Mechanochemical Signaling Directs Cell-Shape Change

Abstract

For specialized cell function, as well as active cell behaviors such as division, migration, and tissue development, cells must undergo dynamic changes in shape. To complete these processes, cells integrate chemical and mechanical signals to direct force production. This mechanochemical integration allows for the rapid production and adaptation of leading-edge machinery in migrating cells, the invasion of one cell into another during cell-cell fusion, and the force-feedback loops that ensure robust cytokinesis. A quantitative understanding of cell mechanics coupled with protein dynamics has allowed us to account for furrow ingression during cytokinesis, a model cell-shape-change process. At the core of cell-shape changes is the ability of the cell’s machinery to sense mechanical forces and tune the force-generating machinery as needed. Force-sensitive cytoskeletal proteins, including myosin II motors and actin cross-linkers such as α-actinin and filamin, accumulate in response to internally generated and externally imposed mechanical stresses, endowing the cell with the ability to discern and respond to mechanical cues. The physical theory behind how these proteins display mechanosensitive accumulation has allowed us to predict paralog-specific behaviors of different cross-linking proteins and identify a zone of optimal actin-binding affinity that allows for mechanical stress-induced protein accumulation. These molecular mechanisms coupled with the mechanical feedback systems ensure robust shape changes, but if they go awry, they are poised to promote disease states such as cancer cell metastasis and loss of tissue integrity.

Main Text

The concept “form begets function begets form” provides an excellent foundation for understanding the behavior of biological systems. Even specialized cells, the smallest unit of complex living systems, perform all of the necessary functions of an organism by assuming distinct shapes, mechanical properties, and physical behaviors. Different cell types use a common set of cytoskeletal elements to provide precise physical support for their distinct functions. For example, red blood cells and neurons have very different shapes that allow them to perform their specific roles. However, they both utilize alternating patterns of actin and spectrin to form cortices with appropriate viscous and elastic properties, albeit in different structural arrangements. Perturbations to this structural network cause a breakdown in the mechanical properties, or the form, of these cells, which inhibits cell function (1, 2).

Fascinatingly, the physical properties of cells are both determined and acted upon by the cytoskeletal apparatus. Cells are capable of modifying their own physical properties and driving changes in cell shape in response to internal and external chemical and mechanical stimuli. These modifications occur through the remodeling of the cell cortex, the network of cytoskeletal proteins directly under the plasma membrane. Much progress has been made recently in deciphering how chemical signals drive mechanical changes, as well as how internally and externally generated mechanical cues modulate chemical signaling in the cell. A more complete mechanistic understanding of the interface between the mechanical and chemical signals that drive cell behavior, including tissue development and cancer metastasis, will be needed to modulate these systems for the treatment of developmental and metastatic diseases.

Force generation by and active remodeling of the cytoskeletal network at the cortex primarily drive cell-shape changes. The cortex contains structural proteins that exhibit distinct physical properties and kinetics of binding and detachment, and are poised to respond dynamically to chemical and mechanical signals to effect shape changes. The cortex is comprised of actin filaments organized in a meshwork ∼200 nm thick (3, 4), cross-linked by actin-cross-linking proteins and nonmuscle myosin IIs, which are the primary drivers of network contraction in cells. Among these structural elements are regulatory proteins that control actin and myosin dynamics, factors that regulate protein turnover, membrane linkers, scaffolding/adaptor proteins, Rho GTPases, Rho GTPase effectors, and Rho GAPs/GEFs (5). The actin filaments in the cortex are quite short: in the social amoeba Dictyostelium, the average actin filament length is ∼100 nm (4, 6). In mammalian cells, identifying a characteristic length is more challenging because of cell-type diversity, but for leukocytes it is ∼300 nm, with the majority being <180 nm in length (7), slightly longer than in Dictyostelium. Cross-linkers anchor these filaments to one another to create the actin meshwork. Cross-linker lengths vary considerably. For example, α-actinin, which binds actin filaments in a parallel or antiparallel orientation, is ∼35 nm in length (8), whereas filamin is 160–190 nm long (9). To actively contract the actin network, myosin II monomers (a functional monomer includes two heavy chains, two essential light chains, and two regulatory light chains) assemble into functional bipolar filaments that are ∼300 nm in length (10). Thus, actin filaments do not dominate the scale of the cortex by length; rather, all of these components are of similar scale (Fig. 1 A). In the same way, the mechanical properties of the cortex are not dominated entirely by the properties of actin filaments, but by this dynamic network of structural and regulatory proteins.

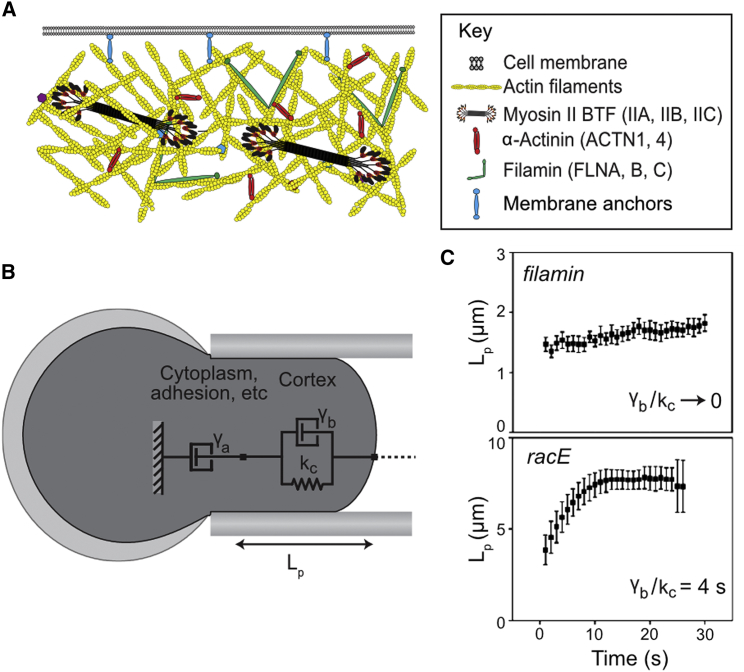
Figure 1.

The structure of the cortex determines its physical properties. (A) Major components of the actin cytoskeleton in the cell cortex, shown roughly to scale for mammalian cells. (B) A simple model of cell mechanics, where the spring k_c and the viscous damper γ_b respectively describe the elastic and viscous contributions from the cortex. The damper γ_a primarily describes the viscous contribution from the cytoplasm. Upon aspiration of Dictyostelium cells into a micropipette using a fixed pressure, the length of the cell protruding into the pipette (L_p) is observed over time. The model in (B) can be accurately used to describe the creep of the cells into the pipette in (C). The slope of the first and second phases of deformation can be used to compute the value of the viscous dampers and γ_a, respectively. The amplitude of the initial length deformation can be used to determine the elastic parameter k_c. In the filamin-null, the contribution of the initial damper γ_b is much smaller than that of k_c, so the initial deformation happens in <1 s. The continued flow can be described by γ_a. In the racE-null, the contribution of γ_b is quite large, causing a slow initial deformation, whereas γ_a is quite small, displaying no creep in the second phase of deformation. To see this figure in color, go online.

Mechanically, the cell cortex can be described as viscoelastic, or having both elastic and viscous characteristics (please see the Glossary of Terms at the end). When probed using very small deformations, such as those imposed by laser-tracking microrheology, the cytoskeleton can be described as having power-law mechanics with the characteristics of a soft glassy material. Elasticity in the material comes from cytoskeletal elements maintaining relatively fixed relationships with one another due to the actin cross-linkers and network entanglements that hold the filament network together. Viscosity, however, requires the ability of these connections from cross-linkers and entanglements to release so that the cytoskeletal elements can rearrange. Furthermore, in cells, active processes that require ATP hydrolysis can also stir these elements, promoting the emergence of a viscous-like character (11, 12). Cell-cortex mechanics at these scales have been analyzed in Dictyostelium (4, 13, 14) and in multiple mammalian cell types (15, 16). In these low-force regimes, cells are predominantly elastic with a mechanical phase angle of ∼10–15°. Further, cells show power-law mechanics over multiple logs of timescale (from submilliseconds to hundreds of milliseconds). However, on longer timescales, active processes in Dictyostelium begin to dominate these low-force-regime mechanics (14).

Cell mechanics at larger force regimes and larger deformations, such as cytokinesis and those imposed by micropipette aspiration, can be described phenomenologically by simpler mechanical models that incorporate elastic springs and viscous dampers (dashpots) (Fig. 1 B). In one arrangement, the so-called Voigt model, a viscous damper (γ_b, nN⋅s/μm³) is placed in parallel with an elastic spring (k_c, nN/μm³) to approximate the cytoskeleton. In addition, many shape-change processes are damped by the viscosity contributed by long-timescale cortex remodeling and the cytoplasm, which can be modeled by incorporating an additional viscous damper, γ_a, placed in series (Fig. 1 B) (17). Upon application of a fixed pressure by micropipette aspiration, the cell will deform and protrude a certain length, L_p, into the pipette (Fig. 1 B) (17). In wild-type and filamin-null Dictyostelium, damper γ_b approaches zero, so the initial deformation is largely elastic and happens in <1 s (Fig. 1 C) (18). However, in some mutants where cytoskeletal regulation is disturbed, such as in the racE-null Dictyostelium, the damper γ_b becomes significant, and the initial deformation occurs over a few seconds (Fig. 1 C) (18). When parameterized with directly measured values, these models help account for cell behavior during retraction from an applied force (18), cytokinesis (19, 20), and cell motility (17, 21).

Forces acting on the cell cortex

The forces acting on the cell cortex during shape-change processes can be divided into inward and outward forces, with inward forces pulling the cortex toward the cell center and outward forces pushing the cortex away from the cell center. Inward forces include Laplace pressure, contraction driven by myosin motors, and actin cross-linker dynamics coupled with actin polymer disassembly (18, 19, 20, 22). An ideal process for studying these inward forces is cytokinesis, where cells must contract inward along the cleavage furrow to divide one cell into two. During normal cell division of almost all eukaryotic cell types, nonmuscle myosin II accumulates at the equatorial region of the cell in response to signals from the mitotic spindle, where it contracts the actin-network to drive furrow ingression. However, in many cell types (Dictyostelium, yeast, and mammalian cells), cells are capable of dividing without myosin II. How is this possible? Studies of myosin II-null Dictyostelium dividing on surfaces indicate that the major driving force for furrow ingression is actually the Laplace pressure (4). Laplace pressure results from the pressure difference (ΔP) between the inside (P_in) and outside (P_out) of a liquid interface, and is proportional to the product of the surface (cortical) tension and local curvature ($\propto$ radius⁻¹) of the fluid surface (19). Because of Laplace pressure, mitotic Dictyostelium cells can divide by traction-mediated cytofission, where adherent cells protrude in two directions, making division across the long axis energetically favorable. The initial increase in curvature in the furrow region upon cell elongation combined with cortical tension leads to increased inward stresses, promoting furrow ingression. Then, as the furrow ingresses, the surface curvature increases, leading to a positive feedback (19). Other types of myosins also contribute to cytokinesis and can do so by impacting these cell mechanics. For example, by providing membrane-cortex linkages, myosin I motors contribute significantly to cortical tension (23). Myosin II-independent cytokinesis is not restricted to Dictyostelium, and likely explains how mammalian cells can divide with myosin II inhibition if the adhesion conditions are appropriate (24), and in tissues when the myosin II-actin-bound state is sufficiently prolonged to last through an entire cytokinesis furrow ingression event (25).

In fact, in Dictyostelium, normal myosin II activity leads to a slowing down of furrow ingression during late stages of cytokinesis (20). Wild-type Dictyostelium cells are more deformable in the polar cortex than at the furrow, whereas myosin II-null cells have a limited mechanical differential (4). This differential leads to two consequences of cell mechanics that likely contribute to this slowdown of furrow ingression in wild-type cells (19, 20). First, as the furrow ingresses, resistive stresses can build in the two daughter cell cortices and cytoplasm, slowing furrow ingression. Genetic mutants devoid of myosin II, key actin cross-linkers, or cytoskeletal regulators that control the polar cortices appear to alleviate this resistive stress (4). Second, the accumulation of the cytokinetic machinery, including myosin II and actin cross-linkers, to the cleavage furrow cortex can lead to strain stiffening of the cytoskeletal network, making it more difficult for the cortex network to remodel (making it more elastic) (19, 22). Most likely, both properties (resistive stresses and strain stiffening) contribute to the wild-type furrow ingression dynamics.

To drive outward force generation, cells primarily use actin assembly and/or pressure-induced blebs. An ideal site for studying the generation of outward forces is the leading edge of a migrating cell. At this edge, the forward-driving force is driven either by the well-defined Arp2/3 Brownian ratchet (26, 27, 28) or by pressure-induced bleb formation due to myosin activity in highly confined, compressed environments (29, 30). The Arp2/3 Brownian ratchet moves the plasma membrane forward by stimulating the creation of many new actin filament branches at the leading edge. Thermal fluctuations in each of these filaments create space for actin monomers to be added to the barbed end of the growing filament, driving the membrane forward (26, 27, 28). In another type of motility, termed lobopodial migration, cells in confined environments pull their nuclei forward by myosin II contraction, using the nucleus as a piston to create enough pressure to drive bleb formation at the cell front (31). These blebs then rapidly fill with actin-cytoskeletal components, creating a new cortex (29, 30). In both cases, the process that allows faster membrane protrusion should determine the dominant behavior.

Chemical and mechanical inputs direct shape change

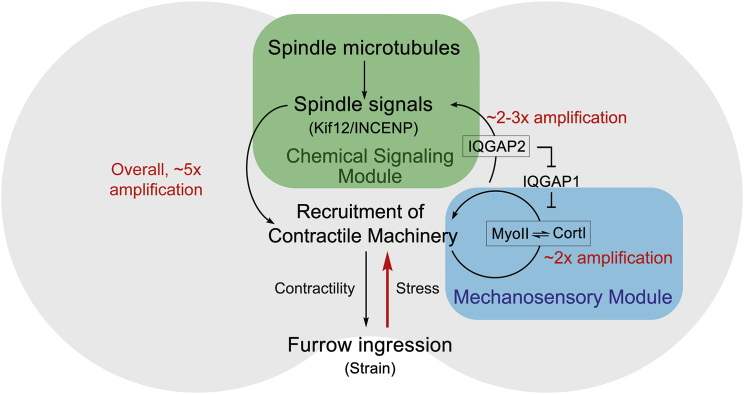
During cell-shape-change behaviors, including cytokinesis and cell migration, two distinct classes of contributions control the direction, magnitude, and robustness of the process: chemical and mechanical inputs. An example of a chemical input is the external chemical gradient of cAMP sensed by Dictyostelium during chemotaxis (32), which drives the directional activation of the branched actin network in pseudopods at the cell front and the contraction of myosin II at the cell back. Chemical signals can also be internal, such as those from the mitotic-spindle-associated chromosomal passenger complex proteins INCENP (inner centromere protein) and kinesin 6, which promote cytokinesis (33, 34). However, the spindle is not essential for symmetrical or asymmetrical cytokinesis in many cell types (35, 36, 37, 38). In reality, the integration of both chemical and mechanical signals drives cytokinesis (Fig. 2). In Dictyostelium, myosin II and cortexillin I, an actin cross-linker, initially accumulate at the cleavage furrow as a result of spindle signaling. However, when mechanical stress is applied to the cortex, the existing myosin II bipolar filaments experience this stress, which leads to a local increase in myosin II concentration. In the context of cytokinesis, this cooperative myosin II assembly occurs even in the absence of spindle-associated chemical-signaling inputs (39, 40, 41). Molecularly, under resistive load, the myosin II lever arms stall in the phase of the power stroke that is the isometric, cooperative binding state, for two reasons. First, the myosin II duty ratio is load sensitive. In mammalian nonmuscle myosin IIB, for example, when a myosin II head imposes a piconewton-range resistive load on another, the second head releases ADP at a 10-fold slower rate than an unloaded head (0.023 ± 0.003 s⁻¹ vs. 0.27 ± 0.06 s⁻¹) (42). Second, in addition to inhibiting ADP release, force can trap the myosin II motor in the cooperative isometric state, which promotes the binding of additional myosin motors to the actin filament nearby due to a propagated conformational change in the actin filament (43, 44, 45). This cooperative binding state was specifically implicated in mechanosensitive accumulation by experiments in which the myosin II lever arm was lengthened or shortened (40). A longer lever arm led to greater accumulation at lower applied stresses, whereas shortening the lever arm led to significantly reduced accumulation across all pressure ranges. Additional controls ruled out myosin II motility velocity as the explanation. This cooperative accumulation can account quantitatively for myosin and cortexillin I accumulation in response to mechanical stress (41). Further, this cooperative accumulation can account for the insertion of myosin II into the cortex of the cleavage furrow, where it promotes additional accumulation of kinesin 6 (Kif12) and INCENP through the cortexillin I-binding IQGAP2 (GapA) (46) (Fig. 2). Thus, the cleavage furrow cortex comprises a mechanochemical feedback loop where both chemical and mechanical signals promote accumulation of the appropriate machinery (46, 47). This system is inherently quite robust: the network of cytokinesis cytoskeletal machinery stabilizes under mechanical load in a manner that is independent of any single protein (22).

Figure 2.

Integrated chemical and mechanical feedback loops drive cleavage furrow ingression. At the cleavage furrow of dividing Dictyostelium, the chemical signaling module, including INCENP and Kif12 (the kinesin 6 family protein), can activate the recruitment of contractile machinery, including cortexillin I (CortI) and myosin II (MyoII). Simultaneously, the contractile machinery, which comprises the mechanosensory module, can accumulate in response to the forces created by furrow ingression and drive the activation of the chemical signaling module through IQGAP2. The overall system allows for an ∼5-fold amplification of myosin II accumulation at the cleavage furrow in response to mechanical stress. To see this figure in color, go online.

Another interesting example of mechanical and chemical signaling integration that drives cell-shape changes can be found in cell-surface proteins that associate between cells. During myoblast fusion in Drosophila, the cell-surface markers Sns and Duf of the fusion-competent cell and founder cell, respectively, associate to activate downstream signaling in both cells (39). In the fusion-competent cell, Sns signaling activates WASP to drive the assembly of an actin focus, which pushes finger-like actin projections into the founder cell. In the founder cell, signaling downstream of Duf drives Rho activation and myosin II contractility, allowing the cell to oppose the projections with enough force to allow cell-cell fusion (39). Interestingly, in the absence of the cytoplasmic domain of Duf, myosin II still accumulates at the site of cell-cell fusion in the founder cell. This accumulation appears to be due to the same force-dependent assembly of myosin II into bipolar filaments (39).

Force sensing by other actin-associated proteins

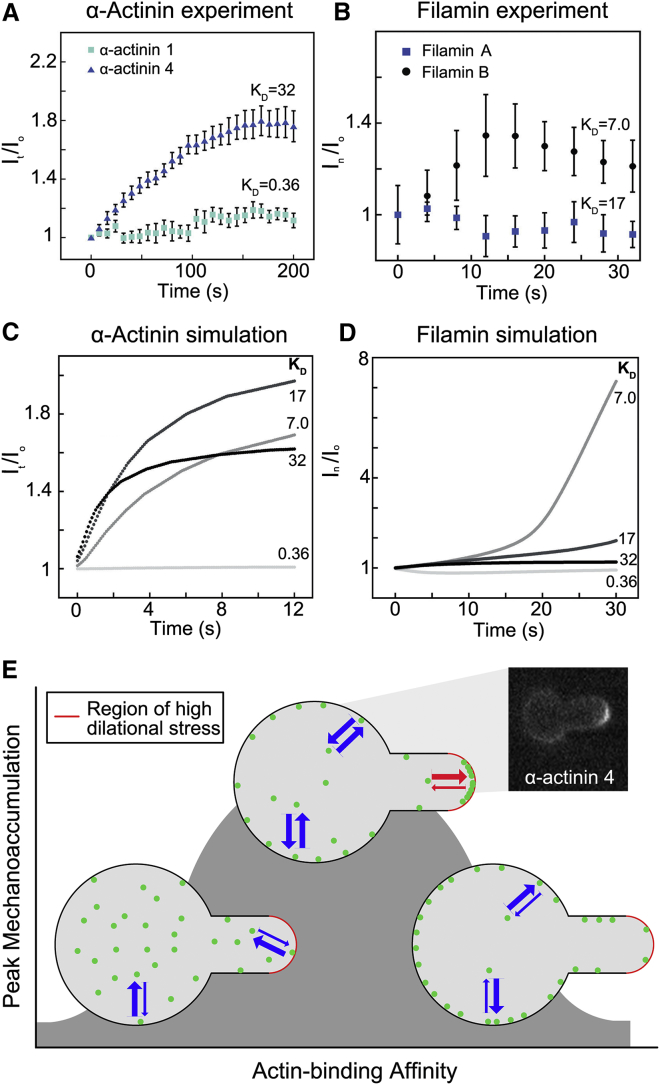
A number of other actin-binding proteins have demonstrated the ability to sense and respond to force. In the adherens junctions of epithelial cells, the minimal cadherin-catenin complex, including α-catenin, β-catenin, and E-cadherin, interacts with actin filaments in a force-dependent manner. Force propagating from the actin cytoskeleton of one cell to another through E-cadherin attachments increases the binding lifetime of the cadherin-catenin complex to actin. In single-molecule experiments, the complex-actin-binding lifetime increases from ∼60 ms at low force to ∼120 ms at 10 pN of applied force (48). At higher forces, these bonds then slip so that they display a catch-slip behavior, depending on the force regime. The catch-slip bond also accounts for the mechanosensitive accumulation (the accumulation of a protein in response to applied stress) of the actin cross-linking protein α-actinin (18, 49) and its recruitment to focal adhesions under high tension (50). In mammalian cells, mechanoaccumulation is unique to the α-actinin 4 paralog, and is not observed for α-actinin 1 (49) (Fig. 3 A). Similarly, the actin cross-linking protein filamin can accumulate in response to shear stress in multiple cell types (18, 49). However, the mammalian paralog filamin B shows higher mechanosensitive accumulation than filamin A (Fig. 3 B). In both cases, reaction-diffusion models (Fig. 3, C and D) for force-dependent binding can predict which paralog will accumulate based on the intrinsic difference in actin-binding affinity of the paralogs (49). These models utilize parameters for cross-linker concentration, diffusion rates, on- and off-rates for actin binding measured in Dictyostelium and mammalian cells, and the catch-slip characteristics of the bonds (18, 49, 51). The models recapitulate the kinetics of protein accumulation over time, capturing a sigmoidal rise for filamin and an exponential rise for α-actinin. The models also illuminate an optimal actin-binding affinity zone for mechanoresponsive proteins. In other words, if the intrinsic actin-binding affinity of a cross-linker is too high, the cell will not have a sufficient monomeric pool available to respond to the applied force, and if the affinity is too low, the protein will not bind actin well enough to stay bound to the network in regions of stress (Fig. 3 E). The exact set-point where the actin-binding affinity is ideal for the mechanoresponse also depends on cooperativity: a model that invokes cooperative actin-binding predicts a lower set-point than one without cooperativity. The cooperativity in the model used to predict filamin accumulation is the reason the filamin model predicts a lower ideal actin affinity for mechanoaccumulation than the α-actinin model (49) (Fig. 3, C and D).

Figure 3.

Mechanoaccumulation by actin-binding proteins is determined by an optimal zone of actin-binding affinity. (A) The low-affinity α-actinin 4, transfected into HeLa cells, accumulates over time in response to micropipette aspiration at a region of high network dilation, the tip of the cell (calculated by fluorescence intensity at the tip, I_t, normalized to the fluorescence intensity at the opposite side of the cell, I_o). The high-affinity α-actinin 1 does not accumulate. All K_D values in panels (A)–(D) have the units of μM. (B) The high-affinity filamin B accumulates to a region of high shear deformation, the neck of the cell, during micropipette aspiration (calculated by the fluorescence intensity at the neck, I_n, normalized to the fluorescence intensity at the opposite side of the cell, I_o). The lower-affinity filamin A does not accumulate. For filamin B, a second phase of myosin II-mediated flow carries the protein to the tip, which accounts for the decrease beginning at ∼12 s. (C) The accumulation of a force-dependent actin-binding protein (e.g., α-actinin) is modeled with four different actin-binding affinities, using a reaction-diffusion model of force-dependent actin binding with physiological G- and F-actin concentrations, cross-linker concentrations, and published actin-binding affinities. (D) The accumulation of filamin is modeled using the same four actin-binding affinities, but considering cooperativity to account for the accelerating rate of accumulation. The results show that an optimal dissociation equilibrium constant (K_D) to actin exists for both noncooperative (α-actinin) and cooperative (filamin) actin-binding proteins where mechanoaccumulation is maximized. Please note that for (C) and (D), the affinities represent the affinities of single actin-binding heads, and not an overall apparent affinity from the complete cross-linking reaction. (A)–(D) are reproduced here from Schiffhauer et al. 2016 (49). (E) At a high actin-binding affinity, actin cross-linking proteins do not have a large enough unbound pool to dynamically respond to force applied during micropipette aspiration. At a very low actin-binding affinity, actin-binding proteins do not bind the cortex with enough affinity to remain locked on at sites of mechanical stress. Thus, there is an optimal zone for actin-binding affinity where mechanoaccumulation is maximal. This is demonstrated by the inset, which shows accumulation of α-actinin 4 during micropipette aspiration. To see this figure in color, go online.

The branched actin network itself also responds to mechanical inputs, affecting cell-shape changes. The forced curvature of actin filaments beyond normal fluctuations in actin filament bending promotes the binding of the Arp2/3 complex to the convex side of the filament (52). This can explain how actin filaments bent along the front edge of a migrating cell ensure the binding of the Arp2/3 complex to the convex side, allowing branching of a new filament in the direction of the plasma membrane. Similarly, the application of load to branched actin networks as they assemble drives an increase in the density and number of actin filaments through the formation of up to 3.5-fold more Arp2/3 complex-mediated actin branches and 3-fold tighter actin filament packing, while not changing the length of the filaments (53). This ability to build variably dense actin networks provides cells the adaptability to push their leading edge through extracellular environments of variable stiffnesses.

Mechanochemical signaling allows dynamic escalation of force production

To accomplish the fundamental processes involved in cell-shape changes, cells integrate chemical and mechanical inputs and ensure robust completion of the task with remarkable versatility. During cytokinesis, Dictyostelium myosin II is likely capable of achieving a 30- to 50-fold dynamic range in force production through a 3- to 5-fold increase from accumulation of myosin II at the furrow by chemical and mechanical signals (46), and a 5- to 8-fold increase in the duty ratio under applied load. This 5- to 8-fold increase due to a shift in the duty ratio assumes that Dictyostelium myosin II exhibits a force-dependent duty ratio similar to that observed for mammalian nonmuscle myosin II (42) (Fig. 2). Even this dynamic range underestimates the cell’s capabilities, because without myosin II, the cells can divide using Laplace pressure, which can be an order of magnitude more powerful than myosin II-mediated contractility (19, 20). Similarly, cells theoretically can increase the motor output of the Arp2/3 complex-actin network at the leading edge by an order of magnitude during migration by force opposition alone (53).

The relative expression of mechanosensory proteins provides yet another level of control by cells. By expressing mechanoresponsive isoforms of myosin II, α-actinin, or filamin, a mammalian cell can tune its ability to respond rapidly to an imposed force. In fact, the mechanoresponsive cross-linker α-actinin 4 was shown to be essential for pancreatic cancer cell migration, to have increased expression in 63% of pancreatic cancer patients, and to be a significant negative predictor of patient survival (54). Thus, understanding how and which proteins are essential for the mechanical stress response may lead to new strategies for stopping the force-dependent processes that are essential for cancer cells, such as division, migration, and metastasis.

In addition, it will be important to delve deeper into the integration of chemical and mechanical signals in cells. For example, chemical signaling from Rac1 is known to activate PKC, which contributes to mammalian myosin light-chain and heavy-chain phosphorylation (55, 56). PKC’s phosphorylation of the myosin IIA heavy chain at S1916 is essential for a cell’s ability to sense and respond to the mechanical input of substrate stiffness at focal adhesions (57). Myosin IIB shows differential mechanoresponsiveness across cell types, and within a cell type, myosin IIB shows differential mechanoaccumulation across the phases of the cell cycle (49). As myosin IIB’s subcellular localization is regulated primarily by a single site of heavy-chain phosphorylation (58), this myosin’s mechanoaccumulative ability may be readily tuned by heavy-chain phosphorylation.

Furthermore, skeletal muscle myosin II can have greater mechanical compliance in the tail region than in the head region (59). Thus, mechanical strain across the myosin filaments could provide a basis for cross talk between the motors and tails under mechanical load. Compliance in the nonmuscle myosin II tail has not yet been definitively demonstrated. However, the ability of a long lever-arm mutant myosin (2xELC) in the context of the phosphomimic (3xAsp) tail mutant to assemble into filaments in vivo is highly consistent with the concept of cross talk between the two parts of the myosin molecule (60). Also, molecular simulations that accurately depict the behavior of nonmuscle myosin II in response to an applied stress require not just force feedback but also strained and unstrained states of myosin II bipolar filaments (in the strained state, the myosin remains assembled until the bipolar filament relaxes) (47). Thus, it is important to determine whether there is compliance in the nonmuscle myosin II tail, and how this compliance affects its mechanosensitive assembly and phosphoregulation. Such knowledge will be essential for learning how to tune the cellular response to the mechanochemical inputs that drive cell-shape-change processes in normal and disease states.

Author Contributions

E.S.S. prepared the figures. E.S.S. and D.N.R. wrote and edited the manuscript.

Editor: Brian Salzberg.

Glossary of Terms

Elasticity: The ability of a solid object to resist deformation and return to its original shape when stress is removed.

Laplace pressure: The pressure differential between the inside and outside of a cell. The Laplace pressure is dependent on the cortical tension and the membrane curvature.

Power-law mechanics: a viscoelastic material characterized by a power law dependency (with exponent β) of the viscoelastic modulus on the time-scale of deformation. In a purely elastic material, β = 0, and in a purely viscous material, β = 1.

Rheological phase angle: Describes the relative contribution of elastic and viscous properties to a viscoelastic material. A pure elastic solid has a 0° phase angle, and a pure viscous fluid has a 90° phase angle.

Soft glassy materials: Compliant materials that have a disordered or amorphous nature (as opposed to crystalline), and have flow characteristics above a stress threshold. These properties arise from discrete, numerous components that interact with each other relatively weakly. Each component occupies a discrete energy well, which cannot be disrupted by thermal fluctuations alone. Discrete components can be dislodged from these wells through the input of energy (defined as ATP-requiring processes in cells). For the cell, these energy wells are established by binding interactions between cytoskeletal elements, entanglements, and steric constraints.

Viscoelastic: a property of a material that exhibits both viscous and elastic characteristics when deformed by force.

Viscosity: The ability of a fluid to resist deformation as a result of drag forces between fluid molecules. The higher the viscosity, the greater the force required for the same speed of deformation.