Mechanical Characterization of Microengineered Epithelial Cysts by Using Atomic Force Microscopy

Abstract

Most organs contain interconnected tubular tissues that are one-cell-thick, polarized epithelial monolayers enclosing a fluid-filled lumen. Such tissue organization plays crucial roles in developmental and normal physiology, and the proper functioning of these tissues depends on their regulation by complex biochemical perturbations and equally important, but poorly understood, mechanical perturbations. In this study, by combining micropatterning techniques and atomic force microscopy, we developed a simple in vitro experimental platform for characterizing the mechanical properties of the MDCK II cyst, the simplest model of lumen-enclosing epithelial monolayers. By using this platform, we estimated the elasticity of the cyst monolayer and showed that the presence of a luminal space influences cyst mechanics substantially, which could be attributed to polarization and tissue-level coordination. More interestingly, the results from force-relaxation experiments showed that the cysts also displayed tissue-level poroelastic characteristics that differed slightly from those of single cells. Our study provides the first quantitative findings, to our knowledge, on the tissue-level mechanics of well-polarized epithelial cysts and offers new insights into the interplay between cyst mechanics and cyst physiology. Moreover, our simple platform is a potentially useful tool for enhancing the current understanding of cyst mechanics in health and disease.

Introduction

Epithelial cysts are soccer ball-like, lumen-enclosing monolayers of polarized cells. As one of two basic building blocks of numerous organs, epithelial cysts, together with tubules, form complex branched tubular structures that function both as conduits for fluid transport and as selective permeability barriers between the body interior and its environment. Besides being biochemically controlled, the formation, maintenance, and function of these tubular structures depend on the coordination of mechanical forces both internally generated and externally applied (1, 2, 3). These forces include, for example, cytoskeletal tension, cell-cell adhesion, cell-extracellular matrix (ECM) adhesion (3), shear stress generated by fluid flow (4), and hydrostatic pressure (5), and act at variable distance ranges and enable cells to sense and respond to subtle changes in the environment. During the past few decades, investigations into these mechanical forces have been greatly facilitated by advances in microsystems engineering (6), such as in the detection of cellular traction force by using micropillars (7, 8); the control of the cell microenvironment by using micropatterning to study cell adhesion, migration, proliferation, differentiation and polarization (9); and the integration of mechanical stretching and shear stress into organ-on-a-chip platforms (10, 11).

Mechanical characterization of epithelial cells at the single-cell, multicellular, and even tissue levels has begun to reveal how mechanical forces govern or are governed by complex biological processes (12, 13, 14); however, we still lack simple in vitro experimental platforms for characterizing tissue-level mechanics and examining its biological implications in a highly physiologically relevant context, such as in the cyst model. Such suitable platforms are lacking mainly because the conventional in vitro method for epithelial cyst formation requires cells to be embedded in a three-dimensional (3D) gel, which renders the cysts inaccessible to most probes (Fig. 1 A) (15).

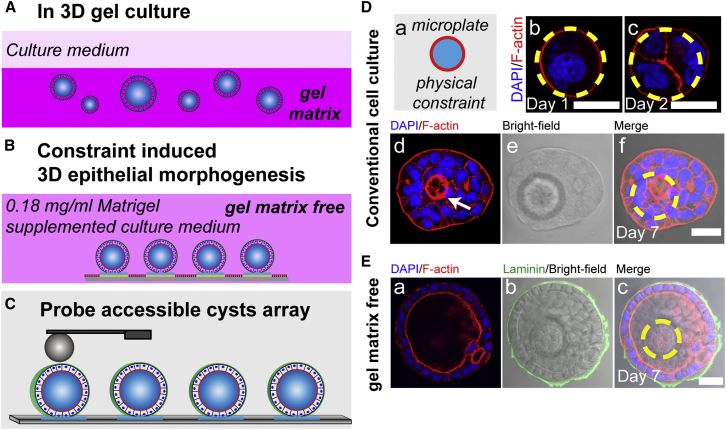
Figure 1.

MDCK II cells form cysts on microdisks under gel-matrix-free culture conditions. Comparison between cyst formation in 3D gel culture (A) and the gel-matrix-free, substrate-constraint-induced cyst formation (B) is provided. The cysts shown in (B) but not (A) are probe-accessible for direct mechanical characterization (C). (D) MDCK II cells cultured on microdisks in conventional cell-culture media did not form cysts on day 7. Representative images showing the morphology of MDCK II cells cultured on microdisks, on days 1 (b), 2 (c), and 7 (f). A small lumen forming in the multilayered cell aggregate was observed on day 7 (d, arrow). Red, F-actin; blue, nuclei. Yellow dashed circles indicate the microdisk boundary. (E) Middle section of a day 7 MDCK II cyst costained for nuclei and F-actin (a) and the ECM protein, laminin (b); the microdisk sitting underneath is shown in bright-field image in (b). F-actin is concentrated in the apical domain and forms a belt traversing the enclosed cell monolayer, and the basally localized laminin closely wraps the entire cyst. Scale bars, 20 μm. To see this figure in color, go online.

Recently, Harris et al. (14) developed an ingenious device to investigate the tensile planar mechanical properties of suspended epithelial monolayers and assessed the effect of the actin cytoskeleton and intercellular adhesion on cell monolayer mechanics. Furthermore, Venugopalan et al. (16) reported creep compression tests on breast epithelial acini and suggested that tissue architecture markedly influences the mechanics. However, with both of these techniques, a tissue of interest, once formed, must be chemically or mechanically extracted from its supporting ECM gel for subsequent mechanical characterization. Although the tissue-extraction procedure minimizes the extent to which the mechanical property of the surrounding gel interferes with that of the tissue, the procedure also eliminates tissue-ECM interactions and might even damage cell-cell interactions and the cells themselves, which can complicate data interpretation.

Therefore, considerable demand exists for generating epithelial cysts that retain a native ECM layer and are concomitantly accessible to probes and convenient for mechanical characterization. However, methods to generate such probe-accessible cysts remain largely unexplored.

Previous work has shown that geometrical confinement of cells, for example, in linear micropatterns (17) and microchannels (18), promotes the formation of endothelial capillary structures. Moreover, findings reported by Rodríguez-Fraticelli et al. (19) and by Shen et al. (20) have suggested that epithelial 3D tissue development and cyst generation can be induced by confining cell spreading and migration on micro- and nanotopographic substrates in ECM gel-matrix-free culture media. However, in these studies, either the efficiency of the cyst formation was low (20) or the mechanically unstable loading conditions used caused the cysts that formed to readily self-detach from the substrates (19). These drawbacks considerably compromise the usefulness of the two approaches for generating cysts for mechanical characterization.

In this study, we demonstrated for the first time, to our knowledge, that MDCK II cells spatially confined on 3 μm-raised microdisks form cyst structures exhibiting normal polarity in gel-matrix-free culture media (Fig. 1 B). Furthermore, atomic force microscopy (AFM) analysis revealed that these cysts are mechanically robust. We used AFM to perform, for the first time, to our knowledge, elasticity and force-relaxation measurements on these MDCK II cysts featuring a native, thin ECM layer, and we determined the Young’s modulus of the MDCK II cyst monolayer and showed that the cyst architecture (the presence of a luminal space) substantially influences cyst mechanics. Furthermore, the force-relaxation studies on the cysts revealed poroelastic signatures at short timescales under a constant strain.

Materials and Methods

Fabrication of parylene microdisk arrays on glass substrates

Microdisk arrays based on parylene C (DPX-C, Specialty Coating Systems, Indianapolis, IN) were fabricated on a glass substrate as previously described (21). Fig. S1 shows the process flow for fabricating the microdisks and the gel-matrix-free cell-culture method for generating MDCK II cysts on the microdisks. Briefly, chemical vapor deposition and standard photolithography were used to produce parylene microdisks (∼3 μm in height). The substrates were passivated with 2-methacryloyloxyethyl phosphorylcholine (MPC) polymer (provided by Prof. K. Ishihara at the University of Tokyo) to inhibit protein absorption and cell adhesion (22). The MPC layer on the patterned region was removed by etching away the sacrificial aluminum layer underneath the MPC by using an alkaline solution (FHD-5, Fujifilm Electronic Materials, Tokyo, Japan), leaving behind the bare parylene surface. The glass substrates containing the microdisk arrays were then diced into chips sized 1 × 1 cm² that were used in the cell-culture experiments.

Cell culture and cyst generation on microdisks

MDCK II cells (Madin-Darby canine-kidney cells, ECACC 00062107) were cultured in Dulbecco’s Modified Eagle Medium/Nutrient Mixture F-12 (DMEM/F-12, Invitrogen, Carlsbad, CA) supplemented with 10% fetal bovine serum (FBS) and maintained at 37°C in a humidified atmosphere of 95% air/5% CO₂. To generate epithelial cysts on microdisk arrays, MDCK II cells were seeded at a density of ∼1 × 10⁴ cells/cm² on the freshly prepared substrate, which was then placed in a 35-mm polystyrene tissue-culture dish and allowed to attach on the microdisk arrays for 12 h; subsequently, unattached cells were removed and the cultures were supplemented with 0.18 mg/mL growth-factor-reduced Matrigel (Corning, Corning, NY, no. 354230, stock concentration 8.9 mg/mL) in the culture medium for the gel-matrix-free culture assays (19, 20). The culture medium was changed once every 3 days.

Immunostaining and confocal microscopy

MDCK II cysts were fixed with 4% paraformaldehyde in phosphate-buffered saline (PBS) and permeabilized with 0.2 M NH₄Cl/PBS containing 0.2% Triton X-100 for 10 min each at room temperature, and then blocked with 3% bovine serum albumin (Sigma-Aldrich, St. Louis, MO) in PBS for 2 h. To characterize cyst morphology, nuclei and F-actin were stained respectively with DAPI (1 μg/mL, Sigma-Aldrich) and phalloidin-TRITC (2 μg/mL, Sigma-Aldrich) for 60 min at room temperature. To characterize MDCK II cyst polarity, cells were first incubated with rabbit polyclonal anti-laminin antibodies (1:25 dilution, Sigma-Aldrich), and/or mouse monoclonal anti-integrin β1 antibodies (1:500 dilution, Abcam, Cambridge, MA), and/or rabbit monoclonal anti-E-cadherin (24E10) antibodies (1:500 dilution, Cell Signaling, Danvers, MA) overnight at 4°C. After washing with PBS thrice (5 min each), the cysts were incubated with fluorescein isothiocyanate (FITC)-conjugated donkey anti-rabbit IgG and TRITC-conjugated donkey anti-mouse IgG antibodies (both 1:200 dilution, Jackson ImmunoResearch, West Grove, PA) for 1 h to detect laminin, β1 integrin, and E-cadherin, respectively. To stain the tight junction protein ZO-1, cysts were incubated with Alexa Fluor (Carlsbad, CA) 594-conjugated mouse monoclonal anti-ZO-1 (1A12) antibodies (5 μg/mL, Life Technologies, Carlsbad, CA) for 1 h at room temperature. Lastly, all samples were washed thrice with PBS (5 min each) and mounted onto microscope slides with Citifluor-AF-1 (Ted Pella, Redding, CA), and then examined under a confocal microscope (LSM710, Zeiss, Oberkochen, Germany).

Assay for testing aquaporin blocking efficiency

To evaluate the efficiency with which aquaporins in MDCK II cysts were blocked by the cysteine-reactive mercurial reagent HgCl₂ (0.1 μM, Sigma-Aldrich) and tetraethylammonium (TEA) chloride (10 mM, Sigma-Aldrich) (23), we recorded the time course of osmotic-gradient-induced volume change of cysts treated with either HgCl₂ or TEA⁺; the recording were obtained using an inverted time-lapse live-cell-imaging microscope (Ti-E; Nikon, Tokyo, Japan). In these experiments, constant ionic strength was maintained by using hypertonic (425 mOsm), isotonic (320 mOsm), and hypotonic (205 mOsm) solutions that were prepared by adding, respectively, 0.29, 0.2, and 0.1 M mannitol to a hypotonic base solution (in millimolar: 40 NaCl, 5 KCl, 1 CaCl₂, 2 MgCl₂, 10 HEPES (pH 7.4), 91 mOsm). After 7-day-old MDCK II cysts were pretreated with HgCl₂ or TEA⁺ in the isotonic solution for 10 min, the bathing medium was successively changed to the hypertonic and isotonic solutions containing HgCl₂ or TEA⁺ (each for 20 min). Cysts were treated as spherical objects, and the cyst volume was analyzed by quantifying the cyst projection by using ImageJ software (NIH).

Atomic force microscopy

For mechanical characterization of MDCK II cysts, we used an AFM instrument (MFP-3D, Asylum Research, Santa Barbara, CA) equipped with a colloidal probe. The cantilevers used in the microscope were silicon microcantilevers (AC240, Olympus, Tokyo, Japan) featuring a spring constant k ≈ 2 N/m. The colloidal probe was assembled as described previously by adhering a glass sphere (∼30 μm in diameter) to the front end of the cantilever (24). The sphere surface was coated with a thin layer of PLL-g-PEG (home-synthesized), which provided a high degree of resistance to protein adsorption and also reduced adhesion on the cyst surface. The entire AFM setup was placed on an active-vibration-isolation table, which was placed in an acoustic-isolation hood (BCH-45, Asylum Research). An air-temperature controller installed inside the acoustic hood maintained the temperature near the cantilever at a constant 37°C. The microengineered cysts together with liquid buffer were placed in an AFM fluidic chamber in a humidified atmosphere of 95% air/5% CO₂.

Before each measurement, we calibrated the in situ spring constant k of the colloidal probe in the liquid buffer by using the thermal power spectral density (PSD) method (24, 25). Measurements of the power spectrum |z(ω)|² of vertical deflections of the cantilever were conducted under the AFM thermal PSD mode. Under this mode, the voltage signal from the position sensitive detector was digitized at a sampling frequency of 5 MHz. Typically, |z(ω)|² was taken with a frequency resolution of 152 Hz and average time of 5 min. To determine the absolute value of |z(ω)|², the output voltage signal from the position sensitive detector was calibrated against known values of the cantilever displacement. The spring constant was finally calculated via k = mω₀², where the effective mass m and the resonant frequency ω₀ of the colloidal probe were obtained from the measured |z(ω)|² (Fig. S2). AFM measurements for characterizing the mechanical properties of the MDCK II cyst were performed in the contact mode by moving the colloidal probe vertically on the top of the cysts. The z-axis piezoelectric actuator of the AFM is controlled to move the probe up or down at a constant speed v in the range of 1–100 μm/s with a travel distance up to 25 μm. When the colloidal probe touches the cyst of interest, it pushes the cyst with an applied force F, which can be accurately detected by the AFM, and the force F increases with the indentation depth δ. The AFM probe retracts when a predetermined maximal indentation force of F_M = 100–300 nN is reached, which gives an indentation strain ε in the range 0.15–0.25. The other measurement obtained was the force-relaxation curves, which was measured after the probe applied a strain ε ≈ 0.15 on the cyst; when the cantilever was held at a constant height, the measured force F(t) (or stress) relaxed over time t (0–40 s) and reached an asymptotic value. The force F was measured at a sampling rate of 2 kHz.

Statistics

Data are expressed as mean ± SE unless specified otherwise. A two-sample independent Student’s t-test was performed to evaluate differences between data sets, and the significance levels were set as follows: statistically significant (0.01 ≤ ^∗p < 0.05), highly significant (0.001 ≤ ^∗∗p < 0.01), and extremely significant (^∗∗∗p < 0.001).

Results and Discussion

Generation and polarity characterization of probe-accessible MDCK II cysts on microdisks

In our pilot study, we generated probe-accessible MDCK II cysts on flat, micropatterned substrates in gel-matrix-free culture media by following the procedures described previously (19). However, the obtained cysts detached readily from the substrates, particularly after the indentation of an AFM probe (data not shown), which precluded mechanical characterization of these cysts by using AFM.

As an alternative, we tested the generation of MDCK II cysts on the 3-μm-raised micropatterns, the parylene-based microdisks in gel-matrix-free culture media (Fig. 1 B); we observed that the cysts adhered tightly to the microdisks, even under the indentation of an AFM probe (see below). The microdisks were patterned on a glass substrate to accommodate single cells, whereas the unpatterned glass surface was coated with MPC polymer to prevent protein adhesion and cell attachment (22) (Fig. S1 A). The diameter and pitch of the microdisks were fixed at 30 and 100 μm, respectively, to locally restrict the spreading and proliferation of single cells on the microdisk islets.

We first tested the culture of MDCK II cells on the microdisks in conventional cell-culture media. After the cells were cultured on the microdisks, they started to divide and spread on the limited space. The periphery of single cells overlapped with the edge of the microdisks (Fig. 1 Db), which implied that out-of-microdisk cell spreading and migration were inhibited, as observed previously (19). However, the cultured MDCK II cells were able to proliferate on the microdisks, and with prolonged cell culture, the cell density increased and the cell formed multilayered cell aggregates with small lumens forming in the center on day 7 (Fig. 1 D). Intriguingly, contrasting this formation of multilayered cell assemblies on the microdisk, in a previous study, 3D cell assemblies formed only on the periphery of larger micropatterns (300 μm in diameter) when the cell density reached 1 cell/100 μm² (26). This micropattern-size-dependent difference in the morphology of the multicellular assemblies in the two studies indicated that geometrical confinement plays a crucial role in imposing an imbalanced force on the border cells and inducing epithelial 3D tissue morphogenesis. Moreover, live imaging of these cell aggregates revealed that they undergo collective, rotational motion (Movie S1). This type of angular motion has also been observed in the case of epithelial cells cultured both on comparatively larger adhesive micropatterns (26, 27) and in a 3D gel matrix (28, 29), and has further been suggested to facilitate the weaving of an organized ECM at the cyst periphery and subsequent polarization of the cyst (29). Because no ECM proteins were included in the conventional cell-culture media used here, an organized ECM layer might not have formed during the rotation of the cell assemblies, which eventually would have led to the formation of small lumens within the multilayered cell aggregates (Fig. 1 D).

In the 3D gel culture (Fig. 1 A), the soft gel matrix not only serves as a supporting material for cell growth and exerts physical constraints on cell migration; the matrix also acts as a chemical cue that guides polarity orientation and lumen development (30, 31). To provide chemical cues for cyst generation on the microdisks, the culture medium was supplemented with soluble ECM proteins (0.18 mg/mL Matrigel, primarily comprising laminin, collagen IV, and entactin) (Fig. 1 B). Notably, MDCK II cells began to form spherical cyst structures on the microdisks on day 4 (Fig. S1, B and C), and on day 7, these cysts clearly displayed a one-cell-thick cell wall and a lumen inside (Fig. S1 B, inset). Staining for F-actin and one essential ECM component, laminin, showed that F-actin mainly formed an apical belt facing the lumen and that laminin assembled into a thin layer that closely wrapped the entire cyst and was not excessively deposited around the cyst (Fig. 1 E).

To verify that the cysts generated on the microdisks are morphologically identical to those generated in the 3D gel culture, we examined the polarity of the cyst monolayer by staining for several domain-specific markers (including β1 integrin, ZO-1, and E-cadherin) when a lumen was clearly visible in a cyst (Fig. 2). Before lumen formation (i.e., on day 3), MDCK II cells formed spherical, solid cell aggregates on the microdisks (Fig. S3). On days 4–5, the MDCK II cysts predominantly featured an inverted polarity, with the basal-specific markers β1 integrin and laminin facing the forming lumen, the lateral-specific marker E-cadherin linking adjacent cells, and the apical-specific marker ZO-1 (a tight junction protein) localized at the cyst periphery, sealing the entire cyst (Fig. 2 B). However, this inverted polarity was reversed on days 7–8 (Fig. 2 C). The process of lumen formation resembled that of MDCK cells cultured in 3D collagen gels, but the apicobasal polarization was slower or less efficient as compared with that of cells cultured in 3D Matrigel (32, 33). Because the concentration of Matrigel (0.18 mg/mL) supplemented in our culture medium was comparatively lower, the added Matrigel might have served as a correspondingly weaker chemical cue for the polarization of MDCK II cells. This slow polarization of MDCK II cells was evidenced by the frequent morphological observation of cysts harboring multiple small lumens even on days 7–8 (Fig. S4) (32, 33).

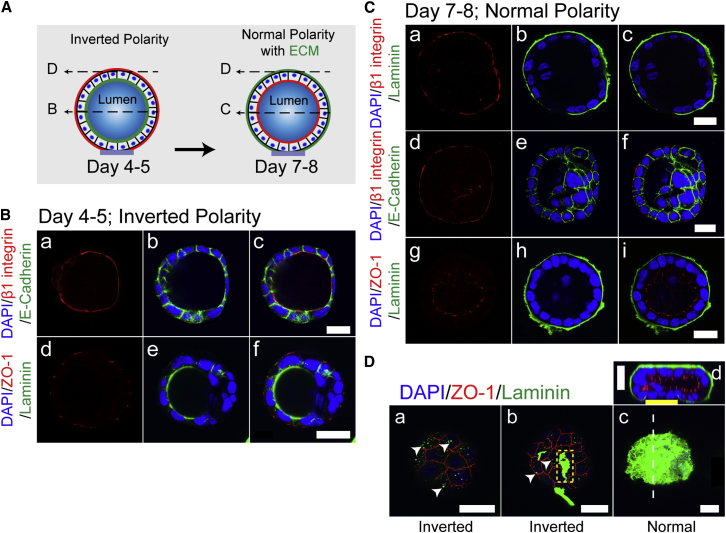
Figure 2.

MDCK II cyst formation on microdisks in gel-matrix-free cultures involves a reversal of polarity from inverted to normal. (A) Schematic of the polarity-reversal process from days 4–5 to 7–8 is shown. The apical domain is shown in red. Dashed arrows in (A) indicate the position of the x-y sections in (B–D). (B) On days 4–5, MDCK II cysts featured an inverted polarity. (C) On days 7–8, the polarity of MDCK II cysts was reversed, with β1 integrin (a and d) and laminin (b) relocalized at the cyst periphery and ZO-1 (g) facing the lumen. (D) Laminin gradually assembled on the apical surface of the cyst (a–c) and the complete assembly of laminin correlated with the reversal of polarity (d). Arrowheads indicate the coexistence of ZO-1 with punctately distributed laminin in (a), and with irregular large laminin patches in (b); the dashed line in (c) indicates the position of the x-z section of the cyst shown in (d). Scale bars, 20 μm. To see this figure in color, go online.

Laminin was previously shown to be effectively weaved around MCF-10A acini in 3D Matrigel cultures (29); however, the laminin assembly on MDCK II cysts generated here on the microdisks was considerably slow, although it was still correlated with the inversion of cyst polarity (Fig. 2 D). Laminin deposition was evident on the microdisks (Fig. S5) and either exhibited a dispersed punctate distribution or appeared as irregular larger patches on the apical surface of days 4–5 cysts until it completely covered the entire cyst by days 7–8 (Fig. 2 D). Notably, the complete assembly of laminin correlated with the polarity inversion that occurred together with the mobilization of ZO-1 to face the lumen. Previous studies showed that the normal cyst phenotype could be sufficiently rescued by exogenous laminin (0.25 mg/mL) even when the partially apically localized β1 integrin was functionally blocked (33, 34, 35), which suggested that laminin alone is adequate for inducing cyst polarization. As compared with the heavy, nonspecific deposition of laminin on the microdisks, the relatively undetectable laminin deposition on cysts that were 4 to 5 days old is intriguing (Fig. S5), and this raises the question of how exogenous (and/or endogenous) laminin signals to the cyst and gradually remodels the apparent laminin-nonadhesive apical surface of the cyst. Nonetheless, we showed that the single-cell-derived cysts generated on the microdisks are morphologically similar to those generated in the 3D gel culture. More importantly, these cysts are accessible to probes for mechanical characterization because of the deposition of a relatively thin layer of laminin around the cysts. Furthermore, these cysts adhered tightly to the substrates, even with the indentation of an AFM probe. The tight adhesion can potentially be attributed to the grasping of the 3-μm-lifted microdisks by the cell protrusions of the cysts (Fig. S6); such protrusions are absent in the cysts generated on flat micropatterns (19).

Measurement of cyst elasticity using AFM force-indentation curves

To analyze the global mechanical property of MDCK II cysts, we performed deep AFM microindentation by using a colloidal probe (30 μm in diameter) that was comparable in size with the cysts and a stiff microcantilever (k ≈ 2 N/m); we sought to apply larger forces over a greater area of the cyst, and thus the probe used here was larger and the cantilever was stiffer than the probe and the cantilever commonly used in measurements of single-cell mechanics (13, 36). After MDCK II cysts had formed on the microdisks patterned on glass cover slips, the samples were transferred, without further processing, to the AFM fluidic chamber for the indentation experiments. First, we measured the force-distance curves of the cysts (Fig. 3, A and B). The target force, F_M, was set as 100–300 nN, which gave an indentation strain ε = 0.15–0.25, to ensure that the ECM-cyst monolayer-lumen composite would be globally deformed by the probe, such that the stretching of the cyst monolayer might contribute to the force-indentation curves (Movie S2).

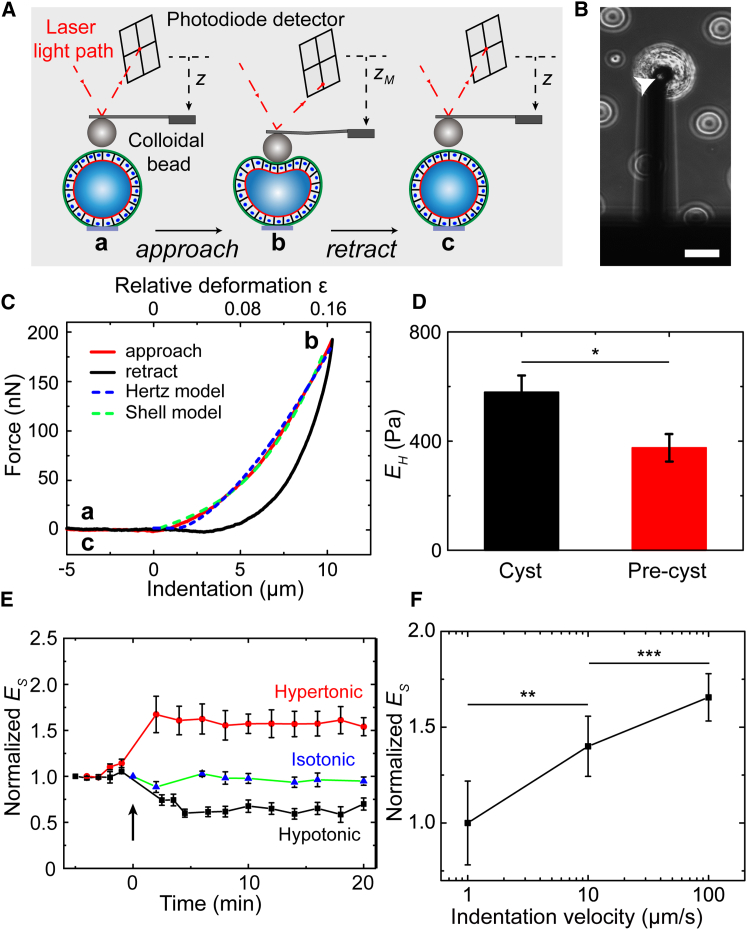
Figure 3.

Cyst elasticity measurement using AFM force-indentation curves. (A) Schematic of the experiment is shown: (a and b) after the colloidal bead is positioned immediately above a cyst, the AFM cantilever is lowered toward the top surface of the cyst at a constant approach velocity, v (1–100 μm/s); (b and c) the cantilever is retracted from the cyst when the target force, F_M, is reached. (B) Phase-contrast image of a microengineered MDCK II cyst under indentation is shown. Arrowhead indicates the colloidal bead glued at the tip of the AFM cantilever. Scale bar, 50 μm. (C) The force-distance curves measured on an MDCK II cyst. The dashed lines are the fit of the approach curve to the Hertz and shell models. Indentation velocity = 1 μm/s. (D) Young’s modulus E_H of MDCK II cysts (N = 20 cysts with n = 6 independent experiments) and precysts (N = 16, n = 3) for F_M = 100 nN, v = 1 μm/s; ^∗p = 0.020. (E) Long-duration monitoring of cyst-monolayer-modulus E_s change upon external hypertonic (425 mOsm; N = 8, n = 8) or hypotonic (205 mOsm; N = 6, n = 6) challenge. Isotonic (320 mOsm); N = 5, n = 5. (F) Normalized Young’s modulus E_s of MDCK II cyst monolayer (N = 5; n = 4) as a function of the indentation velocity, v, under indentation of F_M = 100 nN. ^∗p = 0.002 and 0.0007, paired sample t-test. The Young’s modulus E_s of the cyst monolayer increased with v. To see this figure in color, go online.

The force-distance curves featured an approach curve and a retraction curve with a hysteresis in between, which indicated the viscoelastic nature of the cysts (Fig. 3 C). Because a highly adhesive, thin ECM layer enwraps the entire cyst, the probe was precoated with a thin layer of PLL-g-PEG to minimize interference from cyst-probe adhesion between successive measurements. Notably, in contrast to the results of the cyclic stretching experiments on suspended MDCK II monolayers, which showed that the elastic modulus of the monolayer decreased substantially after repetitive stretching (14), our force-distance curves measured from the repetitive indentation of the MDCK II cysts were highly reproducible (Fig. S7 A); this finding suggests that the cyst monolayer is more resilient than the suspended monolayer and/or that our approach is less invasive than previous methods with regard to the mechanical architecture of the cyst monolayer. Although the cysts contained a fluid-inflated lumen, a hydrostatic-pressure-driven, transepithelial fluid flow did not appear to occur during the cyst compression process; otherwise, the slope of the approach curves would have decreased considerably over the repetitive indentation.

The following measured approach curves were found to be well described by the Hertz model (37, 38):

$$\mathit{F}=\frac{4}{3\left(1-{\upsilon }^2\right)}{\mathit{E}}_{\mathit{H}}{\mathit{R}}^{\frac{1}{2}}{\delta }^{\frac{3}{2}},$$ (1)

where E_H is the Young’s modulus of the entire cyst obtained with the Hertz model, υ is the Poisson ratio (υ = 0.5 for the incompressible assumption), R = 1/(1/R₁ + 1/R₂) is the effective radius of the probe R₁ and the cyst R₂, and δ is the indentation depth. In Fig. 3 C, the blue dashed line shows the validity of the Hertz model for describing the measured forces, and the best fitting gives E_H = 0.58 ± 0.07 kPa, which is in the same order as that determined for other epithelial tissues (39). To further include the effect of the fluid-filled lumen and obtain the Young’s modulus of the cyst monolayer, a shell model was adopted with the assumption that the cyst monolayer is impermeable to water during the indentation (40), as given by this equation:

$$\mathit{F}=\frac{4}{3}{\mathit{E}}_{\mathit{s}}{\mathit{h}}^2\epsilon +\frac{16\pi }{3}{\mathit{E}}_{\mathit{s}}\mathit{h}{\mathit{R}}_2{\epsilon }^3,$$ (2)

where E_s denotes the Young’s modulus of the cyst monolayer obtained with the shell model, h is the monolayer thickness (h = 5–8 μm for MDCK II cells), and the indentation strain ε is defined as the relative deformation ε = δ/2R₂. The data of approach curves can also be well described by the shell model and yielded a Young’s modulus of the cyst monolayer of E_s = 8.2 ± 4.2 kPa, which is comparable with that reported for single MDCK II cells (5–7 kPa) (41) and suspended MDCK II monolayers (20 ± 2 kPa) (14). Because both Hertz model and shell model do not take the adhesion of the cyst surface to the colloidal probe into account and the probe-approaching process is less influenced by adhesion, we chose the measured approach curves rather than the retraction curves for the modulus characterization.

To investigate the influence of a fluid-filled lumen on the cyst mechanics, 3-day-old MDCK II precysts—the spherical, solid cell aggregates—were analyzed in parallel by using the Hertz model (Figs. S3 and S7 B). Intriguingly, the Young’s modulus E_H of the MDCK II precysts (0.38 ± 0.05 kPa) was smaller than that of the cysts containing a lumen (Fig. 3 D). This appears to contrast the previous finding obtained in creep compliance experiments, which indicated that MCF10A acini were softer than MCF10A lumen-lacking pre-acini (16). One possible reason for this difference is that MCF10A acini do not form tight junctions (29), a hallmark of apicobasal polarity, which might compromise the junctional integrity of the acinus monolayer, which is crucial for tissue-level mechanics (42).

The Young’s modulus E_H of MDCK II cysts and precysts depends substantially on indentation velocity (Fig. S8 A), which implied the viscoelastic property is intrinsic to both tissues, regardless of their structural difference; but this modulus-dependence is relatively less on the cyst size (Fig. S8 B).

Next, we examined whether the change of single-cell mechanics would affect the Young’s modulus of the cyst monolayer by challenging the cyst with an osmotic stress. Previous studies have shown that single MDCK II cells displayed an elasticity increase upon hypertonic treatment and elasticity decrease upon hypotonic treatment (41, 43). Cyst size decreased ≥30% or increased ≥10% upon a hypertonic or hypotonic challenge, respectively (Fig. 4 D; Fig. S9). Here, we monitored the cyst-monolayer-modulus E_s change of the same cyst during this process to avoid the effect of cyst-to-cyst variation. Remarkably, the Young’s modulus E_s of MDCK II cyst monolayer increased ∼60% upon hypertonic treatment and decreased ∼35% upon hypotonic treatment (Fig. 3 E). This elasticity change in the cyst monolayer upon an osmotic stress agrees with the change of its constituents as in the case of single MDCK II cells, which could be explained by the poroelastic model that cells behave like poroelastic materials such as physical hydrogels (43, 44); according to this view, changes in the osmolarity of the external bath solution result in corresponding changes in the diffusion pore size of the cytoplasm and thus alter the cyst stiffness.

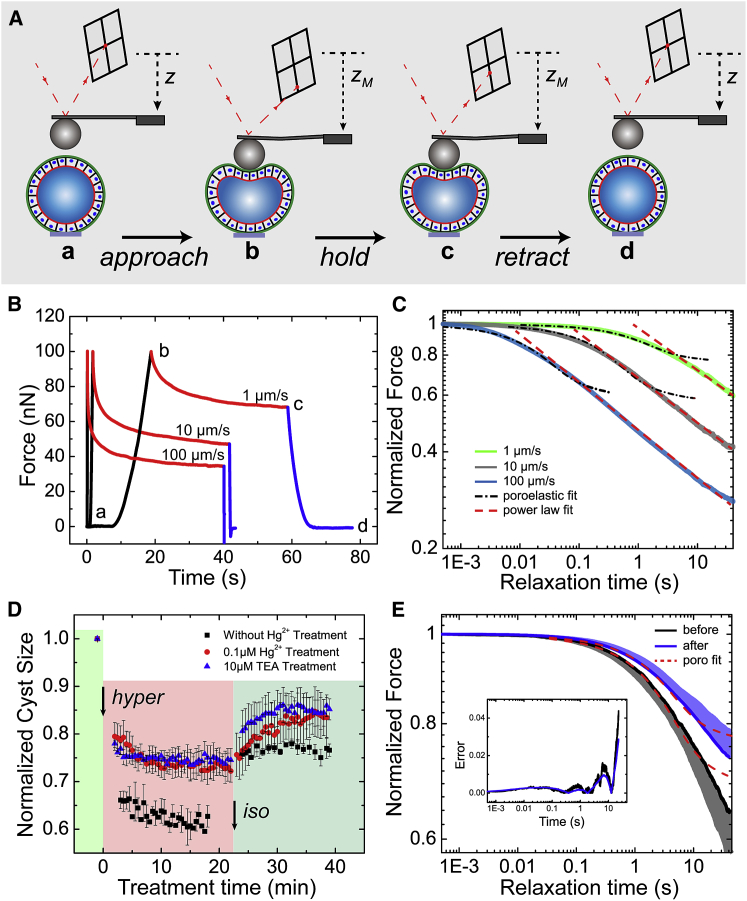
Figure 4.

Force-relaxation experiments on MDCK II cysts. (A) Schematic of the experimental procedures is shown: the approach phase (a and b) is same as that in cyst elasticity measurements; the cantilever is held at a fixed position for 40 s when the target force, F_M, is reached (b and c), and then, retracted from the cyst (c and d). (B) Typical force-relaxation curves obtained for MDCK II cysts, featuring three distinct regions: approach (black; a and b), relaxation (red; b and c), and retraction (blue; c and d); v = 1, 10, and 100 μm/s. (C) Population-averaged force-relaxation curves (b and c) obtained for MDCK II cysts at distinct loading velocities (shaded lines), plotted in a log-log scale. The force-relaxation curves do not reach a plateau within 40 s. Curves are averages of N = 8, 7, and 4 MDCK II cysts (n = 4) for loading velocities of v = 1, 10, and 100 μm/s, respectively. The black dot-dashed lines and red dashed lines are the fittings of the experimental force relaxation with the poroelastic and power-law relaxations, respectively. To obtain the best fitting for the poroelastic fit, we selected the first 6, 3, and 0.2 s (t < t_trans) of the averaged force relaxation with loading velocities of v = 1, 10, and 100 μm/s, respectively. R² = 0.976, 0.971, and 0.971, respectively. For the power-law fit, the ranges of the selected data were set as follows: relaxation time t = 6–40, 3–40, and 0.2–40 s (t_trans < t < 40 s) for v = 1, 10, and 100 μm/s, with power-law exponent β = 0.128, 0.133, and 0.138, and R² = 0.996, 0.995, and 0.993, respectively. (D) Effects of aquaporin blocking on cyst-size change upon consecutive replacement of the external buffering solution with the hypertonic solution (425 mOsm) and isotonic solution (320 mOsm) are shown. Cysts pretreated with 0.1 μM HgCl₂ (N = 4, n = 4) or 10 μM TEA⁺ (N = 3, n = 3) displayed a similar reduction in size (∼25%) upon hypertonic challenge that was less than that of control cysts (∼40%; N = 5, n = 5), which indicated that aquaporins were partially blocked by HgCl₂ or TEA⁺ treatment. (E) Population-averaged force-relaxation curves obtained for MDCK II cysts before and after treatment with 0.1 μM HgCl₂, under loading velocity v = 1 μm/s and target force F_M = 150 nN are shown. The dashed curves are the fittings to the poroelastic model, with the range of the selected data optimized as t = 0–23 s. R² = 0.968 and 0.965 for cysts before and after Hg²⁺ treatment, respectively. The shaded areas above and below the average curves represent the SD(±) of the data; N = 5, n = 5. The inset shows the percentage error, defined as |F(t) − F_fit|/F(t). To see this figure in color, go online.

Only minor fluctuation was detected in the stiffness tracking of control cysts under isotonic challenge (Fig. 3 E), which implied that the intrinsic elastic modulus of MDCK II cyst monolayers might not actively respond to extrinsic mechanical perturbations within the experimental timescale (∼30 min). The fluctuation was increased when the cyst volume changed drastically upon either hypotonic or hypertonic challenge, presumably reflecting, at least partially, unstablized cyst-microdisk adhesion by the drastic cyst volume change. Again, we noticed that the Young’s modulus of the cyst monolayer also depended substantially on indentation velocity (Fig. 3 F).

Force relaxation of MDCK II cysts

To investigate time-dependent cellular behavior of the MDCK II cysts, we performed force-relaxation measurements (Fig. 4, A and B; Movie S3). After the MDCK II cysts were subjected to an applied strain (ε ≈ 0.15 under F_M = 100–150 nN), the height of the cantilever was kept constant (<1% rise of the indentation depth over the relaxation period of 40 s), so that the force-relaxation was measured under an approximately constant strain (Fig. S10 A). Previous studies revealed differences in the timescales in which distinct components of the cyst contribute markedly to the force-relaxation process either biologically or physically, such as in the case of actin-cytoskeleton turnover (45), the highly deformation-magnitude-dependent timescale of cellular poroelastic behavior (43), or the junctional relaxation time (14, 42). To avoid the mutual masking of the contributions from such components, the loading velocity (v) was chosen to be 1, 10, and 100 μm/s. After the initial cyst deformation by the probe, the measured force-relaxation curves at different loading velocities all exhibited two distinct behaviors with an exponential decay in the short-time regime followed by a power-law decay in the long-time regime (Fig. 4 C). As the loading velocity increased, the force curve decayed faster in the short-time regime and the transition to the power-law decay occurred at an earlier time compared with the slow loading case. The transition time t_trans to the power-law decay was found to be t_trans = 6, 3, and 0.2 s, respectively, for v = 1, 10, and 100 μm/s (Fig. 4 C). At the longest decay time t = 40 s, we found that the force amplitude was reduced to F [t = 40]/F [t = 0] = 0.597 ± 0.021, 0.414 ± 0.018, and 0.280 ± 0.034, respectively.

Such a crossover behavior between the two time regimes was also reported previously in the AFM force-relaxation experiments for articular chondrocytes (46), MCF-7 cells (47), and particularly HeLa and MDCK cells (43). In these experiments, a poroelastic model was proposed to explain the initial exponential decay (43). To further test the model, we fitted the force relaxation data to the poroelastic model (Fig. 4 C; Supporting Material) and found that the data could be well described by the poroelastic model when t < t_trans (black dot-dashed lines). For poroelastic materials, the force relaxation is caused by water movement out of the porous matrix in the deformed region and the corresponding timescale is given by, t_p ∼ R₁δ/D_p, with D_p being the poroelastic diffusion coefficient. The characteristic time t_p under our experimental conditions ranged from 2 to 200 s (43, 44), and therefore poroelastic relaxation should contribute substantially to the initial force relaxation when the force loading time, t_approach, was shorter than t_p (t_approach < t_p for fast loadings with v = 10 and 100 μm/s). Interestingly, for MDCK II cysts under slow force loading (v = 1 μm/s, t_approach ∼10 s), the data could also be well fitted to the poroelastic model for timescales up to 3 s (for v = 10 and 100 μm/s, the well-fitted region was considerably shorter). This fitting was slightly better compared with the fast force loading case (Fig. 4 C; Fig. S10 C).

Conceivably, as observed for the single MDCK cells, the poroelastic relaxation should work better at higher loading velocities, because t_approach at higher loading velocity was shorter. By contrast, we observed that the poroelastic relaxation for the MDCK II cysts worked better at slow loading velocities. An important difference between the tissue-level and single-cell mechanics is that there are many junctional complexes in a cyst monolayer (14, 42), whose relaxation might correspond to the power-law relaxation observed in the long-time regime. For fast indentations (t_approach < 2 s), the power-law relaxation moved to the short-time regime that may mask some of the concurrent poroelastic signatures.

Another interesting phenomenon is that the slow power-law decay in the long-time regime lasted beyond the longest record time t = 40 s. The obtained power-law exponent, β, ranging from 0.128 to 0.138, was insensitive to the change of the loading velocity. This value of β is very close to that obtained in the creep experiment for the suspended MDCK II monolayer (β ∼0.15) but is markedly smaller than the reported value for single cells (β ∼0.3–0.5) (14). Our findings thus suggested that the MDCK II cyst behaves more like suspended monolayers than single cells under fast loadings.

From the above discussions, we conclude that relaxation of the MDCK II cysts is a more complex process than a simple uniform poroelastic relaxation even in the short-time regime and may involve water leakage through both junctional complexes and cell membrane. On the theoretical level, one needs to incorporate the relaxation of the junctional complexes and of the poroelastic behavior of individual cells into the model to better explain both the initial exponential force relaxation in the short-time regime and the power-law relaxation in the long-time regime. On the experimental level, one needs to examine both the real-time relaxation of the junctional complexes and the cytoskeleton dynamics to uncover the biological origin of the complex rheological behavior of the MDCK II cysts.

The force relaxation of MDCK II precysts displayed similar relaxation behavior as the MDCK II cysts (Fig. S10 B), suggesting that the filling of the luminal space does not abolish the poroelastic response at short timescales. However, the poroelastic fitting of the force-relaxation data showed that the poroelastic diffusion coefficient, D_p, for the MDCK II cysts was substantially smaller than that for precysts (Fig. S10 D); this implies that the force relaxation of the MDCK II precysts involved a more rapid force dissipation and that the precysts were more permeable to water.

In principle, MDCK II cysts under AFM-probe compression must experience an increased luminal hydrostatic pressure that potentially facilitates the subsequent hydrostatic-pressure-driven water transport across the epithelial-monolayer barrier during force relaxation. The water could be transported either transcellularly, across the cell membranes (through molecules such as aquaporin) and the enclosed cytoplasm, or paracellularly through tight junctions (23, 48, 49). Previous studies evaluating the hydraulic permeability of transwell-cultured epithelial monolayers showed that the paracellular route is the most dominant route for hydrostatic-pressure-driven transepithelial water transport (50, 51). This notion was supported by the results of our force-relaxation experiments performed on MDCK II cysts, in which the transcellular water-transport pathway was partially inhibited by adding HgCl₂, a commonly used aquaporin blocker (Fig. 4, D and E) (23). Here, we first confirmed that basolaterally applied 0.1 μM HgCl₂ blocked the osmotic-gradient-induced water transport and that this was comparable with the effect of another commonly used aquaporin blocker, TEA⁺ (Fig. 4 D). After HgCl₂ treatment, the force relaxation of MDCK II cysts was slowed slightly (Fig. 4 E), but the treatment did not measurably affect the poroelastic diffusion coefficient obtained by the fitting of the force-relaxation curves (Fig. 4 E; Fig. S10 E), which implies that little intracyst water leaked transcellularly during the force relaxation.

The luminal fluid occupies 30% to 50% of the cyst volume, and cysts maintain an initial outward hydrostatic pressure across the monolayer before indentation (6.7 mm H₂O for MDCK cysts (52)); however, the D_p of MDCK II cysts, which are commonly recognized as an electrically leaky epithelial-monolayer model, was still smaller than that of MDCK II precysts. This finding coupled with the observations that 1) the Young’s modulus E_H of MDCK II cysts was higher than that of the MDCK II precysts and 2) the force-distance curves of MDCK II cysts were highly reproducible under repetitive indentations (Fig. 3 D; Fig. S6 A) led us to conclude that paracellular fluid flows were also negligible here. This conclusion, although derived indirectly from mechanical measurements, agrees with that from previous optical measurements (53).

In summary, we have demonstrated a novel approach, to our knowledge, for generating probe-accessible MDCK II cysts in gel-matrix-free culture media for use in AFM-based mechanical characterization. Our approach offers several advantages: 1) cyst preparation is simple and noninvasive to the cells because of the gel-matrix-free configuration; 2) the sensitivity is high because of use of AFM; 3) the reproducibility is high (Fig. 3 E; Fig. S6), which enables the changes in the mechanical property of the same cyst to be examined after drug treatment and thereby markedly enhances the efficiency and reliability of the mechanical characterization; and 4) high throughput can be achieved in generating probe-accessible cyst arrays. This lays a foundation for potentially high-throughput mechanics characterization, particularly when using high-throughput assays such as those involving the use of magnetic tweezers.

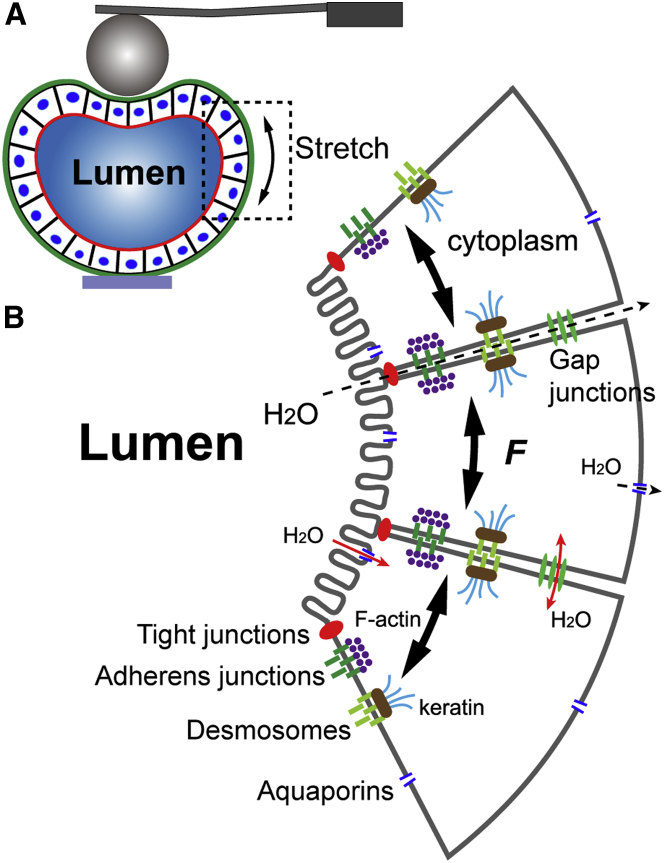
We have also shown for the first time, to our knowledge, that the tissue-level mechanics of MDCK II cyst, as well as its complex rheology. Mechanical compression of MDCK II cysts by an AFM probe might substantially stretch the cyst monolayer because of the presence of a fluid-filled lumen and the tight junctions that seal neighboring cells (Fig. 5). The stretching of the cyst monolayer might cause a deformation of the junctional complexes and the constituent cells; this, in turn, would initiate the response of F-actin and keratin and other intermediate filaments (14) that are connected to adherens junctions and desmosomes, respectively, which are integral to the monolayer mechanics (42). We could expect that individual cells are in series with junctional complexes and presumably assumes a smaller spring constant, and thus play a dominant role in determining the elasticity of the cyst monolayer (Fig. 3 E).

Figure 5.

Possible factors at the cellular and subcellular levels (B) that contribute to the complex rheological behaviors of MDCK II cysts under indentation (A). To see this figure in color, go online.

Moreover, a cyst-compression-induced increase in intracyst hydrostatic pressure might facilitate the efflux of water from the lumen through tight junctions (although our results here did not indicate substantial water efflux) and the aquaporin channels located at both the apical and basolateral membranes (our results also did not indicate substantial transcellular water efflux), as well as an exchange of fluid between neighboring cells through gap junctions. We propose that such water redistribution through the monolayer cytoplasm ultimately may contribute to the poroelastic behaviors observed during the force relaxation of MDCK II cysts.

The mechanical properties of epithelial tissues play critical roles in development, normal physiology, and disease given that epithelial salt and water secretion serves diverse functions in various organ systems (2, 48, 54, 55). For instance, polarization-induced fluid accumulation within an enclosed area generates an outward hydrostatic pressure that opens and expands a luminal space sealed by a stretched monolayer (1, 2, 5, 56), which accounts for one of the most fundamental processes in development, and abnormal luminal-fluid hydrostatic pressure resulting from unregulated fluid secretion leads to diseases such as autosomal-dominant polycystic disease (55). A major driving force for abnormal enlargement of kidney cysts is considered to be cAMP-induced transepithelial chloride secretion, and growing evidence suggests that chloride channels such as cystic fibrosis transmembrane conductance regulator (CFTR) and anoctamin 1 (ANO1) and aquaporins are involved in this process (57, 58, 59, 60). However, all of these previous studies relied heavily on measuring the change in cyst volume after drug treatment, which typically takes days to occur. By contrast, our sensitive AFM experimental setup allows immediate examination of the changes in the mechanical properties of MDCK II cysts under similar circumstances; this will enable future studies to address questions such as whether an increase in cAMP causes an immediate build-up of cyst monolayer tension and how CFTR and ANO1 respond to the tension increase (especially considering that CFTR is mechanosensitive (61, 62) and ANO1 and CFTR are modulated by mechanosensitive Ca²⁺ and ATP signaling), and whether the water permeability of the cyst monolayer is affected by the tension.

Author Contributions

Y.S., D.G., P.T., L.Y., and P.H. conceived the original concept. Y.S. and D.G. designed and executed most of the experiments. D.S. and Y.S. prepared the microdisks. Y.S., D.G., P.T., L.Y., and P.H. analyzed the data and, with comments from D.S. and S.T., wrote the manuscript. P.H., L.Y., and P.T. supervised the study.

Editor: Alexander Dunn

Supporting Material

Movie S1. A 6.5-h Live Imaging of Rotating MDCK II Cell Aggregates on Microdisks on Day 7 of Culture in Conventional Culture Medium without Matrigel Supplement

Images were captured at 1 frame/min. Scale bar, 30 μm.

Movie S2. One Cycle of AFM Cantilever Approach and Retraction for Measuring Force-Distance Curves

The blue dashed curves show the lumen outline before indentation, and the red curves show the outline when the target force, FM, is reached. The cyst monolayer was slightly stretched during the indentation. Scale bar, 30 μm.

Movie S3. The Cantilever Loading Procedure for Stress-Relaxation Experiments on MDCK II Cysts and Precysts

The procedure includes approach, hold, and retraction processes (one each per cycle). Scale bar, 30 μm.