Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Nov 25;138(50):16345–16354. doi: 10.1021/jacs.6b09243

NMR Spectroscopic Characterization of Charge Assisted Strong Hydrogen Bonds in Brønsted Acid Catalysis

Nils Sorgenfrei 1, Johnny Hioe 1, Julian Greindl 1, Kerstin Rothermel 1, Fabio Morana 1, N Lokesh 1, Ruth M Gschwind 1,*
PMCID: PMC5266430  PMID: 27936674

Abstract

graphic file with name ja-2016-092438_0012.jpg

Hydrogen bonding plays a crucial role in Brønsted acid catalysis. However, the hydrogen bond properties responsible for the activation of the substrate are still under debate. Here, we report an in depth study of the properties and geometries of the hydrogen bonds in (R)-TRIP imine complexes (TRIP: 3,3′-Bis(2,4,6-triisopropylphenyl)-1,1′-binaphthyl-2,2′-diylhydrogen phosphate). From NMR spectroscopic investigations 1H and 15N chemical shifts, a Steiner–Limbach correlation, a deuterium isotope effect as well as quantitative values of 1JNH,2hJPH and 3hJPN were used to determine atomic distances (rOH, rNH, rNO) and geometry information. Calculations at SCS-MP2/CBS//TPSS-D3/def2-SVP-level of theory provided potential surfaces, atomic distances and angles. In addition, scalar coupling constants were computed at TPSS-D3/IGLO-III. The combined experimental and theoretical data reveal mainly ion pair complexes providing strong hydrogen bonds with an asymmetric single well potential. The geometries of the hydrogen bonds are not affected by varying the steric or electronic properties of the aromatic imines. Hence, the strong hydrogen bond reduces the degree of freedom of the substrate and acts as a structural anchor in the (R)-TRIP imine complex.

Introduction

Hydrogen bonding impacts the energetics and structures of molecules as well as the reactivity and stereoselectivity of their reactions and is therefore of utmost significance in nature.1 Nowadays, hydrogen bonding is more and more recognized by chemists as potential activation mode for electrophilic substrates such as carbonyl compounds or imines in the field of asymmetric catalysis.2−4 A “privileged class” of asymmetric Brønsted acid catalysts constitute BINOL (1,1′-binaphtol) derived phosphoric acids, which were introduced by Akiyama and Terada2,5−7 and found applications in a wide pool of reactions with imines as substrates, including Mannich reactions, cycloadditions, aza-ene-type reactions, hydrocyanations and transfer-hydrogenations.7,8 Especially, for the asymmetric reductions of imines with Hantzsch 1,4-dihydropyridine ester 1 this class of chiral phosphoric acids provides high stereoselectivities and yields as, e.g., published by the groups of Rueping,9,10 List11 and MacMillan.12 The proposed catalytic cycle for this asymmetric reduction is shown in Figure 1a.3,9,11 The phosphoric acid protonates the imine and forms a chiral hydrogen bond assisted ion pair, which reacts subsequently with the Hantzsch ester 1 to form the chiral amine. Several DFT studies of the groups of Himo and Goodman addressed the issue of enantioselectivity in this catalytic reaction.13−16

Figure 1.

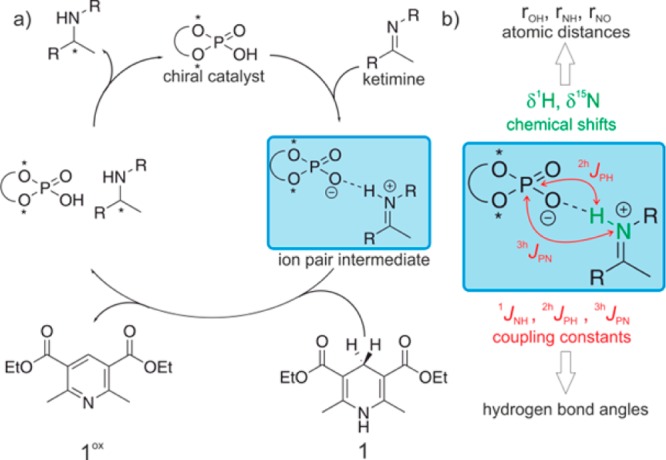
Figure 1

Open in a new tab

(a) Catalytic cycle proposed for the Brønsted acid catalyzed enantioselective reduction of imines with Hantzsch-1,4-dihydropyridine ester 1.9,11 (b) Experimental observables used in this study to characterize the hydrogen bond interaction in (R)-TRIP imine complexes.

They proposed a fast acid–base equilibrium between imine and catalyst followed by an E/Z isomerization of the iminium ion. Next a ternary complex is formed between the ion pair and the Hantzsch ester, which is stabilized by an additional hydrogen bond between the NH of the Hantzsch ester and the phosphoric acid. The absolute stereochemistry of the product and the enantiomeric excess (ee) is then determined by the relative energy of the ternary transitions states of the E and Z iminium ion, respectively.13−17

Furthermore, a detailed experimental study was published by Tang et al., regarding the basis of enantioselectivity in the Brønsted acid catalyzed reduction of imines with gaseous H2 as reduction agent and an achiral iridium complex as cocatalyst.8 Again, a ternary complex and the corresponding transition states were proposed to be responsible for the stereodiscrimination.

However, in the whole field of Brønsted acid catalysis detailed experimental data providing structural insights are extremely rare. Thus, so far not even the hydrogen bond situation in the binary ion pair intermediate has been clarified. The concept of full protonation of basic substrates such as imines by acidic catalysts—often proposed by synthetic chemists and theoreticians—is an oversimplification and an extreme point of view as noted by Toste et al.4 For example, purely hydrogen bonded complexes were proposed in a computational and NMR spectroscopic study of the activation of N-Boc protected imines by a chiral phosphoric acid.18 Furthermore, in a preceding NMR study of our group investigating achiral diphenylphosphoric acid (DPP) imine complexes, both hydrogen bonded complexes and ion pairs were proposed to coexist in solution.19 There, a typical temperature dependent ratio was observed, high temperatures favor hydrogen bonding, whereas at low temperatures ion pairs are more stabilized.19 Contrary results were obtained studying complexes of DPP with 2-methylquinoline at elevated temperatures.20 There, ion-pairing was found to be the dominant interaction motif.20 However, to our knowledge detailed experimental studies about the hydrogen bond properties in ketimine complexes with the chiral phosphoric acids have not been reported so far.

Therefore, in this work we present the first detailed, NMR based experimental investigations on the hydrogen bond activation of imines by chiral phosphoric acids. The hydrogen bonds in these binary catalyst substrate complexes were experimentally characterized by 1H, 15N chemical shifts and trans hydrogen bond scalar couplings. From the chemical shifts the individual atomic distances (rOH, rNH, rNO) within the hydrogen bonds were derived and the 2hJPH and 3hJPN scalar couplings give information about the angles (Figure 1b). These detailed experimental data are compared with high level theoretical calculations about the atomic distances, scalar couplings of the hydrogen bonds and structures of the binary complexes. This reveals not only unprecedented insights into the hydrogen bond activation of Brønsted acid catalysis but also the limitations of both experimental and theoretical models.

Results and Discussion

Model Systems

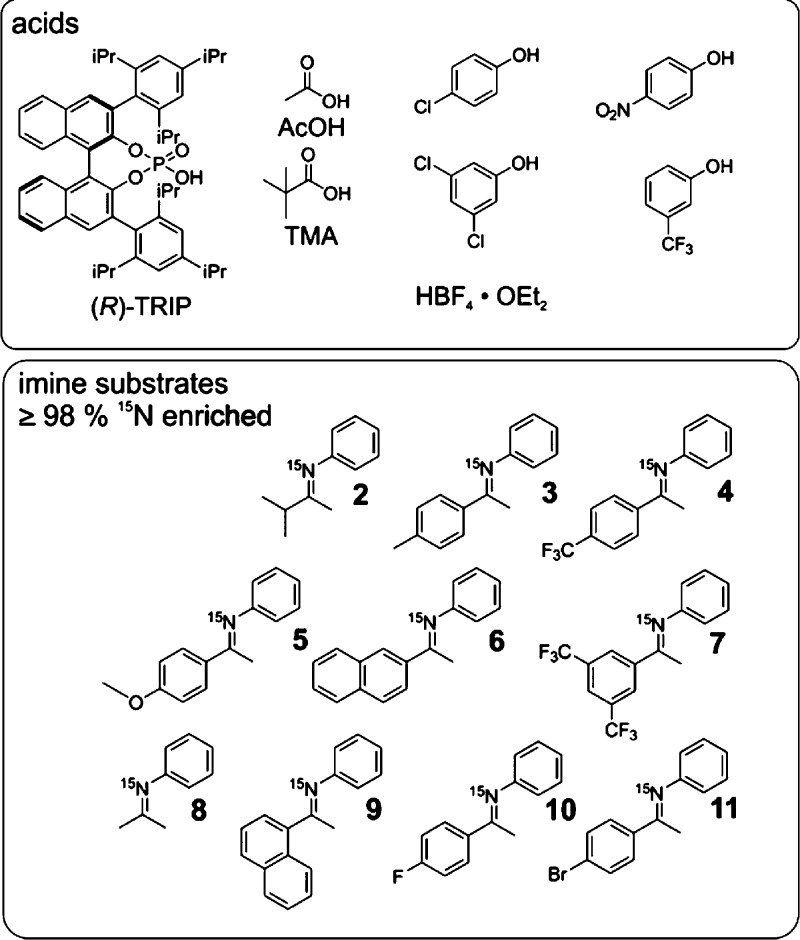
(R)-TRIP 3,3′-bis(2,4,6-triisopropylphenyl)-1,1′-binaphthyl-2,2′-diylhydrogen phosphate was chosen as catalyst, because structural information based on NOE data was available for some (R)-TRIP imine complexes (see below).21 In addition, imines with different steric and electronic properties were selected (Figure 2) to rationalize the influence of the substrate on the hydrogen bonding properties of the ion pairs. Furthermore, tetrafluoroboric acid, was selected to mimic purely ionic complexes. Acetic acid (AcOH), trimethyl acetic acid (TMA) as well as phenols (4-chlorophenol, 4-nitrophenol, 3,5-dichlorphenol, 3-(trifluoromethyl)phenol) were chosen to form strictly neutral hydrogen bonded complexes. The preparation of 15N-labeled imines and representative methods for sample preparation are described in the Supporting Information. All acid imine and phenol imine complexes were investigated in CD2Cl2 and/or freonic mixtures by NMR spectroscopy, because in these solvents the best NMR properties were detected in terms of chemical shift dispersion and line widths (for spectra in toluene see Supporting Information). Extremely low temperatures between 180 and 130 K were used to reach the slow hydrogen bond exchange regime. These low temperatures in combination with the selection of phosphoric acids and up to 98% 15N enriched imines allowed for the detection of 2hJPH and 3hJPN as sensors for hydrogen bond angles and atomic distances.22

Figure 2.

Figure 2

Open in a new tab

Model systems for hydrogen bond studies; Brønsted acid catalyst (R)-TRIP and other acidic compounds were used as donors; all imines 2 – 11, tested as acceptors were 98% 15N enriched to enable the detection of Δδ15N and 3hJPN.

Computational Details

The binary complexes consisting of (R)-TRIP and imines 3–5 and 8 were chosen as models in the theoretical calculations. The structures are optimized at RI-DFT level of theory using meta-GGA functional TPSS-D3 with def2-SVP basis set in the gas phase and in the continuum of dichloromethane (SMD model).23−25 A dielectric constant of 16.2 was used to simulate the low temperature measurement at 180 K. Bond parameters (distances and angles) were averaged over large conformational space (due to isopropyl rotation) according Boltzmann distributions at 180 K. The final free energies of the conformations were evaluated at SCS-RI-MP2/CBS level of theory (for extrapolation procedure see Supporting Information).26 Solvation energies were added subsequently to the Gibbs free energy using SMD solvation model at 180 K in dichloromethane. The 1H and 15N chemical shifts, respectively the scalar coupling constants (1JNH, 2hJPH and 3hJPN), were computed at TPSS with IGLO-III basis set using the complete model, respectively the reduced model.27 The 2,4,6-triisopropylphenyl groups were replaced with hydrogens, and subsequently subjected to frozen optimization. For the geometry optimization, free energy of solvation and scalar coupling constant calculation Gaussian09 version D.01 was used. For single point calculation ORCA3.0.3 was used.28,29

Detection and Characterization of Hydrogen Bonds by NMR

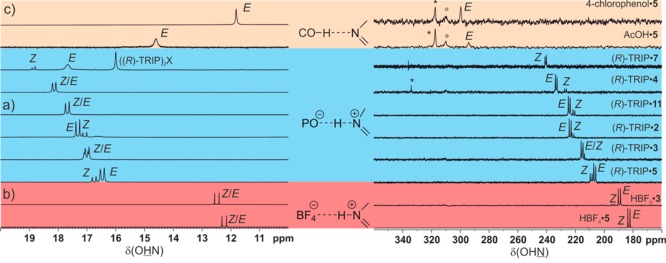
For most of the chiral phosphoric acid imine complexes ((R)-TRIP 2–11), two main ion pair species were detected representing hydrogen bridged ion pairs with E and Z configured imines. Therefore, in the following this general pattern and its assignment is described exemplarily on the hydrogen bonded complex of (R)-TRIP and 5 in CD2Cl2 at 180 K (Figure 3). For (R)-TRIP·5E and (R)-TRIP·5Z the proton in the hydrogen bond is detected at 16.47 and 16.75 ppm, respectively (Figure 3a). Such chemical shifts larger than 16 ppm are usually observed for hydrogen atoms in “strong” or “low-barrier hydrogen bonds”.1,30,31 Both signals are doublets with 1JNH coupling constants of 79.7 and 81.2 Hz showing the covalent connectivity to 15N and the existence of an ion pair structure (for further support see 1H,15N-HMQC spectra in the Supporting Information).19 The E and Z configurations of the imines were assigned based on 3JNH couplings constants between 15N of imine and methyl protons and as well as by NOESY measurements (for details see Supporting Information). The ionic character of both isomers is further corroborated by the significant high-field shift of the 15N resonances to 206.7 and 209.2 ppm for E and Z, respectively (Figure 3b and d), compared to the free base 5 at 321.0 ppm (Figure 3e); Δδ15N > 110 ppm), which is a clear indicator for the proton transfer to the lone pair of the nitrogen.32 Also the 13C low field shifts of the imino groups (Δδ ∼ 13.7 and Δδ ∼ 16.0 ppm for E and Z, respectively; see Figure 3d and e) corroborate this analysis.33,34

Figure 3.

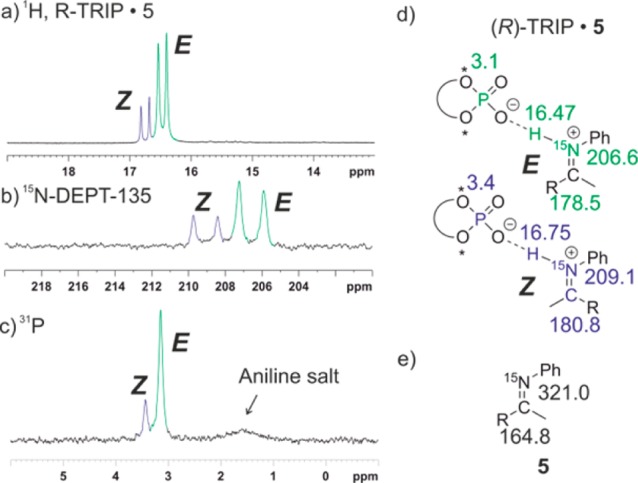
Figure 3

Open in a new tab

(a–c) Sections of the 1H, 15N-DEPT-135 and 31P spectra of a 1:1 complex of (R)-TRIP and 5 (CD2Cl2, 180 K, 600 MHz), clearly showing the coexistence of both E and Z complexes; (d) chemical shifts of (R)-TRIP·5E/Z; (e) chemical shifts of unbound 5.

For (R)-TRIP imine complexes the large 1JNH coupling constants, the significant high field shift of the 15N resonances upon complex formation and the refined spectroscopic and theoretical analysis of the data (see below) indicate a strong preference for the ionic hydrogen bond1,35 (Figure 3d) except for imine 7, in which the two CF3-groups significantly reduce the basicity. The hydrogen bonded complex can be involved in association/dissociation equilibria with the isolated molecules or the separated ion pairs.36−38 In case of imines with low basicity (e.g., 4 or 7) or in the presence of an excess of imine a separated 15N signal of the free non protonated imine is observed at 180 K, which is in slow exchange with the imine in the complex.

Considering our experimental conditions (e.g., low temperatures and the noncoordinative CD2Cl2 as solvent) and the estimated strength of the formed hydrogen bonds (>70 kJ/mol),1 the formation of solvent separated ion pairs in (R)-TRIP complexes is negligible.39 This is substantiated by detection of large 2hJPH and 3hJPN coupling constants (see below).40 Thus, the 1H and 15N chemical shifts observed for the binary substrate complexes of (R)-TRIP with the imines at 180 K are the “intrinsic” chemical shifts of the individual hydrogen bonded species and can be used for the analysis of the hydrogen bond situation of these complexes.35,41

Hydrogen Bond Analysis Based on δ1H, δ15N and 1JNH

In 1H NMR spectra, chemical shifts above 16 ppm are usually observed for hydrogen atoms in “strong” or “low-barrier hydrogen bonds”.1,30,31 According to literature the formation of strong hydrogen bonds is associated with a “proton-transfer reaction”13,8 between hydrogen bond donor and hydrogen bond acceptor. The progress of the proton transfer is dependent on the acidity of the hydrogen bond donor and the basicity of the acceptor, and as well as the polarity of the solvent.1,36,38,39,42 Therefore, empirical correlations of 1H “{δ(OHN)}” and 15N “{δ(OHN)}” chemical shifts, as well as 1JNH “{1J(OHN)}” coupling constants with the atomic distances can be used to determine the position of the proton inside the hydrogen bond, as previously developed by Limbach and Denisov in their studies of OHN hydrogen bonds in pyridine acid complexes (eqs 1–5).35,41,43,44 Using an extended set of complexes with varying acidic and basic properties of their hydrogen bond donors and acceptors, the proton position within the hydrogen bond can be varied stepwise. There, the parabolic dependence of δ(OHN) on δ(OHN) was used to determine the valence bond orders pOHH and pNHH by employing the empirical correlations presented in eqs 1–2.

graphic file with name ja-2016-092438_m001.jpg 1
graphic file with name ja-2016-092438_m002.jpg 2

Furthermore, they proposed a correlation between 1J(OHN) and the valence bond orders as well.35,41,43,44

graphic file with name ja-2016-092438_m003.jpg 3

The determined pOHH and pNHH for a hydrogen bond are then consulted to derive the corresponding atomic distances (rOH, rNH, rNO) according to eqs 4–5.

graphic file with name ja-2016-092438_m004.jpg 4
graphic file with name ja-2016-092438_m005.jpg 5

For a detailed explanation of the empirical equations and constants applied in this study for the acid imine complexes see Supporting Information. To enable a reliable parametrization of the constants {δ(OH)°; δ(HN)°; δ(HN)°; δ(N)°; 1J(HN)°; δ(OHN)*; δ(OHN)*, 1J(OHN)*} used in eqs 1–3, it was necessary to cover a wide range of the valence bond orders pOHH and pNHH. Hence, the database was extended from (R)-TRIP imine complexes with “strong” hydrogen bonds to ionic and neutral acid imine complexes with “moderate” hydrogen bond strength.1,35,41 As mentioned earlier, for the strictly ionic acid imine complexes, tetrafluoroboric acid was selected, which was already used in our previous study.19

Acetic acid (AcOH) and trimethylacetic acid (TMA) as well as several substituted phenols were selected for the strictly neutral acid imine complexes. The plot of δ(OHN)ref against δ(OHN) of all acid imine complexes is shown in Figure 4. Representative 1H and 15N spectra related to the different hydrogen bond types are shown in Figure 5. In strictly ionic complexes with “moderate” hydrogen bonds (HBF4·3, HBF4·5) δ(OHN) values between 12 and 13 ppm and high values of 1JNH about 92.6 Hz are observed indicating a complete proton transfer reaction and therefore short rNH (Figure 4b, Figure 5b).1 With decreasing acidity of the hydrogen bond donor (R)-TRIP and decreasing basicity of the acceptor (5 > 3 > 2 > 11 > 4 > 7) the proton is shifted toward the center of the hydrogen bond, which is interpreted as an increase of strength of the hydrogen bond (Figure 4a; Figure 5a).1,35,41 In the case of (R)-TRIP·7E, the proton is even shifted beyond the maximum indicating a decrease of the hydrogen bond strength and a considerable population of the neutral hydrogen bonded complex. In the predominant ionic complexes high proton chemical shifts are observed from 16.47 ppm ((R)-TRIP·5E) to 18.85 ppm ((R)-TRIP·7Z) in combination with reduced absolute 1JNH coupling constants from 82.2 Hz ((R)-TRIP·5E) to 60.6 Hz ((R)-TRIP·7Z). In contrast, for the neutral hydrogen bonded complex (R)-TRIP·7E a reduced 1JNH coupling constant (42 Hz at 170 K) was observed, which is in full agreement with the trend in the Steiner–Limbach correlation curve. Continuing to the less acidic donors AcOH and 4-chlorophenol the proton is now shifted further on, toward the oxygen atom (Figure 4c, Figure 5c). This leads again to a weakening of the hydrogen bonds, visible by the high field shift of the proton signal at 11.81 ppm for 4-chlorphenol·5. Now with the proton close to the oxygen, the splitting due to the 1JNH coupling vanishes. In contrast, the 15N resonance of the hydrogen bonded complexes is shifted continuously from 182.2 ppm for HBF4·5E over 230.2 ppm for (R)-TRIP·4Z to 299.7 ppm for 4-chlorophenol·5 (Figure 5a–c).

Figure 4.

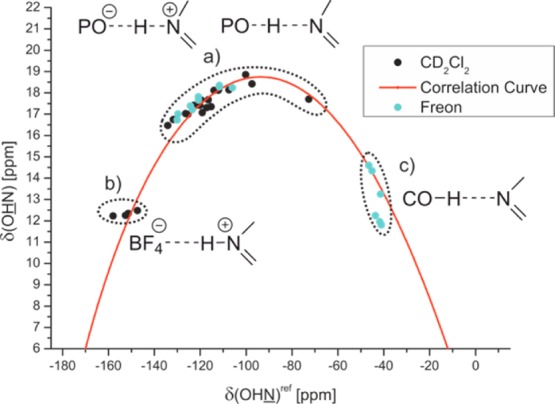
Figure 4

Open in a new tab

Plot of δ(OHN)ref against the δ(OHN) of the hydrogen bonded complexes; (a) (R)-TRIP with 2 – 11; (b) HBF4 with 3 and 5; (c) carboxylic acids and phenols with 3 and 5; the 15N chemical shifts of all complexes are referenced to 7 {δ(OHN)ref = δ(OHN) – 340.8 ppm}; spectra corresponding to the different hydrogen bond types are shown in Figure 5; for details see Supporting Information.

Figure 5.

Figure 5

Open in a new tab

Dependence of δ(OHN) and δ(OHN) on the hydrogen bond strength in the E and Z acid imine complexes shown by selected of 1H (low field sections) and 15N spectra in CD2Cl2 and freonic mixtures between 180 to 130 K; the shown spectra correspond to the hydrogen bond types in Figure 4; (a) (R)-TRIP imine complexes; (b) HBF4·3 and HBF4·5; (c) AcOH·5 and 4-chlorophenol·5; for the 15N spectra of (R)-TRIP·7, (R)-TRIP·5 and HBF4·5 polarization transfer experiments were used (INEPT and DEPT); (*) signals of free imine; (deg) impurity or artifact; in case of R-TRIP·7 signals of ((R)-TRIP)2X complexes are observed;35,55 a list of δ(OHN) and δ(OHN) of the individual complexes is provided in the Supporting Information Table S9–S12.

A satisfying curve fit of the data points was achieved, employing eq 1 and eq 2 (Figure 4, red curve; for details and fitting parameters see Supporting Information). The observed parabolic dependence of δ(OHN) on δ(OHN) is in good agreement with the previous investigations on pyridine-acid complexes by Limbach and co-workers.35,41 For (R)-TRIP imine complexes the continuous progression of the data points on the correlation curve is indicative for a strong hydrogen bond and excludes a tautomeric equilibrium between two proton positions in a classical double well potential (data points on two intersecting straight lines).35 Regarding the 1JNH coupling constants of the investigated Brønsted acid imine complexes, a good characterization by the valence bond model is achieved as well, shown by the plots of 1J(OHN) against δ(OHN) and δ(OHN) (see Supporting Information). The magnitude of the measured coupling constants (60.6–82.2 Hz) reflects again the above-described predominant ionic character of the (R)-TRIP imine complexes and the signitifcantly reduced value of (R)-TRIP·7E (42–46 Hz) corroborates the shift toward neutral hydrogen bonds.

On the basis of the δ(OHN) of the Brønsted acid imine complexes (see Table S9–12 in the Supporting Information) and the fitted correlation curve (Figure 4), the bond orders pOHH and pNHH of the individual (R)-TRIP imine complexes were obtained (see Supporting Information Table S13). Next eqs 4–5 are used to determine the atomic distances rOH, rNH and rNO. These experimentally derived values for rNH and rOH, are depicted in Figure 8 and discussed below together with the results from the theoretical calculations. For all values including rNO see Table S13 in the Supporting Information. All hydrogen bond distances are in the range of strong OHN hydrogen bonds1 and vary between 111 and 136 pm for rNH, 114–146 pm for rOH, and 249–257 pm for rNO. In addition, the obtained average proton donor distances—in the case of (R)-TRIP complexes rOH—below 160 pm indicate the partial covalent character of the formed hydrogen bonds.45,46

Figure 8.

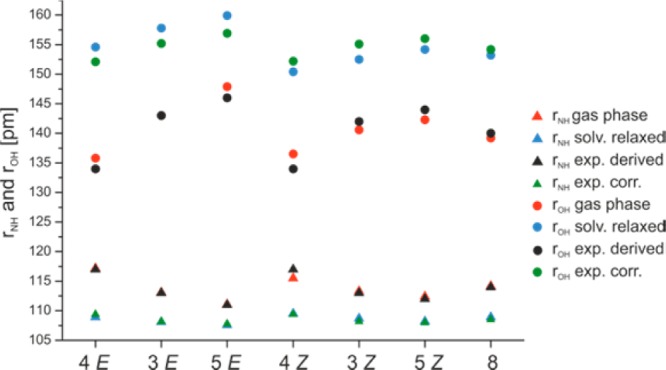
Figure 8

Open in a new tab

Comparison of the experimentally derived and calculated rNH and rOH distances of (R)-TRIP·3–5 and (R)-TRIP·8.

Comparison of NMR Data and Theoretical Calculations

Ion Pair Structures

Next the results of this study were correlated with our recent NMR spectroscopic and computational study regarding the general structures of (R)-TRIP complexes with the aromatic imines (3–5) to gain further insight into the hydrogen bond interaction.21 In general two binding modes of E/Z-imines and catalyst (R)-TRIP are theoretically possible, which are stabilized by dispersive interactions.

For E-imines (3–5) theoretical calculations showed that the orientation, in which the para-substituted ketone moiety reclines on the chiral BINOL aromatic surface is majorly populated for all aromatic imines investigated (Figure 6a). However, initial experimental and theoretical structural studies with short aliphatic imines (2 and 8) and doubly substituted imines21 indicate the second orientation with a 180° rotated imine (structure not shown) to be also populated. In case of Z-imine complexes ((R)-TRIP·3–5) also, NOESY spectra predict that the two binding modes in the complex to be populated. The most stable one is depicted in Figure 6b.21 Furthermore, 1H spectra, which showed only one averaged signal set for the protons at the BINOL moiety, suggested that the Z isomers of the (R)-TRIP imine complexes are extremely dynamic even at very low temperatures. The theoretical calculations predicted that both orientations differ only by 4.5–6 kJ/mol. It is very likely that the compact structure of Z-imines allows the rotation and translation of the imines in the binary complex.21 Fortunately, the actual interpretation of the hydrogen bonds is not affected by this structural diversity, because the geometries of the hydrogen bonds are extremely similar in both conformations. For further discussion of hydrogen bond geometry (atomic distances and angles) and the interpretation of scalar coupling constants (1JNH, 2hJPH, 3hJPN), only Boltzmann averaged values over two orientations and the isopropyl rotation were considered.

Figure 6.

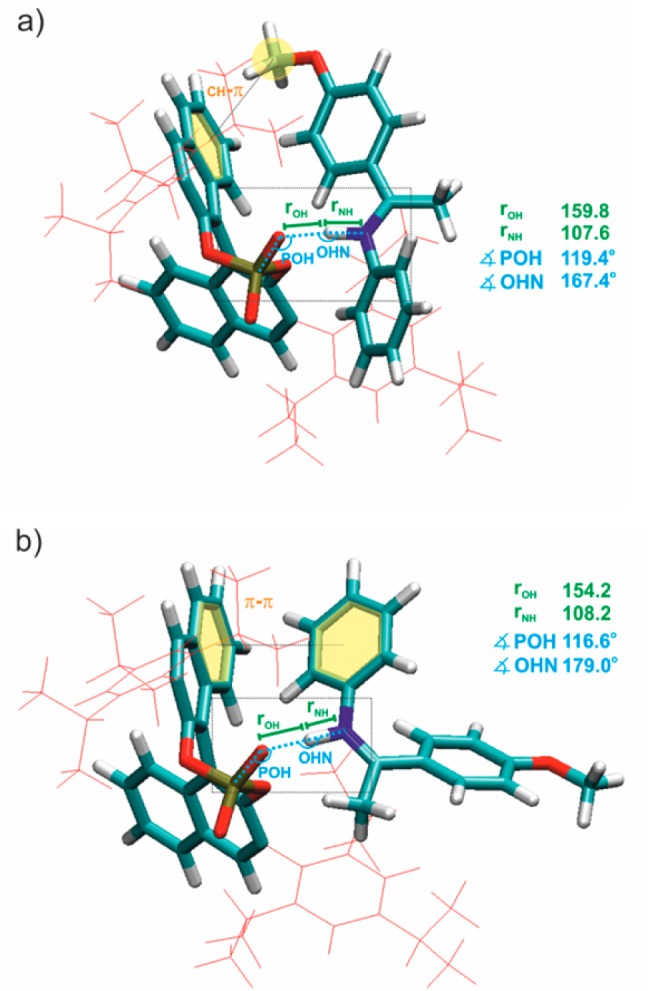
Figure 6

Open in a new tab

Global minima of (R)-TRIP·5 in CD2Cl2 at 180 K (ε = 16.20), optimized at DFT level of theory (for computational details see Supporting Information); (a) (R)-TRIP·5E; (b) (R)-TRIP·5Z.

Potential Surface of the Hydrogen Bond Complexes

The theoretical calculations showed that the alteration of hydrogen bond situation strongly depends on the dielectric medium, in which the complex is simulated (Figure 7a–c). In the gas phase, ion pair- and neutral hydrogen bond-complexes are true minima (Figure 7a). Without any solvent correction, the latter is thermally more stable (ca. 8–13 kJ/mol) and therefore almost exclusively populated. However, the solvent correction at 180 K (ε = 16.20) to the gas phase structure (nonrelaxed) leads to a significant stabilization of the charge separated contact ion pair minima and inverts the population (Figure 7b).

Figure 7.

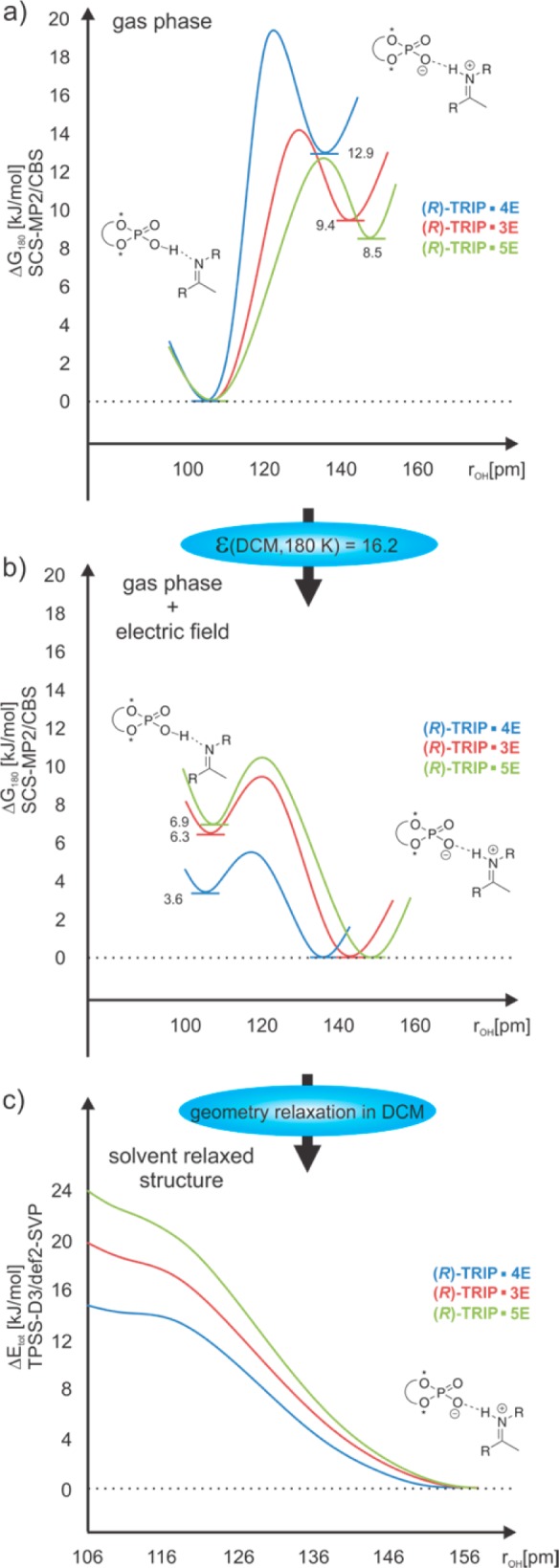
Figure 7

Open in a new tab

(a) Schematic gas phase potential energy profiles of (R)-TRIP/imine complexes. (b) Schematic solvent corrected (in DCM 180 K, nonrelaxed) potential energy profiles of (R)-TRIP/imine complexes. (c) Relaxed scan over rOH of the complexes in DCM continuum at 180 K (ε = 16.20).

After the relaxation in the continuum, the minimum of the neutral hydrogen bonded complex even disappeared and the potential surface becomes an asymmetric single well potential (Figure 7c).47 Furthermore, weaker hydrogen bonds are calculated indicated by longer rOH and rNO as well as shorter rNH values (for rOH and rNH see Figure 8). However, the calculated atomic distances of the solvent relaxed structures are still in the range of strong OHN hydrogen bonds (rNO ≤ 265 pm, for details see Supporting Information).31

From the experimental data available, it is difficult to assess whether the second minimum of the neutral hydrogen bond really disappears in solution at 180 K. The most indicative parameter for a single well or double well potential is the deuterium isotope effect.31,48 For (R)-TRIP·3,5E a small positive isotope effect was measured ((R)-TRIP·3E Δδ(1H–2H, 180 K, CH2Cl2) = 0.15 ppm, ((R)-TRIP·5E Δδ(1H–2H, 180 K, CH2Cl2) = 0.27 ppm, for spectra see Supporting Information), while a slightly larger isotopic effect was obtained for (R)-TRIP·4E (Δδ(1H–2H, 180 K, CH2Cl2) ∼ 0.36 ppm). The slightly larger value for (R)-TRIP·4E could be caused by a flattened shape of the potential surface along the proton transfer coordinates and a vibrational motion of the proton near to the flattened surface,30 and is in agreement with its potential energy profile (see Figure 7c). The effects of the flattened surface and the dynamic motion of the proton near to the surface are further supported by the considerable deviation between experimental and theoretical values of 1JNH in (R)-TRIP·4E (see discussion below). Furthermore, complexes with less basic imines and considerable contributions of neutral hydrogen bonds such as (R)-TRIP·7E let expect the existence of double well potentials. Nevertheless, all accessible experimental isotope effects so far are in agreement with an asymmetric single well potential as shown in Figure 7c.48

Validation of Theoretical Models Based on Atomic Distances, 1JNH, and Chemical Shifts

To further validate the applicability of the different theoretical models for the interpretation of the experimental data, next the theoretically calculated atomic distances were compared with those derived from the “Steiner–Limbach correlation” (Figure 8) for the normal case, the predominantly ionic complexes. The calculated distances of the contact ion pairs in the gas phase are very close to the values derived from the “Steiner–Limbach correlation”, which was at first glance very surprising. However, it is known that in the previous work of Limbach and co-workers35,41 the parameters and constants (rOH°, rNH°, bOH, bNH) were fitted with a solid state data set49 and compared to gas phase data.

To circumvent potential systematic offsets connected with indirectly derived NMR parameters, next 1JNH coupling constants as directly measurable values were selected.

Experimental 1JNH values between 68.6 Hz–82.2 Hz indicate the predominant occupation of the ion pair minimum. Therefore, in the following discussion of the theoretical values the limiting case of exclusive population of ion pairs was assumed, i.e., exclusively the values of the contact ion pair minima are considered even in the gas phase. Our results show that using the gas phase structures even for the exclusive interpretation of the ion pairs, the calculated 1JNH values are significant smaller than the directly measured coupling constants (red bars in Figure 9, for details see Supporting Information). By the application of solvent relaxed structures a significant improvement was achieved in the prediction of the 1JNH coupling constants for E and Z complexes of (R)-TRIP·3,5,8 (blue bars in Figure 9).

Figure 9.

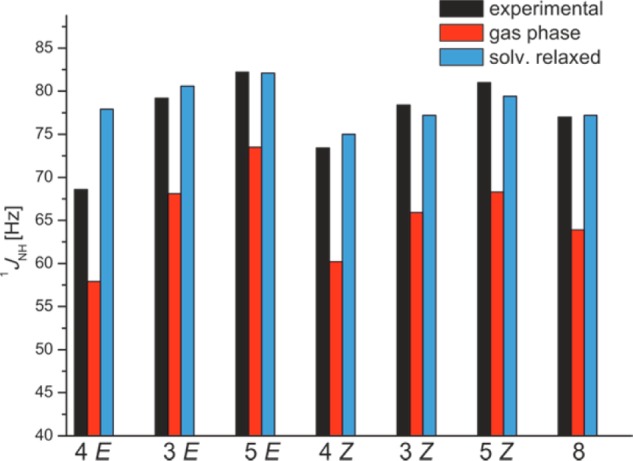
Figure 9

Open in a new tab

Comparison of experimental (black bars) and calculated (blue and red bars) 1JNH values of (R)-TRIP·3,4,5,8 show an excellent agreement between experimental values and calculated values using solvent relaxed structures, with the exception of (R)-TRIP·4E; only ion pair structures are considered in the calculations; values of the E/Z isomers were Boltzmann averaged over the two experimentally observed conformations, see text.

In these cases the absolute deviation between experiment and calculation is mostly marginal and amounts to ∼2 Hz (Figure 9). Therefore, the relaxed structures in the solvent model are considered to represent the experimental condition/observation more realistically and are used for the further discussion. The only significant deviation (8.8 Hz for E) is obtained for (R)-TRIP·4E, which provides the strongest/shortest hydrogen bond due to the electron withdrawing CF3 substituent in the imine 4 (Figure 9). A partial decoupling of the 1JNH due to chemical exchange with the unbound imine would be a potential explanation for the reduced 1JNH values. However, an experiment with 2-fold excess of 4 revealed, that neither the chemical shift nor the observed 1JNH are affected significantly (see Supporting Information). This excludes a significant influence of chemical exchange on the 1JNH under our experimental conditions. (R)-TRIP·4 is the complex with the highest probability of a population of the neutral hydrogen bonded complex (see discussion about the potential above and Figure 7c). Now this reduced 1JNH scalar coupling constant can be an indication for the existence of a second minimum for the neutral hydrogen bonded complexes in solution. The next probable explanation is that the low basicity of 4 leads to a significant delocalization of the proton within the asymmetric single well potential. These dynamic motions of the proton can only be reproduced by dynamic calculation, which would be extremely costly for a system of this size. Both scenarios are in principal possible; however our current interpretation of isotopic effect favors the asymmetric potential picture as depicted in Figure 7c. In summary the application of the Steiner–Limbach correlation based on the chemical shifts and 1JNH coupling constants confirm the formation of strong hydrogen bonds in the (R)-TRIP imine complexes and the predominance of the contact ion pair structure. For (R)-TRIP complexes with highly basic imines theoretical and experimental data indicate an asymmetric single well potential. The comparison of the atomic distances reveals that the classical Steiner–Limbach correlation reproduces the distances of the gas phase structures. However, the comparison of the “direct” observables 1JNH with the different theoretical models demonstrates that the solvent relaxed structures resemble the experimental data the most, which was also corroborated by the analysis of the 1H,15N chemical shifts and NBO50 (for details see Supporting Information). Despite of this substantial improvement, the large deviation between the calculated and experimental values for (R)-TRIP·4E demonstrated somewhat the limit of the applied theoretical treatment, which failed to describe either the correct shape of the potential surface or the dynamic motion of the proton in extreme cases.

The described offset in combination with our theoretical data about the solvent relaxed structures can now be used to introduce a solvent correction term (see eq 6) in the empirical correlation between chemical shifts and atomic distances for phosphoric acid imine complexes.51

graphic file with name ja-2016-092438_m006.jpg 6

The solvent correction term depends implicitly on the experimental condition (e.g., solvent, temperature) and explicitly on the bond order difference (Δp = pOHH – pOHH) from the Steiner–Limbach model. This difference in bond order indicates the strengths of the hydrogen bond, the position in the Steiner–Limbach curve and the sign of the correction term to be applied. By considering the parabolic form of the Steiner–Limbach curve, the correction term should be larger with stronger hydrogen bond character and approaches a maximum with the strongest hydrogen bond. Therefore, Gauss-functions were applied for the correction term (see eq 7 and for fitting procedures Supporting Information).

graphic file with name ja-2016-092438_m007.jpg 7

The constants A, B and C were obtained via fitting to the available theoretical data (for data see Supporting Information). Accordingly, the corrected empirical values are now very close to the predicted values in the solution phase (see Figure 8). A first cross validation of this solvent correction term derived from the TRIP complexes on a binary complex using another catalyst ((R)-3,3′-Bis(3,5-bis(trifluoromethyl)phenyl)-1,1′-binaphthyl-2,2′-diyl hydrogen phosphate)9 and 3E provided only marginal offsets (deviation without correction: 2.1 pm for NH bond distance, respectively 6.1 pm for OH bond distance; with correction: 0.7 pm for NH bond distance, respectively 2.1 pm for OH bond distance) between the empirical value and the solvent relaxed structure. This suggest a general applicability to phosphoric acid imines complexes, however the full potential will be subject to further studies.

Analysis of Hydrogen Bond Geometry Based on 2hJPH and 3hJPN.

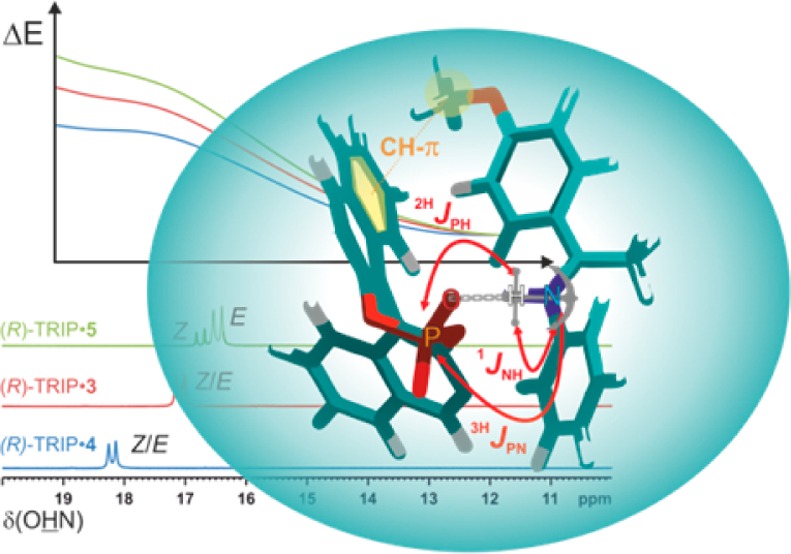
Trans-hydrogen bond scalar couplings can serve as valuable sensors for changes in hydrogen bond geometry.22 Therefore, next calculated and measured 2hJPH and 3hJPN scalar couplings52 (Figure 1b) were interpreted to get insight into the geometrical properties of the hydrogen bonds in (R)-TRIP imine complexes. In all calculated (R)-TRIP imine structures nearly linear hydrogen bonds were found (see Figure 6 for (R)-TRIP·5), which is expected for strong hydrogen bonds.1 The calculated angles (POH, OHN) and dihedral angles (α) vary only insignificantly between gas phase and solvent relaxed structures. Furthermore, there are only minor deviations between the imines 3–5 and 8, regarding the POH and OHN hydrogen bond angles (for data, see Supporting Information). The 2hJPH couplings between the NH protons and 31P were measured qualitatively by 1D/2D 1H,31P-HMBC spectra and 3D HNPO spectra and quantitatively by spin echo difference experiments as reported previously53 (for spectra and pulse sequences, see Supporting Information). The sign of the 2hJPH and 3hJPN scalar couplings was not determined and therefore only absolute values are stated. Figure 10 shows a plot of the 1H chemical shift of the hydrogen bonded proton δ(OHN) against the experimental 2hJPH coupling constants.

Figure 10.

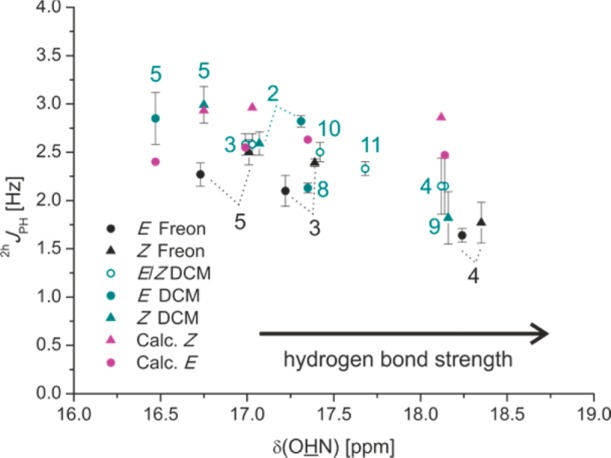
Figure 10

Open in a new tab

Plot of 2hJPH values versus δ(OHN); experimental values black and cyan (180 K, except (R)-TRIP·8 200 K and (R)-TRIP·4 170 K); calculated, Boltzmann averaged values of (R)-TRIP·3,4,5,8 magenta.

With increasing δ(OHN) a continuous decrease of the 2hJPH is observed (from 2.99 ± 0.19 Hz for (R)-TRIP·5Z, CD2Cl2, 180 K to 1.64 ± 0.07 Hz for (R)-TRIP·4E, 170 K, Freon). In general, slightly smaller values were measured for the complexes in Freon mixtures, which is in agreement with the higher 1H chemical shifts indicating a stronger hydrogen bond. From protein nucleotide complexes54 and their model systems22 the 2hJPH angle coupling constant is known to depend on rNO and the POH angle. Considering the small variance of the POH-angles in our system ((R)-TRIP·3–5,8E 117°–118° and (R)-TRIP·3–5,8Z 115°–117°), the observed decrease of the 2hJPH should be connected with the increasing hydrogen bond strength and therefore decreasing rOH (see above) and rNO (see Supporting Information). In the study of Brüschweiler et al. increasing 2hJPH values are predicted for decreasing rNO. In our (R)-TRIP imine systems the opposite trend is observed. Therefore, the 2hJPH coupling constants of (R)-TRIP·3–5,8 in CD2Cl2 were calculated for the ion pair minima. First of all, the calculated 2hJPH values successfully reproduce the order of the magnitude of the experimental data (Figure 10). However, the trend in the experimental data, i.e., decreasing 2hJPH with increasing hydrogen bond strength could not be found. Considering the discussion about the 1JNH scalar coupling constants of (R)-TRIP·4, any effect of a population of the neutral hydrogen bond or vibrational effects should also affect the corresponding 2hJPH data. The calculations reveal a negative sign for 2hJPH coupling constants similar to previous studies of protein nucleotide complexes22,54 and a positive sign for 2hJPH for the neutral hydrogen bonded complex. Thus, both a small population of the neutral hydrogen bonded complex as well as vibrations of the proton toward oxygen should result in reduced scalar coupling values as detected for (R)-TRIP·4.

Next the 3hJPN coupling constants were investigated to get insight into the geometric properties regarding the dihedral angles POHN. The experimental 3hJPN coupling constants are in the range of ∼3.25–2.50 Hz (see Figure 11).

Figure 11.

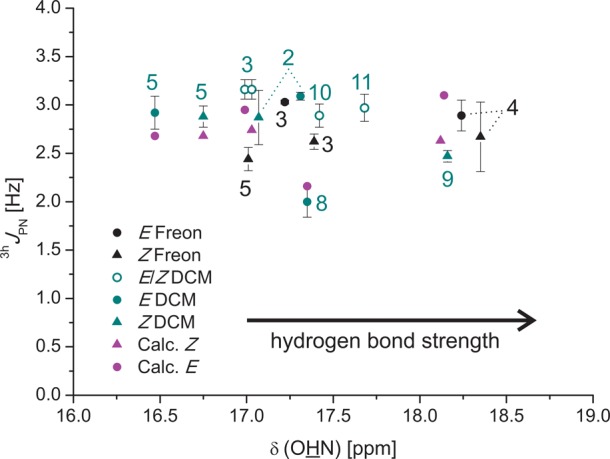
Figure 11

Open in a new tab

Plot of 2hJPH values versus δ(OHN); experimental values black and cyan (180 K, except (R)-TRIP·8 200 K and (R)-TRIP·4 170 K); calculated, Boltzmann averaged values of (R)-TRIP·3,4,5,8 magenta.

The absolute magnitude of the 2hJPH and 3hJPN coupling constants is significantly larger than that reported by Mishima et al. for weak hydrogen bonds providing similar POH angles of around 107° to 120°.53 This can be rationalized by the different electron density distribution due to the strong and partially covalent hydrogen bond character in (R)-TRIP imine systems.1,45,46 Also for 3hJPN the calculations were able to reproduce the order of the magnitude and revealed a negative sign for 3hJPN. However, both experimental and calculated 3hJPN values lack a clear dependence on the 1H chemical shifts (Figure 11). Similar independence of the hydrogen bond strength was observed previously for 2hJFN in HF collidine complexes.36 From the calculated structures dihedral angles POHN around 90° ± 15° are predicted (see Supporting Information). Exactly for this range of dihedral angles the smallest absolute values and smallest variations of 3hJPN are expected. Additionally, the OHN-angles are very linear (165°–175° for (R)-TRIP E-imine and 170°–180° for (R)-TRIP Z-imine; see Supporting Information for the complete data). Thus, the slight decrease of the 2hJPH and the stability of 3hJPN confirm the marginal variance of the hydrogen bond geometry found in the calculations.

Conclusion

Thorough NMR and computational investigations of the activation of imine substrates via hydrogen bonding by (R)-TRIP, a catalyst with broad applicability in Brønsted acid catalysis, were conducted for the first time. A strong hydrogen bond constitutes the dominant interaction between (R)-TRIP and imine. The analysis of its 1H, 15N chemical shifts as well as its 1JNH values reveals mostly a predominantly ionic character of the hydrogen bonded complexes. For (R)-TRIP·7E, including the imine with the lowest basicity, also contributions of neutral hydrogen bonds were found. Individual atomic distances of the hydrogen bonds were elucidated by applying a “Steiner–Limbach correlation” based on 1H, 15N chemical shifts, which are in good agreement with the gas phase structures from the DFT based calculations, therefore a solvent correction term was introduced. Indeed, a comparison with 1JNH values as direct experimental data demonstrates the solvent relaxed structures to describe the system more realistic. The continuous shift of the proton by variation of the imine basicity is indicative for a strong hydrogen bond character. Theoretical calculations of the potential surface reveal a major population of the neutral hydrogen bond complex in the gas phase and an inverted population in solution phase. Moreover, in (R)-TRIP·4E/Z, the complex with the strongest hydrogen bond calculated, the comparison between theoretical and experimental coupling constants suggests a potential participation of neutral hydrogen bond complexes or a strongly delocalized hydrogen atom due to vibrational motion, which cannot be described by our theoretical treatment. For the weaker but more neutral (R)-TRIP·7E complex even a double well potential is expected. The magnitude of deuterium isotope effect corroborates an asymmetric single well potential for (R)-TRIP·3–5E complexes. Furthermore, the trans hydrogen scalar couplings 3hJPN and 2hJPH were detected via 1H,31P-HMBC and 3D-HNPO experiments and quantified via spin echo experiments. These experimental values in combination with structure and coupling constant calculations give a detailed insight into the spatial arrangement of the hydrogen bond atoms. Nearly linear hydrogen bonds are formed with minimal variations within one structural type independent of the imine investigated. That means, the variation of the steric and electronic properties of aromatic imines does not affect the structure as well as the hydrogen bond geometry. Thus, in the (R)-TRIP imine complexes investigated, the hydrogen bond acts as structural anchor in the precatalytic complex.

Preliminary results showed that the product formation is faster with stronger hydrogen bonds in the precatalytic (R)-TRIP imine complex. Further investigations about the formation, stability and the hydrogen bond interaction of ternary complexes are currently conducted.

Acknowledgments

The authors are grateful to Dr. Ilya Shenderovich for the extensive discussions about hydrogen bonds. Financial Support was provided by the European Research Council (ERC-CoG 614182 − IonPairsAtCatalysis).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.6b09243.

  • Procedures for the preparation of 15N enriched imines and samples. Complete set of 1H, 15N and 31P spectra of the investigated Brønsted acid imine complexes. E/Z ratios of the (R)-TRIP imine complexes. Detailed description of the correlation of NMR parameters with the valence bond orders and the atomic distances. Employed pulse sequences for qualitative and quantitative detection of 2hJPH and 3hJPN coupling constants. 1D/2D 1H,31P-HMBC and 3D-HNPO spectra for measuring magnetization transfer via 2hJPH or 3hJPN respectively. (PDF)

The authors declare no competing financial interest.

Supplementary Material

ja6b09243_si_001.pdf (10.9MB, pdf)

References

  1. Steiner T. Angew. Chem., Int. Ed. 2002, 41, 48.. [DOI] [PubMed] [Google Scholar]
  2. Taylor M. S.; Jacobsen E. N. Angew. Chem., Int. Ed. 2006, 45, 1520. 10.1002/anie.200503132. [DOI] [PubMed] [Google Scholar]
  3. Mahlau M.; List B. Angew. Chem., Int. Ed. 2013, 52, 518. 10.1002/anie.201205343. [DOI] [PubMed] [Google Scholar]
  4. Phipps R. J.; Hamilton G. L.; Toste F. D. Nat. Chem. 2012, 4, 603. 10.1038/nchem.1405. [DOI] [PubMed] [Google Scholar]
  5. Uraguchi D.; Terada M. J. Am. Chem. Soc. 2004, 126, 5356. 10.1021/ja0491533. [DOI] [PubMed] [Google Scholar]
  6. Akiyama T.; Itoh J.; Yokota K.; Fuchibe K. Angew. Chem., Int. Ed. 2004, 43, 1566. 10.1002/anie.200353240. [DOI] [PubMed] [Google Scholar]
  7. Zamfir A.; Schenker S.; Freund M.; Tsogoeva S. B. Org. Biomol. Chem. 2010, 8, 5262. 10.1039/c0ob00209g. [DOI] [PubMed] [Google Scholar]
  8. Tang W.; Johnston S.; Iggo J. a; Berry N. G.; Phelan M.; Lian L.; Bacsa J.; Xiao Angew. Chem., Int. Ed. 2013, 52, 1668. 10.1002/anie.201208774. [DOI] [PubMed] [Google Scholar]
  9. Rueping M.; Sugiono E.; Azap C.; Theissmann T.; Bolte M. Org. Lett. 2005, 7, 3781. 10.1021/ol0515964. [DOI] [PubMed] [Google Scholar]
  10. Rueping M.; Azap C.; Sugiono E.; Theissmann T. Synlett 2005, 2367. 10.1055/s-2005-872251. [DOI] [PubMed] [Google Scholar]
  11. Hoffmann S.; Seayad A. M.; List B. Angew. Chem. 2005, 117, 7590. 10.1002/ange.200503062. [DOI] [PubMed] [Google Scholar]
  12. Storer R. I.; Carrera D. E.; Ni Y.; MacMillan D. W. C. J. Am. Chem. Soc. 2006, 128, 84. 10.1021/ja057222n. [DOI] [PubMed] [Google Scholar]
  13. Simón L.; Goodman J. M. J. Am. Chem. Soc. 2008, 130, 8741. 10.1021/ja800793t. [DOI] [PubMed] [Google Scholar]
  14. Marcelli T.; Hammar P.; Himo F. Chem. - Eur. J. 2008, 14, 8562. 10.1002/chem.200800890. [DOI] [PubMed] [Google Scholar]
  15. Marcelli T.; Hammar P.; Himo F. Adv. Synth. Catal. 2009, 351, 525. 10.1002/adsc.200800613. [DOI] [Google Scholar]
  16. Simón L.; Goodman J. M. J. Org. Chem. 2011, 76, 1775. 10.1021/jo102410r. [DOI] [PubMed] [Google Scholar]
  17. Reid J. P.; Simón L.; Goodman J. M. Acc. Chem. Res. 2016, 49, 1029. 10.1021/acs.accounts.6b00052. [DOI] [PubMed] [Google Scholar]
  18. Gridnev I. D.; Kouchi M.; Sorimachi K.; Terada M. Tetrahedron Lett. 2007, 48, 497. 10.1016/j.tetlet.2006.11.017. [DOI] [Google Scholar]
  19. Fleischmann M.; Drettwan D.; Sugiono E.; Rueping M.; Gschwind R. M. Angew. Chem., Int. Ed. 2011, 50, 6364. 10.1002/anie.201101385. [DOI] [PubMed] [Google Scholar]
  20. Kim H.; Sugiono E.; Nagata Y.; Wagner M.; Bonn M.; Rueping M.; Hunger ACS Catal. 2015, 5, 6630. 10.1021/acscatal.5b01694. [DOI] [Google Scholar]
  21. Greindl J.; Hioe J.; Sorgenfrei N.; Morana F.; Gschwind R. M. J. Am. Chem. Soc. 2016, 10.1021/jacs.6b09244. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Czernek J.; Brüschweiler R. J. Am. Chem. Soc. 2001, 123, 11079. 10.1021/ja011618r. [DOI] [PubMed] [Google Scholar]
  23. Tao J.; Perdew J. P.; Staroverov V. N.; Scuseria G. E. Phys. Rev. Lett. 2003, 91, 146401. 10.1103/PhysRevLett.91.146401. [DOI] [PubMed] [Google Scholar]
  24. Grimme S.; Antony J.; Ehrlich S.; Krieg H. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  25. Marenich A. V.; Cramer C. J.; Truhlar D. G. J. Phys. Chem. B 2009, 113, 6378. 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
  26. Grimme S. J. Chem. Phys. 2003, 118, 9095. 10.1063/1.1569242. [DOI] [Google Scholar]
  27. Kutzelnigg W.; Fleischer U.; Schindler M.. Interpretation of NMR Chemical Shifts and Magnetic Susceptibilities; Springer-Verlag: Heidelberg, 1990; Vol. 23. [Google Scholar]
  28. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09, Revision D.01; Gaussian, Inc., Wallingford CT, 2009.
  29. Neese F. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73. 10.1002/wcms.81. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Frey P. a. Magn. Reson. Chem. 2001, 39, 190. 10.1002/mrc.953. [DOI] [Google Scholar]
  31. Frey P. a; Whitt S. a; Tobin J. B. Science 1994, 264, 1927. 10.1126/science.7661899. [DOI] [PubMed] [Google Scholar]
  32. Günther H.NMR Spectroscopy Basic Principles, Concepts, and Applications in Chemistry, 3rd ed.; Wily-VCH Verlag GmbH& Co. KGaA: Weinheim, 2013. [Google Scholar]
  33. Olah G. A.; Kreienbuh P. J. Am. Chem. Soc. 1967, 15, 4756. 10.1021/ja00994a033. [DOI] [Google Scholar]
  34. Olah G. A.; Donovan D. J. J. Org. Chem. 1978, 43, 860. 10.1021/jo00399a013. [DOI] [Google Scholar]
  35. Sharif S.; Denisov G. S.; Toney M. D.; Limbach H. J. Am. Chem. Soc. 2007, 129, 6313. 10.1021/ja070296+. [DOI] [PubMed] [Google Scholar]
  36. Golubev N. S.; Shenderovich I. G.; Smirnov S. N.; Denisov G. S.; Limbach H.-H. Chem. - Eur. J. 1999, 5, 492.. [DOI] [Google Scholar]
  37. Shenderovich I. G.; Burtsev A. P.; Denisov G. S.; Golubev N. S.; Limbach H.-H. Magn. Reson. Chem. 2001, 39, 91. 10.1002/mrc.938. [DOI] [Google Scholar]
  38. Ishikita H.; Saito K. J. R. Soc., Interface 2014, 11, 20130518. 10.1098/rsif.2013.0518. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Reichhardt C.; Welton T. In Solvents and Solvent Effects in Organic Chemistry; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, 2011; pp 136–138. [Google Scholar]
  40. Anderson K. M.; Esadze A.; Manoharan M.; Brüschweiler R.; Gorenstein D. G.; Iwahara J. J. Am. Chem. Soc. 2013, 135, 3613. 10.1021/ja312314b. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Limbach H.-H.; Pietrzak M.; Sharif S.; Tolstoy P. M.; Shenderovich I. G.; Smirnov S. N.; Golubev N. S.; Denisov G. S. Chem. - Eur. J. 2004, 10, 5195. 10.1002/chem.200400212. [DOI] [PubMed] [Google Scholar]
  42. Reichhardt C.; Welton T. In Solvents and Solvent Effects in Organic Chemistry; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, 2011; pp 417–422. [Google Scholar]
  43. Benedict H.; Shenderovich I. G.; Malkina O. L.; Malkin V. G.; Denisov G. S.; Golubev N. S.; Limbach H. J. Am. Chem. Soc. 2000, 122, 1979. 10.1021/ja9907461. [DOI] [Google Scholar]
  44. Limbach H.-H.; Pietrzak M.; Benedict H.; Tolstoy P. M.; Golubev N. S.; Denisov G. S. J. Mol. Struct. 2004, 706, 115. 10.1016/j.molstruc.2004.03.006. [DOI] [Google Scholar]
  45. Grabowski S. J. Chem. Rev. 2011, 111, 2597. 10.1021/cr800346f. [DOI] [PubMed] [Google Scholar]
  46. Grabowski S. J.; Sokalski W. A.; Dyguda E.; Leszczyn J. J. Phys. Chem. B 2006, 110, 6444. 10.1021/jp0600817. [DOI] [PubMed] [Google Scholar]
  47. The y-axis in Figure 7c has a scale in total energy due to the vanishing neutral hydrogen bond minima (no stationary point can be found; hence, no vibrational analysis can be performed).
  48. Smirnov S. N.; Golubev N. S.; Denisov G. S.; Benedict H.; Schah-Mohammedi P.; Limbach H.-H. J. Am. Chem. Soc. 1996, 118, 4094. 10.1021/ja953445+. [DOI] [PubMed] [Google Scholar]
  49. Steiner T. J. Phys. Chem. A 1998, 102, 7041. 10.1021/jp981604g. [DOI] [Google Scholar]
  50. Glendening E. D.; Badenhoop J. K.; Reed A. E.; Carpenter J. E.; Bohmann J. A.; Morales C. M.; Landis C. R.; Weinhold F.. NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, 2013.
  51. The adjustment of the constants employed in eqs 4 and 5 (bXH° and rXH°) to our theoretical data (see Supporting Information) is not suitable, because it impairs the weak neutral hydrogen bonded systems.
  52. For the description of the trans-hydrogen bond scalar couplings the definition of Dingley et al. is used. The abbreviation 3hJPN stands for scalar coupling between 15N and 31P over three bonds including a hydrogen bond and 2hJPH for scalar coupling between a 1H and 31P over two bonds. For reference, see:Dingley A. J.; Cordier F.; Grzesiek S. Concepts Magn. Reson. 2001, 13, 103–127. . [DOI] [Google Scholar]
  53. Federwisch G.; Kleinmaier R.; Drettwan D.; Gschwind R. M. J. Am. Chem. Soc. 2008, 130, 16846. 10.1021/ja807042u. [DOI] [PubMed] [Google Scholar]
  54. Mishima M.; Hatanaka M.; Shigeyuki Y.; Takahisa I.; Wälchli M.; Ito Y.; Shirakawa M. J. Am. Chem. Soc. 2000, 122, 5883. 10.1021/ja000005w. [DOI] [Google Scholar]
  55. Detering C.; Tolstoy P. M.; Golubev N. S.; Denisov G. S.; Limbach H. Dokl. Phys. Chem. 2001, 379, 191. 10.1023/A:1019290114622. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja6b09243_si_001.pdf (10.9MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES