Robust Estimation of Transition Matrices in High Dimensional Heavy-tailed Vector Autoregressive Processes

Abstract

Gaussian vector autoregressive (VAR) processes have been extensively studied in the literature. However, Gaussian assumptions are stringent for heavy-tailed time series that frequently arises in finance and economics. In this paper, we develop a unified framework for modeling and estimating heavy-tailed VAR processes. In particular, we generalize the Gaussian VAR model by an elliptical VAR model that naturally accommodates heavy-tailed time series. Under this model, we develop a quantile-based robust estimator for the transition matrix of the VAR process. We show that the proposed estimator achieves parametric rates of convergence in high dimensions. This is the first work in analyzing heavy-tailed high dimensional VAR processes. As an application of the proposed framework, we investigate Granger causality in the elliptical VAR process, and show that the robust transition matrix estimator induces sign-consistent estimators of Granger causality. The empirical performance of the proposed methodology is demonstrated by both synthetic and real data. We show that the proposed estimator is robust to heavy tails, and exhibit superior performance in stock price prediction.

1. Introduction

Vector autoregressive models are widely used in analyzing multivariate time series. Examples include financial time series (Tsay, 2005), macroeconomic time series (Sims, 1980), gene expression series (Fujita et al., 2007; Opgen-Rhein & Strimmer, 2007), and functional magnetic resonance images (Qiu et al., 2015).

Let X₁, …, X_T ∈ ℝ^d be a stationary multivariate time series. We consider VAR models¹ such that

$${\mathit{X}}_t=\mathbf{A}{\mathit{X}}_{t-1}+{\mathit{E}}_t\text{ for }t=2,\dots ,T,$$

where A is the transition matrix, and E₂, …, E_T are latent innovations. The transition matrix characterizes the dependence structure of the VAR process, and plays a fundamental role in forecasting. Moreover, the sparsity pattern of the transition matrix is often closely related to Granger causality. In this paper, we focus on estimating the transition matrix in high dimensional VAR processes.

VAR models have been extensively studied under the Gaussian assumption. The Gaussian VAR model assumes that the latent innovations are i.i.d. Gaussian random vectors, and are independent from past observations (Lütkepohl, 2007). Under this model, there is vast literature on estimating the transition matrix under high dimensional settings. These estimators can be categorized into regularized estimators and Dantzig-selector-type estimators. The former can be formulated by

$${\mathbf{Â}}^{\text{reg}}≔\underset{\mathbf{M}\in {ℝ}^{d\times d}}{\text{argmin}}l(\mathbf{Y}-\mathbf{M}\mathbf{X})+P_{\rho }(\mathbf{M}),$$ (1.1)

where Y ≔ (X₁, …, X_{T − 1}) ∈ ℝ^d×(T−1), X ≔ (X₂, …, X_T) ∈ ℝ^d×(T−1), l(·) is a loss function, and P_ρ(·) is a penalty function with penalty parameter ρ. Common choices of the loss function include least squares loss and negative log-likelihood (Hamilton, 1994). For the penalty function, various ℓ₁ penalties (Wang et al., 2007; Hsu et al., 2008; Shojaie & Michailidis, 2010) and ridge penalty (Hamilton, 1994) are widely used. Theoretical properties of ℓ₁ penalized estimators are studied in Narki & Rinaldo (2011), Song & Bickel (2011), and Basu & Michailidis (2013).

In parallel to the penalized minimum loss estimators, Han & Liu (2013) proposed a Dantzig-selector-type estimator, which is formulated as the solution to a linear programming problem. In contrast to the ℓ₁ regularized estimators, consistency of the Dantzig-selector-type estimator do not rely on restricted eigenvalue conditions. These conditions do not explicitly account for the effect of serial dependence. Moreover, the Dantzig-selector-type estimator weakens the sparsity assumptions required by the ℓ₁ regularized estimators.

Although extensively studied in the literature, Gaussian VAR models are restrictive in their implications of light tails. Heavy-tailed time series frequently arise in finance, macroeconomics, signal detection, and statistical physics, to name just a few (Feldman & Taqqu, 1998). For analyzing these data, more flexible models and robust estimators are desired.

In this paper, we develop a unified framework for modeling and estimating heavy-tailed VAR processes. In particular, we propose an elliptical VAR model that allows for heavy-tailed processes. The elliptical VAR model covers the Gaussian VAR model as a special case. Under this model, we show that the transition matrix is closely related to quantile-based scatter matrices. The relation serves as a quantile-based counterpart of the Yule-Walker equation² (Lütkepohl, 2007). Motivated by this relation, we propose a quantile-based robust estimator of the transition matrix. The estimator falls into the category of Dantzig-selector-type estimators, and enjoys similar favorable properties as the estimator in Han & Liu (2013). We investigate the asymptotic behavior of the estimator in high dimensions, and show that although set in a more general model, it achieves the same rates of convergence as the Gaussian-based estimators. The effect of serial dependence is also explicitly characterized in the rates of convergence.

As an application of the framework developed in this paper, we investigate Granger causality estimation under the elliptical VAR process. We show that just as in Gaussian VAR models, Granger causality relations are also captured by the sparsity patterns of the transition matrix. The robust transition matrix estimator developed in this paper induces sign-consistent estimators of these relations.

2. Background

In this section, we introduce the notation employed in this paper, and provide a review on elliptical distributions and robust scales. Elliptical distributions provide a basis for our model, while robust scales motivate our methodology.

2.1. Notation

Let v = (υ₁, …, υ_d)^⊤ be a d-dimensional real vector, and M = [M_jk] ∈ ℝ^{d₁ × d₂} be a d₁ × d₂ matrix with M_jk as the (j, k) entry. Denote by v_I the subvector of v whose entries are index by a set I ⊂ {1, …, d}. Similarly, denote by M_U,V the submatrix of M whose entries are indexed by U ⊂ {1, …, d₁} and V ⊂ {1, …, d₂}. Let M_U,* = M_{U,{1, …, d2}}. For 0 < q < ∞, we define the vector ℓ_q norm of v as ${\Vert \mathbf{v}\Vert }_q≔{({\sum }_{j=1}^d|{\upsilon }_j|)}^{1/q}$, and the vector ℓ_∞ norm of v as ${\Vert \mathbf{v}\Vert }_{\infty }≔{\text{max}}_{j=1}^d|{\upsilon }_j|$. Let the matrix ℓ_max norm of M be ‖M‖_max ≔ max_jk |M_jk|, the matrix ℓ_∞ norm be ${\Vert \mathbf{M}\Vert }_{\infty }≔{\text{max}}_j{\sum }_{k=1}^d|{\mathbf{M}}_{jk}|$, and the Frobenius norm be ${\Vert \mathbf{M}\Vert }_F≔\sqrt{{\sum }_{jk}{M}_{jk}^2}$. Let X = (X₁, …, X_d)^⊤ and Y = (Y₁, …, Y_d)^⊤ be two random vectors. We write $\mathit{X}\stackrel{\mathrm{d}}{=}\mathit{Y}$ if X and Y are identically distributed. We use 0, 1, … to denote vectors with 0, 1, … at every entry.

2.2. Elliptical Distribution

Definition 2.1 (Fang et al. (1990))

A random vector X ∈ ℝ^d follows an elliptical distribution with location μ ∈ ℝ^d and scatter S ∈ ℝ^d×d if and only if there exists a nonnegative random variable ξ ∈ ℝ, a rank k matrix R ∈ ℝ^d×k with S = RR^⊤, a random vector U ∈ ℝ^k independent of ξ and uniformly distributed in the k dimensional sphere, 𝕊^k−1, such that

$$\mathit{X}\stackrel{\mathrm{d}}{=}\mathit{\mu }+\xi \mathbf{R}\mathit{U}.$$ (2.1)

In this case, we denote X ~ EC_d(μ, S, ξ). S is called the scatter matrix, and ξ is called the generating variate.

Remark 2.2

(2.1) is often referred to as the stochastic representation of the elliptical random vector X. Of note, by Theorem 2.3 in Fang et al. (1990) and the proof of Theorem 1 in Cambanis et al. (1981), Definition 2.1 is equivalent if we replace “$\stackrel{\mathrm{d}}{=}$” with simply “=”.

Proposition 2.3 (Theorems 2.15 and 2.16 in Fang et al. (1990))

Suppose X ~ EC_d(μ, S, ξ) and rank(S) = k. Let B ∈ ℝ^p×d be a matrix and ν ∈ ℝ^p be a vector. Denote l = rank(BSB^⊤). Then, we have

$$\mathit{\nu }+\mathbf{B}\mathit{X}~\mathrm{E}{\mathrm{C}}_p(\mathit{\nu }+\mathbf{B}\mathit{\mu },\mathbf{B}\mathbf{S}{\mathbf{B}}^{\top },\xi \sqrt{B}),$$

where B ~ Beta(l/2, (k−l)/2) follows a Beta distribution if k > l, and B = 1 if k = l.

2.3. Robust Scales

Let X ∈ ℝ be a random variable with a sequence of observations X₁, …, X_T. Denote F as the distribution function of X. For a constant q ∈ [0, 1], we define the q-quantiles of X and ${\{X_t\}}_{t=1}^T$ to be

$$Q(X;q)=Q(F;q)≔\text{inf}\{x:\mathbb{P}(X\le x)\ge q\},$$

$$\hat{Q}({\{X_t\}}_{t=1}^T;q)≔X^{(k)}\text{ where }k=\text{min}\{t:\frac{t}{T}\ge q\}.$$

Here X⁽¹⁾ ≤ ⋯ ≤ X^(T) are the order statistics of the sample ${\{X_t\}}_{t=1}^T$. We say Q(X; q) is unique if there exists a unique x such that ℙ(X ≤ x) = q. We say $\hat{Q}({\{X_t\}}_{t=1}^T;q)$ is unique if there exists a unique $X\in {\{X_t\}}_{t=1}^T$ such that X = X^(k). Following Rousseeuw & Croux (1993), we define the population and sample quantile-based scales as

$${\sigma }^{\mathrm{Q}}(X)≔Q(|X-\tilde{X}|;1/4),$$ (2.2)

$${\hat{\sigma }}^{\mathrm{Q}}({\{X_t\}}_{t=1}^T)≔\hat{Q}({\{|X_s-X_t|\}}_{1\le s\le t\le T};1/4),$$

where X̃ is an independent copy of X. ${\hat{\sigma }}^{\mathrm{Q}}({\{X_t\}}_{t=1}^T)$ can be computed using O(T log T) time and O(T) storage (Rousseeuw & Croux, 1993).

3. Model

In this paper, we model the time series of interest by an elliptical VAR process.

Definition 3.1

A sequence of observations X₁, …, X_T ∈ ℝ^d is an elliptical VAR process if and only if the following conditions are satisfied:

1. X₁, …, X_T follow a lag-one VAR process

   $${\mathit{X}}_t=\mathbf{A}{\mathit{X}}_{t-1}+{\mathit{E}}_t,\mathit{\text{ for }}t=2,\dots ,T,$$ (3.1)

   where A ∈ ℝ^d×d is the transition matrix, and E₂, …, E^T ∈ ℝ^d are latent innovations.
2. ${\{{({\mathit{X}}_t^{\top },{\mathit{E}}_{t+1}^{\top })}^{\top }\}}_{t=1}^{T-1}$ are stationary and absolutely continuous elliptical random vectors:

   $$\left(\begin{array}{c}\hfill {\mathit{X}}_t\hfill \\ \hfill {\mathit{E}}_{t+1}\hfill \end{array}\right)~\mathrm{E}{\mathrm{C}}_{2d}(\mathbf{0},(\begin{array}{cc}\hfill \mathbf{\Sigma }\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{\Psi }\hfill \end{array}),\xi ),$$ (3.2)

   where Σ and Ψ are positive definite matrices, and ξ > 0 with probability 1.

Remark 3.2

The elliptical VAR process in Definition 3.1 can be generated by an iterative algorithm following Rémillard et al. (2012). In detail, by the property of elliptical distributions, the density function of ${({\mathit{X}}_t^{\top },{\mathit{E}}_{t+1}^{\top })}^{\top }$ can be written by $h(\mathbf{x},\mathbf{e})=1/\sqrt{|\mathbf{\Sigma }||\mathbf{\Psi }|}g({\mathbf{x}}^{\top }{\mathbf{\Sigma }}^{-1}\mathbf{x}+{\mathbf{e}}^{\top }{\mathbf{\Psi }}^{-1}\mathbf{e})$ for some function g, and the density function of X_t and the conditional density function of E_t+1 given X_t can be written by

$$h_1(\mathbf{x})=\frac{1}{\sqrt{|\mathbf{\Sigma }|}}{g}_1({\mathbf{x}}^{\top }{\mathbf{\Sigma }}^{-1}\mathbf{x})$$

$$\text{and }{h}_2(\mathbf{e}|\mathbf{x})=\frac{1}{\sqrt{|\mathbf{\Psi }|}}{g}_2({\mathbf{e}}^{\top }{\mathbf{\Psi }}^{-1}\mathbf{e}),$$

where g₁ and g₂ are defined by

$$g_1(r)={\int }_{{ℝ}^d}g({\Vert \mathbf{z}\Vert }_2^2+r)d\mathbf{z}\text{ and }{g}_2(r)=\frac{g(r+{\mathbf{x}}^{\top }{\mathbf{\Sigma }}^{-1}\mathbf{x})}{g_1({\mathbf{x}}^{\top }{\mathbf{\Sigma }}^{-1}\mathbf{x})}.$$

The elliptical VAR process X₁, …, X_T can be generated by the following algorithm:

1. Generate X₁ from h₁ (x).

2. For t = 2, …, T,

   1. generate E_t from h₂(e | X_t−1);
   2. set X_t = AX_t−1 + E_t.

Remark 3.3

By definition, it follows that an elliptical VAR process is a stationary process. A special case of the elliptical VAR process is the Gaussian VAR process. An elliptical VAR process is Gaussian VAR if (3.2) is replaced by

$$\left(\begin{array}{c}\hfill {\mathit{X}}_t\hfill \\ \hfill {\mathit{E}}_{t+1}\hfill \end{array}\right)~N_{2d}(\mathbf{0},(\begin{array}{cc}\hfill \mathbf{\Sigma }\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{\Psi }\hfill \end{array}\left)\right).$$

The elliptical VAR process generalizes the Gaussian VAR process in two aspects. First, the elliptical model generalizes the Gaussian model by allowing heavy tails. This makes robust methodologies necessary for estimating the process. Secondly, the elliptical VAR model does not require that the observations are independent from future latent innovations.

Next, we show that there exists an elliptical random vector $\mathit{L}={({\mathit{X}}_1^{\top },\dots ,{\mathit{X}}_T^{\top },{\mathit{E}}_2^{\top },\dots ,{\mathit{E}}_T^{\top })}^{\top }$ such that the two conditions in Definition 3.1 are satisfied. To this end, let ${\mathit{L}}_0≔{({\mathit{X}}_1^{\top },{\mathit{E}}_2^{\top },\dots ,{\mathit{E}}_T^{\top })}^{\top }~\mathrm{E}{\mathrm{C}}_{Td}(\mathbf{0},\text{diag}(\mathbf{\Sigma },\mathbf{\Psi },\dots ,\mathbf{\Psi }),\zeta )$ and define

$$\mathit{L}={({\mathit{X}}_1^{\top },\dots ,{\mathit{X}}_T^{\top },{\mathit{E}}_2^{\top },\dots ,{\mathit{E}}_T^{\top })}^{\top }≔\mathbf{B}{\mathit{L}}_0,$$ (3.3)

where

$$\mathbf{B}≔\left(\begin{array}{ccccc}\hfill \mathbf{I}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \cdots \hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{A}\hfill & \hfill \mathbf{I}\hfill & \hfill \mathbf{0}\hfill & \hfill \cdots \hfill & \hfill \mathbf{0}\hfill \\ \hfill {\mathbf{A}}^2\hfill & \hfill \mathbf{A}\hfill & \hfill \mathbf{I}\hfill & \hfill \cdots \hfill & \hfill \mathbf{0}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \cdots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill {\mathbf{A}}^{T-1}\hfill & \hfill {\mathbf{A}}^{T-2}\hfill & \hfill {\mathbf{A}}^{T-3}\hfill & \hfill \cdots \hfill & \hfill \mathbf{I}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{I}\hfill & \hfill \mathbf{0}\hfill & \hfill \cdots \hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{I}\hfill & \hfill \cdots \hfill & \hfill \mathbf{0}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \cdots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \cdots \hfill & \hfill \mathbf{I}\hfill \end{array}\right)\in {ℝ}^{(2T-1)d\times Td}.$$

By Proposition 2.3, L is an elliptical random vector. The next Lemma gives sufficient and necessary conditions for L to satisfy the two conditions in Definition 3.1.

Lemma 3.4

1. L ~ EC(_2T−1)d(0, Ω, ζ) satisfies Condition 1. Partition the scatter Ω according to the dimensions of ${\{{\mathit{X}}_t\}}_{t=1}^T$ and ${\{{\mathit{E}}_t\}}_{t=2}^T$:

   $$\mathbf{\Omega }≔\left(\begin{array}{cc}\hfill {\mathbf{\Omega }}_X\hfill & \hfill {\mathbf{\Omega }}_{XE}\hfill \\ \hfill {\mathbf{\Omega }}_{XE}^{\top }\hfill & \hfill {\mathbf{\Omega }}_E\hfill \end{array}\right).$$ (3.4)

   We have

   $${\mathbf{\Omega }}_E=\left(\begin{array}{ccc}\hfill \mathbf{\Psi }\hfill & \hfill \hfill & \hfill \mathbf{0}\hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \mathbf{0}\hfill & \hfill \hfill & \hfill \mathbf{\Psi }\hfill \end{array}\right)\in {ℝ}^{(T-1)d\times (T-1)d}.$$ (3.5)
2. L satisfies Condition 2 if and only if the following equations hold:

   $${\mathbf{\Omega }}_X=\left(\begin{array}{cccc}\hfill \mathbf{\Sigma }\hfill & \hfill {\mathbf{\Sigma }}_{12}\hfill & \hfill \cdots \hfill & \hfill {\mathbf{\Sigma }}_{1T}\hfill \\ \hfill {\mathbf{\Sigma }}_{12}^{\top }\hfill & \hfill \mathbf{\Sigma }\hfill & \hfill \cdots \hfill & \hfill {\mathbf{\Sigma }}_{2T}\hfill \\ \hfill \hfill & \hfill \cdots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill {\mathbf{\Sigma }}_{1T}^{\top }\hfill & \hfill {\mathbf{\Sigma }}_{2T}^{\top }\hfill & \hfill \cdots \hfill & \hfill \mathbf{\Sigma }\hfill \end{array}\right)\in {ℝ}^{Td\times Td},$$ (3.6)

   $$\mathbf{\Sigma }=\mathbf{A}\mathbf{\Sigma }{\mathbf{A}}^{\top }+\mathbf{\Psi },$$ (3.7)

   $${\mathbf{\Sigma }}_{t,t+u}=\mathbf{\Sigma }{({\mathbf{A}}^{\top })}^u,$$ (3.8)

   $$\mathit{\text{and }}{({\mathbf{\Omega }}_{XE})}_{I_j{I}_k}=\{\begin{array}{cc}\mathbf{0},\hfill & \mathit{\text{if}}j\le k;\hfill \\ {\mathbf{A}}^{j-k-1}\mathbf{\Psi },\hfill & \mathit{\text{if}}j>k,\hfill \end{array}$$ (3.9)

   for t = 1, …, T − 1, u = 1, …, T − t, j = 1, …, T, and k = 2, …, T − 1. Here Ω_XE = [(Ω_XE)_IjIk] is a partition of Ω_XE into d × d matrices, where I_l ≔ {(l − 1)d + 1, …, ld} for l = 1, …, T.

Lemma 3.4 is a consequence of Proposition 2.3. Detailed proof is collected in the supplementary material. Lemma 3.4 shows that there exists an elliptical random vector $\mathit{L}={({\mathit{X}}_1^{\top },\dots ,{\mathit{X}}_T^{\top },{\mathit{E}}_2^{\top },\dots ,{\mathit{E}}_T^{\top })}^{\top }$ that satisfies the two conditions in Definition 3.1. On the other hand, the algorithm in Remark 3.2 generate a unique sequence of random vectors X₁, …, X_T, E₂, …, E_T. Therefore, we immediately have the following proposition.

Proposition 3.5

Let X₁, …, X_T be an elliptical VAR process with latent innovations E₂, …, E_T. Then $\mathit{L}={({\mathit{X}}_1^{\top },\dots ,{\mathit{X}}_T^{\top },{\mathit{E}}_2^{\top },\dots ,{\mathit{E}}_T^{\top })}^{\top }$ is an absolutely continuous elliptical random vector.

Denote Σ₁ ≔ Σ_t,t+1. We call Σ a scatter matrix of the elliptical VAR process, and Σ₁ a lag-one scatter matrix. For any c > 0, since L ~ EC_d(0, Ω, ζ) implies $\mathit{L}~\mathrm{E}{\mathrm{C}}_d(\mathbf{0},c\mathbf{\Omega },\zeta /\sqrt{c})$, cΣ and cΣ₁ are also scatter matrix and lag-one scatter matrix of the elliptical VAR process.

Next, we show that the scatter matrix and lag-one scatter matrix are closely related to the robust scales defined in Section 2.3. In particular, we show that the robust scale σ^Q motivates an alternative definition of the scatter matrix and lag-one scatter matrix.

Let X₁, …, X_T be an elliptical VAR process with X_t = (X_t1, …, X_td)^⊤. We define

$${\mathbf{R}}^{\mathrm{Q}}=[{\mathbf{R}}_{jk}^{\mathrm{Q}}]\text{ and }{\mathbf{R}}_1^{\mathrm{Q}}=[{({\mathbf{R}}_1^{\mathrm{Q}})}_{j\prime k\prime }],$$ (3.10)

where the entries are given by

• ${\mathbf{R}}_{jj}^{\mathrm{Q}}≔{\sigma }^{\mathrm{Q}}{(X_{1j})}^2$, for j = 1, …, d,

• ${\mathbf{R}}_{jk}^{\mathrm{Q}}≔\frac{1}{4}[{\sigma }^{\mathrm{Q}}{(X_{1j}+X_{1k})}^2-{\sigma }^{\mathrm{Q}}{(X_{1j}-X_{1k})}^2]$, for j ≠ k,

• ${({\mathbf{R}}_1^{\mathrm{Q}})}_{j\prime k\prime }≔\frac{1}{4}[{\sigma }^{\mathrm{Q}}{(X_{1j\prime }+X_{2k\prime })}^2-{\sigma }^{\mathrm{Q}}{(X_{1j\prime }-X_{2k\prime })}^2]$, for j′, k′ = 1, …, d.

The next theorem shows that R^Q and ${\mathbf{R}}_1^{\mathrm{Q}}$ are scatter matrix and lag-one scatter matrix of the elliptical VAR process.

Theorem 3.6

For the elliptical VAR process in Definition 3.1, we have

$${\mathbf{R}}^Q=m^{\mathrm{Q}}\mathbf{\Sigma }\mathit{\text{ and }}{\mathbf{R}}_1^{\mathrm{Q}}=m^{\mathrm{Q}}{\mathbf{\Sigma }}_1,$$ (3.11)

where m^Q is a constant.

The proof of Theorem 3.6 exploits the summation stability of elliptical distributions and Proposition 2.3. Due to space limit, the detailed proof is collected in the supplementary material. Combining Lemma 3.4 and Theorem 3.6, we obtain the following theorem.

Theorem 3.7

For the elliptical VAR process in Definition 3.1, let R^Q and ${\mathbf{R}}_1^{\mathrm{Q}}$ be defined as in (3.10). Then, we have

$${\mathbf{R}}_1^{\mathrm{Q}}={\mathbf{R}}^{\mathrm{Q}}{\mathbf{A}}^{\top }.$$ (3.12)

(3.12) serves as a quantile-based counterpart as the Yule Walker equation Var(X₁) = Cov(X₁, X₂)A^⊤. Theorem 3.7 motivates the robust estimator of A introduced in the next section.

4. Method

In this section, we propose a robust estimator for the transition matrix A. We first introduce robust estimators of R^Q and ${\mathbf{R}}_1^{\mathrm{Q}}$. Based on these estimators, the transition matrix A can be estimated by solving an optimization problem.

Let X₁, …, X_T be an elliptical VAR process. We define

$${\hat{\mathbf{R}}}^{\mathrm{Q}}≔[{\hat{\mathbf{R}}}_{jk}^{\mathrm{Q}}]\text{ and }{\hat{\mathbf{R}}}_1^{\mathrm{Q}}≔[{({\hat{\mathbf{R}}}_1^{\mathrm{Q}})}_{jk}],$$

where the entries are given by

• ${\hat{\mathbf{R}}}_{jj}^{\mathrm{Q}}≔{\hat{\sigma }}^{\mathrm{Q}}{({\{X_{tj}\}}_{t=1}^T)}^2$, for j =1, …, d,

• ${\hat{\mathbf{R}}}_{jk}^{\mathrm{Q}}≔\frac{1}{4}[{\hat{\sigma }}^{\mathrm{Q}}{({\{X_{tj}+X_{tk}\}}_{t=1}^T)}^2-{\hat{\sigma }}^{\mathrm{Q}}{({\{X_{tj}-X_{tk}\}}_{t=1}^T)}^2]$, for j ≠ k ∈ {1, …, d},

• ${({\hat{\mathbf{R}}}_1^{\mathrm{Q}})}_{jk}≔\frac{1}{4}[{\hat{\sigma }}^{\mathrm{Q}}{({\{X_{tj}+X_{t+1,k}\}}_{t=1}^{T-1})}^2-{\hat{\sigma }}^{\mathrm{Q}}{({\{X_{tj}-X_{t+1,k}\}}_{t=1}^{T-1})}^2]$, for j, k = 1, …, d.

Motivated by Theorem 3.7, we proposed to estimate A by

$$\mathbf{Â}={\text{argmin}}_{\mathbf{M}\in {ℝ}^{d\times d}}{\sum }_{jk}|{\mathbf{M}}_{jk}|$$ (4.1)

$$\mathrm{s}.\mathrm{t}.{\Vert {\hat{\mathbf{R}}}^{\mathrm{Q}}{\mathbf{M}}^{\top }-{\hat{\mathbf{R}}}_1^{\mathrm{Q}}\Vert }_{\text{max}}\le \lambda .$$

The optimization problem (4.1) can be further decomposed into d subproblems (Han & Liu, 2013). Specifically, the j-th row of  can be estimated by

$${\mathbf{Â}}_{j*}={\text{argmin}}_{\mathbf{v}\in {ℝ}^d}{\Vert \mathbf{v}\Vert }_1$$ (4.2)

$$\mathrm{s}.\mathrm{t}.{\Vert {\hat{\mathbf{R}}}^{\mathrm{Q}}\mathbf{v}-{({\hat{\mathbf{R}}}_1^{\mathrm{Q}})}_{*j}\Vert }_{\infty }\le \lambda .$$

Thus, the d rows of A can be estimated in parallel. (4.2) is essentially a linear programming problem, and can be solved efficiently using the simplex algorithm.

Remark 4.1

Since σ̂^Q can be computed using O(T log T) time (Rousseeuw & Croux, 1993), the computational complexity of R̂^Q and ${\hat{\mathbf{R}}}_1^{\mathrm{Q}}$ are O(d²T log T). Since T ≪ d in practice, R̂^Q and ${\hat{\mathbf{R}}}_1^{\mathrm{Q}}$ can be computed almost as efficiently as their moment-based counterparts

$$\mathbf{Ŝ}=\frac{1}{T}\sum _{t=1}^T{\mathit{X}}_t{\mathit{X}}_t^{\top }\text{ and }{\mathbf{Ŝ}}_1=\frac{1}{T-1}\sum _{t=1}^{T-1}{\mathit{X}}_t{\mathit{X}}_{t+1}^{\top },$$ (4.3)

which have O(d²T) complexity and are used in Han & Liu (2013).

5. Theoretical Properties

In this section, we present theoretical analysis of the proposed transition matrix estimator. Due to space limit, the proofs of the results in this section are collected in the supplementary material.

The consistency of the estimator depends on the degree of dependence over the process X₁, …, X_T. We first introduce the ϕ-mixing coefficient for quantifying the degree of dependence.

Definition 5.1

Let {X_t}_t∈Z be a stationary process. Define ${ℱ}_{-\infty }^0≔\sigma (X_t:t\le 0)$ and ${ℱ}_n^{\infty }≔\sigma (X_t:t\ge n)$ to be the σ-fileds generated by {X_t}_t≤0 and {X_t}_t≥n, respectively. The ϕ-mixing coefficient is defined by

$$\varphi (n)≔\underset{B\in {ℱ}_{-\infty }^0,A\in {ℱ}_n^{\infty },\mathbb{P}(B)>0}{\text{sup}}|\mathbb{P}(A|B)-\mathbb{P}(A)|.$$

Let {X_t}_t∈ℤ be an infinite elliptical VAR process in the sense that any contiguous subsequence of {X_t}_t∈ℤ is an elliptical VAR process. For brevity, we also call {X_t}_t∈ℤ an elliptical VAR process. Let ϕ_j(n), ${\varphi }_{jk}^{+}(n),{\varphi }_{jk}^{-}(n),{\psi }_{j\prime k\prime }^{+}(n)$, and ${\psi }_{j\prime k\prime }^{-}(n)$ be the ϕ-mixing coefficients of {X_tj}_t∈ℤ, {X_tj + X_tk}_t∈ℤ, {X_tj − X_tk}_t∈ℤ, {X_tj′ + X_{t+1, k′}}_t∈ℤ, and {X_tj′ − X_t+1,k′}_t∈ℤ, respectively. Here j, k, j′, k′ ∈ {1, …, d} but j ≠ k. Define

$$\mathrm{\Phi }(n)=\underset{j,k,j\prime ,k\prime }{\text{sup}}\{{\varphi }_j(n),{\varphi }_{jk}^{+}(n),{\varphi }_{jk}^{-}(n),{\psi }_{j\prime k\prime }^{+}(n),{\psi }_{j\prime k\prime }^{-}(n)\},$$

and $\mathrm{\Theta }(T)≔{\sum }_{n=1}^T\mathrm{\Phi }(n)$. Φ and Θ characterize the degree of dependence over the multivariate process {X_t}_t∈ℤ.

Next, we introduce an identifiability condition on the distribution function of X₁.

Condition 1

Let X̃₁ = (X̃₁₁, …, X̃_1d)^⊤ and X̃₂ = (X̃₂₁, …, X̃_2d)^⊤ be independent copies of X₁ and X₂. Let F_j, $F_{jk}^{+},F_{jk}^{-},G_{j\prime k\prime }^{+}$, and $G_{j\prime k\prime }^{-}$ be the distribution functions of |X_1j − X̃_1j|, |X_1j + X_1k − X̃_1j − X̃_1k|, |X_1j − X_1k − X̃_1j + X̃_1k|, |X_1j′ + X_2k′ − X̃_1j′ − X̃_2k′|, and |X_1j′ − X_2k′ − X̃_1j′ + X̃_2k′|. We assume that there exist constants κ > 0 and η > 0 such that

$$\underset{|y-Q(F;1/4)|\le \kappa }{\text{inf}}\frac{d}{dy}F(y)\ge \eta$$

for any $F\in \{F_j,F_{jk}^{+},F_{jk}^{-},G_{j\prime k\prime }^{+},G_{j\prime k\prime }^{-}:j\ne k\mathit{\text{ and }}j,k,j\prime ,k\prime =1,\dots ,d.\}$.

Then next lemma presents the rates of convergence for R̂^Q and ${\hat{\mathbf{R}}}_1^{\mathrm{Q}}$.

Lemma 5.2

Let {X_t}_t∈ℤ be an elliptical VAR process satisfying Condition 1. Let X₁, …, X_T be a sequence of observations from {X_t}_t∈ℤ. Suppose that log d/T → 0 as T → ∞. Then, for T large enough, with probability no smaller than 1 − 8/d², we have

$${\Vert {\hat{\mathbf{R}}}^{\mathrm{Q}}-{\mathbf{R}}^{\mathrm{Q}}\Vert }_{\text{max}}\le r(T),$$ (5.1)

$${\Vert {\hat{\mathbf{R}}}_1^{\mathrm{Q}}-{\mathbf{R}}_1^{\mathrm{Q}}\Vert }_{\text{max}}\le r_1(T),$$ (5.2)

where the rates of convergence are defined by

$$r(T)=\text{max}\{\frac{2}{{\eta }^2}{[\sqrt{\frac{8(1+2\mathrm{\Theta }(T))\text{ log }d}{T}}+\frac{4\mathrm{\Theta }(T)}{T}]}^2,\frac{4{\sigma }_{\text{max}}^{\mathrm{Q}}}{\eta }[\sqrt{\frac{8(1+2\mathrm{\Theta }(T))\text{ log }d}{T}}+\frac{4\mathrm{\Theta }(T)}{T}\left]\right\},$$ (5.3)

$$r_1(T)=\text{max}\{\frac{1}{{\eta }^2}{[\sqrt{\frac{16(1+2\mathrm{\Theta }(T))\text{ log }d}{T}}+\frac{8\mathrm{\Theta }(T)}{T}]}^2,\frac{2{\tau }_{\text{max}}^{\mathrm{Q}}}{\eta }[\sqrt{\frac{16(1+2\mathrm{\Theta }(T))\text{ log }d}{T}}+\frac{8\mathrm{\Theta }(T)}{T}\left]\right\}.$$ (5.4)

Here ${\sigma }_{\text{max}}^{\mathrm{Q}}≔\text{max}\{{\sigma }^{\mathrm{Q}}(X_{1j}),{\sigma }^{\mathrm{Q}}(X_{1j}+X_{1k}),{\sigma }^{\mathrm{Q}}(X_{1j}-X_{1k}):j\ne k\in \{1,\dots ,d\}\},{\tau }_{\text{max}}^{\mathrm{Q}}≔\text{max}\{{\sigma }^{\mathrm{Q}}(X_{1j}+X_{2k}),{\sigma }^{\mathrm{Q}}(X_{1j}-X_{2k}):j,k\in \{1,\dots ,d\}\}$.

Based on Lemma 5.2, we can further deliver the rates of convergence for  under the matrix ℓ_max norm and ℓ₁ norm. We start with some additional notation. For α ∈ [0, 1), s > 0, and M_T > 0 that may scale with T, we define the matrix class

$$ℳ(\alpha ,s,M_T)≔\{\mathrm{M}\in {ℝ}^{d\times d}:\underset{1\le j\le d}{\text{max}}\sum _{k=1}^d{|{\mathrm{M}}_{jk}|}^{\alpha }\le s,{\Vert \mathrm{M}\Vert }_1\le M_T\}.$$

ℳ(0, s, M_T) is the set of sparse matrices with at most s non-zero entries in each row and bounded ℓ₁ norm. ℳ(α, s, M_T) is also investigated in Cai et al. (2011) and Han & Liu (2013).

Theorem 5.3

Let {X_t}_t∈ℤ be an elliptical VAR process satisfying Condition 1, and X₁, …, X_T be a sequence of observations. Suppose that log d/T → 0 as T → ∞, the transition matrix A ∈ ℳ(α, s, M_T), and R^Q is non-singular. Define

$$r_{\text{max}}(T)=\text{max}\{\frac{2}{{\eta }^2}{[\sqrt{\frac{16(1+2\mathrm{\Theta }(T))\text{ log }d}{T}}+\frac{8\mathrm{\Theta }(T)}{T}]}^2,\frac{4\text{ max}({\sigma }_{\text{max}}^{\mathrm{Q}},{\tau }_{\text{max}}^{\mathrm{Q}})}{\eta }[\sqrt{\frac{16(1+2\mathrm{\Theta }(T))\text{ log }d}{T}}+\frac{8\mathrm{\Theta }(T)}{T}\left]\right\}.$$

If we choose the tuning parameter

$$\lambda =(1+M_T)r_{\text{max}}(T)$$

in (4.1), then, for T large enough, with probability no smaller than 1 − 8/d², we have

$${\Vert \mathbf{Â}-\mathbf{A}\Vert }_{\text{max}}\le 2{\Vert {({\mathbf{R}}^{\mathrm{Q}})}^{-1}\Vert }_1(1+M_T)r_{\text{max}}(T),$$ (5.5)

$${\Vert \mathbf{Â}-\mathbf{A}\Vert }_{\infty }\le 4s{[2{\Vert {({\mathbf{R}}^{\mathrm{Q}})}^{-1}\Vert }_1(1+M_T)r_{\text{max}}(T)]}^{1-\alpha }.$$ (5.6)

Remark 5.4

If we assume that η ≥ C₁ and ${\sigma }_{\text{max}}^{\mathrm{Q}},{\tau }_{\text{max}}^{\mathrm{Q}}$, ‖(R^Q)⁻¹‖₁ ≤ C₂ for some absolute constants C₁, C₂ > 0, the rates of convergence in Theorem 5.3 reduces to

$${\Vert \mathbf{Â}-\mathbf{A}\Vert }_{\text{max}}=O_P\left(M_T\sqrt{\frac{\mathrm{\Theta }(T)\text{ log }d}{T}}\right),$$

$${\Vert \mathbf{Â}-\mathbf{A}\Vert }_{\infty }=O_P\left[s{\left(M_T\sqrt{\frac{\mathrm{\Theta }(T)\text{ log }d}{T}}\right)}^{1-\alpha }\right].$$

Here $\mathrm{\Theta }(T)={\sum }_{n=1}^T\mathrm{\Phi }(n)$ characterizes the degree of serial dependence in the process {X_t}_t∈ℤ. If we further assume polynomial decaying ϕ-mixing coefficients

$$\mathrm{\Phi }(n)\le 1/n^{1+\epsilon }\text{ for some }\epsilon >0,$$ (5.7)

we have $\mathrm{\Theta }(T)\le {\sum }_{n=1}^{\infty }1/n^{1+\epsilon }<\infty$ and the rate of convergence are further reduced to ${\Vert \mathbf{Â}-\mathbf{A}\Vert }_{\text{max}}=O_P(M_T\sqrt{\text{log}d/T})$ and ${\Vert \mathbf{Â}-\mathbf{A}\Vert }_{\infty }=O_P[s{(M_T\sqrt{\text{log}d/T})}^{1-\alpha }]$, which are the parametric rates obtained in Han & Liu (2013) and Basu & Michailidis (2013). Condition (5.7) has been commonly assumed in the time series literature (Pan & Yao, 2008)

6. Granger Causality

In this section, we demonstrate an application of framework developed in this paper. In particular, we discuss the characterization and estimation of Granger causality under the elliptical VAR model. We start with the definition of Granger causality.

Definition 6.1 (Granger (1980))

Let {X_t}_t∈ℤ be a stationary process, where X_t = (X_t1, …, X_td)^⊤. For j ≠ k ∈ {1, …, d}, {X_tk}_t∈ℤ Granger causes {X_tj}_t∈ℤ if and only if there exists a measurable set A such that

$$\mathbb{P}(X_{t+1,j}\in A|{\{{\mathit{X}}_s\}}_{s\le t})\ne \mathbb{P}(X_{t+1,j}\in A|{\{{\mathit{X}}_{s,\backslash k}\}}_{s\le t}),$$

for all t ∈ ℤ, where X_s,\k is the subvector obtained by removing X_sk from X_s.

For a Gaussian VAR process {X_t}_t∈ℤ, we have that {X_tk}_t∈ℤ Granger causes {X_tj}_t∈ℤ if and only if the {j, k) entry of the transition matrix is non-zero (Lütkepohl, 2007). In the next theorem, we show that a similar property holds for the elliptical VAR process.

Theorem 6.2

Let {X_t}_t∈ℤ be an elliptical VAR process with transition matrix A. Suppose X_t has finite second order moment, and Var(X_tk | X_s,\k}_s≤t ≠ 0 for any k ∈ {1, …, d}. Then, for j ≠ k ∈ {1, …, d}, we have

1. If A_jk ≠ 0, then {X_tk}_t∈ℤ Granger causes {X_tj}_t∈ℤ.

2. If we further assume that E_t+1 is independent of {X_s}_s≤t for any t ∈ ℤ, we have that {X_tk}_t∈ℤ Granger causes {X_tj}_t∈ℤ if and only if A_jk ≠ 0.

The proof of Theorem 6.2 exploits the autoregressive structure of the process X₁, …, X_T, and the properties on conditional distributions of elliptical random vectors. We refer to the supplementary material for the detailed proof.

Remark 6.3

The assumption that Var(X_tk | X_s,\k}_s≤t ≠ 0 requires that X_tk cannot be perfectly predictable from the past or from the other observed random variables at time t. Otherwise, we can simply remove {X_tk}_t∈ℤ from the process {X_t}_t∈ℤ, since predicting {X_tk}_t∈ℤ is trivial.

Assuming that E_t+1 is independent of {X_s}_s≤t for any t ∈ ℤ, the Granger causality relations among the processes {{X_jt}_t∈ℤ : j = 1, …, d} is characterized by the non-zero entries of A. To estimate the Granger causality relations, we define à = [Ã_jk], where

$${\mathbf{Ã}}_{jk}≔{\mathbf{Â}}_{jk}I(|{\mathbf{Â}}_{jk}|\ge \gamma ),$$

for some threshold parameter γ. To evaluate the consistency between à and A regarding sparsity pattern, we define function sign(x) ≔ I(x > 0) − I(x < 0). For a matrix M, define sign(M) ≔ [sign(M_jk)].

The next theorem gives the rate of γ such that à recovers the sparsity pattern of A with high probability.

Theorem 6.4

Assume that the conditions in Theorem 5.3 holds, and A ∈ ℳ(0, s, M_T). If we set

$$\gamma =2{\Vert {({\mathbf{R}}^{\mathrm{Q}})}^{-1}\Vert }_1(1+M_T)r_{\text{max}}(T),$$

then, with probability no smaller than 1 − 8/d², we have sign(Ã) = sign(A), provided that

$$\underset{\{(j,k):{\mathbf{A}}_{jk}>0\}}{\text{min}}|{\mathbf{A}}_{jk}|\ge 2\gamma .$$ (6.1)

Theorem 6.4 is a direct consequence of Theorem 5.3. We refer to the supplementary material for a detailed proof.

7. Experiments

In this section, we demonstrate the empirical performance of the proposed transition matrix estimator using both synthetic and real data. In addition to the proposed robust Dantzig-selector-type estimator (R-Dantzig), we consider the following two competitors for comparison:

1. Lasso: an ℓ₁ regularized estimator defined in (1.1) with $l(\mathbf{Y}-\mathbf{M}\mathbf{X})={\Vert \mathbf{Y}-\mathbf{M}\mathbf{X}\Vert }_F^2$ and P_ρ(M) = ρ ∑_jkM_jk.

2. Dantzig: the estimator proposed in Han & Liu (Han & Liu, 2013), which solves (4.1) with R̂^Q and ${\hat{\mathbf{R}}}_1^{\mathrm{Q}}$ replaced by Ŝ and Ŝ₁ defined in (4.3).

Lasso is solved using R package glmnet. Dantzig and R-Dantzig are solved by the simplex algorithm.

7.1. Synthetic Data

In this section, we demonstrate the effectiveness of R-Dantzig under synthetic data. To generate the time series, we start with an initial observation X₁ and innovations E₂, …, E_T. Specifically, we consider three distributions for ${({\mathit{X}}_1^{\top },{\mathit{E}}_2^{\top },\dots ,{\mathit{E}}_T^{\top })}^{\top }$:

• Setting 1: a multivariate Gaussian distribution: N(0, Φ);

• Setting 2: a multivariate t distribution with degree of freedom 3, and covariance matrix Φ;

• Setting 3: an elliptical distribution with log-normal generating variate, log N(0, 2), and covariance matrix Φ.

Here the covariance matrix Φ is block diagonal: Φ = diag(Σ, Ψ, …, Ψ) ∈ ℝ^Td×Td. We set d = 50 and T = 25. Using ${({\mathit{X}}_1^{\top },{\mathit{E}}_2^{\top },\dots ,{\mathit{E}}_T^{\top })}^{\top }$, we can generate ${({\mathit{X}}_1^{\top },\dots ,{\mathit{X}}_T^{\top })}^{\top }$ by

$${({\mathit{X}}_1^{\top },\dots ,{\mathit{X}}_T^{\top })}^{\top }=\mathbf{G}{({\mathit{X}}_1^{\top },{\mathit{E}}_2^{\top },\dots ,{\mathit{E}}_T^{\top })}^{\top },$$

where G is given by

$$\mathbf{G}≔\left(\begin{array}{ccccc}\hfill \mathbf{I}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \cdots \hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{A}\hfill & \hfill \mathbf{I}\hfill & \hfill \mathbf{0}\hfill & \hfill \cdots \hfill & \hfill \mathbf{0}\hfill \\ \hfill {\mathbf{A}}^2\hfill & \hfill \mathbf{A}\hfill & \hfill \mathbf{I}\hfill & \hfill \cdots \hfill & \hfill \mathbf{0}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \cdots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill {\mathbf{A}}^{T-1}\hfill & \hfill {\mathbf{A}}^{T-2}\hfill & \hfill {\mathbf{A}}^{T-3}\hfill & \hfill \cdots \hfill & \hfill \mathbf{I}\hfill \end{array}\right)\in {ℝ}^{Td\times Td}.$$

By Proposition 2.3, ${({\mathit{X}}_1^{\top },\dots ,{\mathit{X}}_T^{\top })}^{\top }$ follows a multivariate Gaussian distribution in Setting 1, a multivariate t distribution in Setting 2, and an elliptical distribution in Setting 3 with the same log-normal generating variate.

We generate the parameters A and Σ following Han & Liu (2013). Specifically, we generate the transition matrix A using the huge R package, with patterns band, cluster, hub, and random. We refer to Han & Liu (2013) for a graphical illustration of the patterns. Then we rescale A so that ‖A‖₂ = 0.8. Given A, we generate Σ such that ‖Σ‖₂ = 2‖A‖₂. Using (3.7), we set Ψ = Σ − AΣA^⊤.

Table 1 presents the errors in estimating the transition matrix and their standard deviations. The tuning parameters λ and ρ are chosen by cross validation. The results are based on 1,000 replicated simulations. We note two observations: (i) Under the Gaussian model (Setting 1), R-Dantzig has comparable performance as Dantzig, and out-performs Lasso. (ii) In Settings 2–3, R-Dantzig produces significantly smaller estimation errors than Lasso and Dantzig. Thus, we conclude that R-Dantzig is robust to heavy tails.

Table 1.

Averaged errors and standard deviations in estimating the transition matrix under the matrix Frobenius norm (ℓ_F), ℓ_max norm, and ℓ_∞ norm. The results are based on 1,000 replications.

		Lasso			Dantzig			R-Danzig
		ℓF	ℓmax	ℓ∞	ℓF	ℓmax	ℓ∞	ℓF	ℓmax	ℓ∞
Setting 1	band	4.26(0.74)	0.60(0.25)	2.15(0.38)	3.24(1.07)	0.49(0.22)	1.10(0.07)	3.65(0.01)	0.50(0.03)	1.06(0.05)
	cluster	3.04(0.65)	0.52(0.19)	1.82(0.35)	2.25(0.39)	0.41(0.11)	1.00(0.58)	2.47(0.01)	0.44(0.01)	1.13(0.04)
	hub	2.77(0.61)	0.66(0.05)	2.53(0.22)	1.87(0.01)	0.64(0.02)	1.87(0.02)	1.90(0.01)	0.65(0.01)	1.90(0.06)
	random	2.71(0.01)	0.47(0.01)	1.08(0.02)	2.58(0.36)	0.48(0.19)	1.21(0.83)	2.74(0.01)	0.47(0.01)	1.19(0.08)
Setting 2	band	9.53(0.58)	1.11(0.22)	10.45(1.29)	3.72(0.19)	0.52(0.10)	1.18(0.66)	3.62(0.01)	0.47(0.02)	0.84(0.08)
	cluster	8.52(0.38)	1.00(0.13)	9.24(1.16)	2.58(0.22)	0.46(0.03)	1.24(0.27)	2.57(0.27)	0.44(0.01)	1.09(0.50)
	hub	8.20(0.28)	0.97(0.09)	8.53(1.02)	3.87(0.01)	0.78(0.03)	3.30(0.02)	1.88(0.01)	0.64(0.01)	1.90(0.06)
	random	8.65(0.19)	0.98(0.10)	9.55(1.42)	2.79(0.07)	0.56(0.01)	1.35(0.15)	2.72(0.02)	0.48(0.01)	1.12(0.10)
Setting 3	band	9.43(0.25)	1.07(0.16)	10.83(1.16)	3.79(0.18)	0.52(0.02)	1.16(0.01)	3.69(0.11)	0.49(0.04)	1.14(0.45)
	cluster	8.59(0.34)	0.94(0.10)	9.70(0.98)	2.66(0.10)	0.44(0.02)	1.51(0.22)	2.55(0.11)	0.43(0.01)	1.32(0.26)
	hub	8.16(0.35)	0.95(0.10)	8.79(0.88)	2.51(0.11)	0.66(0.03)	2.34(0.15)	2.01(0.23)	0.64(0.01)	2.07(0.30)
	random	8.81(0.43)	1.04(0.12)	9.31(1.25)	2.71(0.13)	0.47(0.01)	1.28(0.16)	2.55(0.10)	0.46(0.01)	1.04(0.29)

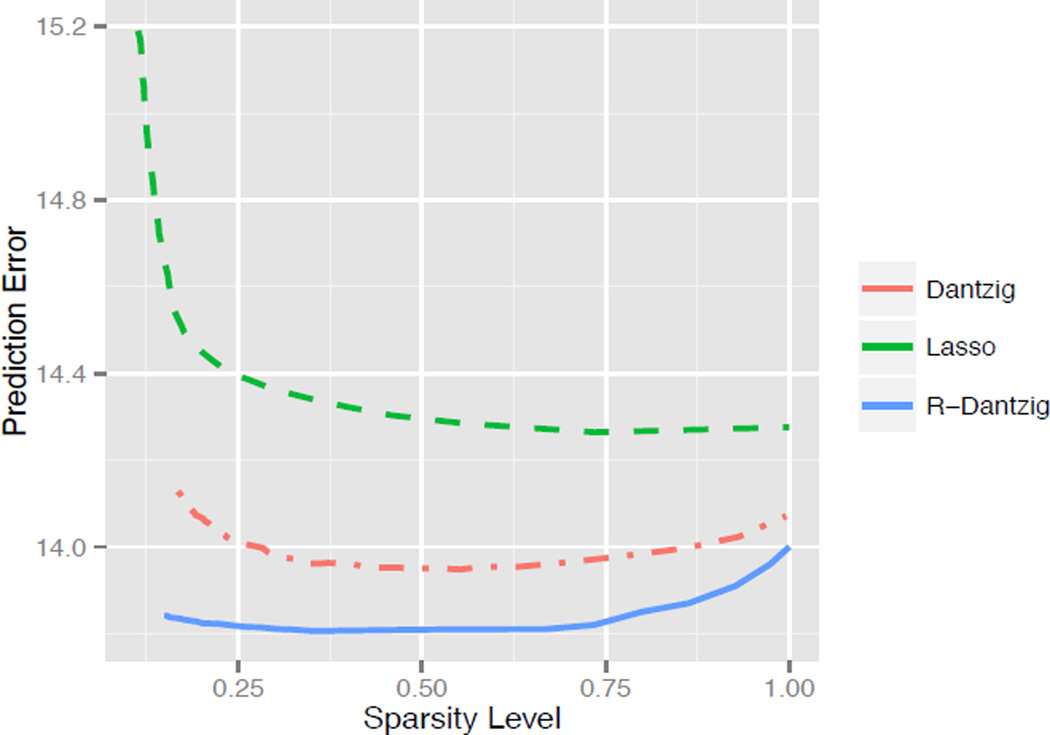
Figure 1 plots the prediction errors ε_s against sparsity s for the three transition matrix estimators. We observe that R-Dantzig achieves smaller prediction errors compared to Lasso and Dantzig.

Figure 1.

Prediction errors in stock prices plotted against the sparsity of the estimated transition matrix.

7.2. Real Data

In this section, we exploit the VAR model in stock price prediction. We collect adjusted daily closing prices³ of 435 stocks in the S&P 500 index from January 1, 2003 to December 31, 2007. This gives us T = 1, 258 closing prices of the 435 stocks. Let X_t be a vector of the 435 closing prices on day t, for t = 1, …, T. We model ${\{{\mathit{X}}_t\}}_{t=1}^T$ by a VAR process, and estimate the transition matrix using Lasso, Dantzig, and R-Dantzig. Let Â_s be an estimate of the transition matrix with sparsity s⁴. We define the prediction error associated with Â_s to be

$${\epsilon }_s≔\frac{1}{T-1}\sum _{t=2}^T{\Vert {\mathit{X}}_t-{\mathbf{Â}}_s{\mathit{X}}_{t-1}\Vert }_2.$$

8. Conclusion

In this paper, we developed a unified framework for modeling and estimating heavy-tailed VAR processes in high dimensions. Our contributions are three-fold. (i) In model level, we generalized the Gaussian VAR model by an elliptical VAR model to accommodate heavy-tailed time series. The model naturally couples with quantile-based scatter matrices and Granger causality. (ii) Methodologically, we proposed a quantile-based estimator of the transition matrix, which induces an estimator of Granger causality. Experimental results demonstrate that the proposed estimator is robust to heavy tails. (iii) Theoretically, we showed that the proposed estimator achieves parametric rates of convergence in matrix ℓ_max norm and ℓ_∞ norm. The theory explicitly captures the effect of serial dependence, and implies sign-consistency of the induced Granger causality estimator. To our knowledge, this is the first work on modeling and estimating heavy-tailed VAR processes in high dimensions. The methodology and theory proposed in this paper have broad impact in analyzing non-Gaussian time series. The techniques developed in the proofs have independent interest in understanding robust estimators under high dimensional dependent data.