Integrating the Escalation and Dose Expansion Studies into a Unified Phase I Clinical Trial

Abstract

We focus on Phase I dose finding studies as they are currently undertaken. The design and analysis of these trials has changed over the last years and, in particular, it is now rare for a Phase I study to not include one or more dose- expansion cohorts (DEC). It is common to see DEC involving several hundred patients, building on an initial dose escalation study that may have no more than 20 to 30 patients. There has been recent focus by researchers on the design of DEC and the analysis of DEC data. It is reasonable to explicitly account for the uncertainty in the estimation of the MTD, the dose upon which the whole of the DEC is currently based. In this paper, we focus on the dose escalation phase prior to the DEC, with the purpose of adapting it to the needs of DEC. Specifically, before beginning the DEC phase, we need to identify those dose levels that will be taken into the DEC. We define a useful concept for this purpose, the co-MTD, and the results support that the estimated MTD and co-MTD contain the true MTD with high probability. We also provide stopping rules for when the data support that the dose escalation can end and the dose expansion can begin. Simulated trials support the use of the proposed approach and provide additional information on how this approach compares with current practice.

1 Introduction and objectives

The landscape of early phase clinical trials has changed rapidly in the last few years.[1, 2] The classic Phase 1 dose escalation design has become more rare and has been almost entirely replaced by a different set-up involving an initial dose finding algorithm followed by the subsequent addition of dose expansion cohorts (DEC). While it remains true that the primary objective of Phase 1 trials is to evaluate safety and identify the maximum tolerated dose (MTD), Phase 1 trials have moved away from the traditional focus on the MTD. Now, dose expansion cohorts are integral to the overall study. Their role is twofold: first, to strengthen the safety evaluation by aiming to refine the initial estimate of the MTD in a more homogenous patient population, and secondly, to exploit any information on secondary endpoints not considered during the initial stage, such as efficacy [3, 4]. A comprehensive analysis of all of this information, together with PK/PD data, is often taken into account before recommending the Phase 2 dose (RP2D).

It has been argued that the old paradigm of a Phase 1 study focused almost exclusively on toxicity followed by a Phase 2 study focused essentially on efficacy in disease-specific groups, is no longer viewed as the design strategy of choice for early drug development [1, 2]. Phase 2 studies now follow the DEC component of the Phase 1 study and are necessarily influenced by the findings of the DEC [5]. Studies larger than previously considered necessary for the Phase 1 safety setting are now common. Phase 2 trials are generally more sharply focused on specific disease categories. In some cases, a Phase 1 + DEC study can be followed directly by a Phase 3 study having entirely skipped the usual Phase 2 design [4], or depending on the treatment effect observed in DEC and how rare the disease is it can lead to an accelerated or conditional drug approval [6]. This represents a very significant departure from the old paradigm.

Statistical analysis of the DEC, following an initial dose-finding trial, has been the subject of recent work [7]. That work, from the perspective of a comprehensive Phase 1 + DEC study, is focused on the second component of the study namely the dose expansion phase. Our purpose here is to focus on the first component of the study, where the initial dose-escalation occurs. We argue that this first component needs to be thought through thoroughly with the second component in mind. The best escalation design will then depend on the particular restrictions and goals of the expansion cohort. We argue that Phase 1 trials need to take into full consideration the fact that DEC are involved at the very beginning of the design rather than adding them on as an unplanned afterthought. The goals of the old Phase 1 design and the goals of the current Phase 1 + DEC design are not the same. The current purpose is not to identify the RP2D based on safety alone, instead the RP2D will be influenced by information on more than a single dose level, and information on efficacy across one or more disease categories (Supplemental Figure 1). The DEC component will sometimes involve more than one level and while it is important to keep a small number of levels in the DEC, it is no less important to ensure that with high probability these levels contain the true MTD.

In this paper, we propose to reduce the error in MTD estimation by bringing forward to the DEC a set of dose levels that contain the true MTD with high probability. The accuracy of the MTD estimate will improve throughout the DEC with the accumulation of safety data while simultaneously gathering information on efficacy and other endpoints that will guide the choice of the RP2D.

2 Overall design

A Phase 1 study without DEC involves several choices relating to design parameters such as the number of dose levels, the actual dose spacing and the overall structure [8, 9]. In this section, we revisit existing guidelines viewed from a different angle, an angle whose focus is the successful structure of the DEC. Our goal is not to elaborate a whole new design, since such a design is not needed. Nonetheless, we do need to keep in mind the requirements of the DEC. In particular we usually want to consider more than a single dose to take forward to the DEC [5]. We need for this set of doses to contain the true MTD with high probability and we would like for certain invariance properties to hold so that, when choosing these doses, the weight of the data is preponderant and the weight of arbitrary model choices is weak. A certain amount of careful tuning is needed. This section outlines the several parts of this construct, put together in a number of sub-sections.

2.1 Ethical and scientific constraints

The constraints, ethical and operational, provide essential guidance. For example, following several authors [8, 10, 11] we propose that for the first part of the Phase 1 + DEC, we sequentially estimate the MTD and treat incoming cohorts at the estimated MTD. This is the same paradigm that underlies most model based designs. Once we move into the DEC part of the study the experimental conditions change: we continue to obtain information on toxicity and we simultaneously collect data on efficacy. The ethical constraint is no longer the same. The compelling ethical restriction whereby each new cohort in a Phase 1 study ought be treated at our best estimate of the MTD no longer holds. This is because information gained during the DEC will not be limited to toxicity alone. Although, for treatment purposes, i.e dose allocation, the first component of these studies only needs to know the best estimate of the MTD, for the purposes of the DEC we need to know something about levels close to the estimated MTD. The MTD may show poor efficacy and a higher level may improve on that without sacrificing much in the way of toxicity. This is true for certain agent classes, and the assumption behind most dose escalation designs is that the higher the dose the higher the efficacy. Conversely, in the case where the MTD is above the target toxicity rate, it may well be that a lower level can exhibit comparable efficacy but more favorable toxicity. Such considerations argue in favor of a DEC that involves more than a single level. Indeed, it can be helpful to view the first part of the study as a means to eliminate doses from consideration rather than as a way to identify a single MTD. Doses that show too little effect, as indicated by a low rate of toxicity, and doses that show too aggressive an effect, as evidenced by too great a rate of toxicity, ought be eliminated from consideration. At the junction between the pure Phase 1 part and the DEC, the question is how many doses to take forward into the expansion.

For the first part of a Phase 1 + DEC design, our proposal is to build on the structure of the continual reassessment method (CRM). As initially structured, the purpose of a CRM design is to identify a single MTD. Such a design can also be used to identify more than a single MTD to take forward into the DEC, and here we show how to achieve this goal. In particular, the CRM, while allowing some arbitrary features such as the model spacing between doses (skeleton), will generally converge to the correct MTD when there is only one. Taking a single dose forward to the DEC is relatively straightforward. When we take 2 or 3 dose levels forward to the DEC we need to know that with high probability, the set chosen contains the true MTD. In order to achieve this, the question of spacing (skeleton) between doses is much more important and needs to be considered. We illustrate this in Section 2.3. The question of the prior is also important, since even for a single MTD, poor prior specification can be too influential on the results. This is examined in Section 2.4. The goal of this proposal is, at the junction of the Phase 1 and DEC components, while maintaining ethical criteria, to be able to propose one or more dose levels that will contain the true MTD with a high probability, and to take these dose levels forward into the DEC. Once we have selected which dose levels (mostly 2-3 levels) to take forward to the DEC based on the probability of one of them being the true MTD, then this part of the study is complete. Analysis of the DEC has been described elsewhere and is not repeated here [12]. Here, we only consider the first component of the Phase 1 + DEC study. This component requires some fine tuning as well as elimination of the arbitrary features in order to integrate it harmoniously into the DEC phase with the purpose of accurately identifying the RP2D. The design is optimized in an operational sense to cater to broad clinical situations, and we illustrate in the following section how to carry out this fine tuning in practice.

2.2 Basic model

We use the simple one parameter dose-toxicity model and CRM [13] as a framework within which we develop the proposed approach. We follow the standard notation here where the trial consists of k ordered dose levels, d₁, d₂, …, d_k, and a total of N patients. The dose level for patient j is denoted as X_j, and the binary dose-limiting toxicity (DLT) outcome, is denoted as Y_j, where a 1 indicates a DLT. At dose X_j = x_j ∈ {d₁, d₂, …, d_k}, the probability that Y_j = 1 is given by:

$$R(x_j)=Pr(Y_j=1|X_j=x_j)\approx \psi (d_i,a)={\alpha }_i^{exp(a)}.$$

where a ∈ [A, B] ∈ (−∞, ∞) is the unknown parameter, and α_i are the standardized units, or skeleton, representing a transformation of the actual dose amount at the discrete dose levels d_i and α_i < α_i+1 for all i. The true MTD is defined to be the dose d_m, 1 ≤ m ≤ k such that, d_m = argmin_di Δ(R(d_i), θ), i = 1, …, k. where Δ(R(d_i), θ) indicates the distance from the target acceptable rate θ. After the inclusion of the first j patients, the log-likelihood can be written as:

$${\mathcal{L}}_j(a)=\sum _{\ell =1}^j{y}_{\ell }log\psi (x_{\ell },a)+\sum _{\ell =1}^j(1-y_{\ell })log(1-\psi (x_{\ell },a))$$ (1)

and is maximized at a = â_j. Once we have calculated â_j we can obtain an estimate of the probability of toxicity at each dose level d_i via: R̂(d_i) = ψ(d_i, â_j), (i = 1, …, k). In the Bayesian setting, we often use a prior distribution denoted as g(a) for the dose-toxicity parameter a. In this context, the starting level d_i assigned to the first patient should be such that ∫_𝒜ψ(d_i, u)g(u)du = θ. This may be a difficult integral equation to solve and, practically, we might take the starting dose to be obtained from ψ(d_i, μ₀) = θ where μ₀ = ∫_𝒜ug(u)du. Given the set Ω_j = {(x₁, y₁),…, (x_j, y_j)} the posterior density for a is;

$$f(a|{\mathrm{\Omega }}_j)=H_j^{-1}exp\{{\mathcal{L}}_j(a)\}g(a);H_j={\int }_{-\infty }^{\infty }exp\{{\mathcal{L}}_j(u)\}g(u)\mathit{\text{du}}.$$ (2)

The dose x_j+1 ∈ {d₁, … d_k} assigned to the (j + 1) th included patient is the dose minimizing the Euclidean distance between θ and $\widehat{R}(d_i)={\alpha }_i^{exp(\widehat{a})}$. The estimated MTD is the dose d̂_m ∈ {d₁, …, d_k}, 1 ≤ m ≤ k such that, d̂_m = argmin_di Δ(R̂(d_i), θ). Choosing a suitable prior, g(a) is a challenge. The challenge is greater when models are misspecified which is the case here. For this reason, it is easier, and more transparent to create a prior, g(a), indirectly via the use of pseudo-data. We illustrate this in Section 2.4.

2.3 Fixing the skeleton using an invariance property

Iasonos and O'Quigley (2013) [14] studied the interplay between the prior and the skeleton and found that each depends heavily on the other. Either parameter can be fixed and the other can be chosen to reflect a strong or weak prior belief on any level being the MTD. It makes more sense for these two model design parameters to be chosen together. We would like to choose a close enough spacing between the skeleton values that, given the prior, enables escalation that is not too slow and a wide enough spacing that prevents escalation from being too rapid. As we will see in the following section, we can bypass the difficulty of calibrating two objects by fixing any prior to coincide exactly with the skeleton. Such a prior is then found in terms of pseudo data at each dose rather than in a density function on the parameter a. It only then becomes necessary to consider the skeleton itself. The following lemma and corollary help us.

Lemma 1 For each 1 ≤ i ≤ k − 1, there exists a unique constant κ_i such that

$$\theta -\psi (d_i,{\kappa }_i)=\psi (d_{i+1},{\kappa }_i)-\theta >0$$

The constants κ_i provide the ingredients to making a partition of the parameter space [A, B] so that

$$[A,B]=\underset{i=1}{\overset{m}{\cup }}{S}_i,\text{where}{S}_1=[A,{\kappa }_1),S_2=[{\kappa }_1,{\kappa }_2),\dots ,S_m=({\kappa }_{m-1},B].$$

This partition enables the following corollary underlining the deterministic aspect of dose allocation given the current information.

Corollary 1 Suppose that â_j is the estimate of the parameter a after the inclusion of j patients. If â_j ∈ S_i then d_i is the level recommended to patient j + 1.

A proof of both the lemma and the corollary are given in O'Quigley (2006) [15]. We would like the following invariance property to hold. Suppose we have data on patients treated at dose levels 2 and 3 and no data elsewhere. Suppose the observed rates are 0/4 at d₂ and 1/3 at d₃ and the recommendation is d₄. If these data are shifted, so that the same patients are now treated at level 3 and level 4 with the same observed rates, i.e. 0/4 at d₃ and 1/3 at d₄ then we would like for the recommendation to be shifted in exactly the same way, i.e., we now recommend level d_i+1 instead of d_i which here would be d₅. This property is not so important when the goal is to home in on a single level. Levels are not favored by the choice of a skeleton or a prior, unless of course that is a deliberate choice and we look at this below. When we are also considering levels adjacent to that of the currently estimated MTD, then it is important that, in some sense, each level is allowed a fair try. The idea is that if, for example, we consider level i to be the most likely candidate for being the MTD, then when considering levels i – 1 and i + 1 as potential MTD candidates, the evidence should be provided by the observations with minimal influence exerted by the choice of skeleton. In other words, the skeleton influence needs to be as weak as possible.

In order for the corollary to apply and provide a recommendation that translates in the same way as the shift in the dose levels, we need for the skeleton spacing to not depend on the parameter a, i.e. the current level. Note that if,

$${\delta }_i=log(-log({\alpha }_i))-log(-log({\alpha }_{i-1}))$$ (3)

does not depend upon i, i.e., δ_i = δ for all i, then we achieve our objective since it depends only on the spacing between the skeleton values and not the unknown parameter. We then calibrate the skeleton spacing so that from one value to the next, on the log(−log) scale the gaps are constant and equal to δ. We call this an equidistant skeleton. For example, for k = 3 a skeleton of 0.3, 0.5, 0.7 is often considered to be of equal distance on the probability scale. Based on the definition of equidistant here, the skeleton values are 0.30, 0.48, 0.64, for δ = −0.5, and 0.3, 0.64, 0.85 for δ = −1 which are different than the values obtained based on equal distance on the probability scale. The value of δ controls how fast or slow we escalate or move across dose levels. In practice, δ should not be too large as this will make escalation very conservative (slow) and very small values of δ will amount to a fast escalation. In general, if we fix the skeleton value for the starting dose to be equal to θ and the last dose to be α_k ≤ 1 – θ, then there are very few values of δ that will result in an equidistant skeleton. Table 1 provides general guidelines for skeletons and corresponding δ values that work well under different true scenarios as a function of k levels and for θ within the interval [0.2 – 0.3]. The skeleton in a particular clinical study should be chosen based on the review of the operating characteristics of a particular clinical scenario and other considerations such as for example use of single or two stage designs which we cover in Section 2.6.

Table 1.

Recommended skeleton values α_i when experimentation starts at dose level 1 and θ = 0.25. Refer to Equation 3 for δ and α_i values.

k	−δ	1	2	3	4	5	6	7
3	0.78	0.25	0.53	0.75
4	0.50	0.25	0.43	0.60	0.73
5	0.39	0.25	0.39	0.53	0.65	0.74
6	0.30	0.25	0.35	0.47	0.57	0.66	0.73
7	0.26	0.25	0.34	0.44	0.53	0.61	0.69	0.75

2.4 Fixing the prior using an invariance property

Our goal is to to fix any prior g(a) for the working parameter a so that it is invariant in the sense described above, and at the same time it is not heavily biased. Indeed in the paper of O'Quigley, Pepe and Fisher (1990) [13], the simple prior that appeared to be relatively non-informative at most of the levels became somewhat more informative at the highest level making those few cases in which the highest level did correspond to the MTD to be quite difficult to attain. The problem can be overcome via the use of pseudo data. For this we need the following lemma;

Proposition 1 For any skeleton α_i, i = 1, …, k, and, for any w > 0 then using likelihood alone, the models ψ(d_i, a) = α_i^exp(a) and $\psi (d_i,a)={({\alpha }_i^w)}^{exp(a)}$ are equivalent.

By equivalent we mean that not only is the final recommendation the same but that at every step all estimates coincide and, in particular, the running estimate of the MTD. The proof is trivial following from an elementary property of likelihood estimators. One consequence of the proposition is that, if we are in the likelihood framework, we are unable to interpret skeleton values as prior probabilities of toxicity since any arbitrary power transformation has no impact on estimates of toxicity rates. Note that, assuming the working model, then in light of the above proposition, there exists some a* so that; ψ^1/w (d_i, a*) = α_i^exp(a*). If we represent any prior via pseudo data, and this is written as R̃(d_i), i = 1, …, k, it follows that

$${\delta }_i=log(-log(\stackrel{\sim }{R}(d_i)))-log(-log(\stackrel{\sim }{R}(d_{i-1})))$$ (4)

which can be compared with Equation 3. A constant δ = δ_i for all i, will satisfy the invariance property that we wish to have but will not of itself guarantee a single unique solution for α_i. As a result of the above proposition there are an infinite number of skeletons that satisfy Equation 4. We lose no generality in allowing the prior pseudo data $\stackrel{\sim }{R}(d_i)=t_i^{\ast }/n_i^{\ast }$, i = 1, …, k, to coincide with the skeleton, i.e., we fix a = 0 but, again, that does not determine our skeleton. It does nonetheless simplify things since we now only have one parameter to be concerned about rather than two. Finally, if we wish to start experimentation at level 2, then it makes sense to fix the skeleton value at level 2 to coincide exactly with the target rate, e.g. α₂ = θ = 0.2. This will also fix the prior data such that R̃(d_i) = 2/10 for example. If we have many levels, and we make use of a two stage design, then it is better to hold off on fixing the skeleton (and prior) until we run into our first DLT [14]. Then, most likely, we would take the level below the level producing the first DLT to coincide with the target rate in order to be fairly conservative.

2.5 Prior distribution, historical data and pseudo-data

It is challenging to choose a parametric function, g(a) that will have the properties that we require [16]. Such a function may be broadly “non-informative” but it will still, in general, favor certain levels over others. Table 2 shows the weights that correspond to each dose level prior to seeing any data under various prior distributions. The weights were calculated by first obtaining the partition S_i, i = 1, …, k, of the parameter space of a to correspond to each level. We then integrate the standardized likelihood at the respective interval to obtain, for i = 1, …, k,

Table 2.

Probability p̂_i at each dose level based on two approaches for given skeletons: exponential prior (upper panel) and pseudodata (lower panel). Refer to Section 2.3 for properties of each skeleton; sections 2.5 and 4.2 for pseudodata.

Skeleton	di = 1	2	3	4	5	6
Exponential prior
s1: 0.05, 0.10, 0.20, 0.30, 0.50, 0.70	0.46	0.11	0.12	0.15	0.13	0.03
s2: 0.01, 0.07, 0.20, 0.38, 0.55, 0.70	0.38	0.17	0.18	0.15	0.09	0.03
s3: 0.05, 0.11, 0.20, 0.30, 0.41, 0.52	0.47	0.11	0.11	0.1	0.09	0.12
s4: 0.01, 0.07, 0.20, 0.38, 0.56, 0.71	0.37	0.17	0.19	0.16	0.09	0.02
s5: 0.05, 0.11, 0.20, 0.31, 0.42, 0.53	0.47	0.11	0.12	0.11	0.09	0.11
Pseudodata
s1: 0.05, 0.10, 0.20, 0.30, 0.50, 0.70	0.11	0.07	0.09	0.18	0.36	0.18
s2: 0.01, 0.07, 0.20, 0.38, 0.55, 0.70	0.07	0.08	0.14	0.22	0.28	0.21
s3: 0.05, 0.11, 0.20, 0.30, 0.41, 0.52	0.12	0.07	0.09	0.13	0.16	0.43
s4: 0.01, 0.07, 0.20, 0.38, 0.56, 0.71	0.07	0.08	0.14	0.22	0.29	0.19
s5: 0.05, 0.11, 0.20, 0.31, 0.42, 0.53	0.12	0.07	0.1	0.13	0.17	0.40

$${\widehat{p}}_i=Pr(d_m=d_i)=H_j^{-1}{\int }_{{\kappa }_{i-1}}^{{\kappa }_i}exp\{{\mathcal{L}}_j(u)\}g(u)\mathit{\text{du}}.$$ (5)

Note that these probabilities are the posterior probabilities of how likely is each level d_i to be the true MTD (d_m) given the data. When the sample size increases without bound and under the conditions in Shen and O'Quigley [21], p̂_m → 1 at the MTD and p̂_i → 0 at all other levels. The estimated rates of toxicity R̂(d_i) which we use to estimate the MTD, d̂_m, approach θ at the MTD as the sample size increases.

The approach becomes much simpler and more transparent when we make use of pseudo-data; $\stackrel{\sim }{R}(d_i)=t_i^{\ast }/n_i^{\ast }$. Following Section 2.4 we make sure that, up to any positive power transformation, R̂(d_i) coincides with the skeleton rates. And no generality is lost by choosing the power transformation to be one. This allows us to reduce the parameter dimensionality and simulation studies shown later confirm that the operating characteristics of such an approach are at least as good as established approaches. For example for a skeleton given by α_i = (0.1, 0.2, 0.3, 0.5, 0.6, 0.7), if we have a total of 60 pseudo-patients, the number of DLTs at each of the 6 dose levels will be 1/10, 2/10, 3/10, 5/10, 6/10, 7/10. The data from the 60 pseudo-patients should not be taken to have equal value as the real patients, but instead the contribution to the likelihood from pseudo-data should be small compared to data obtained from treated patients. We suggest to divide the sum of contributions from pseudo-data to the log likelihood function by the total number of pseudo-patients, for example 60, which is equivalent to equating data from pseudo-patients as 1 real patient. In other words, pseudo-patients correspond to a single theoretical patient divided into 60 contributions spread across all levels. If we denote ℒ_n*(a) as the log likelihood from n* pseudo patients, and g(u) is defined in terms of pseudo data, i.e. g(u) = exp{(1/n*)ℒ_n*(u)}, the probabilities given in Equation 5 are given by: ${\widehat{p}}_i=Pr(d_m=d_i)=H_j^{-1}{\int }_{{\kappa }_{i-1}}^{{\kappa }_i}exp\{{\mathcal{L}}_j(u)+(1/n^{\ast }){\mathcal{L}}_{n^{\ast }}(u)\}\mathit{\text{du}}$ where $H_j={\sum }_{{\kappa }_i}{\int }_{{\kappa }_{i-1}}^{{\kappa }_i}exp\{{\mathcal{L}}_j(u)+(1/n^{\ast }){\mathcal{L}}_{n^{\ast }}(u)\}\mathit{\text{du}}$.

In Table 2 we show these probabilities calculated for the exponential prior and for a prior based on pseudodata. The results show that the exponential prior is not as flat as we expect, as indicated by how far it is from an equal weight of 1/6 for each dose level. The proposed skeleton and prior based on pseudodata have weights that are still not equal to 1/6 at all levels but are closer to 0.2.

Here we illustrate how to use pseudodata to form a prior and solve for the unknown dose toxicity parameter a. Let us denote the pseudo patients at each level as $n_i^{\ast }$, with $n\ast ={\sum }_i^k{n}_i^{\ast }$ and the pseudo toxicities at each level as $t_i^{\ast }$ then the score function based on the pseudo observations alone is:

$${\mathcal{U}}_{n_{\ast }}(a)=\sum _{i=1}^k[t_i^{\ast }\frac{{\psi }^{\prime }}{\psi }(d_i,a)+(n_i^{\ast }-t_i^{\ast })\frac{-{\psi }^{\prime }}{1-\psi }(d_i,a)],$$ (6)

whereas the score function based on the data alone is 𝒰_j(a|Ω_j) = ∂ℒ_j(a)/∂a. Our estimates are based on the equation ${\mathcal{U}}_j^{+}(a)=0$ where ${\mathcal{U}}_j^{+}(a)={\mathcal{U}}_j(a|{\mathrm{\Omega }}_j)+(1/n^{\ast }){\mathcal{U}}_{n^{\ast }}(a)$. In this way the “weight” of the pseudo-observations corresponds to a single patient, so, in a study with 25 patients, we can say that roughly (since it depends on an unknown reality), about 4% (1/25) of the information has been “added-in” by the prior (the existing data are 25 patients and the added information is 1 patient). This approach makes the prior contribution more explicit so that if 4% is deemed too strong, it can be readily reduced to a figure considered acceptable. It can equally well be made stronger by using a smaller value of n* and all of the prior data can be changed to mirror prior beliefs or simply to obtain some particular kind of operating behavior. Our purpose here is to fine tune a design that can be used in most clinical situations. Operating characteristics over many simulated trials will evaluate the robustness of the design to the choice of these parameters as shown in Section 4.2.

2.6 Initial escalation

A large number of studies, both theoretical and via simulations, show that CRM based designs work well and perform close to the optimal design [17, 18]. This is particularly true when there is a fixed number of levels under study, preferably around 6 levels. For more than 8 levels, it becomes difficult for any method, even the optimal, to locate the MTD with reasonable accuracy given the sample sizes of Phase 1 trials (20-30 patients). Sometimes we do not know in advance just how many levels there may be, and only by experimentation do we discover the answer. If there are more than 8 levels, or there is a reasonable chance that there may be more than 8 levels, then our suggestion is to use a two-stage design. An initial stage, in a two-stage design, will start off at a low, and usually the lowest, level and gradually escalate according to clinical rules pre-specified in the protocol, not based on a model. The first DLT completes the first stage and the second stage then kicks in as per usual for a model based design. Two stage designs have been studied extensively [19, 14].

At the start of the second stage, the design and model parameters need to be defined. It may seem prudent to continue experimentation at one level below that at which the first DLT was observed. This seems reasonable whether the first observed DLT corresponds to one patient out of one, one out of two or, indeed, one out of three. This level can be our first best guess at being the level corresponding to the target, typically 0.20, in which case both the skeleton and the prior data would correspond to 0.20. The skeleton can be centered around this level by calling this as “level 3”, leaving two available levels just below it. The skeleton for these levels is obtained from equal shifts in δ_i. The same procedure is applied to the levels above level 3. What do we make of the observations we already have on non-toxicities before the first observed toxicity? Information obtained at 3 levels or lower from the current best estimate of the MTD will be very small and, for practical purposes, negligible [14].

3 Estimation and inference

3.1 Defining an MTD and a co-MTD

The traditional definition of the MTD in model-based designs is the dose that is closest to θ, the target DLT rate, based on the predicted DLT rates at the trial completion. We define a co-MTD as the next dose closest to θ following the MTD. Since R̂(d_i) < θ < R̂(d_i+1) and d̂_m = d_i or d̂_m = d_i+1 depending on the euclidean distance, then the estimated co-MTD is d_i if d̂_m = d_i+1, or the co-MTD is d_i+1 if d̂_m = d_i. In the illustrative example below, d₂ is the MTD and d₃ is the co-MTD. An important question is how often do these two dose levels contain the true MTD and how often do we expose patients to high risk if we select a level above the MTD. This is assessed via simulations below. If we find that under the restrictive small sample sizes of Phase 1 trials (25) we are still able to select 2 levels that include the true MTD with high probability then we will feel confident that we were able to locate the true MTD and thus experiment in a therapeutic window in later phase trials.

3.2 Estimated probability of having located the MTD

Performance of any dose escalation design is usually judged on the basis of the 2 criteria: the accuracy of final recommendation, i.e. the percent of trials with correct selection of the MTD or PCS, as well as safety, typically measured as the number of patients treated at and above the MTD. While still using these two criteria to drive our method we will also wish to introduce a new emphasis: the posterior estimated probability that any dose is in fact the true MTD. This is given based on Equation 5 as p̂_i = Pr(d_m = d_i)

On the basis of this equation we can calculate, and illustrate, our running estimates of the probability of any level being the MTD. In practice, simulations confirm that very quickly in most cases, the probability mass is concentrated around just a few levels and tending to just two levels as the sample size gets larger and this is shown with an example of a clinical trial below. For the purpose of comparing with other established criteria, one could use the highest probability to determine an estimate of the MTD p̂_i, as argmax_ip̂_i. For simplicity here we will report the distribution of values of p̂_i, i = d_m, at the estimated MTD and co-MTD.

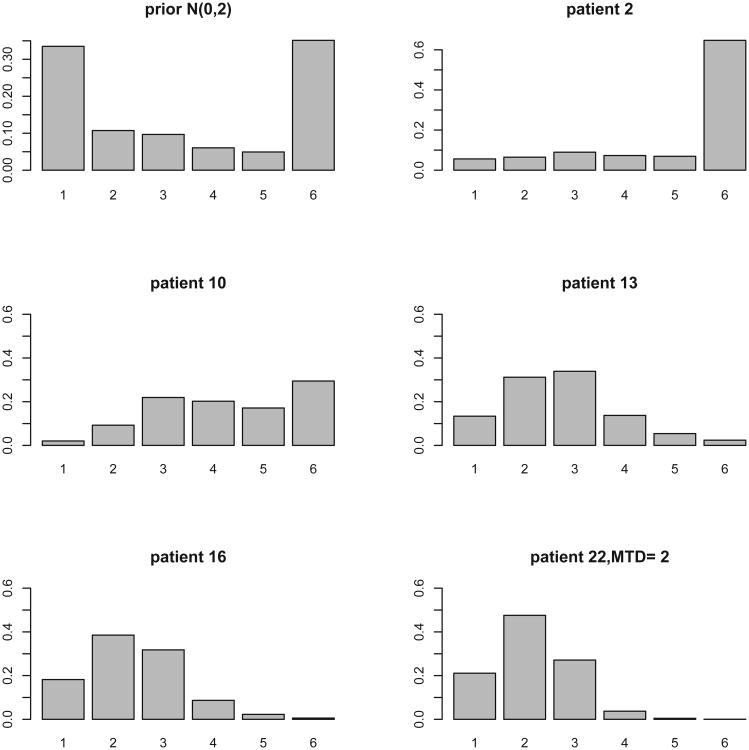
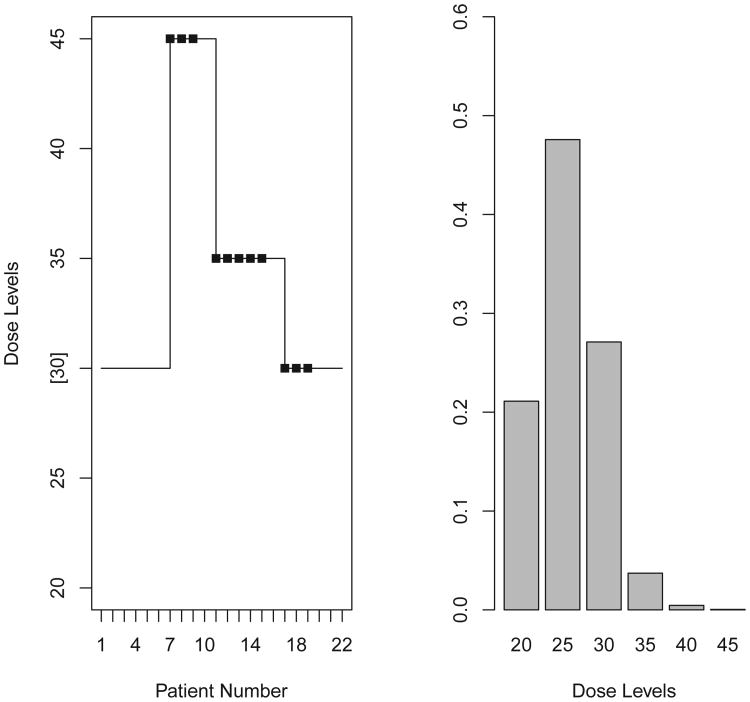
To illustrate the above measure, we use a Phase 1 trial of platelet-derived growth factor receptor inhibitor imatinib mesylate and docetaxel in prostate cancer patients. [22] The study consisted of a lead-in period, where patients were treated with imatinib mesylate at 600 mg/m2 daily in single or divided doses for 30 days, and a combination therapy phase. Patients who received at least 80% of the prescribed drug were eligible for combination therapy where they received intravenous docetaxel at one of the 6 tested dose levels for 4 consecutive weeks (days 1,8,15, 22). Dose escalation for docetaxel with imatinib at a fixed dose was guided by CRM, starting from 30 mg/m2 as the initial dose level and treating patients in cohorts of 6. The MTD was defined as the dose of docetaxel in combination with imatinib at 600 mg/m2 that achieved a DLT rate closest to 30%. The study enrolled 28 patients, 22 were evaluable for toxicity assessment within cycle 1. The trial used the power model $\psi (a)={\alpha }_i^{exp(a)}$, with Normal (0,2) as a prior distribution on a; α_i = (0.07, 0.16, 0.30, 0.40, 0.46, 0.53). Figure 2 shows the trial history starting experimentation from level 3. The trial skipped two levels, and once DLTs were observed there was de-escalation to levels 4 and 3. Although the model based estimate of the MTD was level 2, level 3 was the RP2D based on the observed toxicity rates at higher levels. Based on the classical definition of MTD, the dose closest to the target rate of 0.3, level 2 is the MTD (predicted rates were 0.16, 0.28, 0.43, 0.53, 0.58, 0.64 for i = 1, …, k respectively). However, based on the observed rate of 3/12 (25%) at level 3 and the fact that no patient was treated at level 2, the RP2D selected by the investigators was level 3. This trial is not a good illustration of how to implement CRM in practice because the use of a large cohort size (6 patients) without frequent model/dose updates along with skipping dose levels resulted in a large number of patients being exposed to high toxicity. However, this example is used to illustrate the calculations of Pr(d_m = d_i) in a real trial. Figure 2 (right panel) shows the estimated Pr(d_m = d_i) at the end of the trial after 22 patients were treated, with the mass concentrated around d₂, and d₃. Based on the observed rates which are 0.25, 0.83, 0.75 at levels 3,4,6 respectively, the weight (probability) on each dose level is being shifted from levels 1,2 to levels 2,3.

Figure 2.

Estimated Pr(d_m = d_i) for 6 levels in the trial reported by Matthew et al 2004 that used a N(0, 2) as a prior distribution on a.

3.3 Determining when to stop the dose-escalation and start the DEC

Typical model-based Phase 1 trials have a fixed sample size or allow the trial to stop when projections based on current data indicate that there is a high chance that future patients will be treated at the same level, ie the method has settled [24]. The theory behind existing stopping rules rely on the single MTD definition. In the era of Phase 1 dose escalation studies followed by dose expansion cohorts, and in the setting where we are interested in more than a single MTD, different stopping rules are needed. The estimated probabilities Pr(d_m = d_i) at each level can help us decide when it is time to stop the Phase 1 escalation phase and move into the DEC phase. When the sum of these probabilities at two levels, the estimated MTD and co-MTD, exceeds a threshold say 80-%-90% then the data based on the dose-escalation phase provide us with sufficient confidence to move into the DEC phase. In the illustrative example, after 22 patients at the end of the trial, dose levels 2 and 3 are the two levels with the highest probabilities Pr(d_m = d_i) among all levels, with level 2 and level 3 having a probability of 0.48 and 0.27 respectively. If a dose expansion trial had followed, then these two levels would be carried forward to DEC. These probabilities can be summed (0.48+0.27) and we can then consider more than a single dose level for the DEC, most often two levels and occasionally three. Before we move forward into the dose expansion cohort we would like the sum of these probabilities to be high, say close to 80-90%.

The choice of the actual threshold that we will use, e.g. 80-90%, depends on many clinical factors such as the drug under investigation, whether this is a single agent or combination regimen, the disease type, the patient population and other factors such as competing studies, drugs in the pipeline, funding and available resources. The simulation study below provides numerical results on how these probabilities can be used to assess our confidence in the estimated MTD and what are the likely values we observe in the setting of a 25 patient study.

3.4 Determining the recommended Phase 2 dose

It has been established that the accuracy of model based designs in terms of how often we find the true MTD is around 50% in contrast to 30% accuracy of simple algorithmic designs [23]. In order to increase accuracy further, we either need to increase the sample size during the dose escalation phase or we need to consider this uncertainty in the design of dose expansion cohorts. As we move away from pure Phase 1 dose escalation studies to Phase 1 + DEC studies, then assigning all patients at a single MTD is likely not going to be useful during the DEC where efficacy or immune endpoints are also taken into account. Refer to [12] for methods on how to address bivariate endpoints during the DEC. Selecting which levels to take into the expansion is not trivial. The estimated probabilities that each dose is the true MTD, given in Equation 5 can inform investigators which levels to take into the DEC. We argue in favor of experimentation at more than a single dose for the DEC and we can take into account the precision or uncertainty in the estimated MTD to inform the choice of levels. If we take the estimated MTD and the co-MTD to the DEC and the two levels contain the true MTD with a very high chance, as measured by p̂_i, then we feel confident that we are now within an active therapeutic window. Once we experiment at two levels during the expansion phase, efficacy or other secondary endpoints such as PK/PD can determine the RP2D. While we may not reduce uncertainty across the board at all levels in all situations there are certain situations in which we clearly can reduce uncertainty. Numerical studies below illustrate the accuracy of this approach compared to other approaches.

4 Operating Characteristics

4.1 Data Illustration

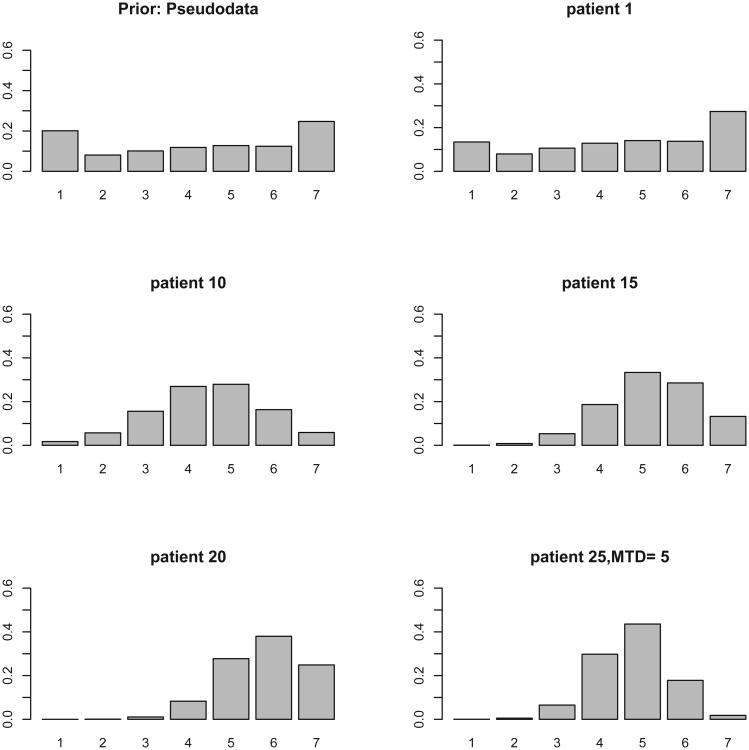
This trial is a hypothetical trial with an equidistant skeleton given by 0.20, 0.30, 0.41, 0.52, 0.62, 0.70, 0.77 which was obtained by equation 3, with k = 7, δ = −0.3 and experimentation starts at level 1 so level 1 has α₁ = θ = 0.2. Pseudo-data are 10 patients per dose, for a total of 70 patients, with DLT rates give by the skeleton. For this prior/skeleton the weight at d₃ before seeing any data is around 0.10 and then as the data accumulates it shifts to around level 5 which is the true MTD (true DLT rates are 0, 0.03, 0.05, 0.1, 0.2, 0.45, 0.7); Figure 3. After 25 patients, the estimated values for Pr(d_m = d_i) are 0.30, 0.44, 0.18 at levels 4, 5, 6 showing that carrying forward only level 5 in a hypothetical dose expansion phase would mean that there is still high uncertainty as to whether level 5 is the MTD (0.56=1-0.44). Carrying two levels leads to 0.26 uncertainty, while carrying three levels forward into the DEC diminishes this uncertainty to 0.08.

Figure 3.

Estimated Pr(d_m = d_i) for 7 levels in a hypothetical trial that used an equidistant skeleton and pseudodata that correspond to this skeleton.

4.2 Simulations

In this section we consider how the proposed approach compares with existing methods for selecting model skeletons. Specifically, we compare the operating characteristics of the proposed skeleton with the method proposed by Lee and Cheung [25] and the original CRM paper [13]. Lee and Cheung [25] proposed the use of a skeleton model which is defined as a skeleton in which the percent correct selection is highest compared to other skeletons, and the method requires that the location of the true MTD is specified. It was suggested by other authors to use Bayesian Model Average whereby more than a single skeleton is used as a way to increase robustness to model choice [16]. Models that may appear to be providing an awkward fit would be weighted down in favour of ones that, at least locally, provide a better description of the accumulating observations. This is an interesting idea but could be computationally complex. The following parameters, and methods were compared; N = 25, k = 6, 7, θ = 0.20 and 1000 simulated trials:

CRMB: Bayesian CRM ( $\psi (a)={\alpha }_i^a$) with exponential prior and α_i = 0.05, 0.10, 0.20, 0.30, 0.50, 0.70 which was used in the original CRM paper [13]

CRML₂: CRM with pseudodata and equidistant skeleton, α_i = 0.01, 0.07, 0.20, 0.38, 0.55, 0.70, δ = 0.5

CRML₃: CRM with pseudodata and equidistant skeleton, α_i = 0.05, 0.11, 0.20, 0.30, 0.41, 0.52, δ = 0.3

CRML₄: CRM with pseudodata and skeleton obtained via the method of [25] with halfwidth=0.08.

CRML₅: CRM with pseudodata and skeleton obtained via the method of [25] with halfwidth 0.05.

For pseudodata, 100 pseudo observations per dose level were used (n* = 600, k = 6 using Equation 6) with toxicity rates equal to the skeleton rates shown above. The proportion of trials that selected each dose level using the above methods under the 5 scenarios used by O'Quigley et al 1990 [13] are presented in Table 3. We see that using equidistant skeletons resulted in improvements in PCS over CRMB across all scenarios except scenario 4, indicating that the skeleton and prior selection used by O'Quigley et al 1990 could be improved especially when the last level was the MTD. This is because the exponential prior in combination with that skeleton is putting a lot of weight on d₁ making it more difficult to attain the last dose. Among the other skeletons evaluated here the difference is in the δ value which controls the separation from adjacent levels. All four skeletons resulted in similar operating characteristics supporting that the recommended approach is as good as the approach developed by Lee and Cheung [25] and these skeletons are easy to obtain (Equation 3) and do not require specification of the true MTD, just the starting dose.

Table 3.

Proportion of trials that selected each dose level as the final MTD out of 1000 trials for a given scenario; R(d_i) denotes true DLT rates. CRMB is the original Bayesian CRM; CRML₂, CRML₃, CRML₄ and CRML₅ use pseudodata and the approach described in Section 4.2 with skeletons s₂, s₃, s₄, s₅ respectively.

Levels	1	2	3	4	5	6
R(di)	0.00	0.00	0.03	0.05	0.11	0.22
CRMB	0.00	0.00	0.00	0.07	0.60	0.32
CRML2	0.00	0.00	0.00	0.06	0.39	0.54
CRML3	0.00	0.00	0.00	0.05	0.30	0.65
CRML4	0.00	0.00	0.00	0.07	0.39	0.55
CRML5	0.00	0.00	0.00	0.05	0.30	0.65
R(di)	0.00	0.00	0.03	0.05	0.06	0.22
CRMB	0.00	0.00	0.00	0.05	0.44	0.52
CRML2	0.00	0.00	0.00	0.04	0.28	0.68
CRML3	0.00	0.00	0.00	0.03	0.22	0.75
CRML4	0.00	0.00	0.00	0.04	0.28	0.68
CRML5	0.00	0.00	0.00	0.03	0.22	0.75
R(di)	0.00	0.00	0.03	0.05	0.10	0.30
CRMB	0.00	0.00	0.00	0.06	0.68	0.26
CRML2	0.00	0.00	0.00	0.06	0.51	0.43
CRML3	0.00	0.00	0.00	0.06	0.42	0.52
CRML4	0.00	0.00	0.00	0.06	0.50	0.44
CRML5	0.00	0.00	0.00	0.05	0.44	0.51
R(di)	0.00	0.00	0.03	0.05	0.10	0.50
CRMB	0.00	0.00	0.00	0.06	0.83	0.10
CRML2	0.00	0.00	0.00	0.06	0.76	0.18
CRML3	0.00	0.00	0.00	0.07	0.70	0.23
CRML4	0.00	0.00	0.00	0.06	0.75	0.19
CRML5	0.00	0.00	0.00	0.07	0.71	0.22
R(di)	0.20	0.90	0.90	0.90	0.90	0.90
CRMB	0.96	4.00	0.00	0.00	0.00	0.00
CRML2	0.96	0.04	0.00	0.00	0.00	0.00
CRML3	0.99	0.01	0.00	0.00	0.00	0.00
CRML4	0.96	0.04	0.00	0.00	0.00	0.00
CRML5	0.99	0.01	0.00	0.00	0.00	0.00

These findings confirmed that CRML₃ is close to CRML₅ and CRML₂ is close to CRML₄ since the skeletons are very close, so we present the estimated Pr(d_m = d_i) for the 3 methods, CRMB, CRML₂, CRML₃ in Supplemental Table 1. The results confirmed that the proposed skeletons and pseudodata approach reduce the uncertainty in the estimated MTD in cases where CRMB was not optimal. Supplemental Table 2 shows the percent of patients being treated at each dose level across many scenarios and confirms the sample size distribution (across dose levels) reported previously [14]. On average at least 70% of patients are being treated at the MTD and co-MTD.

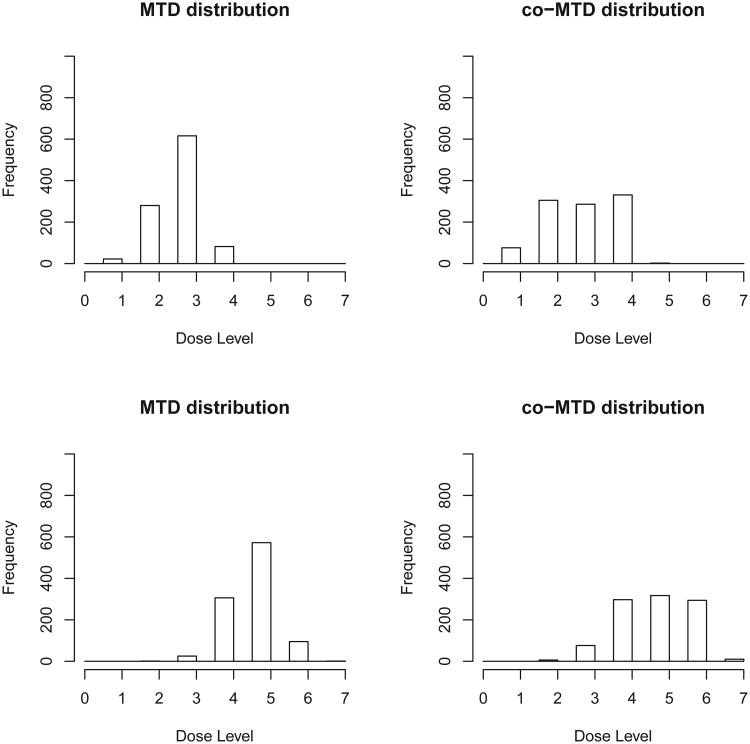
Supplemental Table 3 shows various skeletons for seven dose levels; k = 7, θ = 0.20, δ = −0.3. The scenarios here were selected such that the location of the MTD varied and k = 7 allowed for centering the prior exactly in the middle. Figure 4 shows that the distribution of the estimated MTD with N = 25 is concentrated around the true MTD. The distribution for the co-MTD is clearly centered at much the same place as the estimated MTD, but it is flatter and more spread out. This is expected since the co-MTD is on either side of the MTD, based on the predicted rates of DLT. Although the co-MTD distribution is more spread out over 3 levels, it is still very reasonable since it concentrates on the doses at and next to the MTD. Scenarios where the MTD is the first or last level were omitted from this assessment since the co-MTD cannot be defined in such cases. In these scenarios, the estimated MTD and co-MTD included the true MTD 90% of the time with sample size of 25 (Table 4). A reviewer pointed out the possibility of the co-MTD being higher than the true MTD and the practical implications of this. Based on the scenarios we examined here this can happen on average between 20-35% of the time. In the context of non cytotoxic agents the dose above the MTD might not necessarily be toxic, nevertheless, it is essential to include safety stopping rules in the dose expansion cohort if a dose is deemed not safe in light of additional data. Safety stopping rules are now required by many protocol review committees as safety is often the primary aim of dose expansion cohorts. [7]

Figure 4.

Distribution of MTD (left) and co-MTD (right panel) for scenario 1 R(d_i)=(0.05,0.1, 0.2,0.5,0.7,0.75,0.8); MTD=3 (top panel), and scenario 2, R(d_i)=(0,0.03,0.05,0.1,0.2,0.45,0.7); MTD=5 (lower panel).

Table 4.

Percent of trials that selected the true MTD (PCS:percent correct selection); %trials with highest probability at true MTD, p̂_dm; % trials with second highest probability at true MTD; % trials where the two highest probabilities, p̂_di, exclude the true MTD; mean estimated value of p̂_dm and p̂_dm−1 over 1000 simulations. R(d_i) denote the true rates and s_i denote different skeletons.

	PCS	% trials with highest p̂dm	% trials with 2nd highest p̂di	% trials where two highest p̂di exclude MTD	p̂dm	p̂dm−1
R(di)=(0.05,0.1, 0.2,0.5,0.7,0.75,0.8)
s6	60	59	32	9	0.38	0.25
s7	62	59	33	8	0.38	0.24
s8	61	61	30	9	0.37	0.25
s9	60	59	33	8	0.37	0.25
R(di)=(0,0.03,0.05,0.1,0.2,0.45,0.7)
s6	54	54	36	10	0.36	0.25
s7	58	58	33	10	0.37	0.24
s8	59	58	34	8	0.37	0.24
s9	58	58	32	9	0.37	0.23
R(di)=(0,0,0,0.03,0.05,0.11,0.22)
s6	52	75	12	13	0.28	0.3
s7	63	81	11	8	0.65	0.24
s8	66	84	9	7	0.68	0.23
s9	69	85	8	6	0.70	0.22
R(di)=(0.2,0.5,0.8,0.9,0.9,0.9,0.9)
s6	93	91	9	1	0.73	0.22
s7	91	91	9	1	0.73	0.22
s8	90	90	9	1	0.72	0.23
s9	90	90	10	0	0.72	0.22

Table 4 compares the percent correct selection to the estimated probabilities Pr(d_m = d_i) and also reports the relative and absolute importance of these estimated probabilities. We see that the percent of trials where the highest probability among the 7 levels is at the true MTD is very close to PCS except for scenario 3 where the probability is much higher than PCS. We also see that on average the chance that the two levels with the highest probabilities exclude the true MTD is 10% or smaller with a sample size of N = 25. We can view these probabilities as error rates, i.e. the chance of missing the right dose after including N patients. In addition, on average the probability at the true MTD given by Equation 5 is typically around 0.40, and it rarely exceeds 0.60 when N = 25 which is consistent with our knowledge of the optimal benchmark and how large can PCS be or the attainable values of PCS [17]. The sum of the probabilities, Pr(d_m = d_i) at the true MTD and co-MTD is on average 0.65 (Table 4, sum of columns 6-7). Supplemental Table 4 shows the entire distribution of the values of Pr(d_m = d_i) at the estimated MTD and co-MTD over 1000 trials. It is also important to evaluate how often the estimated MTD or co-MTD are above the true MTD. In the scenarios we examined on average the estimated MTD is higher than the true MTD 4-24% of trials which is consistent with the reported literature on how often we choose a level above the true MTD as the recommended dose [26, 27]. The highest percentage (24%) occurs when the true rates below and above the MTD are 0.15 and 0.50 respectively and we target a dose with a target rate of 0.25 (data not shown). The estimated co-MTD is above the true MTD on average 30%. An important question is what is the observed DLT rate at these 2 levels i.e. how many patients are exposed to DLTs, and simulations confirmed the DLT rate is acceptable (mean observed DLT rate is 0.2 and interquartile range is 0.17-0.22 for the scenarios of Table 4).

In the scenarios we examined, 83-88% of the time the set of two levels, namely the MTD and co-MTD obtained based on R̂(d_i) were also the two levels that had the highest and second highest Pr(d_m = d_i) among all levels. The two sets of estimated MTD, and co-MTD included the true MTD on average 90% of the time regardless of which method was used to select the set. Simulations with larger sample size (N=50) showed that the value of the sum of the two probabilities at MTD and co-MTD increase with sample size and this can be used as evidence of whether to increase the sample size during dose-escalation phase before going into the dose expansion phase (data not shown). These measures also serve as an indication of whether we need to continue experimentation in order to reduce the uncertainty in the dose taken forward, or whether to take more than a single dose into the DEC phase.

5 Discussion

There has been a lot of progress in the field of dose finding methodology in oncology, and numerous model based dose escalation designs have been introduced. For example, Pan et al developed a Phase I/II design that aims to find a desirable dose in terms of both safety and efficacy thresholds, and thus efficacy is used to decide which levels to carry over to Phase II. In the Pan et al [3] design, the phase I and II phases are being carried out simultaneously, not subsequently, while promising dose levels leave the phase I phase and go into phase II but both phases are open for enrollment simultaneously. The clinical problem we focus on here is when efficacy is not part of the decision on which levels to take forward into the dose expansion cohort, and only safety determines the dose escalation part. The dose escalation is typically small (< 25 patients), which is different than existing designs with bivariate endpoints of safety and efficacy that require a much larger sample size in order to address both aims simultaneously [3].

The underlying assumption to all model based designs used for cytotoxic agents is that the higher the dose the higher the rate of both efficacy and toxicity. The scientific objective in the simple setting is typically to determine the MTD with as few patients as possible, and treat most patients close to the MTD, while still maintaining safety at all times. CRM was introduced as a sequential method that meets the ethical, scientific and safety criteria while treating patients at the best estimate of the MTD. Many modifications followed in an attempt to mimic the clinical practice more closely, such as starting experimentation at the lowest dose and preventing dose jumps. Other extensions examined the theoretical or large sample properties and proposed ways to fine tune certain parameters. Escalation with overdose control (EWOC) was proposed in order to favor estimates below the MTD rather than symmetric approaches [26]. Currently, there are a number of designs and models one could choose from to use in a dose escalation study with an MTD objective. Moreover, the literature suggests that there are no advantages to using a more complicated design in basic dose escalation trials like the ones described above, and a simpler, more parsimonious model is adequate [28, 29].

This work proposes a skeleton and a prior in the form of pseudodata that coincide with the skeleton, thus eliminating 1 of the 2 parameters required in the original CRM paper and providing measures on how to decide which two levels to take into the dose expansion phase. While we provided one possible criterion based on equal spacing of doses and the invariance property, other criteria might be developed, especially in cases where we have strong prior information against certain dose levels or favoring other dose levels. Variable distances may help in such situations and this is something that could benefit from deeper study. In addition, the pseudodata can be built from historical data if available, but note that the actual weight that the historical data have relative to the actual data should be investigated and it should be chosen based on clinical considerations. We do not want to give a large weight and in our experience, a weight of 1/n* where n* is the number of pseudo observations or historical data has performed well. Refer to Iasonos, Wages, Conaway et al (2016) for recommendations on using historical data and more detailed discussion on model parameterization. The proposed approach of estimating the co-MTD might be extended in settings where ordinal longitudinal data (repeated cycles) and cumulative toxicities are being used possibly leading to further increasing the ability to detect the pair of MTD and co-MTD. Multiple other strategies could integrate the co-MTD approach such as EWOC and designs that explore different distance measures.

This paper provides a unified phase 1 clinical trial design that addresses the current objectives of Phase 1 trials, which are different than the ones that involved a pure Phase 1 dose escalation study [7, 2]. Only a few years ago the DEC were almost unknown in this context, and clearly the objectives of Phase 1 trials have changed. We described the dose escalation phase as dose selection where investigators want to eliminate dose levels that are too toxic or too low therapeutically by identifying a region, a narrow therapeutic window of one or two levels where we should focus experimentation during the dose expansion phase. We showed that the current practice of taking 1 level into DEC is associated with higher error. In order to decrease this error, we can either increase the sample size before initiating the dose expansion phase and thus reduce the uncertainty (increase precision), or take 2 levels in DEC leaving the sample size of the dose-escalation phase unchanged.

Figure 1.

Illustrative trial. Left panel: trial history reported by Matthew et al 2004 that used a N(0, 2) as a prior distribution on a. Right panel: estimated Pr(d_m = d_i) for 6 levels after N=22 patients are treated, d_m is the true MTD. Squares show dose limiting toxicities.