Separation of rotational and translational segmental momentum to assess movement coordination during walking

Abstract

This investigation presents an analysis of segmental angular momentum to describe segmental coordination during walking. Generating and arresting momentum is an intuitive concept, and also forms the foundation of Newton-Euler dynamics. Total segmental angular momentum is separated into separate components, translational angular momentum (TAM) and rotational angular momentum (RAM), which provide different but complementary perspectives of the segmental dynamics needed to achieve forward progression during walking. TAM was referenced to the stance foot, which provides insight into the mechanisms behind how forward progression is achieved through coordinated segmental motion relative to the foot. Translational and rotational segmental moments were calculated directly from TAM and RAM, via Euler’s 1^st and 2^nd laws in angular momentum form, respectively, and are composed of the effects of intersegmental forces and joint moments. Using data from 14 healthy participants, the effort required to generate and arrest momentum were assessed by linking the features of segmental angular momentum and the associated segmental moments to well-known spatiotemporal and kinetic features of the gait cycle. Segmental momentum provides an opportunity to explore and understand system-wide dynamics of coordination from an alternative perspective that is rooted in fundamentals of dynamics, and can be estimated using only segmental kinematic measurements.

1. Introduction

Total segmental angular momentum is a foundational concept and quantity on which Newton-Euler mechanics are based. Generating and arresting momentum is an intuitive concept that is broadly and correctly used in nonscientific arenas (e.g., sports); however, in dynamic systems, momentum is primarily used as a stepping stone through which equations of motion are calculated (forward dynamics) or moments and forces are obtained (inverse dynamics). Joint kinetics, which are calculated using an iterative Newton-Euler method via inverse dynamics, are commonly used to describe both normal and pathologic human movement patterns and depend upon the total angular momentum of the surrounding segments (Robertson et al., 2004; Carollo & Matthews, 2009). Joint moments represent the net effect of forces (active muscle forces and passive tissues that cross a joint) that are used to generate and absorb power, and are used as a surrogate representation of joint demand during movement (Winter, 1984). Joint demand is often used to quantify the demands placed on the musculoskeletal system due to external biomechanical loads or muscle forces required for stabilization/segmental motion.

Theoretically, the Newton-Euler formulation on which joint kinetics are calculated provides a direct formulation of how forces and moments regulate segmental momentum. Euler’s First Law relates the forces to a segment to motion through the time rate of change of momentum:

$${\mathbf{F}}_{\mathit{\text{seg}}}=\frac{{}^{I}d}{dt}({}^I\mathbf{P}_{\mathit{\text{seg}}})=\frac{I_d}{dt}(m_{\mathit{\text{seg}}}{}^I\mathbf{v}_{\mathit{\text{seg}}})$$ (1)

where ^Ip_seg is the linear momentum of a segment (segment mass times linear velocity) observed in an inertial reference frame. Although the aggregate effect of walking is translational (moving from point A to point B), legged locomotion is accomplished through coordinated segmental rotations relative to other segments about shared axes at the joints, which is driven by joint moments (Kadaba et al., 1990). When a segment with mass rotates and translates, it has angular momentum that is related to external joint forces and moments through Euler’s Laws. Similar to Newton’s Second Law, Euler’s Second Law of rotational motion relates the applied forces and moments to a segment to motion through a statement of momentum:

$${\mathbf{M}}_o=\frac{I_d}{dt}({}^I\mathbf{h}_o)$$ (2)

where M_o is the sum of moments with respect to the inertially fixed point O applied to the segment and ^Ih_o is the total angular momentum of the segment with respect to O. Total angular momentum of a segment is composed of two independent components that result from the rotation of the segment relative to a reference point as well as the rotation about its center of mass (COM) (Kasdin & Paley, 2011), which we label as translational angular momentum (TAM) and rotational angular momentum (RAM), respectively. Considering the changes of TAM and RAM, which are separate components of segmental angular momentum, provides insight into segmental kinetics. The change in TAM over time of a segment is roughly proportional to the net external force applied to the segment at the joints (intersegmental forces), at the muscle attachment points on the segment, and by gravity (referred to as Newton’s Law in angular momentum form). The change in RAM over time is roughly proportional to the net moment provided by the muscles and connective tissue at each end of the segments.

Forward progression during walking is achieved through both translational and angular motion of individual segments, and therefore segment-based analysis of generating and arresting segmental angular momentum may provide additional insight into how the body coordinates segmental control. Because segmental angular momentum is embedded in inverse dynamic calculations that are commonly used to describe joint demand, we propose that kinetics derived from segmental momentum can provide insight into the effort required during movement (through segmental moments). Two investigations have employed a segmental angular momentum in walking by using principal component analysis (PCA) to examine contributions of total angular momentum of segment relative to the body COM to the sum of total angular momentum from all body segments, known as whole-body angular momentum (WBAM) using. Herr and Popovic (2008) concluded that despite large total segmental angular momentum with respect to the body COM, segment-to-segment cancellations occur to minimize WBAM. Bennett et al., (2010) accounted for synergistic control of segmental angular momenta using three principal components in each plane, and the synergies did not change with the gait speed. Although PCA demonstrates segmental synergies in orthogonal parameter spaces created by directions of variance (principal components), to our knowledge, the actual shapes and patterns of individual segmental angular momenta over time are less commonly reported. Two recent investigations have assessed the relative contributions of grouped segmental momenta (upper and lower body) to WBAM in patients with cerebral palsy (Russell et al., 2011) and patients with amputation (Pickle et al., 2016). Although this approach is useful for identifying strategies for maintaining balance and overall control of the system, we propose that more detailed analyses of individual segmental angular momentum can provide additional insight into coordinated segmental motion. The identification of individual segmental movement patterns is what is done in a clinical movement retraining setting, but has not been accomplished using individual segmental momenta.

Measurement of segmental angular momentum is relevant to both observational and instrumented analyses because it depends on segment kinematics that can be used to gain inference on joint kinetics via Euler’s Laws. Assessment of segmental kinematics is common in both observational and instrumented gait analyses, which are both used to identify movement dysfunction and assess outcomes of interventions that target movement quality (Saleh & Murdoch, 1985; Shull et al., 2014). Although important for guiding clinical reasoning, observational gait analysis lacks diagnostic standardization (particularly outside of level walking) and sensitivity (Toro et al., 2003), which can result in misidentification of compensatory movement patterns (Shores, 1980; Robinson & Smidt, 1981; Holden et al., 1984; Frigo et al., 1998) due to poor observer training, observer bias, parallax error, and poor intrarater reliability (Krebs et al., 1985; Coutts, 1999). Instrumented gait analysis, in contrast to observational gait analysis, is currently the gold standard for accurately quantifying human movement (through the measurement of segment velocities, accelerations, forces, moments, and muscle activity); however, it is not commonly used in a clinical setting due to high monetary, computational, and time expenses. By contrast, angular momentum can be easily measured using wearable sensors. At this time, however, the theoretical foundations of using segmental angular momentum to provide insight regarding kinetics and the subsequent interpretation of the waveforms to identify movement patterns remains unknown.

The objective of this investigation was to explore the use of segmental angular momentum to describe coordination and effort during overground walking. We chose to apply this analysis to walking because gait is the most commonly assessed and taught task in biomechanics, and provides an opportunity to link it to other well-known aspects of gait biomechanics. Total angular momentum of each segment is described using the independent components TAM and RAM, and the segmental moments calculated by the time rate of change of TAM and RAM.

2. Dynamic Theory of Separation of Segmental Angular Momentum

2.1. Selection of the Reference point

Selecting a reference point is critical for interpreting the translational component of segmental angular momentum. We propose that separate analysis of TAM referenced to the foot in contact with the ground and RAM will provide a unique insight into the mechanisms behind how forward progression is achieved with respect to the stance foot. Reference TAM to the foot during the stance period allows for interpretable insight using segmental kinetics about that point through the application of Euler’s Laws of rotational motion.

2.2. Mathematical Foundations

The principle of angular momentum separation demonstrates that the total angular momentum (with respect to a chosen point) of a segment is the sum of two independent components: 1) the angular momentum of the segment center of mass (with respect to the same point), often referred to as the “orbital” component, and 2) the angular momentum about the segment center of mass, often referred to as the “spin” component (Kasdin & Paley, 2011).

Total angular momentum of a segment with respect to the stance foot is the sum of segmental TAM (^Ih_seg/foot) and segmental RAM (^Ih_seg):

$${}^I\mathbf{h}_{\text{foot}}={}^I\mathbf{h}_{\mathit{\text{seg}}}{}_{/}{}_{\text{foot}}+{}^I\mathbf{h}_{\mathit{\text{seg}}}$$ (3)

TAM of a segment is defined as the angular momentum of the center of mass (seg) of the segment relative to the reference point at the stance foot COM (foot):

$${}^I\mathbf{h}_{\mathit{\text{seg}}}{}_{/}{}_{\text{foot}}={\mathbf{r}}_{\mathit{\text{seg}}/\text{foot}}\times m_{\mathit{\text{seg}}}{}^I\mathbf{v}_{\mathit{\text{seg}}}{}_{/}{}_{\text{foot}}$$ (4)

where r_seg/foot is the position vector of the segment relative to the stance foot, ^Iv_seg/foot is the velocity of the COM of the segment relative to the stance foot as observed in an inertial reference frame i, and m_seg is the mass of the segment (Figure 1a). RAM of the segment is the angular momentum about its own COM:

$${}^I\mathbf{h}_{\mathit{\text{seg}}}={\mathbf{I}}_{\mathit{\text{seg}}}·{\mathbf{\omega }}_{\mathit{\text{seg}}}$$ (5)

where I_seg is the inertial tensor of the segment and ω_seg is the angular velocity of the segment as observed in the inertial reference frame i (Figure 1a).

Figure 1.

(a) An illustration of the stance limb just before midstance and the vectors used to calculate translational angular momentum (TAM) about the Foot. TAM is a cross product of the position vector with the linear momentum of the segment, which can be thought of as the “moment of momentum”. The in length of the position vector is relatively invariant during the stance period for the stance limb segments and rotates similar to an inverted pendulum. (b) The free-body diagram of the thigh just before midstance, which shows all the forces and moments applied to the segment. The rotational segmental moment is net moment about the COM applied (external) created by the hip and knee joint moments and the moments about the segment COM due to hip and knee joint intersegmental forces. For clarity, the net segmental moment is the summation of all moments due to external forces applied to the segment and joint moments. Therefore, it does not provide the detailed breakdown of moments and forces calculated from inverse dynamic analyses.

We can demonstrate the relationship of TAM and RAM to translational and rotational segmental kinetics by taking the time derivative of both sides of Equation 3.

$${}^I\mathbf{h}_{\text{foot}}={}^I\mathbf{h}_{\mathit{\text{seg}}}{}_{/}{}_{\text{foot}}+{}^I\mathbf{h}_{\mathit{\text{seg}}}\frac{I_d}{dt}({}^I\mathbf{h}_{\text{foot}})=\frac{I_d}{dt}({}^I\mathbf{h}_{\mathit{\text{seg}}}{}_{/}{}_{\text{foot}}+{}^I\mathbf{h}_{\mathit{\text{seg}}})\frac{I_d}{dt}({}^I\mathbf{h}_{\text{foot}})=\frac{I_d}{dt}({}^I\mathbf{h}_{\mathit{\text{seg}}}{}_{/}{}_{\text{foot}})+\frac{I_d}{dt}({}^I\mathbf{h}_{\mathit{\text{seg}}})$$ (6)

The two independent time derivatives on the right-hand side of the Equation 6 provide alternative expressions for Euler’s Laws applied to the segment. The time derivative of translational angular momentum is an expression of Euler’s 1^st Law in angular momentum form:

$$\frac{I_d}{dt}({}^I\mathbf{h}_{\mathit{\text{seg}}}{}_{/}{}_{\text{foot}})={\mathbf{M}}_{\mathit{\text{seg}}/\text{Foot}}+({\mathbf{r}}_{\mathit{\text{seg}}/\text{foot}}\times m_{\mathit{\text{seg}}}{}^I\mathbf{a}_{\text{foot}})$$ (7)

where r_seg/foot × m_seg I a_foot is the corrective inertial moment of the segment relative to the stance foot and is required to satisfy Euler’s law when the stance foot accelerates at the end of the stance period.

The right hand side is the translational segmental moment about the stance foot, expressed as:

$${\mathbf{M}}_{\mathit{\text{seg}}/\text{foot}}={\mathbf{r}}_{\mathit{\text{seg}}/\text{foot}}\times {\mathbf{F}}_{\mathit{\text{seg}}}^{\text{Ext}}$$ (8)

where ${\mathbf{F}}_{\mathit{\text{seg}}}^{\text{Ext}}$ is the resultant force of all external forces applied to the segment (Figure 1b).

The time derivative of rotational angular momentum is the more familiar expression of Euler’s 2^nd Law:

$$\frac{I_d}{dt}({}^I\mathbf{h}_{\mathit{\text{seg}}})={\mathbf{M}}_{\mathit{\text{seg}}}^{\text{Ext}}$$ (9)

The right hand side is the rotational segmental moment expressed as:

$${\mathbf{M}}_{\mathit{\text{seg}}}=\sum _{i=1}^N{\mathbf{M}}_i^{\text{Ext}}+\sum _{i=1}^N({\mathbf{r}}_{i/\mathit{\text{seg}}}\times {\mathbf{F}}_i^{\text{Ext}})$$ (10)

where i is the distal and proximal locations of forces and moments. In a link segment model of the human body, M_seg is the net moment created by adding sum of the applied (external) proximal and distal joint moments to the moments about the segment COM due to proximal and distal forces (Figure 1b):

$${\mathbf{M}}_{\mathit{\text{seg}}}={\mathbf{M}}_{\text{distal}}+{\mathbf{M}}_{\text{proximal}}+({\mathbf{r}}_{\text{distal/COM}}\times {\mathbf{F}}_{\text{distal}})+({\mathbf{r}}_{\text{proximal/COM}}\times {\mathbf{F}}_{\text{proximal}})$$ (11)

3. Experimental Methods

3.1. Participants

Fourteen healthy participants (3F, 11M, age: 61.5 ± 8.4 years, BMI: 25.2 ± 2.8 kg/m²) provided informed consent to the Colorado Multiple Institutional Review Board approved protocol.

Each participant performed three gait trials at 1 m/s (± 5% measured through gait timers) and was instrumented with 63 reflective markers, sampled at 100 Hz (Vicon, Centennial, CO). Kinematic data were low-pass filtered with a 4^th-order Butterworth filter (6 Hz cutoff frequency). A 15-segment participant-specific model was created for each participant (see tables for complete segment list) and used to obtain segment kinematics (Visual 3D, C-Motion, Inc., Germantown, MD) (Figure 2). Segment masses were based on percentage of total body weight (Dempster, 1955) and segment inertias were based on segment geometry (Hanavan, 1964).

Figure 2.

All momentum and moment vectors were expressed in a basis with respect to the path of the body COM (defined by e_sagittale_frontal, and e_transverse axes) to facilitate planar analyses.

3.2. Calculations

To facilitate anatomically planar analyses that considers the progression of the body through space, all angular momenta were expressed in a basis with respect to the path of the body COM: e_frontal (tangent to the horizontal path of the body COM), e_transverse (opposite direction of the gravity), and e_sagittal (e_frontal × e_transverse) (Figure 2).

We calculated segmental TAM (Eq. 4) and the translational segmental moment (M_seg/foot) about the stance foot (Eq. 8) only during the stance period (heel strike to toe off) because the foot accelerates, and becomes non-inertial after toe off. Calculation of the segment RAM (Eq. 5) and the rotational segmental moment about the segment COM (Eq. 10) was performed during the entire gait cycle because the calculations do not depend on the point of reference being stationary.

3.3. Analyses of Segmental Contributions

Peak values of TAM and the translational segmental moment about the stance foot were identified during stance. Peak values of RAM and the rotational segmental moment about the segment COM were identified over the entire gait cycle. We chose to identify peak values of TAM and RAM, and their time derivatives, because they quantify the period of generating the most momentum (zero to peak value) and period of arresting momentum (peak value to zero), and the associated torques required (time derivatives). Using the patterns of segmental generation and arresting of TAM and RAM, and the associated segmental torques, we qualitatively describe movement patterns used to achieve forward progression during walking.

4. Results and Interpretation

4.1. Translational Angular Momentum

Segmental translational angular momentum (TAM) and the translational segmental moments (M_seg) demonstrated similar shapes with respect to the stance foot across segments within planes and generally larger magnitudes with increasing distance from the foot in segments in the stance limb and axial skeleton (Table 2). The progressively larger magnitudes of superior segments with larger mass corresponds well with the inverted pendulum model of forward progression during gait, which represents the aggregate effect of translation and rotation of all body segments (identified through the body COM trajectory) about the fixed fulcrum point at the stance foot.

Table 2.

Mean ± SD peak (minimum and maximum) segmental translational moment about the stance foot during the stance period (right heel strike to right toe off). Units are (N·m) (Eq. (7)).

	Sagittal Plane		Frontal Plane		Transverse Plane
Segment	Minimum	Maximum	Minimum	Maximum	Minimum	Maximum
Trunk	−74.61 ± 18.48	79.55 ± 20.63	−36.62 ± 13.21	30.43 ± 16.12	−7.31 ± 5.11	7.81 ± 4.66
Pelvis	−35.27 ± 11.22	29.49 ± 7.38	−17.09 ± 6.92	16.49 ± 7.28	03.74 ± 1.79	6.55 ± 2.61
Head	−13.28 ± 5.80	12.86 ± 5.30	−12.47 ± 4.43	10.98 ± 4.32	−2.67 ± 1.21	1.20 ± 0.41
Right Thigh	−27.92 ± 7.54	25.54 ± 7.48	−6.50 ± 1.72	11.39 ± 3.46	−3.22 ± 1.05	5.11 ± 1.80
Left Thigh	−26.15 ± 6.00	24.43 ± 7.09	−11.92 ± 4.45	6.70 ± 2.60	−7.86 ± 2.76	9.07 ± 3.50
Right Shank	−9.36 ± 2.11	4.96 ± 1.66	−1.21 ± 0.47	3.23 ± 1.19	−0.84 ± 0.46	1.76 ± 0.73
Left Shank	−14.11 ± 4.38	12.04 ± 9.03	−8.65 ± 20.86	2.80 ± 1.25	−9.07 ± 2.50	7.39 ± 2.27
Right Foot	0.00	0.00	0.00	0.00	0.00	0.00
Left Foot	−6.99 ± 2.08	4.37 ± 1.51	−1.70 ± 0.63	1.88 ± 1.44	−2.81 ± 0.73	3.96 ± 1.78
Right Upper Arm	−6.85 ± 3.03	5.94 ± 1.75	−3.17 ± 0.99	2.80 ± 0.97	−1.55 ± 0.47	1.13 ± 0.65
Left Upper Arm	−5.18 ± 1.18	7.26 ± 1.91	−4.04 ± 1.44	3.91 ± 1.78	−1.32 ± 0.47	1.51 ± 0.68
Right Forearm	−4.19 ± 1.75	4.12 ± 1.41	−1.61 ± 0.49	1.05 ± 0.37	−0.94 ± 0.31	0.95 ± 0.42
Left Forearm	−2.98 ± 1.04	2.65 ± 0.93	−1.65 ± 0.61	1.66 ± 0.77	−1.13 ± 0.36	1.11 ± 0.34
Right Hand	−1.57 ± 0.66	2.00 ± 0.60	−0.66 ± 0.20	0.49 ± 0.36	−0.82 ± 0.31	0.48 ± 0.18
Left Hand	−1.34 ± 0.39	1.73 ± 0.68	−0.80 ± 0.35	0.72 ± 0.33	−0.74 ± 0.23	0.72 ± 0.33

In the sagittal plane (Figure 3), TAM of all segments is negative at heel strike, which corresponds with generation of anterior translational momentum with respect to the stance foot, and then is amplified during weight acceptance (0–12% of the gait cycle). The generation of anterior TAM during weight acceptance is accomplished by net forces applied to each segment resulting in anterior segment translation with respect to the stance foot. This is likely a result of power generation from the contralateral limb during push-off as the weight is transferred between limbs to achieve forward progression. This increase in external forces applied to each segment from push-off creates a negative translational moment with respect to the stance foot, which coincides with an anterior (clockwise) moment direction in the path reference frame (Figure 2). During the first half of single limb support (12–30% of the gait cycle), TAM of all segments is slightly arrested (less negative), which is accomplished by positive translational segmental moments (creating posterior translation) about the stance foot. The direction of segmental translational moment is a result of a posterior position of the segments with respect to the stance foot and the external vertical force due to gravity, which creates a posterior (counterclockwise) moment direction in the path reference frame (Figure 2). It is likely the musculoskeletal system takes advantage of the force due to gravity during early single limb support to prevent continuance or extenuated of “falling forward”. During the second half of single limb support (30–50% of the gait cycle), additional TAM of all segments is slightly generated (decreases), which corresponds with negative translational segmental moments (creating anterior translation) with respect to the stance foot. The translational moment becomes negative as the position vector of the body segments with respect to the foot shifts anteriorly, creating an anterior (clockwise) moment direction in the path reference frame (Figure 2). The largest translational moments occur during double support, which is likely due to high intersegmental forces, and remains small throughout single limb support.

Figure 3.

Mean ± 1SD translational angular momentum (TAM) and translational segmental moment about the stance foot of (a) the axial segments (head, trunk, pelvis) and (b) the lower extremities (bilateral thighs and shanks) in the sagittal, frontal, and transverse planes. TAM and the translational segmental moment about the stance foot were only calculated during the stance period (0–60% of the gait cycle) because that is the phase where the support limb is stationary (MacKinnon & Winter, 1993). Note the different scales between planes.

In the frontal plane (Figure 3), TAM of all segments is positive at heel strike, which corresponds to angular momentum in the direction of the stance limb, and then rapidly decreases (arrested) during weight acceptance (0–12% of the gait cycle), which is accomplished by negative translational moments (creating segment translation away from foot) with respect to the stance foot. The rapid arresting translational angular momentum, and the associated segmental torques, of the body away from the planted limb is required to arrest lateral translation and maintain the position of the body COM with respect to the medial border of the support foot (Shimba, 1984). Throughout the duration of the stance period, the translational segmental moments are negative (creating frontal plane segment translation away from the stance foot), which is likely due to the moment due to the external gravitational force and the relatively constant moment arms of the segments with respect to the stance foot. This negative (clockwise) translational segment moment in the path reference frame (Figure 2) corresponds with the mediolateral trajectory of the of the body COM during the swing limb advancement of the contralateral limb in preparation for weight transfer between limbs (MacKinnon & Winter, 1993; Perry & Burnfield, 2010).

In the transverse plane (Figure 3), TAM of all segments is positive at heel strike, corresponding to axial angular momentum away from the stance foot, and rapidly arrested during weight acceptance, which is accomplished by negative translational segmental moments (creating axial segmental rotation toward the stance foot) during weight acceptance (0–12% of the gait cycle). Similar to the sagittal plane, the increased external forces from the power generation of the contralateral limb push off likely create the negative (clockwise) translational segment moment in the path reference frame (Figure 2). During single limb support (12–50% of the gait cycle), transverse angular momentum remains constant, no applied segmental translational moments, which is likely a strategy used as a progression mechanism and straight line motion because axial angular momentum is not generated or arrested.

4.2. Rotational Angular Momentum

Unlike segmental TAM or translational moments, rotational angular momentum (RAM) and the rotational moments of each segment had a unique shape. In addition, the magnitude of segmental RAM is one to two orders of magnitude smaller than segmental TAM. The TAM magnitude is largely influenced by the choice of reference point, and the moment arms can be large relative to the stance foot. However, because segmental RAM and TAM are both dynamically and geometrically independent from one another, and total segmental angular momentum (TAM + RAM) is not included in the present investigation, the difference in magnitude does not affect the current interpretation. The rotational moments represent the net moment about the segment COM due to the external moments (i.e., joint moments) and external forces at the proximal and distal ends of each segment (i.e., joint intersegmental forces). Because the rotational moment is driven by biomechanical loads, they are related to joint moments that are referred to as demand or effort moments (Carollo & Matthews, 2009). The relationship expressed in Eq. 9 enables a straightforward interpretation of RAM changes by kinetic principles of external demands.

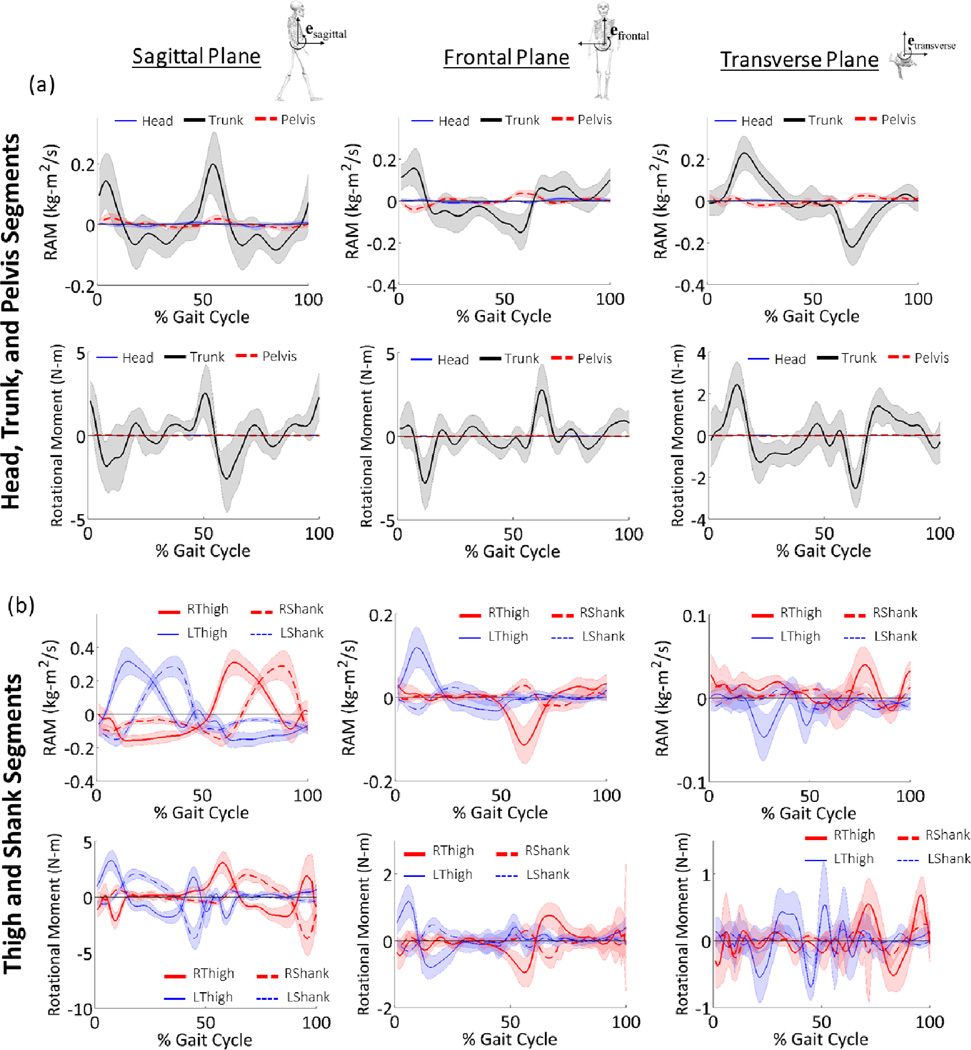
In the sagittal plane, thigh and shank RAM were larger than any other segment (Figure 4). The symmetry across segments and limbs and timing of generation and arresting of segmental RAM curves correspond to the coordinated motion during swing limb advancement used to achieve forward progression. When not supporting the weight of superior segments, timing of the peak thigh and shank rotational moments late in the swing period correspond with the external knee flexor moment required to arrest lower extremity momentum in preparation for foot placement.

Figure 4.

Mean ± 1SD rotational angular momentum (RAM) and translational segmental moment about the COM of the segment of (a) the axial segments (head, trunk, pelvis) and (b) the lower extremities (bilateral thighs and shanks) in the sagittal, frontal, and transverse planes. Note the different scales between planes.

In the frontal plane, the RAM of the trunk and thighs are larger than other segments, and occur primarily during loading and unloading periods of the stance limb (Figure 4, Table 3). During weight acceptance (2–12% of the gait cycle), trunk RAM is generated toward the stance foot. During loading, Trunk RAM is rapidly arrested by a distinct rotational moment away from the stance limb (negative), and then RAM is generated away from the stance foot throughout the duration of single limb support. Frontal plane trunk rotational moments are consistent with the low back lateral bend moments presented by Hendershot et al., (2014), likely to position the body COM away from the stance foot in preparation for contralateral heel strike. This pattern is inversely repeated when loading the contralateral limb. Peak frontal plane thigh RAM and the associated rotational moment away from the stance foot corresponds with the external hip abduction moment that occurs early in the swing period required for foot clearance.

Table 3.

Mean ± SD peak (minimum and maximum) segmental rotational angular momentum (RAM) during the gait cycle (right heel strike to right heel strike). Units of RAM are (kg·m²/s) (Eq. (5)).

	Sagittal Plane		Frontal Plane		Transverse Plane
Segment	Minimum	Maximum	Minimum	Maximum	Minimum	Maximum
Trunk	−0.14 ± 0.04	0.23 ± 0.08	−0.19 ± 0.08	0.20 ± 0.10	−0.23 ± 0.09	0.25 ± 0.09
Pelvis	−0.02 ± 0.01	0.03 ± 0.01	−0.04 ± 0.01	0.04 ± 0.01	−0.04 ± 0.01	0.04 ± 0.01
Head	−0.01 ± 0.01	0.01 ± 0.01	−0.01 ± 0.01	0.01 ± 0.01	−0.005 ± 0.00	0.01 ± 0.00
Right Thigh	−0.19 ± 0.04	0.34 ± 0.07	−0.12 ± 0.05	0.05 ± 0.02	−0.03 ± 0.01	0.06 ± 0.02
Left Thigh	−0.18 ± 0.05	0.33 ± 0.08	−0.05 ± 0.02	0.12 ± 0.05	−0.06 ± 0.02	0.03 ± 0.01
Right Shank	−0.15 ± 0.04	0.30 ± 0.07	−0.03 ± 0.02	0.12 ± 0.05	−0.02 ± 0.01	0.03 ± 0.01
Left Shank	−0.16 ± 0.03	0.29 ± 0.05	−0.03 ± 0.01	0.04 ± 0.03	−0.04 ± 0.07	0.02 ± 0.01
Right Foot	−0.02 ± 0.01	0.02 ± 0.00	−0.01 ± 0.00	0.01 ± 0.00	0.00 ± 0.00	0.00 ± 0.00
Left Foot	−0.02 ± 0.01	0.01 ± 0.00	−0.01 ± 0.00	0.01 ± 0.00	0.00 ± 0.00	0.00 ± 0.00
Right Upper Arm	−0.02 ± 0.01	0.02 ± 0.01	−0.01 ± 0.00	0.01 ± 0.00	−0.01 ± 0.00	0.01 ± 0.00
Left Upper Arm	−0.02 ± 0.01	0.02 ± 0.01	−0.01 ± 0.00	0.01 ± 0.00	−0.01 ± 0.0	0.01 ± 0.01
Right Forearm	−0.01 ± 0.01	0.01 ± 0.00	−0.004 ± 0.00	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00
Left Forearm	−0.01 ± 0.01	0.01 ± 0.00	−0.003 ± 0.00	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00
Right Hand	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00
Left Hand	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00

In the transverse plane, the RAM of the trunk and pelvis are the larger than the other segments (Figure 4, Table 3). During loading response (0–2% of the gait cycle), RAM of the trunk is absent, and the rotational trunk moment is small, which indicates that no torques are required when loading the limb (Figure 4) and reflects the primarily sagittal plane motion. Transverse RAM of the trunk is generated for the duration of weight acceptance (2–12% of the gait cycle), and indicates axial rotation away from the stance foot (Figure 2). Transverse trunk RAM is then arrested for the duration of single limb support (12–50% of the gait cycle), which creates rotation toward the stance foot, until and then absent during weight acceptance of the contralateral limb. Trunk rotational moments away from the stance limb during loading and toward the stance foot during single limb stance are correspond with the low back axial twist moments by Hendershot et al. (2014). Transverse RAM of the pelvis follows similar patterns in comparison to the trunk, but with smaller peak magnitudes, which is explained by the smaller inertia of the pelvis (Figure 4).

5. Discussion

This investigation analyzed the individual contributions of total segmental angular momentum during walking, and the associated kinetics used to generate and arrest segmental angular momentum. The translational angular momentum (TAM) taken about the stance foot provides a coherent interpretation of forward progression during stance. The rotational angular momentum (RAM) about the segment COM can be used to identify specific movement patterns that are used to achieve forward progression through the variations in segmental angular velocity during the gait cycle. In addition, RAM is related to the net external moment through the rotational moment, and therefore represents an external biomechanical load that is representative of effort (Carollo & Matthews, 2009).

A key feature of segmental momentum and segmental moments is that they can be calculated using only kinematics, and may be more suitable for clinical implementation than inverse dynamics calculations. TAM requires segment localization, and is currently the more difficult of the two components to calculate outside of a motion capture laboratory. However, RAM may be achieved through small gyroscopes made possible by microelectromechanical systems (MEMS). MEMS sensors have been used to measure kinematics and spatiotemporal parameters during walking (Sinclair et al., 2013; Patterson et al., 2014; López-Nava et al., 2015) and used for movement retraining (Wall et al., 2009). As wearable sensors become more widely used in a clinical setting (typically for activity monitoring) (Butte et al., 2012; Redfield et al., 2013; Fulk et al., 2014), we anticipate more explorations will focus on how the implementation of wearable sensors can be used to measure or infer biomechanically useful information outside of a traditional motion capture laboratory.

Although joint and muscle-based analyses are the most commonly used in human movement biomechanics, segmental-based analyses provide unique opportunities to examine how dynamic variables are transferred through the system to achieve the desired outcome (in this case, forward progression). Analysis of segmental angular momentum and segmental moments in combination with musculoskeletal simulation equations of motion will enhance our understanding of how momentum is generated, transferred, and arrested between segments. We also anticipate that the two components of total segmental angular momentum can be incorporated into system-based analyses related to flow of power across segments. Changes in segmental momentum intuitively correspond with altered segmental power, and linked to segmental power flow through systematic analyses such as bond graphs (Karnopp et al., 2012). Segment power flow has been presented in several investigations of human movement (Gordon et al., 1980; Neptune et al., 2001; McGibbon et al., 2002; Zajac et al, 2002), but is not ubiquitous within the biomechanics community, particularly in clinical applications where these analyses may be used to inform diagnoses and treatment.

Developing a clearer understanding of how segmental angular momentum and segmental moments are coordinated could assist in reinforcing or correcting movement patterns through muscle strengthening and retraining in the clinic. For example, lateral trunk lean toward the stance limb during gait is a common compensation due to weakness of the hip abductor muscles (Krautwurst et al., 2013). Quantification of peak trunk segment momentum during stance can be used to document this movement compensation and potentially support the effectiveness of interventions, such as hip abductor strengthening, which are intended to change the altered movement pattern. The use of segmental moments in a clinical setting could be beneficial in identifying a potential consequential movement pattern, which is often diagnosed through increased joint demand that lead to overuse injuries (e.g., osteoarthritis). The current results demonstrate a large difference in magnitude of segmental moments between double and single limb support phases, which is consistent with differences of joint moments (identified via inverse dynamics) across these phases. This difference is due to increased power generation by the hip and ankle joints that is required to translate the body COM forward (Cappozzo et al., 1976; Wells, 1981; Winter, 1984; Winter et al., 1990; Hof, 2000) is consistent with previous angular momentum results showing larger changes in segmental angular momentum during double support (Robert et al., 2009). Future experimental work using these variables with clinical populations is needed to determine what deviations in segmental angular momentum and moments exist, and how sensitive and specific these variables for identifying movement deficits, and which are associated with consequential effects on the musculoskeletal system.

TAM provides a helpful framework to interpret intersegmental dynamics needed to maintain forward momentum of the body. TAM captures momentum generation during weight acceptance, little to no momentum generation through midstance (likely due to no hip or ankle power), and momentum arresting during pre-swing. The translational moments reflect the effects of muscle forces and that may or may not be attached to the segment. For instance, the soleus and gastrocnemius are primary drivers of trunk acceleration and deceleration, respectively (Neptune et al., 2001; Zajac et al., 2003; Zmitrewicz et al., 2007), and are represented in the trunk translational moment. As a result, deviations in trunk translational moment may be indicator of problematic or ineffective plantar flexor function. With additional development and exploration through experiments and simulation, TAM and translational moments, which are calculated using only kinematics and inertial properties, may enhance in clinical inference and treatment.

Segmental RAM, which are segment angular velocities scaled by segment inertia, can enable analyses of kinematic strategy and effort (or demand). Because RAM is directly related to angular velocity, timing of segmental motion is easily observed and, for walking can be used to assess coordination of spatiotemporal events (Gaffney et al., 2016; Sigward et al., 2016). Scaling the angular velocity by segment inertia (calculating RAM) allows interpretation of the magnitudes in the context of effort needed to cause rotation. Intuitively, it is more difficult to generate and arrest momentum of segments with large inertia versus segments with small inertia. The rotational moment, which captures the kinetic effort needed to generate or arrest RAM includes both the joint moments and the moments due to proximal and distal forces (Equation 11), which are driven by segment motion and forces that propagate through the kinetic chain. However, it is important to note that the rotational moment does not provide the detailed breakdown of moments and forces calculated from inverse dynamic analyses. Therefore, this should not be used as a surrogate to inverse dynamic calculations, but rather used to provide insight regarding joint kinetics when instrumentation is not available (e.g. within a clinical setting). With further exploration through experiments and simulation, the interactions and relationships between segmental RAM and rotational moments, and traditional biomechanical variables such joint moments and joint powers can be understood and applied. In support of this idea, a recent investigation by (Sigward et al., 2016) demonstrated a strong association of shank angular velocity with knee extensor moment during weight acceptance in patients following ACL reconstruction. This result suggests that analysis of the underlying dynamics through RAM and rotational moment of the shank during heel rocker may facilitate additional insight into the interactions between shank angular velocity, knee extensor moment, and the simultaneously occurring ankle dorsiflexor moment.

There are several limitations to this investigation that should be considered. First, this analysis should be limited to overground walking. During movements containing ballistic motion (e.g. flight phases of sports activities), angular momentum with respect to the body COM is a more appropriate analysis; and using the foot as a reference point is no longer valid. Second, all participants walked at the same speed. Segment patterns identified using this analysis will vary with gait speed. Future work should investigate how segmental movement patterns are altered to accommodate for a change in gait speed. Third, segmental RAM and TAM were calculated using kinematics measured from reflective markers placed on the skin, which are subject to error primarily through skin motion artifact and marker placement error. Finally, qualitative associations between rotational moments and joint moments were based off of well-known waveforms within the literature of joint moments calculated through inverse dynamics; and therefore specific quantitative associations between rotational moments and joint kinetics remain unknown. Future work should establish these associations to determine how the net external moment on a body segment, as determined through the time rate of change of RAM, is associated with joint demand.

6. Conclusion

This investigation assessed the individual contributions of each component of total segmental angular momentum (TAM and RAM) and the kinetics used to generate and arrest segmental angular momentum during walking. The timing and waveforms of the generation and arresting of TAM and RAM describe the coordinated segmental movement patterns used to achieve forward progression during walking. Through Euler’s rotational laws, the time derivative of TAM and RAM can be used to describe the underlying external forces and moments applied to each segment that cause motion. Because these forces and moments are representative of an external biomechanical load, the generation and arresting of segmental angular momentum is likely an indicator of the demand placed on the musculoskeletal system.

Table 1.

Mean ± SD peak (minimum and maximum) segmental translational angular momentum (TAM) during the stance period (right heel strike to right toe off). Units of TAM are (kg·m²/s) (Eq. (4)).

	Sagittal Plane		Frontal Plane		Transverse Plane
Segment	Minimum	Maximum	Minimum	Maximum	Minimum	Maximum
Trunk	−36.94 ± 8.08	0.40 ± 3.18	−8.30 ± 2.10	7.65 ± 3.92	−1.14 ± 0.46	2.48 ± 1.01
Pelvis	−11.35 ± 2.34	−0.36 ± 0.96	−2.97 ± 0.82	2.29 ± 1.04	−0.42 ± 0.24	1.22 ± 0.40
Head	−10.99 ± 2.39	0.44 ± 1.02	−3.04 ± 0.98	2.92 ± 1.41	−0.17 ± 0.17	1.22 ± 0.40
Right Thigh	−5.92 ± 1.30	−2.89 ± 0.83	−1.07 ± 0.26	0.68 ± 0.37	0.17 ± 0.11	0.63 ± 0.21
Left Thigh	−8.33 ± 1.88	0.42 ± 0.54	−1.62 ± 0.40	1.32 ± 0.53	−1.89 ± 0.46	1.10 ± 0.22
Right Shank	−0.84 ± 0.23	−0.14 ± 0.06	−0.08 ± 0.04	0.08 ± 0.03	−0.03 ± 0.04	0.06 ± 0.05
Left Shank	−2.66 ± 0.59	−0.34 ± 0.17	−0.40 ± 0.09	0.28 ± 0.10	−1.24 ± 0.33	0.71 ± 0.14
Right Foot	0.00	0.00	0.00	0.00	0.00	0.00
Left Foot	−0.53 ± 0.15	0.10 ± 0.07	−0.13 ± 0.05	0.08 ± 0.03	−0.62 ± 0.17	0.26 ± 0.05
Right Upper Arm	−3.42 ± 0.83	0.48 ± 0.28	−0.62 ± 0.18	0.53 ± 0.31	0.08 ± 0.09	0.60 ± 0.16
Left Upper Arm	−2.76 ± 0.59	−0.39 ± 0.31	−0.97 ± 0.25	0.86 ± 0.33	−0.57 ± 0.12	0.10 ± 0.06
Right Forearm	−1.84 ± 0.48	0.39 ± 0.18	−0.18 ± 0.06	0.19 ± 0.12	−0.03 ± 0.07	0.46 ± 0.10
Left Forearm	−1.22 ± 0.27	−0.32 ± 0.11	−0.50 ± 0.14	0.41 ± 0.16	−0.38 ± 0.08	−0.01 ± 0.05
Right Hand	−0.63 ± 0.18	0.13 ± 0.07	−0.06 ± 0.02	0.06 ± 0.04	−0.05 ± 0.04	0.20 ± 0.05
Left Hand	−0.36 ± 0.08	−0.06 ± 0.08	−0.17 ± 0.05	0.12 ± 0.04	−0.14 ± 0.04	0.00 ± 0.02

Table 4.

Mean ± SD peak (minimum and maximum) segmental rotational moment about the stance foot during the gait cycle (right heel strike to right heel strike). Units are (N·m) (Eq. (8)).

	Sagittal Plane		Frontal Plane		Transverse Plane
Segment	Minimum	Maximum	Minimum	Maximum	Minimum	Maximum
Trunk	−3.79 ± 1.47	3.43 ± 1.26	−3.62 ± 2.38	3.46 ± 1.54	−2.94 ± 0.90	3.18 ± 1.29
Pelvis	−0.41 ± 0.19	0.48 ± 0.20	−0.74 ± 0.26	0.66 ± 0.22	−0.83 ± 0.35	0.80 ± 0.29
Head	−0.35 ± 0.23	0.28 ± 0.11	−0.22 ± 0.08	0.22 ± 0.08	−0.06 ± 0.03	0.07 ± 0.06
Right Thigh	−3.25 ± 1.39	3.89 ± 1.20	−1.27 ± 0.49	0.16 ± 0.40	−0.88 ± 0.29	1.02 ± 0.30
Left Thigh	−2.70 ± 0.93	3.35 ± 0.80	−0.91 ± 0.28	1.26 ± 0.46	−0.94 ± 0.26	0.98 ± 0.35
Right Shank	−4.24 ± 1.40	2.24 ± 0.51	−0.71 ± 0.42	0.93 ± 1.66	−0.55 ± 0.60	0.46 ± 0.33
Left Shank	−3.91 ± 0.89	2.65 ± 1.59	−0.76 ± 0.98	0.57 ± 0.21	−0.33 ± 0.11	1.19 ± 3.24
Right Foot	−0.28 ± 0.22	0.41 ± 0.31	−0.29 ± 0.65	0.16 ± 0.37	−0.18 ± 0.42	0.16 ± 0.31
Left Foot	−0.22 ± 0.06	0.35 ± 0.09	−0.06 ± 0.02	0.12 ± 0.04	−0.08 ± 0.04	0.07 ± 0.04
Right Upper Arm	−0.15 ± 0.06	0.14 ± 0.07	−0.09 ± 0.05	0.07 ± 0.03	−0.18 ± 0.13	0.14 ± 0.10
Left Upper Arm	−0.13 ± 0.05	0.14 ± 0.06	−0.10 ± 0.08	0.11 ± 0.07	−0.22 ± 0.25	0.25 ± 0.23
Right Forearm	−0.12 ± 0.05	0.10 ± 0.04	−0.04 ± 0.02	0.04 ± 0.02	−0.03 ± 0.01	0.03 ± 0.01
Left Forearm	−0.11 ± 0.04	0.09 ± 0.03	−0.03 ± 0.01	0.03 ± 0.01	−0.03 ± 0.01	0.04 ± 0.01
Right Hand	−0.01 ± 0.00	0.01 ± 0.00	0.00 ± 0.00	0.00 ± 0.00	−0.01 ± 0.00	0.01 ± 0.00
Left Hand	−0.01 ± 0.00	0.01 ± 0.00	0.00 ± 0.00	0.00 ± 0.00	−0.01 ± 0.00	0.01 ± 0.01

Research Highlights.

• Segmental angular momentum components demonstrate coordinated movement patterns

• Euler’s rotational laws describe underlying segmental kinetics that cause motion

• Generating and arresting momentum is indicator of musculoskeletal effort and demand