Developmental Delays in Executive Function from 3 to 5 Years of Age Predict Kindergarten Academic Readiness

Abstract

Substantial evidence has established that individual differences in executive function (EF) in early childhood are uniquely predictive of children’s academic readiness at school entry. The current study tested whether growth trajectories of EF across the early childhood period could be used to identify a subset of children who were at pronounced risk for academic impairment in kindergarten. Using data that were collected at the age 3, 4, and 5 home assessments in the Family Life Project (N = 1,120), growth mixture models were used to identify 9% of children who exhibited impaired EF performance (i.e., persistently low levels of EF that did not show expected improvements across time). Compared to children who exhibited typical trajectories of EF, the delayed group exhibited substantial impairments in multiple indicators of academic readiness in kindergarten (Cohen’s ds = 0.9–2.7; odds ratios = 9.8–23.8). Although reduced in magnitude following control for a range of socioeconomic and cognitive (general intelligence screener, receptive vocabulary) covariates, moderate-sized group differences remained (Cohen’s ds = 0.2–2.4; odds ratios = 3.9–5.4). Results are discussed with respect to the use of repeated measures of EF as a method of early identification, as well as the resulting translational implications of doing so.

Executive functions (EFs) refers to a broad set of cognitive abilities that are utilized in the service of novel problem-solving efforts and more generally for successful self-management. Substantial evidence has implicated EFs as an important predictor of social and academic aspects of school readiness (Blair, 2002; Ursache, Blair, & Raver, 2012). This derives, in part, from the rapid changes that occur in EF abilities across early childhood prior to school entry but more centrally due to the nature of EF abilities themselves. EFs represent a set of domain-general processes that facilitate children’s learning how to learn and that contribute to adaptive behavior. There are a number of studies that have suggested that EFs are related to learning disabilities in both reading and math when assessed at school age. These studies have tried to identify specific aspects of EF, such as working memory, that might be associated with current or later learning disabilities (Cutting, Materek, Cole, Levine, & Mahone, 2009; Swanson, Howard, & Saez, 2006; Toll, Van der Ven, Kroesbergen, & Van Luit, 2011). Although these studies have been valuable in identifying EFs as important in understanding basic deficits in school-age children with learning problems, these studies were not able to identify precursors in early childhood EFs that might be predictive of later learning problems at school age. The current study examined EF longitudinally in early childhood as a potentially unique predictor of early school achievement.

There is growing recognition that poverty undermines a variety of skills that are associated with school readiness, in part, through its proximal effects on EF (Fitzpatrick, McKinnon, Blair, & Willoughby, 2014; Hackman & Farah, 2009; Hackman, Farah, & Meaney, 2010; Nesbitt, Baker-Ward, & Willoughby, 2013). Although poverty is not a causal variable, it stands for processes in the environment that may inhibit the development of optimal EF. For example, income constrains families’ choices regarding housing, child care, and neighborhood quality. On average, children from low-income families are disproportionally more likely to be exposed to risky contexts and to less predictable living conditions (Evans & Schamberg, 2009; Raver, Blair, Willoughby, & Family Life Project Investigators, 2013). Poverty also is associated with less optimal parenting that in turn is related to poorer EF skills in children (Bernier, Carlson, & Whipple, 2010; Blair et al., 2011). Thus, studying EF in the context of poverty may be particularly important in understanding how EF processes contribute to school readiness skills.

Previous studies that exclusively involved young children and that investigated the association between EFs and academic school readiness can be distinguished on the basis of their research design and associated analytic approach. A first set of studies used cross-sectional designs and reported contemporaneous associations between preschool (or kindergarten) children’s performance on direct assessments of EF and their performance on direct assessments of (pre)academic achievement (Espy et al., 2004; Miller, Muller, Giesbrecht, Carpendale, & Kerns, 2013; Smith-Donald, Raver, Hayes, & Richardson, 2007; Willoughby, Blair, Wirth, Greenberg, & Family Life Project Investigators, 2012). Although these studies consistently established positive associations between EF and achievement, given their use of cross-sectional designs and limited control of potential confounder variables, they provided a weak basis of inference regarding the unique contributions of EF to academic readiness.

A second set of studies utilized short-term (e.g., fall-spring) longitudinal designs. These studies have demonstrated prospective associations between earlier measures of EF (typically in preschool but sometimes in kindergarten) and later measures of academic functioning (Barnes et al., 2014; Blair & Razza, 2007; Bull, Espy, & Wiebe, 2008; Clark, Pritchard, & Woodward, 2010; Fitzpatrick & Pagani, 2012; Masten et al., 2012; Monette, Bigras, & Guay, 2011; Sabol & Pianta, 2012). The consistent evidence of prospective associations between earlier EF and later achievement across studies, which differed in the interval of time between assessments and in the number and type of covariates that were considered, increased confidence that EF may be uniquely predictive of early academic achievement.

A third set of studies used short-term longitudinal designs but measured EF (including the Head Toes Knees Shoulders task, which is conceptually and empirically related to direct assessments of EF) and academic achievement at both assessment points. These studies consistently demonstrated that earlier measures of EF were uniquely predictive of later measures of achievement above and beyond the lagged effects of earlier achievement (Brock, Rimm-Kaufman, Nathanson, & Grimm, 2009; Matthews, Ponitz, & Morrison, 2009; McClelland et al., 2007). The fact that EF explained unique variation in later achievement beyond that attributable to earlier achievement provided some of the strongest evidence to date of the role of EF in predicting later academic achievement.

A fourth set of studies used longitudinal designs that included three or more assessments that spanned at least two academic years. The availability of three or more assessments of EF and academic achievement provides an expanded set of opportunities for making stronger tests of the potentially unique contributions of early EF on later achievement. At least two studies used autoregressive cross-lagged path models to test bidirectional associations between emerging EF and academic achievement (Fuhs, Farran, & Nesbitt, 2013; Welsh, Nix, Blair, Bierman, & Nelson, 2010). Both studies indicated that early EF contributed to intermediate improvements in both EF and achievement, each of which subsequently contributed to later achievement. These studies also provided some evidence for bidirectionality of effects between early math achievement and EF. The work of Fuhs et al. (2013) and Welsh et al. (2010) essentially extended the benefits of a lagged analytic approach from short-term longitudinal designs (described above) across a broader period of time. Although helpful, these studies did not fully capitalize on the attributes of repeated-measures designs. Specifically, repeated-measures data on achievement and EF provide the opportunity to use fixed effect analyses (FEAs), which adjust for all measured and unmeasured time-invariant covariates (see Willoughby, Kupersmidt, & Voegler-Lee, 2012 ). McClelland et al. (2014) used FEAs to demonstrate that changes in EF (i.e., the Head Toes Knees Shoulders task) across four assessments that spanned pre-K and kindergarten years were associated with corresponding changes in academic achievement across the same time period. Those analyses provided the strongest evidence to date that preschool EF was uniquely and potentially causally associated with academic school readiness. Unfortunately, we were unable to use FEAs in this current study, as repeated measurements of academic functioning were not available at the same times in which EF was measured.

In light of mounting evidence that preschool EF is uniquely predictive of academic school readiness and given that early childhood represents an initial period of rapid improvements in EF abilities (De Luca & Leventer, 2008; Munakata, Snyder, & Chatham, 2012; Thatcher, North, & Biver, 2008; Weintraub et al., 2013), the present study tested whether individual differences in this rate of improvement in EF across early childhood might be used to identify that subset of children who were at greatest risk for academic problems or learning disabilities at school onset and who may thus have benefited most from the receipt of services immediately upon or prior to school onset. To the best of our knowledge, no previous study on this topic has utilized repeated-measures data in this way.

Given the costs and logistical challenges of repeatedly measuring EF across early childhood, a corollary question was whether the identification of children who exhibited atypical patterns of EF growth was uniquely predictive of kindergarten academic outcomes above and beyond norm-referenced measures of cognitive and language functioning that were obtained during the period of time that spanned the assessment of EF. Whereas previous studies have established that individual differences in EF predict academic functioning above and beyond indexes of general intellectual or language ability (Blair & Razza, 2007; Duckworth & Seligman, 2005; Espy et al., 2004), the current study tested a more stringent question—namely, whether group membership (a categorical variable) was predictive of academic readiness outcomes above and beyond indexes of general intellectual and receptive language ability. To the extent that this was true, it would provide initial empirical justification for using repeated measurements of EF as a means of early identification.

A majority of previous studies that have investigated the association between preschool EF and academic school readiness have focused nearly exclusively on standardized tests of achievement (e.g., Woodcock Johnson). In the current study, we supplemented academic achievement tests with teacher ratings of children’s academic readiness and impairment in functioning (e.g., probability of grade promotion, need for and/or use of learning-related services). These outcomes provided a broader characterization of academic readiness than has been considered in previous studies.

In sum, this study addressed three questions. The first question was whether we could empirically identify a subgroup of children who were characterized by low levels and slow rates of change in EF from 3 to 5 years of age. The second question was whether these children, as a group, exhibited impairments in multiple aspects of academic readiness in kindergarten relative to peers who exhibited age-typical trajectories of EF. The third question was whether any observed group differences persisted after inclusion of a broad set of covariates, including cognitive and language functioning as well as indexes of socioeconomic risk, which are all well-established predictors of academic readiness.

Methods

Participants

The Family Life Project was designed to study young children and their families who lived in two major geographical areas of the United States with high poverty rates. Specifically, three counties each in eastern North Carolina and central Pennsylvania were selected to be indicative of the Black South and Appalachia, respectively. The Family Life Project adopted a developmental epidemiological design in which sampling procedures were employed to recruit a representative sample of 1,292 children whose families resided in one of the six counties at the time of the child’s birth. Low-income families in both states and African American families in North Carolina were oversampled (African American families were not oversampled in Pennsylvania because the target communities were at least 95% non–African American). Full details of the sampling procedure appear elsewhere (Vernon-Feagans, Cox, and Family Life Project Key Investigators, 2013).

Of those families interested and eligible and selected to participate in the study, 1,292 families completed a home visit at 2 months of child age, at which point they were formally enrolled in the study. The current analyses are limited to children for whom a direct assessment of EF was available at 3-, 4-, and/or 5-year assessment(s). Families and children who did not participate in any of the 3-, 4-, or 5-year assessments (n = 171), and hence who were not included in the current analysis, did not differ from families and children who did participate (N = 1,121) with respect to state of residence (36% vs. 41% residing in Pennsylvania, respectively, p = .26), child gender (56% vs. 50% male, p = .19), child race (37% vs. 43% African American, p = .15), or being recruited in the low-income stratum (77% vs. 78% poor, p = .75; note that for sampling purposes only, membership in the low-income stratum was defined as household income-needs ratios of ≤ 2.0, use of federal assistance programs that required proof of poverty, or head of household whose highest education was a high school degree or less). Caregivers of children who did not participate had slightly lower levels of educational attainment than caregivers of participating children (81% vs. 87% had a GED or high school diploma, respectively, p = .03).

Procedures

Families participated in regularly scheduled home visits beginning when children were 2 months old. Demographic data were drawn from multiple home visits that spanned age 2 months through age 3 years. EF data were drawn from the 3-, 4-, and 5-year home visits. Children completed pre-K assessments prior to their enrollment in kindergarten. Pre-K visits were completed in centers or homes contingent on the child’s care arrangement. In the fall of children’s kindergarten year, teachers completed ratings on children, including impressions of their academic ability, need for/receipt of services, and likelihood of grade promotion. In the spring of the kindergarten year, children completed direct assessments of academic achievement.

Measures

The EF battery consisted of seven tasks. Because these tasks have been extensively described and evaluated elsewhere (Willoughby, Blair, Wirth, Greenberg, & Family Life Project Investigators, 2010; Willoughby & Blair, 2011; Willoughby, Wirth, et al., 2012), we provide only abbreviated descriptions here.

Working Memory Span (working memory)

This span-like task required children to perform the operation of naming and holding in mind two pieces of information simultaneously (i.e., the name of colors and animals in pictures of “houses”) and to activate one of them (i.e., animal name) while overcoming interference occurring from the other (i.e., color name). Items were more difficult as the number of houses (each of which included a picture of a color and animal) increased.

Pick the Picture Game (PTP; working memory)

This self-ordered pointing task presented children with a series of 2, 3, 4, and 6 pictures in a set. Children were instructed to continue picking pictures within each set until each picture had “received a turn.” This task requires working memory because children have to remember which pictures in each item set they have already touched (spatial location of pictures changes across trials and was uninformative). PTP was too difficult for many 3-year-olds and was administered only at the 4- and 5-year assessments.

Silly Sounds Stroop (inhibitory control)

This task presented children with pictures of cats and dogs and asked children to make the sound opposite of that which was associated with each picture (e.g., meow when showed picture of a dog). This task requires inhibitory control as children have to inhibit the tendency to associate bark and meow sounds with dogs and cats, respectively.

Spatial Conflict (SC; inhibitory control)

This task presented children with a response card that had a picture of a car and boat. Initially, all stimuli (pictures of cars or boats identical to that on the response card) were presented in locations that were spatially compatible with their placement on the response card (e.g., pictures of cars always appeared above the car on the response card). Subsequently, test items required a contralateral response (e.g., children were to touch their picture of the car despite the fact that it appeared above the boat). This task required inhibitory control as children had to override the spatial location of test stimuli with reference to their response card. The SC was administered at the 3-year assessment.

Spatial Conflict Arrows (inhibitory control)

This task was identical in format to the SC task (above) with the exception that the response card consisted of two black dots (“buttons”) and the test stimuli were arrows that pointed to the left or right. Children were instructed to touch the button to which the arrow pointed. Initially, all left (right)–pointing arrows pointed to the (left) right. Subsequently, test items pointed in the opposite direction. Spatial Conflict Arrows was administered at the 4- and 5-year assessments.

Animal Go/No-Go (inhibitory control)

This is a standard go/no-go task in which children were instructed to click a button (which made an audible sound) every time that they saw an animal (i.e., go trials) except when it was a pig (i.e., no-go trials). Varying numbers of go trials appeared prior to each no-go trial, including, in standard order, 1-go, 3-go, 3-go, 5-go, 1-go, 1-go, and 3-go trials. No-go trials required inhibitory control.

Something’s the Same Game (attention shifting)

This task presented children with a pair of pictures for which a single dimension of similarity was noted (e.g., both pictures were the same color). Subsequently, a third picture was presented, and children were asked to identify which of the first two pictures was similar to the new picture. This task required the child to shift his or her attention from the initial label to a new dimension of similarity (e.g., from color to size).

EF Task Scoring and Composite Formation

As previously discussed (Willoughby, Wirth, et al., 2012), EF task scoring was facilitated by drawing a calibration sample of children—all of whom were deemed to have high-quality data (e.g., data collectors did not report interruptions, children completed multiple tasks)—from across the 3-, 4-, and 5-year assessments (no child contributed data from more than one assessment). Item response theory (IRT) models were used for task evaluation. Specifically, graded response models were used to score the two tasks with polytomous item response formats (i.e., PTP, Working Memory Span), while two-parameter logistic models were used to score the remaining tasks (all of which involved dichotomous items response formats) in the calibration sample. The set of item parameters that was obtained from calibration sample was applied to all children’s EF data across all assessments, resulting in a single IRT-based (i.e., expected a-posteriori [EAP]) score for each task, all of which were on a common developmental scale. Elsewhere, we provided a didactic presentation of this general approach, using a subset of the data that are presented here (see Willoughby, Wirth, & Blair, 2011). An essential idea is that IRT-based scores for each task represent an estimate of a child’s true ability that is free of measurement error and that makes maximal use of item-level information (i.e., scores different weight items on the basis of their difficulty and discrimination parameters). Individual EAP scores for each EF task were scaled such that they took on a mean value of 0 at the age 4 assessment. Although we do not make use of any individual task scores (i.e., see the rationale for the formation of an overall EF composite score below), we provide descriptive statistics for all task scores at each assessment in Table 1. As discussed elsewhere (Willoughby et al., 2010; Willoughby, Wirth, et al., 2012), the rates of task completion varied across assessment periods, with children completing approximately 3.5 of the 5 tasks that were administered at the age 3 assessment and approximately 5.8 of the 6 tasks that were administered at the age 5 assessment.

Table 1.

Descriptive Statistics for Task Scores That Contributed to Executive Function Composite.

	Age 3					Age 4					Age 5
Task	n	M	SD	F%	C%	n	M	SD	F%	C%	n	M	SD	F%	C%
SC	880	0.00	0.85	3.1	11.5	—	—	—	—	—	—	—	—	—	—
SCA	—	—	—	—	—	984	0.09	0.93	4.7	5.9	1,032	0.60	0.93	2.5	16.6
SSS	478	−0.51	0.80	0.9	0.4	893	−0.09	0.86	0.2	1.2	994	0.21	0.78	0.1	3.0
GNG	443	−0.43	0.95	9.0	24.2	795	−0.15	0.87	4.9	28.1	979	0.28	0.69	1.6	47.2
WMS	787	−0.93	0.66	21.7	0.5	957	−0.12	0.84	1.1	0.0	982	0.34	0.68	0.4	0.1
PTP	—	—	—	—	—	933	−0.32	0.88	0.0	0.1	1,003	0.28	0.82	0.0	0.8
STS	841	−0.60	0.78	2.4	0.6	970	0.04	0.71	0.1	3.3	1,023	0.17	0.95	0.1	12.1

Note. F% = percentage of children exhibiting floor effect; C% = percentage of children exhibiting a ceiling effect; SC = Spatial Conflict; SCA = Spatial Conflict Arrows; SSS = Silly Sounds Stroop; GNG = Animal Go/No-Go; WMS = Working Memory Span; PTP = Pick the Picture; STS = Something’s the Same Game. Dashes indicate that a given task was not administered at the given assessment period.

In our previously published studies, we used individual EF task (i.e., EAP) scores as reflective indicators of a latent variable of EF (e.g., Willoughby & Blair, 2011; Willoughby, Blair, et al., 2012); Willoughby et al., 2010). However, more recently, on the basis of both conceptual and statistical criteria, we have determined that individual EF task scores are better combined into a composite EF score (Willoughby, Blair, & Family Life Project Investigators, 2015; Willoughby, Holochwost, Blanton, & Blair, 2014). This EF composite was formed by taking the mean of each child’s EAP scores (i.e., across as many tasks as a given child was able to complete) at each assessment and represented the aggregate set of EF abilities at each age.

Teacher-rated academic function and impairment

Teachers rated a child’s relative academic standing in the class with respect to reading/preliteracy skills (Item 1), math skills (Item 2), and overall academic function (Item 3). Items were derived from the Head Start REDI Academic Performance Questions (http://headstartredi.ssri.psu.edu/). Each item was rated on a 5-point Likert-type scale (0 = near the very bottom of your class, 1 = in the bottom half of your class, 2 = in the solid middle of your class, 3 = in the top half of your class, 4 = near the very top of your class). The mean response across the three items was used as a continuous indicator of class standing. An additional question asked the teacher’s impression regarding the likelihood that the child would be promoted to first grade (“Do you think that this child will proceed to first grade next year?”). This item was rated on a 4-point Likert-type scale (0 = highly unlikely, 1 = there are some serious concerns, probably not, 2 = there are some concerns but probably yes, 3 = definitively yes). Finally, teachers rated a series of items regarding a child’s need for or receipt of learning-related services. The specific items used in this study included “Have you been concerned about how this child is developing, learning, or behaving?” “Does this child have an individual education plan or IEP?” and “Has this child received wrap-around or early intervention services?” Each item was rated as yes or no. Teacher ratings were intended to supplement children’s performance on standardized achievement tests with ecologically valid indicators of kindergarten academic readiness.

Woodcock-Johnson III Tests of Achievement (WJ III; Woodcock, McGrew, & Mather, 2001)

WJ III is a conormed set of tests for measuring general scholastic aptitude, oral language, and academic achievement. The Letter Word Identification and Picture Vocabulary subtests were used as indicators of early reading achievement, while the Applied Problems subtest was used as an indicator of early math achievement. Norm-referenced standardized scores (M = 100, SD = 15) were used for each subtest. The validity and reliability of WJ III have been established elsewhere (Woodcock et al., 2001).

Covariates

Demographic variables that were used as covariates included household income-to-needs ratio (i.e., the total household income of anyone who resided in the household divided by the federal poverty threshold for a family of that size and composition), primary caregiver highest education (in years), and child race, sex and age. In addition, as elaborated below, a number of indicators of children’s general cognitive abilities were also included as covariates.

Wechsler Preschool and Primary Scales of Intelligence (WPPSI; Wechsler, 2002)

At the 3-year home visit, children completed the Vocabulary and Block Design subscales of the WPPSI, which were combined to create an estimate of intellectual functioning (Sattler, 2001). At the pre-K visit, children completed symbol search and coding subscales of the WPPSI, which were used as indicators of processing speed. General intellectual function and processing speed both contribute to academic readiness and served as covariates.

Peabody Picture Vocabulary Test, Fourth Edition (Dunn & Dunn, 2007)

The Peabody Picture Vocabulary Test, fourth edition, is a norm-referenced instrument that measures children’s receptive vocabulary; it was administered at the pre-K visit. Receptive vocabulary has been established as an important indicator of children’s cognitive and linguistic development and served as a covariate.

Analytic Strategy

The first research question was whether there was a subset of children who exhibited developmental delays in their linear rate of EF development from age 3 to 5. A series of growth mixture models (GMMs) were estimated to test this question. GMMs use a categorical latent variable to represent heterogeneity in growth parameters (B. Muthén & Shedden, 1999). Following best practice (Nylund, Asparouhov, & Muthen, 2008), a combination of empirical (i.e., [adjusted] Bayesian Information Criterion [BIC], Lo-Mendell-Rubin [LMR] test statistic for K-1 classes, statistical significance of parameter estimates for intercepts and slopes) and substantive (i.e., proportion of children assigned to each class) criteria were used to determine the optimal number of classes.

The second and third research questions were whether children who exhibited slower rates of change in the developmental of EF from age 3 to 5 years (i.e., represented by GMM class membership) exhibited worse academic performance in kindergarten (Question 2), after adjustment for socioeconomic and cognitive covariates (Question 3). Although it is common in the applied literature to assign children to the GMM class for which they have the highest posterior probability (i.e., membership becomes a categorical predictor variable), this practice ignores measurement imprecision regarding class membership and potentially introduces bias into predictive models. We used a recently developed three-step procedure to circumvent this problem (see Asparouhov & Muthen, 2014). This approach involved regressing academic outcomes, one at a time, onto an indicator that represented a child’s most likely GMM class membership (i.e., that trajectory that most closely approximated their data). Importantly, this model also used information about the classification probabilities, which was obtained from the standard output of the unconditional GMM, to represent the measurement error that was associated with forcing children into a particular GMM class. Although the three-step approach did not provide a coefficient that explicitly tested the association between GMM class membership and outcomes (because class membership is probabilistic), we tested the cross-group equivalence of adjusted intercepts (for continuous outcomes) and thresholds (for categorical outcomes) to make these inferences. All models were estimated using Version 7.1 of Mplus (L. K. Muthén & Muthén, 1998–2013) and took into account the complex sampling design (stratification and oversampling).

Results

Descriptive Statistics

Descriptive statistics for all study variables appear in Tables 2 and 3. Four points were noteworthy with respect to descriptive data. First, individual differences in EF at 3-year (|r| = .11–.33), 4 (|r| = .20–.50), and 5 (|r| = .22–.49) assessments were each correlated with academic readiness indicators in kindergarten (see Table 2). Second, individual differences in EF were also correlated with demographic factors—including household income–needs ratio, parental education, and race (|r| = .23–.34), as well as cognitive factors (|r| = .18–.55)—including intellectual ability, receptive language, and processing speed that were used as covariates in subsequent predictive models (see Table 2). Third, socioeconomic status and indicators of general cognitive function were as strongly correlated with indicators of academic readiness as were measures of EF (see Table 2). Fourth, as previously described (Willoughby, Wirth, et al., 2012), children exhibited linear increases in EF scores from age 3 to 5 (see Table 3). Collectively, these results were consistent with expectations that demographic, general cognitive, and EF variables were all correlated with each other and with indicators of academic readiness. The overarching question was whether we could distinguish children on the basis of developmental changes in EF across time and whether children who exhibited delayed EF across time were uniquely impaired on kindergarten academic outcomes above and beyond demographic and general cognitive factors.

Table 2.

Unweighted Bivariate Correlations Between All Study Variables.

Variable	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1. Income/Needs	—
2. Parent Edu	.61	—
3. Child age	.05	.03	—
4. Child IQ	.39	.39	.07	—
5. Child Recept	.40	.43	.07	.63	—
6. Child PS-Code	.20	.22	−.11	.35	.34	—
7. Child PS-SS	.29	.30	−.02	.44	.43	.53	—
8. EF (age 3)	.23	.24	.00	.41	.38	.18	.27	—
9. EF (age 4)	.28	.33	.08	.55	.55	.34	.43	.37	—
10. EF (age 5)	.26	.29	.04	.48	.53	.34	.34	.32	.59	—
11. WJ-LW	.28	.29	−.28	.31	.37	.32	.33	.17	.30	.29	—
12. WJ-PV	.34	.32	−.08	.46	.62	.21	.28	.23	.41	.37	.43	—
13. WJ-AP	.32	.33	−.15	.51	.58	.36	.42	.33	.50	.49	.54	.56	—
14. Acad Skill	.28	.32	.21	.44	.49	.32	.33	.24	.41	.40	.53	.40	.47	—
15. Prob Promo	.25	.25	.19	.39	.46	.25	.29	.25	.34	.40	.39	.33	.40	.68	—
16. Black	−.39	−.25	−.19	−.38	−.45	−.11	−.20	−.30	−.34	−.27	−.01	−.23	−.29	−.15	−.24	—
17. Male	.04	.01	.02	−.16	−.06	−.23	−.10	−.09	−.14	−.13	−.06	.05	−.02	−.05	−.08	.01	—
18. IES	−.12	−.08	.02	−.22	−.19	−.16	−.11	−.11	−.20	−.22	−.23	−.21	−.28	−.20	−.19	−.00	.07	—
19. Services	−.14	−.18	−.08	−.28	−.27	−.16	−.17	−.14	−.25	−.28	−.16	−.19	−.24	−.31	−.31	.10	.06	.32	—
20. Concerns	−.22	−.27	−.15	−.37	−.41	−.24	−.26	−.18	−.37	−.40	−.34	−.30	−.38	−.61	−.56	.15	.14	.18	.33	—

Note. Parent Edu = parent education; Child Recept = child receptive language; PS = processing speed; Code = coding; SS = symbol search; EF = executive function; WJ = Woodcock Johnson; LW = Letter Word Identification; PV = Picture Vocabulary; AP = Applied Problems; Acad Skill = academic skill rating; Prob Promo = probability of promotion; IEP = Individualized Education Program. Children were assigned to typical and delay EF groups on the basis of posterior probabilities from the growth mixture models and were assigned solely for purposes of sample description.

Table 3.

Unweighted Descriptive Statistics for Total Sample and Executive Function Subgroups.

	Totala			Typicalb		Delayc
Variable	N	M	SD	n	M	n	M
Income/needs	1,112	1.9	1.5	991	1.9	121	1.3
Parent education (years)	1,120	12.7	2.1	997	12.8	123	11.9
Child age (K)	1,047	6.0	0.3	928	6.0	119	6.0
Child estimated IQ (age 3)	1,036	93.9	16.1	926	95.4	110	81.3
Child Receptive Vocab (pre-K)	956	94.1	15.7	854	96.0	102	78.4
Child PS-Coding (pre-K)	859	96.3	14.2	788	97.2	71	85.6
Child PS-Search (pre-K)	759	96.3	14.1	734	97.0	61	88.0
EF (age 3)	972	−0.5	0.5	888	−0.5	84	−0.7
EF (age 4)	1,008	−0.1	0.5	899	−0.1	109	−0.6
EF (age 5)	1,037	0.3	0.5	917	0.4	120	−0.6
WJ-LW (K)	1,039	107.5	12.0	920	108.4	119	100.8
WJ-PV (K)	1,038	99.2	9.9	919	100.2	119	91.1
WJ-AP (K)	1,039	100.8	13.5	920	102.6	119	87.2
Academic skills (K)	958	2.3	1.3	853	2.4	105	1.3
Probability promotion (K)	958	2.5	0.9	853	2.6	105	1.9
	n	%		n	%	n	%
Child race (African American)	1,120	43		997	41	123	59
Child gender (male)	1,120	50		997	49	123	60
IEP (K)	958	9		853	7	105	27
Wrap/Early Services (K)	959	12		854	9	105	32
Concerns about student (K)	959	42		854	37	105	78

Note. Vocab = vocabulary; PS = processing speed; EF = executive function; WJ = Woodcock Johnson; LW = Letter Word Identification; PV = Picture Vocabulary; AP = Applied Problems; IEP = Individualized Education Program. Children were assigned to typical and delay EF groups on the basis of posterior probabilities from the growth mixture models and were assigned solely for purposes of sample description.

^aN = 1,120.

^bn = 997.

^cn = 123.

GMMs

A series of unconditional GMMs were estimated that differed solely in the number of assumed classes (2–6). Each model assumed a linear functional form of change with variation in intercepts and slopes across all classes. Inspection of the BIC favored a two-class solution (BICs: 3797.5, 3802.3, 3815.6, 3829.4, 3843.002 for Classes 2–6, respectively). Inspection of the sample size–adjusted BIC favored a three-class solution (adjusted BICs: 3762.6, 3757.8, 3761.6, 3765.9, 3769.947 for Classes 2–6, respectively); however, one of the classes consisted of 1% of participants. The Lo-Mendell-Rubin (LMR) test statistic, which has a null hypothesis that one fewer classes than the number being estimated is sufficient, was significant for the two-class (p < .0001) but not three-class (p = .22) solution (i.e., LMR favored a two-class solution). Collectively, these results indicated that a two-class solution was optimal.

Additional modifications were considered to the two-class model. First, we removed the default constraint of equal (co)variances for the latent intercept and slopes terms across classes. Second, the residual variance for EF at age 5 was not statistically significant in either group and was fixed to 0. Third, the latent variance for the linear slope term in the smaller of the two classes was not statistically significant and also fixed to 0.

Approximately 91% of children had data that most resembled the first class (average posterior probability of .96). These children exhibited average levels of EF at age 4 that increased linearly across time (μ_intercept = .01, p = .57; μ_slope = .46, p < .001). Within this group, there was significant variability in both level (φ²_intercept = .09, p < .001) and rate of linear change (φ²_slope = .03, p < .001), though individual differences in level of EF were uncorrelated with rates of change (φ = −.05, p = .60). Children in this first group were designated as typically developing with respect to EF.

Approximately 9% of children had data that resembled the second class (average posterior probability of .84). These children exhibited below-average levels of EF at age 4 that did not significantly increase across time (μ_intercept = −.53, p < .001; μ_slope = .07, p = .09). Although there was significant variability in level of EF in Class 2 (φ²_intercept = .19, p < .001), the nonsignificant variance in slopes had been fixed to 0 in the model-trimming process described above. Children in this second group were designated as developmentally delayed with respect to EF. That is, whereas children in the former group exhibited nearly one half of a standard deviation unit change per year (μ_slope = .46), children in this latter group exhibited less than one tenth of a standard deviation unit change per year (μ_slope = .07). These results implied a diverging set of EF abilities that would become increasingly accentuated across time.

Prediction of Kindergarten Outcomes

Although membership in GMM groups was probabilistic, we assigned children to groups solely for purposes of description (i.e., to compute descriptive statistics for study variables). As summarized in Table 2, children who were most likely to be associated with the delayed group tended to come from more disadvantaged households (lower income-needs ratio, less parental education) and to have performed appreciably worse on every direct indicator of cognitive and academic performance between age 3 and kindergarten. The final set of GMMs was parameterized such that each academic readiness outcome could be compared across groups while still taking into account the probabilistic nature of group membership by treating it as a latent variable with measurement error. Specifically, two separate two-class GMMs were estimated for each academic outcome. The first model provided unadjusted group differences on each outcome (i.e., similar to the simple group comparisons in Table 2 but without having to assign children to a specific class). The second model provided adjusted group differences (i.e., covariates included family income-needs ratio; primary caregiver education; child race, sex, and age at the time of the kindergarten assessment; estimated IQ at age 3; and receptive language and processing speed at pre-K) on each outcome. For continuous outcomes, Cohen’s d effect sizes were computed by dividing (un) adjusted group differences in means by the observed standard deviations (per Table 2). For dichotomous outcomes, odds ratios (ORs) were computed by exponentiating (un)adjusted group differences in thresholds.

Continuous outcomes

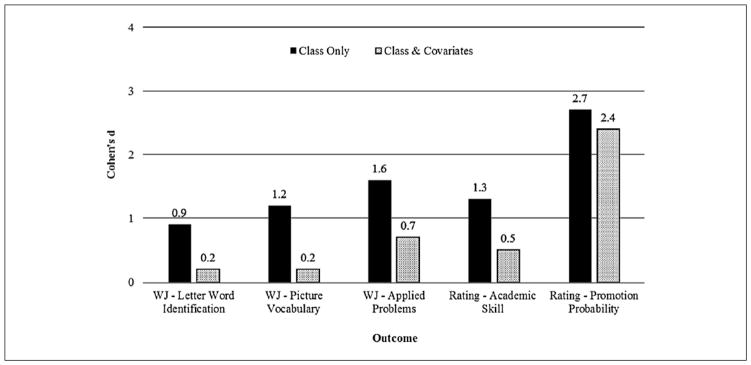
For the WJ III Letter Word Identification subtest, typical and delayed groups had an unadjusted difference of 10.8 points on standardized scores, which was statistically significant and indicative of a large effect (Wald χ²₍₁₎ = 44.8, p < .0001, Cohen’s d = 0.90). However, after adjustment for covariates, the group difference was reduced to a 2.3-point difference in standard scores, which was not statistically significant and indicative of a small effect (Wald χ²₍₁₎ = 1.7, p = .19, Cohen’s d = 0.19). For the WJ III Picture Vocabulary subtest, typical and delayed groups had an unadjusted difference of 11.5 points on standardized scores, which was statistically significant and indicative of a large effect (Wald χ²₍₁₎ = 54.6, p < .0001, Cohen’s d = 1.16). After adjustment for covariates, the group difference was reduced to a 2.3-point difference in standard scores, which was statistically significant and indicative of a small effect (Wald χ²₍₁₎ = 4.0, p = .05, Cohen’s d = 0.23). For the WJ III Applied Problems subtest, typical and delayed groups had an unadjusted difference of 20.9 points on standardized scores, which was statistically significant and indicative of a large effect (Wald χ²₍₁₎ = 100.0, p < .001, Cohen’s d = 1.55). After adjustment for covariates, the group difference was reduced to a 10.0-point difference in standard scores, which was statistically significant and indicative of a moderately large effect (Wald χ²₍₁₎ = 31.6, p < .0001, Cohen’s d = 0.74).

For teacher ratings of children’s overall academic ability, typical and delayed groups had an unadjusted difference of 1.7 points, which was statistically significant and indicative of a large effect (Wald χ²₍₁₎ = 121.5, p < .001, Cohen’s d = 1.29). After adjustment for covariates, the group difference was reduced to a 0.6-point difference, which was statistically significant and indicative of a medium-sized effect (Wald χ²₍₁₎ = 7.6, p = .006, Cohen’s d = 0.46). For teacher ratings of a child’s likelihood of being promoted to first grade, typical and delayed groups had an unadjusted difference of 2.1 points, which was statistically significant and indicative of a large effect (Wald χ²₍₁₎ = 115.4, p < .001, Cohen’s d = 2.68). After adjustment for covariates, the group difference was reduced to a 1.9-point difference, which was statistically significant and still indicative of a large effect (Wald χ²₍₁₎ = 354.4, p < .001, Cohen’s d = 2.42). A visual summary of group differences is depicted in Figure 1.

Figure 1.

Effect size estimates for the prediction of continuous indicators of kindergarten academic readiness from preschool executive function class membership.

Dichotomous outcomes

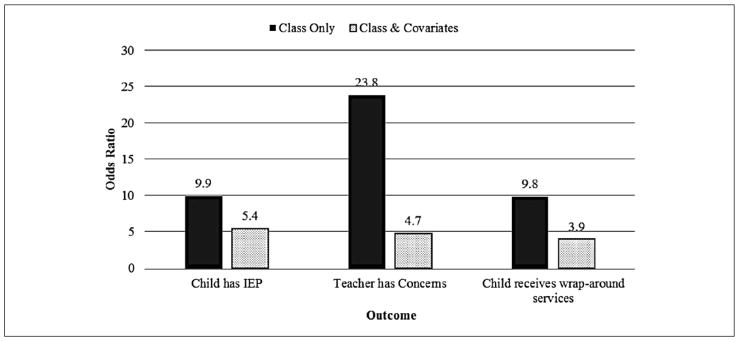
The unadjusted odds of children in the delayed group having an Individualized Education Program (IEP) were 9.9 times greater than the odds of children in the typical group having an IEP, which was statistically significant and indicative of a large effect (Wald χ²₍₁₎ = 34.5, p < .0001, OR = 9.9). After adjustment for covariates, the odds of the delay group’s having an IEP was 5.4 times greater than the odds of the typical group’s having an IEP, which was statistically significant and indicative of a large effect (Wald χ²₍₁₎ = 7.6, p = .006, OR = 5.4). The unadjusted odds of a teacher’s having concerns about learning or behavior for children in the delayed group were 23.8 times greater than the odds of a teacher’s having concerns about children in the typical group, which was statistically significant and indicative of a large effect (Wald χ²₍₁₎ = 23.5, p < .001, OR = 23.8). After adjustment for covariates, the odds of teacher concerns for the delay group was 4.7 times greater than the odds for the typical group, which was statistically significant and indicative of a medium effect (Wald χ²₍₁₎ = 8.4, p = .004, OR = 4.7). Finally, the unadjusted odds of a child in the delayed group receiving wrap-around services were 9.8 times greater than the odds for children in the typical group, which was statistically significant and indicative of a large effect (Wald χ²₍₁₎ = 39.9, p < .0001, OR = 9.8). After adjustment for covariates, the odds of a child in the delayed group receiving wrap-around services was 3.9 times greater than the odds for a child in the typical group receiving wrap-around services, which was statistically significant and indicative of a medium effect (Wald χ²₍₁₎ = 6.1, p = .01, OR = 3.9). A visual summary of group differences is depicted in Figure 2.

Figure 2.

Effect size estimates for the prediction of dichotomous indicators of kindergarten academic readiness from preschool executive function class membership.

Postscript: Overlap of GMM Class Membership and Lowest Decile of EF at Each Age

These results indicate that children who did not exhibit age-graded improvements in EF across early childhood had pronounced academic problems in kindergarten. In light of these results, it was of interest to describe the overlap between membership in the delayed GMM group and being in the lowest decile of overall EF scores at each assessment. Although this was not an explicit research question, it informed an ad hoc question about the extent to which the trajectory-based approach for child identification was comparable to simply identifying children who performed poorly at a single point in time. This was accomplished by cross-tabulating membership in the delayed trajectory group with children whose observed EF composite was in the lowest decile at each assessment. Among the 972 children who had an EF composite score at the age 3 assessment, 18.4% (18/98) of children who were in the bottom 10% of observed scores were in the delayed trajectory group. This represented a statistically significant association, χ²₍₁₎ = 13.1, p = .0003. Among the 1,008 children who had an EF composite score at the age 4 assessment, 36.6% (37/101) of children who were in the bottom 10% of observed scores were in the delayed trajectory group. This represented a statistically significant association, χ²₍₁₎ = 77.6, p < .0001. Finally, among the 1,037 children who had an EF composite score at the age 5 assessment, 96.2% (100/104) of children who were in the bottom 10% of observed scores were in the delayed trajectory group. This also represented a statistically significant association, χ²₍₁₎ = 808.2, p < .0001.

Discussion

EFs are a set of domain-general processes that contribute to children’s school readiness. Moreover, early childhood is understood to be a period of rapid improvement in EF abilities. The overarching objectives of this study were to test whether we could identify a subset of children who exhibited atypical or otherwise delayed improvement in EF between 3 and 5 years of age and to test whether this group of children exhibited impairments in academic functioning during kindergarten. Results indicated that approximately 9% of children were characterized by low levels of EF that did not exhibit expected age-graded improvements between ages 3 and 5 years. Relative to their typically developing peers, these children exhibited moderate to large-sized differences in multiple indexes of academic function in kindergarten, even after adjustment for numerous demographic and general cognitive factors that are well-established risks for academic problems.

This study benefited from the use of a large representative sample of children who were born in predominantly low-income communities. The weighted estimate of 9% of children who exhibited delayed development of EF is interesting in light of estimates that 7% to 10% of children have learning or learning-related (e.g., attention-deficit/hyperactivity disorder) disabilities—and these estimates have continued to grow across time (Altarac & Saroha, 2007; Boyle et al., 2011; Houtrow, Larson, Olson, Newacheck, & Halfon, 2014). There appears to be a high degree of overlap between children who fail to show expected patterns of improvement in EF across early childhood and their risk for learning-related problems at school onset. An important direction for future research is to delineate more specifically what proportion of children who exhibit delayed patterns of EF end up in special education placements or receiving specific learning-related services.

This study also benefited from direct assessments of EF tasks that have undergone rigorous psychometric evaluation and that were scaled to facilitate meaningful inferences regarding individual change. Direct assessments of EF correlate poorly (rs ≈ .20) with questionnaire-based assessment of EF (Toplak, West, & Stanovich, 2013). It is not clear that questionnaire-based methods are sufficiently sensitive to age-related changes in EF abilities to have been used in the way that direct assessments were used here. This is an important direction for future research.

Most previous studies that have examined the association between EF and school readiness have focused on children’s performance on standardized tests of academic achievement. Consistent with previous results, children in the delayed EF group performed more poorly on direct and teacher-rated assessments of early reading and math achievement, with effects’ being larger for math than reading. A distinguishing feature of the current study was consideration of a broader set of academic readiness indicators that capitalized on the unique perspectives of kindergarten teachers. Interestingly, group differences on teacher reports of children’s overall academic skills (Cohen’s d = 0.5) were intermediate between children’s direct performance on early reading (Cohen’s d = 0.2) and math (Cohen’s d = 0.7) abilities. In contrast to small- to moderate-sized differences in observed and rated academic ability, teachers reported that the delayed EF group was at markedly increased risk for grade retention (Cohen’s d = 2.4). Moreover, there were 370% increased odds that a teacher had concerns about learning or behavior for children in the delayed versus typically developing group, and children in the delayed EF group had 290% to 440% increased odds of having an IEP or receiving wrap-around or early intervention services relative to children in the typically developing group. Importantly, all of these effects were adjusted for covariates. This expanded set of outcomes underscored the importance of expanding definitions of academic readiness beyond direct measures of academic achievement. Risk for grade retention and need for/use of educational services are ecologically valid indicators of academic impairment.

Collectively, these results raise the prospect of incorporating direct assessments of EF into early child care (or health care) settings as a strategy for identifying children who may benefit from early intervention services and/or services immediately upon enrollment in kindergarten. Knowing whether a child exhibited developmental delays in the progression of his or her EF abilities conveyed information that was uniquely predictive of academic readiness. Children’s progression of EF was based on three annual assessments that took, on average, 30 to 40 min each to complete (approximately 2 hours of assessment time that spanned 2 years). An important question for future research is whether similar discriminations of children could be accomplished across shorter periods of time (e.g., three assessments across a 1-year assessment period). Despite the conceptual appeal of using trajectory-based methods for early identification, post hoc analyses demonstrated that nearly all of the children in the delayed trajectory group could have been identified by selecting children who performed in the bottom 10% of scores at the age 5 assessment. Obviously, this single assessment is more cost and time effective and would still provide the opportunity to identify children who may benefit from services prior to enrollment in kindergarten.

This study had at least three limitations. First, we focused exclusively on a composite variable that represented aggregate EF abilities. Specific tasks or subdomains of EF (e.g., working memory) may be differentially predictive of academic outcomes. Unfortunately, this study was not well suited to address these questions, given that some tasks were not administered at all three assessments. Second, repeated-measures data and designs are expensive. The benefits of using developmental trajectories as a means of early identification should be weighed against these costs. If timed correctly (e.g., just prior to or coincident with enrollment in kindergarten), a single assessment in conjunction with normative data may accomplish the same benefits of a repeated-measures approach with far less cost. Third, although we characterized the delayed group as not exhibiting developmental change in EF across time, the point estimate of the slope for that group was positive (not 0). Although the slope estimate was not distinguishable from (i.e., the confidence interval included) 0, with a larger sample size it may have been. It is probably best to characterize these children as exhibiting slower (vs. no) growth in EF abilities than expected. In a related vein, inferences about the rate of improvement in EF should not be extended beyond the age period studied. It is entirely possible that these children will exhibit pronounced improvements in their EF abilities following enrollment in school (e.g., catch up).

In sum, as evidence continues to mount regarding the contributions of EF to academic school readiness, it will be important for the field to consider ways in which this information can be optimized for purposes of early identification and early intervention. The descriptive results of observational studies like those presented here underscore the importance of developing an array of intervention approaches (from individualized programs to classroom curricula) that can be used to enhance EF across the early childhood period. The results of this study further suggest that monitoring growth in EF across the academic year may be useful for evaluating the benefits of those efforts. These efforts hold the potential for addressing long-standing discrepancies in school readiness that exist between children from low- and middle-income households.