Insights into genome architecture deduced from the properties of short Lac repressor-mediated DNA loops

Abstract

Genomic DNA is vastly longer than the space allotted to it in a cell. The molecule must fold with a level of organization that satisfies the imposed spatial constraints as well as allow for the processing of genetic information. Key players in this organization include the negative supercoiling of DNA, which facilitates the unwinding of the double-helical molecule, and the associations of DNA with proteins, which partition the DNA into isolated loops, or domains. In order to gain insight into the principles of genome organization and to visualize the folding of spatially constrained DNA, we have developed new computational methods to identify the preferred three-dimensional pathways of protein-mediated DNA loops and to characterize the topological properties of these structures. Here, we focus on the levels of supercoiling and the spatial arrangements of DNA in model nucleoprotein systems with two topological domains. We construct these systems by anchoring DNA loops in opposing orientations on a common protein–DNA assembly, namely the Lac repressor protein with two bound DNA operators. The linked pieces of DNA form a covalently closed circle such that the protein attaches to two widely spaced sites along the DNA. We examine the effects of operator spacing, loop orientation, and long-range contacts on overall chain configuration and topology, and discuss our findings in the context of classic experiments on the effects of supercoiling and operator spacing on Lac repressor-mediated looping and recent work on the role of proteins as barriers that divide genomes into independent topological domains.

Introduction

The long strings of DNA that comprise the genomes of all organisms undergo several layers of compaction in order to fit and function inside the tight confines of a cell. A key feature in this organization is the formation of DNA loops held in place by proteins that are bound to widely spaced sites along the genome (Postow et al. 2004; Dillon and Dorman 2010; Cavalli and Misteli 2013; Dekker and Misteli 2015). The proteins act as topological barriers that inhibit communication between elements on different loops and localize fragments of DNA with different levels of intertwining, or supercoiling, of the double-helical strands. Whereas the looser wrapping of strands characteristic of regions of negative supercoiling generally promotes genetic activities, the tighter wrapping found in regions of positive supercoiling tends to repress such functions (Liu et al. 2009).

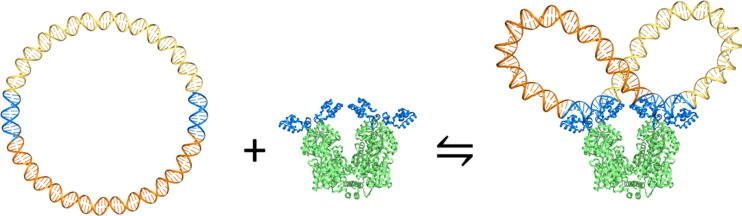
Insulator-like elements constructed by the binding of the Lac repressor protein to separated operator sites on DNA plasmids capture many of the features of DNA topological organization observed in vivo. The formation of a stable Lac repressor–operator complex introduces two protein-mediated loops on a covalently closed circular duplex (Fig. 1). The recognition elements on the protein simultaneously contact two different sites on the DNA and constrain the pathways of the intervening pieces of the closed chain. The binding of the repressor to distant operator sites on plasmids of a few thousand base pairs (bp) thus inhibits communication between transcriptional elements located on the different halves of the DNA (Bondarenko et al. 2003) and divides the DNA into two separate topological domains, in which the level of supercoiling in one domain is independent of the other (Leng et al. 2011). Conversely, the formation and sites of Lac repressor-mediated loops on DNA plasmids depend upon the level of supercoiling. Negative supercoiling enhances and stabilizes the association of the repressor with distant operators (Borowiec et al. 1987; Whitson et al. 1987; Krämer et al. 1988; Eismann and Müller-Hill 1990), and the level of supercoiling dictates the distances between operators most readily incorporated in the paired loops (Krämer et al. 1988; Eismann and Müller-Hill 1990). Changes in supercoiling imposed through direct manipulation of single DNA molecules capture the interconversion of looped and unlooped states implicated in the mix of repressor–operator complexes on circular DNA (Normanno et al. 2008). Moreover, the single-molecule studies reveal two distinct looped states that respectively build up and die off in phase with direct manipulation of one end of the DNA. Like the plasmids, the linear chains are spatially constrained, albeit in extended rather than closed configurations and with one rather than two protein-mediated loops.

Fig. 1.

Molecular images illustrating the partition of a 182-bp DNA minicircle into equally sized, independent topological domains through the binding of the Lac repressor protein. Images rendered in PyMOL (http://www.pymol.org) with the DNA backbones depicted by tubes, the DNA bases by sticks, and the protein by ribbons. The DNA operators and the recognition headpieces on protein are highlighted in blue. The intervening segments of DNA are shown in different shades of gold and the remainder of the protein in green. Here, the operators attach in opposing antiparallel orientations to the binding headpieces of the protein

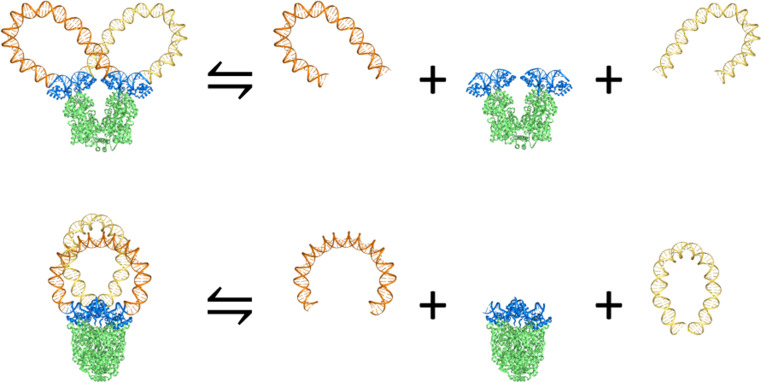
Estimates of the free energies of DNA looping based on treatments of the double helix as an elastic rod offer insights into how a closed circular molecule may adapt to the constraints of protein binding. The ease of DNA looping depends upon the length of the molecule and the relative spatial disposition of its binding sites on protein (Tobias et al. 1994). The requirements of binding are best met if the ends of the DNA are appropriately phased with the ~10.5-bp DNA helical repeat (Swigon et al. 2006; Czapla et al. 2013). Chains differing in length by 5–6 bp accordingly close with lesser ease against the given protein. The DNA chain length further determines the orientation of the loops anchored to the protein (Czapla et al. 2013). For example, when the DNA chain is relatively short, the most easily formed loops attach to the Lac repressor in antiparallel orientations and the less easily closed loops in parallel orientations (described below). Whereas the antiparallel loops follow U-shaped pathways with the ends of the molecule (i.e., the protein-bound lac operator sequences) pointed in roughly opposing directions, the parallel loops describe helical arcs of low pitch with the DNA ends pointed in nearly the same direction. As each operator may bind to either of the repressor headpieces, the DNA loops can attach to the protein in four distinct ways (Geanacopoulos et al. 2001): an antiparallel form and a parallel form (respectively termed A₁ and P₁) that connect the first binding headpiece to the second and two opposing antiparallel and parallel forms (termed A₂ and P₂) that connect the second headpiece to the first.1 Moreover, pairs of opposing loops (A₁A₂ and P₁P₂) may simultaneously bind the same set of operators and, thereby, describe a continuous DNA chain. The Lac repressor complexes that partition closed circular duplexes form such pairs of loops (Fig. 2).

Fig. 2.

Configurations of Lac repressor-partitioned minicircles obtained by concatenating the structures of pairs of 92-bp energy-minimized loops , including the bound DNA fragments of the repressor–operator complex. The closed pathways constructed from antiparallel (A₁, A₂) loops (upper row) differ significantly from those formed from parallel (P₁, P₂) loops (lower row), illustrated here by the combination of A₁ or P₁ (light gold) and A₂ or P₂ (dark gold) loops. The molecular components of the former construct are oriented in the same viewpoint (down the axis perpendicular to the “V” formed by the arms of the protein assembly) as in Fig. 1, and those in the latter from the vantage point obtained upon 45° rotation of the protein as a whole about the vertical axis through the center of the “V”. See the legend to Fig. 1 for molecular color-coding and styles

The ease of dividing a closed DNA molecule into independent topological domains with an insulator protein thus depends upon the lengths and types of imposed loops. Here, we estimate that cost from the relative elastic energies of short, Lac repressor-anchored fragments of ideal, naturally straight DNA. The optimized energies (Perez et al. 2014) mirror the looping propensities and modes of chain attachment found in simulations of Lac repressor-mediated DNA chain closure (Czapla et al. 2013) and capture chain-length-dependent variations in DNA loop formation determined experimentally (Han et al. 2009; Johnson et al. 2012). We also take account of long-range contacts between looped segments that may influence the formation of the protein–DNA assembly. We determine the preferred placement of operators at various positions along an ideal, 182-bp closed duplex and the likely configurations of the resulting loops. We identify conditions under which the modeled DNA may assume different levels of supercoiling and find that the binding of repressor to evenly spaced operator sites brings the energies of different topoisomers within close range of one another. We ignore the large-scale opening of the Lac repressor detected in low-resolution structural studies (McKay et al. 1982; Ruben and Roos 1997; Taraban et al. 2008), the effects of non-specific architectural proteins on looping (Becker et al. 2005; Czapla et al. 2011), the fluctuations in DNA operator sequences on the repressor headpieces (Spronk et al. 1999; Colasanti et al. 2013), and the local, sequence-dependent structural and energetic properties of DNA (Olson et al. 1998). The present article thus serves as a starting point for further investigation of the contributions of repressor deformability, architectural proteins, operator motions, minicircle chain length, and base-pair sequence to DNA topological organization.

Approach

Configurations of closed circular DNA molecules divided into separate topological domains by the binding of the Lac repressor were obtained by concatenating the structures of pairs of loops anchored in opposing orientations on the binding headpieces of the protein (Fig. 2). The structures of the loops were identified with a new procedure that optimizes the energy of a collection of base pairs, in which the first and last pairs are held fixed (Clauvelin and Olson 2014). The DNA is treated at the level of base-pair steps, using six rigid-body parameters to specify the arrangements of successive residues (Lu and Olson 2003, 2008) and a potential that allows for elastic deformations of the parameters from their equilibrium rest states (Czapla et al. 2006). The base-pair steps are assigned the properties of an ideal, inextensible, naturally straight polymer, with isotropic bending deformations, independent fluctuations of twist, and a helical rest state with 10.5 bp per turn and successive residues displaced by 3.4 Å. The reported energies do not take account of the stabilizing interactions between protein and DNA, which are fixed in value by the assumed rigid repressor–operator model (see below).

The Lac repressor is represented by a rigid, V-shaped model, constructed by superposition of the structures of two well-resolved crystallographic complexes (Swigon et al. 2006; Swigon and Olson 2008), specifically the 2.6-Å resolution structure of the protein dimer bound to a symmetric DNA operator (Bell and Lewis 2000) and the 2.7-Å resolution structure of the tetrameric form of the protein without DNA-binding headpieces (Lewis et al. 1996). The modeled operator DNA is assigned the rigid-body parameters adopted in the former complex and the full repressor is included as a “side group” of the DNA. That is, the atoms of protein are expressed in the reference frame of one of the bases in the full assembly. The reported loop lengths correspond to the number of base-pair steps between the centers of the bound DNA operators, namely seven of the 13 steps attached to each arm of the modeled repressor–operator assembly plus the DNA steps subjected to configurational variation. The reported lengths of the loops are, accordingly, 14-bp steps longer than the lengths of the optimized, ligand-free segments of DNA, and the length of the circular DNA formed upon concatenation of two protein-mediated loops is 12-bp steps longer than the combined lengths of the two ligand-free segments.2

The DNA loops include configurations from two competing families of Lac repressor-mediated structures associated with each orientational setting on the protein (Colasanti et al. 2013). The energies of the loops in the two families, here termed F1 and F2, exhibit similar ~21-bp periodic dependencies on chain length. The oscillations of energy with chain length, however, differ in phase by a helical turn such that the valleys in the energy profile of one family of looped structures coincide with the peaks in the other and vice versa. The energy minima occur at chain lengths where the uptake of twist is minimal and the ends of the DNA fall in nearly perfect register with the binding sites on the repressor. Opposing pairs of antiparallel or parallel loops may, accordingly, attach in four distinct ways to a specified pair of operators on a closed duplex. That is, opposing antiparallel loops may combine as A^F1₁A^F1₂, A^F1₁A^F2₂, A^F2₁A^F1₂, or A^F2₁A^F2₂ pairs and opposing parallel loops as P^F1₁P^F1₂, P^F1₁P^F2₂, P^F2₁P^F1₂, or P^F2₁P^F2₂ pairs. The relative populations of the different forms depend upon the levels of torsional and bending stress associated with the assumed orientations and spacings of the DNA operators and the length of the DNA as a whole. Here, we consider DNA minicircles of 182 bp and allow for all possible orientations of loops with center-to-center operator spacings between 73 and 111 bp.3 The loops that divide this minicircle in half contain the natural 92-bp center-to-center operator spacing found in Escherichia coli.

The topology of the repressor-partitioned minicircles, which follows from the combination of loop configurations, is described in terms of a discrete ribbon constructed from the origins and reference frames of four successive base pairs (Britton et al. 2009; Clauvelin et al. 2012). In contrast to the twist angle included in the six rigid-body parameters used to specify the relative spatial arrangements of successive base pairs (mentioned above), the values of twist reported here, the so-called twist of supercoiling (Britton et al. 2009), can be combined with the writhing number of a closed structure to obtain the correct linking number, an integer if the edges of the DNA ribbon are connected and the surface bounded by the ribbon is free of self-contact (Călugăreanu 1961; White 1969; White and Bauer 1987). The “closed” DNA includes the two constrained loops and both protein-bound operators. The values of twist reveal the extent to which the protein contributes to DNA topology and how torsional stress is distributed along the constrained molecule.

DNA looping on closed circular DNA

Lac repressor-partitioned minicircles

Lac repressor-mediated loops with the natural 92-bp center-to-center operator spacing found in Escherichia coli adopt a mix of energy-optimized configurations with subtle differences in three-dimensional structure (Colasanti et al. 2013; Perez et al. 2014). The antiparallel loops either under- or overwind, by ~2°/bp relative to ideal B DNA, to fit against the protein headpieces, and the DNA, as a whole, swings back and forth relative to the repressor structure (unpublished results). The loops anchored in some of the more highly bent parallel orientations are subject to less torsional stress and, thus, comparable in total elastic energy to the combined bending and twisting energies of the antiparallel loops.

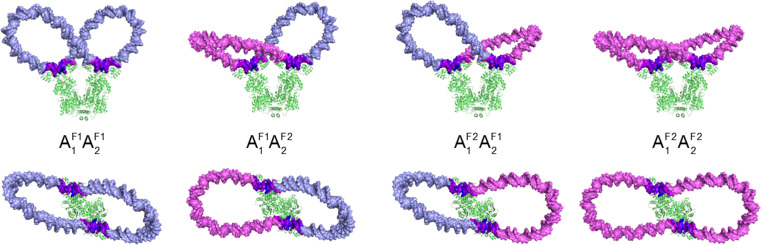
Concatenation of the optimized 92-bp loops yields five major classes of Lac repressor-bound minicircles, four from the combination of antiparallel loops and one from the combination of parallel loops. The structures formed from the antiparallel loops follow similar spatial pathways with a narrow protein-bound “waist” connecting two roughly U-shaped lobes (Fig. 3). The lobes, however, adopt different configurations with respect to the protein and assume different levels of supercoiling. Both lobes may underwind, both overwind, or one lobe underwind and the other overwind relative to B DNA. The base pairs along the two underwound loops, which are incorporated in the A^F1₁A^F1₂ protein-anchored construct, deviate as much as 60 Å from the corresponding residues along the two overwound loops included in the A^F2₁A^F2₂ construct. The latter minicircle is more extended and less contorted than the former, with loop apices separated by intramolecular distances of up to 240 Å versus maximum distances of 213 Å in the more compact form. The respective writhing numbers of the two constructs, −0.5 and −0.2, reflect the closed and open arrangements of the DNA lobes relative to the protein assembly.

Fig. 3.

Molecular images showing the overall folding and torsional stress in a 182-bp DNA minicircle found upon attaching a pair of evenly spaced operators in all possible antiparallel orientations to the Lac repressor. Configurations are denoted by the settings and families of the energy-optimized loops anchored to the protein (see text). Views looking perpendicular to (upper row) and down (lower row) the symmetry axis of the V-shaped protein assembly. The torsional stress is expressed in terms of the net change in the twist of supercoiling, relative to B DNA, at individual base-pair steps along the closed molecule. DNA is color-coded such that the most underwound steps (located on the operators) are depicted in deep blue and the most overwound steps (also on the operators) in deep magenta, with intermediate regions of negative, null, and positive deviations in twist varying respectively from blue to white to magenta. The uniform twist along the protein-free lobes reflects the treatment of DNA as an ideal elastic rod

Although the Lac repressor unwinds the highly kinked CG base-pair steps at the centers of the DNA operators by more than 9° relative to B DNA, the protein headpiece introduces a net increase in twist over the bound operators (~5° over each 13-step fragment).4 The changes in twist along the protein-free DNA fragments are substantially larger. The ~150° net decrease in twist within each lobe of the A^F1₁A^F1₂ minicircle occurs in the context of a topoisomer with linking number Lk of 16 and the nearly comparable increase in twist within the arms of the A^F2₁A^F2₂ minicircle in the context of a topoisomer with Lk = 18. The protein-bound minicircles made up of one underwound and one overwound loop have the same linking number (Lk = 17) as a protein-free DNA minicircle of the same length. In contrast to the protein-free minicircle, where a ±1 change in Lk increases the energy substantially over that of the Lk = 17 topoisomer, the binding of the Lac repressor to operator sites spaced by 92-bp on the DNA equalizes the energies of these topoisomers. That is, the differences in elastic energy between the topoisomers decrease from tens to fractions of k _B T if the V-shaped protein attaches to operators with 92-bp center-to-center spacing. Although the local DNA deformations in the Lac-partitioned minicircle are much more costly than the bending and twisting of the free minicircle, the energies of the protein-mediated loops are not appreciably affected by the mode of protein attachment and associated levels of supercoiling.

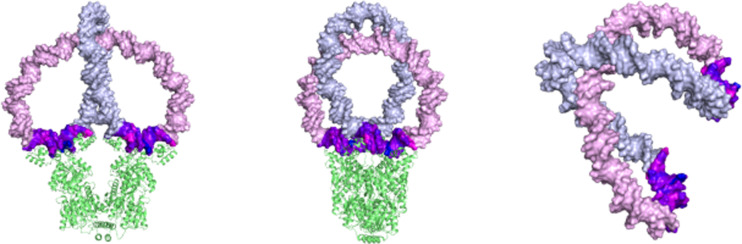
The low-energy Lac repressor-bound construct formed from the pairwise combination of parallel (P^F1₁, P^F2₂) loops brings the centers of the two protein-free segments into close, potentially favorable, contact (Fig. 4). The outer P^F1₁ loop runs roughly perpendicular to the inner P^F2₂ loop with the edges of the grooves close enough to associate with a common ligand. The DNA, as a whole, follows a more highly folded but much less torsionally stressed pathway than the DNA attached to the repressor in the four antiparallel arrangements. The accumulated change in twist along each lobe—roughly −100° along the P^F1₁ lobe and +40° along the P^F2₂ lobe, relative to B DNA—is much lower than the corresponding changes in twist in the constructs with antiparallel attachments. The writhing number Wr of −1.2 and linking number Lk of 16 are consistent with the folded, plectonemic DNA pathway evident from certain views of the structure. The DNA follows similar folded pathways of comparable writhe but much greater torsional stress if bound to protein through other parallel attachments. For example, the accumulated changes in twist underwind a P^F2₁ loop by nearly −300° and overwind a P^F1₂ loop by almost 250°. Thus, the only feasible way to divide a 182-bp minicircle in half through parallel attachments to the modeled repressor is with the P^F1₁P^F2₂ construct.

Fig. 4.

Molecular images illustrating the plectonemic folding, torsional stress, and long-range contacts of a 182-bp DNA minicircle formed upon binding a pair of evenly spaced operators in parallel (P^F1₁P^F2₂) orientations to the Lac repressor. Views of the protein-bound assembly looking perpendicular to the axis joining operator centers (left), from the standpoint, used in the lower row of Fig. 2, to illustrate the loop composition (center), and from a perspective, in the absence of protein, that highlights the interwinding of the DNA as a whole (right). Torsional stress color-coded as in Fig. 3

Influence of operator spacing on protein uptake

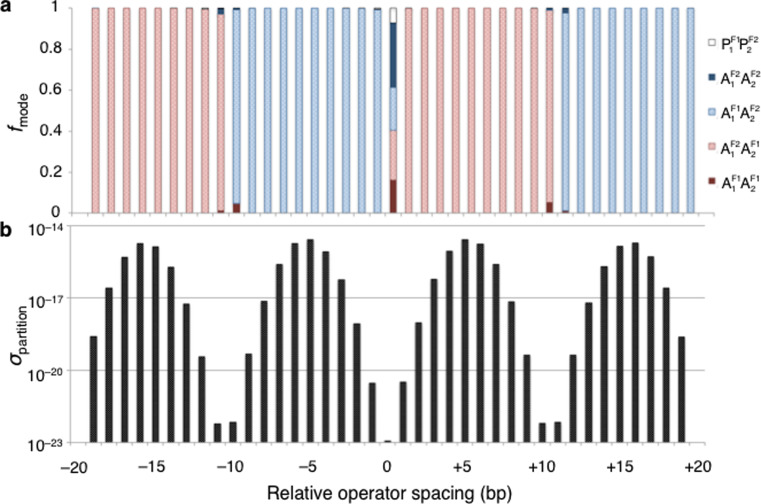
Repositioning the lac operators on the 182-bp minicircle has a profound effect on the elastic energies and configurations of the repressor-bound system. A shift in operator spacing by a single base pair from the evenly spaced, or symmetric, attachment of protein considered above reduces the mix of feasible repressor-bound configurations to a single state (Figs. 5a and 6). The changes in spacing alter the DNA torsional stress, with a 1-bp decrease in the separation of operators reducing the build-up of twist in A^F1₁ and A^F1₂ loops by ~25° and a 1-bp increase in spacing doing roughly the same in A^F2₁ and A^F2₂ loops. The net twist increases in magnitude by ~20° and the energy rises precipitously with changes in spacing of the opposite sense in the same loops, i.e., an increase in operator spacing along the first set of loops and a decrease along the second. Thus, a single configuration dominates a 182-bp minicircle unevenly divided by repressor attachments at sites 91- and 93-bp apart. The shorter lobe adopts an A^F1₁ or A^F1₂ configuration that is slightly less underwound and the longer lobe an A^F2₂ or A^F2₁ configuration that is slightly less overwound than the lobes formed upon symmetric protein attachment. The multiple configurations associated with the latter placement of protein accordingly serve as a “transition state” between the A^F1₁A^F2₂ and A^F2₁A^F1₂ repressor-bound constructs that respectively dominate the configurational landscape when the spacing between the first and second operators is smaller or larger than that between the second and first.

Fig. 5.

Profiles, as a function of operator spacing, of (a) the fraction f _mode of 182-bp, Lac repressor-bound DNA minicircles in each of the energetically favored modes of loop attachment to the V-shaped protein assembly and (b) the relative ease of partitioning the DNA into two domains at these sites. Operator spacing is expressed in terms of the displacement of the recognition sequences, in base-pair steps, relative to the even positioning at 0 associated with the formation of equally sized loops having the 92-bp center-to-center spacing found in the Escherichia coli lac operon. That is, one of the protein-anchored loops is altered in size by the specified difference in spacing and the other by its negative. The ease of DNA partitioning σ _partition is given by the sum of the Boltzmann factors of the elastic energies of the modeled Lac repressor-bound minicircles at each spacing. Note the much lower chances of dividing the minicircle in half compared to partitioning it at other sites

Fig. 6.

Gallery of molecular images illustrating the changes in overall folding and torsional stress in a 182-bp, Lac repressor-partitioned DNA minicircle upon selective displacement of operators relative to the even spacing entailed in the formation of two 92-bp loops. Configurations are labeled, color-coded, and oriented as in Fig. 3, with the favored arrangements at the specified spacings outlined in blue. The upper and lower signs in the ∓ and ± symbols denote the respective changes in the lengths of the A1 and A2 loops. Structures are shown in the absence of protein to draw attention to the subtle differences among DNA structures

The torsional stress on DNA nearly vanishes when the operator spacing changes by ±5 bp relative to the symmetric placement of repressor on the minicircle (Fig. 6). The elastic energy attains its lowest values when the operator centers lie 87- and 97-bp apart and the recognition elements on DNA lie in almost perfect register with the repressor headpieces. The lobes of these structures fall in the same A^F1₁A^F2₂ and A^F2₁A^F1₂ conformational classes as those formed on repressor-bound minicircles with operators shifted ±1-bp from their sites on the evenly divided minicircle. The Boltzmann factors of the ±5-bp shifted states are roughly eight orders of magnitude greater than the combined Boltzmann factors of the five types of Lac repressor-bound minicircles that comprise the set of evenly partitioned minicircles with 92-bp operator spacing (Fig. 5b). The Boltzmann factors associated with two other protein-divided minicircles, formed when the operator spacing differs by ±16 bp relative to the evenly divided minicircle, are nearly as large. The lobes of these low-energy structures, however, fall into different conformational categories from those with ±5-bp operator displacements. The shorter lobes adopt A^F2₁ or A^F2₂ configurations and the longer lobes A^F1₂ or A^F1₁ configurations (Fig. 5a). Transitions between the configurational families associated with the two low-energy forms occur at operator spacings of ±10–11 bp. The mix of configurational states at these points (Fig. 6) is less varied than that found for minicircles with repressor-mediated loops of the same size. One of the antiparallel loop combinations dominates the configurational landscape on either side of the transition points, with a small proportion of minicircles divided by repressor through A^F1₁A^F1₂ and/or A^F2₁A^F2₂ attachments (Fig. 5a). The single low elastic energy construct formed from the combination of unevenly sized parallel loops (a P^F2₁ loop 20–24 bp shorter than its P^F1₂ partner) self-intersects. The linking numbers of the configurations that comprise the “transition states”, nevertheless, span the same range of values (16–18) found in the evenly divided minicircles (Fig. 7). The Lk = 17 topoisomer dominates in all of the unevenly divided minicircles, including the “transition states” with ±10–11-bp operator spacings.

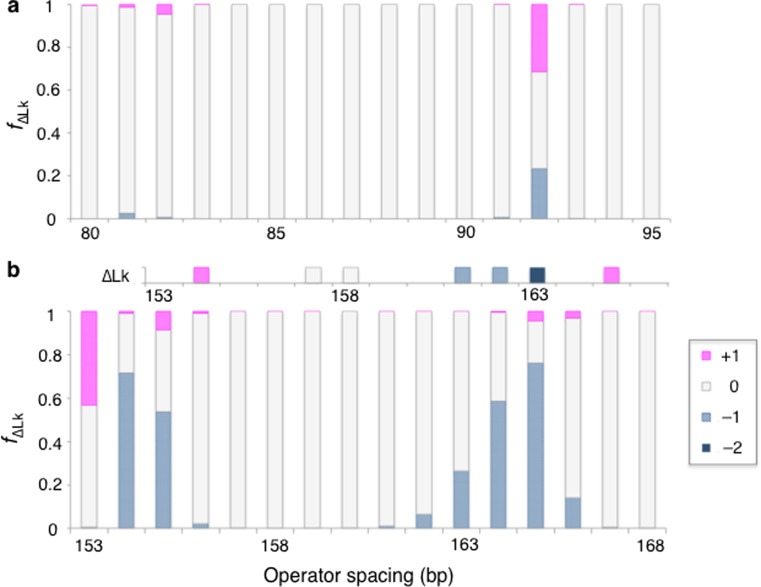
Fig. 7.

Profiles, as a function of operator spacing, of the distribution of topoisomers in (a) 182-bp and (b) 318-bp Lac repressor-partitioned minicircles generated from eight modes of DNA loop attachment to the V-shaped protein assembly. Operator spacing is expressed in terms of the center-to-center distances of one of the two DNA lobes formed upon protein binding and DNA topology in terms of the differences in linking number ∆Lk = Lk – Lk₀ of the topoisomers with respect to the relaxed state. Values of Lk₀ are the linking numbers of the constructs of lowest torsional stress, Lk = 17 in (a) and Lk = 30 in (b). The fraction f _∆Lk of minicircles with a given value of ∆Lk is proportional to the sum of the Boltzmann factors of those constructs. The predictions in (b) mirror the effects of supercoiling on the stability of loops of the same size formed in 452-bp Lac repressor-divided minicircles (Krämer et al. 1988) if offset by 2 bp (note the shifted histogram of observed ∆Lk values above the predicted data). The discrepancy in phase disappears upon a slight increase in the assumed DNA helical repeat (see text)

Concluding remarks

Although this article focuses on the configurations of a single short DNA minicircle bound at widely separated operator sites to the Lac repressor protein, the patterns of looping in the optimized structures reveal principles that can be related to the general, protein-mediated topological organization of DNA. For example, the preferred mode of DNA attachment to the repressor—with operators pointed in opposing, roughly antiparallel directions against the protein binding headpieces (Figs. 3 and 6)—may contribute to the low levels of communication found to occur between the two halves of a Lac repressor-partitioned plasmid (Bondarenko et al. 2003). The U-shaped pathways of the looped DNA segments lie on either side of the V-shaped protein, and, unless appreciably long (Huang et al. 2001), cannot deform to the extent needed to generate sequentially distant, intersegmental contacts. Indeed, looping of this type provides a useful model of the compaction of chromatin during mitosis (Dekker and Mirny 2016). The configurational properties of chromatin, however, reflect numerous factors, such as the precise sites and number of bound histone proteins, that influence the likelihood and pathways of loop formation. For example, simulated chromatin fibers exhibit a wide range of polymeric behaviors depending upon the spacing of nucleosomes (Clauvelin et al. 2015). On the other hand, the DNA loops formed by the strings of nucleosomes in chromatin, although orders of magnitude longer than the currently modeled loops in terms of the number of base pairs, resemble the bare DNA fragments in terms of the number of potentially deformable structural variables. A fully saturated chromatin construct of 1548 bp, with nine nucleosomes spaced at 172-bp increments, contains the same number of free base-pair steps as a 225-bp fragment of bare DNA. Chromatin fibers densely covered by a few hundred nucleosomes thus contain only a few thousand base-pair steps. Such fibers may close along the same lines as the loops considered here, with the naturally stiff base-pair steps inducing the nucleosome-decorated DNA to close in an antiparallel orientation with limited contacts to adjacent loops. The generally more costly partitioning of closed circular DNA, and potentially certain chromatin fibers, through the parallel alignment of operators on the repressor brings the two protein-free segments into close contact, especially if the chain is divided into comparably sized pieces (Fig. 4). Most modes of such attachment, however, introduce sterically impossible DNA–DNA and/or protein–DNA contacts that rule out these structures (Fig. 5a).

The changing mix of configurational states found upon repositioning lac operators on the modeled repressor-divided minicircles (Figs. 5 and 6) offers a rationale for the known influence of DNA supercoiling on the spacing of operators optimal for loop formation (Krämer et al. 1988). The differences in torsional stress among the various modes of DNA attachment to protein give rise to a variety of topoisomers at each operator setting. The levels of torsional stress depend upon the operator spacings and attain their lowest values when the operators lie in close register with the repressor headpieces. A single low-energy topoisomer dominates the configurational landscape if both lobes of the repressor-bound DNA are torsionally relaxed, such as the lobes with 87- and 97-bp spacing anchored in antiparallel settings on a 182-bp minicircle of linking number 17 (Figs. 6 and 7a). The much higher energies of minicircles with different modes of loop attachment and DNA topologies, i.e., the Lk = 16 and 18 topoisomers of the 182-mer with the same 87- and 97-bp operator spacings, preclude these occurrences. Operator spacings that introduce comparable, non-zero levels of torsional stress in different types of loop attachments yield a wide range of repressor-bound topoisomers, such as the topoisomers of a 182-bp minicircle of linking numbers 16–18 formed from the combination of under- and overwound 92-bp loops (Figs. 3 and 7a). The mix of topoisomers tends to be greatest when the spacing of operators differs by roughly a half helical turn (5–6 bp) from the operator separation distances of lowest torsional stress. The similar energies of these systems suggest that the repressor will bind to different topoisomers. The models further illustrate how different levels of torsional stress can build up in protein-divided minicircles (Leng et al. 2011) and how different looped states can build up and die off in phase with direct manipulation of one end of a tethered DNA molecule (Normanno et al. 2008).

The measured effects of supercoiling on the binding of the Lac repressor to a larger repressor-partitioned minicircle (Krämer et al. 1988) follow directly from these principles. The tetrameric protein assembly successfully divides a torsionally relaxed 452-bp closed circular DNA into lobes with 158- and 294-bp spacing but fails to bind to topoisomers of different linking number, a system analogous to the 182-bp minicircle with lobes of 74 and 84 bp that persists exclusively in the relaxed state. In addition, the protein shows minimal binding to a relaxed 452-bp minicircle with 163- and 289-bp operator spacings but associates readily with topoisomers of lesser linking number, a system analogous to the 182-bp minicircle divided into lobes of 79 bp with different topologies. The predicted distribution of topoisomers of a 318-bp ideal DNA minicircle partitioned by the V-shaped Lac repressor model into lobes ranging in size between 153 and 168 bp captures the relative spacings of operators found to associate with different topoisomers of the 452-bp minicircle (Fig. 7b). The modeled systems are constructed, as described above, by concatenation of the energy-optimized loops from competing families of Lac repressor-mediated structures of the selected lengths and the distribution of linking numbers is proportional to the sum of the Boltzmann factors of the variously combined structures. The total length of the minicircle is limited by the size of currently available energy-minimized loop structures (unpublished results).5 The slight discrepancies in the looping propensities of linear DNA, optimal at operator spacings of 160 bp in the modeled system versus 158 bp in the corresponding experimental construct (Krämer et al. 1987), give rise to the offset in predicted versus observed loop topologies at different operator spacings (displaced histogram at the top of Fig. 7b).

Slight changes in the DNA model, such as an increase in the assumed double-helical repeat from 10.5 to ~10.7 bp/turn, remove the difference in predicted versus observed phasing of linking numbers, and, as reported elsewhere (Hirsh et al. 2011), so does the opening of the V-shaped Lac repressor assembly. The DNA helical repeat reflects the underlying nucleotide sequence with values spanning a range, e.g., a tenfold repeat in the poly dA·poly dT homopolymer versus a 10.6–10.7-bp repeat in poly dG·poly dC (Wang 1979; Peck and Wang 1981; Rhodes and Klug 1981), much wider than the change noted above. The binding of a few nonspecific architectural proteins, such as the bacterial HU protein, can also account for the discrepancy in twist. The uptake of HU not only changes the torsional alignment of DNA against a loop-mediating protein but also enhances its propensity to adopt a closed structure (Czapla et al. 2008, 2011, 2013). On the other hand, whether the Lac repressor adopts an opened state in the 452-bp protein-divided minicircle remains an open question. Whereas the opening of the repressor is needed to mirror the DNAase I cutting patterns (Krämer et al. 1987) of very short (52- and 74-bp) Lac repressor-mediated loops (Swigon et al. 2006), it is not necessary to hypothesize such deformations (Perez et al. 2014) to account for the looping propensities deduced from tethered particle motions studies of longer (110–130-bp), Lac repressor-mediated loops (Han et al. 2009; Johnson et al. 2012). All other evidence supporting the opening of the repressor derives from studies of the isolated protein or complexes of the protein with the operator alone (Steitz et al. 1974; McKay et al. 1982; Ruben and Roos 1997; Taraban et al. 2008). In this regard, we are investigating the effects of Lac repressor deformation on the preferred spatial pathways of the DNA looped between its binding headpieces and the implications of these changes on the partitioning of closed circular DNA by the protein assembly.

Compliance with ethical standards

Conflicts of interest

Pamela J. Perez declares that she has no conflict of interest.

Wilma K. Olson declares that she has no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed byany of the authors.