Abstract
We introduce a novel Bayesian nonparametric model that uses the concept of disease trajectories for disease subtype identification. Although our model is general, we demonstrate that by treating fractions of tissue patterns derived from medical images as compositional data, our model can be applied to study distinct progression trends between population subgroups. Specifically, we apply our algorithm to quantitative emphysema measurements obtained from chest CT scans in the COPDGene Study and show several distinct progression patterns. As emphysema is one of the major components of chronic obstructive pulmonary disease (COPD), the third leading cause of death in the United States [1], an improved definition of emphysema and COPD subtypes is of great interest. We investigate several models with our algorithm, and show that one with age, pack years (a measure of cigarette exposure), and smoking status as predictors gives the best compromise between estimated predictive performance and model complexity. This model identified nine subtypes which showed significant associations to seven single nucleotide polymorphisms (SNPs) known to associate with COPD. Additionally, this model gives better predictive accuracy than multiple, multivariate ordinary least squares regression as demonstrated in a five-fold cross validation analysis. We view our subtyping algorithm as a contribution that can be applied to bridge the gap between CT-level assessment of tissue composition to population-level analysis of compositional trends that vary between disease subtypes.
I. Introduction
Disease subtyping is the process of identifying subpopulations of people who share similar disease characteristics, and it can be an important step in the search for distinct biological mechanisms that can explain disease etiology. Examples of heterogeneous diseases that have been studied from the perspective of disease subtyping include brain cancer [2], Parkinson’s disease [3], autism [4], autoimmune disease [5], and Chronic Obstructive Pulmonary Disease (COPD) [6]. In the case of progressive diseases such as COPD, the challenge is to identify subpopulations in which progression characteristics are similar; distinct disease trajectories suggest underlying biological and/or genetic similarity within subtypes. As COPD is the fourth leading cause of death worldwide [7] with an estimated global financial cost of $2.1 trillion, identifying meaningful subtypes that can lead to more targeted patient care is especially important.
COPD is characterized by airflow limitation resulting from chronic inflammatory responses in the airways and lungs to noxious particles or gases. There are two basic components of COPD: emphysema (destruction and loss of lung tissue) and small airways disease (inflammation and thickening of airway walls). Patients often undergo high resolution computed tomography (CT) scanning, which enables the direct evaluation of the lungs with both visual and quantitative methods. Recently, the Fleischner Society, a multidisciplinary medical society for thoracic radiology, released a statement defining the phenotypic abnormalities that characterize emphysema as evident on CT [8]. Patterns include centrilobular emphysema (subdivided into trace, mild, moderate, confluent, and advanced desctructive), panlobular, and paraseptal (subdivided into mild and substantial). There has also been a significant amount of work to classify patterns of emphysema on CT using computer algorithms [9], [10], [11], [12], [13], [14]. However, there has been comparatively little work to assess the change of these patterns over time and in response to smoke exposure across large cohorts of subjects, so the etiology of these patterns and the manner in which they progress remains unclear.
In this paper we introduce a general, Bayesian nonparametric model that uses the concept of disease trajectories to define subtypes. The model can be applied to a wide range of disease measures; here we demonstrate that by treating the fractions of different lung tissue types identified on CT as compositional data, our model can be effectively used as a means to investigate distinct emphysema progression patterns.
Researchers have previously applied the concept of trajectory clustering in a number of contexts. Schulam et al [5] introduced a probabilistic subtyping model and used it to identify subtypes of scleroderma. Their model uses longitudinal data to search for a fixed number of trajectory clusters. Wang et al [15] use continuous-time Markov jump processes to model the progression of COPD using comorbidity information. Their analysis focused on discovering a single disease progression model for COPD rather than a mixture of trajectory subtypes. McCulloch et al [16] illustrate the utility of latent class mixed models by identifying subgroup structure in longitudinal prostate cancer data, and Nagin and Odgers [17] apply the phrase group-based trajectory modeling to refer to the same underlying concept of identifying subgroups that evolve in time in distinct ways. An issue faced by all of these methods is how to identify the number of trajectories that best explain the data. A typical approach is to investigate a range of possible group numbers and apply a measure such as the Bayesian information criterion (BIC) [18] or the Akaike information criterion (AIC) [19] to select the final number of groups that best balances the goodness of fit and model complexity.
The model we introduce here is nonparametric and automatically determines the number of trajectories that best explain the data. Our approach is similar in spirit to a model we presented previously [20]. In both cases we are interested in clustering individuals using disease trajectories; however, whereas before we used Gaussian processes to represent trajectories, here we use linear functions of the predictors to represent them. This has the disadvantage of being more restrictive in terms of the functions can be modeled, but it has the advantage of making the relationship between predictors and disease measures more interpretable. Both models also leverage constraints between data points in order to guide the fitting process. We previously described using so-called “must-link” and “cannot-link” constraints between data pairs to flexibly capture auxiliary information about the data set, such as expert input specifying that a pair of points should or should not be grouped together. Here we expand this mechanism to accommodate longitudinal data, which forces observations from the same individual into the same trajectory during the inference procedure (the use of “must-link” and “cannot-link” constraints is less rigid, coaxing the algorithm rather than forcing the algorithm). Lastly, we previously made the variance on each target variable a constant and required that it be specified by the user. Here we learn these variances during the inference procedure and allow each trajectory to have a unique variance for each target variable.
Although our model can be applied to a wide range of applications and disease severity measures, we focus here on the analysis of quantitative emphysema measures derived from CT data. The paper is laid out as follows: in Section I we provide a detailed description of the emphysema data used in our experiments (Section II-A), our model formulation (Section II-B), the variational inference procedure (Section II-C), our experimental design (Section II-D), and the methods by which we validate our model (Section II-E). In Section III we give results, and we conclude in Section IV.
II. Materials and Methods
In this section we detail our Bayesian model and the variational inference procedure we use to compute a posterior probability over our model’s latent variables. The Bayesian paradigm is attractive because it enables specification of prior knowledge through model parameter selection. Additionally, by adopting a Bayesian approach, the over-fitting problem (which arises when making point estimates of parameters) can be avoided [21]. We begin by describing the emphysema data that we use for our experiments and later describe the experimental setup and validation criteria we apply to the posterior probabilities and disease trajectories discovered by our model.
A. Data
Between 2007 and 2011, 10,192 non-Hispanic white (6, 784) and African-American (3, 408) smokers were enrolled into the COPDGene Study, a previously described multicenter study designed to investigate the genetic and epidemiologic associations of COPD [22]. Participants with a history of active lung disease other than asthma, emphysema, or COPD were excluded from COPDGene. The age of enrollment ranges from 45 years old to over 90 years old, and participants present with a range of disease severity. A wide array of data exists for study participants including image-based disease measures computed from CT scans, spirometric measures of lung function, comorbidity information, demographic data, genetic profiles, and history of smoke exposure. The COPDGene study is currently in its second round of funding, and the subjects originally recruited are now returning at an interval of 5 years from their first visit for a repeat collection of the same data obtained during their first visit.
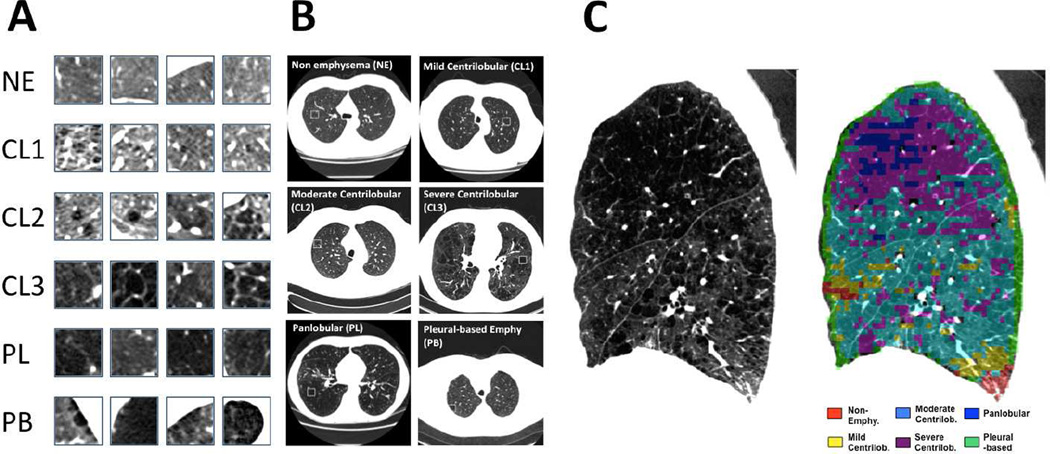
In this paper we demonstrate our Bayesian subtyping framework by identifying subpopulations of individuals whose emphysema patterns progress in distinct ways. We assume that progression potentially depends on a number of factors including increasing age and smoke exposure, current smoking status, gender, and race. We use a tissue classification scheme based on the local histogram of lung density [14] to characterize the percentage of six tissue patterns in CT scans acquired through the COPDGene study: non-emphysematous (NE), mild centrilobular emphysema (CL1), moderate centrilobular emphysema (CL2), severe centrilobular emphysema (CL3), panlobular emphysema (PL), and pleural-based emphysema (PB). Figure 1 illustrates tissue classification using the local histogram method. As mentioned in the Section I, alternative methods exist for classifying emphysema patterns in CT images. We choose the local histogram method because of its available implementation and the encouraging associations between classified image patterns and a wide array of measures of respiratory physiology and function [23]. However, it is important to note that the Bayesian framework presented in this paper could be used equally well with data derived from other classification approaches.
Fig. 1.
Prototypic lung computed tomography (CT) patches for each local histogram emphysema pattern as regions of interest (A) and in context (B). Local histogram emphysema classification results for a sagittal slice of the right lung corresponding to a COPDGene subject with severe emphysema (C).
The local histogram data can be treated as compositional data [24] by considering the fraction of the whole lung region accounted for by non-emphysematous tissue and each type of emphysema. Each individual in the COPDGene study is then associated with a 6 dimensional vector, [fNE, fCL1, fCL2, fCL3, fPL, fPB], where each element represents the fraction of each type of tissue in the lung, and the sum of all vector elements equals 1. Because of the summation contraint, the distribution over this space is confined to a 5-simplex. Egozcue et al introduced the isometric log-ratio (ILR) transformation and showed that it can be applied to compositional data vectors in order to map them from the simplex space to the real space [25]. The ILR transformation is given by
| (1) |
where in our case fn is the 6-dimensional compositional data vector of the nth subject, Yn is the 5-dimensional transformed vector in the real space, and Ψ is the 5 × 6 contrast matrix (details below). This transformation has the property that it preserves distance relationships between points. Additionally, the multivariate normal distribution in the real space has an analogue in the simplex space [26], and if a random composition is distributed according to the normal distribution on the simplex, then the ILR transformation of that random composition is distributed according to the multivariate normal in the real space.
The rows of the contrast matrix, Ψ, are associated with an orthonormal basis in the simplex, and there are multiple ways to define such a basis. We choose the approach based on a sequential binary partition (SBP) of the compositional data elements ([27], [28]) given its intuitive construction and the ease in interpreting the resulting coordinates. The SBP is a hierarchy of the parts of a composition. In the first order of the hierarchy, all parts are split into two groups. In subsequent steps, each group is in turn spit into two groups. The particular scheme we adopted for our problem is provided in Table I, which gives the sign matrix used to encode the sequential binary partition and build an orthonormal basis. Columns correspond to elements of the compositional data vector, and rows relate to elements of the transformed data vector. For a given row, a +1 indicates that the compositional element appears in the numerator of the transformed data vector, and a −1 indicates that it appears in the denominator. 0s indicate that the compositional data element is not involved in vector element of the transformed data. Given the sign matrix, the contrast matrix can readily be derived (see [27], [28] for details). Importantly, Table I provides an interpretation of each element of the vector in the ILR-transformed space, which are in terms of ratios between groups of compositional data elements. For example, the first row of the sign matrix corresponds to the first element of the ILR-transformed vector. This element captures the proportion of pleural-based emphysema vs all other tissue types (non-emphysematous, each type of centrilobular emphysema, and panlobular emphysema). Since the logarithm is taken in Equation 1, this means that a negative value indicates there is less pleural-based emphysema compared to all other tissue types, a positive value means there is more, and 0 indicates that are equal amounts.
TABLE I.
Sign matrix used to encode the sequential binary partition of the compositional data and to build an orthonormal basis for the constrast matrix, Ψ. The right-most column provides and interpretation of each element of the transformed data vector. “Non-Pleural-based” indicates all tissue types other than “Pleural-based Emphysema”. “Non Pleural-based Emphysema” represents all types of emphysema other than pleural-based emphysema. “Centrilobular” represents mild, moderate, and severe centrilobular emphysema.
| NE | CL1 | CL2 | CL3 | PL | PB | Interpretation |
|---|---|---|---|---|---|---|
| −1 | −1 | −1 | −1 | −1 | +1 | Pleural-based Emphysema / Non-Pleural-based |
| −1 | +1 | +1 | +1 | +1 | 0 | Non Pleural-based Emphysema / Non-Emphysematous |
| 0 | −1 | −1 | −1 | +1 | 0 | Panlobular / Centrilobular |
| 0 | −1 | −1 | +1 | 0 | 0 | Severe Centrilobular / Non-Severe Centrilobular |
| 0 | −1 | +1 | 0 | 0 | 0 | Moderate Centrilobular / Mild Centrilobular |
The ILR transformation is useful because it allows a conjugate model formulation as we describe below. However, we need a principled way of dealing with lung tissue type fractions that are equal to zero, which cause the natural log function to be undefined. For this we use the multiplicative substitution strategy proposed by [29] given as follows
| (2) |
Here δ is chosen to be 5 × 10−7, which is roughly equal to the fraction of a typical lung region accounted for by one image voxel (i.e. the detection limit of the imaging system).
In this study we consider all COPDGene round 1 data as well as the round 2 data available at the time of this study (1, 338 samples). Gender is coded as −1 (males) and 1 (females); race is coded as −1 (non-Hispanic whites) and 1 (African Americans); and smoking status is coded as −1 (current non-smoker) and 1 (current smoker). Cumulative smoke exposure is measured as pack-years, defined as the number of cigarette packs smoked per day multiplied by the number of years the person has smoked.
B. Model Formulation
In this section we describe our Bayesian formulation. We begin with a brief review of Markov random fields and Dirichlet process mixtures, two key elements of our model.
1) Markov Random Fields
A Markov random field (MRF) is represented by an undirected graphical model in which the nodes represent variables or groups of variables and the edges indicate dependence relationships [30]. An important property of MRFs is that a collection of variables is conditionally independent of all others in the field given the variables in their Markov blanket. The Hammersley-Clifford theorem states that the distribution, p (Z), over the variables in a MRF factorizes according to
| (3) |
where 𝒵 is a normalization constant called the partition function, 𝒞 is the set of all cliques in the MRF, Zc are the variables in clique c, and Hc is the energy function over clique c ([31], [32]). The energy function captures the desired configuration of local variables. Here we use a MRF to force longitudinal data instances belonging to the same individual to be in the same subtype cluster.
2) Dirichlet Process Mixtures
Ferguson [33] first introduced the Dirichlet process (DP) as a measure on measures. It is parameterized by a base measure, G0, and a positive scaling parameter α:
| (4) |
The notion of a Dirichlet process mixture (DPM) arises if we treat the kth draw from G as a parameter of the distribution over some observation [34]. DPMs can be interpreted as mixture models with an infinite number of mixture components.
More recently, Blei and Jordan [35] described a variational inference algorithm for DPMs using the stick-breaking construction introduced in [36]. The stick-breaking construction represents G as
| (5) |
| (6) |
where is the Kronecker delta, and the vi are distributed according to a beta distribution: vi ~ Beta (1, α), and . We use a DPM in our model to automatically identify the number of disease trajectories that best explain our data.
3) Our Model
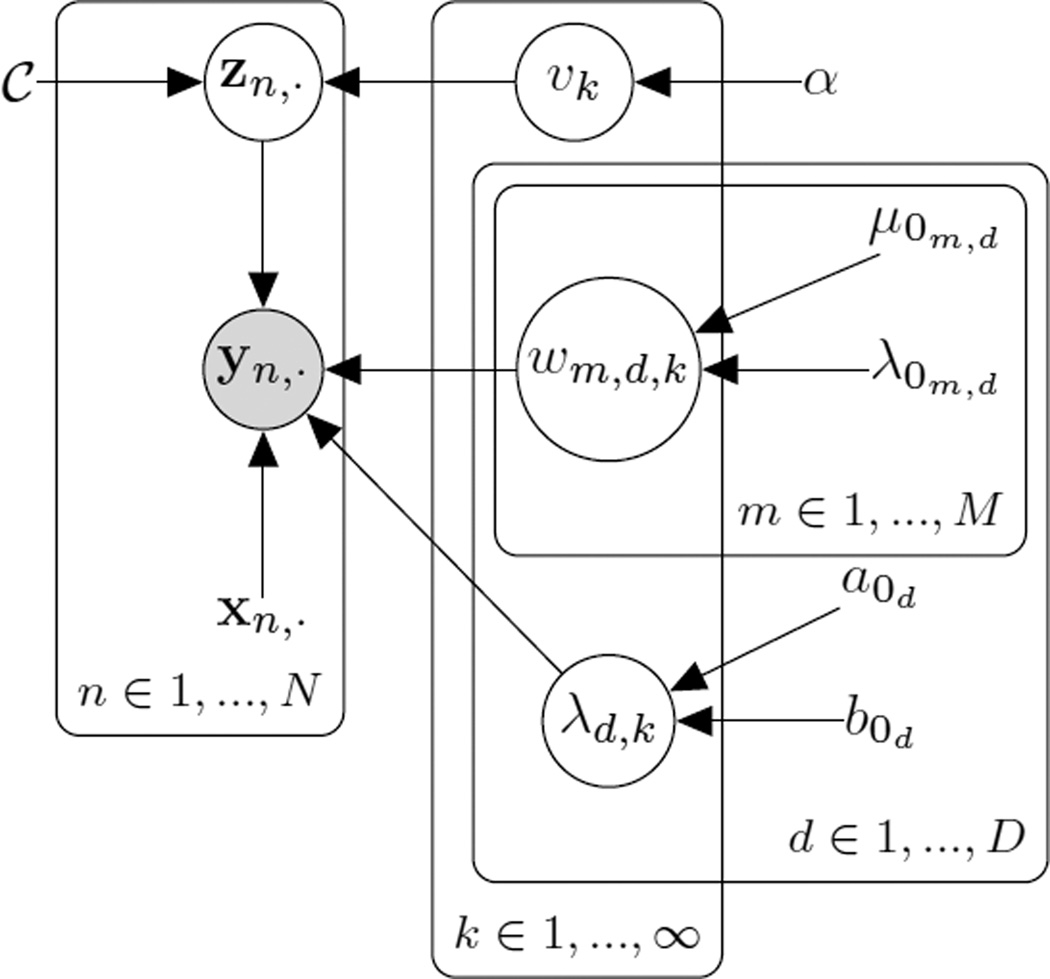
Let X = [x1 ⋯ xM] be the N × M matrix of observed predictors where N is the number of instances and M is the dimension of the predictor space. Let Y = [y1 ⋯ yD] be the N × D matrix of corresponding target values, where D represents the dimension of the target variables. In our experiments, Y are the transformed local histogram data given by Equation 1. We introduce the N × ∞ binary indicator matrix, Z, to represent the association between the data instances and the latent regression functions. W is the M × D × ∞ matrix of predictor coefficients that we wish to learn, along with λ, the D × ∞ matrix of precision values on each of D target variables.
The probabilistic graphical model describing our formulation can be seen in Figure 2. The set 𝒞 is a collection of data instances that are associated longitudinally – i.e. that represent the same patient at multiple time points. α, μ0, λ0, a0, and b0 are hyperparameters in our model that control the shape of the the prior distributions. A summary of the variables in our model is given in Table II. With these quantities defined, we give the joint distribution as
| (7) |
where
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
Fig. 2.
Probabilistic graphical model for our Bayesian nonparametric disease subtyping model. Shaded circles represent observed random variables, unshaded circles represent unobserved (latent) variables. Variables with no circle represent constants or hyperparameters. Plates indicated repeated sets of variables/constants.
TABLE II.
Description of variables in our probabilistic model. See text for details.
| Variable | Description |
|---|---|
| N | Number of data instances |
| D | Dimension of target variables |
| M | Dimension of predictor space |
| Y | N × D matrix of target variables |
| X | N × M matrix of observed predictors |
| W | M × D × ∞ matrix of predictor coefficients |
| Z | N × ∞ binary indicator matrix |
| λ | D × ∞ matrix of precision values |
| 𝒞 | Set of longitudinal constraints |
| v | Beta-distributed random variable in stick-breaking construction |
| α | Hyperparameter for prior over v |
| μ0, λ0 | Hyperparameters for prior over W |
| a0, b0 | Hyperparameters for prior over λ |
The likelihood in our model is given in Equation 8 and is represented as a multivariate normal distribution that factorizes over data instances, target variables, and trajectories. The mean is given by the inner product between an instance’s predictors and the associated coefficients in theW matrix; the variance is given by inverse precision for the corresponding target variable and trajectory.
Equation 9 describes the distribution over Z and consists of two terms: the first is a MRF that captures the pairwise longitudinal constraints, and the second is a multinomial distribution with parameters drawn for a Dirichlet process using the stick-breaking construction. The energy function for the MRF used in our experiments is given by
| (13) |
where < zi,·, zj,· > represents the inner product between zi,· and zj,·. This energy function is similar to the one we used previously [20], but here we have adapted it to force longitudinal data pairs to be associated with the same disease trajectory. Note that any number of longitudinal data points for an individual can be handled with this framework by simply forming a link between each data point and the data point from the previous visit.
Equation 10 expresses the distribution over the variable, v, used for the stick-breaking process, and α is the concentration parameter. The distribution over the predictor coefficients, given by Equation 11, is a multivariate normal distribution that factorizes over predictors, target variables, and trajectories. Our prior belief about each of these coefficients is represented by the mean, μ0m,d, and our confidence in those choices is captured by the precision, λ0m,d. Lastly, the prior over each target variable’s precision is modeled as a gamma distribution (Equation 12), which is the conjugate prior to the normal distribution’s precision parameter. The shape of this distribution is controlled by the hyperparameters a0 and b0.
C. Inference
In this section we give the variational inference update equations used in our model. Variational inference is a method of approximate inference that makes assumptions (typically a factorization) over the distribution of interest, and it turns an inference problem into an optimization problem [37], [38].
For our application, we are interested in the distribution over the latent variables in our model given our observations: p (Z, v, W, λ|Y, X, 𝒞, α, μ0, λ0, a0, b0). The posterior probability is approximated by optimizing the variational lower bound. The standard variational inference approach is to assume a factorized approximation of this distribution, in our case: p* (Z) p* (v) p* (W) p* (λ). In order to derive the expression for one of these factors, the expectation with respect to the other factors is considered. Derivation of the variational distributions begins with the following expressions
| (14) |
| (15) |
| (16) |
| (17) |
We give expressions for each factor without derivation. First, p* (v) is given by
| (18) |
K is an integer chosen by the user for the truncated stick-breaking process (set to 20 in our experiments).
The variational distribution for p* (Z) is given by
| (19) |
where
| (20) |
and
| (21) |
In Equation 19, 𝒱 represents a set of sets. Each element V of 𝒱 is a set of data indices belonging to a connected subgraph of the constraint MRF. In our experiments, this set of data indices corresponds to pairs of COPDGene data samples representing the same individual at baseline and 5-year follow-up. Because the set of constraints is sparse, the MRF can be characterized by a collection of disconnected subgraphs. (If the constraint set is dense, we can approximate the distribution by truncating the neighborhood to enforce low cardinality). It is important to note that the distribution factorizes over the resultant subgraphs. Given that each subgraph cardinality is small, it is feasible to compute the corresponding partition function, 𝒵V. This in turn enables efficient computation of 𝔼Z {Z}.
The variational distribution over λ is given by a gamma distribution with parameters a and b:
| (22) |
| (23) |
| (24) |
Finally, the variational distribution over the coefficients W is given by a multivariate normal distribution that factorizes over the predictors, targets, and subtype clusters:
| (25) |
| (26) |
| (27) |
The − in w−,d,k and xn,− indicates all but the mth predictor.
Inference proceeds by iteratively updating Equations 18, 19, 22, and 25. The variational lower bound is guaranteed to increase with each iteration and can be monitored to assess convergence. For our experiments, we terminate algorithm execution when the percent increase in the lower bound falls below 1 × 10−10.
D. Experimental Design
As stated above, our goal is to demonstrate our Bayesian subtyping framework by identifying distinct populations of people with similar emphysema progression characteristics. We explore several models with various subsets of the following predictors: age, pack years, (age)2, (pack years)2, smoking status, race, gender, and an intercept term. The Bayesian paradigm involves specifying prior knowledge (or lack thereof) through model hyperparameter selection. In our case, we must select values for the hyperparameters α, μ0, λ0, a0, and b0. The hyper-parameter α is set to 5 for all of our experiments. This value encodes our general belief about how many trajectories exist: smaller α values reflect the belief that only a few trajectories exist and vice versa. For all experiments, a0 and b0 were set to 0.01, corresponding to gamma distributions with mean 1.0 and a variance 100.0 (Equation 12).We place vague priors over each of the predictor coefficients by setting μ0 = 0 and λ0 = 10−4. In Section III we show the results of a sensitivity analysis that investigates how stable disease trajectory assignments are to perturbations of these parameter settings.
E. Model Comparison and Validation
We compare each of the models considered in our experiments by estimating their predictive accuracy. For this we use two approaches: 1) a version of the Watanabe-Akaike information criteria (WAIC) that uses a correction for the effective number of parameters to adjust for overfitting ([39], [40]), and 2) a five-fold cross validation study. The WAIC is given by:
| (28) |
where lppd is the log pointwise predictive density given by
| (29) |
Here ppost (·) represents the posterior distribution over all our latent variables which we collectively represent as θ. The correction term, pWAIC, is given by
| (30) |
which is a sum over the posterior variance for each sample point. Both lppd and pWAIC are estimated by sampling from the posterior distribution. Other measures exist for estimating model predictive accuracy such as the deviance information criterion (DIC) and the Akaike information criterion (AIC), but we use WAIC as given in Equation 28 because it is a more fully Bayesian measure: it averages over the posterior distribution rather than conditioning on a point estimate of θ [40].
For the five-fold cross validation study we divide the set of 1, 338 round 2 data points into five evenly-sized groups. For each fold we hold out one of the five round 2 groups and run our algorithm using the round 1 data and the remaining four round 2 groups. After the algorithm converges, we predict the target values (the ILR-transformed compositional data) for each data point in the hold-out set. For a given individual in the hold-out set, i, we estimate the expected value of his/her round 2 target variables by averaging samples from i’s posterior density but using i’s round 2 predictor values. We report the average mean squared error (MSE) between actual and predicted target values for each fold. We compare our predictions to those made by multiple, multivariate ordinary least-squares regression, a standard analysis method which implicitly assumes a single disease trajectory.
We use the predictive accuracy to select from the various candidate models that we explore. Once selected, we are interested in evaluating whether the posterior estimates of our model’s latent variables are sensible based on our prior knowledge. If a model does not significantly violate our assumptions it does not prove that the model is correct, but if assumptions are flagrantly violated, then the model is suspect. For example, we generally expect that the proportion of emphysema patterns relative to the amount of normal tissue should increase with increasing age and smoke exposure. Significant departures from this expectation will signal an issue with our model. We also expect that draws from our posterior distribution will resemble our observed data in substantive ways. This can be checked graphically by plotting histograms of our observed data overlaid with draws from the posterior. Areas of significant discrepancy can pinpoint possible issues with the model that may need to be addressed.
Finally, our goal is to identify subpopulations of individuals whose emphysema patterns evolve in distinct ways, which we assume occurs because of common underlying biology. To evaluate this, we consider the association of the discovered subtypes to seven single nucleotide polymorphisms (SNPs) known to be associated with COPD at genome-wide significance levels: rs12914385, rs13141641, rs4416442, rs754388, rs626750, rs4846480, and rs2070600. We perform an ordered logistic regression on each SNP and perform a likelihood ratio test between two models: the first, adjusted for age, pack-years of smoking, and principal components of genetic ancestry to adjust for population stratification, and the second, with the addition of subtypes as a categorical variable. Results are given in Section III.
III. Results and Discussion
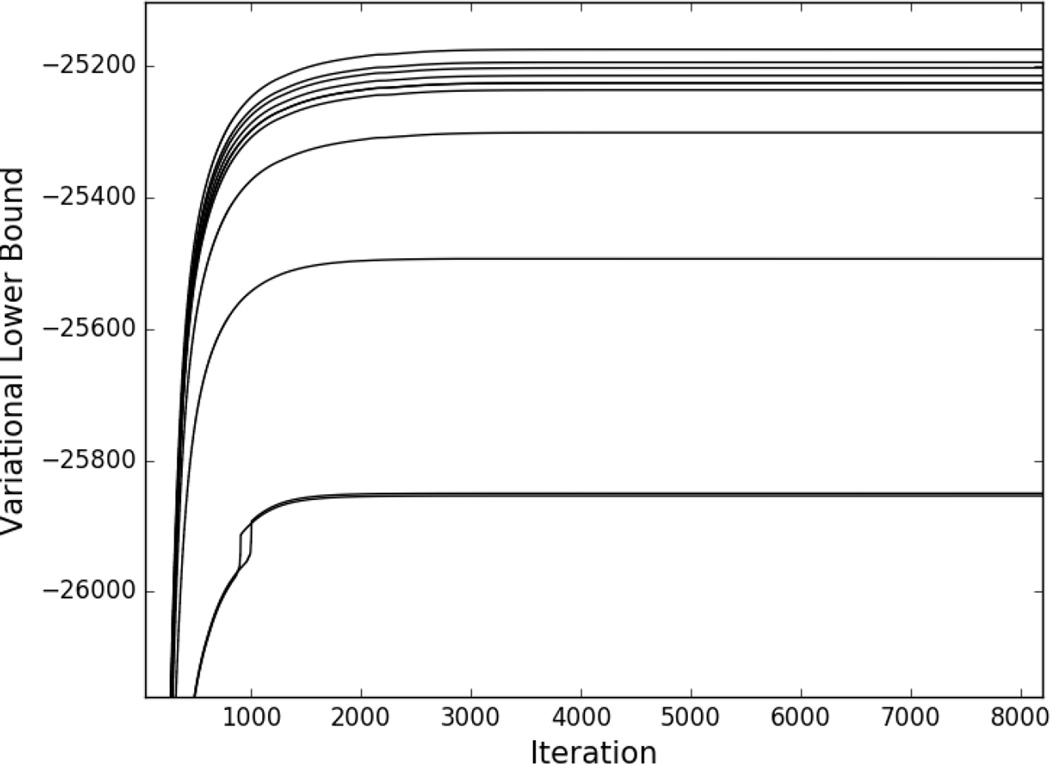
Our algorithm was run to convergence for each model explored in our study using the termination criterion given in Section II-C. Figure 3 shows the variational lower bound (the variational inference objective function) as a function of iteration number for each model. In each case, the algorithm converged within approximately 8, 000 iterations. (Note that the rank ordering of the models in terms of variational lower bound values at convergence does not correspond to the same rank ordering in terms of model WAIC scores, as these quantities capture different things). In the following sections we provide a comparison of the models and choose a model for further investigation (Section III-A), give a detailed description of the selected model (Section III-B), show results of checks on the selected model (Section III-C), and present results of genetic analysis (Section III-D).
Fig. 3.
Variational lower bound as a function of iteration number for the models explored in our study. From bottom (most negative lower bound value) to top (least negative lower bound value) models are ordered as M7, M9, M6, M3, M10, M1, M4, M5, M8, M2.
A. Model Comparison and Selection
Table III gives WAIC scores and cross validation MSEs for the top ten performing models explored in our experiments. All models included age, pack years, and an intercept term as predictors. For each fold in the cross validation study, the mean squared error is given for our approach (unshaded column) and for multiple, multivariate ordinary least squares regression (adjacent shaded column). The MSEs for our model are noticeably lower for each model across all five folds. The last column shows the folds average for each model. We note that models M3 and M5 have the lowest average MSE but that the values do not vary considerably across the models. Therefore, we select model M1, which has the lowest WAIC score, for further analysis.
TABLE III.
Predictive accuracy results for the top ten performing models in our study. All models contain as predictors age, pack years, and an intercept term. The Additional Predictors column lists other predictors that each model uses. Models are ordered according to WAIC scores, with lower scores indicating improved, estimated predictive accuracy while minimizing the effective number of model parameters. Mean squared error values are given for each fold of the cross validation study (unshaded: our approach, shaded: multiple, multivariate ordinary least squares regression).
| Model | Additional Predictors | WAIC | Fold 1 | Fold 2 | Fold 3 | Fold 4 | Fold 5 | Folds Average | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M1 | smoking status | 112455 | 18.2 | 27.9 | 16.2 | 26.0 | 16.1 | 24.0 | 14.7 | 23.8 | 16.5 | 25.5 | 16.3 | 25.6 |
| M2 | - | 113678 | 18.4 | 27.6 | 16.6 | 26.1 | 16.2 | 25.1 | 15.1 | 23.8 | 16.4 | 26.1 | 16.5 | 25.7 |
| M3 | (pack years)2 | 114532 | 17.5 | 28.5 | 14.9 | 26.6 | 16.1 | 25.9 | 14.9 | 24.9 | 17.0 | 29.0 | 16.1 | 27.0 |
| M4 | smoking status, race, gender, (pack years)2 | 114879 | 18.2 | 26.6 | 16.4 | 25.3 | 15.9 | 23.9 | 14.6 | 22.6 | 16.6 | 24.3 | 16.3 | 24.5 |
| M5 | smoking status, gender, (pack years)2, age2 | 115280 | 17.9 | 26.7 | 16.1 | 25.1 | 15.9 | 24.0 | 14.5 | 22.6 | 16.3 | 24.7 | 16.1 | 24.6 |
| M6 | smoking status, gender, (pack years)2 | 115346 | 18.3 | 26.8 | 16.3 | 25.2 | 16.2 | 24.9 | 14.7 | 22.7 | 16.8 | 24.6 | 16.4 | 24.7 |
| M7 | smoking status, gender | 115368 | 18.1 | 26.8 | 16.2 | 25.2 | 16.2 | 23.9 | 14.7 | 22.8 | 16.9 | 24.6 | 16.4 | 24.6 |
| M8 | race, gender | 115392 | 18.8 | 26.4 | 16.2 | 25.4 | 16.3 | 23.9 | 14.8 | 22.6 | 16.7 | 24.6 | 16.4 | 24.5 |
| M9 | race, gender, (pack years)2 | 115558 | 18.1 | 26.4 | 16.4 | 25.4 | 16.3 | 24.0 | 14.8 | 22.6 | 16.8 | 24.6 | 16.5 | 24.6 |
| M10 | smoking status, (pack years)2, age2 | 115600 | 18.6 | 27.8 | 16.4 | 25.8 | 16.2 | 25.0 | 14.7 | 23.6 | 16.6 | 25.6 | 16.5 | 25.6 |
B. Selected Model Description
Using model M1, our algorithm identified nine subtypes. Table IV summarizes the number of individuals in each subtype and the percentage of individuals in each group with longitudinal constraints.
TABLE IV.
Summary of subtype sizes and the percentage of individuals in each subtype with longitudinal contraints (model M1).
| Subtype | Size | Constraint Percentage |
|---|---|---|
| 1 | 446 | 11.9 |
| 2 | 1,088 | 39.8 |
| 3 | 637 | 5.7 |
| 4 | 1,793 | 14.6 |
| 5 | 684 | 6.2 |
| 6 | 1,126 | 6.2 |
| 7 | 1,458 | 7.9 |
| 8 | 847 | 14.1 |
| 9 | 1,364 | 14.8 |
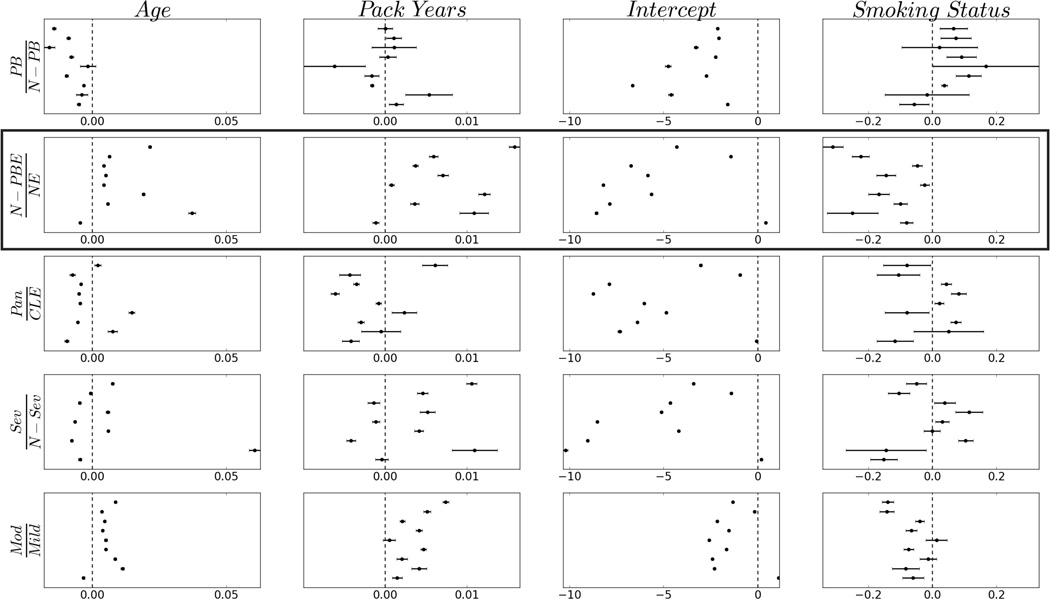
We display mean coefficients and probability intervals for each predictor in Figure 4. We highlight the second row as the target vector element most closely associated with the overall amount of emphysema (panlobular plus centrilobular) relative to the amount of non-emphysematous tissue (generally, the amount of pleural-based emphysema accounts for a small fraction of the overall composition). We observe that in all but subtype one, the amount of (non-pleural-based) emphysema increases with increasing age and smoke exposure and that these rates vary from subtype to subtype. We also note that the amount of (non-pleural-based) emphysema relative to non-emphysematous tissue appears to decrease in current smokers as opposed to current non-smokers (row two, column four). This can potentially be explained by an inflammatory response in the lungs caused by current smoke exposure which would increase lung density and decrease the amount of apparent emphysema. These trends are mirrored in the last row of Figure 4, which captures the relative amounts of moderate and mild emphysema. Overall, these results tend to align with our assumption that smoke exposure provokes an inflammatory response and that emphysema tends to progress with age and cumulative exposure. The effect of the predictors on the other target variables (rows one, three, and four) are more mixed, suggesting a more nuanced effect on the progression of these patterns, although the apparent decrease in pleural-based emphysema with increasing age (row 1, column 1) is unexpected.
Fig. 4.
Model M1 coefficient means and probability intervals covering 95% of each posterior density. Each column corresponds to one of M1’s predictors, and each row corresponds to an element of the ILR-transformed compositional data vector. PB: pleural-based emphysema; N-PB: non-pleural-based tissue; N-PBE: non-pleural-based emphysema; NE: non-emphysematous; Pan: panlobular; CLE: centrilobular; Sev: severe centrilobular; N-Sev: non-severe centrilobular; Mod: moderate centrilobular; Mild: mild centrilobular. Subtypes are ordered along the y-axis (subtype 1 at bottom of each panel). The 0-centered vertical dashed lines serve as a visual reference: values to the left indicate ratios less than 1.0, and values to right indicate ratios greater than 1.0. Boxed row highlights target vector element most closely associated with the overall amount of emphysema relative to the amount of normal tissue. See text for further details.
It is notable that non-pleural-based emphysema patterns do not appear to progress in subtype one. We note that the intercept for this subtype is greater than zero (Figure 4, row two, column three), indicating that these individuals have more emphysematous than non-emphysematous tissue at the outset; i.e., they are very sick early on. It is unlikely that these individuals actually improve as our model suggests (emphysema is known to be a progressive disease). It is more likely that they die before reaching an advanced age as a result of their severe condition. This reveals one of the limitations of our approach: given that we do not explicitly incorporate mortality data in our model, it is difficult to accurately capture such trends.
C. Selected Model Checking
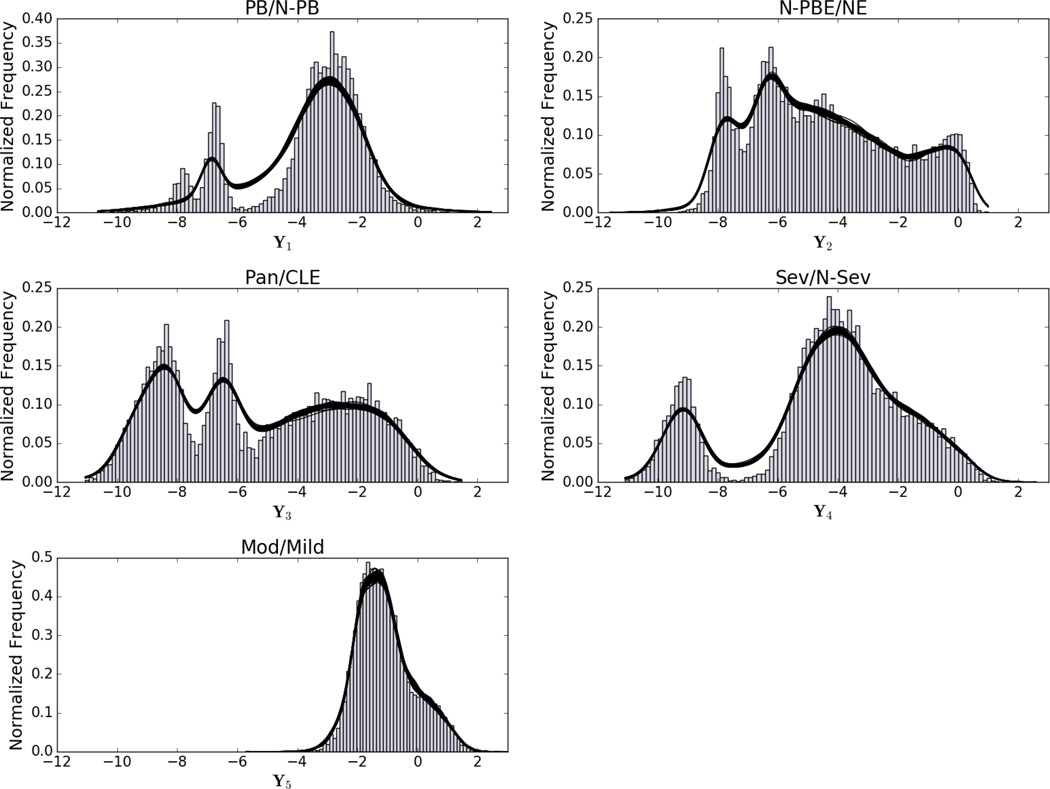
As a check of model M1’s posterior probability density, we show in Figure 5 50 random draws from the posterior overlaid on the data histograms of the five-dimensional transformed space, Y. Overall, model M1 does a very good job of capturing the major modes in each of the marginal densities. An exception that indicates a possible area for improvement is the leftmost mode in the PB/N − PB density, which M1 does not capture. This is the only target variable that involves the pleural-based emphysema pattern; the discrepancy could possibly be explained by the local histogram method’s relative difficulty in accurately classifying the pleural-based emphysema pattern, although further investigation is required to verify this.
Fig. 5.
50 Random draws from M1’s posterior overlaid on the data histograms. Kernel density estimation is used to represent each draw, depicted as a solid black lines (the similarity of each draw make the line overlays appear as a single thick line). PB: pleural-based emphysema; N-PB: non-pleural-based tissue; N-PBE: non-pleural-based emphysema; NE: non-emphysematous; Pan: panlobular; CLE: centrilobular; Sev: severe centrilobular; N-Sev: non-severe centrilobular; Mod: moderate centrilobular; Mild: mild centrilobular.
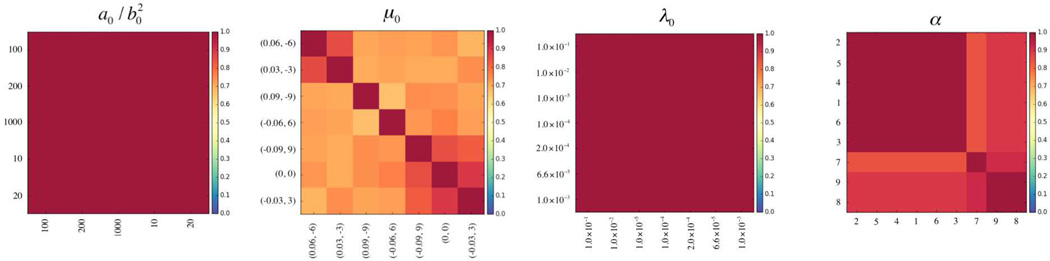
We are also interested to know how sensitive our results are to perturbations in our parameter and prior choices. We consider how trajectory assignments differ as we adjust the variance of the gamma distribution in Equation 12, the mean and precision in Equation 11, and the α parameter in Equation 10; when adjusting one quantity, the others are held fixed at the values specified in Section II-D. Results of the sensitivity analysis are shown in Figure 6, where we use normalized mutual information (NMI) ([41]) for pairwise trajectory assigment comparisons. Letting A and B represent two different trajectory assignments, the NMI is given by , where H(·) is the entropy. Higher NMI values indicate greater agreement, with a value of 1.0 indicating perfect agreement. The figure shows that trajectory assignments are quite stable for a range of parameter and prior choices, indicating the strength of the data – as opposed to the priors – in defining the final solution. This tends to be somewhat less so for the mean values in Equation 11 and highlights the specification of trajectory shape (via predictor coefficients) as an area of focus for future experimentation.
Fig. 6.
Normalized mutual information (NMI) results of sensitivity analysis for hyperparameter choices in our model. Left: comparison of subtype assignments for different variances in the gamma distribution given in Equation 12. Middle left: comparison of assignments for different μ0 combinations (slope, intercept) in Equation 11. Middle right: comparison of assignments for different precision values in Equation 11. Right: comparison of assignments as a function of the α parameter given in Equation 10.
D. Selected Model Genetic Analysis
Finally, Table V shows the results of the genetic association study for models M1 and M2 and for results generated using K-means clustering as described in Castaldi et al [42]. Models M1 and M2 show significant associations for all SNPs (model M1 gives a p-value just over 0.05 for SNP rs754388 on the RIN3 gene). Notably, no significant association is found between the K-means clustering solution and the rs2070600 SNP on the AGER gene, yet there are strong associations with the M1 and M2 subtypes.
TABLE V.
Single nucleotide polymorphisms (SNPs), genes on which they are located, and p-values indicating significance of association to the subtypes discovered by models M1 and M2 and by the K-means method described in [42].
| SNP | Gene | M1 | M2 | K-Means |
|---|---|---|---|---|
| rs12914385 | CHRNA3 | 1.19 × 10−5 | 7.53 × 10−8 | 6.09 × 10−4 |
| rs13141641 | HHIP | 2.37 × 10−3 | 4.23 × 10−4 | 1.57 × 10−5 |
| rs4416442 | FAM13A | 6.44 × 10−3 | 2.89 × 10−3 | 1.50 × 10−2 |
| rs754388 | RIN3 | 5.13 × 10−2 | 2.78 × 10−2 | 1.20 × 10−2 |
| rs626750 | MMP12 | 1.56 × 10−3 | 4.92 × 10−4 | 5.79 × 10−3 |
| rs4846480 | TGFB2 | 5.27 × 10−3 | 2.89 × 10−3 | 5.23 × 10−3 |
| rs2070600 | AGER | 2.04 × 10−5 | 1.53 × 10−5 | 2.61 × 10−1 |
IV. Conclusion
In this paper we introduce a Bayesian nonparametric approach for identifying disease subtypes and demonstrate its use on emphysema data derived from the COPDGene study. Our model has several features which make it attractive. First, it is nonparametric and is able to automatically discover the number of trajectory subtypes that best explains the data. Second, our algorithm identifies the precision of each target variable for each subtype (latent variable λ). Alternative approaches attempt to model individual random effects, acknowledging that some subpopulation members may vary from the group trend in ways that are not explicitly modeled. By learning subtypes variances separately for each target variable, we are able to represent the possibility that some subtypes may exhibit more within-group variability for a given target variable than others. We also introduce a flexible way to represent constraints imposed by longitudinal data, extending a mechanism that we introduced previously for capturing “must-link” and “cannot-link” constraint information between data points.
We chose to use vague priors for the latent variables in our model. Given that ours is a new probabilistic model applied to a new data set (isometric log-ratio transformed emphysema data), we did not have strong evidence to choose more specific priors for the predictor coefficients. However, given the genetic associations with the discovered trajectory clusters and the encouraging predictive accuracy shown in the results section, we now have some measure of confidence that the posterior distributions over the coefficients have some meaning. Furthermore, the size of our data set makes the prior specification less important than it would be for smaller data sets. The relative insensitivity of the subtype assignments to hyperparameter perturbations shown in the sensitivity analysis demonstrates the effect of the data in driving the solution. We could conceivably now apply our model to a new cohort with a more limited number of data samples using the posteriors discovered from the COPDGene data as priors for the new data set. In such a setting with more limited data, the influence of the prior becomes more pronounced, and the strength of the Bayesian approach is brought to bear.
We note that the recent emphysema definitions released in the Fleischner Society statement conflict slightly with the classification categories we imposed during the development of our previously described local histogram method. In particular, our “pleural-based” category attempts to capture the paraseptal emphysema pattern, which can also occur near lobar fissures – not reflected in our local histogram data set. Additionally, severe centrilobular emphysema (the Fleischner Society’s advanced destructive emphysema) appears very similar to panlobular emphysema on a local level. Labeling both advanced destructive emphysema and true panlobular as panlobular potentially conflates patterns arising from distinct biological mechanisms, making it difficult to further tease out progression patterns. Furthermore, panlobular, centrilobular, and paraseptal emphysema – while understood to be distinct phenotypes – may manifest within the same individual [43], [44]. These facts help to explain not only why the subtypes determined by our approach exhibit a mixture of these components, but also why our results show some issues representing pleural-based emphysema (PB/N − PB in Figure 5; row one, column one in Figure 4) and some ambiguity in the relative progression of panlobular and centrilobular patterns (rows three and four in Figure 4).
Despite these issues, our primary goal is to enrich the purity of subtype definition enough to identify biological or genetic factors that may be at the root cause of disease etiology. We found significant associations between model M1’s discovered subtypes and seven SNPs known to associate with COPD. This is an encouraging result, but targeted follow-up studies would be needed to determine the possible role of the affected genes in the emphysema progression process.
In summary, our algorithm produced interesting and encouraging results on emphysema data from the COPDGene study. The probabilistic model we describe here is general and can be applied to any number of disease measures that can be modeled (or transformed to model) as draws from a multivariate normal distribution. Although we have used emphysema measures generated from the local histogram classification approach, data produced from other lung tissue classification approaches can be analyzed just as easily. As such, we view our subtyping algorithm as a contribution that can be applied to bridge the gap between CT-level assessment of tissue composition to population-level analysis of compositional trends that vary between disease subtypes.
Acknowledgments
This work was supported by United States National Institute of Health grants R01 HL089856, R01 HL089897, and K25 HL130637.
Contributor Information
James C. Ross, Brigham and Women’s Hospital, Harvard Medical School, Boston, Massachusetts, USA
Peter J. Castaldi, Brigham and Women’s Hospital, Harvard Medical School, Boston, Massachusetts, USA
Michael H. Cho, Brigham and Women’s Hospital, Harvard Medical School, Boston, Massachusetts, USA
Junxiang Chen, Department of Electrical and Computer Engineering, Northeastern University, Boston, Massachusetts, USA.
Yale Chang, Department of Electrical and Computer Engineering, Northeastern University, Boston, Massachusetts, USA.
Jennifer G. Dy, Department of Electrical and Computer Engineering, Northeastern University, Boston, Massachusetts, USA
Edwin K. Silverman, Brigham and Women’s Hospital, Harvard Medical School, Boston, Massachusetts, USA
George R. Washko, Brigham and Women’s Hospital, Harvard Medical School, Boston, Massachusetts, USA
Raúl San José Estépar, Brigham and Women’s Hospital, Harvard Medical School, Boston, Massachusetts, USA.
References
- 1.Murphy SL, et al. Deaths: final data for 2010. National vital statistics reports. 2013;61 [PubMed] [Google Scholar]
- 2.Verhaak RG, et al. Integrated genomic analysis identifies clinically relevant subtypes of glioblastoma characterized by abnormalities in pdgfra, idh1, egfr, and nf1. Cancer cell. 2010;17:98–110. doi: 10.1016/j.ccr.2009.12.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lewis S, et al. Heterogeneity of parkinsons disease in the early clinical stages using a data driven approach. Journal of Neurology, Neurosurgery & Psychiatry. 2005;76:343–348. doi: 10.1136/jnnp.2003.033530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Doshi-Velez F, et al. Comorbidity clusters in autism spectrum disorders: an electronic health record time-series analysis. Pediatrics. 2014;133:e54–e63. doi: 10.1542/peds.2013-0819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schulam P, et al. Clustering longitudinal clinical marker trajectories from electronic health data: Applications to phenotyping and endotype discovery; Twenty-Ninth AAAI Conference on Artificial Intelligence; 2015. [Google Scholar]
- 6.Castaldi PJ, et al. Cluster analysis in the COPDGene study identifies subtypes of smokers with distinct patterns of airway disease and emphysema. Thorax. 2014 doi: 10.1136/thoraxjnl-2013-203601. thoraxjnl–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Decramer M, et al. Chronic obstructive pulmonary disease. The Lancet Respiratory Medicine. 2012;379 doi: 10.1016/S2213-2600(12)70060-7. [DOI] [PubMed] [Google Scholar]
- 8.Lynch DA, et al. Ct-definable subtypes of chronic obstructive pulmonary disease: A statement of the fleischner society. Radiology. 2015 doi: 10.1148/radiol.2015141579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Uppaluri R, et al. Quantification of pulmonary emphysema from lung computed tomography images. American journal of respiratory and critical care medicine. 1997;156:248–254. doi: 10.1164/ajrccm.156.1.9606093. [DOI] [PubMed] [Google Scholar]
- 10.Sørensen L, et al. Quantitative analysis of pulmonary emphysema using local binary patterns. Medical Imaging, IEEE Transactions on. 2010;29:559–569. doi: 10.1109/TMI.2009.2038575. [DOI] [PubMed] [Google Scholar]
- 11.Park YS, et al. Texture-based quantification of pulmonary emphysema on high-resolution computed tomography: comparison with density-based quantification and correlation with pulmonary function test. Investigative radiology. 2008;43:395–402. doi: 10.1097/RLI.0b013e31816901c7. [DOI] [PubMed] [Google Scholar]
- 12.Depeursinge A, et al. Lung tissue classification using wavelet frames. Engineering in Medicine and Biology Society, 2007. EMBS 2007; 29th Annual International Conference of the IEEE, IEEE; 2007. pp. 6259–6262. [DOI] [PubMed] [Google Scholar]
- 13.Prasad M, et al. Multi-level classification of emphysema in hrct lung images. Pattern Analysis and Applications. 2009;12:9–20. [Google Scholar]
- 14.Mendoza CS, et al. Emphysema quantification in a multi-scanner hrct cohort using local intensity distributions. Biomedical Imaging (ISBI); 2012 9th IEEE International Symposium on, IEEE; 2012. pp. 474–477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang X, et al. Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM; 2014. Unsupervised learning of disease progression models; pp. 85–94. [Google Scholar]
- 16.McCulloch C, et al. Discovering subpopulation structure with latent class mixed models. Statistics in medicine. 2002;21:417–429. doi: 10.1002/sim.1027. [DOI] [PubMed] [Google Scholar]
- 17.Nagin DS, Odgers CL. Group-based trajectory modeling in clinical research. Annual Review of Clinical Psychology. 2010;6:109–138. doi: 10.1146/annurev.clinpsy.121208.131413. [DOI] [PubMed] [Google Scholar]
- 18.Raftery AE. Bayesian model selection in social research. Sociological methodology. 1995;25:111–164. [Google Scholar]
- 19.Akaike H. A new look at the statistical model identification. Automatic Control, IEEE Transactions on. 1974;19:716–723. [Google Scholar]
- 20.Ross J, Dy J. Nonparametric mixture of gaussian processes with constraints; Proceedings of the 30th International Conference on Machine Learning (ICML-13); 2013. pp. 1346–1354. [Google Scholar]
- 21.Bishop CM. Pattern Recognition and Machine Learning (Information Science and Statistics) Secaucus, NJ, USA: Springer-Verlag New York. Inc.; 2006. [Google Scholar]
- 22.Regan EA, et al. Genetic epidemiology of COPD (COPDGene) study design. COPD: Journal of Chronic Obstructive Pulmonary Disease. 2011;7:32–43. doi: 10.3109/15412550903499522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Castaldi PJ, et al. Distinct quantitative computed tomography emphysema patterns are associated with physiology and function in smokers. American journal of respiratory and critical care medicine. 2013;188:1083–1090. doi: 10.1164/rccm.201305-0873OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Aitchison J. The statistical analysis of compositional data. 1986 [Google Scholar]
- 25.Egozcue JJ, Pawlowsky-Glahn V, Mateu-Figueras G, Barcelo-Vidal C. Isometric logratio transformations for compositional data analysis. Mathematical Geology. 2003;35:279–300. [Google Scholar]
- 26.Figueras GM, Glahn VP, Rubí JJE. The normal distribution in some constrained sample spaces. SORT: statistics and operations research transactions. 2013;37:29–56. [Google Scholar]
- 27.Egozcue JJ, Pawlowsky-Glahn V. Groups of parts and their balances in compositional data analysis. Mathematical Geology. 2005;37:795–828. [Google Scholar]
- 28.Pawlowsky-Glahn V, Egozcue JJ. Exploring compositional data with the coda-dendrogram. © Austrian Journal of Statistics. 2011;40(1–2):103–113. 2011. [Google Scholar]
- 29.Martín-Fernández JA, et al. Dealing with zeros and missing values in compositional data sets using nonparametric imputation. Mathematical Geology. 2003;35:253–278. [Google Scholar]
- 30.Kindermann R, Snell L. Markov random fields and their applications. 1980 [Google Scholar]
- 31.Geman S, Geman D. Stochastic relaxation, gibbs distributions, and the bayesian restoration of images. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 1984:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- 32.Besag J. Spatial interaction and the statistical analysis of lattice systems. Journal of the Royal Statistical Society. Series B (Methodological) 1974:192–236. [Google Scholar]
- 33.Ferguson TS. A bayesian analysis of some nonparametric problems. The annals of statistics. 1973:209–230. [Google Scholar]
- 34.Antoniak CE. Mixtures of dirichlet processes with applications to bayesian nonparametric problems. The annals of statistics. 1974:1152–1174. [Google Scholar]
- 35.Blei DM, Jordan MI. Variational inference for dirichlet process mixtures. Bayesian Analysis. 2006;1:121–143. [Google Scholar]
- 36.Sethuraman J. A constructive definition of dirichlet priors. Technical report, DTIC Document. 1991 [Google Scholar]
- 37.Jordan M, et al. An introduction to variational methods for graphical models. Machine learning. 1999;37:183–233. [Google Scholar]
- 38.Jaakkola TS. 10 tutorial on variational approximation methods. Advanced mean field methods: theory and practice. 2001:129. [Google Scholar]
- 39.Watanabe S. Asymptotic equivalence of bayes cross validation and widely applicable information criterion in singular learning theory. The Journal of Machine Learning Research. 2010;11:3571–3594. [Google Scholar]
- 40.Gelman A, et al. Bayesian data analysis. Vol. 2. Taylor & Francis: 2014. [Google Scholar]
- 41.Strehl A, Ghosh J. Cluster ensembles—a knowledge reuse framework for combining multiple partitions. The Journal of Machine Learning Research. 2003;3:583–617. [Google Scholar]
- 42.Castaldi PJ, Dy J, Ross J, Chang Y, Washko GR, Curran-Everett D, Williams A, Lynch DA, Make BJ, Crapo JD, et al. Cluster analysis in the COPDGene study identifies subtypes of smokers with distinct patterns of airway disease and emphysema. Thorax. 2014 doi: 10.1136/thoraxjnl-2013-203601. thoraxjnl–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lynch DA, Austin JH, Hogg JC, Grenier PA, Kauczor HU, Bankier AA, Barr RG, Colby TV, Galvin JR, Gevenois PA, et al. Ct-definable subtypes of chronic obstructive pulmonary disease: A statement of the fleischner society. Radiology. 2015 doi: 10.1148/radiol.2015141579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kim W, Eidelman DH, Izquierdo JL, Ghezzo H, Saetta MP, Cosio MG. Centrilobular and panlobular emphysema in smokers. Am Rev Respir Dis. 1991;144:1385–1390. doi: 10.1164/ajrccm/144.6.1385. [DOI] [PubMed] [Google Scholar]