Performance of toxicity probability interval based designs in contrast to the continual reassessment method

Abstract

Toxicity probability interval designs have received increasing attention as a dose-finding method in recent years. In this study, we compared the two-stage, likelihood-based continual reassessment method (CRM), modified toxicity probability interval (mTPI), and the Bayesian optimal interval design (BOIN) in order to evaluate each method's performance in dose selection for Phase I trials. We use several summary measures to compare the performance of these methods, including percentage of correct selection (PCS) of the true maximum tolerable dose (MTD), allocation of patients to doses at and around the true MTD, and an accuracy index. This index is an efficiency measure that describes the entire distribution of MTD selection and patient allocation by taking into account the distance between the true probability of toxicity at each dose level and the target toxicity rate. The simulation study considered a broad range of toxicity curves and various sample sizes. When considering PCS, we found that CRM outperformed the two competing methods in most scenarios, followed by BOIN, then mTPI. We observed a similar trend when considering the accuracy index for dose allocation, where CRM most often outperformed both the mTPI and BOIN. These trends were more pronounced with increasing number of dose levels.

1. Introduction

The continual reassessment method (CRM) [1] and other model-based designs were developed to improve phase I clinical trial efficiency by constantly updating the estimated toxicity rates based on new safety data [2]. These designs are considered to be statistically and computationally complex, leading many to perceive dose allocations as coming from a “black box” [3]. Although less transparent, CRM provides a versatile framework which can be extended to allow for more complicated settings [4], such as delayed toxicity [5], drug combinations [6], treatment schedules [7], patient heterogeneity [8], and bivariate outcomes [9]. Use of CRM and other model-based designs has been limited in actual clinical trials in favor of the less efficient 3+3 design [10,11]. The limited use of innovative approaches in practice has lead to a recent push to introduce simpler methods centered on toxicity probability intervals, with the aim of greater feasibility and likelihood of being implemented. The modified toxicity probability interval (mTPI) [12] design was developed to blend the simplicity of designs like 3+3 while incorporating parametric methods [3]. The Bayesian optimal interval (BOIN) [13] design is another toxicity probability interval design that is also simple to implement.

Each of the three methods considered in this manuscript (CRM, mTPI, and BOIN) have previously been compared to the standard 3+3 method and simulations show that these modern designs have superior operating characteristics [13–15]. Only limited scenarios have been used to directly compare CRM, mTPI, and BOIN. The aims of this manuscript are to:

1. compare these methods in a greater variety of scenarios, both in the number of dose levels considered and in the variety in shape of the dose toxicity curves;

2. consider CRM design specifications that are representative of decisions that would be made in practice by incorporating a stopping bound to terminate the trial if the lowest dose generates excessive toxicities;

3. compare these methods using an accuracy index, which includes information at all dose levels and allows one to assess the ability of a method to both recommend the MTD and allocate current trial patients to a dose close to the MTD; and

4. apply the accuracy index to dose allocation of trial patients.

2. Dose-finding methods

In this section, we describe the three dose finding designs discussed in Section 1. Care was taken in selection of model specifications in order to use these methods as intended by the authors. The target probability of toxicity is given by θ. Suppose there are K available dose levels and denote the probability of dose limiting toxicity (DLT) at dose level k by π_k, where k = 1 … K. The number of patients assigned to dose level k is given by n_k and y_k denotes the number of subjects on dose k who have experienced a DLT.

2.1. Continual reassessment method

The continual reassessment method (CRM), given by O'Quigley et al. [16] is the most widely recognized model-based method for dose finding designs. The simulations presented in Section 4 utilize the two-stage likelihood version of CRM given by O'Quigley and Shen [1]. This design uses a one-parameter working model for the probability of toxicity at dose d_k that assumes a monotonically increasing dose-toxicity relationship. A practical choice is the power model, given by:

$$\psi (d_k,a)=p_k^{exp(a)},$$ (1)

where k = 1,…, K denotes the dose level, a is a scalar parameter, and 0 < p₁ < p₂ < ⋯ < p_K < 1 are pre-specified constants referred to as the “skeleton” values. Although skeleton values are important, the skeleton spacing is more important than the values themselves. The skeleton values do not need to be close to the true toxicity probabilities. The method of Lee and Cheung [17] is used in these simulations to obtain a skeleton with adequate spacing between skeleton values. The likelihood version of CRM requires heterogeneity in DLT responses before the second stage sequential approach can begin. These simulations allow for a first stage consisting of a rule-based design with cohort size of 1, where single patient cohorts are assigned escalating doses, beginning with the first dose, and continuing until one DLT and one non-DLT are observed. Once heterogeneity of responses is observed, the trial proceeds into the second stage where the estimate of the parameter a is found by maximizing the likelihood, given by:

$$L(a,n_k,y_k)=\prod _{k=1}^K{\left(p_k^{exp(a)}\right)}^{y_k}{(1-p_k^{exp(a)})}^{n_k-y_k}.$$ (2)

CRM design specifications for the simulation study include a stopping bound to terminate the trial due to excessive toxicity in the lowest dose. This stopping bound allows for trial termination if the lower limit of the 90% confidence interval for the first dose is greater than the target toxicity probability, θ. This augmentation was made in order to allow the CRM design to function in a way that is more representative of decisions that would be made in practice during a clinical trial. Also, this allowed the CRM simulations to be more comparable to the modified toxicity probability interval designs, which terminate the trial when the first dose is overly toxic. Simulation results for the CRM design were obtained using the crmout function in R package dfcrm, specifying the “mle” method and “empiric” model. The skeleton was specified using the getprior [17] function within the dfcrm package, specifying a halfwidth of 0.06 and prior guess of MTD of dose 2. Iasonos and O'Quigley [18] and Jia, Lee, and Cheung [19] provide additional information on design aspects of CRM.

2.2. Modified toxicity probability interval

The modified toxicity probability interval (mTPI) [12] was developed to combine the simplicity of the 3+3 method while allowing for specification of a target toxicity probability. Consider a trial in progress where the current dose is d_k, with n_k subjects already treated at this dose level and y_k observed toxicities. Investigators will either choose to treat the next patient at a lower dose (de-escalate to d_k−1), remain at the same dose (d_k), or treat at the next higher dose (escalate to d_k+1). This decision is made by partitioning the interval (0, 1) into 3 subintervals, given by [0, θ − ε₁), [θ – ε₁, θ + ε₂), and [θ + ε₂, 1), where ε₁ and ε₂ are pre-specified constants. The unit probability mass (UPM) is calculated for each subinterval, (l, u), and is defined as the posterior probability that toxicity probability, π_k, is in the subinterval, divided by the width of the subinterval. The mTPI method assumes that the toxicity probabilities π_k, k = 1,…, K, have independent beta distributions with shape parameters (α_k, β_k). The UPM is given by:

$$\mathit{\text{UPM}}(l,u)=\frac{1}{u-l}[F_{{\alpha }_k,{\beta }_k}(u)-F_{{\alpha }_k,{\beta }_k}(l)],$$ (3)

where F_αk,βk is the beta cumulative distribution function with parameters α_k = α + y_k and β_k = β + n_k − y_k. The interval with the highest UPM dictates the dose decision for the next patient, where the dose de-escalating, remaining the same, or escalating is associated with the intervals [0, θ – ε₁), [θ – ε₁, θ + ε₂), and [θ + ε₂, 1), respectively. Safety rules are also incorporated which prevent escalation to a dose that has previously been deemed too toxic and trial termination for a decision of de-escalation when currently at the lowest dose.

The mTPI webtool, found at http://www.compgenome.org/NGDF/, was used to implement the mTPI method for these simulations. The design specifications include the default values of ε₁ = ε₂ = 0.05. To make simulations more comparable, cohorts of size 1 are used for results presented in the manuscript. Results using cohorts of size 3 are given in the Supplemental Material.

2.3. Bayesian optimal interval (BOIN) design

The BOIN method [13] allocates patients to doses based on the specification of lower and upper cut-off values, denoted γ_1k(n_j, θ) > 0 and γ_2k(n_j, θ) > 0, such that 0 < γ_1k(n_j, θ) < γ_2k(n_j, θ) <1. Optimal values of γ_1k(n_j, θ) and γ_2k(n_j, θ) are derived in Liu and Yuan [13]. The values of γ_1k(n_j, θ) and γ_2k(n_j, θ) are generated from specifications of θ₁ > θ and θ₂ < θ, where θ₁ is the highest DLT probability that is regarded as sub-therapeutic indicating escalation should be considered and θ₂ (> θ₁) is the lowest DLT probability that is regarded as too toxic indicating that de-escalation should be considered. In practical situations, given a target rate of θ, the specifications of θ₁ ∈ [0.5θ, 0.7θ ] and θ₂ ∈ [1.3θ, 1.5θ ] are appropriate and yield good operating characteristics. The default values recommended by the authors of the BOIN method are θ₁ = 0.6θ and θ₂ = 1.4θ.

Suppose the current cohort of patients is treated at d_k, and let π̂_k = y_k/n_k be the estimated DLT rate, where y_k is the number of observed DLTs and n_k is the number of patients treated at d_k. The BOIN method allocates patient cohorts according to the following dose-finding algorithm.

1. Allocate the first cohort of patients to the lowest dose d₁

2. Based on the treatment of the current cohort at dose d_k

   1. If π̂_k ≤ γ_1k(n_j, θ), escalate to dose d_k+1
   2. If π̂_k ≥ γ_2k(n_j, θ), de-escalate to dose d_k−1
   3. Otherwise, if γ_1k(n_j, θ) < π̂_ij < γ_2k(n_j, θ), stay at the same dose d_k

3. Continue this allocation procedure until the maximum sample size is reached.

After accrual of the maximum sample size into the study, estimates of the DLT rates, π̃_k, at each dose are generated using isotonic regression (Barlow et al., [20]). The MTD that is selected at the conclusion of the trial is that with the estimated DLT rate closest to θ. To make simulations more comparable, cohorts of size 1 are used for results presented in the manuscript. Results using cohorts of size 3 are given in the Supplemental Material.

3. Methods of comparison

In this section, we consider several summary measures used in comparing the dose-finding designs outlined in Section 2. A variety of measures are considered in order to focus on different goals of an early phase clinical trial: to select the best dose to move forward to future trials and to allocate subjects to the most appropriate dose within the current clinical trial. The summary measures include the accuracy index and percent correct selection. There are benefits and shortcomings to each measure considered, such as the ability of accuracy index to incorporate information at all dose levels into a single summary measure and the idea that PCS only considers information from the dose which has a probability of toxicity closest to the target toxicity probability, θ.

3.1. Accuracy index

Accuracy index is a summary measure used to assess performance of a method by incorporating information on dose selection at all dose levels into one number, among simulations that make a dose recommendation. This measure penalizes the method for selecting doses further from the true MTD. Accuracy index, outlined by Cheung [21], is given by

$$A_N=1-K\times \frac{{\sum }_{k=1}^K{\rho }_k\times \text{Probability of selecting dose}k}{{\sum }_{k=1}^K{\rho }_k},$$ (4)

where K is the number of doses, ρ_k = |π_k − θ|, π_k is the true toxicity probability at dose k, and θ is the target toxicity probability. Other measures of distance such as the squared distance, ρ_k = (π_k − θ)², could also be used. This measure achieves a balance of incorporating information at all dose levels by penalizing for allocation based on the absolute difference between the probability of toxicity at that dose level and the target probability of toxicity.

Two main goals for early phase clinical trials are to select the best dose to move forward to future trials but also to most appropriately allocate subjects within the current clinical trial. The above mentioned accuracy index achieves the first of these goals. In order to assess method performance for subject allocation, the accuracy index can be used by substituting the probability of selecting dose k in (4) with the proportion of subjects allocated to dose k. Accuracy index is calculated with results from simulations that make a dose recommendation.

3.2. Percent correct selection

Another summary measure used to compare the methods under consideration is the percent correct selection (PCS). PCS is the probability of selecting the true MTD, given by the proportion of simulations which select the dose that minimizes |π_k − θ|. For overly toxic scenarios (4 dose levels: scenarios 9 and 12; 6 dose levels: scenario 1), trial termination is the correct selection and PCS in these scenarios is given by the proportion of simulations which terminate the trial without a dose recommendation. Given that one of the primary goals of an early phase trial is to select the best dose to move forward to future studies, this is an effective measure in terms of focusing on the single best dose. However, it is not unlikely that several doses may have a probability of toxicity that are close to the target, θ. Consider a case where the target probability of toxicity is θ = 0.25 and doses 3 and 4 have a probability of toxicity π₃ = 0.21 and π₄ = 0.28. In this case, the difference between the doses' probability of toxicity and the target probability are essentially the same and both doses may be of equal interest. If we were relying on PCS as our summary measure for the methods, we would miss valuable information. In light of this type of scenario, we consider the percent acceptable selection within 5% of the target probability of toxicity. In the example above, the percent acceptable selection within 5% will capture information from doses with a probably of toxicity within the interval [0.2, 0.3].

4. Simulations

In this section, we discuss the design of simulations, selection of dose toxicity curves, and results of simulations in order to compare the characteristics of three dose-finding trial designs. In all simulations, the target toxicity rate is θ = 0.2 and 2,000 simulations were run. Simulations include curves with 4, 6, and 8 dose levels. The simulations study a wide variety of situations. A large number of other situations and indeed any specific situation can be generated using the user-friendly software available for each method. Dose toxicity curves with 4, 6, and 8 dose levels correspond to a sample size of 24, 36, and 48, respectively.

Dose toxicity curves

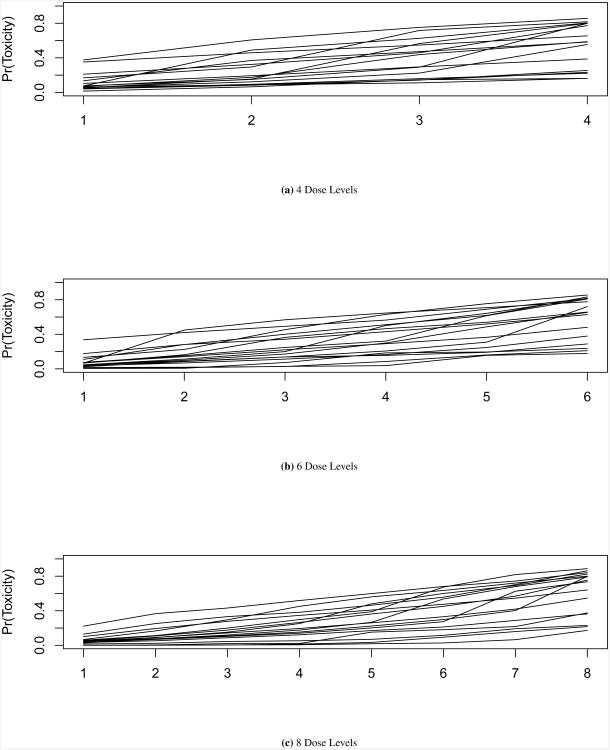
Sixteen dose toxicity curve scenarios were created for each number of dose levels considered. Rather than simply choosing 16 curves to compare these methods, 12 curves were generated by considering 1,000 8-level dose toxicity curves generated from order statistics of a Beta distribution with shape parameters (1, 2). K-means clustering was used to partition the curves into 12 groups. Within each of the 12 curve groups, toxicity probabilities were averaged at each dose level to obtain the final 12 scenarios to be used in simulations. This process was considered in order to obtain a variety of dose toxicity spacing and curve shape. To generate scenarios with 6 dose levels, 6 doses in each of the original 1,000 8-dose level curves were randomly selected to remain. The same process of K-means clustering, as described above for 8 dose levels, was used to create 12 dose toxicity scenarios. The same process was repeated to obtain the 4 dose level curves. As this procedure produced dose toxicity curves with the MTD at lower doses, 4 additional curves were generated in each dose level set to allow for observing the MTD at the highest doses (4 dose levels: 4 curves with MTD at dose level 4; 6 dose levels: 2 curves each with MTD at dose levels 5 and 6; 8 dose levels: 2 curves each with MTD at dose levels 7 and 8). The method proposed by Paoletti et al. [22] was used to generate the 4 additional curves, where the probability of toxicity at the MTD and the difference in probability of toxicity between dose levels were drawn from normal distributions, 𝒩(ϕ⁻¹ (0.2), 0.15) and 𝒩(0.6, 0.25), respectively. To display the variety of scenarios, the 16 curves for each set of dose levels are given in Figure 1. Tables with the probability of toxicity for these curves are given in the supplementary material.

Figure 1. Dose Toxicity Curves.

Results

The simulation results assess the ability of these designs to address the two main goals of an early phase clinical trial: to select the best dose to move forward to future trials and to allocate subjects to the most appropriate dose within the current clinical trial. It is important to note that the scenarios were independently created for each set of dose level curves: 4, 6, and 8 dose levels. Because of this, the scenario labels between varying number of doses are not related. The proportion of simulations that end without a dose recommendation and the proportion of simulations recommending the true MTD are given in Tables 1 and 2, respectively.

Table 1. Proportion of simulations with early termination.

Scenario
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
4 Dose Levels
CRM	0.00	0.02	0.05	0.12	0.04	0.06	0.01	0.01	0.47	0.01	0.01	0.66	0.00	0.01	0.00	0.00
mTPI	0.05	0.10	0.16	0.29	0.08	0.22	0.05	0.06	0.67	0.08	0.08	0.80	0.02	0.04	0.06	0.03
BOIN	0.00	0.03	0.07	0.22	0.02	0.12	0.01	0.01	0.67	0.01	0.01	0.76	0.00	0.01	0.01	0.01
6 Dose Levels
CRM	0.54	0.03	0.04	0.06	0.01	0.01	0.01	0.01	0.01	0.01	0.00	0.03	0.00	0.00	0.00	0.00
mTPI	0.73	0.12	0.14	0.24	0.03	0.05	0.09	0.05	0.08	0.06	0.04	0.07	0.03	0.00	0.01	0.01
BOIN	0.74	0.05	0.08	0.15	0.00	0.00	0.01	0.00	0.01	0.01	0.00	0.01	0.00	0.00	0.00	0.00
8 Dose Levels
CRM	0.15	0.01	0.00	0.03	0.00	0.00	0.00	0.00	0.01	0.00	0.01	0.02	0.00	0.00	0.00	0.00
mTPI	0.38	0.07	0.05	0.14	0.04	0.02	0.04	0.04	0.06	0.03	0.05	0.11	0.00	0.02	0.00	0.00
BOIN	0.34	0.01	0.01	0.07	0.00	0.00	0.01	0.01	0.01	0.01	0.01	0.03	0.00	0.00	0.00	0.00

Table 2. Proportion of simulations recommending the true MTD.

Scenario
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
4 Dose Levels
CRM	0.51	0.44	0.66	0.68	0.71	0.64	0.77	0.51	0.50	0.67	0.55	0.34	0.74	0.54	0.72	0.53
mTPI	0.39	0.33	0.60	0.40	0.87	0.43	0.74	0.51	0.26	0.60	0.42	0.19	0.60	0.46	0.58	0.46
BOIN	0.44	0.40	0.67	0.53	0.87	0.54	0.82	0.56	0.30	0.66	0.49	0.24	0.65	0.48	0.69	0.48
6 Dose Levels
CRM	0.43	0.49	0.56	0.53	0.38	0.66	0.42	0.54	0.41	0.69	0.47	0.65	0.35	0.34	0.68	0.55
mTPI	0.22	0.35	0.49	0.39	0.26	0.57	0.30	0.40	0.27	0.58	0.32	0.88	0.29	0.23	0.54	0.43
BOIN	0.24	0.40	0.54	0.48	0.36	0.63	0.32	0.49	0.33	0.67	0.42	0.90	0.34	0.26	0.63	0.52
8 Dose Levels
CRM	0.76	0.65	0.38	0.46	0.32	0.51	0.40	0.48	0.47	0.44	0.56	0.50	0.40	0.37	0.92	0.57
mTPI	0.53	0.47	0.22	0.32	0.22	0.34	0.24	0.34	0.32	0.28	0.37	0.32	0.37	0.22	0.65	0.44
BOIN	0.58	0.59	0.32	0.38	0.31	0.43	0.33	0.43	0.42	0.36	0.47	0.44	0.37	0.34	0.80	0.47

Accuracy index for dose selection

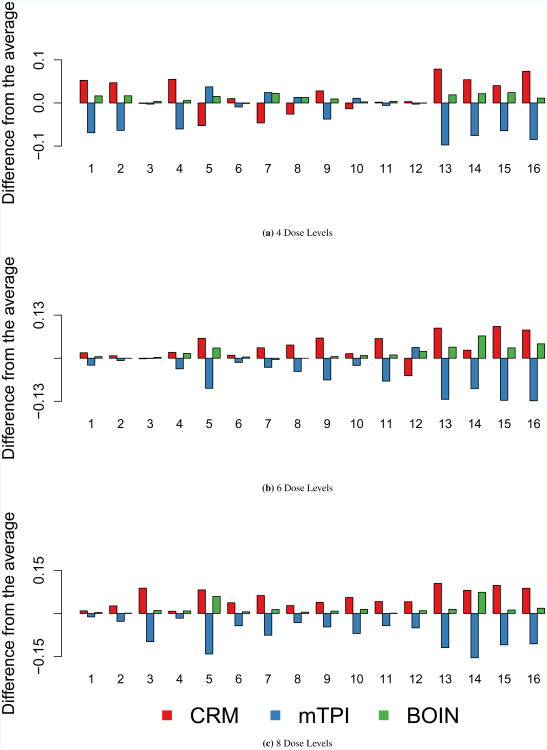
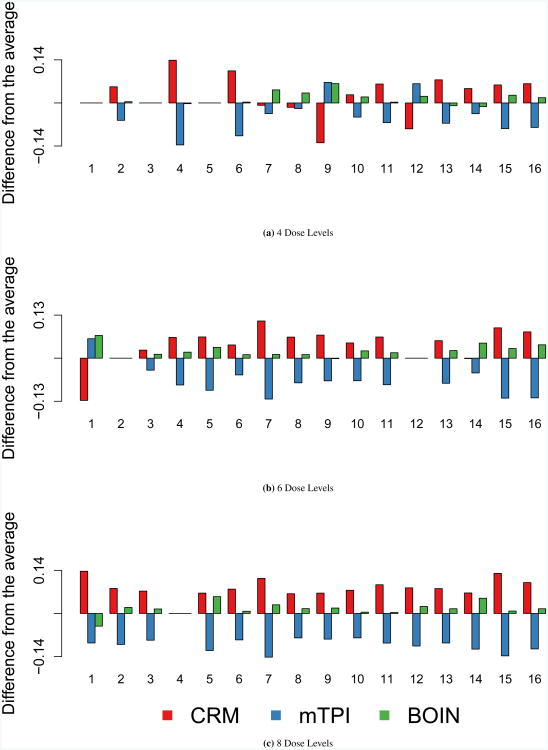
Figure 2 displays the accuracy index for dose selection. As the number of dose levels increases, there is movement toward separation of the methods. In the set of scenarios with 8 dose levels, there is a distinct ranking of methods where CRM achieves the highest accuracy index values, followed by BOIN and mTPI.

Figure 2. Accuracy Index for Dose Selection.

Accuracy index for subject allocation

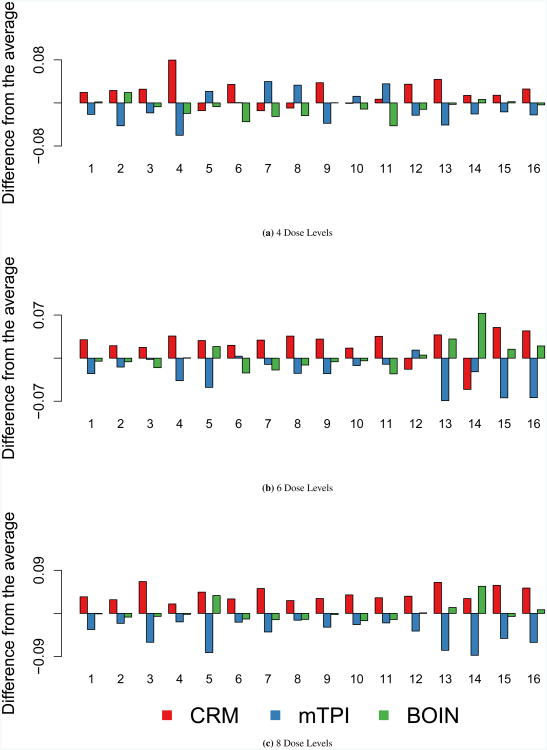
Figure 3 displays the accuracy index for subject allocation. Overall, each of the methods performs similarly with respect to subject allocation. With 4 dose levels, the toxicity probability interval methods occasionally outperform CRM, but the difference in index values is very small. As the number of dose levels increase, there is a distinct ranking of methods where CRM achieves the highest accuracy index values, followed by BOIN and mTPI.

Figure 3. Accuracy Index for Subject Allocation.

Percent correct selection

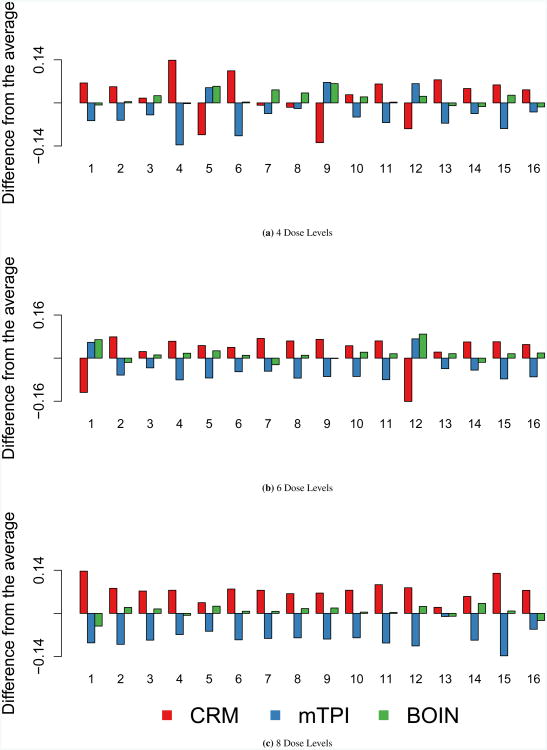
Figure 4 displays results for PCS. Results for PCS are similar to the accuracy index for dose recommendation. As the number of dose levels increases, there is clear separation of the methods. Similar to the accuracy indexes, with a greater number of dose levels, 6 and 8, CRM outperforms the toxicity probability methods. Although PCS is very similar in the toxicity probability interval methods, BOIN tends to outperform mTPI when 8 dose levels are considered. PCS is calculated by selecting the single dose which has an estimated probability of toxicity closest to the target, θ.

Figure 4. Percent Correct Selection.

Percent acceptable selection within 5%

Figure 5 displays results for the percent acceptable selection within 5%. Scenarios are only considered if the dose toxicity curve included a dose whose probability of toxicity was within 5% of the target, θ. These results have a similar trend as the accuracy indexes and PCS, where there is not a clear indication for a superior method at smaller dose levels but separation of the methods occurs as the number of dose levels increase.

Figure 5. Percent Acceptable Selection within 5%.

5. Conclusion

In this manuscript, we compared the performance of the likelihood based continual reassessment method (CRM) [1], modified toxicity probability interval (mTPI) [12], and the Bayesian optimal interval (BOIN) design [13]. Although each of these methods has been individually shown to outperform the 3+3 design, there have been few scenarios considered in comparing the three methods to each other. The aims of this manuscript were to: 1) compare these methods using a variety of scenarios; 2) consider CRM design specifications that are representative of decisions that would be made in practice by incorporating a stopping bound to terminate the trial for excessive toxicity in the lowest dose; 3) use the accuracy index in comparing methods to allow for information on dose recommendation and subject allocation at all dose levels; and 4) to apply the accuracy index to dose allocation of trial patients.

The summary measures used to compare methods were selected in their ability to assess two goals of a Phase I dose-finding trial: to select the best dose to move forward to future trials and to allocate subjects to the most appropriate dose within the current clinical trial. Simulation results show that when evaluating dose recommendation in dose toxicity curves with 6 or 8 doses, CRM outperforms the competing methods, followed by BOIN. With 4 dose levels, the relationship between the methods is less clear. This pattern of results was seen in the accuracy indexes for dose recommendation and subject allocation, percent correct selection (PCS), and percent acceptable selection within 5%.

Ease of use for methods should be considered, along with the method performance, when selecting a design to use in practice. These simulations show that CRM tends to outperform the toxicity probability interval methods as the number of dose levels increases, but use in practice can be more difficult with CRM than the toxicity probability interval designs, where dose assignment decisions for mTPI and BOIN can be displayed in a spreadsheet. Use of novel designs in clinical trial protocols presents a challenge in understanding by the clinical investigators who review the protocols, and these protocols must include sufficient information to show validity and safety of the design [2].