Light Harvesting for Organic Photovoltaics

Abstract

The field of organic photovoltaics has developed rapidly over the last 2 decades, and small solar cells with power conversion efficiencies of 13% have been demonstrated. Light absorbed in the organic layers forms tightly bound excitons that are split into free electrons and holes using heterojunctions of electron donor and acceptor materials, which are then extracted at electrodes to give useful electrical power. This review gives a concise description of the fundamental processes in photovoltaic devices, with the main emphasis on the characterization of energy transfer and its role in dictating device architecture, including multilayer planar heterojunctions, and on the factors that impact free carrier generation from dissociated excitons. We briefly discuss harvesting of triplet excitons, which now attracts substantial interest when used in conjunction with singlet fission. Finally, we introduce the techniques used by researchers for characterization and engineering of bulk heterojunctions to realize large photocurrents, and examine the formed morphology in three prototypical blends.

1. Introduction

Sunlight is the most abundant renewable energy resource and underpins life on our planet. Nature has evolved complex photosynthetic processes to harvest this light for the generation of chemical energy.¹⁻³ While chemical energy underpins the natural world, electrical energy is a more easily transmittable form in human societies. Consequently, harvesting of sunlight for the generation of electrical energy is highly desirable, and great developments in the conversion efficiency of photovoltaic cells have been made over the last 50 years.⁴ A desire for low-cost, low toxicity, large-area, thin-film technologies has led to organic photovoltaic cells showing promise to satisfy all of these properties.⁵ In organic photovoltaics, the absorbing material is a thin (∼100 nm) layer of organic semiconducting material that is sandwiched between two electrical contacts. Light absorbed in the organic layer forms tightly bound excitons that with clever choices of materials and device architectures are split into free electrons and holes, which are then extracted at electrodes to give useful electrical power.

Organic semiconductors have several attractive features for photovoltaics. They enable simple fabrication either by vacuum sublimation, printing from solution, or spray-coating.⁵ Thin films of organic semiconductors show a high absorption coefficient of ∼10⁵ cm^–1, which is very attractive for photovoltaic applications because very little material is needed: layers of only 100 nm can absorb nearly 90% of the incident light in a double pass using reflection from the metal electrode.⁶⁻¹⁰ Thin and lightweight photovoltaic panels can be made on a wide range of substrates, including flexible ones.⁵ Flexibility also enables roll-to-roll printing, easy transportation, and simple installation. Chemical synthesis presents almost endless opportunities to tune optical, electronic, and mechanical properties of organic materials through molecular engineering, miscibility, and self-assembly. Organic photovoltaic materials and devices for solar energy conversion have been researched extensively in the last 2 decades, and remarkable progress has been achieved, with recorded power conversion efficiencies over 10% for organic solar cells.⁶⁻¹⁰

In order to harvest sunlight for the generation of electrical energy, the active layer of a photovoltaic solar cell has to perform several functions: it has to absorb the solar light that then has to generate free charge carriers, and these carriers need to reach the electrodes to give photovoltage and photocurrent. The highest occupied molecular orbital (HOMO) of a neutral organic molecule in the ground electronic state contains two electrons with opposite spins. Upon absorption of a photon (Figure 1A), one electron is promoted to the lowest unoccupied molecular orbital (LUMO) and its spin is conserved; therefore, the primary photoexcitations have singlet (spin zero) character. As they consist of a bound electron–hole pair, they are usually referred to as singlet excitons. A key difference from inorganic semiconductors is that primary photoexcitations in organic semiconductors are strongly bound Frenkel and charge transfer excitons.^11,12 Typical binding energies of singlet excitons have been reported to be between 0.1 and 0.4 eV.¹³⁻¹⁵ In order to split an exciton into a charge pair, a heterojunction of electron donor and acceptor materials is used in which the HOMO and LUMO energies of the acceptor are lower than those of the donor¹⁶ (Figure 1B,C). This energy offset drives electron transfer from the excited electron donor to acceptor and hole transfer from the excited electron acceptor to donor. Its function is analogous to a type II heterojunction (staggered gap) in inorganic semiconductors. For simplicity in organic photovoltaics a “heterojunction” usually means a type II heterojunction by default.

Figure 1.

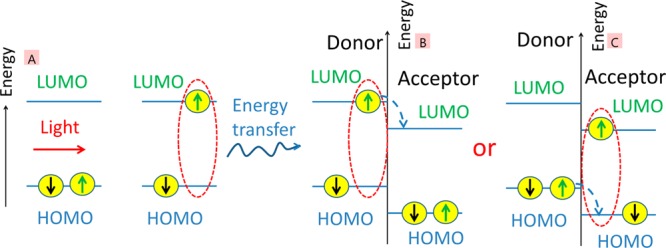
Schematic illustration of charge generation in organic photovoltaic materials which involves (A) light absorption and the generation of a singlet exciton with opposite “up” and “down” spins, followed by energy transfer to a type II heterojunction of an electron donor and acceptor and then (B) electron or (C) hole transfer at the heterojunction. Charge transfer can also occur from triplet excitons if the energy level offset is sufficient.

It has been shown experimentally that the rate of photoinduced electron transfer (k_ET) decreases exponentially with the distance (R_DA) between donor and acceptor¹⁷⁻²⁰

1

Here k₀ is the electron transfer rate at the donor–acceptor contact and β is the attenuation factor. These findings suggest that quantum mechanical tunnelling is the dominant mechanism.²¹ The β parameter in covalently linked donor–bridge–acceptor systems was found to be bridge-specific and also to depend on the orientation between donor and acceptor as well as their electronic properties.¹⁸⁻²⁰ For dispersed donors and acceptors in solution or in organic glasses, as well as for pairs linked through nonconjugated bridges, values of β > 1 Å^–1 are usually observed.¹⁷ These results indicate that electron transfer is limited to subnanometer distances between the donor and acceptor. Excitons must migrate to a heterojunction between the electron donor and the electron acceptor in order to generate charge carriers. Excitons can be transported to a heterojunction by Förster resonance energy transfer (FRET) between the electron donor and electron acceptor and by exciton diffusion in the donor or acceptor materials. Two organic photovoltaic architectures of donor and acceptor materials are generally used to harvest sunlight. In the first, shown on the left in Figure 2, the donor and acceptor materials are deposited as a simple bilayer structure, while on the right, the two are mixed throughout the active layer to form a bulk heterojunction.

Figure 2.

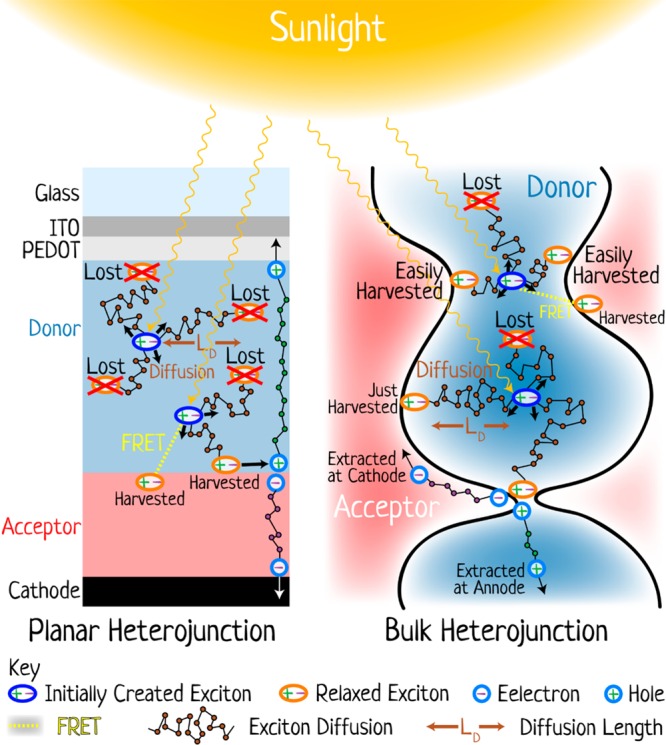
The two main architectures of organic photovoltaic devices and the processes occurring in them (not to scale). On the left is a cross section of a planar heterojunction; on the right is a magnified region of a bulk heterojunction. In both diagrams, the donor region is light blue and the acceptor region is red, and the key defines the other elements. Sunlight incident on the devices leads to the formation of excitons that then diffuse (and/or transfer energy by FRET) to the heterojunction where charge separation occurs. Some excitons do not reach the heterojunction and are lost. These processes are discussed in more detail throughout the review.

In the bilayer structure excitons can only be harvested at a limited distance from the heterojunction that is determined by the sum of a FRET distance (L_FRET) and of an exciton diffusion length (L_D). Here—and throughout this review—we use the term light harvesting to mean the successful conversion of absorbed photons into free charge carriers. We emphasize this definition as if any one element of all the processes fails or leads to a bottleneck then the ultimate device performance is determined by it, not the many other steps that are well-optimized; thus, the concept of light harvesting is important when one wants to connect the fundamental processes occurring in devices with the ultimate performance. In a bilayer, both the diffusion length and FRET distance are limited by a finite exciton lifetime to distances typically less than 20 nm in organic films;²²⁻²⁷ therefore, a maximum useful thickness of donor or acceptor layers in a bilayer is <40 nm, even with an optimized exciton diffusion length and FRET. Because of a limited width of the absorption spectra of organic materials, for the best coverage of the solar spectrum, one has to use donor and acceptor materials with distinct absorption spectra. A maximum absorption coefficient in organic materials of 10⁵ cm^–1 means that a layer of 40 nm can absorb only up to 55% of the incident light in a double pass at the peak and less far away from the absorption maximum. Power conversion efficiencies (PCE) of around 6% have been achieved in research solar cells with 1 cm² active area using organic bilayers.²⁸ It is worth noting that high-efficiency bilayer solar cells typically have a rough interface between donor and acceptor layers (about 16 nm RMS) that increases the interface area and helps to harvest excitons from donor and acceptor layers.²⁸ The roughness occurs naturally by vacuum sublimation of polycrystalline films or by sequential deposition of donor and acceptor layers from solution using different solvents for each layer.²⁹

The limited number of excitons reaching the acceptor gives poor light harvesting in bilayers and so severely limits their PCE. An elegant solution to improve light harvesting in planar heterojunctions is to use multilayer architectures of materials with efficient FRET between layers. Recently, a PCE of 8.4% has been achieved with a three-layer structure comprising two electron acceptors and a donor and utilizing FRET between the acceptor layers.²⁸ We describe this approach in more detail in section 2.5.

An alternative way to improve light harvesting is to increase the interface area of the heterojunction even more than the roughness of the layers allows. This has been successfully implemented by blending electron donor and acceptor materials, where spontaneous separation of donor and acceptor phases forms a nanostructure that is known as a bulk heterojunction.³⁰⁻³² This approach (Figure 2, right) enables light harvesting from materials with a short exciton diffusion length. Blends can be deposited from solution using a common solvent or a mixture of solvents or by coevaporation of donor and acceptor materials. In the overall schematic shown in Figure 2, the bulk heterojunction is shown at a nanoscale level, with a donor phase (light blue) surrounded by an acceptor phase (light red). Absorption of light in the donor phase leads to the formation of excitons (dark blue ellipse) that may be some distance from the acceptor phase. If the two components mix well, then every single donor molecule is close enough to an acceptor molecule and almost every exciton can migrate to the donor–acceptor interface. This can proceed by site-to-site exciton diffusion within the donor phase until the exciton reaches the interface with the acceptor, or it can occur by direct FRET from the donor to the acceptor. The small length scale of the bulk heterojunction phase separation enables good harvesting of excitons, with only a few example tracks for the drawn excitons in Figure 2 being lost, with most harvested (some easily and some only just, depending on the initial position and the path followed). This contrasts with the bilayer case, where many are lost inside the donor layer unless it is significantly thinner than needed for light absorption, as already discussed. In the bulk heterojunction, once the exciton is at the donor–acceptor interface it dissociates into a geminate electron–hole pair. This charge pair has to overcome Coulomb attraction in order to separate into free charges. The holes are transported in the donor phase and electrons in the acceptor phase; therefore, the charge transport pathways in the planar heterojunction solar cell are straightforward provided there is a sufficient built-in electric field from the difference of the work functions of the electrodes. Recent studies of bulk heterojunctions have shown that the blend morphology has to be just right for the charge pair to dissociate into free carriers, and we discuss this in more detail in section 4.2. The free carrier generation and their transport to the correct electrodes in bulk heterojunctions relies on continuous and uninterrupted donor and acceptor phases. Even with continuous charge transport pathways, both electrons and holes must navigate the labyrinth of the complex morphology to the electrodes. If a free electron encounters a hole, they form a nongeminate pair that can recombine or dissociate again into free carriers. The rate of nongeminate charge recombination in bulk heterojunctions depends on its morphology.³³⁻³⁵ In a heterojunction with small donor and acceptor domains and very high interface area, a charge is more likely to encounter the interface with the other component of the blend and hence more likely to recombine with its opposite charge. This complex series of steps involved in light harvesting has led to intensive research efforts on bulk heterojunction solar cells, and recently, multiple 1 cm² active area research cells have been demonstrated with PCE above 10%.³⁶⁻⁴⁰ The progress was achieved by rational design of donor and acceptor materials with efficient light absorption and good charge transport, morphology optimization of the active layers, and development of new charge transporting layers. Recent advances in bulk heterojunction solar cells using conjugated polymers as electron donors are described in a review by Yu and co-workers.⁷

In summation, the key steps of converting light into electrical power in organic photovoltaics are (a) light absorption, (b) energy transfer (by exciton diffusion and/or FRET) to a heterojunction, (c) exciton splitting into an electron–hole pair, (d) dissociation of bound charge pairs into free carriers, and (e) charge extraction to the electrodes. In this review we discuss recent advances toward understanding of processes b, c, and d and improving their efficiencies in planar and bulk heterojunctions. We present an overview of energy transfer mechanisms, methods to measure exciton transport, and recent efforts to improve light harvesting in planar heterojunctions by enhancing the exciton diffusion length, by encouraging interlayer FRET, and by directing exciton diffusion. We briefly discuss harvesting of triplet excitons, which now attracts substantial interest when used in conjunction with singlet fission, where one high-energy singlet exciton can generate two triplet excitons and so double the charge carrier yield. Then we review the main experimental findings and inferred mechanisms of charge pair generation and dissociation into free carriers. In particular, we discuss the role of the morphology of bulk heterojunctions, which has to be “just right” for the best solar conversion efficiency. We introduce the main techniques for measuring the morphology of bulk heterojunctions and discuss optimized morphologies for photovoltaic performance. Charge extraction and nongeminate recombination are not discussed here, and we refer the reader to recent reviews on these topics.³³⁻³⁵ Light capture by microstructures and plasmonics are also excluded from this review but have been covered in detail recently by others.⁷

2. Excitation Energy Transfer to Heterojunction

Because electron transfer in organic materials occurs only at subnanometre distances between molecules, excitons must migrate to a heterojunction between the electron donor and the electron acceptor in order to generate charge carriers. In this section we discuss the mechanisms of energy transfer, the techniques to measure exciton diffusion, and recent efforts to enhance the exciton harvesting range by increasing their diffusion length and by directing exciton transport.

2.1. Intermolecular Interactions and Energy Transfer Mechanisms

Electronic energy transfer between molecules can be radiative or nonradiative. Radiative, or “trivial”, energy transfer involves emission of a photon from one molecule and absorption of that photon by another molecule. Nonradiative energy transfer occurs by two different types of intermolecular interactions: (1) Coulombic interaction of a transition dipole moment responsible for the luminescence of an exciton with the absorption transition dipole of a nearby molecule and (2) electron exchange interactions, which involve simultaneous exchange of electrons in HOMOs and LUMOs between nearest neighbors (Figure 3).

Figure 3.

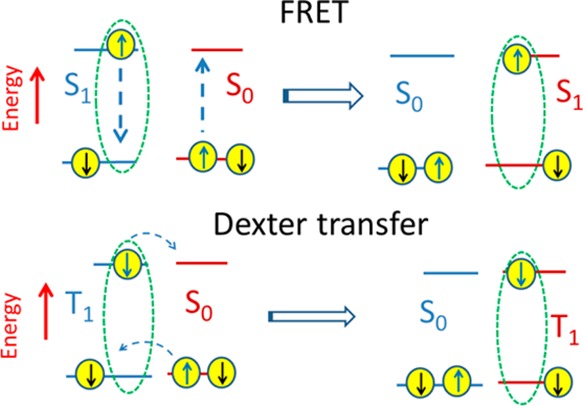
Schematic illustration of nonradiative Förster resonance energy transfer of singlet exciton S₁ and Dexter transfer of triplet exciton T₁. The “up” and “down” arrows illustrate electron spins, and S₀ denotes a chromophore in the ground state.

Nonradiative energy transfer dominates over radiative transfer in organic thin films. Energy transfer by Coulombic coupling is usually referred to as Förster resonance energy transfer, in recognition of the contribution of the German scientist Theodor Förster to the theory.⁴¹ In the weak coupling limit the rate of FRET can be calculated using the Fermi golden rule

2

where V is the electronic coupling energy between the exciton and energy-accepting chromophore; s is the dielectric screening of the interaction by the surrounding medium; J is the spectral overlap between the homogeneous spectral profiles of exciton luminescence f^hom(E) and absorption of energy-accepting chromophore a^hom(E), which have each been normalized to unit area on an energy scale, 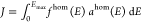; and E_max is the upper energy of the luminescence and absorption spectra.⁴² In a dipole approximation, s = 1/n², where n is the refractive index of the surrounding medium, typically in the range of 1.5–2 for organic semiconductors. When the emitting and absorbing dipoles can be approximated as point dipoles, the energy transfer rate has a simple expression⁴¹

3

where τ is the luminescence lifetime of the excited chromophore in the absence of energy transfer, R is the distance between the exciton emission dipole and the energy-accepting dipole, and R₀ is the Förster radius, which depends on the photoluminescence quantum yield of the excited chromophore, the angle between the donor emission and acceptor absorption transition dipole moments, and the spectral overlap J, which was defined above. The point dipole approximation is only accurate when the distance between the interacting chromophores is much larger than the size of the exciton. When these distances are comparable, calculations of the electrostatic interaction between transition dipoles require more sophisticated methods, such as transition density calculations or multicentric monopole expansion.^42,43 For elongated chromophores, such as conjugated polymers, a line-dipole approximation gives satisfactory results with modest computational resources.⁴⁴⁻⁴⁶

While fluorescent singlet excitons move predominantly by FRET, triplet excitons have an electronic spin of 1 and therefore are spin-forbidden from emitting light. The absorption of neutral molecules from a singlet ground state to a triplet excited state is also spin-forbidden. As efficient FRET requires strong spectral overlap of absorption and emission, FRET from the triplet to singlet state is inefficient, and triplet–triplet FRET is very inefficient. The dominant transport mechanism of triplet excitons is by electron exchange, which is often referred to as Dexter transfer. This requires an overlap of molecular orbitals of neighboring molecules; therefore, the transfer rate decreases exponentially with a distance between molecules and operates effectively only over a distance of less than 2 nm.^42,47,48

Localized excitons move by spontaneously hopping from one site to another by FRET or Dexter transfer. However, in an ideal molecular aggregate, when the interaction energy between molecules is higher than the energetic disorder and the dissipation of electronic excitation energy is slow, the exciton is delocalized between participating units and can transfer energy coherently in a wavelike motion. Recent experiments suggested that coherent energy transfer takes place in photosynthetic pigment–protein complexes.⁴⁹ Macroscopic spatial coherence reaching tens of micrometers has been observed in ordered single chains of a conjugated polymer polydiacetylene at cryogenic temperatures.⁵⁰ Several experimental studies suggested that primary excitons in conjugated polymers are delocalized along the chain in the first 100 fs after excitation, even at room temperature.⁵¹⁻⁵³ Theoretically it has been shown that correlated fluctuations of electronic transition energy in molecular aggregates can help to preserve the electronic coherence between excitonic states and only uncorrelated fluctuations result in loss of coherence.⁵⁴ Correlated exciton relaxation has been reported in poly(3-hexylthiophene), which suggests that indeed coherent energy transfer can occur in conjugated polymers on a 100 fs time scale.⁵⁵ The signatures of delocalized primary excitons have also been reported in helical π-stacks of self-assembled perylene bisimides⁵⁶ and in star-shaped molecules.^57,58 Generally, exciton localization on fewer units of a polymer or an aggregate is observed in 100–300 fs at room temperature and is attributed to exciton self-trapping driven by structural relaxation of excited units.^{51−53,57,58} However, recent observations of efficient exciton transport over micrometer-scale distances in individual self-assembled nanofibers suggest the existence of delocalized singlet excitons at room temperature in well-ordered H-type aggregates which significantly enhance the distance of energy transfer.^59,60 Nevertheless, in most circumstances, excitons hop from chromophore to chromophore in the material, and methods to measure this diffusion are the topics under discussion in the next sections.

2.2. Methods To Measure Exciton Transport

In this section, we review the main techniques to measure the distances over which singlet and triplet excitons can be transported in their finite lifetime. For excitons, which move by random walk, the convention is to quote their average diffusion length , where D is the exciton diffusivity, τ is the exciton lifetime, and Z = 1, 2, or 3 for one-dimensional, two-dimensional, and three-dimensional diffusion, respectively. In the case of time-dependent exciton diffusivity, the integral of D over the time interval τ should be used.

2.2.1. Surface Quenching of Photoluminescence

A film of the organic material under study is deposited on a surface that quenches the luminescence of the organic material, as depicted in Figure 4. For this measurement, the studied material has to be at least weakly luminescent. The advantage of this technique is that it measures energy transfer to the donor–acceptor interface in a bilayer and is directly linked to light harvesting in planar heterojunctions. The quenching can be measured by either steady-state or time-resolved photoluminescence (PL).⁶¹⁻⁶⁹ In steady-state measurements, one has to take into account a variation of the amount of light absorbed because of the optical interference, which in turn requires a detailed knowledge of optical constants and a calculation.⁷⁰ The overall quenching dynamics involves two consecutive processes: exciton transport to the surface and quenching by charge transfer to a quencher or by FRET. To measure exciton transport it is very important that the exciton is quenched very quickly at the interface so that the quenching dynamics are transport-limited. When quenching at the interface is slower than exciton transport, the overall quenching kinetics are monoexponential and very different from transport-limited quenching.⁷¹ Time-resolved measurements have an advantage in being able to distinguish between the transport-limited quenching and surface-limited quenching.

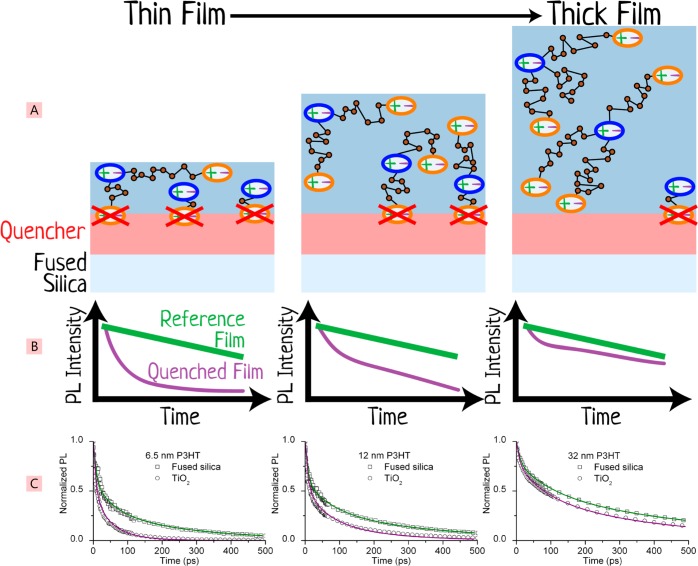
Figure 4.

Schematic of the surface quenching technique. (A) Varying thicknesses of the material of interest (blue block in the stack) are deposited on top of a quencher material (red block), and the time-resolved PL decays are measured (schematically shown in panel B) and compared against a reference film of the material prepared without the quencher layer. The thickness dependence of the time-resolved quenching can be used to determine the exciton diffusion coefficient. Shown in panel C are experimental data of surface quenching in 6.5, 12, and 32 nm thick films of the polymer P3HT deposited on titania (the quencher). Panel C is modified and reprinted with permission from ref (65). Copyright 2008 John Wiley and Sons.

If exciton transport is studied in an electron donor material, then it is best to use a layer of an electron acceptor as a quencher and vice versa. The luminescence intensity at time t is proportional to the concentration of excitons, N(x,t), integrated over the thickness of the film; here x is the distance from the exciton to the quencher surface. It is assumed that excitons move by a random walk, and the results can then be modeled using a one-dimensional diffusion equation

4

where G(x,t) is the exciton generation rate, D is the exciton diffusivity in the direction perpendicular to the quenching interface, k_Q(x) is the rate constant of surface quenching, which depends on the distance to the quenching interface, and k_s is the rate constant of spontaneous exciton decay measured in the reference film of the same thickness but on a nonquenching surface (for example, fused silica). The fluorescence intensity at time t is proportional to the integral of N(x,t) over the thickness of the film. In the simplest analysis and estimation of the exciton diffusion length, it is usually assumed that exciton diffusivity is time-independent;⁶⁵⁻⁶⁸ however, different models have been proposed to describe time-dependent exciton diffusivity in materials with significant energetic disorder,⁷²⁻⁷⁵ and we discuss this in more detail in section 2.3. To study exciton diffusion in electron donor materials it is common to use a layer of fullerene molecules as a quencher, which can quench by electron transfer and FRET.^26,69 When using a vacuum-deposited C₆₀ fullerene as a quencher, care must be taken to avoid interdiffusion of C₆₀ molecules with the donor molecules, which would lead to an overestimation of the exciton diffusion length (Figure 5).⁶⁷ For this purpose, the C₆₀ derivatives can be cross-linked⁶⁷ or tethered to the substrate.²⁶

Figure 5.

Fluorescence quenching efficiency in the 26 nm polymer film as a function of time after evaporation of C₆₀ on top. The C₆₀ evaporation starts at t = 0. The inset shows the increase of the apparent exciton diffusion distance with time, which indicates intermixing of the evaporated C₆₀ molecules with the soft polymer layer. This leads to an overestimate of the intrinsic exciton diffusion length. Reprinted with permission from ref (67). Copyright 2005 American Chemical Society.

When a long-distance FRET to the quencher is active as a quenching mechanism, it has to be included in the rate constant k_Q(x) in eq 4 to get an accurate measurement of the exciton diffusion length. For example, Luhman and Holmes have obtained consistent values of the singlet exciton diffusion length in films of boron subphthalocyanine chloride using three different electron acceptors with very different Förster radii R₀ for FRET to the acceptor, which they measured independently.⁶⁹

2.2.2. Volume Quenching of Photoluminescence

This technique can be used to study exciton diffusion in luminescent materials. Sometimes it is referred to as bulk quenching because it uses dispersed quenchers of PL in the bulk of the film and therefore measures three-dimensional exciton diffusion.^26,76,77 Very low concentrations of quenchers are used to ensure that they are homogeneously dispersed throughout the film. The measurement involves recording time-integrated or time-resolved PL intensity with varying concentration of the quencher, as depicted in Figure 6.

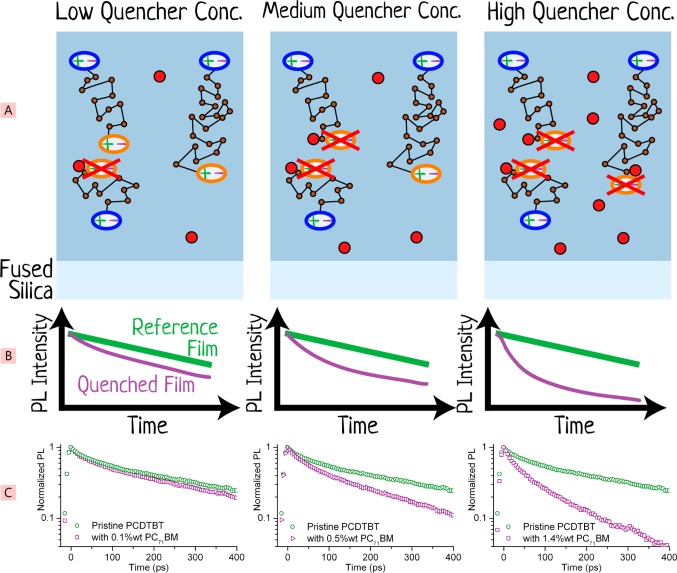
Figure 6.

Schematic illustration of the volume-quenching technique in which quenchers are dispersed throughout the layer of the material to be studied. Shown in panel A from left to right are three films of the material under investigation (blue block) with increasing concentrations of a dispersed quencher (red solid circles). Excitons are more readily quenched with increasing quencher concentration, and this is measured with time-resolved PL and compared against a reference film without any dispersed quenchers, as shown in panel B schematically and in panel C as experimentally measured data of the polymer PCDTBT mixed with the quencher PC₇₁BM. Panel C adapted and reprinted from ref (26) with permission. Copyright 2012 American Chemical Society.

Time-resolved PL measurements have several advantages over steady-state measurements: they enable the quenching mechanisms and time-dependence of exciton diffusion to be studied, they are less susceptible to thin-film interference effects, and modeling of the data is strongly constrained, as an entire decay curve is obtained for each concentration of quencher. The PL intensity at time t is proportional to the exciton concentration N(t). The decay rate of excitons in a blend is the sum of the spontaneous decay rate with the rate constant k_s and a quencher-induced decay rate with the rate constant k_q

5

where G is the exciton generation rate and Q is the quencher concentration, which is, of course, time-independent. For such a monomolecular quenching process, the PL quenching rate constant k_q is easily isolated from the rate constant of the unquenched, spontaneous decay of excitons by differentiating the natural logarithm of the PL ratio using²⁶

6

where N_doped is the exciton density in the film doped with quenchers and N_pristine is the exciton density in the pristine reference film. With this technique, it is particularly important that the exciton is quenched on the first encounter with the quencher and to include all active quenching mechanisms in the analysis. For example, long-distance FRET to the quencher has to be taken into account, as well as exciton diffusion to the quencher, and analytical expressions for k_q exist for both processes.^26,78,79 Alternatively, Monte Carlo simulation of 3D exciton diffusion in the blend can be used to fit the quenching dynamics and to determine exciton diffusivity.^76,80 This approach can be used even when the quencher distribution is not uniform but it has to be included in the model.

Ward et al. showed that the quenching rate of PL in films of the conjugated polymer PTB7 by electron transfer is at a maximum for an energy offset of ∼0.4 eV between the electron affinities of PTB7 and acceptor molecules.⁸¹ This dependence was described well by the Marcus theory of electron transfer.⁸² For the optimum energy offset, the exciton is quenched on the first encounter with the quencher and the above-described analysis can be used. However, when the energy level offset is not an optimum and the rate of electron transfer is lower, the exciton can escape quenching by diffusing away. In some cases, it is possible to include an exciton escape rate into the analysis.⁸¹ If that is not possible, then the measured exciton diffusivity and diffusion length can only be considered as a lower limit.

2.2.3. Exciton–Exciton Annihilation

This process occurs at high excitation densities when one exciton transfers its energy to another exciton and brings it to a higher-energy excited state. The higher-energy excited state relaxes rapidly, and overall an exciton is lost. In so far as quenching occurs throughout the volume of the sample, this measurement resembles volume quenching, but with excitons acting as their own quenchers. In these experiments, typically high light intensities are used, far higher than used under solar illumination conditions, and the consequences of this have to be taken into account when analyzing the data. For example, there is a finite probability for a singlet exciton in the higher-energy excited state to split into an electron–hole pair^83,84 or into two triplet excitons;⁸⁵ in that case, both singlet excitons are lost. The electron–hole pairs and triplets can also quench singlet excitons; hence, very high light intensities should be avoided.⁸⁶ The process can be measured using time-resolved photoluminescence, as its intensity is proportional to exciton population (Figure 7), or transient absorption, which can probe stimulated emission from an exciton or its absorption to higher excited states.

Figure 7.

Schematic illustration of exciton–exciton annihilation measurement methodology to determine the exciton diffusion coefficient. (A) The material under investigation (blue block) is excited with a laser of increasing power (left to right). At higher powers more excitons are created, and they are closer to each other. As they diffuse they will meet and annihilate, producing a time dependence of the PL intensity as shown schematically in panel B. If this is compared with a reference PL decay taken at low power, then the exciton diffusion coefficient can be derived. Experimental data from films of P3HT are shown in panel C and are reprinted with permission from ref (65). Copyright 2008 John Wiley and Sons.

When excitons can be treated as point particles and energy transfer occurs by incoherent hopping, the exciton concentration N is described by a kinematic rate equation⁸⁷

7

where G is the exciton generation rate, k_s is the exciton decay rate in the absence of annihilation, and γ is the annihilation rate.

Exciton–exciton annihilation involves two consecutive processes: multistep exciton hopping from an excited to an unexcited chromophore (exciton diffusion) and energy transfer to an excited chromophore (annihilation). When exciton diffusion is restricted to one dimension (1D) a time dependence of γ ∝ t^–1/2 is observed.⁸⁸⁻⁹⁰ The same time dependence is observed in a three-dimensional system if excitons are immobile and exciton–exciton annihilation occurs by direct Förster energy transfer onto an excited chromophore (static annihilation). The strong time-dependence of γ in both cases can be explained by a nonuniform spatial distribution of excitons because of the fast annihilation of excitons at the nearest distance; in that case, the annihilation process depends on the history of excitation dynamics and is therefore non-Markovian. In the case of fast exciton diffusion in three-dimensional (3D) systems, a uniform distribution of excitons is quickly restored by exciton diffusion and the annihilation rate is time-independent on a long time scale. When excitons annihilate on the first encounter, the annihilation rate is limited by diffusion and in 3D systems can be described by the solution of the Smoluchowski equation⁹¹

8

where D is exciton diffusivity and R_a is the annihilation radius. Here it is assumed that only one exciton is lost per encounter. For typical values of D ≈ 10^–3 cm² s^–1 and R_a ≈ 1 nm, the time-dependent component becomes negligible for t > 16 ps and eq 8 is reduced to the time-independent form of γ_3D = 4πR_aD. A time-independent annihilation rate has been observed at long times in films of poly(3-hexylthiophene) (P3HT)⁶⁵ as well as other polythiophenes and poly(phenylenevinylene) derivatives, which indicates that annihilation is controlled by 3D exciton diffusion.⁹²⁻⁹⁴ At early times after excitation the annihilation rate is often time-dependent. For example, Masri et al. observed a decrease of the γ value in the first 20 ps after the excitation pulse in P3HT films and fitted it to an equation derived for diffusion-limited annihilation in the case of preferentially 1D diffusion and a spherical annihilation volume with a radius r_a(86)

9

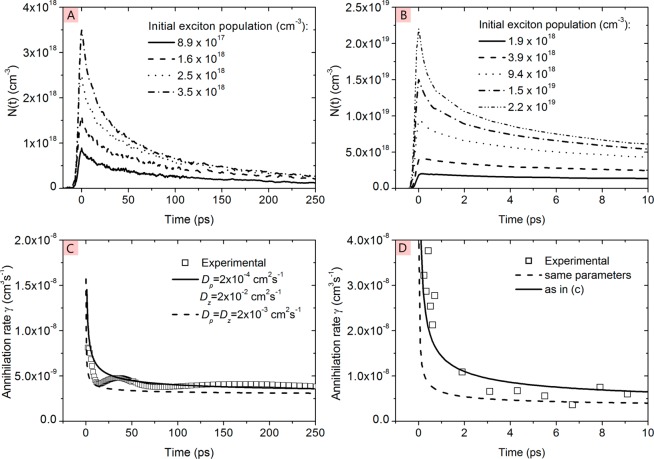
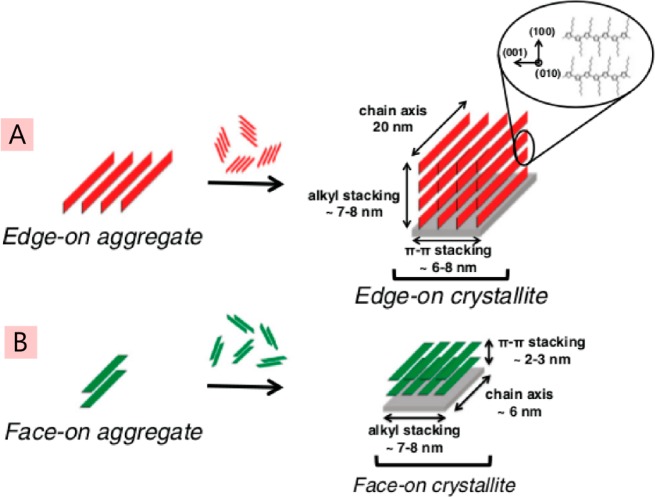
here D_z is a high diffusivity in a preferred direction and D_p is a much lower diffusivity in a direction perpendicular to z. They obtained D_z ≈ 100D_p and attributed D_z to exciton diffusion along the π-stack of P3HT chromophores (Figure 8).

Figure 8.

Time dependence of exciton population N(t) in P3HT film measured for different excitation densities by (A) time-resolved fluorescence after excitation at 2.2 eV and (B) transient absorption after excitation at 2.4 eV. (C) Annihilation rate obtained from time-resolved fluorescence data using eq 7 and (D) annihilation rate obtained from transient absorption data using eq 7; solid line and dotted lines are simulated rates using eq 9 with D_p and D_z values given in the legend. Reprinted with permission from ref (86). Copyright 2013 John Wiley and Sons.

Tamai et al. also studied exciton–exciton annihilation in P3HT films but used selective excitation of the crystalline regions of the polymer with low-energy photons at 2 eV.⁹⁵ They observed the γ ∝ t^–1/2 time-dependence up to 100 ps and attributed it to strictly one-dimensional exciton diffusion in the crystalline domains (Figure 9). This time-dependence of γ has been observed in the quasi-one-dimensional organic semiconductor phthalocyanines and in 4,9,10-perylenetetracarboxylic dianhydride.⁸⁸⁻⁹⁰

Figure 9.

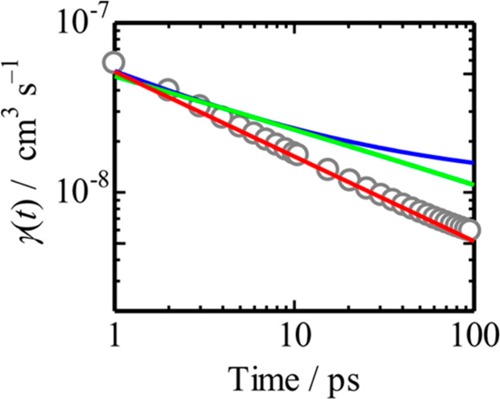
Annihilation rate for a P3HT film excited at 2 eV obtained using eq 7. The red line represents the fitting curve using γ ∝ t^–1/2. The blue and green lines represent the annihilation rate coefficient calculated by the 3D (eq 8) and 2D models, respectively. Reprinted with permission from ref (95). Copyright 2014 American Chemical Society.

These results indicate that the technique is useful not only to estimate the exciton diffusivity but also to evaluate the dimensionality of energy transfer. Like other techniques for measuring exciton diffusion, exciton–exciton annihilation has various advantages and disadvantages. An important advantage is that the measurements can be made on a single sample. A serious disadvantage is that in order to determine the diffusion coefficient, the annihilation radius needs to be known and there are not convenient ways of determining it independently.

2.2.4. Direct Imaging of Exciton Motion

The vast majority of measurements of exciton diffusion have used experiments such as those described above; however, under some circumstances, it has been possible to image the motion of excitons directly. The basic idea of these experiments is very simple: excite a small spot, image the resulting fluorescence, and watch it spread out. Of course in practice it is challenging, because the exciton diffusion length is small compared with the excitation spot. This type of experiment has mainly been applied to materials with high diffusion coefficients, such as molecular crystals. Ern et al. studied triplet diffusion in anthracene crystals, by detecting delayed blue fluorescence resulting from triplet–triplet annihilation. By varying the spatial distribution of the exciting red light, they were able to deduce a diffusion constant of 2 × 10^–4 cm²/s for triplet diffusion in the ab plane on anthracene crystals at room temperature.⁹⁶ Direct imaging of the motion of excitons and trions (negatively charged excitons) was studied by Sanvitto et al.⁹⁷ and Pulizzi et al.⁹⁸ in GaAs/AlGaAs quantum wells at a temperature of 4.2 K. They used a 40× microscope objective to focus the beam of a Ti:sapphire laser to a spot of 1.6 μm diameter, and the same objective imaged the spot through a spectrograph to give spatial information on one axis and spectral information on the other. The neutral excitons were found to be more diffusive than the trions and spread out to a total spatial extent of 10 μm, corresponding to a diffusion coefficient of 120 cm² s^–1. It should be remembered, however, that this value is for an inorganic semiconductor at low temperature; it serves to demonstrate the technique, though it is not in itself relevant to OPV.

Recent studies of exciton diffusion in organic crystals have used closely related approaches. Irkhin and Biaggio studied a rubrene crystal.⁹⁹ Excitation from a steady-state laser was focused using a microscope objective, and the same objective imaged PL onto a CCD camera. The emission was assigned to delayed fluorescence due to triplet–triplet annihilation, with many of the triplets forming as a result of singlet fission. In contrast to the work of Sanvitto and Pulizzi, spectral selection was provided by a filter, thereby allowing exciton diffusion throughout the plane (rather than just in one direction) to be imaged. This led to the spectacular images shown in Figure 10. The upper panel shows the excitation spot, and the lower panel shows the PL detected. The emission has spread much more in the b direction than in the a direction: the exciton diffusion is highly anisotropic and the elliptical shape of the lower panel directly shows this. The spread to ±2 μm in each direction actually corresponds to triplets diffusing ±4 μm from the center because the measurement detects delayed fluorescence due to triplet–triplet annihilation, which is a bimolecular process and therefore follows the square of the triplet density. These results show exciton diffusion over micron distances at room temperature in steady-state measurements on the organic crystal, rubrene. However, these authors noted they were not able to observe exciton diffusion directly in tetracene.

Figure 10.

Direct imaging of exciton diffusion. Contour plot of the intensity distribution of the excitation light (A) and the of the PL at the surface of a rubrene crystal (B). Reprinted with permission from ref (99). Copyright 2011 American Physical Society.

Akselrod et al.¹⁰⁰ refined the above measurement in two ways and then applied it to image exciton transport in tetracene. The refinements were to increase the magnification to ×500, thereby improving the spatial resolution, and to make time-resolved measurements. Müller and Bardeen¹⁰¹ had shown that a streak camera could be used to image the motion of molecular excited states with picosecond time resolution and 150 nm spatial resolution, but Akselrod used a simpler approach of translating an avalanche photodiode (APD) across the image of the emission. Although the excitation spot is diffraction-limited, its spread can be imaged with subwavelength resolution. At first this seems surprising because of the Abbe criterion, which gives a wavelength-scale limit on resolving two spots. However, monitoring exciton diffusion does not require two spots to be distinguished, so more accurate measurements are possible and indeed are now commonly demonstrated in super-resolution microscopy. By translating the APD across the image of the emission spot, the spreading of the emission could be resolved in time, leading to the results shown in Figure 11.

Figure 11.

Time-resolved imaging of exciton diffusion in tetracene. Panel A shows the emission pattern as it evolves in space and time along the crystal a axis. The distribution at a particular time has been normalized to emphasize changes in the distribution width. Panel B shows cross sections of the emission intensity map at four time points showing spatial broadening of the intensity distribution. Panel C shows the time evolution of the mean square displacement of triplet excitons. Reprinted with permission from ref (100). Copyright 2014 Nature Publishing Group.

The initial intensity distribution was described by a Gaussian with a width of 229 nm that rapidly broadened in the first 2 μs, followed by a slower expansion to 701 nm at 7 μs. In the first 2 μs, the process could be described by a diffusion coefficient (in the a direction) of (1.35 ± 0.01) × 10^–3 cm²/s. When combined with the triplet lifetime of 1.37 μs for the crystal studied, this leads to a diffusion length √(2Dt) of 0.61 μm. The authors note that ultrapure tetracene can have lifetimes up to 58 μs, which for the same diffusion coefficient would enable diffusion up to 4 μm. As in the case of other exciton diffusion measurements, time-resolved measurements provide additional information, in particular how the excitons spread as a function of time. This is summarized in panel C of Figure 11, where it is found that exciton diffusion becomes slower at longer time, and this is attributed to trapping associated with energetic disorder. The anisotropy of exciton diffusion is also reported by making the same measurement along different crystal directions. For the b direction, the diffusion coefficient is (2.28 ± 0.07) × 10^–3 cm²/s, and for the c direction, it is (0.31 ± 0.02) × 10^–3 cm²/s.

A transient absorption microscope has also been used to image exciton diffusion in tetracene.¹⁰² In this experiment, the pump beam is held at a fixed position and the probe beam is scanned to form an image. This measurement works best on picosecond and few nanosecond time scales and so allows both singlet and triplet dynamics to be studied. For delay times between 1 and 7 ns, the triplet diffusion coefficients appeared to be more than an order of magnitude higher than those deduced from transient luminescence. The authors propose that this effective enhancement of triplet exciton transport on picosecond and nanosecond time scales is due to the interconversion of triplet and singlet excitons enabling singlets to assist in triplet diffusion. Modeling of their data suggests that the singlet-mediated process alone would give a diffusion length for triplets of 1.9 μm. Pure triplet diffusion alone would give a diffusion length of 5.4 μm if a lifetime of 62.5 μs is assumed, and the two processes together would give a diffusion length of 5.6 μm.

The demonstrations of direct imaging of exciton diffusion are very impressive. However, so far they have been only been applied to a very restricted range of organic semiconductors with rather high order. It would be much more demanding to apply them to the most widely used OPV materials, including conjugated polymers, so there is a continuing need for the many other techniques described in this section.

2.2.5. Modeling of Photocurrent

As explained at the start of this review, charge generation in an organic solar cell arises primarily from the migration of photogenerated excitons to a heterojunction; hence, device characteristics can be used to learn about exciton diffusion. In a planar heterojunction, only excitons within a diffusion length of the heterojunction will reach it and contribute to photocurrent. The situation is very similar to surface quenching measurements described above, except that the loss of the exciton is detected by current instead of as a loss of fluorescence. By studying the influence of layer thickness and excitation wavelength it is possible to estimate the exciton diffusion length, though typically it is necessary to assume that all the charges generated at the interface are extracted from the device.

This type of approach was applied to molecular crystals in the 1960s.^103,104 In an extensive and detailed study of anthracene, Mulder used steady-state excitation spectra of fluorescence and of photocurrent as methods for measuring exciton diffusion lengths.¹⁰⁴ The results were analyzed in terms of a diffusion model that also included reabsorbance of fluorescence. The results of the exciton diffusion length deduced from fluorescence and from photocurrent were compared. The latter appeared to depend on the choice of electrode, but it was found that consistent results could be obtained by the use of alkaline electrode solutions. The resulting exciton diffusion length was in the region of 30 nm and was consistent with values obtained from fluorescence studies. The exact value depended on the method of preparation of the crystal and the orientation measured. Higher (but unreliable) values were obtained for nonalkaline electrode solutions, which was attributed to charge generation not only occurring at the surface (as assumed in the exciton diffusion model) but also at deeper centers such as oxygen molecules and hydrogen ions penetrating from the (acidic) electrode solution into a thin layer of the crystal next to the electrode. Photocurrent studies were applied to study the effect of introducing dopants on exciton diffusion and to study other materials, obtaining a diffusion length of 29 nm for tetracene and 10 nm for β-perylene.

Ghosh and Feng¹⁰⁵ also derived diffusion equations and used photocurrent excitation spectra to study exciton diffusion. In their case, they studied a solar cell consisting of a layer of merocyanine in between aluminum and silver contacts. The main differences from the earlier work are the materials studied, the contacts used, and the fact that the built-in potential of the contacts rather than an applied external field was used to extract charge. Using the spectrum from 440 nm to longer wavelengths, an exciton diffusion length of 6 nm was deduced. The same approach was used by Bulovic and Forrest¹⁰⁶ to study excitons in 3,4,9,10-perylenetetracarboxylic dianhydride (PTCDA). Two distinct excitonic features with different diffusion lengths were reported. One was assigned to a self-trapped charge transfer state with a diffusion length of 225 ± 15 nm; the other was a triplet with a diffusion length of 88 ± 6 nm.

Modeling of the photocurrent in an early polymer solar cell consisting of the polymer poly(p-phenylenevinylene) [PPV] and a perylene acceptor layer was performed by Halls and Friend.¹⁰⁷ It was assumed that all excitons excited within a diffusion length of the interface are ionized at the interface, lead to separated charges, and are then extracted. The resulting exciton diffusion length was 9 ± 1 nm. A fuller model of the photocurrent excitation spectrum of a polymer solar cell was described by Pettersson et al.¹⁰⁸ The treatment of exciton diffusion and photocurrent generation is similar to that of the earlier papers, but the paper pays particular attention to modeling the electric field distribution inside the device, which of course also determines the spatial profile of photogenerated excitons. The optical model used complex indices of refraction and layer thicknesses determined by spectroscopic ellipsometry. The paper concluded that exciton diffusion has a major effect on device efficiency. The work also found that it was important to take into account the optical field distribution and found that both layers in their device contributed to the photocurrent. The resulting values of the diffusion length were 4.7 nm for poly(3-(4′-(1″,4″,7″-trioxaoctyl)phenyl)thiophene) (PEOPT) and 7.7 nm for C₆₀. We note, however, that the latter value is lower than the value of 20 nm in another report.^109,110 Many subsequent studies have followed the approach of using a full optical and diffusion model of photocurrent excitation spectra to deduce exciton diffusion length. Two contrasting studies applied the approach to pentacene. Yoo et al.¹¹¹ reported an exciton diffusion length of at least 60 nm. Subsequently it has become clear that pentacene undergoes singlet fission, leading to the generation of two triplets. After taking account of this effect, Tabachnyk et al.¹¹² measured a triplet exciton diffusion length of 40 nm in pentacene.

2.2.6. Time-Resolved Microwave Conductivity and Transient Absorption

Exciton transport in nonluminescent materials can be studied using a planar heterojunction to generate charge carriers and to detect them instantly with electrodeless techniques, so that the response time is limited by energy transfer to heterojunction. Researchers at Delft University of Technology have used a microwave probe to measure an increase in conductivity in the sensing layer when an exciton reaches it and injects charge.^113,114 Only excitons within a diffusion length of the heterojunction or FRET distance contribute to photoconductivity. Using this technique, a singlet diffusion length of 7 nm has been found in evaporated C₆₀ films¹¹⁵ and a triplet diffusion length of 28 nm in palladium tetrakis(4-carboxyphenyl)porphyrin (PdTPPC) films.¹¹⁶ Alternatively, transient absorption can be used to detect radical cations or anions in a planar heterojunction that is within an exciton diffusion length of a heterojunction.¹¹⁷

2.3. The Influence of Disorder on Exciton Diffusivity

Because of the conformational and positional disorder present in organic semiconductors, as well as dispersive interactions between molecules that are caused by rapid fluctuations of electron densities, the same electronic state has slightly different energies on different chromophores.^11,12 Singlet exciton transport occurs predominantly by FRET-controlled hopping from chromophore to chromophore. According to eqs 2 and 3, in order to get fast exciton hopping, one requires a high oscillator strength of luminescence and absorption, a short distance between chromophores, and high spectral overlap of homogeneous spectral profiles of luminescence and absorption. Two factors reduce the spectral overlap: the reorganization energy of individual chromophores in the excited state and energetic disorder. The spectral overlap is high for excitations hopping downhill in transition energy, whereas it is much smaller for excitations hopping uphill and often needs thermal activation to get to the resonant transition energy. Many theoretical and experimental studies have explored the influence of energetic disorder on exciton diffusion. More than 30 years ago Movaghar et al. derived an analytical theory to describe the time dependence of exciton diffusion by incoherent hopping by assuming uncorrelated free energies of adjacent sites and a Gaussian distribution of site energies.¹¹⁸Figure 12 shows the diffusivity as a function of time for different values of the disorder width normalized to the thermal energy. The theory predicts two different time regimes of exciton diffusion: an initial dispersive regime, where exciton diffusivity is decreasing with time when excitations migrate downhill in energy, and an equilibrium regime with a constant diffusivity D_∞, where transport occurs through low energy sites. They found that the crossover time t_r to long-time behavior (marked by an arrow on each curve) and diffusivity at long time D_∞ roughly obey the relation t_r^βD_∞ ≈ const with β = 0.45. The analytical theory was compared with Monte Carlo simulations in a cubic lattice, and very good agreement was obtained. Using a simple thermodynamic argument, Movaghar et al. predicted that the mean long-time energy is lower than the peak energy of the Gaussian density of states by a value ΔE = a²/kT, where a is the half-width of the Gaussian disorder and kT is the thermal energy.

Figure 12.

Plot of log₁₀ of the diffusivity D(t) versus log₁₀ of time for different values of a/kT, where a is the half-width of the Gaussian disorder and kT is the thermal energy; the crossover time to long-time behavior D_∞ is denoted by an arrow on each curve; the time axis is scaled with ν₀, which is the hopping rate downhill in energy. The inset shows the long-time (equilibrium) value D_∞(T) and the crossover time t_r plotted versus (a/kT)². Reprinted with permission from ref (118). Copyright 1986 American Physical Society.

The Gaussian disorder model described above has been very successful in describing the time evolution of photoluminescence and phosphorescence spectra at different temperatures^{46,72,119−121} and the temperature dependence of the time-averaged exciton diffusivity. For example, Mikhnenko et al. measured the time-averaged diffusivity of singlet exciton in films of the poly(p-phenylenevinylene) derivative MDMO-PPV using surface quenching of the photoluminescence and found that the exciton diffusivity decreased by a factor of 2 when cooling the sample from room temperature to 150 K (Figure 13).⁸⁰ They explained this result by a decrease of the thermally activated hopping rate at lower temperature. Below 150 K, exciton diffusivity was almost temperature-independent, suggesting that thermally activated hopping is inefficient at very low temperature and excitons migrated only downhill in energy. They also found a strong correlation between the temperature dependence of exciton diffusivity and the PL (0–0) vibronic peak position, suggesting that the width of energetic disorder can be estimated simply by measuring the temperature dependence of the PL spectrum. Ribierre et al. observed a similar temperature dependence of the time-averaged hopping rate of triplet excitons in phosphorescent iridium-cored metal–ligand charge transfer complexes using triplet–triplet annihilation.¹²²

Figure 13.

(A) Temperature dependence of the exciton diffusion length L_D (red circles) and the time-averaged diffusivity ⟨D⟩ (green squares) in films of the poly(p-phenylenevinylene) derivative MDMO-PPV. (B) Temperature dependence of the time-integrated photoluminescence spectrum vibronic (0–0) peak position. Two temperature regimes are observed: a low-temperature regime (up to 150 K) highlighted in blue and a high-temperature regime. Reprinted with permission from ref (80). Copyright 2008 American Chemical Society.

Later models have adopted the Gaussian disorder model but used eq 2 or 3 to calculate the hopping rate with a time-dependent Förster radius R₀ or spectral overlap term J used instead of a Boltzmann term.⁷²⁻⁷⁵ This approach better describes an exciton hopping downhill in energy on an early time scale after excitation.

2.4. Increasing Diffusion Length of Singlet Excitons

The one-dimensional diffusion length of singlet excitons in organic films typically ranges from 5 to 20 nm.²⁴ To absorb most of the incident light, the thickness of donor and acceptor layers has to be at least 100 nm; therefore, there is a strong drive to increase the exciton diffusion length in order to improve light harvesting in planar heterojunctions. In addition to the strength of electronic coupling between molecules, two other main factors influence exciton diffusivity. These are the spectral overlap integral of the absorption and fluorescence spectra (term J in eq 2) and energetic disorder. Raisys et al. showed a direct correlation between the spectral overlap integral (term J) and the exciton diffusivity in triphenylamine derivatives with different side arms.¹²³ They observed an enhancement of diffusivity by a factor of 5 and have obtained a good agreement with Monte Carlo simulations using the measured optical properties of the films. Generally longer diffusion lengths are observed in crystalline materials,^61,62 and this can be explained by lower energetic disorder that results in higher exciton diffusivity on a long time scale where energy transport is thermally activated.

Sometimes it is possible to increase the exciton lifetime and maintain high diffusivity. Menke et al. showed an increase of the exciton diffusion length from 11 to 15 nm in the electron donor boron subphthalocyanine chloride by diluting it into a wide-energy-gap host material UGH2.¹²⁴ The main reason for the increased exciton diffusion length was a 6-fold increase of the exciton lifetime. Using this approach, they made planar-heterojunction solar cells with the fullerene C₆₀ as an electron acceptor and obtained a power conversion efficiency of 4.4%, which is 30% higher than that of the control cell made using undiluted subphthalocyanine molecules.

However, dilution of chromophores does not always help to increase exciton lifetime. For example, the dilution of metal-free phthalocyanine molecules in UGH2 to 25% resulted in a 3-fold decrease of the exciton lifetime, showing that the nonradiative decay of singlet excitons is very sensitive to intermolecular interactions.¹²⁵

2.5. Interlayer Förster Resonance Energy Transfer

As the diffusion proceeds in a donor material by a random walk, the range is limited, as excitations are as likely to hop away from the acceptor as toward it. There is therefore a strong desire to direct energy transport to planar heterojunctions between electron donors and acceptors. In contrast to exciton diffusion, FRET between electron donor and acceptor materials is directional and can bring excitons directly to a heterojunction. FRET can enhance the exciton harvesting distance in bulk heterojunctions;²⁶ however, much bigger enhancement can be gained in planar heterojunctions.^{22−25,27,69} The general equation to describe the rate of FRET from a point donor to a slab of acceptor molecules of thickness Δ is¹²⁶

10

where z is the distance between the excited donor and the acceptor film, τ is the PL decay time of the donor in the absence of energy transfer, and d₀ is the critical transfer distance (Figure 14). The parameter d₀ is typically 2–3 times larger than the Förster radius R₀ and is proportional to the density of energy of accepting chromophores in the acceptor layer.^22−26,126 The transfer rate decreases much more slowly with distance than in the case of energy transfer between single chromophores, so interlayer FRET can be efficient over long distances. It has been shown that ∼90% of excitons can be transferred over 20 nm distance and ∼50% of excitons over 35 nm.^22−27,69

Figure 14.

Schematic of FRET from an exciton in a donor layer to a slab of acceptor molecules.

Cnops et al. designed a three-layer planar heterojunction solar cell using an α-sexithiophene (α-6T) electron donor, a boron subnaphthalocyanine chloride (SubNc) electron acceptor, and an additional light-harvesting layer of boron subphthalocyanine chloride (SubPc) (Figure 15).²⁸ In this structure, excitons generated in SubPc transfer their energy to SubNc and subsequently dissociate at both interfaces by hole or electron transfer. They have demonstrated a PCE of 8.4% (7.77% certified) in a 1 cm² active area cell with an external quantum efficiency in the range of 50–80% over a broad wavelength ranging from 400 to 720 nm. All three absorbing materials have contributed to the photocurrent in these devices. Endres et al. studied the same structure using X-ray photoemission spectroscopies and found that there is a small energy barrier between SubNc and SubPc, which may limit the efficiency of electron extraction in this configuration.¹²⁷ These results suggest that even higher efficiencies could be attained by aligning the electron affinities of these materials. Reid and Rumbles used experimentally verified Monte Carlo simulations to evaluate the maximum achievable efficiencies in planar multilayer heterojunctions with energy cascades.¹²⁸ They found that a PCE of 10% is plausible and 15% is theoretically possible, assuming a typical 0.6 eV energy loss at the heterojunction.

Figure 15.

Schematic representation of the device architecture with three active layers and the energy-level diagram of the active layers illustrating an interlayer FRET from SubPc to SubNc followed by hole transfer to α-6T and charge extraction. Reprinted with permission from ref (28). Copyright 2014 Nature Publishing Group.

These results show that multilayered structures with interlayer FRET are very promising for light harvesting in organic photovoltaics. This approach allows optimization of the ordering and thicknesses of different layers to maximize light absorption in each one by tuning optical interference. In combination with long-range interlayer FRET, this is very likely to enable more efficient solar cells with reproducible performance.

2.6. Directing Energy Transport

Use of multilayer heterojunctions with energy cascades discussed in the previous section is one of the ways to achieve directional exciton transport and efficient light harvesting.¹²⁸ Menke et al. have explored a different approach to direct energy transport from a diluted to a neat layer of the same organic semiconductor SubPc.¹²⁹ In such a structure, there is no energy gradient between layers and energy transfer occurs in both directions. However, as there is a higher concentration of energy-accepting molecules in the neat layer, forward energy transfer to the neat layer is faster than back energy transfer. They demonstrated a light-harvesting efficiency of 50% in a trilayer made of a diluted 20-nm-thick outer layer of SubPc, a 10-nm-thick layer of neat SubPc, and a layer of the electron acceptor NTCDA.¹²⁹ Although this efficiency is lower than that in energy-cascade structures, it can potentially give a higher open circuit voltage because there is no loss of excitation photon energy in its transfer between layers.

A high level of control of the energetic disorder and directional energy transport has been demonstrated by inclusion of fluorescent molecules into ordered one-dimensional nanochannels made of optically inert host materials.^130,131 Such systems are very attractive for basic studies of guest–host and guest–guest interactions, as well as molecular dynamics in confined geometries, and they can enable exciton transport over distances longer than 50 nm according to calculations.¹³²

2.7. Prospects for Singlet Fission and Triplet Exciton Harvesting

Light absorption in organic semiconductors generates singlet excitons. The intersystem crossing rate from the singlet to the triplet state is usually slower than the radiative and nonradiative decay of singlet excitons; therefore, the triplet exciton yield is usually small. Triplet exciton transport now attracts substantial interest when used in conjunction with singlet fission, where each singlet exciton can split into two triplet excitons and so can potentially double the charge carrier yield and photocurrent.^133,134 Singlet fission can be efficient in molecules with a triplet exciton energy less than half the energy of the singlet exciton and is an attractive way to utilize high-energy photons of the solar spectrum. The most researched material is polycrystalline pentacene, which shows very fast singlet fission in about 80 fs.¹³⁵ Planar heterojunction organic solar cells have been reported with a peak external quantum efficiency of up to 126% in a small portion of the visible spectrum using pentacene, demonstrating the generation of more than one electron per incident photon.^136,137 Tabachnyk et al. determined the triplet exciton diffusion length in polycrystalline pentacene to be about 40 nm by modeling the photovoltaic spectral response.¹¹² These studies suggest that harvesting of triplet excitons is a bottleneck for charge carrier generation in bilayer solar cells using polycrystalline pentacene, where the triplet exciton lifetime is on the order of 5 ns.¹³⁸ Much longer lifetimes of triplet excitons are observed in single pentacene crystals (on the order of 0.4–2 μs),¹³⁹ so it may be possible to increase the triplet lifetime and diffusion length in thin films by increasing crystallinity. It has been shown that triplet exciton lifetime in other materials can be increased by controlling intermolecular interactions,^140−142 so there might be an opportunity to increase triplet diffusion length by molecular engineering.

Measuring triplet exciton transport is also challenging because only some materials are phosphorescent. An interesting technique to study triplet diffusion was suggested by Mikhnenko et al., who used a thin layer of a metal–ligand charge transfer complex with very fast intersystem crossing rate to generate triplet excitons and inject them into the studied material.¹⁴³ A phosphorescent detector layer was deposited on the other side of the studied material to detect the transported triplet excitons. To demonstrate the technique, they measured the triplet exciton diffusion length in films of N,N′-di-[(1-naphthyl)-N,N⁰-diphenyl]-1,10-biphenyl-4,40-diamine (NPD) and found a value of 87 nm.

3. Free Carrier Generation

Because charge transfer between electron donor and acceptor is a short-range process, initially an exciton is split into a bound geminate electron–hole pair. This charge pair then has to overcome recombination and dissociate into free carriers in order to contribute to photocurrent, and this process usually limits the device performance.^77,144−148 In this section, we briefly discuss the main experimental findings and concepts suggested to explain free carrier generation in bulk and planar heterojunctions. For a more detailed description of the theoretical models, we refer the reader to recently published perspectives.^149−151

3.1. The Influence of Photon Energy

Charge carrier generation has been studied extensively using ultrafast spectroscopy. The most common technique is ultrafast transient absorption spectroscopy, where the formation of characteristic absorption bands of radical cations in an electron donor and radical anions in an electron acceptor can be observed. On the basis of experimental findings, several different mechanisms of free carrier generation have been proposed and they are shown schematically in Figure 16. It has been suggested that ballistic charge separation can occur in higher-energy (hot) charge transfer (CT) states if it can outcompete the electronic relaxation in the manifold of CT states and vibrational cooling. For example, extremely fast charge generation within 50 fs has been reported by Grancini et al. in a photovoltaic blend of the conjugated polymer PCPDTBT and the soluble fullerene PC₆₁BM.¹⁵² They observed very different transient absorption spectra when exciting the polymer with an excess photon energy of 1 eV above the optical band gap as compared to excitations with lower-energy photons and suggested that higher-energy exciton states convert almost resonantly into hot CT states that dissociate into free charge carriers in less than 200 fs by ballistic charge transport. This study suggests that electron transfer can be faster than electronic and vibrational relaxation of the exciton. Faster electron transfer from hot vibronic states is also supported by theoretical studies.¹⁵³ Even the lowest-energy exciton in the donor or acceptor material, which is marked S₁ in Figure 16, can couple almost resonantly to a hot CT state, where one of the carriers is delocalized and it can experience a short-distance ballistic transport before it forms a polaron. Such a process can generate a loosely bound charge pair with an effective separation distance of several nanometers, which then dissociates into free carriers by one carrier hopping away from its counter charge. Jailaubekov et al. studied the relaxation of hot CT states generated in planar heterojunctions of copper phthalocyanine and electron acceptors C₆₀ and C₇₀ using transient two-photon photoemission spectroscopy.¹⁵⁴ In this technique, a pump pulse generated CT states by splitting excitons at the heterojunction, whereas a probe pulse was incident upon the same spot after a variable time delay and led to ionization of the sample. They analyzed the kinetic energy of the photoelectrons emitted from the sample, identified hot CT states at ∼0.3 eV higher energy than the relaxed CT states, and observed relaxation of hot CT states within ∼1 ps. This study suggests that in order to assist free carrier generation, the dissociation of hot CT states has to be faster than 1 ps.

Figure 16.

Hypothetical potential energy surfaces along the charge separation coordinate illustrating different free carrier generation mechanisms proposed in the literature. Vertical arrows represent light absorption in the ground state (G.s.) to generate exciton states S₁...S_n or charge transfer (CT) states. The straight horizontal arrows illustrate ballistic transport of delocalized carriers in hot CT states suggested by some studies. The bent arrows indicate incoherent carrier hopping between sites on donor or acceptor, with red bent arrows representing thermally activated hopping.

However, several studies have shown that the internal quantum efficiency (the ratio of collected charges and absorbed photons at the short circuit condition) in high-performance bulk heterojunctions is independent of the energy of absorbed photons, including a direct excitation of the relaxed intermolecular CT states formed between donor and acceptor with very low photon energy (indicated by a dashed line in Figure 16).^155−160 The fraction of light absorbed by these CT states was determined using electroluminescence measurements and was found to be lower by 4 orders of magnitude as compared to intramolecular absorption by the donor and acceptor.^155−160 Direct excitation of CT states without excess energy can generate an electron–hole pair only on the nearest-neighbor donor–acceptor pair with a separation distance of less than 1 nm. The high efficiency of photocurrent generation observed by direct excitation of the relaxed CT states indicates that a charge pair in this state is loosely bound and can dissociate into free carriers with the help of a rather weak built-in electric field. Ballistic charge transport is unlikely in the relaxed CT state; thus, dissociation is expected to occur by incoherent carrier hopping, and some of its steps have to be thermally activated. These findings are consistent with observations of rather slow charge generation in efficient photovoltaic blends of poly(3-hexylthiophene) (P3HT) with fullerene acceptors prepared by thermal annealing, where the majority of charge pairs were found to be generated on a picosecond time scale, presumably limited by exciton diffusion to a heterojunction.^161−164 Annealing has been shown to triple the power conversion efficiency of P3HT:fullerene bulk-heterojunction solar cells to ∼4%,^165,166 suggesting that slower charge generation in these materials is not an obstacle to device efficiency. Slower charge generation in annealed blends suggests larger domain sizes of donor and acceptor, which help dissociation of bound charge pairs into free carriers, as discussed in section 4.2.2. In very efficient photovoltaic blends of the electron-donating polymer PTB7 with the acceptor PC₇₁BM, charge pair generation has been observed on a 100–300 fs time scale.^77,167 These results suggest that the rate of electron transfer at the heterojunction does not have to be ultrafast to achieve high device efficiencies in organic photovoltaics. In the next section, we discuss recent findings on how the rate depends on the energy offset between donor and acceptor.

3.2. The Dependence on Driving Force

The difference of the Gibbs free energy between the relaxed neutral excited state (exciton) and the relaxed CT state (electron–hole pair) is known as the “driving force” for electron transfer. In organic photovoltaics, it is desirable to have the smallest driving force necessary to generate free charge carriers, as any excess will be converted into heat and will reduce the photovoltage (and consequently the power conversion efficiency). A recent study by Coffey et al. showed the existence of an optimal driving force for the highest yield of mobile charge carriers that was measured by microwave conductivity¹⁶⁸ (Figure 17). They observed a decrease of the mobile carrier yield when the optimal driving force was exceeded and explained their results using the Marcus theory of electron transfer.⁸² These findings highlighted the importance of the reorganization energy in charge generation.

Figure 17.

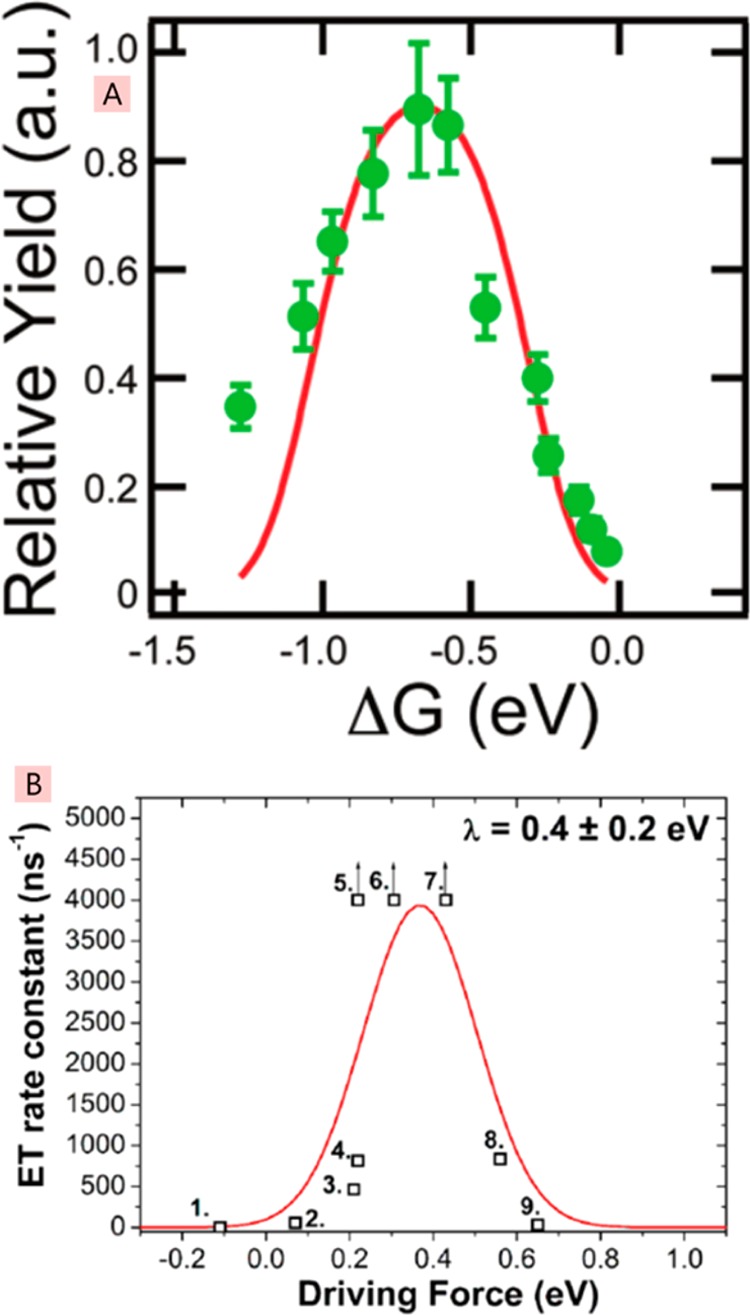
Yield of mobile charge carriers (A) and the rate constant for electron transfer (B) plotted against the driving force ΔG. Points 5–7 in the bottom panel have arrows denoting that they are lower limits. Panel A reprinted with permission from ref (168). Copyright 2012 American Chemical Society. Panel B reprinted from ref (81) and licensed under CC-BY-4.0.

Ward et al. measured electron transfer rates from thermally relaxed excitons in the conjugated polymer PTB7 to different electron acceptors in the blends using time-resolved fluorescence quenching.⁸¹ Measurements with very low and very high loadings of acceptor were used to separate electron transfer at a short distance to an acceptor (<1 nm) from exciton diffusion in the PTB7 phase. They found very fast electron transfer in <2 ps for values of the driving force between 0.2 and 0.6 eV. Higher and lower driving forces outside this range gave slower rates of electron transfer, as expected from the Marcus theory of electron transfer. These results show that electron transfer is very fast and efficient when the driving force equals the reorganization energy. Fitting to the Marcus model gave a reorganization energy of ∼0.4 eV. These results suggest that the energy loss at the donor–acceptor interface can be reduced by reducing the reorganization energy and maintaining the optimum offset of electron affinities or ionization potentials.

Although the driving force influences the rate of electron transfer from donor to acceptor, its effect on dissociation of photogenerated charge pairs into free carriers is not significant. This is indicated by the high photocurrent efficiency observed after direct excitation of the relaxed CT states^155−157 and dissociation of bound charge pairs on a picosecond time scale that is much slower than the cooling of hot CT states.^145−148 These findings imply that it should be possible to design efficient photovoltaic materials with small reorganization energies that would give high open circuit voltages without a trade-off in photocurrent.

3.3. Charge Pair Generation Inside Donor or Acceptor Domains

Excitons can split into charge pairs in the bulk of an organic semiconductor, albeit with a lower efficiency than at heterojunctions. For example, charge pair generation with 15–20% efficiency has been observed in films of conjugated polymers that are used as electron donors,^169−171 and neat films of fullerene derivatives, which are commonly used as acceptors.^148,172

Generation of bound charge pairs inside donor or acceptor domains can be detrimental to device performance because these pairs often recombine before they can be spatially separated into donor and acceptor phases. To avoid recombination losses, the morphology of bulk heterojunction has to support fast extraction of holes and electrons into the donor and acceptor domains, respectively, where they can be transported to the correct electrodes, and this is discussed in section 4.2 of this review.

3.4. Dissociation of Bound Charge Pairs

Charge pair dissociation into free carriers is a crucial step in the operation of organic solar cells; therefore, its understanding is very important for the development of efficient heterojunctions. However, the mechanism is not understood and is actively debated. The observations of efficient dissociation of relaxed charge transfer states in high-performance bulk heterojunctions suggest that hot CT states are not required to achieve charge pair dissociation.^155−157 The free carrier yield is independent of the internal electric field in efficient bulk heterojunctions or shows very weak dependence, indicating that the potential barrier for charge pair dissociation is very small.^145,173 Gao et al. have estimated an activation energy of around 9 meV for charge pair dissociation in optimized P3HT:PC₆₁BM bulk heterojunctions.¹⁷⁴ There are several possible explanations for a low potential barrier. Several studies suggested that Coulomb attraction is compensated by the free energy cascade from interfacial CT states to spatially separated charged states in the bulk of donor and acceptor domains.^{77,145,175−178} This concept is supported by observations of mixed donor–acceptor phases in the boundaries between pure domains in bulk heterojunctions^77,179 and findings that the difference in ionization potentials and electron affinities is favorable for directional charge transport from a mixed phase into pure donor and acceptor domains.^176,180,181 Higher entropy of spatially separated charges as compared to CT states can also contribute to the free energy gain.¹⁷⁵ Gao et al. have estimated that the entropy contribution is sufficient to diminish the activation energy needed for pair dissociation when it is spaced by just 4 nm, assuming uninterrupted three-dimensional charge transport at 300 K and a dielectric constant of 3.5.¹⁷⁴ In that case, charge pairs separated by >4 nm can be considered unbound and can dissociate into free carriers provided there are continuous donor and acceptor domains to support charge transport. It has been suggested that long-range charge-separated states (up to 4 nm separation) can be accessed through ballistic transport of delocalized carriers in hot CT states^182−184 or very fast initial carrier hopping.^{145−148,161,185,186}

Fewer studies of charge pair dissociation have been conducted in planar heterojunctions. The dissociation efficiency has been shown to increase with increasing electric field up to 0.05–0.5 MV cm^–1 and to saturate above these values.^148,187,188 The dissociation efficiency was found to saturate at lower field values when polymers with longer conjugation length were used as electron donors. This suggests that an increase of hole delocalization along the conjugated chain decreases the binding energy of the geminate electron pair and helps its dissociation into free carriers.^187,188

In summary, the rate of charge generation has been shown to depend on the driving force for electron transfer, and in some cases, charge generation was found to be faster than electronic and vibrational relaxation. However, in high-performance photovoltaic blends, the free carrier yield was found to be independent of photon energy and electric field, indicating that hot charge transfer states do not play a major role. Free carrier generation in these blends occurs through relaxed charge transfer states and is influenced by blend morphology, energetics of mixed and pure donor and acceptor phases, charge delocalization, and carrier mobility. More studies are needed to understand the role of each of these factors. Free carrier generation in planar heterojunctions has been found to depend on applied electric field and conjugation length of the electron donor, indicating that the mechanism could be different from that in the bulk heterojunction. It is possible that there is no universal mechanism and more than one mechanism is involved in some cases.

4. Optimum Morphologies of Bulk Heterojunctions

So far we have recounted that absorption of light by donor and acceptor materials in a bulk heterojunction readily occurs; however, harvesting that light requires, among other things, getting the formed exciton to the donor:acceptor interface via exciton diffusion or FRET and getting free charges through the active layer to their respective electrodes to be extracted, as discussed above. Consequently, it is clear that the structural arrangement of the donor and acceptor in the blend—the morphology—is of vital importance to enable light harvesting. If the donor and acceptor are too far apart, then excitons will not be able to traverse the distance to enable them to be split into charge pairs, and if the distance is too short, then while excitons will easily dissociate, sufficiently separate pathways of material will not be available to suppress recombination of the readily formed charge pairs. The optimal distance between the two materials is on the order of 10–20 nm, approximately the exciton diffusion length. Measuring the morphology on such length scales is very challenging; the donor and acceptor are typically both carbon-based materials, soft in nature, with similar physical properties. In this section, we will review the principal methods of measuring the morphology of BHJ blends, discuss some of the key results published to date and their implications for light harvesting in organic photovoltaics, and highlight the challenges that remain. This is not meant to be an exhaustive treatment of morphology in organic photovoltaic blends, which more detailed singular reviews already cover in great detail,^189−194 but rather an overview of how it links to light harvesting for organic photovoltaics.

4.1. Measurement Techniques

The length scale of merit for BHJs as discussed above is ∼10–20 nm, this is much smaller than the optical diffraction limit, and thus, alternative techniques to classical optical microscopy have been used to measure the blend morphology.

4.1.1. Atomic Force Microscopy

A key technique to measure nanoscale morphology is atomic force microscopy (AFM) and variants thereof.¹⁹⁵ Here a cantilevered tip honed to a 10–20 nm point is scanned across the sample. Atomic repulsion forces can be used to keep the tip a constant distance from the actual sample (giving topographical information), and the frequencies of an oscillating tip can be used to derive more information on surface force response, revealing finer details (so-called “phase” images). In the context of organic photovoltaics, AFM can give information on the surface and subsurface topography of the film.

Conventional topography images simply show the surface of the film and can give information on the organization of the two materials in the blend only when they fully phase separate into clear separate domains, e.g., in a polymer–polymer blend, as shown in Figure 18A. Rarely is this the case in good OPV blends, and thus phase images instead can be used to reveal more subtle details, as shown in Figure 18B,C.

Figure 18.

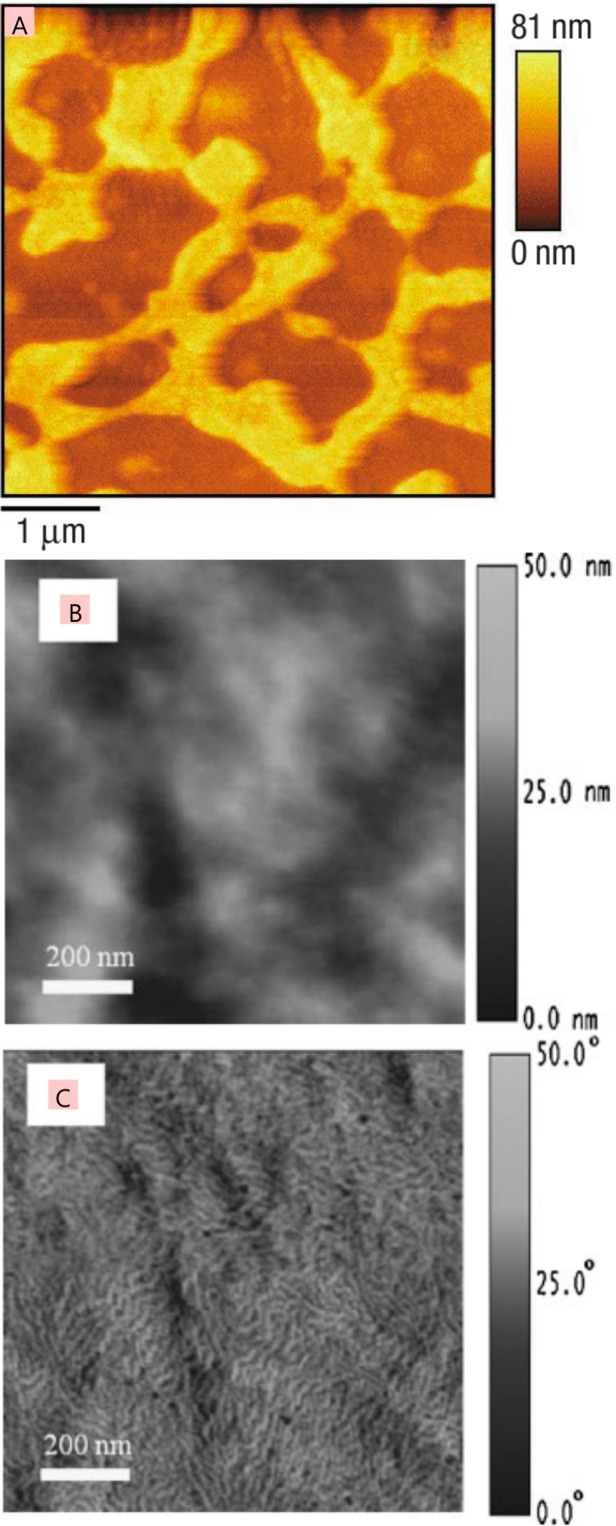
(A) AFM topography of a blend film of PFO and F8BT, showing clear phase separation. (B) Topography and (C) phase image of the same area of a P3HT:PC₆₁BM blend film, indicating the finer details that the phase measurement reveals. The image in panel A is reprinted with permission from ref (196). Copyright 2003 Nature Publishing Group. The images in panels B and C are reprinted with permission from ref (197). Copyright 2008 John Wiley and Sons.

Unfortunately, frequently in high-performance OPV blends the blend morphology is such that there are subtle degrees of mixing between the two materials, leading overall to a relatively featureless image in AFM topography and phase. Here instead an extension of the AFM concept can be used, wherein a metal-coated AFM tip is used as a conductivity probe as it is scanned across the sample surface, giving rise to the technique of conductive AFM (C-AFM). Material composition can be derived by exploiting the clear conductivity differences between p-type electron donors and n-type electron acceptors used in the BHJ blend. Given the small contact area between the sample and the AFM tip (of diameter ∼40 nm), the measured currents tend to be very small (pico or nanoamps), and significant biases (a few volts) are typically used to ensure clear current maps that have distinguishable features measurable above the noise floor. An extension of the conductivity map is to measure photoconductivity with an AFM (PC-AFM).¹⁹⁸ Here light is shone onto the sample, creating excitons that dissociate in the blend into charge pairs. Extraction of the charge pairs by the metal-coated AFM tip under bias with respect to the sample substrate contact leads to a measured photocurrent, which then will vary depending upon blend composition as the tip is scanned across the sample, as depicted in Figure 19. This enables a photocurrent map to be built that can be qualitatively analogous to the donor:acceptor concentration.

Figure 19.

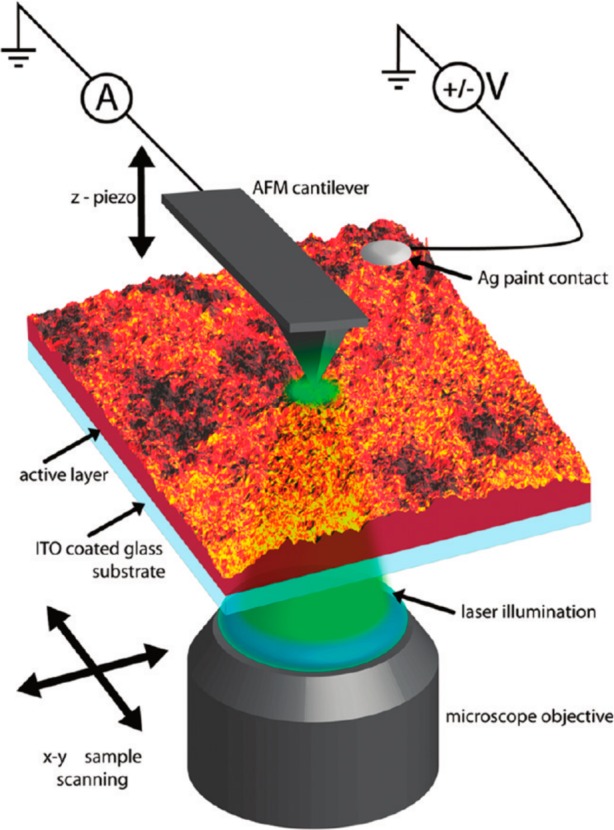
Schematic illustration of a photoconductive AFM setup. Illumination of a sample leads to the generation of excitons that dissociate into charges. These charges are then extracted by the metal AFM tip, which is under bias with respect to the sample substrate. Spatial scanning of the sample (or the tip) allows a 2D photocurrent map to be recorded. Reprinted with permission from ref (198). Copyright 2010 American Chemical Society.

4.1.2. Scanning Near-Field Optical Microscopy

The length scale of interest, 10–50 nm, as indicated above, is well below the diffraction limit enabled with conventional confocal optical microscopy; however, this is just within the capabilities of another optical microscopy technique, scanning near-field optical microscopy (SNOM).^199−202 Here an AFM is used, either with a tip that has a ∼50 nm aperture in it that light is coupled into or with a solid tip that light is scattered off of. In both cases, the evanescent wave of light from the end of the tip is coupled into the sample below, leading to a spatial resolution below the diffraction limit. Transmission and reflection of the excitation light can be collected, as well as fluorescence from the sample under investigation. Additionally, Raman spectroscopy of the scattered incident excitation light can be performed. All of these modes can contribute to discriminating the blend morphology in a bulk heterojunction. Despite the promising path for SNOM in helping with BHJ morphology, typically that has proved challenging in reality. This can be attributed to the advanced nature of the suite of SNOM techniques, along with the challenges in reaching the headline spatial resolution of <50 nm. Additionally, mixing between the donor and acceptor tends to “blur” the SNOM images, making high resolutions difficult to achieve. Nevertheless, successful investigations of organic semiconductors using SNOM techniques have been made. In Figure 20, a blend of poly(9,9′-dioctylfluorene) and poly(9,9′-dioctylfluorene-alt-benzothiadiazole) is investigated with SNOM.¹⁹⁶ In this system, the two polymers show clear phase separation, and this allows nanoscale mapping of the fluorescence from each of them to be made. OPV blends were investigated by Schubert et al., who looked at the absorption of light by the donor and acceptor to build up maps of the two materials.²⁰³ Shown in Figure 20 are maps of the donor P3HT absorption in blends cast from different solvents, indicating both the changes in nanomorphology and the mixing enhancements that lead to loss of contrast with the acceptor. Exploring the Raman properties of materials, a recent paper has investigated the nanoscale composition of materials, as also shown in Figure 20, finding that materials can be distinguished by their vibrational responses.²⁰⁴

Figure 20.

Scanning near-field optical microscopy of the blend of the conjugated polymers PFO and F8BT showing the AFM topography (A) and F8BT near-field PL (B); arrow 1 indicates regions of F8BT, while arrow 2 shows PFO. Reprinted with permission from ref (196). Copyright 2003 Nature Publishing Group. (C and D) Optical density (absorption) measurements of P3HT blended with a naphthalene-polymer-based acceptor. Casting from p-xylene (C) gives large-scale phase separation, while casting from a 1:1 mixture of p-xylene and chloronapthalene (D) gives a well-mixed blend. Reprinted with permission from ref (203). Copyright 2012 John Wiley and Sons. (E and F) Block-co-polymer of polystyrene and poly(methyl methacrylate) measured with AFM phase (E) and near-field Raman imaging of the 1735 cm^–1 carbonyl mode (F). Reprinted with permission from ref (204). Copyright 2014 Nature Publishing Group.

4.1.3. Electron Microscopy

At first glance, the most practical route to achieving the high spatial resolution required for observing BHJ morphology is the use of electron microscopy.^205−207 The de Broglie wavelength of accelerated electrons can reach the picometer length scale, and while other practicalities of electron microscopy restrict the spatial resolution to the angstrom scale, this is still well within the requirements for measuring the length scales of interest in OPV blends. The qualifier on this promising route is that both the donor and acceptor in OPV blends are primarily carbon-based, and thus, the two materials have a very similar response to electrons, thus measuring contrast can be challenging and frequently requires the application of specific blends with favorable contrast and advanced measurement techniques or sample preparation.

In classical bright-field transmission electron microscopy (TEM), an electron gun is imaged onto a sample, and the transmitted intensity is measured on a phosphor screen. The whole thickness of the sample is imaged, and thus, absorption of electrons through the sample volume will lead to a reduced signal in the image plane, while transmission of electrons will lead to a higher signal. Contrast differences between materials are required to see features. Typically, for all-organic BHJ films very limited contrast exists, and thus, only specific blends with fortuitous compositions can readily be imaged with bright-field conventional TEM, such as choosing a blend with a high purity of phases, as demonstrated in Figure 21A.

Figure 21.

(A) Bright-field transmission electron microscopy of MDMO-PPV:PC₆₁BM blend. Strong demixing leads to easily measurable phase separation, with fullerene regions appearing dark. Reprinted with permission from ref (208). Copyright 2009 The Royal Society of Chemistry. (B) TEM tomography reconstruction of P3HT:ZnO blend, with regions of ZnO being yellow, P3HT appearing transparent, and the gray region on top being the aluminum top contact. Reprinted with permission from ref (209). Copyright 2009 Nature Publishing Group.

Conventional TEM images are simple projections of the sample volume onto a plane; however, 3D information can be derived if multiple projections are made at different sample angles with respect to the electron beam plane, enabling computer-aided TEM tomography to be performed. High contrast between blend components is required as a prerequisite before attempting tomography, as the reconstruction process is challenging; however, as shown in Figure 21B, when a suitable system is measured, the results can lead to detailed and valuable information on the full three-dimensional morphology of the blend, leading to a large amount of secondary information, such as mean free paths of material and connectivity analysis. The stunning image shown illustrates the remarkable level of detail that can be achieved in a best-case situation. However, a hybrid solar cell, i.e., an organic donor with an inorganic acceptor, is a situation that gives strong contrast. For organic/organic bulk heterojunctions, a range of advanced TEM techniques discussed below have proved useful to enhance contrast and/or give compositional information.^206,207

In energy-filtered transmission electron microscopy (EFTEM), inelastically scattered electrons from the sample are selectively filtered for detection. Such inelastic scattering can occur with different amounts of energy loss for different elements, e.g., due to different energies of core electron transitions. Selective transmission of specific scattered electron energies, e.g., carbon K edge, sulfur, or fluorine, can be made and imaged, leading to elemental maps. This can be used to distinguish between the components of a photovoltaic blend, for while carbon is generally a constituent in both blend materials, the polymer will typically include sulfur or fluorine atoms that can be used to give contrast.

In high-resolution transmission electron microscopy (HRTEM), the highest spatial resolution is achieved, at the potential cost of not having discriminatory compositional information. This technique is thus most useful for resolving crystalline regions of material, commonly associated with OPV blend materials, such as P3HT, that show high degrees of local ordering. Advanced defocusing techniques may be used to enhance the resolved image; however, caution has to be applied when doing this, as the dangers of misinterpretation are significant. Shown in Figure 22 is a HRTEM image of a blend of the small molecule donor material p-DTS(FBTTh₂)₂ with PC₆₁BM. Highly ordered regions are observed, indicating both the lattice spacing and the domain boundaries of the crystallite. As noted above, compositional information is lacking; thus, it is not known if the crystallite is set within the amorphous material of the donor itself or of the acceptor.

Figure 22.

High-resolution transmission electron microscopy of a blend film of p-DTS(FBTTh₂)₂ with PC₆₁BM when processed with 0.4% diiodooctane. Regions of crystalline order are observed. Reprinted with permission from ref (210). Copyright 2014 American Chemical Society.

4.1.4. Time-Resolved Photophysics

To probe the local morphology at the smallest length scales, angstroms to nanometers, there exists the possibility to use the time-dependent light emission or absorption from the organic materials in the blend themselves as nanoscale probes of the local composition. This has the added advantage of determining the exciton harvesting of the blend itself directly, with the population of excitons formed from light absorption being measured and the degree of quenching by the other component of the blend quantified. With this technique, transient photoluminescence (TPL) or transient absorption (TA) can be used to determine certain geometric shapes, if the exciton diffusion coefficient is known. For example, as shown schematically in Figure 23, if the exciton diffusion coefficient of a donor material (blue) is known, and it is surrounded by an acceptor material (red), then with sufficient time resolution, the Smoluchowski equation can be used to determine the radius, r, of the donor domain. This method relies on a presumed knowledge of the geometry of the donor domain (spherical, cylindrical, oblate spheroid, etc.) and for easiest modeling an analytical solution to the Smoluchowski equation for that geometry.

Figure 23.

Schematic of time-resolved PL derived morphology with donor material (blue region in center) surrounded by an acceptor (red region). An exciton generated in the center of the donor region has an exciton diffusion radius (L_D) denoted by the dashed line, which should correspond to the natural unquenched PL lifetime. Measured shorter PL lifetimes can enable (presuming a spherical geometry) the radius to the acceptor (r) to be determined.

The main advantage of this technique is that it is sensitive on the very smallest scale in the immediate vicinity surrounding the polymer or fullerene. A disadvantage is that the blend chosen for this technique has to be amenable to analysis, with relatively pure phases of material present to enable modeling of the diffusion to a quenching surface; if the quencher is too dispersed in the blend, i.e., if the blend has a significant mixed phase, then excitons are quenched without having to diffuse to the donor:acceptor interface. The blend ratios used in devices are typically on the order of 1:1 and have significant mixed phase components, thus leading to kinetics that may be too complicated to model and understand correctly using accessible analytical fitting methods. However, in systems amenable to analysis, the technique can give important information. Shown in Figure 24 is the derived domain size distribution in a blend of two polymers, PFB and F8BT, when the ratio between the two components is modified. One can immediately grasp why this technique has powerful conclusions when applied correctly, as such small length scale domain distributions would be very difficult to observe with the multitude of morphology techniques discussed above in the previous sections.

Figure 24.

Derived probability density of exciton diffusion length as a function of distance for different blends of PFB:F8BT. Mass ratios of PFB:F8BT are as follows: squares are 90:10, circles are 75:25, upward triangles are 50:50, and downward triangles are 20:80. The solid line indicates the theoretical exciton diffusion length distribution for a sphere of 2 nm radius and the dashed line for a 5 nm sphere radius. Reprinted with permission from ref (211). Copyright 2008 American Physical Society.

4.2. Key Blend Morphologies

With an understanding of the key techniques to measure morphology, we now turn our attention to study the key donor:acceptor blend morphologies that have been reported over the last 15 years. In discussing the morphology here, we are particularly thinking of its role in light harvesting and the operation of the device: as already explained, in order to harvest light in a bulk heterojunction organic photovoltaic cell, the donor and acceptor domains need to be within an exciton diffusion length (typically ∼10 nm) of where the light is absorbed. In looking at the morphology of OPV blends, we aim to examine why systems do and do not work and any common themes that we can deduce between different blends. The number of donor:acceptor combinations in the development of OPVs is very large, so we focus on three key generations of OPV donor polymer materials, namely, poly[2-methoxy-5-(3,7-dimethyloctyloxy)-1,4-phenylenevinylene] (MDMO-PPV), poly[3-hexylthiophene-2,5-diyl] (P3HT), and poly[[4,8-bis[(2-ethylhexyl)oxy]benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl][3-fluoro-2-[(2-ethylhexyl)carbonyl]thieno[3,4-b]thiophenediyl]] (PTB7). The chemical structures for these three key donor materials are shown in Figure 25.

Figure 25.

Chemical structures of three donor materials (MDMO-PPV, P3HT, PTB7) and two acceptor materials (PC₆₁BM, PC₇₁BM) that are examined in this section.

Each donor material represents a key generational point in the development of OPVs, with MDMO-PPV blends reaching power conversion efficiencies of 1–3%,^212−214 P3HT 3–5%,^{165,215−218} and PTB7 7–10%.^36,37,219 Here we will examine the efforts to understand the morphology of blends containing these donor materials to date. It is worth noting that recently small molecule donors have begun to match the performance of polymeric materials.^220−223 The morphologies discussed in this review can be pertinent to small molecule BHJs, but we have chosen not to feature any specific study of a small molecule blend owing to the potentially different physics and chemistry at play in material organization (e.g., crystallinity, miscibility). A variety of acceptors have been used in fabricating BHJ cells based on these donors, but generally, fullerene derivatives such as [6,6]-phenyl-C₆₁-butyric acid methyl ester (PC₆₁BM) or [6,6]-phenyl-C₇₁-butyric acid methyl ester (PC₇₁BM), both chemical structures shown in Figure 25, have been used.

4.2.1. MDMO-PPV

MDMO-PPV was one of the earliest successful OPV donor materials, giving reliable power conversion efficiencies in the region of 1–2%,²¹² with the highest efficiency of 3% being reached when blended with PC₇₁BM.²¹³ Almost no spectral coverage in the red part of the visible spectrum and relatively low external quantum efficiencies are responsible for the overall power conversion efficiency of ∼2%. The completely amorphous nature of MDMO-PPV prevents the use of X-ray diffraction techniques to study the polymer or bulk heterojunction blends, so information on the structural arrangement of the materials relies solely on other techniques, as detailed below.

The morphology of the MDMO-PPV:fullerene system has been extensively studied.^224−227 The fullerene was found to mix intimately with MDMO-PPV up to ∼50% mass ratio.²²⁵ On the face of it, such fine mixing is ideal for light harvesting, as it will give very strong exciton dissociation and good charge-pair generation. Unfortunately, while maximizing surface area for charge separation, the large surface area associated with such fine mixing also leads to strong charge recombination, as opposite charges can readily meet again. Hence, charge extraction is very problematic is such a finely mixed structure. It was found that if the blend has more than 50% fullerene, then phase separation starts to occur, leading to the formation of pure unmixed domains comprised solely of PC₆₁BM.²²⁵ The best device performance was obtained with 80% fullerene:20% MDMO-PPV by mass. At this blend ratio pure fullerene domains form that give rise to percolation pathways for electrons, thus spatially separating the charges and suppressing recombination. The phase separation is, however, relatively uncontrolled, and at the optimal fullerene loading ratio of 80%, large 60–500 nm fullerene domains form, with the size dependent on the casting solvent used for the blend.²²⁷ These sizes and high degrees of purity enable observation with TEM (Figure 26A,B), SEM (Figure 26C,D), and AFM (Figure 26E,F). An overall schematic of the morphology is shown in Figure 27, with charge transport and extraction to a tip contact indicated. Such morphology is clearly not the most advantageous for photovoltaic cells. Fullerene domains that form near the top of the active layer promote good electron and hole extraction to their electrodes and could be thought of in effect as equivalent to not being too far away from ideal nanoscale-ordered heterojunctions. On the other hand, when the fullerene is buried inside the blend, then electrons have to transverse regions that only contain 50% fullerene (meaning recombination with holes is likely), while, more critically, holes have to get through near-pure fullerene domains, an unlikely occurrence. These restrictions are partly responsible for the relatively low external quantum efficiency of this optimized blend and indicate how the morphology has an important role to play in determining the overall light harvesting and photovoltaic performance of organic BHJ blends.

Figure 26.

Microscopy images of MDMO-PPV:PC₆₁BM blends spin-coated from toluene (top row, A, C, E) and chlorobenzene (bottom row, B, D, F) when measured with bright-field TEM (A, B), cross-section imaging with SEM (C, D), and AFM topography (E, F). Large pure fullerene domains form when spin-coated from toluene, which get smaller but are still distinct from MDMO-PPV when spin-coated from chlorobenzene. Images in panels C–F are reprinted with permission from ref (227). Copyright 2006 Elsevier. Image in panel A reprinted with permission from ref (224). Copyright 2003 Elsevier. Image in panel B reprinted with permission from ref (208). Copyright 2009 The Royal Society of Chemistry.

Figure 27.

Schematic of the morphology in MDMO-PPV:PC₆₁BM blends when large pure fullerene domains are formed, indicating relative charge transport and extraction to an AFM tip. Reprinted with permission from ref (228). Copyright 2007 American Chemical Society.

The large size of the pure fullerene domains does have the distinct advantage of making them easier to characterize, and in particular, the work of Coffey et al. in measuring the electrical characteristics on and off the domains with PC-AFM enabled novel nanoscale electrical behavior to be explored.²²⁸ Positioning the PC-AFM tip on different regions of the blend enables local I–V curves to be constructed, as shown in Figure 28. One can thus correlate regions of high and low current at different biases with the AFM topography and other morphological information to understand how the electrical behavior of the blend is related to the physical organization of the material.

Figure 28.

Photoconductive AFM of MDMO-PPV:PC₆₁BM blend. (A) Schematic of the experimental setup. (B) AFM topography of blend film. (C) Photocurrent map of the same region as in panel B, at 0 V bias, showing regions high and low in current. (D) I–V curves for specific points as indicated by the symbols on panels B and C. Reprinted with permission from ref (228). Copyright 2007 American Chemical Society.

Finally, it is worth noting that the overall morphological structure of MDMO-PPV:PC₆₁BM described here has become a recurring theme in a number of OPV blends with higher than 50% fullerene weighting and has helped in understanding high-performance blends such as PTB7:PC₇₁BM (vide infra) a number of years after the original work was reported. This indicates that knowledge derived for one blend, while specific to that blend, can also contain general information or indicators for others.

4.2.2. P3HT

P3HT was the prototypical OPV donor polymer for a significant number of years and continues to be important as a benchmark system to study and understand. Power conversion efficiencies range between 3 and 5% for P3HT blended with PC₆₁BM.^{165,215−218}

In contrast to the completely amorphous polymer MDMO-PPV discussed above, P3HT is characterized by its semicrystalline nature, where regions of P3HT are amorphous and small regions, ∼10 × 10 × 20 nm are ordered into crystallites.²²⁹ This semicrystalline nature of the polymer is important to the photovoltaic performance of the material and has major effects on the morphology and light harvesting in the blend. These effects are both positive (crystalline structures lead to higher mobility and enable diffractive experimental techniques to be used to characterize the morphology) and negative (the details of the crystalline and mixed phases are complicated, with unknowns in both the spatial and size distributions along with complications in varieties of crystalline ordering controlled by chemical structure variations). Consequently, while the P3HT:PC₆₁BM blend has been very heavily studied and is an important blend to understand, a straightforward conclusive morphological narrative for it has failed to gain acceptance. The aim here is to highlight some informative studies that have been completed on the P3HT-based blends to date and attempt to build an overall sense of the likely morphology. It should be noted that some studies that will be covered here do not use PC₆₁BM as the acceptor but alternatives that can help to provide better contrast for measures of morphology.

Starting with an examination of the crystallinity aspects of the polymer, P3HT itself is comprised of repeat units of a thiophene monomer with a hexyl side chain at the 3-position. The monomers can be arranged such that the hexyl side chain is at the same position on every ring (regioregular, RR). This gives high crystallinity, as the side chains of the polymer can interleave, as shown in Figure 29, to form a periodic structure. π-Stacking of the thiophene backbones can also occur to give large three-dimensional aligned structures, which one can call crystallites and, as noted above, can grow to ∼10 × 10 × 20 nm in size.

Figure 29.

Crystalline organization of P3HT chains, which can form edge-on (A) or face-on (B) aggregates to the substrate. Reprinted with permission from ref (229). Copyright 2012 American Physical Society.

As might be anticipated, these periodic regions of P3HT are important in the photovoltaic performance of the material. The reasons for this are multiple. The hole mobility in crystalline P3HT can be close to double that of amorphous P3HT.^230,231 The ability for charges to move with high mobilities in P3HT is an obvious advantage when one aims to get holes to the electrode and extract them quickly before they have a chance to meet an electron and recombine. This aim is also enhanced by the crystallinity in a second sense in that crystalline regions do not—by definition—contain any PC₆₁BM molecules. Thus, recombination of holes with electrons on fullerene molecules is suppressed inside the crystallite, allowing the hole to move freely without being lost. Crystalline P3HT thus seems like an ideal candidate for use in photovoltaic blends; there are, however, many challenges in bringing together each of the advantageous properties in the correct way to enable the optimal light harvesting. For example, holes may well have high mobilities and low recombination probabilities inside P3HT crystallites, but unless that crystallite connects to the anode, the holes will have to transverse other more disordered regions to be extracted. The morphology of the entire blend, ordered and disordered polymer and fullerene, thus determines the overall light-harvesting and photovoltaic performance of the system. Where does one begin with such a complex question as to what is the morphology in P3HT-based blends?

Compositionally, large-scale phase separation does not occur in blends of P3HT:PC₆₁BM, and this makes the determination of compositional maps challenging. Initial bright-field TEM studies²³² were able to discern some features, but the low contrast hampered strong interpretation of the data. A strategy of creating contrast by shrewd choice of blend components thus arose as a method for understanding the morphology. In work by Roehling et al.,²³³ an endohedral fullerene was used as the acceptor. Here a heavy-metal lutetium-based trimetallic nitride, Lu₃N, is contained within a solubilized C₈₀ fullerene cage. Blends of P3HT with Lu₃N–PC₈₁BH produce power conversion efficiencies of up to 4%,²³⁴ with advantageous open circuit voltages of ∼0.8 V, and so are a valid blend composition for investigation of morphology. The heavy metal contained within the fullerene affords strong contrast with the P3HT in the high-angle annular dark-field scanning transmission electron microscopy tomography experiments that the authors report.²³³ Examination of the three phases (P3HT, fullerene-rich, and mixed) in as-cast films and annealed films that give optimal power conversion efficiencies show strong differences that explain the differing light harvesting. In the as-cast films, the P3HT and fullerene are separated into distinct, small domains surrounded by a large mixed-phase component (Figure 30, left side). The role of thermal annealing is clear in the morphological evolution of the blend (Figure 30, right side), as fullerene-rich and P3HT domains have become larger and connected together to form networks. Crucially, the tomography technique enables the morphology in the z direction (i.e., perpendicular to the substrate) to be determined. For the annealed blend, one can see in cross-sectional reconstructions (Figure 30, bottom row) that the P3HT and fullerene-rich domains have extended in the z direction as well as the x and y directions. This is important, for charges are flowing in primarily the z direction, and one can see that clear continuous phases of P3HT and fullerene exist throughout this direction, enabling charges to be extracted with low recombination probabilities.

Figure 30.

TEM tomography reconstructions of as cast (left column) and thermally annealed (right column) P3HT:Lu-PC₆₁BM blend films. Shown are identified P3HT regions (first row), fullerene-rich regions (second row), mixed-phase regions (third row), and cross-sectional composites of all three (fourth row). Scale bars are 100 nm. Reprinted with permission from ref (233). Copyright 2013 John Wiley and Sons.

The large endohedral fullerene molecules are not frequently used, so there is a desire for determination of the three-dimensional morphology of more commonly studied blends. To this end, another way of obtaining high contrast was to study the hybrid inorganic blend of P3HT with zinc oxide. Power conversion efficiencies in these devices can reach 2%,^209,235 and it is an interesting candidate for photovoltaic cells, as the inorganic component carries distinct advantages (high dielectric constant, high charge mobility), so the formed morphology is important. The organic:inorganic blend gives rise to high contrast in transmission electron microscopy, enabling TEM tomography to be performed.²⁰⁹ We chose to highlight this tomography study owing to both the exceptional contrast that is garnered from the blend components and the analysis that the authors have provided, which goes beyond simple pictorial representations of the morphology into a more detailed quantitative investigation. Three thicknesses of P3HT:ZnO films were investigated, 57, 100, and 167 nm thick, and the tomography of each was measured, as shown in Figure 31A–C, where ZnO is highlighted in yellow and P3HT is transparent. It can be seen that the thinnest film contains a great degree of phase separation, with large areas of P3HT surrounded by small clusters of ZnO. When the films are made thicker, the ZnO becomes more distributed inside the film volume and the P3HT domains are substantially reduced in size. The work does not just end at the 3D reconstruction of the morphology, however, but applies the now known 3D organization of the materials to look at the efficiency of quenching of P3HT excitons by applying a diffusion model with the known exciton lifetime and diffusion coefficient. This enables a 3D model of the exciton quenching to be generated, as shown in Figure 31D–F. These results are now determining quantitative information on how the blend behaves in a photovoltaic context at harvesting light and are a gold standard for others to aim at in quantifying light harvesting of a blend as opposed to simply showing images.

Figure 31.

Morphology of P3HT:ZnO blend films of three thicknesses (57 nm, first column; 100 nm, second column; and 157 nm, third column). Panels A–C show the reconstructed TEM tomography for the films, with ZnO yellow and P3HT transparent. Panels D–F show modeled exciton harvesting for each determined morphology when using the known P3HT exciton diffusion coefficient, with red regions corresponding to near-unity harvesting and blue/black regions to almost none. Reprinted with permission from ref (209). Copyright 2009 Nature Publishing Group.

The modeled exciton quenching reveals that large areas of the 57 nm thick film have no or very little light harvesting at all. Doubling of the thickness to 100 nm shows a dramatic improvement, with only a very small region of the film not able to contribute to light harvesting. Finally, at a film thickness of 167 nm, there are no regions of the film that do not contribute, and the worst areas are only a few small domains that have only 50% probability of light harvesting. It is clear from this study that the most powerful way to examine light harvesting in bulk heterojunction organic photovoltaic blends is with the ability to combine detailed morphological information with photophysical knowledge.

The best examination of the morphology and light-harvesting properties of P3HT would be with PC₆₁BM, as this is the most common blend combination and is the most well understood blend in terms of other electrical and photophysical studies.^{65,145,163,236−247} The challenge, however, as already noted, is that poor contrast exists between the materials to enable discrimination of the composition. Consequently, more advanced microscopy techniques have been used. The most promising study made use of a variant of energy-filtered TEM and significant computational image analysis to enable the production of material maps looking through the film²⁴⁸ (Figure 32). Here P3HT and PC₆₁BM domains could be mapped, along with a mixed phase of the two materials, showing that isolated domains of both materials are found embedded in a mixed-phase matrix. The compositional maps of as-cast films of the blend were compared with those of thermally annealed films.

Figure 32.

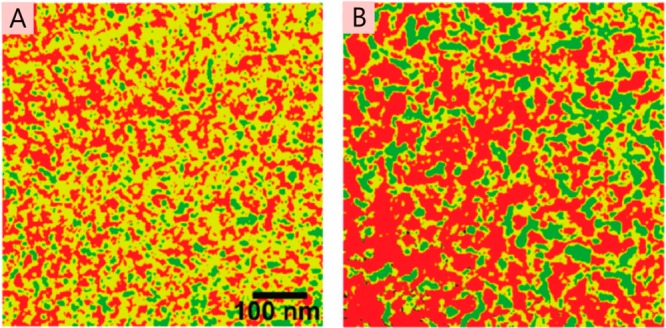
EFTEM of P3HT:PC₆₁BM blend as-cast (A) and after thermal annealing (B). Green areas show P3HT, red areas PC₆₁BM, and yellow areas a mixture of the two. Reprinted with permission from ref (248). Copyright 2011 American Chemical Society.

Thermal annealing is a postdeposition processing step commonly used to greatly enhance device efficiency.^{165,217,249−251} In thermal annealing, the film is heated, leading to it softening and the possibility of both the polymer and fullerene rearranging their packing in the film. In particular, when the film is heated to a temperature above the glass transition temperature (T_g) of the polymer, the polymer enters a “rubbery” phase that enables the chains to move, bend, and reshape themselves to enable crystalline order between or among the chains to be formed. Alternatively, solvent vapor annealing (SVA) can be used^252,253 to enhance crystallinity. Here a film is exposed to solvent vapor, which causes it to swell, thereby allowing rearrangement of the polymer chains (and fullerene) and enabling crystallinity to increase. Upon thermal annealing, the domains of P3HT and PC₆₁BM are found to grow, joining together to form in-plane bicontinuous networks, with a feature size of 14–100 nm found by analyzing the spectral power density of the image in Figure 32B. This result is consistent with the endohedral fullerene STEM tomography measurements already presented above and gives good confidence that thermal annealing consistently increases domain size and purity to enhance charge transport networks in the active layer.

This result is a good starting point for understanding P3HT:PC₆₁BM light-harvesting morphologies, but there are many unknowns remaining, as primarily the plane parallel to the substrate was mapped, with the compositional information integrated along the z direction, as is commonly the case with TEM-based techniques. Extracting z information is possible with spectroscopic ellipsometry,²⁵⁴ but at the cost of not having lateral information (x and y directions) on the same sample volume. Ideally, one would like full three-dimensional information. Two ways to obtain such information have been found. In the first, Masters et al. have developed a novel energy filtering of secondary electrons in scanning electron microscopy for use with organic BHJ blends.²⁵⁵ The advantage of this is that only the top few (1–3) nanometers are able to contribute to the EFSEM signal, ensuring the observations give only xy plane morphology rather than the full-film thickness z-integrated morphology that was measured above with EFTEM. If one were to selectively remove layers of the sample with etching, then 3D information could be derived. The EFSEM measurements were as much a proof-of-principle on using the technique with all-organic BHJ blends as a detailed examination of morphology, but the authors did choose to investigate P3HT:PC₆₁BM to validate their methods. With confidence that only the surface of the film is being imaged, the authors first find a P3HT “skin” layer on top of the blend that they need to remove with plasma treatment. Once that has been removed, they were able to use energy filtering to directly observe P3HT-rich, mixed, and PC₆₁BM-rich phases before and after thermal annealing (Figure 33), finding typical phase sizes of 16 and 28 nm. Such phase sizes are indicative of why P3HT:PC₆₁BM works well as a BHJ OPV blend, as they are on the correct order for ensuring that excitons created are able to diffuse to the interface and be separated into charge pairs, as already discussed in this review. Consequently, with such phase sizes, good light harvesting can be achieved. These results corroborate what has been observed previously, but do so with the distinction that they are definitively only looking at a very thin plane of the morphology rather than z-integrated results.

Figure 33.

Novel energy-filtered SEM image of P3HT:PC₆₁BM blends as cast (A) and after thermal annealing (B), with red indicating P3HT-rich areas and blue PC₆₁BM rich areas, while gray denotes mixed regions. Reprinted from ref (255). Licensed under CC-BY-4.0.

The second way to address the problem of getting z information for P3HT:PC₆₁BM is the use of computer aided TEM tomography as already discussed, but this is extremely challenging with the limited contrast available in conventional bright-field TEM. Recent pioneering studies have utilized energy-filtered TEM tomography²⁵⁶ and energy-filtered scanning electron microscopy on a different OPV blend, indicating that such techniques are possible. Consequently, for P3HT:PC₆₁BM-based blends some alternative strategies have been used to enable the generation of contrast. In work in 2009, van Bavel et al.²⁰⁸ undertook TEM tomography on P3HT:PC₆₁BM blend films to determine the three-dimensional organization of the blend. Using relatively low molecular weight P3HT (19.4 kDa) that preferentially forms highly crystalline nanorods,²⁵⁷ contrast was enabled for tomography. The work enabled full 3D reconstructions of the blend morphology in as-cast, thermally annealed, and solvent-annealed samples. In the as-cast film, few features were seen, owing to the primarily amorphous nature of the P3HT being indistinguishable from the PC₆₁BM. However, in the two annealed samples, strong P3HT nanorod crystallization was induced and strong contrast was formed. The 3D reconstruction allows information on the composition perpendicular to the substrate (the z direction) to be deduced, as shown in Figure 34. The proportion of crystalline P3HT nanorods as a function of depth through the film can be measured and shows that the majority lie close to the bottom of the film. This is an important result and is consistent with good device performance, as hole extraction is through the ITO anode at the bottom of the film.

Figure 34.

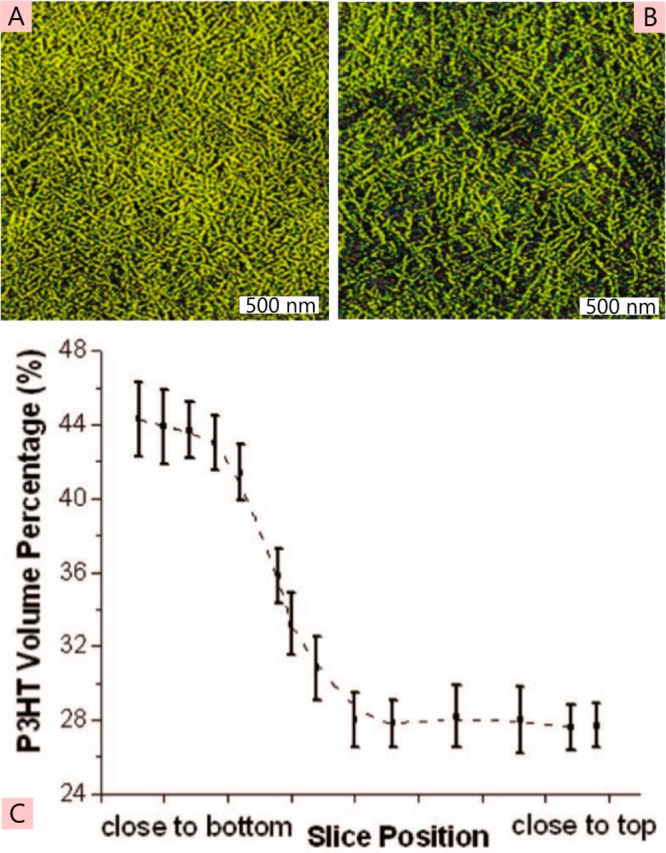
TEM tomography slices of a 100–200 nm thick P3HT:PC₆₁BM blend film, with P3HT indicated by the color yellow. Slices are taken toward the bottom of the film (A) and toward the top of the film (B), indicating differences in the amount of P3HT. This can enable the P3HT volume percentage as a function of z-position in the film, as shown in panel C, to be measured. Reprinted with permission from ref (208). Copyright 2009 American Chemical Society.

The disadvantages of the study, as the authors concede, is that contrast is only provided with the highly crystalline P3HT nanorods; thus, no information is deduced on the amorphous P3HT. In addition, the relatively low molecular weight of the P3HT used is a little different from the values typically used in devices, where such nanorods are not commonly observed. However, these limitations must be viewed in the context of the aim of truly observing the three-dimensional nanomorphology of the blend, which was achieved.

The second part of the P3HT:PC₆₁BM light-harvesting morphology narrative, as discussed at the beginning of this section, is the crystallinity of the P3HT. This is a difficult and challenging set of variables to measure, but numerous diffraction techniques can aid in understanding. Given the number of studies that have been undertaken on P3HT,^257−263 we have selected only a few that offer the most comprehensive overall impression of crystallinity in the polymer as it pertains to OPV blends. To examine the blend crystallinity it is pertinent to begin by just looking at the organization in films of P3HT on its own. A comprehensive investigation by Duong et al.²²⁹ using grazing-incidence X-ray diffraction (GIXRD) was able to quantify the orientation, size, and spatial placement of crystalline P3HT regions within neat films. By analyzing the intensities of edge-on and face-on diffraction peaks in situ during film formation, along with optical absorption spectra, a picture is able to be drawn of the overall evolution of film crystallinity formation and orientations, as shown in Figure 35.

Figure 35.

Schematic of how P3HT films form during spin-coating deposition. Initial edge-on aggregates align on the substrate (A), which grow into crystallites (B), followed by the formation of face-on aggregates higher up in the film (C), which grow into crystallites (D) before all the elements finally form a tightly packed structure (E). Reprinted with permission from ref (229). Copyright 2012 American Physical Society.

The term “aggregate” was used to describe one-dimensional π-stacking, while “crystallite” was used to describe lamellae of those aggregates giving two-dimensional ordering.²²⁹ It was found that edge-on P3HT crystallites, 20 × 10 × 10 nm in size dominate at the substrate–film boundary, before giving way to face-on orientated crystallites 6 × 8 × 3 nm in size further inside the film. The ratio of the overall edge- and face-on orientations was dependent on the casting solvent used, with chloroform giving predominantly face-on aggregates in the bulk of the film, while dichlorobenzene gave primarily edge-on.

For light harvesting, the structure of the P3HT:PC₆₁BM BHJ blends is important, and it is found that some of the same observations hold true. In the as-cast blend, P3HT crystallites are primarily edge-on to the substrate, while after thermal annealing it was found that these reorientate to face-on.²⁶² The size of the crystallites increases upon annealing,²⁰⁸ and in another study, it was found that the inclusion of PC₆₁BM somewhat restricts the size that the P3HT crystallites can grow to upon annealing when compared to films of neat P3HT.²⁶² A detailed discussion of the complex results that can be obtained from diffraction techniques is outside the scope of this work, but we note that a number of studies have investigated polymer:fullerene blends (typically P3HT:PC₆₁BM) and attempted to place those results within the context of other morphological, electrical, and photophysical knowledge on the blend,^264−269 and a comprehensive review of the topic has also been published by Rivnay et al. that goes into far greater detail.²⁷⁰ One final application of diffraction techniques that we do wish to highlight is their use for in situ studies of the evolution of order in thin films as they are annealed. This can also be in combination with other photophysical measurements, such as variable-angle spectroscopic ellipsometry (VASE) or field-effect mobility measurements to give a greater understanding of the annealing process.²⁷¹ Observing the evolution of the material crystallinity during annealing can give new insights into how the crystalline regions form and grow under the influence of heat, as shown for P3HT:PC₆₁BM films in Figure 36.²⁷² Here grazing-incidence X-ray diffraction measurements have been made continuously while the blend film has been annealed, and the out-of-plane [100] crystallite domain size has been calculated from the scattering peak size with the Scherrer equation. It can be seen that as soon as heat is applied to the film, the domain size increases and is then followed by a slower period of growth lasting for ∼10 min of annealing. Annealing longer than 10 min leads to a subtle loss of domain size over time, consistent with the optimal annealing time in devices being in the 10–15 min range. When the film is cooled, a clear drop in the P3HT domain size is observed and may be linked to some disorder being reintroduced now that less thermal energy is available. From these results, one can see that dynamical experiments to study annealing can give unique information on the morphology of BHJ blends, and a number of important studies have been reported that indicate the power of this methodology.^272−274

Figure 36.

Time evolution of [100] out-of-plane (OOP) domain sizes for P3HT calculated from Scherrer’s equation on the recorded grazing incidence X-ray diffraction peaks. The sample is heated (the temperature is indicated by the black line, right-hand axis) and the domain size is monitored for different weight percentages of P3HT:PC₆₁BM blend films. Overall, the domain size increases when the film is heated for ∼15 min. A small reduction in domain sizes occurs when the film is cooled, but the overall sizes are still substantially larger than before annealing. Reprinted with permission from ref (272). Copyright 2011 American Chemical Society.

Finally, to draw all of the knowledge presented on the morphology of P3HT:PC₆₁BM together, we present an overall schematic of the as-cast organization of the material and how that is altered by thermal annealing, as depicted in Figure 37.

Figure 37.

Overall P3HT:PC₆₁BM morphology, in-plane (A) and laterally (B) of as-cast blend films (left column) and after thermal annealing (right column), with P3HT-rich shown as shades of blue and PC₆₁BM-rich as shades of red. Initially, small spatially isolated domains of both materials form, which after thermal annealing join up to make contiguous domains in three dimensions. Thermal annealing promoted the formation of pure crystalline domains of P3HT, which are shown as the darkest blue regions in the annealed sample. The impact of the morphology on the charge recombination in transient absorption is shown in panel C, and here the as-cast film is the black open squares and the black line and shows fast geminate recombination owing to a higher degree of mixing, while the annealed sample (red open circles, red line) has markedly less geminate recombination. Image in panel C reprinted with permission from ref (163). Copyright 2010 American Chemical Society.

After casting P3HT:PC₆₁BM solution by spin-coating we have a primarily mixed blend of the two materials, with phase separation promoted on small length scales. Small P3HT crystallites align edge-on to the substrate, but overall, light harvesting in an OPV configuration is hindered owing to the small isolated domains of both materials that will enhance exciton dissociation but strongly hamper charge transport and extraction. Thermal annealing of P3HT:PC₆₁BM blends has been shown to triple the power conversion efficiency,^165,166 and morphology studies can explain why. In this blend, the light harvesting is optimized owing to the larger phase separation that leads to bicontinuous pathways of polymer and fullerene that form in-plane and out-of-plane. A mixed phase of the two materials still exists, but it constitutes a smaller fraction of the overall film after annealing. These results are consistent with transient absorption studies that showed that charge generation is much slower in thermally annealed P3HT:PC₆₁BM blends than in as-cast blends and presumably is limited by exciton diffusion to a heterojunction.^161−164 The charge recombination mechanism also changes upon thermal annealing of P3HT:PC₆₁BM blends: while as-cast blends show substantial geminate recombination, in annealed blends, recombination is predominantly bimolecular, indicating that charge pairs dissociate more efficiently into free carriers in annealed blends.^{161−163,275} Geminate recombination is suppressed by thermal annealing, but the network is still spatially fine enough to ensure that all excitons reach heterojunction by diffusion and give efficient charge generation.

4.2.3. PTB7

The final material that we will examine in detail for how light harvesting is dependent on optimization of the morphology is the high-performance polymer PTB7. With optimized electrodes and interlayers, PTB7-based blends are capable of reaching power conversion efficiencies in the range of 9–10%.^36,37 The material has proven important in propelling organic photovoltaic devices to and across the 10% efficiency barrier, an important milestone not just psychologically, but also to enable OPVs to be potentially competitive with amorphous silicon PV as a low-cost power generation technology.

Nearly always, the highest efficiencies are achieved with the use of the high boiling point additive 1,8-diiodooctane (DIO). DIO is added at 3% by volume to the solution prior to spin-coating and is found to double the efficiency.²¹⁹ Current–voltage curves and external quantum efficiency spectra for as-cast and additive-treated PTB7:PC₇₁BM devices are shown in Figure 38, with efficiencies slightly lower than in optimum devices^36,37 owing to nonoptimized contacts and lack of interlayers, but the blends have active layer deposition conditions (blend ratio, concentration, spin speed, etc.) identical to those of the highest-efficiency devices. The doubling of the efficiency with the use of DIO is a good question to investigate in the context of the interplay between the blend morphology and its effect on light harvesting, for such dramatic device performance improvements are at the heart of understanding why bulk heterojunctions work well and how the can be fully optimized.

Figure 38.

I–V curves (A) and external quantum efficiencies (B) for PTB7:PC₇₁BM devices from chlorobenzene as cast (black lines) and with 3% diiodooctane (DIO) added to the casting solvent (red lines). Device efficiency doubles with the use of DIO. Reprinted from ref (77). Licensed under CC-BY-3.0.

Without the use of the additive DIO, the blend films of PTB7 with PC₇₁BM at a ratio of 1:1.5 show large quasi-periodic round features 150–200 nm in diameter^179,219 that are clearly visible in AFM and TEM images (Figure 39), not dissimilar to the observed morphology of MDMO-PPV:PC₆₁BM (vide supra).

Figure 39.

AFM topography (A) and bright-field TEM (B) of PTB7:PC₇₁BM blend films from chlorobenzene as-cast. Image in panel A reprinted with permission from ref (276). Copyright 2015 The Royal Society of Chemistry. Image in panel B reprinted with permission from ref (219). Copyright 2010 John Wiley and Sons.

For such strong TEM contrast there must be a high degree of material purity between the PTB7 and PC₇₁BM regions, and the fullerene can be identified as the main constituent of the large 150–200 nm domains from its interactions with electrons that form the TEM image. In OPV blends containing PC₇₁BM, the fullerene contributes significantly (up to half) of the photocurrent, absorbing strongly in the blue and green. With large pure fullerene domains this should lead to a low degree of light harvesting from the fullerene, for excitons that form inside such a large volume will only be able to diffuse ∼3 nm before decaying to the ground state.⁷⁷ It is thus surprising when time-resolved photoluminescence of the fullerene was measured in the blend and showed a very fast decay, with an average lifetime of 67 ps, indicating that there was a significant amount of quencher (i.e., PTB7) in the immediate vicinity of the fullerene molecules.⁷⁷ This is in contrast to the AFM and TEM images, which show homogeneous, presumed pure, domains of PC₇₁BM.

The average lifetime is in fact comprised of a number of components, including a fast ∼300 fs decay that is consistent with fullerene exciton dissociation due to hole transfer to PTB7 that has to be right next to the fullerene molecules. Slower picosecond decays represent exciton diffusion within regions of PC₇₁BM before quenching due to hole transfer to PTB7. As the diffusion coefficient of PC₇₁BM has been determined,⁷⁷ the morphology can be derived from the time-resolved PL decays. A best-fit is found for a region of pure fullerene material, spherical in shape with a diameter of 60 nm, as shown in Figure 40A, well below the observed fullerene domain size of 150–200 nm. This led to a further examination of the morphology, and upon closer investigation, a “skin” layer of PTB7 was observed to be covering the active layer (Figure 40B), similar to some MDMO-PPV and P3HT blends, as briefly mentioned in their respective sections above. This skin layer is polymer-rich in character, blankets the top of the film, and therefore obscures the structural organization of the material beneath it when probed with surface characterization techniques such as AFM. By removing this skin layer with plasma etching, the true morphology of the as-cast blend could then be observed with AFM (Figure 40C), and the blend displays a remarkable ordered morphology, with the large fullerene domains appearing to actually comprise numerous small fullerene spheres 20–60 nm in size, surrounded by a PTB7-rich matrix.^77,276

Figure 40.

Morphology of PTB7:PC₇₁BM blend film spin-coated from chlorobenzene without DIO. (A) Results of time-resolved PL decay modeling, using the PC₇₁BM exciton diffusion coefficient to determine that pure fullerene spheres ∼60 nm in size exist, much smaller than what is observed from the initial morphology measurements. (B) SEM cross-sectional image of the blend, showing the “skin” on top of the blend layer that was obscuring the true morphology. (C) After removal of the skin with plasma ashing, AFM topography shows that the large domains actually consist of a large number of small fullerene domains, 20–60 nm in size, agreeing well with the time-resolved PL data in panel A. Reprinted from ref (77). Licensed under CC-BY-3.0.

This work is a good example of utilizing time-resolve photophysics to derive nanoscale morphology in an OPV blend, for with a cursory glance the fullerene domains would be presumed to be ∼200 nm in diameter, whereas in fact they are ∼60 nm. The small pure-fullerene spheres sit in a PTB7-rich matrix, which studies have shown to be ∼70% PTB7 and 30% PC₇₁BM.¹⁷⁹ The matrix and skin layer are presumed to be a quintessentially mixed phase, with polymer and fullerene completely mixed together at the smallest length scales with no discernible phase separation. An overall picture of the morphology without additive is thus able to be built and explains the low power conversion efficiencies that are obtained. Absorption of light and dissociation of excitons into charge pairs by the polymer and fullerene are both good, but charge separation, transport, and extraction are made difficult owing to the morphology. The small pure-fullerene spheres lead to regions where there is a large surface area for dissociation but no continuous network for electron transport. Furthermore, the intimately mixed-phase regions will promote charge recombination, for there are no separated domains to keep charges apart. Finally, the polymer-rich skin at the top of the film acts as a partial electron-blocking layer, which is not the most advantageous arrangement next to the electron-extracting cathode in the device stack. Consequently, this morphology tells us that even when one does have good exciton dissociation and clear domains of material, light harvesting may not be possible owing to the fact that all parts of the photovoltaic process need to be satisfied to turn absorbed photons into extracted charges.

With the use of a solvent additive, the device performance of PTB7:PC₇₁BM solar cells doubles.²¹⁹ As the morphology of blends without additive was found to be particularly unattractive for good devices, it was speculated that this is where major improvements must occur. The use of solvent additives with OPVs has occurred for a number of different blends,^220,277,278 generally to control the evaporation rates of the host solvent and to enable the correct amount of crystallization or phase separation to occur. The type of additive, its boiling point, and the volume percentage used are typically determined by trial and error in order to achieve the optimal device performance. For PTB7:PC₇₁BM, the additive found to work best is DIO, and the volume added is 3% into chlorobenzene for an overall 25 mg mL^–1 solute concentration (10 mg of PTB7 and 15 mg of PC₇₁BM).²¹⁹ AFM or TEM studies of the optimized blend with DIO show a uniformly mixed blend (Figure 41A,B) with no discernible features.^179,219 This is consistent with the time-resolved PL from the blend, which shows a very fast predominantly 100 fs decay of fullerene excitons.⁷⁷ Using X-ray microscopy, the miscibility of the fullerene into PTB7 is measured¹⁷⁹ and found to be ∼60%, with variations existing between 52 and 68%, creating regions that are slightly polymer-rich and regions that are fullerene-rich; however, the spatial resolution of the technique does not allow any quantifiable information on that spatial concentration variability.

Figure 41.

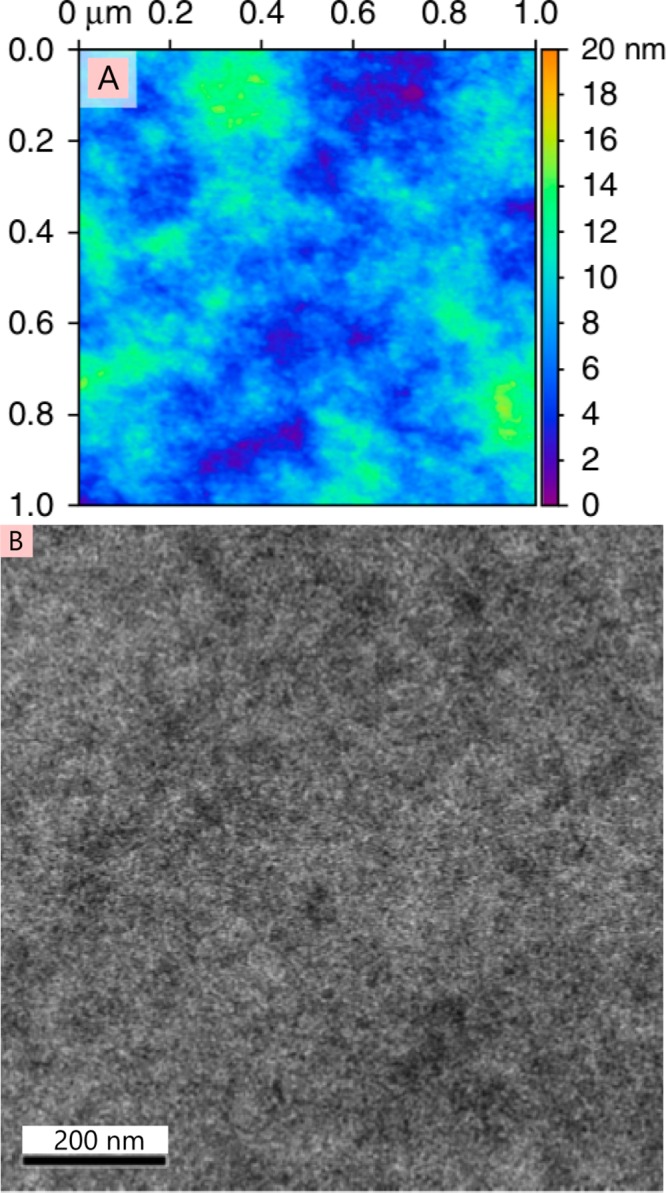
AFM topography (A) and bright-field TEM (B) of PTB7:PC₇₁BM blend cast from chlorobenzene with 3% DIO added to the solution prior to spin-coating. Image in panel A reprinted from ref (77). Licensed under CC-BY-3.0. Image in panel B reprinted with permission from ref (219). Copyright 2010 John Wiley and Sons.

As shown, AFM and TEM do not have the ability to discriminate between the two materials with such a high degree of mixing between them. Consequently, more advanced techniques have been applied. The greatest success was seen with photoconductive AFM (Figure 42), where remarkable contrast in photocurrent was observed, with feature sizes down to a few tens of nanometers.⁷⁷ The PC-AFM photocurrent map shows swirling linear features of high and low photocurrent. Light for the generation of photocurrent is provided by the AFM tip laser at 670 nm and thus is primarily absorbed in regions that are rich in PTB7, leading to high photocurrent, while low photocurrent is due to regions rich in PC₇₁BM. While the observed morphology is in the substrate plane, and current flow is perpendicular to that, what is observed is still relevant, as charges may have to move laterally before finding vertical pathways. If a closer look is taken at the morphology (Figure 42B), then one can see that the PTB7-rich and PC₇₁BM-rich domains form extended elongated shapes, with transitionary photocurrent measured between the domains (i.e., the photocurrent transition follows a gradual linear dependence rather than a sharp step function between the domains).

Figure 42.

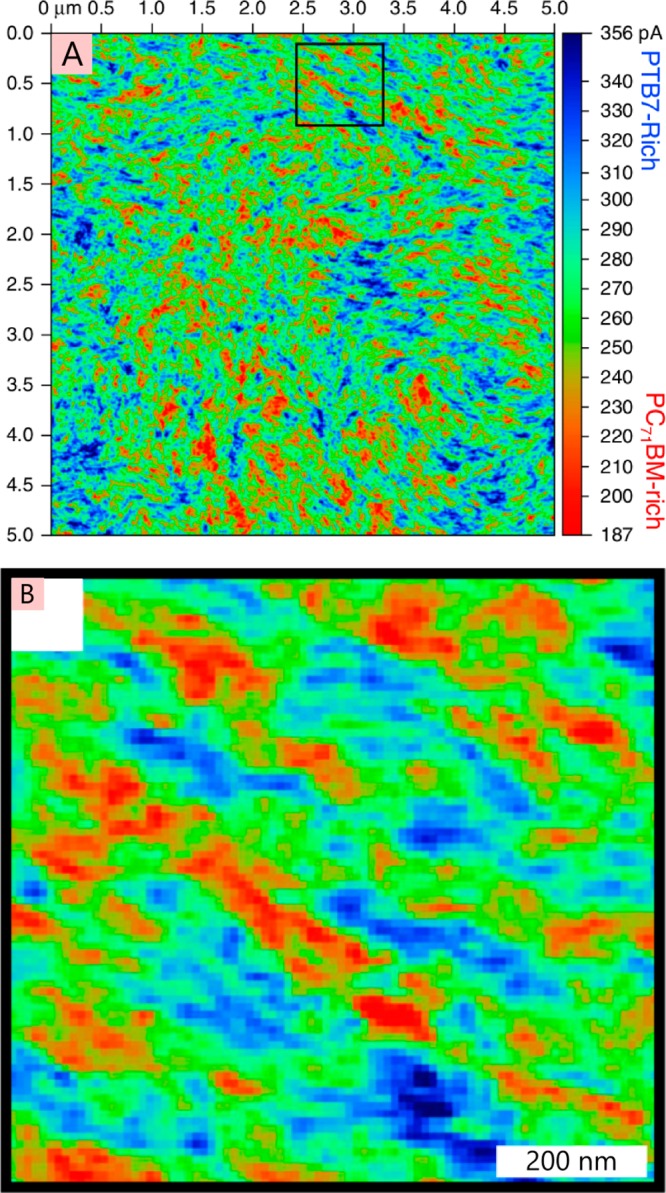
(A) Photocurrent map of PTB7:PC₇₁BM blends spin-coated from chlorobenzene solution with 3% DIO. Measurements were made by photoconductive AFM at a bias of −3 V and with photoexcitation at 670 nm. PTB7-rich regions are shown in blue, mixed-phase regions in green, and PC₇₁BM-rich regions in red. In panel B is shown a close-up of the boxed region in panel A, indicating that the two materials form elongated fiberlike domains with respect to each other. Reprinted from ref (77). Licensed under CC-BY-3.0.

Examination has also been made of the crystallinity of PTB7 by X-ray diffraction experiments.^279,280 In work by Hammond et al.,²⁷⁹ PTB7 was measured in blends with and without DIO, and when combined with spectroscopic ellipsometry, information on the alignment of the polymer chains and the degree of crystallinity can be obtained. What was found was that PTB7 was not highly crystalline; indeed, by one measure only ∼21% of the polymer chains were aligned in blend films. However, this does not mean that the majority of PTB7 is amorphous, as the authors comment that paracrystallinity is an important consideration in the blend films, i.e., partial local ordering aided by lattice strain. In addition, there is some evidence from other work²⁸¹ that polymers very similar to PTB7 readily aggregate, and while this is not crystalline order, it is not what one would class as a truly amorphous polymer either. Hammond et al. also found that DIO plays no role in enhancing the crystallinity in the blend films, with XRD being almost identical in blends with and without DIO. The crystals that form are small by the standards of P3HT discussed above, with typical dimensions of 1.5 × 5 nm (i.e., ca. four π-stacked chains, by ca. three d-spacings).

Thus, overall the morphology generated with 3% DIO is highly advantageous for light harvesting in a photovoltaic cell, creating a blend with large surface areas between donor and acceptor for efficient exciton dissociation into charge pairs and quite small, interconnected, pure domains of both materials for charge separation and transport with minimal recombination losses. It is clear that in PTB7:PC₇₁BM the morphology plays a very important role in light harvesting, for if the morphology is as it is when no DIO additive is used, solar cell efficiency is halved. The role of DIO in the blend is to enable the highly advantageous morphology for OPV performance; however, why DIO has that role is still not fully understood. The common function of DIO as a high boiling point solvent to slow the evaporation process to enhance crystallinity is not relevant here, where neither material is highly crystalline. Instead, DIO seems to help mixing and miscibility of PTB7 and PC₇₁BM, with fullerene miscibility into the polymer enhanced from 30 to 60% when DIO is used. However, the improved miscibility not only leads to well-mixed materials but also to an optimal fiberlike nanoscale organized morphology, thereby enabling not only efficient light harvesting to generate charge, but also extraction of those charges.

Although the highest efficiencies with PTB7 are obtained with PC₇₁BM, BHJs can also be made with PC₆₁BM, with power conversion efficiencies in the region of 3–4%. As a testament to how complex BHJ morphology can be, the organization of the two materials in the PC₆₁BM blend is completely different from the PC₇₁BM one discussed above.²⁸⁰ The higher miscibility of PC₆₁BM than PC₇₁BM²⁸² leads to a higher degree of mixing and a more complex nanoscale morphology. Small crystallites a few nanometers in size of polymer and fullerene form near to each other, embedded in a more disordered matrix of both materials. A subtle large-scale phase separation on the order of 150 nm exists, but is not as well-defined and impactful as in the PC₇₁BM blends. Overall the role of DIO in the PC₆₁BM blends is less important, with the additive enhancing mixing when chlorobenzene is used as the casting solvent but otherwise not changing measured parameters drastically. This is borne out by the overall device efficiency, which only increases by a third with the use of DIO, compared to the doubling of device efficiency for PC₇₁BM-based blends with chlorobenzene.

4.3. Morphology Summary

To conclude this section, we can see that the morphology—the spatial organization of the donor and acceptor materials in the blend—is vitally important to successful harvesting of sunlight in photovoltaic devices. The optimal morphology for each blend combination frequently reduces to a compromise of competing photophysical and electrical requirements for light absorption, charge generation, transport, and extraction. If the donor and acceptor are too spatially disconnected into phase-separated domains, then exciton diffusion is unable to ensure that absorbed light can be converted into charge pairs. Conversely, if the two materials are too well mixed, then charge pairs form easily but cannot be readily separated or kept apart for long enough to enable extraction. If crystallinity in some of the OPV materials is not great enough, then the charge mobility is too low; if the crystallinity is too high, then charge-pair generation is restricted. The morphology in OPV blends is a delicate balancing act, the formed morphology has to be “just right”, as otherwise losses in device performance are incurred. Almost always this “just right” morphology is found by trial-and-error device fabrication runs, combining different solvents, additives, deposition methods, and postdeposition treatments (solvent vapor annealing, thermal annealing, etc.) until an optimum is obtained. Material scientists then explore these morphologies with a suite of techniques, as detailed in this section to determine what this “optimal” morphology is. Scientifically this is not the most efficient way of improving device performance and finding the best deposition methodologies. It is thus a pressing problem to attempt to understand the actual nanoscale organizational physics of how these materials interact and blend with each other and then determine/predict what the resultant morphology would be. Computationally and in terms of physics understanding this is obviously a “grand challenge”, all the more challenging because each blend combination of donor and acceptor forms a different morphology. The combination of donor and acceptor materials in terms of synthetic chemistry capabilities is near infinite; thus, exploring these via trial-and-error device fabrication with all the possible solvents, additives, etc. is simply impossible. Significant improvements have been realized, as this section demonstrates, with approximate doubling of device efficiencies at each “node” on the path of progress, from 1 to 2% efficiencies with MDMO-PPV, through 3–4% with P3HT and now 7–10% with PTB7. To continue this progress, new materials with advantageous photovoltaic properties will need to be created and optimal morphologies for them determined, preferably predictively rather than retrospectively, to enable the best light harvesting.

5. Summary and Outlook

In this review, we have provided a detailed picture of the main processes and variables that govern light harvesting in organic photovoltaic cells. The great strength of organic materials for photovoltaic applications is the strong absorption of light that enables the use of thin films on the order of 100 nm from nontoxic, relatively stable, plastic materials. The materials can be deposited from solution by simple coating processes, and they offer the prospect of simple fabrication of large areas of solar cells at low cost and with low energy of manufacture. As the primary photoexcitations are tightly bound Frenkel excitons, a key step in light harvesting is splitting them into free charges which is achieved using a charge-accepting material (normally an electron acceptor, if as is most often the case the absorbing material is an electron donor). A combination of exciton diffusion and FRET leads to exciton transport to the acceptor. Two main device structures are used: planar and bulk heterojunctions. Since excitons in most materials diffuse <20 nm, planar heterojunctions are limited to be thin organic layers that do not fully absorb the incident light. This is overcome by creating a bulk heterojunction throughout the full 100 nm thickness of the film, with separation between the electron donor and acceptor on the order of 20 nm. The bulk heterojunction is used out of necessity rather than desire, as it creates a wide-range of complications in designing materials for efficient harvesting of light. The efficient operation of a bulk heterojunction requires a particular arrangement of the donors and acceptors (morphology) that facilitates excitons reaching the heterojunction and also enables charge separation and extraction. At present it is not known in advance if a new material will be able to make a suitable morphology, and progress in the field is slowed by needing to explore a wide range of processing conditions with no guarantee of success.

There are three main ways in which this situation could be improved. The first is by making so-called ordered heterojunctions in which either donor or acceptor are patterned and the other material added to make the desired morphology.^283−285 The length scales involved are demanding, and so far efficiencies using this approach have been limited.^286,287 Nevertheless, progress in self-assembly and in nanoimprint lithography could help to achieve this. The second main approach is to enhance the effective exciton diffusion length; a factor of ∼5 increase would enable planar heterojunctions to harvest almost all of the incident sunlight. This would simplify fabrication, avoid the time-consuming optimization of donor–acceptor morphology, and enable materials to be used that do not form appropriate BHJ morphologies. The suggested increase in the exciton diffusion length is clearly very challenging, but advances in materials, processing, and possibly device structure combined with the advanced experimental techniques and synthetic chemistry available today could enable it to be realized. The third approach is further improvement of the bulk heterojunction by moving from an empirical to a predictive approach. Understanding of exciton diffusion and dissociation and charge separation, transport, and extraction in bulk heterojunctions all convolved with a complex nanoscale morphological arrangement of the materials has reached a remarkable degree of maturity, given the complexity of the blends. Moving from a regime of reactive understanding of the systems created to predictive control of such systems with the use of advanced electrical, photophysical, morphological, theoretical, and synthetic chemical scientific techniques is a prospect with serious merit and one that could transform the relatively trial-and-error approach that has been used thus far into a powerful predictive method for improving or optimizing solar cell efficiencies.

Finally, it is worth pausing to consider the remarkable progress that has been made in organic photovoltaics, with power conversion efficiencies of OPVs increasing by a factor of 5 in the last 20 years, with lab-based devices now regularly exceeding 10%. In this review we have described the key processes that all have to be present in order for the successful harvesting of light in an organic solar cell, and have detailed how understanding of these processes has contributed to such performance increases. With good prospects for further understanding and optimization, future improvements in device efficiency are anticipated. The external quantum efficiencies at short-circuit conditions now reach 70–80% in record-efficiency organic photovoltaic cells over spectral regions of strong light absorption. However, the open-circuit voltage from single-junction cells is only about 0.8 V or lower and potentially can be increased. There are several factors that make the open-circuit voltage much lower than the energy of the absorbed photon could allow. First, the higher-energy exciton states usually relax to the lowest-energy exciton before splitting into an electron–hole pair. These energy losses can be avoided by developing tandem cells or multijunction cells that use a combination of different absorbers. In such cells, higher energy photons are absorbed and converted in a subcell with higher band gap materials.²⁸⁸ In February 2016, the German company Heliatek demonstrated a record power conversion efficiency of 13.2% in small organic solar cells using this approach with their proprietary materials.

A second source of energy loss is the energy offset between exciton states and charge transfer states, which is the driving force for charge pair generation. We have discussed recent findings that the optimum driving force for charge separation equals the reorganization energy in sections 3.1 and 3.2. This implies that photovoltaic materials with small reorganization energies and a small driving force can minimize the loss of open-circuit voltage at a heterojunction without a trade-off of photocurrent. A further loss of open-circuit voltage of typically 0.5 V is associated with charge extraction.²⁸⁹ Multiple factors were suggested to contribute here, including energetic disorder for charge transport, the nature of the electrical contacts, and carrier recombination. The main findings on this topic have been reviewed several times.^290−292 Overcoming limitations in the open-circuit voltage outlined above can be expected to lead to further progress in the power conversion efficiency of organic photovoltaic devices.

Biographies

Gordon J. Hedley received his M.Sc. in Physics & Astronomy from the University of Durham in 2005. He obtained his Ph.D. in 2010 with Ifor D. W. Samuel at the University of St Andrews, where he investigated the ultrafast photophysics of transition-metal complexes. His research then focused on the ultrafast photophysics and morphology of organic photovoltaic materials with postdoctoral positions at the Organic Semiconductor Centre at the University of St Andrews. He is currently a postdoctoral researcher at the University of Regensburg in Germany, where he studies the single molecule spectroscopy of organic semiconductors.

Arvydas Ruseckas studied physics at Vilnius University and received his Ph.D. in 1999 from Lund University in Sweden and Institute of Physics in Lithuania under the guidance of Villy Sundström and Algimantas Undzėnas. He is a research fellow at the University of St Andrews, and his current research mainly focuses on the development and application of ultrafast spectroscopic techniques to study energy and charge transport in organic semiconductors and hybrid structures for photovoltaic and light-emitting devices.

Ifor D. W. Samuel is professor of physics at the University of St Andrews. He received his M.A. and Ph.D. from the University of Cambridge, working on the optical spectroscopy of organic semiconductors. He was a research fellow at Christ’s College, Cambridge, UK, and also performed postdoctoral work at CNET-France Telecom in Paris, before setting up his own research group on light-emitting polymers and dendrimers at the University of Durham. In 2000, he moved to the University of St Andrews, where he founded and leads the Organic Semiconductor Centre. His current work concerns the photophysics of organic semiconductor materials and devices, including organic light-emitting diodes, solar cells, and lasers, and their applications, and he has published approximately 400 journal papers. He is a fellow of the Royal Society of Edinburgh, the Institute of Physics, SPIE, and the Royal Society of Chemistry.

The authors declare no competing financial interest.