Age-Specific Variation in Adult Mortality Rates in Developed Countries

Abstract

This paper investigates historical changes in both single-year-of-age adult mortality rates and variation of the single-year mortality rates around expected values within age intervals over the past two centuries in 15 developed countries. We apply an integrated Hierarchical Age-Period-Cohort—Variance Function Regression Model to data from the Human Mortality Database. We find increasing variation of the single-year rates within broader age intervals over the life course for all countries, but the increasing variation slows down at age 90 and then increases again after age 100 for some countries; the variation significantly declined across cohorts born after the early 20th century; and the variation continuously declined over much of the last two centuries but has substantially increased since 1980. Our further analysis finds the recent increases in mortality variation are not due to increasing proportions of older adults in the population, trends in mortality rates, or disproportionate delays in deaths from degenerative and man-made diseases, but rather due to increasing variations in young and middle-age adults.

Introduction

Most developed countries have experienced substantial mortality declines and continuous life expectancy increases over the past two centuries (Oeppen and Vaupel 2002). Initial mortality declines resulted from decreasing mortality risks from infectious and parasitic diseases among young people as a result of better nutrition, hygiene, vaccines and medical advances. During the late 19^th century and early 20^th century, individuals saved from infectious disease-related deaths survived into middle and older ages and then faced an elevated risk of dying from degenerative or man-made diseases (Omran 1982), which caused the age-of-death distribution to progressively shift from the young to the old. Beginning in the late 1960s, the United States and other developed nations experienced unexpectedly rapid declines in mortality rates for the major degenerative diseases (e.g., heart disease, cancer and stroke) (Olshansky and Ault 1986), which caused the age distribution of deaths to further shift to the older ages (Kannisto 2001).

This widespread demographic and epidemiologic transition has important implications for temporal trends in mortality dispersions, i.e., variability in age at death, measured either by the standard deviation around the mean or modal age of death (Cheung et al. 2005; Myers and Manton 1984a; Kannisto 2001), or by the distance between the lower and upper quartiles of the age distribution of death (“interquartile range”) (Wilmoth and Horiuchi 1999), or by the Gini coefficient of age at death (Shkolnikov et al. 2003). Studies of mortality dispersion focus either on unconditional mortality dispersion (Robine 2001), i.e., variability of age at death across the entire life span or conditional mortality dispersion (Edwards and Tuljapurkar 2005; Nusselder and Mackenbach 1996; Smits and Monden 2009), i.e., variability of age at death above certain age. Mortality dispersion has been viewed as an indicator of population health disparities (Edwards and Tuljapurkar 2005). Prior studies have found all-life-span mortality dispersion decreases over time while mortality dispersion at older ages is increasing (Myers and Manton 1984b), which suggests an increasing postponement of health disparities to older ages (Engelman et al. 2010).

Building on this prior research, the present paper examines variation in single-year-of-age-specific mortality rates around mean rates within age intervals (e.g., age 30-40), period, and cohort, which we call mortality variation. This new measurement captures the variability in risk of death within each temporal group defined by age, period and cohort. Despite the difference between traditional measures of mortality dispersion and this new measure of mortality variation, both measures are related to variability in the risk of death within a population. The former tackles the variability within whole population or subpopulation above a certain age; the latter addresses the variability within each age group, period and cohort. Our approach makes two important contributions. The first is a methodological contribution. Prior studies calculated measures of mortality dispersion either from period or cohort life tables, and so were not able to simultaneously disentangle the effects of both factors on the trend of mortality dispersion. In this sense, our study extends and shed lights on the literature on mortality dispersion.

The second is a conceptual contribution. Using this approach, we are able to investigate the variability in risk of death not only across periods or cohorts like prior studies but also throughout life course which then reveals the whole picture of variability in risk of death across three temporal dimensions: age, period and cohort. This research is relevant to several research literatures; e.g., the relative contribution of mortality selection and cumulative advantage on the trend of health disparities across life course; the relative contribution of mortality selection and cohort evolution on the trend of health disparities across birth cohorts; and the relative contribution of mortality decline and epidemiologic transition on the trend of health disparities across periods. Our analyses yield some findings on the temporal components of mortality rates and variation that are consistent with prior research as well as some findings that are novel and that flow from the empirical application of the new statistical model. They also point to new questions and avenues for future research.

The remainder of the paper is organized as follows. The next section reviews prior research on historical changes in mortality rates and mortality dispersions, from which hypotheses are stated that embody our expectations about the age, time period, and cohort dependence of these rates and variation. This is followed by sections on data and methods and a methodological discussion of the relationship between mortality dispersion and mortality variation. Findings then are presented. A discussion and conclusion section ends the paper.

Temporal Changes in Mortality Rates

The temporal dependence of mortality rates on age has been a topic of study by demographers since Graunt's (1662) classical study of the “Bills of Mortality” in London. Generally, these studies show exponentially accelerating increases in mortality rates across the adult ages, as embodied in Gompertz's (1825) classical law of mortality. A principal topic of recent research is whether the exponential increase decelerates to a plateau of high but stable rates at the oldest ages and, if so, at what age does the deceleration begin (Gavrilov and Gavrilova 2011; Vaupel 1997).

Recent studies of historical trends of mortality rates also have found patterns of cohort mortality declines that may have resulted from decreased exposures to physiological risk factors for chronic morbidities such as infection and inflammation (Finch and Crimmins 2004), increased health capital brought about by technophysio evolution (Fogel and Costa 1997), or a combination of these and other factors across birth cohorts (Zheng 2014). Period mortality declines may be attributable to a changing mix of socioeconomic development, lifestyle changes, and medical innovations in each period (Omran 1971; Olshansky and Ault 1986). Systematic regression analyses that disentangle confounding time-related variables also suggest that, during the second half of the twentieth century, cohort effects have been strong while period effects have been relatively weak (Yang 2008). Nonetheless, period effects that impact mortality for all or most ages and cohorts are expected during wars or infectious disease epidemics (Omran 1982; Wilmoth 1990).

Temporal Changes in Mortality Dispersions and Their Implications on Mortality Variations

Prior studies of mortality dispersion examine either unconditional variability of age at death across the entire life span or conditional variability of age at death above certain age. Some scholars (Robine 2001) suggested including deaths of all age groups to calculate mortality dispersion and then examined all-life-span mortality dispersion over time, while others focused on the dependence of the trend of mortality dispersion on age. For example, Myers and Manton (1984a) found that all-life-span mortality dispersion in the U.S. is negatively correlated with the level of life expectancy, but mortality dispersion over age 60 is positively correlated with the level of life expectancy. These findings recently have been updated and extended to mortality data on 23 developed national populations with at least five decades of data by Engelman et al. (2010) who show that survivors to ages 75 and over have grown increasingly heterogeneous in their mortality risk even though all-life-span mortality dispersion decreases over time in these 23 countries despite some minor differences in the extent of mortality dispersion across countries.

There are at least two topics of theoretical interest to demographers for which measures of mortality dispersion are salient. One is related to the question of mortality compression and the limit to human life span (Caselli and Vallin 2001), and the other is related to health disparities within populations. We take up the latter one and further extend the measure of variability of risk of death to residual mortality variation around the mean of age-specific mortality rates within age intervals, time periods and cohorts. As compared to prior studies on mortality dispersion which look exclusively at life tables where the effects of age structure have been removed, mortality variation in our study is affected by all three temporal dimensions: age, time period, and cohort. The conceptual distinction of these three components is essential as they are confounded with each other and affect trends in mortality variation. For instance, an increase in mortality variation across time periods may result from either cohort replacement in which cohorts with larger within-cohort mortality variation succeed cohorts with smaller within-cohort mortality variation or an aging society wherein the elderly, who usually have larger within-age mortality variation than younger people, increase their proportionate share in the population structure, or from some combination of the two. Similarly, a widening mortality variation with age may be confounded with other temporal patterns. That is, period patterns in mortality variation may affect age variability in mortality variation. And a widening mortality variation across age groups may also be influenced by cohort patterns.

Age Pattern in Mortality Variations

Many theoretical and empirical studies in demography, medical sociology and social epidemiology suggest distinct patterns of mortality variation across age, period, and cohort. Population heterogeneity theory conceptualizes populations as heterogeneous, composed with individuals or subpopulations with different physiological vulnerability to mortality or demographic frailty (Vaupel et al. 1979). In aggregate mortality data, frailty cannot be directly measured as it represents unobserved heterogeneity within populations (Vaupel et al. 1979; Vaupel and Yashin 1985). Individual frailty is assumed to be fixed at birth and the mortality hazard tends to remove individuals with higher level of frailty at earlier ages. This leaves individuals with lower level of frailty surviving to older ages and thereby reduces the unobserved heterogeneity in populations at older ages. For example, Manton et al. (1981) found both the means and variances of frailty decreases across age groups, which is consistent with the operation of selective mortality across the life span. In brief, this line of research suggests that the convergence in health disparities and mortality variation in late life observed in empirical studies may be due to selective mortality. But other studies suggest the convergence may also result from diminished socioeconomic differences in exposure to risk factors, postponement of morbidity and functional limitations for higher socioeconomic status (SES) people, and universal biological frailty (House et al. 1994; House et al. 2005). Biological frailty, different from demographic frailty, has been found to increase over age as the capacity of the human body to resist destruction and mortality decreases in response to accumulated environmental stressors (Arking 2006; Strehler and Mildvan 1960; Zheng et al. 2011b). At the same time, cumulative advantage theory prevalent in medical sociology and social epidemiology argues that the advantageous status in early life will be accumulated and magnified across the life course, which leads to widening health disparities and variation in mortality risk across the life span (Lauderdale 2001; Lynch 2003).

Period Pattern in Mortality Variations

In terms of change in mortality variation across time periods, current studies may also imply different trends. As noted, in prior studies demographers have found increasing life expectancy and declining mortality rates are associated with declining all-life-span mortality dispersion. That is, all-age-inclusive mortality dispersion in advanced human societies has been decreasing over time since the mid-nineteenth century when the mortality rate started declining due to socioeconomic development, improved nutrition, improving living standards, medical advances, and better public health practices. Demographic transition theory is echoed by epidemiologic transition theory (Olshansky and Ault 1986; Omran 1971) which states that advanced human societies have gone through the three stages of transition (the age of pestilence and famine, the age of receding pandemics, and the age of degenerative and man-made diseases) and currently are at the fourth stage (the age of delayed degenerative diseases) in which advances in medical technology and health care programs have further delayed the age at death (Myers and Manton 1987; Olshansky and Ault 1986). Mortality variation declined when these degenerative diseases affected all population when they underwent the third stage of epidemiologic transition, but then increased afterwards when medical technology and health care programs started disproportionately benefiting higher SES groups (Glied and Lleras-Muney 2008; Lynch 2003). As a result, in contrast to the reduced mortality dispersion based on demographic research, time period influences may lead to the expectation of a widening mortality variation in the fourth stage of epidemiologic transition. Re-emerging infectious diseases (Olshansky et al. 1997) may further contribute to the enlarged mortality variation in younger ages.

Cohort Pattern in Mortality Variations

Temporal trends of mortality variation may be dominated by period effects when the major causes of deaths are wars or acute infectious diseases, e.g., tuberculosis, influenza, and pneumonia, as these diseases affected all age groups. But when the causes of deaths shifted from acute to chronic diseases in the 20^thcentury, cohort patterns of mortality variation may have emerged similarly to those found for mortality rates (Yang 2008). Similar to the two possible explanations of the period pattern cited above, there may exist different implications for mortality variation across cohorts. As overall mortality rates decrease and life expectancies increase, we thus may expect decreasing mortality dispersion for cohorts born in the 20^th century (Myers and Manton 1984a). This empirical prediction is supported by “technophysio evolution” theory (Fogel and Costa 1997) and “cohort morbidity phenotype” theory (Finch and Crimmis 2004). Both theories propose that recent cohorts either have better initial endowment of health capital and experience slower rates of depreciation of health capital over age or face lessened risk factors in early life, which would have produced cohorts composed with more robust individuals and thereby reduce the mortality variation. But research on increasing health disparities across cohorts (Lynn 2003) implies possible increasing mortality variation across cohorts. Another unique mechanism contributing to cohort patterns is mortality selection. The theory of heterogeneity (Vaupel et al. 1979) proposes that frail members of a cohort who are more vulnerable to mortality risk tend to die earlier. Due to medical advances, individuals with high frailty in the later cohorts are more likely to survive into adulthood than those in earlier cohorts which then increases the heterogeneity and subsequent mortality variation in the adulthood in later cohorts, especially in older ages (Engelman et al. 2010). In brief, the mortality selection mechanism may further contribute to increasing mortality variation across cohorts.

Hypotheses

In sum, prior demographic research leads to relatively clear predictions about how the age, time period, and cohort dimensions should relate to temporal trends in mortality rates. By comparison, there is less consensus on expectations for how these dimensions relate to trends in mortality dispersions. These differences are embodied in the following hypotheses:

Hypothesis 1 – Mortality Rates

We expect that temporal changes in mortality rates will show strong increases with age, and decreases among more recent cohorts. Period dependence will be weaker, but mortality increases due to wars or infectious disease epidemics will be evident.

Hypothesis 2 – Mortality Variations across Age

Cumulative advantage theory leads to the expectation that mortality variations will be positively related to age from young adulthood to the middle and older ages. A mortality selection mechanism, however, may reduce mortality variation over the life course.

Hypothesis 3 – Mortality Variations across Periods

Period effects may be present during periods of war or infectious epidemics. Decreasing mortality rates predict decreasing mortality variation over time, while epidemiologic transition theory would suggest a decreasing and then increasing mortality variation trend.

Hypothesis 4 – Mortality Variations across Cohorts

Cohort pattern should be evident across the twentieth century when the major causes of death shifted from acute diseases to chronic illnesses. Technophysio evolution theory and cohort morbidity phenotype theory predict decreasing mortality variation across cohorts, while the health disparities literature suggests an increasing mortality variation trend. A mortality selection mechanism may further contribute to increasing mortality variation across cohorts as weaker individuals are more likely to survive in later cohorts which increases the heterogeneity of population composition.

Data and Methods

Data

This study examines the variations in single-year-of-age-sex-specific mortality rates and mortality variations across time periods, cohorts, and age in the advanced societies. Data are from Human Mortality Database (http://www.mortality.org/) which includes reliable and complete life table and time series of data on mortality (population occurrence/exposure) rates. Analysis is based on 15 developed countries: Australia, Belgium, Denmark, England and Wales, Finland, France, Iceland, Italy, Japan, Netherlands, New Zealand, Norway, Sweden, Switzerland, and U.S.A. Mortality data date back to 1750 for Sweden, and to mid- or late-19^th century for most other countries. The data analyzed are annual, single-year-of-age-and-period-specific mortality rates across the age range from age 18 to 109 with a final open-ended age 110 and over category. In total, there are 204,414 mortality rates for each of the male and female categories. Table 1 presents a summary of the numbers of mortality rates, time periods, and birth cohorts for each country in the present analysis.

Table 1. Summary of Data: Numbers of Mortality Rates, Time Periods, and Birth Cohorts for Each Country.

Country	Number of age-specific mortality rates	Period	Cohort
Australia	8091	1921-2007	1811-1989
Belgium	15717	1841-2009	1731-1991
Denmark	16275	1835-2009	1725-1991
England and Wales	15717	1841-2009	1731-1991
Finland	12276	1878-2009	1768-1991
France	18042	1816-2009	1706-1991
Iceland	15903	1838-2008	1728-1990
Italy	12741	1872-2008	1762-1990
Japan	5859	1947-2009	1837-1991
Netherlands	14880	1850-2009	1740-1991
New Zealand	10044	1901-2008	1791-1990
Norway	15252	1846-2009	1736-1991
Sweden	24180	1751-2010	1641-1992
Switzerland	12462	1876-2009	1766-1991
USA	6975	1933-2007	1823-1989

Statistical Model

Prior analyses of trends in mortality levels and dispersions therein (Myers and Manton 1984b; Engleman et al. 2010) first converted observed age-specific mortality rates into life tables. From the life table survivorship functions, life expectancies at various ages (e.g., ages 0, 10, 50, 75) and single-year-age-at-death frequency distributions then were calculated, and, from these, standard deviations as measures of dispersions of the death frequency distributions around the life expectancies at the corresponding ages. Trends in the standard deviations then were studied by period or cohort.

The present study takes a different approach. First, we focus on the adult ages from age 18 to the end of life. Within this age range, we partition age into intervals – the analyses reported here are for 10-year age intervals, but similar results are obtained for 5-year, 15-year, or 20-year intervals. Within these age intervals and separately for each country and sex, we perform an integrated analysis of temporal trends in both single-year-of-age mortality rates and variations in those rates around expected values by applying recently developed Hierarchical Age-Period-Cohort-Variance Function Regression (HAPC-VFR) Models (Zheng et al. 2011a). This integrated regression analysis filters variability in both the single-age mortality rates and age-specific variations of the rates around expected values within the age intervals into their age, period and cohort components. An integrated analysis of temporal trends in both mortality rates and variances has not been conducted previously due to the lack of a statistical model that can jointly assess the age and temporal trends of both mortality rates and mortality variation.

The HAPC-VFR model simultaneously assesses the effects of age, period, and cohort in the mean and variance of an outcome by embedding a Variance Function Regression model (Western and Bloome 2009) within the framework of a Hierarchical Age-Period-Cohort model (Yang and Land 2006). More specifically, the HAPC-VFR model is a mixed (fixed and random) effects model that estimates the conditional mean and conditional variance equations of the variance function regression model by treating the effects of age as fixed and those of cohorts and periods as random.¹

In brief, for each of the 15 countries in the present analysis, this HAPC-VFR model is estimated by a two-step algorithm:

Step 1: Estimate the β regression coefficient vectors for between-group variation across age, period and cohort

We use the restricted maximum likelihood (REML) estimator (Raudenbush and Bryk 2002) to estimate the first step. The algebra for this algorithm is:

Level-1 or “Within-Cell” Model²

$$\begin{array}{cc}M{R}_{ijk}={\beta }_{0jk}+{\beta }_1\mathit{\text{age}}{18}_{ijk}+{\beta }_2\mathit{\text{age}}{30}_{ijk}+{\beta }_3\mathit{\text{age}}{40}_{ijk}+{\beta }_4\mathit{\text{age}}{50}_{ijk}+{\beta }_5\mathit{\text{age}}{70}_{ijk}+{\beta }_6\mathit{\text{age}}{80}_{ijk}+{\beta }_7\mathit{\text{age}}{90}_{ijk}+{\beta }_8\mathit{\text{age}}{100}_{ijk}+e_{ijk},\hfill & e_{ijk}~N(0,{\sigma }^2)\end{array}$$ (1)

Level-2 or “Between-Cell” Model

$${\beta }_{0jk}={\gamma }_0+u_{0j}+v_{0k},u_{0j}~N(0,{\tau }_u),v_{0k}~N(0,{\tau }_v)$$ (2)

for i = 1, 2, …, n_jk age-specific mortality rates within cohort j and period k;

j = 1, …, J birth cohorts;

k = 1, …, K time periods;

where within each birth cohort j and time period k, the single-year-of-age-specific mortality rate, MR_ijk, is modeled as a function of a set of 10-year age group dummies age18_ijk, age30_ijk, …, age100_ijk, the reference age group is ages 60-69 in birth cohort j and time period k, and e_ijk is the random cell residual.

The intercept β_0jk varies by birth cohort and time period. γ₀ is the expected mean of mortality rates of the reference age group (age 60-69) averaged over all periods and cohorts; u_0j is the residual random effect of cohort j, that is, the contribution of cohort j averaged over all periods, on β_0jk, assumed normally distributed (Gaussian) with mean 0 and variance τ_u; and v_0k is the residual random effect of period k, that is, the contribution of period k averaged over all cohorts, assumed normally distributed with mean 0 and variance τ_v. In addition, β_0j = γ₀ + u_0j is the cohort MR score averaged over all periods for the reference age group; and β_0k = γ₀ + v_0k is the period MR score averaged over all cohorts for the reference age group.

This step produces 15 sets of estimates of fixed-effects coefficients (for the age group dummies), random-effects (for cohorts and periods), and a random variance components matrix which evaluates the contributions of these age group dummies and period and cohort contextual variables to the explanation of variance in the conditional expected value or conditional mean of the outcome variable. In other words, for each of the countries, this first step regression estimates variability in the conditional mean of mortality rates across age, period, and cohort.

According to Hypothesis 1, we would expect that the coefficients (β₁ to β₈) for age groups to increase with age, β_0j significantly declines among more recent cohorts, and β_0k is significant and positive in periods when wars or infectious disease epidemics happened.

Step 2: Estimate the λ regression coefficient vectors for within-group variation across age, period, and cohort

For each country, we next calculate the residuals, ${\widehat{e}}_{ijk}=M{R}_{ijk}-{\widehat{MR}}_{ijk}=M{R}_{ijk}-({\widehat{\beta }}_1\mathit{\text{age}}{18}_{ijk}+\cdots +{\widehat{\beta }}_8\mathit{\text{age}}{100}_{ijk})$, from the Step 1 regression, for each age i, and calculate the squared residuals, ${\widehat{e}}_{ijk}^2$ or denoted as ${\sigma }_{ijk}^2$. We then apply the residual pseudo-likelihood (RSPL) estimator to estimate the second step. For normally distributed errors, the squared residuals will have a gamma distribution, and the second step then is estimated in generalized linear mixed model form—as a gamma regression of ${\widehat{e}}_{ijk}^2$ on the age18_ijk, …, age100_ijk using a log link function (Western and Bloome 2009:300; see also Nelder and Lee 1991).

The algebra for this algorithm can be stated as follows:

Level-1 or “Within-Cell” Model

$$log({\sigma }_{ijk}^2)={\lambda }_{0jk}+{\lambda }_1\mathit{\text{age}}{18}_{ijk}+{\lambda }_2\mathit{\text{age}}{30}_{ijk}+{\lambda }_3\mathit{\text{age}}{40}_{ijk}+{\lambda }_4\mathit{\text{age}}{50}_{ijk}+{\lambda }_5\mathit{\text{age}}{70}_{ijk}+{\lambda }_6\mathit{\text{age}}{80}_{ijk}+{\lambda }_7\mathit{\text{age}}{90}_{ijk}+{\lambda }_8\mathit{\text{age}}{100}_{ijk},$$ (3)

Level-2 or “Between-Cell” Model

$${\lambda }_{0jk}={\pi }_0+{\omega }_{0j}+{\phi }_{0k},{\omega }_{0j}~N(0,{\psi }_{\omega }),{\phi }_{0k}~N(0,{\psi }_{\phi })$$ (4)

where λ_0jk is the intercept, that is, the mean log(σ²) of age-specific mortality rates of the reference age group (60-69) which belong to birth cohort j and time period k; π₀ is the expected mean of log(σ²) at the reference age group (age 60-69) averaged over all periods and cohorts; ω_0j and φ_0k are the residual random effects of cohort j and period k, respectively, assumed normally distributed with mean 0 and variance ψ_ω and ψ_φ. In addition, λ_0j = π₀ + ω_0j is the cohort log(σ²) score averaged over all periods for the reference age group; and λ_0k = π₀ + ω_0k is the period log(σ²) score averaged over all cohorts for the reference age group.

This step produces 15 sets of estimated fixed-effects coefficients (for the age group dummies), random-effects (for cohorts and periods), and a random variance components matrix which evaluates the contributions of these variables to the explanation of variance in the logarithm of the residual variances $log({\sigma }_i^2)$. That is, for each of the 15 countries, this step estimates variability in the conditional variances of the mortality rates (or mortality variation) across age, period, and cohort.

According to Hypothesis 2, if cumulative advantage theory dominates mortality variations across age, the coefficients for age groups (λ₁ to λ₈) increase with age; if mortality selection is the main mechanism, the coefficients will decrease with age. According to Hypothesis 3, λ_0k is significant and positive during periods of war or infectious epidemics. Decreasing mortality rates over time predict decreasing λ_0k over time, while epidemiologic transition theory predicts a decreasing and then increasing λ_0k over time. According to Hypothesis 4, λ_0j becomes significant since the beginning of the 20^th century. Technophysio evolution theory and cohort morbidity phenotype theory predict decreasing λ_0j across cohorts; while the mortality selection mechanism would produce increasing λ_0j across cohorts.

Even though each of these two steps produces a set of restricted maximum likelihood or residual pseudo-likelihood estimates for the hierarchical age-period-cohort part of the model, the algorithm must be iterated in order to obtain maximum likelihood (ML) estimators for the variance function regression model (Aitkin 1987).³ As Western and Bloome (2009:301) indicate, the fitted values $({\widehat{\sigma }}_{ijk}^2)$ from an application of the twosteps should be saved and used in a weighted regression of MR_ijk on age18_ijk, age30_ijk, …, age100_ijk with weights $(1/{\widehat{\sigma }}_{ijk}^2)$. Estimates of the residuals from Step 1 then are updated, Step 2 is computed, and so forth until convergence. Western and Bloome (2009:301) note that the ML estimator may perform poorly in small samples, in which case a REML or Bayes estimator can be used. In the empirical application in this study, however, the sample sizes are large, in which case the adjustments in the REML made for the loss of degrees of freedom resulting from estimation of the regression parameters will be very small, if not trivial. We used the SAS PROC MIXED and PROC GLIMMIX procedures to estimate the first- and second-step regressions, respectively.

Relation to Prior Measures of Mortality Dispersion

How do the measures of dispersions in mortality rates – estimated as age-specific residual variation among the single-age rates around expected values within age intervals in this statistical model – relate to those used in prior studies? As a point of comparison, one of the most recent research contributions, Engelman et al. (2010), similarly used data from the Human Mortality Database. They first separately calculated period- and cohort-specific life tables for each of 23 national populations from which the life table age-specific functions for the expected number of deaths at age x, d(x), were obtained for each population. This calculation of the age-dependence of the distribution of deaths is similar to the statistical estimation of the age-interval effect coefficients in Equation (1) of our Step 1 above, except that the death distributions of the Engleman et al. analyses are standardized to the stationary population distribution of the life table.

For each age-specific distribution of deaths, any given initial age a, and any given year t, Engelman et al. (2010) then calculated the variance of the distribution of remaining deaths by averaging the squared distance of all ages at death from their mean value, the expected years of life remaining at age x, and then obtained estimates of the standard deviations as the square root of the variance. This calculation of the age-dependence of the standard deviations in the death distributions is similar, for the specific ages for which the calculations were made by Engleman et al. (2010) (ages 0, 10, 50, and 75), to the estimation of Equation (3) of our Step 2 above.

There are, however, three differences between the estimates of variability of Engleman et al. (2010) and those reported here. First, we specified the regression equations directly with the observed country-single-year-of-age-period-specific mortality rates as the outcome variable rather than the expected age-specific numbers of deaths from period-specific life tables calculated from the rates. Second, we estimated dispersions in mortality rates as age-specific residual heterogeneity among the single-age rates around expected values within age intervals rather than as standard deviations of life table ages of death from their expected values from selected ages to the end of life. Third, the analyses of Engleman et al. (2010) of trends in the calculated standard deviations of the life table age-at-death distributions proceed along either age-period or age-cohort lines, whereas our application of the HAPC-VFR statistical model facilitates the simultaneous filtering of trends in the mortality variations into their age, period, and cohort components.

Findings

Variability in Mortality Rates across Age, Period, and Cohort

For the 15 countries in the present analysis, the three panels of Figure 1 display the predicted mortality rates based on the estimated conditional expectation functions of the HAPC model across the three temporal dimensions – age, period, and cohort.⁴ Each line represents one country; the same for all subsequent figures.

Figure 1. Variability in Predicted Mortality Rates across Age, Period and Cohort for Males and Females in 15 Populations.

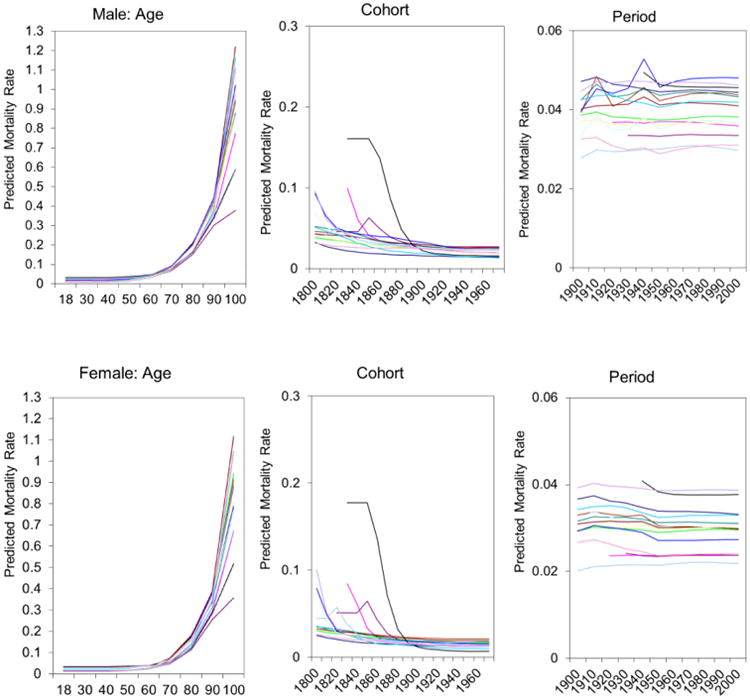
Note: Each line represents one country. The lowest lines in old age in the Age panel represent the U.S. The lines with the steepest decline in the Cohort panel represent Japan.

For both males and females, we find that the conditional means of mortality rates accelerate up to age 100 in all the countries, except for the U.S. (the lowest lines in the figures), where mortality rates increase at a lower rate after age 90. Mortality rates are very similar in young and middle adulthoods across countries, but differences widen in older adulthood, and U.S. men and women have substantial lower mortality rates than other countries after age 90.

There also are strong similarities of the male and female temporal patterns in the cohort panels of Figure 1. Generally, the mortality rates show decreases across cohorts for all the countries since the early 19^th century. Japan, described as an accelerated pattern of the classical model of epidemiological transition by Omran (1971), experienced substantial and rapid mortality decline beginning with the 1860 birth cohort as demonstrated by the curve with the steepest decline. The estimated period effects, by comparison, show no substantial trends in the second half of the twentieth century, after controlling for confounded age and cohort effects.⁵ Two spikes occurred in 1910-1919 and 1940-1949 due to World War I, the 1918 influenza epidemic, and World War II; these spikes are more pronounced for males than females.

Overall, these findings on the age, period, and cohort dependence of changes in mortality rates across the twentieth century are consistent with our Hypothesis 1. Our primary focus, however, is on temporal changes in mortality variations, to which we now turn.

Variability in Age Interval Residual Mortality Variations across Age, Period, and Cohort

Figure 2 shows that the estimated age interval residual mortality variations increase over the life course for all the countries, but slow down at age 80 and increase again after age 90 for some countries, e.g., Japan, England, and the U.S. National differences in age interval residual mortality variations are small during adulthood from age 40 to 80, but are larger at both the lower and upper ends of the adult age range. These findings are generally similar for males and females.

Figure 2. Variability in Predicted Mortality Variations across Age for Males and Females in 15 National Populations.

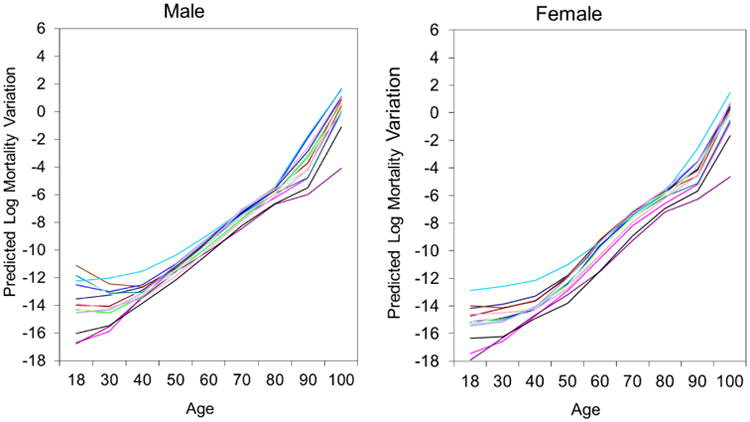
Note: Each line represents one country.

Figure 3 portrays the variability in the estimated age interval residual mortality variations across cohorts. For cohorts born before the 20^th century, the residual mortality variations are generally flat, slightly decrease, or have random variation, but there are significant declines across cohorts born after the early 20^th century. We caution, however, that the estimated rapid declines in residual mortality variations in the most recent cohorts (e.g., born after 1960) may be less statistically reliable, as these cohorts are relatively young and most of them have not experienced large numbers of death events yet. These findings are generally similar for males and females, while national differences in mortality variations across cohorts are relatively larger for females than for males.

Figure 3. Variability in Predicted Mortality Variations across Cohorts for Males and Females in 15 National Populations.

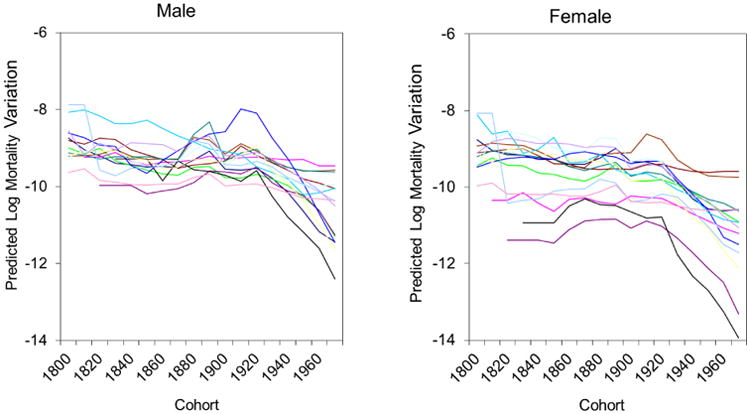
Note: Each line represents one country.

Figure 4 portrays the change in estimated residual mortality variations across time periods.⁶ Generally, these estimated period effects show downward trends from 1900 to 1980. These downward trends are interrupted by two upward spikes, more pronounced for males than females, during the 1910-1919 and 1940-1949 periods, indicative of the mortality impacts of World War I, the 1918 influenza epidemic, and World War II. In other words, in addition to increasing the expected values of mortality rates (Figure 1), these period-specific historical events also increased their expected variances. Also of note in Figure 4 is that, net of the age and cohort effects, the long-term downward trends in period effects show reversals since 1980 in all 15 countries.

Figure 4. Variability in Predicted Mortality Variations across Time Periods for Males and Females in 15 National Populations.

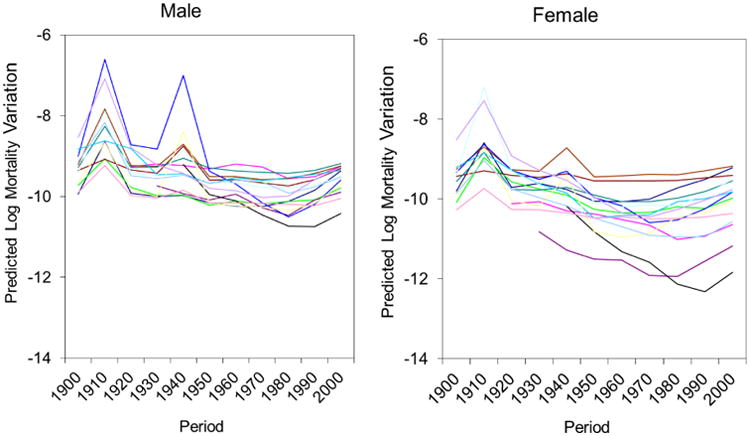
Note: Each line represents one country.

Discussion

Based on the research literature reviewed earlier, we examined several possible explanations for the increasing residual mortality variations in the recent decades since 1980 in all 15 countries, including aging populations, the intrinsic relationship between mortality rates and mortality dispersion, and epidemiologic transition.

First, aging national populations may contribute to this phenomenon. The elderly have larger within-age-interval residual mortality variations than younger people; therefore increases in their proportionate shares in population structures will increase the residual mortality variations in the whole society. We created a period-level variable, the proportion of population age 65 and over, and entered it as an explanatory variable in the integrated HAPC-VFR model. As Table 2 shows, this variable has a statistically significant negative regression coefficient in the estimated residual mortality variation equations for both sexes and each of the 15 countries. In other words, for each country a time period with a larger proportion of population age 65 and over is associated with a smaller all-ages expected mortality variation, thus aging national populations do not contribute to this phenomenon. This is consistent with the findings of Myers and Manton (1984a) that all-life-span mortality dispersion is negatively correlated with the level of life expectancy, as the proportion of population age 65 and over is an indirect indicator of life expectancy.

Table 2. Estimated Regression Coefficients of the Proportion of Population Age 65 and Over on Mortality Variation by Country and Gender.

Country	Female	Male
Australia	-4.53 ***	-7.12 ***
Belgium	-13.01 ***	-12.05 ***
Denmark	-12.17 ***	-15.96 ***
England	-12.17 ***	-12.22 ***
Finland	-11.94 ***	-17.24 ***
France	-10.12 ***	-8.37 ***
Iceland	-4.75 ***	-31.53 ***
Italy	-16.79 ***	-16.50 ***
Japan	-8.12 ***	-5.02 ***
Netherlands	-3.91 ***	-1.94 **
New Zealand	-6.22 ***	-20.29 ***
Norway	-14.51 ***	-13.87 ***
Sweden	-10.16 ***	-18.75 ***
Switzerland	-24.45 ***	-36.09 ***
USA	-8.20 **	-8.69 *

^*indicates p<.05;

^**indicates p<.01;

^***indicates p<.001.

Second, the recent increases in period effects on residual mortality variations (Figure 4) may result from either an increasing mortality rate or a declining life expectancy. Some studies suggest a positive relationship between mortality and mortality variation or a negative relationship between life expectancy and mortality variation; therefore the recent increase in residual mortality variation may result from increasing mortality rates or decreasing life expectancy. This explanation, however, is unlikely to be true, as mortality rates are relatively flat in recent decades, net of age and cohort effects (see the Period panels in Figure 1).

Third, a disproportionate delay in deaths from degenerative diseases may contribute to the increasing residual mortality variation in recent decades. From the beginning to the middle of the twentieth century, infectious and parasite diseases receded and degenerative diseases (e.g., cancer, heart diseases) became the leading causes of death for all, which narrowed the mortality variation. But, since 1960, public health measures and medical advances have especially benefited higher socioeconomic status groups, which may have led to the increasing mortality variation in the more recent decades. If this is true, we should observe an even larger increase in residual mortality variation among the elderly in recent decades as degenerative diseases tend to kill people at old ages. In order to test this hypothesis, we focus the analysis on the elderly (ages 65 and over). Figure 5 portrays trends in the estimated period effects for each of the 15 countries in residual mortality variation for males and females within this age group. Surprisingly, the estimated residual mortality variation among the elderly decreased in recent decades in 14 developed countries except for the U.S. which experienced a large increase in residual mortality variation, especially since 1970 (the bolded line is the U.S.). Therefore, for most countries, a disproportionate delay in deaths from degenerative diseases is not the cause of the increasing residual mortality variation in recent decades.

Figure 5. Variability in Predicted Mortality Variations across Time Periods for Males and Females aged 65 and Older in 15 National Populations.

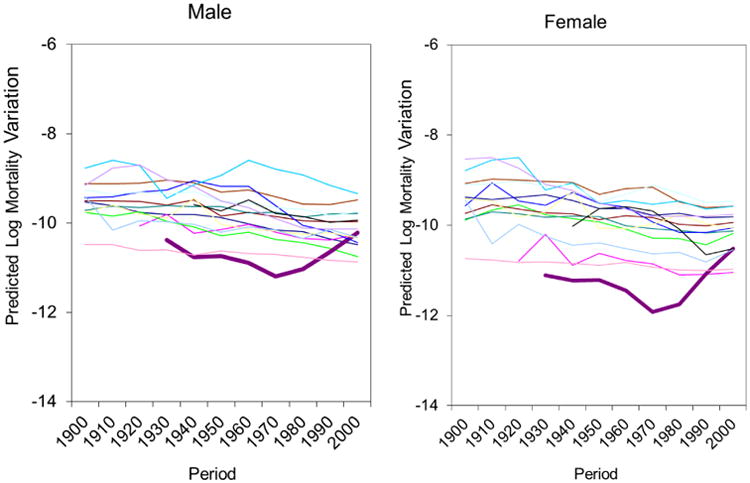
Note: Each line represents one country. The bolded lines represent the U.S.

Fourth, Olshansky et al. (1997) documented the re-emergence of infectious diseases (e.g., the Human Immunodeficiency Virus/Acquired Immunodeficiency Syndrome (HIV/AIDS) infection), which have disproportionately affected and caused deaths among people at different socioeconomic statuses (Rubin et al. 2009). These infectious diseases have been concentrated among younger people; therefore, we examine whether residual mortality variation among young- and middle-aged adults (ages 18 to 64) has increased in recent decades. Figure 6 shows that the residual mortality variation among young- and middle-aged adults substantially increased since 1980 in all 15 countries. It is evident from this figure that the period trend in residual mortality variation in recent time periods is driven by the trend for young- and middle-aged adults rather than for older adults, which is consistent with the differential age impacts of HIV/AIDS (Rubin et al. 2009).

Figure 6. Variability in Predicted Mortality Variations across Time Periods for Males and Females aged 18-64 in 15 National Populations.

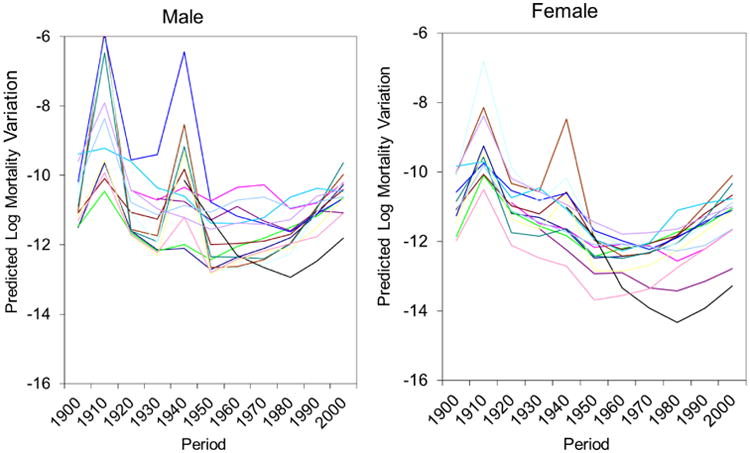
Note: Each line represents one country.

Conclusion

We investigated historical changes in mortality rates and residual mortality variations within 10-year age intervals across the adult ages over the past two centuries in 15 developed countries using an integrated HAPC-VFR Model. This model embeds a variance function regression model in the framework of a hierarchical age-period-cohort model. Its application to mortality involves two steps. In the first step, we estimated changes in mortality rates across the age, period, and cohort dimensions. In the second step, we estimated changes in residual mortality variations within age intervals across these temporal domains. Previous studies reported distinct age, period, and cohort components of trends in mortality rates (Osmond 1985; Yang 2008). The same distinctions may also apply to the trends in mortality variation.

Based on data from the Human Mortality Database, and consistent with prior demographic research, we found that, net of period and cohort effects, mortality rates accelerate across the adult ages among all countries. The one exception to an acceleration of the mortality rates to the highest age group in our analysis (100 and over years) is the U.S., where mortality rates increase at a slower rate after age 90 (Figure 1). With respect to this finding for the U.S., note that errors in age reporting may be a factor, as Gavrilov and Gavrilova (2011), using the more accurate age records of the Social Security Administration Death Master File, found no deceleration in the exponential increase in cohort mortality rates in the U.S. until after age 100.

We also found that men and women have substantially lower mortality rates in the U.S. than in other countries after age 90 (Figure 1). Similar findings were reported in Manton and Vaupel (1995) and Ho and Preston (2010). For example, Manton and Vaupel (1995) found the United States had higher life expectancy at age 80 and more favorable survival from age 80 to 100 than Sweden, France, England and Japan. They attributed this relative advantage to intensive and effective medical care among the U.S. elderly and persistent cohort effects of earlier conditions (e.g., relatively higher education among earlier cohorts in the U.S. than other countries, the healthy immigrant effect, higher mortality in young ages leaving less frail survivors in old ages in the U.S.) Ho and Preston (2010) also found a favorable mortality ranking at very old ages in the U.S. relative to other developed countries. They dismissed health care access (e.g., Medicare) and health behavior (e.g., smoking) as the major explanations for the relative advantage (Preston and Ho 2010), but attributed this to a more effective U.S. health care system for older patients although they could not dismiss mortality selection as a possible mechanism.

In addition, net of age and period effects, our analysis showed that mortality rates substantially declined across cohorts for all countries, while, net of age and cohort effects, they are relatively flat across time periods. These findings are consistent with Yang's (2008) conclusion, based on an age-period-cohort analysis, that mortality decline is more of a cohort than a period driven phenomenon. These findings also support the theory of technophysio evolution, which implies health capital and physiological capacities increased across successive cohorts (Fogel and Costa 1997). Later cohorts have been exposed to fewer risk factors across their life course, less inflammation in early life (Finch and Crimmins 2004), better nutrition, better health care and public and personal health practices (Fogel 2004), and better education (Lauderdale 2001). These advantages accumulate along life course and so increase life expectancy and reduce mortality risk across successive cohorts.

In our analysis of trends in residual mortality variations, we found that, net of period and cohort effects, these variations increase over the life course for all countries, but slow down at age 80 and then increase again after age 90 for some countries, e.g., Japan, England, and the U.S. These findings are consistent with the “cumulative disadvantage” hypothesis in the health disparities literature (House et al. 2005). This also indirectly suggests a fixed frailty across the life span is relatively unlikely as a fixed frailty and selective mortality will reduce the mortality variation in old age (Manton et al. 1981). This also suggests that, although mortality selection may operate throughout the life course, this mechanism is not strong enough to reverse the overall increasing mortality variation over ages.

Net of age and period effects, we found that the estimated residual mortality variations were relatively flat for cohorts born before the 20^th century but significantly declined across cohorts born after the early 20^th century. These findings suggest that when major causes of death were shifted from infectious diseases to chronic disease in the late 19^th and early 20^th century this cohort pattern emerged. These findings are generally consistent with Myers and Manton (1984a)'s finding that mortality dispersion with all deaths included is negatively correlated with the level of life expectancy. While the Myers and Manton study pertains to a period pattern, our finding distinguishes the period and cohort components of the change. The substantial decline we found for most recent cohorts may also result from the relative young age of these cohorts. These findings support the prediction of increasing prevalence of robust individuals in younger cohorts from technophysio evolution theory and cohort morbidity phenotype theory. All in all, these findings suggest that, although frail individuals are more likely to survive into adulthood in later cohorts due to socioeconomic development and medical advances, which possibly increases the heterogeneity among later cohorts, this selective survival mechanism is not strong enough to reverse the overall reducing mortality variation trend across cohorts due to the continually increasing health capital and decreasing mortality rate at the population level (Zheng 2014).

With regard to period patterns of residual mortality variation, we found that, net of age and cohort effects, the variations continuously declined over much of the last two centuries but have substantially increased since 1980. Further analysis suggested the recent increases in the residual mortality variations are not due to increasing proportions of older adults in the population, which instead may explain the continual downward trend of mortality variation before 1980 as this indicator indirectly measures life expectancy. The reversal of the period trend in residual mortality variation after 1980 is also not due to the period trend in mortality rate as it is very flat across time periods after controlling for age and cohort effects as displayed in Figure 1. This also does not result from a disproportionate delay in deaths from degenerative and man-made diseases as mortality variation among population aged 65 and older continued declining after 1980 among these 15 countries except the U.S. We also found that residual mortality variation among young- and middle-aged adults (age 18 to 64) has increased in recent decades. In fact, the whole period trend in residual mortality variation is driven by the trend within young- and middle-aged adults. A re-emergence of infectious diseases such as HIV (Olshansky et al. 1997) and a widening mortality risk from these diseases across socioeconomic strata (Rubin et al. 2009) appears to be related to this trend, as these diseases tend to kill young- and middle-aged adults, but additional explanations should be explored in future research.

This study has several limitations. First, although the Human Mortality Database is considered to be of high quality, and has been widely used for cross-national and historical research on old-age mortality (Ho and Preston 2010; Wilmoth and Horiuchi 1999; Yashin et al. 2001), we cannot totally dismiss the possibility that our results may be biased by age misreporting in the death rates. Second, we only focus on more developed nations; therefore it is still unknown whether the patterns found in this paper could be generalized to less developed countries, especially given that they experienced demographic and epidemiologic transition at different timings and through different mechanisms.

In conclusion, using integrated HAPC-VFR models, this study yields some important findings. We find that residual mortality variation generally increases over the life course into the older ages, which supports the “cumulative advantage” theory and suggests that, although mortality selection may operate throughout life course, it does not reverse the overall increasing residual mortality variation over ages. We also find that residual mortality variation started declining in cohorts born after the early 20^th century when the major causes of death shifted from infectious diseases to chronic illnesses. The declining residual mortality variation across cohorts was a result of continual mortality decline, which suggests although increasing survival may increase heterogeneity among younger cohorts, this force does not override the declining mortality rate to increase mortality variation. Net of age and cohorts effect, residual mortality variations continuously declined over much of the last two centuries but have substantially increased since 1980. The recent increases in residual mortality variations are not due to increasing proportions of older adults in the population, trends in mortality rates, or disproportionate delays in the deaths from degenerative and man-made diseases, but rather due to increasing variations in young and middle-age adults. This is a somewhat surprising finding.

Many developed countries currently are at the fourth stage (the age of delayed degenerative diseases) of epidemiologic transition in which advances in medical technology and health care programs have further decreased mortality selection in younger ages, delayed the age at death, and improved survival at increasingly older ages (Wilmoth et al. 2000), which is supposed to increase heterogeneity within older populations (Engelman et al. 2010). But, in terms of mortality, our study does not find increasing residual variation at the older ages for more recent time periods or birth cohorts. One, however, should not infer that variations in other outcomes are not increased. For example, the variation in morbidity, disability, and functional impairment may increase due to the increasingly complex composition of older population, which is related to the morbidity compression or expansion debate (Fries 1980; Gruenberg 1977). Besides that, it is also important to investigate what factors may contribute to the increasing residual mortality variation in young and middle-age adults. The re-emergence of infectious illness (e.g., HIV) and sedentary life style related risk factors (e.g., obesity) may certainly play a role in the increasing heterogeneity among young and middle-age adults, but this new phenomenon merits further extensive attention and investigation. The public policy implications of the findings from this study are that, in order to reduce mortality variation and health disparities in the future, efforts should focus on relatively earlier stages of the life course rather than on the older ages.