Accelerated Path-following Iterative Shrinkage Thresholding Algorithm with Application to Semiparametric Graph Estimation

Abstract

We propose an accelerated path-following iterative shrinkage thresholding algorithm (APISTA) for solving high dimensional sparse nonconvex learning problems. The main difference between APISTA and the path-following iterative shrinkage thresholding algorithm (PISTA) is that APISTA exploits an additional coordinate descent subroutine to boost the computational performance. Such a modification, though simple, has profound impact: APISTA not only enjoys the same theoretical guarantee as that of PISTA, i.e., APISTA attains a linear rate of convergence to a unique sparse local optimum with good statistical properties, but also significantly outperforms PISTA in empirical benchmarks. As an application, we apply APISTA to solve a family of nonconvex optimization problems motivated by estimating sparse semiparametric graphical models. APISTA allows us to obtain new statistical recovery results which do not exist in the existing literature. Thorough numerical results are provided to back up our theory.

1 Introduction

High dimensional data challenge both statistics and computation. In the statistics community, researchers have proposed a large family of regularized M-estimators, including Lasso, Group Lasso, Fused Lasso, Graphical Lasso, Sparse Inverse Column Operator, Sparse Multivariate Regression, Sparse Linear Discriminant Analysis (Tibshirani, 1996; Zou and Hastie, 2005; Yuan and Lin, 2005, 2007; Banerjee et al., 2008; Tibshirani et al., 2005; Jacob et al., 2009; Fan et al., 2012; Liu and Luo, 2015; Han et al., 2012; Liu et al., 2015). Theoretical analysis of these methods usually rely on the sparsity of the parameter space and requires the resulting optimization problems to be strongly convex over a restricted parameter space. More details can be found in Meinshausen and Bühlmann (2006); Zhao and Yu (2006); Zou (2006); Rothman et al. (2008); Zhang and Huang (2008); Van de Geer (2008); Zhang (2009); Meinshausen and Yu (2009); Wainwright (2009); Fan et al. (2009); Zhang (2010a); Ravikumar et al. (2011); Liu et al. (2012a); Negahban et al. (2012); Han et al. (2012); Kim and Kwon (2012); Shen et al. (2012). In the optimization community, researchers have proposed a large variety of computational algorithms including the proximal gradient methods (Nesterov, 1988, 2005; NESTEROV, 2013; Beck and Teboulle, 2009b,a; Zhao and Liu, 2012; Liu et al., 2015) and coordinate descent methods (Fu, 1998; Friedman et al., 2007; Wu and Lange, 2008; Friedman et al., 2008; Meier et al., 2008; Liu et al., 2009; Friedman et al., 2010; Qin et al., 2010; Mazumder et al., 2011; Breheny and Huang, 2011; Shalev-Shwartz and Tewari, 2011; Zhao et al., 2014c).

Recently, Wang et al. (2014) propose the path-following iterative soft shrinkage thresholding algorithm (PISTA), which combines the proximal gradient algorithm with path-following optimization scheme. By exploiting the solution sparsity and restricted strong convexity, they show that PISTA attains a linear rate of convergence to a unique sparse local optimum with good statistical properties for solving a large class of sparse nonconvex learning problems. However, though the PISTA has superior theoretical properties, it is empirical performance is in general not as good as some heuristic competing methods such as the path-following coordinate descent algorithm (PCDA) (Tseng and Yun, 2009b,a; Lu and Xiao, 2013; Friedman et al., 2010; Mazumder et al., 2011; Zhao et al., 2012, 2014a). To address this concern, we propose a new computational algorithm named APISTA (Accelerated Path-following Iterative Shrinkage Thresholding Algorithm). More specifically, we exploit an additional coordinate descent subroutine to assist PISTA to efficiently decrease the objective value in each iteration. This makes APISTA significantly outperform PISTA in practice. Meanwhile, the coordinate descent subroutine preserves the solution sparsity and restricted strong convexity, therefore APISTA enjoys the same theoretical guarantee as those of PISTA, i.e., APISTA attains a linear rate of convergence to a unique sparse local optimum with good statistical properties. As an application, we apply APISTA to a family of nonconvex optimization problems motivated by estimating semiparametric graphical models (Liu et al., 2012b; Zhao and Liu, 2014). PISTA allows us to obtain new sparse recovery results on graph estimation consistency which has not been established before. Thorough numerical results are presented to back up our theory.

NOTATIONS

Let υ = (υ₁, …, υ_d)^T ∈ ℝ^d, we define ‖υ‖₁ = ∑_j |υ_j|, ${\Vert \mathit{\upsilon }\Vert }_2^2={\sum }_j{\upsilon }_j^2$, and ‖υ‖_∞ = max_j |υ_j|. We denote the number of nonzero entries in υ as ‖υ‖₀ = ∑_j 𝟙(υ_j ≠ 0). We define the soft-thresholding operator as ${𝒮}_{\lambda }(\mathit{\upsilon })={[\text{sign}({\upsilon }_j)·(|{\upsilon }_j|-\lambda )]}_{j=1}^d$ for any λ ≥ 0. Given a matrix A ∈ ℝ^d×d, we use A_*j = (A_1j, …, A_dj)^T to denote the j^th column of A, and A_k* = (A_k1, …, A_kd)^T to denote the k^th row of A. Let Λ_max(A) and Λ_min(A) denote the largest and smallest eigenvalues of A. Let ψ₁(A), …, ψ_d(A) be the singular values of A, we define the following matrix norms: ${\Vert \mathbf{A}\Vert }_{\mathrm{F}}^2={\sum }_j{\Vert {\mathbf{A}}_{*j}\Vert }_2^2$, ‖A‖_max = max_j ‖A_*j‖_∞, ‖A‖₁ = max_j ‖A_*j‖₁, ‖A‖₂ = max_j ψ_j(A), ‖A‖_∞ = max_k ‖A_k*‖₁. We denote υ_\j = (υ₁, …, υ_j−1, υ_j+1, …, υ_d)^T ∈ ℝ^d−1 as the subvector of υ with the j^th entry removed. We denote A_\i\j as the submatrix of A with the i^th row and the j^th column removed. We denote A_i\j to be the i^th row of A with its j^th entry removed. Let 𝒜 ⊆ {1, …, d}, we use υ_𝒜 to denote a subvector of υ by extracting all entries of υ with indices in 𝒜, and A_𝒜𝒜 to denote a submatrix of A by extracting all entries of A with both row and column indices in 𝒜.

2 Background and Problem Setup

Let ${\mathit{\theta }}^{*}={({\theta }_1^{*},\dots ,{\theta }_d^{*})}^T$ be a parameter vector to be estimated. We are interested in solving a class of regularized optimization problems in a generic form:

$$\underset{\mathit{\theta }\in {ℝ}^d}{\text{min}}\underset{{ℱ}_{\lambda }(\mathit{\theta })}{\underbrace{ℒ(\mathit{\theta })+{ℛ}_{\lambda }(\mathit{\theta })}},$$ (2.1)

where ℒ(θ) is a smooth loss function and ℛ_λ(θ) is a nonsmooth regularization function with a regularization parameter λ.

2.1 Sparsity-inducing Nonconvex Regularization Functions

For high dimensional problems, we exploit sparsity-inducing regularization functions, which are usually continuous and decomposable with respect to each coordinate, i.e., ${ℛ}_{\lambda }(\mathit{\theta })={\sum }_{j=1}^d{r}_{\lambda }({\theta }_j)$. For example, the widely used ℓ₁ norm regularization decomposes as $\lambda {\Vert \mathit{\theta }\Vert }_1={\sum }_{j=1}^d\lambda |{\theta }_j|$. One drawback of the ℓ₁ norm is that it incurs large estimation bias when $|{\theta }_j^{*}|$ is large. This motivates the usage of nonconvex regularizers. Examples include the SCAD (Fan and Li, 2001) regularization

$$r_{\lambda }({\theta }_j)=\lambda |{\theta }_j|·𝟙(|{\theta }_j|\le \lambda )-\frac{{\theta }_j^2-2\lambda \beta |{\theta }_j|+{\lambda }^2}{2(\beta -1)}·𝟙(\lambda <|{\theta }_j|\le \lambda \beta )+\frac{(\beta +1){\lambda }^2}{2}·𝟙(|{\theta }_j|>\lambda \beta )\text{ for }\beta >2,$$

and MCP (Zhang, 2010a) regularization

$$r_{\lambda }({\theta }_j)=\lambda (|{\theta }_j|-\frac{{\theta }_j^2}{2\lambda \beta })·𝟙(|{\theta }_j|<\lambda \beta )+\frac{{\lambda }^2\beta }{2}·𝟙(|{\theta }_j|\ge \lambda \beta )\text{ for }\beta >1.$$

Both SCAD and MCP can be written as the sum of an ℓ₁ norm and a concave function ℋ_λ(θ), i.e., ℛ_λ(θ) = λ‖θ‖₁ + ℋ_λ(θ). It is easy to see that ${\mathscr{H}}_{\lambda }(\mathit{\theta })={\sum }_{j=1}^d{h}_{\lambda }({\theta }_j)$ is also decomposable with respect to each coordinate. More specifically, the SCAD regularization has

$$h_{\lambda }({\theta }_j)=\frac{2\lambda |{\theta }_j|-{\theta }_j^2-{\lambda }^2}{2(\beta -1)}·𝟙(\lambda <|{\theta }_j|\le \lambda \beta )+\frac{(\beta +1){\lambda }^2-2\lambda |{\theta }_j|}{2}·𝟙(|{\theta }_j|>\lambda \beta ),$$

$$h_{\lambda }^{\prime }({\theta }_j)=\frac{\lambda \text{sign}({\theta }_j)-{\theta }_j}{\beta -1}·𝟙(\lambda <|{\theta }_j|\le \lambda \beta )-\lambda \text{sign}({\theta }_j)·𝟙(|{\theta }_j|>\lambda \beta ),$$

and the MCP regularization has

$$h_{\lambda }({\theta }_j)=-\frac{{\theta }_j^2}{2\beta }·𝟙(|{\theta }_j|<\lambda \beta )+\frac{{\lambda }^2\beta -2\lambda |{\theta }_j|}{2}·𝟙(|{\theta }_j|\ge \lambda \beta ),$$

$$h_{\lambda }^{\prime }({\theta }_j)=-\frac{{\theta }_j}{\beta }·𝟙(|{\theta }_j|\le \lambda \beta )-\lambda \text{sign}({\theta }_j)·𝟙(|{\theta }_j|>\lambda \beta ).$$

In general, the concave function h_λ(·) is smooth and symmetric about zero with h_λ(0) = 0 and $h_{\lambda }^{\prime }(0)=0$. Its gradient $h_{\lambda }^{\prime }(·)$ is monotone decreasing and Lipschitz continuous, i.e., for any ${\theta }_j^{\prime }>{\theta }_j$, there exists a constant α ≥ 0 such that

$$-\alpha ({\theta }_j-{\theta }_j^{\prime })\le h_{\lambda }^{\prime }({\theta }_j)-h_{\lambda }^{\prime }({\theta }_j^{\prime })\le 0.$$ (2.2)

Moreover, we require $h_{\lambda }^{\prime }({\theta }_j)=-\lambda \text{sign}({\theta }_j)$ if |θ_j| ≥ λβ, and $h_{\lambda }^{\prime }({\theta }_j)\in (-\lambda ,0)$ if |θ_j| ≤ λβ.

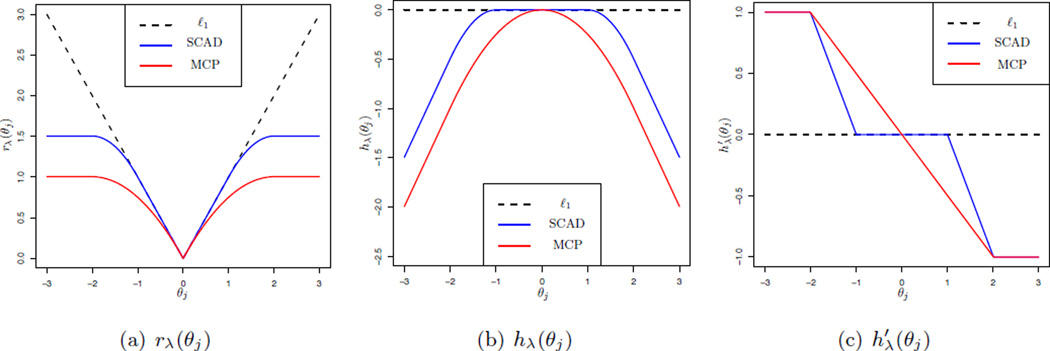
It is easy to verify that both SCAD and MCP satisfy the above properties. In particular, the SCAD regularization has α = 1/(β − 1), and the MCP regularization has α = 1/β. These nonconvex regularization functions have been shown to achieve better asymptotic behavior than the convex ℓ₁ regularization. More technical details can be found in Fan and Li (2001); Zhang (2010a, b); Zhang and Zhang (2012); Fan et al. (2014); Xue et al. (2012); Wang et al. (2014, 2013); Liu et al. (2014). We present several illustrative examples of the nonconvex regularizers in Figure 2.1.

Figure 2.1.

Two illustrative examples of the nonconvex regularization functions: SCAD and MCP. Here we choose λ = 1 and β = 2.01 for both SCAD and MCP.

2.2 Nonconvex Loss Function

A motivating application of the method proposed in this paper is sparse transelliptical graphical model estimation (Liu et al., 2012b). The transelliptical graphical model is a semiparametric graphical modeling tool for exploring the relationships between a large number of variables. We start with a brief review the transelliptical distribution defined below.

Definition 2.1 (Transelliptical Distribution)

Let ${\{f_j\}}_{j=1}^d$ be a set of strictly increasing univariate functions. Given a positive semidefinite matrix Σ^* ∈ ℝ^d×d with rank(Σ^*) = r ≤ d and ${\mathbf{\Sigma }}_{jj}^{*}=1$ for j = 1, …, d, we say that a d-dimensional random vector X = (X₁, …, X_d)^T follows a transelliptical distribution, denoted as X ~ TE_d(Σ^*, ξ, f₁, …, f_d), if X has a stochastic representation

$${(f_1(X_1),\dots ,f_d(X_d))}^T\stackrel{\mathrm{d}}{=}\xi \mathbf{A}\mathit{U},$$

where Σ^* = AA^T, U ∈ 𝕊^{r − 1} is uniformly distributed on the unit sphere in ℝ^r, and ξ ≥ 0 is a continuous random variable independent of U.

Note that Σ^* in Definition 2.1 is not necessarily the correlation matrix of X. To interpret Σ^*, Liu et al. (2012b) provide a latent Gaussian representation for the transelliptical distribution, which implies that the sparsity pattern of Θ^* = (Σ^*)⁻¹ encodes the graph structure of some underlying Gaussian distribution. Since Σ^* needs to be invertible, we have r = d. To estimate Θ^*, Liu et al. (2012b) suggest to directly plug in the following transformed Kendall’s tau estimator into existing gaussian graphical model estimation procedures.

Definition 2.2 (Transformed Kendall’s tau Estimator)

Let x₁, …, x_n ∈ ℝ^d be n independent observations of X = (X₁, …, X_d)^T, where x_i = (x_i1, …, x_id)^T. The transformed Kendall’s tau estimator Ŝ ∈ ℝ^d×d is defined as $\mathbf{Ŝ}=[{\mathbf{Ŝ}}_{kj}]=[\text{sin}(\frac{\pi }{2}{\hat{\tau }}_{kj}\left)\right]$, where τ̂_kj is the empirical Kendall’s tau statistic between X_k and X_j defined as

$${\hat{\tau }}_{kj}=\{\begin{array}{cc}\hfill \frac{2}{n(n-1)}\sum _{i<i\prime }\text{sign }((x_{ij}-x_{i\prime j})(x_{ik}-x_{i\prime k}))\hfill & \hfill \text{if}j\ne k,\hfill \\ \hfill 1\hfill & \hfill \text{otherwise}.\hfill \end{array}$$

We then adopt the sparse column inverse operator to estimate the j^th column of Θ^*. In particular, we solve the following regularized quadratic optimization problem (Liu and Luo, 2015),

$$\underset{{\mathbf{\Theta }}_{*j}\in {ℝ}^d}{\text{min}}\frac{1}{2}{\mathbf{\Theta }}_{*j}^T\mathbf{Ŝ}{\mathbf{\Theta }}_{*j}-{\mathbf{I}}_{*j}^T{\mathbf{\Theta }}_{*j}+{ℛ}_{\lambda }({\mathbf{\Theta }}_{*j})\text{ for}j=1,\dots ,d.$$ (2.3)

For notational simplicity, we omit the column index j in (2.3), and denote Θ_*j and I_*j by θ and e respectively. Throughout the rest of this paper, if not specified, we study the following optimization problem for the transelliptical graph estimation

$$\underset{\mathit{\theta }\in {ℝ}^d}{\text{min}}\frac{1}{2}{\mathit{\theta }}^T\mathbf{Ŝ}\mathit{\theta }-{\mathbf{e}}^T\mathit{\theta }+{ℛ}_{\lambda }(\mathit{\theta }).$$ (2.4)

The quadratic loss function used in (2.4) is twice differentiable with

$$\nabla ℒ(\mathit{\theta })=\mathbf{Ŝ}\mathit{\theta }-\mathbf{e},{\nabla }^2ℒ(\mathit{\theta })=\mathbf{Ŝ}.$$

Since the transformed Kendall’s tau estimator is rank-based and could be indefinite (Zhao et al., 2014b), the optimization in (2.3) may not be convex even if ℛ_λ(θ) is a convex.

Remark 2.1

It is worth mentioning that the indefiniteness of Ŝ also makes(2.3) unbounded from below, but as will be shown later, our proposed algorithm can still guarantee a unique sparse local solution with optimal statistical properties under suitable solutions.

Remark 2.2

To handle the possible nonconvexity, Liu et al. (2012b) estimate ${\mathbf{\Theta }}_{*j}^{*}$ based on a graphical model estimation procedure proposed in Cai et al. (2011) as follows,

$$\underset{{\mathbf{\Theta }}_{*j}\in {ℝ}^d}{\text{min}}{\Vert {\mathbf{\Theta }}_{*j}\Vert }_1\text{ subject to }{\Vert \mathbf{Ŝ}{\mathbf{\Theta }}_{*j}-{\mathbf{I}}_{*j}\Vert }_{\infty }\le \lambda \text{ for}j=1,\dots ,d.$$ (2.5)

(2.5) is convex regardless the indefiniteness of Ŝ. But a major disadvantage of (2.5) is the computation. Existing solvers can only solve (2.5) up to moderate dimensions. We will present more empirical comparison between (2.3) and (2.5) in our numerical experiments.

3 Method

For notational convenience, we rewrite the objective function ℱ_λ(θ) as

$${ℱ}_{\lambda }(\mathit{\theta })=\underset{{\widetilde{ℒ}}_{\lambda }(\mathit{\theta })}{\underbrace{ℒ(\mathit{\theta })+{\mathscr{H}}_{\lambda }(\mathit{\theta })}}+\lambda {\Vert \mathit{\theta }\Vert }_1.$$

We call ℒ̃_λ(θ) the augmented loss function, which is smooth but possibly nonconvex. We first introduce the path-following optimization scheme, which is a multistage optimization framework and also used in PISTA.

3.1 Path-following Optimization Scheme

The path-following optimization scheme solves the regularized optimization problem (2.1) using a decreasing sequence of N + 1 regularization parameters ${\{{\lambda }_K\}}_{K=0}^N$, and yields a sequence of N + 1 output solutions ${\{{\hat{\mathit{\theta }}}^{\{K\}}\}}_{K=0}^N$ from sparse to dense. We set the initial tuning parameter as λ₀ = ‖∇ℒ(0)‖_∞. By checking the KKT condition of (2.1) for λ₀, we have

$$\underset{\mathit{\xi }\in \partial {\Vert \mathbf{0}\Vert }_1}{\text{min}}{\Vert \nabla {\widetilde{ℒ}}_{\lambda }(\mathbf{0})+{\lambda }_0\mathit{\xi }\Vert }_{\infty }=\underset{\mathit{\xi }\in \partial {\Vert \mathbf{0}\Vert }_1}{\text{min}}{\Vert \nabla ℒ(\mathbf{0})+\nabla {\mathscr{H}}_{\lambda }(\mathbf{0})+{\lambda }_0\mathit{\xi }\Vert }_{\infty }=0,$$ (3.1)

where the second equality comes from ‖ξ‖_∞ ≤ 1 and $\nabla {\mathscr{H}}_{\lambda }(\mathbf{0})={(h_{\lambda }^{\prime }(0),h_{\lambda }^{\prime }(0),\dots ,h_{\lambda }^{\prime }(0))}^T=\mathbf{0}$ as introduced in §2.1. Since (3.1) indicates that 0 is a local solution to (2.1) for λ₀, we take the leading output solution as θ̂^{0} = 0. Let η ∈ (0, 1), we set λ_K = ηλ_{K − 1} for K = 1, …, N. We then solve (2.1) for the regularization parameter λ_K with θ̂^{{K − 1}} as the initial solution, which leads to the next output solution θ̂^{K}. The path-following optimization scheme is illustrated in Algorithm 1.

3.2 Accelerated Iterative Shrinkage Thresholding Algorithm

We then explain the accelerated iterative shrinkage thresholding (AISTA) subroutine, which solves (2.1) in each stage of the path-following optimization scheme. For notational simplicity, we omit the stage index K, and only consider the iteration index m of AISTA. Suppose that AISTA takes some initial solution θ^[0] and an initial step size parameter L^[0], and we want to solve (2.1) with the regularization parameter λ. Then at the m^th iteration of AISTA, we already have L^[m] and θ^[m]. Each iteration of AISTA contains two steps: The first one is the proximal gradient descent iteration, and the second one is the coordinate descent subroutine.

Algorithm 1.

Path-following optimization. It solves the problem (2.1) using a decreasing sequence of regularization parameters ${\{{\lambda }_K\}}_{K=0}^N$. More specifically, λ₀ = ‖ℒ(0)‖_∞ yields an all zero output solution θ̂^{0} = 0. For K = 1, …, N, we set λ_K = ηλ_{K − 1}, where η ∈ (0, 1). We solve (2.1) for λ_K with θ̂^{{K − 1}} as an initial solution. Note that AISTA is the computational algorithm for obtaining θ̂^{K + 1} using θ̂^K as the initial solution. L_min and ${\{{\hat{L}}^{\{K\}}\}}_{K=0}^N$ are corresponding step size parameters. More technical details on AISTA are presented are Algorithm 3.

Algorithm: ${\{{\hat{\mathit{\theta }}}^{(K)}\}}_{K=0}^N\leftarrow \mathtt{\text{APISTA}}({\{{\lambda }_K\}}_{K=0}^N)$

Parameter: η, Lmin

Initialize: λ0 = ‖∇ℒ(0)‖∞, θ̂{0} ← 0, L̂{0} ← Lmin

For: K = 0, …., N − 1

λK+1 ← ηλK, {θ̂{K+1}, L̂{K+1}} ← AISTA(λK+1, θ̂{K}, L̂{K})

End for

Output: ${\{{\hat{\mathit{\theta }}}^{(K)}\}}_{K=0}^N$

(I) Proximal Gradient Descent Iteration

We consider the following quadratic approximation of ℱ_λ(θ) at θ = θ^[m],

$${𝒬}_{\lambda ,L^{[m+1]}}(\mathit{\theta };{\mathit{\theta }}^{[m]})={\widetilde{ℒ}}_{\lambda }({\mathit{\theta }}^{[m]})+{(\mathit{\theta }-{\mathit{\theta }}^{[m]})}^T\nabla {\widetilde{ℒ}}_{\lambda }({\mathit{\theta }}^{[m]})+\frac{L^{[m+1]}}{2}{\Vert \mathit{\theta }-{\mathit{\theta }}^{[m]}\Vert }_2^2+\lambda {\Vert \mathit{\theta }\Vert }_1,$$

where L^[m+1] is the step size parameter such that 𝒬_λ,L^[m+1] (θ; θ^[m]) ≥ ℱ_λ(θ). We then take a proximal gradient descent iteration and obtain θ^[m] by

$${\mathit{\theta }}^{[m+0.5]}=\underset{\mathit{\theta }\in {ℝ}^d}{\text{argmin}}{𝒬}_{\lambda ,L^{[m+1]}}(\mathit{\theta };{\mathit{\theta }}^{[m]})=\underset{\mathit{\theta }\in {ℝ}^d}{\text{argmin}}\frac{L^{[m+1]}}{2}{\Vert \mathit{\theta }-{\tilde{\mathit{\theta }}}^{[m]}\Vert }_2^2+\lambda {\Vert \mathit{\theta }\Vert }_1,$$ (3.2)

where θ̃^[m] = θ^[m] − ∇ℒ̃_λ(θ^[m])/L^[m+1]. For notational simplicity, we write

$${\mathit{\theta }}^{[m+0.5]}={𝒯}_{\lambda ,L^{[m+1]}}({\mathit{\theta }}^{[m])}).$$ (3.3)

For sparse column inverse operator, we can obtain a closed form solution to (3.2) by soft thresholding

$${\mathit{\theta }}^{[m+0.5]}={𝒮}_{\lambda /L^{[m+1]}}({\tilde{\mathit{\theta }}}^{[m+0.5]}).$$

The step size 1/L^[m+1] can be obtained by the backtracking line search. In particular, we start with a small enough L^[0]. Then in each iteration of the middle loop, we choose the minimum nonnegative integer z such that L^[m+1] = 2^zL^[m] satisfies

$${ℱ}_{\lambda }({\mathit{\theta }}^{[m+0.5]})\le {𝒬}_{\lambda ,L^{[m+1]}}({\mathit{\theta }}^{[m+0.5]};{\mathit{\theta }}^{[m]})\text{ for }m=0,1,2,\dots .$$ (3.4)

(II) Coordinate Descent Subroutine

Unlike the proximal gradient algorithm which repeats (3.3) until convergence at each stage of the path-following optimization scheme, AISTA exploits an additional coordinate descent subroutine to further boost the computational performance. More specifically, we define ${𝒜}^{\perp }=\{j|{\theta }_j^{[m+0.5]}=0\}$ and solve the following optimization problem

$$\underset{\mathit{\theta }}{\text{min}}{ℱ}_{\lambda }(\mathit{\theta })\text{ subject to }{\mathit{\theta }}_{{𝒜}^{\perp }}=\mathbf{0}$$ (3.5)

using the cyclic coordinate descent algorithm (CCDA) initiated by θ^[m+0.5]. For notational simplicity, we omit the stage index K and iteration index m, and only consider the iteration index t of CCDA. Suppose that the CCDA algorithm takes some initial solution θ⁽⁰⁾ for solving (2.1) with the regularization parameter λ. Without loss of generality, we denote 𝒜 = {1, …, |𝒜|}. At the t^th iteration, we have θ^(t). Then at the (t + 1)^th iteration, we conduct the coordinate minimization cyclically over all active coordinates. Let w^(t+1,k) be an auxiliary solution of the (t + 1)^th iteration with the first k − 1 coordinates updated. For k = 1, we have w^(t+1,1) = θ^(t). We then update the k^th coordinate to obtain the next auxiliary solution w^(t+1,k+1).

More specifically, let ∇_kℒ̃_λ(θ) be the k^th entry of ∇ℒ̃_λ(θ). We minimize the objective function with respect to each selected coordinate and keep all other coordinates fixed,

$$w_k^{(t+1,k+1)}=\underset{{\theta }_k\in ℝ}{\text{argmin}}{ℒ}_{\lambda }({\theta }_k;{\mathit{w}}_{\backslash k}^{(t+1,k)})+r_{\lambda }({\theta }_k).$$ (3.6)

Once we obtain $w_k^{(t+1,k+1)}$, we can set ${\mathit{w}}_{\backslash k}^{(t+1,k+1)}={\mathit{w}}_{\backslash k}^{(t+1,k)}$ to obtain the next auxiliary solution w^(t+1,k+1). For sparse column inverse operator, let ${\tilde{w}}_k^{(t+1,k)}=e_k-{\mathbf{Ŝ}}_{\backslash kk}^T{\mathit{w}}_{\backslash k}^{(t+1,k)}$, we have

$$w_k^{(t+1,k+1)}=\underset{{\theta }_k\in ℝ}{\text{argmin}}\frac{1}{2}{\mathbf{Ŝ}}_{kk}{\theta }_k^2+e_k-{\mathbf{Ŝ}}_{\backslash kk}^T{\mathit{w}}_{\backslash k}^{(t+1,k)}{\theta }_k-e_k{\theta }_k+r_{\lambda }({\theta }_k)=\underset{{\theta }_k\in ℝ}{\text{argmin}}\frac{1}{2}{({\theta }_k-{\tilde{w}}_k^{(t+1,k)})}^2+r_{\lambda }({\theta }_k),$$ (3.7)

where the last equality comes from the fact Ŝ_kk = 1 for all k = 1, …, d. By setting the subgradient of (3.7) equal to zero, we can obtain $w_k^{(t+1,k+1)}$ as follows:

• For the ℓ₁ norm regularization, we have $w_k^{(t+1,k+1)}={𝒮}_{\lambda }({\tilde{w}}_k^{(t+1,k)})$.

• For the SCAD regularization, we have

  $$w_k^{(t+1,k+1)}=\{\begin{array}{cc}{\tilde{w}}_k^{(t+1,k)}\hfill & \text{if}|{\tilde{w}}_k^{(t+1,k)}|\ge \gamma \lambda ,\hfill \\ \frac{{𝒮}_{\gamma \lambda /(\gamma -1)}({\tilde{w}}_k^{(t+1,k)})}{1-1/(\gamma -1)}\hfill & \text{if}|{\tilde{w}}_k^{(t+1,k)}|\in [2\lambda ,\gamma \lambda ),\hfill \\ {𝒮}_{\lambda }({\tilde{w}}_k^{(t+1,k)})\hfill & \text{if}|{\tilde{w}}_k^{(t+1,k)}|<2\lambda .\hfill \end{array}$$
• For the MCP regularization, we have

  $$w_k^{(t+1,k+1)}=\{\begin{array}{cc}{\tilde{w}}_k^{(t+1,k)}\hfill & \text{if}|{\tilde{w}}_k^{(t+1,k)}|\ge \gamma \lambda ,\hfill \\ \frac{{𝒮}_{\lambda }({\tilde{w}}_k^{(t+1,k)})}{1-1/\gamma }\hfill & \text{if}|{\tilde{w}}_k^{(t+1,k)}|<\gamma \lambda .\hfill \end{array}$$

When all |𝒜| coordinate updates in the (t + 1)^th iteration of CCDA finish, we set θ^(t+1) = w^{(t+1,|𝒜|+1)}. We summarize CCDA in Algorithm 2. Once CCDA terminates, we denote its output solution by θ^[m+1], and start the next iteration of AISTA. We summarize AISTA in Algorithm 3.

Algorithm 2.

The cyclic coordinate descent algorithm (CCDA). The cyclic coordinate descent algorithm cyclically iterates over the support of the initial solution. Without loss of generality, we assume 𝒜 = {1, …, |𝒜|}.

Algorithm: θ̂ ← CCDA(λ, θ(0)).

Initialize: t ← 0, 𝒜 = supp(θ(0))

Repeat:

w(t+1,1) ← θ(t)

For k = 1, …, |𝒜|

$w_k^{(t+1,k+1)}\leftarrow {\text{argmin}}_{{\theta }_k\in ℝ}{ℒ}_{\lambda }({\theta }_k;{\mathit{w}}_{\backslash k}^{(t+1,k)})+r_{\lambda }({\theta }_k)\text{ and }{\mathit{w}}_{\backslash k}^{(t+1,k+1)}\leftarrow {\mathit{w}}_{\backslash k}^{(t+1,k)}$

End for

θ(t+1) ← w(t+1,|𝒜|+1), t ← t + 1

Until convergence

θ̂ ← θ(t)

Remark 3.1

The backtracking line search procedure in PISTA has been extensively studied in existing optimization literature on the adaptive step size selection (Dennis and Schnabel, 1983; Nocedal and Wright, 2006), especially for proximal gradient algorithms (Beck and Teboulle, 2009b,a; NESTEROV, 2013). Many empirical results have corroborated better computational performance than that using a fix step size. But unlike the classical proximal gradient algorithms, APISTA can efficiently reduce the objective value by the coordinate descent subroutine in each iteration. Therefore we can simply choose a constant step size parameter L such that

$$L\ge \underset{\mathit{\theta }\in {ℝ}^d}{\text{sup}}{\mathrm{\Lambda }}_{\text{max}}({\nabla }^2ℒ(\mathit{\theta })).$$ (3.8)

The step size parameter L in (3.8) guarantees 𝒬_λ,L(θ; θ^[m]) ≥ ℱ_λ(θ) in each iteration of AISTA. For sparse column inverse operator, ∇²ℒ(θ) = Ŝ does not depend on θ. Therefore we choose

Algorithm 3.

The accelerated iterative shrinkage thresholding algorithm (AISTA). Within each iteration, we exploit an additional coordinate descent subroutine to improve the empirical computational performance.

Algorithm: {θ̂, L̂} ← AISTA(λ, θ[0], L[0])

Initialize: m ← 0

Repeat:

z ← 0

Repeat:

L [m+1] ← 2z L[m], θ[m+0.5] ← 𝒯λ,Ω,L[m+1] (θ[m]), z ← z + 1

Until: 𝒬λ,L[m+1] (θ[m+0.5]; θ[m]) ≥ ℱλ(θ[m+1])

θ[m+1] ← CCDA(λ, θ[m+0.5]), m ← m + 1

Until convergence

θ̂ ← θ[m−0.5], L̂ ← L[m]

Output: {θ̂, L̂}

L = Λ_max(Ŝ). Our numerical experiments show that choosing a fixed step not only simplifies the implementation, but also attains better empirical computational performance than the backtracking line search. See more details in §5.

3.3 Stopping Criteria

Since θ is a local minimum if and only if the KKT condition min_{ξ∈∂‖θ‖1} ‖∇ℒ̃_λ(θ) + λξ‖_∞ = 0 holds, we terminate AISTA when

$${\omega }_{\lambda }({\mathit{\theta }}^{[m+0.5]})=\underset{\mathit{\xi }\in \partial {\Vert {\mathit{\theta }}^{[m+0.5]}\Vert }_1}{\text{min}}{\Vert \nabla {\widetilde{ℒ}}_{\lambda }({\mathit{\theta }}^{[m+0.5]})+\lambda \mathit{\xi }\Vert }_{\infty }\le \epsilon ,$$ (3.9)

where ε is the target precision and usually proportional to the regularization parameter. More specifically, given the regularization parameter λ_K, we have

$${\epsilon }_K={\delta }_K{\lambda }_K\text{ for }K=1,\dots ,N,$$ (3.10)

where δ_K ∈ (0, 1) is a convergence parameter for the K^th stage of the path-following optimization scheme. Moreover, for CCDA, we terminate the iteration when

$${\Vert {\mathit{\theta }}^{(t+1)}-{\mathit{\theta }}^{(t)}\Vert }_2^2\le {\delta }_0^2{\lambda }^2,$$ (3.11)

where δ₀ ∈ (0, 1) is a convergence parameter. This stopping criterion is natural to the sparse coordinate descent algorithm, since we only need to calculate the value change of each coordinate (not the gradient). We will discuss how to choose δ_K’s and δ₀ in §4.1.

4 Theory

Before we present the computational and statistical theories of APISTA, we introduce some additional assumptions. The first one is about the choice of regularization parameters.

Assumption 4.1

Let δ_K’s and η saitsify

$$\eta \in [0.9,1)\text{ and }\underset{0\le K\le N}{\text{max}}{\delta }_K\le {\delta }_{\text{max}}=1/4,$$

where η is the rescaling parameter of the path-following optimization scheme, δ_K’s are the convergence parameters defined in (3.10), and δ₀ is the convergence parameter defined in (3.11). We have the regularization parameters

$${\lambda }_0>{\lambda }_1\dots >{\lambda }_N\ge 8{\Vert \nabla ℒ({\mathit{\theta }}^{*})\Vert }_{\infty }.$$

Assumption 4.1 has been extensively studied in existing literature on high dimensional statistical theory of the regularized M-estimators (Rothman et al., 2008; Zhang and Huang, 2008; Negahban and Wainwright, 2011; Negahban et al., 2012). It requires the regularization parameters to be large enough such that irrelevant variables can be eliminated along the solution path. Though ‖∇ℒ(θ^*)‖_∞ cannot be explicitly calculated (θ^* is unknown), we can exploit concentration inequalities to show that Assumption 4.1 holds with high probability (Ledoux, 2005). In particular, we will verify Assumption 4.1 for sparse transellpitical graphical model estimation in Lemma 4.8.

Before we proceed with our second assumption, we define the largest and smallest s-sparse eigenvalues of the Hessian matrix of the loss function as follows.

Definition 4.1

Given an integer s ≥ 1, we define the largest and smallest s-sparse eigenvalues of ∇²ℒ(θ) as

• Largest s-Sparse Eigenvalue : ${\rho }_{+}(s)=\underset{\mathit{\upsilon }\in {ℝ}^d,{\Vert \mathit{\upsilon }\Vert }_0\le s}{\text{sup}}\frac{{\mathit{\upsilon }}^T{\nabla }^2ℒ(\mathit{\theta })\mathit{\upsilon }}{{\Vert \mathit{\upsilon }\Vert }_2^2}$,

• Smallest s-Sparse Eigenvalue : ${\rho }_{-}(s)=\underset{\mathit{\upsilon }\in {ℝ}^d,{\Vert \mathit{\upsilon }\Vert }_0\le s}{\text{inf}}\frac{{\mathit{\upsilon }}^T{\nabla }^2ℒ(\mathit{\theta })\mathit{\upsilon }}{{\Vert \mathit{\upsilon }\Vert }_2^2}$.

Moreover, we define ρ̃₋(s) = ρ₋(s) − α and ρ₊(s) = ρ₊(s) for notational simplicity, where α is defined in (2.2).

The next lemma shows the connection between the sparse eigenvalue conditions and restricted strongly convex and smooth conditions.

Lemma 4.1

Given ρ₋(s) > 0, for any θ, θ′ ∈ ℝ^d with |supp(θ) ∪ supp(θ′)| ≤ s, we have

$$ℒ(\mathit{\theta }\prime )\le ℒ(\mathit{\theta })+{(\mathit{\theta }\prime -\mathit{\theta })}^T\nabla ℒ(\mathit{\theta })+\frac{{\rho }_{+}(s)}{2}{\Vert \mathit{\theta }\prime -\mathit{\theta }\Vert }_2^2,$$

$$ℒ(\mathit{\theta }\prime )\ge ℒ(\mathit{\theta })+{(\mathit{\theta }\prime -\mathit{\theta })}^T\nabla ℒ(\mathit{\theta })+\frac{{\rho }_{-}(s)}{2}{\Vert \mathit{\theta }\prime -\mathit{\theta }\Vert }_2^2.$$

Moreover, if ρ₋(s) > α, then we have

$${\widetilde{ℒ}}_{\mathit{\lambda }}(\mathit{\theta }\prime )\le {\widetilde{ℒ}}_{\lambda }(\mathit{\theta })+{(\mathit{\theta }\prime -\mathit{\theta })}^T\nabla {\widetilde{ℒ}}_{\lambda }(\mathit{\theta })+\frac{{\rho }_{+}(s)}{2}{\Vert \mathit{\theta }\prime -\mathit{\theta }\Vert }_2^2,$$

$${\widetilde{ℒ}}_{\mathit{\lambda }}(\mathit{\theta }\prime )\ge {\widetilde{ℒ}}_{\lambda }(\mathit{\theta })+{(\mathit{\theta }\prime -\mathit{\theta })}^T\nabla {\widetilde{ℒ}}_{\lambda }(\mathit{\theta })+\frac{{\tilde{\rho }}_{-}(s)}{2}{\Vert \mathit{\theta }\prime -\mathit{\theta }\Vert }_2^2,$$

and for any ξ ∈ ∂‖θ‖₁,

$${ℱ}_{\lambda }(\mathit{\theta }\prime )\ge {ℱ}_{\lambda }(\mathit{\theta })+{(\nabla {\widetilde{ℒ}}_{\lambda }(\mathit{\theta })+\lambda \mathit{\xi })}^T(\mathit{\theta }\prime -\mathit{\theta })+\frac{{\tilde{\rho }}_{-}(s)}{2}{\Vert \mathit{\theta }\prime -\mathit{\theta }\Vert }_2^2.$$

The proof of Lemma 4.1 is provided in Wang et al. (2014), therefore omitted. We then introduce the second assumption.

Assumption 4.2

Given ‖θ^*‖₀ ≤ s^*, there exists an integer s̃ satisfying

$$\tilde{s}\ge (144{\kappa }^2+250\kappa )·s^{*},{\rho }_{+}(s^{*}+2\tilde{s})<+\infty ,\text{ and }{\tilde{\rho }}_{-}(s^{*}+2\tilde{s})>0,$$

where κ = ρ₊(s + 2s̃)ρ̃₋(s + 2s̃).

Assumption 4.2 requires that ℒ̃_λ(θ) satisfies the strong convexity and smoothness when θ is sparse. As will be shown later, APISTA can always guarantee the number of irrelevant coordinates with nonzero values not to exceed s̃. Therefore the restricted strong convexity is preserved along the solution path. We will verify that Assumption 4.2 holds with high probability for the transellpitical graphical model estimation in Lemma 4.9.

Remark 4.2 (Step Size Initialization)

We take the initial step size parameter as L_min ≥ ρ₊(1). For sparse column inverse operator, we directly choose L_min = ρ₊(1) = 1.

4.1 Computational Theory

We develop the computational theory of APISTA. For notational simplicity, we define $𝒮=\{j|{\theta }_j^{*}\ne 0\}$ and ${𝒮}^{\perp }=\{j|{\theta }_j^{*}=0\}$ for characterizing the the solution sparsity. We first start with the convergence analysis for the cyclic coordinate descent algorithm (CCDA). The next theorem presents its rate of convergence in term of the objective value.

Theorem 4.3 (Geometric Rate of Convergence of CCDA)

Suppose that Assumption 4.2 holds. Given a sparse initial solution satisfying ${\Vert {\mathit{\theta }}_{{𝒮}^{\perp }}^{(0)}\Vert }_0\le \tilde{s}$, (3.5) is a strongly convex optimization problem with a unique global minimizer θ̄. Moreover, for t = 1, 2…, we have

$${ℱ}_{\lambda }({\mathit{\theta }}^{(t)})-{ℱ}_{\lambda }(\overline{\mathit{\theta }})\le {\left(\frac{(s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})}{(s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})+{\tilde{\rho }}_{-}(1){\tilde{\rho }}_{-}(s^{*}+\tilde{s})}\right)}^t[{ℱ}_{\lambda }({\mathit{\theta }}^{(0)})-{ℱ}_{\lambda }(\overline{\mathit{\theta }})].$$

The proof of Theorems 4.3 is provided in Appendix A. Theorem 4.3 suggests that when the initial solution is sparse, CCDA essentially solves a strongly convex optimization problem with a unique global minimizer. Consequently we can establish the geometric rate of convergence in term of the objective value for CCDA. We then proceed with the convergence analysis of AISTA. The next theorem presents its theoretical rate of convergence in term of the objective value.

Theorem 4.4 (Geometric Rate of Convergence of AISTA)

Suppose that Assumptions 4.1 and 4.2 hold. For any λ ≥ λ_N, if the initial solution θ^[0] satisfies

$${\Vert {\mathit{\theta }}_{{𝒮}^{\perp }}^{[0]}\Vert }_0\le \tilde{s},{\omega }_{\lambda }({\mathit{\theta }}^{[0]})\le \lambda /2,$$ (4.1)

then we have ${\Vert {\mathit{\theta }}_{{𝒮}^{\perp }}^{(m)}\Vert }_0\le \tilde{s}$ for m = 0.5, 1, 1.5, 2, …. Moreover, for m = 1, 2, …, we have

$${ℱ}_{\lambda }({\mathit{\theta }}^{[m]})-{ℱ}_{\lambda }({\overline{\mathit{\theta }}}^{\lambda })\le {(1-\frac{1}{8\kappa })}^m[{ℱ}_{\lambda }({\mathit{\theta }}^{(0)})-{ℱ}_{\lambda }(\overline{\mathit{\theta }})],$$

where θ̄^λ is a unique sparse local solution to (2.1) satisfying ω_λ(θ̄^λ) = 0 and ${\Vert {\overline{\mathit{\theta }}}_{{𝒮}^{\perp }}^{\lambda }\Vert }_0\le \tilde{s}$.

The proof of Theorem 4.4 is provided in Appendix B. Theorem 4.4 suggests that all solutions of AISTA are sparse such that the restricted strongly convex and smooth conditions hold for all iterations. Therefore, AISTA attains the geometric rate of convergence in term of the objective value. Theorem 4.4 requires a proper initial solution to satisfy (4.1). This can be verified by the following theorem.

Theorem 4.5 (Path-following Optimization Scheme)

Suppose that Assumptions 4.1 and 4.2 hold. Given θ satisfying

$${\Vert {\mathit{\theta }}_{{𝒮}^{\perp }}\Vert }_0\le s\text{ and }{\omega }_{{\lambda }_{K-1}}(\mathit{\theta })\le {\delta }_{K-1}{\lambda }_{K-1},$$ (4.2)

we have ω_λK(θ) ≤ λ_K/2.

The proof of Theorem 4.5 is provided in Wang et al. (2014), therefore omitted. Since θ^{0} naturally satisfies (4.2) for λ₁, by Theorem 4.5 and induction, we can show that the path-following optimization scheme always guarantees that the output solution of the (K − 1)^th stage is a proper initial solution for the K^th stage, where K = 1, …, N. Eventually, we combine Theorems 4.3 and 4.4 with Theorem 4.5, and establish the global geometric rate of convergence in term of the objective value for APISTA in the next theorem.

Theorem 4.6 (Global Geometric Rate of Convergence of APISTA)

Suppose that Assumptions 4.1 and 4.2 hold. Recall that δ₀ and δ_K’s are defined in §3.3, κ and s̃ are defined in Assumption 4.2, and α is defined in (2.2). We have the following results:

1. At the K^th stage (K = 1, …, N), the number of coordinate descent iterations within each CCDA is at most C₁ log (C₂/δ₀), where

   $$C_1=2{\text{ log}}^{-1}\left(\frac{(s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})}{(s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})+{\tilde{\rho }}_{-}(1){\tilde{\rho }}_{-}(s^{*}+\tilde{s})}\right)\text{ and }{C}_2=\sqrt{\frac{21s^{*}}{{\tilde{\rho }}_{-}(s^{*}+\tilde{s}){\tilde{\rho }}_{-}(1)}};$$
2. At the K^th stage (K = 1, …, N), the number of the proximal gradient iterations in each AISTA is at most C₃ log (C₄/δ_K), where

   $$C_3=2{\text{ log}}^{-1}(1-\frac{1}{8\kappa })\text{ and }{C}_4=10\sqrt{\kappa s^{*}};$$
3. To compute all N + 1 output solutions, the total number of coordinate descent iterations in APISTA is at most

   $$C_1\text{ log }(C_2/{\delta }_0)\sum _{K=1}^N{C}_3\text{ log }(C_4/{\delta }_K);$$ (4.3)
4. At the K^th stage (K = 1, …, N), we have

   $${ℱ}_{{\lambda }_N}({\hat{\mathit{\theta }}}^{\{K\}})-{ℱ}_{{\lambda }_N}({\overline{\mathit{\theta }}}^{{\lambda }_N})\le [𝟙(K<N)+{\delta }_K]·\frac{105{\lambda }_K^2{s}^{*}}{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})};$$

The proof Theorem 4.6 is provided in Appendix C. We then present a more intuitive explanation about Result (3). To secure the generalization performance in practice, we usually tune the regularization parameter over a refined sequence based on cross validation. In particular, we solve (2.1) using partial data with high precision for every regularization parameter. If we set δ_K = δ_optλ_K for K = 1, …N, where δ_opt is a very small value (e.g. 10⁻⁸), then we can rewrite (4.3) as

$$N{C}_1\text{ log }\left(\frac{C_2}{{\delta }_0}\right)C_3\text{ log }\left(\frac{C_4}{{\delta }_{\text{opt}}}\right)=𝒪\left(N\text{ log }\right(\frac{1}{{\delta }_{\text{opt}}}\left)\right),$$ (4.4)

where δ₀ is some reasonably large value (e.g. 10⁻²) defined in §3.3. The iteration complexity in (4.4) depends on N.

Once the regularization parameter is selected, we still need to solve (2.1) using full data with some regularization sequence. But we only need high precision for the selected regularization parameter (e.g., λ_N), and for K = 1, …, N − 1, we only solve (2.1) for λ_K up to an adequate precision, e.g., δ_K = δ₀ for K = 1, …, N − 1 and δ_N = δ_optλ_N. Since 1/δ_opt is much larger than N, we can rewrite (4.3) as

$$C_1\text{ log }\left(\frac{C_2}{{\delta }_0}\right)((N-1)C_3\text{ log }(\frac{C_4}{{\delta }_0})+C_3\text{ log }(\frac{C_4}{{\delta }_{\text{opt}}}\left)\right)=𝒪\left(\text{log}\right(\frac{1}{{\delta }_{\text{opt}}}\left)\right).$$ (4.5)

Now the iteration complexity in (4.5) does not depend on N.

Remark 4.7

To establish computational theories of APISTA with a fixed step size, we only need to slightly modify the proofs of Theorems 4.4 and 4.6 by replacing ρ₊(s^* + 2s̃) and ρ₊(s^* + s̃) by their upper bound L defined in (3.8). Then a global geometric rate of convergence can also be derived, but with a worse constant term.

4.2 Statistical Theory

We then establish the statistical theory of the SCIO estimator obtained by APISTA under transelliptical models. We use Θ^* and Σ^* to denote the true latent precision and covariance matrices. We assume that Θ^* belongs to the following class of sparse, positive definite, and symmetric matrices:

$${𝒰}_{{\psi }_{\text{max}},{\psi }_{\text{min}}}(M,s^{*})=\{\mathbf{\Theta }\in {ℝ}^{d\times d}|\mathbf{\Theta }={\mathbf{\Theta }}^T,\underset{j}{\text{ max }}{\Vert {\mathbf{\Theta }}_{*j}\Vert }_0\le s^{*},{\Vert \mathbf{\Theta }\Vert }_1\le M,0<{\psi }_{\text{max}}^{-1}\le {\mathrm{\Lambda }}_{\text{min}}(\mathbf{\Theta })\le {\mathrm{\Lambda }}_{\text{max}}(\mathbf{\Theta })\le {\psi }_{\text{min}}^{-1}<\infty \},$$

where ψ_max and ψ_min are positive constants, and do not scale with (M, s^*, n, d). Since Σ^* = (Θ^*)⁻¹, we also have ψ_min ≤ Λ_min(Σ^*) ≤ Λ_max(Σ^*) ≤ ψ_max.

We first verify Assumptions 4.1 and 4.2 in the next two lemmas for transelliptical models.

Lemma 4.8

Suppose that $\mathit{X}~T{E}_d({\mathbf{\Sigma }}^{*},\xi ,{\{f_j\}}_{j=1}^d)$. Given ${\lambda }_N=8\sqrt{2\pi }M\sqrt{\text{log }d/n}$, we have

$$\mathbb{P}({\lambda }_N\ge 8{\Vert \nabla ℒ({\mathit{\theta }}^{*})\Vert }_{\infty })\ge 1-\frac{1}{d^2}.$$

The proof of Lemma 4.8 is provided in Appendix D. Lemma 4.8 guarantees that the selected regularization parameter λ_N satisfies Assumption 4.1 with high probability.

Lemma 4.9

Suppose that $\mathit{X}~T{E}_d({\mathbf{\Sigma }}^{*},\xi ,{\{f_j\}}_{j=1}^d)$. Given α = ψ_min/2, there exist universal positive constants c₁ and c₂ such that for $n\ge 4{\psi }_{\text{min}}^{-1}{c}_2(1+2c_1)s^{*}\text{log }d$, with probability at least 1 − 2/d², we have

$$\tilde{s}=c_1{s}^{*}\ge (144{\kappa }^2+250\kappa )s^{*},{\tilde{\rho }}_{-}(s^{*}+2\tilde{s})\ge \frac{{\psi }_{\text{min}}}{4},{\rho }_{+}(s^{*}+2\tilde{s})\le \frac{5{\psi }_{\text{max}}}{4},$$

where κ is defined in Assumption 4.2.

The proof of Lemma 4.9 is provided in Appendix E. Lemma 4.9 guarantees that if the Lipschitz constant of $h_{\lambda }^{\prime }$ defined in (2.2) satisfies α = ψ_min/2, then the transformed Kendall’s tau estimator Ŝ = ∇²ℒ(θ) satisfies Assumption 4.2 with high probability.

Remark 4.10

Since Assumptions 4.1 and 4.2 have been verified, by Theorem 4.6, we know that APISTA attains the geometric rate of convergence to a unique sparse local solution to (2.3) in term of the objective value with high probability.

Recall that we use θ to denote Θ_*j in (2.4), by solving (2.3) with respect to all d columns, we obtain ${\hat{\mathbf{\Theta }}}^{\{N\}}=[{\hat{\mathbf{\Theta }}}_{*1}^{\{N\}},\dots ,{\hat{\mathbf{\Theta }}}_{*d}^{\{N\}}]$ and ${\overline{\mathbf{\Theta }}}^{{\lambda }_N}=[{\overline{\mathbf{\Theta }}}_{*1}^{{\lambda }_N},\dots ,{\overline{\mathbf{\Theta }}}_{*d}^{{\lambda }_N}]$, where ${\overline{\mathbf{\Theta }}}_{*j}^{{\lambda }_N}$ denotes the output solution of APISTA corresponding to λ_N for the j^th column (j = 1, ‥d), and ${\overline{\mathbf{\Theta }}}_{*j}^{{\lambda }_N}$ to denote the unique sparse local solution corresponding to λ_N for the j^th column (j = 1, ‥d), which APISTA converges to. We then present concrete rates of convergence of the estimator obtained by APISTA under the matrix ℓ₁ and Frobenius norms in the following theorem.

Theorem 4.11. [Parameter Estimation]

Suppose that $\mathit{X}~T{E}_d({\mathbf{\Sigma }}^{*},\xi ,{\{f_j\}}_{j=1}^d)$, and α = ψ_min/2. For $n\ge 4{\psi }_{\text{min}}^{-1}{c}_2(1+2c_1)s^{*}\text{log }d$, given ${\lambda }_N=8\sqrt{2}\pi M\sqrt{\text{log }d/n}$, we have

$${\Vert {\hat{\mathbf{\Theta }}}^{\{N\}}-{\mathbf{\Theta }}^{*}\Vert }_1=O_P\left(M{s}^{*}\sqrt{\frac{\text{log }d}{n}}\right),\frac{1}{d}{\Vert {\hat{\mathbf{\Theta }}}^{\{N\}}-{\mathbf{\Theta }}^{*}\Vert }_{\mathrm{F}}^2=O_P\left(\frac{M^2{s}^{*}\text{log }d}{n}\right).$$

The proof of (4.11) is provided in Appendix F. The results in Theorem 4.11 show that the SCIO estimator obtained by APISTA achieves the same rates of convergence as those for subguassian distributions (Liu and Luo, 2015). Moreover, when using the nonconvex regularization such as MCP and SCAD, we can achieve graph estimation consistency under the following assumption.

Assumption 4.3

Suppose that $\mathit{X}~T{E}_d({\mathbf{\Sigma }}^{*},\xi ,{\{f_j\}}_{j=1}^d)$. Define ${ℰ}^{*}=\{(k,j)|{\mathbf{\Theta }}_{kj}^{*}\ne 0\}$ as the support of Θ^*. There exists some universal constant c₃ such that

$$\underset{(k,j)\in {ℰ}^{*}}{\text{min}}|{\mathbf{\Theta }}_{kj}^{*}|\ge c_{3}M·\sqrt{\frac{s^{*}\text{ log }d}{n}}.$$

Assumption 4.3 is a sufficient condition for sparse column inverse operator to achieve graph estimation consistency in high dimensions for transelliptical models. The violation of Assumption 4.3 may result in underselection of the nonzero entries in Θ^*.

The next theorem shows that, with high probability, Θ̅^λ_N and the oracle solution Θ̂^o are identical. More specifically, let ${𝒮}_j=\text{supp}({\mathbf{\Theta }}_{*j}^{*})$ for j = 1, …, d, ${\hat{\mathbf{\Theta }}}^{\mathrm{o}}=[{\hat{\mathbf{\Theta }}}_{*1}^{\mathrm{o}},\dots ,{\hat{\mathbf{\Theta }}}_{*d}^{\mathrm{o}}]$ defined as follows,

$${\hat{\mathbf{\Theta }}}_{{𝒮}_{j}j}^{\mathrm{o}}=\underset{{\mathbf{\Theta }}_{{𝒮}_{j}j}\in {ℝ}^{|{𝒮}_j|}}{\text{argmin}}\frac{1}{2}{\mathbf{\Theta }}_{{𝒮}_{j}j}^T{\mathbf{Ŝ}}_{{𝒮}_j{𝒮}_j}{\mathbf{\Theta }}_{{𝒮}_{j}j}-{\mathbf{I}}_{{𝒮}_{j}j}^T{\mathbf{\Theta }}_{{𝒮}_{j}j}\text{ and }{\hat{\mathbf{\Theta }}}_{{𝒮}_j^{\perp }j}^{\mathrm{o}}=\mathbf{0}\text{ for }j=1,\dots ,d.$$ (4.6)

Theorem 4.12. [Graph Estimation]

Suppose that $\mathit{X}~T{E}_d({\mathbf{\Sigma }}^{*},\xi ,{\{f_j\}}_{j=1}^d)$, α = ψ_min/2, and Assumption 4.3 holds. There exists a universal constant c₄ such that $n\ge 4{\psi }_{\text{min}}^{-1}{c}_2(1+2c_1)s^{*}\text{log }d$, if we choose ${\lambda }_N=c_4\sqrt{2}\pi M\sqrt{s^{*}\text{log }d/n}$, then we have

$$\mathbb{P}({\overline{\mathbf{\Theta }}}^{{\lambda }_N}={\hat{\mathbf{\Theta }}}^{\mathrm{o}})\ge 1-\frac{3}{d^2}.$$

The proof of Theorem 4.12 is provided in Appendix G. Since Θ̂^o shares the same support with Θ^*, Theorem 4.12 guarantees that the SCIO estimator obtained by APISTA can perfectly recover ℰ^* with high probability. To the best of our knowledge, Theorem 4.12 is the first graph estimation consistency result for transelliptical models without any post-processing procedure (e.g. thresholding).

Remark 4.13

In Theorem (4.12), we choose ${\lambda }_N=c_4\sqrt{2}\pi M\sqrt{\text{log }d/n}$, which is different from the selected regularization parameter in Assumption 4.8. But as long as we have $c_4\sqrt{s^{*}}\ge 8$, which is not an issue under the high dimensional scaling

$$M,s^{*},n,d\to \infty \text{ and }M{s}^{*}\text{log}d/n\to 0,$$

λ_N ≥ 8‖∇ℒ(θ^*)‖_∞ still holds with high probability. Therefore all computational theories in §4.1 hold for Θ̅^λ_N in Theorem 4.12.

5 Numerical Experiments

In this section, we study the computational and statistical performance of APISTA method through numerical experiments on sparse transelliptical graphical model estimation. All experiments are conducted on a personal computer with Intel Core i5 3.3 GHz and 16GB memory. All programs are coded in double precision C, called from R. The computation are optimized by exploiting the sparseness of vector and matrices. Thus we can gain a significant speedup in vector and matrix manipulations (e.g. calculating the gradient and evaluating the objective value). We choose the MCP regularization with varying β’s for all simulations.

5.1 Simulated Data

We consider the chain and Erdös-Rényi graph generation schemes with varying d = 200, 400, and 800 to obtain the latent precision matrices:

• Chain. Each node is assigned a coordinate j for j = 1, …, d. Two nodes are connected by an edge whenever the corresponding points are at distance no more than 1.

• Erdös-Rényi. We set an edge between each pair of nodes with probability 1/d, independently of the other edges.

Two illustrative examples are presented in Figure 5.1. Let 𝒟 be the adjacency matrix of the generated graph, and ℳ₂ be the rescaling operator that converts a symmetric positive semidefinite matrix to a correlation matrix. We calculate

$${\mathbf{\Sigma }}^{*}={ℳ}_2[{(\widetilde{𝒟}+(1-{\mathrm{\Lambda }}_{\text{min}}(𝒟))\mathbf{I})}^{-1}].$$

We use Σ^* as the covariance matrix to generate n = ⌈60 log d⌉ independent observations from a multivariate t-distribution with mean 0 and degrees of freedom 3. We then adopt the power transformation g(t) = t⁵ to convert to the t-distributed data to the transelliptical data. Note that the corresponding latent precision matrix is Ω^* = (Σ^*)⁻¹. We compare the following five computational methods:

1. APISTA: The computational algorithm proposed in §3.

2. F-APISTA: APISTA without the backtracking line search (using a fixed step size instead).

3. PISTA: The pathwise iterative shrinkage thresholding algoritm proposed in Wang et al. (2014).

4. CLIME: The sparse latent precision matrix estimation method proposed in Liu et al. (2012b), which solves (2.5) by the ADMM method (Alternating Direction Method of Multipliers, Li et al. (2015); Liu et al. (2014)).

5. SCIO(P): The SCIO estimator based on the positive semidefinite projection method proposed in Zhao et al. (2014b). More specifically, we first project the possibly indefinite Kendall’s tau matrix into the cone of all positive semidefinite matrices. Then we plug the obtained replacement into (2.3), and solve it by the coordinate descent method proposed in Liu and Luo (2015).

Figure 5.1.

Different graph patterns. To ease the visualization, we only present graphs with d = 200.

Note that (4) and (5) have theoretical guarantees only when the ℓ₁ norm regularization is applied. For (1)–(3), we set δ₀ = δ_K = 10⁻⁵ for K = 1, …, N.

We first compare the statistical performance in parameter estimation and graph estimation of all methods. To meet this end, we generate a validation set of the same size as the training set. We use the regularization sequence with N = 100 and ${\lambda }_N=0.5\sqrt{\text{log }d/n}\approx 0.0645$. The optimal regularization parameter is selected by

$$\hat{\lambda }=\underset{\lambda \in \{{\lambda }_1,\dots ,{\lambda }_N\}}{\text{argmin}}{\Vert {\hat{\mathbf{\Theta }}}^{\lambda }\tilde{\mathbf{S}}-\mathbf{I}\Vert }_{\text{max}},$$

where Θ̂^λ denotes the estimated latent precision matrix using the training set with the regularization parameter λ, and S̃ denotes the estimated latent covariance matrix using the validation set. We repeat the simulation for 100 times, and summarize the averaged results in Tables 5.1 and 5.2. For all settings, we set δ₀ = δ_K = 10⁻⁵. We also vary β of the MCP regularization from 100 to 20/19, thus the corresponding α varies from 0.01 to 0.95. The parameter estimation performance is evaluated by the difference between the obtained estimator and the true latent prediction matrix under the Forbenius and matrix ℓ₁ norms. The graph estimation performance is evaluated by the true positive rate (T. P. R.) and false positive rate (F. P. R.) defined as follows,

$$\mathrm{T}.\mathrm{P}.\mathrm{R}.=\frac{{\sum }_{k\ne j}𝟙({\hat{\mathbf{\Theta }}}_{kj}^{\hat{\lambda }}\ne 0)·𝟙({\mathbf{\Theta }}_{kj}^{*}\ne 0)}{{\sum }_{k\ne j}𝟙({\mathbf{\Theta }}_{kj}^{*}\ne 0)},\mathrm{F}.\mathrm{P}.\mathrm{R}.=\frac{{\sum }_{k\ne j}𝟙({\hat{\mathbf{\Theta }}}_{kj}^{\hat{\lambda }}\ne 0)·𝟙({\mathbf{\Theta }}_{kj}^{*}\ne 0)}{{\sum }_{k\ne j}𝟙({\mathbf{\Theta }}_{kj}^{*}\ne 0)}.$$

Table 5.1.

Quantitive comparison among different estimators on the chain model. Since APISTA and F-APISTA can output valid results for large α’s, their estimator attains better performance than other competitors. The SCIO(P) and CLIME estimators use the ℓ₁ norm regularization with no bias reduction. Thus their performance is worse than the other competitors in both parameter estimation and graph estimation.

Method	d	‖Θ̂−Θ‖F	‖Θ̂−Θ‖1	T. P. R.	F. P. R.	α
PISTA	200	4.1112(0.7856)	1.0517(0.1141)	1.0000(0.0000)	0.0048(0.0079)	0.20
	400	6.4507(0.9062)	1.0756(0.0717)	1.0000(0.0000)	0.0007(0.0004)	0.20
	800	8.2640(1.1456)	1.0434(0.0673)	1.0000(0.0000)	0.0003(0.0006)	0.20
APISTA	200	2.5162(0.2677)	0.7665(0.1583)	0.9993(0.0012)	0.0001(0.0001)	0.95
	400	3.3664(0.2735)	0.8298(0.0986)	1.0000(0.0000)	0.0002(0.0000)	0.67
	800	5.0244(0.7984)	0.9312(0.1226)	1.0000(0.0000)	0.0002(0.0004)	0.50
F-APISTA	200	2.5163(0.2670)	0.7658(0.1559)	0.9994(0.0015)	0.0001(0.0002)	0.95
	400	3.3629(0.2702)	0.8253(0.0959)	1.0000(0.0000)	0.0002(0.0000)	0.67
	800	5.0237(0.7963)	0.9373(0.1289)	1.0000(0.0000)	0.0002(0.0005)	0.50
SCIO(P)	200	6.1812(1.2924)	1.2245(0.0777)	1.0000(0.0000)	0.0165(0.0220)	0.00
	400	8.9991(0.9894)	1.2255(0.0785)	1.0000(0.0000)	0.0058(0.0047)	0.00
CLIME	200	6.4771(0.8617)	1.2187(0.0358)	1.0000(0.0000)	0.0126(0.0043)	0.00
	400	9.1221(0.9997)	1.2177(0.0629)	1.0000(0.0000)	0.0043(0.0032)	0.00

Table 5.2.

Quantitive comparison among different estimators on the Erdös-Rényi model. Since A-PISTA and F-APISTA can output valid results for large α’s, their estimators attains better performance than other competitors. The SCIO(P) and CLIME estimators use the ℓ₁ norm regularization with no bias reduction. Thus their performance is worse than the other competitors in both parameter estimation and graph estimation.

Method	d	‖Θ̂−Θ‖F	‖Θ̂−Θ‖1	T. P. R.	F. P. R.	α̂
PISTA	200	3.2647(0.1235)	1.6807(0.2675)	1.0000(0.0000)	0.0587(0.0013)	0.20
	400	4.5609(0.7666)	2.2113(0.3358)	1.0000(0.0000)	0.0295(0.0091)	0.20
	800	5.0751(0.3832)	2.5718(0.2826)	1.0000(0.0000)	0.0099(0.0020)	0.20
APISTA	200	2.2888(0.1141)	1.1644(0.2343)	1.0000(0.0000)	0.0193(0.0005)	0.33
	400	3.2206(0.2733)	1.4974(0.2778)	1.0000(0.0000)	0.0067(0.0100)	0.33
	800	4.0929(0.1862)	1.6347(0.2023)	1.0000(0.0000)	0.0036(0.0008)	0.50
F-APISTA	200	2.2890(0.1161)	1.1647(0.2390)	1.0000(0.0000)	0.0197(0.0007)	0.33
	400	3.2251(0.2702)	1.4928(0.2731)	1.0000(0.0000)	0.0060(0.0102)	0.33
	800	4.0984(0.1891)	1.6397(0.2096)	1.0000(0.0000)	0.0034(0.0009)	0.50
SCIO(P)	200	3.4277(0.5405)	1.5213(0.3223)	1.0000(0.0000)	0.0618(0.0170)	0.00
	400	5.7144(0.8158)	1.9057(0.2933)	0.9994(0.0017)	0.0341(0.0145)	0.00
CLIME	200	3.6297(0.6103)	1.4876(0.2855)	1.0000(0.0000)	0.0581(0.0159)	0.00
	400	5.9206(0.8385)	1.8246(0.2817)	1.0000(0.0000)	0.0320(0.0112)	0.00

Since the convergence of PISTA is very slow when α is large, we only present its results for α = 0.2. APISTA and F-APISTA can work for larger α’s. Therefore they effectively reduces the estimation bias to attain the best statistical performance in both parameter estimation and graph estimation among all estimators. The SCIO(P) and CLIME methods only use ℓ₁ norm without any bias reduction, their performance is worse than the other competitors. Moreover, due to the poor scalability of their solvers, SCIO(P) and CLIME fail to output valid results within 10 hours when d = 800.

We then compare the computational performance of all methods. We use a regularization sequence with N = 50, and λ_N is proper selected such that the graphs obtained by all methods have approximately the same number of edges for each regularization parameter. In particular, the obtained graphs corresponding to λ_N have approximately 0.1 · d(d − 1)/2 edges. To make a fair comparison, we choose the ℓ₁ norm regularization for all methods. We repeat the simulation for 100 times, and the timing results are summarized in Tables 5.3 and 5.4. We see that F-APISTA method is up to 10 times faster than PISTA algorithm, and APISTA is up to 5 times after than PISTA. SCIO(P) and CLIME are much slower than the other three competitors.

Table 5.3.

Quantitive comparison of computational performance on the chain model (in seconds). We see that the F-APISTA method attains the best timing performance among all methods. The SCIO(P) and CLIME methods are much slower than the other three methods.

d	PISTA	APISTA	F-APISTA	SCIO(P)	CLIME
200	0.8342(0.0248)	0.2693(0.0031)	0.1013(0.0022)	2.6572(0.1253)	8.5932(0.5396)
400	3.8782(0.0696)	1.2103(0.0368)	0.4559(0.0308)	25.451(2.5752)	48.235(5.3494)
800	30.014(0.3514)	6.5970(0.2338)	2.4283(0.2605)	315.87(34.638)	460.12(45.121)

Table 5.4.

Quantitive comparison of computational performance on the Erdös-Rényi model (in seconds). We see that the F-APISTA method attains the best timing performance among all methods. The SCIO(P) and CLIME methods are much slower than the other three methods.

d	PISTA	APISTA	F-APISTA	SCIO(P)	CLIME
200	0.5401(0.0248)	0.2048(0.0056)	0.1063(0.0110)	2.712(0.13558)	7.1325(0.7891)
400	3.0501(0.0829)	0.9982(0.0453)	0.4555(0.0071)	26.140(2.1503)	45.160(4.9026)
800	28.581(0.3517)	6.8417(0.7543)	2.7037(0.2145)	332.90(30.115)	442.57(50.978)

5.2 Real Data

We present a real data example to demonstrate the usefulness of the transelliptical graph obtained by the sparse column inverse operator (based on the transformed Kendall’s tau matrix). We acquire closing prices from all stocks of the S&P 500 for all the days that the market was open between January 1, 2003 and January 1, 2005, which results in 504 samples for the 452 stocks. We transform the dataset by calculating the log-ratio of the price at time t + 1 to price at time t. The 452 stocks are categorized into 10 Global Industry Classification Standard (GICS) sectors.

We adopt the stability graphs obtained by the following procedure (Meinshausen and Bühlmann, 2010; Liu et al., 2010):

1. Calculate the graph path using all samples, and choose the regularization parameter at the sparsity level 0.1;

2. Randomly choose 50% of all samples without replacement using the regularization parameter chosen in (1);

3. Repeat (2) 100 times and retain the edges that appear with frequencies no less than 95%.

We choose the sparsity level 0.1 in (1) and subsampling ratio 50% in (2) based on two criteria: The resulting graphs need to be sparse to ease visualization, interpretation, and computation; The resulting graphs need to be stable. We then present the obtained stability graphs in Figure 5.2. The nodes are colored according to the GICS sector of the corresponding stock. We highlight a region in the transelliptical graph obtained by the SCIO method and by color coding we see that the nodes in this region belong to the same sector of the market. A similar pattern is also found in the transelliptical graph obtained by the CLIME method. In contrast, this region is shown to be sparse in the Gaussian graph obtained by the SCIO method (based on the Pearson correlation matrix). Therefore we can see that the SCIO method is also capable of generating refined structures as the CLIME method when estimating the transelliptical graph.

Figure 5.2.

Stock Graphs. We see that both transelliptical graphs reveal more refined structures than the Gaussian graph.

6 Discussions

We compare F-APISTA with a closely related algorithm – the path-following coordinate descent algorithm (PCDA¹) in timing performance. In particular, we give a failure example of PCDA for solving sparse linear regression. Let X ∈ ℝ^n×d denote design matrix and y ∈ ℝⁿ denote the response vector. We solve the following regularized optimization problem,

$$\underset{\mathit{\theta }}{\text{min}}\frac{1}{2n}{\Vert \mathit{y}-\mathbf{X}\mathit{\theta }\Vert }_2^2+{ℛ}_{\lambda }(\mathit{\theta }).$$

We generate each row of the design matrix X_i* from a d-variate Gaussian distribution with mean 0 and covariance matrix Σ ∈ ℝ^d×d, where Σ_kj = 0.75 if k ≠ j and Σ_kk = 1 for all j, k = 1, …, d. We then normalize each column of the design matrix X_*j such that ${\Vert {\mathbf{X}}_{*j}\Vert }_2^2=n$. The response vector is generated from the linear model y = Xθ^* + ε, where θ^* ∈ ℝ^d is the regression coefficient vector, and ε is generated from a n-variate Gaussian distribution with mean 0 and covariance matrix I. We set n = 60 and d = 1000. We set the coefficient vector as ${\theta }_{250}^{*}=3,{\theta }_{500}^{*}=2,{\theta }_{750}^{*}=1.5$, and ${\theta }_j^{*}=0$ for all j ≠ 250, 500, 750. We then set α = 0.95, N = 100, ${\lambda }_N=0.25\sqrt{\text{log }d/n}$, and δ_c = δ_K = 10⁻⁵.

We then generate a validation set using the same design matrix as the training set for the regularization selection. We denote the response vector of the validation set as ỹ ∈ ℝⁿ. Let θ̂^λ denote the obtained estimator using the regularization parameter λ. We then choose the optimal regularization parameter λ̂ by

$$\hat{\lambda }=\underset{\lambda \in \{{\lambda }_1,\dots ,{\lambda }_N\}}{\text{argmin}}{\Vert \mathit{ỹ}-\mathbf{X}{\hat{\mathit{\theta }}}^{\lambda }\Vert }_2^2.$$

We repeat 100 simulations, and summarize the average results in Table 6. We see that F-APISTA and PCDA attain similar timing results. But PCDA achieves worse statistical performance than F-APISTA in both support recovery and parameter estimation. This is because PCDA has no control over the solution sparsity. The overselection irrelevant variables compromise the restricted strong convexity, and make PCDA attain some local optima with poor statistical properties.

Table 6.1.

Quantitative comparison between F-APISTA and PCDA. We see that F-APISTA and PCDA attain similar timing results. But PCDA achieves worse statistical performance than F-APISTA in both support recovery and parameter estimation.

Method	‖θ̂−θ*‖2	‖θ̂𝒮‖0	‖θ̂𝒮c‖0	Correct Selection	Timing
F-APISTA	0.8001(0.9089)	2.801(0.5123)	0.890(2.112)	667/1000	0.0181(0.0025)
PCDA	1.1275(1.2539)	2.655(0.7051)	1.644(3.016)	517/1000	0.0195(0.0021)

Appendix

A Proof of Theorem 4.3

Proof

Since ‖θ⁽⁰⁾‖₀ ≤ s^* + s̃ implies that |𝒜| ≤ s^* + s̃, by Assumption 4.2 and Lemma 4.1, we know that (3.5) is strongly convex over θ_𝒜. Thus it has a unique global minimizer. We then analyze the amount of successive decrease. By the restricted strong convexity of ℱ_λ(θ), we have

$${ℱ}_{\lambda }({\mathit{w}}^{(t+1,k)})-{ℱ}_{\lambda }({\mathit{w}}^{(t+1,k+1)})\ge ({\nabla }_k{ℒ}_{\lambda }({\mathit{\theta }}_k^{(t+1)},{\mathit{w}}_{\backslash k}^{(t+1,k)})+\lambda {\xi }_k^{(t+1)})({\mathit{\theta }}_k^{(t)}-{\mathit{\theta }}_k^{(t+1)})+\frac{\tilde{\rho }-(1)}{2}{({\mathit{\theta }}_k^{(t)}-{\mathit{\theta }}_k^{(t+1)})}^2,$$ (A.1)

where ${\xi }_k^{(t+1)}\in \partial |{\theta }_k^{(t+1)}|$ satisfies the optimality condition of (3.6),

$${\nabla }_k{\widetilde{ℒ}}_{\lambda }({\theta }_k^{(t+1)},{\mathit{w}}_{\backslash k}^{(t+1,k)})+\lambda {\xi }_k^{(t+1)}=0.$$ (A.2)

By combining (A.1) with (A.2), we have

$${ℱ}_{\lambda }({\mathit{w}}^{(t+1,k)})-{ℱ}_{\lambda }({\mathit{w}}^{(t+1,k+1)})\ge \frac{\tilde{\rho }-(1)}{2}{({\theta }_k^{(t+1)}-{\theta }_k^{(t)})}^2,$$

which further implies

$${ℱ}_{\lambda }({\mathit{\theta }}^{(t)})-{ℱ}_{\lambda }({\mathit{\theta }}^{(t+1)})\ge \frac{\tilde{\rho }-(1)}{2}{\Vert {\mathit{\theta }}^{(t)}-{\mathit{\theta }}^{(t+1)}\Vert }_2^2.$$ (A.3)

We then analyze the gap in the objective value yet to be minimized after each iteration. For any θ′, θ ∈ ℝ^d with ${\mathit{\theta }}_{{𝒜}^{\perp }}^{\prime }={\mathit{\theta }}_{{𝒜}^{\perp }}=\mathbf{0}$, by the restricted strong convexity of ℱ_λ(θ), we have

$${ℱ}_{\lambda }(\mathit{\theta }\prime )\ge {ℱ}_{\lambda }(\mathit{\theta })+{(\nabla {\widetilde{ℒ}}_{\lambda }(\mathit{\theta })+\lambda \mathit{\xi })}^T(\mathit{\theta }\prime -\mathit{\theta })+\frac{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}{2}{\Vert \mathit{\theta }\prime -\mathit{\theta }\Vert }_2^2,$$ (A.4)

where ξ ∈ ℝ^d with ξ_𝒜 ∈ ∂‖θ_𝒜‖₁ and ξ_𝒜^⊥ = 0. We then minimize both sides of (A.4) with respect to ${\mathit{\theta }}_{𝒜}^{\prime }$ and obtain

$${ℱ}_{\lambda }({\mathit{\theta }}^{(t+1)})-{ℱ}_{\lambda }(\overline{\mathit{\theta }})\le \frac{1}{2{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}{\Vert {\nabla }_{𝒜}{\widetilde{ℒ}}_{\lambda }({\mathit{\theta }}^{(t+1)})+\lambda {\mathit{\xi }}_{𝒜}^{(t+1)}\Vert }_2^2\stackrel{(\mathrm{i})}{=}\frac{1}{2{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}\sum _{k=1}^{|𝒜|}{[{\nabla }_k{\widetilde{ℒ}}_{\lambda }({\mathit{\theta }}^{(t+1)})-{\nabla }_k{\widetilde{ℒ}}_{\lambda }({\mathit{\theta }}_k^{(t+1)},{\mathit{w}}_{\backslash k}^{(t+1,k)})]}^2\stackrel{(\mathrm{i}\mathrm{i})}{\le }\frac{{\rho }_{+}^2(s^{*}+\tilde{s})}{2{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}\sum _{k=1}^{|𝒜|}{\Vert {\mathit{\theta }}^{(t+1)}-{\mathit{w}}^{(t+1,k)}\Vert }^2\le \frac{(s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})}{2{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}{\Vert {\mathit{\theta }}^{(t+1)}-{\mathit{\theta }}^{(t)}\Vert }^2,$$ (A.5)

where (i) comes from (A.2) and (ii) comes from the restricted strong smoothness of ℒ̃_λ(θ).

Eventually, by combing (A.5) with (A.3), we obtain

$${ℱ}_{\lambda }({\mathit{\theta }}^{(t+1)})-{ℱ}_{\lambda }(\overline{\mathit{\theta }})\le \frac{(s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})}{{\tilde{\rho }}_{-}(1){\tilde{\rho }}_{-}(s^{*}+\tilde{s})}[{ℱ}_{\lambda }({\mathit{\theta }}^{(t)})-{ℱ}_{\lambda }({\mathit{\theta }}^{(t+1)})]\le \frac{(s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})}{{\tilde{\rho }}_{-}(1){\tilde{\rho }}_{-}(s^{*}+\tilde{s})}([{ℱ}_{\lambda }({\mathit{\theta }}^{(t)})-{ℱ}_{\lambda }(\overline{\mathit{\theta }})]-[{ℱ}_{\lambda }({\mathit{\theta }}^{(t+1)})-{ℱ}_{\lambda }(\overline{\mathit{\theta }})]),$$

which further implies

$${ℱ}_{\lambda }({\mathit{\theta }}^{(t+1)})-{ℱ}_{\lambda }(\overline{\mathit{\theta }})\le \left(\frac{s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})}{(s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})+{\tilde{\rho }}_{-}(1){\tilde{\rho }}_{-}(s^{*}+\tilde{s})}\right)[{ℱ}_{\lambda }({\mathit{\theta }}^{(t)})-{ℱ}_{\lambda }(\overline{\mathit{\theta }})].$$ (A.6)

By recursively applying (A.6), we complete the proof.

B Proof of Theorem 4.4

Proof

Before we proceed with the proof, we first introduce several important lemmas.

Lemma B.1

Suppose that Assumptions 4.1 and 4.2 hold. For any λ ≥ λ_N, if θ satisfies,

$${\Vert {\mathit{\theta }}_{{𝒮}^{\perp }}\Vert }_0\le \tilde{s}\text{ and }{\omega }_{\lambda }(\mathit{\theta })\le \lambda /2,$$ (B.1)

then we have

$${\Vert \mathit{\theta }-{\mathit{\theta }}^{*}\Vert }_2\le \frac{21\lambda \sqrt{s^{*}}}{8{\tilde{\rho }}_{-}(s^{*}+\tilde{s})},{\Vert \mathit{\theta }-{\mathit{\theta }}^{*}\Vert }_1\le \frac{21\lambda s^{*}}{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})},\text{ and }{ℱ}_{\lambda }(\mathit{\theta })\le {ℱ}_{\lambda }({\mathit{\theta }}^{*})+\frac{21{\lambda }^2{s}^{*}}{2{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}.$$

Lemma B.2

Suppose that Assumptions 4.1 and 4.2 hold. For any λ ≥ λ_N, if θ satisfies,

$${\Vert {\mathit{\theta }}_{{𝒮}^{\perp }}\Vert }_0\le \tilde{s}\text{ and }{ℱ}_{\lambda }(\mathit{\theta })\le {ℱ}_{\lambda }({\mathit{\theta }}^{*})+\frac{21{\lambda }^2{s}^{*}}{2{\tilde{\rho }}_{-}(s^{*}+\tilde{s})},$$

then we have ‖[𝒯_L,λ(θ)]_𝒮^⊥‖₀ ≤ s̃ for any L ≤ 2ρ₊(s^* + 2s̃).

The proofs of Lemmas B.1 and B.2 are provided in Wang et al. (2014), therefore omitted. Since the initial solution θ^[0] satisfies the approximate KKT condition. By Lemma B.1, we know that θ^[0] satisfies

$${ℱ}_{\lambda }({\mathit{\theta }}^{[0]})\le {ℱ}_{\lambda }({\mathit{\theta }}^{*})+\frac{21{\lambda }^2{s}^{*}}{2{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}.$$ (B.2)

We assume L^[m] ≤ 2ρ₊(s^* + 2s̃). Since ${\Vert {\mathit{\theta }}_{{𝒮}^{\perp }}^{[0]}\Vert }_0\le \tilde{s}$, by (B.2) and Lemma B.2, we have θ^[0.5] = 𝒯_L,λ(θ^[0]) and ${\Vert {\mathit{\theta }}_{{𝒮}^{\perp }}^{[0.5]}\Vert }_0\le \tilde{s}$. Since the coordinate descent subroutine iterates over 𝒜 = supp(θ^[0.5]), its output solution θ^[1] also satisfies ${\Vert {\mathit{\theta }}_{{𝒮}^{\perp }}^{[1]}\Vert }_0\le \tilde{s}$. Since the proximal gradient descent iteration and coordinate descent subroutine decrease the objective value, by (B.2), we also have

$${ℱ}_{\lambda }({\mathit{\theta }}^{[1]})\le {ℱ}_{\lambda }({\mathit{\theta }}^{[0.5]})\le {ℱ}_{\lambda }({\mathit{\theta }}^{[0]})\le {ℱ}_{\lambda }({\mathit{\theta }}^{*})+\frac{21{\lambda }^2{s}^{*}}{2{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}.$$

Then by induction, we know that all successive θ^[m]’s satisfy ${\Vert {\mathit{\theta }}_{{𝒮}^{\perp }}^{[m]}\Vert }_0\le \tilde{s}$ for m = 1.5, 2, 2.5, ….

Now we verify L^[m] ≤ 2ρ₊(s^* + 2s̃). Since we start with a small enough L = ρ₊(1) ≤ 2ρ₊(s^* + 2s̃). If L does not satisfy the stopping criterion for the backtracking line search in (3.4), then we multiply L by 2. Once L attains the interval ∈ [ρ₊(s^* + 2s̃), 2ρ₊(s^* + 2s̃)], it stops increasing. Because by the restricted strong smoothness of ℒ̃_λ(θ), such a step size parameter always guarantees that the algorithm iterates from a sparse θ^[m] to a sparse θ^[m+0.5], and meanwhile satisfies the stopping criterion of the backtracking line search. Thus L^[m] ≤ 2ρ₊(s^* + 2s̃) is verified.

The existence and uniqueness of θ̄^λ has been verified in Wang et al. (2014). Therefore the proof is omitted. We then proceed to derive the geometric rate of convergence to θ̄^λ by the next lemma.

Lemma B.3

Suppose that Assumptions 4.1 and 4.2 hold. For any λ ≥ λ_N, if θ satisfies

$${\Vert {\mathit{\theta }}_{{𝒮}^{\perp }}\Vert }_0\le \tilde{s}\text{ and }{ℱ}_{\lambda }(\mathit{\theta })\le {ℱ}_{\lambda }({\mathit{\theta }}^{*})+\frac{21{\lambda }^2{s}^{*}}{2{\tilde{\rho }}_{-}(s^{*}+\tilde{s})},$$ (B.3)

given L ≤ 2ρ₊(s^* + 2s̃), then we have

$${ℱ}_{\lambda }({𝒯}_{\lambda ,L}(\mathit{\theta }))-{ℱ}_{\lambda }({\overline{\mathit{\theta }}}^{\lambda })\le (1-\frac{1}{8\kappa })[{ℱ}_{\lambda }(\mathit{\theta })-{ℱ}_{\lambda }({\overline{\mathit{\theta }}}^{\lambda })].$$

The proof of Lemma B.3 is provided in Wang et al. (2014), therefore omitted. Since we have verified that all θ^[m]’s satisfy (B.3) and all L^[m]’s satisfy L^[m] ≤ 2ρ₊(s^* + 2s̃) for m = 0, 1, 2, …, Lemma B.3 implies

$${ℱ}_{\lambda }({\mathit{\theta }}^{[m+1]})-{ℱ}_{\lambda }({\overline{\mathit{\theta }}}^{\lambda })\le {ℱ}_{\lambda }({\mathit{\theta }}^{[m+0.5]})-{ℱ}_{\lambda }({\overline{\mathit{\theta }}}^{\lambda })\le (1-\frac{1}{8\kappa })[{ℱ}_{\lambda }({\mathit{\theta }}^{[m]})-{ℱ}_{\lambda }({\overline{\mathit{\theta }}}^{\lambda })],$$ (B.4)

where the first inequality holds because the coordinate descent subroutine decreases the objective value. Then by recursively applying (B.4), we compete the proof.

C Proof of Theorem 4.6

Proof

Before we proceed with the proof of Result (1), we first introduce the following lemma.

Lemma C.1

Suppose that Assumptions 4.1 and 4.2 hold. For any λ ≥ λ_N, if θ satisfies

$${\Vert {\mathit{\theta }}_{{𝒮}^{\perp }}\Vert }_0\le \tilde{s}\text{ and }{\omega }_{\lambda }(\mathit{\theta })\le {\delta }_{\text{max}}\lambda ,$$

then for any λ′ ∈ [λ_N, λ], we have

$${ℱ}_{\lambda \prime }(\mathit{\theta })-{ℱ}_{\lambda \prime }({\overline{\mathit{\theta }}}^{\lambda \prime })\le \frac{21[{\delta }_{\text{max}}\lambda +2(\lambda -\lambda \prime )](\lambda +\lambda \prime )s^{*}}{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}.$$

The proof of Lemmas C.1 is provided in Wang et al. (2014), therefore omitted. If we take λ = λ′ = λ_K and θ = θ̂^{K−1}, then Lemma C.1 implies

$${ℱ}_{{\lambda }_K}({\hat{\mathit{\theta }}}^{\{K-1\}})-{ℱ}_{{\lambda }_K}({\overline{\mathit{\theta }}}^{{\lambda }_K})\le \frac{21s^{*}{\lambda }_K^2}{2{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}.$$ (C.1)

Recall (A.3) in Appendix A. Within each coordinate descent subroutine for λ_K, we have

$${\Vert {\mathit{\theta }}^{(t)}-{\mathit{\theta }}^{(t+1)}\Vert }_2^2\le \frac{2[{ℱ}_{{\lambda }_K}({\mathit{\theta }}^{(t)})-{ℱ}_{{\lambda }_K}({\mathit{\theta }}^{(t+1)})]}{{\tilde{\rho }}_{-}(1)}\le \frac{2[{ℱ}_{{\lambda }_K}({\mathit{\theta }}^{(t)})-{ℱ}_{{\lambda }_K}(\overline{\mathit{\theta }})]}{{\tilde{\rho }}_{-}(1)}.$$ (C.2)

By combining Theorem 4.3 with (C.2), we have

$${\Vert {\mathit{\theta }}^{(t)}-{\mathit{\theta }}^{(t+1)}\Vert }_2^2\le 2{\left(\frac{(s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})}{(s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})+{\tilde{\rho }}_{-}(1){\tilde{\rho }}_{-}(s^{*}+\tilde{s})}\right)}^t\frac{[{ℱ}_{{\lambda }_K}({\mathit{\theta }}^{(0)})-{ℱ}_{{\lambda }_K}(\overline{\mathit{\theta }})]}{{\tilde{\rho }}_{-}(1)}.$$

Therefore given

$$t\ge \text{log}\left(\frac{2[{ℱ}_{{\lambda }_K}({\mathit{\theta }}^{(0)})-{ℱ}_{{\lambda }_K}(\overline{\mathit{\theta }})]}{{\tilde{\rho }}_{-}(1){\delta }_0^2{\lambda }_K^2}\right)/{\text{log}}^{-1}\left(\frac{(s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})}{(s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})+{\tilde{\rho }}_{-}(1){\tilde{\rho }}_{-}(s^{*}+\tilde{s})}\right),$$ (C.3)

we have

$${\Vert {\mathit{\theta }}^{(t)}-{\mathit{\theta }}^{(t+1)}\Vert }_2^2\le 2{\left(\frac{s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})}{(s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})+{\tilde{\rho }}_{-}(1){\tilde{\rho }}_{-}(s^{*}+\tilde{s})}\right)}^t\frac{[{ℱ}_{{\lambda }_K}({\mathit{\theta }}^{(0)})-{ℱ}_{{\lambda }_K}(\overline{\mathit{\theta }})]}{{\tilde{\rho }}_{-}(1)}\le {\delta }_0^2{\lambda }_K^2,$$

which satisfies the stopping criterion of CCDA for λ_K. Since both the proximal gradient descent iteration and coordinate descent subroutine decrease the objective value, we have

$${ℱ}_{{\lambda }_K}({\hat{\mathit{\theta }}}^{\{K-1\}})\ge {ℱ}_{{\lambda }_K}({\mathit{\theta }}^{(0)})\ge {ℱ}_{{\lambda }_K}(\overline{\mathit{\theta }})\ge {ℱ}_{{\lambda }_K}({\overline{\mathit{\theta }}}^{{\lambda }_K})$$ (C.4)

within each coordinate descent subroutine for the K^th stage. By combining (C.1) and (C.3) with (C.4), we have

$$t\ge \text{log}\left(\frac{21s^{*}}{{\tilde{\rho }}_{-}(s^{*}+\tilde{s}){\tilde{\rho }}_{-}(1){\delta }_0^2}\right)/{\text{log}}^{-1}\left(\frac{(s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})}{(s^{*}+\tilde{s}){\rho }_{+}^2(s^{*}+\tilde{s})+{\tilde{\rho }}_{-}(1){\tilde{\rho }}_{-}(s^{*}+\tilde{s})}\right).$$

Before we proceed with the proof of Result (2), we first introduce the following lemma.

Lemma C.2

Suppose that Assumptions 4.1 and 4.2 hold. For any λ ≥ λ_N, if θ satisfies,

$${\Vert {\mathit{\theta }}_{{𝒮}^{\perp }}\Vert }_0\le \tilde{s}\text{ and }{ℱ}_{\lambda }(\mathit{\theta })\le {ℱ}_{\lambda }({\mathit{\theta }}^{*})+\frac{21{\lambda }^2{s}^{*}}{2{\tilde{\rho }}_{-}(s^{*}+\tilde{s})},$$ (C.5)

given L ≤ 2ρ₊(s^* + 2s̃), we have

$${\omega }_{\lambda }({𝒯}_{\lambda ,L}(\mathit{\theta }))\le 3\sqrt{{\rho }_{+}(s^{*}+2\tilde{s})[{ℱ}_{\lambda }({𝒯}_{\lambda ,L}(\mathit{\theta }))-{ℱ}_{\lambda }(\mathit{\theta })]}.$$

The proof of Lemma C.2 is provided in Wang et al. (2014), therefore omitted. Recall that in Appendix B, we have shown that at the K^th stage, θ^[m] satisfies (C.5). The backtracking line search guarantees L^[m+1] ≤ 2ρ₊(s^* + 2s̃). Thus by Lemma C.2, we have

$${\omega }_{{\lambda }_K}({\mathit{\theta }}^{[m+0.5]})\le 3\sqrt{{\rho }_{+}(s^{*}+2\tilde{s})[{ℱ}_{{\lambda }_K}({\mathit{\theta }}^{[m+0.5]})-{ℱ}_{{\lambda }_K}({\mathit{\theta }}^{[m]})]}\le 3\sqrt{{\rho }_{+}(s^{*}+2\tilde{s})[{ℱ}_{{\lambda }_K}({\mathit{\theta }}^{[m+1]})-{ℱ}_{{\lambda }_K}({\overline{\mathit{\theta }}}^{{\lambda }_K})]},$$ (C.6)

where the last inequality holds since the coordinate descent subroutine decreases the objective value. By combining (C.6) with Theorem 4.4, we obtain

$${\omega }_{{\lambda }_K}({\mathit{\theta }}^{[m+0.5]})\le 3\sqrt{{\rho }_{+}(s^{*}+2\tilde{s}){(1-\frac{1}{8\kappa })}^{m+1}[{ℱ}_{{\lambda }_K}({\mathit{\theta }}^{[0]})-{ℱ}_{{\lambda }_K}({\overline{\mathit{\theta }}}^{{\lambda }_K})]}.$$

Thus as long as

$$m\ge \text{log}\left(\frac{9{\rho }_{+}(s^{*}+2\tilde{s})[{ℱ}_{{\lambda }_K}({\mathit{\theta }}^{[0]})-{ℱ}_{{\lambda }_K}({\overline{\mathit{\theta }}}^{{\lambda }_K})]}{{\delta }_K^2{\lambda }_K^2}\right)/{\text{log}}^{-1}(1-\frac{1}{8\kappa }),$$ (C.7)

we have

$${\omega }_{{\lambda }_K}({\mathit{\theta }}^{[m+0.5]})\le 3\sqrt{{\rho }_{+}(s^{*}+2\tilde{s}){(1-\frac{1}{8\kappa })}^m[{ℱ}_{{\lambda }_K}({\mathit{\theta }}^{[0]})-{ℱ}_{{\lambda }_K}({\overline{\mathit{\theta }}}^{{\lambda }_K})]}\le {\delta }_K{\lambda }_K,$$

which satisfies the stopping criterion of AISTA at the K^th stage. By combining (C.1) with (C.7), we have

$$m\ge \text{log}\left(\frac{189\kappa {\lambda }_K^2{s}^{*}}{2{\delta }_K^2{\lambda }_K^2}\right)/{\text{log}}^{-1}(1-\frac{1}{8\kappa }).$$

Result (3) is just a straightforward combination of Results (1) and (2).

To prove Result (4), we need to use Lemma C.1 again. In particular, for K < N, we take λ′ = λ_N, λ = λ_K and θ = θ̂^{K}. We then have

$${ℱ}_{{\lambda }_N}({\hat{\mathit{\theta }}}^{\{K\}})-{ℱ}_{{\lambda }_N}({\overline{\mathit{\theta }}}^{{\lambda }_N})\le \frac{21({\lambda }_K+{\lambda }_N)({\omega }_{{\lambda }_K}({\hat{\mathit{\theta }}}^{\{K\}})+2({\lambda }_K-{\lambda }_N))s^{*})}{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}.$$ (C.8)

Since we have λ_K > λ_N for K = 1, …, N − 1, (C.8) implies

$${ℱ}_{{\lambda }_N}({\hat{\mathit{\theta }}}^{\{K\}})-{ℱ}_{{\lambda }_N}({\overline{\mathit{\theta }}}^{{\lambda }_N})\le \frac{105{\lambda }_K^2{s}^{*}}{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}.$$ (C.9)

For K = N, (C.8) implies

$${ℱ}_{{\lambda }_N}({\hat{\mathit{\theta }}}^{\{N\}})-{ℱ}_{{\lambda }_N}({\overline{\mathit{\theta }}}^{{\lambda }_N})\le \frac{105{\delta }_N{\lambda }_N^2{s}^{*}}{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}.$$ (C.10)

By combining (C.9) with (C.10), we prove Result (4).

D Proof of Lemma 4.8

Proof

Before we proceed with the proof, we need to introduce the following lemma.

Lemma D.1

Suppose that $\mathit{X}~T{E}_d({\mathbf{\Sigma }}^{*},\xi ,{\{f_j\}}_{j=1}^d)$. We have

$$\mathbb{P}({\Vert \mathbf{Ŝ}-{\mathbf{\Sigma }}^{*}\Vert }_{\text{max}}\le \sqrt{2}\pi \sqrt{\frac{\text{log }d}{n}})\ge 1-\frac{1}{d^2}.$$ (D.1)

The proof of Lemma D.1 is provided in Liu et al. (2012a), therefore omitted. We consider the following decomposition,

$${\Vert \nabla ℒ({\mathit{\theta }}^{*})\Vert }_{\infty }={\Vert \mathbf{Ŝ}{\mathit{\theta }}^{*}-\mathit{e}\Vert }_{\infty }={\Vert (\mathbf{Ŝ}-{\mathbf{\Sigma }}^{*}){\mathit{\theta }}^{*}\Vert }_{\infty }\le {\Vert {\mathit{\theta }}^{*}\Vert }_1{\Vert \mathbf{Ŝ}-{\mathbf{\Sigma }}^{*}\Vert }_{\text{max}}.$$ (D.2)

Then by combining (D.1) and (D.2) with the fact ‖θ^*‖₁ ≤ ‖Θ^*‖₁ ≤ M, we have

$$\mathbb{P}({\Vert \nabla ℒ({\mathit{\theta }}^{*})\Vert }_{\infty }\le \sqrt{2}\pi M\sqrt{\frac{\text{log }d}{n}})\ge 1-\frac{1}{d^2},$$

which completes the proof.

E Proof of Lemma 4.9

Proof

Before we proceed with the proof, we first introduce the following lemma.

Lemma E.1

Suppose that $\mathit{X}~T{E}_d({\mathbf{\Sigma }}^{*},\xi ,{\{f_j\}}_{j=1}^d)$. There exists a universal constant c₂ such that

$$\mathbb{P}(\underset{{\Vert \mathit{\theta }\Vert }_0\le s}{\text{sup}}|{\mathit{\theta }}^T(\mathbf{Ŝ}-{\mathbf{\Sigma }}^{*})\mathit{\theta }|\le \frac{c_{2}s\text{ log }d}{n}{\Vert \mathit{\theta }\Vert }_2^2)\ge 1-\frac{2}{d^2}.$$ (E.1)

The proof of Lemma E.1 is provided in Han and Liu (2015), therefore omitted. We consider the decomposition

$${\mathit{\theta }}^T\mathbf{Ŝ}\mathit{\theta }={\mathit{\theta }}^T{\mathbf{\Sigma }}^{*}\mathit{\theta }+{\mathit{\theta }}^T(\mathbf{Ŝ}-{\mathbf{\Sigma }}^{*})\mathit{\theta }.$$ (E.2)

By assuming ‖θ‖₀ ≤ s^* + 2s̃ and

$$|{\mathit{\theta }}^T(\mathbf{Ŝ}-\overline{\mathbf{\Sigma }})\mathit{\theta }|\le c_2\frac{(s^{*}+2\tilde{s})\text{log }d}{n}{\Vert \mathit{\theta }\Vert }_2^2/n,$$

we further have

$${\mathit{\theta }}^T\mathbf{Ŝ}\mathit{\theta }\le {\mathrm{\Lambda }}_{\text{max}}({\mathbf{\Sigma }}^{*})·{\Vert \mathit{\theta }\Vert }_2^2+|{\mathit{\theta }}^T(\mathbf{Ŝ}-{\mathbf{\Sigma }}^{*})\mathit{\theta }|\le {\psi }_{\text{max}}{\Vert \mathit{\theta }\Vert }_2^2+c_2\frac{(s^{*}+2\tilde{s})\text{ log }d}{n}{\Vert \mathit{\theta }\Vert }_2^2,$$ (E.3)

$${\mathit{\theta }}^T\mathbf{Ŝ}\mathit{\theta }\le {\mathrm{\Lambda }}_{\text{min}}({\mathbf{\Sigma }}^{*})·{\Vert \mathit{\theta }\Vert }_2^2-|{\mathit{\theta }}^T(\mathbf{Ŝ}-{\mathbf{\Sigma }}^{*})\mathit{\theta }|\le {\psi }_{\text{min}}{\Vert \mathit{\theta }\Vert }_2^2-c_2\frac{(s^{*}+2\tilde{s})\text{ log }d}{n}{\Vert \mathit{\theta }\Vert }_2^2.$$ (E.4)

Thus for $n\ge 4{\psi }_{\text{min}}^{-1}{c}_2(s^{*}+2\tilde{s})\text{log }d$, we have

$$3{\psi }_{\text{min}}{\Vert \mathit{\theta }\Vert }_2^2/4\le {\mathit{\theta }}^T\mathbf{Ŝ}\mathit{\theta }\le 5{\psi }_{\text{max}}{\Vert \mathit{\theta }\Vert }_2^2/4.$$

Given α = ψ_min/2, we have

$${\rho }_{+}(s^{*}+2\tilde{s})\le 5{\psi }_{\text{max}}/4,{\tilde{\rho }}_{-}(s^{*}+2\tilde{s})\ge {\psi }_{\text{min}}/4,\kappa \le 5{\psi }_{\text{max}}/{\psi }_{\text{min}}.$$ (E.5)

Since we need to secure s̃ = c₁s^* ≥ (144κ² + 250κ)s^*, we take

$$c_1=3600{\psi }_{\text{max}}^2/{\psi }_{\text{min}}^2+1250{\psi }_{\text{max}}/{\psi }_{\text{min}}\ge 72(1+\gamma ){\kappa }^2+250\kappa .$$ (E.6)

In another word, we need

$$n\ge 4{\psi }_{\text{min}}^{-1}{c}_2(1+2c_1)s^{*}\text{log }d\ge 4{\psi }_{\text{min}}^{-1}{c}_2(s^{*}+2\tilde{s})\text{log }d.$$

Eventually by combining (E.1) and (E.5) with (E.6), we complete the proof.

F Proof of Theorem 4.11

Proof

Recall that the output solution θ̂^{N} satisfies ${\Vert {\hat{\mathit{\theta }}}_{{𝒮}^{\perp }}^{\{N\}}\Vert }_0\le \tilde{s}$ and ω_λN ≤ δ_Nλ_N. By Lemma B.1, we have

$${\Vert {\hat{\mathit{\theta }}}^{\{N\}}-{\mathit{\theta }}^{*}\Vert }_1\le \frac{21{\lambda }_N{s}^{*}}{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}\text{ and }{\Vert {\hat{\mathit{\theta }}}^{\{N\}}-{\mathit{\theta }}^{*}\Vert }_2^2\le \frac{7{\lambda }_N^2{s}^{*}}{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}.$$ (F.1)

By the definition of the matrix ℓ₁ and Frobenius norms, we have

$${\Vert {\hat{\mathbf{\Theta }}}^{\{N\}}-{\mathbf{\Theta }}^{*}\Vert }_1=\underset{1\le j\le d}{\text{max}}{\Vert {\mathbf{\Theta }}_{*j}^{\{N\}}-{\mathbf{\Theta }}_{*j}^{*}\Vert }_1\text{ and }{\Vert {\hat{\mathbf{\Theta }}}^{\{N\}}-{\mathbf{\Theta }}^{*}\Vert }_{\mathrm{F}}^2=\sum _{j=1}^d{\Vert {\mathbf{\Theta }}_{*j}^{\{N\}}-{\mathbf{\Theta }}_{*j}^{*}\Vert }_2^2.$$ (F.2)

Recall that we use θ̂^{N} to denote arbitrary column of Θ̂^{N}. By combining (F.2) with (F.1), we have

$${\Vert {\hat{\mathbf{\Theta }}}^{\{N\}}-{\mathbf{\Theta }}^{*}\Vert }_1\le \frac{21{\lambda }_N{s}^{*}}{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}\text{ and }\frac{1}{d}{\Vert {\hat{\mathbf{\Theta }}}^{\{N\}}-{\mathbf{\Theta }}^{*}\Vert }_{\mathrm{F}}^2\le \frac{7{\lambda }_N^2{s}^{*}}{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}.$$

Since all above results rely on Assumptions 4.1 and 4.2, by Lemma 4.8 and 4.9, we have

$${\Vert {\hat{\mathbf{\Theta }}}^{\{N\}}-{\mathbf{\Theta }}^{*}\Vert }_1\le \frac{168\sqrt{2}\pi s^{*}M}{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}\sqrt{\frac{\text{log }d}{n}}\text{ and }\frac{1}{d}{\Vert {\hat{\mathbf{\Theta }}}^{\{N\}}-{\mathbf{\Theta }}^{*}\Vert }_{\mathrm{F}}^2\le \frac{896{\pi }^2{s}^{*}{M}^2\text{log }d}{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})n}$$

with probability 1 − 3d⁻², which completes the proof.

G Proof of Theorem 4.12

Proof

For notational simplicity, we omit the column index j, and use 𝒮 and θ̂^o ∈ ℝ^d to denote the true support 𝒮_j and corresponding oracle estimator Θ̂^o respectively for the j^th column. In particular, we can rewrite (4.6) as follows,

$${\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}=\underset{{\mathit{\theta }}_{𝒮}\in {ℝ}^{|𝒮|}}{\text{argmin}}\frac{1}{2}{\mathit{\theta }}_{𝒮}^T{\mathbf{Ŝ}}_{𝒮𝒮}{\mathit{\theta }}_{𝒮}-{\mathit{e}}_{𝒮}^T{\mathit{\theta }}_{𝒮}\text{ and }{\hat{\mathit{\theta }}}_{{𝒮}^{\perp }}^{\mathrm{o}}=\mathbf{0}.$$ (G.1)

Suppose that Assumption 4.2 holds. We have

$${\mathrm{\Lambda }}_{\text{min}}({\mathbf{S}}_{𝒮𝒮})\ge {\rho }_{-}(s^{*})\ge {\rho }_{-}(s^{*}+2\tilde{s})={\tilde{\rho }}_{-}(s^{*}+2\tilde{s})+\alpha >\alpha ,$$

which implies that S_𝒮𝒮 is positive definite. Thus (G.1) is strongly convex and θ̂^o is a unique minimizer. In our following analysis, we also assume

$${\Vert \mathbf{Ŝ}-{\mathbf{\Sigma }}^{*}\Vert }_{\text{max}}\le \sqrt{2}\pi \sqrt{\frac{\text{log }d}{n}}.$$ (G.2)

By the strong convexity of (G.1), we have

$$0\stackrel{(i)}{\ge }\frac{1}{2}{({\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}})}^T{\mathbf{Ŝ}}_{𝒮𝒮}{\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}-{\mathit{e}}_{𝒮}^T{\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}-\frac{1}{2}{({\mathit{\theta }}_{𝒮}^{*})}^T{\mathbf{Ŝ}}_{𝒮𝒮}{\mathit{\theta }}_{𝒮}^{*}+{\mathit{e}}_{𝒮}^T{\mathit{\theta }}_{𝒮}^{*}\ge {({\mathbf{Ŝ}}_{𝒮𝒮}{\mathit{\theta }}_{𝒮}^{*}-\mathit{e})}^T({\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}-{\mathit{\theta }}_{𝒮}^{*})+\frac{{\rho }_{-}(s^{*})}{2}{\Vert {\mathit{\theta }}_{𝒮}^{*}-{\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}\Vert }_2^2,$$ (G.3)

where (i) comes from the fact that θ̂^o is the minimizer to (G.1). For notational simplicity, we denote ${\hat{\mathbf{\Delta }}}_{𝒮}^{\mathrm{o}}={\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}-{\mathit{\theta }}_{𝒮}^{*}$. By the Cauchy-Schwarz inequality, (G.3) can be rewritten as

$$\frac{{\rho }_{-}(s^{*})}{2}{\Vert {\hat{\mathbf{\Delta }}}_{𝒮}^{\mathrm{o}}\Vert }_2^2\le -{({\mathbf{Ŝ}}_{𝒮𝒮}{\mathit{\theta }}_{𝒮}^{*}-{\mathit{e}}_{𝒮})}^T{\hat{\mathbf{\Delta }}}_{𝒮}^{\mathrm{o}}\le {\Vert {\mathbf{Ŝ}}_{𝒮𝒮}{\mathit{\theta }}_{𝒮}^{*}-{\mathit{e}}_{𝒮}\Vert }_{\text{max}}{\Vert {\hat{\mathbf{\Delta }}}_{𝒮}^{\mathrm{o}}\Vert }_1\le {\Vert \mathbf{Ŝ}{\mathit{\theta }}^{*}-\mathit{e}\Vert }_{\text{max}}\sqrt{s^{*}}{\Vert {\hat{\mathbf{\Delta }}}_{𝒮}^{\mathrm{o}}\Vert }_2,$$

where the last inequality comes from (G.2) and the fact that Δ̂^o contains at most s^* entries. By simple manipulations, we obtain

$${\Vert {\hat{\mathbf{\Delta }}}_{𝒮}^{\mathrm{o}}\Vert }_2\le \frac{2\sqrt{s^{*}}{\Vert \mathbf{Ŝ}{\mathit{\theta }}^{*}-\mathit{e}\Vert }_{\text{max}}}{{\rho }_{-}(s^{*})}\le \frac{2\sqrt{s^{*}}{\Vert {\mathit{\theta }}_{𝒮}^{*}\Vert }_1{\Vert {\mathbf{Ŝ}}_{𝒮𝒮}-{\mathbf{\Sigma }}_{𝒮𝒮}^{*}\Vert }_{\text{max}}}{{\rho }_{-}(s^{*})}\le \frac{2\sqrt{2}\pi M}{{\rho }_{-}(s^{*})}\sqrt{\frac{s^{*}\text{log }d}{n}},$$ (G.4)

where the last inequality comes from the fact ‖θ^*‖₁ ≤ ‖Θ^*‖₁ ≤ M. By combining (G.4) with Assumption 4.3, we obtain

$$\underset{j\in 𝒮}{\text{min}}|{\hat{\theta }}_j^{\mathrm{o}}|\ge \underset{j\in 𝒮}{\text{min}}|{\hat{\theta }}_j^{*}|-{\Vert {\hat{\mathbf{\Delta }}}_{𝒮}^{\mathrm{o}}\Vert }_{\infty }\stackrel{(i)}{\ge }\underset{j\in 𝒮}{\text{min}}|{\theta }_j^{*}|-{\Vert {\hat{\mathbf{\Delta }}}_{𝒮}^{\mathrm{o}}\Vert }_2=(c_3-\frac{2\sqrt{2}\pi }{{\rho }_{-}(s^{*})})M\sqrt{\frac{s^{*}\text{log }d}{n}},$$

where (i) comes from the fact ${\Vert {\hat{\mathbf{\Delta }}}_{𝒮}^{\mathrm{o}}\Vert }_{\infty }\le {\Vert {\hat{\mathbf{\Delta }}}_{𝒮}^{\mathrm{o}}\Vert }_2$. Now we assume $c_3\ge 2\sqrt{2}\pi {\rho }_{-}^{-1}(s^{*})+c_4\sqrt{2}\pi \beta$ for some constant c₄ (will be discussed later). We then have

$$\underset{j\in 𝒮}{\text{min}}|{\hat{\theta }}_j^{\mathrm{o}}|\ge c_4\sqrt{2}\pi M\sqrt{\frac{s^{*}\text{log }d}{n}}\ge {\lambda }_N\beta .$$

Now we show that θ̂^o is a sparse local solution to (2.4). In particular, we have the following decomposition,

$$ℒ{\hat{\mathit{\theta }}}^{\mathrm{o}}=\mathbf{Ŝ}{\hat{\mathit{\theta }}}^{\mathrm{o}}-\mathit{e}=\left[\begin{array}{cc}{\mathbf{Ŝ}}_{𝒮𝒮}\hfill & {\mathbf{Ŝ}}_{𝒮{𝒮}^{\perp }}\hfill \\ {\mathbf{Ŝ}}_{{𝒮}^{\perp }𝒮}\hfill & {\mathbf{Ŝ}}_{{𝒮}^{\perp }{𝒮}^{\perp }}\hfill \end{array}\right]\left[\begin{array}{c}{\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}\hfill \\ \mathbf{0}\hfill \end{array}\right]-\left[\begin{array}{c}{\mathit{e}}_{𝒮}\hfill \\ \mathbf{0}\hfill \end{array}\right].$$

Since ${\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}$ is the minimizer to (G.1), by the KKT condition of (G.1), we have

$${\mathbf{Ŝ}}_{𝒮𝒮}{\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}-{\mathit{e}}_{𝒮}=\mathbf{0}.$$ (G.5)

Moreover, since ${\text{min}}_{j\in 𝒮}|{\hat{\theta }}_j^{\mathrm{o}}|\ge {\lambda }_N\beta$, we have

$$\partial {ℛ}_{{\lambda }_N}({\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}})=-\nabla {\mathscr{H}}_{{\lambda }_N}({\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}})+{\lambda }_N\partial {\Vert {\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}\Vert }_1=\mathbf{0}.$$ (G.6)

By combining (G.5) with (G.6), we have

$${\mathbf{Ŝ}}_{𝒮𝒮}{\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}-{\mathit{e}}_{𝒮}-\nabla {\mathscr{H}}_{{\lambda }_N}({\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}})+{\lambda }_N\partial {\Vert {\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}\Vert }_1=\mathbf{0}.$$ (G.7)

Now we consider

$${\Vert {\mathbf{Ŝ}}_{{𝒮}^{\perp }𝒮}{\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}\Vert }_{\infty }=({\mathbf{Ŝ}}_{{𝒮}^{\perp }𝒮}-{\overline{\mathbf{\Sigma }}}_{{𝒮}^{\perp }𝒮}+{\overline{\mathbf{\Sigma }}}_{{𝒮}^{\perp }𝒮})({\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}-{\mathit{\theta }}_{𝒮}^{*}+{\mathit{\theta }}_{𝒮}^{*})={\Vert ({\mathbf{Ŝ}}_{{𝒮}^{\perp }𝒮}-{\overline{\mathbf{\Sigma }}}_{{𝒮}^{\perp }𝒮}){\hat{\mathbf{\Delta }}}_{𝒮}^{\mathrm{o}}\Vert }_{\infty }+{\Vert {\overline{\mathbf{\Sigma }}}_{{𝒮}^{\perp }𝒮}{\hat{\mathbf{\Delta }}}_{𝒮}^{\mathrm{o}}\Vert }_{\infty }+{\Vert {\mathbf{Ŝ}}_{{𝒮}^{\perp }𝒮}-{\overline{\mathbf{\Sigma }}}_{{𝒮}^{\perp }𝒮}{\mathit{\theta }}^{*}\Vert }_{\infty }=\sqrt{s^{*}}{\Vert {\mathbf{Ŝ}}_{{𝒮}^{\perp }𝒮}-{\overline{\mathbf{\Sigma }}}_{{𝒮}^{\perp }𝒮}\Vert }_{\text{max}}{\Vert {\hat{\mathbf{\Delta }}}_{𝒮}^{\mathrm{o}}\Vert }_2+{\Vert {\hat{\mathbf{\Delta }}}_{𝒮}^{\mathrm{o}}\Vert }_{\infty }+{\Vert {\mathbf{Ŝ}}_{{𝒮}^{\perp }𝒮}-{\overline{\mathbf{\Sigma }}}_{{𝒮}^{\perp }𝒮}\Vert }_{\infty }{\Vert {\mathit{\theta }}^{*}\Vert }_1=\frac{4{\pi }^{2}M{s}^{*}\text{log }d}{{\rho }_{-}(s^{*})n}+\frac{2\sqrt{2}\pi M}{{\rho }_{-}(s^{*})}\sqrt{\frac{s^{*}\text{log }d}{n}}+\sqrt{2}\pi M\sqrt{\frac{\text{log }d}{n}}=(\frac{\sqrt{2}\pi {\psi }_{\text{min}}{c}_2}{(1+2c_3){\rho }_{-}(s^{*})}+\frac{2}{{\rho }_{-}(s^{*})}+1)\sqrt{2}\pi M\sqrt{\frac{s^{*}\text{log }d}{n}}.$$

Therefore as long as

$$c_4\ge \frac{\sqrt{2}\pi {\psi }_{\text{min}}{c}_2}{(1+2c_3){\rho }_{-}(s^{*})}+\frac{2}{{\rho }_{-}(s^{*})}+1,$$

we have ${\Vert {\mathbf{Ŝ}}_{{𝒮}^{\perp }𝒮}{\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}\Vert }_{\infty }\le {\lambda }_N$, which implies that there exists ξ ∈ ∂‖0‖₁ such that

$${\mathbf{Ŝ}}_{{𝒮}^{\perp }𝒮}{\hat{\mathit{\theta }}}_{𝒮}^{\mathrm{o}}-\nabla {\mathscr{H}}_{{\lambda }_N}(\mathbf{0})+{\lambda }_N\mathit{\xi }=\mathbf{0}.$$ (G.8)

By combining (G.7) with (G.8), we know that θ̂^o satisfies the KKT condition and is a local solution to (2.4).

Now we will show that θ̂^o and θ̄^λ_N are identical. Since $\Vert {\overline{\mathit{\theta }}}_{{𝒮}^{\perp }}^{{\lambda }_N}\Vert \le \tilde{s}$ and $\Vert {\hat{\mathit{\theta }}}_{{𝒮}^{\perp }}^{\mathrm{o}}\Vert =0$, we have

$$|\text{supp}({\hat{\mathit{\theta }}}^{\mathrm{o}})\cup \text{supp}({\overline{\mathit{\theta }}}^{{\lambda }_N})|\le s^{*}+\tilde{s}.$$

By the restricted strong convexity of ℱ_λN, we have

$${ℱ}_{{\lambda }_N}({\overline{\mathit{\theta }}}^{{\lambda }_N})\ge {ℱ}_{{\lambda }_N}({\hat{\mathit{\theta }}}^{\mathrm{o}})+{(\nabla {\widetilde{ℒ}}_{{\lambda }_N}({\hat{\mathit{\theta }}}^{\mathrm{o}})+{\lambda }_N{\tilde{\mathit{\xi }}}^{\mathrm{o}})}^T({\overline{\mathit{\theta }}}^{{\lambda }_N}-{\hat{\mathit{\theta }}}^{\mathrm{o}})+\frac{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}{2}{\Vert {\overline{\mathit{\theta }}}^{{\lambda }_N}-{\hat{\mathit{\theta }}}^{\mathrm{o}}\Vert }_2^2,={ℱ}_{{\lambda }_N}({\overline{\mathit{\theta }}}^{{\lambda }_N})+\frac{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}{2}{\Vert {\overline{\mathit{\theta }}}^{{\lambda }_N}-{\hat{\mathit{\theta }}}^{\mathrm{o}}\Vert }_2^2,$$ (G.9)

$${ℱ}_{{\lambda }_N}({\hat{\mathit{\theta }}}^{\mathrm{o}})\ge {ℱ}_{{\lambda }_N}({\overline{\mathit{\theta }}}^{{\lambda }_N})+{(\nabla {\widetilde{ℒ}}_{{\lambda }_N}({\overline{\mathit{\theta }}}^{{\lambda }_N})+{\lambda }_N\tilde{\mathit{\xi }})}^T({\hat{\mathit{\theta }}}^{\mathrm{o}}-{\overline{\mathit{\theta }}}^{{\lambda }_N})+\frac{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}{2}{\Vert {\hat{\mathit{\theta }}}^{\mathrm{o}}-{\overline{\mathit{\theta }}}^{{\lambda }_N}\Vert }_2^2,={ℱ}_{{\lambda }_N}({\overline{\mathit{\theta }}}^{{\lambda }_N})+\frac{{\tilde{\rho }}_{-}(s^{*}+\tilde{s})}{2}{\Vert {\overline{\mathit{\theta }}}^{{\lambda }_N}-{\hat{\mathit{\theta }}}^{\mathrm{o}}\Vert }_2^2,$$ (G.10)

where ξ̃ and ξ̃^o are defined as

$$\tilde{\mathit{\xi }}=\underset{\xi \in \partial {\Vert {\overline{\mathit{\theta }}}^{{\lambda }_N}\Vert }_1}{\text{argmin}}{\Vert \nabla {\widetilde{ℒ}}_{{\lambda }_N}({\overline{\mathit{\theta }}}^{{\lambda }_N})+{\lambda }_N\mathit{\xi }\Vert }_{\infty }\text{ and }{\tilde{\mathit{\xi }}}^{\mathrm{o}}=\underset{\xi \in \partial {\Vert {\hat{\mathit{\theta }}}^{\mathrm{o}}\Vert }_1}{\text{argmin}}{\Vert \nabla {\widetilde{ℒ}}_{{\lambda }_N}({\hat{\mathit{\theta }}}^{\mathrm{o}})+{\lambda }_N\mathit{\xi }\Vert }_{\infty }.$$

By combining (G.9) with (G.10), we have ${\Vert {\hat{\mathit{\theta }}}^{\mathrm{o}}-{\overline{\mathit{\theta }}}^{{\lambda }_N}\Vert }_2^2=0$, i.e., θ̂^o = θ̄^λ_N. Note that we choose ${\lambda }_N=c_4\sqrt{2}\pi M\sqrt{\text{log }d/n}$, which is different from the selected regularization parameter in Assumption 4.8. But as long as we have $c_4\sqrt{s^{*}}\ge 8$, which is not an issue under the high dimensional scaling

$$M,s^{*},n,d\to \infty \text{ and }M{s}^{*}\text{log }d/n\to 0,$$

λ_N ≥ 8‖∇ℒ(θ^*)‖_∞ still holds with high probability. Since the above results universally hold over all columns of Θ̅^λ_N and Θ^* under Assumptions 4.1 and (4.2), by Lemmas 4.8 and 4.9, we obtain Θ̂^o = Θ̅^λ_N, which completes the proof.