Abstract
Facial action unit (AU) detection from video has been a long-standing problem in automated facial expression analysis. While progress has been made, accurate detection of facial AUs remains challenging due to ubiquitous sources of errors, such as inter-personal variability, pose, and low-intensity AUs. In this paper, we refer to samples causing such errors as hard samples, and the remaining as easy samples. To address learning with the hard samples, we propose the Confidence Preserving Machine (CPM), a novel two-stage learning framework that combines multiple classifiers following an “easy-to-hard” strategy. During the training stage, CPM learns two confident classifiers. Each classifier focuses on separating easy samples of one class from all else, and thus preserves confidence on predicting each class. During the testing stage, the confident classifiers provide “virtual labels” for easy test samples. Given the virtual labels, we propose a quasi-semi-supervised (QSS) learning strategy to learn a person-specific (PS) classifier. The QSS strategy employs a spatio-temporal smoothness that encourages similar predictions for samples within a spatio-temporal neighborhood. In addition, to further improve detection performance, we introduce two CPM extensions: iCPM that iteratively augments training samples to train the confident classifiers, and kCPM that kernelizes the original CPM model to promote nonlinearity. Experiments on four spontaneous datasets GFT [15], BP4D [56], DISFA [42], and RU-FACS [3] illustrate the benefits of the proposed CPM models over baseline methods and state-of-the-art semisupervised learning and transfer learning methods.
Index Terms: Transfer learning, semi-supervised learning, support vector machine (SVM), confident classifiers, self-paced learning, easy-to-hard, facial action unit (AU) detection
I. Introduction
Facial expressions convey varied and nuanced meanings. Small variations in the timing and packaging of smiles, for instance, can communicate a polite greeting, felt enjoyment, embarrassment, or social discomfort. To analyze information afforded by facial expressions, the most widely used approach is the Facial Action Coding System (FACS) [24]. FACS describes facial activities in terms of anatomically based Action Units (AUs). AUs can occur alone or in combinations to represent nearly all possible facial expressions. AUs have a temporal envelope that minimally includes an onset (or start) and an offset (or stop), and may include changes in intensity. There has been an encouraging progress on automated facial AU detection during the past decades, especially for posed facial actions [14], [20], [47], [52], [59].
Accurate detection of facial AUs remains challenging due to numerous sources of errors, including quality and quantity of annotations [40], head yaw [28], low intensity [29], and individual differences [1], [13], [48], [54]. To address these variabilities, one typical option is a nonlinear model, which, yet, often leads to overfitting and thus impairs generalizability. Standard supervised methods, such as a linear SVM [25] or AdaBoosting [27], aim to separate positive and negative samples using a single classifier. Single-classifier approaches may perform well on AUs with high intensities and frontal faces. However, they often fail on subtle AUs or AUs with appearance changes caused by head poses or illumination.
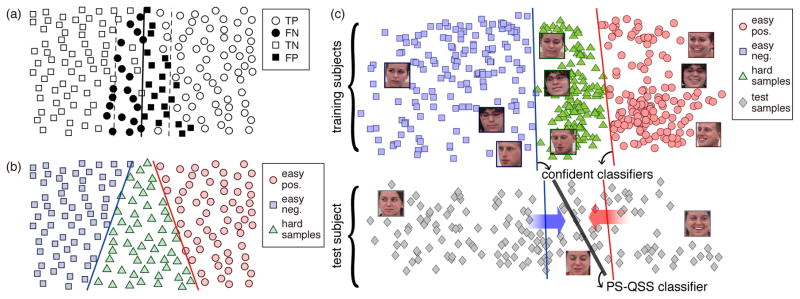
Single-classifier approaches are limited due to the lack of a hyperplane with confident separation. Fig. 1(a) illustrates a linear SVM separating samples from two overlapped classes. Most samples within the SVM margin consist of false positives (FP) and false negatives (FN), which result in undesirable ambiguities for training a reliable classifier. Throughout this paper, we refer to these ambiguous samples as hard samples, and the remaining as easy samples. To address the learning with the hard samples, we propose to train two confident classifiers. Fig. 1(b) depicts the confident classifiers learned on the two overlapped classes. Unlike standard single-classifier approaches, each confident classifier separates easy samples of one class from all else, and thus is able to focus on predicting one class with high confidence.
Fig. 1.
The main idea of Confidence Preserving Machine (CPM): (a) A standard single-margin classifier identifies true positive (TP), true negative (TN), false positive (FP) and false negative (FN). Data within the margin (dashed lines) consist of mostly FP and FN, producing undesired ambiguities for training a classifier. (b) The proposed confident classifiers, two hyperplanes that are not necessarily parallel, reveal easy and hard samples for preserving confident predictions in each class. (c) The proposed CPM, consisting of confident classifiers and a person-specific (PS) classifier using a quasi-semi-supervised (QSS) learning strategy, is trained to propagate predictions from confident test samples (easy test samples) to hard ones.
With the confident classifiers, this paper proposes the Confidence Preserving Machine (CPM), a novel two-stage learning framework that combines multiple classifiers following an “easy-to-hard” strategy. Fig. 1(c) illustrates the CPM framework. During the training stage, CPM learns two confident classifiers, which identify hard samples as the ones lying between the two hyperplanes and easy samples as the ones that both classifiers give the same prediction. Given a test video in the second stage, CPM learns a person-specific (PS) classifier using a quasi-semi-supervised (QSS) learning strategy. We term this classifier a PS-QSS classifier. Specifically, CPM first uses confident classifiers to assign “virtual” labels to easy test samples. Then, CPM learns the PS-QSS classifier by propagating from the virtual labels to hard test samples based on an assumption of spatio-temporal smoothness. That is, frames that are closer in both the feature space and the temporal space should share similar predictions.
In addition, we show that the proposed CPM can be further extended to improve the detection performance. Specifically, we propose two extensions of CPM: (1) iCPM learns the confident and PS-QSS classifiers by iteratively adding easy test samples into the training set. Confident classifiers retrained on this augmented set can potentially yield improvement due to extra information from the test domain. (2) kCPM learns the classifiers in a kernelized manner. Unlike standard kernel methods with complexity quadratic in the number of samples, we develop a sample selection strategy that effectively reduces the sample size for training confident classifiers. Evaluation was performed on four benchmark datasets, namely GFT [15], BP4D [56], DISFA [42], and RU-FACS [3]. Comprehensive experiments show that both iCPM and kCPM outperformed the regular CPM, baseline methods (e.g., SVM and AdaBoosting) and state-of-the-art methods based on supervised learning, semi-supervised learning, and transfer learning.
A preliminary version of this work appeared as [55]. In this paper, we provide technical details in solving the PS-QSS classifier, present extended results with more comparisons and datasets, and offer an in-depth analysis of the hard samples discovered by CPM. The rest of the paper is organized as follows. We review the related work in Sec. II. Sec. III introduces the framework of CPM and each of its components. In Sec. IV, we present the two methods of iCPM and kCPM, and provide detailed comparisons between CPM and other related learning techniques. Sec. V experimentally evaluates and compares CPM with alternative approaches. In Sec. VI, we conclude and describe future direction.
II. Related Work
Facial expression analysis is known challenging for numerous sources of errors. Below we review previous efforts to reduce such errors, and semi-supervised learning and transfer learning that motivate the proposed CPM.
Errors reduction
There have been several efforts in facial expression analysis to address previously identified or suspected sources of error. To recognize subtle expressions, prior studies have investigated various combinations of features and classifiers, such as spatio-temporal directional features extracted by robust PCA [51], and a temporal interpolation {SVM,MKL,RF} classifiers [45]. Another source of error involves head pose. For such cases, previous work sought to model head pose and expression simultaneously, e.g., using a particle filter with multi-class dynamics [19] or a variable-intensity template [38]. Individual differences also cause errors, and can be approached using domain adaption methods [13], [48]. Other works seek to jointly recognize face identity and facial expression using a dictionary-based component separation algorithm [50]. However, other sources of error, such as human aging [35], are possible, and others may be unknown. Addressing specific sources of error individually may impair generalizability and fails to address unknown sources of error, which can further impair generalizability.
Instead of dealing with specific factors, CPM is a nonspecific method that copes with sources of error both recognizable and not. Regardless of the type of error, CPM is able to automatically identify easy samples from hard ones, preserve confident knowledge using confident classifiers, and then transfer to a person-specific classifier.
Semi-supervised learning (SSL)
SSL has emerged as a promising approach to incorporate unlabeled data for training. This approach makes one or more assumptions on relationships between input and label space [9]. The smoothness assumption enforces samples within a neighborhood to share similar labels, and can be typically modeled by a graph-based method [41]. The cluster assumption encourages clusters of samples to obtain same labels. This assumption has been shown to be equivalent to low-density separation [10], and can be extended to entropy minimization [32]. The manifold assumption considers that samples lie on a low-dimensional manifold. As the closest approach to CPM, Laplacian SVM (Lap-SVM) [5], [43] incorporated this assumption as a regularization for learning an SVM. Other work explored the combination of the three assumptions using a boosting framework [12]. Interested readers are referred to [9], [58] for a more extensive review.
Notwithstanding the progress that has been made by pursuing these assumptions, they could be insufficient. As noted, many sources of error may not be modeled or even known. In the AU detection scenario where feature distribution across subjects could change significantly [13], [48], the smoothness and manifold assumptions in standard SSL could be violated because closer data may contain different labels. CPM utilizes a quasi-semi-supervised approach that preserves spatial-temporal smoothness on unlabeled test samples.
Transfer learning
Transfer learning considers discrepancy caused by domain differences. Presuming that each domain can be represented as a linear subspace, several studies proposed to find intermediate spaces so that the domain mismatch can be reduced. Techniques include subspace alignment [26], and geodesic distances on a Grassmann manifold [30], [31]. The discrepancy between raw features can be alleviated by learning a transformation [36], [44]. Some explore the idea of importance re-weighting to adapt one or multiple training domain(s) to a test domain [7], [34], [49]. Following this direction, Selective Transfer Machine (STM) [13] was proposed to personalize classifiers for facial AU detection by selecting a subset of training samples that form a distribution close to the test subject. Recently, there have been several studies that describe a training domain as classifier parameters, and assume that an ideal classifier for the test domain can be represented as a combination of the learned classifiers [1], [21], [22], [53].
CPM differs from transfer learning in three ways. One, most transfer learning methods emphasize errors caused by individual differences, head pose or AU intensity; CPM has no such assumption. Two, most transfer learning methods are frame-based; CPM considers a spatial-temporal smoothness for video data. Three, most transfer learning methods seek multiple sources domains [21], [22], [48] or importance re-weighting [13], [49], which could be computationally expensive; CPM avoids so using a sample selection strategy.
III. Confidence Preserving Machine (CPM)
A. Overview of CPM for AU detection
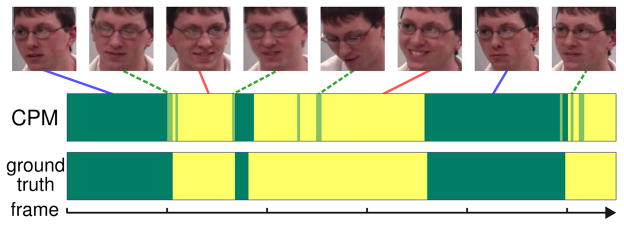
Facial AU detection typically deals with data in the form of videos, i.e., each subject has at least a clip of video instead of a single image. Among these videos, some frames are easier to tell an AU presence than others. Fig. 2 shows the easy and hard frames from a particular video. Because hard samples are intrinsically inseparable, treating easy and hard samples equally would degrade the performance of a standard single-hyperplane classifier (e.g., SVM [25]).
Fig. 2.
Illustration of CPM on identifying AU12 from a real video. Dashed lines (light green) indicate the hard frames due to low intensities and head pose; solid lines indicate the easy samples for positive (light yellow) and negative (dark green) ones.
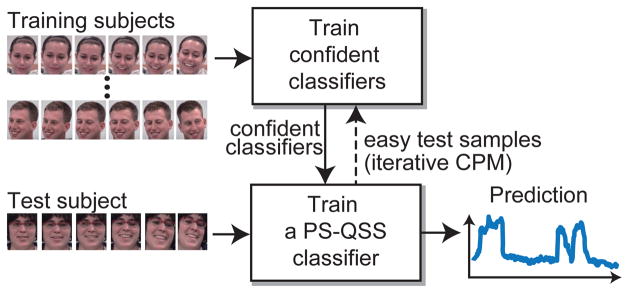
To address these issues, we propose the CPM, a two-stage framework that exploits multiple classifiers with an easy-to-hard strategy. Fig. 3 illustrates the CPM framework. The first stage, training confident classifiers, aims to find a pair of classifiers that distinguish easy and hard samples in training subjects. We define the easy samples as the ones on which the predictions of the confident classifiers agree with each other, and the hard samples otherwise. Compared to the standard approaches that use a single classifier, each confident classifier focuses on predicting one class. The confident classifiers, therefore, are able to identify whether an unseen sample is easy or not, and predict confidently on it. In the second stage, training a person-specific classifier, we first identify easy test samples by applying the trained confident classifiers. With confident predictions on easy test samples, we introduce a quasi-semi-supervised approach to train a person-specific classifier, which we term as a PS-QSS classifier. The PS-QSS classifier determines the label of the hard samples by propagating consistently the predictions in space and time.
Fig. 3.
The proposed two-stage CPM framework: Given training videos, the confident classifiers are first trained, and then are passed to train a PS-QSS classifier, which makes the final predictions on the test video. In iterative CPM, easy test samples are selected to iteratively expand the training set.
B. Train confident classifiers
The first stage in CPM is to train the confident classifiers, a pair of classifiers that aim to cooperatively identify and separate easy and hard samples in the training set with index 𝒟 = {1, 2, . . . , n}, where yi∈{+1,−1} denotes a label and n is the size of the training set.
In this paper, we cast the AU detection problem as a binary classification problem, although multi-label formulations have been proposed (e.g.., [57]). We formulate CPM in the context of maximum margin learning extending the support vector machine (SVM), but it can be applicable to any other supervised learning paradigm. The intuition behind the confident classifiers is to learn two classifiers, one for the positive class, represented by a hyperplane w+, and will predict confidently positive samples; similarly, w− is for the negative class. We consider the easy samples ℰ as the subset of training samples where both classifiers make the same prediction and hard samples ℋ otherwise. It is important to note that w+ and w− classify the easy positive and negative samples respectively and they are not necessarily parallel. Mathematically speaking,
| (1) |
where ℰ and ℋ denote the index sets of easy samples and hard samples, and we denote the confident classifiers (w+,w−), or wy. Learning the confident classifiers can be done iteratively by maximizing the margin as:
| (2) |
where yi is the ground truth label, is a relabel of a hard training sample xj that will be explained below. ξi and ξj are non-negative slack variables for easy samples and hard samples respectively, to take into account misclassification. The easy samples will preserve the original labels yi, whereas we will relabel the hard samples as for w+ and as for w−, to make the classifiers as confident as possible.
Alg. 1 summarizes the alternating procedure of solving (2), which involves the easy samples ℰ, the hard samples ℋ, and the confident classifiers (w+,w−). Given ℰ and ℋ, the confident classifiers (w+,w−) are solved as standard SVMs [25]. Given (w+,w−), ℰ and ℋ are inferred using Eq. (1).
Note that the convergence of this alternating procedure is not guaranteed; instead we set a maximum iteration. The set of hard samples is initialized as empty. In the later iterations, hard samples are updated as those misclassified by both w+ and w−. The relabeling strategy enables w+ and w− to preserve confident predictions in each class by adjusting the labels for hard samples. Here, we explore two relabeling strategies:
Holistic relabeling: The most straightforward strategy is to relabel all hard samples as +1 when training w−, and −1 when training w+, i.e., , ∀xj ∈ ℋ. We term this strategy holistic relabeling. The main advantage of holistic relabeling is its low computational complexity.
- Localized relabeling: Holistic relabeling may result in some unnecessary hard samples if signal noise exists. To gain more robustness against signal noise, we relabel an hard sample xj as +1 only when there exists a neighboring support instance xk with positive ground truth label, and similarly for relabeling xj as −1. We term this localized relabeling. Denote the set of samples with support instances as 𝒮y = {j ∈ ℋ|∃k ∈ ℋ : d(xj, xk) ≤ r, yk = y}, where r is a threshold and d(xj, xk) is the distance between xj and xk. The relabeling is formulated as
(3)
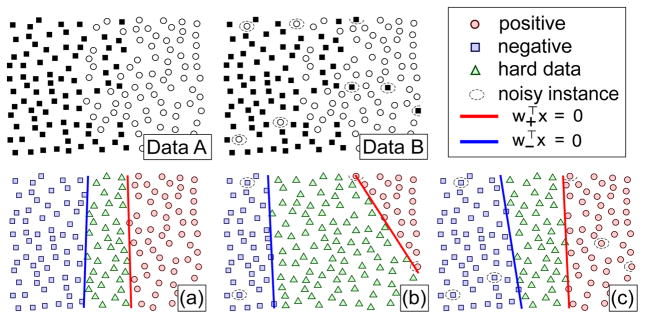
For simplicity, both strategies use binary labels. Note that other relabeling strategies are directly applicable, e.g., weighting the relabels similar to those in DA-SVM [7], or introducing the concepts of bags as in MIL [2]. Fig. 4 illustrates the two relabeling strategies on synthetic examples. (a) and (b) illustrate the confident classifiers learned using holistic relabeling on A and B, respectively. As can be seen, the confident classifiers move toward the noisy instances in (b), showing that the holistic relabeling is improper for the presence of noise. Fig. 4(c) illustrates the result using localized relabeling, which is more robust to noisy instances.
Fig. 4.
Illustration of two relabeling strategies. Data A and B are two synthetic data without and with noisy instances, respectively. (a)~(c) show the confident classifiers learned on the relabeled data using holistic relabeling on A, holistic relabeling on B, and localized relabeling on B, respectively.
Algorithm 1.
Train confident classifiers
| Input: Data and its index set 𝒟 = {1, 2, . . . , n} | |
| Output: Confident classifiers (w+,w−), easy samples ℰ and hard samples ℋ | |
| 1: | Init: ℰ ←𝒟; ℋ←∅; |
| 2: | repeat |
| 3: | (w+,w−) ← solve (2) with fixed ℰ and ℋ; |
| 4: | Update easy and hard samples (ℰ,ℋ) using (1); |
| 5: | Update relabels ; |
| 6: | until convergence or exceed max iteration |
C. Train a person-specific (PS) classifier using a quasi-semisupervised (QSS) strategy
In the previous section, we have discussed how to train the confident classifiers. As pointed out first by Chu et al. [13], a generic classifier trained on many subjects is unlikely to generalize well to an unseen subject because of the domain discrepancy between the training and the test distributions that vary according to camera model, intra-personal variability, illumination, etc. Chu et al. [13] showed that person-specific (PS) and a personalized model outperformed existing methods. The distinction between PS and personalized models are as follows. PS classifiers are referred to the ones trained in only one subject. Personalized classifiers are generic classifiers that are adapted to a particular subject.
Recall our goal is to train a PS classifier for a test subject. To obtain such a classifier, CPM first collects “virtual labels” from the predictions of confident classifiers w+ and w−. Since the confident classifiers are trained with many subjects, they are likely to generalize well to easy samples. However, there remain hard samples that CPM finds difficult to identify. To disambiguate the hard samples, CPM adopts a person-specific classifier using a quasi-semi-supervised (QSS) strategy. In particular, we adopt a Laplacian to enforce label smoothness on spatially and temporally neighboring samples.
Let us assume that we have a m-frame test video denoted by Xte = [x1, x2, . . . , xm]⊤ with index 𝒟te = {1, 2, . . . , m}. CPM first identifies the easy test samples ℰt as the ones on which the confident classifiers predict consistently, i.e., , and is a virtual label for an easy test sample. Once these virtual labels are obtained, CPM propagates labels to the hard samples with a semi-supervised strategy minimizing:
| (4) |
where γs and γI control the importance of regularizations.
S(wt,Xte) is defined as the smoothness term. The intuition behind S is to preserve spatial-temporal relations in the label space, and we propose the smoothness regularizer as:
| (5) |
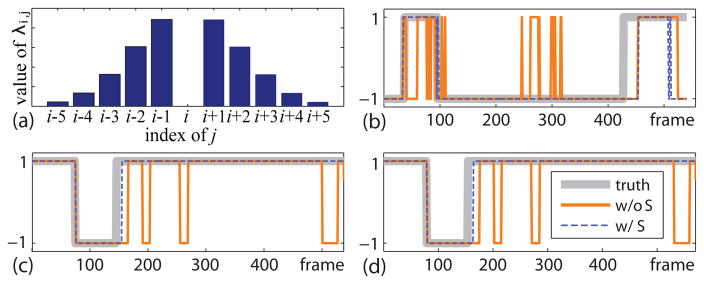
where is the PS classifier prediction on sample x, Xte are the test samples, T controls the window size for which frames to include in the smoothing, and λij is a weight parameter that emphasizes closer temporal neighbors than further ones (i.e., the closer in time two frames are the more similar their decision values are). We determine λij using a Gaussian distribution centered at the frame of interest, as illustrated in Fig. 5(a) where T = 5. We define a selection parameter , excluding the frames that are far away in feature space. dij is the distance of frame i and j in feature space. Zi is the normalization term such that . After some linear algebra, we can rewrite Eq. (5) in matrix form as
Fig. 5.
(a) an example of λ with T = 5. (b)~(d) show the effectiveness of the smoothness term S on AU6 on video 2F01_11, AU12 on video 2F01_09, and AU17 on video 2F01_09, respectively. The y-axis denotes AU occurrence (+1: presence, −1: absence).
| (6) |
where D ∈ ℝm×m, .
The sums of D’s rows equal zeros, i.e., Σj Dij = 0. Therefore, the smoothness matrix D enforces the neighboring samples in both the feature space and the temporal space to have similar predictions. Please refer details for solving wt to Appendix A.
Relations to Laplacian Matrix
Denote C = D⊤D for notational convenience. Both C and Laplacian matrix L imposing smoothness on neighboring samples. They share several properties, e.g., they are positive semidefinite, sum of each row and column are zero. However, C considers both temporal and spatial constrains while L only consider spatial constrains. Consequently, they have mathematically differences in formulation. D assembles the incidence matrix ∇ where L = ∇⊤∇. Both D and ∇ can be interpreted by a directed graph, but in different ways. Let’s denote their corresponding graphs as 𝒢D = {ℰD, 𝒱D} and 𝒢∇ = {ℰ∇, 𝒱∇}, respectively. The i-th row of ∇ ∈ ℤ|ℰ∇|×|𝒱∇| denotes a directed edge 〈j, k〉, with non-zero entries ∇ij = −1 and ∇ik = +1. While D ∈ ℝ|𝒱D|×|𝒱D|, a non-zero element Dij < 0, i ≠ j corresponds to a directed edge 〈j, i〉 in 𝒢. The absolute value of Dij is the weight of edge 〈j, i〉. Note that if there exists an edge 〈j, i〉, then edge 〈i, j〉 exists. But their weights are not necessary the same, thus D is not symmetric. Differences can also be found if we regard L and C as two operators. Taking an operation on f = [f(x1), . . . , f(xm)]⊤, f⊤ Lf =Σi>j wij (f(xi) – f(xj))2, where wij denotes the weight. While, f⊤ Cf = S(wt,Xte), as Eq. (5) shown, has a form of f⊤Cf =Σi>j aij (f(xi) – f(xj))2+Σi>j bijf(xi)f(xj)+ c, where aij, bij, and c are coefficients. The extra item of f(xi)f(xj) ascribes to the temporal constrain.
Fig. 5 shows the effectiveness of the smoothness term S on 3 AUs in the BP4D dataset [56]. To start the label propagation, 2.5% frames were randomly selected from each video as the estimated labels of easy instances. We compare the prediction on the rest 97.5% frames by training a linear SVM only using the labeled frames, and one with the smoothness term S over all the labeled and unlabeled data. As can be seen, compared to the ground truth, the prediction with the smoothness term performs more consistent result across three AUs.
In some cases, easy test samples are unavailable, and thus cause Eq. (4) failing to learn wt. Most singular cases occur in unbalanced AUs with few positive samples. For instance, the appearance of AU1 in a test subject is relatively rare. In such cases, the confident classifiers are unlikely to discover easy positive samples from the test subject. We are unable to learn wt by Eq. (4) because none easy positive samples are detected. To address these cases, we found heuristically that provides good predictions.
IV. Extensions of CPM
While CPM has reported good results, this section describes two extensions: (1) Iterative CPM (iCPM) incorporates a progressive labeling strategy by gradually including test data in the training set. (2) Kernel CPM (kCPM) extends CPM to incorporate non-linear decision boundaries.
A. Iterative CPM (iCPM)
CPM learns in sequential fashion the confident classifiers (Sec. III-B) and the PS-QSS classifier (Sec. III-C). So, the PS-QSS classifier depends indirectly on the training data through confident classifiers. However, it is likely that there is mismatch between the training and test data [13], [48], and the confident classifiers might not generalize well even in the easy samples. To address this issue, we propose iterative CPM (iCPM) that jointly learns the confident and PS classifiers.
Algorithm 2.
Iterative Confidence Preserving Machine
| Input: labeled training data with index set 𝒟 = {1, 2, . . . , n}, unlabeled test data with index set 𝒟te = {1, 2, . . . , m} | ||
| Output: person-specific classifier wt | ||
| 1: | ℰ ←𝒟, ℋ←∅; | |
| 2: | (w+,w−) ← solve (2); | |
| 3: | (ℰ,ℋ) using (1); | |
| 4: | repeat | |
| 5: | Update relabels , ∀j ∈ ℋ; | |
| 6: | (w+,w−) ← solve (2) with fixed ℰ and ℋ; | |
| 7: | Estimate virtual labels , | |
|
|
||
| 8: | ; | |
| 9: | if ∃i, j ∈ ℰt, s.t. ŷi = −1, ŷj = 1 then | |
| 10: | wt ← solve (4) given Xte and ; | |
| 11: | else | |
| 12: | ; | |
| 13: | end if | |
| 14: | Update ; | |
| 15: | Update (ℰ,ℋ) ← (1); | |
| 16: | ℰ ←ℰ ∪ℰt; | |
| 17: | until convergence | |
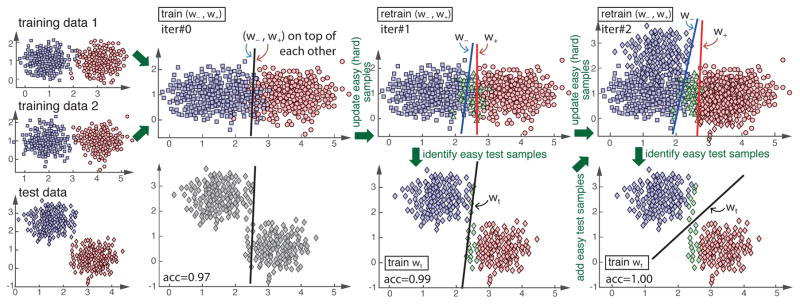
In iCPM, at each iteration, the easy test samples are selected to be part of the training for the confident classifiers, so the confident classifiers is trained with test data (but no labels of test data are provided). Alg. 2 summarizes the steps for iCPM algorithm. Fig. 6 illustrates a synthetic example. In Fig. 6, the training and test distributions are different. In the initialized step, all the training data are labeled as easy-samples, so the confident classifiers are basically a standard SVM, and the two confident classifiers are the same. This classifier achieves 97% accuracy on test data. In the first iteration, we update the hard-samples (green triangles) and re-train the confident classifiers. The confident classifiers identify easy samples (blue and red diamonds) in test data, and the PS-QSS classifier labels the hard-samples (green diamonds), and learns the PS-QSS classifier (the black line), achieving 99% of accuracy. Finally, in the second iteration, the easy and hard samples are again updated to train the confident classifiers and the PS-QSS classifier achieving 100% of classification accuracy.
Fig. 6.
A Synthetic example of iCPM. The first column illustrates two training subjects (rectangles and circles) and a test subject (diamonds). A same color indicates the same class. The second, third, and forth column illustrates the initialization and two iterations in Alg. 2, respectively. Points in blue and red colors are easy samples, while those in green are hard ones. (This figure is best shown in color copies).
Complexity
As in standard transfer learning methods [21], [49], iCPM incorporates all the training data to compute a PS-QSS classifier. In every iteration, iCPM learns each of the two confident classifier from the union of training samples and easy test samples, and learns a PS-QSS classifier from the test samples. Despite the fact that every iteration involves learning two confident classifiers and a PS-QSS classifier, iCPM is relatively efficient in training due to the learning of linear classifiers. In Alg. 2, solving (2) with fixed ℰ and ℋ and solving (4) are both linear with complexity 𝒪(max(n, d)min(n, d)2) [8], where d is the dimension of features; n is the number of samples in ℰ ∪ℋ in (2), or the number of test samples in (4).
B. Kernel CPM (kCPM)
CPM and iCPM are efficient to learn because they assume a linear decision boundary. However, most practical cases would require a non-linear decision boundary to separate real data. Non-linear boundaries are likely to lead a better separation between easy and hard samples. A simple approach to extend our proposed CPM model is to directly apply kernel tricks in (2) and (4). However, the directly kernelization of CPM is time and memory consuming since the training of confident classifiers (2) involves around 100,000 samples. To reduce the computational burden, we design a strategy to select samples in the training of the confident classifiers. Below, we present the details to kernelize the two steps of kCPM, i.e., training confident classifiers and training PS-QSS classifier.
Algorithm 3.
Sample selection for kCPM
| Input: Positive training samples 𝒟+, negative training samples 𝒟−, distance threshold r, order flag positive_first. | |
| Output: Selected points set 𝒮 | |
| 1: | 𝒮 ←∅; |
| 2: | if positive_first then |
| 3: | 𝒟 = 𝒟+ ∪𝒟−, where 𝒟+ occur first. |
| 4: | else |
| 5: | 𝒟 = 𝒟− ∪𝒟+, where 𝒟− occur first. |
| 6: | end if |
| 7: | for all xi in 𝒟 in order do |
| 8: | if minxj∈𝒮 d(xi, xj) > r then |
| 9: | Add xi into 𝒮; |
| 10: | end if |
| 11: | end for |
Train confident classifiers
Unlike the linear CPM mentioned in Sec. III, training nonlinear confident classifiers involves an n × n kernel matrix that is expensive to store and compute. Instead, we propose a sample selection strategy to reduce the size of training samples.
Alg. 3 describes the sample selection algorithm. The intuition is to reduce the training size by selecting only one representative sample in a region with radius r. That is, a sample is selected if and only if none of its r-radius neighbors are selected. This process proceeds until all samples are examined. The resulting distribution tends to be uniform, and contains much less samples than the original distribution. Denote the desired size of training samples as n′, we determined the radius r according to an empirical distance estimation. Specifically, we first randomly select n′ samples, compute for each sample the distance to its nearest neighbor, and then assign r as the average over n′ distances. The ordering of sample selection varies for training the confident classifiers (f+, f−). To get f+, we perform the sample selection process for negative samples before positive samples. This ensures that each selected positive sample has a neighborhood of only positive samples in the original distribution. Thus, f+ trained on such selected samples is confident on its positive predictions. To get f−, we apply the same strategy with a reversed order (positive samples first).
Fig. 7 illustrates an example of the sample selection strategy. As seen in Fig. 7(b), negative samples are selected in the middle region where original positive and negative samples are messed up. As a result, the learned f+ lies to the right side of a typical kernel SVM (black line in Fig. 7(a)). Similarly, in Fig. 7(c), f− lies to the left side. The selected samples in Fig. 7(b)–(c) distribute uniformly, and are much less than those in original dataset as shown in Fig. 7(a).
Fig. 7.
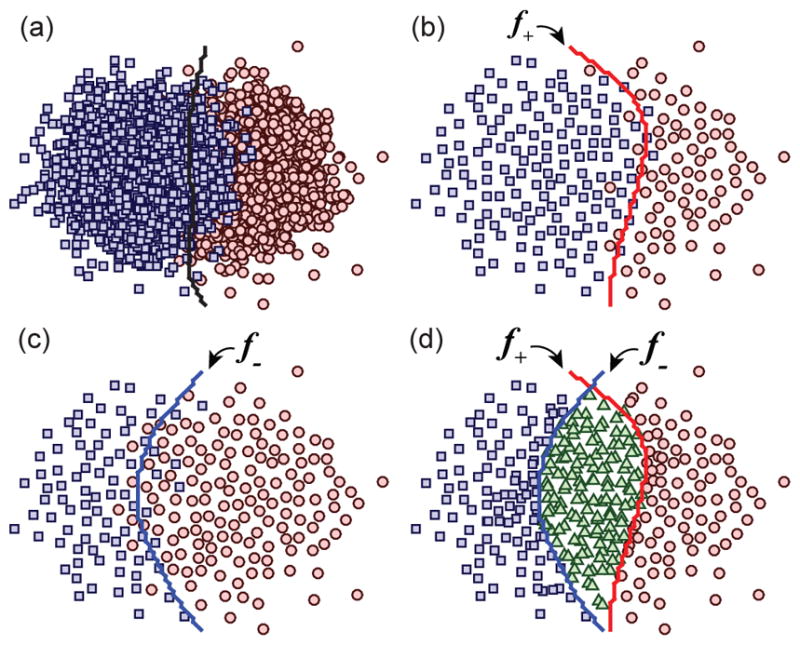
An illustration of kCPM: Easy negative, easy positive, and hard samples are denoted as blue rectangles, red circles, and green triangles, respectively. (a) A standard kernel SVM trained on original samples. (b)–(c) Confident classifiers f+ and f− trained on selected points under positive-first order and negative-first order, respectively. (d) Confident classifiers cooperatively separate easy and hard samples.
The sample selection algorithm shows its advantages on two-folds. First, it is feasible to train kernel machines on the selected samples, which are much smaller in size than the original dataset while well represent the kernel space. Although other instance selecting algorithms can also reduce the size of original dataset (e.g., sparse modeling representative selection [18], multi-class instance selection [11]), they lack the mechanisms to train two biased classifiers. The second advantage of the proposed sample selection strategy is that confident classifiers trained on the two sets of points are able to predict confidently on opposite sides of the margin. Specifically, the classifier is confident in its negative predictions if it is trained on the samples selected under a positive-first order. And similar is the other one.
Train the PS-QSS classifier
Using Alg. 3, we are able to select a set of positive-first samples { }, a set of negative-first samples { }, and learn the nonlinear confident classifiers (f+, f−). For notational convenience, we use the notation y ∈ {+, −} in Sec. III-B to denote the selected samples as , and the confident classifiers as fy. Given fy, the prediction on a test sample xte becomes , where αy = [αy1, . . . , αyny ]⊤ ∈ ℝny are the parameters of fy, and 〈., .〉ℋ denotes the inner product in a reproducing kernel Hilbert space. In this paper, we use . Similar to the regular linear CPM, test samples with consistent predictions from the confident classifiers are identified as easy test samples, i.e., ℰt = {i ∈ 𝒟te|f+(xi)f−(xi) > 0}. Then, we train a nonlinear person-specific (PS) classifier in a quasisemi-supervised (QSS) manner as discussed in Sec. III-C using the nonlinear form of Eq. (4):
| (7) |
where Kt ∈ ℝm×m is a kernel matrix computed from m test samples, and S(αt,Kt) is the nonlinear smoothness term defined as:
| (8) |
The prediction of a test sample x is then computed as , where is the i-th element of αt.
C. Discussion on related work
The proposed CPM and its extensions (referred as CPMs) are related to existing methods that use multiple classifiers [27], [37], methods that follow an “easy-to-hard” strategy [4], [33], [39], semi-supervised learning [6], [43], [46], and transfer learning [23]. Table I compares CPMs against related methods in terms of their properties.
TABLE I.
Comparison of properties between CPMs and alternative methods (✓: applicable, ×: inapplicable)
| Method | Multiple classifiers | Identify easy/hard | Unlabeled data | Distribution mismatch | Smoothness assumption | Non-parallel hyperplanes | Progressive labeling |
|---|---|---|---|---|---|---|---|
| Boosting [27] | ✓ | × | × | × | × | × | × |
| TW-SVM [37] | ✓ | × | × | × | × | ✓ | × |
| Self-paced learning [39] | × | ✓ | × | × | × | × | × |
| RO-SVM [4], [33] | × | ✓ | × | × | × | × | × |
| Self-training [46] | × | × | ✓ | × | × | × | ✓ |
| Co-training [6] | ✓ | × | ✓ | × | × | × | ✓ |
| Lap-SVM [43] | × | × | ✓ | × | ✓ | × | × |
| DAM [21] | ✓ | × | ✓ | ✓ | ✓ | × | ✓ |
| CPM (proposed) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
A crucial property of CPMs is the use of multiple classifiers, which are also exploited in boosting methods [27] and Twin SVMs (TW-SVMs) [37]. The goal of using multiple classifiers is to generate multiple non-parallel hyperplanes that yield better separation than standard methods with a single hyperplane. Boosting methods train a set of weak classifiers and sequentially combine them into a strong classifier. In TW-SVMs, each hyperplane of the twin classifiers is close to one class and far from the other. Similarly, CPM uses the confident classifiers that form two non-parallel hyperplanes to preserve confident predictions.
Other methods also employ the mechanism of identify easy and hard samples, such as self-paced learning [39] and SVM with reject options (RO-SVM) [4], [33]. Self-paced learning models the “easiness” as latent variables, and assigns less weights to samples that are potentially hard to classify. RO-SVM designs new loss functions for hard samples in the “rejection region”. However, all these methods focus on classification without using unlabeled data.
Semi-supervised learning (SSL) is a technique known for the use of unlabeled data. Examples include self-training [46], co-training [6] and Laplacian SVM (Lap-SVM) [43]. Self-training progressively adds unlabeled data with high confidence to retrain the classifier. Co-training adopts unlabeled data by training two or more classifiers so that the most confident samples from one classifier are used to train another. Lap-SVM utilizes unlabeled data by propagating labeled samples to unlabeled ones through a smoothness assumption. However, common to these methods is the assumption that labeled and unlabeled data are drawn from the same distribution.
Mismatches in data distribution can be addressed by transfer learning approaches. Closest to CPM is DAM [23] due to their common properties such as the use of multiple classifiers, smoothness assumptions, the use of unlabeled test data, and progressively labeling. One major difference between CPM and DAM is how a test sample is identified as easy or hard. DAM used a manually-determined threshold to reject a hard test sample. On the contrary, CPM automatically identifies easy and hard samples using a principled easy-to-hard strategy. Compared to the aforementioned methods, CPMs possess all properties as summarized in Table I.
V. Experiments
In this section, we experimentally validate the proposed CPM and its extensions. First, we describe the datasets and settings used in the experiments. Then, we provide an objective evaluation on CPM components, and compare CPM with alternative methods, including a baseline SVM, semi-supervised learning methods, transfer learning methods, and boosting methods. Finally, we provide hard sample analysis in terms of AU intensities, head poses, and individual differences.
A. Datasets and settings
This section describes datasets and settings used throughout the experiments. We chose to use four largest spontaneous facial expressions datasets:
GFT [15] are recorded when three unacquainted young adults sat around a circular table for a 30-minute conversation with drinks. Moderate out-of-plane head motion and occlusion are presented in the videos which makes the AU detection challenging. In our experiments, 50 subjects are selected and each video is about 5000 frames.
BP4D [56] is a spontaneous facial expression dataset in both 2D and 3D videos. The dataset includes 41 participants aging from 18 to 29 associating with 8 tasks, which are covered with an interview process and a series of activities to elicit eight emotions. Frame-level ground-truth for facial actions are obtained using FACS. In our experiments, we only use the 2D videos.
DISFA [42] recorded 27 subjects’ spontaneous expressions when they were watching video clips. DISFA not only codes the AUs, but also labels the intensities. In our experiments, we use the frames with intensities equal or greater than A-level as positive, the rest as negative. The dataset consist of 27 videos with 4845 frames each.
RU FACS [3] consists of 100 subjects participating in a “false opinion” paradigm that shows a wide rage of emotional expressions. 33 subjects have been FACS-coded. Like the other three, it includes spontaneous behavior such as speech. We selected 28 of the coded 33 participants with sequence length of about 7000 frames.
All experiments were conducted under a same protocol where each dataset was reorganized in 10 disjoint splits. Each split designated numerous (5 in GFT, 4 or 5 in BP4D, 2 or 3 in DISFA and RU FACS) subjects as test data and the rest as training data, i.e., each subject was treated as the test data in turns during the 10 splits. For each frame, we tracked 49 facial landmarks using IntraFace [16], and registered faces onto a 200×200 template. Then, SIFT descriptors were extracted on 32×32 regions centered at each facial landmark.
For evaluation, we reported both conventional frame-based F1 score (F1-frame) and event-based F1 score (F1-event) [17]. The former is prevalent in binary classification problems, while the latter can evaluate detection performance at event-level. An “event” is defined as a max continuous period with an AU presence. In this sense, F1-event captures the agreement between the ground truth events and the predicted events, by measuring the event-based recall ER as the fraction of true events being correctly predicted, and the event-based precision EP as the fraction of predicted events being true. An event-level agreement holds true if an overlap score between a ground truth event and a predicted event is above a certain threshold. F1-event was computed as the area under the curve by adjusting the overlapping threshold in [0,1].
B. Objective evaluation on CPM components
Recall that two major components in CPM are the confident classifiers and the person-specific (PS) classifier learned with quasi-semi-supervised (QSS) learning strategy. To validate their effectiveness, we conducted comparisons with a baseline linear SVM [25], confident classifiers only (Conf), and CPM (i.e., Conf+QSS). In Conf, we trained confident classifiers using Alg. 1, and then passed them to train a PS classifier without a smoothness assumption. Conf checks whether the confident classifiers are effective when compared with a standard single-hyperplane SVM. CPM differs from Conf by learning the PS classifier with the spatial-temporal smoothness as discussed in Sec. III-C. In this way, CPM verifies the effectiveness of the PS-QSS classifier on propagating labels with smoothness assumptions. We also conducted iCPM to validate the iterative integration in CPM, and kCPM see how a non-linear boundary would influence the performance.
Fig. 8 reports the results of the above four experiments on GFT, BP4D, DISFA, and RU-FACS datasets, respectively. The values of F1-frame and F1-event were reported as the average over all AUs. Comparing the results between SVM and Conf, confident classifiers showed positive affects on the performance. The effectiveness of applying smoothness assumptions was indicated by the results between Conf and CPM. Out of the results, iCPM outperformed CPM in most cases, validating the effectiveness of the proposed iterative integration. kCPM shows its advantages over CPM because non-linear boundaries are more accurate than linear ones. When compared with iCPM, kCPM only has a better F1-frame performance. An explanation is that iCPM has an iterative mechanism, which iteratively strengthens the spatiotemporal smoothness. Thus, a better F1-event is achieved.
Fig. 8.
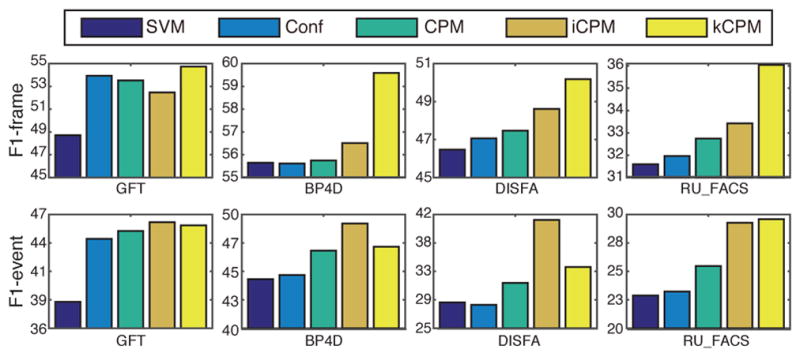
Results of SVM, confident, CPM, iCPM, and kCPM. The values are averaged over different AUs. In each dataset, different amounts of AUs are involved: 11 in GFT, 12 in BP4D, 8 in DISFA, 7 in RU FACS. Note that the scales in each dataset are different for display purpose.
C. Comparisons with alternative methods
This section compares the proposed CPM with alternative methods discussed in Sec. IV-C, including baseline methods, semi-supervised learning (SSL), and transfer learning. Note that typical transfer learning methods treat each dataset as a domain, while this subject treats each subject as a domain. For baselines, we used LibLinear [25] and Matlab toolbox for Adaboost [27]. For SSL, we implemented a linear version of Laplacian SVM (Lap) [43]. Its kernel version is computationally prohibitive because our experiments contain more than 100,000 samples. For transfer learning, we compared to state-of-the-art methods including Geodesic Flow Kernel (GFK) [30], Domain Adaption Machine (DAM) [21], and Multi-source Domain Adaptation (MDA) [49]. GFK computed the geodesic flow kernel from training to test sample, and then used it as a kernel in SVM. DAM fitted a classifier for test subject as a linear combination of classifiers of training subjects. Note that DAM is able to tackle with unlabeled test data. We did not use its extended version DSM [22] because DSM requires to enumerate all the possible selections of source domains, which are as much as 245 in our experiment. MDA performed unsupervised domain adaptation by re-weighting both source domains and training instances. All methods, except for SVM and Ada, learned a specific classifier for each test subject. Codes of other competitive methods were either downloaded from author’s web page or provided by the authors. To show a more fair comparison, we also implemented Hidden Markov Model (HMM) as a post-processing for smoothing the prediction of SVM, Lap, and Ada. Note that HMM was not directly applicable for DAM, MDA, and GFK because their scores of the frame-level labeling output were available only for test data.
Table II~V show the results reported with the best parameters. SVM and Ada outperformed well in some AUs. Despite this, the overall performances of Ada were worse than iCPM, because Adaboost is a supervised method without investigating unlabeled test data. Overall, Lap had the worst performance due to its unsuitable assumption for spontaneous facial expression detection, which enforced the data to have similar decision values with their neighbors. Such assumption was not guaranteed across training and test subjects drawn from different distributions. Lap achieved better results on one or two AUs in BP4D. This is because most frames in BP4D dataset were frontal and thus had less appearance differences.
TABLE II.
F1 scores on the GFT dataset [15]. “H” stands for an extra post-processing with HMM.
| F1-frame | F1-event | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AU | SVM|H | Ada|H | Lap|H | DAM | MDA | GFK | iCPM | kCPM | SVM|H | Ada|H | Lap|H | DAM | MDA | GFK | iCPM | kCPM |
| 1 | 30.3|16.8 | 20.3|15.4 | 12.1|16.4 | 1.7 | 29.2 | 30.9 | 29.9 | 30.4 | 20.3|17.9 | 15.3|28.2 | 5.4| 9.7 | 2.1 | 21.3 | 21.6 | 27.1 | 23.4 |
| 2 | 25.6|18.4 | 14.8|21.8 | 26.0|19.3 | 5.3 | 25.8 | 29.3 | 25.7 | 28.0 | 20.2|21.1 | 12.2|30.7 | 18.2|16.6 | 4.7 | 21.3 | 22.5 | 24.8 | 26.0 |
| 6 | 66.2|66.4 | 62.1|47.3 | 2.7|40.7 | 58.0 | 63.8 | 66.1 | 67.3 | 70.2 | 49.1|56.8 | 47.5|43.4 | 4.4|37.5 | 50.0 | 47.0 | 50.2 | 56.8 | 57.3 |
| 7 | 70.9|72.2 | 69.6|50.0 | 24.0|50.3 | 66.0 | 66.6 | 72.2 | 72.5 | 74.4 | 50.4|59.8 | 50.7|44.0 | 21.6|48.3 | 41.7 | 49.2 | 52.1 | 60.1 | 58.1 |
| 10 | 65.5|65.5 | 65.5|43.7 | 56.7|61.2 | 64.9 | 65.4 | 67.5 | 67.0 | 70.7 | 50.2|57.8 | 50.2|46.6 | 46.5|57.5 | 53.1 | 51.6 | 54.3 | 58.1 | 55.6 |
| 12 | 74.2|75.9 | 73.0|54.5 | 64.8|69.0 | 72.9 | 71.9 | 72.7 | 75.1 | 78.3 | 56.3|65.0 | 54.7|59.9 | 54.9|64.4 | 61.9 | 52.0 | 54.3 | 65.0 | 65.3 |
| 14 | 79.6|78.1 | 77.7|59.2 | 76.7|51.2 | 79.5 | 74.0 | 79.8 | 80.7 | 82.1 | 63.8|70.8 | 62.3|59.9 | 81.5|61.2 | 64.6 | 63.7 | 64.8 | 74.7 | 71.4 |
| 15 | 34.1|17.5 | 20.3|20.5 | 19.3|13.9 | 1.4 | 31.8 | 31.7 | 43.5 | 38.9 | 28.1|20.1 | 17.7|41.8 | 15.9|20.2 | 2.3 | 25.4 | 26.8 | 32.2 | 32.0 |
| 17 | 49.2|50.6 | 48.2|38.6 | 42.5|21.2 | 34.6 | 47.4 | 48.9 | 49.1 | 57.1 | 42.9|53.1 | 37.1|38.5 | 36.4|25.9 | 29.6 | 41.4 | 41.3 | 52.3 | 50.2 |
| 23 | 28.3|29.8 | 19.4|20.7 | 27.1|25.1 | 2.8 | 26.0 | 26.7 | 35.0 | 28.6 | 27.7|35.9 | 16.8|36.7 | 9.5|19.5 | 4.4 | 26.7 | 27.1 | 25.9 | 31.5 |
| 24 | 31.9|21.0 | 22.3|25.8 | 25.7|16.9 | 3.0 | 31.8 | 33.0 | 31.6 | 43.6 | 30.3|21.8 | 20.8|26.4 | 21.7|13.9 | 4.9 | 30.0 | 30.5 | 31.8 | 34.6 |
| Av. | 48.7|46.6 | 44.8|36.1 | 32.8|35.0 | 35.5 | 48.5 | 48.6 | 52.5 | 54.8 | 38.6|43.7 | 35.0|41.5 | 27.3|34.1 | 29.0 | 39.1 | 38.9 | 46.3 | 45.9 |
Both DAM and MDA assumed the person-specific classifier is a linear combination of multiple source classifiers. When positive and negative data were extremely imbalanced, e.g., AU1 on GFT, DAM performed poorly because each source classifier was unreliable. MDA performed better than DAM because MDA learned the weights for training data and source-domains instead of using fixed weights, meanwhile, MDA had a smooth assumption over test data. GFK performed similarly to SVM, although it did not provide a way to deal with multiple sources. GFK regarded all the training videos as a domain and represented data on the Grassmann manifold from training data to the test data. Across three datasets, iCPM consistently outperformed three transfer learning methods.
With few exceptions, iCPM consistently outperformed the alternative methods in both metrics. Because iCPM incorporated the spatial-temporal smoothness term (Sec. III-C), it showed an obvious increase on F1-event compared to F1-frame. Recall that AU detection aims for detecting temporal events, we believe this spatial-temporal smoothness would significantly improve the detection result. Note that the experiments with HMM did not show consistent improvements on either F1-frame or F1-event as iCPM did. A possible explanation is that a trivial enforcement of temporal consistency is likely to make some frames similar to their misclassified neighbors, or over-smooth some short events. It indicated that the performance edge of iCPM was given by both separating easy/hard samples and its temporal-spatial smoothness.
D. Hard sample analysis
Automated facial AU detector could fail due to various sources of errors. These errors are ubiquitous in AU detection, but few existing studies address or systematically identify them. In this section, we utilize CPM’s nature to identify the errors as “hard samples”, in hope to provide a better understanding in challenges of automated AU detection. Specifically, we rigorously investigate the properties of hard samples using the original CPM (Section III). The properties for investigation include AU intensity, head pose, and proportions of hard samples in different individuals or AUs.
AU intensity
AU intensity measures the strength of an AU, telling if an AU is obvious or not. Because annotations of AU intensity is available only in the DISFA dataset, we used DISFA for this investigation. Intensity ranges from ‘A’ to ‘E’; ‘E’ reflects the most obvious AU. Fig. 9 illustrates the statistic analysis in terms of AU intensity. We consider hard samples in two cases. First, we investigate the percentage of hard samples from each of 8 AUs in every intensity, as shown in the upper row of Fig. 9. As can been seen, in almost all cases, the lower the intensity, the more hard samples are discovered. This observation is the most clear when we average over all AUs, confirming that low-intensity AUs tend to be hard samples with high probability. Second, we investigate the percentage of each intensity within positive hard samples, as shown in the lower row. As can be seen, most positive hard samples (those with present AUs) have low level intensities, and no E-level AUs were identified as hard samples. This finding suggests that AUs in hard samples have relatively low intensities, providing a proof that most hard positive samples come from low-intensity AUs, while all E-level AUs are identified as easy samples. Note that each figure in lower row does not sum to 1, because we have excluded the ones with intensity ‘0’ (negative samples) from the statistic.
Fig. 9.
Analysis on CPM-selected hard samples in terms of AU intensities using the DISFA dataset: (Upper) the percentage of hard samples within each intensity; (lower) the percentage of each AU intensity within positive hard samples.
Low-intensity AUs v.s. head poses
Given above AU intensity analysis, our findings suggest that subtle AUs (AU with low intensities) are the majority of hard samples. In addition, we have known that head pose could influence the performance [19], [38]. Here we investigate the effects of AU subtleness and head poses on GFT, BP4D, and DISFA datasets. Because intensity annotations were unavailable in these datasets, we measured the subtleness of an AU at frame xi by its similarity to onset or offset frames:
| (9) |
where ℐ denotes the index set of onset/offset frames, d(xi, xj) is the distance (we used Euclidean distance) between frames xi and xj, z and β are parameters that normalize the similarity to (0, 1]. The head pose of a frame was measured by its rotation angle to the frontal face. In particular, given a rotation matrix R ∈ ℝ3×3, the angle θ(R) between the face axis and the optical axis of the camera is calculated as
| (10) |
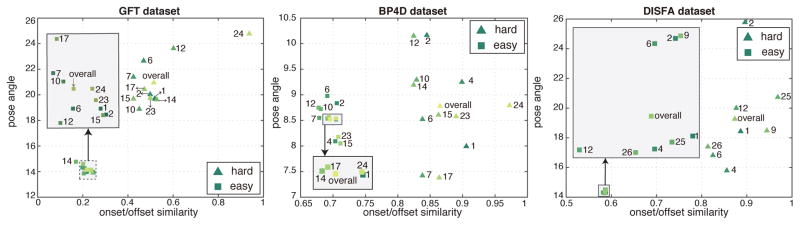
where is the projection of rotation on the optical axis of camera (z-axis). R33 is the element of R in the third row and third column. Denote as an averaged similarity over a set of frames ℐ, and as an averaged pose angle. Let frames with high similarities with onset/offset frames be ℐh = {s(xi) ≥ τs̄ε, ∀i ∈ ℋ}, and frames with low similarity ℐℓ = ℋ\ℐh. τ is a scaling factor controlling the factor, which we empirically set τ = 1.5. For each AU, we computed their statistics in AU subtleness and head poses as s̄ℐh and θ̄ℐℓ, respectively. Generally, subtle AUs in frontal faces lead to large values in similarities, while large head poses could lead to small values in similarities. Fig. 10 illustrates the CPM-identified hard and easy training samples in the similarity-angle space of (s̄ℐh, θ̄ℐℓ). For three datasets, each AU is represented as two points in the 2D space: one for easy samples and the other for hard samples. As can be seen, easy samples consistently lie on the bottom-left corner in the similarity-angle space, showing that easy sample typically comes from frontal faces with low similarity to onset/offset frames. On the other hand, hard samples consistently lie on the right-up of the similarity-angle coordinates. This justifies that sources of “sample hardness” can be traced back to subtleness of an AU or large head poses.
Fig. 10.
Analysis on CPM-selected hard and easy training samples in terms of head pose angle and the similarity with onset/offset frames. Triangles and rectangles indicate hard and easy samples, respectively. A number indicate an AU; “overall” indicates the average over all data.
Biases in individuals and AUs
We validated biases in individual and AUs by investigating the proportions of hard samples in different subjects or different AUs. We employed GFT dataset for this experiment because it contains the most frames and subjects of all considered datasets. Fig. 11 illustrates the proportions of hard samples in GFT dataset. The left figure shows an average proportion of hard samples in different subject. As can been seen, the proportions vary between different subjects. For instance, some contains about three times more hard samples than others. The right figure shows the average proportion for each AU. The dark green bars denote the proportions of hard positive samples computed as , and similarly did the hard negative samples were computed (light green bars). As can be seen, the proportion differs across AUs. Note that for all AUs except 14, proportion of hard positive samples are higher than those for negative ones. That is because only AU14 has more positive samples than negative ones.
Fig. 11.
A proportion of hard training samples that CPM selected from the GFT dataset. (Left) Each bar denotes an averaged portion of hard samples over 11 AUs for a subject. (Right) Each bar denotes an averaged proportion over 50 subjects for each AU.
VI. Conclusion
In this study, we proposed confidence preserving machine (CPM) for facial AU detection. CPM exploits an easy-to-hard strategy that first recognizes easy samples by a pair of confident classifiers, and then tackles hard samples by propagating predictions from easy samples to hard ones. Considering that the confident classifiers could be influenced by different distributions between training and test data, we designed an iterative CPM (iCPM) that iteratively adds easy test samples to the training process of confident classifiers. We also developed an efficient kernel CPM (kCPM) to capture non-linear boundaries between easy and hard samples. Results on four spontaneous facial expression datasets show that our methods outperform state-of-the-art semi-supervised learning, transfer learning methods, and a boosting method. Current CPM and its extensions are offline AU detectors. Future work includes an “online” extension of CPM by incrementally updating the confident classifiers and the QSS classifier, e.g., augmenting the easy training samples ε for every t frames.
TABLE III.
F1 scores on the BP4D dataset [56]. “H” stands for an extra post-processing with HMM.
| F1-frame | F1-event | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AU | SVM|H | Ada|H | Lap|H | DAM | MDA | GFK | iCPM | kCPM | SVM|H | Ada|H | Lap|H | DAM | MDA | GFK | iCPM | kCPM |
| 1 | 46.0|43.4 | 41.5|37.7 | 43.8|29.0 | 38.2 | 39.6 | 42.4 | 46.6 | 48.2 | 29.2|38.1 | 29.8|41.7 | 29.2|27.8 | 26.7 | 30.5 | 29.7 | 35.3 | 38.9 |
| 2 | 38.5|38.4 | 12.4|25.5 | 17.6|27.8 | 27.3 | 37.0 | 35.8 | 38.7 | 40.8 | 29.3|36.1 | 12.9|32.4 | 24.8|27.1 | 12.3 | 28.2 | 28.9 | 32.5 | 32.6 |
| 4 | 48.5|41.6 | 39.4|30.4 | 27.2|26.1 | 29.1 | 45.7 | 47.3 | 46.5 | 53.2 | 33.5|37.4 | 28.9|28.3 | 30.5|26.5 | 22.3 | 32.8 | 32.8 | 39.4 | 35.4 |
| 6 | 67.0|62.0 | 71.7|61.2 | 71.5|26.1 | 67.5 | 69.2 | 71.2 | 68.4 | 76.0 | 53.7|37.4 | 54.4|58.5 | 53.7|26.5 | 55.4 | 52.9 | 54.4 | 60.9 | 51.7 |
| 7 | 72.2|56.5 | 74.7|53.7 | 71.6|52.2 | 72.6 | 70.2 | 72.5 | 73.8 | 77.3 | 59.0|55.3 | 55.2|49.2 | 56.2|57.6 | 61.1 | 58.4 | 54.9 | 62.1 | 57.2 |
| 10 | 72.7|54.6 | 75.7|62.1 | 72.8|55.3 | 74.4 | 71.0 | 74.2 | 74.1 | 80.9 | 61.3|52.8 | 59.3|67.8 | 60.7|60.6 | 68.6 | 57.5 | 59.7 | 65.1 | 58.6 |
| 12 | 83.6|65.4 | 84.3|62.6 | 84.3|55.3 | 76.4 | 81.8 | 83.9 | 84.6 | 87.5 | 62.5|52.8 | 63.9|60.8 | 64.2|60.6 | 60.8 | 59.9 | 65.6 | 71.4 | 69.3 |
| 14 | 59.9|49.2 | 61.0|50.9 | 62.6|26.3 | 59.9 | 57.8 | 57.2 | 62.2 | 62.0 | 49.5|46.3 | 51.7|56.7 | 51.9|26.9 | 53.3 | 50.2 | 48.7 | 55.9 | 57.1 |
| 15 | 41.1|39.9 | 30.6|30.4 | 35.2|25.5 | 15.9 | 41.4 | 40.6 | 44.3 | 44.3 | 33.7|39.0 | 24.4|39.0 | 25.4|25.4 | 12.7 | 28.2 | 31.1 | 37.4 | 36.3 |
| 17 | 55.6|57.8 | 56.6|47.8 | 59.1|46.3 | 52.9 | 50.1 | 55.4 | 57.5 | 60.7 | 46.0|56.1 | 44.0|51.5 | 44.0|41.7 | 51.5 | 39.6 | 44.0 | 49.9 | 53.3 |
| 23 | 40.8|39.4 | 33.0|32.8 | 33.6|27.6 | 3.9 | 36.2 | 39.9 | 41.7 | 41.1 | 36.4|44.0 | 28.2|41.4 | 27.2|22.2 | 5.8 | 30.7 | 33.3 | 41.9 | 41.0 |
| 24 | 42.1|19.3 | 34.2|26.7 | 40.5|16.9 | 4.9 | 41.1 | 41.7 | 39.7 | 43.1 | 37.7|16.0 | 30.9|35.7 | 34.8|13.8 | 3.6 | 35.4 | 35.6 | 38.7 | 34.3 |
| Av. | 55.7|47.3 | 51.3|43.5 | 54.7|36.9 | 42.6 | 53.4 | 55.2 | 56.5 | 59.6 | 44.3|44.8 | 40.3|46.9 | 41.9|36.5 | 36.2 | 42.0 | 43.2 | 49.2 | 47.2 |
TABLE IV.
F1 scores on the DISFA dataset [42]. “H” stands for an extra post-processing with HMM.
| F1-frame | F1-event | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AU | SVM|H | Ada|H | Lap|H | DAM | MDA | GFK | iCPM | kCPM | SVM|H | Ada|H | Lap|H | DAM | MDA | GFK | iCPM | kCPM |
| 1 | 26.5|14.4 | 17.1|12.4 | 13.1|16.2 | 7.9 | 19.0 | 23.2 | 29.5 | 30.7 | 14.5|17.6 | 16.1|21.2 | 9.6|11.6 | 5.4 | 11.6 | 18.1 | 18.7 | 13.0 |
| 2 | 24.0|15.3 | 20.1|10.5 | 6.4|12.6 | 13.1 | 9.5 | 16.3 | 24.8 | 23.7 | 10.8|17.6 | 17.3|17.0 | 11.4|11.0 | 12.1 | 16.4 | 17.4 | 19.2 | 19.6 |
| 4 | 56.1|48.5 | 59.8|26.4 | 21.1|23.4 | 40.4 | 59.3 | 60.3 | 56.8 | 65.7 | 31.6|37.2 | 32.5|27.7 | 15.9|16.2 | 32.4 | 28.6 | 28.3 | 41.8 | 39.0 |
| 6 | 40.9|34.9 | 31.9|22.1 | 22.1|19.9 | 19.2 | 21.1 | 41.9 | 41.7 | 41.0 | 30.3|29.2 | 28.3|25.9 | 23.7|13.5 | 22.6 | 30.8 | 30.6 | 36.9 | 34.3 |
| 9 | 30.5|10.9 | 29.3|17.4 | 12.1|10.9 | 11.9 | 7.6 | 30.3 | 31.5 | 26.4 | 23.4|13.2 | 22.7|39.9 | 7.8| 8.3 | 14.3 | 27.4 | 14.6 | 31.7 | 16.2 |
| 12 | 65.6|70.1 | 69.4|46.3 | 33.7|32.2 | 50.9 | 63.1 | 69.6 | 71.9 | 70.5 | 49.9|57.1 | 51.9|61.6 | 33.2|20.7 | 44.3 | 42.1 | 46.2 | 56.6 | 53.7 |
| 25 | 78.3|84.1 | 83.9|70.5 | 35.3|30.3 | 56.2 | 81.3 | 80.0 | 81.6 | 85.4 | 31.9|76.7 | 38.0|58.8 | 42.5|21.2 | 56.4 | 46.5 | 36.1 | 76.7 | 52.5 |
| 26 | 50.0|51.5 | 59.6|50.5 | 18.9|25.5 | 43.2 | 51.1 | 54.6 | 51.3 | 58.0 | 38.6|51.7 | 38.7|49.5 | 48.7|18.4 | 38.4 | 36.4 | 37.3 | 47.7 | 45.1 |
| Av. | 46.5|41.2 | 46.6|32.0 | 20.3|21.4 | 30.4 | 39.0 | 47.0 | 48.6 | 50.2 | 28.9|37.5 | 30.7|37.7 | 24.1|15.1 | 28.2 | 30.0 | 28.6 | 41.2 | 34.2 |
TABLE V.
F1 scores on the RU-FACS dataset [3]. “H” stands for an extra post-processing with HMM.
| F1-frame | F1-event | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AU | SVM|H | Ada|H | Lap|H | DAM | MDA | GFK | iCPM | kCPM | SVM|H | Ada|H | Lap|H | DAM | MDA | GFK | iCPM | kCPM |
| 1 | 26.8|25.8 | 23.0|15.9 | 21.2|15.0 | 18.9 | 27.3 | 23.5 | 26.7 | 32.4 | 30.5|31.9 | 27.1|30.7 | 17.7|36.7 | 24.8 | 26.0 | 30.9 | 40.7 | 36.0 |
| 2 | 22.2|17.8 | 14.0|14.4 | 16.5|14.0 | 16.7 | 17.7 | 19.7 | 22.5 | 26.9 | 17.8|14.9 | 12.5|13.0 | 10.1| 3.4 | 16.3 | 16.3 | 17.5 | 21.7 | 22.2 |
| 6 | 36.5|17.3 | 35.1| 9.9 | 27.6|10.1 | 26.6 | 30.8 | 32.7 | 41.1 | 44.5 | 21.9| 9.5 | 22.8|16.1 | 13.4| 4.3 | 19.9 | 18.3 | 20.2 | 25.0 | 34.1 |
| 12 | 64.3|58.4 | 59.1|24.5 | 48.9|25.8 | 39.4 | 59.8 | 63.7 | 67.6 | 65.0 | 39.9|36.5 | 36.7|24.9 | 30.5| 7.5 | 30.8 | 36.4 | 35.2 | 45.1 | 46.2 |
| 14 | 17.4|10.6 | 13.7|12.0 | 1.3| 9.4 | 12.8 | 15.9 | 18.7 | 15.4 | 19.9 | 14.3|12.2 | 10.6|19.4 | 2.3|13.4 | 9.7 | 14.0 | 13.5 | 19.2 | 18.7 |
| 15 | 12.7| 6.6 | 8.2| 7.8 | 1.3| 5.0 | 6.8 | 12.1 | 12.6 | 16.9 | 14.7 | 9.2| 8.5 | 7.4|12.2 | 2.1| 4.2 | 5.2 | 10.9 | 9.8 | 15.7 | 14.2 |
| 17 | 41.2|12.9 | 47.8|48.4 | 10.0| 9.5 | 20.7 | 36.9 | 36.3 | 43.8 | 48.8 | 26.6|10.5 | 34.3|32.1 | 9.7| 5.1 | 23.8 | 18.3 | 19.6 | 37.5 | 35.7 |
| Av. | 31.6|21.3 | 28.7|19.0 | 18.1|12.7 | 20.3 | 28.6 | 29.6 | 33.4 | 36.1 | 22.9|17.7 | 21.6|21.2 | 12.3|10.7 | 18.6 | 20.0 | 21.0 | 29.3 | 29.6 |
Acknowledgments
Research reported in this paper was supported in part by National Natural Science Foundation of China (No. 61272350), the State Key Laboratory of Software Development Environment (No. SKLSDE-2016ZX-24), US National Institutes of Health under MH096951, and National Institutes of Mental Health R21 MH099487-01A1. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. Jiabei Zeng also thanks China Scholarship Council, and the Fundamental Research Funds for the Central Universities for supporting of this work.
Biographies

Jiabei Zeng is a Ph.D. candidate at the School of Computer Science and Engineering, Beihang University, Beijing, China. She received her B.S. degree of computer science from Beihang University in 2011. Her research interests include computer vision and machine learning.

Wen-Sheng Chu is currently a Ph.D. candidate at the Robotics Institute, Carnegie Mellon University. His research interests lie in the development and use of machine learning techniques for computer vision problems. He is a student member of the IEEE and a member of the Phi Tau Phi Scholastic Honor Society.

Fernando De la Torre is an Associate Research Professor in the Robotics Institute at Carnegie Mellon University. He received his B.Sc. degree in Telecommunications, as well as his M.Sc. and Ph. D degrees in Electronic Engineering from La Salle School of Engineering at Ramon Llull University, Barcelona, Spain in 1994, 1996, and 2002, respectively. His research interests are in the fields of Computer Vision and Machine Learning. Currently, he is directing the Component Analysis Laboratory (http://ca.cs.cmu.edu) and the Human Sensing Laboratory (http://humansensing.cs.cmu.edu) at Carnegie Mellon University. He has over 150 publications in referred journals and conferences and is Associate Editor at IEEE TPAMI. He has organized and co-organized several workshops and has given tutorials at international conferences on component analysis.

Jeffrey F. Cohn is Professor of Psychology and Psychiatry at the University of Pittsburgh and Adjunct Professor of Computer Science at the Robotics Institute at Carnegie Mellon University. He leads interdisciplinary and inter-institutional efforts to develop advanced methods of automatic analysis and synthesis of facial expression and prosody; and applies those tools to research in human emotion, social development, non-verbal communication, psychopathology, and biomedicine. He has served as Co-Chair of the 2008 IEEE International Conference on Automatic Face and Gesture Recognition (FG2008), the 2009 International Conference on Affective Computing and Intelligent Interaction (ACII2009), the Steering Committee for IEEE International Conference on Automatic Face and Gesture Recognition, and the 2014 International Conference on Multimodal Interfaces (ACM 2014). He has co-edited special issues of the Journal of Image and Vision Computing and is a Co-Editor of IEEE Transactions in Affective Computing (TAC).

Zhang Xiong is a full professor in School of Computer Science of Engineering in Beihang University and director of the Engineering Research Center of Advanced Computer Application Technology, Ministry of Education. He has won a National Science and Technology Progress Award. He is now the chief scientist of smart city project supported by the National High Technology Research and Development Program of China. Prof. Xiong serves as members of several national committees, e.g., the National Computer Science and Technology Teaching Steering Committee of Ministry of Education. His research interests and publications span from computer vision, wireless sensor networks and information security. He is the executive Editors-in-Chief of Frontiers of Computer Science (FCS).
Appendix A Solution to PS-QSS Classifier wt
This appendix provides details about the derivation of solving the PS-QSS classifier in Problem (4), Sec. III-C. Without loss of generality, we multiply Problem (4) by to ease a multiple of 2 during the derivation:
| (11) |
where ℰt is the index set of easy test samples, ℓ(y, t) = max(0, 1 − yt)2 is a quadratic loss, ŷi is the virtual label that confident classifiers assign to a easy test sample, and is the smooth regularizer detailed in Sec. III-C. We use ŷ ∈ ℝ|ℰt| interchangeably to denote a vector of ŷi. To solve Eq. (11), we use the Newton’s method for solving the convex optimization problem. We denote the Hessian matrix of Eq. (11) as H and the step size as α. A Newton step at iteration (τ + 1) for wt follows the update:
| (12) |
where the first order Jacobian function ∇wt and the second order Hessian matrix H are computed as:
| (13) |
| (14) |
where Xℰ ∈ ℝ|ℰt|×d denotes the samples in ℰt, Id is an d × d identity matrix, and Esv ∈ ℝ|ℰt|×|ℰt| is a diagonal matrix that indicates support vectors in Xℰ, i.e., Esv,ii = 1 if the i-th sample of ℰt is the support vector, and 0 otherwise. Specifically, support vectors are the frames with non-zero loss. From Eqs. (13) and (14), we obtain:
| (15) |
Substituting Eq. (15) into the Newton step in Eq. (12), we obtain the update for solving wt:
| (16) |
Note that the second term in Eq. (16) involves an expensive computation of matrix inverse. We avoid such inversion by computing (H−1EsvXℰ ŷ) as the solution to the linear system Hx = EsvXℰŷ.
Contributor Information
Jiabei Zeng, Engineering Research Center of Advanced Computer Application Technology, Ministry of Education, Beihang University, Beijing 100191, China, and School of Computer Science and Engineering, Beihang University.
Wen-Sheng Chu, Robotics Institute, Carnegie Mellon University.
Fernando De la Torre, Robotics Institute, Carnegie Mellon University.
Jeffrey F. Cohn, Robotics Institute, Carnegie Mellon University. Department of Psychology, University of Pittsburgh
Zhang Xiong, Engineering Research Center of Advanced Computer Application Technology, Ministry of Education, Beihang University, Beijing 100191, China, and School of Computer Science and Engineering, Beihang University.
References
- 1.Almaev T, Martinez B, Valstar M. Learning to transfer: transferring latent task structures and its application to person-specific facial action unit detection. ICCV. 2015 [Google Scholar]
- 2.Andrews S, Tsochantaridis I, Hofmann T. Support vector machines for multiple-instance learning. NIPS. 2002 [Google Scholar]
- 3.Bartlett MS, Littlewort GC, Frank MG, Lainscsek C, Fasel IR, Movellan JR. Automatic recognition of facial actions in spontaneous expressions. Journal of Multimedia. 2006;1(6):22–35. [Google Scholar]
- 4.Bartlett PL, Wegkamp MH. Classification with a reject option using a hinge loss. Journal of Machine Learning Research. 2008;9:1823–1840. [Google Scholar]
- 5.Belkin M, Niyogi P, Sindhwani V. Manifold regularization: A geometric framework for learning from labeled and unlabeled examples. Journal of Machine Learning Research. 2006;7:2399–2434. [Google Scholar]
- 6.Blum A, Mitchell T. Combining labeled and unlabeled data with co-training. CoLT. 1998 [Google Scholar]
- 7.Bruzzone L, Marconcini M. Domain adaptation problems: A dasvm classification technique and a circular validation strategy. TPAMI. 2010;32(5):770–787. doi: 10.1109/TPAMI.2009.57. [DOI] [PubMed] [Google Scholar]
- 8.Chapelle O. Training a support vector machine in the primal. Neural Computation. 2007;19(5):1155–1178. doi: 10.1162/neco.2007.19.5.1155. [DOI] [PubMed] [Google Scholar]
- 9.Chapelle O, Schölkopf B, Zien A, et al. Semi-supervised learning. Vol. 2 MIT Press Cambridge; 2006. [Google Scholar]
- 10.Chapelle O, Zien A. Semi-supervised classification by low density separation. AISTATS. 2005 [Google Scholar]
- 11.Chen J, Zhang C, Xue X, Liu C-L. Fast instance selection for speeding up support vector machines. Knowledge-Based Systems. 2013;45:1–7. [Google Scholar]
- 12.Chen K, Wang S. Semi-supervised learning via regularized boosting working on multiple semi-supervised assumptions. TPAMI. 2011;33(1):129–143. doi: 10.1109/TPAMI.2010.92. [DOI] [PubMed] [Google Scholar]
- 13.Chu W-S, De la Torre F, Cohn JF. Selective transfer machine for personalized facial action unit detection. CVPR. 2013 doi: 10.1109/CVPR.2013.451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cohn JF, De la Torre F. The Oxford Handbook of Affective Computing. 2014 ch. Automated Face Analysis for Affective Computing. [Google Scholar]
- 15.Cohn JF, Sayette MA. Spontaneous facial expression in a small group can be automatically measured: An initial demonstration. Behavior Research Methods. 2010;42(4):1079–1086. doi: 10.3758/BRM.42.4.1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.De la Torre F, Chu W-S, Xiong X, Vicente F, Ding X, Cohn JF. Intraface. FG. 2015 doi: 10.1109/FG.2015.7163082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ding X, Chu W-S, De la Torre F, Cohn JF, Wang Q. Facial action unit event detection by cascade of tasks. ICCV. 2013 doi: 10.1109/ICCV.2013.298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dornaika F, Aldine IK. Decremental sparse modeling representative selection for prototype selection. Pattern Recognition. 2015;48(11):3714–3727. [Google Scholar]
- 19.Dornaika F, Davoine F. Simultaneous facial action tracking and expression recognition in the presence of head motion. IJCV. 2008;76(3):257–281. [Google Scholar]
- 20.Du S, Tao Y, Martinez AM. Compound facial expressions of emotion. Proceedings of the National Academy of Sciences. 2014;111(15):E1454–E1462. doi: 10.1073/pnas.1322355111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Duan L, Tsang IW, Xu D, Chua T-S. Domain adaptation from multiple sources via auxiliary classifiers. ICML. 2009 [Google Scholar]
- 22.Duan L, Xu D, Chang S-F. Exploiting web images for event recognition in consumer videos: A multiple source domain adaptation approach. CVPR. 2012 [Google Scholar]
- 23.Duan L, Xu D, Tsang IW. Domain adaptation from multiple sources: A domain-dependent regularization approach. IEEE Trans on Neural Networks and Learning Systems. 2012;23(3):504–518. doi: 10.1109/TNNLS.2011.2178556. [DOI] [PubMed] [Google Scholar]
- 24.Ekman P, Rosenberg EL. What the face reveals: Basic and applied studies of spontaneous expression using the Facial Action Coding System (FACS) Oxford University Press; 1997. [Google Scholar]
- 25.Fan R-E, Chang K-W, Hsieh C-J, Wang X-R, Lin C-J. Liblinear: A library for large linear classification. Journal of Machine Learning Research. 2008;9:1871–1874. [Google Scholar]
- 26.Fernando B, Habrard A, Sebban M, Tuytelaars T. Unsupervised visual domain adaptation using subspace alignment. ICCV. 2013 [Google Scholar]
- 27.Freund Y, Schapire RE. A decision-theoretic generalization of on-line learning and an application to boosting. Journal of Computer and System Sciences. 1997;55(1):119–139. [Google Scholar]
- 28.Girard JM, Cohn JF, Jeni LA, Lucey S, De la Torre F. How much training data for facial action unit detection? FG. 2015 doi: 10.1109/FG.2015.7163106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Girard JM, Cohn JF, la Torre FD. Estimating smile intensity: A better way. Pattern Recognition Letters. 2014 doi: 10.1016/j.patrec.2014.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gong B, Shi Y, Sha F, Grauman K. Geodesic flow kernel for unsupervised domain adaptation. CVPR. 2012 [Google Scholar]
- 31.Gopalan R, Li R, Chellappa R. Domain adaptation for object recognition: An unsupervised approach. ICCV. 2011 [Google Scholar]
- 32.Grandvalet Y, Bengio Y. Semi-supervised learning by entropy minimization. NIPS. 2005 [Google Scholar]
- 33.Grandvalet Y, Rakotomamonjy A, Keshet J, Canu S. Support vector machines with a reject option. NIPS. 2009 [Google Scholar]
- 34.Gretton A, Smola A, Huang J, Schmittfull M, Borgwardt K, Schölkopf B. Covariate shift by kernel mean matching. Dataset shift in machine learning. 2009;3(4):5. [Google Scholar]
- 35.Guo G, Guo R, Li X. Facial Expression Recognition Influenced by Human Aging. IEEE Trans on Affective Computing. 2013;4(3):291–298. [Google Scholar]
- 36.Jhuo I-H, Liu D, Lee D, Chang S-F. Robust visual domain adaptation with low-rank reconstruction. CVPR. 2012 [Google Scholar]
- 37.Khemchandani R, Chandra S, et al. Twin support vector machines for pattern classification. TPAMI. 2007;29(5):905–910. doi: 10.1109/tpami.2007.1068. [DOI] [PubMed] [Google Scholar]
- 38.Kumano S, Otsuka K, Yamato J, Maeda E, Sato Y. Pose-invariant facial expression recognition using variable-intensity templates. IJCV. 2009;83(2):178–194. [Google Scholar]
- 39.Kumar MP, Packer B, Koller D. Self-paced learning for latent variable models. NIPS. 2010 [Google Scholar]
- 40.Li Y, Chen J, Zhao Y, Ji Q. Data-free prior model for facial action unit recognition. IEEE Trans on Affective Computing. 2013;4(2):127–141. [Google Scholar]
- 41.Liu W, Wang J, Chang SF. Robust and scalable graph-based semi-supervised learning. Proceedings of the IEEE. 2012;100(9):2624–2638. [Google Scholar]
- 42.Mavadati SM, Mahoor MH, Bartlett K, Trinh P, Cohn JF. Disfa: A spontaneous facial action intensity database. IEEE Trans on Affective Computing. 2013 Apr;4(2):151–160. [Google Scholar]
- 43.Melacci S, Belkin M. Laplacian support vector machines trained in the primal. Journal of Machine Learning Research. 2011;12:1149–1184. [Google Scholar]
- 44.Muandet K, Balduzzi D, Schölkopf B. Domain generalization via invariant feature representation. ICML. 2013 [Google Scholar]
- 45.Pfister T, Li X, Zhao G, Pietikainen M. Recognising spontaneous facial micro-expressions. ICCV. 2011 [Google Scholar]
- 46.Rosenberg C, Hebert M, Schneiderman H. Semi-supervised self-training of object detection models. WACV. 2005 [Google Scholar]
- 47.Rudovic O, Pavlovic V, Pantic M. Context-sensitive dynamic ordinal regression for intensity estimation of facial action units. TPAMI. 2015 May;37(5):944–958. doi: 10.1109/TPAMI.2014.2356192. [DOI] [PubMed] [Google Scholar]
- 48.Sangineto E, Zen G, Ricci E, Sebe N. We are not all equal: Personalizing models for facial expression analysis with transductive parameter transfer. ACM MM. 2014 [Google Scholar]
- 49.Sun Q, Chattopadhyay R, Panchanathan S, Ye J. A two-stage weighting framework for multi-source domain adaptation. NIPS. 2011 [Google Scholar]
- 50.Taheri S, Patel VM, Chellappa R. Component-Based Recognition of Facesand Facial Expressions. IEEE Trans on Affective Computing. 2013;4(4):360–371. [Google Scholar]
- 51.Wang S-J, Yan W-J, Zhao G, Fu X, Zhou C-G. Microexpression recognition using robust principal component analysis and local spatiotemporal directional features. ECCVW. 2014 [Google Scholar]
- 52.Whitehill J, Bartlett MS, Movellan JR. Social Emotions in Nature and Artifact. 2014 ch. Automatic facial expression recognition. [Google Scholar]
- 53.Yang J, Yan R, Hauptmann AG. Cross-domain video concept detection using adaptive SVMs. ACM MM. 2007 [Google Scholar]
- 54.Yang S, Rudovic O, Pavlovic V, Pantic M. Personalized modeling of facial action unit intensity. Advances in Visual Computing. 2014 [Google Scholar]
- 55.Zeng J, Chu W-S, De la Torre F, Cohn JF, Xiong Z. Confidence preserving machine for facial action unit detection. ICCV. 2015 doi: 10.1109/TIP.2016.2594486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Zhang X, Yin L, Cohn JF, Canavan S, Reale M, Horowitz A, Liu P. A high-resolution spontaneous 3d dynamic facial expression database. FG. 2013 [Google Scholar]
- 57.Zhao K, Chu W-S, De la Torre F, Cohn J, Zhang H. Joint patch and multi-label learning for facial action unit detection. CVPR. 2015 doi: 10.1109/CVPR.2015.7298833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zhu X. Semi-supervised learning. In: Sammut C, Webb G, editors. Encyclopedia of Machine Learning. 2010. pp. 892–897. [Google Scholar]
- 59.Zhu Y, De la Torre F, Cohn JF, Zhang YJ. Dynamic cascades with bidirectional bootstrapping for spontaneous facial action unit detection. IEEE Trans on Affective Computing. 2011;2:79–91. doi: 10.1109/T-AFFC.2011.10. [DOI] [PMC free article] [PubMed] [Google Scholar]