Abstract
We address the nature of unintentional changes in performance in two papers. This first paper tested a hypothesis that unintentional changes in performance variables during continuous tasks without visual feedback are due to two processes. First, there is a drift of the referent coordinate for the salient performance variable toward the actual coordinate of the effector. Second, there is a drift toward minimum of a cost function. We tested this hypothesis in four-finger isometric pressing tasks that required the accurate production of a combination of total moment and total force with natural and modified finger involvement. Subjects performed accurate force/moment production tasks under visual feedback, and then visual feedback was removed for some or all of the salient variables. Analytical inverse optimization was used to compute a cost function. Without visual feedback, both force and moment drifted slowly toward lower absolute magnitudes. Over 15 s, the force drop could reach 20% of its initial magnitude while moment drop could reach 30% of its initial magnitude. Individual finger forces could show drifts toward both higher and lower forces. The cost function estimated using the analytical inverse optimization reduced its value as a consequence of the drift. We interpret the results within the framework of hierarchical control with referent spatial coordinates for salient variables at each level of the hierarchy combined with synergic control of salient variables. The force drift is discussed as a natural relaxation process toward states with lower potential energy in the physical (physiological) system involved in the task.
Keywords: optimization, cost function, finger, force, unintentional movement
Introduction
The unintentional drift of performance is a well-documented phenomenon. It is observed during both unperturbed continuous trials (Slifkin et al. 2000; Vaillancourt and Russell 2002), in response to transient force perturbations (Wilhelm et al. 2013; Zhou et al. 2014), and over repeated trials (Heijnen et al. 2012). Within this context, we use the word “unintentional” for changes in performance that happen in the absence of changes in the external force field and distortions in the natural sensory feedback, and without the actor’s knowledge. For example, when a person is asked to maintain accurate constant force by an effector under visual feedback and then the feedback is removed, a slow drift in force, typically to lower values, is observed (Vaillancourt and Russell 2002; Shapkova et al. 2008). A similar, but much faster, drift is observed when the effector is subjected to a transient perturbation (Wilhelm et al. 2013; Reschechtko et al. 2014). If a person is asked to walk toward an obstacle, step over it, and continue walking, over repeated trials the clearance between the foot and the obstacle gets smaller (particularly for the trailing foot), and sometimes the foot touches the obstacle (Heijnen et al. 2012, 2014). The cited earlier studies offered interpretations of these phenomena based on a variety of concepts such as limitation of the working memory, boredom, inattention, minimization of energy expenditure, and fatigue.
Recently, we have offered a conceptually different interpretation for unintentional drifts in performance based on two concepts. The first is the control of voluntary actions with changes in referent coordinates (RCs) for the involved effectors (Feldman and Levin 1995; Feldman 2015). The second is the idea of synergic control of redundant systems (note that all natural actions involve redundant sets of effectors, Bernstein 1967) based on the principle of abundance (Latash 2012). For example, producing a constant force by an effector is associated with setting its RC (and possibly apparent stiffness k, Latash and Zatsiorsky 1993) and keeping it unchanged with the help of visual feedback. When the feedback becomes unavailable, RC may drift toward the actual coordinate (AC) of the effector (e.g., the actual coordinate of the fingertip) and cause a slow force decrease. In isometric conditions AC is constant, force magnitude F = k(RC – AC), and a drift in RC is reflected in the drift in force. This hypothetical mechanism has been referred to as RC-back-coupling (Reschechtko et al. 2014; Ambike et al. 2015; Zhou et al. 2015). Along similar lines, moment of force (M) production may be viewed as a consequence of a change in referent orientation (RO) of the object with respect to its actual orientation (AO): M = kR(RO – AO) where kR is rotational apparent stiffness (Latash et al. 2010; Parsa et al. 2016). Unintentional changes in M are viewed as consequences of a drift of RO toward AO, which is another example of the hypothetical RC-back-coupling mechanism. Figure 1 illustrates the notions of actual coordinate (AC), referent coordinate (RC), actual orientation (AO), and referent orientation (RO) in panel A, and RC-back-coupling in panel B. Note that RC-back-coupling can potentially lead to an increase or a decrease in the force by individual effectors (finger) depending on the relative drifts in RC and RO (Parsa et al. 2016).
Figure 1.
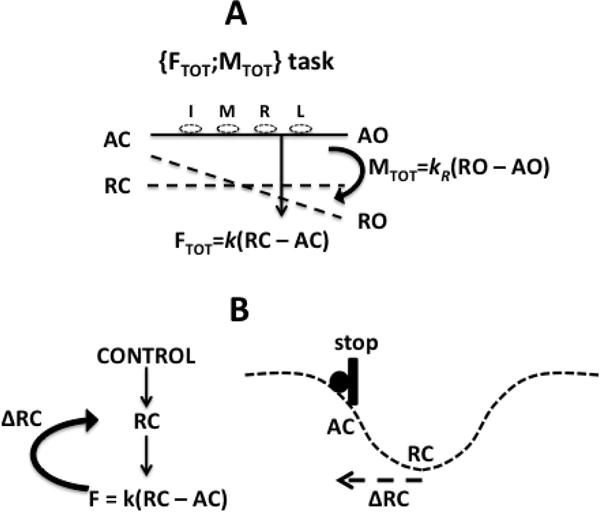
A: A schematic illustration of the notions of actual coordinate (AC), actual orientation (AO), referent coordinate (RC), and referent orientation (RO) for the task of four-finger force-moment production. Note that total force (FTOT) is a linear function of (RC – AC), while total moment (MTOT) is a function of (RO – AO). B: A schematic illustration of the concept of RC-back-coupling. Direct process starts with a change in RC resulting in a change in force (F). A slower process leading to a change in RC (ΔRC) toward AC results in a force drop. The scheme on the right shows a potential field (dashed line) corresponding to a value of RC. Apparent stiffness and apparent rotational stiffness are shown as k and kR.
Typical tasks involve redundant sets of effectors. For such a task, the effector space can be decomposed into two subspaces based on the effect that the effectors have on a salient performance variable. The uncontrolled manifold (UCM, Scholz and Schöner 1999) is a subspace corresponding to no change in that variable, while the orthogonal to the UCM subspace (ORT) corresponds to changes in this variable. During steady-state tasks, processes in the UCM are usually less stable as compared to ORT (reviewed in Latash et al. 2002, 2007). Note that processes in less-stable spaces are slower as compared to more-stable spaces (cf. motion of a mass on a weak spring – less stable, and on a stiff spring – more stable). Hence, slower drift is expected within the UCM while faster drift is expected within ORT. When the system is perturbed leading to a change in the salient performance variable, the perturbation by definition affects the ORT space resulting in a fast RC-back-coupling process and fast change in that performance variable. During continuous steady-state tasks, transient relaxation processes are slow reflecting the lower stability within the UCM. A degree of coupling between the two subspaces has been hypothesized leading to the slow force drift observed during continuous tasks (Ambike et al. 2015).
The concepts of RC and synergic control were used to explain the overall change in the salient performance variable and its stability as reflected, for example, in the structure of inter-trial variance within the UCM and ORT spaces (reviewed in Latash et al. 2007). In this study, we focus on a third characteristic of actions by abundant systems, namely the average across trials sharing of the salient performance variable among the elements. Sharing has been addressed based on optimality principles (reviewed in Prilutsky and Zatsiorsky 2002). Recently, a method of analytical inverse optimization (ANIO) has been introduced (Terekhov et al. 2010) that allows computing a cost function based on observed behavior of a redundant system over a broad range of task constraint values.
Our main hypothesis is unintentional changes in performance variables during continuous tasks without visual feedback are due to two processes. First, there is the aforementioned RC-back-coupling leading to a drift of the RC towards the actual coordinate of the effector. Second, there is a drift within the UCM toward a minimum of the cost function reflected in coordinated drifts of the elemental variables (variables produced by individual effectors at the selected level of analysis). We tested this hypothesis in multi-finger isometric pressing tasks that required the accurate production of a combination of total moment and total force, {MTOT; FTOT} (similar to Park et al. 2010, 2013).
To test the first set of predictions, we quantified the drifts in FTOT and MTOT observed when the subjects continued performing such tasks without visual feedback. We predicted that FTOT would drop (similarly to Vaillancourt and Russell 2002; Ambike et al. 2015a) while MTOT drift would depend on the initial magnitude and direction of MTOT and directed toward its zero magnitude corresponding to the horizontal actual orientation of the hand. This prediction is based on the idea that MTOT production may be viewed as a shift of the referent orientation of the plane of fingertip coordinates (RO) away from its actual orientation (AO) scaled with an apparent stiffness coefficient (kO): MTOT = kO(RO − AO).
To test the second set of predictions, we required our subjects to vary their preferred sharing of the task among the four fingers using visual feedback. Namely, we asked them to produce the same {MTOT; FTOT} combination but with the force of the middle finger (FMID) reduced by 50%. Any finger could be chosen as a candidate for this manipulation. We selected the middle finger because: (1) its effects on MTOT are relatively small and could be easily compensated for by adjustments in other finger forces; and (2) it is a strong finger with substantial contribution to FTOT (Li et al. 1998). After visual feedback had been turned off, we expected the forces to drift towards their preferred sharing pattern corresponding to a minimum of the cost function reconstructed using the ANIO method. Since no perturbations were used, we expected all the processes to be relatively slow (e.g., as in Ambike et al. 2015a,b). To explore the interaction among the hypothesized processes, we quantified the drifts in performance under a variety of visual feedback conditions, from no feedback at all to feedback presented selectively on only a subset of the three constraints, FTOT, MTOT, and FMID. We expected consistent drifts in the no-feedback variables only.
Methods
Subjects
Six male and five female subjects (age 27.27 ± 5.44 years, mass 74.18 ± 14.73 kg, height 171.18 ± 8.30 m), all right-handed, volunteered to participate in the study. All subjects were healthy and without any history of neuropathy or any other upper-limb disorders. Nine subjects performed the experiment entirely. For technical reasons, for one of the conditions, the data for two subjects were unavailable (see later in Methods). All the procedures were approved by the Office for Research Protection of the Pennsylvania State University.
Equipment
Four force transducers (Nano-17 sensors, ATI Industrial Automation, Garner, NC, USA) were mounted on an aluminum plate, which was attached to a wooden board. The whole setup was fixed with a clamp to a table (Figure 2). The sensors were covered with sandpaper, the friction coefficient with the fingerpads was approximately 1.4–1.5 (Savescu et al. 2008). Visual feedback was shown on a 19″ monitor placed at the eye level, about 0.6 m away from subjects.
Figure 2.
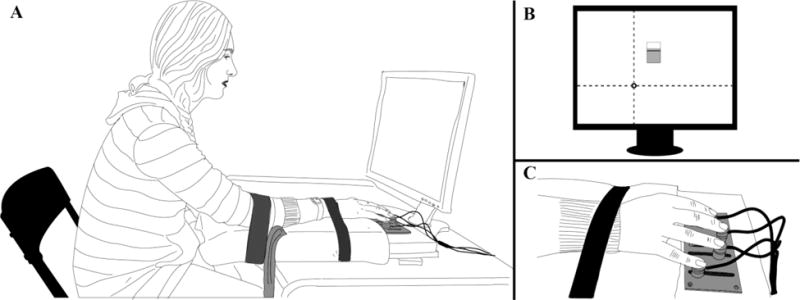
The setup. A: The subject’s position. B: Visual feedback defined total force and total moment target, {FTOT, MTOT}, as the intersection of two lines. The “tank with water” in the middle of the screen presented the feedback on the middle finger force. C: Hand placement on the sensors.
Twenty-four analog signals (4 sensors × 6 components) were digitized at 100 Hz by a 12-bit analog-digital converter (PCI-6031, National Instruments, Austin, TX). The programs for visual feedback and data collection were written in Labview 2010. Off-line analysis was done using Matlab 2014.
Experimental procedure
During the test, subjects sat in a chair at the table and placed the right-hand fingertips on the sensors. Two Velcro straps were used to maintain a steady hand and forearm position (Figure 1). The wooden plate was covered with a soft sponge layer for comfort. Sensor position in the anterior-posterior direction was adjusted for subject’s hand anatomy.
At the beginning of every trial, the experimenter asked the subject to place the fingertips on the sensors and relax the hand. The sensor readings were set to zero so that during data collection only the downward active force of the fingers was recorded.
The vertical axis on the visual feedback monitor screen showed the total pressing force (FTOT, the sum of the pressing forces of all four fingers), and the horizontal axis showed the total moment of force (MTOT) computed about the anterior-posterior axis passing in-between the sensors for the ring and middle fingers (Figure 2). Note that MTOT was a nominal moment value computed based on the vertical force magnitudes that did not take into account possible effects of the shear forces. As shown in Figure 1, subjects controlled the cursor position by adjusting FTOT and MTOT. (MTOT, FTOT) = (0, 0) corresponded to a cursor location in the mid-bottom of the screen. Pronation (PR) moment was considered negative while supination (SU) moment was positive.
The experiment consisted of three parts. The first part involved the maximum voluntary contraction (MVC) by all four fingers (MVC-4) and by the index finger alone (MVC-I). During these trials, the subjects were given feedback on the force produced by all four fingers (in MVC-4), or by the index finger (in MVC-I). Subjects performed two trials at each task with at least 30 s between the trials; the trial with the maximal value of the instructed force was chosen to set further tasks.
The second part involved data collection for analytical inverse optimization (ANIO). In this part, the subjects were required to press with the four fingers in a natural way, with minimal effort, to reach a target shown on the screen corresponding to a combination of MTOT and FTOT, {MTOT; FTOT}. To set tasks, we defined the unit of MTOT as 7% of MVC-I multiplied by the index finger nominal lever arm (0.045 m). Nine total force levels (5–45% of MVC-4 with steps of 5%), and seventeen-moment levels (0–4PR and 0–4SU with steps of 0.5) were used resulting in a total of eighty-one {MTOT; FTOT} combinations that filled a triangular shape with {(4PR, 45%MVC), (0, 5%MVC), (4SU, 45%MVC)} as vertices (as in Park et al. 2013). Subjects had 6 s to reach the target and stay there. There were 10-s intervals between trials, and additional 1-min rest periods after each 10-trial block.
The third part involved the main task. During this task, subjects were required to press with four fingers to reach the presented {MTOT; FTOT} target in a natural way, as in the second part. Three targets were used with FTOT always equal to 20% of MVC-4, while MTOT was 1.5PR, 0, or 1.5SU.
All the subjects were able to reach the prescribed {MTOT; FTOT} target within 3 s. After 5 s from the trial initiation, additional feedback was shown in the middle of the screen (not interfering with the original feedback on {MTOT; FTOT}). The additional feedback showed the force of the middle finger, FMID, as a vertical rectangular chart (Fig. 2). The subjects were required to reduce FMID to 50% of the average FMID level they had been producing over the 4.5–5 s time interval from the trial initiation (computed online). They were given 10 s to reach a new steady finger force combination that would satisfy the original {MTOT; FTOT} constraint and the new FMID constraint.
At that time (15 s into the trial), visual feedback was manipulated. There were seven feedback conditions: no feedback on any of the three variables (None), feedback on FTOT only, feedback on MTOT only, feedback on FMID only, feedback on FTOT and FMID (FTOT+FMID), feedback on FTOT and MTOT (MTOT+FTOT), and feedback on MTOT and FMID (MTOT+FMID). For nine of the subjects, an eighth condition was also used, in which all the feedback remained on the screen until the end of the trial (All). For technical reasons, data for the remaining two subjects for the “All” condition were unavailable. The subjects were always instructed to continue pressing with the same finger forces: “keep doing what you have been doing”. The conditions were presented in a fully randomized order. Three trials were performed under each condition.
Before starting the data collection, subjects performed ten practice trials to get acquainted with the main task. Conditions for the practice trials were selected randomly. No data were recorded in those trials.
A 10-s break was enforced between trials to prevent fatigue. After every ten trials, a one-minute break was given. Subjects were encouraged to ask for more rest during the experiment as needed. None of the subjects reported fatigue after the experiment.
Data processing
All data analysis was done in Matlab software. The finger forces were low-pass filtered at 5 Hz using a zero lag, fourth-order Butterworth filter. Three phases were selected in each trial for data analysis. Phase-1 corresponded to the time interval between 4.7 and 4.8 s; Phase-2 corresponded to the time interval between 14.7 and 14.8 s, and Phase-3 corresponded to the time interval between 29.7 and 29.8 s. These three 100-ms long time intervals were selected to reflect the steady states under the original two constraints, {MTOT; FTOT}, under the combination of three constraints, {MTOT; FTOT} and FMID, and at the end of the trial. Figure 3 illustrates these three phases for a sample trial using the FTOT time series.
Figure 3.
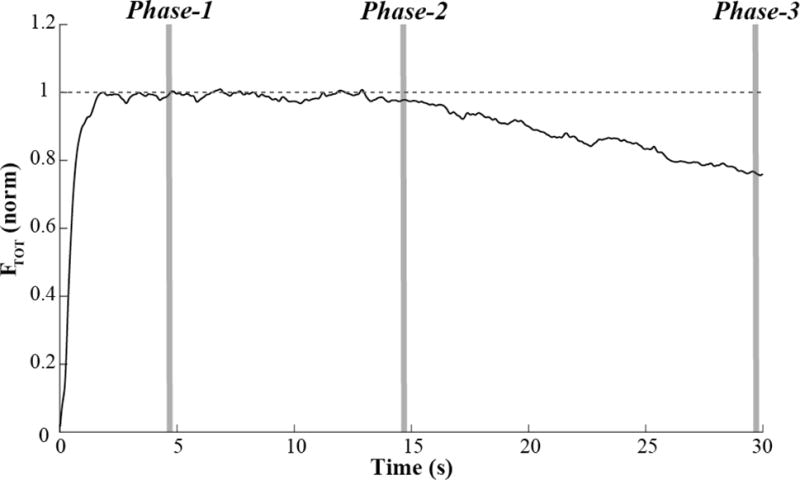
A typical example of total force (FTOT) time series during the task with no feedback after Phase-2. The three phases are shown by gray vertical columns. Phase-1 corresponded to the time interval between 4.7 and 4.8 s (performance under the original task, {FTOT, MTOT}); Phase-2 corresponded to the time interval between 14.7 and 14.8 s (performance under the added constraint on the middle finger force), and Phase-3 corresponded to the time interval between 29.7 and 29.8 s (the end of the trial).
Analysis of the drift in performance variables
The drift in the main performance variables, FTOT, MTOT, and FMID was estimated as the difference in the values of these variables averaged over Phase-3 and Phase-2 (ΔFTOT, ΔMTOT, and ΔFMID, respectively). For each subject, the average drift values were computed across three repetitions over each condition separately. Since the initial values of the two main task-related variables, FTOT and MTOT, were well matched to the task values by the subjects (see Results), we expected the drifts to reflect the final values of those variables. For other variables that could show substantial variability across conditions, such as individual finger forces, we analyzed both initial (Phase-2) and final (Phase-3) values in addition to their changes. These comparisons in normalized (to MVC) units were made since the force drift magnitude is known to change proportionally with the initial force value (e.g., Ambike et al. 2015). For across-subjects comparisons, the drifts in all performance variables and finger forces were normalized by the corresponding average values within Phase-2.
ANIO and computation of the cost function
The Analytical Inverse Optimization (ANIO) method (Terekhov et al. 2010) was used for approximating the cost function. The method used the data collected in the second part of the study, that is, during accurate production of 81 different {MTOT; FTOT} tasks. For each trial, we computed the average finger forces during the time interval {5.7 s; 5.9 s} from the trial initiation. We tested the planarity of the collected data sets within each subject using principal component analysis (PCA). In previous studies, we used the criterion of >90% of the variance explained by the first two PC vectors (Park et al. 2010, 2011, 2012). Compared to the cited earlier studies, we softened the criterion for data acceptance into ANIO. This was done because two subjects showed about 85% of the data explained by the two first PCs. Otherwise, the results in those two subjects were not different from all other subjects. Hence, to be able to include those data in our analysis, we chose 80% to be the threshold. All the subjects, except one, produced data sets that satisfied this criterion (see Table 1). This justified using a second-order polynomial of finger forces as a cost function (Terekhov et al. 2010; Park et al. 2011):
| (1) |
where i stands for fingers (index, middle, ring, and little), subscript n stands for normal forces, ki and wi are coefficients selected to provide the best fit to the original data. Further, the cost functions were used to compute optimal solutions for the same {MTOT; FTOT} tasks for each subject. For consistency, we used this equation for the data of the only subject who failed to satisfy the 80% criterion. The dihedral angle (D-angle) between the plane of optimal solutions for the same {MTOT; FTOT} combinations and the plane of original data (spanned by PC1 and PC2) was computed. The D-angle is a metric reflecting the goodness of fit provided by the computed cost function. The dihedral angle equal to zero means that the two planes are parallel. The noise analysis and a description of why the dihedral angle is an adequate measure for goodness of fit was discussed in earlier publications (Terekhov et al. 2010; Terekhov and Zatsiorsky 2011). A more detailed description of the method can be found in the Appendix.
Table 1.
Summary of the results of ANIO
| Subject | Quadratic coefficients (ki) | D–angle (deg) | % Variance |
|---|---|---|---|
| 1 | [0.53 0.26 0.44 0.67] | 1.82 | 89.89 |
| 2 | [0.81 0.26 0.26 0.45] | 5.06 | 89.75 |
| 3 | [0.83 0.15 0.22 0.49] | 6.08 | 93.93 |
| 4 | [0.45 0.08 0.41 0.79] | 12.89 | 77.21 |
| 5 | [0.68 0.27 0.36 0.58] | 2.86 | 85.08 |
| 6 | [0.94 0.17 0.14 0.25] | 11.24 | 88.23 |
| 7 | [0.97 0.13 0.06 0.21] | 1.66 | 85.88 |
| 8 | [0.16 0.31 0.29 0.89] | 8.56 | 83.08 |
| 9 | [0.77 0.53 0.31 0.53] | 0.01 | 86.60 |
| 10 | [0.45 0.34 0.64 0.53] | 2.96 | 93.77 |
| 11 | [0.85 0.32 0.31 0.28] | 7.30 | 87.99 |
The coefficients at quadratic terms computed for individual subjects, D-angle, and the percent of total variance accounted for by the first two PC vectors.
Equation (1) was further used to compute the cost values (CANIO) within Phase-2 and Phase-3 for the data collected during the main part of the experiment. The change in CANIO was computed between the two phases (ΔCANIO). The average values of ΔCANIO across the three repetitions at each condition were used for statistical purposes. In general, as defined by Eq. (1), CANIO = 0, corresponding to zero finger forces, may be viewed as optimal. However, this could never happen in the experiment, as people were explicitly instructed not to take their hand off the sensors. So, we expected CANIO to move closer to zero from Phase-2 to Phase-3, as compared to its initial value.
Statistical analysis
Data are presented in the text and Figures as means ± standard errors unless stated otherwise. To test the first hypothesis, a two-way repeated measure ANOVA was run on ΔFTOT, ΔMTOT, and ΔFMID, separately with the factors Feedback (None, FTOT, MTOT, FMID, FTOT+FMID, FTOT+ MTOT, MTOT+FMID, and All) and Moment (PR, ZE, and SU). To include the “All” condition, the analysis was repeated for nine subjects who had performed all of the conditions; however, the main effects were studied for 11 subjects without including the “All” feedback condition. To test the second hypothesis, the same ANOVA design was applied to ΔCANIO.
Furthermore, to study changes in finger forces during the main task, a two-way MANOVA with repeated measures was used with the factors Finger (index, middle, ring, and little), Feedback and Moment. In all of the analysis, significant effects of ANOVA and MANOVA were further explored using pairwise contrasts with Bonferroni adjustments. The adjustments were selected based on the actual number of levels of factors with significant main effects or on the number of permutations of levels in significant interaction effects.
All the data sets were checked for normality and sphericity using the Mauchly criterion. In cases of sphericity violations, the Greenhouse-Geisser correction was applied. The nominal critical p-value (before Bonferroni adjustments) in all of the analysis was set at 0.05. The actual critical p-values depended on specific contrasts.
Results
Analytical Inverse Optimization (ANIO)
Principal component analysis (PCA) applied to the individual finger force data collected over the sets of 81 trials with different combinations of total moment and total force, {MTOT; FTOT}, led in all subjects, except one, to well over 80% of total variance accounted for by the first two PCs (Table 1). Only subject #4 failed to satisfy the 80% criterion, while the average value across subjects was 87.4±1.43%.
For consistency, we applied ANIO to the data of all subjects including subject #4. The second column in Table 1 shows the coefficients (ki) at the second-order terms of the cost function; see Equation (1) in Methods. Note that all these coefficients were positive, which is an important criterion for applicability of ANIO (Terekhov et al. 2010; Terekhov and Zatsiorsky 2011). The positive ki values mean that ANIO found a solution for the inverse optimization problem.
The dihedral angle (D-angle), the goodness of fit index (see Methods) was, on average 5.49±1.25°. Two subjects showed larger values of the D-angle (>10°); one of them was subject #4 who also showed the lowest percentage of variance accounted for by the two PCs.
Drifts in task-related performance variables
All the subjects were able to perform the {MTOT; FTOT} tasks, even after the additional constraint on FMID had been added. Note that the main task was very simple, especially given that the {MTOT; FTOT} values were normalized with respect to the MVC. We did not have specific error requirements, but the subjects could place the cursor on the target with no visible deviations in both Phase-1 and Phase-2. As a result, the drifts in the two main task-related variables, FTOT and MTOT, reflected final values since initial values were closely matched (in normalized units). Figure 3 shows the individual finger time series during a typical trial with an initial pronation moment, as well as the computed performance variables related to the task constraints, FTOT, MTOT, and FMID. During the early portion of the task (until Phase-1), the subject achieved a certain finger force combination that satisfied the {MTOT; FTOT} constraint. By Phase-2, the subject was able to reduce FMID by 50% (as required by the task) while still producing the same {MTOT; FTOT} combination. After the visual feedback on all three performance variables, FTOT, MTOT, and FMID, was turned off, the finger forces showed consistent drifts leading to a drop in FTOT, a drop in the magnitude of MTOT, and an increase in FMID (see Phase-3 in Figure 3).
Keeping visual feedback on some of the performance variables helped the subjects to avoid drift in those variables, while drifts in the variables without visual feedback persisted. Figure 4 illustrates two typical trials with the initial moment into supination and into pronation. After Phase-2, visual feedback on FTOT only was preserved, while the feedback on MTOT and FMID was turned off. The Figure shows a consistent level of FTOT throughout the trial, while the magnitude of MTOT drifts to lower absolute values and the magnitude of FMID drifts toward higher values.
Figure 4.
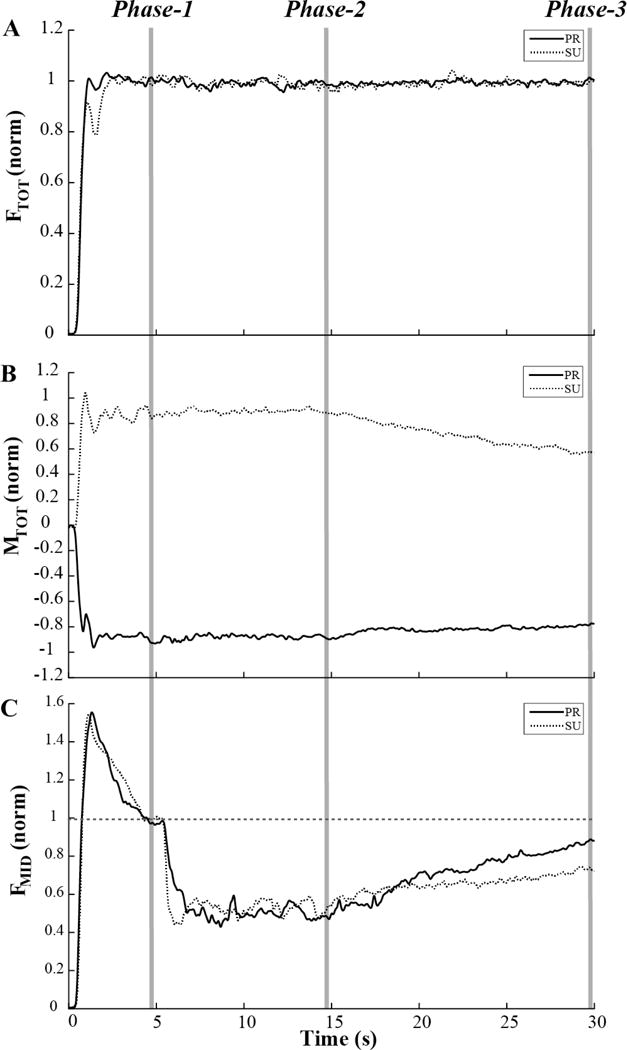
Typical performance under the FTOT feedback condition (no feedback on total moment and middle finger force). A: Total force, FTOT did not drift. B: Total moment, MTOT magnitude decreased. C: Middle finger force, FMID increased over the time interval with modified visual feedback. Note that MTOT drifted in opposite directions under the initial pronation (PR) and initial supination (SU) conditions. Solid lines – performance under the initial PR conditions; dashed lines – performance under the initial SU conditions. Averages over 3 trials in each condition for a representative subject are shown.
Overall patterns of the drifts in the three task-related variables are illustrated in Figure 5. Panel A of Figure 5 shows the averaged across subjects magnitude of the drift in FTOT (ΔFTOT) from Phase-2 (full feedback) to Phase-3 (modified feedback) as a function of feedback condition. Note the very low drift magnitudes when FTOT feedback was present and large consistent drifts to lower FTOT values (negative ΔFTOT) when FTOT feedback was turned off. The drift in FTOT showed only minor changes with the initial MTOT magnitude, but it showed smaller values when MTOT feedback was present.
Figure 5.
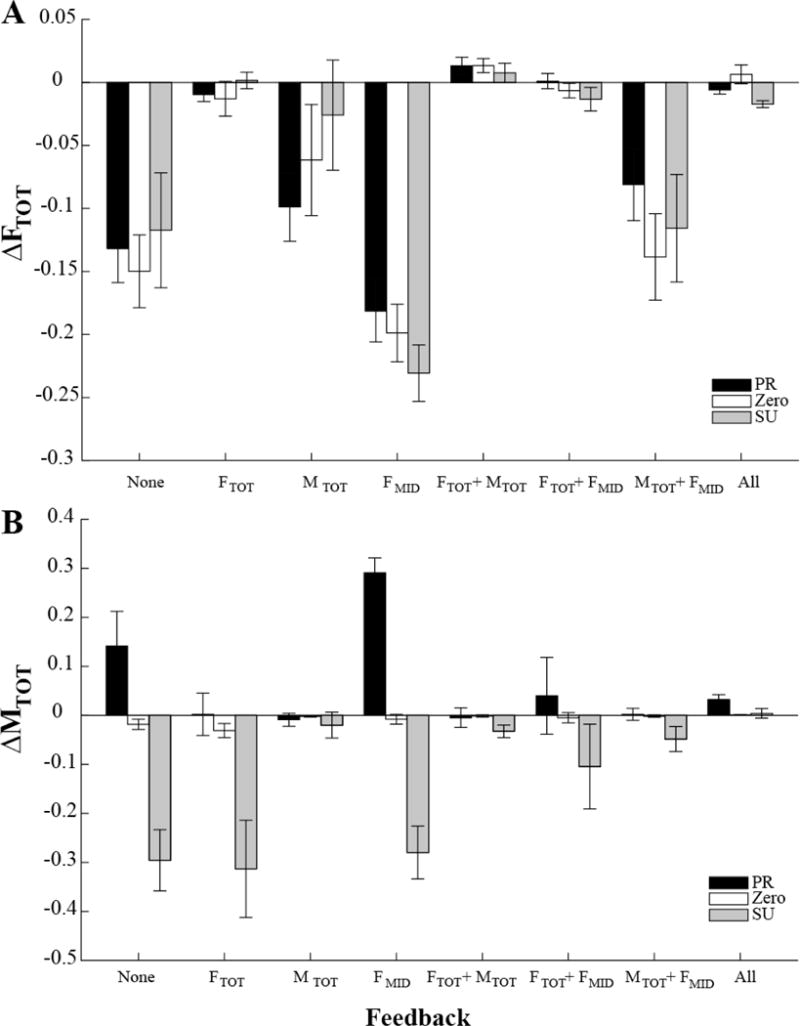
Across-subjects means and standard errors for the change in total force (A, ΔFTOT) and in the total moment, (B, ΔMTOT) between Phase-2 and Phase-3. The data are shown separately for the three initial MTOT condition, pronation (PR, black bars), supination (SU, gray bars) and zero initial moment (ZERO, white bars) and the different feedback conditions (X axis). FMID stands for the middle finger force. Note the consistent FTOT drop under conditions without FTOT feedback, and different directions of MTOT change under conditions without MTOT feedback for the initial PR and SU conditions.
Two-way ANOVA, Moment × Feedback, on ΔFTOT over the time of modified feedback confirmed a significant effect of Feedback (F[2.574, 25.741] = 22.394, p < 0.001). Pairwise contrasts confirmed that the drop was larger in conditions without FTOT feedback (on average, 12.76 ± 1.68% of the target FTOT), compared to conditions when FTOT feedback was kept over the whole trial (on average, 0.19 ± 0.037% of the target FTOT, p < 0.001). It also confirmed larger magnitudes of ΔFTOT for the “None” and “FMID” condition (no feedback on FTOT and MTOT) compared to the “MTOT” and “MTOT+FMID” conditions (p < 0.05).
The drift in MTOT depended strongly on both the initial MTOT value and feedback. As illustrated in panel B of Figure 5, this drift was very small and inconsistent when feedback on MTOT was available throughout the trial. The drift was large when MTOT feedback was unavailable for both initial PR (black bars) and SU (gray bars) MTOT values. The difference in the sign of ΔMTOT in the PR and SU conditions reflected the fact that MTOT drifted toward zero value. The average decrease in MTOT in the absence of visual feedback was 11.84%±6.45%, 1.56%±0.59%, and 24.83%±4.84% of the original value in PR, ZERO, and SU moment condition, respectively. When the feedback was shown, these values decreased to 1.20%±0.69%, 0.15%±0.03%, and 2.63%±0.94% of the original value, respectively.
Two-way ANOVA, Moment × Feedback, on ΔMTOT confirmed a significant effect of Moment (F[1.324, 13,236] = 28.314 p < 0.001) and a significant Moment × Feedback interaction (F[3.668, 36.684] = 11.374, p < 0.001). The effect of Moment reflected significant differences within each pairs of the three levels, PR, SU and ZERO (p < 0.05). The interaction reflected the different magnitudes of the drift between conditions with and without MTOT feedback (p < 0.001). Effect of Feedback was not significant because of its opposite effects depending on the initial moment.
Drifts in finger forces
The regularities in the drifts of FTOT and MTOT were reflected in drifts of the individual finger forces. Figure 6 illustrates the averaged across subjects values of individual finger forces in Phase-2 and Phase-3. Since we have been primarily interested in the finger force drifts during the time with no visual feedback, i.e., from the end of Phase-2 to the end of Phase-3, further analysis was applied to the force changes during that time interval expressed in normalized units (see Methods). Panel B of Figure 7 illustrates the drifts in the middle finger force, FMID. In trials, when visual feedback on FMID was provided, no consistent drifts in FMID were observed. In contrast, when FMID feedback was unavailable, FMID showed a consistent tendency to increase. These effects were the strongest in the SU tasks (gray bars in Fig. 5B) and weakest in the PR tasks (black bars in Fig. 5B). In the absence of feedback on FMID, 20.89%±8.27%, 31.01%±4.73%, and 64.21%±12.17% increase in FMID was observed in the PR, ZERO, and SU conditions, respectively.
Figure 6.
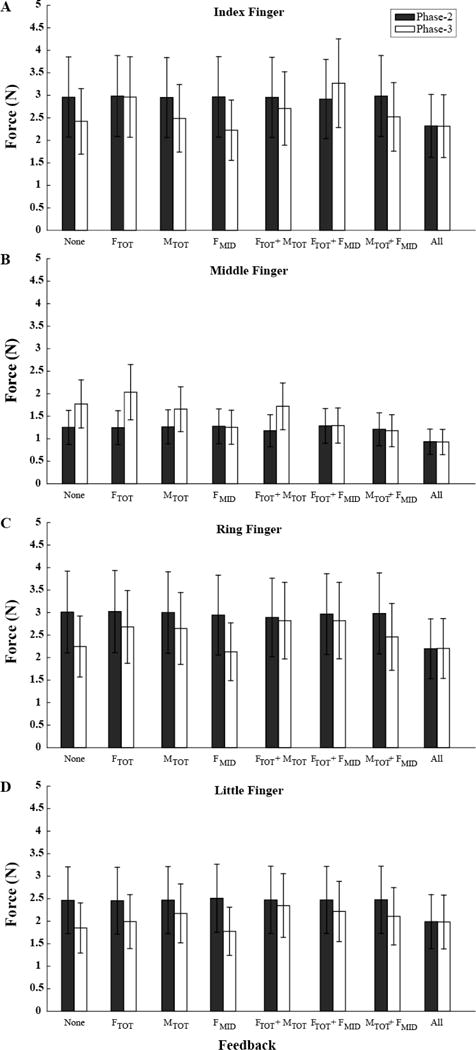
Across-subjects means and standard errors for the index finger force (A), middle finger force (B), ring finger force (C), and little finger force (D) in Phase-2 (solid bars) and Phase-3 (empty bars) for the different feedback conditions (X axis). The data have been averaged over the three initial MTOT conditions. FMID stands for the middle finger force. Note the consistent FMID increase in Phase-3 under conditions without FMID feedback.
Figure 7.
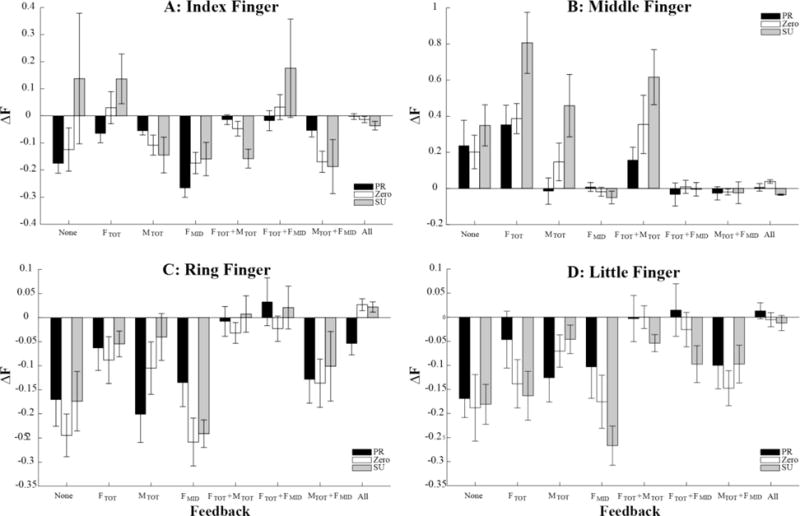
Across-subjects means and standard errors for the change in the index finger force (A), middle finger force (B), ring finger force (C), and little finger force (D) between Phase-2 and Phase-3. The data are shown separately for the three initial MTOT condition, pronation (PR, black bars), supination (SU, gray bars) and zero initial moment (ZERO, white bars) and the different feedback conditions (X axis). FMID stands for the middle finger force. Note the consistent FMID increase under conditions without FMID feedback.
Two-way ANOVA, Moment × Feedback, on ΔFMID confirmed significant effects of both Moment (F[2, 20] = 11.028, p < 0.001) and Feedback (F[2.710, 27.102] = 13.582, p < 0.001). There was also a significant Moment × Feedback interaction (F[4.644, 46439] = 3.143, p < 0.05). Pairwise comparisons confirmed the larger ΔFMID for SU compared to both PR and ZERO conditions (p < 0.05). The effect of Feedback reflected larger drift values for conditions without feedback on FMID compared to conditions with FMID feedback (p < 0.05). The interaction reflected the smaller effects of Moment on ΔFMID for the “None” condition as compared to other conditions without FMID feedback (p < 0.05).
In contrast to the ΔFMID patterns, the forces produced by the other three fingers (index, ring, and little) typically showed drifts toward smaller values (panels A, C, and D of Fig. 7). These drifts were smaller for the trials under “All” and “FTOT+MTOT” visual feedback conditions and larger under the “None” and “FMID” conditions. These observations were supported by a significant effect of Feedback (F[3.624,144.962] = 15.910, p < 0.001). There was also a significant effect of Moment reflecting the tendency of more positive (less negative) values of force changes for the SU tasks (F[2, 80] = 7.964, p < 0.001), particularly pronounced for the index finger (Moment × Finger interaction, F[6, 80] = 6.880, p < 0.01). Other significant effects, including the three-way interaction Moment × Feedback × Finger (F[17.649, 235.316] = 2.895, p < 0.01) reflected the complex pattern of individual finger force adjustments. Since these effects were not directly related to the specific hypotheses and their discussion, we do not present these results.
Cost value drifts
To test the second hypothesis on the drift within the UCM toward a minimum of the cost function, we quantified the cost function, CANIO at the end of Phase-2 and Phase-3 (with modified visual feedback). These values are shown in panels A and B of Figure 8. Note that, under most conditions, CANIO values were lower at the end of Phase-3 compared to the end of Phase-2. This is illustrated in panel C of Figure 8 that shows the change in CANIO (ΔCANIO) over that time interval. Under most conditions, the cost function showed a drop as illustrated by the negative values in Figure 8C. The largest magnitudes of ΔCANIO were seen under the “FMID” and “None” conditions while the smallest changes, close to zero, were observed under the “All”, “FTOT+MTOT” and “FTOT+FMID” conditions. These patterns did not show any clear effects of initial moment value. These results were reflected in the significant effect of Feedback in the Moment × Feedback ANOVA (F[1.347, 13.474] = 5.550, p < 0.05). No other effects reached significance. Note that, while the plot in Figure 8C resembles the one for the changes in FTOT (Fig. 5A), there is a significant difference. In the FTOT feedback condition, ΔFTOT was close to zero while ΔCANIO was negative (p < 0.05).
Figure 8.
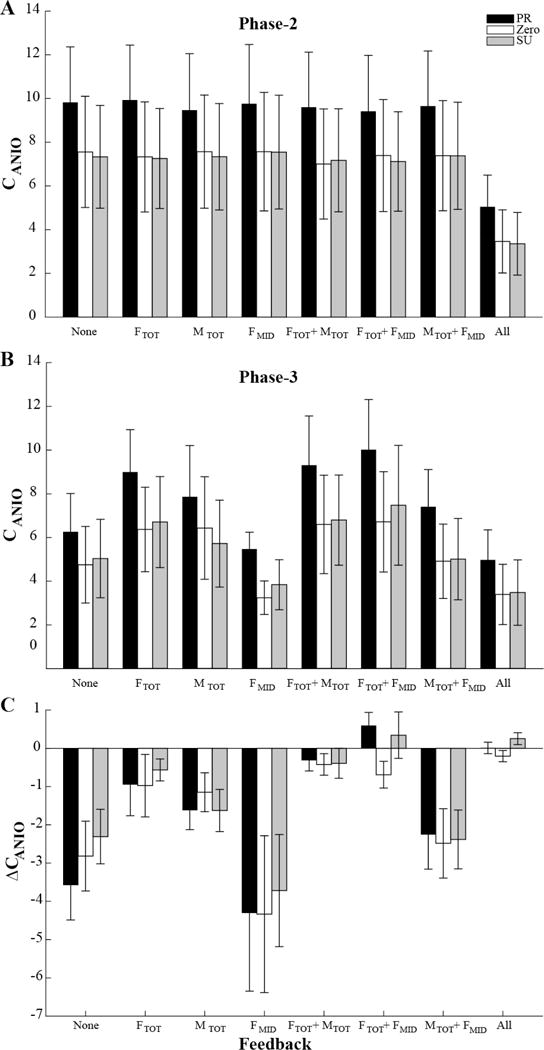
Across-subjects means and standard errors for the magnitude of the cost function, CANIO, at the end of Phase-2 (panel A) and at the end of Phase-3 (panel B). The changes in CANIO (ΔCANIO) between Phase-2 and Phase-3 are shown in panel C. The data are shown separately for the three initial MTOT condition, pronation (PR, black bars), supination (SU, gray bars) and zero initial moment (ZERO, white bars) and the different feedback conditions (X axis). FMID stands for the middle finger force. Note the mostly negative ΔCANIO values.
Discussion
The results of our study provide support for the main hypothesis formulated in the Introduction. We suggested that two factors contributed to the observed drift in finger forces in the absence of visual feedback. First, drift of the referent coordinate (RC) for a salient task-specific variable toward its actual coordinate was assumed (cf. Ambike et al. 2015). The experiments showed a drift of total force (FTOT) to lower values across conditions without FTOT feedback. They also showed a drift of the total moment of force (MTOT) towards lower absolute values when no MTOT related feedback was shown; the direction of the drift depended on the initial MTOT magnitude. The idea of control with RC implies, in particular, that active force is approximately proportional to the difference between the referent and actual fingertip coordinates, while active moment is proportional to the difference between the referent and actual hand orientations (Latash et al. 2010). Given that the actual finger position and configuration were always the same, our current observations support the assumed RC drift toward actual fingertip coordinates and hand orientation.
Second, we also assumed that a drift would happen within the uncontrolled manifold (UCM; Scholz and Schöner 1999) for the salient performance variables toward a state corresponding to minimum of a cost function defined in the space of elemental variables. The initial cost of the finger force combination computed based on the cost function reconstructed with analytical inverse optimization (ANIO, Terekhov et al. 2010) dropped across conditions including the condition when feedback was provided on FTOT and no changes in that variable took place. Moreover, we observed an atypical drift of the middle finger force (FMID) to higher values in trials when the subjects reduced FMID intentionally as compared to the preferred finger force combination. Note that all earlier studies reported downward drifts of finger forces after turning visual feedback off unless the initial forces were very low (Slifkin et al. 2000; Vaillancourt and Russell 2002; Ambike et al. 2015).
Some of the current findings are similar to those in a recent paper that studied the across-trials structure of variance in force-moment production tasks performed without visual feedback (Parsa et al. 2016). That study involved many trials per condition and, consequently, it explored only two conditions. In this paper, we explored effects of changes in the initial sharing pattern (leading to changes in the cost function, CANIO) on the drifts. Due to the number of conditions, we could not possibly run the across-trials variance analysis. Hence, we limited ourselves to the analysis of motor equivalence and explored stability of force-moment under such enforced changes in the sharing pattern (covered in the companion paper).
Factors that define unintentional changes in performance
Unintentional motor performance has been known for many years. One of the classical examples is the so-called Kohnstamm phenomenon (Kohnstamm 1915; Ivanenko et al. 2006): An unintentional motion of an extremity following a long-lasting strong isometric contraction. Unintentional changes in locomotion have been reported following walking on a rotating platform (the podokinetic effect, Weber et al. 1998; Scott et al. 2011) and under vibration applied to the leg muscles (Gurfinkel et al. 1998; Ivanenko et al. 2000).
Recently, the phenomenon of unintentional finger force drop has been studied in experiments with accurate force production when the previously available visual feedback was turned off (Slifkin et al. 2000; Vaillancourt and Russell 2002; Shapkova et al. 2008). Similar effects have been observed in grasping studies following a slow transient change in the aperture (Ambike et al. 2014), while faster unintentional changes in arm position and finger forces were reported in experiments with transient perturbations applied to the effectors (Wilhelm et al. 2014; Zhou et al. 2014, 2015).
Some of the earlier studies invoked the notion of working memory limitations as the cause for the unintentional force drop (Vaillancourt et al. 2001; Vaillancourt and Russell 2002). Potential involvement of working memory in these phenomena was based on a body of literature describing connections between prefrontal and premotor cortices with the dorsolateral prefrontal cortex and posterior parietal cortex during tasks requiring memory in nonhuman primates (Goldman-Rakic 1988; Selemon and Goldman-Rakic 1988). It has also been supported by studies of cortical activation using MRI-based methods (Vaillancourt et al. 2003) as well as by EEG studies (Poon et al. 2012). On the other hand, involvement of working memory has been challenged in a recent study (Jo et al. 2016) based on an observation that resting during a comparable time interval led to no consistent force drift.
In a recent study, Ambike et al. (2015) also reported a force drift in the opposite direction, to higher values, but only in fingers that started the task with very low forces. These trends were weak (although statistically significant in some cases). While they remind the FMID drift to higher forces in our study, the initial FMID magnitudes in our experiment were typically higher (about 10% of the MVC force) than the values leading to finger force drift toward higher force reported by Ambike and colleagues (under 5% of that finger’s MVC force). Besides, the magnitude of the FMID drift in our study was of about the same magnitude as the more typical downward force drift in other fingers (Figure 5), while in the Ambike et al. study the upward force drift was an order of magnitude smaller than the typical downward drifts.
Several earlier studies (Ambike et al. 2014, 2015; Zhou et al. 2015) offered a conceptually different interpretation for the unintentional force drifts, which views these phenomena as specific examples of the well-known general tendency of all physical systems to move toward states with lower potential energy. The unintentional force drift has been interpreted within the hypothesis assuming that the neural control of movements is based on shifts of referent spatial coordinates for salient variables (the RC-hypothesis, reviewed in Feldman 2015). Within the RC-hypothesis, force production in isometric conditions is associated with setting RC for the effector that differs from its actual coordinate (AC). The difference between AC and RC produces force via a scaling coefficient, apparent stiffness (cf. Pilon et al. 2007). An unintentional drop in force means that RC moves towards AC and/or the apparent stiffness decreases; for simplicity, we consider only the former mechanism. Note that when RC = AC, the system produces no force, and muscle activation is minimal for the given effector configuration. This state may be viewed as the state with minimal potential energy of the effector. A hypothesis has been suggested that, when the CNS does not implement sensory-based corrections, the physical/physiological system participating in the task relaxes toward a state with minimal potential energy, i.e., AC attracts RC leading to a force drift toward smaller magnitudes. Our current results on the FTOT and MTOT drifts provide support for this idea.
A novel hypothesis offered in this study is that, when an abundant set of effectors participates in a task, a drift toward preferred solution is expected in the space of elemental variables. We estimated preferred solutions using the analytical inverse optimization (ANIO) method (Terekhov et al. 2010) and then used the computed cost functions to estimate the changes in cost associated with the changing finger force combinations. Asking the subjects to perform the {FTOT; MTOT} tasks with a reduced contribution from the middle finger forced them to deviate from the naturally preferred solution corresponding to a minimum of the cost function. The observed downward drift of the cost supports the idea that a drift took place in the space of finger forces leading to more natural finger force combinations (closer to the minimum of the cost function).
Taken together, our observations suggest superposition of two processes: a drift of RC toward AC and a drift in the space of finger forces directed at reducing the cost of the action. Figure 9 illustrates this idea for a two-finger task of producing a value of total force: F1 + F2 = FTOT. Assume that the subject has a preferred pattern of sharing FTOT between the two fingers, e.g., 50:50 (the large black dot), corresponding to a minimum of the cost function (shown with parabolic dashed lines). Other solutions for the task are possible shown by the lines with negative slope – UCMs for this task. The initial force level corresponds to a certain distance between RC and AC. Imagine now that the subject was asked to perform this task with an unusual force combination, i.e. lower contribution of finger #1 (the open circle). This point corresponds to a higher cost of the action (see the dashed circle, a projection of the point on the cost function). After visual feedback on both FTOT and F1 has been turned off, two processes will take place. First, RC will drift towards AC illustrated by the drift of the solution space (UCM) toward smaller FTOT values (compare the thick and thinner UCM lines in Fig. 9). At the same time, a drift in the {F1; F2} space will take place moving the actual finger force values closer to the bottom of the cost function. The resultant drift is shown as the dashed line with the arrow. Our observations suggest that the two processes proceed at comparable time scales, but this issue requires further investigation. Note that unintentional drifts at two time scales have been reported so far, slow (typical times of 10–20 s; Vaillancourt and Russell 2002; Ambike et al. 2014, 2015) and fast (typical times of 1–2 s; Wilhelm et al. 2013; Zhou et al. 2014, 2015; Ambike et al. 2016).
Figure 9.
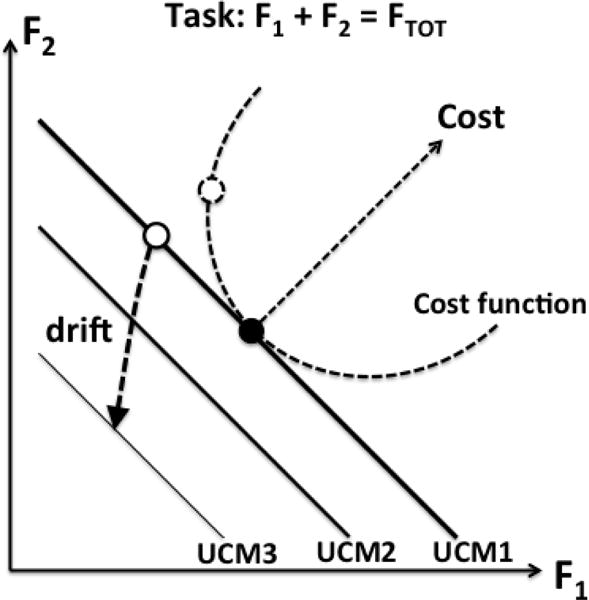
An illustration of the two components of the unintentional finger force changes using a two-finger task of producing a value of total force: F1 + F2 = FTOT. The solution space is shown as a line with negative slope, UCM1. The preferred sharing of FTOT between the two fingers is shown with the large black dot; it is assumed to correspond to a minimum of the cost function (the parabolic dashed line). If the subject performs this task with an unusual force combination (the open circle), the cost is higher (the dashed circle). After visual feedback has been turned off, (F1 + F2) will drift to lower values due to the assumed referent coordinate (RC) drift resulting in new solution spaces shown by thinned lines (UCM2 and UCM3). At the same time, a drift along UCM toward the bottom of the cost function will take place. The resultant drift is shown as the dashed line with the arrow.
Hierarchical control with referent coordinates
Two approaches dominate the field of motor control. One of them is motivated by ideas from the field of control theory. This approach assumed that the central nervous system performs computational operations with neural variables reflecting specific sensory or mechanical variables, for example computing integrals of certain functions of those variables over movement time before movement initiation or in the process of movement. A typical example is the optimal feedback control schemes that are based on minimizing cost of action given the goal and current state of the effectors (Todorov and Jordan 2002; Diedrichsen et al. 2010). These methods have been successful in describing certain non-trivial features of voluntary movements and their corrections. While assuming an appropriate computational process within the central nervous system is probably able to account for all the data presented in our study, we are reluctant to accept the idea of neural computations based on both philosophical grounds (this topic is too broad to be covered here; for a recent review see Latash 2016) and the lack of direct demonstrations of such computations.
The alternative approach originates from physics, i.e., study of natural laws that describe behavior of any objects, animate and inanimate (reviewed in Latash 2012, 2014, 2016). This approach does not assume that the central nervous system performs computational operations but that it behaves according to laws of nature (some of these laws are unknown to us at this time). We use the physical approach, following established traditions of motor control (Bernstein 1947; Kugler and Turvey 1987; Feldman 2015). In particular, we accept the idea of control with referent coordinates that reflect changes in subthreshold depolarization of neuronal pools (reviewed in Feldman 2015).
The RC-hypothesis implies a hierarchical system of control with the RC for salient, task-specific variables defined at the highest level of the hierarchy. Further, this low-dimensional set of RCs maps on RCs at lower levels of the control hierarchy, which are typically higher-dimensional, and defines RCs for limbs, joints, digits, and muscles. Such transformations are associated with synergic adjustments among RCs within abundant sets at lower levels, possibly via back-coupling loops (Latash et al. 2005; Martin et al. 2009). This scheme predicts relatively consistent behavior in the space of salient task-specific variables combined with a relatively variable behavior at the level of elements (Schöner 1995).
This prediction has been tested in a number of studies within the UCM hypothesis (Scholz and Schöner 1999). Some of those studies (reviewed in Latash et al. 2007; Latash 2008) compared inter-trial variance within a space where salient variables do not change (within UCM, VUCM) and within a space where those variables change (orthogonal to the UCM, VORT). The inequality VUCM > VORT, where both indices are quantified per dimension in the corresponding spaces, has been used as a signature of a synergy stabilizing those salient variables. Another group of studies quantified deviations along the UCM and along the ORT space during quick corrective actions (Mattos et al. 2011, 2014). Note that deviations along the UCM by definition cannot correct deviations of salient variables. Nevertheless, large such deviations have been observed reflecting the lower stability of the system within the UCM as compared to the ORT directions.
In our study, we observed most consistent across subjects patterns of unintentional drifts in the task-related variables such as FTOT and MTOT when the corresponding feedback was turned off (Fig. 4). The drifts in some of the individual finger forces were less consistent (Fig. 5) suggesting that much of the finger force drifts took place within the UCM for FTOT and MTOT. This issue is analyzed in detail in the companion paper (Parsa et al. 2016).
Is optimization real?
The original formulation of the problem of motor redundancy (Bernstein 1935) stated explicitly that the main problem of motor control was the elimination of redundant degrees of freedom. This could be done by adding constraints to the system (for example, self-imposed, intentional constraints, e.g. Hu and Newell 2011), or by using optimization approaches, i.e., looking for a solution from an infinite set that minimizes (or maximizes) a cost function. A number of cost functions have been explored (reviewed in Nelson 1984; Prilutsky and Zatsiorsky 2002), such as minimal time, minimal energy expenditure, minimal jerk, minimal fatigue, minimal discomfort, and many others. Researchers selected specific cost functions rather arbitrarily, typically reflecting their intuition and experience.
Two questions emerge. First, can arbitrary choice of cost functions be avoided and replaced with a computational, data based, method? Second, are optimization approaches useful for analysis of natural, biological movements?
An answer to the first question was offered by the ANIO method (Terekhov et al. 2010: Terekhov and Zatsiorsky 2011). This method allows computing a cost function based on experimental observations under certain assumptions, in particular that the cost function is additive with respect to outputs of the elements. A number of studies have shown that ANIO produces consistent cost functions that allow describing multi-finger tasks with better accuracy than typical cost functions used in the literature (Niu et al. 2012), and that this method is sensitive to fatigue, healthy aging, and neurological disorders (Park et al. 2010, 2011b, 2012). Our current study makes another step in supporting applicability of ANIO to actions by abundant systems. As in the cited earlier studies, ANIO was able to reconstruct cost functions that generated solutions approximating the experimental data with good accuracy: The angle between the planes of actual solutions and ANIO-based solutions was, on average, about 5 degrees. Moreover, unintentional finger force changes after the visual feedback had been turned off led to a significant drop in the cost of the action based on the ANIO results.
ANIO is a method of fitting a data set based on a set of assumptions (described in detail in Terekhov et al. 2010). It produces a cost function that may or may not be able to describe the action in terms of optimization (for recent examples of ANIO failures see Xu et al. 2012; Parsa et al. 2016). In our tasks, however, ANIO was able to produce feasible cost functions (cf. Terekhov et al. 2010). In earlier studies, cost functions produced by ANIO were compared to other, more traditional, cost functions: ANIO-derived costs showed superior performance to most other functions and were not surpassed by any. Day-to-day changes in the ANIO-derived cost functions were also studied. Since these issues have been covered in earlier studies (Terekhov and Zatsiorsky 2011; Niu et al. 2012a,b), we have decided not to review them again but rather to accept ANIO as a viable method of finding cost functions for the studied tasks.
With respect to the second question, we view the drift of the cost (ΔCANIO; see Fig. 6) to lower values, as providing strong support for the idea that the CNS is indeed driven by some kind of an optimization process, i.e., it is naturally moved to solutions corresponding to minimum values of a cost function. The optimization process does not assume that the brain “computes” an optimal solution given a cost function, instead it may reflect intrinsic neural feedbacks, which attract the finger forces towards magnitudes corresponding to smaller values of the cost function (Martin et al 2013), similar to how gravity pulls a ball toward the local lowest point of a landscape. As a consequence, the optimization does not have to be absolute, just “good enough” (Simon 1956; Loeb 1999), corresponding to the relatively low stability along the corresponding UCM. Our instruction to the subjects to drop FMID by 50% before the visual feedback was turned off (Phase 2) apparently took the subjects away from the “good enough” region. As a result, a drift leading to lower cost values was seen including, in particular, the non-trivial drift of FMID to higher values in contrast to the dominant downward trend in the other finger forces.
Note that the drift in CANIO potentially got contributions from two factors. First, CANIO dropped with FTOT as it could be expected given its functional form, Eq. (1). Second, when feedback was provided on FTOT (and, as a result, no drift in FTOT took place), CANIO still showed a drift toward smaller values (see the negative values of ΔCANIO in Fig. 8C). This allows drawing a conclusion that a drift within the UCM for FTOT likely took place directed toward states with smaller CANIO.
Concluding comments
The main results of our study include support for the hypothesis on two sources of the observed unintentional finger force drift: The drift of RC towards AC and the drift of cost toward lower values. The observed drifts were relatively slow, comparable to earlier reports on the force drift in the absence of visual feedback (Vaillancourt and Russell 2002; Shapkova et al. 2008; Ambike et al. 2015). It suggested processes within a subspace characterized by relatively low stability of its elements, i.e. primarily within the UCM for the task. Since the effects were observed in the salient performance variables, these observations also suggest a degree of coupling between the UCM and ORT spaces, a hypothesis (Ambike et al. 2015, 2016) that is still in need of more direct experimental confirmation.
Acknowledgments
We are very much grateful to Dr. Satyajit Ambike for the productive discussions at early stages of this project. The study was in part supported by NIH grants NS035032 and AR048563.
APPENDIX: ANALYTICAL INVERSE OPTIMIZATION (ANIO)
The purpose of this method it to use the data collected during an experiment to approximate a hypothetical objective function for the explored range of elemental variables (see Martin et al 2013). Mathematical proofs and computational details can be found in Terekhov et al. 2010; Terekhov and Zatsiorsky 2011. In this study we determined a cost function explaining the distribution of the normal finger forces in the force and moment production task, The constraints were the prescribed total force and total moment, {FTOT, MTOT} combination. Thus, the ANIO problem was defined in the following way:
| (A1) |
| (A2) |
| (A3) |
where is the vector of normal finger forces ( , i = 1,…,4); the numbers 1 to 4 stand for the index, middle, ring, and little finger, respectively, gi is an arbitrary continuously differentiable function (gi belongs to Cn with n ≥ 2 in the feasible region); r = [r1, r2, r3, r4]T is the vector of moment arms, which was [−0.045, −0.015, 0.015, 0.045]T meters in this experiment. Pronation (PR) was considered as the negative moment. The equations can be written in matrix form:
| (A4) |
where,
| (A5) |
| (A6) |
First, we verified that the problem was not “splittable” (Terekhov et al. 2010), which means that our optimization problem could not be represented as a set of smaller optimization problems solved independently. Second, we tested whether the experimental data are distributed in a plane using PCA (see Methods) as it was observed in several earlier studies (Park et al. 2010; Niu et al. 2012a,b). If this was true, then the unknown cost function had to be a second-order polynomial (Terekhov et al. 2010; Martin et al. 2013).
The third step was computing the coefficients of the objective function within the class of second-order polynomials:
| (A7) |
where, Ja is the objective function reconstructed from the data, ki is the ith quadratic term coefficient, and wi is the ith linear term coefficient. Indices i = 1, 2, 3, and 4 refer to the index, middle, ring, and little finger, respectively.
Writing the Lagrange principle for the problem 〈Ja, C〉 in matrix form we get:
| (A8) |
where,
| (A9) |
Ĉ is a matrix of rank 2, and is a vector consisting of partial derivatives of Ja (gradient vector). Substituting equation A7 in A8 gives the plane of optimal solutions:
| (A10) |
where K is the diagonal matrix of quadratic coefficients, and w is the vector of linear coefficients. Rank of Ĉ is 2; therefore, equation 9 defines a plane in the four-dimensional space. ANIO finds the coefficients by minimizing the dihedral angle (D-angle) between the optimal plane defined by equation A10 and the experimental data plane determined by the first two PCs (see Martin et al. 2013). The objective functions were constructed for each participant separately. The “fmincon” function (“active-set” algorithm) from the Matlab optimization toolbox was used to minimize the D-angle. The coefficients of the objective function were normalized by the square root of the sum of squared quadratic coefficients (as in Terekhov and Zatsiorsky 2011; Martin et al. 2013).
References
- Ambike S, Paclet F, Zatsiorsky VM, Latash ML. Factors affecting grip force: anatomy, mechanics, and referent configurations. Exp Brain Res. 2014;232:1219–1231. doi: 10.1007/s00221-014-3838-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ambike S, Zatsiorsky VM, Latash ML. Processes underlying unintentional finger-force changes in the absence of visual feedback. Exp Brain Res. 2015;233:711–721. doi: 10.1007/s00221-014-4148-x. [DOI] [PubMed] [Google Scholar]
- Ambike S, Mattos D, Zatsiorsky VM, Latash ML. The nature of constant and cyclic force production: Unintentional force-drift characteristics. Exp Brain Res. 2016;234:197–208. doi: 10.1007/s00221-015-4453-z. [DOI] [PubMed] [Google Scholar]
- Bernstein NA. The problem of interrelation between coordination and localization. Archives of Biological Science. 1935;38:1–35. (in Russian) [Google Scholar]
- Bernstein NA. On the Construction of Movements. Medgiz; Moscow: 1947. (in Russian) [Google Scholar]
- Bernstein NA. The Co-ordination and Regulation of Movements. Pergamon Press; Oxford: 1967. [Google Scholar]
- Diedrichsen J, Shadmehr R, Ivry RB. The coordination of movement: optimal feedback control and beyond. Trends Cogn Sci. 2010;14:31–39. doi: 10.1016/j.tics.2009.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman AG. Referent control of action and perception: Challenging conventional theories in behavioral science. Springer; NY: 2015. [Google Scholar]
- Feldman AG, Levin MF. Positional frames of reference in motor control: their origin and use. Behav Brain Sci. 1995;18:723–806. [Google Scholar]
- Goldman-Rakic PS. Topography of cognition: parallel distributed networks in primate association cortex. Ann Rev Neurosci. 1988;11:137–156. doi: 10.1146/annurev.ne.11.030188.001033. [DOI] [PubMed] [Google Scholar]
- Gurfinkel VS, Levik YS, Kazennikov OV, Selionov VA. Locomotor-like movements evoked by leg muscle vibration in humans. Eur J Neurosci. 1998;10:1608–1612. doi: 10.1046/j.1460-9568.1998.00179.x. [DOI] [PubMed] [Google Scholar]
- Heijnen MJH, Muir BC, Rietdyk S. Factors leading to obstacle contact during adaptive locomotion. Exp Brain Res. 2012;223:219–231. doi: 10.1007/s00221-012-3253-y. [DOI] [PubMed] [Google Scholar]
- Heijnen MJH, Romine NL, Stumpf DM, Rietdyk S. Memory guided obstacle crossing: more failures were observed for the trail limb versus lead limb. Exp Brain Res. 2014;232:2131–2142. doi: 10.1007/s00221-014-3903-3. [DOI] [PubMed] [Google Scholar]
- Hu X, Newell KM. Modeling constraints to redundancy in bimanual force coordination. J Neurophysiol. 2011;105:2169–2180. doi: 10.1152/jn.01086.2010. [DOI] [PubMed] [Google Scholar]
- Ivanenko YP, Wright WG, Gurfinkel VS, Horak F, Cordo P. Interaction of involuntary post-contraction activity with locomotor movements. Exp Brain Res. 2006;169:255–260. doi: 10.1007/s00221-005-0324-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanenko YP, Grasso R, Lacquaniti F. Influence of leg muscle vibration on human walking. J Neurophysiol. 2000;84:1737–1747. doi: 10.1152/jn.2000.84.4.1737. [DOI] [PubMed] [Google Scholar]
- Jo HJ, Ambike S, Lewis MM, Huang X, Latash ML. Finger force changes in the absence of visual feedback in patients with Parkinson’s disease. Clin Neurophysiol. 2016;127:684–692. doi: 10.1016/j.clinph.2015.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohnstamm O. Demonstration einer katatonieartigen erscheinung beim gesunden (katatonusversuch) Neurol Zentral. 1915;Bl. 34S:290–291. [Google Scholar]
- Kugler PN, Turvey MT. Information, Natural Law, and the Self-Assembly of Rhythmic Movement. Hillsdale, NJ: Erlbaum; 1987. [Google Scholar]
- Latash ML. Synergy. Oxford University Press; New York: 2008. [Google Scholar]
- Latash ML. The bliss (not the problem) of motor abundance (not redundancy) Exp Brain Res. 2012;217:1–5. doi: 10.1007/s00221-012-3000-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML. Motor control: On the way to physics of living systems. In: Levin MF, editor. Progress in Motor Control: Skill Learning, Performance, Health, and Injury. Springer; New York, NY: 2014. pp. 1–16. [Google Scholar]
- Latash ML. Towards physics of neural processes and behavior. Neurosci Biobehav Rev. 2016;69:136–146. doi: 10.1016/j.neubiorev.2016.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Friedman J, Kim SW, Feldman AG, Zatsiorsky VM. Prehension synergies and control with referent hand configurations. Exp Brain Res. 2010;202:213–229. doi: 10.1007/s00221-009-2128-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schöner G. Motor control strategies revealed in the structure of motor variability. Exerc Sport Sci Rev. 2002;30:26–31. doi: 10.1097/00003677-200201000-00006. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schöner G. Toward a new theory of motor synergies. Motor Control. 2007;11:276–308. doi: 10.1123/mcj.11.3.276. [DOI] [PubMed] [Google Scholar]
- Latash ML, Shim JK, Smilga AV, Zatsiorsky V. A central back-coupling hypothesis on the organization of motor synergies: a physical metaphor and a neural model. Biol Cybern. 2005;92:186–191. doi: 10.1007/s00422-005-0548-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Zatsiorsky VM. Joint stiffness: Myth or reality? Hum Move Sci. 1993;12:653–692. [Google Scholar]
- Loeb GE. What might the brain know about muscles, limbs and spinal circuits? Prog Brain Res. 1999;123:405–409. doi: 10.1016/s0079-6123(08)62875-7. [DOI] [PubMed] [Google Scholar]
- Martin V, Scholz JP, Schöner G. Redundancy, self-motion, and motor control. Neural Comput. 2009;21:1371–1414. doi: 10.1162/neco.2008.01-08-698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin JR, Terekhov AA, Latash ML, Zatsiorsky VM. Optimization and variability of motor behavior in multi-finger tasks: What variables does the brain use? J Mot Behav. 2013;45:289–305. doi: 10.1080/00222895.2013.792234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattos D, Latash ML, Park E, Kuhl J, Scholz JP. Unpredictable elbow joint perturbation during reaching results in multijoint motor equivalence. J Neurophysiol. 2011;106:1424–1436. doi: 10.1152/jn.00163.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattos D, Schöner G, Zatsiorsky VM, Latash ML. Motor equivalence during accurate multi-finger force production. Exp Brain Res. 2015;233:487–502. doi: 10.1007/s00221-014-4128-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson W. Physical principles for economies of skilled movements. Biol Cyberns. 1983;46:135–147. doi: 10.1007/BF00339982. [DOI] [PubMed] [Google Scholar]
- Niu X, Latash ML, Zatsiorsky VM. Reproducibility and variability of the cost functions reconstructed from experimental recordings in multi-finger prehension. J Mot Behav. 2012a;44:69–85. doi: 10.1080/00222895.2011.650735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niu X, Terekhov AV, Latash ML, Zatsiorsky VM. Reconstruction of the unknown optimization cost functions from experimental recordings during static multi-finger prehension. Motor Control. 2012b;16:195–228. doi: 10.1123/mcj.16.2.195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Zatsiorsky VM, Latash ML. Optimality vs. variability: An example of multi-finger redundant tasks. Exp Brain Res. 2010;207:119–132. doi: 10.1007/s00221-010-2440-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Singh T, Zatsiorsky VM, Latash ML. Optimality vs. variability: Effect of fatigue in multi-finger redundant tasks. Exp Brain Res. 2012;216:591–607. doi: 10.1007/s00221-011-2963-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Sun Y, Zatsiorsky VM, Latash ML. Age-related changes in optimality and motor variability: An example of multi-finger redundant tasks. Exp Brain Res. 2011;212:1–18. doi: 10.1007/s00221-011-2692-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Jo HJ, Lewis MM, Huang X, Latash ML. Effects of Parkinson's disease on optimization and structure of variance in multi-finger tasks. Exp Brain Res. 2013;231:51–63. doi: 10.1007/s00221-013-3665-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parsa B, O’Shea DJ, Zatsiorsky VM, Latash ML. On the nature of unintentional action: A study of force/moment drifts during multi-finger tasks. J Neurophysiol. 2016;116:698–708. doi: 10.1152/jn.00180.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parsa B, Zatsiorsky VM, Latash ML. Optimality and stability of intentional and unintentional actions: II. Motor equivalence and structure of variance. 2017 doi: 10.1007/s00221-016-4806-2. (The companion paper) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pilon J-F, De Serres SJ, Feldman AG. Threshold position control of arm movement with anticipatory increase in grip force. Exp Brain Res. 2007;181:49–67. doi: 10.1007/s00221-007-0901-8. [DOI] [PubMed] [Google Scholar]
- Poon C, Chin-Cottongim LG, Coombes SA, Corcos DM, Vaillancourt DE. Spatiotemporal dynamics of brain activity during the transition from visually guided to memory-guided force control. J Neurophysiol. 2012;108:1335–1348. doi: 10.1152/jn.00972.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prilutsky BI, Zatsiorsky VM. Optimization-based models of muscle coordination. Exerc Sport Sci Rev. 2002;30:32–38. doi: 10.1097/00003677-200201000-00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reschechtko S, Zatsiorsky VM, Latash ML. Stability of multi-finger action in different spaces. J Neurophysiol. 2014;112:3209–3218. doi: 10.1152/jn.00395.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savescu AV, Latash ML, Zatsiorsky VM. A technique to determine friction at the fingertips. J Appl Biomech. 2008;24:43–50. doi: 10.1123/jab.24.1.43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholz JP, Schöner G. The uncontrolled manifold concept: Identifying control variables for a functional task. Exp Brain Res. 1999;126:289–306. doi: 10.1007/s002210050738. [DOI] [PubMed] [Google Scholar]
- Schöner G. Recent developments and problems in human movement science and their conceptual implications. Ecol Psychol. 1995;8:291–314. [Google Scholar]
- Scott JT, Lohnes CA, Horak FB, Earhart GM. Podokinetic stimulation causes shifts in perception of straight ahead. Exp Brain Res. 2011;208:313–321. doi: 10.1007/s00221-010-2480-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selemon LD, Goldman-Rakic PS. Common cortical and subcortical targets of the dorsolateral prefrontal and posterior parietal cortices in the rhesus monkey: evidence for a distributed neural network subserving spatially guided behavior. J Neurosci. 1988;8:4049–4068. doi: 10.1523/JNEUROSCI.08-11-04049.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapkova EY, Shapkova AL, Goodman SR, Zatsiorsky VM, Latash ML. Do synergies decrease force variability? A study of single-finger and multi-finger force production. Exp Brain Res. 2008;188:411–425. doi: 10.1007/s00221-008-1371-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon HA. Rational choice and the structure of the environment. Psychol Rev. 1956;63:129–138. doi: 10.1037/h0042769. [DOI] [PubMed] [Google Scholar]
- Slifkin AB, Vaillancourt DE, Newell KM. Intermittency in the control of continuous force production. J Neurophysiol. 2000;84:1708–1718. doi: 10.1152/jn.2000.84.4.1708. [DOI] [PubMed] [Google Scholar]
- Terekhov AV, Pesin YB, Niu X, Latash ML, Zatsiorsky VM. An analytical approach to the problem of inverse optimization: An application to human prehension. J Math Biol. 2010;61:423–453. doi: 10.1007/s00285-009-0306-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terekhov AV, Zatsiorsky VM. Analytical and numerical analysis of inverse optimization problems: conditions of uniqueness and computational methods. Biol Cybern. 2011;104:75–93. doi: 10.1007/s00422-011-0421-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nature Neurosci. 2002;5:1226–1235. doi: 10.1038/nn963. [DOI] [PubMed] [Google Scholar]
- Vaillancourt DE, Russell DM. Temporal capacity of short-term visuomotor memory in continuous force production. Exp Brain Res. 2002;145:275–285. doi: 10.1007/s00221-002-1081-1. [DOI] [PubMed] [Google Scholar]
- Vaillancourt DE, Slifkin AB, Newell KM. Visual control of isometric force in Parkinson’s disease. Neurophysiologia. 2001;39:1410–1418. doi: 10.1016/s0028-3932(01)00061-6. [DOI] [PubMed] [Google Scholar]
- Vaillancourt DE, Thulborn KR, Corcos DM. Neural basis for the processes that underlie visually guided and internally guided force control in humans. J Neurophysiol. 2003;90:3330–3340. doi: 10.1152/jn.00394.2003. [DOI] [PubMed] [Google Scholar]
- Weber KD, Fletcher WA, Gordon CR, Melvill Jones G, Block EW. Motor learning in the “podokinetic” system and its role in spatial orientation during locomotion. Exp Brain Res. 1998;120:377–385. doi: 10.1007/s002210050411. [DOI] [PubMed] [Google Scholar]
- Wilhelm L, Zatsiorsky VM, Latash ML. Equifinality and its violations in a redundant system: multi-finger accurate force production. J Neurophysiol. 2013;110:1965–1973. doi: 10.1152/jn.00461.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Y, Terekhov AV, Latash ML, Zatsiorsky VM. Forces and moments generated by the human arm: Variability and control. Exp Brain Res. 2012;223:159–175. doi: 10.1007/s00221-012-3235-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou T, Solnik S, Wu Y-H, Latash ML. Unintentional movements produced by back-coupling between the actual and referent body configurations: Violations of equifinality in multi-joint positional tasks. Exp Brain Res. 2014;232:3847–3859. doi: 10.1007/s00221-014-4059-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou T, Zhang L, Latash ML. Intentional and unintentional multi-joint movements: their nature and structure of variance. Neurosci. 2015;289:181–93. doi: 10.1016/j.neuroscience.2014.12.079. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]


