Abstract
We address the nature of unintentional changes in performance in two papers. This second paper tested hypotheses related to stability of task-specific performance variables estimated using the framework of the uncontrolled manifold (UCM) hypothesis. Our first hypothesis was that selective stability of performance variables would be observed even when the magnitudes of those variables drifted unintentionally because of the lack of visual feedback. Our second hypothesis was that stability of a variable would depend on the number of explicit task constraints. Subjects performed four-finger isometric pressing tasks that required the accurate production of a combination of total moment and total force with natural or modified finger involvement under full visual feedback, which was removed later for some or all of the salient variables. We used inter-trial analysis of variance and drifts in the space of finger forces within the UCM and within the orthogonal to the UCM space. The two variance components were used to estimate a synergy index stabilizing the force/moment combination, while the two drift components were used to estimate motor equivalent and non-motor equivalent force changes, respectively. Without visual feedback, both force and moment drifted toward lower absolute magnitudes. The non-motor equivalent component of motion in the finger force space was larger that the motor equivalent component for variables that stopped receiving visual feedback. In contrast, variables that continued to receive visual feedback showed larger motor equivalent component, compared to non-motor equivalent component, over the same time interval. These data falsified the first hypothesis; indeed, selective stabilization of a variable over the duration of a trial allows expecting comparably large motor equivalent components both with and without visual feedback. Adding a new constraint (presented as a target magnitude of middle finger force) resulted in a drop in the synergy index in support of the second hypothesis. We interpret the force drift as a natural relaxation process toward states with lower potential energy in the physical (physiological) system involved in the task. The results show that presenting sensory feedback on a performance variable makes synergies stabilizing that variable dependent on that particular sensory feedback.
Keywords: synergy, motor equivalence, finger, force, unintentional movement
Introduction
In this paper, we address the famous problem of motor redundancy (Bernstein 1967): For all natural actions, the number of variables produced by elements involved in an action (elemental variables) is larger than the number of constraints. This results in an infinite number of possible solutions, and the problem has traditionally been formulated as: How does the central nervous system (CNS) select specific solutions for such tasks? Recently, this problem has been revisited based on the principle of abundance (Gelfand and Latash 1998; Latash 2012). According to this principle, the CNS does not select a specific solution, but instead families of solutions are facilitated equally able to solve the task. This results in different stability properties in different directions within the space of elemental variables. In this context, we use the term “stability” to imply ability of a system to return toward a steady state or a trajectory following a brief, small perturbation.
The related notion of task-specific stability introduced by Schöner (1995) suggests that the CNS acting in a multi-dimensional space of elemental variables can selectively stabilize processes in directions leading to changes in salient task-specific performance variables. For a given performance variable, the space of elemental variables may be viewed as composed of two sub-spaces, the uncontrolled manifold (UCM, Scholz and Schöner 1999) where the performance variable stays unchanged, and the orthogonal to the UCM (ORT) space where this variable changes. If the central nervous system stabilizes this performance variable, processes in the ORT space are expected to show relatively high stability while processes within the UCM are expected to show relatively low stability. Note that variations of the elemental variables (e.g., finger forces in multi-finger tasks) within the UCM do not affect the performance variables (e.g., total force and moment). Variations of elemental variables within the ORT do not compensate for each other and affect the performance variables.
The most direct method to assess stability quantitatively would be to apply an unexpected brief perturbation and quantify deviations of the system from the unperturbed state or trajectory. This method, however, is not always practical because the intact central nervous system reacts to perturbations with reflexes and reflex-like reactions (so-called, pre-programmed reactions or long-loop reflexes, Hammond 1954; Tatton et al. 1978; Shemmel et al. 2010) as well as voluntary corrections that may be themselves viewed as additional perturbations and changes in the control process. Two indirect methods have been used to assess stability in different spaces within the abundant space of elemental variables. Both methods produce quantitative indices that may be viewed as proxies of stability. The first method quantifies inter-trial variance. It is based on the idea that trajectories tend to diverge in less stable directions and converge in more stable directions. Hence, if processes within the UCM are less stable than within ORT, VUCM > VORT is expected (each variance index, V, is computed per degree-of-freedom in the corresponding space). The notion of a synergy stabilizing a performance variable has been introduced, and a synergy index (ΔV) has been used reflecting the normalized difference between VUCM and VORT (reviewed in Latash et al. 2007; Latash 2008).
The second method is based on an observation that a quick action or reaction leads to motion of the system in both desired directions and undesired directions. For example, if you try to compress quickly a typical spring from a pen between the thumb and index finger, the spring will likely buckle and jump away from the hand (e.g., Venkadesan et al. 2007). This happens because the spring is more stiff (and stable) along its main axis and is more compliant (less stable) orthogonal to this axis. In this situation, the quick desired action plays a role of an input into a physical system that shows large deviations in directions of low stability. During quick actions, different stability within the UCM and ORT sub-spaces is reflected in the phenomenon of motor equivalence, defined as motion within the UCM (Mattos et al. 2011; Scholz et al. 2011). Note that motion within the UCM by definition has no effect on the salient performance variable and is addressed as motor equivalent (ME). Motion within ORT changes the performance variable and is called non-motor equivalent (nME). Large amounts of ME motion have been documented in kinematic, kinetic, and electromyographic spaces in tasks that required quick corrections of performance variables in response to external perturbations (Mattos et al. 2011, 2013, 2015). These large ME motions have been interpreted as reflecting the relatively low stability of processes within the corresponding UCM as compared to processes in ORT, which is a reflection of selective stabilization of the salient performance variables. Note that the nME motion may be larger or smaller than ME motion depending on the task: If the task requires no change in the salient performance variable, nME is expected to be smaller; however, if the variable changes during the time of observation, nME may be equal to or even bigger than ME.
While the inequality VUCM > VORT and large amounts of ME motion have been documented in many studies (reviewed in Latash et al. 2007; Latash and Zatsiorsky 2016), there is no agreement on the origin of these phenomena. Within the computational approach to motor control, applications of the optimal feedback control theory have been able to account for such observations (Todorov and Jordan 2002; Diedrichsen et al. 2007). An alternative approach does not assume computations within the central nervous system but views motor behavior as a consequence of natural laws (Kugler and Turvey 1986; Latash 2010). Within the latter approach, the idea of control with referent body coordinates (RCs, produced by physiological variables, such as subthreshold depolarization of neuronal pools, reviewed in Feldman 2015) coupled with the idea of hierarchical control and central back-coupling loops (Latash et al. 2005; Latash 2010) has been able to account for features of synergic behaviors, such as VUCM > VORT and large ME motion. In this study, we accept this approach as the one based on physics and physiology.
In this study, we explored stability of performance variables during their unintentional drifts. So far, only one experiment with multi-joint positional tasks and external transient perturbations addressed this issue (Zhou et al. 2015). To the best of our knowledge, this is the first study to explore indices of performance stability during unintentional drifts in performance in steady-state tasks. Our first hypothesis was that selective stability of performance variables would be observed even when the magnitudes of those variables drift unintentionally. This hypothesis assumes hierarchical control of such actions with magnitudes of salient performance variables defined at a higher level of the hierarchy (e.g., via changes in the relevant RCs). Stability of those variables is assumed to be defined at a lower level, possibly via back-coupling projections (Martin et al. 2009). As a result, a drift of the RCs is expected to lead to a drift in the performance variables without changes in their stability properties. We tested this hypothesis with respect to variables that showed no drift (because of the presence of visual feedback) and with respect to variables that drifted (because their visual feedback was turned off, Slifkin et al. 2000; Vaillancourt et al. 2002). In the experiments, the subjects were required to produce accurate total force and total moment of force {FTOT; MTOT} combinations and then to modify their preferred pattern of sharing the task among the four fingers by decreasing the middle finger force (FMID) by 50% while producing the same {FTOT; MTOT} magnitudes. We used the ME and nME indices as quantitative proxies of stability; note that the more commonly used analysis of inter-trial variance was not possible given only a few trials per feedback condition.
We also explored whether stability of a variable depended on the number of explicit task constraints. This was a secondary goal of the study unrelated to the issue of unintentional drifts in performance. Earlier studies explored this issue indirectly by varying the number of explicitly involved elemental variables (e.g., Latash et al. 2001). They showed, in particular, that some performance variables showed higher stability indices (similar to ΔV) with an increase in the number of elemental variables. In our current study, no change in the number of elemental variables took place – the subjects always performed all tasks with four fingers of the right (dominant) hand. However, adding a constraint related to the required magnitude of FMID was expected to reduce the range of available solutions. Based on the aforementioned earlier studies, our second hypothesis was that indices of stability for {FTOT; MTOT} would drop after the subjects purposefully reduced FMID to 50% of its preferred value.
Methods
Subjects
Eleven subjects voluntarily participated in this study, five females and six males (age: 27.27 ± 5.44 years, mass: 74.18 ± 14.73 kg, height: 171.18 ± 8.30 m. All our subjects were right-handed and healthy. Nine of the subjects completed the whole experiment. For technical reasons, data for two subjects were unavailable for one of the conditions. As a result, the number of subjects in different comparisons varied between nine and eleven. All subjects signed the consent form approved by the Office of Research Protections of The Pennsylvania State University.
Apparatus
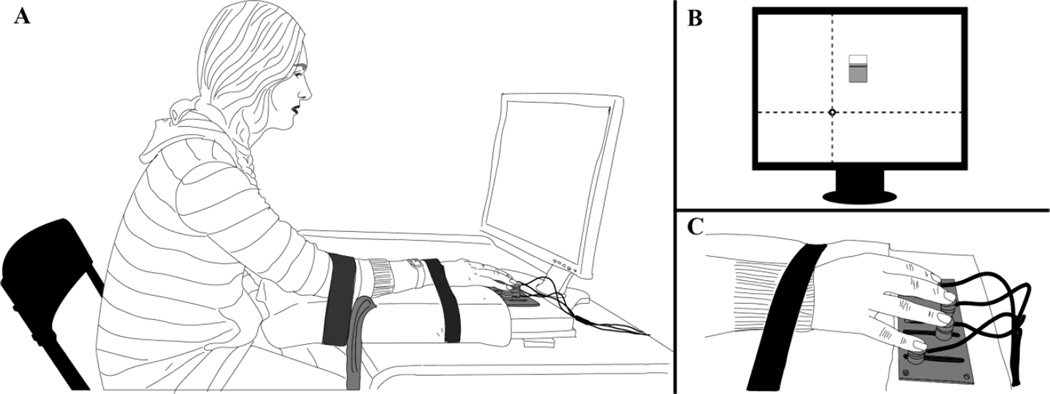
The setup is described in more detail in the first paper of this two-part series (Parsa et al. 2017; see Fig. 1). The subject sat in front of the monitor, which was used to provide visual feedback and define tasks. The four fingers of the right hand were placed comfortably on six-component force sensors (ATI), while the right lower arm was fixed comfortably to the wooden plate with two sets of Velcro straps (Fig 1A,C). The screen provided feedback on three variables (Fig. 1B): The total normal force produced by the fingers (FTOT, along the Y-axis), the total moment (MTOT, along the X-axis) produced by the normal fingers forces with respect to a horizontal line in a sagittal plane passing in-between the middle and ring fingers, and the normal force produced by the middle finger (FMID, as the level in a tank-with-water graph; see Fig. 1B) located in such a way that it did not interfere with the first two feedback signals. The latter feedback was used at specific times only (described later).
Figure 1.
The setup. A: The subject’s position. B: Visual feedback defined total force and total moment target values, {FTOT, MTOT}, as the intersection of two lines. The “tank with water” in the middle of the screen presented the feedback on the middle finger force. C: Hand placement on the sensors.
Twenty-four analog signals (4 sensors × 6 components) were digitized by a 12-bit analog-digital converter (PCI-6031, National Instruments, Austin, TX) at 100 Hz. A Labview program was written for data acquisition and to provide visual feedback. All further data analyses were done using MATLAB 2014.
Experimental procedure
Subjects first placed their fingertips on the sensors and relaxed; then the sensor readings were set to zero; as a result only active downward forces were measured. The experiment consisted of three parts. The first two parts involved maximal force production trials (MVC) and trials with accurate production of various combinations {FTOT; MTOT} described in detail in the companion paper. The data presented and analyzed in this paper were collected in the third part.
Each trial started with a {FTOT; MTOT} target shown on the screen (Fig. 1B). FTOT was always equal to 20% of the four-finger MVC, while MTOT could be 1.5PR, 0, or 1.5SU. A unit of the moment into pronation (PR) or supination (SU) was defined as in an earlier study (Park et al. 2010) as 7% of the index finger MVC multiplied by the index finger nominal lever arm (0.045 m). The subjects were given 5 s to match the {FTOT; MTOT} task combination.
Five seconds after the trial initiation, a third feedback on FMID appeared on the screen and subjects were instructed to adjust their middle finger force to match the level shown by the tank feedback without changing the {FTOT; MTOT} level. The target level for FMID was set at half of the average force this finger produced within the time interval 4.7–4.8 s from the trial initiation. The subjects were given 10 s to reach a new steady finger force combination that would satisfy the original {FTOT; MTOT} constraint and the new FMID constraint.
At that time (15 s into the trial), visual feedback was manipulated. We had eight main conditions: no feedback on any of the three variables (None), feedback on one of the three performanca variables (FTOT; MTOT, or FMID), feedback on two of the performance variables (FTOT&FMID, MTOT&FTOT, and MTOT&FMID), and all the feedback remaining on the screen until the end of the trial (All). Under each condition, three trials were performed in a row with 10-s intervals.
Data processing
Finger force data were low-pass filtered at 5 Hz using a zero lag, fourth-order Butterworth filter. We selected three phases in each trial for data analysis to represent three steady states: under the original set of constraints, {FTOT; MTOT}, under the combination of three constraints, {FTOT; MTOT} and FMID, and at the end of the time with modified visual feedback. Correspondingly, Phase-1 was defined as the time interval between 4.7 and 4.8 s; Phase-2 corresponded to the time interval between 14.7 and 14.8 s, and Phase-3 corresponded to the time interval between 29.7 and 29.8 s.
Analysis of motor equivalence
The task constraints can be represented as a set of linear equations:
| (1) |
| (2) |
| (3) |
where FI, FM, FR, and FL stand for index, middle, ring, and little finger forces; MTOT could be 1.5PR, 1.5SU, or Zero depending on the task; and FMID* is the middle finger force by the subjects at the end of Phase-1. The coefficients in Eq. (2) are the nominal moment arms of the finger forces. We can rewrite the task in a matrix form:
| (4) |
where C is the m × n constraint matrix defining the task, F is the n-dimensional vector of finger forces (elemental variables in our analysis), and P is the m-dimensional vector of performance variables. Changes in the elemental and performance variables:
| (5) |
where ΔF is the vector of changes in the finger force between two phases. It could be computed between Phase-2 and Phase-1 (ΔF21) and between Phase-3 and Phase-2 (ΔF32). Since Eqs (4–5) are linear, the Jacobian (J) of the system is the same as the C matrix.
Performance remains unchanged (ΔP = 0) if the changes in elemental variables occur in the null space of the J [e = null(J)]. Hence, the projection of ΔF onto the null-space was defined as the ME component, while the projection of ΔF orthogonal to the null-space was defined as the nME components. ME and nME components were normalized by the square root of the corresponding space dimensionality (cf. Mattos et al. 2011).
We also performed similar analyses with respect to subsets of performance variables that received (PVISION) and did not receive (PNO-VISION) visual feedback. These analyses used respectively changed Jacobians:
| (6) |
| (7) |
where JVISION is k × n matrix where k is the number of performance variables that received visual feedback, and JNO-VISION is j × n matrix where j is the number of performance variables that did not receive visual feedback
Analysis of inter-trial variance
The UCM hypothesis (Scholz and Schöner 1999) allows partitioning the inter-trial variance within a redundant space of elemental variables into two components; one of them keeps salient performance variables unchanged (VUCM), while the other leads to changes in these variables (VORT). We analyzed the data across all trials in Phase-1 and Phase-2 because in those phases the visual feedback was always available for the task-specific performance variables. At each time sample, inter-trial variance was computed within the null-space of J (which is the UCM for tasks with linear constraints) and within its orthogonal complement (ORT space). Further, an index of synergy (ΔV) was defined as the normalized difference between VUCM and VORT:
| (6) |
where VTOT stands for total variance and n with subscripts stand for the dimensionality of the corresponding spaces. Since ΔV by its computation is bounded, for statistical analysis ΔV values were log-transformed using the modified Fisher’s z-transform (Solnik et al. 2013).
Statistics
We present the data in the text and figures as means ± standard errors unless stated otherwise. All data sets were tested for normality and sphericity using the Mauchly criterion, and in cases of sphericity violations, the Greenhouse-Geisser correction was used. We set the critical p-value at 0.05 for all the analysis.
Changes in the ME and nME components under different feedback conditions were tested between Phase-3 and Phase-2 to address the first specific hypothesis. We computed the two components with respect to the Jacobian representing variables that received visual feedback (JVISION) as well as with respect to the Jacobian representing variables that stopped receiving visual feedback (JNO-VISION). Both analyses used three-way repeated-measures ANOVA with the factors Component (ME, nME), Moment (PR, Zero, SU), and Feedback (seven levels). The “All” condition was left out of the JNO-VISION analysis because J becomes empty, while the “None” feedback condition was left out of the JVISION analysis because J becomes empty.
To address the second specific hypothesis, we tested the effects of adding an additional constraint on the ME vs. nME indices and on the structure of inter-trial variance computed for the {FTOT; MTOT} task between Phase-2 (two constraints) and Phase-1 (three constraints). Note that full feedback was available in both phases. The analysis of motor equivalence used repeated-measures ANOVA with factors Component (ME, nME), Phase (1 and 2), and Moment (PR, Zero, SU). The analysis of the z-transformed synergy index ΔVZ was done with a two-way ANOVA, Phase × Moment. We also explored the effects of adding the FMID constraint on the two variance components using an additional factor Variance (VUCM and VORT). The variance components and ΔVZ were also computed in Phase-2 with respect to all three constraints: FTOT, MTOT, and FMID. Significant effects were further explored by pairwise comparisons with Bonferroni corrections.
Results
All the subjects were able to adjust their finger forces from Phase-1 to Phase-2 to accommodate the additional constraint (reduce FMID by 50%) while keeping the required magnitude of total force and total moment, {FTOT; MTOT}. This change in the finger forces was associated with a large ME motion and very small nME motion reflecting the fact that accuracy of performance with respect to the original set of constraints was nearly unchanged. Turning visual feedback off resulted in drifts in the variables without feedback: FTOT and MTOT typically drifted toward lower absolute magnitudes, while FMID typically drifted toward higher magnitudes. Variables with preserved feedback showed no visible drifts. These findings were reflected in the relative magnitudes of ME and nME motion.
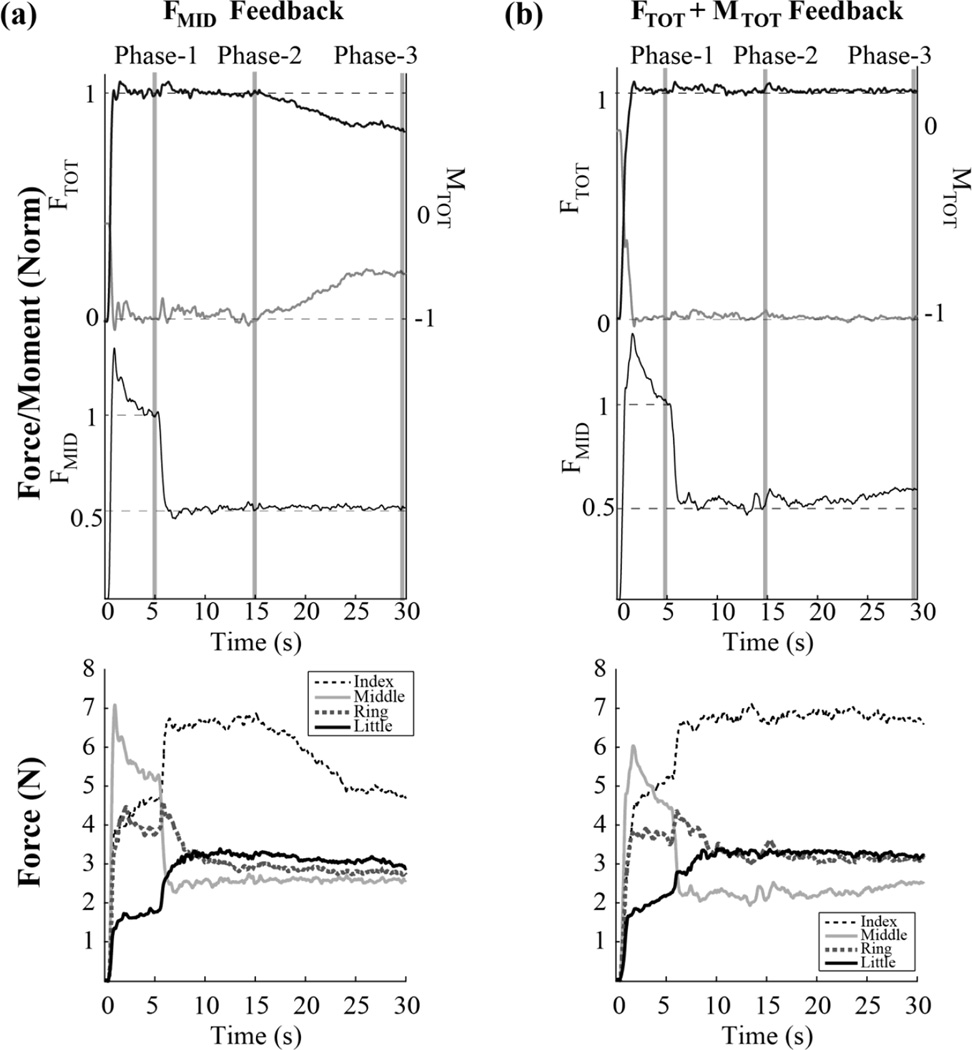
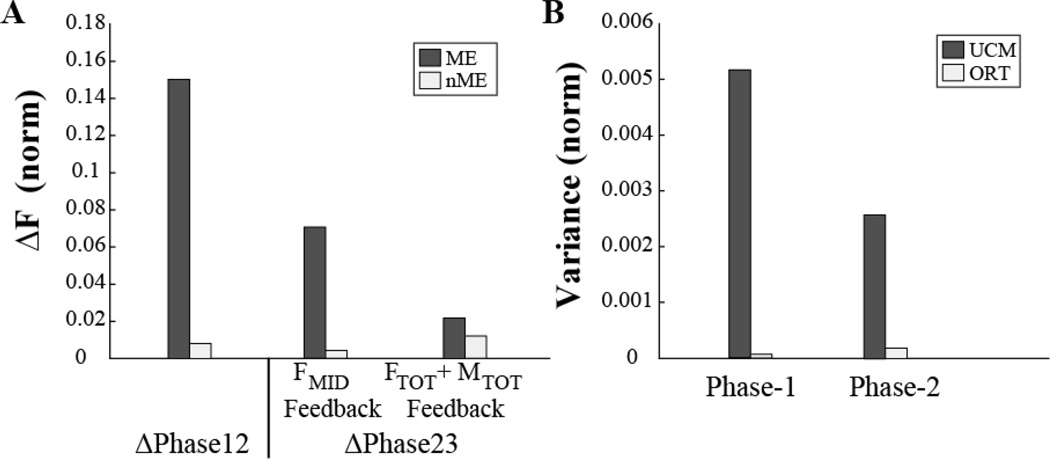
Typical performance by a representative subject is illustrated in Figure 2 for the task involving pronation moment under two conditions, with feedback on FMID only (panel A) and with feedback on FTOT and MTOT (panel B). The lines in the top panels show averaged across three trials time series of FTOT, MTOT, and FMID. The two bottom panels show the corresponding time profiles of individual finger forces. Figure 3 presents the results of motor equivalence analysis (ME and nME) between Phase-1 and Phase-2 (ΔPhase12) and between Phase-2 and Phase-3 (ΔPhase23) in panel A, while panel B shows the results of the inter-trial variance analysis (VUCM and VORT) over Phase-1 and Phase-2. Details on the magnitudes of drifts are presented in the companion paper. Here we focus on changes in the ME and nME components and structure of variance.
Figure 2.
Typical example of FTOt (top black lines), MTOT (middle gray lines), and FMID (bottom lines) time profiles for two feedback conditions: (a) only on the middle finger force - FMID; (b) on the combination of total force and total moment - FToT+MToT. Each of the three performance variables was normalized by their value at Phase-1. Averages over three trials by a representative subject are shown for the initial MTOT into pronation. Panels (c) and (d) show the corresponding time profiles of individual finger forces in absolute values (newtons).
Figure 3.
A: the motor equivalent (ME) and non-motor equivalent (nME) components computed for two time intervals (ΔPhase12 and ΔPhase23). B: The two inter-trial variance components (VUCM and VORT) in Phase-1 and Phase-2 computed with respect to the {FTOT; MTOT} task. The values are presented for the data illustrated in Fig. 2.
Motor equivalence analysis
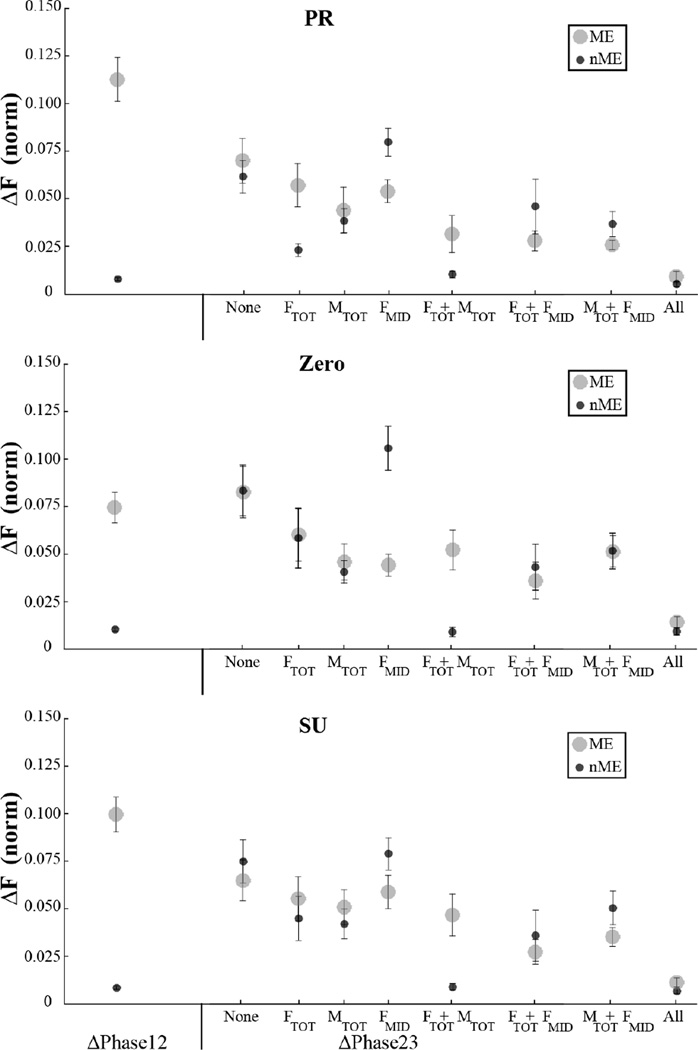
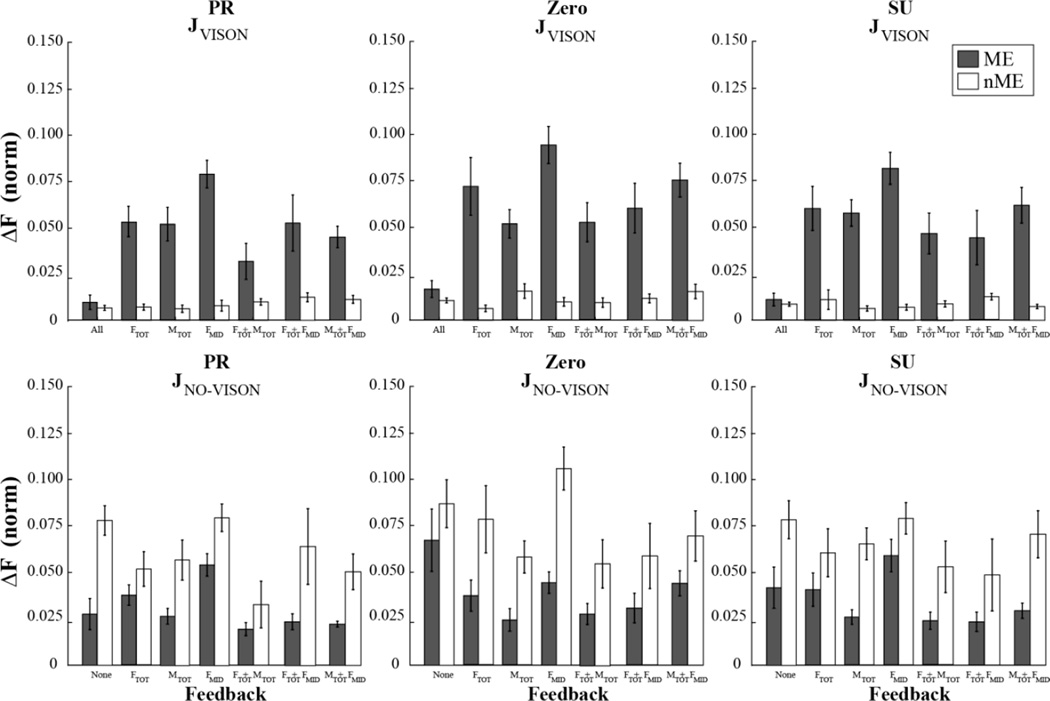
To address the first specific hypothesis, we explored the magnitudes of ME and nME components for variables that did and did not received visual feedback. The magnitudes of the ME and nME components computed with respect to the {FTOT; MTOT} set of constraints are shown in Figure 4. Averaged across subjects data with standard error bars are shown for the three tasks with different initial MTOT magnitudes, PR, Zero, and SU. The left side of each panel shows the results over the interval from Phase 1 to Phase 2 (ΔPhase12), while the right side shows the results over the interval from Phase 2 to Phase 3 (ΔPhase23). In all three panels, the magnitude of ME over ΔPhase12 (when visual feedback was available on all the main variables) is much larger than the magnitude of nME (effect of Component; F[1, 8] = 37.33, p < 0.001). The difference between the two components was smaller for the Zero MTOT condition (Component × Moment interaction; F[2, 16] = 5.15, p < 0.05).
Figure 4.
Motor equivalent (ME) and non-motor equivalent (nME) components averaged across subjects with standard error bars for ΔPhase12 and ΔPhase23 for different moment and feedback conditions. The two components were computed with respect to the {FToT; MTOT} task.
The relative magnitude of the ME and nME components differed depending on the available visual feedback over ΔPhase23 as illustrated in the right parts of Fig. 4. Under conditions with feedback on both FTOT and MTOT, the nME component remained very low, much lower than the ME component. A three-way ANOVA with repeated measures, Component × Moment × Feedback confirmed significant effects of Component (F[1, 10] =101.79, p < 0.001) reflecting the overall larger ME magnitudes.
The difference between the two components became smaller if only one of the two original constraints received visual feedback, and nME became significantly larger than ME if feedback on FMID only was available (Component × Feedback interaction; F[2.40, 23.96] = 7.87, p < 0.01). These effects were consistent across MTOT conditions although the trials with MTOT = 0 were characterized by lower ME and nME magnitudes (Component × Moment interaction; F[2, 20] = 9.41, p < 0.001). The three-way ANOVA, Component × Moment × Feedback, also confirmed significant effects of Component (F[1, 10] =101.79, p < 0.001) reflecting the overall larger ME magnitudes, and Feedback (F[2.12, 21.19] = 5.507, p < 0.05) reflecting multiple pairwise differences that can be seen in Fig. 4.
Figure 5 shows clearly that ME > nME for variables with feedback (top row) while the inequality reverses, nME > ME, for variables without feedback (bottom row). This was due to both smaller ME magnitudes and larger nME magnitudes for the no-vision Jacobian analysis (in all comparable feedback and moment conditions). Note also the special set of data for the “All” condition in the top row: When all three variables remained specified throughout the trial, the subjects showed very small ME motion compared to all other conditions when at least one of the constraints was without the corresponding feedback.
Figure 5.
The ME and nME components for ΔPhase23 averaged across subjects with standard error bars and shown for the three moment conditions, PR - pronation, Zero, and SU - supination. Top: With respect to the Jacobian reflecting constraints with the feedback that remained on the screen throughout the trial (JVISION). Bottom: With respect to the Jacobian reflecting constraints without feedback (JNO-VISION) between Phase-2 and Phase-3. Note that ME > nME in the top panels and nME > ME in the bottom panels.
A three-way repeated measures ANOVA, Jacobian (feedback, no-feedback) × Moment × Feedback was run on ME and nME components separately. ANOVA on ME showed significant effects of Moment (F[2, 20] = 5.26, p < 0.05), Feedback (F[5, 50] = 8.49, p < 0.001), and Jacobian (F[1, 10] = 28.29, p < 0.001), and a significant interaction Moment × Jacobian (F[2, 20] = 15.11, p < 0.001). Pairwise contrast confirmed that the ME component was the largest when the feedback was provided on FMID only compared to conditions with feedback on other subsets of constraints (p < 0.05). It is obvious from Fig. 5 that the nME values were much larger for the No-Feedback Jacobian than for the Feedback Jacobian (F[1, 10] = 33.55, p < 0.001). ANOVA showed no significant effect of Feedback, while there was an effect of Moment (F[2, 20] = 7.29, p < 0.005) reflecting larger nME magnitudes for the Zero MTOT condition compared to the PR condition.
Analysis of the structure of variance
This analysis could only be run over Phase-1 and Phase-2 because only three trials were available for any given feedback conditions between Phase-2 and Phase-3. Note also that the data for one of the subjects were over four standard deviations away from the mean; hence, we considered that subject as an outlier and performed statistical analysis on the data from ten subjects only. In both Phase-1 and Phase-2, strong synergies stabilizing the {FTOT; MTOT} combination were observed. These synergies were reflected in the much higher inter-trial variance component leading to no changes in {FTOT; MTOT} compared to the variance component leading to changes in {FTOT; MTOT}, VUCM > VORT (effect of Variance; F[1, 9] = 35.76; p < 0.005).
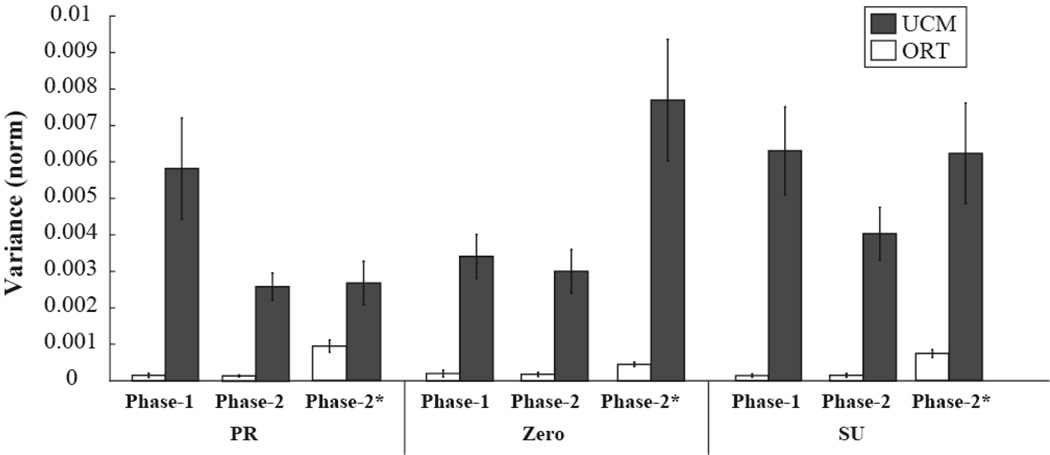
With respect to our second specific hypothesis, adding the new constraint (FMID) led to very small effects on VORT; in contrast, there was a consistent drop in the magnitude of VUCM (Phase × Variance interaction, F[1, 9] = 12.05; p < 0.01). These results are illustrated in Figure 6. Note the very small VORT magnitudes (white bars) compared to the VUCM (black bars) and a drop in VUCM from Phase-1 to Phase-2.
Figure 6.
The two inter-trial variance components (VUCM and VORT) for Phase-1 and Phase-2 computed with respect to the {FTOT; MTOT} Jacobian for the three moment conditions, PR – pronation, Zero, and SU - supination. The data labeled Phase-2* show the variance components for Phase-2 computed with respect to the Jacobian reflecting all three constraints: {FTOT; MTOT} and FMID.
These results were reflected in the synergy index ΔV values that were consistently positive across conditions and phases. The synergy indices were larger in Phase-1 (on average, z-transformed values were 1.85 ± 0.074 for Phase-1, and 1.56 ± 0.071 for Phase-2, effect of Phase F[1, 9] = 12.53, p < 0.01). The synergy indices were the largest for MTOT = 0 (effect of Moment; F[2, 18] = 6.423, p<0.01), and the difference between the phases was the smallest for MTOT = 0 (Moment × Phase interaction, F[2,18] = 3.65, p < 0.05).
When the analysis in Phase-2 was run with respect to all three constraints (FTOT, MTOT, and FMID), both the VORT and VUCM values became significantly larger when normalized by dimensionality of the spaces (compare the data for “Phase-2” and “Phase-2*” in Fig. 6; the data with * refer to the analysis with respect to all three constraints; p < 0.05). Note that VTOT was the same for the two analyses. The difference between the phases was due to the fact that the UCM is two-dimensional for the analysis with respect to {FTOT; MTOT}, and it is one-dimensional with respect to the three constraints. So, the total VUCM was in fact smaller for the analysis with respect to the three constraints, but the normalized values were larger. These results were reflected in the significantly larger ΔVZ indices computed with respect to the two original constraints in Phase-2 as compared to the ΔVZ indices computed with respect to all three constraints (1.55±0.38 vs. 0.93±0.41; effect of Constraint F[1, 9] = 22.2, p<0.001). As in the earlier analysis of ΔVZ data, there was a significant effect of Moment (F[2, 18] = 14.0, p<0.001) and a significant Moment × Jacobian interaction (F[2, 18] = 18.7, p<0.01) reflecting the largest values of ΔVZ for MTOT = 0 and the smallest difference between the two analyses for MTOT =0.
We also explored correlations between the indices of motor equivalence during the transition from Phase-1 to Phase-2 and the inter-trial variance indices available for Phase-2. This analysis was done across all subjects. The only consistently significant correlations were observed between the nME index and VORT (R2 ranged between 0.462 and 0.624; p < 0.05 for all three moment conditions). There were no significant correlations between VUCM and ME and between ME/nME and ΔVZ indices.
Discussion
Our first hypothesis was that selective stability of performance variables would be observed even when the magnitudes of those variables drifted unintentionally. This hypothesis has been falsified in the analysis of motor equivalence (cf. Mattos et al. 2011, 2015). Indeed, under complete visual feedback (between Phase-1 and Phase-2 and also under the “All” condition between Phase-2 and Phase-3), the finger force deviations led to only very small changes in the directions that changed the magnitudes of performance variables related to the explicit task constraints (non-motor equivalent, nME). In contrast, finger force deviations were large in directions that led to no changes in those variables (motor equivalent, ME > nME). When the analysis was run for variables that stopped receiving visual feedback between Phase-2 and Phase-3, the ME deviations became smaller while the nME deviations increased leading to an inequality nME > ME. While quantitative analysis of the ME and nME indices has to be interpreted with care (cf. Scholz and Schöner 2014; also see later in the Discussion), the counter-directional changes in the two components suggest that visual feedback was crucial to ensure stability of the task-related variables. This general conclusion is supported by results from earlier studies by Ranganathan and Newell (2008, 2009) as well as by a recent study exploring changes in the structure of inter-trial variance during unintentional drifts in performance (Parsa et al. 2016).
Our second hypothesis was related to changes in the structure of inter-trial variance after adding a new constraint to the ongoing task of producing a combination of total force and total moment, {FTOT; MTOT}. We hypothesized that the synergy index (reviewed in Latash et al. 2007) would drop after the subjects purposefully reduced FMID to 50% of its preferred value, and the results have supported this hypothesis. Indeed, while the inequality VUCM > VORT was present at both phases, during Phase-2, there was a significant drop in the synergy index (ΔV).
Further, we discuss implications of these results for stability of performance variables that are produced with or without appropriate visual feedback.
Synergies and the number of constraints
Our understanding of synergies links this central concept in motor control (Babinski 1899; Bernstein 1947, 1967) to stability of performance (Schöner 1995). Stability is an absolutely crucial feature of functional movements because all such movements are performed in the presence of unpredictable and time-varying neural states in the unpredictable and time-varying environment. This makes the current concept of synergy different from those used in clinical studies (DeWald et al. 1995) and in studies of motor behavior that imply under this term sets of performance variables produced by effectors that show parallel changes (d’Avella et al. 2003; Ivanenko et al. 2004; Ting and Mcpherson 2005).
In many earlier studies within the framework of the UCM hypothesis, inter-trial variance indices were used as proxies of stability (reviewed in Latash et al. 2002, 2007). To make the indices comparable between spaces with different dimensionalities, VUCM and VORT were normalized per dimension. We used the same method to compare variance indices between Phase-1 (when the subject performed the task under the two original constraints, FTOT and MTOT) and Phase-2 (when the third constraint related to FMID was added). Adding the third constraint forced the subjects to use a sub-space in the original UCM (in Phase-1) compatible with the required value of FMID. This naturally was expected to lead to a drop in VUCM, which was observed in the experiment, resulting in a drop in the synergy index ΔV.
Effects of changes in the number of task-related constraints were explored in several earlier studies. In one of the very first studies using the UCM-based approach, quick-draw shooting actions were analyzed with respect to performance variables of different dimensionality (Scholz et al. 2000). No effects of dimensionality were noticed. In a study of bimanual actions by Diedrichsen (2007), motion of two hands was correlated if the two hands controlled a single cursor (one constraint). The correlation disappeared when the two hands moved two different cursors (two constraints). Note, however, that the condition with two cursors differed from the condition with a single cursor not only in the number of constraints but also in the nature of the task that required either independent motion of the two arms or a synergic action. In another study, reaching to a spherical target (three constraints) and a cylindrical target (five constraints) was accompanied by similar indices of the structure of variance (Mattos et al. 2011). Changing the number of constraints in the course of an action, to our knowledge, has never been explored.
Earlier studies with the production of accurate sine patterns of FTOT with 2, 3, and 4 fingers of a hand led to an unexpected result (Latash et al. 2001; Scholz et al. 2002): When the subjects performed the task with two fingers only, they showed a pattern of variance compatible with stabilization of MTOT although it was not specified as a performance variable, and the subjects had no visual feedback on MTOT. This led to lack of synergies stabilizing FTOT. Adding a third finger led to even stronger MTOT-stabilizing synergies without FTOT-stabilizing synergies. Only in the four-finger condition, the subjects showed stabilization of MTOT (stabilized over the whole cycle) and of FTOT (stabilized only within a narrow phase range corresponding to relatively high force magnitudes). Taken together, the results of those studies and of the current study confirm the idea that: (a) a new constraint is incorporated into the original solution space leading to a reduction in the size of the solution space used by the CNS; and (b) reducing the number of elements leads to shrinking the solution space, which primarily affects stability of less salient variables, even if they are prescribed by an explicit instruction.
The analysis with respect to all three constraints in Phase-2 (data shown as Phase-2* in Fig. 6) showed a somewhat counter-intuitive picture: Both VUCM and VORT increased for the three-constraint analysis (as compared to the two-constraint analysis) while total variance remained unchanged. This was possible because of two factors, the different dimensionality of the UCM and ORT spaces in the two analyses and the very different magnitudes of the variance components (VUCM >> VORT). Indeed, VUCM dropped in the three-constraint analysis, while VORT increased by the same magnitude. Because of the normalization per dimension, the normalized magnitude of VUCM increased. On the other hand, the added variance to VORT was so much bigger as compared to its original magnitude that, even after normalization by the increased dimensionality of ORT, it remained significantly larger as compared to the two-constraint analysis. The data in Figure 6 show that comparing variance indices across tasks with different numbers of constraints may lead to seemingly controversial results.
Stability and its reflections in motor equivalence and structure of variance
The two methods of analysis used in this study, structure of variance and motor equivalence, have been used in earlier studies as proxies of stability with respect to task-specific, salient performance variables (reviewed in Scholz and Schöner 2014; Latash and Zatsiorsky 2016). The two indices (ME/nME and ΔV) are not 100% equivalent. This was shown in earlier studies that documented somewhat different behaviors of the two indices (Mattos et al. 2011, 2014). The ΔV index reflects the structure of variance in the space of elemental variables; therefore, it is not sensitive to possible changes in mean values of these variables. In contrast, nME is expected to be very low if the action interval starts and ends with similar values of the task-related variables. It is expected to be much higher if the task-related variables change their values, either intentionally or unintentionally (as in our study). In general, reducing two indices to a single metric, such as VUCM and VORT to ΔV, and ME and nME to ME/nME, should be done with care (cf. Latash et al. 2010). While these operations reduce the number of outcome variables, one has to keep in mind that differences in such metrics could reflect differences in one, the other, or both of the original variables. This happens, for example, during anticipatory synergy adjustments – changes in the synergy index observed during steady state in preparation to a quick action (Olafsdottir et al. 2005; Latash and Huang 2015).
In our study, two inequalities (VUCM > VORT and ME > nME) were seen consistently for the data at Phase-1 and Phase-2 when the subjects had full feedback on all the relevant variables. The two inequalities are both consistent with the idea of selective stabilization of the two performance variables related to the original set of constraints, {FTOT; MTOT}. Correlation analysis, however, revealed significant correlations between VORT and nME only. In other words, subjects who showed larger nME deviations during the transition from the two-constraint phase to the three-constraint phase were also the ones who showed larger VORT at the end of this transition. Large nME reflects larger violations of the original {FTOT; MTOT} constraints during the transition. These larger changes in {FTOT; MTOT} led to larger inter-trial variance in those variables (VORT), possibly reflecting the so-called signal-dependent noise (Newell and Carlton 1993; Harris and Wolpert 1998).
The lack of correlation between ME and VUCM is non-trivial. Indeed, larger ME deviations imply larger changes of finger forces in directions that did not affect {FTOT; MTOT}. The idea of signal-dependent noise suggests that inter-trial variance in those directions should also be larger. This was not the fact, however: Correlations between VUCM and ME across MTOT conditions could be both positive and negative with the R2 values always under 0.11. So, signal-dependent noise seems to define variance in directions leading to changes in task-related performance variables (i.e., in ORT) but not in directions that keep those variables unchanged (i.e., in UCM). This conclusion is consistent with the idea that changes in magnitudes of variables are defined at a higher level of a control hierarchy while stability of those variables in defined as a hierarchically lower level (see the Introduction and Latash et al. 2010). This general idea is consistent with recent observations of changes in the performance of motor tasks and synergic control in patients with cortical and subcortical disorders (Park et al. 2012; Jo et al. 2016; reviewed in Latash and Huang 2015).
The relations between the outcome variables of the ME and variance analyses remain unclear and have to be explored in future studies. While both sets of indices seem to reflect stability of relevant performance variables (cf. Mattos et al. 2011; Scholz and Schöner 2014), they should be viewed as complementary rather than repetitive.
In conditions with visual feedback on only some of the performance variables, nME motion for the variables with feedback was expected to be low while nME motion was expected to be higher for the variables without feedback reflecting the drift in those variables. This prediction has been confirmed in the analysis of the ME and nME motion with respect to two Jacobians, JVISION and JNO-VISION (see Figure 5). Less expectedly, the differences in the ME component computed with respect to JVISION and JNO-VISION were also significant: ME was smaller for JNO-VISION. This result is consistent with earlier studies exploring the effects of manipulations of visual feedback (Ranganathan and Newell 2008, 2009) on sets of goal-equivalent solutions in two-finger force production tasks. Those earlier studies showed, in particular, that error compensation between the two fingers (which may be seen as equivalent to ME motion) decreased without the visual feedback. Our current findings show counter-directional changes in the ME and nME motion components suggesting a redistribution of the relatively invariant total drift in the space of elemental variables between the two sub-spaces.
Stability during unintentional drift in performance
In the companion paper (Parsa et al. 2017), we present arguments in favor of a scheme that views unintentional drifts in performance as consequences of two processes. First, there is a drift of referent coordinates (RCs) for the salient task-specific variables toward their actual coordinates (ACs). This is a natural process expected in any physical system moving toward minimum of potential energy; it is expected within the hypothesis on the neural control of movements with changes in RCs for salient variables (Latash 2010, 2016; Feldman 2015). A recent study has provided direct experimental evidence confirming RC drift during unintentional force changes (Ambike et al. 2016). Second, there is a drift of an abundant system toward states with smaller values of a cost function as defined within the ideas of optimal control: If a system is forced to perform using non-optimal contributions of elemental variables, it is expected to show a drift toward configurations that are closer to the optimal one. We modeled this situation by asking the subjects to produce {FTOT; MTOT} values using finger force combinations that differed from the preferred ones, namely with the middle finger force reduced by 50%.
This scheme is an example of a general approach to the neural control of movement based on physics and physiology, not on assumed computational processes within the central nervous system (as, for example, in approaches based on optimal feedback control ideas, Todorov and Jordan 2002; Diedrichsen et al. 2010). While assuming relevant computations can potentially account for any experimental observation, this very fact makes this approach non-disprovable. Let us reiterate that there is a qualitative difference between discovering laws of nature acting in a system and using computational means to reproduce its behavior. In particular, some of the findings in our study suggest that no single optimization method can account for these phenomena. Indeed, the large magnitudes of ME motion are by definition wasteful: they are accompanied by muscle activations that do not move the system with respect to task-related variables. Within the physical approach, large ME motion is a natural consequence of the low stability of the system within the UCM.
Within this general scheme, both ME and nME drifts are expected. The consistent drifts in FTOT and MTOT in the absence of visual feedback (cf. Slifkin et al. 2000; Vaillancourt and Russell 2002; Parsa et al. 2016) are leading to nME deviations. The drifts within the UCM, directed toward preferred finger force combinations (modeled as those with smaller costs, Parsa et al. 2017), lead to ME deviations. A priori, we could not predict the relative magnitude of the two drifts. Based on earlier studies and on the general scheme of hierarchical control with RCs (Latash 2010; Ambike et al. 2015, 2016), we expected to see synergies stabilizing variables that showed consistent drifts after the relevant visual feedback had been turned off. The main result, however, falsified this hypothesis. Indeed, visual feedback manipulations led to the typical inequality ME > nME for the variables that continued to receive feedback, while the inequality reversed, nME > ME, for the variables without visual feedback (Fig. 5). This was associated with counter-directional changes in both ME and nME: Overall, the ME components decreased after the removal of visual feedback, while the nME components increased.
Unfortunately, because of the large number of feedback conditions, we could not collect enough trials per condition to perform the analysis of the structure of inter-trial variance in Phase-3. This was done in another study using only a few conditions and multiple trials per condition (Parsa et al. 2016). So, in this study, we have only ME data reflecting stability of the variables that continued to receive visual feedback vs. those that stopped receiving this feedback. The contrast between the two is striking. It suggests that visual feedback plays a very important role in ensuring stability of performance variables. While this result corroborates findings in several earlier studies (Ranganathan and Newell 2008, 2009) and is compatible with several hypotheses on the origin of synergies (Todorov and Jordan 2003; Latash et al. 2005; Martin et al. 2009), it suggests that the central back-coupling loops by themselves were unable to bring about stability of variables without the help of visual feedback. It is possible that the formulation of the task biased the subjects toward relying on visual feedback to ensure stable performance in our experiment. We plan to explore this possibility by using similar tasks performed primarily under somatosensory control and/or based on memory.
For example, if the unintentional drift in performance is a consequence of a slow drift of the referent coordinate of the effector (RC) toward its actual coordinate (AC) without contribution from memory and/or computational processes, we would expect this drift to be much smaller or disappear if the subject is asked to memorize a magnitude of a performance variable and reproduce it after a comparable time interval of rest. We also expect the drift to disappear if the subject is asked to perform intentional changes in the performance variable rather than keeping it constant: The system may be expected to re-set after each episode of a change in performance such that no consistent drift is accumulated. An even stronger prediction can be made if a person is asked to produce a magnitude of a performance variable (e.g., finger force) without visual feedback, based on somatosensory feedback only. Since the feedback would be available throughout the trial, we expect corrections of the hypothesized RC drift, possibly even overcorrections (a drift toward higher forces) given that force-sensitive receptors may show adaptation and require higher forces to produce comparable perceptions. We cannot see how similar predictions could be drawn based on alternative ideas such as memory deficiency or computational processes. Performing these experiments is in our immediate plans.
Concluding comments
To summarize, we learned the following main lessons from the results presented in this series of two papers. Unintentional changes in performance can be seen in different performance variables – individual finger forces, total force, and total moment of force – following removal of the visual feedback. The variables showing the drift fail to show stabilization by the adjusted contributions of individual fingers, while variables that continue to receive visual feedback show signatures of selective stability. We interpret the main finding within the introduced hierarchical scheme of the neural control of movement based on physics and physiology: Motor actions are controlled by parameters (such as RCs for the involved effectors) defined at various levels of a hypothetical hierarchy. At the higher level of the hierarchy, this control process is relatively low-dimensional, reflecting task-related variables. At lower levels, the number of parameters (RCs) is increased, the system becomes abundant, and RCs show synergic co-variation that stabilizes task-specific parameters. Within this scheme, unintentional performance drifts reflect two processes: (a) a drift of the referent coordinate of a variable toward its actual coordinate; and (b) a drift in the abundant space of elements toward configurations with lower magnitude of a cost function. This scheme allows accounting for the phenomena of unintentional changes in performance without invoking cognitive and/or computational processes.
Acknowledgments
We are very much grateful to Dr. Satyajit Ambike for the productive discussions at early stages of this project. The study was in part supported by NIH grants NS035032 and AR048563.
References
- Ambike S, Mattos D, Zatsiorsky VM, Latash ML. Unsteady steady-states: Central causes of unintentional force drift. Exp Brain Res. 2016 doi: 10.1007/s00221-016-4757-7. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ambike S, Zatsiorsky VM, Latash ML. Processes underlying unintentional finger force changes in the absence of visual feedback. Exp Brain Res. 2015;233:711–721. doi: 10.1007/s00221-014-4148-x. [DOI] [PubMed] [Google Scholar]
- Babinski F. De l’asynergie cerebelleuse. Rev Neurologique. 1899;7:806–816. [Google Scholar]
- Bernstein NA. On the Construction of Movements. Medgiz: Moscow (in Russian); 1947. [Google Scholar]
- Bernstein NA. The Co-ordination and Regulation of Movements. Oxford: Pergamon Press; 1967. [Google Scholar]
- d’Avella A, Saltiel P, Bizzi E. Combinations of muscle synergies in the construction of a natural motor behavior. Nat Neurosci. 2003;6:300–308. doi: 10.1038/nn1010. [DOI] [PubMed] [Google Scholar]
- DeWald JP, Pope PS, Given JD, Buchanan TS, Rymer WZ. Abnormal muscle coactivation patterns during isometric torque generation at the elbow and shoulder in hemiparetic subjects. Brain. 1995;118:495–510. doi: 10.1093/brain/118.2.495. [DOI] [PubMed] [Google Scholar]
- Diedrichsen J. Optimal task-dependent changes of bimanual feedback control and adaptation. Curr Biol. 2007;17:1675–1679. doi: 10.1016/j.cub.2007.08.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diedrichsen J, Shadmehr R, Ivry RB. The coordination of movement: optimal feedback control and beyond. Trends Cogn Sci. 2010;14:31–39. doi: 10.1016/j.tics.2009.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman AG. Referent control of action and perception: Challenging conventional theories in behavioral science. NY: Springer; 2015. [Google Scholar]
- Gelfand IM, Latash ML. On the problem of adequate language in movement science. Motor Control. 1998;2:306–313. doi: 10.1123/mcj.2.4.306. [DOI] [PubMed] [Google Scholar]
- Hammond PH. Involuntary activity in biceps following the sudden application of velocity to the abducted forearm. J Physiol. 1954;127:23P–25P. [PMC free article] [PubMed] [Google Scholar]
- Harris CM, Wolpert DM. Signal-dependent noise determines motor planning. Nature. 1998;394:780–784. doi: 10.1038/29528. [DOI] [PubMed] [Google Scholar]
- Ivanenko YP, Poppele RE, Lacquaniti F. Five basic muscle activation patterns account for muscle activity during human locomotion. J Physiol. 2004;556:267–282. doi: 10.1113/jphysiol.2003.057174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jo HJ, Maenza C, Good DC, Huang X, Park J, Sainburg RL, Latash ML. Effects of unilateral stroke on multi-finger synergies and their feed-forward adjustments. Neurosci. 2016;319:194–205. doi: 10.1016/j.neuroscience.2016.01.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kugler PN, Turvey MT. Information, Natural Law, and the Self-Assembly of Rhythmic Movement. Hillsdale, NJ: Erlbaum; 1987. [Google Scholar]
- Latash ML. Synergy. New York: Oxford University Press; 2008. [Google Scholar]
- Latash ML. Motor synergies and the equilibrium-point hypothesis. Motor Control. 2010;14:294–322. doi: 10.1123/mcj.14.3.294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML. The bliss (not the problem) of motor abundance (not redundancy) Exp Brain Res. 2012;217:1–5. doi: 10.1007/s00221-012-3000-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML. Towards physics of neural processes and behavior. Neurosci Biobehav Rev. 2016;69:136–146. doi: 10.1016/j.neubiorev.2016.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Huang X. Neural control of movement stability: Lessons from studies of neurological patients. Neurosci. 2015;301:39–48. doi: 10.1016/j.neuroscience.2015.05.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Levin MF, Scholz JP, Schöner G. Motor control theories and their applications. Medicina. 2010;46:382–392. [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Scholz JF, Danion F, Schöner G. Structure of motor variability in marginally redundant multi-finger force production tasks. Exp Brain Res. 2001;141:153–165. doi: 10.1007/s002210100861. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schöner G. Motor control strategies revealed in the structure of motor variability. Exerc Sport Sci Rev. 2002;30:26–31. doi: 10.1097/00003677-200201000-00006. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schöner G. Toward a new theory of motor synergies. Motor Control. 2007;11:276–308. doi: 10.1123/mcj.11.3.276. [DOI] [PubMed] [Google Scholar]
- Latash ML, Shim JK, Smilga AV, Zatsiorsky V. A central back-coupling hypothesis on the organization of motor synergies: a physical metaphor and a neural model. Biol Cybern. 2005;92:186–191. doi: 10.1007/s00422-005-0548-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Zatsiorsky VM. Biomechanics and Motor Control: Defining Central Concepts. New York, NY: Academic Press; 2016. [Google Scholar]
- Martin V, Scholz JP, Schöner G. Redundancy, self-motion, and motor control. Neural Comput. 2009;21:1371–1414. doi: 10.1162/neco.2008.01-08-698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattos D, Latash ML, Park E, Kuhl J, Scholz JP. Unpredictable elbow joint perturbation during reaching results in multijoint motor equivalence. J Neurophysiol. 2011;106:1424–1436. doi: 10.1152/jn.00163.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattos D, Kuhl J, Scholz JP, Latash ML. Motor equivalence (ME) during reaching: Is ME observable at the muscle level? Motor Control. 2013;17:145–175. doi: 10.1123/mcj.17.2.145. [DOI] [PubMed] [Google Scholar]
- Mattos D, Schöner G, Zatsiorsky VM, Latash ML. Motor equivalence during accurate multi-finger force production. Exp Brain Res. 2015;233:487–502. doi: 10.1007/s00221-014-4128-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newell KM, Carlton LG. Force variability in isometric responses. J Exp Psychol: Hum Percept Perform. 1993;14:37–44. [PubMed] [Google Scholar]
- Olafsdottir H, Yoshida N, Zatsiorsky VM, Latash ML. Anticipatory covariation of finger forces during self-paced and reaction time force production. Neurosci Lett. 2005;381:92–96. doi: 10.1016/j.neulet.2005.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Wu Y-H, Lewis MM, Huang X, Latash ML. Changes in multi-finger interaction and coordination in Parkinson’s disease. J Neurophysiol. 2012;108:915–924. doi: 10.1152/jn.00043.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parsa B, O’Shea DJ, Zatsiorsky VM, Latash ML. On the nature of unintentional action: A study of force/moment drifts during multi-finger tasks. J Neurophysiol. 2016;116:698–708. doi: 10.1152/jn.00180.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parsa B, Terekhov A, Zatsiorsky VM, Latash ML. Optimality and stability of intentional and unintentional actions: I. Origins of drifts in performance. Exp Brain Res. 2017 doi: 10.1007/s00221-016-4809-z. (the companion paper) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranganathan R, Newell KM. Motor synergies: feedback and error compensation within and between trials. Exp Brain Res. 2008;186:561–570. doi: 10.1007/s00221-007-1259-7. [DOI] [PubMed] [Google Scholar]
- Ranganathan R, Newell KM. Influence of augmented feedback on coordination strategies. J Mot Behav. 2009;41:317–330. doi: 10.3200/JMBR.41.4.317-330. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Danion F, Latash ML, Schöner G. Understanding finger coordination through analysis of the structure of force variability. Biol Cybern. 2002;86:29–39. doi: 10.1007/s004220100279. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Dwight-Higgin T, Lynch JE, Tseng YW, Martin V, Schöner G. Motor equivalence and self-motion induced by different movement speeds. Exp Brain Res. 2011;209:319–332. doi: 10.1007/s00221-011-2541-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholz JP, Schöner G. The uncontrolled manifold concept: Identifying control variables for a functional task. Exp Brain Res. 1999;126:289–306. doi: 10.1007/s002210050738. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Schöner G. Use of the uncontrolled manifold (UCM) approach to understand motor variability, motor equivalence, and self-motion. Adv Exp Med Biol. 2014;826:91–100. doi: 10.1007/978-1-4939-1338-1_7. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Schöner G, Latash ML. Identifying the control structure of multijoint coordination during pistol shooting. Exp Brain Res. 2000;135:382–404. doi: 10.1007/s002210000540. [DOI] [PubMed] [Google Scholar]
- Schöner G. Recent developments and problems in human movement science and their conceptual implications. Ecol Psychol. 1995;8:291–314. [Google Scholar]
- Shemmel J, Krutky MA, Perreault EJ. Stretch sensitive reflexes as an adaptive mechanism for maintaining limb stability. Clin Neurophysiol. 2010;121:1680–1689. doi: 10.1016/j.clinph.2010.02.166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slifkin AB, Vaillancourt DE, Newell KM. Intermittency in the control of continuous force production. J Neurophysiol. 2000;84:1708–1718. doi: 10.1152/jn.2000.84.4.1708. [DOI] [PubMed] [Google Scholar]
- Solnik S, Pazin N, Coelho C, Rosenbaum DA, Scholz JP, Zatsiorsky VM, Latash ML. End-state comfort and joint configuration variance during reaching. Exp Brain Res. 2013;225:431–442. doi: 10.1007/s00221-012-3383-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tatton WG, Bawa P, Bruce IC, Lee RG. Long loop reflexes in monkeys: an interpretive base for human reflexes. Prog Clin Neurophysiol. 1978;4:229–245. [Google Scholar]
- Ting LH, Macpherson JM. A limited set of muscle synergies for force control during a postural task. J Neurophysiol. 2005;93:609–613. doi: 10.1152/jn.00681.2004. [DOI] [PubMed] [Google Scholar]
- Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nat Neurosci. 2002;5:1226–1235. doi: 10.1038/nn963. [DOI] [PubMed] [Google Scholar]
- Vaillancourt DE, Russell DM. Temporal capacity of short-term visuomotor memory in continuous force production. Exp Brain Res. 2002;145:275–285. doi: 10.1007/s00221-002-1081-1. [DOI] [PubMed] [Google Scholar]
- Venkadesan M, Guckenheimer J, Valero-Cuevas FJ. Manipulating the edge of instability. J Biomech. 2007;40:1653–1661. doi: 10.1016/j.jbiomech.2007.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou T, Zhang L, Latash ML. Intentional and unintentional multi-joint movements: their nature and structure of variance. Neurosci. 2015;289:181–193. doi: 10.1016/j.neuroscience.2014.12.079. [DOI] [PMC free article] [PubMed] [Google Scholar]