Preconditioned Total Field Inversion (TFI) Method for Quantitative Susceptibility Mapping

Abstract

Purpose

To investigate systematic errors in traditional quantitative susceptibility mapping (QSM) where background field removal and local field inversion (LFI) are performed sequentially, to develop a total field inversion (TFI) QSM method to reduce these errors, and to improve QSM quality in the presence of large susceptibility differences.

Theory and Methods

The proposed TFI is a single optimization problem which simultaneously estimates the background and local fields, preventing error propagation from background field removal to QSM. To increase the computational speed, a new preconditioner is introduced and analyzed. TFI is compared with the traditional combination of background field removal and LFI in a numerical simulation and in phantom, 5 healthy subjects and 18 patients with intracerebral hemorrhage.

Results

Compared with the traditional method PDF+LFI, preconditioned TFI substantially reduced error in QSM along the air-tissue boundaries in simulation, generated high-quality in vivo QSM within similar processing time, and suppressed streaking artifacts in intracerebral hemorrhage QSM. Moreover, preconditioned TFI was capable of generating QSM for the entire head including the brain, air-filled sinus, skull, and fat.

Conclusion

Preconditioned total field inversion improves the accuracy of QSM over the traditional method where background and local fields are separately estimated.

Introduction

Quantitative susceptibility mapping (QSM) extracts the spatial distribution of tissue magnetic susceptibility from the gradient echo signal phase (1-9). Current QSM methods consist of two steps (1): i) background field removal to determine the local field generated by tissue, and ii) inversion from the local field to the tissue susceptibility. This allows a fairly robust mapping of the central brain regions, particularly for iron deposition in the mid brain nuclei (1). However, several technical challenges remain.

A major challenge is imprecise separation of background and tissue fields caused by the assumptions made in background field removal methods. This is particularly problematic near the brain boundary where a large tissue-air susceptibility difference is present (1). To avoid the separate fitting of background and local field, Laplacian-based QSM methods have been proposed (10-14) based on the partial differential formulation of the forward signal equation (5,15). The Laplacian operation implicitly eliminates the background field. However, the practical implementation of the Laplacian requires a trade-off between robustness to error amplification and the integrity of the visualized cortical brain tissue (16). The necessary erosion of the brain mask may prevent visualization of certain structures at the brain boundary, such as the superior sagittal sinus.

The presence of a large susceptibility dynamic range within the region of interest (ROI) is similarly a challenge in QSM, often leading to streaking artifacts (17-21). For example, the susceptibility difference between intracerebral hemorrhage (ICH) and surrounding tissue can exceed 1.6 ppm (17). Using a nonlinear QSM model of ICH signal (21) can reduce these streaking artifacts, but does not eliminate them. Recent work has focused on this challenge by separating the fitting processes for sources of strong (such as ICH) and weak (normal brain) susceptibilities, hence preventing ICH-related artifact from permeating into the normal brain (17,18). However, these methods require carefully choosing the regularization parameter (18) or threshold (17) for detecting ICH to minimize artifacts in the subsequent inversion for weak susceptibilities.

In this work, we address both challenges using a generalized inverse problem that is suitable for large dynamic ranges in susceptibility. We propose a preconditioned QSM to perform total field inversion (TFI), strongly reducing the error propagation associated with imprecise background field removal, and suppressing streaking artifacts in intracerebral hemorrhage QSM.

Theory

For QSM, the total magnetic field is conventionally decomposed into two components: the local field f_L defined as the magnetic field generated by the susceptibility χ_L inside a given region of interest M (local susceptibility), and the background field f_B defined as the magnetic field generated by the susceptibility χ_B outside M (background susceptibility) (22):

$$f=f_B+f_L=d\ast ({\chi }_B+{\chi }_L)$$ [1]

Here ∗ is the convolution operator, and d is the the field generated by a unit dipole with Lorentz sphere correction (23). The components f_B and f_L may be estimated separately: estimation of χ_B or f_B is referred to as background field removal. A variety of background field removal methods have been proposed, such as high-pass filtering (HPF)(4), projection onto dipole fields (PDF)(22) or Laplacian based methods (24-26). χ_L is then obtained from the local field f − f_B, typically using regularization (2,7,21,27). This step is referred to as local field inversion (LFI). Errors in the background field propagate into the subsequent local field, ultimately leading to errors in the final susceptibility. Although recent work (28) allows updating the background field during local field inversion, it requires a prior susceptibility atlas and co-registration to estimate the background susceptibility first.

Here, we propose to estimate χ_B and χ_L jointly using a total field inversion (TFI):

$${\chi }^{\ast }={\text{argmin}}_{\chi }\frac{1}{2}\parallel w(f-d\ast \chi ){\parallel }_2^2+\lambda \parallel M_G\nabla \chi {\parallel }_1,$$ [2]

thus using the same formulation as the traditional QSM inversion problem (1). Here χ = χ_L + χ_B represents the total susceptibility in the entire image volume. The data weighting w can be derived from the magnitude images by calculating the error propagation from the MRI data into the total field (2). A weighted total variation term is used to suppress the streaking artifacts induced by the presence of zeroes in the dipole kernel d (2,21).

The use of iterative optimization algorithms, such as conjugate gradient (CG) (29), in solving Eq. 2 can lead to slow convergence, as illustrated in a healthy brain in Figure 1. Here, Eq. 2 is linearized at χ = 0 and solved using CG. During early iterations, part of the background field is fitted as local field, generating an unreasonable local susceptibility map (Figure 1d). To address this problem, we use prior-enhanced preconditioning (30) to improve convergence. In (30), it is shown that if the solution χ is a Gaussian random vector with mean 0 ∈ ℝⁿ and covariance matrix Γ ∈ ℝ^n×n, then a right-hand preconditioner P (see below) that approximates the covariance matrix Γ, by P^H P ≈ Γ, will increase convergence speed. For TFI, a binary diagonal preconditioner P is constructed as follows:

$$P_i=\{\begin{array}{cc}1,\hfill & i\in M\hfill \\ P_B(P_B>1),\hfill & i\notin M^{}\hfill \end{array}\phantom{\}},$$ [3]

where i denotes the voxel, and M the tissue ROI. It is designed such that the difference in the matrix P^HP between a voxel inside and outside M is approximately equal to the difference in susceptibility between the local and the background region, which includes bone and air (1). We further modify this P to account for strong susceptibility within M (e.g. intracerebral hemorrhage) by thresholding the R2* map: M_R2* ≔R2* < $R{2}_{th}^{\ast }$, assuming that voxels with high R2* have strong susceptibility. Thus, P is defined as:

$$P_i=\{\begin{array}{cc}1,\hfill & i\in M\cap M_{R{2}^{\ast }}\hfill \\ P_B(P_B>1),\hfill & otherwise\hfill \end{array}\phantom{\}}$$ [4]

The preconditioned TFI problem then becomes:

$$y^{\ast }={\text{argmin}}_y\Phi \left(y\right)=\underset{y}{\text{argmin}}\frac{1}{2}\parallel w(f-d\ast Py){\parallel }_2^2+\lambda \parallel M_G\nabla Py{\parallel }_1$$ [5]

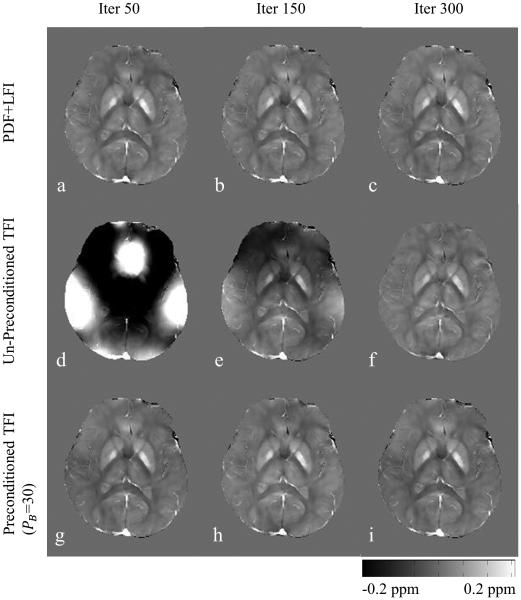
Figure 1.

Human brain QSM reconstructed using traditional PDF+LFI, un-preconditioned TFI and preconditioned TFI at different CG iterations. In order to produce a QSM similar to PDF+LFI with 50 iterations, TFI without preconditioning required 300 iterations. Preconditioning reduces this number down to 50.

The final susceptibility is computed as χ* = Py*. Eq. 5 is solved using a Gauss-Newton method (see Appendix).

A number of recently proposed methods similarly circumvent background field removal to estimate susceptibility directly from the total field (10-14). These methods are based on the partial differential formulation (15,31) of the signal equation (Eq. 1):

$$\Delta f=\Delta (d\ast ({\chi }_B+{\chi }_L))=\left(\frac{1}{3}\Delta -\frac{{\partial }^2}{\partial z^2}\right){\chi }_L$$ [6]

Here, Δ denotes the Laplacian. Notice that the contribution from background sources χ_B disappears after applying the Laplacian. Two examples of these methods are: 1) Single-Step QSM (SSQSM) (10):

$${\chi }^{\ast }={\text{argmin}}_{\chi }\frac{1}{2}\parallel \Delta f-\left(\frac{1}{3}\Delta -\frac{{\partial }^2}{\partial z^2}\right)\chi {\parallel }_2^2+\lambda \parallel M_G\nabla \chi {\parallel }_2^2,$$ [7]

where M_G is a binary mask derived from the magnitude image. It can be efficiently optimized using a preconditioned conjugate gradient solver (32).

2) Differential QSM (12):

$${\chi }^{\ast }={\text{argmin}}_{\chi }\frac{1}{2}\parallel w(e^{i\text{GML}f}-e^{i\text{GMP}\chi }){\parallel }_2^2+\lambda \parallel M_G\nabla \chi {\parallel }_1$$ [8]

with $\text{GML}f\left(r\right)\stackrel{\text{def}}{=}{\int }_M\frac{1}{\mid r-r^{\prime }\mid }\Delta f\left(r^{\prime }\right)d{r}^{\prime }\text{and}\text{GMP}\chi \left(r\right)\stackrel{\text{def}}{=}{\int }_M\frac{1}{\mid r-r^{\prime }\mid }\left(\frac{1}{3}\Delta -\frac{{\partial }^2}{\partial z^2}\right)\chi \left(r^{\prime }\right)d{r}^{\prime }$.

Laplacian-based methods enable QSM reconstruction within a single step. However, the practical implementation of Laplacian necessitates the erosion of the ROI M. The amount of erosion depends on the width of the kernel used for computing the Laplacian.

Methods

For developing and evaluating the proposed total field inversion (TFI) with preconditioning, we performed simulations, phantom imaging, in vivo imaging of the brain of healthy subjects using COSMOS as a reference and of patients suffering from hemorrhages. Finally, we explored whole head QSM.

The optimal P_B in Eq. 4 was empirically determined to ensure that, for a given number of CG iterations, the Gauss-Newton solver arrived at a solution with minimal error with respect to a reference susceptibility. Then this P_B value was used for other similar datasets. In this work, we used $R{2}_{th}^{\ast }=30s^{-1}$. The performance of the proposed TFI method in phantom and in vivo was compared with SSQSM and Differential QSM. In this work, the Spherical Mean Value (SMV) with variable kernel size (16) was used to implement the Laplacian in SSQSM and Differential QSM, where the kernel diameter was varied from d to 3 voxels, and the ROI mask was eroded accordingly for these two methods. The kernel diameter d at the most central ROI was optimized as described below.

Simulation

Accuracy of Sequential Inversion and TFI

We constructed a numerical brain phantom of size 80 × 80 × 64. Brain tissue susceptibilities were set to 0 ppm, except for a single point susceptibility source of 0.1 ppm. Background susceptibilities were set to 0, and the total field was computed with the forward model f = Md* χ. Both LFI and TFI without preconditioning (P_B = 1) were used, and the estimation for the point source χ_S was compared to the truth χ_ST (0.1 ppm). For sequential inversion, both PDF (22) and LBV (26) were used for background field removal and MEDI (21) for local field inversion. This process was repeated by moving the point source across the entire ROI, which generated an error map showing the spatial variation of the estimation error |χ_S − χ_ST |/ χ_ST for each method. The regularization parameter λ was set to 10⁻³ for PDF+LFI, LBV+LFI and TFI.

Effect of the preconditioner P in TFI

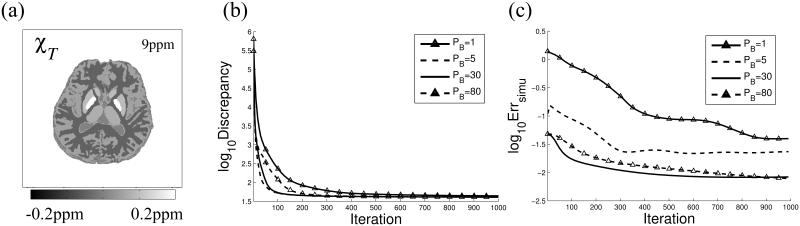
A numerical brain phantom of size 256 × 256 × 98 (33) was constructed with known susceptibilities simulating different brain tissues: white matter (WM) −0.046 ppm, gray matter (GM) 0.053 ppm, globus pallidus (GP) 0.19 ppm, and cerebrospinal fluid (CSF) 0. Background susceptibilities were set to 9 ppm to simulate air outside the ROI. The total field was computed from the true susceptibility map χ_T (Figure 3a) using the forward model. Gaussian white noise (SNR = 200) was added to the field. We applied the proposed TFI method using four different preconditioners: P_B = 1 (no preconditioning),5,30 and 80 and using Eq. 3. During reconstruction, the discrepancy $\parallel M(f-d\ast \chi )\parallel {}_2$ and the root mean square error (RMSE) ${\text{Err}}_{\text{simu}}=\parallel M\chi -M{\chi }_T{\parallel }_2∕\sqrt{n}$ between the estimated susceptibility Mχ and the true susceptibility Mχ_T (n is the number of voxels inside M) were examined to compare convergence. The regularization parameter λ was set to 10⁻³.

Figure 3.

True susceptibility map (a) used in simulation. Discrepancy (b) and Error (c) between estimated and true brain QSM in simulation with different preconditioning weights P_B.

Phantom experiment

To examine the accuracy of our TFI method, a phantom was prepared, where 5 gadolinium solution filled balloons were embedded in agarose (1%), with expected magnetic susceptibilities χ_ref of 0.049, 0.098, 0.197, 0.394 and 0.788 ppm, respectively. The measured susceptibilities were referenced to the agarose background. The phantom was scanned at 3T (GE, Waukesha, WI) using a multi-echo gradient echo sequence with monopolar Cartesian readout (anterior/posterior) without flow compensation. Imaging parameters were: FA = 15, FOV = 13 cm, TE₁ = 3.6 ms, TR = 71 ms, #TE = 8, ΔTE = 3.5 ms, acquisition matrix = 130 × 130 × 116, voxel size = 1 × 1 × 1 mm³, BW = ±31.25 kHz and a total scan time of 13 min.

Next, PDF+LFI, TFI, SSQSM and Differential QSM were performed on the same phantom data. Nonlinear field map estimation (21) followed by graph-cut-based phase unwrapping (34) was used to generate the total field. We optimized P_B in Eq. 4, by repeating the TFI methods for a range of P_B values (1,2,5,10,20,30,40,50,60,70,80) and selecting the value that produced the smallest error between the mean estimated susceptibility χ for each balloon and its corresponding reference susceptibility ${\chi }_{ref}:{\text{Err}}_{\text{phantom}}={\sum }_{i=1}^5{\left(({\chi }_i-{\chi }_{refi})∕{\chi }_{refi}\right)}^2$ at the end of the 300th CG iteration. The regularization parameter λ was determined by minimizing Err_phantom for PDF+LFI, which was then also used for TFI. For SSQSM and Differential QSM, λ and the maximum kernel diameter d for the variable radius SMV were jointly determined by minimizing Err_phantom.

In vivo experiment: healthy brain

The brain of 5 healthy subjects was imaged using multi-echo GRE at 3T (GE, Waukesha, WI) with monopolar readout without flow compensation. All studies in this work were conducted with the approval of our institutional review board. Imaging parameters were: FA = 15, FOV = 24 cm, TE₁ = 3.5 ms, TR = 40 ms, #TE = 6, ΔTE = 3.6 ms, acquisition matrix = 240×240×46, voxel size = 1×1×3 mm³, BW = ±62.5 kHz and a total scan time of 9 min. For each subject, 3 orientations were imaged, and the reference brain QSM χ_Lref was reconstructed using COSMOS (35). For PDF+LFI, TFI, SSQSM and Differential QSM, only one orientation was used. The ROI was obtained automatically using BET (36,37). Data from one subject was used to optimize P_B in Eq. 4 by minimizing the RMSE ${\text{Err}}_{\text{invivo}}=\parallel {\chi }_L-{\chi }_{Lref}{\parallel }_2∕\sqrt{n}$ between the estimated susceptibility χ_L and the reference χ_Lref at the end of the 300th CG iteration (n is the number of voxels inside the ROI). The obtained weight P_B was then used for the remaining 4 subjects. The CSF was chosen as the reference for the in vivo susceptibility value in this work. Susceptibilities were measured within ROIs of the globus pallidus (GP), putamen (PT), thalamus (TH) and caudate nucleus (CN) for quantitative analysis. The relative difference $({\chi }_{\text{GP}}-{\chi }_{\text{GP}}^{\text{COSMOS}})∕{\chi }_{\text{GP}}^{\text{COSMOS}}$ was calculated for each subject, with χ_GP the mean susceptibility measurement of GP for each subject. The regularization parameter λ was chosen by minimizing Err_invivo for PDF+LFI, while TFI used the same λ. The maximum kernel diameter d and the regularization parameter λ were jointly determined by minimizing Err_invivo for SSQSM and Differential QSM.

In vivo experiment: brain with hemorrhage

We acquired human data in 18 patients, each with intracerebral hemorrhage (ICH), using multi-echo GRE at 3T (GE, Waukesha, WI) with monopolar readout without flow compensation. Imaging parameters were: FA = 15, FOV = 24 cm, TE₁ = 5 ms, TR = 45 ms, #TE = 8, ΔTE = 5 ms, acquisition matrix = 256 × 256 × 28~52, voxel size = 1 × 1 × 2.8 mm³, BW = ±31.25 kHz and parallel imaging factor R = 2. Total scan time was proportional to the number of slices (about 10 slices/min). For each case, we applied PDF+LFI, TFI, SSQSM and Differential QSM to estimate the QSM of brain with ICH. For TFI, Eq. 4 was used and P_B was determined from the previous in vivo COSMOS experiment. The $R{2}^{\ast }$ threshold was $R{2}_{th}^{\ast }=30s^{-1}$, which, in our preliminary studies, was empirically determined to effectively distinguish the hemorrhage site from surrounding brain tissue. The regularization parameter λ was chosen using L-curve analysis for PDF+LFI, SSQSM and Differential QSM, while TFI used the same λ as in PDF+LFI. The same kernel diameters d as in the COSMOS experiment were used here for SSQSM and Differential QSM, respectively. To quantify the shadow artifact around ICH, the mean susceptibility within a 5mm wide layer surrounding each ICH was computed for PDF+LFI and TFI. The reduction in standard deviation (SD) in non-ICH regions was also computed as a measure for ICH-related artifact reduction (17). It was defined as $R=(\text{SD}({\chi }_{\text{MEDI}}\mid M_{\text{non-ICH}})-\text{SD}({\chi }_{\text{TFI}}\mid M_{\text{non-ICH}}))∕\text{SD}({\chi }_{\text{MEDI}}\mid M_{\text{non-ICH}})$, where $\chi \mid M_{\text{non-ICH}}$ denotes the susceptibilities in the non-ICH region.

In vivo experiment: whole head QSM

Since the proposed method no longer separates background field removal and local field inversion, it is possible to generate a susceptibility map for the entire head by including tissues outside the brain (e.g. scalp, muscles and oral soft tissues) into the ROI M in Eq. 5. We acquired one healthy human brain data at 3T (GE, Waukesha, WI) using a multi-echo gradient echo sequence with monopolar 3D radial readout for large spatial coverage. Flow compensation was off. Imaging parameters were: FA = 15, FOV = 26 cm, TE₁ = 1 ms, TR = 34 ms, #TE = 9, ΔTE = 3 ms, acquisition matrix = 256×256×256, voxel size = 1 × 1 × 1 mm³, BW = ±62.5 kHz, number of radial projections = 30000, scan time of 15 min, and reconstruction using regridding (38). TFI was used with P_B determined from the previous in vivo COSMOS experiment. The ROI M in Eq. 5 was determined by thresholding the magnitude image I: M ≔ I > 0.1 max(I). The total field was estimated using SPURS (34). Differential QSM with d = 3 was also applied using this ROI (12). For comparison, QSM of only the brain was also reconstructed with TFI using the mask obtained from BET. The regularization parameter λ was chosen using L-curve analysis for brain-only TFI, Differential QSM and whole head TFI.

All computations in this work were performed in MATLAB on a desktop computer with a 6-core CPU (Intel Core i7) and 32GB memory.

Results

Simulation

Accuracy of Sequential Inversion and TFI

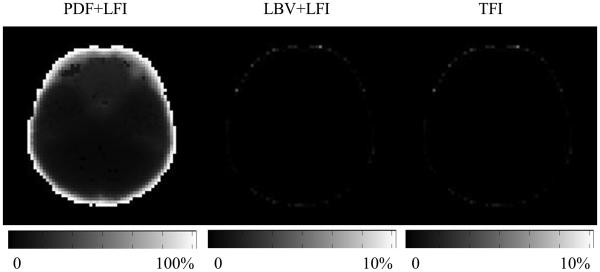
In Figure 2, the PDF+LFI method shows an estimation error of less than 10%, except near the boundary of the ROI: when the source was within 4 voxels of the boundary, the error was at least 40%. In contrast, the maximum error for both LBV+LFI and the proposed TFI were 4.8% throughout the ROI, including the boundary.

Figure 2.

Error map for PDF+LFI, LBV+LFI and TFI for the 0.1ppm point source simulation. When the point source is close to the ROI boundary, the error when using TFI is significantly smaller than that using PDF+LFI.

Effect of preconditioner P in TFI

Figure 3b shows that for P_B > 1, the discrepancy between the measured and the estimated total field decreased faster compared to using no preconditioning (P_B = 1). Figure 3c shows that, for large enough CG iteration numbers (>1000), the preconditioned solvers converged to Err_simu <0.04 with respect to the reference for all P_B values. On the other hand, at CG iteration 100, P_B = 30 achieved a smaller Err_simu (Figure 3c) compared to P_B = 5 or 80.

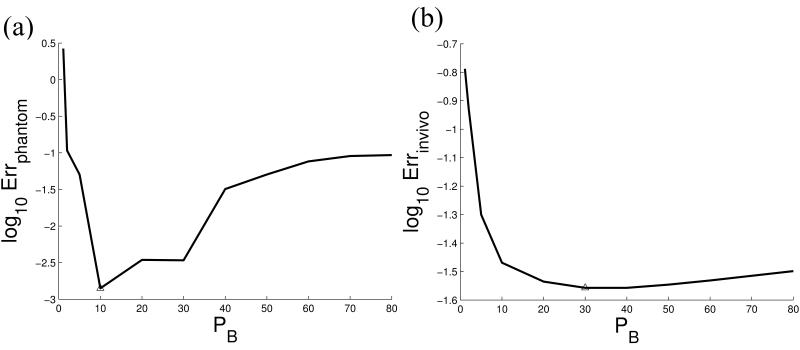
Phantom

The optimized regularization parameter λ was 2 × 10⁻² for both PDF+LFI and TFI, 5 × 10⁻¹ for SSQSM and 5 × 10⁻³ for Differential QSM. The optimized kernel diameter d was 13 for SSQSM and 3 for Differential QSM. The weight P_B = 10 was found to be optimal here (Figure 4a). Linear regression between the estimated (y) and reference (x) balloon susceptibilities were: PDF+LFI y = 0.978x − 0.004 (R = 1.000); TFI y = 0.973x + 0.004 (R = 1.000); SSQSM y = 0.833x + 0.019 (R = 0.999); Differential QSM y = 0.971x + 0.004 (R = 1.000). Err_phantom were: PDF+LFI: 0.0158, TFI: 0.0050, SSQSM: 0.0350, Differential QSM: 0.0010.

Figure 4.

The weight P_B in preconditioner is optimized by minimizing the error between the estimated QSM and the reference value both in the phantom (a) and in vivo (b).

In vivo imaging: healthy brain

Figure 1 shows brain QSMs reconstructed using PDF+LFI, un-preconditioned TFI (P_B = 1) and preconditioned TFI (P_B = 30), at different CG iterations. With preconditioning (P_B = 30), CG generated a local tissue susceptibility similar to that obtained with PDF+LFI in 50 iterations, while the un-preconditioned TFI needed 300 iterations to reach a comparable solution. P_B = 30 was determined by minimizing Err_invivo (Figure 4b). The average reconstruction time was 232 seconds for PDF+LFI, 270 seconds for TFI, 50 seconds for SSQSM and 284 seconds for Differential QSM. The regularization parameter χ was 10⁻³ for both PDF+LFI and TFI, 5 × 10⁻² for SSQSM and 1 × 10⁻³ for Differential QSM. The maximum kernel diameter d was 17 for SSQSM and 3 for Differential QSM.

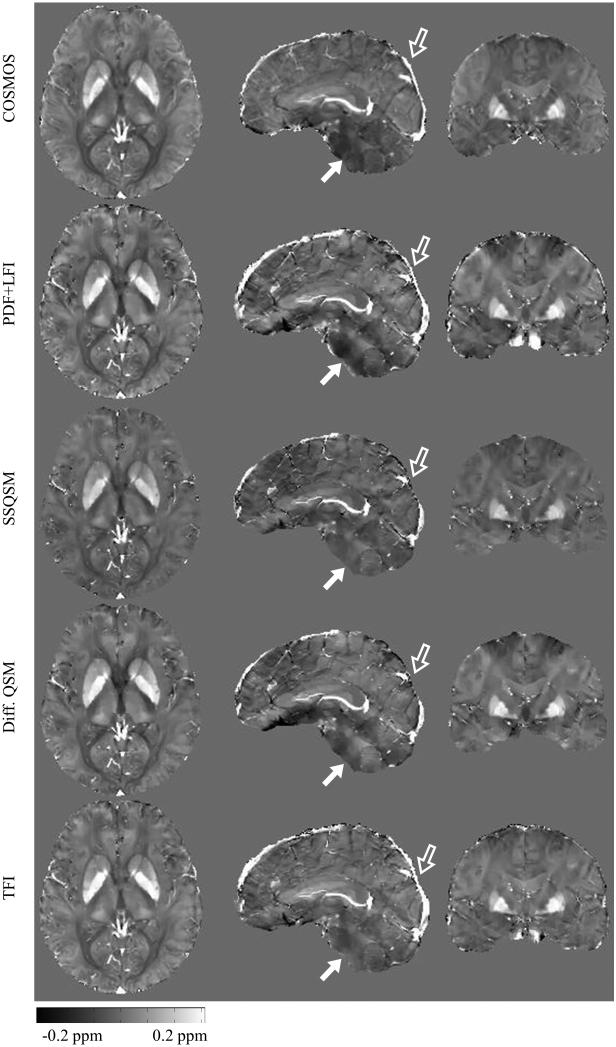
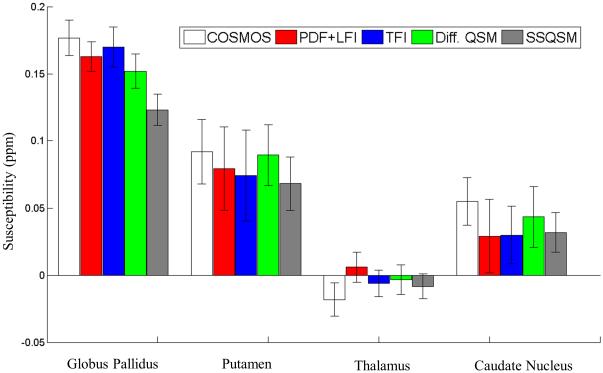
Figure 5 shows that the QSM for all methods were consistent with the COSMOS map near the center of the brain. Meanwhile, homogeneity of QSM in the lower cerebrum (solid arrow in Figure 5) was improved using TFI compared to PDF+LFI. The superior sagittal sinus was better visualized with PDF+LFI and TFI than with SSQSM and Differential QSM, especially at the posterior brain cortex (hollow arrow in Figure 5). The measured susceptibilities for deep GM are shown in Figure 6. Using COSMOS as reference, significant underestimation was observed for SSQSM in the measurement of GP susceptibility compared to Differential QSM, PDF+LFI or TFI. This underestimation was observed in other subjects as well (Table 1). SSQSM underestimated the susceptibility of the GP by 27.4% on average, compared to 5.4%, 9.6% and 8.9% for PDF+LFI, TFI and Differential QSM, respectively.

Figure 5.

In vivo healthy QSM estimated with COSMOS, PDF+LFI, SSQSM, Differential QSM and proposed TFI. Both PDF+LFI and TFI give more complete depiction of superior sagittal sinus than SSQSM or Differential QSM, especially at posterior brain boundary (hollow arrow). At the bottom of the cerebrum (solid arrow), TFI’s result is more homogeneous than PDF+LFI.

Figure 6.

Mean and standard deviation of measured susceptibilities of globus pallidus, putamen, thalamus and caudate nucleus in Figure 5 for COSMOS, PDF+LFI, TFI, Differential QSM and SSQSM. These 5 methods show comparable measurement for putamen, thalamus and caudate nucleus. For globus pallidus, SSQSM shows significant underestimation than COSMOS, PDF+LFI, TFI or Differential QSM.

Table 1.

Mean susceptibility of globus pallidus in all 5 healthy subjects using COSMOS, PDF+LFI, TFI, Differential QSM and SSQSM. Underestimation in SSQSM are observed in all cases, compared with PDF+LFI, TFI and Differential QSM.

Method	χ GP1 (ppm)	χ GP2 (ppm)	χ GP3 (ppm)	χ GP4 (ppm)	χ GP5 (ppm)	Average relative difference
COSMOS	0.147	0.143	0.163	0.175	0.177
PDF+LFI	0.139	0.139	0.160	0.159	0.163	−5.4%
TFI	0.133	0.125	0.147	0.154	0.170	−9.6%
Diff. QSM	0.139	0.133	0.147	0.158	0.153	−8.9%
SSQSM	0.124	0.112	0.104	0.117	0.123	−27.4%

In vivo imaging: brain with hemorrhage

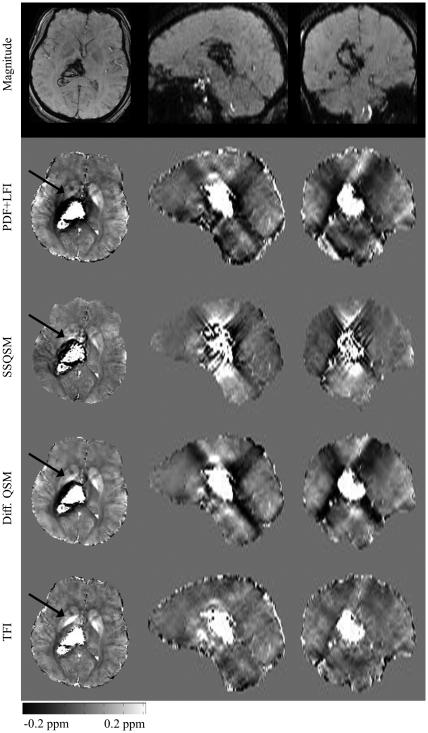
All hemorrhage patient brain images were reconstructed using P_B = 30 for TFI. The average reconstruction time was 328 seconds for PDF+LFI, 325 seconds for TFI, 50 seconds for SSQSM and 344 seconds for Differential QSM. The regularization parameter λ was 10⁻³ for both PDF+LFI and TFI, 2 × 10⁻³ for SSQSM and 5 × 10⁻⁴ for Differential QSM. Maximum kernel diameter d was 17 for SSQSM and 3 for Differential QSM. Figure 7 shows one example with reduced shadowing artifacts around the ICH site using the proposed preconditioned TFI method as compared to using PDF+LFI, SSQSM or Differential QSM. In particular, we observed that the GP structure was more discernible with the shadowing artifact removed (as indicated by arrows in Figure 7). Considering that the shadow artifact around ICH manifests itself as negative susceptibility (17,18), the increase in the mean susceptibility within ICH’s vicinity (Table 2) indicates a reduction of the artifact. The standard deviation reduction shown in Table 2 similarly points to the reduction of this shadow artifact.

Figure 7.

In vivo result in one patient suffering from intracerebral hemorrhage. From top to bottom: T2*-weighted magnitude image, QSM reconstructed using PDF+LFI, SSQSM, Differential QSM and proposed TFI.

Table 2.

Artifact reduction quantification for ICH patients.

Patient number	Age(years) /Gender	MEDI non-ICH mean susceptibility (ppm)	TFI non-ICH mean susceptibility (ppm)	STD reduction (R)
1	52/M	−0.158	0.008	63%
2	51/M	0.047	0.013	38%
3	43/M	−0.003	0.006	31%
4	70/F	−0.041	0.000	6%
5	65/M	−0.020	0.021	17%
6	60/M	−0.224	0.023	29%
7	77/M	−0.008	0.009	10%
8	41/M	−0.053	0.020	25%
9	78/M	−0.117	0.017	59%
10	72/F	0.006	0.032	3%
11	48/F	−0.077	0.022	26%
12	72/M	0.021	0.032	1%
13	63/M	−0.005	0.019	1%
14	70/M	−0.062	−0.019	12%
15	47/M	−0.018	0.005	11%
16	62/M	−0.010	0.036	27%
17	47/M	−0.019	0.014	5%
18	47/M	−0.018	0.014	5%

In Vivo Experiment: Whole-Head QSM

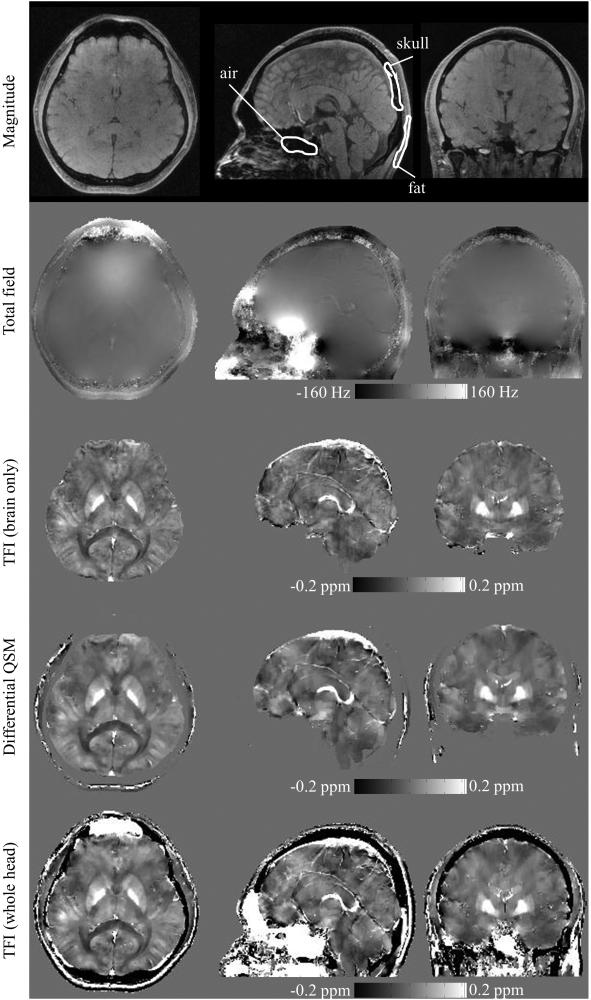
The whole head QSM was compared with the magnitude/phase image and brain QSM (Figure 8). The reconstruction time was 13.4 minutes for brain-only TFI, 19 minutes for Differential QSM and 14.2 minutes for whole head TFI. The regularization parameter λ was 10⁻³ for both brain-only TFI and Differential QSM, and 2.5 × 10⁻³ for whole head TFI. The results show that the intracerebral map in whole head TFI QSM was consistent with the brain-only TFI, although the brain-only TFI generated slightly better homogeneity at top part of the brain as seen in the sagittal and coronal view. Meanwhile, whole head QSM also provided additional mapping of susceptibility for extracerebral structures, such as the skull, air-filled sinuses and subcutaneous fat. Since the ROI was determined by thresholding magnitude images, the exterior of the brain was more distinct in whole head QSM compared to brain-only QSM, especially at brain stem and cerebellum. Additionally, whole head QSM clearly discriminated the skull and sinus air, which were hard to distinguish in the magnitude image due to the loss of MR signal in both regions. Example ROIs were delineated for sinus air, skull and fat, as in Figure 8, and the mean susceptibility was calculated to be 7.38 ppm for the sphenoidal sinus, −1.36 ppm for the skull, and 0.64 ppm for fat. These susceptibility values are consistent with prior literature (19,39,40). When comparing Differential QSM and whole head TFI, a similar susceptibility map was obtained within the brain, while Differential QSM did not depict the susceptibilities of the skull and sinus air.

Figure 8.

Magnitude (first row), total field (second row), TFI-generated brain QSM (third row), Differential QSM (fourth row) and TFI-generated whole head QSM (bottom row) are shown in axial (left column), sagittal (middle column) and coronal (right column) views. The susceptibility distribution for skull, air filled sinuses and subcutaneous fat is clearly depicted with whole head TFI. Example ROIs are shown and mean susceptibility values are calculated for: nasal air = 7.38 ppm, skull = −1.36 ppm and fat = 0.64 ppm.

Discussion

Our data demonstrate that total field inversion (TFI) for QSM eliminates the need for separate background field removal and local field inversion (LFI), and that preconditioning can accelerate TFI convergence. Compared to the traditional PDF+LFI approach, TFI provides more robust QSM in regions near high susceptibility regions such as those containing air or hemosiderin present in hemorrhages, within similar reconstruction time. It is also demonstrated that TFI is able to generate the whole head QSM without the need for brain extraction.

The sequential background field removal and LFI process the same data using the same Maxwell equations but require an assumption or regularization (1) to differentiate the background field and the local field. For the background field removal exemplified here using PDF, it is assumed that the Hilbert space L spanned by all possible local unit dipole fields f_dL is orthogonal to the Hilbert space B spanned by all possible background unit dipole fields f_dB (22). However, this orthogonality assumption is not valid when the local unit dipole is close to the ROI boundary (22), and will cause error in PDF. This error or similar error introduced by any other background field removal method propagates into the subsequent LFI and produces an inaccurate local susceptibility estimation. However, there is no need to break the problem of fitting MRI data with the Maxwell equations into two separate background field removal and LFI problems. Our proposed TFI eliminates this separation and avoids the associated error propagation. Improvement of TFI over PDF+LFI is shown in Simulation (Figure 2) and in vivo (Figure 5), especially when the local source of interest is close to the ROI boundary. It is noted that LBV+LFI also outperforms PDF+LFI in separating local and background fields, but in order to exclude noisy phase from Laplacian operation (26) at ROI boundary, LBV requires an accurate ROI mask, which might be challenging for in vivo brain QSM.

Preconditioning is necessary to achieve practical performance with TFI. Figure 1 shows that for brain QSM, non-preconditioned TFI takes 300 CG iterations to converge to a solution comparable to PDF+LFI, but the latter method takes only 50 iterations. Here we introduced a prior-enhanced right-preconditioner specific to our TFI problem (Eq. 4). Similar work on a prior-enhanced preconditioner can be found in MR dynamic imaging (41), where a right-preconditioner is constructed as a smoothing filter which incorporates the prior knowledge that coil sensitivities are generally spatially smooth. In a QSM scenario, we consider the susceptibility gap between strong susceptibility sources (e.g. air, skull or hemorrhage) and weak susceptibility sources (e.g. normal brain tissue), by assigning a larger weight (P_B > 1) to the strong susceptibility regions in the preconditioner (Eq. 4). This preconditioner P is aimed to approximate a covariance matrix Γ by P^H P ≈ Γ, under the assumption that the solution χ for Eq. 2 is a Gaussian random vector χ ~ N(0,Γ). Calvetti et al. (30) indicates that the convergence of iterative Krylov subspace solvers (such as the CG) can be improved using this preconditioner. This is confirmed with our result shown in Figure 1, where preconditioning reduced the required number of CG iterations by a factor of 6 for TFI. The proposed preconditioner is different from the preconditioner proposed by Bilgic et al. for QSM (32). There, the system matrix for local field inversion is approximated by a diagonal matrix and used as a preconditioner after inverting. It may therefore be possible to combine both preconditioners in TFI for further speedup.

Since our preconditioner is designed for a large dynamic range of susceptibilities, it straightforwardly applies to intracerebral hemorrhage (ICH). As shown in Figure 7, preconditioned TFI effectively suppresses the artifact near the hemorrhage site and enhances the QSM quality for ICH. Previous work in handling a large range of susceptibilities is based on the piecewise constant model – either explicitly specified as in (20), or implicitly using a strong edge regularization (17-19). In these methods, different regularization parameters need to be carefully chosen for strong and weak susceptibilities, respectively. Otherwise, under-regularization would induce streaking artifacts near the hemorrhage site (17,18), or over-regularization would sacrifice fine detail in weak susceptibility regions (19,20). Our proposed TFI method utilizes preconditioning to improve convergence towards an artifact-reduced solution, as opposed to using multiple levels of regularization. This eliminates the need for combining QSMs from multiple local field inversion instances (17,18). For whole head QSM (Figure 8), our proposed preconditioned TFI produces intracerebral (weak) and extracerebral (strong) QSM simultaneously, whereas the intracerebral component is less well seen in (19) due to over-regularization.

Laplacian-based methods, SSQSM (10) and Differential QSM (12) use the harmonic property of the background field f_B (Δf_B = 0 within the ROI) to eliminate both phase unwrapping and background field removal, enabling local susceptibility estimation in a single step. SSQSM further speeds up by omitting the SNR weighting and using L2 norm for regularization (10). However, Laplacian-based methods suffer from brain erosion: The Laplacian is implemented using the finite difference operator or the spherical kernel operator (1,24,25,42), both requiring the ROI mask to be eroded. As a consequence, erosion of superior sagittal sinus can be seen in SSQSM and Differential QSM (Figure 5). This brain erosion problem is avoided in PDF+LFI and TFI that do not evaluate the Laplacian. Furthermore, SSQSM suffers from substantial susceptibility underestimation in phantom and in vivo, compared to Differential QSM, PDF+LFI and TFI. This underestimation was also observed for a range of values for the regularization parameter λ around the reported value (results not shown). This may be caused by the use of L2-norm regularization, which has been shown to underestimate susceptibility compared to L1-norm regularization (27). Moreover, Differential QSM does not estimate the susceptibilities of the skull and sinus air (Figure 8). This is consistent with previous literature (12). The reason is that, since ROI is determined by thresholding the magnitude image, the skull and sinus air are not included and are considered as “background”. Therefore the Laplacian operation removes the field generated by the skull and sinus air. On the contrary, TFI preserves the field they generate and depicts their susceptibilities (Figure 8).

There are limitations to our preliminary implementation of preconditioned TFI. First, the current choice of the preconditioner P is empirical and performance may be improved by selecting a patient specific value or model. Further work might focus on determining P from physical or statistical models of the susceptibility distribution for better approximation of the covariance matrix Γ. A prior QSM estimation, which can be calculated very fast by methods such as SSQSM (10), might also be helpful in modeling this distribution and constructing the preconditioner. Second, the construction of our preconditioner requires R2^∗ map to extract intracerebral region with strong susceptibility, such as ICH. If the R2^∗ information is not available, especially when only single-echo image is acquired, the preconditioned TFI might be less effective in suppressing ICH-based shadow artifact. In future work, we will focus on incorporating other contrast (magnitude, T1-weighted or T2-weighted image) into constructing the preconditioner. Third, for whole head QSM, the skull has very short T2^∗, such that the multi-echo GRE sequence fails to acquire skull MR signal for field estimation. In future work, the use of an ultra-short echo time (UTE) (43) pulse sequence to provide phase information in the skull will likely lead to a more accurate susceptibility map. The magnitude signal from UTE sequence might also be used for differentiating skull and air-filled sinus, hence enabling more effective preconditioning by assigning different weight P_B for these regions. Finally, the proposed TFI method uses a linear signal model but can be extended to a non-linear formulation similar to that of (21), in order to bypass the phase unwrapping step and improve the noise modeling. However, caution is needed because the non-linear and non-convex objective function has multiple local minimum. Given the fact that the desired solution is fairly large outside the ROI, such as that of air, the all-zero initial guess used in this work may cause the solver to converge to an incorrect local minimum. Future work will be focused on construction of an initial guess robust against this problem. The current linear solution may provide such an initial guess.

Conclusion

In this article, we propose a total field inversion (TFI) algorithm for QSM reconstruction. This eliminates the need for sequential background field removal and local field inversion, and it achieves a higher accuracy at the boundary of the susceptibility map. We also introduce a preconditioner to improve convergence. We show that the proposed preconditioned TFI suppresses streaking artifacts in QSM of intracerebral hemorrhage. TFI is also capable of mapping the susceptibility of the entire head including brain tissue, skull, air-filled sinus and subcutaneous fat.

Appendix. A. Gauss-Newton Method for Preconditioned Total Field Inversion

The matrix formulation for Eq. 5 is:

$$y^{\ast }={\text{argmin}}_y\Phi \left(y\right)=\underset{y}{\text{argmin}}\frac{1}{2}\parallel W(f-F^{H}DFPy){\parallel }_2^2+\lambda \parallel M_{G}GPy{\parallel }_1$$ [A1]

Where F is the Fourier transform, $D\left(k\right)=\frac{1}{3}-\frac{k_z^2}{k^2}$ is the k-space dipole kernel and G the finite difference operator. At the n-th Newton iteration, Φ is linearized at the current solution y_n:

$$\Phi (y_n+d{y}_n)=\frac{1}{2}\parallel W((f-F^{H}DFP{y}_n)-F^{H}DFPd{y}_n){\parallel }_2^2+\lambda \parallel M_{G}GP(y_n+d{y}_n){\parallel }_1$$ [A2]

Using weak derivatives, the update dy_n is found by solving:

$$\begin{array}{cc}\hfill & 0={\nabla }_{d{y}_n}\Phi =-{\left(W{F}^{H}DFP\right)}^{H}W((f-F^{H}DFP{y}_n)-F^{H}DFPd{y}_n)+\hfill \\ \hfill & \lambda {\left(M_{G}GP\right)}^H\text{diag}\left\{\frac{1}{\sqrt{{\mid M_{G}GP{y}_n\mid }^2+\in }}\right\}{M}_{G}GP(y_n+d{y}_n)\hfill \end{array}$$

Or:

$$\begin{array}{cc}\hfill & \left[P{F}^{H}DF{W}^2{F}^{H}DFP+\lambda P{G}^H{M}_G\text{diag}\left\{\frac{1}{\sqrt{{\mid M_{G}GP{y}_n\mid }^2+ϵ}}\right\}{M}_{G}GP\right]d{y}_n=\hfill \\ \hfill & \left[P{F}^{H}DF{W}^2(f-F^{H}DFP{y}_n)-\lambda P{G}^H{M}_G\text{diag}\left\{\frac{1}{\sqrt{{\mid M_{G}GP{y}_n\mid }^2+ϵ}}\right\}MGP{y}_n\right],\hfill \end{array}$$ [A3]

which is solved using the conjugate gradient (CG) method (29). Note that we use $M_{G}GP{y}_n\approx \sqrt{{\mid M_{G}GP{y}_n\mid }^2+ϵ}$ where ϵ = 10⁻⁶ to avoid division by zero. The stopping criteria are: maximum number of iterations = 100 or relative residual < 0.01. The Gauss-Newton method is terminated when the relative update $\parallel d{y}_n{\parallel }_2∕\parallel y_n{\parallel }_2$ is smaller than 0.01.