OPTIMAL SLICE TIMING CORRECTION AND ITS INTERACTION WITH FMRI PARAMETERS AND ARTIFACTS

Abstract

Due to the nature of fMRI acquisition protocols, slices in the plane of acquisition are not acquired simultaneously or sequentially, and therefore are temporally misaligned with each other. Slice timing correction (STC) is a critical preprocessing step that corrects for this temporal misalignment. Interpolation-based STC is implemented in all major fMRI processing software packages. To date, little effort has gone towards assessing the optimal method of STC. Delineating the benefits of STC can be challenging because of its slice-dependent gain as well as its interaction with other fMRI artifacts. In this study, we propose a new optimal method (Filter-Shift) based on the fundamental properties of sampling theory in digital signal processing. We then evaluate our method by comparing it to two other methods of STC from the most popular statistical software packages, SPM and FSL. STC methods were evaluated using 338 simulated and 30 real fMRI data and demonstrate the effectiveness of STC in general as well as the superiority of the proposed method in comparison to existing ones. All methods were evaluated under various scan conditions such as motion level, interleave sequence, scanner sampling rate, and the duration of the scan itself.

Graphical Abstract

1. Introduction

Typically, fMRI data are acquired slice by slice through a fast acquisition technique called echo planar imaging (EPI) in which each slice’s acquisition takes about 30–100 ms and follows a single radio frequency (RF) pulse excitation (Stehling et al., 1991). By rapidly acquiring and stacking 2D slice images, a 3D brain volume image can be constructed anywhere between fractions of a second to several seconds, depending on the number of slices and the slice’s in-plane resolution. Such sequential acquisition results in an accumulating offset delay between the first slice and the remaining ones. Furthermore, to eliminate or attenuate leakages of a single slice RF pulse excitation to adjacent slices, interleaved slice acquisition techniques are performed regularly in fMRI scanners. In interleaved slice acquisition, slices are not acquired sequentially, a process which imposes non-monotonic acquisition delay to the adjacent slices. Even-odd interleave is the most common interleaved slice acquisition in fMRI scanning in which first even slices are acquired sequentially, followed by odd slices. Other kinds of interleaved sequences with different numbers of slices being skipped between two consecutive slice acquisition have also been used in the field (Parker et al., 2014). For instance, Philips scanners use square root of the number of slices in the volume as the interleave parameter in slice acquisition. No matter what kind of interleave is being used, they all give rise to the same issue, which is the non-monotonic offset delay in the acquisition time of the adjacent slices. We formulate the slice timing problem in the next subsection and then demonstrate the existing methods to resolve this issue based on their interpolation kernel. In section 2, we introduce our proposed optimal STC method and explain how to evaluate its effectiveness in comparison to the existing methods using simulated and real fMRI data.

In the existing STC method evaluations (Calhoun et al., 2000; Sladky et al., 2011), fMRI artifacts and in particular motion, as the most destructive contaminating factor in fMRI data analysis, is not taken into account. Motion deteriorates the gain that we can achieve from STC, therefore in our evaluation we stratified the gain of the STC on different levels of motion to demonstrate their interaction.

In addition, we preform two more experiments to examine the effectiveness of STC on different fMRI parameters. First, we study the effect of scan length, spanning from 300 volumes to just 10 volumes, on the effectiveness of the STC. Second, we investigate the effect of various TR’s, spanning from short (0.5s) to long (5.0s) on simulated 10 minute scans, on the effectiveness of STC. The experimental results are then presented in the results section in the same order they are presented in section 2. Finally, a discussion on each of the results is provided in the discussion section.

1.1 The Slice Timing Problem

An ideal imaging system would capture the entire brain volume at one instance. While sequential acquisition of slices is tolerable for many aspects of fMRI analysis, interleaved acquisition becomes problematic for any process that requires voxels spanning over more than one slice. Spatial smoothing with a 3D kernel is one such process that becomes problematic with interleaved acquisition. Involuntary head motion during the scan is also challenging to model and correct with interleaved data. To resolve this problem, slice timing correction (STC) is proposed and widely used in the field (Sladky et al., 2011). STC accounts for a given slice’s temporal offset by interpolating the signal in the reverse direction of the imposed offset delay. The benefits of STC have been shown in numerous studies (Henson et al., 1999; Vogt K et al., 2009). However, all the existing methods are interpolation based, which estimates the signal values between two sampling points. Because of this, they are all considered to be essentially sub-optimal methods.

In this study, we aim to completely reconstruct the signal from its sampled version with no sub-optimal interpolation. According to Shannon-Nyquist sampling theorem (Proakis and Manolakis, 1988) such a reconstructed signal will be independent from the offsets of sampling and thus eventually eliminate the need for STC altogether. We first describe the existing STC methods from a signal processing point of view, and next describe in detail our proposed method.

Assessing the quality of STC methods is challenging due to its interaction with motion (Kim et al., 1999), and the fact that its improvement is dependent on the amount of the offset delay of each slice. For instance, the signal from a voxel in a slice with no delay (acquired at the beginning of the TR) will show little to no improvement after STC, no matter what correction technique we use. Because of this, if slices with high offset delay do not fall on a region of observed significant activation, it is likely that there will be little difference in results between STC and uncorrected data. Furthermore, depending on an individual’s brain size, position and head orientation in scanner, voxels with the same offset delay may represent different regions from one subject to another. In this manner, any given ROI may fall on different slices with different delays across subjects. This makes it extremely difficult to compare STC methods on a given region across subjects. Registration would not help in this instance, as it may redistribute the voxels across slices, thus destroying the ability to compare high-delay slices to low-delay slices. In our evaluation, we generated simulated data with the same subject brain morphology to control for brain shape differences. For real data, we used only the voxels in subject’s native space that are located in slices with moderate offset delay and have significant activation.

1.2 Existing Methods of STC

Almost all the existing STC methods are based on interpolation techniques that estimate the signal value between sample points. If f (s,t) is the underlying true fMRI signal at location s (s = (x,y,z) in Cartesian coordinate system) and time instant t, then the sampled version of the true signal will be

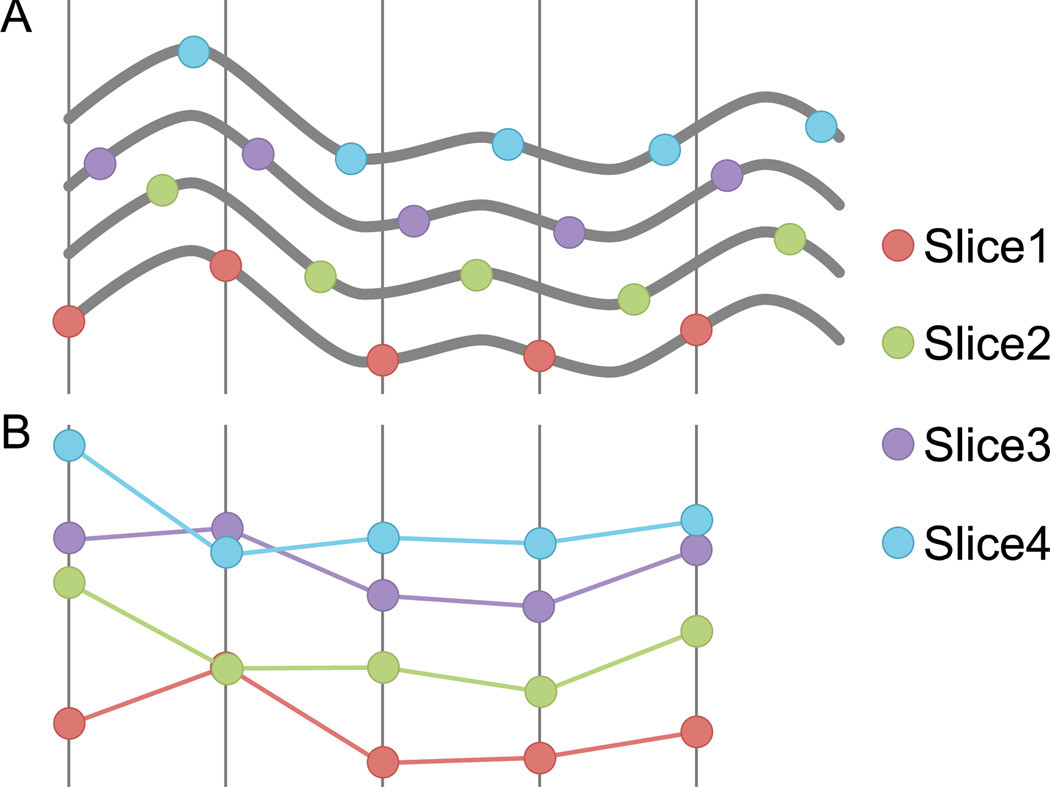
$$F[s,n]=f(s,{\mathit{\text{nT}}}_s+\phi (z))$$ (1)

$$\phi (z)=\frac{\gamma }{\delta }{\mathit{\text{mod}}}_{\gamma }(z)+\mathit{\text{floor}}(z/\gamma )$$

where T_s is the sampling period (TR), z is the slice number, γ is the total number of slices, δ is the interleaved parameter, and φ(z) is the offset delay imposed for each slice by interleaved acquisition. For simplicity and without loss of generality we assumed δ is a factor of γ. The slice-timing problem arises from the fact that offset φ(z) changes as a function of z. Figure 1 sketches the effect of such dependency in the sample’s offset delay for four adjacent voxels with different z coordinates. The goal of STC is to correct for these irregular offset delays. Conventional interpolation-based techniques attempt to operate on the discrete signals (Figure 1B) and estimate the signal value between the sample points. Mathematically, this can be represented by the convolution of the sampled signal, F[s,n] with an interpolation kernel h:

$$\widehat{f}[s,n]=\sum _{k=0}^{N-1}F[s,k]h({\mathit{\text{nT}}}_s-k-\phi (z))$$ (2)

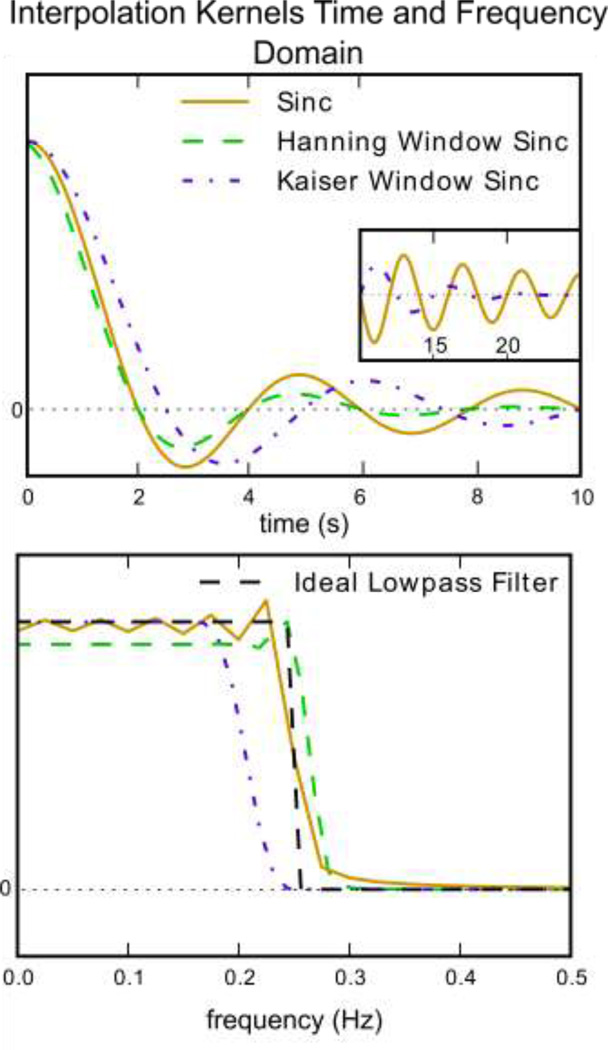
where f̂ is the shifted/interpolated signal. Linear, cubic spline, sinc, or a windowed sinc are commonly used in the literature for the purpose of STC. Figure 2 shows the time and frequency domain of different sinc interpolation kernels.

Figure 1. The slice-timing problem: the same signal sampled at different offsets yields signals that do not look the same.

(A) Five adjacent slices acquired with interleaved acquisition all sample the same underlying bold signal. (B) Without correction, reconstruction yields five different signals despite having the same underlying shape.

Figure 2. Time and frequency domain plots of kernels for sinc, Hanning window sinc and Kaiser window sinc.

A) The time domain representation of various kernels and B) the frequency domain of these kernels. It is easy to see from this the impact various kernel will have on a signal’s frequency spectrum. Inset: An example of using a window function to facilitate a smoothly terminating sinc function. The purple dashed line is a sinc function multiplied with a Kaiser window, which greatly reduces rippling in the both the frequency and time domain. A non-windowed sinc (gold) ends abruptly, which causes rippling in the frequency domain. The green line is truncated at 10s, so it does not exist in the inset window.

Two widely used fMRI data analysis software packages, statistical parametric mapping (SPM) (Friston et al., 1994) and FMRIB software library (FSL) (Jenkinson et al., 2012), use different version of sinc interpolation (SPM: sinc, FSL: Hanning window sinc) for their STC module. Because of this, we will focus on sinc interpolation in our comparison. Sinc interpolation can be represented as convolution of the fMRI signal with the following kernel,

$$h_s(t)=\frac{\text{sin}(\pi t/T_s)}{\pi t/T_s}$$ (3)

Figure 2 shows the time and frequency domain of this kernel. It should be emphasized that ripples in the pass band of the sinc kernel are due to truncation of the signal in the time domain, and become worse as the signal is truncated shorter. To attenuate the rippling artifact, a smooth window function such as Hanning has been proposed by FSL to be applied to the sinc kernel,

$$w_{\mathit{\text{hann}}}(n)=0.5(1-\text{cos}(\frac{2\pi {\mathit{\text{nT}}}_s}{T_{s}N-1}\left)\right)$$ (4)

where N is the length of the sequence. By examining the frequency domain of this kernel we can see that ripples are removed at the expense of a more gradual filter stop-band.

2. Materials and Methods

In the previous section we have formulated the existing interpolation-based STC techniques as filtering of the sampled fMRI signal with different kernels with irregular and slice dependent offset delay φ(z). It is important to note that such irregular offset delay has no effect on the magnitude of the frequency domain of the signal. In other words, no matter what φ(z) is, the frequency domain of the sampled fMRI signal F [s, n] will be the same. From the signal theory standpoint, since all slices are acquired with the same sampling rate, as long as the sampling rate is twice the maximum bandwidth of the underlying BOLD signal of interest, it can be optimally recovered (Shannon-Nyquist sampling theory). This means all sampled signals in Figure 1b from all the slices can be reconstructed to give the signals in Figure 1a, no matter what the offset of the sampling.

If we assume that the canonical double gamma HRF curve (commonly used in linear modeling of hemodynamic response) is realistically close to the shape of the real HRF, then spectral analysis of this curve reveals that the hemodynamic response function has 99.9% of its energy in the frequency range of [0, 0.21] Hz. For a typical fMRI sampled at 0.5 Hz (TR = 2 seconds), this is sufficient to reconstruct the signal completely according to the sampling theorem. This theoretical concept is the foundation of our proposed optimal method for STC that is described next.

2.1 Filter-shift slice timing correction

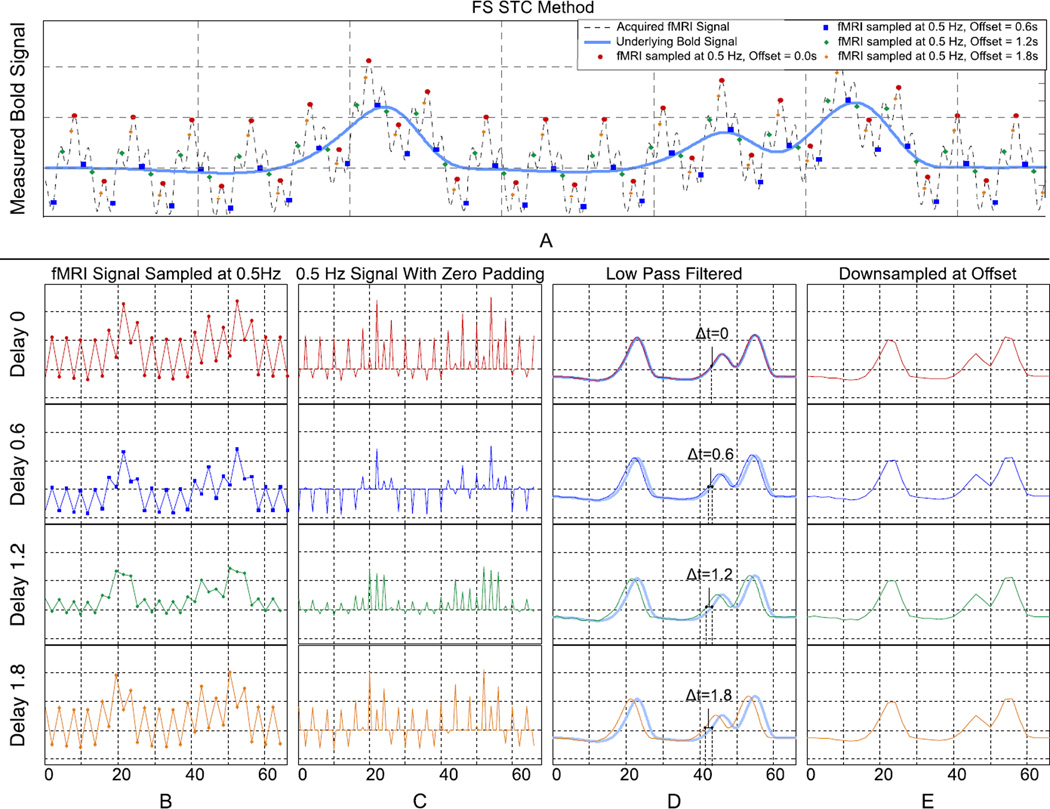
A simplified representation of our filter-shift (FS) method for optimal STC is presented in Figure 3 using simulated fMRI data for illustrative purposes. Figure 3A shows the underlying BOLD signal (light blue) as well as the contaminated fMRI signal (dash-line) with simplified physiological noise. For simplicity and illustration purposes we only add exaggerated physiological noise and ignore the other fMRI artifacts, contaminants, and noise. Multiple fMRI signals with different offsets are then sampled with the same frequency, simulating the effect of irregular sampling of the adjacent slices in fMRI data. Figure 3B shows those sampled signals separately, highlighting the apparent difference between them. Figure 3C shows the signal upsampled by padding with zeros between samples, and Figure 3D shows the upsampled signal after lowpass filtering with a delay that is equivalent to their offset in original sampling. By lowpass filtering, we band limit our signal to the frequencies of interest, which provides a significant advantage over other STC techniques. The original signal can optimally be recovered from irregular sampling only by filtering and shifting, as seen in Figure 3D. Finally to obtain the recovered signal in the same sampling rate, we down sample the data to the scanner’s sampling rate (TR=2 seconds, 0.5Hz) as shown in Figure 3E.

Figure 3. A visual description of the Filter Shift STC method showing high frequency simulated data, the effect of down-sampling at various offsets, and how the original signal can be reconstructed with upsampling and low pass filtering regardless of offset.

(A) An underlying bold signal is contaminated with physiological noise and sampled at 0.5Hz with different offsets. (B) Each offset yields visually different low-frequency signals. (C & D) These signals are upsampled and LPF to remove noise. The result is a shifted version of the original bold signal. (E) By resampling the high frequency with the same offset results in identical low frequency signals.

Since we can upsample the data to any sampling rate by adding zeros between the original sampling points, the signal can be resampled and shifted to the appropriate offset with no need for interpolation. It is worth mentioning that upsampling and lowpass filtering is essentially considered the standard method for signal reconstruction from sampled data in the digital signal-processing field, due to the preservation of the signal’s frequency response. Therefore, we can eliminate the need for sub-optimal and interpolation-based STC by just performing standard signal reconstruction. The only caveat is that the upsampling needs to be done with frequency high enough to accommodate the lowest offset delay that is encountered in the acquisition process.

Figure 3 also schematically illustrates the effect of eliminating STC from the fMRI preprocessing pipeline. Figure 3B shows that the four sampled signals with different offset can be significantly different even though they all represent the same underlying BOLD signal. FMRI data analysis without STC is equivalent to processing the four time series in Figure 3B whereas the actual BOLD signals are the ones in Figure 3E.

One issue we encounter is that the limited length of the fMRI data prevents us from using a high order optimal or near optimal lowpass filter due to the lengthy initialization period. Generally, any digital filter needs to operate on a certain number of initial time points to function properly. The number of time points is the initialization period, which is ½ the order of the filter. Thus, for any signal filtered with filter order N, the first N/2 and last N/2 time points of the filtered signal are not considered accurate. In this study we addressed this issue with two different tactics. First, we mirror pad half of the data to both ends to generate a contiguous circular signal. This allows us to increase the order of our filter without introducing initialization artifacts to the signal. This is implemented in the following steps: the time series is split in half, and the first half is mirrored and padded onto the front of the original signal. Likewise, the second half is mirrored and padded onto the end of the original signal. This ensures a periodic, circular signal with similar frequency characteristics, and allows us to use higher order filters with larger initialization periods. Second, a Kaiser window is added to the sinc interpolation kernel to help smooth the ends of the signal and remove any discontinuities, allowing for a shorter sampling of the sinc function, resulting in a lower order filter. This can be seen in the inset of Figure 2 where a Kaiser windowed sinc function tapers off gently, while the non-windowed sinc ends abruptly. A Kaiser multiplicative windowing function offers less pass band rippling and faster stop-band drop off than a Hanning window. This window is created with equation 5

$$w_{\mathit{\text{kaiser}}}(n)=\{\frac{I_0(\pi \alpha )\left(\sqrt{1-{(\frac{2{\mathit{\text{nT}}}_s}{T_{s}N-1}-1)}^2}\right)}{\underset{0}{I_0(\pi \alpha )}}\underset{\mathit{\text{otherwise}}}{0\le n\le N-1}$$ (5)

where I₀ is the zero order modified Bessel function of the first kind, and α is an arbitrary shaping coefficient. This kernel in plotted in Figure 2 for the comparison purpose. It is clear from Figure 2 (bottom) that Kaiser window preserves the BOLD signal and removes the undesired signal variability more effectively than the Hanning window.

The parameters used for the full FS method are as follows. First, the fMRI signal was mirror padded with half a length of the data on either side as described above. The signal was then upsampled to 20 Hz. This signal is then lowpass filtered with a 908 order Kaiser windowed sinc Finite Impulse Response (FIR) filter with a cutoff frequency of 0.21Hz (to preserve 99.9% of the energy in the canonical HRF), and stop gain of −60dB. This cutoff frequency could be adjusted to encompass the spectrum of subject specific HRFs with no loss of performance. The output of this process is a 20 Hz reconstructed BOLD signal. The signal was then trimmed to its original length and resampled to 0.5 Hz at any desired time shift. Because each slice has the same offset over all its voxels, this process can be parallelized so that each slice is operated on independently and reincorporated into the final image. All computations were carried out using python. The code is available for download from our website¹.

2.2 Simulated Data

Real fMRI data sets are problematic for evaluating the quality of one method over another because the true underlying BOLD signal is always unknown. Because of this, simulated datasets were used so that processed images could be compared to a known, true underlying BOLD signal. The generated simulated data in this paper were used to: i) evaluate the performance of our proposed FS method in comparison to existing STC methods with controlled levels of motion and noise, ii) examine the effect of different interleave acquisition sequences on STC, iii) examine the effect of short scan length on our proposed method, and iv) to examine the effect of TR on STC.

The morphology of our simulated fMRI scans comes from a real subject’s data by temporally averaging all its volumes. Reconstructing the same subject’s structural image with FreeSurfer (Fischl et al., 2004, 2002) and inter-modal rigid-body registration with FSL (Greve and Fischl, 2009) gives us the ROI masks in the fMRI space. Then neuronal activity stimuli consisting of sequences of 20 boxcar pulses with jittered onsets (at least 10 s apart) and randomly generated durations (0.5 to 3.5 s) were created for each ROI. Each ROI had a randomly generated boxcar pulse sequence, though only one was examined in this study. The neuronal stimulus for each voxel was convolved with the canonical HRF included in SPM to generate the hemodynamic response. Both HRF and neuronal stimuli were sampled at a frequency high enough to simulate interleaved slice acquisition for a given TR and number of slices (upsampled to a frequency equal to γ/TR, where γ is the total number of slices. This allows for one sample for each slice, and eliminates any need for further interpolation.). For a TR of 2, with 37 slices, we upsampled to 20 Hz. Null data (random noise) were assigned to voxels outside all ROIs. To simulate cardiac and respiratory variations in the fMRI signal, a simplified approach was taken, using a single sinusoid at f_c=1.23 Hz for cardiac and another sinusoid at f_r=0.25 Hz for respiratory noise. The magnitude of the cardiac signal is modulated with the inverse of the distance of the voxel from the nearest artery. In this manuscript, no physiological noise correction is applied, as it falls outside the scope of this study. Here we seek only to address the implications of slice timing correction and the errors introduced by temporal shifting. Thermal noise was then added to the signal. The temporally averaged volume is used to obtain the mean value at each voxel, which was used to shift the mean of the hemodynamic signal and to scale the standard deviation of the signal to 1% of the mean value comparable to a robust signal in the visual cortex. We used the same averaged volume for all simulated data sets to control for the significant difference in the morphology of the brain, which eliminates the need for spatial normalization to compare the results.

To have the most realistic simulation of motion’s interaction with interleaved slice acquisition, we have simultaneously simulated the motion and slice acquisition. Motion parameters were extracted from real subjects by taking the inverse of their spatial realignment transformation matrices at the original sampling rate (TR). We then upsampled these motion parameters (6 parameters) using spline interpolation to the same sampling frequency that the BOLD signals were generated for each ROI (20 Hz). By applying the upsampled parameters to the volume at the initial point we can specify the exact position of the volume at any fractional time between the two original sampling points. Since we have the orientation of the brain volume at any time (TR/ ) between the two sampling points, we know what part of the brain volume is imaged at each slice acquisition depending on the slice offset delay. This results in the most realistic simulation of the interaction between slice timing and motion. It should be noted that our motion measurements are limited to the observed head position at each TR, and the accuracy of the spline interpolation for between TRs; therefore we are unable to model any fast or nonlinear motion between TRs, which can occur in real data. Different interleave types (even-odd or Philips) can be simply simulated by sampling the slices in an appropriate offset delay of each interleave type.

Twenty simulated scans were used for the evaluation of our proposed FS method and the effect of noise and motion on STC. Each fMRI scan was simulated with twelve different combinations of noise and motion levels. Three different thermal noise levels were used, consisting of white noise that made up 0, 20, and 40% of the signal’s energy. For each noise level, four different motion profiles were simulated: high, medium, low, and no motion. The motion levels were classified by a set of real subjects’ mean frame-wise displacement (mFWD) inside the scanner (low: mFWD < 0.1mm, med: 0.25mm < mFWD < 0.4mm, high: 0.6mm < mFWD < 0.7mm) (Power et al., 2012). Generated fMRI scans consisted of 10 minutes of scanning with an in-plane acquisition matrix of 112 112, and 37 slices. The voxel size was set to 2 2 3 mm³. Since our real data are acquired with Philips scanner and with an interleave type in which every other $\sqrt{\gamma }$ slices are acquired, we also simulated the same interleave type by skipping 6 slices between any two consecutive slice acquisition. The default TR was equal to 2 seconds for these experiments. Thus, with 20 scans each simulated under 12 different conditions, we created 240 unique fMRI scans. In addition, 13 more fMRI scans were simulated and resampled at 6 different TR’s ranging from 0.5s to 5s for an additional 78 fMRI scans. In total, 338 fMRI scans were simulated for this study.

2.3 Real Data

The ideal task for testing the effectiveness STC should have high temporal sensitivity and a robust bold signal across all subjects. Higher level cognitive tasks are not robust enough across subjects, and it would be difficult to say for certain whether any changes in the statistics are closer to the true underlying neuronal activity or not. Block design tasks are typically more robust, but lack the temporal sensitivity necessary and would be unsuitable for examining small temporal inaccuracies (Sladky et al., 2011). Because the BOLD signal due to visual stimuli generates robust activation in the primary visual cortex, an event related visual stimulus was used for evaluation of STC methods using real subjects’ fMRI data. Thirty right-handed healthy subjects (17/18 young/old; percent female: 0.53/0.61, age mean ± std: 25.5/64.9 ± 2.4/2.2 years) were presented with visual (flashing checker boards) stimuli with random onset and duration (event-related design) while undergoing functional magnetic resonance imaging. To ensure attention to the stimuli, subjects were asked to respond with a button press at the conclusion of each visual stimulus. Functional images were acquired using a 3.0 Tesla Achieva Philips scanner with a field echo echo-planar imaging (FE-EPI) sequence [TE/TR = 20ms/2000ms; flip angle = 72 degrees; 112×112 matrix size; in-plane voxel size = 2.0 mm x 2.0 mm; slice thickness = 3.0 mm (no gap); 41 transverse slices per volume, 6:1 Philips interleaved, in ascending order. Participants were scanned for 5.5 minutes with at least 37 events of visual stimuli.

Subjects were stratified based on their mFWD over the entire scan period. Ten low motion (mFWD < 0.14 mm), ten medium motion (0.14mm ≤ mFWD < 0.2mm), and ten high motion (mFWD ≥ 0.2mm) subjects were selected for each group.

2.4 fMRI Data Processing and Statistical Analysis

Both simulated and real data were first motion corrected (spatial realignment) using rigid-body registration of all volumes to the middle one by FSL (mcflirt (Jenkinson et al., 2002)). Then STC (temporal realignment) was performed using our proposed FS method as well as the FSL and SPM default techniques. No other preprocessing steps were carried out, in order to minimize confounds. To have control over all aspects of the statistical analysis, we have developed a standard generalized linear model (GLM) in Python and used it to model observed fMRI data Y at each voxel as a linear combination of regressors X which were created by convolving the double gamma HRF with the stimulus function. The data is modeled as

$$\mathit{Y}=\mathit{X}\cdot \beta +\mathit{e}$$

where β coefficients were obtained using the least-square estimate and given by,

$$\beta ={({\mathit{X}}^T\mathit{X})}^{-1}{\mathit{X}}^T\mathit{Y}$$

To obtain the significance level of the voxel’s activation associated with the stimuli of interest, standard GLM statistical inference was performed to obtain the t-statistics for each voxel independently (Friston et al., 1995). We used voxel-wise t-statistics as the evaluation criteria for our method comparisons as well as investigating the effect of different acquisition settings and artifacts on the effectiveness of STC. All statistics used in the results are from this native-space, subject-level analysis.

For simulated data, we selected the left superior frontal (LSF) region as our region of interest (ROI). We chose this ROI because it spans 19 slices in the z-axis, covering a wide range of simulated delays, and also because it’s relatively large compared to other segmented gray matter ROIs. Furthermore, it spans from the tip of the frontal cortex to the middle of the brain, which will capture motion artifacts at various points in the brain. Only voxels in the LSF ROI were used in all simulated data analysis, and the known underlying BOLD signal assigned to the LSF ROI was used as our regressor. An LSF ROI mask was created from the template subject’s Freesurfer (https://surfer.nmr.mgh.harvard.edu/fswiki) segmented image.

For real data, such prior information of the underlying BOLD signal did not exist. Therefore an ROI mask has been generated in each subject’s native space to delineate the voxels that we expect significant activation (native visual ROI). These masks were generated by transferring the group level activation mask for the visual stimulus back into each subject’s native space. The group level activation mask was obtained by running a full default FSL first level analysis including: a) spatial realignment, b) STC, c) 3D smoothing with FWHM=5mm, d) intensity normalization, e) temporal filtering (125s cutoff), f) GLM with prewhitening. The parameter estimates and variance were passed into a default FSL mixed effects second level analysis including: a) spatial normalization, b) full Bayesian linear model, as described in (Beckmann et al., 2003; Woolrich et al., 2004), and c) cluster-wise multiple comparison correction (z threshold 2.3, cluster significance threshold p = 0.05). Only voxels in the native visual ROI were used in all real data analysis. It should be emphasized that this analysis was only used for masking purposes, and the statistics from it are never used in the results.

The STC comparison on simulated data was rather straightforward due to the fact that we had prior knowledge about the true underlying bold signal and well defined ROIs where our signals were generated. Real data is significantly more complicated to evaluate. We created a “gold standard” method to compare STC techniques by constructing a slice-dependent shifted regressor for each slice. These shifted regressors account for the slice dependent acquisition offset delay. In theory, the slice-dependent shifted regressor should produce the best results in the absence of 3D smoothing. To have a fair comparison the fMRI time series is upsampled and filtered with the same lowpass filter we used in the FS method, since all the STC methods discussed here have inherent lowpass filtering.

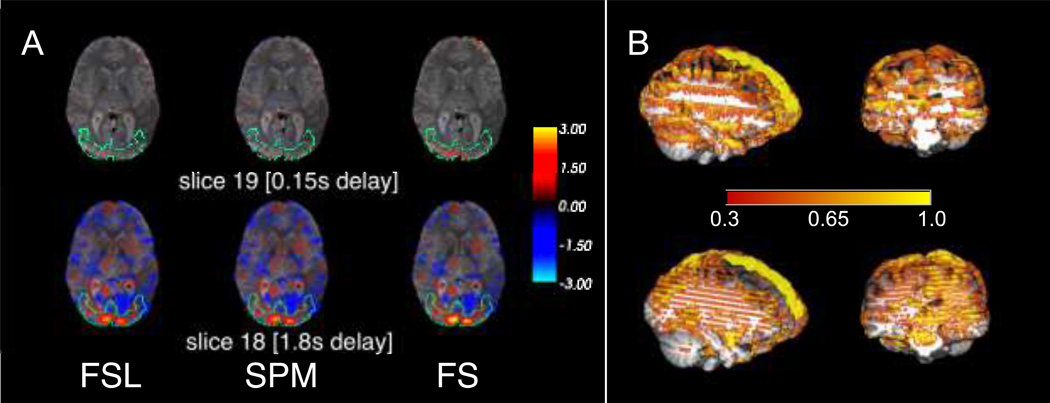
Another challenging aspect of evaluating STC methods is its slice-dependent gain. We demonstrated this challenge by showing how the improvement due to STC was dependent on the acquisition offset delay in typical real subject’s fMRI data. We selected two adjacent brain slices with maximum offset delay difference from the area of highest activation due to visual stimuli. While both slices present the same level of activation, we expect the slice with low offset delay to show significantly less improvement due to STC than the high offset delay slice (see Figure 4). For this reason, all evaluations in this work were performed in the following manner. For any given subject, the same 20 voxels were compared across all STC methods. These were selected by identifying the 20 voxels with the highest t-statistics from the parametric map generated by the gold standard. Furthermore, only voxels from a slice with high delay in either the native visual ROI or the LSF ROI were considered for this selection. This identifies the 20 voxels whose signal most resembles our regressor. For real data, we identified slice 17, and for simulated data we identified slice 18 (1.78s delay from first slice for Philips interleave 6, 1.46s delay from first slice for even-odd interleave). We then extracted the t-statistics of those same 20 voxels for every other method of STC. Voxel selection ROI’s were the same as mentioned previously: LSF for simulated data and the native visual ROI for real data. We then used a pair-wise t-test on these values to compare the effectiveness of each method in each level of motion.

Figure 4. Difference in t values between STC and uncorrected data on two adjacent slices with different acquisition delays in real data.

The benefit of STC varies from slice to slice, depending on the acquisition delay. A) Two adjacent slices exhibit very different STC results. Slice 18 (1.8s delay) has t values significantly larger than those in uncorrected data with differences as large as 3. Slice 19 (0.15s delay) has very few differences from uncorrected data. Note that because this is a difference map, this simply indicates that all methods, including uncorrected, perform similarly well on low-delay slices. B) A 3D visualization of the difference between t values in the FS STC data and uncorrected data. The stripes along the z axis are present at high acquisition delay slices in data collected with Phillips interleave 6 (top), and even-odd.

2.5 Comparison of FS with the existing STC methods

The goal of this experiment is first to show the necessity of performing STC on fMRI data, and then to demonstrate the superiority of our proposed optimal STC technique (FS) in comparison to the exiting ones using simulated and real data. In addition, we investigated the effect of fMRI artifacts (involuntary head motion and noise) on the effectiveness of performing STC on fMRI data. For simulated data, three different levels of noise and four different levels of motion were synthesized to contaminate the fMRI data, as explained in section 2.2, whereas in real data we stratified subjects based their head motion profile to three different levels as explained in section 2.3.

Data corrected with four different STC methods (the gold standard shifted regressors (SR), proposed FS, and FSL/SPM default interpolation based methods), as well as uncorrected data were fed to the processing pipeline explained in section 2.4 to generate five parametric maps for each condition in both simulated and real data.

For each combination of motion and noise level in simulated data we obtained the activation parametric maps associated with one regressor containing the underlying neuronal stimuli for the LSF ROI for simulated data and the visual stimuli timecourse in real data. We used the voxel-wise parametric maps (t-statistics) in the aforementioned ROI obtained from uncorrected and slice timing corrected fMRI data as the evaluation metric in our comparison. Higher t-statistics indicates the superiority of a method as compared to the others since it could recover the original underlying BOLD signal with more accuracy.

The interaction between STC gain and level of motion/noise can also be examined using the voxel-wise t-statistics. We anticipate that increasing motion will reduce the benefit of STC, since motion has much higher destructive effect than the slice timing offset delay. If increasing the motion/noise level would result in smaller t-statistics, then we can conclude that there is a significant interaction between the STC gain and level of motion/noise.

2.6 STC on fMRI data with short length

Because FS STC employs a filter (908 order filter at 20Hz), there is an inherent initialization period that cannot be ignored. The number of samples in the initialization period of a filter is equal to its order. At 20 Hz, a 908 order filter is equivalent to 45.4 seconds initialization time. In our studies, all fMRI data have a TR of 2s (0.5 Hz). This makes the initialization period roughly equal to 23 volumes in an fMRI time series.

Our method is employed with substantial padding to avoid any such problems; however, scans with fewer time points may be more susceptible to initialization artifacts. If the data is not padded sufficiently, or is padded incorrectly, this initialization period may introduce artifacts into the data, reducing its accuracy. We examine the validity of our method as compared to FSL and SPM STC techniques, as they have no initialization period. Our goal then is to show that the statistics from our method remain in agreement with FSL and SPM, two of the most widely used software packages available, for all practical scan lengths.

As the number of samples in a scan decreases, the statistical power of the measurement also decreases. By reducing the number of time points in a scan, we expect to see the statistics gradually decrease. Because our method employs an FIR lowpass filter with a large initialization period, we would also expect that once the time series is short enough that the half-length mirrored padding becomes shorter than the filter order, our method will begin to perform significantly poorer than the others. This was experimentally tested on a subset of 5 simulated subjects (no motion, no noise) as well as 5 real (low motion) subjects. Both the real and simulated data were truncated step-wise with decremental steps of 10 volumes, down to a length of 20 volumes. After each truncation, STC and a GLM regression were run, and the statistics were saved for further analysis. As described in section 2.5, the voxels with the top 20 t-statistics were extracted from SR method within the real/simulated ROIs in the full-length data case, and the same voxel’s t-statistics were used from each truncated data set.

2.7 STC on short and long TRs

It has been suggested that for short (<2s) TRs, the benefit of STC is not worth the possible errors introduced by the process (Poldrack et al., 2011). With modern multi-echo pulse sequences able to acquire images with very short TRs on the order of hundreds of milliseconds, it is important to address the usefulness of STC on data with high temporal resolution. We examined the benefits of STC on various TRs. To do this, we simulated 13 additional subjects with low motion and low noise, in the same manner as described in section 2.2 (10 minute scan with random event related stimuli). Each subject’s high-resolution BOLD signal was resampled at 2, 1, 0.5, 0.33, 0.25, and 0.2 Hz, to simulate TRs of 0.5, 1, 2, 3, 4, and 5 seconds. This resulted in 6 data sets per subject. The full 10 minutes were sampled at each TR value so that the length of the simulated scan varied as a function of TR. We then performed all 4 STC methods on each subject’s data. Each TR was separately evaluated by identifying the top 20 voxels from the shifted regressor method as described in section 2.4. The values of these voxels were then extracted across all other STC methods in the TR. This was repeated for all TRs, and the average t-statistics of each STC method were plotted as a function of sampling rate.

3. Results

We first start by showing the slice dependency of the STC gain, which justifies our method of comparison based on focusing on slices with maximal offset delay in the activated area. Figure 4 shows the difference in t-statistics before and after STC on two adjacent slices with maximum offset delay difference (slices 18 and 19 with 1.78 and 0.15 seconds offset delay respectively) in real data after being smoothed with a 5mm 2D Gaussian kernel. Warm colored areas indicate an improvement in t-statistics compared to uncorrected data. This illustrates the challenges involved in evaluating STC methods using real fMRI data over one typical subject’s brain morphology. Figure 4A shows that the t-statistics in slice 19 have very little benefit from performing STC, as the difference between the uncorrected statistics is small. However, their adjacent voxels in slice 18, even though they presented the same level of activation (delineated by green lines in Figure 4A), have significant improvement over uncorrected data. The decreases in T value compared to uncorrected data (blue regions) do not indicate poorer performance on the part of the STC data. A decrease in T statistics can be an improvement in the following ways: 1) An uncorrected time series from a voxel unrelated to the task is erroneously correlating with a regressor (Type I error), and this correlation is removed or reduced after the time series is shifted during STC, or 2) An uncorrected time series from a voxel that is negatively correlated to the task is erroneously calculated to be uncorrelated (Type II error), and the correlation can be seen after the time series is shifted during STC. An example of this would be with the default mode network, which has significant deactivations. STC is going to improve the deactivations t-stats by making them more negative, which shows up as a reduction in t-stats.

This clearly demonstrates the slice dependency of STC performance. Figure 4B visualizes the same concept in the 3D view of the slice with both Philips interleave (top), as well as even-odd (bottom), where the color overlay represents the t-statistics difference between STC data and uncorrected data. Note that in regions of activation, this difference is significantly higher than the color bar indicates. In order to show whole-brain differences and capture the spatial pattern induced by interleaved acquisition, the threshold has been set artificially low. It is clear from this figure that slices acquired in the beginning of the TR benefit significantly less from STC than slices acquired at the later time. The same phenomenon has been shown for sequentially acquired data in previous studies (Henson et al., 1999). Therefore, only voxels within slices that were acquired with large offset delay and located inside the activated ROI are selected to have the most effective comparison.

3.1 STC Method Comparison

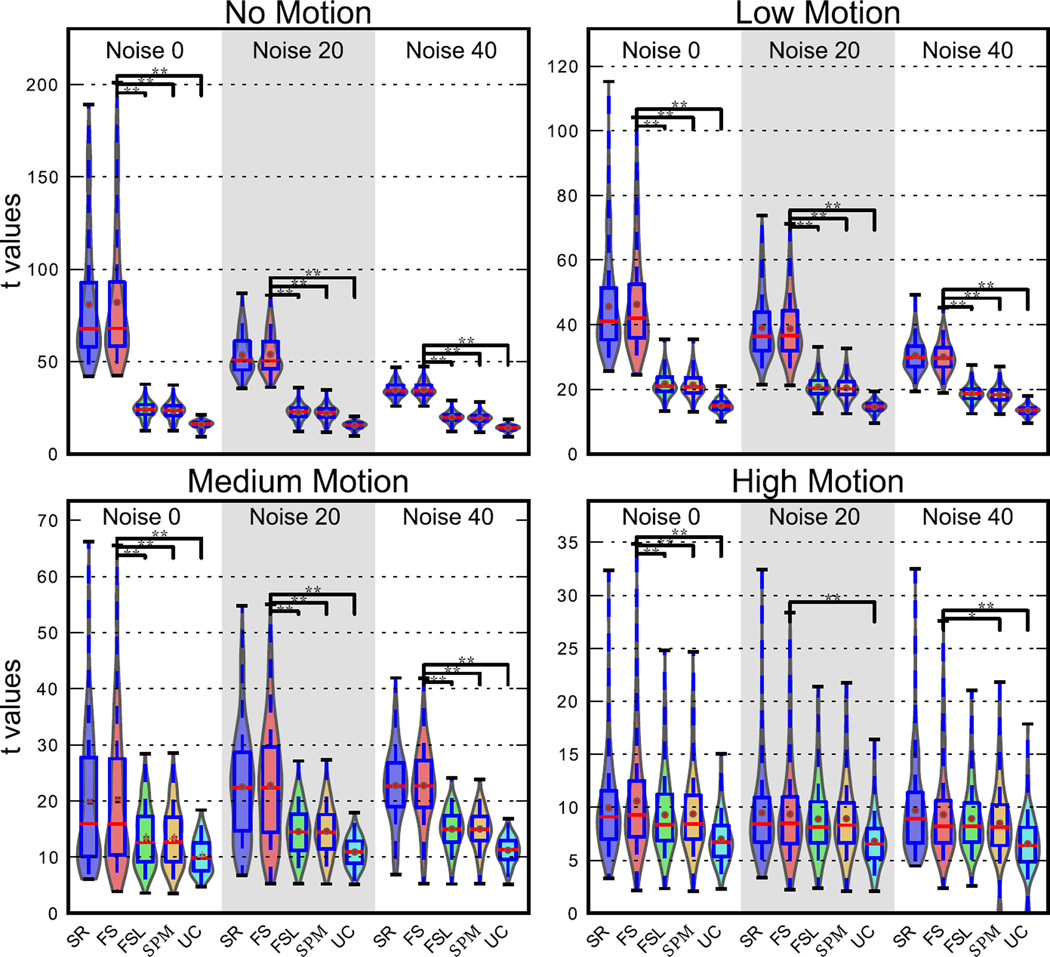
Figure 5 shows the t-statistics from the parametric maps obtained from uncorrected and STC simulated data (Philip’s interleave). The fact that for all conditions the mean t-value for STC data is always greater than the mean t-value for uncorrected data indicates that it is always beneficial to perform STC. Specifically, Figure 5 shows that FS STC outperforms all other methods, except for in high motion/high noise conditions. In the no motion, no noise case, which has the most optimal conditions for signal reconstruction, FS t-statistics were 415% higher than uncorrected data, while FSL and SPM were 51% and 47% higher respectively. FS yields significantly higher t-statistics than all other STC methods (p<0.001) for all levels of motion and noise, except for high motion with 20% and 40% noise levels. At high motion and no noise, FS still significantly outperforms FSL and SPM, where FS t-statistics were 51% higher than uncorrected data, and FSL and SPM were 32% and 33% higher respectively. Adding noise to this condition reduced all the t-statistics to a point where the differences were insignificant (p>0.05). Still, the high motion and high noise case shows that the application of any STC is still beneficial, and each method improved the t-statistics by on average 33%.

Figure 5. voxel-wise t statistic comparison from STC data and uncorrected data in the LSF ROI in simulated data for various noise and motion levels with interleave 6.

STC was carried out with three methods: FSL, SPM, and FS. The analysis was carried out for high, medium, and low motion cases, as well as three different SNR conditions (Noise 20 indicates that 20% of the signal’s energy is from white noise, and so on). Each violin plot contains values from 20 scans. Higher values indicate that a STC method had higher z scores than data that was analyzed with no STC. Two stars indicate that these z differences are also significantly different from our method (FS), t<0.001, one star indicates significance p<0.05.

The twofold interaction of noise and motion on STC gain is also shown in Figure 5. The effect of adding noise to data is that the average t-statistics decrease linearly, but at different rates. This results in lower variance between methods, meaning they all improve the t-statistics more similarly. While the variance of the mean t-statistics between STC methods decreases exponentially, meaning all methods become more similar in performance. In reference to the no noise no motion case, mean FS t-statistics decrease 34% and 54% with the addition of 20% and 40% noise respectively (noise 20 and noise 40 in Figure 5). FSL and SPM both decrease 6% for the noise 20 case and 17% for the noise 40 case. Finally, uncorrected data reduces just 3% and 12% respectively.

Motion has a similar effect, in that it decreases the average t-statistics and reduces the variance; however, its overall effect is larger. From the no noise no motion case, the addition of low, medium, and high motion reduces FS t-statistics by 44%, 75%, and 87% respectively. FSL’s t-statistics were reduced by 11%, 44%, and 61%, while SPM’s t-statistics were reduced by 9%, 43%, and 58%. Finally, uncorrected data was reduced by 6%, 36%, and 55%. The variance of the mean t-statistics for each method also decreased much faster with the addition of motion. It’s clear from these results that the presence of noise and motion both reduce the effectiveness of all STC techniques, however FS remains significantly better for most cases, and never performs worse than FSL or SPM, even in the high noise/high motion case. It should be emphasized that by using simulated data, these results were obtained while controlling for differences in baseline fMRI activity and brain morphology, both of which have a stronger deteriorating effect on the results than the offset delay in slice acquisition.

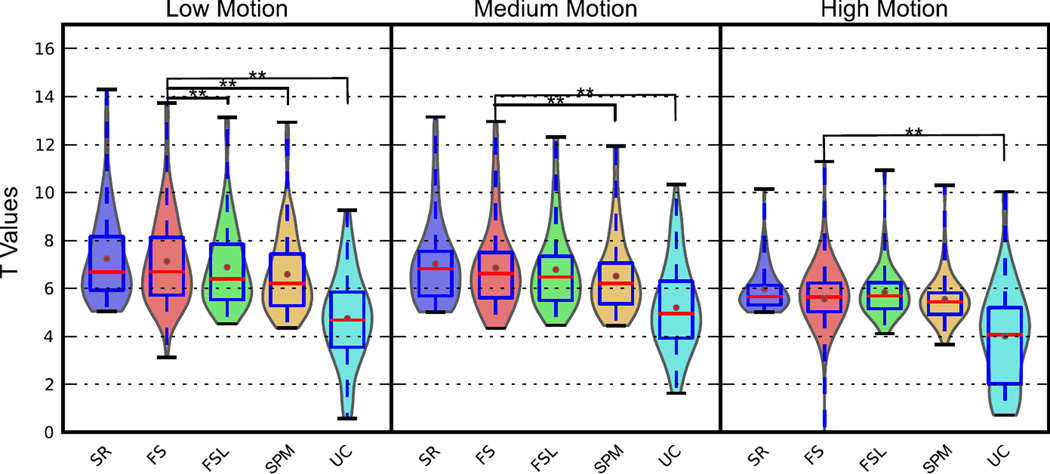
Figure 6 shows the t-statistics from the top 20 voxels in slice 17 in the SR (gold standard) case, extracted from all methods from real data. As with the simulated data, Figure 6 shows that STC is always beneficial in processing real fMRI data, regardless of the technique, even though the degree of its improvement significantly decreases with any increase in the level of motion. With low motion, t-statistics from FS were 33% greater than uncorrected, while FSL and SPM were 31% and 28% greater, respectively. This illustrates the superiority of the our proposed FS method as compared to the FSL and SPM methods, since the voxel-wise paired t test shows a significant increase in the t-statistics of the resulted parametric maps with FS (p<0.001). Higher levels of motion decrease these values and the differences between them, and in the medium level of motion the t-statistics from FS are only significantly higher than SPM and uncorrected data. Finally, in high motion subjects FS shows no significant superiority to the other STC techniques (p>0.05) whereas it still significantly improves the t-statistics in comparison to uncorrected data (p<0.001). The t-statistics from subjects with medium motion were on average 4% lower in FS, and 1% lower in FSL and SPM, as compared to the low motion subjects. High motion subjects had t-statistics 19% lower for FS, 14% lower for FSL, and 15% lower for SPM.

Figure 6. Voxel-wise t statistic from STC data and uncorrected data in the visual ROI in real data for various motion levels with interleave 6.

The top 20 voxels from the Shifted-Regressor method were identified from the slice with high delay (Slice 17) that intersected the region of significant activation. The values from these voxels were then extracted from all other STC methods for comparison. (30 subjects’ real data with three levels of motion.) Methods that are significantly different than the proposed method (p < 0.001) are indicated with a star, pair-wise t-test.

Figure 6 also presents the results of the gold standard (SR) STC method. In all levels of motion, FS performed closest to the SR method, indicating that it is more optimal than FSL and SPM.

In real data, the contamination from thermal noise, motion, and physiological noise is much more complex than in the simulated data. It is also apparent from this that the effects of motion are not as obvious as in the simulated data due to the additional sources of contamination in real data.

3.2 Effect of Scan Length on STC

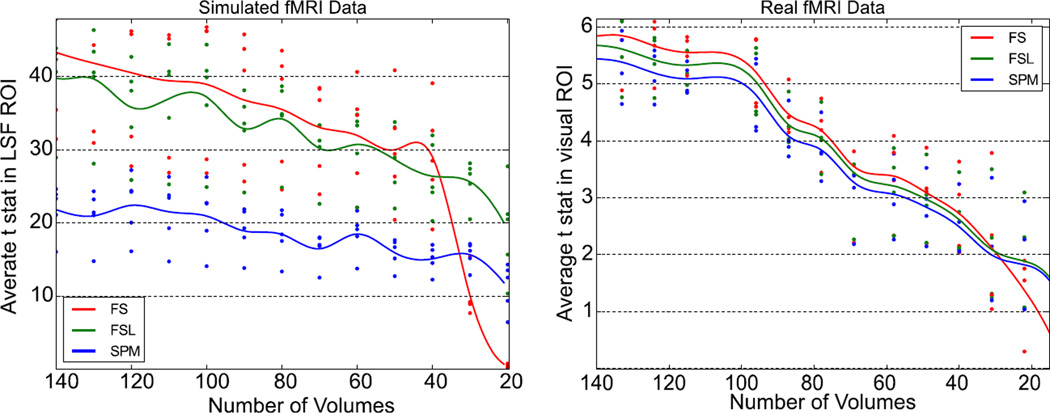
Figure 7 shows the top 20 voxel’s mean t-statistics from five low-motion subjects plotted against the length of the truncated signal for both real and simulated data. As expected, our method performs better than both FSL and SPM for the majority of the scan lengths. In the simulated data, the fluctuations in the statistics from FSL and SPM appear to be exaggerated. This is likely due to the sensitive nature of the GLM on a very clean signal. Similar fluctuations are present in the FS data, however the amplitude is much lower. In the real data, we see a much better example of how all the statistical methods have similar slope at each point. This is important, as it verifies the consistency and reliability of each method against the others. In both the simulated and real data, there is a critical scan length where the FS method no longer outperforms FSL and SPM. In real data, this value is at approximately 30 time points, which is comparable to the calculated length of the filter’s initialization period, 23 scans. For the simulated data, FS performs worse than FSL at 38 time points, and performs worse than SPM at 33. Given how well the statistics agree for all lengths greater than this, we can assume that this divergence is due to the required half-length mirror padding required for initialization for low pass filter in the FS method.

Figure 7. Performance of STC methods compared to the length of the initial fMRI time series on simulated and real data.

(Left) Simulated data: top 20 t statistics vs length of scan by method for five subjects, extracted from the slice with maximum delay (slice 17) in the region with significant activation. Divergence between our STC method and controls occurs at ~ 38 volumes. (Right) Real data: top 20 t stats vs length of scan by method for five subjects. Divergence occurs at ~ 27 volumes

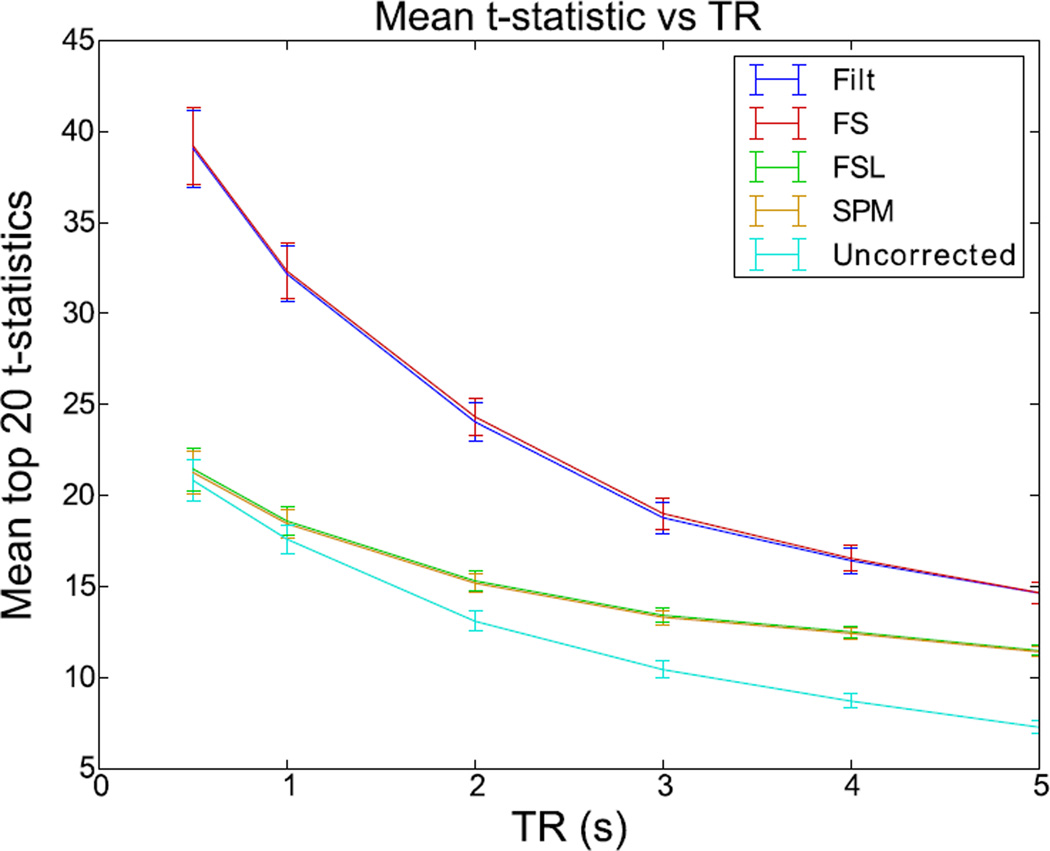
3.5 STC and TR

Figure 8 shows the mean t-statistics of each method from the experiment described in section 2.9 plotted as a function of TR. As the TR increases, the average t value of the selected voxels decreases in all slice timing methods, including the shifted regressor and FS. Uncorrected data decreases significantly in their t-statistics as the TR increases due to an increasing temporal misalignment between the model-predicted signal and the observed fMRI signal, as well as the general effect of a lowering number of sample points. In addition, we expect the difference between the STC data and the uncorrected ones to increase with TR, as an indication of the benefit of the STC. Even though this is the case for FSL and SPM STC data, we do not see such behavior for SR and FS STC data. This is in agreement with the sentiments from the literature that there is minimal benefit of STC for TRs less than 2s for FSL and SPM STC methods (Poldrack et al., 2011). At a TR of 2, FSL and SPM are performing 15.6% better than uncorrected data, while SR and FS perform 85.6% better. These values gradually increase, to where TR=5, FSL and SPM perform 55.7% better than uncorrected, while SR and FS perform 101.1% better. For the lower TRs of 1.0 and 0.5 seconds, FSL and SPM converge to the uncorrected data, to where the difference becomes insignificant (a 5% and 2.2% difference respectively). However, SR and FS continue to outperform uncorrected data by 83.2% for a TR of 1s, and 88.0% for a TR of 0.5s. This is mainly due to the aliasing of the physiological signals in fMRI data into the frequency spectrum of the BOLD signal. By increasing the sampling rate, the aliased artifacts from physiological noise move outside the BOLD signal spectrum, and can be removed by filtering with same cutoff frequency (0.21 Hz).

Figure 8. Effect of increasing TR on the STC gain on simulated data.

T values from LSF region in simulated data with TRs varying from 0.5 to 5 seconds extracted from a slice with maximal delay (slice 18). Error bars represent the 95% confidence interval, calculated from the extracted t values for each method across all 13 subjects.

4. Discussion

Reconstructing a true underlying signal from its sampled version by upsampling and lowpass filtering has been a common practice in digital signal processing field for quite some time (Parker et al., 1983; Proakis and Manolakis, 1988). However, such a simple and optimal technique has not been fully utilized in fMRI data processing. Using a sampled version of a signal in fMRI data is definitely more convenient and practically more feasible. Upsampling the fMRI data from typical TR=2s (0.5 Hz) to 20 Hz will increase the size of the fMRI scan 40 times. This means typical 200 Mbyte fMRI data file will increase in size to 8 Gbyte. Just loading such a huge data will crash many of today’s computers. In addition, fMRI data contains many contaminating artifacts and noises (e.g. cardiac and respiration), which might have a dynamic and much broader frequency spectrum which essentially complicate the optimal signal reconstruction process. Considering all practical issues one might conveniently decide to process the sampled version of the signal instead of going through the complete signal reconstruction process. In this paper we showed that one of the benefits of performing complete signal reconstruction is that it circumvents the need for sub-optimal interpolation based STC. It also eliminates the lowpass filtering step which is part of many fMRI data analysis pipelines. To address the practical feasibility, we implemented the method in a way that the final results are always saved in a down sampled version whereas all the processing is performed on the upsampled and fully reconstructed data. The current version the Python code takes 8 minutes to process each slice on each computing node (12GB Memory, two 8 core Intel Xeon CPU’s 2.4GHz). With full parallelization it should not take more than 8 minutes to run for entire volume. Optimizing the code and converting to C will eventually lower the execution time significantly.

We have demonstrated the benefit of STC on fMRI data in both real and simulated data which had already been shown in the literature (Calhoun et al., 2000; Henson et al., 1999; Sladky et al., 2011; Vogt K et al., 2009). However, the slice-timing problem is fundamentally intertwined with many confounding factors such as involuntary head motion during scanning. Because of all the interactions between these factors, it’s often difficult to intuitively say if slice-timing correction would provide any benefit to the analysis. We examined the effect of motion on the effectiveness of STC, and showed that even though the effectiveness of STC deteriorates with increasing levels of artifacts it still remains beneficial to be executed as a preprocessing step. In addition, we showed that our proposed method (FS) outperformed both FSL and SPM’s STC in every case, aside from the highest level of motion. However, the achieved STC gain became very small when addition artifacts such as motion and noise are introduced. It should be emphasized that while all interpolation can be represented as upsampling, filtering, and downsampling, it is the shape of a kernel’s frequency response H(ω) that determines the quality of the reconstructed signal. A perfect boxcar frequency response (dashed line in Figure 2) would perfectly reconstruct the sampled signal, reducing interpolation error when resampling at an offset. Therefore, the interpolation kernel with a frequency response that most resembles the dashed line will most accurately reconstruct the sampled signal.

Simulated data showed the absolute superiority of our proposed FS method in optimal and even slightly noise/motion-contaminated conditions. In real data, FS still outperformed the existing method, however the gain was much smaller than in simulated data with the same level of motion contamination. This suggests that there are remaining harmful sources of error that we have not taken into account in our simulation. The differences in brain morphology or the disturbance in the homogeneity of the magnetic field due to other factors may be some of these sources. Despite this, our method generated better than or comparable results to the existing STC methods for all level of motions in real data. Studies may acquire subjects with higher levels of motion than those here, but we can gather from the simulated data that it’s unlikely FS will ever perform worse than FSL or SPM. In fact, the highest noise/motion level present in our subjects (mFWD > 0.6mm) has been shown to cause un-resolvable problems in functional connectivity analysis of resting state fMRI data, so it’s unlikely that data with significantly more noise/motion would be considered useable (Power et al., 2012).

Although very short scan lengths did have a significant impact on the FS STC technique, there was no detectable effect on scans until the scan length is shortened to about 35 time points. Typically, fMRI scans are much longer than this, and it would be very rare for this case to present itself in a research or clinical study. Furthermore, it’s possible that a more sophisticated padding routine could further improve upon this method. Presently, the length of the scan determines padding, where ½ the scan length is padded on either end of the signal, doubling the scan length. In future work, padding could be determined by the order of the filter. To show that the proposed FS method is in fact an optimal method that produces the same results as the gold standard (SR) technique, we chose a very high order FIR filter. However, this filter order can be reduced significantly with tolerable amount of inaccuracy. One can anticipate that with tolerating only 5% error, the filter order would drop one order of magnitude, which essentially is equal to two or three volumes for filter initialization. Regardless, it takes about two to five volumes acquisition for the net magnetization to reach its equilibrium which often requires discarding the first few volumes from fMRI data. Another possibility is to use infinite impulse response (IIR) filter, which requires much lower order filter to achieve the same level of accuracy. However, one might face the non-linear phase issue of the IIR filter, which needs to be addressed before being able to utilize it for fMRI data.

Both of our simulated and real data are based on event-related design, which requires fast (< 5 s) and random stimuli duration. Conversely, block-designed experiments have much longer (>10 s) stimulus duration, thus making it less susceptible to the acquisition offset delay (<TR). It is already shown in the literature that block design accompanying with moderate 3D smoothing may not benefit substantially from STC (Sladky et al., 2011). Therefore we decided not to repeat that experiment again in this work. Nevertheless, extremely high TRs (TR>5s) could not be tolerated even for block-designed experiments and might require STC.

TR proved to play an interesting and significant role in STC. For traditional interpolation techniques, we were able to show that the benefit of STC is indeed minimal and insignificant at very short TRs. It may seem unusual that SR and FS STC do not converge with the other methods as the TR decreases. In theory, the errors introduced by interpolation through FSL and SPM’s STC should become smaller and smaller, and approach the quality of the proposed FS method. Additionally, the sampling rate should not affect the quality of the shifted regressor or FS as long as the signal is band limited and the sampling rate is twice the Nyquist frequency.

The inherent low pass filter present in our method is responsible for the significant increase in t statistics at shorter TR. The BOLD signal contains high-frequency physiological noise, which can alias into the BOLD signal bandwidth, contaminating the signal in a way that cannot be removed by lowpass filtering. Increasing the sampling rate decreases the amount of aliased noise, until all the contaminants lie outside the pass band. Once the noise is outside of the passband, the filter is significantly more effective, and is able to remove more noise from the signal. In our simulated data, the frequencies chosen for physiological noise alias into the pass-band of our filter for TRs of 5, 4, and 3 s. This further attributes to the degradation of the average t value in these methods. Finally, while you may expect the average t-statistics to converge for all methods when the TR becomes small, the cutoff frequency remains constant at 0.21 Hz for every TR in FS. In interpolation based STC (FSL, and SPM), the interpolation kernel expands with increasing sampling rate, encompassing almost the entire sampled frequencies in the pass-band. Thus, as the aliased artifacts move out of the 0.21 Hz range, our method is able to effectively remove all of our simulated physiological noise through lowpass filtering, while FSL expands the pass-band, which encompasses both higher frequency physiological and thermal noises. If such filtering were to be done on the data before FSL or SPM STC was performed, it is likely that the statistics would be more similar to the SR and FS method. Furthermore, while the overall t values are lower for all methods at a high TR, the percent improvement is larger, suggesting that STC is very important in these conditions, regardless of whether filtering is carried out or not. In the future, this method can be tested on real data with various low and high TRs.

One shortcoming of this method is that it still treats STC as an independent procedure from motion correction, when in reality there is significant interaction between the motion correction and STC problem. STC is not independent of motion correction, and vice-versa, however they have traditionally been treated as such. Lately, there has been a significant amount of work done to address this problem, either by accounting for the slice acquisition time in the motion correction routine (Bannister et al., 2007; Beall and Lowe, 2014), as well as attempting to combine the motion correction and STC processing steps, and simultaneously solving for both (Roche, 2011). Other methods examine which native space slice each voxel came from in the motion corrected volume (Jones et al., 2008). By taking into account the true sampling delay of each voxel, an accurate voxel-wise estimate of physiological noise can be created to account for such delays. Future work could involve studying how to integrate motion correction and STC methods that take into account orientation and slice acquisition time in an attempt to resolve these interactions.

5. Conclusion

Based on a signal theory approach of sampling and reconstruction, we have proposed and developed an optimal signal recovery technique. This optimal method has the disadvantage of requiring significant padding, which results in increased computation time. From these data sets, we have shown that our method resulted in significantly higher t-statistics over all noise conditions, as well as low and medium motion conditions. Motion proved to be the largest source of contamination in the simulated data, and also greatly reduced the effectiveness of all STC techniques in real and simulated data.

Future work involves examining STC with multiband image acquisition, as it’s currently assumed that the TRs are short enough to completely forgo STC. We further hope to examine the padding performed on data for the FS method in hopes that the minimum volume limitations can be improved on.

This paper provided an in-depth look at many common situations in which STC may be implemented. We have shown that in all such cases, STC is a valuable addition to the preprocessing pipeline. We were able to optimize STC and eliminate the error introduced with traditional interpolation methods, which significantly increased voxel wise statistics due to a more accurate reconstruction of the true BOLD signal.

Highlights.

• We propose a new, optimal method of preforming slice timing correction (STC)

• We simulate 338 fMRI images, and acquire 30 real images to evaluate our method

• We examine the effect of noise, motion, and scan length on STC

• Our method outperforms FSL and SPM’s method except in high motion