Diamond Family of Nanoparticle Superlattices

Abstract

Diamond lattices formed by atomic or colloidal elements exhibit remarkable functional properties. However, building such structures via self-assembly has proven to be challenging due to the low packing fraction, sensitivity to bond orientation, and local heterogeneity. We report a strategy for creating a diamond superlattice of nano-objects via self-assembly, and demonstrate its experimental realization by assembling two variant diamond lattices, one with and one without atomic analogs. Our approach relies on the association between anisotropic particles with well-defined tetravalent binding topology and isotropic particles. The constrained packing of triangular binding footprints of truncated tetrahedra on a sphere defines a unique three-dimensional lattice. Hence, the diamond self-assembly problem is solved via its mapping onto two-dimensional triangular packing on the surface of isotropic spherical particles.

The diamond lattice holds a special significance among known crystal structures as it is simultaneously simple, yet non-trivial. Tetravalent atoms, such as carbon or silicon, and molecular system like water, form this lattice under appropriate conditions. However, due to the openness of the lattice, whose volume fraction is only 34% of the hard-sphere limit, higher density packings frequently prevail. The structure of atomic diamond gives rise to its unique properties, such as extreme mechanical hardness, and a combination of high thermal conductivity and electrical insulation(1). The immense historical interest in colloidal diamond lattices has been due to the predicted optical response, in particular its potential application as a full three-dimensional (3D) photonic band gap material(2). Yet, building 3D diamond lattices from nano- and micro-scale particles by means of self-assembly has proven to be remarkably difficult.

Computationally, it was predicted that a delicate balance of isotropic interactions and packing effects might permit the formation of diamond(3–6). Indeed, diamond-like structures of isotropically interacting systems were observed in polymers(7, 8) and in a binary system of charged nanoparticles (NPs)(9). However, the interactions are typically highly system-specific; thus, it is difficult to generalize such a strategy for the rational assembly of a diamond lattice. Alternatively, engineered anisotropic interactions have been considered. For example, precisely truncated tetrahedra were computationally predicted to show a diamond lattice(10). Micron-scale colloids with tetrahedrally-arranged binding sites(11), known as “patchy” particles, were developed experimentally (12–14). Similar to the tetrahedral symmetry of covalent bonds in atomic systems, e.g. carbon or silicon, such patchy particles should naturally form diamond lattices. However, recent computational studies proved that at equilibrium, cubic diamond (CD) is degenerate with its hexagonal counterpart when there are only short-range interactions(12). Moreover, both these structures compete with an amorphous tetrahedral “liquid”, which is thermodynamically favored unless the bonding is highly directional(15–17). Free rotation about bonds easily introduces defects, including a mixture of both cubic and hexagonal local structures, leading to a kinetically-arrested, disordered state. Thus, tetrahedral motifs on their own are not sufficient for the robust assembly of a diamond crystal. Furthermore, the high sensitivity of the lattices to the position of binding spots imposes exceptionally stringent requirements on the fidelity of particle fabrication. Combined, these complications have hindered the rational assembly of diamond from either micro- or nanoscale particles.

Here, we demonstrate self-assembly of nanoscale cubic diamond superlattices. In our approach, the 3D assembly problem is transformed into a two-dimensional (2D) packing problem, thereby bypassing the enumerated challenges. Specifically, our central hypothesis is that the assembly of a diamond structure might be realized without imposing strict requirements on the position, orientation and shape of binding spots, but rather by relying on the self-organization of the binding “footprints” of shaped particles on the surface of isotropic spherical particles (Fig. 1). Although this assembly scenario might seem hopelessly unconstrained, we demonstrate experimentally that our approach leads to the desired diamond structure, drastically streamlining the assembly process. In essence, the engineered topology of interparticle connections encodes a 3D lattice, due to the unique way the footprints of these particles can organize on the surface of the isotropic particles. We show the fabrication of a family of lattices based on the diamond motif using NPs of different types.

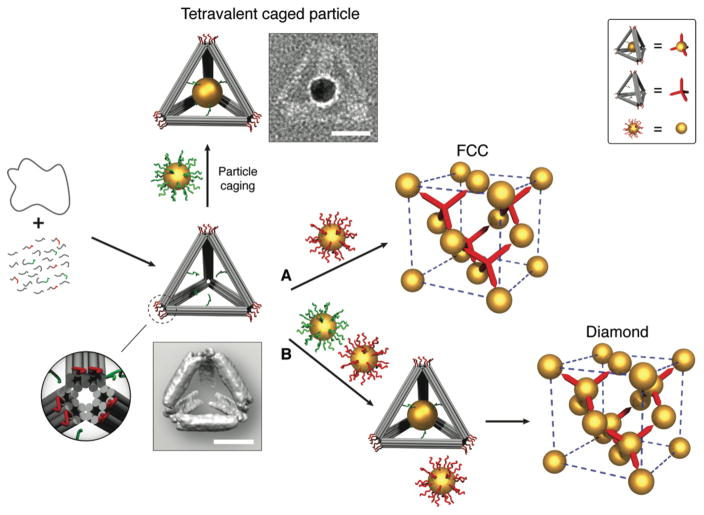
Fig. 1. Schematic illustration of the experimental strategy.

A circular single-stranded M13 DNA genome is folded by a set of helper strands to generate a rigid tetrahedral DNA origami cage containing two sets of sticky-ended DNA strands. One set (green) is projected from the inner faces of the edges, functioning as an anchor to encapsulate and hold the guest particle (uniformly coated with green strands) inside the cage; another set (red) is installed at each vertex of the tetrahedral cage, acting as a sticky patch to provide binding to the basis particles (uniformly coated with red strands). Zoom in: a detailed view of the vertex (truncated) of the tetrahedron cage; image blow the tetrahedron model: a reconstructed cryo-EM density map of the tetrahedron. The guest and the basis particles coated with corresponding complementary DNA can either individually interact with the tetrahedral cages to form tetravalent caged particles and FCC superlattices (route A, empty cages) respectively, or together hybridize with the tetrahedral cages to create diamond crystals (route B, with caged particle). A representative of a constructed tetravalent caged particle is shown in a negative-staining TEM image beside the model. Top right box is a visual definition of the system components for simplified illustration of shown FCC and diamond superlattices. Scale bars, 20 nm.

Given its unique selectivity of interactions and structural plasticity, DNA provides a versatile tool for the programmable assembly of finite-sized and extended nanoparticle structures(18–22) and close packed lattices(23–26). Our strategy allows for assembly of the diamond family of lattices by employing tetrahedral cages, constructed using DNA origami technology(27, 28), as topological linkers between isotropic NPs. Since the size of the origami structure is comparable to a nanoparticle diameter, the tetrahedral linker can be viewed practically as a vertex-truncated tetrahedron (see zoom-in view in Fig. 1) with a triangular footprint, which can bind to the isotropic DNA-coated gold NPs via hybridization (Fig. 1).

Isotropic particles and tetrahedral origami self-assemble into an open face-centered cubic (FCC) lattice (Fig. 1, route A). By caging an additional NP inside each tetrahedron, co-assembly with uncaged, isotropic NPs (Fig. 1, route B) instead gives rise to a diamond lattice.

The DNA origami tetrahedron cage is constructed with each of its six edges containing a rigid 36-nm 10-helix bundle (Fig. 1) with cross-section of ~ 9 nm × 6 nm. This design creates roughly triangular footprints at the vertices, which contain 6 dangling single-stranded (ss) DNA (red strands in Fig. 1) for binding of isotropically DNA-coated “basis particles” (melting temperature for DNA links T_m ≈ 42.3 °C). Selected tetrahedral edges are encoded with a different ssDNA sequence that projects toward the interior (green strands in Fig. 1). These internal strands contain ssDNA overhangs (T_m ≈ 48 °C) that anchor the “guest particles” (up to ≈ 26 nm in diameter) inside the tetrahedra, forming tetravalent caged particles (see supplementary materials for details). To achieve single particle encapsulation, we used gold NPs with a core diameter of 14.5 nm (excluding DNA shell).

We examined the assembled constructs using transmission electron microscopy (TEM). The structure of the DNA origami tetrahedron was resolved using cryo-EM and single-particle 3D reconstruction techniques; showing excellent agreement between reconstruction and design (Fig. 1 and fig. S3A). Negative-stain TEM images reveal the high-fidelity positioning of the central guest particle within the tetrahedron, as well as the undistorted cage-particle construct (Fig. 1 and fig. S3B).

We asked whether these nano-components—basis isotropic particles, tetrahedra, and tetravalent caged NPs—could be assembled into superlattices. We first tested the assembly of the basis particles (core diameter 14.5 nm) with the tetrahedral cages, whose vertices host complementary ssDNA (Fig. 1, route A). We mixed and annealed the two components, and probed the assembled structure by in-situ small angle x-ray scattering (SAXS). The 2D scattering pattern and the associated structure factor S(q) revealed a series of sharp scattering peaks. The ratio of the positions of the peaks (q ⁿ/q¹) matches $1:\sqrt{4/3}:\sqrt{8/3}:\sqrt{11/3}:2:\sqrt{16/3}\dots$, indicating the formation of a well-defined FCC lattice (Fig. 2, A and C). Our modeling of S(q), which accounts for particle size, origami dimensions, and lattice correlation length (see supplementary materials for a description of the SAXS modeling), is in excellent agreement with the experimental curve (29) (Fig. 2C, top channel, and fig. S10). Figure 2D illustrates how the basis particles are linked by DNA tetrahedra in the FCC lattice. The interparticle distance d is 71.9 nm, consistent with the spacing calculated from the sizes of our components (see detailed calculation in supplementary materials). Formation of the FCC lattice per se is remarkable, given the rotational freedom of the tetrahedra when they interact with isotropic particles in the lattice.

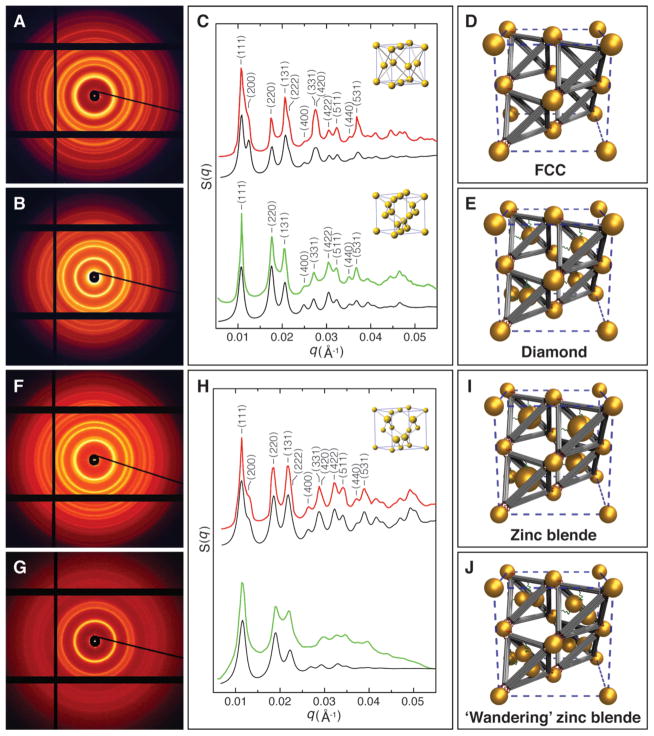
Fig. 2. SAXS characterization of the diamond family of nanoparticle superlattices.

(A) 2D SAXS pattern of the FCC superlattices constructed with basis particles (core diameter 14.5 nm) and tetrahedral DNA origami cages. (B) 2D SAXS pattern of the diamond superlattices formed from basis particles (core diameter 14.5 nm) and tetravalent caged particles (core diameter 14.5 nm). (C) Integrated 1D patterns. Top channel: Experimental (red) and calculated (black) 1D SAXS patterns for the FCC crystals. Bottom channel: Experimental (green) and calculated (black) 1D SAXS patterns for the diamond crystals. Insets are standard FCC and diamond unit cells respectively. (D) Unit cell model of the assembled FCC superlattice. (E) Unit cell model of the constructed diamond crystal. (F) 2D SAXS pattern of the zinc blende lattices constructed with basis particles (core diameter 8.7 nm) and tetravalent caged particles (core diameter 14.5 nm). (G) 2D SAXS pattern of the ‘wandering’ zinc blende lattices formed from basis particles (core diameter 8.7 nm) and guest particle pairs (core diameter 8.7 nm) caged inside the tetrahedra. (H) Integrated 1D patterns. Top channel: Experimental (red) and modeled (black) structure factors, S(q), for the zinc blende crystals (inset: standard zinc blende unit cell). Bottom channel: Experimental (green) and modeled (black) structure factors for the ‘wandering’ zinc blende lattices. (I) Unit cell model of the assembled zinc blende superlattice. (J) Unit cell model of the ‘wandering’ zinc blende lattice, where caged particle pairs have no unique orientation in the tetrahedra.

The FCC structure provides a platform for the assembly of a CD lattice, because the unit cell of diamond can be viewed as an FCC cell with four additional objects located at (1/4, 1/4, 1/4), (3/4, 3/4, 1/4), (1/4, 3/4, 3/4), and (3/4, 1/4, 3/4); i.e. the exact centers of the tetrahedra (Fig. 1). Thus, to assemble a CD lattice, we use isotropic gold NPs of 14.5 nm core diameter both as the basis particles and the guest particles. Using a one-pot slow annealing process, we mixed an equal molar ratio of two types of NPs coated with different DNA (see supplementary materials for sequence designs, and table S1). Due to the separation of melting temperatures of anchoring strands inside tetrahedra and at the vertices, the lattice assembly occurs in two distinct steps (Fig. 1): The guest particles with DNA shells complementary to inner (green) strands were first trapped inside the cages, forming the tetravalent caged particles; these caged particles subsequently hybridized with the basis particles to form lattices. The SAXS reveals a crystalline organization with a remarkable degree of long-range order, as evident from >15 sharp diffraction peaks (Fig. 2, B and C). The peak positions correspond to $q^{\mathrm{n}}/q^1\approx 1:\sqrt{8/3}:\sqrt{11/3}:\sqrt{16/3}:\sqrt{19/3}:\sqrt{8}:3\dots$, which is in precise agreement with a cubic diamond lattice. The measured lattice constant is $100.7\text{nm}(2\pi \sqrt{3}/q^1)$, consistent with the 43.7 nm center-to-center distance between the basis and caged particles ( $a\sqrt{3}/4$) and the 71.2 nm distance between the two basis particles ( $a/\sqrt{2}$). The good agreement between the calculated and experimental S(q) profiles further confirms the formation of a well-ordered diamond lattice (Fig. 2C, bottom channel, and fig. S11), whose unit cell model is shown in Fig. 2E.

Based on the same strategy, we built two variant lattices in the CD family: a zinc blende lattice and another lattice for which there is no known atomic analog. The zinc blende lattice was obtained by replacement of the 14.5 nm basis particles in the CD with smaller 8.7 nm particles. Our assembled zinc blende structures exhibited excellent long-range crystalline order (Fig. 2, F and H, and fig S4). Again, we observe a precise correspondence between experimental and modeled scattering curves (Fig. 2H, top channel, and fig. S12), confirming the formation of the designed zinc blend lattice shown in Fig. 2I.

To assemble the second variety of the CD family lattice, we used a pair of 8.7 nm core diameter guest NPs for caging inside the tetrahedra and NPs with a core diameter of 8.7 nm as the basis particles. The tetrahedron interiors were decorated with two additional anchoring strands, for a total of 6 ssDNA. The reduced NP size and the increased anchor points allow for the caging of two particles within one DNA origami tetrahedron (see fig. S8). We call the assembled structure a ‘wandering’ zinc blende lattice, since the guest particles have greater positional freedom. Its X-ray diffraction pattern is similar to that of the canonical zinc blende structure, but of a lower quality (Fig. 4, G and H). The absence of higher order diffraction peaks is likely due to the random occupancy of the two distinct but equally sized particles within the tetrahedra. Our SAXS modeling in this case assumed that the two caged particles were randomly and isotropically oriented. The modeled profile approximately matches the experimental curve (Fig. 4H, bottom channel, and fig. S13), supporting our predicted structural organization (Fig. 4J). This binary organization is remarkable, because one nano-component (the basis particle) is well positioned, while another component (the guest particle pair) has a local freedom.

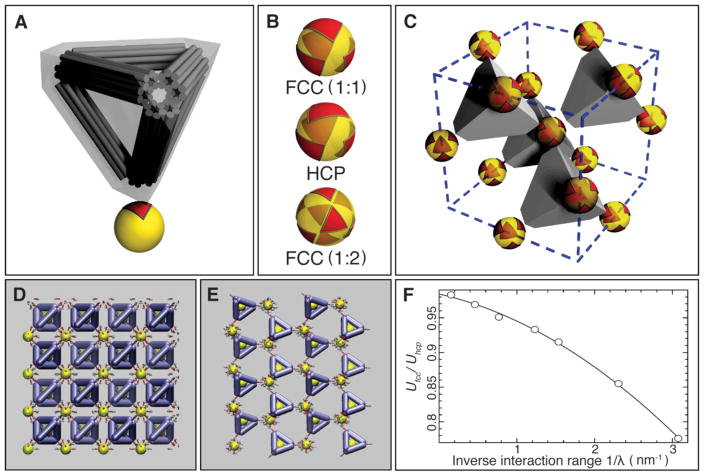
Fig. 4. Mechanism of the formation of the FCC and diamond superlattices.

(A) Model of the binding interaction between the DNA tetrahedral cage and the nanoparticle. The DNA tetrahedral cage was modeled as a truncated tetrahedron completely encompassing the cage. The binding of the tetrahedral cage to the nanoparticle leaves an equilateral triangular footprint on the particle surface. (B) Triangle-on-a sphere arrangement. Top: for the FCC superlattice (with 1:1 NP to DNA cage ratio). Middle: for the HCP superlattice. Bottom: the FCC superlattice (with 1: 2 NP to DNA cage ratio). (C) Illustration of the FCC lattice of isotropic particles formed due to their connection by truncated tetrahedra in the regime shown in (B) (top, FCC (1:1)). (D) Snapshot of the simulation for FCC (or cubic diamond) configuration. (E) Snapshot of the simulation for HCP (or hexagonal diamond) configuration. (F) Ratio of electrostatic energy for FCC (or CD) and HCP (or HD) organizations, based on screened Coulombic interactions between the negatively charged DNA bundles that comprise the tetrahedral cages. The lower energy of FCC organizations is favored.

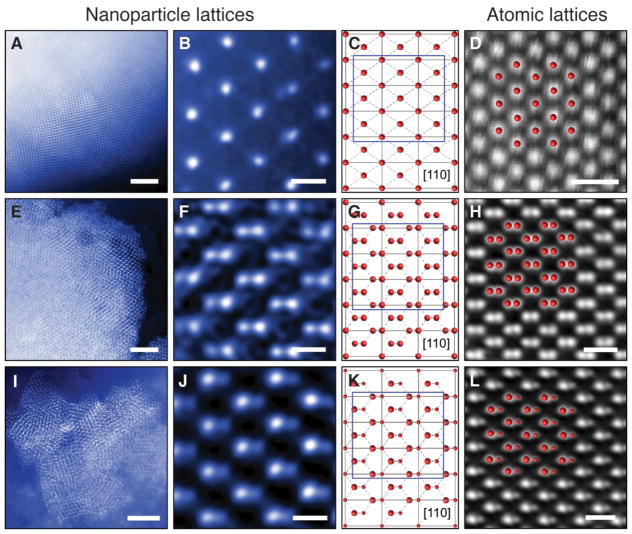
We also applied cryo-scanning transmission electron microscopy (cryo-STEM) to directly visualize the assembled lattices. Figure 3 shows the cryo-STEM images of the assembled diamond-family superlattices, plunge-frozen from their native liquid environment (also see fig. S5–S7). In this experiment, the image formation is dominated by Rutherford scattering from the atomic nuclei in the sample. Thus, the image reflects the projected atomic mass contrast, where areas with gold would have intensities higher than those of ice. As can be seen in Fig. 3, A, E, and I respectively, all three assemblies—FCC, diamond, and zinc blende—exhibit well-ordered lattices of NPs. The enlarged images of each self-assembled superlattices shown in Fig. 3, B, F, and J respectively, match the [110] projections of their corresponding models (Fig. 3, C, G, and K). To draw an analogy between our self-assembled superlattices and naturally occurring atomic crystals, Figures 3, D, H, and L present the atomic-resolution images of silicon (CD), platinum (FCC), and zinc telluride (zinc blende) along the [110] zone axis, respectively. The self-assembled nanoparticle superlattices (Fig. 3, B, F, and J) closely match their atomic analogs.

Fig. 3. Cryo-STEM images of the diamond family of nanoparticle superlattices.

(A and B) FCC superlattices constructed with basis particles (core diameter 14.5 nm) and tetrahedral DNA origami cages. (A) Low magnification image. (B) High magnification image taken along the [110] zone axis. (C) Schematic projection of a FCC lattice along [110] zone axis. (D) HAADF-STEM image of platinum viewed in the [110] direction. (E and F) Diamond superlattices formed from basis particles (core diameter 14.5 nm) and tetravalent caged particles (core diameter 14.5 nm). (E) Low magnification image. (F) High magnification image taken along the [110] zone axis. (G) Schematic projection of a diamond lattice along [110] zone axis. (H) HAADF-STEM image of silicon viewed along the [110] direction. (I and J) Zinc blende lattices constructed with basis particles (core diameter 8.7 nm) and tetravalent caged particles (core diameter 14.5 nm). (I) Low magnification image. (J) High magnification image taken along the [110] zone axis. (K) Schematic projection of a zinc blende lattice along [110] zone axis. (L) HAADF-STEM image of zinc telluride viewed along the [110] direction. The match between the nanoparticle lattices and the atomic analogues confirm a successful assembly of the diamond family of nanoparticle superlattices. Scale bars, 500 nm in A, E, and I; 50 nm in B, F, and J; 0.5 nm in D, H, and L.

The mechanism of formation for these diamond-family lattices is quite intricate. Over short ranges, the energy of the FCC lattice is identical to that of the hexagonally closed packed (HCP) lattice, as well as their derivatives such as CD, zinc blende, and hexagonal diamond (HD). The CD and HD lattices are indistinguishable from the point of view of the nearest-neighbor coordination, since, in both scenarios, tetrahedra can connect to four particles. Furthermore, while the DNA tetrahedron binds anisotropically, the basis particles interact isotropically. In other words, there is seemingly substantial freedom in the way in which the tetrahedra can attach to a particle surface.

Below, we present a simple model that explains the formation of the observed superlattices. This model attributes their robust self-assembly to the specific truncated architecture of the DNA cages (Fig. 4A), not merely to their overall tetrahedral symmetry. In this model, steric and electrostatic repulsion between the cages is represented by the rigid-body interaction between the truncated tetrahedra.

Each tetrahedron binds to a spherical particle, through a large “footprint” on its surface, as shown in Fig. 4A (red triangle), owing to its truncation. This footprint is approximately an equilateral triangle with side length b ≈10σ ≈20nm (where σ ≈ 2nm is the diameter of a DNA duplex). For the combination of sizes used in our experiments, the hard-core constraint between truncated tetrahedra is equivalent to the requirement of no overlap between their respective footprints on the spherical particle surface. In this way, we map the 3D assembly of NPs and cages onto the 2D arrangement of triangles on a spherical surface. In this mapping, the sphere corresponds to a NP with its DNA shell, including the dsDNA segments formed upon hybridization with the cages. The diameter D of this sphere in our experiments is D ≈35nm, out of which 14.5 nm is the gold core, and 10 nm is an approximate thickness of the ssDNA/dsDNA shell.

Figure 4B shows three examples of the triangle-on-a-sphere arrangements that correspond to three plausible superlattices: FCC (with 1:1 NP to DNA cage ratio, as shown in Fig. 4C), HCP, and FCC (with 1:2 ratio). FCC (1:1) clearly corresponds to the most compact footprint arrangement. While FCC (1:2) can be discarded as geometrically impossible for our size ratio (b / D≈0.6), in the case of HCP, the non-compact footprint arrangement translates into a significant entropic cost compared to FCC (1:1). As we show (see Supplementary Material), this entropy is associated primarily with rotational degrees of freedom of DNA cages, and the corresponding correction to the free energy per cage is:

$$\mathrm{\Delta }F\approx 2\mathit{kT}ln\left(\frac{b^{\ast }-b}{b^{\ast }/2-b}\right)$$

Here $b^{\ast }=\sqrt{6D^2-8b^2}$. In our case (b / D ≈ 0.6) a substantial thermodynamic advantage to FCC is given by ΔF ≈ 2.8kT. In addition, electrostatics and steric repulsions between cages would also favor FCC over HCP.

To further validate this conclusion, we performed numerical simulations of ground state structures of the DNA-origami linked nanoparticle structures using a coarse-grained representation, previously validated experimentally (30). We examined configurations of basis particles linked by tetrahedra in either FCC or HCP arrangements. In the FCC (or CD) configuration, the faces of tetrahedra are aligned (Fig. 4D), while in the HCP (or HD), only alternating planes align (Fig. 4E). Consequently, the longer-ranged repulsion between edges results in an energy gap that favors FCC (Fig. 4F). The size of this gap is related to the screening length of the potential. Thus, the medium-ranged repulsion of the truncated tetrahedral linkers provides another thermodynamic driving force to stabilize FCC (or CD) over otherwise similar structures.

Thus, we have demonstrated how packing of linker footprints on the surface of isotropic nanoparticles can enforce the formation of a desired lattice, including the experimental realization of the elusive diamond superlattice and its derivatives.