A simulation study on the constancy of cardiac energy metabolites during workload transition

Abstract

Key points

• The cardiac energy metabolites such as ATP, phosphocreatine, ADP and NADH are kept relatively constant during physiological cardiac workload transition.

• How this is accomplished is not yet clarified, though Ca²⁺ has been suggested to be one of the possible mechanisms.

• We constructed a detailed mathematical model of cardiac mitochondria based on experimental data and studied whether known Ca²⁺‐dependent regulation mechanisms play roles in the metabolite constancy.

• Model simulations revealed that the Ca²⁺‐dependent regulation mechanisms have important roles under the in vitro condition of isolated mitochondria where malate and glutamate were mitochondrial substrates, while they have only a minor role and the composition of substrates has marked influence on the metabolite constancy during workload transition under the simulated in vivo condition where many substrates exist.

• These results help us understand the regulation mechanisms of cardiac energy metabolism during physiological cardiac workload transition.

Abstract

The cardiac energy metabolites such as ATP, phosphocreatine, ADP and NADH are kept relatively constant over a wide range of cardiac workload, though the mechanisms are not yet clarified. One possible regulator of mitochondrial metabolism is Ca²⁺, because it activates several mitochondrial enzymes and transporters. Here we constructed a mathematical model of cardiac mitochondria, including oxidative phosphorylation, substrate metabolism and ion/substrate transporters, based on experimental data, and studied whether the Ca²⁺‐dependent activation mechanisms play roles in metabolite constancy. Under the in vitro condition of isolated mitochondria, where malate and glutamate were used as mitochondrial substrates, the model well reproduced the Ca²⁺ and inorganic phosphate (P_i) dependences of oxygen consumption, NADH level and mitochondrial membrane potential. The Ca²⁺‐dependent activations of the aspartate/glutamate carrier and the F₁F_o‐ATPase, and the P_i‐dependent activation of Complex III were key factors in reproducing the experimental data. When the mitochondrial model was implemented in a simple cardiac cell model, simulation of workload transition revealed that cytoplasmic Ca²⁺ concentration ([Ca²⁺]_cyt) within the physiological range markedly increased NADH level. However, the addition of pyruvate or citrate attenuated the Ca²⁺ dependence of NADH during the workload transition. Under the simulated in vivo condition where malate, glutamate, pyruvate, citrate and 2‐oxoglutarate were used as mitochondrial substrates, the energy metabolites were more stable during the workload transition and NADH level was almost insensitive to [Ca²⁺]_cyt. It was revealed that mitochondrial substrates have a significant influence on metabolite constancy during cardiac workload transition, and Ca²⁺ has only a minor role under physiological conditions.

Key points

• The cardiac energy metabolites such as ATP, phosphocreatine, ADP and NADH are kept relatively constant during physiological cardiac workload transition.

• How this is accomplished is not yet clarified, though Ca²⁺ has been suggested to be one of the possible mechanisms.

• We constructed a detailed mathematical model of cardiac mitochondria based on experimental data and studied whether known Ca²⁺‐dependent regulation mechanisms play roles in the metabolite constancy.

• Model simulations revealed that the Ca²⁺‐dependent regulation mechanisms have important roles under the in vitro condition of isolated mitochondria where malate and glutamate were mitochondrial substrates, while they have only a minor role and the composition of substrates has marked influence on the metabolite constancy during workload transition under the simulated in vivo condition where many substrates exist.

• These results help us understand the regulation mechanisms of cardiac energy metabolism during physiological cardiac workload transition.

Abbreviations

ACO

aconitase

AGC

aspartate/glutamate carrier

AGC A_Ca

Ca²⁺‐activation term of AGC

ALT

alanine aminotransferase

AST

aspartate aminotransferase

[Ca²⁺]_cyt

cytoplasmic Ca²⁺ concentration

[Ca²⁺]_mit

mitochondrial Ca²⁺ concentration

C3 A_Pi

P_i‐activation term of Complex III

CaUni

Ca²⁺ uniporter

C_m

electrical capacitance of mitochondrial inner membrane

DCT

dicarboxylate transporter

ΔΨ

mitochondrial membrane potential

ICDH

isocitrate dehydrogenase

k_ATPuse

coefficient of ATP usage

KHE

K⁺/H⁺ exchanger

KUni

K⁺ uniporter

MCT

monocarboxylate transporter

MDH

malate dehydrogenase

$\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$

oxygen consumption

NCX

mitochondrial Na⁺/Ca²⁺ exchanger

NHE

mitochondrial Na⁺/H⁺ exchanger

OGC

2‐oxoglutarate/malate carrier

OGDH

2‐oxoglutarate dehydrogenase

PC

pyruvate carboxylase

PCr

phosphocreatine

PDHC

pyruvate dehydrogenase

P_i

inorganic phosphate

P_iC

phosphate carrier

[P_i]_cyt

cytoplasmic P_i concentration

[P_i]_mit

mitochondrial P_i concentration

SCS

succinyl‐CoA synthase

SN

F₁F_o‐ATPase

SN A_Ca

Ca²⁺‐activation term of SN

TCT

tricarboxylate transporter

Introduction

The heart is a continuously working pump that is energetically driven by hydrolysis of ATP. In the heart, mitochondrial oxidative phosphorylation is the major source of ATP, and ATP is consumed mainly by ATPases such as the Na⁺/K⁺‐ATPase, the sarcoplasmic reticulum Ca²⁺‐ATPase and the myosin‐ATPase (Katz, 2010). Since the amount of ATP in the heart is small (∼0.7 g in the human heart; Ingwall, 2002), ATP synthesis by mitochondrial oxidative phosphorylation must increase so as to adapt to a rise in cardiac ATP demand. This adaptation was well demonstrated by a rapid increase in cardiac oxygen consumption ($\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$) during workload augmentation (Hata et al. 1994), resulting in a linear relationship between $\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$ and workload (Khouri et al. 1965; Hata et al. 1994). During a change in the heart's physiological workload, energy metabolites such as ATP, phosphocreatine (PCr), ADP and NADH are maintained at almost constant levels (Balaban et al. 1986; Katz et al. 1989; Balaban, 2009 a). Mechanisms underlying the constancy of energy metabolites have been extensively studied. However, the details have not yet been clarified.

Chance and Williams were the first to propose feedback control by ADP (Chance & Williams, 1956), which has been recognized as the fundamental mechanism controlling energy homeostasis (Saks et al. 2012). Recently Beard and his colleagues suggested, based on analyses of mathematical mitochondrial model and literature experimental data, that P_i is the primary feedback signal stimulating mitochondrial oxidative phosphorylation in vivo (Beard, 2006; Wu et al. 2008, 2009). The increase of P_i at high cardiac workload was reported by several studies (Bache et al. 1999; Gong et al. 2003) although Katz et al. (1989) could not detect the P_i increase.

ADP and P_i, which are products of ATP hydrolysis, enter mitochondria and become substrates for ATP synthesis by the mitochondrial F₁F_o‐ATPase (SN). Rapid transfer of ATP and ADP between mitochondria and extra‐mitochondrial ATP‐consuming systems is mediated by phosphotransfer pathways, e.g. creatine kinase, adenylate kinase and glycolysis (Andrienko et al. 2003; Saks et al. 2012). However, feedback control may not be sufficient to maintain the metabolite constancy. Korzeniewski and his colleagues demonstrated in theoretical studies that the feedback control by ADP and P_i induced large changes in energy metabolites during a physiological workload change (Korzeniewski et al. 2005; Korzeniewski, 2007). They demonstrated that metabolite constancy can be achieved only by a direct activation of all oxidative phosphorylation complexes and substrate dehydrogenation in parallel with an increase in ATP usage (parallel activation). Zhou et al. supported the parallel activation hypothesis, using a more detailed mitochondrial model including metabolic pathways and NADH generation (Zhou et al. 2006). However, molecular mechanisms underlying parallel activation have not been experimentally clarified so far.

It has been suggested for years that Ca²⁺ plays roles in the regulation of mitochondrial ATP generation (Balaban, 2009 b; Glancy & Balaban, 2012). Ca²⁺ directly activates mitochondrial dehydrogenases: pyruvate dehydrogenase (PDHC), isocitrate dehydrogenase (ICDH), and 2‐oxoglutarate dehydrogenase (OGDH) (McCormack et al. 1990). The importance of the Ca²⁺‐dependent activation of mitochondrial dehydrogenases was also demonstrated by several mathematical models including ours (Cortassa et al. 2006; Jo et al. 2006), in which transient changes of mitochondrial NADH were successfully reproduced by assuming Ca²⁺‐dependent activation of mitochondrial dehydrogenases. Several studies have suggested that SN is activated by Ca²⁺ (Harris, 1993; Territo et al. 2000, 2001), although the mechanism is not yet clear. The aspartate/glutamate carrier (AGC), which consists of a malate–aspartate shuttle together with a 2‐oxoglutarate/malate carrier (OGC), has a Ca²⁺‐binding domain facing the cytoplasm and is activated by cytoplasmic Ca²⁺ concentration ([Ca²⁺]_cyt) (Murphy et al. 1979; Pardo et al. 2006; Satrustegui et al. 2007).

It is, however, uncertain whether these Ca²⁺‐dependent activation mechanisms, which were revealed mainly in in vitro conditions, e.g. isolated mitochondria, contribute significantly to the constancy of energy metabolites during an in vivo workload change. Indeed, in mice lacking mitochondrial Ca²⁺ influx via the mitochondrial Ca²⁺ transporter (CaUni encoded by MCU), cardiac function was unaffected (Holmstrom et al. 2015) or almost normal except for acute cardiac responses following catecholamine stimulation (Kwong et al. 2015; Wu et al. 2015). The stability of energy metabolites during workload change was not investigated in these studies. In addition, an increase of cardiac workload is not always accompanied by an increase in [Ca²⁺]_cyt. Stretching cardiac muscle increases cardiac contraction, a phenomenon known as the Frank–Starling law of the heart. The stretching, however, does not immediately augment Ca²⁺ transients (Allen & Kurihara, 1982; Shimizu et al. 2002). Furthermore, allosteric activation by P_i of OGDH (Rodriguez‐Zavala et al. 2000) and Complex III of the respiratory chain (Bose et al. 2003) was proposed as a possible mechanism to maintain metabolite constancy (Beard, 2006; Wu et al. 2008).

In this study, we investigated, by utilizing mathematical modelling and simulation, whether the in vitro experimental Ca²⁺‐ and P_i‐activation mechanisms sufficiently account for metabolite constancy during in vivo cardiac workload change. Under the experimental condition of isolated mitochondria using malate and glutamate as substrates, the Ca²⁺‐dependent activation of AGC and SN and the P_i‐dependent activation of Complex III were found to be key factors. However, under a simulated in vivo condition, where other mitochondrial substrates were included, the energy metabolites were more stable and NADH level was almost insensitive to [Ca²⁺]_cyt. Results revealed that mitochondrial substrates greatly influence NADH level during cardiac workload transition, and Ca²⁺ has only a minor role in maintaining metabolite constancy under physiological in vivo conditions.

Methods

Computational method

We constructed a mathematical model of cardiac mitochondria, using a Java‐based simulation platform, simBio (Sarai et al. 2006). The ordinary differential equations were integrated with the fourth order Runge–Kutta method. The time step was adaptively changed in a range from 10^–6 to 10^–1 ms to shorten the calculation time. The equations and parameters of enzymes and transporters were determined by fitting to data from isolated heart mitochondria as far as possible. The source code (S1) of Java classes and XML files (S1–4) are available as Supporting Information.

Construction of a cardiac mitochondrial model

The mitochondrial model consisted of oxidative phosphorylation, the citric acid cycle, the pyruvate pathway, substrate transporters and ion transporters (Fig. 1). Simulation analyses were performed in the in vitro condition of isolated mitochondria, namely without the components shown inside the dotted box in Fig. 1, or in the in vivo cardiomyocyte condition with the components shown inside the dotted box in Fig. 1. The model structure was essentially similar to previously published models (Korzeniewski et al. 2005; Cortassa et al. 2006; Jo et al. 2006; Nguyen et al. 2007; Wu et al. 2007; Dzbek & Korzeniewski, 2008; Wu et al. 2008; Bazil et al. 2010; Wei et al. 2011). The main feature of our model was that major mitochondrial ion/substrate transporters and all the possible Ca²⁺‐ and P_i‐dependent mechanisms were formulated so as to simulate mitochondrial ion dynamics, substrate metabolism and ATP production. Details are described in Supporting Information, Appendix and Figs S1–S17. The process of β‐oxidation of fatty acids was omitted in this model because the experiments referred to in this study were carried out without fatty acids.

Figure 1. A scheme of the mitochondrial model .

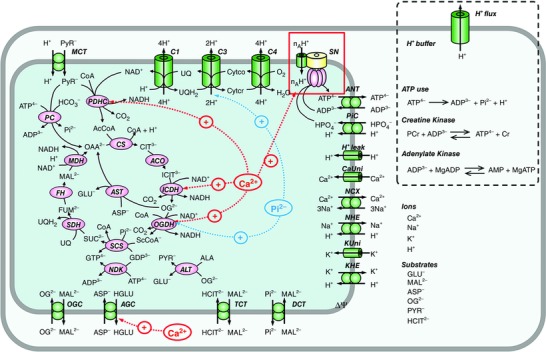
Allosteric regulation by Ca²⁺ and P_i is indicated by red and blue arrows, respectively. Shown inside the dotted box are additional cytoplasmic and plasmalemmal components to simulate an in vivo workload change of cardiomyocytes with mitochondria incorporated. AcCoA, acetyl‐CoA; ALA, alanine; ANT, adenine nucleotide translocase; ASP^–, aspartate; C1, Complex I of the respiratory chain; C3, Complex III of the respiratory chain; C4, Complex IV of the respiratory chain; CS, citrate synthase; Cytco, oxidized form of cytochrome c; Cytcr, reduced form of cytochrome c; FH, fumarate hydratase; FUM^2–, fumarate; GLU^–, glutamate; HCIT^2–, citrate; MAL^2–, malate; NDK, nucleoside diphosphate kinase; OAA^2–, oxaloacetate; OG^2–, 2‐oxoglutarate; PYR^–, pyruvate; SDH, succinate dehydrogenase; SUC^2–, succinate; UQH2; ubiquinol; ScCoA, succinyl‐CoA.

The oxidative phosphorylation model was adapted from the model of Dzbek & Korzeniewski (2008). The dependences of Complex I on NADH and ubiquinone, and of Complex III on reduced ubiquinone and cytochrome c were newly added to fit the model to experimental time courses reported by Bose et al. (2003) (Fig. S14). Similarly, the dependence of Complex III on P_i was added according to the experiment by Bose et al. (2003).

Kinetic models of enzymes in the citric acid cycle were formulated based on experimental data and previous models (see Supporting Information, Appendix and Figs S1–S8 and S10 for details). Consequently, the process of substrate dehydrogenation used by Dzbek & Korzeniewski (2008) was replaced with a newly formed detailed model of the citric acid cycle. The pyruvate pathways, which consisted of PDHC, pyruvate carboxylase (PC), and alanine aminotransferase (ALT), and the substrate transporters such as the monocarboxylate transporter (MCT), the dicarboxylate transporter (DCT), the tricarboxylate transporter (TCT), OGC and AGC were formulated. Validation of each elemental model is demonstrated in Figs S11–S13.

Mitochondrial ions (Ca²⁺, Na⁺ and K⁺) change dynamically and are important for mitochondrial function (Bernardi, 1999; Takeuchi et al. 2015). Mitochondrial ion dynamics were reconstructed by incorporating models of CaUni (Nguyen et al. 2007), the Na⁺/Ca²⁺ exchanger (NCX) (Kim & Matsuoka, 2008), the Na⁺/H⁺ exchanger (NHE) (Nguyen et al. 2007), the K⁺ uniporter (KUni) (Dzbek & Korzeniewski, 2008) and the K⁺/H⁺ exchanger (KHE) (Dzbek & Korzeniewski, 2008). The CaUni model well reproduced the [Ca²⁺]_cyt dependences of CaUni (Kirichok et al. 2004). The NCX model, which assumed a 3Na⁺/1Ca²⁺ exchange, well reproduced our experimental data on the cytoplasmic Na⁺ and [Ca²⁺]_cyt dependences of NCX (Kim & Matsuoka, 2008). In addition, the time course of mitochondrial Ca²⁺ concentration ([Ca²⁺]_mit) decline upon activation of NCX was comparable to the experimental data (Kim & Matsuoka, 2008) (Fig. S15A). Consequently, the steady state relationship between [Ca²⁺]_cyt and [Ca²⁺]_mit (Wan et al. 1989) was well reproduced (Fig. S15B).

Mitochondrial membrane potential (ΔΨ) is determined mainly by the electron transfer system (Complex I, III and IV) and by other electrogenic channels and transporters. Here ΔΨ was calculated as follows:

$$\frac{\mathrm{d}\mathrm{\Psi }}{\mathrm{d}t}=-\frac{\left(4v_{\mathrm{C}1}+2v_{\mathrm{C}3}+4v_{\mathrm{C}4}-n_{\mathrm{A}}{v}_{\mathrm{SN}}-v_{\mathrm{LK}}-v_{\mathrm{ANT}}+v_{\mathrm{AGC}}-v_{\mathrm{KUni}}-2v_{\mathrm{CaUni}}-v_{\mathrm{NCX}}\right)}{C_{\mathrm{m}}}$$

where, C _m is electrical capacitance of mitochondrial inner membrane (0.001 mm mV⁻¹) (Dzbek & Korzeniewski, 2008).

The activation of PDHC, ICDH and OGDH by [Ca²⁺]_mit (McCormack et al. 1990) was well reconstructed, as shown in Fig. S16A–D. It has been reported that Ca²⁺ activates SN (Harris, 1993; Territo et al. 2000; Territo et al. 2001), although the mechanisms are not yet clarified. We hypothesized that SN is activated by [Ca²⁺]_mit, based on the experimental finding by Territo et al. that entry of Ca²⁺ into mitochondria was necessary for SN activation (Territo et al. 2000) (Fig. S16E). AGC has a Ca²⁺ binding domain facing the extra‐mitochondrial space and therefore is activated by [Ca²⁺]_cyt (Murphy et al. 1979; Pardo et al. 2006; Satrustegui et al. 2007). However, since the precise [Ca²⁺]_cyt dependence of AGC was not available, the [Ca²⁺]_cyt‐dependent activation was expressed as a simple Hill equation in this study (Fig. S16F). The parameters of Ca²⁺‐dependent activation of SN and AGC were determined by fitting the models to experimental data (Territo et al. 2000; Bose et al. 2003).

The activation by mitochondrial P_i concentration ([P_i]_mit) of OGDH (Rodriguez‐Zavala et al. 2000) and of Complex III (Bose et al. 2003) was determined by fitting the models to experimental data (Fig. S17A and C). The [P_i]_mit dependence of succinyl‐CoA synthase (SCS) was reconstructed to reproduce experimental data (Cha & Parks, 1964), as shown in Fig. S17B.

Simulation procedures

To simulate in vitro experiments on the [Ca²⁺]_cyt dependence of isolated mitochondria performed by Territo et al. (Figs 2 A and 4) (Territo et al. 2000), [Ca²⁺]_cyt was changed from 10^–6 μm to various values (10^–6–2.0 μm) for 1 h in the presence of 5 mm malate and 5 mm glutamate as substrates. To simulate in vitro experiments on the cytoplasmic P_i concentration ([P_i]_cyt) dependence of isolated mitochondria performed by Bose et al. (Figs 2 B and 5) (Bose et al. 2003), [P_i]_cyt was increased from 10^–6 mm to various values (10^–6–10 mm) for 10 min in the presence of malate/glutamate as substrates. For both simulation procedures, cytoplasmic reactions (shown inside the dotted box in Fig. 1) were omitted. Other initial conditions are listed in Appendix (Supporting Information).

Figure 2. Dependences of $\mathit{}\mathrm{m}\dot{\mathit{V}}{}_{{\mathit{}\mathrm{O}}_{\mathit{}\mathbf{2}}}$ , NADH and ΔΨ on [Ca²⁺]_cyt and [P_i]_cyt .

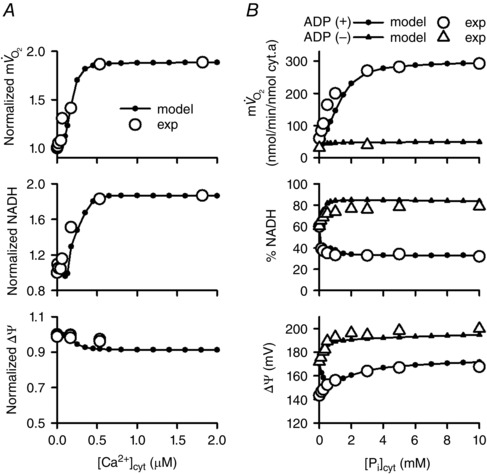
Simulations were performed using the model of isolated mitochondria with the experimental conditions of Territo et al. (2000) (A) and Bose et al. (2003) (B). A, [Ca²⁺]_cyt dependence. Experimental data (exp; open circles) are from Territo et al. (2000). Simulation data (model; filled circles) were normalized to those at 10^–6 μm [Ca²⁺]_cyt. B, [P_i]_cyt dependence. Simulation data (model) were in state III (with ADP, filled circles) and state IV (without ADP, filled triangles). Experimental data (exp; open circles and triangles) were from Bose et al. (2003).

Figure 4. Contribution of the Ca²⁺‐ and P_i‐dependent activation mechanisms to the [Ca²⁺]_cyt dependences in the isolated mitochondrial model .

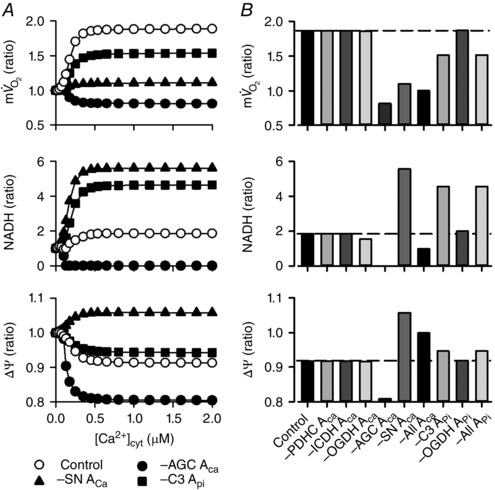
The basic simulation condition was the same as that of Fig. 2 A. The Ca²⁺‐dependent activation terms of PDHC, ICDH, OGDH, AGC and SN, that is, PDHC A_Ca, ICDH A_Ca, OGDH A_Ca, AGC A_Ca and SN A_Ca, were removed from the mathematical formula individually or at the same time. In addition, the P_i‐dependent activation terms of Complex III and OGDH, that is, C3 A_Pi and OGDH A_Pi, were removed individually or at the same time. A, removal of AGC A_Ca, SN A_Ca and C3 A_Pi. Open circles represent the control model, and filled symbols represent the absence of AGC A_Ca, SN A_Ca and C3 A_Pi. B, summary of the simulation results. Ratios of $\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$, NADH and ΔΨ at 10^–6 μm [Ca²⁺]_cyt to those at 0.535 μm [Ca²⁺]_cyt were plotted. Dotted lines indicate the ratios obtained from the control model. –All A_Ca: Ca²⁺‐dependent activation terms were removed from all components; –All A_Pi: P_i‐dependent activation terms were removed from all components.

Figure 5. Contribution of the Ca²⁺‐ and P_i‐dependent activation mechanisms to the [P_i]_cyt dependences in the isolated mitochondrial model .

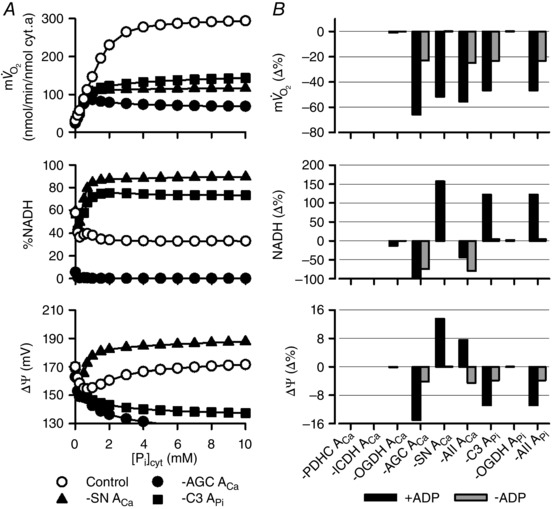
The basic simulation conditions were the same as those of Fig. 2 B. Removal of the Ca²⁺‐dependent activation term and P_i‐dependent activation term was the same as in Fig 4. A, removal of AGC A_Ca, SN A_Ca and C3 A_Pi under the condition of state III (with [P_i]_cyt and ADP in addition to malate/glutamate). Open circles represent the control model, and filled symbols represent the absence of AGC A_Ca, SN A_Ca and C3 A_Pi. B, summary. Values of $\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$, NADH and ΔΨ at 2 mm [P_i]_cyt were expressed as percentage difference from the control model. Data are from state III (black) and state IV (with only [P_i]_cyt in addition to malate/glutamate; grey).

Simulations of cardiomyocytes in vivo (Figs 6, 7, 8, 9, 10, 11) were performed by incorporating the cardiac mitochondrial model into a simple cardiac cell model (Fig. 1 including the components inside the dotted box) according to the method of Korzeniewski et al. (2005). This simple cardiac cell model included cytoplasmic ATP use, creatine kinase, adenylate kinase, cytoplasmic H⁺ buffer and H⁺ efflux from the cytosol to the extracellular space, in addition to mitochondria. In the model, mitochondrial H⁺ leak was reduced to 1% to adjust $\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$ level without cardiac workload (Gobel et al. 1978; Katz et al. 1989; Korzeniewski, 2007). For simulation of in vitro experiments with isolated mitochondria (Bose et al. 2003), a larger mitochondrial H⁺ leak was required to reproduce a mitochondrial pH of 7.14. In the simulations using the simple cardiac cell model, [Ca²⁺]_cyt was changed from 10^–3 to 10 μm, and the coefficient of ATP usage (k _ATPuse) was changed from 1.5 × 10^–5 to 1.88 × 10^–4 mm ms^–1 to cover the range of $\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$ in dog heart: about 2–11 mm min⁻¹ (Boerth et al. 1969; Katz et al. 1989; Korzeniewski et al. 2005). Other initial conditions for each simulation are listed in Appendix (Supporting Information).

Figure 6. Workload and [Ca²⁺]_cyt dependences of energy metabolites in the simple cardiac cell model .

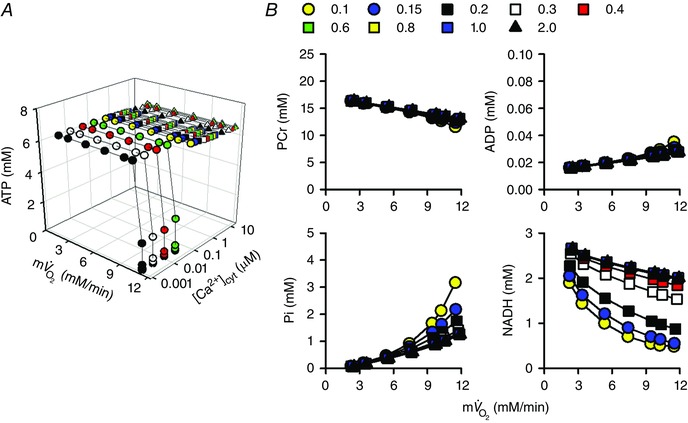
The coefficient of ATP usage, k _ATPuse, was changed from 1.5 × 10^–5 to 1.88 × 10^–4 mm ms⁻¹, and [Ca²⁺]_cyt was changed from 0.001 to 10 μm. A, total cytoplasmic ATP. B, cytoplasmic PCr, ADP and P_i, and mitochondrial NADH. Data at 0.1 to 2.0 μm [Ca²⁺]_cyt are shown.

Figure 7. Effects of additional substrate on the workload and [Ca²⁺]_cyt dependences of NADH in the simple cardiac cell model .

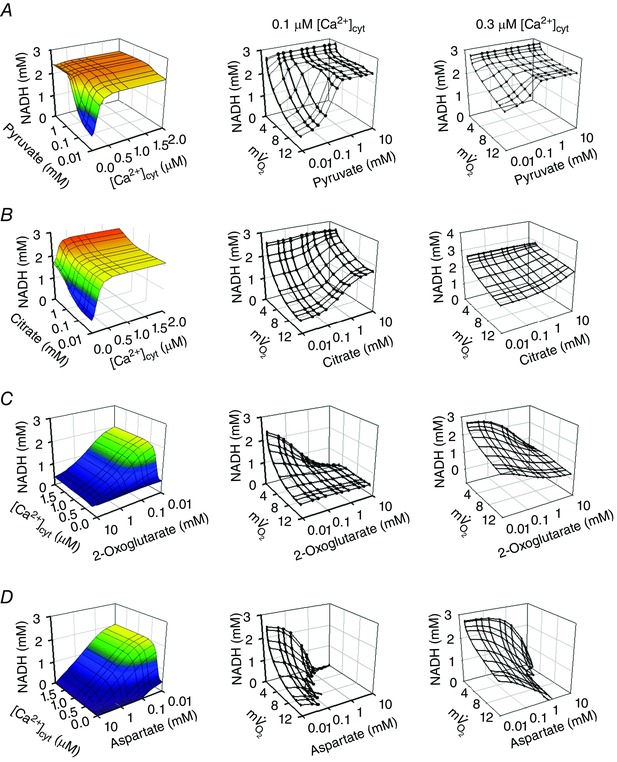
Pyruvate (A), citrate (B), 2‐oxoglutarate (C) and aspartate (D) were added to the cytoplasm of the simple cardiac cell model, in addition to malate/glutamate. The middle and right panels show the results of simulations at 0.1 and 0.3 μm [Ca²⁺]_cyt, respectively. Unit for $\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$ is mm min^–1.

Figure 8. Activities of representative enzymes and substrate transporters at different combinations of substrates in the simple cardiac cell model .

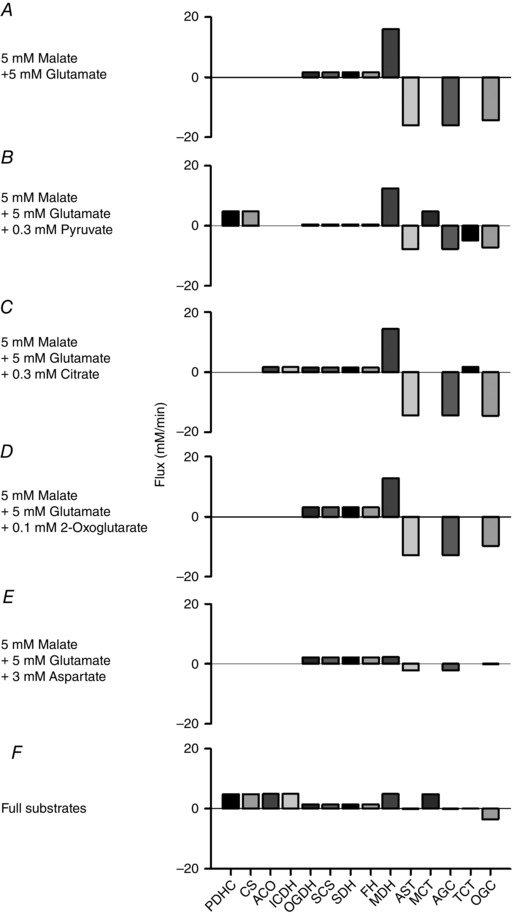
A, 5 mm malate and 5 mm glutamate. B, 5 mm malate, 5 mm glutamate and 0.3 mm pyruvate. C, 5 mm malate, 5 mm glutamate and 0.3 mm citrate. D, 5 mm malate, 5 mm glutamate and 0.1 mm 2‐oxoglutarate. E, 5 mm malate, 5 mm glutamate and 3 mm aspartate. F, full substrates; 1 mm malate, 5 mm glutamate, 0.3 mm pyruvate, 0.3 mm citrate, 0.1 mm 2‐oxoglutarate and 3 mm aspartate. All the simulations were done at 0.3 μm [Ca²⁺]_cyt and 1.5 × 10^–4 mm ms⁻¹ k _ATPuse ($\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$ = 8.8 mm min⁻¹ except for E, 3.2 mm min⁻¹).

Figure 9. Workload and [Ca²⁺]_cyt dependences of energy metabolites in the simple cardiac cell model with multiple mitochondrial substrates: 1 mm malate, 5 mm glutamate, 0.3 mm pyruvate, 0.3 mm citrate, 0.1 mm 2‐oxoglutarate and 3 mm aspartate .

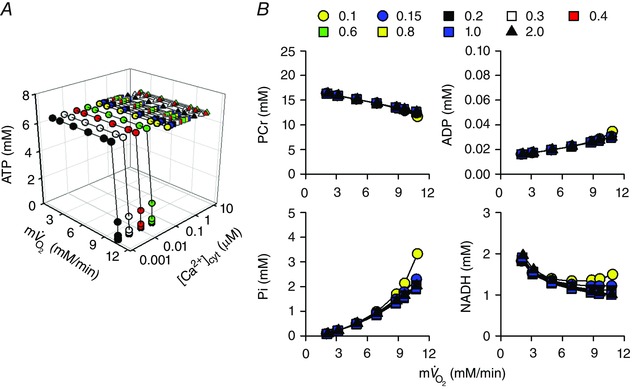
The same protocols as in Fig. 6 were used. A, total cytoplasmic ATP. B, cytoplasmic PCr, ADP, P_i and mitochondrial NADH.

Figure 10. [Ca²⁺]_cyt dependence of four dehydrogenases, AGC and OGC .

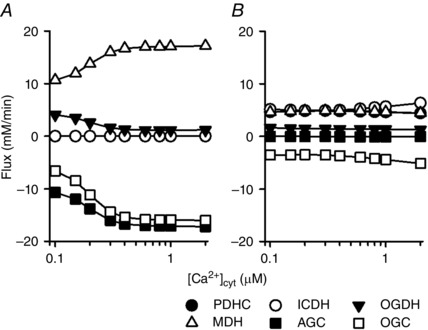
A, 5 mm malate and 5 mm glutamate condition. B, full substrates condition: 1 mm malate, 5 mm glutamate, 0.3 mm pyruvate, 0.3 mm citrate, 0.1 mm 2‐oxoglutarate and 3 mm aspartate. k _ATPuse = 1.5 × 10^–4 mm ms⁻¹ ($\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$ = 9.4 – 9.8 mm min⁻¹ in A, 8.8 – 8.9 mm min⁻¹ in B).

Figure 11. Substrate dependence of NADH in the simple cardiac cell model .

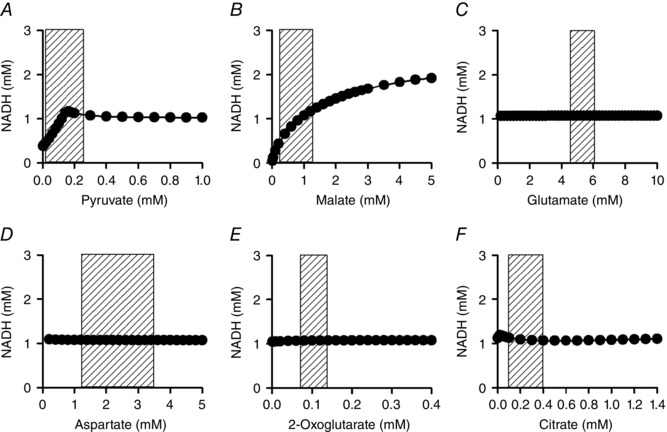
The basic combination of substrates was the same as in Fig. 9. Pyruvate (A), malate (B), glutamate (C), aspartate (D), 2‐oxoglutarate (E) and citrate (F) were systematically increased in the presence of 0.3 μm [Ca²⁺]_cyt. k _ATPuse was set to 1.5 × 10^–4 mm ms⁻¹ ($\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$ = 8.6–8.9 mm min⁻¹). Shaded areas show physiological range of each substrate (Albe et al. 1990; Kato et al. 2010).

Results

Roles of allosteric Ca²⁺‐ and P_i‐dependent activation

First, we simulated in vitro experiments with isolated mitochondria to examine the basic characteristics of the model (Fig. 2). Steady state dependences of $\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$, NADH and ΔΨ on [Ca²⁺]_cyt and [P_i]_cyt were well fitted to experimental data from isolated mitochondria (Territo et al. 2000; Bose et al. 2003). To study how an individual component contributes to $\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$, NADH and ΔΨ, sensitivity analysis was performed (Fig. 3). As expected, components of oxidative phosphorylation had a great influence on mitochondrial function. The components relating to Ca²⁺‐dependent activation, SN and AGC were influential. In addition, the phosphate carrier (P_iC) and the allosteric P_i‐dependent activation of Complex III were also influential. The analysis suggested that Ca²⁺ and P_i have essential roles in mitochondrial function.

Figure 3. Sensitivity analysis of the isolated mitochondrial model .

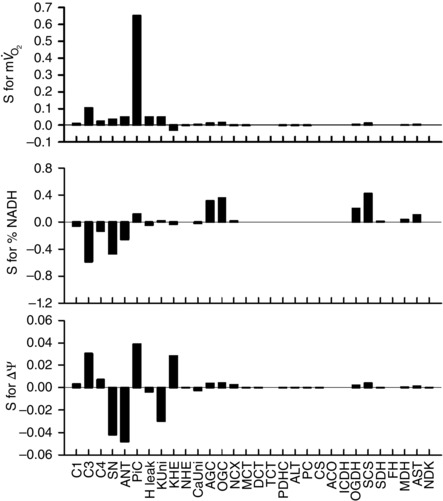
The simulation conditions were the same as those of Fig. 2 A, with [Ca²⁺]_cyt = 1.0 μm. Sensitivity (S) for parameter X (X = $\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$, NADH and ΔΨ) was calculated as the relative change by ±5% change of the expression level of each component: $S=\frac{|X_{+5\%}-X_{-5\%}|}{0.1X_{\mathrm{original}}}$.

Then the contributions of Ca²⁺‐ and P_i‐dependent activation on [Ca²⁺]_cyt dependence were studied by eliminating individual allosteric regulation by Ca²⁺ or P_i in the simulation of Territo's experimental protocol (Territo et al. 2000). In Fig. 4 A, [Ca²⁺]_cyt dependences of $\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$, NADH and ΔΨ without Ca²⁺‐dependent activation of AGC (AGC A_Ca) or SN (SN A_Ca), and without the P_i‐dependent activation of Complex III (C3 A_Pi), are presented. The ratios of changes in the above parameters when [Ca²⁺]_cyt was increased from 10^–6 to 0.535 μm are summarized in Fig. 4 B. The removal of AGC A_Ca, SN A_Ca, and C3 A_Pi had marked effects on the [Ca²⁺]_cyt dependences. Since malate/glutamate were used as mitochondrial substrates, similarly to Territo's protocol (Territo et al. 2000), OGC and AGC functioned to supply malate and glutamate to mitochondria (the malate‐aspartate shuttle). That is, OGC‐mediated malate influx stimulated malate dehydrogenase (MDH) to produce NADH and oxaloacetate. Oxaloacetate was then converted by aspartate amino transferase (AST) to aspartate, leaving mitochondria through AGC. Therefore, AGC functioned to maintain the driving force of OGC to transport malate into mitochondria. The elimination of AGC A_Ca therefore reduced [Ca²⁺]_cyt‐dependent malate supply through the malate‐aspartate shuttle, resulting in the reduction of MDH activity to produce NADH. As a result, NADH was depleted, $\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$ decreased, and ΔΨ depolarized as [Ca²⁺]_cyt increased. The elimination of SN A_Ca almost abolished the [Ca²⁺]_cyt‐dependent increase of $\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$ and augmented the [Ca²⁺]_cyt‐dependent increase of NADH. These alternations were due to the attenuation of function of the respiratory chain. The decline of ΔΨ was reversed, or the mitochondrial membrane was hyperpolarized, due to a lower H⁺ influx through SN. The elimination of C3 A_Pi attenuated the [Ca²⁺]_cyt‐dependent increase of $\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$ and increased NADH because of the attenuation of respiratory chain function. These analyses indicated that the Ca²⁺‐dependent activation of AGC and SN, and the P_i‐dependent activation of Complex III are important factors for the [Ca²⁺]_cyt dependences of isolated mitochondrial function.

Similar analyses were performed in Bose's protocol (0.5 μm [Ca²⁺]_cyt) with various [P_i]_cyt (Bose et al. 2003) (Fig. 5). These analyses also demonstrated that the Ca²⁺‐dependent activation of AGC and SN, and the P_i‐dependent activation of Complex III are important for the [P_i]_cyt dependences of isolated mitochondria.

Metabolite stability and cardiac workload

In order to study the workload dependence of energy metabolites, we used the simple cardiac cell model (Fig. 6). Workload was altered by changing k _ATPuse to cover the physiological range of $\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$ in dog heart: about 2–11 mm min⁻¹ (Boerth et al. 1969; Katz et al. 1989; Korzeniewski et al. 2005). Then simulation was performed at various [Ca²⁺]_cyt, from 0.001 to 10 μm. At higher workload, i.e. at higher $\mathrm{m}\dot{V}{}_{{\mathrm{O}}_2}$, cytoplasmic ATP was depleted when [Ca²⁺]_cyt was lower than 0.1 μm, while it was kept constant when [Ca²⁺]_cyt was 0.1 μm or higher. The workload dependences of other metabolites (PCr, ADP, P_i and mitochondrial NADH) at [Ca²⁺]_cyt between 0.1 and 2.0 μm are plotted in Fig. 6 B. As workload was augmented, ADP and P_i increased, inducing feedback stimulation. The larger increase in P_i than ADP is consistent with previous simulation studies (Beard, 2006; Wu et al. 2008; Wu et al. 2009). NADH, as well as P_i, was [Ca²⁺]_cyt dependent, suggesting an important role of Ca²⁺‐dependent activation systems for NADH and P_i levels. The [Ca²⁺]_cyt dependence of NADH was mainly due to Ca²⁺‐dependent activation of AGC, as demonstrated in Fig. 4.

It should be noted that the model simulations were performed in the presence of malate/glutamate as mitochondrial substrates, according to the experiments by Bose et al. (2003) and Territo et al. (2000). Under this condition, the activities of Ca²⁺‐dependent dehydrogenases (PDHC, ICDH and OGDH) were low, as demonstrated later in Fig. 8. It was conceivably possible that NADH was more or differently dependent on [Ca²⁺]_cyt if these dehydrogenases were more active. To test this hypothesis, we studied the dependences of energy metabolites on workload and [Ca²⁺]_cyt at different substrate conditions.

Substrate dependences of metabolite stability

Pyruvate was added at various concentrations between 0.01 and 10 mm to the cytoplasm, to activate PDHC (Figs 7 A and 8 B). When pyruvate concentration was lower than 0.5 mm, mitochondrial NADH increased with increasing [Ca²⁺]_cyt but was almost independent of [Ca²⁺]_cyt at pyruvate concentrations higher than 1 mm (Fig. 7 A, left panel). This is because higher concentrations of pyruvate stimulated PDHC, overcoming the lower activity of PDHC at low Ca²⁺ concentrations. At a [Ca²⁺]_cyt level in the diastolic heart (0.1 μm; Fig. 7 A, middle panel), NADH markedly decreased with higher workload when pyruvate concentration was low, while at the mean [Ca²⁺]_cyt level (0.3 μm; Fig. 7 A, right panel), NADH became relatively stable during workload transition, even at lower pyruvate concentrations. In the physiological range of pyruvate (rat heart: 0.039–0.26 mm) (Albe et al. 1990; Kato et al. 2010), higher pyruvate concentrations increased NADH level and attenuated the Ca²⁺ dependence of NADH, suggesting the importance of glycolytic flux for NADH stability.

The addition of citrate had a similar tendency to the addition of pyruvate (Fig. 7 B). Citrate stimulated aconitase (ACO) and ICDH, inducing NADH production by ICDH (Fig. 8 C). In the physiological range of citrate (0.07–0.39 mm) (Albe et al. 1990) and at the mean [Ca²⁺]_cyt level of 0.3 μm, NADH was stable during the workload transition (Fig. 7 B, right panel).

The addition of 2‐oxoglutarate decreased NADH level at all [Ca²⁺]_cyt levels (Fig. 7 C), although it stimulated NADH production by OGDH (Fig. 8 D). At physiological concentrations of 2‐oxoglutarate (0.07–0.14 mm) (Albe et al. 1990), NADH level was dependent on [Ca²⁺]_cyt and was relatively stable during the workload transition at 0.3 μm [Ca²⁺]_cyt (Fig. 7 C, right panel). An addition of aspartate also markedly decreased mitochondrial NADH (Fig. 7 D), because high aspartate inhibited conversion by AST from glutamate to aspartate.

The above analyses indicated that mitochondrial substrates significantly affect the [Ca²⁺]_cyt dependence of NADH level and the NADH stability during workload transition.

To investigate the stability of mitochondrial NADH under physiological conditions, simulation analysis was performed in the presence of all six substrates at physiological concentrations (Fig. 9): 1 mm malate, 5 mm glutamate, 0.3 mm pyruvate, 0.3 mm citrate, 0.1 mm 2‐oxoglutarate and 3 mm aspartate (Albe et al. 1990; Kato et al. 2010). Under this condition, all of the enzymes of the citric acid cycle and PDHC were active (Fig. 8 F). Similarly to the malate/glutamate condition (Fig. 6), cytoplasmic ATP could not be maintained at high cardiac workload when [Ca²⁺]_cyt was less than 0.1 μm. Changes of PCr, ADP and P_i were also similar to those under the malate/glutamate condition. However, contrary to the malate/glutamate condition, mitochondrial NADH was almost independent of [Ca²⁺]_cyt and was almost stable during workload change (Fig. 9 B). [Ca²⁺]_cyt dependence of four dehydrogenases, AGC and OGC were compared between the malate/glutamate condition and this condition in Fig. 10. Under the malate/glutamate condition, the absence of cytoplasmic 2‐oxoglutarate and aspartate favoured cytoplasmic malate–mitochondrial 2‐oxoglutarate exchange via OGC and cytoplasmic glutamate–mitochondrial aspartate exchange via AGC, respectively. Therefore the fluxes through OGC and AGC are large (Fig. 10 A). The increase of [Ca²⁺]_cyt from 0.1 to 2 μm stimulated AGC resulting in augmentation of NADH production by MDH (the malate–aspartate shuttle). Under the full substrates condition, the presence of cytoplasmic 2‐oxoglutarate attenuated the cytoplasmic malate–mitochondrial 2‐oxoglutarate exchange via OGC due to a decreased driving force for outward transport of 2‐oxoglutarate. The presence of aspartate also attenuated the cytoplasmic glutamate–mitochondrial aspartate exchange via AGC due to decreased driving force for outward transport of aspartate (see the equations of OGC and AGC in Supporting Information, Appendix). Therefore, the fluxes through OGC and AGC were smaller than those under the malate/glutamate condition. NADH production by four dehydrogenases was almost independent of [Ca²⁺]_cyt because of very low activity of AGC, lower Ca²⁺ affinity of ICDH (Fig. S15A), and the relatively small Ca²⁺‐sensitive component of PDHC (Fig. S16B). Under the full substrates condition, pyruvate and malate had significant influence on NADH level, as shown in Fig. 11, where concentration of one substrate was changed at each analysis. Under this condition, the augmentation of mitochondrial influxes of ADP and P_i by their cytoplasmic increases has a pivotal role in the metabolite constancy. Therefore, the metabolite constancy could not be maintained when the augmentation of ANT by increased ADP_cyt (Fig. S18A and B) or the augmentation of P_iC by increased [P_i]_cyt (Fig. S18C and D) was eliminated. Allosteric P_i regulation of OGDH and Complex III made a moderate contribution to the metabolite constancy (Fig. S18E and F).

Discussion

We constructed a mathematical model of cardiac mitochondria including oxidative phosphorylation, substrate metabolism, and ion/substrate transporters, and studied whether the Ca²⁺‐dependent activation mechanisms play roles in metabolite constancy during workload change. The Ca²⁺‐dependent activation mechanisms were prominent at [Ca²⁺]_cyt concentrations below physiological minimum level ([Ca²⁺]_cyt at diastole; approximately 0.1 μm) in cardiomyocytes. When malate and glutamate were sole mitochondrial substrates, as in many experiments using isolated mitochondria, the Ca²⁺‐dependent activation of AGC and SN, and the P_i‐dependent activation of Complex III were found to be key factors, and mitochondrial NADH level was increased by [Ca²⁺]_cyt in the physiological range. However, under simulated physiological levels of [Ca²⁺]_cyt and mitochondrial substrates, mitochondrial NADH was relatively constant over the physiological workload change and almost insensitive to [Ca²⁺]_cyt. Therefore, it was revealed that mitochondrial substrates greatly influence the NADH level during cardiac workload transition, and Ca²⁺ has only a minor role in maintaining metabolite constancy under physiological conditions.

It has been suggested for years that Ca²⁺ plays roles in the regulation of mitochondrial ATP generation (Balaban, 2009 a; Glancy & Balaban, 2012). Indeed, implementation of Ca²⁺‐activated systems was inevitable to reproduce experimental data using isolated mitochondria under the malate/glutamate condition (Figs 4 and 5). In addition, Ca²⁺ had pivotal roles in the transient change of NADH upon rapid workload transition, as demonstrated in cardiomyocytes, trabeculae and model simulations (Brandes & Bers, 2002; Cortassa et al. 2006; Jo et al. 2006). However, under the in vivo physiological ranges of [Ca²⁺]_cyt and mitochondrial substrates, the Ca²⁺‐activated systems do not seem to contribute significantly to the steady‐state metabolite constancy during workload transition (Fig. 9). At higher workload and lower [Ca²⁺]_cyt below diastolic level (approximately 0.1 μm), energy balance collapsed, suggesting that the basal activation of SN and AGC by Ca²⁺ had significant influences on metabolite constancy. However, since the heart is continuously beating, and [Ca²⁺]_cyt hardly ever decreases below 0.1 μm, the enzymes and transporters could be constitutively activated by Ca²⁺ under physiological conditions. Additionally, the allosteric effects of Ca²⁺ were nearly saturated at the mean [Ca²⁺]_cyt level of cardiomyocytes and could not be expected to have marked influences on mitochondrial metabolism in the physiological range of [Ca²⁺]_cyt.

The in vitro experiments referred to in this study used a high cytoplasmic Mg²⁺ (Territo et al. 2000; Bose et al. 2003; 5 mm), which attenuates Ca²⁺ influx through CaUni (Bragadin et al. 1979). Therefore, the Ca²⁺ influx may be larger under physiological conditions (approximately 1 mm Mg²⁺) and [Ca²⁺]_mit may become higher than the present simulation condition. This possibility was tested in an additional simulation under a condition of increased CaUni activity to fit a [Ca²⁺]_cyt–[Ca²⁺]_mit relation with 1 mm Mg²⁺ (Fig. S19A). Cytoplasmic ATP at high cardiac workload became stable even at lower [Ca²⁺]_cyt (0.03 μm; Fig. S19B) and the metabolites became further insensitive to [Ca²⁺]_cyt (Fig. S18C). These results further support our conclusion that Ca²⁺ has only a minor role in maintaining metabolite constancy under physiological conditions.

The [Ca²⁺]_cyt‐dependent activation of AGC had a significant influence on mitochondrial NADH level under the malate/glutamate condition. This result suggested that in addition to [Ca²⁺]_mit, [Ca²⁺]_cyt also had a direct contribution to maintaining mitochondrial NADH level. This result is consistent with recent experiments in brain mitochondria, where the [Ca²⁺]_cyt‐dependent activation of AGC was found to be a key factor in adjusting mitochondrial energization to the requirements of neurons (Gellerich et al. 2012). However, the contribution of AGC to NADH may be dependent on mitochondrial substrates as shown in Fig. 10.

The stability of NADH and its Ca²⁺ dependence significantly depended on the substrate, especially on pyruvate. Several lines of experimental evidence are consistent with our finding. Wan et al. demonstrated that PDHC was almost 100% activated and NADH was insensitive to Ca²⁺ in the presence of pyruvate and malate, whereas PDHC was only 20% active in the absence of pyruvate and Ca²⁺, and NADH level was activated by Ca²⁺ (2‐oxoglutarate/malate condition) (Wan et al. 1989). Recently, Vinnakota et al. also reported that mitochondrial NADH level was almost insensitive to Ca²⁺ when pyruvate and malate were used as mitochondrial substrates (Vinnakota et al. 2011, 2016 b). The present simulation study is in line with these results. However, since glutamate was omitted in Vinnakota et al.’s experiments, the contribution of AGC might have been underestimated. Minor roles of Ca²⁺ in mitochondrial metabolism are also consistent with data from mice lacking MCU, which showed normal or slightly reduced cardiac function (Holmstrom et al. 2015; Kwong et al. 2015; Wu et al. 2015).

P_i had pivotal roles in stimulating mitochondrial ATP production. In our model simulation, the allosteric activation of Complex III by P_i was a key factor in reproducing the experimental data (Figs 4 and 5). In the simple cardiac cell model, P_i increased with increasing workload (Figs 6 and 9), though the level was still within the physiological concentration range (3–5 mm) (Dos Santos et al. 2000; Shen et al. 2001). This tendency of P_i level was similar to the model simulation by Wu et al. (2008). Wu et al. (2008) also demonstrated the workload‐dependent increase in P_i by analysing experimental data in the literature (Bache et al. 1999; Gong et al. 2003). The pooled data, however, had a large variation. On the other hand, Katz et al. (1989 a) reported that P_i did not increase with increasing workload. Since detection of a low level of P_i is technically difficult, a new experimental technique is needed for more clearly detecting the increase of P_i during the cardiac workload transition. Most recently Vinnakota et al. (2016 a) reported that P_i did not modulate the activity of Complex III in isolated mitochondria, in conflict with a previous report by Bose et al. (2013). Further studies are needed to determine whether or not P_i directly regulates Complex III.

Our cardiac mitochondrial model includes oxidative phosphorylation, substrate metabolism, and ion/substrate transporters. The main feature is that the major mitochondrial ion/substrate transporters and all the possible Ca²⁺‐ and P_i‐activated mechanisms are formulated so as to simulate mitochondrial ion dynamics, substrate metabolism and ATP production. To date, many mitochondrial models have been published, and some models can simulate additional mitochondrial functions such as reactive oxygen species formation (Yugi & Tomita, 2004; Korzeniewski et al. 2005; Cortassa et al. 2006; Jo et al. 2006; Zhou et al. 2006; Nguyen et al. 2007; Wu et al. 2007; Dzbek & Korzeniewski, 2008; Wu et al. 2008; Bazil et al. 2010; Wei et al. 2011; Kembro et al. 2013). However, to the best of our knowledge, this is the first simulation study to investigate the effects of mitochondrial substrate composition and Ca²⁺ on metabolite stability during workload transition. Many of the previous model studies did not extensively investigate the stability of metabolites during workload transition, and the regulatory effects of Ca²⁺ and P_i were not fully incorporated. Korzeniewski's group (Korzeniewski et al. 2005; Dzbek & Korzeniewski, 2008) studied metabolite stability, but their models did not include the citric acid cycle, metabolite transporters and mitochondrial Ca²⁺ dynamics. Wu et al. (2007, 2008) took a similar approach to ours in the study of metabolite stability and demonstrated that P_i was a primary feedback signal for stimulating oxidative phosphorylation. However, they did not consider the Ca²⁺‐dependent regulatory mechanisms, so that their model could not reproduce the experimental results of Territo et al. (2000).

The present simulation study has several limitations. Firstly, we based the model mainly on experimental data from isolated cardiac mitochondria, and the kinetics of enzymes and transporters in intact myocytes may be different from those in isolated mitochondria. Further improvement of the model will be required. However, in the present situation, it is practically impossible to obtain the kinetic parameters for mitochondrial enzymes and transporters in vivo. The simulation approach based on existing experimental data, as conducted in our present study, is the most promising way to understand mitochondrial function and energy metabolism in vivo. Secondly, glycolysis and β‐oxidation of fatty acid were not incorporated in this model. We do not expect that the inclusion of glycolysis and β‐oxidation would affect the main conclusion of this study because all of the components of the citric acid cycle, and PDHC, are activated by the substrates. However, it would be interesting to test in the future how flux balance between glycolysis and β‐oxidation affects metabolite stability during workload transition. Lastly, although our model is based on existing experimental data, the mechanisms of some phenomena, such as Ca²⁺‐dependent activation of SN and P_i‐dependent activation of Complex III, have not been well clarified. Further experimental studies to obtain the mechanistic insights are obviously needed to create a more realistic mathematical model.

Additional information

Competing interests

The authors declare that they have no conflicts of interest with the contents of this article.

Author contributions

All studies were performed at Kyoto University, Ritsumeikan University and University of Fukui. R.S. created most of models of enzymes and transporters. A.T. created a simple cardiac cell model implemented with mitochondria, analysed the model and wrote the paper. Y.H. created models of ion transporters. N.I. conceived the idea for the project. S.M. conceived the idea for the project, analysed the model, and wrote the paper with A.T. All authors approved the final version of the manuscript and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

This work was supported by the leading project for Biosimulation (A.T., N.I. and S.M.), the Biomedical Cluster Kansai project (Y.H., N.I. and S.M.), and JSPS KAKENHI grant Numbers 26670101 (S.M.), 15H04674 (S.M.), and 26291019 (A.T.).

Supporting information

Disclaimer: Supporting information has been peer‐reviewed but not copyedited.

Appendix. Model variables, parameters and equations.

Source Code S1. Source codes of components written in Java class.

XML S1. An XML file to execute simulations of isolated mitochondrial experiments by Bose et al. (2003).

XML S2. An XML file to execute simulations of isolated mitochondrial experiments by Territo et al. (2000).

XML S3. An XML file to execute simulations using a simple cardiac cell model with full substrates.

XML S4. An XML file to execute simulations using a simple cardiac cell model with malate/glutamate.

Figure S1. Kinetic studies of the reaction catalysed by CS.

Figure S2. Kinetic studies of the reaction catalysed by ACO.

Figure S3. Kinetic studies of the reaction catalysed by ICDH.

Figure S4. Kinetic studies of the reaction catalysed by OGDH.

Figure S5. Kinetic studies of the reaction catalysed by SCS.

Figure S6. Kinetic studies of the reaction catalysed by SDH.

Figure S7. Kinetic studies of the reaction catalysed by FH.

Figure S8. Kinetic studies of the reaction catalysed by MDH.

Figure S9. Kinetic studies of the reaction catalysed by NDK.

Figure S10. Kinetic studies of the reaction catalysed by AST.

Figure S11. Kinetic studies of the reaction catalysed by PDHC.

Figure S12. Kinetic studies of the reaction catalysed by PC.

Figure S13. Kinetic studies of the reaction catalysed by ALT.

Figure S14. Time courses of NADH and ΔΨ changes in the simulation of experiment by Bose et al. (2003).

Figure S15. [Ca²⁺]_cyt dependence of mitochondrial model.

Figure S16. Ca²⁺ dependences of enzymes and transporters.

Figure S17. [P_i]_mit dependences of OGDH, SCS and C3.

Figure S18. Workload and [Ca²⁺]_cyt dependences of energy metabolites in the simple cardiac cell model without metabolite controls.

Figure S19. Workload and [Ca²⁺]_cyt dependences of energy metabolites in the simple cardiac cell model with increased activity of CaUni.