Modelling individual difference in visual categorization

Abstract

Recent years has seen growing interest in understanding, characterizing, and explaining individual differences in visual cognition. We focus here on individual differences in visual categorization. Categorization is the fundamental visual ability to group different objects together as the same kind of thing. Research on visual categorization and category learning has been significantly informed by computational modeling, so our review will focus both on how formal models of visual categorization have captured individual differences and how individual difference have informed the development of formal models. We first examine the potential sources of individual differences in leading models of visual categorization, providing a brief review of a range of different models. We then describe several examples of how computational models have captured individual differences in visual categorization. This review also provides a bit of an historical perspective, starting with models that predicted no individual differences, to those that captured group differences, to those that predict true individual differences, and to more recent hierarchical approaches that can simultaneously capture both group and individual differences in visual categorization. Via this selective review, we see how considerations of individual differences can lead to important theoretical insights into how people visually categorize objects in the world around them. We also consider new directions for work examining individual differences in visual categorization.

Categorization is a fundamental building block of human visual cognition. We need to be able to recognize objects in the world as kinds of things because we rarely see the exact same object twice and things we learn about one object should generalize to other objects of the same kind. Kinds of things are called categories. Recognizing an object as a kind of thing is called categorization. Once an object is categorized, whatever knowledge we have about that category can be used to make inferences and inform future actions. Humans and animals need to categorize friend from foe, edible from poisonous, and then act accordingly (e.g., Goldstone, Kersten, & Carvalho, 2003; Murphy, 2002; Richler & Palmeri, 2014). Without our ability to categorize, every visual experience would be a brand new experience, eliminating the benefit of past experience and its successes and failures as a guide to future understanding and future action. Categorization is also a gateway to conceptual knowledge, whereby we can combine an infinite variety of possible thoughts into structured groups, communicate via a set of common concepts, and decrease the amount of information we need to handle in each moment.

Cognitive psychologists and vision scientists often aim to identify general mechanisms that underlie human perception and cognition. Significant progress has been made developing and testing theories that embody general mechanisms to explain behavior on average. But anyone who has ever conducted a behavioral experiment quickly realizes that people vary tremendously in how they perform different kinds of tasks. Individual differences in performance can occur for many different reasons, ranging from uncontrolled differences in experimental context, to variation in past experience, to different levels of motivation, to the selection of different visual and cognitive strategies, to relatively stable individual differences in ability, however defined. We can treat all this variability as a mere nuisance – noise or error variance in the common parlance – or we can try to characterize, understand, and explain how and why people vary. While some research areas, like intelligence (e.g., Conley, 1984; Gohm, 2003) and working memory (e.g., Engle, Kane, & Tuholski, 1999; Kane & Engle, 2002; Lewandowsky, 2011; Unsworth & Engle, 2007), have a rich history of examining individual differences, only relatively recently have researchers in visual cognition begun to examine individual differences systematically (e.g., Duchaine & Nakayama, 2006; Gauthier et al., 2013; Lee & Webb, 2005; McGugin, Richler, Herzmann, Speegle, & Gauthier, 2012; Vandekerckhove, 2014).

Why study individual differences? Theories of perception and cognition in psychology, vision science, and neuroscience are intended to be theories of individual behavior, quite unlike theories of group behavior in the social sciences, which often intend to explain the aggregate. We need to understand not only the average, but the causes of variability in perception and cognition (Cronbach, 1975; Plomin & Colledge, 2001); both general patterns and individual differences in behavior are basic characteristics of human perception and cognition that our theories must explain. Any viable theory must account not only for aggregate behavior, but also group differences and true individual subject differences, and we can ultimately reject theories that offer no explanation at all for individual behavior. As we will see, theories that make similar predictions about the aggregate may make quite different predictions when it comes to the individuals. Moreover, ignoring individual differences in favor of group averages can give rise to a misleading account of behavior because the act of averaging or aggregating can produce results that are qualitatively different from the behavior of any individual within that aggregate (e.g., Estes, 1956)

In this paper, we discuss and review work examining individual differences in visual object categorization. Specifically, because research on visual categorization has long had formal computational modeling as a pivotal component of theory development (Wills & Pothos, 2012), our discussions will center on how models of visual categorization have addressed individual differences and have been informed by individual differences. Numerous review papers and books have provided a gallery of models of categorization (e.g., Kruschke, 2005, 2008; Lee & Vanpaemel, 2008; Pothos & Wills, 2011; Richler & Palmeri, 2014; Wills & Pothos, 2012). Our goal is to examine how these models address individual differences, not to chronicle the corpus of proposed models, so our review will be selective in order to highlight models most relevant to our discussion. Furthermore, unlike many reviews that outline individual categorization models independently from one another, we chose instead to juxtapose the major formal models by outlining their common components and their critical differences in terms of how objects are perceptually represented (Perceptual Representation), how categories are represented (Category Representation), and how decisions are made (Decision Process).

We begin by describing the components of many formal models of categorization and highlight how those components might vary across individuals to predict and explain individual differences in categorization behavior. We then provide a selective review highlighting examples of how computational modeling has treated individual differences and how individual differences have informed our theoretical understanding of visual categorization.

Overview of Visual Categorization Models

The models we will discuss all explain how we decide that an object is a kind of thing. In a visual categorization experiment with real objects, we can test people on how well and how quickly they know that some objects are planes, others are trains, and others are automobiles. In a visual category learning experiment with novel objects, people might first learn that some objects are mogs, others are bliks, and others are rabs, and we can later test them on how well they apply that knowledge to learned objects or generalize to new objects (e.g., Richler & Palmeri, 2014). Models instantiate hypotheses we have about the mechanisms that underlie these categorization decisions and we evaluate models by comparing their predictions to observed categorization behavior.

Many categorization models decompose their internal mechanisms into at least three key components: the perceptual representation of an object, internal representations of categories, and a decision process that determines category membership based on the available evidence from matching a perceptual representation to internal category representations. Each component – perceptual representation, category representation, and decision process – can be specified in different ways, and these differences can often be the focus of vigorous debate. Often, different visual categorization models can be described as different combinations of these components (Kruschke, 2005, 2008; Lee & Vanpaemel, 2008). For example, two competing models might share the same assumptions about perceptual representations (e.g., that objects are represented along multiple psychological dimensions) and decision processes (e.g., that decisions are made according to the relative category evidence) but differ in their assumptions about category representations (e.g., that categories are represented in terms of prototypes vs. exemplars) (e.g., Ross, Deroche, & Palmeri, 2014; Shin & Nosofsky, 1992).

In what follows, we step through these three major components, discuss various ways they are implemented in different models, and discuss how different specifications of each component might incorporate individual differences. Much of our discussion will focus on asymptotic models of object categorization, but will include some discussion of models of category learning as well (for one review, see Kruschke, 2005). Because our focus is on the components of models and how they can vary across individuals, we will not discuss in great detail all of the various empirical and theoretical studies that purport to support or falsify particular models in this article (e.g., see Ashby & Maddox, 2005; Pothos & Wills, 2011; Richler & Palmeri, 2014).

Perceptual Representations

All models of object categorization assume that an internal perceptual representation of a target object is compared to stored representations of category knowledge in order to decide which category that object belongs to. Models traditionally referred to as object recognition models often describe in great detail the complex neural network that starts with the retina and runs through the hierarchy of ventral visual cortical areas; at the top of that hierarchy are nodes of the network that make categorization decisions (e.g., Riesenhuber & Poggio, 2000; Serre, Oliva, & Poggio, 2007; Tong, Joyce, & Cottrell, 2005). Much of the effort in developing these models focuses on the transformations that take place from the retinal image to high-level object representations (how the object itself is mentally represented), with far less discussion of alternative assumptions about category representations (how its kind is mentally represented) and decision making (how a specific choice of its kind is made) (for further discussion, see also Palmeri & Cottrell, 2009; Palmeri & Gauthier, 2004).

That contrasts with most categorization models and category learning models.¹ Many of these models simply assume that objects are represented as vectors of features or dimensions without specifying in much detail how those features or dimensions are derived from the retinal image of an object. Instead, the features or dimensions of an object’s perceptual representation might be based on what features or dimensions are explicitly manipulated by the experimenter, they might simply reflect a statistical distribution of within- and between-category feature overlap (e.g., Hintzman, 1986; Nosofsky, 1988), or they might be derived using techniques like multidimensional scaling (e.g., Nosofsky, 1992; Shepard, 1980). Whereas the perceptual representation of an object is the penultimate stage of processing in some object recognition models, the perceptual representation is the input stage of many categorization models. That said, it is possible in principle to use the perceptual representation created by an object recognition model as the input to an object categorization model (e.g., Mack & Palmeri, 2010; Ross et al., 2014).

There is an interesting and rich history of debate regarding featural versus dimensional representations of objects and how similarities based on the presence or absence of qualitative features or geometric distances in a continuous space defined by dimensions are defined ( Shepard, 1980; Tversky, 1977; Tversky & Gati, 1982). Because many models have been formalized assuming that objects are represented along psychological dimensions (but see Lee & Navarro, 2002), that is where we focus here for illustration. Object dimensions can be simple, like size and brightness (e.g., Goldstone, 1994), more complex but local, like object parts (e.g., Nosofsky, 1986; Sigala & Logothetis, 2002), or more global properties of object shape (e.g., Folstein, Gauthier, & Palmeri, 2012; Goldstone & Steyvers, 2001). Objects are often represented as points in a multidimensional psychological space (Nosofsky, 1992).

The similarity between two objects is often defined as being inversely proportional to their distance in that space (e.g., Nosofsky, 1986; Shepard, 1987). Some categorization models assume that the same stimulus (X, Y) does not always produce the same percept (x, y) because sensory-perceptual processes are inherently noisy (e.g., Ashby & Gott, 1988; Ashby & Townsend, 1986), in a sense representing a stimulus as a probability distribution or a sample from a probability distribution in multidimensional psychological space rather than as a fixed point in that space. And some categorization models assume that different stimulus dimensions become available to the perceiver more quickly than others depending on their perceptual salience (e.g., Lamberts, 2000).

To make things concrete, let us consider, for example, a model like the Generalized Context Model (GCM; Nosofsky, 1984, 1986; see also Kruschke, 1992; Lamberts, 2000; Nosofsky & Palmeri, 1997a). Objects are represented as points in a multidimensional psychological space. The distance d_ij between representations of objects i and j is given by

$$d_{\mathit{\text{ij}}}={\left[\sum _{m=1}^M{w}_m{|i_m-j_m|}^r\right]}^{1/r},$$ (1)

where m indexes the dimensions in psychological space, M is the total number of dimensions, w_m is the weight given to dimension m, as described later, and r specifies the distance metric; and similarity s_ij is given by

$$S_{\mathit{\text{ij}}}=\text{exp}(-c\cdot d_{\mathit{\text{ij}}}),$$ (2)

where c is a sensitivity parameter that scales distances in psychological space. Variants of these representational formalizations are used in a range of models, including exemplar (Nosofsky, 1986), prototype (Smith & Minda, 2000), and rule-based (Nosofsky & Palmeri, 1998) models of categorization.

In a model assuming no systematic individual differences, all subjects would share the same psychological space (i_m, j_m), with the same dimensional weightings (w_m) and sensitivity scalings (c) for computing distances (d_ij) and similarities (s_ij) between represented objects. Alternatively, and perhaps more likely, different subjects could differ in their psychological representations of objects. While it is theoretically possible that different subjects could have entirely different multidimensional psychological spaces, with different numbers and types of dimensions and different relative positions of objects in that space, it may be more likely that subjects differ from one another quantitatively rather than qualitatively; for example, subjects may share the same relative positioning of objects in psychological space but weight the dimensions differently when computing similarities (e.g., see Palmeri, Wong, & Gauthier, 2004).

Examples of potential individual differences in perceptual representations are illustrated in Figure 1. For example, some combination of learning and experience, or maturation and genetics, could cause some subjects to have greater (or lesser) perceptual discriminability or lesser (or greater) perceptual noise in object representations in psychological space. This would be reflected by a relative expansion (or contraction) of psychological space for those subjects, for example comparing subjects P1 and P2 in Figure 1. In effect this relative expansion (or contraction) of perceptual space makes distances between objects relatively larger (or smaller), which in turn makes similarities relatively smaller (or larger), which makes perceptual confusions relatively lower (or higher).

Figure 1.

Illustration of some potential individual differences in perceptual representations. Each symbol represents an object as a point in a two-dimensional psychological space; in this example, consider circle symbols as objects from one category and triangle symbols as objects from another category. Different individuals can have relatively low overall perceptual discriminability (P1) or high overall perceptual discriminability (P2); the space can be stretched along dimension 1 and shrunken along dimension 2 (P3), or vice-versa (P4).

In addition to expanding or contracting the entire psychological space, different subjects could stretch or shrink particular dimensions differently, for example comparing subjects P3 and P4 in Figure 1. This relative stretching or shrinking of particular dimensions could reflect past experience with objects, for example based on how diagnostic particular dimensions have been for learned categorizations. Stretching along a relevant dimension makes diagnostic distinctions between objects larger, making objects that vary along that dimension easier to categorize. Two forms of stretching and shrinking have been considered (e.g., Folstein, Palmeri, Van Gulick, & Gauthier, 2015). One form of relative stretching along diagnostic dimensions is top-down and flexible, weighting certain dimensions more than others when computing similarities in a particular categorization task, mathematically formalized in models like the GCM via the dimension weight parameter (w_m). Different categorizations might be based on different diagnostic dimensions (e.g., Nosofsky, 1986, 1992), and different subjects might weight those dimensions more or less effectively. In addition to facilitating categorization in a flexible manner, the relative stretching of object representations along particular dimensions could reflect long-lasting changes to how we perceive and represent objects. Objects that vary along a dimension relevant to previously learned categories can remain more perceptually discriminable in tasks that may not even require categorization (e.g., Goldstone, 1994), with differences along particular dimensions remaining more salient even when those dimensions are not diagnostic for the current task (e.g., Folstein et al., 2012; Folstein, Palmeri, & Gauthier, 2013; Viken, Treat, Nosofsky, McFall, & Palmeri, 2002). Different subjects can stretch different dimensions to different degrees, as reflected in the contrast between subject P3 and P4 in Figure 1².

Category Representations

Models differ considerably in what they assume about category representations. Categorization is a form of abstraction in that we treat different objects as kinds of things, and perhaps the greatest source of debate is whether such abstraction requires that category representations themselves be abstract. On one extreme are models that assume that categories are represented by abstract prototypes or rules and on the other extreme are models that assume that categories are represented by the specific exemplars that have been experienced; we explain the differences between these kinds of category representations below. For illustration, here we consider only representations on the extremes of the abstraction continuum and do not consider models that assume more nuanced intermediate forms of abstraction (e.g., Anderson, 1991; Love, Medin, & Gureckis, 2004).

To describe different formal models of categorization in a common mechanistic language, we assume that for all models, an object representation is compared to stored representations of different possible categories and that the result of this comparison is the evidence that an object belongs to each of possible categories. For the simple case of two categories, A and B, we use the notation E_iA and E_iB to denote the evidence that object i belongs to Category A or Category B, respectively. In the next section, we describe how these evidences are used to make a categorization decision.

Classic research on categorization suggested that natural categories have a graded structure characterized by notions of “family resemblance” (e.g., Rosch & Mervis, 1975). It is easier, for example, to categorize a robin as a bird than an ostrich as a bird because a robin is more similar to the prototypical or average bird, suggesting that the bird category is defined by its prototype. Analogously, when trained on category exemplars that are distortions of a prototype, during transfer tests after learning, people categorize a previously unseen prototype on average as well as, and sometimes better than, trained category exemplars, suggesting that a prototype had been abstracted from the experienced exemplars during learning (e.g., Homa, Cross, Cornell, Goldman, & Shwartz, 1973; Posner & Keele, 1968). As the name implies, in prototype models, each category is represented by its own prototype (Smith & Minda, 1998), which is often assumed to be the average of all the instances of a category that have been experienced. The evidence E_iA that object i is a member of Category A is simply given by similarity between the representation of object i and the representation of the prototype P_A.

$$E_{\mathit{\text{iA}}}=S_{{\mathit{\text{iP}}}_A},$$ (3)

where S_iPA is specified by Equations 1 and 2. As illustrated in Figure 2, one potential source of individual differences is that different people form different prototypes, perhaps because they have experienced different category instances, or the quality of those stored prototypes could vary as well because of individual differences in learning mechanisms (see the Prototypes row in Figure 2).

Figure 2.

Illustration of various quantitative and qualitative individual differences in category representations. The four rows illustrate qualitative individual differences in types of category representations, exemplars, prototypes, rules, or decision bounds. The two columns illustrate quantitative differences for individuals sharing the same qualitative category representation (e.g., different quality of exemplar representations, different category prototypes, different kinds of rules or decision bounds).

Rather than assume abstraction, exemplar models assume that a category is represented in terms of visual memories for all of the particular instances that have been experienced and those stored exemplars are activated according to their similarity to the object to be categorized. The degree to which an object is similar to exemplars from just a single category determines how well that object will be categorized. Categorization behaviors that seem to suggest abstraction, such as the prototype abstraction, are well-predicted by exemplar models that assume no abstraction (e.g., Hintzman, 1986; Palmeri & Nosofsky, 2001; Shin & Nosofsky, 1992) .

Mathematically, for models like the GCM (Nosofsky, 1984, 1986), the evidence that object i is a member of Category A (denoted C_A), is given by the summed similarity of that object to all previously stored exemplars of that category,

$$E_{\mathit{\text{iA}}}=\sum _{j\in C_A}{N}_j{S}_{\mathit{\text{ij}}},$$ (4)

where s_ij is specified by Equations 1 and 2; N_j is an exemplar-strength parameter, which can reflect, for example, the differential frequency with which an individual has encountered particular exemplars. Both the particular collection of stored exemplars and the strength of those exemplars could vary across individuals. In addition, the quality of exemplar memories could vary across individuals as well. One way to mathematically instantiate this idea is to allow different values of the sensitivity parameter c in Equation 2 for different subjects (see the Exemplars row in Figure 2). In much the same way that individuals can differ in the quality of their perceptual representations, they can also differ in the quality of the stored memory representations, as reflected by the steepness of the generalization gradients defined by the sensitivity parameter (e.g., Nosofsky & Zaki, 1998; Palmeri & Cottrell, 2009).

Prototype and exemplar models both assume that categorization depends on similarity to stored category representations. An alternative conception is that categorization depends on boundaries that carve perceptual space into response regions or abstract rules that specify necessary and sufficient conditions for category membership. Early accounts often equated category learning with logical rule learning (e.g., Bourne, 1970; Trabasso & Bower, 1968). These early rule-based accounts were largely rejected in favor of similarity-based accounts until the 1990s when a series of models combining rules with other forms of representation began to be proposed (e.g., Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Erickson & Kruschke, 1998; Nosofsky, Palmeri, & McKinley, 1994; Nosofsky & Palmeri, 1998; Palmeri, 1997).

Rules can take on logical forms having a wide range of complexity (e.g., Feldman, 2000). Consider first a simple single-dimension rule, for example that dark objects are in Category A and light objects are in Category B. This simple rule carves psychological space into response regions such that objects on one side of the darkness-lightness boundary are an A regardless of the values along other dimensions. In its simplest form, if object i falls in the A region defined by the boundary, then E_iA=1 and E_iB=0; if it falls in the B region, then E_iA=0 and E_iB=1. But as we will see in the next section, the addition of decisional noise can turn a deterministic categorization into one that is more probabilistic.

It is natural to imagine that different individuals might form different rules (as illustrated in the Rules row in Figure 2). Indeed, the rule-plus-exception (RULEX) model (Nosofsky, Palmeri, et al., 1994; Nosofsky & Palmeri, 1998) explicitly assumes that different individuals can learn different rules to ostensibly the same object categorization problem because they select different dimensions to evaluate as potential candidates, have different criteria for accepting perfect versus imperfect rules, or have different preferences for simple rules versus more complex rules. Some people might learn to form a rule along one dimension, others might learn to form a rule along another dimension, and still others might learn a conjunction of two other dimensions. RULEX allows people to learn imperfect rules, and assumes that they memorize to varying degrees any exceptions to learned rules, hence the “EX” in “RULEX”. As we will see in more detailed later, variability in categorization across individuals according to RULEX is assumed to reflect the idiosyncratic rules and exceptions that different people learn when confronted with the same categorization problem to solve.

The idea that boundaries can be learned to divide psychological space into response regions is generalized in so-called decision boundary models, as instantiated with General Recognition Theory (GRT Ashby & Gott, 1988; Ashby & Townsend, 1986). These boundaries can correspond to rules along individual dimensions (e.g., Ashby et al., 1998), but they can also carve psychological space using various forms of linear or nonlinear boundary to separate different categorization regions; decision boundaries can correspond to simple rules along a single dimension that are easy to verbalize or to quite complex multidimensional nonlinear discriminations that are non-verbalizable. Decision boundaries for different individuals can differ qualitatively in their type (linear vs. quadratic), quantitatively in their locations, or some combination of both (e.g., Danileiko, Lee, & Kalish, 2015) (as illustrated in the Decision Bounds row in Figure 2).

Individual differences in category representation can be a major source of individual differences in visual categorization performance. Individuals can differ within the same system of category representation. If everyone forms prototypes, where is the location of their prototype? If everyone learns exemplars, what exemplars do they have stored in memory and how well are they stored? And if everyone forms rules, what kind of rules have they formed? Alternatively, different individuals can form different kinds of category representations. Some might abstract a prototype, others might learn exemplars, and still others might create rules. And if people create hybrid representations combining different kinds of representations, then individuals can differ in their particular combinations of representations. For example, some might use both rules and exemplars, otherwise might use prototypes and exemplars. Later in this article, we will discuss example approaches of considering individual differences in category representations of these sorts.

Decision Processes

Matching the perceptual representation of an object with learned category representations yields evidence that the object belongs to each possible category. The decision process translates this collection of evidence measures into a classification response, which can predict, for example, the probability of each possible categorization of the object and the response time to make a categorization decision. We will continue to illustrate using a simple example of a decision between two possible categories, A and B, with evidence values E_iA and E_iB that object i belongs to each category, but recognize that all of these decision mechanisms can be extended beyond the simple two-choice scenario.

We first consider decision processes that only predict response probabilities. A purely deterministic decision favors category A whenever E_iA is greater than E_iB. Allowing for possible response biases, category membership is simply given by:

$$P_{\mathit{\text{iA}}}=1,\mathit{\text{ if }}{E}_{\mathit{\text{iA}}}+b_A>E_{\mathit{\text{iB}}}+b_B,$$ (5)

where b_A and b_B are the biases of responding with Category A and B, respectively.

Alternatively, we can imagine that when E_iA and E_iB are relatively close in value that the same object might sometimes be classified as a member of Category A, and other times as a member of Category B. One well-known probabilistic decision mechanism, harkening back to the classic Luce choice rule (Luce, 1963), gives the probability of classifying the object i as a member of Category A by:

$$P_{\mathit{\text{iA}}}=\frac{b_A{E}_{\mathit{\text{iA}}}}{b_A{E}_{\mathit{\text{iA}}}+b_B{E}_{\mathit{\text{iB}}}},$$ (6)

where b_A and b_B are the bias of responding Category A and B, respectively. Response biases present in both deterministic and probabilistic decision processes are a common source of individual differences in categorization and a whole host of other cognitive phenomena.

Deterministic and probabilistic decision processes represent two ends of a continuum. Purely deterministic decisions can become more probabilistic when there is noise the decision process:

$$P_{\mathit{\text{iA}}}=1,\mathit{\text{ if }}{E}_{\mathit{\text{iA}}}+b_A>E_{\mathit{\text{iB}}}+b_B+\epsilon ,$$ (7)

where ε is from a normal distribution with a mean of 0 and a standard deviation of 𝝈. And probabilistic decisions can become more deterministic with a nonlinear rescaling of the Luce choice rule:

$$P_{\mathit{\text{iA}}}=\frac{{[b_A{E}_{\mathit{\text{iA}}}]}^{\gamma }}{{[b_A{E}_{\mathit{\text{iA}}}]}^{\gamma }+{[b_B{E}_{\mathit{\text{iB}}}]}^{\gamma }},$$ (8)

where γ is a parameter that reflects the degree of determinism in responding (Maddox & Ashby, 1993; Nosofsky & Palmeri, 1997b; see Kruschke, 2008, for other extensions); as γ approaches infinity, purely deterministic responding is predicted, and as γ approaches 1, probabilistic responding is predicted. In both formalizations, individuals can differ from one another in the amount of noise (Equation 7) or relative determinism (Equation 8) in their decision process.

Decision processes that only predict response probabilities ignore time. Time is not only an informative component of categorization behavior (e.g., Mack & Palmeri, 2011, 2015) but also an important potential source of individual differences, including factors like well-known trade-offs between speed and accuracy (e.g., Pew, 1969; Wickelgren, 1977). One popular class of decision models that predict response times and response probabilities are well-known sequential sampling, also known as accumulation of evidence, models (for a review of different classes of sequential sampling models, see Ratcliff & Smith, 2004), including diffusion (Ratcliff & McKoon, 2008; Ratcliff, 1978) and random walk models (Nosofsky & Palmeri, 1997a; Nosofsky & Stanton, 2005), and the linear ballistic accumulator model (Brown & Heathcote, 2005, 2008).

Sequential sampling models assume that evidence accumulates over time towards response thresholds associated with alternative choices and that variability in this accumulation of evidence over time is an important source of variability in categorization response time and response choices. As illustrated in Figure 3, these models decompose response times into a non-decision time associated with the time to perceive an object (and the time to execute a motor response) and a decision time associated with the accumulation of evidence to a response threshold. The decision process itself assumes a starting point for evidence, which can be biased toward some responses over other responses, an average rate of evidence accumulation, which is often referred to as drift rate, and the response threshold, which can be adjusted up or down to control the trade-off between speed and accuracy. The variants of these models assume some form of variability within or between trials, which gives rise to variability in predicted behavior. The parameters of such models have intuitive psychological interpretations that have been validated empirically (e.g., Donkin, Brown, Heathcote, & Wagenmakers, 2011; Ratcliff & Rouder, 1998; Voss, Rothermund, & Voss, 2004) and all can be potential sources of individual differences (as illustrated in Figure 3).

Figure 3.

Illustration of potential individual differences in the decision process as instantiated by a stochastic accumulator model. Within or across conditions, individuals can vary in their non-decisional time, drift rate, threshold, or bias. A: individuals with longer non-decisional time than the others (τ); B: individuals with higher drift rate than the others (δ); C: individuals with larger threshold than others (α); D: individuals who are more biased toward the upper boundary than others (β).

Sequential sampling models provide a generic decision mechanism that can be incorporated into models of a wide array of perceptual and cognitive processes. Nosofsky and Palmeri (1997a; Palmeri, 1997) proposed the Exemplar-Based Random Walk (EBRW) model of categorization that combined the random walk sequential sampling architecture with what is essentially a theory of the drift rate parameters. In EBRW, accumulation rates driving a random walk are built mathematically from assumptions embodied in the GCM combined with key temporal components borrowed from the instance theory of automaticity (Logan, 1988). Specifically, the probability of taking a step toward category A for stimulus i is defined as

$$p_i=\frac{E_{\mathit{\text{iA}}}}{E_{\mathit{\text{iA}}}+E_{\mathit{\text{iB}}}}.$$ (9)

And the speed with which steps are taken is based on some additional temporal assumptions that go beyond the scope of this article (see Nosofsky & Palmeri, 1997a, 2015). This combination of GCM and sequential sampling models created a model that can explain a wide array of categorization behavior, including predictions about variability in errors and response times for individual objects and how these changes with learning and experience (e.g., Mack & Palmeri, 2011; Nosofsky & Palmeri, 2015).

Modeling Individual Differences in Categorization

We now turn to examining both how formal models of visual categorization have captured individual differences and how individual difference have informed the development of formal models. As we noted before, our selection of examples will intentionally provide a bit of an historical perspective, starting with modeling approaches that ignore individual differences, to those that capture group differences, to those that predict individual differences, and to more recent hierarchical approaches that aim to simultaneously capture both group and individual differences in visual categorization.

Accounting for Average Data

Not unlike most areas of psychology, a significant amount of early research in categorization either ignored individual differences or treated individual differences as little more than uninteresting error variance. That error variance is mitigated by averaging subject data, highlighting the systematic variance across conditions or across stimuli. When evaluating computational models, those models are often tested on how well they can account for particular qualitative and quantitative aspects of this average data.

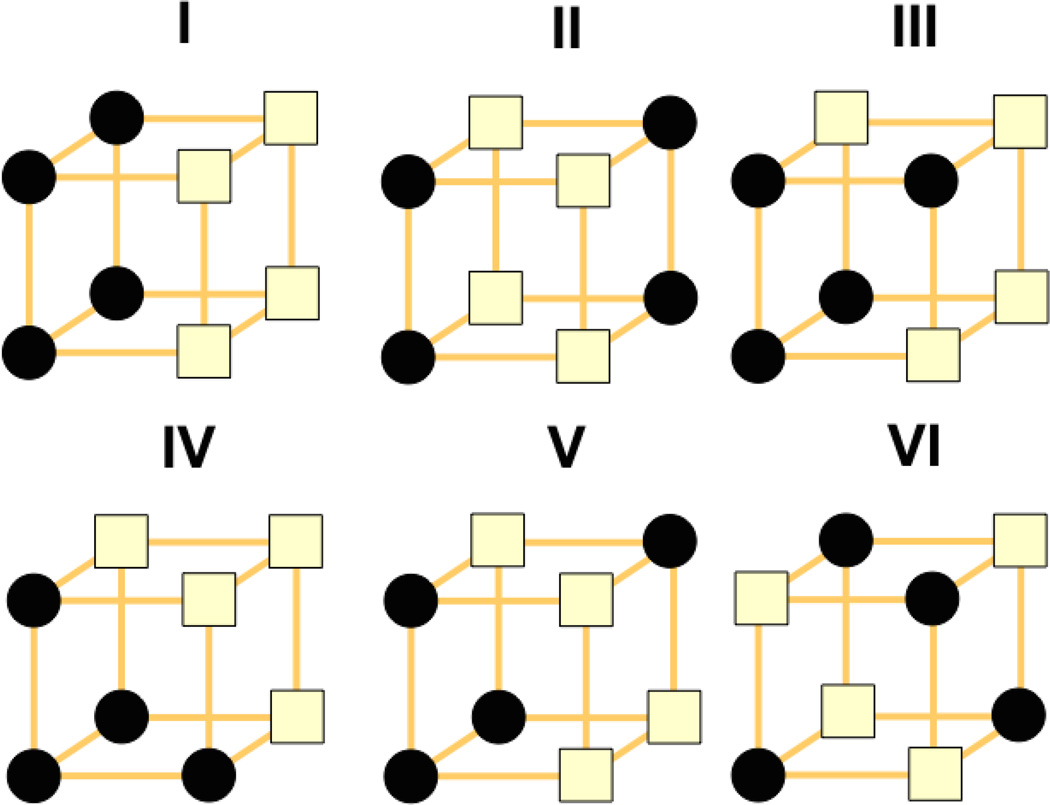
Let us consider first the classic study by Shepard, Hovland, and Jenkins (1961). The abstract stimulus structure and category structures are illustrated in Figure 4. There are three binary-valued dimensions, for example shape, color, and size, yielding eight possible stimuli. When arranging these eight stimuli into two categories with four items per category, there are six possible category structure types, allowing for rotation and reflection (see also Feldman, 2000). In Figure 4, the eight vertices of a cube represent the eight possible stimuli, with black vertices representing members of one category and white vertices representing members of the other category for each of the six types. For Type I, only a single dimension is relevant; for Type II, two dimensions are relevant, as part of a logical exclusive-or problem; for Types III, IV, and V, all three dimensions are relevant to varying degrees; and Type VI essentially requires a unique identification of each item since all items are adjacent to members of the opposite category. For each problem type, subjects were presented with stimuli one at a time, tried to categorize each stimulus as a member of one of the two categories, and received corrective feedback after their response; the ultimate goal was to try to learn to categorize all eight stimuli correctly.

Figure 4.

Illustration of six types of categorization structures tested by Shepard, Hovland, and Jenkins (1961; see also Nosofsky, Gluck, Palmeri, McKinley, & Glauthier, 1994). The eight vertices of each cube represent abstractly the eight possible stimuli constructed from three binary-valued stimulus dimensions. Vertices depicted by black circles are those assigned to on category and vertices depicted by light squares are those assigned to the other category.

The key data are either the average number of errors made when learning each problem type (Shepard et al., 1961) or the average proportion of errors for each type in each block of training (Nosofsky, Gluck, Palmeri, McKinley, & Glauthier, 1994). For stimuli composed of separable dimensions, Type I is the easiest to learn, followed by Type II, then by Types III, IV, and V of roughly equally difficulty, and finally by Type VI (see Nosofsky & Palmeri, 1996, for the case of stimuli composed of integral dimensions). The qualitative ordering of categorization problem difficulty and the quantitative learning curves have been benchmark data for evaluating categorization models (e.g., Kruschke, 1992; Love et al., 2004; Nosofsky, Palmeri, et al., 1994).

Note that for the Shepard, Hovland, and Jenkins category structure, models are not only evaluated on how well they account for learning and performance averaged across subjects, they are also typically evaluated on how well they account for problem difficulty averaged across items (but see Nosofsky, Gluck, et al., 1994). Individual subject effects and individual item effects are often companion pieces in traditional discussions in the individual differences literature, especially in the area of psychometrics (Wilson, 2004). While early work in categorization modeling largely ignore individual differences, a significant body of work has focused on predictions of item effects: how easy or difficult it is to learn particular members of categories, what kinds of errors are made categorizing particular items, and how learned categorizations are generalized to particular untrained transfer items.

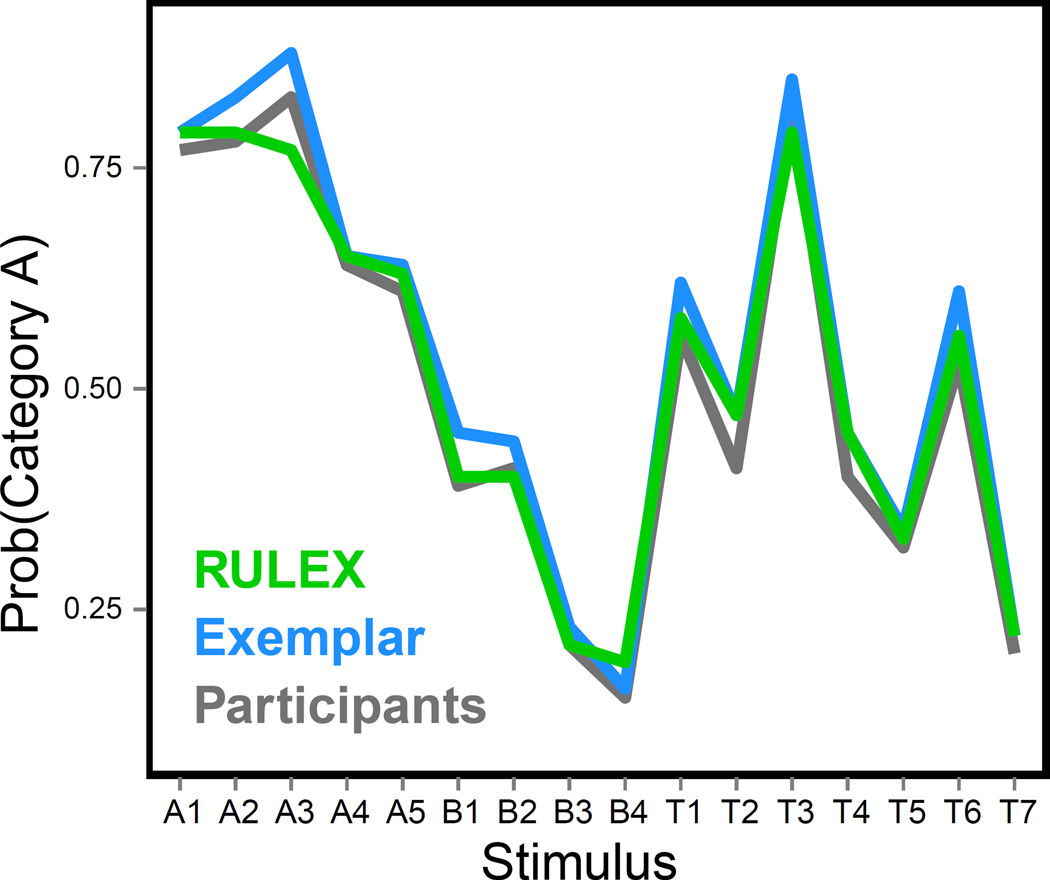
Consider, for example, a classic experiment from Medin and Schaffer (1978), which has been replicated dozens of times (e.g., Johansen & Palmeri, 2002; Love et al., 2004; Mack, Preston, & Love, 2013; Medin, Altom, & Murphy, 1984; Nosofsky, 2000; Nosofsky, Palmeri, et al., 1994; Palmeri & Nosofsky, 1995; Rehder & Hoffman, 2005; Smith & Minda, 2000). The abstract category structure from their most widely replicated Experiment 2 is shown in Table 1. Stimuli vary on four binary-valued dimensions, yielding 16 possible stimuli. Many variants of stimulus dimensions have been used over the years; in Medin and Schaffer, the dimensions were form (triangle or circle), size (large or small), color (red or green), and number (one or two objects). Five stimuli (A1-A5) are assigned to Category A; four (B1-B4) are assigned to Category B; the remaining seven (T1-T7) are so-called transfer stimuli that subjects did not learn but on which they were tested after training. Subjects first learn to categorize the 9 training stimuli (A1-A5 and B1-B4), shown one at a time, into Category A or Category B with feedback over several training blocks. After training, subjects complete a transfer task in which all 16 stimuli are presented, including both the 9 training stimuli and the 7 transfer stimuli, with no feedback. The classification probabilities P(A) for each stimulus during transfer are averaged across all subjects. Observed data from one replication of this classic study is shown in Figure 5 (from Nosofsky, Palmeri, et al., 1994).

Table 1.

Category Structure from Experiment 2 of Medin and Schaffer (1978)

Stimulus	Dimension
	1	2	3	4
Category A
A1	1	1	1	2
A2	1	2	1	2
A3	1	2	1	1
A4	1	1	2	1
A5	2	1	1	1
Category B
B1	1	1	2	2
B2	2	1	1	2
B3	2	2	2	1
B4	2	2	2	2
Transfer
T1	1	2	2	1
T2	1	2	2	2
T3	1	1	1	1
T4	2	2	1	2
T5	2	1	2	1
T6	2	2	1	1
T7	2	1	2	2

Entries are the value of each stimulus along each of the four binary-valued dimensions. A1-A5 refer to the 5 stimuli assigned to category A. B1-B4 refer to the 4 stimuli assigned to category B. T1-T7 refer to the 7 stimuli that were not learned but tested in the transfer phase.

Figure 5.

Fits of an exemplar model (the context model of Medin & Schaffer, 1978) and the RULEX (rule-plus-exception) model (Nosofsky et al., 1994) to the averaged transfer data from a replication and extension of Medin & Schaffer (1978); from Experiment 1 of Nosofsky, Palmeri, and McKinley (1994).

The Medin and Schaffer (1978) category structure was originally designed specifically to contrast predictions of exemplar and prototype models by examining errors categorizing particular items. Specifically, a prototype model predicts that A2 would be more difficult to learn than A1 because A2 is less similar to the Category A modal prototype than A1; in contrast, an exemplar model predicts that A2 would be easier to learn than A1 because A2 is relatively similar to other exemplars of Category A and dissimilar to exemplars of Category B, whereas A1 is similar to exemplars of category B³. Since then, predicting categorization of all training and transfer items, not just A1 and A2, in this classic structure and its empirical variants has been a benchmark result for evaluating categorization models (e.g., Johansen & Palmeri, 2002; Medin et al., 2004; Mack et al., 2013; Nosofsky, Palmeri, et al., 1994; Rehder & Hoffman, 2005; Smith & Minda, 2000). Models are fitted to the averaged data, finding parameters that minimize the discrepancy between predicted and observed classification probabilities (e.g., Lewandowsky & Farrell, 2011). As illustrated in Figure 5, models assuming very different kinds of category representations – in this case exemplars for the context model and rules plus exceptions for the RULEX model – can produce similar accounts of the average data (for details, see Nosofsky, Palmeri, et al., 1994). As we will see later, considering individual differences in categorization may help tease apart how people learn categories defined by this category structure in ways that are masked when considering only average performance data.

Accounting for Group Differences

A step towards considering individual differences is considering group differences. Groups can differ because of brain damage, disease, age, experience, and a whole host of other factors, and from a theoretical perspective, computational models can be used to account for and explain those group differences. Moreover, the presence of those group differences can provide potentially challenging test of the mechanistic assumptions underlying computational models.

For example, Nosofsky and Zaki (1998) investigated whether an exemplar model could explain the observed dissociation between categorization and recognition observed when comparing groups with amnesia to control groups, as reported by Knowlton and Squire (1993). Using a variant of the classic dot pattern task of Posner and Keele (1968), Knowlton and Squire either exposed people to distortions of a prototype dot pattern and later asked them to classify new dot patterns in a categorization task, or they exposed people to a collection of random dot patterns and later asked them to judge dot patterns as new or old in a recognition memory task. Not surprisingly, given their memory impairments, Knowlton and Squire observed that individuals with amnesia performed significantly worse than controls at recognition memory. What was noteworthy was that they observed no significant difference between the groups at categorization. This dissociation between recognition and categorization was interpreted by Knowlton and Squire (1993) as support for multiple memory systems, a hippocampal system responsible for explicit recognition memory, which is damaged in amnesia, and another implicit category learning system, which is preserved.

By contrast, exemplar models assume that the same exemplar memories are used to recognize objects as old or new and to categorize objects as different kinds. Knowlton and Squire cited their observed dissociation as evidence that appears to falsify exemplar models outright. They claimed that a theory that assumes a single memory system supporting recognition and categorization, like the exemplar model, cannot account for a dissociation between recognition and categorization resulting from brain damage.

To formally test this claim, Nosofsky and Zaki (1998) generated predictions for two simulated groups of subjects, one with poor exemplar memory representations, simulating the group of individuals with amnesia, and one with normal exemplar memory representations, simulating the control group. These memory differences were instantiated by a single parameter that was allowed to vary between groups. Recall that the sensitivity parameter, c, in Equation 2 controls the scaling between distance in psychological space and similarity. When c is high, small differences in distance translate into large differences in similarity, but when c is low, large differences in distance are needed to generate comparable differences in similarity. As a consequence, relatively poorer memory representations can be simulated with relatively smaller values of c, making items that are far apart in terms of distance seem similar or confusable psychologically. Instantiating group differences with this single parameter difference, Nosofsky and Zaki showed that the exemplar model can indeed predict large significant differences in old-new recognition memory accompanied by only small nonsignificant difference in categorization (see also Palmeri & Flanery, 2002). The recognition task requires fine distinctions between old and new items, causing performance to be significantly impacted by poorer memory representations, whereas the categorization task requires broad generalization to experienced exemplars, causing performance to be relatively unaffected by poorer memory representations. A single memory-system exemplar model simulating memory differences between groups via a single parameter difference was capable of explaining the observed neuropsychological dissociation.

The parameters of computational models are often key engines for explaining individual and group differences. The core model components regarding how objects and categories are represented, how similarities and evidence are computed, and how evidence is accumulated to make a particular categorization at a particular time are commonly assumed to be the same across groups (or individuals within a group). What varies between groups (or individuals) is how those representations and processes are parameterized. As one example, differences between experts and novices can be explained in part by the quality of their visual percepts and visual memories (e.g., Palmeri et al., 2004; Palmeri & Cottrell, 2009). As another example, differences between individuals at risk for bulimia and those who are not can be explained in part by how much they weight body size dimensions in their categorizations (e.g., Viken et al., 2002).

But using computational models to account for group differences has limitations. Within a group, individual differences are averaged together, so accounting for group differences has many of the same limitations as accounting for average data. In addition, whether an empirical study or a computational modeling effort, dichotomizing potentially continuous individual differences – amnesic versus control, expert versus novice, bulimic versus control – potentially misses critical structure present in the fine-grained data – a continuum of memory impairment, a continuum of expertise, a continuum of eating disorder. Whether the relationship between the continuum and model mechanisms are linear, exponential, or other form of function, is lost when we aggregate individual differences into two or more groups (e.g., Vandekerckhove, 2014).

Accounting for Individual Subject Performance

At least since the classic work of Estes (1956), there have long been cautions about analyzing and modeling data aggregated across individual subjects. Estes considered the case of learning curves. Imagine that all individual subject learning curves follow a step function that rises from chance to perfect performance in an instant, but they do so at different time points. In this sense, every subject exhibits all-or-none learning, but “get it” at different times. Averaging over these individual step functions will result in an average learning curve will misleadingly show a gradual, continuous rise rather than all-or-none learning. Estes said that any given mean learning curve could have “arisen from any of an infinite variety of populations of individual curve” (Estes, 1956, p. 134), with averaging especially problematic when the averaged data does not faithfully reflect individual behavioral patterns (Estes & Maddox, 2005; Estes, 1956).

Nosofsky, Palmeri, and McKinley (1994) demonstrated how considering individual subject behavior can help to distinguish different models of categorization that are indistinguishable based on averaged data. They first showed that the rule-based RULEX model and the exemplar-based context model could both account equally well for a replication of the classic Medin & Schaffer (1978) experiment when fitted to average subject categorization of old training items and new transfer items (see Figure 5).

They next distinguished the two models based on how they accounted for individual subject behavior. Rather than simply fit the models to the average probability of classifying individual stimuli as members of Category A or Category B (Figure 5), they fitted the models to the generalization patterns individual subjects exhibited when tested on the new transfer items (Figure 6), as described next.

Figure 6.

Distributions of generalization patterns from Experiment 1 of Nosofsky et al. (1994) and Experiment 1 of Palmeri and Nosofsky (1995); both are replications and extensions of Experiment 2 of Medin and Schaffer (1978). Each of the 32 generalization patterns is one of the possible ways that a subject could classify the five critical transfer items (T1, T2, T4, T5, and T6, respectively) from the category structure shown in Table 1; for example, pattern AABBB denotes classifying T1–T2 as members of category A and T4–T6 as members of category B. White bars highlight the two prominent rule-based generalization patterns. The hatched bar highlights the prominent exemplar-based generalization pattern. From “Are there representational shifts during category learning?” by M. K. Johansen, & T. J. Palmeri, 2002, Cognitive Psychology, 45, p. 482–553. Copyright 2002 by Academic Press. Reprinted with permission.

Consider the category structure shown in Table 1. Imagine that during the category learning phase, an individual notices that information along the first stimulus dimension is partially diagnostic and forms a simple, yet imperfect, rule along that dimension. If stimulus dimension one corresponds to size, and value 1 corresponds to small and value 2 corresponds to large, then small stimuli are put into category A and large stimuli are put into category B. In the following transfer phase, when that subject applies that learned rule to the seven transfer stimuli (that they have not seen before) they would categorize T1-T3 (the small stimuli) in Category A and T4-T7 (the large stimuli) in Category B by a simple application of that rule. We can represent this as the generalization pattern AAABBBB. Now imagine that during the category learning phase, another individual notices that information along the third dimension is partially diagnostic and forms a rule along that dimension. If stimulus dimension three corresponds to color, and value 1 corresponds to red and value 2 corresponds to green, then red stimuli are put into category A and green stimuli are put into category B. When applying this rule during the transfer phase, they would show the generalization pattern BBAABAB, categorizing the red transfer stimuli as A’s and the green transfer stimuli as B’s. Nosofsky et al. tested over 200 subjects and for each individual subject they tallied the generalization pattern they exhibited during the transfer phase to create a distribution of generalization patterns across all subjects; Palmeri and Nosofsky (1995) replicated this experiment with additional training trials. To simplify the illustration of the distribution of generalization patterns from these two studies, Figure 6 leaves out T3 (which is nearly always categorized as a member of Category A) and T7 (which is nearly always categorized as a member of Category B) from the generalization patterns; hence AAABBBB becomes AABBB and BBAABAB becomes BBABA.

Whereas the rule-based RULEX model and the exemplar-based context model made similar prediction regarding average categorization, they made different predictions regarding the distributions of generalization patterns – in other words, they made different predictions at the individual subjects level. Subjects showed prominent rule-based generalization, as predicted by RULEX (Nosofsky, Palmeri, et al., 1994; see also Nosofsky, Clark, & Shin, 1989), as shown in the left panel of Figure 6. When Palmeri and Nosofsky (1995) followed up with more training, they observed a relative increase in the proportion of ABBA generalizations, as shown in the right panel of Figure 6, which turned out to be the modal generalization predicted by exemplar models (see also Anderson & Betz, 2001; Palmeri & Johansen, 2002; Raijmakers, Schmittmann, & Visser, 2014).

Ashby, Maddox, and Lee (1994) also investigated the potential dangers of testing categorization models based on their fits to averaged data. They used both real and simulated data for identification, a special case of categorization in which each stimulus defines its own category. The similarity-choice model (Luce, 1959), a theoretical precursor to the generalized context model (Nosofsky, 1984), generally provided far better fits to averaged data than to individual subject data. In one case, they simulated data from the identification version of the decision-bound model, in which each stimulus forms its own category (Ashby & Townsend, 1986; Ashby & Gott, 1988; Ashby & Lee, 1991). Perhaps not surprisingly, the decision-bound model provided a better account of individual subject data than the similarity-choice model since the data were simulated from the former model. If there were no averaging artifact, then whether fitting individual subject data or averaged data, the decision-bound model should be recovered as the true model since that is the model that generated the data. However, when fitted to averaged data, the similarity-choice model provided better fits than the decision-bound model that actually generated the data. Testing models based on fits to averaged data can lead to erroneous conclusions about the underlying mental processes.

Individual subject analyses can provide more accurate information regarding categorization processes than group analysis since the structure within average data may not faithfully reflect that within individual subject data. An obvious cost of individual subject analyses is significantly less statistical power. And parameter estimation does not benefit from the noise reduction provided by aggregation. Generally, fitting models to individual subject data requires an adequate number of observations from each subject and will likely be outperformed by fitting to group data if insufficient data are obtained (Brown & Heathcote, 2003; Cohen, Sanborn, & Shiffrin, 2008; Lee & Webb, 2005; Pitt, Myung, & Zhang, 2002). With too little data, inferences based on individual subject analyses can be so noisy and unreliable that averaging seems an acceptable trade-off, despite the possible distortions (Cohen, Sanborn, & Shiffrin, 2008; Lee & Webb, 2005). The Nosofsky, Palmeri, et al. (1994) work described at the outset of this section provides something akin to an intermediate step between individual subject fitting and group fitting; the distributions of generalization patterns across the individuals in the group were fitted, not each individual subject’s data or the group data. A more formalized means of fitting group and individual subject data involves hierarchical modeling, as described next.

Hierarchical Modeling

Modeling group averages can fail to recognize meaningful individual differences in the population, while modeling individual subject data may lack sufficient power to detect important patterns between individuals or even allow quantitative model fitting to individual subject data of any sort.⁴ A solution to this dilemma is to model both group and individual differences simultaneously using what is called a hierarchical modeling approach (e.g., Gelman & Hill, 2006; Lee & Webb, 2005; Rouder, Lu, Speckman, Sun, & Jiang, 2005). In hierarchical modeling, individuals are assumed to be samples from a certain population or group, with model parameters defining both the group and individuals sampled from the group. In its most general form, quantitative individual differences can be captured by the parameter differences within a group, while at the same time, qualitative group differences can be described by parameter differences between groups (Lee, 2011; Shiffrin, Lee, Kim, & Wagenmakers, 2008). While fitting individuals and groups simultaneously might appear little more than a complication of an already complicated modeling problem, in practice, the techniques used for hierarchical modeling actually allow both individual and group parameters to be modeled more precisely because information at multiple levels is shared (Kreft & de Leeuw, 1998; Lee, 2011; Shiffrin et al., 2008).

In a lot of traditional cognitive model parameter estimation, whether fitting group data or individual data, best-fitting parameters are those that maximize or minimize some objective function, such as likelihood or χ², that quantifies the deviation between observed data and model predictions (e.g., Lewandowsky & Farrell, 2011). While maximum likelihood can be used to fit certain classes of linear hierarchical models and hierarchical variants of other classical statistical models (e.g., Gelman & Hill, 2006), hierarchical cognitive models quickly become too computationally challenging or entirely intractable to use such traditional model fitting methods. A Bayesian modeling framework provides a natural alternative, with a coherent and principled means for statistical inference (e.g., see Gelman, Carlin, Stern, & Rubin, 1995; Kruschke, 2010) and enabling modeling of flexible and complex cognitive phenomena at the group and individual differences level (Lee & Wagenmakers, 2014). The vector of model parameters, θ, can be estimated from the observed data, D, by a conceptually straightforward application of Bayes’ rule: p(θ | D) = p(D | θ) p(θ) / p(D); a conceptually straightforward causal chaining of conditional probabilities, often called a graphical model (e.g., Griffiths, Kemp, & Tenenbaum, 2008), allows a complex hierarchy of group and individual subject parameters to be specified. In practice, the solution to a multivariate, hierarchical Bayesian specification of a cognitive model requires computationally intensive Monte Carlo techniques that have only been possible to implement on computer hardware that have become available in the past few years, hence the recent explosion of interest in Bayesian modeling approaches. The combination of hierarchical cognitive modeling with a Bayesian framework is called Bayesian hierarchical cognitive modeling.

Consider first a Bayesian hierarchical version of the diffusion model (e.g., Vandekerckhove, Tuerlinckx, & Lee, 2011) or of the linear ballistic accumulator model (e.g., Annis, Miller, & Palmeri, in press) of perceptual decision making. Recall that these models explain variability in response times and response probabilities via a combination of drift rate, response threshold, starting point, non-decision time (for debates regarding variability in these parameters, see Heathcote, Wagenmakers, & Scott, 2014; Jones & Dzhafarov, 2014; Smith, Ratcliff, & McKoon, 2014). While it is possible in principle to simply fit the diffusion model to individual subject data, the model requires fits to full correct and error response time distributions, which requires a relatively large number of observations per subject per condition. Sometimes large data sets are impossible to obtain, for example in online experiments (e.g., Shen, Mack, & Palmeri, 2015). Bayesian hierarchical approaches specify group-level parameters for the drift rate, response threshold, and so forth, and assume that individual subject parameters are random samples from those distributions. This imposed hierarchy helps constrain individual subject parameter estimates, even in the face of inadequate or even missing data (e.g., Gelman & Hill, 2006).

The simplest individual differences model specified within a Bayesian hierarchy is one that assumes a single multivariate distribution of model parameters for a single group, with individual subject parameters sampled from that group. A more complex version might allow certain model parameters to vary systematically with a person or item covariate, or even single-trial covariates from neural data such as EEG measures (Nunez, Vandekerckhove, & Srinivasan, 2016). It is certainly possible to fit a model like the diffusion model or LBA to each individual subject separately and then, say, correlate their parameter estimates with some other subject factor, like intelligence or age (e.g., Ratcliff, Thapar, & McKoon, 2006; Ratcliff, Thapar, & McKoon, 2011). Simultaneously fitting all subjects at the same time in a hierarchical manner allows direct statistical tests of explanatory models of the parameter differences between individual subjects in a far more statistically powerful manner. For example, we have recently tested how perceptual decision making that underlies categorization and memory changes with real-world expertise, specifying explanatory models of drift rate and other accumulator model parameters with equations that include a (potential) covariate for individual subject domain expertise (Annis & Palmeri, 2016; Shen, Annis, & Palmeri, 2016). In our case, rather than estimate drift rate on an individual subject basis and correlate that parameter with expertise – which cannot be done because we are testing online subjects with few observations per condition, making individual subject fitting largely impossible – we test directly variants of accumulator models that incorporate expertise in an explanatory model of the accumulator model parameters.

Multiple qualitative groups can also be specified within a Bayesian hierarchical framework. For example, Bartlema et al. (2014) used hierarchical modeling to investigate how individuals differ in their distribution of selective attention to the dimensions of stimuli as a consequence of category learning in a set of data originally reported by Kruschke (1993). Subjects learned the category structure shown in the top panel of Figure 7. Stimuli were “boxcars” that varied in the position of a bar in the box and the height of the box, as illustrated. The dashed line in the figure illustrates the boundary separating stimuli into Category A and B. Both dimension are relevant to the categorization, and when the GCM (Nosofsky, 1986) was fitted to average categorization data, best-fitting parameters revealed that attention weights were applied to both the position and height dimensions.

Figure 7.

Top: The category structure that participants learned. The eight stimuli varied along two dimensions: the height of the box and the position of the bar within the box. The stimuli below and above the diagonal line are assigned to category A and B, respectively. Middle: The posterior mean of the membership probability (attending to height, attending to position, contaminant) of each participant. Bottom: Modal behavioral patterns of the three different groups. Above each stimulus, the red and yellow bars represent the averaged frequencies of the stimuli being classified into A (yellow) and category B (red) by members of the group. From “A Bayesian hierarchical mixture approach to individual differences: Case studies in selective attention and representation in category learning” by A. Bartlema, M. Lee, R. Wetzels, & W. Vanpaemel, 2014, Journal of Mathematical Psychology, 59(1), p. 135–138. Copyright 2014 by Elsevier. Reprinted with permission.

Bartlema et al. (2014) instead considered the possibility that different latent groups of subjects might show qualitatively different patterns of dimensional weighting (also described as dimensional selective attention). Rather than assuming that everyone attended to (weighted) both dimensions equally, subjects might attend to only one of the dimensions (attend position group or attend height group), or not attend to (weight) any dimension and simply guessed (contaminant group); in addition to these qualitative groups, there could also be quantitative differences in parameters between subjects within each group. A mixture component with three latent groups was added to the Bayesian hierarchical analysis, which identified a latent group membership for each subject. The results showed that indeed, subject appeared to fall within one of three latent groups. The middle panel of Figure 7 shows the group membership probability (y axis) as a function of subject number (x axis). The bottom panel of Figure 7 illustrates the different behavioral patterns shown by subjects in the different groups. Thus a mixture-model Bayesian hierarchical analysis can provide a unique picture of categorization behavior of groups of subjects within the population, a pattern that would be completely missed by fitting average categorization data collapsed across subjects.

Groups of subjects can also differ qualitatively in the kinds of category representations they learn and use. Theoretical work often asks whether an exemplar model or a prototype model provide a better account of categorization (e.g., Palmeri & Nosofsky, 2001; Shin & Nosofsky, 1992). Bartlema et al. (2014) considered instead the possibility that some subjects might learn exemplars and other might form prototypes. Subjects learned a category structure based on Nosofsky (1989), which is shown in the top panel of Figure 8. The eight training stimuli are labeled in the figure with their category membership (A or B) and a unique number; the remaining eight stimuli were only used during the transfer test. In fits to average categorization data, the exemplar model showed an advantage over the prototype model. Using a Bayesian hierarchical approach, allowing for each subject’s data to match the result of prediction by either exemplar- or prototype-learning, a more interesting story emerged, with both prototype and exemplar learners present in the collection of subjects. The middle panel of Figure 8 showed the estimated group membership of each subject (exemplar or prototype). The bottom panel showed the characteristic behavioral pattern of prototype and exemplar learners. In this hierarchical approach, individual subjects are allowed to be part of qualitative groups and to different quantitatively from one another within a group, capturing nuances of individual differences in categorization not possible using non-hierarchical approaches.

Figure 8.

Top: The category structure, based on Nosofsky (1989). The stimuli varied along two dimensions: the angle of the bar and the size of the half circle. The 8 training stimuli were numbered 1–8, along with their category assignment A or B. Middle: The posterior mean of the membership probability (prototype or exemplar) of each participant. Bottom: Behavioral patterns of the three different groups. Above each stimulus, the red and yellow bars represent the averaged frequencies of the stimuli being classified into A (yellow) and category B (red) by members of the group. From “A Bayesian hierarchical mixture approach to individual differences: Case studies in selective attention and representation in category learning” by A. Bartlema, M. Lee, R. Wetzels, & W. Vanpaemel, 2014, Journal of Mathematical Psychology, 59(1), p. 140–143. Copyright 2014 by Elsevier. Reprinted with permission.

Discussion

In this article, we showed how considering individual differences has grown to become important for theoretical research on visual categorization. We outlined key components of computational models of categorization, illustrating how individual differences might emerge from variability in perceptual input representations, category representations, and decision processes. Our semi-historical review outlined a progression of approaches, from fitting average data, to fitting group data, to considering individual differences in various ways, including current emerging approaches using Bayesian hierarchical modeling. In addition to simply extending current models to incorporate individual differences, we discussed how considering individual differences can be key to unraveling the underlying representations and processes instantiated within computational models.

Why study individual differences in categorization? With respect to testing predictions of computational models, it has been well documented at least since Estes (1956) that inferences based on averaged, group data can be misleading. A model, and more generally, a theory, may be able to capture well patterns of data averaged across subjects. But if few, if any, of those subjects actually exhibits the qualitative pattern of data exhibited by the group average, then the model is accounting for a statistical fiction, not accounting for actual human behavior. Models of cognitive and perception are ultimately intended to be models of individuals, not models of group averages.

At a surface level, we can ask whether there are individual differences in a cognitive process like categorization and then try to describe them if there are any. Given a finite number of observations per subject, there must be individual differences observed simply because of mere statistical noise. Beyond that, in just about any behavioral task, there are bound to be individual differences because of differences in motivation and attentiveness. We are generally interested in explaining and understanding systematic individual differences, answering the question of why people differ from one another.

In some respects, the way we have considered individual differences in the present article may appear different from traditional work on individual differences. A baseline approach might be to measure behavior in one task and try to understand individual differences in that task by correlating performance with another measured factor like general intelligence (e.g., Craig & Lewandowsky, 2012; Kane & Engle, 2002; Little & McDaniel, 2015; Unsworth & Engle, 2007). This approach is well illustrated in the domain of categorization, for example, in Lewandowsky, Yang, Newell, and Kalish (2012). They had subjects learn rule-based and so-called information-integration categorization problems (Ashby & Maddox, 2005) and asked whether measured working memory capacity (Lewandowsky, Oberauer, Yang, & Ecker, 2010; Oberauer, Süβ, Schulze, Wilhelm, & Wittmann, 2000) differentially predicted learning of the two types of categorization problems. They used structural equation modeling (e.g., Tomarken & Waller, 2005) to attempt to explain variability in category learning in the two types of categorization problems via variability in working memory capacity.

In a traditional approach to individual differences, the most reasonable way to explain why people differ in some primary task is to correlate their performance in that task with another measure like intelligence, age, working memory capacity, and so forth. With computational models, performance is decomposed into component processes, often characterized by the value of a model parameter that reflects some latent characteristic of a given individual subject. That could be response threshold in a decision process, a dimensional selective attention weight that stretches perceptual representations, or scaling of perceptual space than expands perceptual and memory discriminability. The question “why do people differ” in a given task is answered by how they vary in the component processes in a model that give rise to performance.

Of course, the values of model parameters for individual subjects, or the states induced within a model by those parameters (e.g., Mack et al., 2013), could also be correlated (or analyzed via a more sophisticated approach like structural equation modeling) with other individual subject measure as well. For example, individual subject parameters like the drift rate or response threshold in a decision model can be related to subject parameters like intelligence and age (Ratcliff, Thapar, & McKoon, 2010; Ratcliff et al., 2011). These parameters can also be related to individual subject brain measures to understand how variability neural mechanisms give rise to variability in human performance (e.g., Nunez, Srinivasan, & Vandekerckhove, 2015; Turner et al., 2013; Turner, Van Maanen, & Forstmann, 2015; Turner et al., in press).

Individual differences are important to consider not only for the field of visual categorization, but also for cognitive science in general. By including individual differences in formal models of cognition, we can avoid being misled by aggregated data. Moreover, considering individual differences moves of closer to understanding the continuum of human ability, performance, and potential.