Towards Globally Optimal Crowdsourcing Quality Management: The Uniform Worker Setting

Abstract

We study crowdsourcing quality management, that is, given worker responses to a set of tasks, our goal is to jointly estimate the true answers for the tasks, as well as the quality of the workers. Prior work on this problem relies primarily on applying Expectation-Maximization (EM) on the underlying maximum likelihood problem to estimate true answers as well as worker quality. Unfortunately, EM only provides a locally optimal solution rather than a globally optimal one. Other solutions to the problem (that do not leverage EM) fail to provide global optimality guarantees as well.

In this paper, we focus on filtering, where tasks require the evaluation of a yes/no predicate, and rating, where tasks elicit integer scores from a finite domain. We design algorithms for finding the global optimal estimates of correct task answers and worker quality for the underlying maximum likelihood problem, and characterize the complexity of these algorithms. Our algorithms conceptually consider all mappings from tasks to true answers (typically a very large number), leveraging two key ideas to reduce, by several orders of magnitude, the number of mappings under consideration, while preserving optimality. We also demonstrate that these algorithms often find more accurate estimates than EM-based algorithms. This paper makes an important contribution towards understanding the inherent complexity of globally optimal crowdsourcing quality management.

1. INTRODUCTION

Crowdsourcing enables data scientists to collect human-labeled data at scale for machine learning algorithms, including those involving image, video, or text analysis. However, since human workers often make mistakes while answering these tasks, crowdsourcing quality management, i.e., jointly estimating human worker quality as well as answer quality—the probability of different answers for the tasks—is essential. While knowing the answer quality helps us with the set of tasks at hand, knowing the quality of workers helps us estimate the true answers for future tasks.

We focus on rating tasks, i.e., tasks where the answer is one from a fixed set of ratings ∈ {1, 2, …, R}. This includes, as a special case, filtering tasks, where the ratings are binary, i.e., {0, 1}. Consider the following example: say a data scientist intends to design a sentiment analysis algorithm for tweets. To train such an algorithm, she needs a training dataset of tweets, rated on sentiment. Each tweet needs to be rated on a scale of {1, 2, 3}, where 1 is negative, 2 is neutral, and 3 is positive. A natural way to do this is to display each tweet, or item, to human workers hired via a crowdsourcing marketplace like Amazon’s Mechanical Turk, and have workers rate each item on sentiment from 1—3. Since workers may answer these rating tasks incorrectly, we may have multiple workers rate each item. Our goal is then to jointly estimate sentiment of each tweet and the accuracy of the workers.

Standard techniques for solving this estimation problem typically involve the use of the Expectation-Maximization (EM). Applications of EM, however, provide no theoretical guarantees. Furthermore, as we will show in this paper, EM-based algorithms are highly dependent on initialization parameters and can often get stuck in undesirable local optima. Other techniques for quality assurance, some specific to only filtering [5, 8, 12], are not provably optimal either, in that they only give bounds on the errors of their estimates, and do not provide globally optimal quality estimates. We cover this and other related work in detail in the next section.

In this paper, we present a technique for globally optimal quality management, that is, finding the maximum likelihood item (tweet) ratings, and worker quality estimates. A straightforward technique for globally optimal quality management is to simply consider all possible mappings from items to ratings, and for each mapping, infer its overall likelihood. (It can be shown that the best worker error rates are easy to determine once the mapping is fixed.) The mapping with the highest likelihood is then the global optimum.

However, even in this simple example, if we have 500 tweets and 3 possible ratings, the total number of mappings from tweets to ratings is 3⁵⁰⁰, an exceedingly large number. Therefore, this straightforward technique is infeasible.

Key Insights.

To reduce this exponential complexity, we use two simple ideas to greatly prune the set of mappings that need to be considered, from 3⁵⁰⁰, to a much more manageable number.

Let us assume that workers are indistinguishable, and they all have the same quality (which is unknown). It is well-understood that at least on Mechanical Turk, the worker pool is constantly in flux, and it is often hard to find workers who have attempted enough tasks in order to get robust estimates of worker quality. (Our techniques also apply to a generalization of this case.)

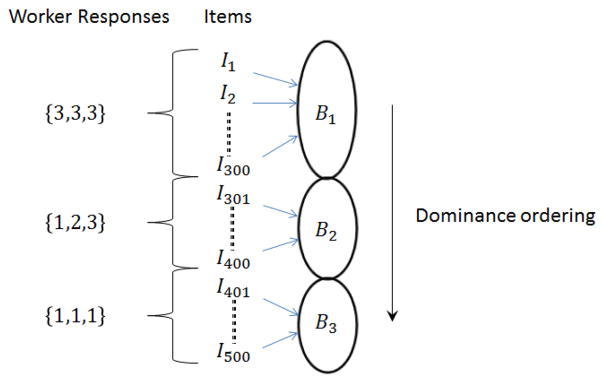
Suppose we have 3 ratings for each tweet—a common strategy in crowdsourcing is to get a small, fixed number of answers for each question. First, we hash “similar” tweets that receive the same set of worker ratings into a common bucket. As shown in Figure 1, suppose that 300 items each receive three ratings of 3 (positive), 100 items each receive one rating of 1, one rating of 2 and one rating of 3, and 100 items each receive three ratings of 1. That is, we have three buckets of items, corresponding to the worker answer sets B₁ = {3, 3, 3}, B₂ = {1, 2, 3}, and B₃ = {1, 1, 1}. We now exploit the intuition that if two items receive the same set of worker responses they should be treated identically. We therefore only consider mappings that assign the same rating to all items (tweets) within a bucket. Now, since in our example, we only have 3 buckets each of which can be assigned a rating of 1,2, or 3, we are left with just 3³ = 27 mappings to consider.

Next, we impose a partial ordering on the set of buckets based on our belief that items in certain buckets should receive a higher final rating than items in other buckets. Our intuition is simple: if an item received “higher” worker ratings than another item, then its final assigned rating should be higher as well. In this example, our partial ordering, or dominance ordering on the buckets is B₁ ≥ B₂ ≥ B₃, that is, intuitively items which received all three worker ratings of 3 should not have a true rating smaller than items in the second or third buckets where items receive lower ratings. This means that we can further reduce our space of 27 remaining mappings by removing all those mappings that do not respect this partial ordering. The number of such remaining mappings is 10, corresponding to when all items in the buckets (B₁, B₂, B₃) are mapped respectively to ratings (3, 3, 3), (3, 3, 2), (3, 3, 1), (3, 2, 2), (3, 2, 1), (3, 1, 1), (2, 2, 2), (2, 2, 1), (2, 1, 1), and (1, 1, 1).

Figure 1.

Mapping Example

In this paper, we formally show that restricting the mappings in this way does not take away from the optimality of the solution; i.e., there exists a mapping with the highest likelihood that obeys the property that all items with same scores are mapped to the same rating, and at the same time obeys the dominance ordering relationship described above.

We primarily focus on the setting where workers independently draw their responses from a common error distribution. That said, we do propose generalizations to the worker model in Appendix B, for instance, when workers are known to come from a small number of distinct classes with separate error distributions. In either case, one concern may be that these assumptions may be too restrictive, relative to the vast body of related work on the topic (Section 1.1). However, we still believe a thorough study of this setting is useful, for three reasons:

• To the best of our knowledge, no related papers provide global optimality guarantees (even for restricted settings), so it is of independent theoretical interest.

• It is common for practitioners to not track individual worker identities, but simply assume them to come from a generic pool, especially given the transient nature of crowdsourcing marketplaces, in which case our setting applies directly.

• Lastly, and most importantly, we find that even when the datasets violate our assumptions (that is, workers have distinct error rates), there are a variety of settings where our algorithms have higher accuracy than EM-based algorithms that take individual worker error rates into account. In fact, these settings correspond precisely to the real-world marketplace scenario where workers are fleeting and have limited attention spans.

Thus, our primary contributions are as follows:

• [Theoretical Insights] We develop an intuitive algorithm based on simple, but key insights that finds a provably optimal maximum likelihood solution to the problem of jointly estimating true item labels and worker error behavior for crowdsourced filtering and rating tasks. Our approach involves reducing the space of potential ground truth mappings while preserving optimality, enabling an exhaustive search on an otherwise prohibitive domain. Our work represents a significant first step towards understanding the nature and complexity of exact globally optimal solutions for the joint estimation problem.

• [Experimental Insights] We perform experiments to evaluate the performance of our algorithm on a variety of different metrics. Though we optimize for likelihood, we show that our algorithm also does well on other metrics such as the accuracy of predicted item labels and worker response distributions, and latency. We also test our algorithm in settings where certain worker model assumptions (uniformity of worker error rate) do not necessarily hold. We show that despite a competitive disadvantage in such settings, our algorithm still performs comparably to state-of-the-art EM-based algorithms, while having the advantage of simplicity and ease of implementation over them.

1.1 Related Literature

Crowdsourcing is gaining importance as a platform for a variety of different applications where automated machine learning techniques don’t always perform well, e.g., filtering [15] or labeling [17, 19, 26] of text, images, or video, and entity resolution [1, 24, 25, 27]. One crucial problem in crowdsourced applications is that of worker quality: since human workers often make mistakes, it is important to model and characterize their behavior in order to aggregate high-quality answers.

EM-based joint estimation techniques

We study the particular problem of jointly estimating hidden values (item ratings) and a related latent set of parameters (worker error rates) given a set of observed data (worker responses). A standard machine learning technique for estimating parameters with unobserved latent variables is Expectation Maximization [9]. There has been significant work in using EM-based techniques to estimate true item values and worker error rates, such as [7, 22, 28], and subsequent modifications using Bayesian techniques [3, 14]. In [18], the authors use a supervised learning approach to learn a classifier and the ground truth labels simultaneously. In general, these machine learning based techniques only provide probabilistic guarantees and cannot ensure optimality of the estimates. We solve the problem of finding a global, provably maximum likelihood solution for both the item values and the worker error rates. That said, our worker error model is simpler than the models considered in these papers—in particular, we do not consider worker identities or difficulties of individual items. However, we study this simpler model in more depth, providing optimality guarantees. Since our work represents the first providing optimality guarantees (even for a restricted setting), it represents an important step forward in our understanding of crowdsourcing quality management. Additionally, anecdotally, even the simpler model is commonly used for platforms like Mechanical Turk, where the workers are fleeting.

Furthermore, we experimentally test our algorithm on the general setting where worker identities are available. Although our algorithm is at a natural disadvantage due to its assumption of identical workers, we find that it compares well against EM-based heuristics that use the available worker-specific information.

Other techniques with no guarantees

There has been some work that adapts techniques different from EM to solve the problem of worker quality estimation. For instance, Chen et al. [4] adopts approximate Markov Decision Processes to perform simultaneous worker quality estimation and budget allocation. Liu et al. [13] uses variational inference for worker quality management on filtering tasks (in our case, our techniques apply to both filtering and rating). Venanzi et al. [23] uses a Bayesian Classifier Combination model and probabilistic inference to determine different classes of worker quality. Like EM-based techniques, these papers do not provide any theoretical guarantees.

Weaker guarantees

There has been a lot of recent work on providing partial probabilistic guarantees or asymptotic guarantees on accuracies of answers or worker estimates, for various problem settings and assumptions, and using various techniques. We first describe the problem settings adopted by these papers, then their solution techniques, and then describe their partial guarantees.

The most general problem setting adopted by these papers is identical to us (i.e., rating tasks with arbitrary bipartite graphs connecting workers and tasks) [29]; most papers focus only on filtering [5, 8, 12], or operate only when the graph is assumed to be randomly generated [11, 12]. Furthermore, most of these papers assume that the false positive and false negative rates are the same.

The papers draw from various techniques, including just spectral methods [5, 8], just message passing [12], a combination of spectral methods and message passing [11], or a combination of spectral methods and EM [29].

In terms of guarantees, most of the papers provide probabilistic bounds [5, 11, 12, 29], while some only provide asymptotic bounds [8]. For example, Dalvi et al. [5], which represents the most recent in a line of papers [8, 11, 12], show that under certain assumptions about the graph structure (depending on the eigenvalues) the error in their estimates of worker quality is lower than some quantity with probability greater than 1 − δ.

Thus, overall, all the work discussed so far provides probabilistic guarantees on their item value predictions, and error bound guarantees on their estimated worker qualities. In contrast, we consider the problem of finding a global maximum likelihood estimate for the correct answers to tasks and the worker error rates.

Other related papers

Joglekar et al. [10] consider the problem of finding confidence bounds on worker error rates. Our paper is complementary to theirs; while they solve the problem of obtaining confidence bounds on the worker error rates, we consider the problem of finding the maximum likelihood estimates to the item ground truth and worker error rates.

Zhou et al. [30, 31] use minimax entropy to perform worker quality estimation as well as inherent item difficulty estimation; here the inherent item difficulty is represented as a vector. Their technique only applies when the number of workers attempting each task is very large; here, overfitting (given the large number of hidden parameters) is no longer a concern. For cases where the number of workers attempting each task is in the order of 50 or 100 (highly unrealistic in practical applications), the authors demonstrate that the scheme outperforms vanilla EM.

Summary

In summary, at the highest level, our work differs from previous works in its focus on finding a globally optimal solution to the maximum likelihood problem. We focus on a simpler setting, but do so in more depth, representing significant progress in our understanding of global optimality. Our globally optimal solution uses simple and intuitive insights to reduce the search space of possible ground truths, enabling exhaustive evaluation. Our general framework leaves room for further study and has the potential for more sophisticated algorithms that build on our reduced space.

2. PRELIMINARIES

We start by introducing some notation, and then describe the general problem that we study in this paper; specific variants will be considered in subsequent sections.

Items and Rating Questions

We let I be a set of |I| = n items. Items could be, for example, images, videos, or pieces of text. Given an item I ∈ I, we can ask a worker w to answer a rating question on that item. That is, we ask a worker: What is your rating r for the item I?. We assume that every item has a true rating in [1, R] that is not known to us in advance, and allow workers to rate items with any value ∈ {1, 2, …, R}.

Example 2.1

Recall our example application from Section 1, where we have R = 3 and workers can rate tweets as being negative (r = 1), neutral (r = 2), or positive (r = 3). Suppose we have two items, I = {I₁, I₂} where I₁ is positive, or has a true rating of 3, and I₂ is neutral, or has a true rating of 2.

Response Set

We assume that each item I is shown to m arbitrary workers, and therefore receives m ratings ∈ [1, R]. We denote the set of ratings given by workers for item I as M(I) and write M(I) = (v_R, v_R−1, …, v₁) if item I ∈ I receives a rating of i, 1 ≤ i ≤ R, from v_i workers. Thus, ${\displaystyle \sum _{i=1}^R}{v}_i=m$. We call M(I) the response set of I, and M the worker response set in general.

Continuing with Example 2.1, suppose we have m = 2 workers rating each item on the scale of {1, 2, 3}. Let I₁ receive one worker response of 2 and one worker response of 3. Then, we write M(I₁) = (1, 1, 0). Similarly, if I₂ receives one response of 3 and one response of 1, then we have M(I₂) = (1, 0, 1).

Modeling Worker Errors

We assume every worker draws their responses from a common (discrete) response probability matrix, p, of size R × R. Thus, p(i, j) is the probability that a worker rates an item with true value j as having rating i. The matrix p is in general not known to us. We aim to estimate both, p and the true ratings of items in I as part of our computation.

Note that we assume that every response to a rating question returned by every worker is independently and identically drawn from this matrix: thus, each worker responds to each rating question independently of other questions they may have answered, and other ratings for the same question given by other workers; and furthermore, all the workers have the same response matrix. We recognize that assuming the same response matrix is somewhat stringent—to mitigate this, we evaluate our algorithm experimentally on settings where distinct workers have different error rates and show that making this assumption is appropriate (and leads to good performance) for certain settings that occur often in practice. We also consider generalizations of our algorithm to the case where we can categorize workers into different classes in Appendix B.

That said, while our (generalized) techniques can still indeed be applied when there are a large number of workers or worker classes with distinct response matrices, they may be impractical. Since our focus is on understanding the theoretical limits of global optimality for a simple case, we defer to future work fully generalizing our techniques to apply to workers with distinct response matrices, or when worker answers are not independent of each other.

Mapping and Likelihood

We call a function f: I → {1, 2, …, R} that assigns ratings to items a mapping. The set of actual ratings of items is also a mapping. We call that the ground truth mapping, T. For instance, for Example 2.1, T(I₁) = 3, T(I₂) = 2.

Let Pr(M|f, p) be the probability of workers providing the responses in M, had f been the ground truth mapping and p been the true worker error matrix. We call this value the likelihood of the pair, f, p. Thus, our goal is to solve the following problem:

Problem 2.1 (Maximum Likelihood Problem)

Given M, I, find $\underset{f,p}{\text{argmax}}Pr(M\mid f,p)$.

We illustrate this concept on our example. Consider the matrix:

$$p=\left[\begin{array}{lll}0.7\hfill & 0.1\hfill & 0.2\hfill \\ 0.2\hfill & 0.8\hfill & 0.2\hfill \\ 0.1\hfill & 0.1\hfill & 0.6\hfill \end{array}\right]$$

Let us compute the likelihood of the pair f, p when f(I₁) = 2, f(I₂) = 2. We have Pr(M|f, p) = Pr(M(I₁)|f, p) Pr(M(I₂)|f, p) assuming that rating questions on items are answered independently. The quantity Pr(M(I₁)|f, p) is the probability that workers drawing their responses from p respond with M(I₁) to an item with true rating f(I₁). Assuming independence of worker responses, this quantity can be written as the product of the probability of seeing each of the responses that I₁ receives. Therefore, the probability of seeing M(1, 1, 0), that is, one response of 3 and one response of 2, is p(3, 2)p(2, 2) = 0.1 × 0.8 = 0.08. Similarly, Pr(M(I₂)|f, p) = p(3, 2) × p(1, 2) = 0.1 × 0.1 = 0.01. Combining, we have Pr(M|f, p) = 0.01 × 0.08 = 8 × 10⁻⁴. A naive solution would be to look at every possible mapping f′, compute $p^{\prime }=\underset{p}{\text{arg}}\text{max}Pr(M\mid f^{\prime },p)$ and choose the f′ maximizing the likelihood value Pr(M|f′, p′). The number of such mappings, R^|I|, is however exponentially large, prompting the need for a more efficient algorithm. We list our notation in Table 1 for ready reference.

Table 1.

Notation Table

Symbol	Explanation
I	Set of items
M	Items-workers response set
f	Items-values mapping
p	Worker response probability matrix
Pr(M|f, p)	Likelihood of (f, p)
m	Number of worker responses per item
T	Ground truth mapping

3. FILTERING PROBLEM

Filtering can be regarded as a special case of rating where R = 2. We discuss it separately, first, because its analysis is significantly simpler, and at the same time provides useful insights that we then build upon for the generalization to rating, that is, to the case where R > 2. For example, consider the filtering task of finding all images of Barack Obama from a given set of images. For each image, we ask workers the question “is this a picture of Barack Obama”. We can represent an answer of “no” to the question above by a score 0, and an answer of “yes” by a score 1. Each item (image) I ∈ I now has an inherent true value in {0, 1} where 1 means that the item is one that satisfies the filter, in this case, the image is one of Barack Obama. Mappings here are functions f: I → {0, 1}.

Next, we formalize the filtering problem in Section 3.1, describe our algorithm in Section 3.2, prove a maximum likelihood result in Section 3.3 and evaluate our algorithm in Section 3.5.

3.1 Formalization

Given the response set M, we wish to find the maximum likelihood mapping f: I → {0, 1} and 2 × 2 response probability matrix, p. For the filtering problem, each item has an inherent true value of either 0 or 1, and sees m responses of 0 or 1 from different workers. If item I receives m − j responses of 1 and j responses of 0, we can represent its response set with the tuple M(I) = (m − j, j).

Consider a worker response probability matrix of $p=\left[\begin{array}{ll}0.7\hfill & 0.2\hfill \\ 0.3\hfill & 0.8\hfill \end{array}\right]$. The first column represents the probabilities of worker responses when an item’s true rating is 0 and the second column represents probabilities when an item’s true rating is 1. Given that all workers have the same response probabilities, we can characterize their response matrix by just the corresponding worker false positive (FP) and false negative (FN) rates, e₀ and e₁. Here, we can describe the entire matrix p with just the two values, e₀ = 0.3 and e₁ = 0.2.

Filtering Estimation Problem

Let M be the observed response set on item-set I. Our goal is to find

$$f^{\ast },e_0^{\ast },e_1^{\ast }=\underset{f,e_0,e_1}{\text{argmax}}Pr(M\mid f,e_0,e_1)$$

Here, Pr(M|f, e₀, e₁) is the probability of getting the response set M, given that f is the ground truth mapping and the true worker response matrix is defined by e₀, e₁.

Dependance of Response Probability Matrices on Mappings

Due to the probabilistic nature of our workers, for a fixed ground truth mapping T, different worker error rates, e₀ and e₁ can produce the same response set M. These different worker error rates, however have varying likelihoods of occurrence. This leads us to observe that worker error rates (e₀, e₁) and mapping functions (f) are not independent and are related through any given M. In fact, we show that for the maximum likelihood estimation problem, fixing a mapping f enforces a maximum likelihood choice of e₀, e₁. We leverage this fact to simplify our problem from searching for the maximum likelihood tuple f, e₀, e₁ to just searching for the maximum likelihood mapping, f. Given a response set M and a mapping, f, we call this maximum likelihood choice of e₀, e₁ as the parameter set of f, M, and represent it as Params(f, M). The choice of Params(f, M) is very intuitive and simple. We show that we just can estimate e₀ as the fraction of times a worker disagreed with f on an item I in M when f(I) = 0, and correspondingly, e₁ as the fraction of times a worker responded 0 to an item I, when f(I) = 1. Under this constraint, we can prove that our original estimation problem, $\underset{f,e_0,e_1}{\text{argmax}}Pr(M\mid f,e_0,e_1)$ simplifies to that of finding $\underset{f}{\text{argmax}}Pr(M\mid f,e_0^{\ast },e_1^{\ast })$ where $e_0^{\ast },e_1^{\ast }$ are the constants given by Params(f, M).

Example 3.1

Suppose we are given 4 items I = {I₁, I₂, I₃, I₄} with ground truth mapping T = (T(I₁), T(I₂), T(I₃), T(I₄)) = (1, 0, 1, 1). Suppose we ask m = 3 workers to evaluate each item and receive the following number of (“1”,“0”) responses for each respective item: M(I₁) = (3, 0), M(I₂) = (1, 2), M(I₃) = (2, 1), M(I₄) = (2, 1). Then, we can evaluate our worker false positive and false negative rates as described above: $e_1=\frac{0+1+1}{3+3+3}=\frac{2}{9}$ (from items I₁, I₃ and I₄) and $e_0=\frac{1}{3}$ (from I₂).

We shall henceforth refer to Pr(M|f) = Pr(M|f, Params(f, M)) as the likelihood of a mapping f. For now, we focus on the problem of finding the maximum likelihood mapping with the understanding that finding the error rates is straightforward given the mapping is fixed. We formally show that the problem of jointly finding the maximum likelihood response matrix and mapping can be solved by just finding the most likely mapping f^* in Section 3.4. The most likely triple f, e₀, e₁ is then given by f^*, Params(f^*, M).

It is easy to calculate the likelihood of a given mapping. We have $Pr(M\mid f)={\displaystyle \prod _{I\in \mathbf{I}}}Pr(M(I)\mid f,e_0,e_1)$, where e₀, e₁ = Params(f, M) and Pr(M(I)|f, e₀, e₁) is the probability of seeing the response set M(I) on an item I ∈ I. Say M(I) = (m − j, j). Then, we have

$$Pr(M(I)\mid f)=\{\begin{array}{ll}{(1-e_1)}^{m-j}{e}_1^j\hfill & \text{for}f(I)=1\hfill \\ e_0^{m-j}{(1-e_0)}^j\hfill & \text{for}f(I)=0\hfill \end{array}$$

This can be evaluated in O(m) for each I ∈ I by doing one pass over M(I). Thus, Pr(M|f) = Π_I∈I Pr(M(I)|f) can be evaluated in O(m|I|). We use this as a building block in our algorithm.

3.2 Globally Optimal Algorithm

In this section, we describe our algorithm for finding the maximum likelihood mapping, given a response set M on an item set I. A naive algorithm could be to scan all possible mappings, f, calculating for each, $e_0^{\ast },e_1^{\ast }=\text{Params}(f,M)$ and the likelihood $Pr(M\mid f,e_0^{\ast },e_1^{\ast })$. The number of all possible mappings is, however, exponential in the number of items. Given n = |I| items, we can assign a value of 0 or 1 to any of them, resulting in 2ⁿ different mappings. This makes the naive algorithm prohibitively expensive.

Our algorithm is essentially a pruning based method that uses two simple insights (described below) to narrow the search for the maximum likelihood mapping. Starting with the entire set of 2ⁿ possible mappings, we eliminate all those that do not satisfy one of our two requirements, and reduce the space of mappings to be considered to O(m), where m is the number of worker responses per item. We then show that just an exhaustive evaluation on this small set of remaining mappings is still sufficient to find a global maximum likelihood mapping.

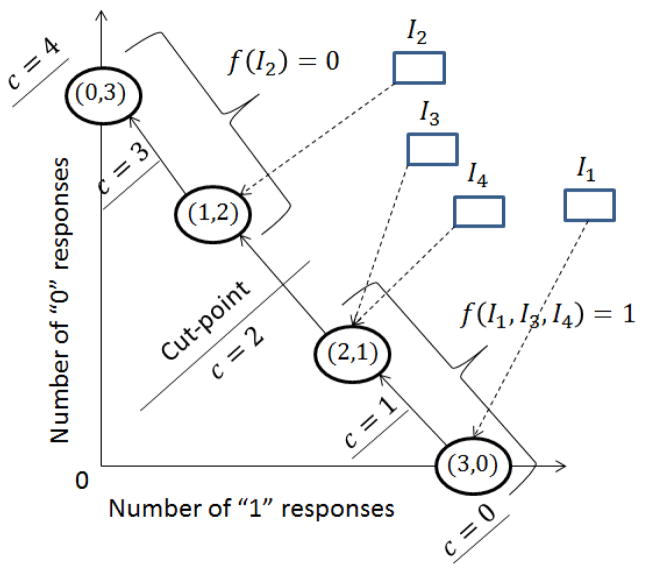
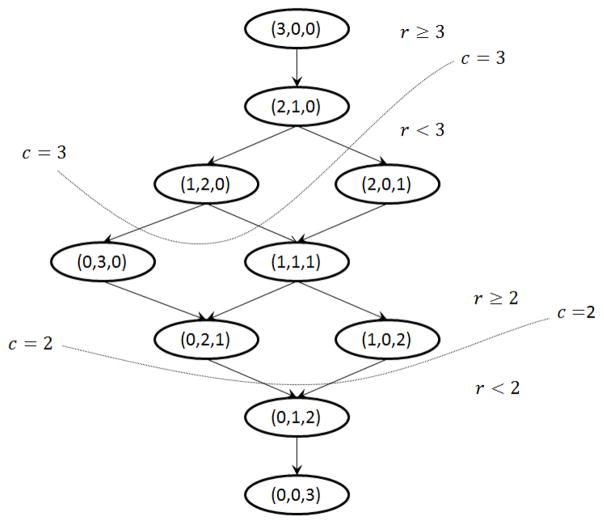
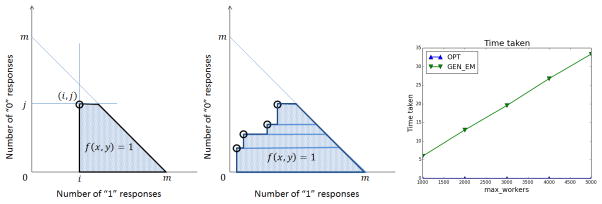
We illustrate our ideas on the example from Section 3.1, represented graphically in Figure 2. We will explain this figure below.

Figure 2.

Filtering: Example 3.1 (cut-point = 2)

Bucketizing

Since we assume (for now) that all workers draw their responses from the same probability matrix p (i.e., have the same e₀, e₁ values), we observe that items with the exact same set of worker responses can be treated identically. This allows us to bucket items based on their observed response sets. Given that there are m worker responses for each item, we have m + 1 buckets, starting from m “1” and zero “0” responses, down to zero “1” and m “0” responses. We represent these buckets in Figure 2. The x-axis represents the number of 1 responses an item receives and the y-axis represents the number of 0 responses an item receives. We hash items into the buckets corresponding to their observed response sets. Intuitively, since all items within a bucket receive the same set of responses and are for all purposes identical, two items within a bucket should receive the same value.

In our example (Figure 2), the set of possible responses to or bucket of any item is {(3, 0), (2, 1), (1, 2), (0, 3)}, where (3 − j, j) represents seeing 3 − j responses of “1” and j responses of “0”. We only consider mappings, f, where items in the same bucket are assigned the same value, that is, f(I₃) = f(I₄). This leaves 2⁴ mappings corresponding to assigning a value of 0/1 to each bucket. In general, given m worker responses per item, we have m + 1 buckets and 2^m+1 mappings that satisfy our bucketizing condition. Although for this example m + 1 = n, typically we have m ≪ n.

Dominance Ordering

Second, we observe that buckets have an inherent ordering. If workers are better than random, we intuitively expect items with more “1” responses to be more likely to have true value 1 than items with fewer “1” responses. Ordering buckets by the number of “1” responses, we have (m, 0) → (m − 1, 1) → … → (1, m − 1) → (0, m). We eliminate all mappings that give a value of 0 to a bucket with a larger number of “1” responses while assigning a value of 1 to a bucket with fewer “1” responses. We formalize this intuition as a dominance relation, or ordering on buckets, (m, 0) > (m − 1, 1) > … > (1, m − 1) > (0, m), and only consider mappings where dominating buckets receive a value not lower than any of their dominated buckets.

Figure 2 shows the dominance relation in the form of directed edges, with the source node being the dominating bucket and the target node being the dominated one. Here, we discard all mappings which assign a value of “0” to a dominating bucket (say response set (3, 0)) while assigning a value of “1” to one of its dominated buckets (say response set (2, 1)).

Dominance-Consistent Mappings

We consider the space of mappings satisfying our above bucketizing and dominance constraints, and call them dominance-consistent mappings. We can prove that the maximum likelihood mapping from this small set of mappings is in fact a global maximum likelihood mapping across the space of all possible “reasonable” mappings: mappings corresponding to better than random worker behavior.

To construct a mapping satisfying our above two constraints, we choose a cut-point to cut the ordered set of response sets into two partitions. The corresponding dominance-consistent mapping then assigns value “1” to all (items in) buckets in the first (better) half, and value “0” to the rest. For instance, choosing the cut-point between response sets (2, 1) and (1, 2) in Figure 2 results in the corresponding dominance-consistent mapping, where {I₁, I₃, I₄}, are mapped to “1”, while {I₂}, is mapped to “0”. We have 5 different cut-points, 0, 1, 2, 3, 4, each corresponding to one dominance-consistent mapping. Cut-point 0 corresponds to the mapping where all items are assigned a value of 0 and cut-point 4 corresponds to the mapping where all items are assigned a value of 1. In particular, the figure shows the dominance-consistent mapping corresponding to the cut-point c = 2. In general, if we have m responses to each item, we obtain m + 2 dominance-consistent mappings.

Definition 3.1

(Dominance-consistent mapping f^c). For any cut-point c ∈ 0, 1, …, m+1, we define the corresponding dominance-point mapping f^c as

$$f^c(I)=\{\begin{array}{ll}1\hfill & ifM(I)\in \{(m,0),\dots ,(m-c+1,c-1)\}\hfill \\ 0\hfill & ifM(I)\in \{(m-c,c),\dots ,(0,m)\}\hfill \end{array}$$

Our algorithm enumerates all dominance-consistent mappings, computes their likelihoods, and returns the most likely one among them. The details of our algorithm can be found in our technical report. As there are (m + 2) mappings, each of whose likelihoods can be evaluated in O(m|I|), (See Section 3.1) the running time of our algorithm is O(m²|I|).

In the next section we prove that in spite of only searching the much smaller space of dominance-consistent mappings, our algorithm finds a global maximum likelihood solution.

3.3 Proof of Correctness

Reasonable Mappings

A reasonable mapping is one which corresponds to a better than random worker behavior. Consider a mapping f corresponding to a false positive rate of e₀ > 0.5 (as given by Params(f, M)). This mapping is unreasonable because workers perform worse than random for items with value “0”. Given I, M, let f: I → {0, 1}, with e₀, e₁ = Params(f, M) be a mapping such that e₀ ≤ 0.5 and e₁ ≤ 0.5. Then f is a reasonable mapping. It is easy to show that all dominance-consistent mappings are reasonable mappings.

Now, we present our main result on the optimality of our algorithm. We show that in spite of only considering the local space of dominance-consistent mappings, we are able to find a global maximum likelihood mapping.

Theorem 3.1 (Maximum Likelihood)

We let M be the given response set on the input item-set I. Let F be the set of all reasonable mappings and F^dom be the set of all dominance-consistent mappings. Then, max_f^*∈F^dom Pr(M|f^*) = max_f∈F Pr(M|f)

Proof

We provide an outline of our proof below. Further details can be found in the Appendix A.1.

• Step 1: Suppose f is not a dominance-consistent mapping. Then, either it does not satisfy the bucketizing constraint, or it does not satisfy the dominance-constraint. We claim that if f is reasonable, we can always construct a dominance-consistent mapping, f^* such that Pr(M|f^*) ≥ Pr(M|f). Then, it trivially follows that max _f^*∈F^dom Pr(M|f^*) = max_f∈F Pr(M|f). We show the construction of such an f^* for every reasonable mapping f below.

• Step 2: (Bucketizing Inconsistency). Suppose f does not satisfy the bucketizing constraint. Then, we have at least one pair of items I₁, I₂ such that M(I₁) = M(I₂) and f(I₁) ≠ f(I₂). Consider the two mappings f₁ and f₂ defined as follows:

  $$\begin{array}{l}{f}_1(I)=\{\begin{array}{ll}f(I_2)\hfill & \text{for}I=I_1\hfill \\ f(I)\hfill & \forall I\in \mathbf{I}\backslash \{I_1\}\hfill \end{array}\\ f_2(I)=\{\begin{array}{ll}f(I_1)\hfill & \text{for}I=I_2\hfill \\ f(I)\hfill & \forall I\in \mathbf{I}\backslash \{I_2\}\hfill \end{array}\end{array}$$

  The mappings f₁ and f₂ are identical to f everywhere except for at I₁ and I₂, where f₁(I₁) = f₁(I₂) = f(I₂) and f₂(I₁) = f₂(I₂) = f(I₁). We show that max(Pr(M|f₁), Pr(M|f₂)) ≥ Pr(M|f). Let f′ = argmax _f1,f2 (Pr(M|f₁), Pr(M|f₂)).

• Step 3: (Dominance Inconsistency). Suppose f does not satisfy the dominance constraint. Then, there exists at least one pair of items I₁, I₂ such that M(I₁) > M(I₂) and f(I₁) = 0, f (I₂) = 1. Define mapping f′ as follows:

  $$f^{\prime }(I)=\{\begin{array}{ll}f(I_2)\hfill & \text{for}I=I_1\hfill \\ f(I_1)\hfill & \text{for}I=I_2\hfill \\ f(I)\hfill & \forall I\in \mathbf{I}\backslash \{I_1,I_2\}\hfill \end{array}$$

  Mapping f′ is identical to f everywhere except at I₁ and I₂, where it swaps their values. We show that Pr(M|f′) ≥ Pr(M|f).

• Step 4: (Reducing Inconsistencies). Suppose f is not a dominance-consistent mapping. We have shown that by reducing either a bucketizing inconsistency (Step 2), or a dominance inconsistency (Step 3), we can construct a new mapping, f′ with likelihood greater than or equal to that of f. Now, if f′ is a dominance-consistent mapping, set f^* = f′ and we are done. If not, look at an inconsistency in f′ and apply steps 2 or 3 to it. We can show that with each iteration, we are reducing at least one inconsistency while increasing likelihood. We repeat this process iteratively, and since there are only a finite number of inconsistencies in f to begin with, we are guaranteed to end up with a desired dominance-consistent mapping f^* satisfying Pr(M|f^*) ≥ Pr(M|f). This completes our proof sketch.

3.4 Calculating error rates from mappings

In this section, we formalize the correspondence between mappings and worker error rates that we introduced in Section 3.1. Given a response set M and a mapping f, say we calculate the corresponding worker error rates e₀(f, M), e₁(f, M) = Params(f, M) as follows:

1. Let I_j ⊆ I ∋ f(I) = 0, M(I) = (m − j, j)∀I ∈ I_j. Then, $e_0=\frac{{\sum }_{j=0}^m(m-j)\mid I_j\mid }{m{\sum }_{j=0}^m\mid I_j\mid }$

2. Let I_j ⊆ I ∋ f(I) = 1, M(I) = (m − j, j)∀I ∈ I_j. Then, $e_1=\frac{{\sum }_{j=0}^{m}j\mid I_j\mid }{m{\sum }_{j=0}^m\mid I_j\mid }$

Intuitively, e₀(f, M) (respectively e₁(f, M)) is just the fraction of times a worker responds with a value of 1 (respectively 0) for an item whose true value is 0 (respectively 1), under response set M assuming that f is the ground truth mapping. We show that for each mapping f, this intuitive set of false positive and false negative error rates, (e₀, e₁) maximizes Pr(M|f, e₀, e₁). We express this idea formally below.

Lemma 3.1 (Params(f, M))

Given response set M, and mapping f, let Pr(e₀, e₁|f, M) be the probability that the underlying worker false positive and negative rates are e₀ and e₁ respectively, conditioned on f being the true mapping. Then,

$$\forall f,\mathit{Params}(f,M)=\underset{e_0,e_1}{\text{argmax}}Pr(e_0,e_1\mid f,M)$$

Next, we show that instead of simultaneously trying to find the most likely mapping and false positive and false negative error rates, it is sufficient to just find the most likely mapping while assuming that the error rates corresponding to any chosen mapping, f, are always given by Params(f, M). We formalize this intuition in Lemma 3.2 below. The details of its proof, which are simple and follow from Lemma 3.1, can also be found in the full technical report [6].

Lemma 3.2 (Likelihood of a Mapping)

Let f ∈ F be any mapping and M be the given response set on I. We have,

$$\underset{f,e_0,e_1}{max}Pr(M\mid f,e_0,e_1)=\underset{f}{max}Pr(M\mid f,\mathit{Params}(f,M))$$

3.5 Experiments

In this section, we evaluate the performance of our algorithm, OPT, on synthetic and real data, and compare it against baselines. We report our performance in terms of (a) accuracy of label predictions, (b) accuracy of worker error rates, and (c) time taken.

We discuss four experiments: our first experiment is on synthetic data, our second experiment is on data from [10] on image comparison, our third experiment is on data from [21] on classification, and our last experiment summarizes results on other datasets.

In all our experiments, our algorithm, OPT, assumes a single error rate across all workers, despite that not holding true, so is at a considerable disadvantage to other algorithms that do take individual worker identities and error rates into account.

We also note that while our gains for the filtering setting are small, as we will see in Section 4.3, the gains are significantly higher for the case of rating, where multiple error rate parameters are being simultaneously estimated. (For the filtering case, only false positive and false negative error rates are being estimated.)

Experiment 1: Synthetic Data Experiments

For the synthetic data, we perform experiments under two settings: In the first setting, data is generated using the assumption that workers draw their responses from a fixed common error distribution. This is the same assumption that is also made by our algorithm, denoted OPT. We compare OPT against an EM baseline that also makes the same assumption. Here, our goal is to explore the effects of optimizing on likelihood on other parameters of interest, e.g., the quality of the predicted item values, or the estimated error rates, on an equal footing with EM baselines.

In the second setting, data is generated using the assumption that different workers draw their responses from different error distributions, with worker identities known. While our algorithm continues to operate as before (with the single error rate assumption), for our EM baseline, we use a richer algorithm that can take worker identities and individual error rates into account. Here, our goal is to study the impact of OPT in settings where our assumptions do not hold, and when worker identities are indeed available.

Setting 1: Identical worker error distribution

Dataset generation

To generate ground truth values for items, given a fixed selectivity s, for each item, we assign a ground truth value of 1 with probability s, and 0 with probability 1 − s. This gives a set of items I, |I| = n, and ground truth mapping T. Then, we generate an underlying worker response probability matrix, with the only constraint that workers are better than random (false positive and false negative rates are ≤ 0.5). We then simulate worker responses based on this matrix to generate a response set M. Different algorithms being compared now take I, M as input and return a mapping f : I → {0, 1}, and a worker response matrix p.

Algorithms

We compare our algorithm, OPT, against the basic EM algorithm that is also solving the same maximum likelihood problem. We discuss details of the EM algorithm in [6]. EM takes an initial estimate or guess for worker error rates as a parameter — we experiment with three different initializations here. EM(1) starts with an initialization of e₀, e₁ = 0.25 (workers are better than random), EM(2) with e₀, e₁ = 0.5 (workers are random), and EM(3) with e₀, e₁ = 0.75 (workers are worse than random). EM(*) is the consolidated algorithm which runs each of the three EM instances and best among them in terms of maximum likelihood.

Setup

We experiment with different choices over both input parameters and comparison metrics over the output. We observe that changing the number of items, n, does not significantly affect our accuracy results, so we set n = 1000. We vary the selectivity, s, and the number of worker responses per item, m; due to space limitations, we show a representative set of results below. Each experiment is repeated across 1000 random trials.

Likelihood

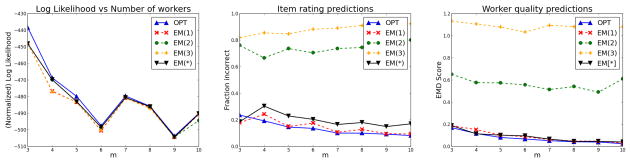
Figure 3(a) shows the likelihoods of mappings returned by OPT and different EM instances on varying the number of worker responses, for s = 0.5. The y-axis is on log scale, with a higher value being more desirable. We observe that OPT returns higher likelihood mappings with the marginal improvement going down as m increases. We believe that in practice it is unlikely that m > 5 (more than 5 answers per item).

Figure 3.

Filtering, Synthetic, Setting 1: (a)Likelihood, s = 0.5 (b) Fraction Incorrect, s = 0.7 (c) EMD Score, s = 0.5

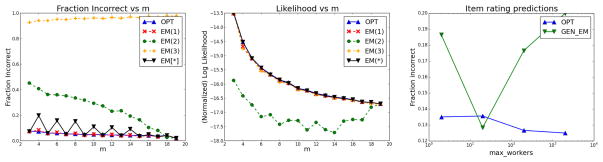
Fraction incorrect

In addition to likelihood, we are also interested in other metrics that measure the quality of our predictions. In Figure 3(b) (s = 0.7), we plot the fraction of item values each of the algorithms predict incorrectly (a lower score is better). Here, again, OPT estimates true values of items with a higher accuracy than EM instances; with EM(2) and EM(3) being especially bad.

EMD score

Then, to evaluate the predicted worker error rates against actual ones, we plot the Earth Movers distance (EMD) between our predicted matrix and the actual one in Figure 3(c) (s = 0.5 – lower better). For a detailed description of distance metrics, see technical report [6]. We observe that OPT’s predictions are closer to the actual probability matrix than all the EM instances. We observe that EM(2) and EM(3) get stuck in bad local minima.

Summary

For all metrics, OPT displays slightly higher accuracy, in addition to giving a global likelihood guarantee. (Our results for rating are even better since there are multiple parameters being estimated.) Our experiments also show that optimizing for likelihood does not adversely affect other metrics of interest. We experiment with additional parameter settings and comparison metrics, and present more extensive results in our technical report [6].

Setting 2: Distinct worker error distributions

Next, we consider the setting where data is generated using distinct worker error rates, with worker identities available to the algorithms. Furthermore, different workers may respond to different items, giving a general item-worker response matrix. For this setting, we consider a generalized version of the previous EM, algorithm GEN_EM, that assumes and estimates a distinct error distribution for each worker. (The previous EM instances assumed a single common error distribution.) OPT, on the other hand, ignores worker identities, and uses a single common error distribution. The item-worker response matrix can be dense or sparse depending on how many items different workers respond to.

Our expectation is that if the matrix is dense, with a small number of workers, each answering many items, then GEN_EM will do well, since it will converge to high-confidence estimates for worker accuracies. If, on the other hand, the matrix is sparse, which is often the case when there is a large and fluid worker pool, with each worker answering a small number of items, then we expect OPT to do as well as GEN_EM, which may extrapolate worker accuracies without much evidence.

Dataset generation, Setup, and Algorithms

We use m′ distinct workers each with a uniformly drawn, independent error rate that is better than random (≥ 0.5). Each of the n items receives responses from m workers randomly sampled from m′, so workers answer an average of nm/m′ items. We keep n constant at 1000, making m/m′ a good measure of the density of the item-worker matrix.

The generalized version of EM for this setting, GEN_EM, starts with an initial error rate estimate for each worker, and then converges to distinct error rates for them. We use the same initialization as EM(1) from the experiments in Setting 1 for each worker, as that was observed to have the best performance.

Accuracy Results

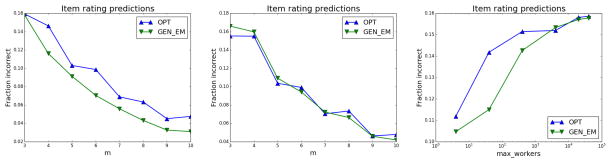
Figure 4(a) depicts the performance as a function of m, when m′ = 50. We observe that GEN_EM performs better throughout. This is not surprising given that with just 50 total workers, each worker would answer 1000 × 10/50 = 200 items for m = 10, giving GEN_EM very fine-grained information about each individual worker. Contrast this to Figure 4(b), where m′ = 1000 — here, the item-worker response matrix is much sparser (average number of responses per worker is 10) and we consequently observe that OPT is comparable to (even marginally better than) GEN_EM in spite of working with a much coarser granularity of information! The latter case is often true in marketplaces where requesters have little control over which workers attempt their tasks, or if the workers are anonymous.

Figure 4.

Filtering, Synthetic, Setting 2: (a) m′ = 50, varying m (b) m′ = 1000, varying m (c) (m = 4), varying m′

In Figure 4(c), we show the performance as a function of the maximum size of the worker pool, m′ (log-scale), while keeping the number of responses per item, m, fixed. While GEN_EM outperforms OPT for smaller m′ (dense response matrix), OPT catches up for m′ > 1000.

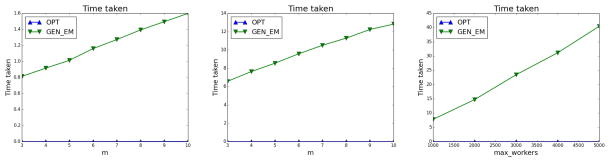
Efficiency Results

In Figures 5(a), 5(b), 5(c), we compare the efficiency of OPT against GEN_EM in terms of actual execution time. As before, we explore the effects of both m and m′. In Figures 5(a), 5(b) we vary m from 3 to 10 along the x-axis, for a fixed value of m′ = 100, 1000 in the two plots respectively. In Figure 5(c), we vary m′ while keeping m fixed at 4. We observe that while the time taken by OPT is typically of the order of 0.001 seconds, GEN_EM (which scales linearly with number of iterations, set at 40 for these plots) takes several seconds to execute for higher values of m′. In fact, OPT is almost not visible in these plots. This further supports the case for OPT in settings with a large worker pool. Note that OPT is linear in m, but its low latency values hide this trend at this scale.

Figure 5.

Filtering, Synthetic, Setting 2; Vary m: (a) m′ = 100 (b) m′ = 1000; Vary m′: (c) m = 4

We also perform experiments where we inject a small fraction of “bad” (random) workers into the worker pool for both the settings above. We observe that for reasonable numbers, this injection does not significantly affect our previous results. More detailed experimental results on this can be found in our technical report.

Experiment 2: Real Data Experiment on [10]

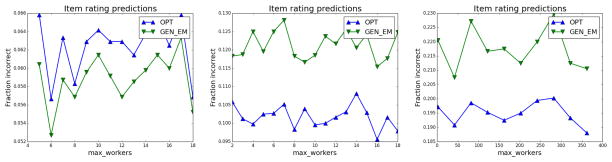
We now describe our results on a real dataset. Since the dataset contains answers from a small worker pool, it is naturally dense, and is therefore unfavorable to OPT. We compare OPT versus GEN_EM here. Additional results can be found in the Appendix. For each of these experiments we “vary” the size of the dataset by hiding some of the worker responses and report results from the different, remaining, partial sets.

Dataset

Our dataset is an image comparison dataset [10], where 19 workers are asked to each evaluate 48 tasks. Each task requires a worker to identify if two images show the same sportsperson. We have ground-truth yes/no answers for each task, but do not know the worker error rates. To evaluate the performance of OPT with GEN_EM, we compare the estimates for the item values (the yes/no answers) against the given ground truth.

Results

While in our synthetic experiments, we had the luxury of generating datasets with arbitrary m′, here, we have m′ ≤ 19. We fix m (number of responses per item) for a given plot and vary m′ (number of total workers present) along the x-axis, and compare the fraction of item values predicted incorrectly along the y-axis. We show our results for m = 5 in Figure 6(a) and for m = 2 in Figure 6(b). Again, we observe that for the denser item-worker response matrix (m = 5), GEN_EM is more accurate than OPT, while for the sparser (m = 2) case, OPT is more accurate than GEN_EM. Thus, even on settings which violate our assumptions, such as this dataset with a finite, small worker pool, OPT is more accurate than GEN_EM for sparse item-worker response matrices.

Figure 6.

Filtering Real Dataset 1 (a) m = 5, (b) m = 2; Filtering Real Dataset 2 (c) m = 2

Experiment 3: Real Data Experiment on [21]

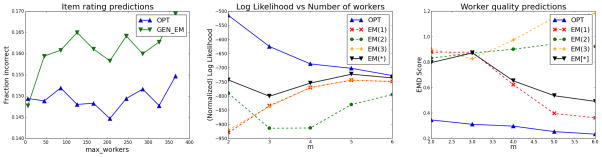
We now present results on our second real dataset, from Tian et al. [21]. This is a dataset of images with simple classification (example, is this an image of the sky) or counting tasks. It contains a set of 64 images each responded to by 402 workers. From this, we selected the subset of 36 images corresponding to the filtering tasks, as opposed to the counting tasks. Below we show plots 6(c) and 7(a) where we keep m fixed for a plot and vary m′ along the x-axis. We observe here that our algorithm OPT predicts item values more accurately than GEN_EM for nearly all parameter settings. Full details of our experimental setup can be found in [6].

Experiment 4: Comparison against other baselines

We also evaluated our approach on a few other datasets and against other baseline algorithms. We present our results on two datasets, TEMP and RTE from [16]—both these datasets are part of the SQUARE benchmark [20]. The TEMP dataset contains judgments for temporal ordering of events in text, while the RTE dataset contains judgments for textual entailment (both binary tasks).

OPT predicts the labels for TEMP with a 93.94% accuracy, similar to that of the best algorithm for this dataset, whose accuracy is 93.9% [20].

On the RTE dataset, OPT predicts labels with an error rate of 11.3% (accuracy of 88.7%). We compare this against the results from [29], where their sophisticated Opt-D&S algorithm has an error rate of 7.1% (while other methods have much poorer performance, for example, KOS — 39.7% [11] and Ghosh-SVD — 49.13% [8]). We argue that while OPT is not the most accurate (since it ignores worker identities), it is competitive in its accuracy while having the advantage of simplicity over some of the more sophisticated baselines such as Opt-D&S.

Indeed, all the datasets in the SQUARE benchmark are dense datasets; if the datasets were sparse (like in Experiment 3), we expect OPT to not just match the performance of these algorithms, but also beat them.

4. RATING PROBLEM

In this section, we extend our techniques from filtering to the problem of rating items. Even though the main change resides in the possible values of items ({0, 1} for filtering and {1, …, R} for rating), this small change adds significant complexity to our dominance idea. We show how our notions of bucketizing and dominance generalize from the filtering case.

4.1 Formalization

Recall from Section 2 that, for the rating problem, workers are shown an item and asked to provide a score from 1 to R, with R being the best (highest) and 1 being the worst (lowest) score possible. Each item from the set I receives m worker responses and all the responses are recorded in M. We write M(I) = (v_R, v_R−1, …, v₁) if item I ∈ I receives v_i responses of “i”, 1 ≤ i ≤ R. Recall that ${\displaystyle \sum _{i=1}^R}{v}_i=m$. Mappings are functions f : I → {1, 2, …, R} and workers are described by the response probability matrix p, where p(i, j) (i, j ∈ {1, 2, …, R}) denotes the probability that a worker will give an item with true value j a score of i. Our problem is defined as that of finding $f^{\ast },p^{\ast }=\underset{f,p}{\text{argmax}}Pr(M\mid f,p)$ given M.

As in the case of filtering, we use the relation between p and f through M to define the likelihood of a mapping. We observe that for maximum likelihood solutions given M, fixing a mapping f automatically fixes an optimal p = Params(f, M). Thus, similar to Filtering, we can focus our attention on the mappings, implicitly finding the maximum likelihood p as well. Intuitively, Params(f, M)(i, j) is just the fraction of times a worker responded i to an item that is mapped by f to a value of j. Let the i^th dimension of the response set of any item I by M_i(I). That is, if M(I) = (v_R, …, v₁), then M_i(I) = v_i. Let I_i ⊆ I ∋ f(I) = i∀i, I ∈ I_i. Then, $\text{Params}(f,M)(i,j)=\frac{{\sum }_{I\in {\mathbf{I}}_{\mathbf{j}}}{M}_i(I)}{m\mid I_j\mid }\forall i$, j.

Denoting the likelihood of a mapping, Pr(M|f, Params(f, M)), as Pr(M|f), our maximum likelihood rating problem is now equivalent to that of finding the most likely mapping. Thus, we wish to solve for $\underset{f}{\text{argmax}}Pr(M\mid f)$.

4.2 Algorithm

Now, we generalize our idea of bucketized, dominance-consistent mappings from Section 3.2 to find a maximum likelihood solution for the rating problem.

Bucketizing

For every item, we are given m worker responses, each in 1, 2, …, R. It can be shown that there are $\left(\begin{array}{c}R+m-1\\ R-1\end{array}\right)$ different possible worker response sets, or buckets. The bucketizing idea is the same as before: items with the same response sets can be treated identically and should be mapped to the same values. So we only consider mappings that give the same rating score to all items in a common response set bucket.

Dominance Ordering

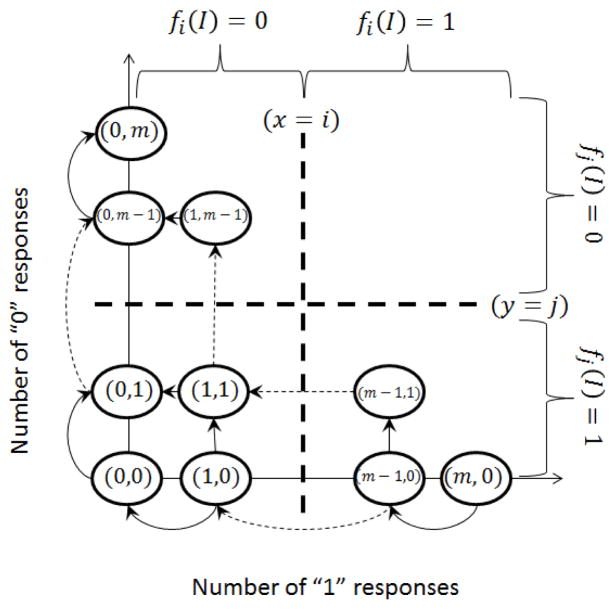
Next we generalize our dominance constraint. Recall that for filtering with m responses per item, we had a total ordering on the dominance relation over response set buckets, (m, 0) > (m − 1, 1) > … > (1, m − 1) > (0, m) where no dominated bucket could have a higher score (“1”) than a dominating bucket (“0”). Let us consider the simple example where R = 3 and we have m = 3 worker responses per item. Let (i, j, k) denote the response set where i workers give a score of “3”, j workers give a score of “2” and k workers give a score of “1”. Since we have 3 responses per item, i + j + k = 3. Intuitively, the response set (3, 0, 0) dominates the response set (2, 1, 0) because in the first, three workers gave items a score of “3”, while in the second, only two workers give a score of “3” while one gives a score of “2”. Assuming a “reasonable” worker behavior, we would expect the value assigned to the dominating bucket to be at least as high as the value assigned to the dominated bucket. Now consider the buckets (2, 0, 1) and (1, 2, 0). For items in the first bucket, two workers have given a score of “3”, while one worker has given a score of “1”. For items in the second bucket, one worker has given a score of “3”, while two workers have given a score of “2”. Based solely on these scores, we cannot claim that either of these buckets dominates the other. So, for the rating problem we only have a partial dominance ordering, which we can represent as a DAG. We show the dominance-DAG for the R = 3, m = 3 case in Figure 8. For arbitrary m, R, we can define the following dominance relation.

Figure 8.

Dominance-DAG for 3 workers and scores in {1, 2, 3}

Definition 4.1 (Rating Dominance)

Bucket B₁ with response set ( $v_R^1,v_{R-1}^1,\dots ,v_1^1$) dominates bucket B₂ with response set ( $v_R^2,v_{R-1}^2,\dots ,v_1^2$) if and only if $\exists 1<r^{\prime }\le R\ni (v_r^1=v_r^2\forall r\notin \{r^{\prime },r^{\prime }-1\})$ and $(v_{r^{\prime }}^1=v_{r^{\prime }}^2+1)\wedge (v_{r^{\prime }-1}^1=v_{r^{\prime }-1}^2-1)$.

Intuitively, a bucket B₁ dominates B₂ if increasing the score given by a single worker to B₂ by 1 makes its response set equal to that of items in B₁. Note that a bucket can dominate multiple buckets, and a dominated bucket can have multiple dominating buckets, depending on which worker’s response is increased by 1. For instance, in Figure 8, bucket (2, 1, 0) dominates both (2, 0, 1) (increase one score from “1” to “2”) and (1, 2, 0) (increase one score from “2” to “3”), both of which dominate (1, 1, 1).

Dominance-Consistent Mappings

As with filtering, we consider the set of mappings satisfying both the bucketizing and dominance constraints, and call them dominance-consistent mappings.

Dominance-consistent mappings can be represented using cuts in the dominance-DAG. To construct a dominance-consistent mapping, we split the DAG into at most R partitions such that no parent node belongs to an intuitively “lower” partition than its children. Then we assign ratings to items in a top-down fashion such that all nodes within a partition get a common rating value lower than the value assigned to the partition just above it. Figure 8 shows one such dominance-consistent mapping corresponding to a set of cuts. A cut with label c = i essentially partitions the DAG into two sets: the set of nodes above all receive ratings ≥ i while all nodes below receive ratings < i. To find the most likely mapping, we sort the items into buckets and look for mappings over buckets that are consistent with the dominance-DAG. We use an iterative top-down approach to enumerate all consistent mappings. First, we label our nodes in the DAG from $1\dots \left(\begin{array}{c}R+m-1\\ R-1\end{array}\right)$ according to their topological ordering, with the root node starting at 1. In the i^th iteration, we assume we have the set of all possible consistent mappings assigning values to nodes 1 … i − 1 and extend them to all consistent mappings over nodes 1 … i. When the last ${\left(\begin{array}{c}R+m-1\\ R-1\end{array}\right)}^{th}$ node has been added, we are left with the complete set of all dominance-consistent mappings. Details of our algorithm appear in [6].

Complexity

As with the filtering problem, an exhaustive search of only the dominance-consistent mappings under this dominance DAG constraint gives us a global maximum likelihood mapping across a much larger space of reasonable mappings. Suppose we have n items, R rating values, and m worker responses per item. The number of buckets of possible worker response sets (nodes in the DAG) is $\left(\begin{array}{c}R+m-1\\ R-1\end{array}\right)$. Then, the number of unconstrained mappings is Rⁿ and number of mappings with just the bucketizing condition, i.e., where items with the same response sets get assigned the same value, is $R^{\left(\begin{array}{c}R+m-1\\ R-1\end{array}\right)}$. It is easy to see that this is an upper bound to the number of dominance-consistent mappings.

We can also derive a reasonable lower bound by observing that one way of generating (a subset of) dominance-consistent mappings is to assign ratings to the DAG such that all nodes at the same depth have identical ratings, and all nodes at any depth have a higher rating than all nodes at the subsequent lower depth. Note that all mappings generated this way are dominance-consistent, as no lower node can dominate a higher one. Furthermore, observe that this bound is achieved in the limiting case when the DAG has a width of 1, i.e., it is a chain. Suppose the DAG has a total depth of d. Then, using the standard combinatorial stars and bars technique, we can show that the number of such mappings is given by $\left(\begin{array}{c}d+R-1\\ d\end{array}\right)$. Now, by observing that the root node (depth 1) is given by (m, 0, 0, …, 0), the bottom node (depth d) is given by (0, 0, …, m), and that the ratings given to any node in depth d sum up to Rm − d + 1, we have d = Rm − m + 1. Substituting this value, we have $\left(\begin{array}{c}Rm-m+R\\ Rm-m+1\end{array}\right)$ as a lower bound for the number of dominance-consistent mappings for the rating problem.

We leave the (challenging) problem of finding a closed form expression for the actual number of dominance-consistent mappings as future work. Instead, we enumerate a sample set of values in Table 2 for n = 100 items. We see that the number of dominance-consistent mappings is significantly smaller than the number of unconstrained mappings. The fact that this greatly reduced set of intuitive mappings contains a global maximum likelihood solution displays the power of our approach. Furthermore, n is typically much larger, which would make the number of unconstrained mappings exponentially larger, while the number of dominance-consistent mappings remains unaffected.

Table 2.

Number of Mappings for n = 100 items

R	m	Unconstrained	Bucketized	Dom-Consistent
3	3	1047	6 × 104	126
3	4	1047	107	462
3	5	1047	1010	1716
4	3	1060	1012	2.8 × 104
4	4	1060	1021	2.7 × 106
5	2	1069	1010	2.8 × 104
5	3	1069	1024	1.1 × 108

4.3 Experiments

In this section, we evaluate the performance of our algorithm, OPT, on synthetic and real rating data. Similar to our analyses in Section 3.5, we report our performance in terms of (a) accuracy of label predictions, (b) accuracy of worker error rates, and (c) time taken. As before, in all our experiments, OPT assumes a single error rate across all workers. Here, we discuss two experiments: our first experiment is on synthetic data, and our second experiment is on data from [2], on website relevance judgment.

Experiment 1: Synthetic Data Experiments

We perform experiments on the identical, as well as distinct worker synthetic data settings using setups similar to those described in Section 3.5. We present a sample of our experiments and results below, and refer interested readers to our technical report for a more extensive experimental analysis.

Setting 1: Identical worker error distribution

Similar to Section 3.5, we first perform experiments under the setting where data generation, OPT, as well as EM are all based on a single error rate matrix. Details of the setup can be found in [6].

Likelihood

Figure 7(b) plots the likelihoods (on log scale) of the mappings output by different algorithms along the y-axis. We observe that the likelihoods of the mappings returned by OPT, are much higher than those of any of the EM algorithms. For example, consider m = 5: we observe that our algorithm finds mappings that are on average 9 orders of magnitude more likely than those returned by EM(*) (here, the best EM instance). As with filtering, the gap between the performance of our algorithm and the EM instances decreases as the number of workers increases.

Figure 7.

(a) Filtering, Real Dataset 2, m = 6; (b) Rating, Synthetic, Setting 1: Likelihood; (c) Rating, Setting 1: Worker Quality Predictions;

Quality of item rating predictions

In Figure 7(c) we compare the predicted ratings of items against actual values. We measure a weighted score based on how far the predicted value is from the true value. This score lies in the range [0, 2] (details in [6]), with a lower score implying more accurate predictions. Again, we observe that in spite of optimizing for, and providing a global maximum likelihood guarantee, our algorithm predicts item ratings with a high degree of accuracy, with significantly better performance than all the EM instances. For example, at m = 2 we observe that OPT deviates from the true rating by less than 0.4 on average, while the EM instances are off by 0.8 or higher.

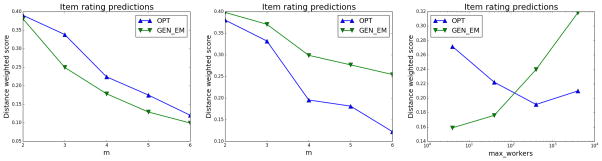
Setting 2: Distinct worker error distributions

Accuracy Results

Here, we compare the distance-weighted scores (plotted along the y-axis) of our algorithm, OPT, against GEN_EM while varying m (number of responses per item) along the x-axis (for a fixed m′). We observe that GEN_EM is more accurate than OPT for the case when m′ = 50 (Figure 9(a)), but is significantly worse than OPT for the sparse item-worker response matrix setting (Figure 9(b)), where the size of the worker pool, m′ = 1000 is large. For example, at m = 5, OPT deviates from the true ratings by less than 0.2 on average, while GEN_EM deviates by nearly 0.3. Comparing these results to those in Section 3.5, our gains in accuracy of item predictions for rating are significantly higher because the number of parameters being estimated is much higher, and the EM algorithm has more “ways” it can go wrong if the parameters are initialized incorrectly. That is, with a higher dimensionality we expect that EM converges more often to non-optimal local maxima.

Figure 9.

Rating, Synthetic: (a) Setting 2, item rating predictions: m′ = 50, (b) m′ = 1000 (c) Rating (m = 4), Synthetic, Vary m′

Similar to Figure 4(c), in Figure 9(c), we also show the results obtained when we vary m′ along the x-axis (log-scale), while keeping m fixed at 4. For m′ < 100 (smaller worker pool, denser item-worker response matrix), GEM_EM outperforms our algorithm, while for higher values of m′, OPT is significantly more accurate.

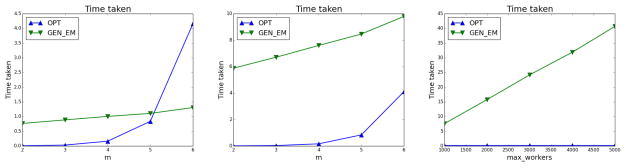
Efficiency Results

In Figures 10(a), 10(b), 10(c), we compare the efficiency of OPT against GEN_EM. Similar to our experiments for filtering, in Figures 10(a), 10(b) we vary m, for fixed values of m′ = 100, 1000 respectively. In Figure 10(c), we vary m′ while keeping m fixed at 4. We observe that OPT appears to scale exponentially in m, and is less efficient than GEN_EM for higher values of m and small values of m′ (m′ ≤ 100, m > 5). However, for a large worker pool (m′ ≥ 1000), we see that OPT is much more efficient. Since typically m is fixed to be a small value by the task requester, we conclude that in practice OPT scales better than GEN_EM. Note again, that although these plots are drawn with GEN_EM performing 40 iterations, reducing the number of iterations (at the cost of accuracy) will only linearly scale down GEN_EM’s latency; it will still be inefficient compared to OPT for higher values of m′.

Figure 10.

Rating, Synthetic, Setting 2; Vary m: (a) m′ = 100 (b) m′ = 1000; Vary m′: (c) m = 4

Again, we conclude that even when distinct worker-level information is available to EM, OPT performs very well in spite of its simplifying assumptions, especially under the very realistic settings where worker pools are large and non-persistent.

Experiment 2: Real Data Experiment on [2]

We also performed experiments on a subset of the HC dataset from [2, 20]. This dataset contains judgements given by Mechanical Turk workers on the relevance of displayed webpages to given search queries. Relevance was judged on a ternary scale: highly relevant, relevant, and non-relevant. From this dataset, we chose the subset where every item (webpage-query pair) had gold truth available and at least 6 worker judgements. On this subset (spanning around 500 workers, 1000 items, 10000 judgements), we observed that both OPT and GEN_EM exactly matched the gold truth labels roughly 46% of the time, as compared to the Median strategy (always predict median of observed labels) which got roughly 35% correct. The distance weighted score (average absolute deviation from gold truth on a scale of 0 to 2) obtained by OPT was 0.65, while that by GEN_EM and Median were 0.74 and 0.85 respectively, showing that OPT predicted values closer to the gold truth in more cases than simple vanilla-EM or Median based strategies.

5. CONCLUSIONS

We have taken a first step towards finding a global maximum likelihood solution to the problem of jointly estimating the item ground truth, and worker quality, in crowdsourced filtering and rating tasks. Given worker ratings on a set of items, we showed that the problem of jointly estimating the ratings of items and worker quality can be split into their two respective, independent estimation problems. We used a few key, intuitive ideas to first find a global maximum likelihood mapping from items to ratings, thereby finding the most likely ground truth. We then showed that the worker quality, modeled by a common response probability matrix, can be inferred automatically from the corresponding maximum likelihood mapping. We develop a novel pruning and search-based approach, in which we greatly reduce the space of (originally exponential) potential mappings to be considered, and prove that an exhaustive search in the reduced space is guaranteed to return a maximum likelihood solution.

Via our experiments, we demonstrated that our algorithm outperforms EM-based algorithms on datasets where worker errors are all alike, and in fact, even outperforms EM-based algorithms on datasets where the worker errors are distinct, as long the worker pools are large. The latter setting is common in practice in crowd-sourcing marketplaces where workers are fleeting and easily distracted. It should be noted that even in the case of real datasets with a small set of distinct workers where our algorithm (due to its ignoring of worker identities) is at a disadvantage, its performance is still comparable to state-of-the-art algorithms while providing the significant benefit of being simple and intuitive. We also demonstrated that despite being optimized for the likelihood of mappings, our algorithm estimates ground truth of item ratings and worker error rates with high accuracy, and performs well on other metrics.

Our algorithms can be generalized to the setting where there is a small number of worker classes, each with their own error rates. Likewise, in this paper we assume a fixed number of responses for each item, but we can be generalized to the case where different items may receive different numbers of responses. We briefly discuss both these generalizations in our Appendix B.

It should be noted that although our framework extends to these generalizations, including the case where each worker has an independent, different quality, the algorithms can be inefficient in practice. We have not considered the problem of item difficulties in this paper, assuming that workers have the same quality of responses on all items. As future work, we hope that the ideas described in this paper can be built upon to design efficient algorithms that find a global maximum likelihood mapping under more general settings.

APPENDIX

A. FILTERING

A.1 Proof of Correctness

In this section, we show that if a mapping, f, is not dominance-consistent for some given response matrix M, then we can construct an alternate, dominance-consistent mapping f′, such that Pr(M|f′) ≥ Pr(M|f). This is Step 3 in the proof for Theorem 3.3, and the proof for Step 2 follows in a similar fashion.

Suppose f does not satisfy the dominance constraint. Then, there exists at least one pair of items I₁, I₂ such that M(I₁) > M(I₂) and f(I₁) = 0, f(I₂) = 1. Define mapping f′ as follows:

$$f^{\prime }(I)=\{\begin{array}{ll}f(I_2)\hfill & \text{for}I=I_1\hfill \\ f(I_1)\hfill & \text{for}I=I_2\hfill \\ f(I)\hfill & \forall I\in \mathbf{I}\backslash \{I_1,I_2\}\hfill \end{array}$$

Let I₁ have realization (m−i, i), that is, it receives m−i responses of 1 and i responses of 0 from workers. Similarly, let I₂ have realization (m − j, j). Now, suppose i < j, that is, M(I₁) > M(I₂) and f(I₁) = 0, f(I₂) = 1, f′(I₁) = 1, f′(I₂) = 0. Now, we need to show that Pr(M|f′) ≥ Pr(M|f).

Let n_k1, n_k0 denote the number of items mapped to 1 and 0 respectively under f (and f′) in I \ {I₁ ∪ I₂} with realization (m − k, k). With this notation, we can compute each of Pr(M|f) and Pr(M|f′).

Likelihood of f′ : I₁ → 1, I₂ → 0.

Let

$$p_{11}^{\prime }=\frac{{\sum }_k{n}_{k1}(m-k)+(m-i)}{{\sum }_k{n}_{k1}m+m}$$

and

$$p_{00}^{\prime }=\frac{{\sum }_k{n}_{k0}(m-k)+j}{{\sum }_k{n}_{k0}m+m}$$

Here, $p_{11}^{\prime }$ (respectively $p_{00}^{\prime }$) represents the underlying (maximum likelihood) probability of a worker responding 1 (respectively 0) for an item with true value 1 (respectively 0). Further, (for ease of exposition), let a₁ = Σ_k n_k1(m − k) + (m − i), a₀ = Σ_k n_k0(m − k) + j, c₁ = Σ_k n_k1m + m, and c₀ = Σ_k n_k0m + m. Then, from the independence of items assumption, we have, $P(M\mid f^{\prime })={(p_{11}^{\prime })}^{a_1}{(1-p_{11}^{\prime })}^{c_1-a_1}{(p_{00}^{\prime })}^{a_0}{(1-p_{00}^{\prime })}^{c_0-a_0}$.

Likelihood of f : I₁ → 0, I₂ → 1.

Similarly, we let

$$p_{11}=\frac{{\sum }_k{n}_{k1}(m-k)+(m-j)}{{\sum }_k{n}_{k1}m+m}$$

and

$$p_{00}=\frac{{\sum }_k{n}_{k0}(m-k)+i}{{\sum }_k{n}_{k0}m+m}$$

Suppose b₁ = Σ_k n_k1(m − k) + (m − j), and b₀ = Σ_k n_k0(m − k)+i, we can similarly show that P(M|f) = (p₁₁)^b₁(1 − p₁₁)^c₁−b₁ × (p₀₀)^b₀(1 − p₀₀)^c₀−b₀.

Therefore, we can write $\frac{P(M\mid f^{\prime })}{P(M\mid f)}$ as X₁X₀, where: $X_1=\frac{{(p_{11}^{\prime })}^{a_1}{(1-p_{11}^{\prime })}^{c_1-a_1}}{{(p_{11})}^{b_1}{(1-p_{11})}^{c_1-b_1}}$, and $X_0=\frac{{(p_{00}^{\prime })}^{a_0}{(1-p_{00}^{\prime })}^{c_0-a_0}}{{(p_{00})}^{b_0}{(1-p_{00})}^{c_0-b_0}}$.

We claim, that for reasonable mappings, X₁, X₀ ≥ 1, which implies that P(M|f′) ≥ P(M|f), thereby completing our proof. We show below that X₁ ≥ 1. The proof for X₀ follows in a similar fashion.

We can rewrite X₁ as $X_1=\frac{{(a_1)}^{a_1}{(c_1-a_1)}^{c_1-a_1}}{{(b_1)}^{b_1}{(c_1-b_1)}^{c_1-b_1}}$. We drop the “1” subscript from this point for ease of notation. Here, we have a < b (follows from i < j). It can be shown that when a < b, a+b ≥ c ⇒ X ≥ 1. It is easy to see that if f and f′ are reasonable mappings, then we have $p_{11}^{\prime }$, p₁₁ ≥ 0.5 (follows from the definition in Section 3.3). But $p_{11}^{\prime }=\frac{a_1}{c_1}$, and $p_{11}=\frac{b_1}{c_1}$. Therefore, $a,b\ge \frac{c}{2}\Rightarrow a+b\ge c\Rightarrow X\ge 1$. This completes our proof.

A.2 Real Data Additional Experiments

Here, we report some additional experiments for our first real dataset [10]. In particular, we would like to estimate the performance of OPT versus vanilla EM instances. Under this setting, OPT, as well as EM assume a single worker error distribution and infer item values based on this assumption and learned error distribution.

Setup

We vary the number of workers used from 1 to 19 and plot the performance of algorithms OPT, EM(1), EM(2), EM(3), EM(*) similar to Section 3.5. We plot the number of worker responses used along the x-axis. For instance, a value of m = 4 indicates that for each item, four random worker responses are chosen. The four workers answering one item may be different from those answering another item. This random sample of the response set is given as input to the different algorithms. Similar to our synthetic data experiments, we average our results across 100 different trials for each data point in our subsequent plots.

Likelihood

Figure 11(b) plots the likelihoods of the final solution for different algorithms. We observe that except for EM(2), all algorithms have a high likelihood. This can be explained as follows: EM(2) which starts with an initialization of e₀ and e₁ rates around 0.5 and converges to a final response probability matrix in that neighborhood. Final error rates of around 0.5 (random) will have naturally low likelihood when there is a high amount of agreement between workers. EM(1) and EM(3) on the other hand start with, and converge to near opposite extremes with EM(1) predicting e₀/e₁ rates ≈ 0 and EM(3) predicting error rates ≈ 1. Both of these, however, result in a high likelihood of observing the given response, with EM(1) predicting that the worker is always correct, and EM(3) predicting that the worker is always incorrect, i.e., adversarial. Even though EM(1) and EM(3) often converge to completely opposite predictions of item-values because of their initializations, their solutions still have similar likelihoods corresponding to the intuitive extremes of perfect and adversarial worker behavior. This behavior thus demonstrates the strong dependence of EM-based approaches on the initialization parameters.

Figure 11.

Filtering, Real, Setting 1: (a) Item predictions, (b) Likelihood; (c) 2 worker classes: Fraction incorrect

Fraction Incorrect

Figure 11(a) plots the fraction of items predicted incorrectly along the y-axis for OPT and the EM algorithms. We observe that both EM(1) and our algorithm OPT do fairly well on this dataset even when a very few number of worker responses are used. However, EM(*), which one may expect would typically do better than the individual EM initializations, sometimes does poorly compared to OPT by picking solutions of high likelihood that are nevertheless not very good. Note that here we assume that worker identities are unknown and arbitrary workers could be answering different tasks — our goal is to characterize the behavior of the worker population as a whole. For larger datasets, we expect the effects of population smoothing to be greater and our assumptions on worker homogeneity to be closer to the truth. So, even though our algorithm provides theoretical global guarantees under somewhat strong assumptions, it also performs well for settings where not all our assumptions are true.

B. EXTENSIONS

In this section we discuss the generalization of our bucketizing and dominance-based approach to some extensions of the filtering and rating problems. Recall our two major assumptions: (1) every item receives the same number (m) of responses, and (2) all workers are randomly assigned and their responses are drawn from a common distribution, p(i, j). We now relax each of these requirements and describe how our framework can be applied.

B.1 Variable number of responses

Suppose different items may receive different numbers of worker responses, e.g. because items are randomly chosen, or workers choose some questions preferentially over others. Note in this section we are still assuming that all workers have the same response probability matrix p.

For this discussion we restrict ourselves to the filtering problem; a similar analysis can be applied to rating. Suppose each item can receive a maximum of m worker responses, with different items receiving different numbers of responses. Again, we bucketize items by their response sets and try to impose a dominance-ordering on the buckets. Now, instead of only considering response sets of the form (m − j, j), we consider arbitrary (i, j). Recall that a response set (i, j) denotes that an item received i “1” responses and j “0” responses. We show the imposed dominance ordering in Figure 13.

Figure 13.

Variable number of responses

We expect an item that receives i “1” responses and j “0” responses to be more likely to have true value “1” than an item with i − 1 “1” responses and j “0” responses, or an item with i “1” responses and j + 1 “0” responses. So, we have the dominance relations (i, j) > (i − 1, j) where i ≥ 1, j ≥ 0, i + j ≤ m, and (i, j) > (i, j + 1) with i, j ≥ 0, i + j + 1 ≤ m. Note that the dominance ordering imposed in Section 3, (m, 0) > (m − 1, 1) > … > (0, m), is implied transitively here. For instance, (m, 0) > (m − 1, 0) ∧ (m − 1, 0) > (m − 1, 1) ⇒ (m, 0) > (m − 1, 1). Also note that this is a partial ordering as certain pairs of buckets, (0, 0) and (1, 1) for example, cannot intuitively be compared.

Again, we can reduce our search for the maximum likelihood mapping to the space of all bucketized mappings consistent with this dominance (partial) ordering. That is, given item set I and response set M, we consider mappings f : I → {0, 1}, where M(I₁) = M(I₂) ⇒ f(I₁) = f(I₂) and M(I₁) > M(I₂) ⇒ f(I₁) ≥ f(I₂). We show two such dominance consistent mappings, f_i and f_j in Figure 13. Mapping f_i assigns all items with at least i “1” worker responses to a value of 1 and the rest to a value of 0. Similarly, mapping f_j assigns all items with at most j “0” responses a value of 1 and the rest a value of 0. We can construct a third dominance-consistent mapping f_ij from a conjunction of these two: f_ij(I) = 1 if and only if f_i = 1 ∧ f_j = 1, that is, f_ij assigns only gives those items that have at least i “1” worker responses and at most j “0” responses, a value of 1. We can now describe f_i and f_j as special instances of the dominance-consistent mapping f_ij when j = m and i = 0 respectively.

We show below that all dominance-consistent mappings for this setting can be described as the union of different f_ijs for a set of 0 ≤ i, j ≤ m, for a total of O(2^m) dominance-consistent mappings. Note that although this expression is exponential in the maximum number of worker responses per item, m, for most practical applications this is a very small constant.

Let f be any dominance-consistent mapping under this setting. Let (i, j) be a response set with i responses of 1 and j responses of 0 such that f(i, j) = 1. Then, by our dominance constraint, we know that f(i + Δi, j + Δj) = 1∀Δi ≥ 0, Δj ≥ 0. We represent this figuratively in Figure 12(a). If f(i, j) = 1, then all response sets, or points, in the shaded area also get mapped to a value of 1.

Figure 12.

Variable number of responses: (a) Dominance constraint 1, (b) Dominance constraint 2; 2 worker classes: (c) Time taken

Now, by applying the dominance constraint as shown in Figure 12(a) to every (i, j) such that f(i, j) = 1, we can show that f can now be described intuitively by its “boundary”. We demonstrate this intuition in Figure 12(b). Every point, (i, j), on f’s boundary satisfies f(i, j) = 1. Additionally, every point “within” the boundary, every point that is to the right of and below the boundary gets mapped to a value of 1 under f. Finally, every point that is not on or within the boundary gets mapped to a value of 0 under f.

It follows from the dominance constraint that every dominance-consistent mapping, f, can be represented by a unique such continuous boundary. Furthermore, it is easy to see that any such boundary satisfies three conditions:

• Its leftmost (corner) point lies on one of the axes.

• Its topmost (corner) point lies on the line x + y = m.

• If (x₁, y₁) and (x₂, y₂) lie on the boundary, then x₁ ≤ x₂ ⇔ y₁ ≤ y₂.

Intuitively the above three conditions give us a constructive definition for any dominance-consistent mapping’s boundary. Every dominance-consistent mapping can be constructed uniquely as follows: (1) Choose a left corner point lying on one of the axes. (2) Choose a topmost corner point (necessarily above and to the right of the first corner point) lying on the line x + y = m. (3) Finally, define the boundary as a unique grid traversal from the left corner to the top corner where you are allowed to extend the boundary only to the right or upwards. Each such boundary corresponds to a unique dominance-consistent mapping where every point on or under the boundary is mapped to 1 and every other point is mapped to 0. Furthermore, every dominance-consistent mapping has a unique such boundary.

Therefore our problem of counting the number of dominance-consistent mappings for this setting reduces to counting the number of such boundaries. We use our constructive definition for the boundary to compute this number. First, suppose the leftmost corner point, L = (p, 0), 0 ≤ p ≤ m, lies on the x-axis (we can calculate similarly for (0, q)). Now, the topmost corner point lies to the right of the first corner point, and on the line x + y = m. Therefore it is of the form T = (p + i, m − (p + i)) for some 0 ≤ i ≤ m − p. The number of unique grid traversals (respectively boundaries) from L to T is given by $\left(\begin{array}{c}m-p\\ i\end{array}\right)$. Combining, we have the number of unique boundaries that have their left corner on the x-axis is ${\displaystyle \sum _{p=0}^m}{\displaystyle \sum _{i=0}^{m-p}}\left(\begin{array}{c}m-p\\ i\end{array}\right)={\displaystyle \sum _{p=0}^m}{2}^{m-p}=2^{m+1}-1$. Calculating similarly for boundaries that start with their leftmost corner on the y-axis ((0, q), 1 ≤ q ≤ m) and including the empty boundary (corresponding to the mapping where all items get assigned a value of 0), we get an additional 2^m boundaries. Therefore, we conclude that there are O(2^m) such boundaries, corresponding to O(2^m) dominance-consistent mappings. It should be noted that although this is exponential in the maximum number of worker responses to an item, typical values of m are small enough that all mappings can very easily be enumerated and evaluated.

B.2 Worker classes

So far we have assumed that all workers are identical, in that they draw their answers from the same response probability matrix, a strong assumption that does not hold in general. Although we could argue that different worker matrices could be aggregated into one average probability matrix that our previous approach discovers, if we have fine-grained knowledge about workers, we would like to exploit it. In this section we consider the setting where there are two of classes of workers, expert and regular workers to evaluate the same set of items. We discuss the generalization to larger numbers of worker classes below.

We now model worker behavior as two different response probability matrices, the first corresponding to expert workers who have low error rates, and the second corresponding to regular workers who have higher error rates. Our problem now becomes that of estimating the items’ true values in addition to both of the response probability matrices. For this discussion, we consider the filtering problem; a similar analysis can be applied to the rating case.

Again, we extend our ideas of bucketizing and dominance to this setting. Let (y_e, n_e, y_r, n_r) be the bucket representing all items that receive y_e and n_e responses of “1” and “0” respectively from experts, and y_r and n_r responses of “1” and “0” respectively from regular workers. A dominance partial ordering can be defined using the following rules. An item (respectively bucket) with response set $B_1=(y_e^1,n_e^1,y_r^1,n_r^1)$ dominates an item (respectively bucket) with response set $B_2=(y_e^2,n_e^2,y_r^2,n_r^2)$ if and only if one of the following is satisfied:

• B₁ sees more responses of “1” and fewer responses of “0” than B₂. That is, $(y_e^1\ge y_e^2)\wedge (y_r^1\ge y_r^2)\wedge (n_e^1\le n_e^2)\wedge (n_e^1\le n_e^2)$ where at least one of the inequalities is strict.

• B₁ and B₂ see the same number of “1” and “0” responses in total, but more experts respond “1” to B₁ and “0” to B₂. That is, $(y_e^1+y_r^1=y_e^2+y_r^2)\wedge (n_e^1+n_r^1=n_e^2+n_r^2)\wedge (y_e^1\ge y_e^2)\wedge (n_e^1\le n_e^2)$ where at least one of the inequalities is strict.

As before, we consider only the set of mappings that assign all items in a bucket the same value while preserving the dominance relationship, that is, dominating buckets get at least as high a value as dominated buckets.

Note that the second dominance condition above leverages the assumption that experts have smaller error probabilities than regular workers. If we were just given two classes of workers with no information about their response probability matrices, we could only use the first dominance condition. In general, having more information about the error probabilities of worker classes allows us to construct stronger dominance conditions, which in turn reduces the number of dominance-consistent mappings. This property allows our framework to be flexible and adaptable to different granularities of prior knowledge.

Example (2 worker classes, 2 responses per item)

We demonstrate the OPT solution for a simple generalization to filtering, where we have two worker classes: “good”, and “bad”, and each item receives 2 responses. Suppose we denote the responses by a good worker as “Y” (yes, or 1) and “N” (no, or 0), and those by a bad worker as “y”, and “n”. Any item can receive one of the following 10 possible sets of responses: (YY), (Yy), (yy), (Yn), (yn), (YN), (yN), (nn), (Nn), (NN). If the only information about these worker classes is that the good class has lower (false positive and false negative) error rates, then the corresponding (least constrained) dominance-consistent DAG is shown in Figure 14. For this DAG, we have 18 dominance-consistent mappings.

Figure 14.

2 worker classes: Dominance DAG

We evaluated the performance of OPT against GEN_EM under this setting on a synthetic dataset. Workers were randomly chosen to belong to one of the two classes. Workers from the good class were uniformly randomly assigned an error rate between 0.9 and 1.0, while workers from the bad class were given an error rate between 0.6 and 0.7. In Figure 11(c) we vary the total size of the worker pool, m′ along the x-axis, and show the fraction of items predicted incorrectly along the y-axis. We also plot the times taken by OPT and GEN_EM (20 iterations) to label all items in Figure 12(c). We observe that OPT is faster, as well as more accurate than GEN_EM under this setting.

Complexity

The complexity introduced by worker classes can not be estimated for the general case, since it is governed not only by the number of worker classes, but also by the input constraints specified on the error rates of workers from different classes. Finer grained constraints imply fewer dominance-consistent mappings and hence, a lower complexity, while coarser grained (or fewer) constraints imply a higher complexity. For instance, in the limiting case where we have no prior information about the worker class error rates, we have no constraints, and the dominance-consistent DAG correspondingly has no edges. Therefore, the complexity of OPT, which scales linearly with the number of mappings, is 𝒪(R^k), where R = 2 for filtering, and k is the number of possible responses (or nodes in the DAG) seen by an item. At the other extreme, when the different error rates of the respective classes are highly constrained (for instance, if we know that one class is significantly better than another, and any responses from workers of the first class dominate all responses of workers from the second class), the dominance-consistent DAG can be reduced to a single chain: in this case, given any pair of sets of responses, it can be calculated exactly which set gives a higher likelihood of an item passing the filter. In this extreme, the resulting complexity of OPT is $\mathcal{O}(\left(\begin{array}{c}k+R-1\\ k\end{array}\right))$ (derivable in a similar fashion to the lower bound shown for rating in Section 4.2). Note that k itself is not easy to compute for arbitrary values of R, m and w (number of worker classes). For m = 1, we have k = wR (each response can be given by any of the worker classes, and can be anything between [1, R]). For arbitrary values, k can scale exponentially with w.

While this extension is reasonable when the number of distinct worker classes is small, it is impractical to generalize it to a large number of classes. One heuristic approach to tackling the problem of a large number of worker classes, or independent workers, could be to divide items into a large number discrete groups and assign a small distinct set of workers to evaluate each group of items. We then treat and solve each of the groups independently as a problem instance with a small number worker classes. We leave the problems of formally computing the complexity, and finding more efficient algorithms for this general setting as a topic for future work.