Effects of Using the Unloaded Configuration in Predicting the In Vivo Diastolic Properties of the Heart

Abstract

Computational models are increasingly being used to investigate the mechanical properties of cardiac tissue. While much insight has been gained from these studies, one important limitation associated with computational modeling arises when using in-vivo images of the heart to generate the reference state of the model. An unloaded reference configuration is needed to accurately represent the deformation of the heart. However, it is rare for a beating heart to actually reach a zero-pressure state during the cardiac cycle. To overcome this, a computational technique was adapted to determine the unloaded configuration of an in-vivo porcine left ventricle (LV). In the current study, in-vivo measurements were acquired using magnetic resonance images (MRI) and synchronous pressure catheterization in the LV (N=5). The overall goal was to quantify the effects of using early–diastolic filling as the reference configuration (common assumption used in modeling) versus using the unloaded reference configuration for predicting the in-vivo properties of LV myocardium. This was accomplished by using optimization to minimize the difference between MRI measured and finite element predicted strains and cavity volumes. The results show that when using the unloaded reference configuration, the computational method predicts material properties for LV myocardium that are softer and less anisotropic than when using the early-diastolic filling reference configuration. This indicates that the choice of reference configuration could have a significant impact on capturing the realistic mechanical response of the heart.

1. Introduction

Realistic computational simulations of the heart are able to provide useful information that cannot be measured clinically and may help to better diagnose and treat cardiac diseases. In finite element (FE) methods, using a good estimate of the initial unloaded configuration is a key factor to obtain realistic deformation and distribution of stress. Such a reference state rarely exists during a normal cardiac cycle, due to a continuously present physiological pressure load. Consequently, magnetic resonance (MR) images of the heart, which are used to construct FE models, can typically only represent loaded states. Some studies have used the early-diastolic geometry of the heart (following the isovolumic relaxation) as the reference state for FE models [1], [2], while others have used the mid-diastolic state [3]. In the majority of these cases the specific reference state was chosen because the LV pressure was “at a minimum”. However, the ventricle was still partially loaded, i.e., none of these states represent the true zero-pressure configuration of the heart [4].

Several methods have been suggested to estimate the unloaded configuration of a deformed structure [5] [6] [7]. Bols et al. proposed the backward displacement method, which is able to solve the inverse problem of finding the unloaded configuration of blood vessels based on fixed-point iterations [8]. The implementation of this method is straightforward and it can easily be used in combination with existing finite element solvers. In the current study, the method of Bols et al. [8] was adapted to unload the geometry of five healthy porcine left ventricle (LV) models, which were created from in-vivo MRI data that was contoured at early-diastolic filling. This provided two FE models for each of the five animals; (1) a model with a reference geometry based on early-diastolic filling and (2) a model with a reference geometry that is based on the numerically unloaded state. Next, passive material parameters of the myocardium were identified using a technique that utilizes a combination of MRI/pressure data, FE modeling, and numerical optimization [9]. The ultimate goal of this study was to estimate the in-vivo material properties of left ventricular myocardium, as well as quantify how the material properties and end-diastolic stress distributions were affected by the choice of reference configuration.

2. Methods

2.1. Finite Element Model

In this study, five healthy adult male pigs weighing approximately 40 kg were used in order to assess in-vivo cardiac function (Table 1). The animals used in this work received care in compliance with the protocols approved by the Institutional Animal Care and Use Committee at the University of Pennsylvania in accordance with the guidelines for humane care (National Institutes of Health Publication 85-23, revised 1996). The data used in the current study is from the same animal cohort that was used in the study of Nikou et al. [9], in which many of the experimental details can be found. Briefly, the endocardium and epicardium of the LV were contoured from the 3D SPAMM (SPAtial Modulation of Magnetization) MR images and fit with 3D surface geometry. Animal-specific FE meshes were generated with approximately 1500 trilinear hexahedral elements, which was based on a convergence study. A homogeneous linear distribution of myofiber orientation angles from −37° (at epicardium) to +83° (at endocardium), with respect to the circumferential direction, was assigned to each element [10]. The application of these fiber angles was confirmed by performing a sensitivity analysis, where the fiber distribution was varied over a range of endocardial and epicardial angles. The measured LV pressure was used as a loading boundary condition in the model. The base of the LV model was constrained to deform in the basal plane.

Table 1.

Physiological LV pressure and cavity volume measured from catheterization and MRI

Case #	Early-diastolic pressure (kPa)	End-diastolic pressure (kPa)	Early-diastolic volume (mL)	End-diastolic volume (mL)
1	0.04	0.90	47.1	61.0
2	0.60	2.78	57.6	71.6
3	0.56	2.22	54.7	68.8
4	0.54	1.92	35.9	57.0
5	0.94	2.17	49.9	56.1

2.2. Material Model

The passive material properties of the myocardium were assumed to be nearly incompressible and transversely isotropic with respect to the local myofiber direction. The diastolic mechanics are described by the following strain energy function [11]

$$\psi =\frac{1}{2}\mathrm{C}({\mathrm{e}}^{\mathrm{Q}}-1)$$ (1)

With transverse isotropy given by

$$\mathrm{Q}={\mathrm{b}}_{\mathrm{f}}{{\mathrm{E}}_{11}}^2+{\mathrm{b}}_{\mathrm{t}}({{\mathrm{E}}_{22}}^2+{{\mathrm{E}}_{33}}^2+{{\mathrm{E}}_{23}}^2+{{\mathrm{E}}_{32}}^2)+{\mathrm{b}}_{\mathrm{f}\mathrm{s}}({{\mathrm{E}}_{12}}^2+{{\mathrm{E}}_{21}}^2+{{\mathrm{E}}_{13}}^2+{{\mathrm{E}}_{31}}^2)$$ (2)

where the constants C, b_f, b_t and b_fs are material parameters, E₁₁ is the Green-Lagrange strain in the fiber direction, E₂₂ is the cross-fiber strain, E₃₃ is the strain in the radial direction and the rest are shear strains. The constitutive model was coded as a user defined material subroutine that was implemented in the nonlinear explicit FE solver LS-DYNA (Livermore Software Technology Corporation, Livermore, CA).

2.3. Material Parameter Estimation

A Genetic algorithm (GA) technique was chosen for the optimization, and was performed using the software LS-OPT (Livermore Software Technology Corporation, Livermore, CA). Briefly, the passive material parameters (C, b_f, b_t, b_fs) were optimized within the ranges previously reported for normal myocardium [12]. Diastolic strain was calculated from the 3D SPAMM MR images using a custom optical flow plug-in for ImageJ to derive 3D displacement flow fields [9]. The objective function that was minimized during the optimization was taken to be the mean squared error (MSE) between MRI measured and FE predicted strains as well as the normalized difference in LV cavity volume. This was done using data from two time points, specifically, at mid-diastole (a point between early diastolic filling and end-diastole) and end-diastole. Utilizing kinematic data from multiple time points allows for better identification of the material parameters, as noted by Xi et al. [19]. The MRI measured strains were computed using early diastolic filling as the reference configuration. Therefore, when the partially loaded FE models were used for parameter estimation, the FE predicted strains were directly compared with the MRI measured strains. However, for the unloaded FE models a multiplicative decomposition of the deformation gradient was used to calculate strains with respect to the early-diastolic filling reference frame and then compared with MRI measured strains. This ensured both sets of optimizations were consistent.

The objective function utilized strains predicted at N=252 positions (located at the centroids of the LV midwall elements) per time point, which were compared to the nearest LV points from the MRI data where strain was measured. The MSE was defined as

$$MSE=\frac{1}{2}\sum _{t=1}^2\sum _{n=1}^{252}\sum _{i,j=1,2,3}{(E_{ij,n}-{Ē}_{ij,n})}_t^2+{\left(\frac{V-\overline{V}}{\overline{V}}\right)}_t^2$$ (3)

where t is the number of kinematic time points, n is the location of the strain point within the myocardium, E_ij,n and V are the FE predicted diastolic strain and diastolic LV cavity volume, respectively, and the corresponding over bar variables represent in-vivo measured values. The factor of $\frac{1}{2}$ was used to calculate the mean over the number of time points, which was 2 in the current study.

2.4. Unloading

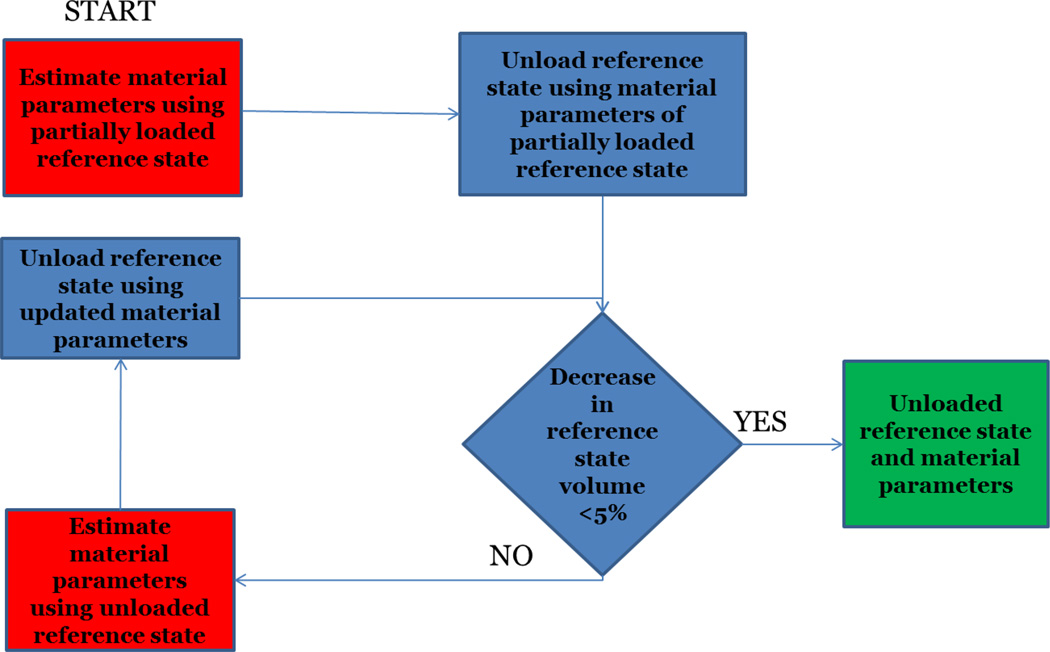
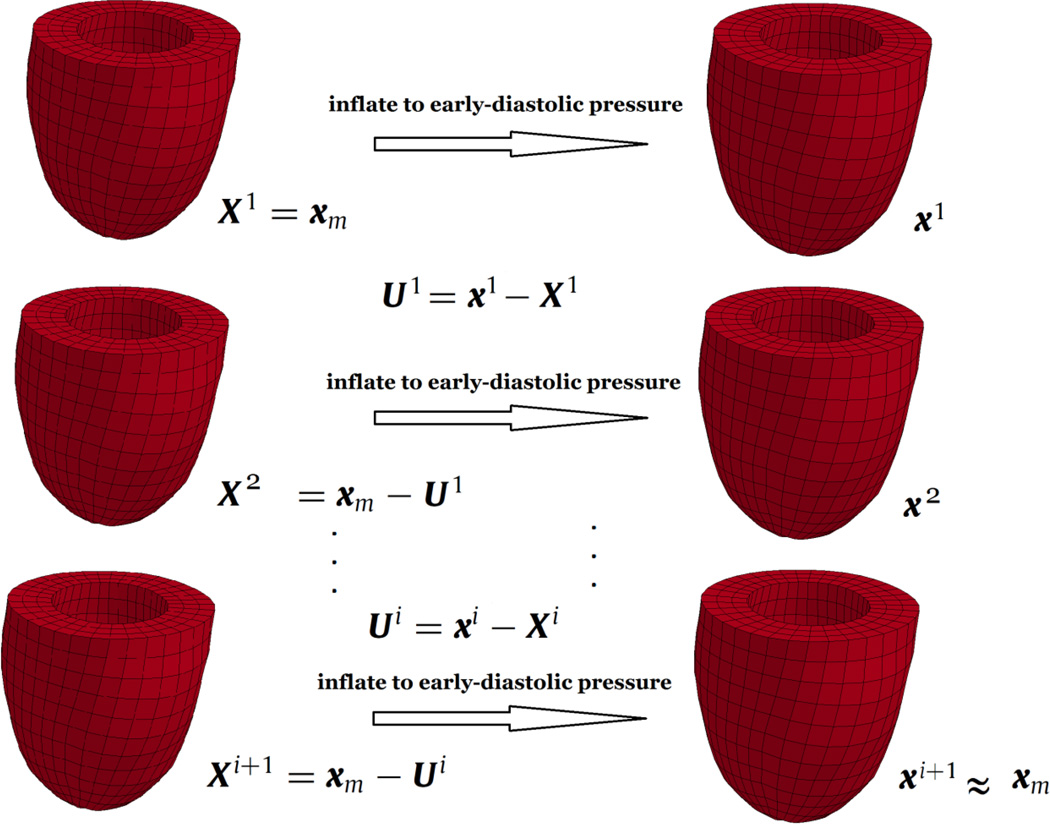
In this study, the unloading of MRI derived geometry is dependent on the material parameters of the constitutive model incorporated in the FE solver, since multiple FE solutions are required to obtain the unloaded configuration [8]. Therefore, material parameter estimation and unloading of the geometry were coupled together. An iterative scheme was designed to estimate the in-vivo material properties and unload the partially loaded reference configuration (Figure 1). In order to unload the LV geometry, the backward displacement method [8] was adapted to LV geometry (Figure 2). The first estimate of the unloaded geometry was chosen to be the early-diastolic geometry and the final estimate was assumed to be the one that, when loaded to the early-diastolic pressure, matches the target geometry best. On average, each case underwent three sets of the material parameter estimation and unloading routines, before reaching the final properties and unloaded state.

Figure 1.

The iterative process designed for in-vivo material parameters estimation and unloading the partially loaded MRI derived reference configuration.

Figure 2.

Backward displacement method applied to the LV model. X represents the nodal coordinates of consecutive estimates of the unloaded geometry and x represents the nodal coordinates of these estimates when inflated to the early-diastolic pressure. x_m represents the nodal coordinates of the target geometry (MRI derived geometry at early-diastole).

3. Results

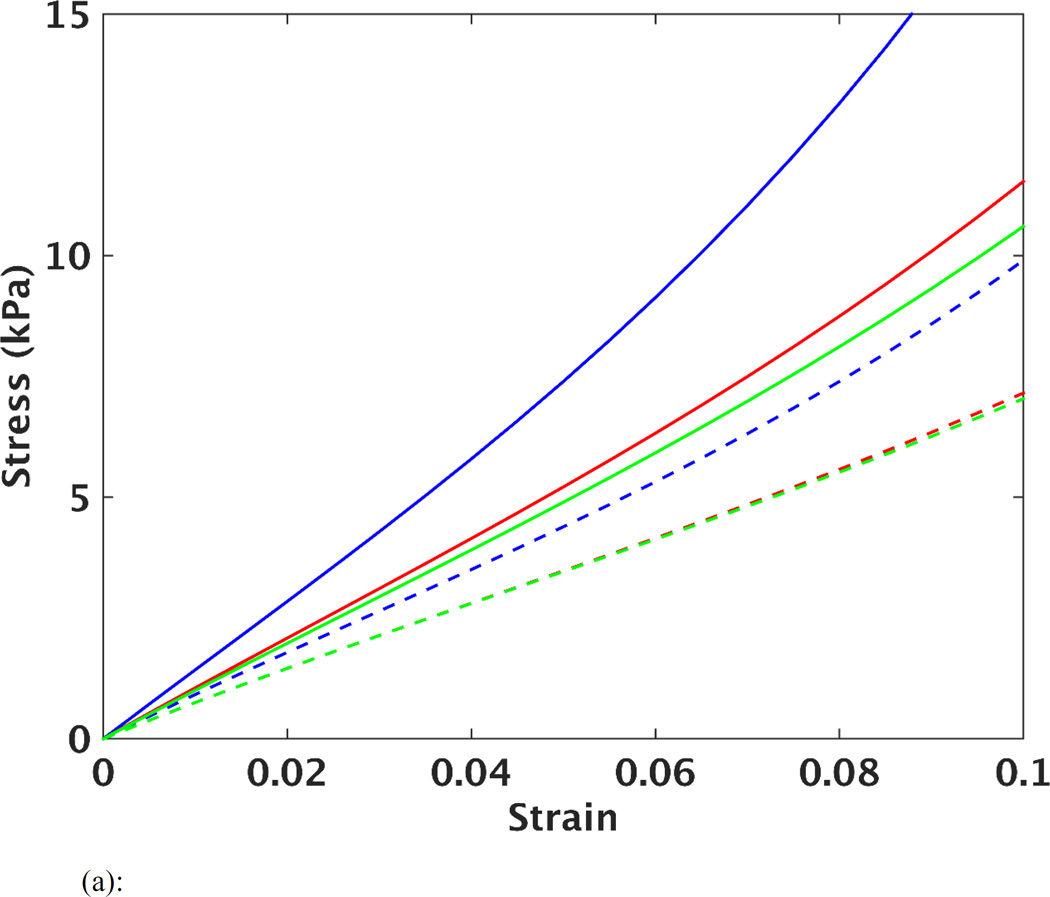
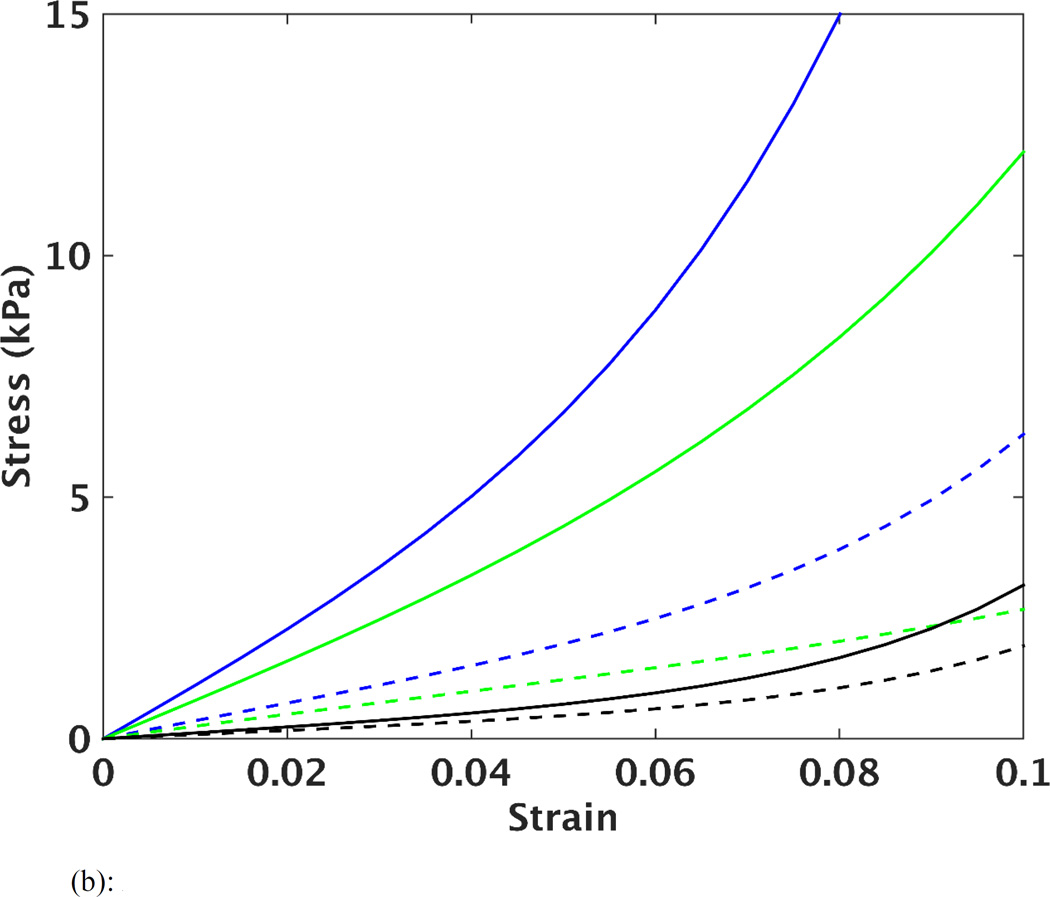
The optimized material parameters before and after unloading are listed in Table 2, as well as the 95% confidence intervals. It should be noted that the agreement between the FE predicted and MRI measured strain (as indicated by the MSE) was comparable in each of the 5 cases, when comparing the results of using the early-diastolic vs. unloaded reference state. However, it can be seen (Table 2) that the size of the confidence intervals of the parameters after the unloading procedure were decreased. This implies that the estimated parameters can be found in a narrower portion of the parameter space, thus improving the identification of these values. In order to visualize the effects of unloading on predictions of stiffness and anisotropy of LV myocardium, the estimated parameters were used to plot stress vs. strain curves based on simulated equi-biaxial extension tests. The curves in Figure 3a show changes in material response for one case (case 2) after each iteration of the unloading/material optimization scheme, while Figure 3b shows the final average of all five cases before and after unloading. In all cases, the computational scheme predicted a softer passive myocardium with decreased anisotropy between fiber and cross-fiber directions after unloading.

Table 2.

Results of the unloading and material parameter estimation routines (estimated parameters and their corresponding confidence intervals). For each case, the first and second row show optimization results when early-diastolic and numerically unloaded geometries were used as the reference configuration of the FE model, respectively.

Case #	FE reference volume (mL)	C (kPa)	bf	bt	bfs	MSE
1	47.1	0.12±0.02	95.97±1.95	14.24±0.30	47.87±1.04	6.75
	43.5	0.11±0.01	65.23±0.76	15.95±0.20	49.93±0.14	6.67
2	57.6	5.73±0.17	14.21±1.65	5.51±0.41	3.1±1.68	14.72
	54.5	7.53±0.18	6.73±1.57	3.44±0.13	1.29±0.60	15.07
3	54.7	0.73±0.43	90.64±3.60	16.75±0.48	25.98±1.36	12.51
	50.0	4.42±0.32	11.39±3.42	2.15±0.39	2.94±1.19	13.06
4	35.9	1.47±0.05	35.56±0.33	2.82±0.10	6.77±0.27	10.27
	29.0	3.75±0.03	8.26±0.26	1.03±0.05	1.21±0.09	10.45
5	49.9	3.79±0.02	55.06±0.62	3.84±0.13	27.84±1.08	4.47
	45.2	3.58±0.05	46.34±0.55	1.10±0.10	13.65±0.98	4.50

Figure 3.

(a): Simulated equi-biaxial stress vs. strain curves in the fiber (solid lines) and cross-fiber (dashed lines) directions for case 2. Each set of curves represents the material properties assessed before unloading (in blue), after first unloading (in red), after second unloading (in green), and after third unloading (in cyan).

(b): Average of the five cases, showing the fiber (solid curves) and cross-fiber (dashed curved) stress vs. strain from the simulated equi-biaxial extension, before unloading (in blue), after final unloading (in green) and results of reference [12] (average of four cases) from excised unloaded porcine LVs (in black).

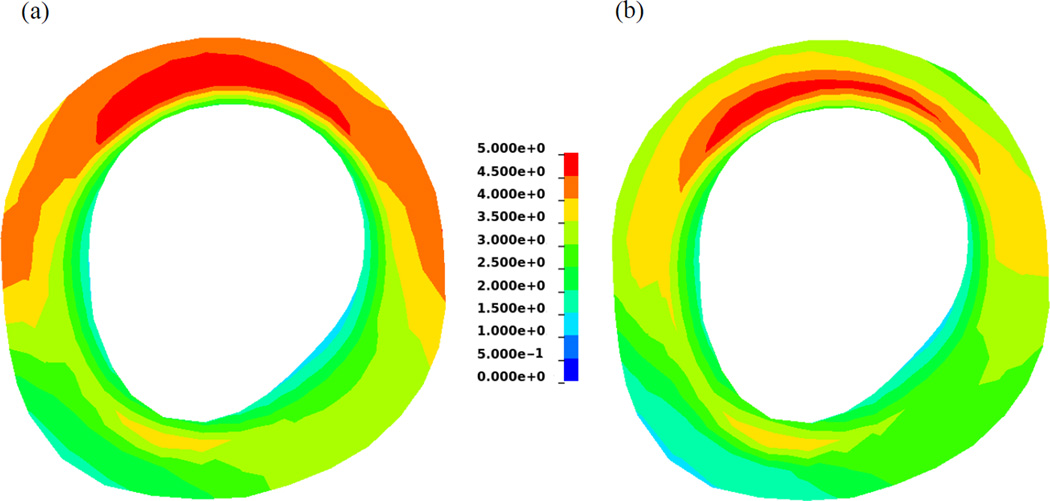
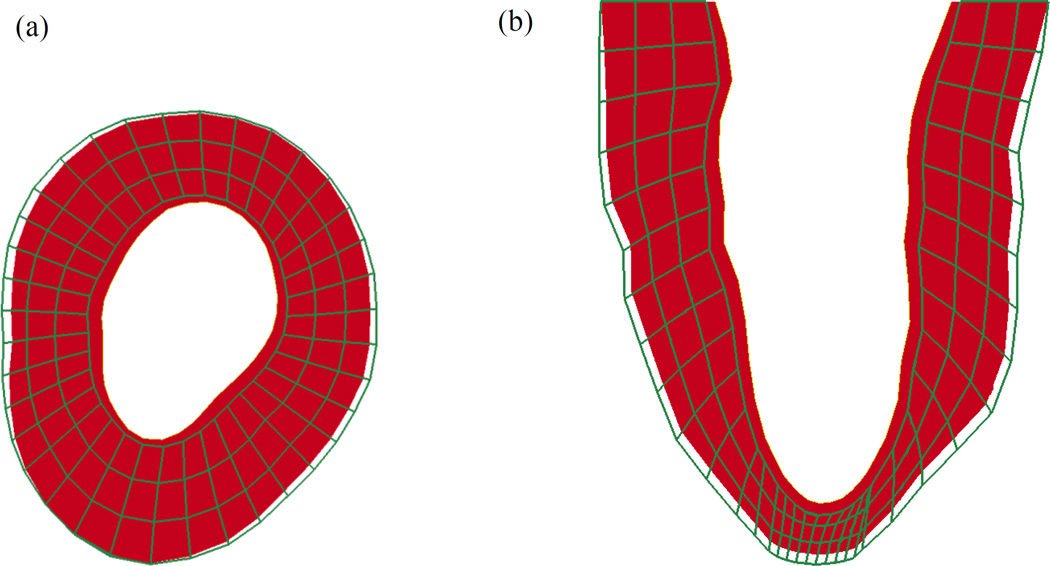
In order to assess changes in LV stress distributions, the estimated material parameters obtained using the early-diastolic and numerically unloaded geometries of one case (case 5) were used to simulate their corresponding FE models to the end-diastolic pressure (Figure 4). It can be seen that the overall magnitude of stress is decreased for the unloaded model. Additionally, the global average of stress in the myofiber direction (at end-diastole) was also decreased in all of the cases (Table 3). The cavity volume of the LV geometry for each reference state is given in Table 2, while an example of the early-diastolic and numerically unloaded geometries for one case (case 4) are shown in Figure 5. It can be seen that the length (base to apex) and diameter of the LV decrease after unloading. However, it should be noted that the total wall volume was preserved, thus leading to an increase in wall thickness in the unloaded state.

Figure 4.

Contours of first principle stress in a mid-ventricle slice at end-diastole before (left) and after (right) unloading.

Table 3.

Global average of LV stress in the myofiber direction at end-diastole (kPa).

Case #	Before unloading	After unloading	% Decrease
1	1.57	1.34	14%
2	9.70	3.33	65%
3	10.02	3.06	69%
4	2.88	2.73	5%
5	3.42	3.00	12%

Note: each case was loaded to the measured end-diastolic pressure to generate the stress in the LV.

Figure 5.

(a) Short axis and (b) long axis views of the LV model for case 4. Note that the green wireframe model represents the early-diastolic geometry and the solid red model represents the geometry after numerical unloading.

4. Discussion

The general trend in each of the cases analyzed in the current study is that using an unloaded reference configuration for the LV FE model results in a prediction of softer passive myocardium, compared to using early-diastolic filling as the reference state. While this result is intuitive, few studies have sought to explicitly quantify the effects of using these two configurations as the reference state on the determination of nonlinear constitutive parameters. Work by Xi et al. [19] used MRI and FE modeling to evaluate the choice of the reference configuration on the prediction of residual active tension in human myocardium. That study also predicted the constitutive parameters for in-vivo passive LV mechanics, but did not assess the effects of the reference configuration on those values.

It should be noted that the optimizations in the current study were also conducted using kinematic data from only end-diastole in the objective function. We observed an average decrease of roughly 11% in the MSE values, in each of the five cases studied, when using two kinematic time points (mid-diastole and end-diastole) instead of only one time point (end-diastole). The decrease in MSE values are consistent with the observations by Xi et al. [19], which suggests that by increasing the amount of kinematic data the identifiability of the parameters is improved. Additionally, it should be pointed out that the contribution of the volume term in the objective function was very small (~0.001) compared to the contribution of the strain. This is driven by the fact that all 6 components of strain were used at 252 locations.

The material parameters determined in the current study showed variability from case to case (Table 2). It should be noted that this type of variability has been observed in several previous studies of normal myocardium, where the values of C, b_f, b_t, and b_s varied by as much as a factor of 5 within the same group of animals [12–14]. Given the results of the current study, as well as previous studies, there appears to be natural variability in ventricular stiffness within an animal group. In terms of the unloading procedure, it can be seen (Table 2) that if the early-diastolic pressure was low, then the material parameters were minimally affected.

Figure 3b shows fiber and cross-fiber stress vs. strain curves before and after unloading, as well as from a previous study that used four isolated arrested pig hearts undergoing passive inflation [12]. After unloading the LV model, the myofiber stiffness in the current study is closer to that predicted by the previous study. The difference in the curves between these two studies could be related to effects of performing ex-vivo vs. in-vivo experiments. Nonetheless, the current results indicate that unloading the heart does have a significant influence on the determination of the myocardial stiffness, when using the combined MRI/modeling approach. Additionally, Figure 3b shows that after unloading, the stress-strain curve in the cross-fiber direction underwent smaller changes compared to the fiber direction. This indicates that the overall anisotropy of the material parameters decreased after unloading. This was quantified further by estimating the moduli over a strain range of 0.05–0.10. It was found that the anisotropy ratio decreased from 5.5 (before unloading) to 3.7 (after unloading).

There are several limitations associated with the presented work. The transversely isotropic constitutive law used in this study is not fully consistent with the anisotropy of left ventricular myocardium, which is shown to be orthotropic [15]. In future works, this material law will be replaced with a structurally based material law [16]. Additionally, in the current study, a homogeneous distribution of average myofiber angles in was assigned to the myocardium. In the future, animal-specific distributions of myofiber angles obtained from diffusion tensor MRI of ex-vivo hearts will be mapped to the in-vivo model [17]. Another limitation is that the contribution of residual stresses in the myocardium was neglected. However, the effect of these stresses are relatively small in diastole [18].

5. Conclusions

In this study, the LV models were numerically unloaded and the passive diastolic material parameters were estimated using both the early-diastolic and unloaded reference state models. Final results indicate that the passive stiffness of myocardium and anisotropy between the fiber and cross-fiber directions decreased when using the unloaded reference state model. This study shows that numerically unloading the MRI-derived model is an important step toward developing a more realistic representation of LV mechanical function. This could play a key role when applying these approaches to build patient-specific computational models for assessing myocardial health.