Evaluating the Treatment Effects Model For Estimation of Cross-sectional Associations Between Risk Factors and Cardiovascular Biomarkers Influenced by Medication Use

Abstract

Purpose

In cross-sectional observational data, evaluation of biomarker-to-exposure associations is often complicated by nonrandom medication use. Traditional approaches often lead to biased estimates, consistent with known results involving confounding by indication. More sophisticated, yet easy to implement approaches such as inverse probability weighting and censored normal regression can address medication use in certain settings, but have poor performance when medication use depends on off-medication biomarker values. More sophisticated approaches are necessary.

Methods

Heckman’s treatment effects model resembles the process which gives rise to cross-sectional data. In this study, we conduct a variety of simulation studies to illustrate why traditional approaches are inappropriate when medication use depends on underlying biomarker values. We illustrate how Heckman’s model can accommodate this feature. We also apply the models to data from the Multi-Ethnic Study of Atherosclerosis.

Results

Inverse probability weighting and censored normal regression are sensitive to how strongly medication use is associated with untreated biomarker values (the untreated value acts as an unmeasured predictor of medication use in this context). Heckman’s model can often adequately remove bias and is robust to certain forms of model misspecification, but relies on knowing important predictors of medication use, even when they are independent of the biomarker. The advantages of Heckman’s model can be negated if the effect of medication on biomarker values is proportionate to the underlying biomarker.

Conclusions

If predictors of medication use are measured, data are cross-sectional, and effects are approximately additive, then Heckman’s model is more accurate relative to alternative approaches.

1. INTRODUCTION

In cross-sectional observational data, estimating the association between an exposure of interest and a biomarker is challenging when participants are on medication intended to alter their biomarker values. Consider using cross-sectional observational data to evaluate the association between diabetes (exposure of interest) and low-density lipoprotein (LDL). Depending on the age distribution of the cohort, many participants may be on medication to lower their LDL, so that their underlying, untreated LDL values (which would theoretically have been observed had they not been on medication at the time of measurement) are unobservable. Medication use occurs most frequently in participants who would have had a high LDL off medication. In addition, medication use is often associated with the exposures of interest (diabetes in this example), and other observable factors such as the Framingham Risk Score and insurance. Data on underlying LDL values are missing according to medication use status, which depends on unobservable and/or observable risk factors. That is, medication use is endogenous.

Methods have been proposed to address nonrandom medication use in a longitudinal setting.¹ Commonly, however, only cross-sectional data are available (e.g., when safety challenges or substantial cost/inconvenience preclude the possibility of repeated measurements). In these cases, we must turn to methods which are applicable to cross-sectional data in order to estimate biomarker associations. Traditional methods such as excluding participants on medication from analysis or adjusting for medication use, despite their frequent use^2–8, require strong assumptions and often result in invalid estimates.

More sophisticated methods that can be applied or generalized to a cross-sectional setting such as inverse probability-of-treatment weighting (IPTW)^9–10 and censored normal regression¹¹ have been proposed, but rely on stringent assumptions that are almost assuredly not satisfied in practice. James Heckman devised what he refers to as a hybrid model with structural shift¹², better known as his “treatment effects model,” which can be used to correct the observed biomarker for the effect of medication use by jointly modeling the biomarker with a latent medication use model. Parameters can be estimated through maximum likelihood.¹³

Figure 1 illustrates the data generation mechanism presumed by the Heckman model, which we believe is a fairly realistic representation of cross-sectional data with endogenous medication use. The Heckman model provides us with a means of addressing nonrandom medication use with an alternative set of assumptions to those made by censored normal regression and IPTW. It is important to better understand the performance of these approaches when medication use depends on participants’ off-medication biomarker values. Thus, there are two primary goals to this study: (1) to demonstrate the lack of plausibility of traditional methods, and (2) to better understand to what extent misspecification of the Heckman model negates its advantages under correct specification. In turn, we apply these models to our motivating example of LDL and diabetes from the Multi-Ethnic Study of Atherosclerosis (MESA).

Figure 1.

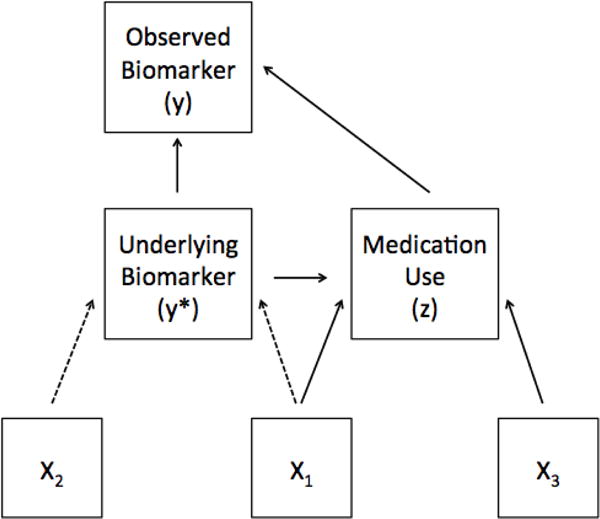
Diagram depicting the presumed data generation mechanism for the Heckman treatment effects model in a cross-sectional setting. All measurements refer to a single point in time. Dashed lines indicate associations of particular interest.

2. THE FAILURE OF TRADITIONAL APPROACHES

We demonstrate the failure of traditional approaches with a simplistic example. Figure 2 depicts the results of fitting three simple approaches based on a single realization of a hypothetical data generating mechanism with endogenous medication use: (i) fitting ordinary least squares (OLS) on the observed data, or “ignoring the issue”, (ii) excluding on-medication participants from analysis, and (iii) adjusting for medication use. The off-medication participants are represented by black circles (these values represent the underlying biomarker value, which is observed). The on-medication participants are depicted by representing their underlying biomarker value as a gray × and the observed value as a gray circle. In Figure 2A, we show the true association with a solid black line, which would be estimable if no participants were on medication. The results from these three models fail to capture the true association well. These methods perform poorly because they rely on assumptions about medication use that are not satisfied. Neither ignoring the issue nor excluding participants is reasonable as each approach presumes that medication use is independent of the underlying biomarker. Adjusting for medication use as though a confounder (as in Figure 2D) presumes that medication use is independent of the underlying biomarker, conditional on the exposure of interest. Based on Figure 1, medication use is not exactly a confounder for the relationship of interest, but is rather a cause of missing data on the underlying biomarker.^14–15 Importantly, the confidence intervals for each of these estimates fail to include the truth.

Figure 2.

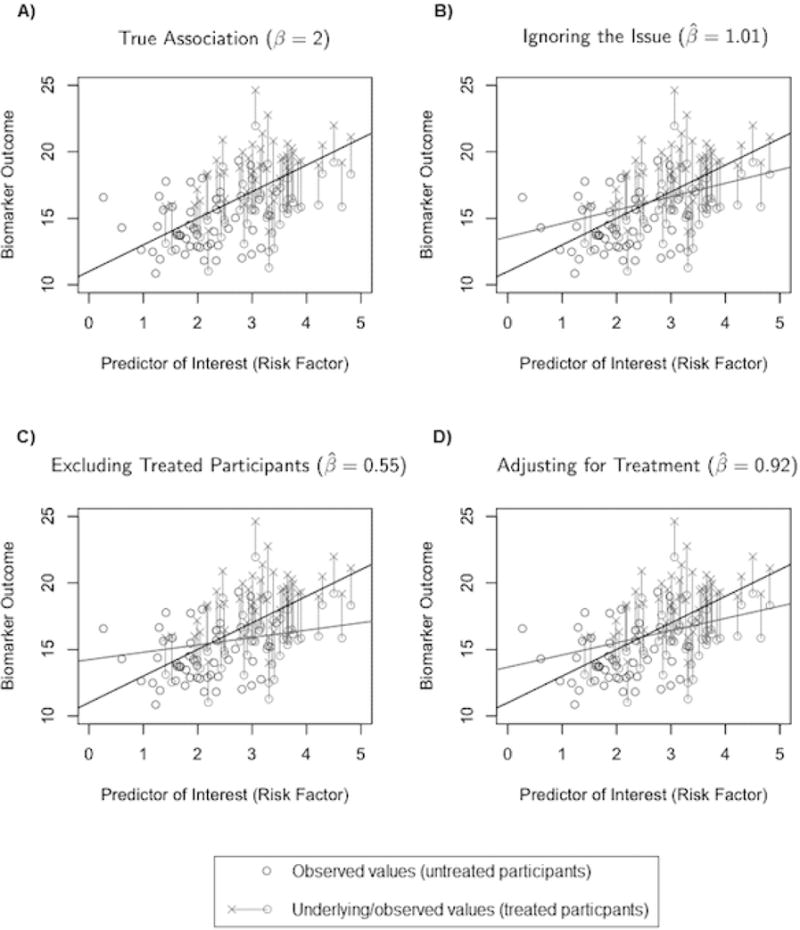
Observed values for untreated participants are shown as black circles; treated participants are in gray; the observed (o) and treated (×) values are connected with a line. The dark black line signifies the true association of β = 2; the gray lines show the results form three traditional approaches: ignoring the issue (panel B), excluding treated participants (panel C), and adjusting for treatment (panel D).

The adjustment approach is sufficient if medication use is random (in the setting of a randomized trial, for instance). More generally, it is sufficient if medication use is independent of the underlying biomarker value. For example, suppose the biomarker in question is systolic blood pressure (SBP) and the medication under consideration is a statin; traditional methods are sufficient since, despite the fact that statins are known to lower SBP, participants do not traditionally take statins for that purpose.¹⁶

3. METHODS

3.1 Regression and Likelihood Methods

In this section, we describe the assumptions of each of the discussed models, and how they are fit. We focus our attention on simple approaches which are easy to implement. Ad hoc methods such as “fixed” or “random” addition¹¹ are not considered in this paper because they rely on external information on study participants or population average treatment effects; such information often does not exist. Let y_i denote the observed biomarker for subject i = 1,…,n and let z_i denote the medication use indicator taking on 1 for a subject on medication and 0 otherwise. We denote the underlying, untreated biomarker value by $y_i^{\ast }$, which is unobservable if z_i = 1. In untreated participants, y_i and $y_i^{\ast }$ are equivalent. Let X = (1, X₁,…,X_K) be the design matrix of the exposures of interest (e.g., age, gender, and race), and β = (β₀,…,β_K)^T be a vector of regression coefficients (fitting an intercept). Suppose that $y_i^{\ast }={\mathit{x}}_i\mathit{\beta }+{\epsilon }_i$, where ε_i are independent, each with mean 0 and variance ${\sigma }_{\epsilon }^2$. The exposure-to-biomarker association, β, is our target of inference. Estimates from traditional models are obtained from fitting the following from OLS using the observed y-values: E[y_i|x_i] = x_iβ (Ignore), E[y_i|x_i, z_i = 0] = x_iβ (Exclude), and E[y_i|x_i, z_i] = x_iβ + z_iη (Adjust). As mentioned in Section 2, these approaches presume that medication use is either completely independent (Ignore and Exclude) or conditionally independent (Adjust) of the underlying biomarker.

3.1.1 Inverse Probability of Treatment Weighting

Wang et al. describe an inverse probability-of-treatment weighting (IPTW) approach for a longitudinal setting, up-weighting study participants who are less likely to be observed in an attempt to reduce bias (namely, participants on medication with lower observed biomarker values, and participants off medication with higher observed biomarker values).^9–10

This approach can be generalized to a cross-sectional setting as well. The probability of being on medication can naïvely be estimated using a (probability of) medication use model from logistic regression on observed X′s: logit(P (z_i = 1|x_i)) = x_iτ, from which stabilized weights can be generated. An analogue to the adjustment model can then be fit with these weights. This method differs from the approach of Wang et al.⁹, as we do not generate weights from the unobservable biomarker value, but it is still truly an IPTW-type approach. Note that only variables which are associated with both the biomarker and medication use are used to generate the weights, excluding variables which predict medication use only; this has been shown to have better behavior than including covariates which predict medication use only.^17–18 Of note is that the IPTW medication use model cannot incorporate what is arguably the most important predictor of treatment in this setting: the (unobservable) untreated biomarker value. This is a meaningful departure from the assumptions of IPTW, under which this model would otherwise be expected to perform well. IPTW also has known challenges when positivity assumptions are violated.

Our approach differs from Wang’s in the following ways: he classifies each participant’s underlying biomarker into two categories (high or low); this category is presumed to be observed, even though the underlying biomarker itself is unobservable. The probability of medication use, in turn, is presumed only to depend on the exposure and the underlying biomarker category (high or low).

3.1.2 Censored Normal Regression

Tobin outlines a censored normal regression approach which attempts to correct the observed biomarker, y_i, in participants on medication by modeling them as right-censored versions of their untreated values.¹¹ The approach is as follows: y_i is modeled according to:

$$y_i^{\ast }\{\begin{array}{l}=y_i\text{if}{z}_i=0\\ \ge y_i\text{if}{z}_i=1\end{array}.$$ (1)

We then may modify the normal likelihood for ordinary least squares linear regression, incorporating this right-censoring: let ϕ and Φ denote the standard normal density and cumulative distribution, respectively, and ${\sigma }_{\epsilon }^2$ the error variance of $y_i^{\ast }$, we have that the likelihood is given by:

$$\mathcal{L}(\beta ,{\sigma }_{\epsilon }^2|Y,Z,X)={{\displaystyle \prod _{i=1}^n\left(\varphi \left(\frac{y_i-x_i\mathit{\beta }}{{\sigma }_{\epsilon }}\right)\right)}}^{1-z_i}{\left(1-\mathrm{\Phi }\left(\frac{y_i-x_i\mathit{\beta }}{{\sigma }_{\epsilon }}\right)\right)}^{z_i}.$$ (2)

To estimate parameters, this likelihood function can be maximized. This model presumes that (i) the medication’s effect is non-negative for each participant; (ii) the untreated value follows a normal distribution; and, (iii) censoring is non-informative. Tobin acknowledges that the non-informative censoring assumption is not quite satisfied, but believes in his motivating example of genetic exposures and blood pressure that this approach well-approximates the association of interest.

3.1.3 Extension to Endogenous Medication Use (Heckman’s Treatment Effects Model)

Let W = (1, W₁,…,W_M) denote a design matrix corresponding to observed covariates which predict medication use (they need not all be distinctly different from the covariates which predict $y_i^{\ast }$). Define $z_i^{\ast }=w_i\alpha +{\gamma }_i$, where α = (α₀,…,α_M) and γ_i is a random error with mean zero and variance ${\sigma }_{\gamma }^2$ Here, $z_i^{\ast }$ is a continuous latent variable. Although $z_i^{\ast }$ is unobserved, medication use, defined by $z_i=1\left(z_i^{\ast }>0\right)$ (the indicator that $z_i^{\ast }$ is positive) is observed. We refer to this as the “medication use” model.

Finally, let $y_i=y_i^{\ast }-{\mu }_{\delta }{z}_i$ denote the observed biomarker value, which is equivalent to $y_i^{\ast }$ for participants off medication (z_i = 0), but is some unknown μ_δ lower than y_i^∗ for participants on medication (z_i = 1). To estimate parameters, this model was originally proposed as a two-stage model¹², but Maddala proposed a more efficient maximum likelihood approach which jointly models (ε_i, γ_i) as bivariate normal, with correlation parameter ρ.¹³ We consider the latter approach. The parameters σ_γ and ρ are weakly identifiable, and hence it is convenient to set ${\sigma }_{\gamma }^2=1$ without loss of generality so that all parameters may be estimated (this is a well known property of the probit model).¹⁹ The likelihood can then be written as follows, letting θ = (α, β, μ_δ, ρ, σ_ε):

$$\mathcal{L}\left(\mathit{\theta }|Y,Z,Z,W\right)={\displaystyle \prod _{i=1}^n\varphi }\left(\frac{y_i-x_i\mathit{\beta }+{\mu }_{\delta }{z}_i}{{\sigma }_{\epsilon }}\right)\mathrm{\Phi }{\left(-r_i\right)}^{1-z_i}\mathrm{\Phi }{\left(r_i\right)}^{z_i}.$$ (3)

The quantity r_i is the conditional mean of $z_i^{\ast }|y_i^{\ast }$, divided by its conditional standard deviation, which can be obtained from standard bivariate normal theory. In this model, our parameters of primary interest (namely, β, σ_ε, and μ_δ) are identifiable. They can be estimated from maximizing this likelihood function.

It turns out that this model very easily accommodates direct dependence of $z_i^{\ast }$ on the underlying biomarker $y_i^{\ast }$: if we add a term λy_i* into the medication use model, it may be expanded as follows: $z_i^{\ast }=w_i\alpha +\lambda x_i\mathit{\beta }+\lambda {\epsilon }_i+{\gamma }_i$. then, if we intentionally include all covariates of X in W, the total error on $z_i^{\ast }$ is λε_i + γ_i, and the total errors are still bivariate normal, just as before. Hence, the model is still correctly specified and provides consistent estimates of β. Since α is not identifiable, there is no need to estimate λ in this procedure.

Additionally, this model indeed allows for the effect of the medication use to be normally distributed around μ_δ across subjects. This introduces heteroscedasticity, and therefore robust “sandwich” based standard errors should be used for valid inference.²⁰

The “medication use” model is somewhat similar in spirit to that of IPTW, except that its total errors are permitted to be correlated to the errors on the biomarker. This is the mechanism by which endogeneity of medication use is incorporated; the alternative approaches described do not have this advantage. Use of the probit model rather than a logistic model as in IPTW is a convenient way to obtain the conditional distribution of $z_i^{\ast }|y_i^{\ast }$. Another key difference in the models is that all predictors of medication use are to be placed in the medication use model, as opposed to IPTW in which this is not the case. This difference will be reflected in how we conduct our simulation studies.

3.2 Simulation Study

3.2.1 Heckman-Ideal Scenario

We designed a number of scenarios with no departures from the Heckman model assumptions for simulation purposes (the assumptions of IPTW and the censored normal model are hence not satisfied). The primary goal of this component of the study is to evaluate the advantage over alternative approaches which have been previously described to address medication use (censored normal regression and IPTW). Note: the simulation setup of Section 2 is a simplified version of the one we present in this section.

Let X = (1, X₁, X₂, X₃) denote a design matrix for all predictors of interest measured in the study. Assume that they are fixed (we generated each X_i independently from a normal distribution with standard deviation 1, and treated them as fixed through all replications of the simulation study). Suppose that the data generating mechanism is given by $z_i^{\ast }=x_{1i}+x_{3i}+\lambda y_i^{\ast }+{\gamma }_i$ so that α = (0, 1, 0, 1)^T, and that $y_i^{\ast }=x_{1i}+x_{2i}+{\epsilon }_i$, so that β = (β₀, β₁, β₂)^T = (0, 1, 1)^T. Thus, in accordance with Figure 1, X₁ predicts the underlying biomarker and medication use, X₂ predicts the underlying biomarker, but not medication use (except through λ), and X₃ predicts medication use, but not the underlying biomarker. Suppose that the effect of the medication is generated as ${\delta }_i\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{~}\mathcal{N}(\mu \delta ,{\sigma }_{\delta }^2)$ to allow inter-individual variation in the effect of treatment. We fixed the variance of the error terms ${\epsilon }_i$ and γ_i to be 4 for all settings. Finally, the observed outcome is generated as follows: $y_i=y_i^{\ast }-{\delta }_i$.

We alter the parameters λ, μ_δ, and ρ to generate four “Heckman-ideal” scenarios, noting that λ is not estimated. In the first, λ = 0.2, μ_δ = 1, and ρ = 0. The other three scenarios alter one of each of these parameters at a time (λ = 0.8 in Scenario 2, μ_δ = 1.5 in Scenario 3, and ρ = 1/16 in Scenario 4). These three alterations can be described as “increasing endogeneity through exposures and correlation,” “increasing effect of medication use,” and “increasing endogeneity through random correlation only,” respectively. For all settings, ${\sigma }_{\delta }^2=1/10$.

Two-thousand replicates were used for each simulation scenario (each based on n = 2000 participants, and the nuisance intercept in the generation of z^∗ was set to yield approximately a 50% prevalence of medication use in each replication). β was estimated from each of the six methods outlined, along with Huber-White sandwich variance estimates to account for the heteroscedasticity.²⁰ We then obtained an estimate of the true standard error by taking the standard deviation of the simulated estimates. We focused our attention on β₁ and β₂, as the intercept is not of interest in most association studies.

Note: although medication use is dichotomized as described in Section 3.1.3, all participants have a nonzero probability of being on medication due to random error in the medication use model; to verify that we have not induced positivity challenges for IPTW, we report descriptive statistics (mean, minimum, and maximum) on the IPTW weights from the simulations.

3.2.2 Formal Sensitivity Analyses

We performed a number of sensitivity analyses in which we altered the data generating mechanism of “Ideal Scenario 1” so that the Heckman model was no longer correctly specified. (NB: the other models remain incorrectly specified even under these modifications). The goal of this component of the study was to evaluate to what extent the advantages of the Heckman model seen in the previous study are negated when we perturb its assumptions.

The first three sensitivity analyses pertain specifically to misspecification of the IPTW and Heckman medication use models. We first consider estimation of β when X₁ is removed from the medication use models, and then when X₂ is removed. Recall that X₃ is not originally included in the IPTW medication use model, so we may only evaluate the Heckman model when X₃ is not included.

The next three sensitivity analyses pertain to distributional/measurement assumption violations commonly encountered in practice: a departure from the normal errors in the biomarker model; measurement error in X₁; and, an effect of medication use that is proportional to the underlying biomarker value, with a mean-variance relationship. Details of the sensitivity analyses are provided in Table 1.

Table 1.

Simulation Setup: Sensitivity Analyses

	Violation	Description
1	Treatment Model Misspecification I	X1 removed from treatment modela
2	Treatment Model Misspecification II	X2 removed from treatment modela
3	Treatment Model Misspecification III	X3 removed from treatment modelb
4	Non-Normal Errors	${\epsilon }_i~\mathrm{Gamma}\left(\alpha =8,\beta =\sqrt{2}\right)-8/\sqrt{2}$
5	Measurement Error	$X_1^{\mathit{obs}}=X_1+{\xi }_i;{\xi }_i~\mathcal{N}(0,{\left(1/20\right)}^2)$
6	Proportional Treatment Effect	${\delta }_i~\mathcal{N}(Y_i^{\ast }/5,{(Y_i^{\ast }/20)}^2)$

^a- Only applies to IPTW and Heckman Model

^b- Only applies to Heckman model

3.3 Application to the Multi-Ethnic Study of Atherosclerosis

We applied these methods to data collected from the Multi-Ethnic Study of Atherosclerosis (MESA). MESA is a prospective cohort study designed to study the progression of subclinical cardiovascular disease. The study includes 6,814 men and women aged 45–84 years who were free of clinical cardiovascular disease at entry. The participants were recruited from six U.S. communities, and included 47% men with an ethnic distribution of 38% white, 28% African-American, 22% Hispanic, and 12% Chinese-American. All subjects gave informed consent. Details of the sampling, recruitment, and data collection have been reported elsewhere.²¹

Specifically, we modeled low-density lipoprotein (LDL) as the biomarker outcome, with diabetes the predictor of interest, and adjusting for: age, gender, race category, smoking & alcohol status, and BMI. The medication use indicator variable was taken to be self-reported use of any lipid-lowering medication. In assigning the weights for IPTW, these variables were all used in the medication use model. For the Heckman medication use model, the following variables were added: insurance status, education status, and Framingham risk score.

All simulations and analyses were conducted using Stata Version 12 (StatCorp, College Station, TX) or R Version 2.14.2 (The R Foundation for Statistical Computing, http://www.R-project.org).^22–23 Censored normal regression can be performed using Stata’s “cnreg” command, and Heckman’s treatment effects model can be performed with the “treatreg” command.

4. RESULTS

4.1. Simulation Studies

4.1.1 Heckman-ideal Simulation Results

Table 2 provides a summary of the estimates, simulated standard errors, estimated (Huber-White) standard errors, and coverage probabilities for Scenario 1. The results for the remaining scenarios are illustrated in Figure 3. In each of these “Heckman-ideal” scenarios, the Heckman model provides valid estimates and inference for all coefficients. In general, Huber-White standard errors estimate the true standard errors well. In estimating β₁, the Heckman model far outperforms the other approaches in coverage probability and bias. The censored normal approach meaningfully overestimates β₁. Traditional methods tend to perform better in estimating β₂ with only modest bias, which is unsurprising since X₂ does not predict medication use as strongly as X₁.

Table 2.

Simulation Results under Heckman-Ideal Scenarios (β₁ = β₂ = 1)

Scenario 1	β1				β2
Default	Estimate	SESim	${\widehat{SE}}_{\mathrm{HW}}$	CP	Estimate	SESim	${\widehat{SE}}_{\mathrm{HW}}$	CP
Ignore	0.81	0.046	0.046	0.02	0.98	0.046	0.045	0.91
Exclude	0.90	0.069	0.069	0.66	0.99	0.066	0.064	0.94
Adjust	0.89	0.049	0.049	0.41	0.99	0.046	0.045	0.94
Censored Normal	1.53	0.064	0.06	0.00	1.07	0.060	0.062	0.81
IPTW	0.88	0.061	0.059	0.49	0.99	0.051	0.050	0.93
Heckman	1.00	0.068	0.068	0.95	1.00	0.046	0.046	0.95

Figure 3.

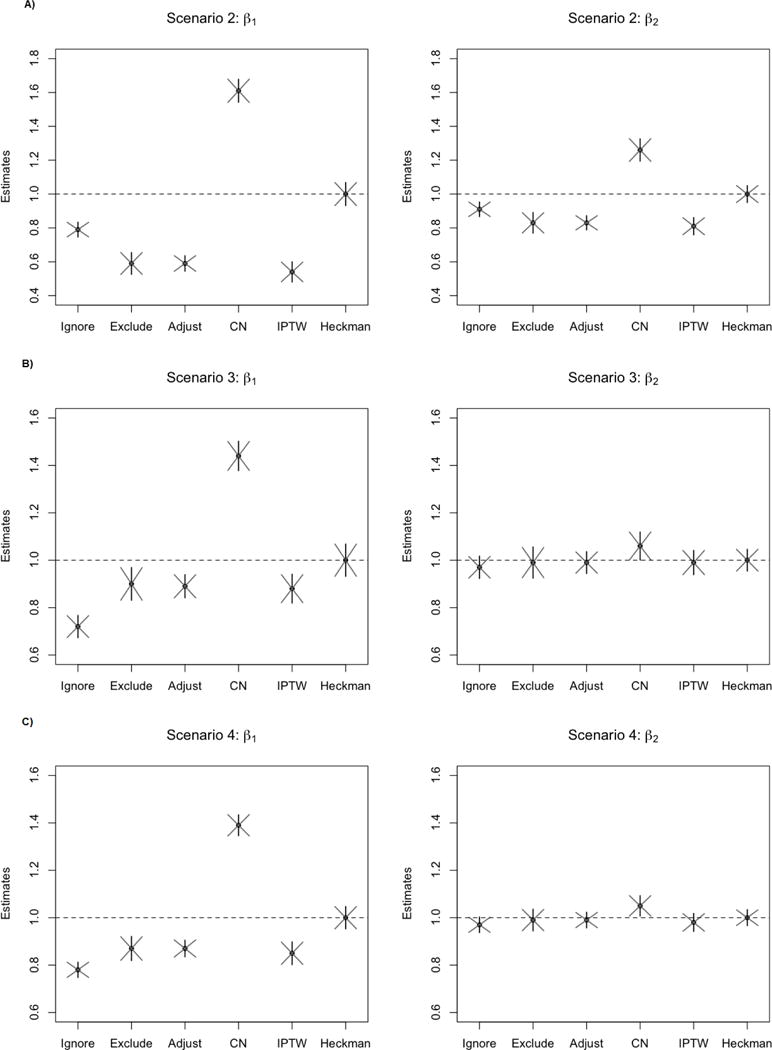
Point estimates are averaged over 2000 replications, denoted as a black dot; vertical lines represent the simulation-standard error, and the diagonal lines denote the estimated Huber-White standard errors. Scenario 2 corresponds to an increase in λ, Scenario 3 corresponds to an increase in μ_δ, and Scenario 4 corresponds to an increase in ρ.

When the strength of dependence of medication use on the underlying biomarker increases (Scenarios 2 and 4), all methods but Heckman’s model show more bias in comparison to Scenario 1. For IPTW, this result is consistent with previous findings that this method is sensitive to increases in endogeneity due to unobservables.²⁴ The weights from IPTW in a single replication ranged from 0.41 to 7.7 (mean 1.0), suggesting that we do not have positivity violations in the data.

When the mean effect of medication is increased from μ_δ = 1.0 to μ_δ = 1.5, the Heckman model still fares well in comparison to other methods. Note that the true mean difference in the underlying biomarker value between treated and untreated participants is approximately 1.38 based on this simulation, so an effect of 1.0 could signify a moderate effect, but an effect of 1.5 is very large. Although the censored normal approach improved marginally when the effect of medication is large, it is clearly sensitive to the level of endogeneity which is not truly estimable from the censored normal approach. Estimates from the exclusion method are trivially equivalent under all possible μ_δ.

We conducted a follow-up simulation study based on these results to evaluate the performance of these methods when medication use was dependent only on the observable covariates (in particular, when λ = 0, but all other parameters were as described in Scenario 1). All methods except ignoring the issue and censored normal regression provided valid estimates and approximately 95% coverage in this case.

4.1.2 Medication Use Model Misspecification

Table 3 provides a summary of the estimates, their variability, and coverage probabilities from the sensitivity analysis involving medication use model misspecification.

Table 3.

Simulation Results Under Treatment Model Misspecification (β₁ = β₂ = 1)

X1 Removed	β1				β2
	Estimate	SESim	${\widehat{SE}}_{\mathrm{HW}}$	CP	Estimate	SESim	${\widehat{SE}}_{\mathrm{HW}}$	CP
IPTW	0.89	0.049	0.049	0.41	0.99	0.046	0.045	0.94
Heckman	0.88	0.049	0.049	0.31	1.00	0.047	0.046	0.95
	β1				β2
X2 Removed	Estimate	SESim	${\widehat{SE}}_{\mathrm{HW}}$	CP	Estimate	SESim	${\widehat{SE}}_{\mathrm{HW}}$	CP
IPTW	0.88	0.061	0.059	0.49	0.99	0.050	0.050	0.93
Heckman	1.00	0.068	0.069	0.95	0.98	0.046	0.045	0.92
	β1				β2
X3 Removed	Estimate	SESim	${\widehat{SE}}_{\mathrm{HW}}$	CP	Estimate	SESim	${\widehat{SE}}_{\mathrm{HW}}$	CP
Heckman	0.95	0.22	0.16	0.73	0.99	0.053	0.052	0.94

Removal of X₁ from the medication use model has a meaningful effect on the bias of ${\widehat{\beta }}_1$ for both IPTW and the Heckman model. The variability of ${\widehat{\beta }}_1$ and ${\widehat{\beta }}_2$ decrease, with coverage of β₂ still being adequate. Removing X₂ from the medication use model has little impact on the bias of ${\widehat{\beta }}_1$, although for the Heckman model, there is a slight bias induced for ${\widehat{\beta }}_2$ and a reduction of coverage by about 2%. The variability of the each of the estimates decreases. Removal of X₃ from the Heckman medication use model results in a downward bias on ${\widehat{\beta }}_1$ with a loss of coverage and substantially higher variability of the estimates. The Huber-White standard error does not estimate the true standard error well in this case. Of note is that estimation of ${\widehat{\beta }}_2$ is not meaningfully impacted by this change. This appears to be the reverse of IPTW.¹⁸

4.1.3 Distributional and Measurement-Based Assumption Violations

None of the methods were heavily influenced by moderate right-skewness of the errors or slight measurement error on X₁ (Table 4). Additional simulations with higher measurement error resulted in shrinkage of the estimates (that is, a tendency for the estimates to be closer to zero), consistent with the known properties of nondifferential misclassification of the exposure.¹⁷

Table 4.

Simulation Results Under Distribution/Measurement Violations (β₁ = β₂ = 1)

Skewed Errors	β1				β2
	Estimate	SESim	${\widehat{SE}}_{\mathrm{HW}}$	CP	Estimate	SESim	${\widehat{SE}}_{\mathrm{HW}}$	CP
Ignore	0.81	0.046	0.046	0.01	0.98	0.046	0.045	0.93
Exclude	0.90	0.067	0.066	0.67	0.99	0.062	0.061	0.94
Adjust	0.89	0.050	0.049	0.40	0.99	0.045	0.045	0.94
Censored Normal	1.54	0.065	0.065	0.00	1.07	0.060	0.062	0.81
IPTW	0.88	0.062	0.059	0.46	0.99	0.051	0.050	0.93
Heckman	1.00	0.072	0.071	0.95	1.00	0.046	0.046	0.95
	β1				β2
Measurement Error	Estimate	SESim	${\widehat{SE}}_{\mathrm{HW}}$	CP	Estimate	SESim	${\widehat{SE}}_{\mathrm{HW}}$	CP
Ignore	0.81	0.045	0.046	0.02	0.98	0.047	0.045	0.91
Exclude	0.89	0.067	0.069	0.66	0.99	0.066	0.064	0.94
Adjust	0.89	0.048	0.049	0.39	0.99	0.047	0.045	0.93
Censored Normal	1.53	0.062	0.064	0.00	1.07	0.061	0.062	0.81
IPTW	0.88	0.060	0.059	0.47	0.99	0.052	0.050	0.93
Heckman	1.00	0.068	0.068	0.95	1.00	0.047	0.046	0.95
	β1				β2
Proportional Treatment	Estimate	SESim	${\widehat{SE}}_{\mathrm{HW}}$	CP	Estimate	SESim	${\widehat{SE}}_{\mathrm{HW}}$	CP
Ignore	0.90	0.042	0.041	0.32	0.90	0.041	0.041	0.30
Exclude	0.90	0.069	0.069	0.66	0.99	0.066	0.064	0.94
Adjust	0.80	0.044	0.044	0.01	0.89	0.041	0.041	0.20
Censored Normal	1.61	0.065	0.065	0.00	1.02	0.062	0.064	0.95
IPTW	0.79	0.055	0.053	0.04	0.89	0.046	0.045	0.30
Heckman	0.90	0.062	0.063	0.63	0.90	0.042	0.042	0.31

When the effect of medication use is multiplicative and not additive, censored normal regression provides higher upward bias. Both the Heckman model and IPTW appear to be sensitive to this violation for both ${\widehat{\beta }}_1$ and ${\widehat{\beta }}_2$, as we see shrinkage and a loss of coverage. Under this example of multiplicative effects, the Heckman model does not show much improvement over the traditional approaches.

4.2 Application to MESA biomarkers

The prevalence of lipid-lowering medication use in the sample was 16.2%. Figure 4 depicts the point estimates and confidence intervals for estimating the diabetes-LDL association from each method. In estimating the association between diabetes and LDL, all traditional methods, as well as IPTW, would suggest protective effects of diabetes on LDL. These results would be inconsistent with the literature.²⁵ Censored normal regression and Heckman provide estimates that are consistent with no such association. This mirrors prior results found by a longitudinal imputation approach.¹ Interestingly, the censored normal approach does not provide the highest estimates; it is possible that the effect of lipid lowering medications is large enough in this setting that censored normal is performing reasonably well.

Figure 4.

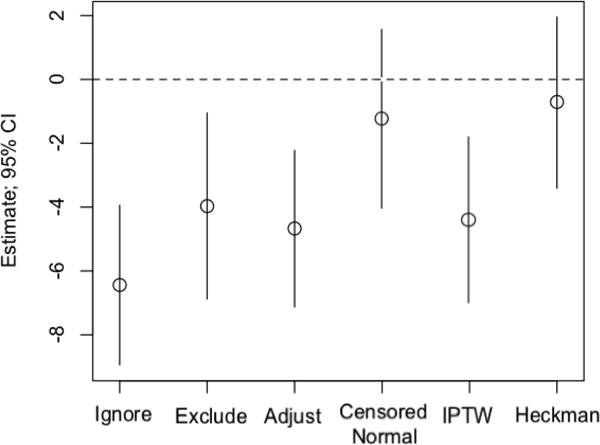
Graphical depiction of the application to diabetes-LDL model in the Multi-Ethnic Study of Atherosclerosis. Estimates are reported in mg/dL.

As noted in Section 3.1.3, Heckman’s model can also be used to estimate the effect of the medication on the biomarker. In this example, we estimate a treatment effect of 47.7 mg/dL (95% CI: [42.5, 52.9]). The adjustment model provides an estimate of 14.8 (95% CI: [12.9, 16.8]), and IPTW provides an estimate of 13.4 (95% CI: [11.2, 15.6]). The estimates provided by Heckman’s model closely resemble estimates obtained from longitudinal data; estimates from the other two approaches are severely attenuated.¹

5. DISCUSSION

We have demonstrated that in cross-sectional data, traditional methods can perform poorly in estimating an exposure-to-biomarker association when medication use depends on untreated biomarker values. Alternative methods such as censored normal regression and IPTW can show poor performance when used without regard to this dependence; however, the Heckman model shows high advantages over alternatives when correctly specified, as expected. Although cross-sectional data have limitations surrounding understanding temporality of events, there are settings in which they are the only means we have to estimate associations. We believe that the assumptions of the Heckman model are more reasonable than those of of the alternatives and hence provide us with estimates that are closer to the truth.

We have confirmed the inappropriateness of IPTW in this setting by noting its sensitivity to the strength of correlation of the biomarker and medication use; when increased, the ability to properly weight participants deteriorates since treated and untreated subjects will be more well-separated, creating challenges with positivity of medication use probability.²⁴ Arguably the most important predictor of medication use (the untreated biomarker), is unobservable and hence not incorporated in the weighting procedure. The Heckman model addresses this by modeling the correlation. The errors (ε_i, γ_i) need not themselves be correlated for there to be endogeneity, as the total errors on the medication use variable and the underlying biomarker are correlated if $\lambda \ne 0$. Medication to lower a biomarker can often be assumed to be endogenous, as those with undesirable biomarker values are likely to be on medication.

The Heckman model presumes that data are collected on X₁ (associated with both the biomarker and medication use) as it is included in the biomarker model. Hence, bias induced by excluding X₁ from the medication use model can be addressed by including it. To that end, this component of the study does not truly describe a limitation of the Heckman model, but confirms that variables strongly associated with the biomaker should be measured.

However, a variable associated with medication use, irrespective of its association with the biomarker, impacts the variability of the estimates when not included. Variables which are strongly associated with the biomarker outcome are typically known and hence collected throughout a study; however, data on variables associated with medication use may not be collected. This is a clear shortcoming of the Heckman model when the target of inference corresponds to a covariate associated with medication use. We recognize in our application to MESA that there are likely unmeasured variables associated with medication use, although the level of association and the extent of their impact is not verifiable. This shortcoming does not hold for IPTW as it does not model variables associated with only medication use.^17–18 In our application to LDL, we have demonstrated that Heckman’s model can provide estimates of both the biomarker association and the effect of the medication that are consistent with longitudinal data, whereas IPTW does not.

The Heckman model is robust to departures from several distributional assumptions (skewness of biomarker errors and measurement error, in particular), still showing advantages over alternative approaches. However, non-additive effects can substantially impact bias. This is a meaningful limitation, since in cross-sectional observational data, there is no reliable way to estimate the distribution of the effect of medication use. Although, this is no more of a limitation for the Heckman model than for adjustment and IPTW, which also presume additive effects of medication. Methods such as ignoring and excluding do not show substantial worsening of bias precisely because they fail to model the effect of medication at all.

While the Heckman model remains robust to certain assumptions, unverifiable misspecification of the medication use model can be difficult to overcome in settings where predictors of medication use are not well understood. However, if predictors of medication use are thought to be known and the effect of medication is to change the biomarker by a fixed amount on average, the Heckman model should be considered as a means of correcting bias. Special consideration of endogeneity and the associations of variables with medication use and biomarkers should inform model selection for estimating biomarker-to-exposure associations. Research to develop further extensions of these models is needed in order to correctly estimate the natural association between a predictor of interest and a biomarker in cross-sectional observational data with endogenous medication use.

Key points.

• Simple, traditional approaches to estimate biomarker associations in cross-sectional observational data tend to be highly biased.

• Common fixes such as inverse probability weighting do not reduce bias in this setting except in rare circumstances.

• Heckman’s treatment effects model resembles the process by which cross-sectional data arise.

• The treatment effects model is reasonably robust to a wide range of assumption violations.