Local and distributed PiB accumulation associated with development of preclinical Alzheimer’s disease

Abstract

Amyloid-beta plaques are a hallmark of Alzheimer’s disease (AD) that can be assessed by amyloid imaging (e.g., Pittsburgh B compound [PiB]) and summarized as a scalar value. Summary values may have clinical utility but are an average over many regions of interest, potentially obscuring important topography. This study investigates the longitudinal evolution of amyloid topographies in cognitively normal older adults who had normal (N = 131) or abnormal (N = 26) PiB scans at baseline. At 3 years follow-up, 16 participants with a previously normal PiB scan had conversion to PiB scans consistent with preclinical AD. We investigated the multivariate relationship (canonical correlation) between baseline and follow-up PiB topographies. Furthermore, we used penalized regression to investigate the added information derived from PiB topography compared to summary measures. PiB accumulation can be local, that is, a topography predicting the same topography in the future, and/or distributed, that is, one topography predicting another. Both local and distributed PiB accumulation was associated with conversion of PiB status. Additionally, elements of the multivariate topography, and not the commonly used summary scalar, correlated with future PiB changes. Consideration of the entire multivariate PiB topography provides additional information regarding the development of amyloid-beta pathology in very early preclinical AD.

1. Introduction

Alzheimer’s disease (AD) is characterized by a long preclinical period wherein pathology accumulates in the absence of overt symptoms (Price et al., 2009). The deposition of amyloid-beta (Aβ), measured via positron emission tomography (PET) using Pittsburgh compound B (PiB) (Klunk et al., 2004), is one of the earliest measurable pathological changes in AD (Braak and Del Tredici, 2012; Jack et al., 2013) and can be monitored longitudinally (Sojkova et al., 2011; Villemagne et al., 2011; Vlassenko et al., 2011). The results of PiB scans are often summarized into a single scalar metric defined as an average over a group of regions known to accumulate the most of Aβ plaques in symptomatic AD. PiB scans assessed in this way are dichotomized as either PiB negative (PiB−) or PiB positive (PiB+) (Mintun et al., 2006). A PiB+ scan in a cognitively normal individual is interpreted as presumptive evidence for preclinical AD (Jack et al., 2012; Morris et al., 2014; Sperling et al., 2011) and predicts clinical progression (Morris et al., 2009). Dichotomizing PiB status is potentially clinically useful but reduces complex and potentially informative topographies to a single scalar metric.

The earliest detectably abnormal amyloid topography is relatively focal but becomes more expansive as the disease progresses (Braak et al., 2011; Thal et al., 2002). Understanding of this early topography, how it differs from the topography of the highest PiB retention at the more advanced stages of AD and how it progresses in the early stage of the disease remains unclear. Multivariate statistical techniques, well suited for examining local and distributed phenomena, may help to characterize better the relationships in longitudinal amyloid topographies as assessed by PiB.

In this study, we followed 157 cognitively normal participants who were PiB− (N = 131) or PiB+ (N = 26) at baseline as assessed by a summary scalar value of mean cortical (MC) standardized uptake value ratio (SUVR). These participants were followed longitudinally (mean follow-up: ~3 years). In participants who developed significant PiB accumulation (i.e., became PiB+), we investigated the topographic progression of PiB accumulation using canonical correlation. Canonical correlation identifies pairs of highly correlated topographies. We then compared the ability of the single scalar value and topographic measures to capture the underlying PiB accumulation associated with the development of preclinical AD.

2. Methods

2.1. Subjects

Participants were community dwelling volunteers (age range 45–85 years) enrolled in the Adult Children Study project at the Washington University in St Louis Knight Alzheimer Disease Research Center. All participants were cognitively normal, both at baseline and at follow-up PiB scans, as assessed by a Clinical Dementia Rating score of 0 (Morris, 1993) and the Mini-Mental Status Examination. Participants were in good general health with no neurological, psychiatric, or systemic medical illness that could disrupt longitudinal participation. Each participant underwent magnetic resonance imaging (MRI) and PiB PET (described in the following section). Baseline scans were dichotomized as either PiB− or PiB+ (criteria described in the following section) and a second scan was performed on average 3.29 years later (standard deviation = 1.22 years; minimum = 0.96 years; maximum = 6.47 years). Participants were divided into 3 groups based on their PiB status at baseline and follow-up: CNnn (cognitively normal, PiB− at both scans, N = 115), CNnp (cognitively normal, PiB− at first scan but PiB+ at second scan, N = 16), or CNpp (cognitively normal, PiB+ at both scans, N = 26). Complete demographic information is shown in Table 1.

Table 1.

Demographic information

Variable	CNnn	CNnp	CNpp	p
N	115	16	26	N/A
Age in y at baseline scan (SD)	59.5 (8.77)	66.4 (8.67)	68.2 (6.3)	<0.001
Gender (male/female)	35/80	5/11	10/16	0.73
Education in y (SD)	16.1 (2.4)	15.4 (2.5)	15.4 (2.4)	0.90
APOE ε4+ (% carriers)	23 (20)	9 (56)	17 (65)	<0.001
MC SUVR at baseline (SD)	0.97 (0.07)	1.17 (0.10)	2.12 (0.60)	<0.001
MC SUVR (follow-up)	1.02 (0.09)	1.47 (0.31)	2.48 (0.56)	<0.001
MMSE at baseline	29.3 (0.86)	29.3 (1.09)	28.9 (1.51)	0.73
MMSE at follow-up	29.4 (0.92)	29.4 (0.96)	29.0 (1.42)	0.89
Follow-up time in y (SD)	3.30 (1.45)	3.26 (1.20)	2.99 (1.26)	0.37

Mean (standard deviation) or counts for demographic variables.

Key: APOE ε4, apolipoprotein E ε4 positive indicates at least one APOE ε4 allele; CNnn, cognitively normal individuals, PiB negative at both scans; CNnp, cognitively normal, PiB-negative at first scan but PiB positive at second scan; MC SUVR, mean cortical standard uptake volume ratio of PiB deposition; MMSE, Mini-Mental Status Examination; SD, standard deviation.

2.2. MRI assessment

MRI consisted of an magnetization-prepared rapid gradientecho T1-weighted image collected on a Siemens (Erlangen, Germany) MR scanner. Images are processed using FreeSurfer software version 5.1 (Martinos Center for Biomedical Imaging, Charlestown, MA, USA) (Fischl et al., 2002). All FreeSurfer parcelations were assessed for accuracy by a skilled investigator (Karl A. Friedrichsen). Only gray matter regions were included in this analysis.

2.3. PET assessment

The PiB PET assessment has been previously described in detail (Su et al., 2013, 2014). Imaging was conducted on a Siemens 962 HR+ ECAT PET scanner or a Siemens Biograph 40 scanner. PET data were analyzed using previously developed methods (Su et al., 2013, 2015). FreeSurfer segmentation (Fischl et al., 2002) (http://freesurfer.net/) was used as the basis for quantitative analysis to obtain regional SUVR with cerebellar gray matter serving as the reference region. Partial volume correction was also performed using a regional spread function technique (Rousset et al., 1998; Su et al., 2015).

PiB positivity was defined using the MC SUVR across the precuneus, prefrontal, gyrus rectus, and temporal FreeSurfer regions of interest (ROIs) (Morris et al., 2010). A cutoff value of 1.42 was used which is comparable to an MC binding potential of 0.18 that was previously defined (Mintun et al., 2006; Su et al., 2013). Characteristic SUVR images are presented in Fig. 1. The equivalence for an MC SUVR of 1.42 and MC-BP of 0.18 was previously determined using regression in an independent sample (unpublished data). Because of the criticality of this cutoff for subsequent analyses, primary results are also replicated using an alternative cutoff determined from this sample (Supplementary Material).

Fig. 1.

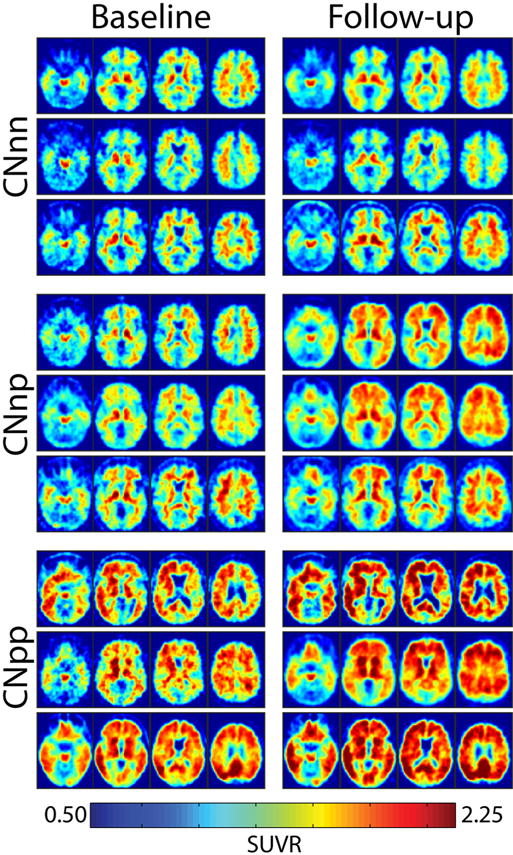
Baseline and follow-up SUVR images for the CNnn, CNnp, and CNpp group. Baseline and follow-up SUVR images for 3 randomly selected participants in each group. Abbreviations: CNnn, cognitively normal, PiB− at both scans; CNnp, cognitively normal, PiB− at first scan but PiB+ at second scan; CNpp, cognitively normal, PiB+ at both scans; SUVR, standardized uptake value ratio.

2.4. Canonical correlation analysis

We investigated the progression of PiB topography in CNnp, CNnn, and CNpp groups separately. To do this, we calculated the canonical correlation between the PiB topography at baseline and the PiB topography at follow-up using 42 ROIs (Hardle and Simar, 2007; Hotelling, 1936). A canonical correlation is the weighted average of variables (termed canonical variables) in one distribution that are maximally correlated with the weighted average of variables from another distribution. There can be multiple significant canonical correlations that isolate unique variance (similar to PCA components).

Let X₁, X₂∈ℝ^N×M index the regional PiB SUVR in N subjects and M = 42 ROIs at time point 1 and 2, respectively. Define:

$${\displaystyle \sum =\left[\begin{array}{cc}{\sum }_1& {\sum }_{12}\\ {\sum }_{21}& {\sum }_2\end{array}\right]}=\left[\begin{array}{cc}{X}_1^T{X}_1& X_1^T{X}_2\\ X_2^T{X}_1& X_2^T{X}_2\end{array}\right]$$

In this case, Σ is rank deficient which precludes matrix inversion. Therefore, define $\widehat{\sum }=\left(1-\alpha \right)\sum +\alpha \mathrm{\Delta }$, where α is an arbitrary parameter and Δ is a shrinkage target (Schafer and Strimmer, 2005). For this analysis, α is calculated in closed form as previously described (Ledoit and Wolf, 2003); Δ is defined as the diagonal matrix of Σ which ensures that $\widehat{\sum }$ is full rank (Ledoit and Wolf, 2004). This approach was recently applied to analyze functional MRI data (Brier et al., 2015).

The number of significant canonical correlations is defined as the dimensionality of ${\widehat{\sum }}_{12}$. Here, we estimate this dimensionality using an information criterion (Minka, 2000). For every significant canonical correlation there exist 2 canonical variables: one corresponding to the baseline PiB topography and another corresponding to the follow-up PiB topography. Let a_i be the ith canonical variable corresponding to the baseline PiB topography; a_i is defined as the ith eigenvector of ${\widehat{\sum }}_1^{-1}{\widehat{\sum }}_{12}{\widehat{\sum }}_2^{-1}{\widehat{\sum }}_{21}$. Similarly, let b_i be the ith canonical variable corresponding to the follow-up PiB topography; b_i is defined as the ith eigenvector of ${\widehat{\sum }}_2^{-1}{\widehat{\sum }}_{21}{\widehat{\sum }}_1^{-1}{\widehat{\sum }}_{12}$. The values of a_i and b_i are unit norm and maximize the correlation between $a_i^T{X}_1$ and $b_i^T{X}_2$.

2.5. Penalized regression

We fit an elastic net penalized regression model which uses the linear combination of an L₁ and L₂ norm of the calculated β values as a penalty (also known as least absolute shrinkage and selection operator [LASSO] and ridge regression, respectively) (Hastie et al., 2001; Tibshirani, 1996; Zou and Hastie, 2005). Penalized regression differs from ordinary least squares (OLS) regression in that it enforces a penalty term that forces some favorable property on the resulting regression βs. The L₁ penalty (LASSO) penalizes nonzero β values and thus forces small β values to 0 and retains a small number of nonzero β values. This results in a model that is more easily interpretable (i.e., has only a few terms to consider). However, in data that are highly colinear the decision to retain one variable and discard a highly correlated variable is arbitrary (Zou and Hastie, 2005). The elastic net accommodates this data feature by allowing highly correlated predictor variables to enter the model simultaneously. This flexibility is accomplished by relaxing the L₁ penalty with some fraction of an L₂ penalty.

We fit 2 separate elastic net models: The first uses follow-up MC SUVR as an outcome variable and the second uses percent change in MC SUVR as an outcome variable. Let y = [y₁, y₂,…, y_N]∈ ℝ be the outcome variable of interest, either follow-up MC SUVR or the percent change in MC SUVR between baseline and follow-up. Furthermore, let X = ℝ^N×[M+1] index the regional PiB SUVR in N subjects and M = 40 ROIs. The M + first region is the baseline MC SUVR value which is included to investigate its sufficiency as a predictor. All variables were mean centered and made unit variance (z-scored). The estimate of penalized regression coefficients then has the form:

$$\underset{\widehat{\beta }}{\arg min}{\Vert y-X\widehat{\beta }\Vert }^2+\lambda \left(\left(1-\alpha \right){\Vert \widehat{\beta }\Vert }^2+\alpha {\Vert \widehat{\beta }\Vert }_1\right)$$

The first term is OLS regression. The second and third terms are the L₂ and L₁ norms, respectively. λ determines the overall penalty severity and α determines the relative contribution of the L₁ and L₂ penalty. Both parameters are selected by leave-one-out cross validation.

To compare the power of baseline MC SUVR and the entire topography to predict follow-up MC SUVR or percentage change in MC SUVR we compared the adjusted-R² values:

$$adj{R}^2=1-\frac{\left(1-R^2\right)\left(N-1\right)}{N-df-1}$$

For OLS, the df is the number of predictors. Similarly, for LASSO regression the number of df is the number of nonzero β values. However, in elastic net regression the number of df is complicated by the potential for colinearity in the selected predictors. Thus, df is defined as:

$$df=Tr\left(X_{\mathcal{A}}{\left(X_{\mathcal{A}}^T{X}_{\mathcal{A}}+\left(\lambda \cdot \left(1-\alpha \right)\right)I\right)}^{-1}{X}_{\mathcal{A}}^T\right)$$

where Tr indicates the trace and $\mathcal{A}$ indicates the active predictor set (Zou and Hastie, 2005).

3. Results

We first investigated the evolution of PiB topography in the CNnp group. The number of significant canonical correlations was determined to be 3 using an information criteria (Minka, 2000). The first canonical correlation was characterized by the baseline topography in Fig. 2A and the follow-up topography in Fig. 2B. The baseline topography was dominated by large positive weights in the posterior cingulate, precuneus, and superior temporal regions balanced by negative weights in lateral frontal regions. At follow-up the topography was similar but now also included inferior and lateral temporal regions. These topographies were highly correlated (Fig. 2C; r = 0.58, p < 10⁻⁴). For example, the precuneus and temporal regions are positive in both topographies and lateral frontal regions are strongly negative. The original regional data are then projected onto these topographies yielding a single scalar value for each subject at baseline and follow-up. Put another way, the weighted average of PiB binding (weighted according to the loadings in the topographies) was calculated at baseline and follow-up. These baseline and follow-up scalar values were highly correlated (Fig. 2D; r = 0.99; p < 10⁻¹⁰) with follow-up significantly higher. Thus, this canonical correlation represents the accumulation of Aβ locally in regions already affected.

Fig. 2.

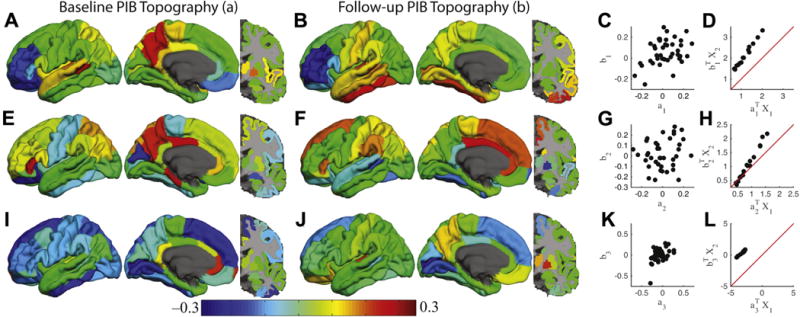
Canonical correlation analysis reveals distinct amyloid accumulation processes. The results corresponding to the first, second, and third canonical correlations are organized as individual rows. The first column (A, E, and I) shows the canonical variable (a) corresponding to the baseline PiB topography. The second column (B, F, and J) shows the canonical variable (b) corresponding to the follow-up PiB topography. These topographies are unit norm. The third column (C, G, and K) shows the correlation between the 2 canonical variables within a single canonical correlation. The fourth column (D, H, and L) shows the projection of the original data onto the canonical variables. Red line is the identity line. Abbreviation: PiB, Pittsburgh compound B. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

The second canonical correlation, isolated after removing the variance related to the first canonical correlation, had a different pattern. The topographies of PiB for the baseline and follow-up scan are shown in Fig. 2E and F, respectively. The baseline topography was dominated by large positive weights in posterior cingulate, precuneus, and lateral parietal regions. In contrast, frontal regions dominated the follow-up topography. In contrast to the first canonical variable, the topographies were not as strongly correlated (Fig. 2G; r = 31; p= 0.04). This indicates that baseline PiB topography predicts PiB values in a different topography at follow-up. Projection of the original data onto these topographies resulted in a strong positive correlation (Fig. 2H; r = 0.99; p < 10⁻¹⁰). The prediction of a distinct topography at follow-up based on a different topography at baseline suggests that this canonical correlation represents the expansion of Aβ topography to additional regions in the CNnp group.

The third canonical correlation has yet a different pattern. The topographies of PiB for the baseline and follow-up scan are shown in Fig. 2I and J and were moderately correlated (Fig. 2K; r = .47, p = 0.002). The baseline topography was dominated by the anterior cingulate, whereas the follow-up topography was dominated by precuneus and subcortical regions. Projection of the original data onto this topography resulted in a strong positive correlation (Fig. 2L; r = 0.99; p < 10⁻¹⁰). This canonical correlation represents a combination of local and distributed processes distinct from the 2 aforementioned processes. These canonical correlation analyses were replicated using an alternative cutoff (Supplementary Material).

One analytic decision present in the previous results is the averaging of homotopic regions into a single bilateral ROI. We sought to determine whether this assumption (similar results on the left and right) was supported by the data. To accomplish this, the number of columns in X was doubled to 2M corresponding to left and right regional SUVR values being represented separately. The number of canonical correlations in this lateralized data set was determined to be 3 by an information criteria (Minka, 2000). This was the same number of canonical correlations identified in the homotopic analysis described previously. There were 2 critical analytic questions to be addressed: (1) were the topographies isolated in the lateralized analysis symmetric across the midsagittal plane and (2) were the same topographies isolated in the lateralized analysis similar to those in the homotopic analysis. To address the first question, within a single topography the loadings on the left were regressed onto the loadings on the right. For all topographies (3 canonical correlations with a baseline and follow-up topography) the left and right loadings were strongly related (all p < 0.05). In each case, the 95% confidence intervals on the regression β crossed 1, suggesting equal values for the left and the right hemispheres. Nevertheless, the maximum likelihood β estimate favored a larger representation in the left hemisphere compared to the right hemisphere but this bias was not significant. We next examined whether the topographies isolated in the lateralized analysis were similar to the topographies isolated in the homotopic analysis. For each canonical correlation (both baseline and follow-up), the topography resulting from the homotopic analysis was highly correlated between the left and right (analyzed separately) hemisphere topographies resulting from the lateralized analysis (all r > 0.65; all p < 0.001). These data suggest a bias toward representation of the left hemisphere, but this difference does not lead to significantly different PiB accumulation with respect to hemisphere.

A single canonical correlation described the relationship between baseline and follow-up PiB topographies in the CNnn group (Fig. 3A and B). The baseline and follow-up topographies were not correlated (Fig. 3C) and did not demonstrate any obvious biological topography. Furthermore, the projected PiB values did not show systematic increases (Fig. 3D), indicating no accumulation, consistent with their CNnn status.

Fig. 3.

Canonical correlation analysis in the CNnn group reveals minimal amyloid accumulation. Canonical correlation analysis in the CNnn group using the same presentation style as Fig. 1 in the main text. (A) and (B) represent the maximally correlated baseline and follow-up topographies, respectively. (C) depicts the correlation between the two topographies. The critical feature here is that the correlated topographies do not exhibit marked accumulation (the data are along the identity line in D). Abbreviations: CNnn, cognitively normal, PiB− at both scans; PiB, Pittsburgh compound B.

A single canonical correlation described the relationship between baseline and follow-up PiB topographies in the CNpp group (Fig. 4). The baseline topography (Fig. 3A) was not significantly correlated with the follow-up topography (Fig. 4B; r = 0.12, p = 0.44). However, the projected PiB values were strongly correlated (r = 0.99; p < 10⁻¹⁰) and a dramatic accumulation was seen at follow-up, as reflected by data above the identity line (Fig. 4D). These results suggest that CNpp individual at baseline continues to have significant accumulation longitudinally.

Fig. 4.

Canonical correlation analysis in the CNpp group reveals substantial amyloid accumulation. Canonical correlation analysis in the CNpp group using the same presentation style as Fig. 1 in the main text. (A) and (B) represent the maximally correlated baseline and follow-up topographies, respectively. (C) depicts the correlation between the two topographies. The critical feature here is that the correlated topographies exhibit marked accumulation (the data are above the identity line in D). Abbreviations: CNpp, cognitively normal, PiB+ at both scans; PiB, Pittsburgh compound B.

We next turned to the question of defining the correlates of future PiB accumulation in those who were PiB− at baseline. Accepting that the MC SUVR is a reliable measure of the level of AD pathology, can follow-up values be understood as a function of the baseline scan? Across all subjects, the baseline and follow-up MC SUVR were highly correlated (r = 0.55, p < 10⁻¹¹, Adj-R² = 0.30) suggesting that, relative to the interindividual variance, MC SUVR values did not dramatically change over a period of 3 years. Importantly, only within just the CNnp group were the baseline and follow-up MC SUVR not correlated (r = 0.24, p = 0.36). Baseline MC SUVR was also not correlated with the percent change in MC SUVR across scans (r = 0.026, p = 0.77, Adj-R² = −0.007). A negative Adj-R² indicates poor model fit. Notably, the baseline MC SUVR and percent change in MC SUVR was negatively correlated in the CNpp group (r = −0.54, p = 0.0047), suggesting a slowing of PiB accumulation within this topography. Thus, an open question is what features in the baseline topography correlates with future change in MC SUVR.

To investigate which features of the baseline topography correlate with the follow-up MC SUVR and percent change in MC SUVR, we fit 2 separate elastic net models using individual regional SUVR values as predictors. The β coefficients corresponding to the minimum cross-validation error for each model are shown in Table 2 and depicted visually in Fig. 5. Positive values predict relatively higher MC SUVR or positive changes in MC SUVR in the first (predicting MC SUVR) and second model (predicting percent change in MC SUVR) and negative values predict relatively lower MC SUVR or negative changes in MC SUVR. Importantly, the baseline MC SUVR only entered the model for predicting follow-up MC SUVR and not for predicting the change in MC SUVR. The correlation between the predicted follow-up MC SUVR and the actual MC SUVR was significantly correlated (r = 0.73, p < 10⁻²²) and after correcting for the number of predictors was better than baseline MC SUVR alone (Adj-R² = 0.50 compared with 0.30). Similarly, the predicted percent change in MC SUVR was significantly correlated with the actual percent change in MC SUVR (r = 0.54, p < 10⁻¹⁰) and, after correcting for the number of predictors, was better than baseline MC SUVR alone (Adj-R² = 0.25 compared with −0.007).

Table 2.

Elastic net regression coefficients

Region	Predictor Value
	Follow-up MC SUVR	% Change in MC SUVR
Posterior cingulate	0.032	0.023
Rostral middle frontal	0.028
Rostral anterior cingulate	0.027	0.014
Precuneus	0.025
Baseline MC SUVR	0.021
Caudate	0.017	0.011
Frontal pole	0.016	0.002
Caudal anterior cingulate	0.010	0.004
Caudal middle frontal	0.005
Parahippocampal gyrus	0.003
Pericalcerine		−0.003
Transverse temporal	−0.001
Insula	−0.004	−0.004
Precentral gyrus	−0.015	−0.016
Postcentral gyrus	−0.027	−0.023

Table of penalized (elastic net) regression coefficients. Blank spaces correspond to coefficients equal to zero.

Key: MC SUVR, mean cortical standard uptake volume ratio.

Fig. 5.

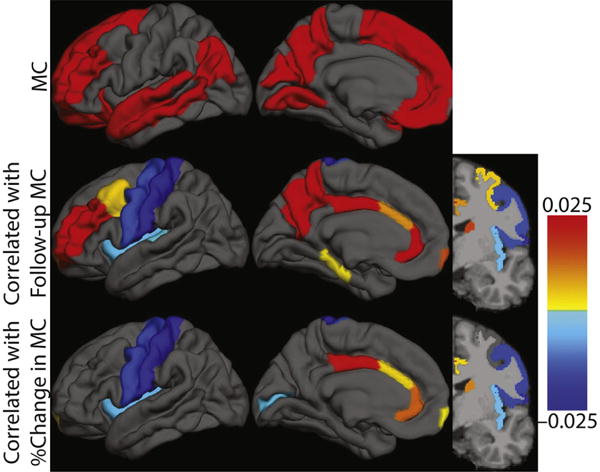
Topography of baseline Pittsburgh compound B deposition that correlates with follow-up and % change in mean cortical standardized uptake value ratio. Graphical representation of the information in Table 2. First row shows MC definition. Color bar indicates regression β values. Abbreviation: MC, mean cortical. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

4. Discussion

This report uses two multivariate techniques (canonical correlation and penalized regression) to describe expanding Aβ topographies, as assessed by PiB, and identifies patterns of deposition correlated with future PiB accumulation. Canonical correlation finds topographies that represent local and distributed accumulation in those who develop preclinical AD as assessed by a scalar cutoff. Critically, within cognitively normal individuals similar accumulation is absent in the group that remains PiB− at both time points but is present in those who became PiB+ at follow-up or who remained PiB+ at both time points. Evidence of Aβ pathology (e.g., in the CNnp group) is sufficient for classification as stage 1 preclinical AD (Jack et al., 2012; Sperling et al., 2011). Given that these participants became PiB + over a 3-year interval, this group represents the very earliest identifiable stages of preclinical AD. One method of operationalizing these criteria is through a scalar cutoff applied to some mean PiB binding index (Mintun et al., 2006). This is a potentially clinically useful method for summarizing the data and is predictive of eventual symptomatic conversion (Morris et al., 2009). However, the baseline MC SUVR failed to strongly correlate with future changes in MC SUVR, limiting its utility in early disease stages. In contrast, the multivariate topography, not restricted to regions typically involved in the late stages of AD, strongly correlated with change in MC SUVR in a penalized regression analysis. Overall, these data demonstrate that accounting for the multivariate PiB topography may help to understand and characterize the development of AD pathology over the different stages of the disease.

The application of multivariate statistics to the study of PiB topographies allows for the investigation of novel neurobiology. Previous work using mass univariate approaches necessarily included a data reduction step, for example, averaging over many regions of interest. This approach is powerful when the relevant topography is known. However, in the earliest stages of preclinical AD the relevant topography is unknown. Canonical correlation and penalized regression consider the entire topography in a minimally biased manner to maximize explanatory power. In this report, the additional power resulting from considering the entire distribution is leveraged to describe the topography of PiB associated with conversion to preclinical AD. Importantly, the identified topography is distinct from the maximally effected topography in late stage AD.

A critical analytic decision in the analysis of PiB data is resolution at which the analysis should be conducted. Currently, 3 analytic strategies dominate the literature: analysis of (1) global PiB binding over the entire cortex, (2) composite PiB binding in an a priori topography, or (3) regional/voxelwise PiB binding. The first 2 approaches are strong data reduction approaches that have demonstrated utility for predicting future symptomatic conversion (Ma et al., 2014; Morris and Price, 2001) though regional analysis may offer diagnostic advantages (Aizenstein et al., 2008). The notable feature of both of these approaches is the definition of a region of interest a priori (the whole cortex in the case of the former, specific topographies in the case of the latter). However, the relevant topography where PiB deposition maximally occurs changes with disease progression (Villain et al., 2012); the topography that predicts symptomatic conversion may not be useful for detecting changes associated with earliest disease onset. Regional analyses allow for the flexibility to identify novel topographies but can yield varied results owing to the increased number of degrees-of-freedom (Engler et al., 2006; Grimmer et al., 2010; Jack et al., 2009; Kadir et al., 2012; Rinne et al., 2010; Villemagne et al., 2011). The presently reported results make use of multivariate techniques well suited to compiling regional data into meaningful topographies. Application of such approaches is especially important when the topographies of interest are not known a priori.

The conversion from PiB− to PiB+ necessarily involves deposition of additional Aβ. That additional deposition is not haphazard but usually follows a stereotypical progression (Braak and Braak, 1997; Thal et al., 2002). We report on distinct processes using canonical correlation analysis. We find evidence of a local and distributed process. In the local process, regions with PiB deposition at baseline simply accumulate more PiB plaques by the follow-up scan. However, in the distributed process, PiB in a particular topography correlates with PiB deposition in a different topography. Specifically, this progression represents the well-documented spread of Aβ deposition from posterior regions to more anterior regions (Thal et al., 2002).

The penalized regression model identifies topography of PiB retention that correlates with future PiB accumulation, either total value or percent change. Critically, the summary scalar was not a strong correlate of future percent change in PiB burden. The regions with positive β values largely overlap with known areas of Aβ retention early in the disease (Thal et al., 2002). However, not all regions overlap with previously defined summary metrics used for operationalizing the PiB+ definition. Notably, the previous scalar metric was defined based on the observations in the symptomatic stage of AD and does not necessary reflect the spatial pattern of PiB deposition in early preclinical stage (Mintun et al., 2006). This may lead to a biased view of early PiB burden using the MC SUVR approach. The caudate nucleus deserves specific discussion. Although it is known that caudate develops Aβ deposits throughout the disease (Thal et al., 2002), it is not commonly noted as a prominent initial contributor to PiB topography in late onset AD (but see Kemppainen et al., 2007). Nevertheless, the caudate nucleus is identified in both penalized regression models. However, it has been noted that individuals with autosomal dominant AD have particularly intense PiB retention in the striatum (Klunk et al., 2007). The independent evidence from this study and the study of autosomal dominant AD suggests some important, or at least reliable, process may be ongoing in the striatum early in AD.

The penalized regression identified several regions which were negatively loaded in both regression models. The presence of these negatively loaded regions demonstrates that the Aβ topography associated with advancing disease is specific. That is, PiB binding alone is not sufficient but rather it must be deposited in the disease causing topography. Amyloid in negatively loaded regions does not contribute to early disease pathophysiology. Indeed, Aβ is only present in the primary motor and sensory cortices much later in the disease (Braak and Braak, 1997), likely after symptoms develop. This potentially reflects that participants who have PiB retention in the precentral gyrus are unlikely to be PiB− at baseline. Thus, negatively loaded regions may serve as control regions by accounting for binding that is not because of Aβ or AD-related processes, especially at early disease stages. The presence of a negatively predictive region indicates that it is not simply high values of PiB retention that predict conversion to PiB+ status but rather PiB deposition in a specific topography.

Only a small number of participants converted from PiB− status to PiB+ status which limits the robustness of this study. Additionally, the definition of converter compared with nonconverter is based on crossing a PiB threshold. Although such thresholds have been demonstrated to be potentially clinically useful (Mintun et al., 2006; Morris et al., 2009), other choices for a cutoff may be equally valid. Regardless of the precise definition, the primary scientific points remain: local and distributed processes are involved in the conversion to preclinical AD and consideration of the entire multivariate Aβ topography identifies correlates of advancing Aβ accumulation. A related point pertains to the prognostic information related to individuals who remain PiB− for the duration of the study but accumulate more PiB than average. These individuals are likely at an increased risk for developing preclinical AD in the future but longer follow-up time is required.

In summary, this study identified canonical correlations between baseline and follow-up PiB topographies in patients who converted from PiB− to PiB+. Penalized regression identified a topography association with future Aβ accumulation. Future studies could validate these regression models for their predictive power.

Appendix A. Supplementary data

Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.neurobiolaging.2015.10.025.