Generation of anatomically realistic numerical phantoms for photoacoustic and ultrasonic breast imaging

Abstract.

Photoacoustic computed tomography (PACT) and ultrasound computed tomography (USCT) are emerging modalities for breast imaging. As in all emerging imaging technologies, computer-simulation studies play a critically important role in developing and optimizing the designs of hardware and image reconstruction methods for PACT and USCT. Using computer-simulations, the parameters of an imaging system can be systematically and comprehensively explored in a way that is generally not possible through experimentation. When conducting such studies, numerical phantoms are employed to represent the physical properties of the patient or object to-be-imaged that influence the measured image data. It is highly desirable to utilize numerical phantoms that are realistic, especially when task-based measures of image quality are to be utilized to guide system design. However, most reported computer-simulation studies of PACT and USCT breast imaging employ simple numerical phantoms that oversimplify the complex anatomical structures in the human female breast. We develop and implement a methodology for generating anatomically realistic numerical breast phantoms from clinical contrast-enhanced magnetic resonance imaging data. The phantoms will depict vascular structures and the volumetric distribution of different tissue types in the breast. By assigning optical and acoustic parameters to different tissue structures, both optical and acoustic breast phantoms will be established for use in PACT and USCT studies.

1. Introduction

Photoacoustic computed tomography (PACT)^1–3 and ultrasound computed tomography (USCT)^4–6 are emerging modalities for breast imaging. PACT employs ultrasonic detection principles and a contrast mechanism based on optical absorption, thereby combining the rich contrast of optical imaging methods with the deep penetration and high spatial resolution of ultrasound imaging methods. The hybrid nature of PACT breast imaging provides both structural information and hemoglobin-related functional information within the breast, which can aid clinical diagnosis. USCT employs various acoustic tissue contrasts, including acoustic reflectivity, acoustic attenuation, and speed of sound, to characterize malignant tissues within the breast. Both PACT and USCT are radiation-free, breast-compression-free, and relatively inexpensive. In addition, the integration of PACT and USCT has drawn increasing attention^7–11 because they provide complementary contrasts, the speed of sound information produced by USCT can improve the accuracy of PACT image reconstruction, and the two imaging modalities can share a common ultrasonic detection system. These advantages make PACT and USCT promising tools for breast cancer screening.

Developing an effective PACT or USCT breast imaging system requires carefully balancing various design constraints. Computer-simulation studies are often conducted to facilitate this task. Furthermore, the development and optimization of advanced reconstruction algorithms also require simulation studies. To date, numerical phantoms employed in many PACT and USCT simulation studies are either two-dimensional (2-D)^12,13 or three-dimensional (3-D) volumes comprised of only simple objects.^12,14–17 These oversimplified phantoms do not reflect the complex anatomical structures within the breast, thus limiting the value of simulation studies in guiding real-world system design and algorithm development. This is particularly true when task-based image quality measures are employed.¹⁸ While some recent works in quantitative PAT have employed realistic numerical phantoms derived from $\mu \mathrm{CT}$ rat and mouse brain images,^19,20 those phantoms were utilized for small animal imaging and therefore provided limited guidance for clinical system designs. As such, there remains a need for the development of anatomically realistic numerical breast phantoms suitable for clinical purposes to advance PACT and USCT technologies.

However, the creation of accurate numerical breast phantoms for PACT and USCT is challenging due to the intertwined networks of vessel, fat, and fibroglandular tissue within the breast. Generation of numerical breast phantoms has been previously addressed by Zastrow et al.²¹ for microwave imaging and by Deng et al.²² for optical imaging. However, with hemoglobin being the key optical contrast of PACT, the development of useful PACT phantoms requires accurate modeling of vessel structures, which were not considered in the aforementioned work. Other groups, including Nie et al.,²³ Chen et al.,²⁴ and Wang et al.,²⁵ have developed methods for segmenting different breast tissues from MRI images. Although their segmentation methods could potentially be utilized to establish PACT phantoms, the vessel structures were not considered in their works either. Marcan et al.²⁶ successfully segmented hepatic vessels from MR images in the liver, but due to the inherently different anatomies of breast and liver, their method cannot be directly employed to establish breast phantoms.

In this work, we report the development of realistic 3-D numerical breast phantoms for PACT and USCT that describe the optical and acoustic properties of the breast. Clinical contrast-enhanced magnetic resonance (MR) data are employed to establish the numerical phantoms. Methods for segmenting skin, vessels, fat tissue, and fibroglandular tissue are developed and applied to the clinical data. Finally, coregistered optical and acoustic phantoms are generated from the segmented tissue types. Furthermore, to promote reproducibility in PACT and USCT research, the phantoms have been made publicly available online.²⁷ The generated phantoms can be readily employed in PACT and USCT simulations.

The remainder of the paper is organized as follows. An overview of the methodology for generating optical and acoustic phantoms from MR datasets is presented in Sec. 2. A comprehensive description of the methodology with implementation details is given in Sec. 3, and examples of generated numerical phantoms are presented in Sec. 4. A PACT simulation study utilizing the generated phantoms is given in Sec. 5. Finally, a summary of the work is provided in Sec. 6.

2. Overview of Methodology

2.1. Overall Scheme

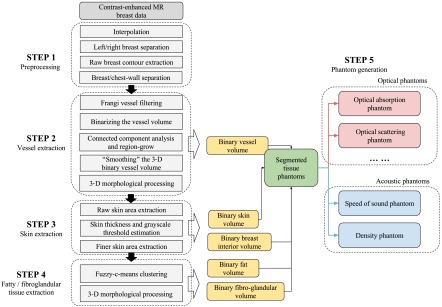
The goal of this work is to develop a computational framework for generating realistic 3-D optical and acoustic breast phantoms from clinical MR data. The general work flow is shown in Fig. 1. To extract vessel structures, contrast-enhanced MR (CE-MR) data are utilized. In CE-MR images, an injected contrast agent results in an increased intensity at vessel locations in the postcontrast images compared to the precontrast images. The input MR data are processed by a four-step procedure to segment different tissues within the breast, which include blood vessels, skin layer, fat, and fibroglandular tissues. By assigning corresponding optical and acoustic property values to each segmented tissue type, a collection of numerical phantoms are created as the final output. An overview of the computational framework is described in the following sections, and a detailed description of the method and its numerical implementation are presented in Sec. 3.

Fig. 1.

Flow chart of the key steps in the breast phantom generation process.

2.2. Clinical Data Collection

Magnetic resonance imaging (MRI) is one of the standard screening tools for breast imaging.^28,29 Skin, fat, and fibroglandular tissues can be well characterized within the breast according to their intensities in MR images. Furthermore, with the aid of contrast agents, blood vessels can also be identified in CE-MR images. MRI retains the natural shape of the breast corresponding to a patient lying in a prone position and provides sufficient resolution for our purpose. Because of these features, the numerical phantoms in our study are based on a database of contrast-enhanced, fat-suppressed MR breast images.

2.3. Step 1: Preprocessing

Each dataset is first interpolated onto a finer 3-D grid to reduce voxelization in the appearance of the MRI images. Left and right breasts are then separated into individual volumes from the centerline and are treated as independent phantoms. A raw contour of the breast is extracted from the interpolated precontrast MR data to separate the breast volume from the background. Finally, the chest wall area is excluded from the breast volume.

2.4. Step 2: Vessel Extraction

The second step of the computational framework involves extracting vessel structures from contrast-enhanced MR data. Hemoglobin is the major optical absorber within human tissue in the visible and NIR spectral ranges. The absorbed energy distribution of blood provides key information for imaging techniques that utilize optical absorption contrast, such as PACT. A newly generated vessel nest may reveal angiogenesis.³⁰ Also, strong signals from major vessels can hinder the detection of weak signals from a nearby structure of interest. Therefore, incorporating anatomically realistic vessel information is crucial for optical phantoms to accurately simulate clinical experiments.

A vessel-enhanced MR image is first computed by averaging three postcontrast MR datasets taken at different time points after injection of the contrast agent and subtracting precontrast data from the averaged data. A Frangi vesselness filter is then applied to the raw vessel-enhanced data.^31,32 The Frangi filter exploits the local Hessian characteristics of different 3-D geometrical surfaces and selectively enhances tube-like structures across multiple tube radii. Hence, the vessel-like structures in the data are enhanced. To segment the data processed by the Frangi filter, an intensity threshold is chosen by analyzing the histogram. This threshold is then applied to binarize the data. By examining all major connected components in the binarized data and manually choosing the ones whose visual appearance represent vessel structures, we can eliminate nonvessel structures with minimal human interactions. The chosen connected components representing vessels are then morphologically processed to smooth unnatural boundaries and are combined to form a 3-D binary vessel volume.²⁶

2.5. Step 3: Skin Extraction

The skin layer defines the breast-air boundary, which plays a vital role in both photon propagation and acoustic wave propagation. To extract the skin layer from fat-suppressed precontrast MR data, the fact that the skin layer has a higher intensity than both the background outside of the breast and the interior adjacent breast tissue (normally fat) is exploited. Meanwhile, since some superficial vessel structures also possess high intensities, the extracted vessels from step 2 are utilized as supplementary information to facilitate the skin extraction procedure to avoid categorizing these vessels as part of the skin layer. First, an approximated skin area is retrieved by finding the outer breast contour using an empirically set intensity threshold for the skin. This approximated skin area contains most of the skin but also other tissues and part of the background. A more accurate skin intensity threshold and a skin thickness range are then estimated by analyzing the histogram within the approximated skin area. Finally, an accurate skin layer is extracted by applying the more accurate skin intensity, and skin thickness at different parts of the breast is adaptively determined to reflect the true thickness in the MR images. Vessel structures located near the breast surface are also avoided.

2.6. Step 4: Fat and Fibroglandular Tissue Extraction

Acoustic heterogeneity in the breast, including the speed of sound and tissue density, plays a crucial role in acoustic wave propagation. The fourth step in our framework describes the segmentation of fat and fibroglandular tissues within the breast. In fat-suppressed MR data, fibroglandular tissues have a higher intensity than fat. Based on this fact, a fuzzy C-means algorithm is applied to the breast volume (with skin layer excluded) to separate fibroglandular tissue from fat.²³ Morphological processing is applied to the binary fibroglandular tissue volume to remove unnatural structures. Finally, the binary fat volume is generated by taking the complement of the fibroglandular tissue volume with respect to the breast volume.

2.7. Step 5: Optical and Acoustic Phantom Generation

Using the methods described above, the breast volume can be segmented into different classes representing vessel, skin, fat, and fibroglandular tissues. A segmented-tissue phantom is created by assigning each voxel to one of these four tissue types according to the segmentation results. The optical absorption phantom, optical scattering phantom, refractive index phantom, and scattering anisotropy phantom are generated by assigning corresponding property values to each tissue type based on the segmented tissue phantom. Acoustic phantoms, including the speed of sound and density phantoms, are generated accordingly.

3. Detailed Description of Methodology and Implementation

The content in Sec. 2 addressed the salient aspects of the proposed methodology for generating optical and acoustic breast phantoms. In this section, a more detailed description of the methodology along with implementation details is presented. The following notations are employed: the $X$, $Y$, $Z$ directions within the breast volume correspond to the medial-lateral, superior-inferior, and anterior-posterior anatomical directions, respectively; the variables starting with $\mathbf{V}$ indicate 3-D volumes with grayscale intensity values, and the variables starting with $\mathbf{B}$ indicate 3-D volumes with binary values (0 and 1).

3.1. Description of MRI Data

A total of 50 contrast-enhanced and fat-suppressed MR datasets were collected from Barnes Jewish Hospital with the approval of the Institutional Review Board. Both precontrast and postcontrast data were acquired using a Siemens 1.5T Espree MRI system, employing a Flash 3-D sequence with a repetition time of 6.06 ms and an echo time of 2.71 to 2.85 ms. Each dataset was comprised of a series of transaxial slices with an in-plane pixel-size of $0.6\mathrm{mm}\times 0.6\mathrm{mm}$ and a slice spacing of 1.0 mm. After a precontrast MR scan was performed, 13 mL of MultiHance contrast agent was injected, and three sequential postcontrast MR scans were performed at different time-points after injection.

3.2. Preprocessing Implementation

The MRI data were preprocessed as follows:

• 1.Both precontrast and postcontrast MR data were interpolated onto a uniform 3-D grid with a voxel size of $0.2\times 0.2\times 0.2{\mathrm{mm}}^3$ using cubic interpolation.
• 2.The left and right breasts were separated from the centerline into two individual volumes and were used to create two distinct phantoms.
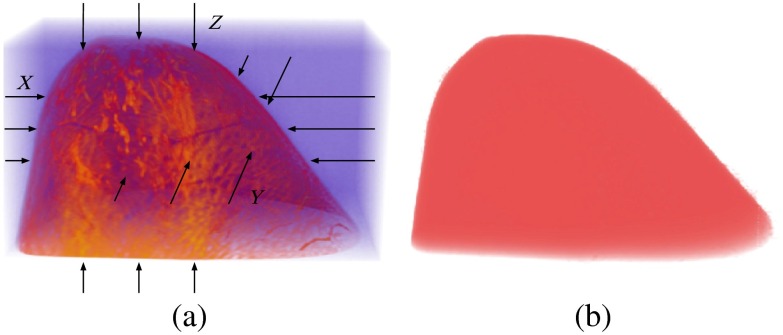
• 3.A raw binary volume of the breast contour, ${\mathbf{B}}_{R\_\text{contour}}$, was extracted from the interpolated precontrast MR data. The technique to retrieve the contour is referred to as 3-D pooling.²¹ This 3-D pooling method created three logical masks along three directions: $X$, $Y$, and $Z$.In each one-dimensional “1-D” column within the breast data, the first and last voxels whose intensities exceed a specified threshold were found, and the voxels between these first and last voxels were set to 1 in the corresponding logical mask. Three logical masks were combined into the raw breast contour volume using the logical and operation. A value of 1 for a given voxel in ${\mathbf{B}}_{R\_\text{contour}}$ indicates the breast, while a value of 0 indicates space outside the breast. An illustration of the pooling method is shown in Fig. 2.
• 4.The original MR data include both breast and a large portion of the chest wall area. Separation of the breast from the chest wall area is accomplished by traversing through the $X\text{-}Y$ (coronal) slices of ${\mathbf{B}}_{R\_\text{contour}}$ and computing the perimeter of the contour’s coronal slices. The perimeter in general follows an increasing trend from nipple to chest wall. Therefore, when the perimeter exceeds a specified threshold, the breast volume is cut at this slice: all slices before were considered to contain part of the breast, while all slices beyond were considered to contain part of the chest wall. The chest wall area was then cropped out from both the interpolated breast data and ${\mathbf{B}}_{R\_\text{contour}}$.

Fig. 2.

(a) Illustration of the pooling method on a precontrast MR dataset. (b) The extracted raw contour volume.

This procedure produced interpolated-and-cropped precontrast and postcontrast MR data, which were denoted by ${\mathbf{V}}_{\mathrm{pre}}$ and ${\mathbf{V}}_{\mathrm{post}}$, along with a cropped binary raw contour volume denoted by ${\mathbf{B}}_{R\_\text{contour}}$.

3.3. Vessel Extraction Implementation

The vessels were extracted according to the following steps:

• 1.Three postcontrast datasets taken at different time-points after injection were first averaged to give ${\mathbf{V}}_{\mathrm{post}}$. A raw vessel-enhanced dataset was then obtained by ${\mathbf{V}}_{R\_\text{enhanced}}={\mathbf{V}}_{\mathrm{post}}-{\mathbf{V}}_{\mathrm{pre}}$.
• 2.A Frangi vesselness filter was applied to ${\mathbf{V}}_{R\_\text{enhanced}}$,^31,32 and the output was further smoothed by a narrow 3-D Gaussian kernel. The smooth filtered data was denoted by ${\mathbf{V}}_{\text{Frangi}}$.
• 3.Because the Frangi vesselness filter enhances but does not segment vessel-like structures, further postprocessing is necessary to separate vessels from other structures. A threshold was chosen at 70% to 90% of the cumulative histogram of ${\mathbf{V}}_{\text{Frangi}}$ and was applied to ${\mathbf{V}}_{\text{Frangi}}$ to create a binary vessel volume ${\mathbf{B}}_{\text{Frangi}}$.
• 4.Connected component analysis was applied to ${\mathbf{B}}_{\text{Frangi}}$ to extract major vessel structures while excluding other nonvessel tube structures.²⁶ Each connected component with a voxel-count larger than a preset threshold was displayed on the screen, and some minimal human interaction (5 to 10 yes/no choices) were required to determine whether the connected component represented a vessel structure or not. Each chosen connected component was subject to a 3-D region-growing operation to fill gaps³³ and a thinning operation to better reflect the true vessel thickness.
• 5.The binary vessel volume after step 4 was then “smoothed” according to the following steps:
  • a.Three maximum intensity projection (MIP) images of the binary vessel volume were computed across all three directions, $X$, $Y$, and $Z$, and were denoted by ${\mathbf{I}}_X$, ${\mathbf{I}}_Y$, and ${\mathbf{I}}_Z$, respectively.
  • b.The region boundaries within each MIP image were extracted using the Moore-Neighbor tracing algorithm modified by Jacob’s stopping criteria (MATLAB’s bwboundaries function).³⁴ The boundaries were essentially collections of 2-D pixels. The $X$ and $Y$ coordinates of each collection of pixels were taken to form two vectors. Both vectors were then smoothed by a 1-D Gaussian kernel and recombined into $X\text{-}Y$ coordinates of pixels to create “smoothed” boundaries. The interior of the “smoothed” boundaries was then filled to form “smoothed” 2-D MIP images, denoted by ${\mathbf{I}}_{\text{smooth}X}$, ${\mathbf{I}}_{\text{smooth}Y}$, and ${\mathbf{I}}_{\text{smooth}Z}$.
  • c.A new “smooth” 3-D binary vessel volume ${\mathbf{B}}_{\text{smooth}}$ was created from ${\mathbf{B}}_{\text{Frangi}}$, ${\mathbf{I}}_{\text{smooth}X}$, ${\mathbf{I}}_{\text{smooth}Y}$, and ${\mathbf{I}}_{\text{smooth}Z}$, employing the following rules: A voxel in ${\mathbf{B}}_{\text{Frangi}}$ was changed from 1 to 0 if the corresponding projected pixel in ${\mathbf{I}}_{\text{smooth}X}$ was 0 and performing such an operation did not change the corresponding pixels in ${\mathbf{I}}_Y$ and ${\mathbf{I}}_Z$. Similar processes were repeated for ${\mathbf{I}}_{\text{smooth}Y}$ and ${\mathbf{I}}_{\text{smooth}Z}$. A voxel in ${\mathbf{B}}_{\text{Frangi}}$ was changed from 0 to 1 if the corresponding projected pixel in ${\mathbf{I}}_{\text{smooth}X}$ was 1 and it had at least two nonzero neighboring voxels in ${\mathbf{B}}_{\text{Frangi}}$. Similar processes were repeated for ${\mathbf{I}}_{\text{smooth}Y}$ and ${\mathbf{I}}_{\text{smooth}Z}$.
• 6.The “smooth” 3-D binary vessel volume was closed using a small solid sphere to remove small holes and sharp corners. Small isolated structures were removed as well.

This procedure produced a binary vessel volume ${\mathbf{B}}_{\text{vessel}}$.

3.4. Skin Extraction Implementation

The skin layer was extracted according to the following steps illustrated in Fig. 3:

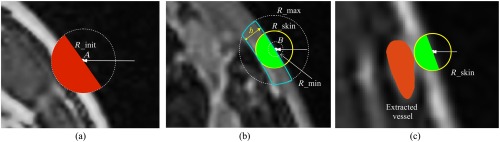
Fig. 3.

Illustration of skin extraction procedure. (a) Extraction of the raw skin area ${\text{Area}}_{\mathrm{RS}}$, where the white arrow is an example of a voxel “column,” $A$ is the first voxel larger than $T_0$ in this “column,” and the red mask forms ${\text{Area}}_{\mathrm{RS}}$. (b) Extraction of the final skin layer, where the dotted circles indicate a sphere with radius ${\mathrm{R}}_{\max }$, the blue line encloses the true skin region, and the yellow circle represents the adaptively chosen skin thickness ${\mathrm{R}}_{\text{skin}}$. The green masks form ${\mathbf{B}}_{\text{skin}}$. (c) Illustration of skin extraction that avoids superficial vessel structures.

• 1.A low-level grayscale threshold $T_0$ and an initial guess of the maximum skin thickness $R_{\mathrm{init}}$ were empirically chosen. The value of $T_0$ was set at 20% of the maximum intensity in ${\mathbf{V}}_{\mathrm{pre}}$, and $R_{\mathrm{init}}$ was set to 3.0 mm, which slightly exceeds the normally accepted skin thickness of 2.0 to 2.5 mm.³⁵
• 2.The raw contour ${\mathbf{B}}_{R\_\text{contour}}$ was first applied to the interpolated precontrast data ${\mathbf{V}}_{\mathrm{pre}}$ to exclude the background. For each column within the generated 3-D volume, the first voxel that was larger than $T_0$ was found and denoted by $A$. A sphere centered at $A$ with a radius of $R_{\mathrm{init}}$ was then identified [dotted circle in Fig. 3(a)], and the hemisphere inside the breast was chosen by computing the local gradient at $A$. The hemisphere [indicated by the red mask in Fig. 3(a)] represented a raw estimation of the skin area. This process was repeated for every voxel “column” in five directions, $\pm X$, $\pm Y$, $+Z$, and all such red hemispheres were combined to form a raw skin area, ${\text{Area}}_{\mathrm{RS}}$.
• 3.${\text{Area}}_{\mathrm{RS}}$ included both the high-contrast true skin layer and some low-contrast voxels representing either background or fat. According to the cumulative histogram of voxel intensities within ${\text{Area}}_{\mathrm{RS}}$, a threshold $T_S$ was chosen at 30% to 50% of the maximum value of the cumulative histogram to represent an estimated skin intensity threshold. We chose the center $X\text{-}Z$ slice of ${\text{Area}}_{\mathrm{RS}}$ to estimate an average skin thickness. Within this slice, the estimated $T_S$ was applied to estimate the total area of the skin within this slice, and 2-D thinning was applied to estimate the “length” of the skin. By dividing skin area by skin “length,” we get an estimated skin thickness $R_{\mathrm{avg}}$. This quantity represents an average skin thickness. However, the thickness at different parts of the breast may vary. Therefore, we define a skin thickness range to be $[R_{\min },R_{\max }]=[R_{\mathrm{avg}}-\mathrm{\Delta }R,R_{\mathrm{avg}}+\mathrm{\Delta }R]$, where $\mathrm{\Delta }R$ is an empirically chosen parameter reflecting the degree of skin thickness variability for a particular patient.
• 4.Step 2 was repeated, but this time, the estimated skin threshold $T_S$ was used. For a particular voxel “column,” the first voxel larger than $T_S$ was denoted by $B$. The radius of the sphere, $R_{\text{skin}}$, was determined by the following procedure:
  • a.A sphere centered at $B$ with a radius of $R_{\max }$ was identified [the dotted circle labeled with $R_{\max }$ in Fig. 3(b)].
  • b.The hemisphere inside the breast was chosen by computing the local gradient at $B$. This hemisphere provides an overestimation of the thickness of the skin layer. Therefore, this hemisphere contains a spherical cap in which the skin is not present. In Fig. 3(b), the blue-line-enclosed area indicates the region of the hemisphere where the skin layer is located. The volume of the skin layer within the hemisphere can be approximated by counting the number of voxels with intensities greater than $T_S$. With knowledge of the volume and the radius of the sphere $R_{\max }$, the height of this skin region can be analytically computed. This height $h$ served as the estimated skin thickness $R_{\text{skin}}$.
  • c.The estimated skin thickness $R_{\text{skin}}$ was projected onto the range $[R_{\min },R_{\max }]$.
  • d.This quantity $R_{\text{skin}}$ was further reduced so that the skin region did not overlap with the extracted vessel structures in ${\mathbf{B}}_{\text{vessel}}$ [see Fig. 3(c)].

The new hemispheres determined by $T_S$ and $R_{\text{skin}}$ are indicated by the green areas in Figs. 3(b) and 3(c), respectively. All such green hemispheres from every voxel “column” were combined to form the final binary skin volume ${\mathbf{B}}_{\text{skin}}$. The volume inside the skin mask representing the interior of the breast was denoted by ${\mathbf{B}}_{\text{interior}}$.

This procedure produced a binary skin volume ${\mathbf{B}}_{\text{skin}}$ and a binary breast-interior volume ${\mathbf{B}}_{\text{interior}}$.

3.5. Fat/Fibroglandular Tissue Extraction Implementation

The fat and fibroglandular tissues within the breast were segmented according to the following steps:

• 1.First, the breast interior mask ${\mathbf{B}}_{\text{interior}}$ was applied to the precontrast data ${\mathbf{V}}_{\mathrm{pre}}$ to obtain the interior volume of the breast ${\mathbf{V}}_{\text{interior}}$. Extracted vessels from step 2 were also excluded.
• 2.A fuzzy C-means clustering method³⁶ was applied to ${\mathbf{V}}_{\text{interior}}$ to separate fat tissue from fibroglandular tissue.²³ The voxels in ${\mathbf{V}}_{\text{interior}}$ were clustered into six clusters according to their intensities. The clusters whose centers had intensities larger than a preset threshold (30% of the maximum intensity) were classified as fibroglandular tissue. Note that the cluster number and threshold value may need to be adjusted according to different datasets.
• 3.The extracted binary fibroglandular volume was then closed with a small solid sphere to remove holes and sharp corners and filtered with a median filter to smooth the structures. Isolated small structures were removed as well. The binary fat volume was created by subtracting the binary fibroglandular volume from the interior mask ${\mathbf{B}}_{\text{interior}}$.

This procedure created a binary fat volume ${\mathbf{B}}_{\text{fat}}$ and a binary fibroglandular volume ${\mathbf{B}}_{\mathrm{fibro}}$.

4. Results

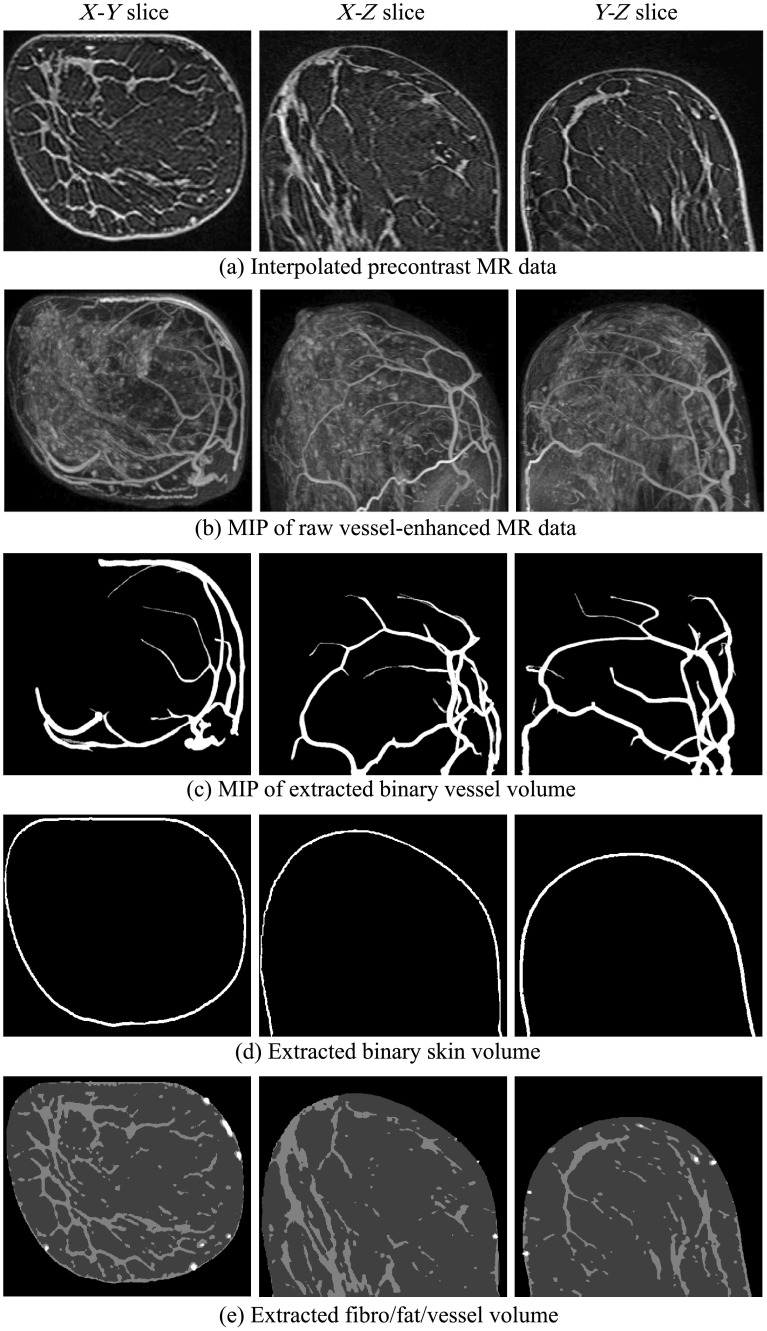
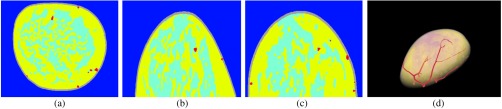
In this section, examples of numerical breast phantoms produced using the proposed methodology are presented. Specifically, three numerical phantoms were created from three patients’ MR data. Each example represents a different BI-RADS breast density level: scattered fibroglandular level (patient 1), heterogeneously dense level (patient 2), and extremely dense level (patient 3). The extracted binary volumes of blood vessels, skin, fat, and fibroglandular tissue for each case are shown in Figs. 4–6, respectively. The generated segmented-tissue phantoms along with their 3-D rendered views are shown in Figs. 7–9. Because the optical and acoustic phantoms all have the same structures and visual appearances as their corresponding segmented-tissue phantoms, differing only in their units and absolute values, these phantoms are not displayed here.

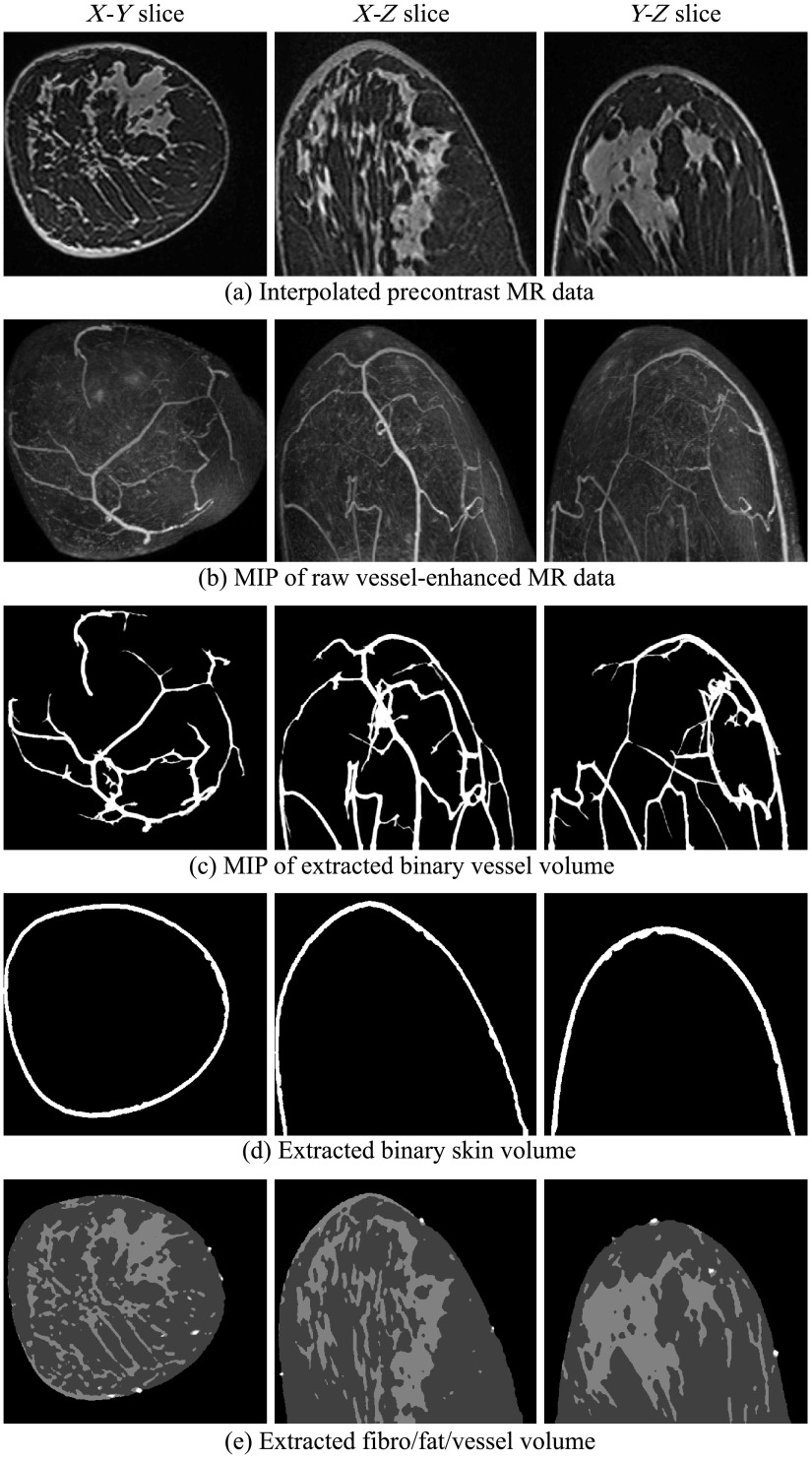
Fig. 4.

Extracted blood vessels, skin, fat, and fibroglandular tissues from patient 1, with scattered fibroglandular breasts. Colors in (e): white, vessel; light gray, fibroglandular; dark gray, fat.

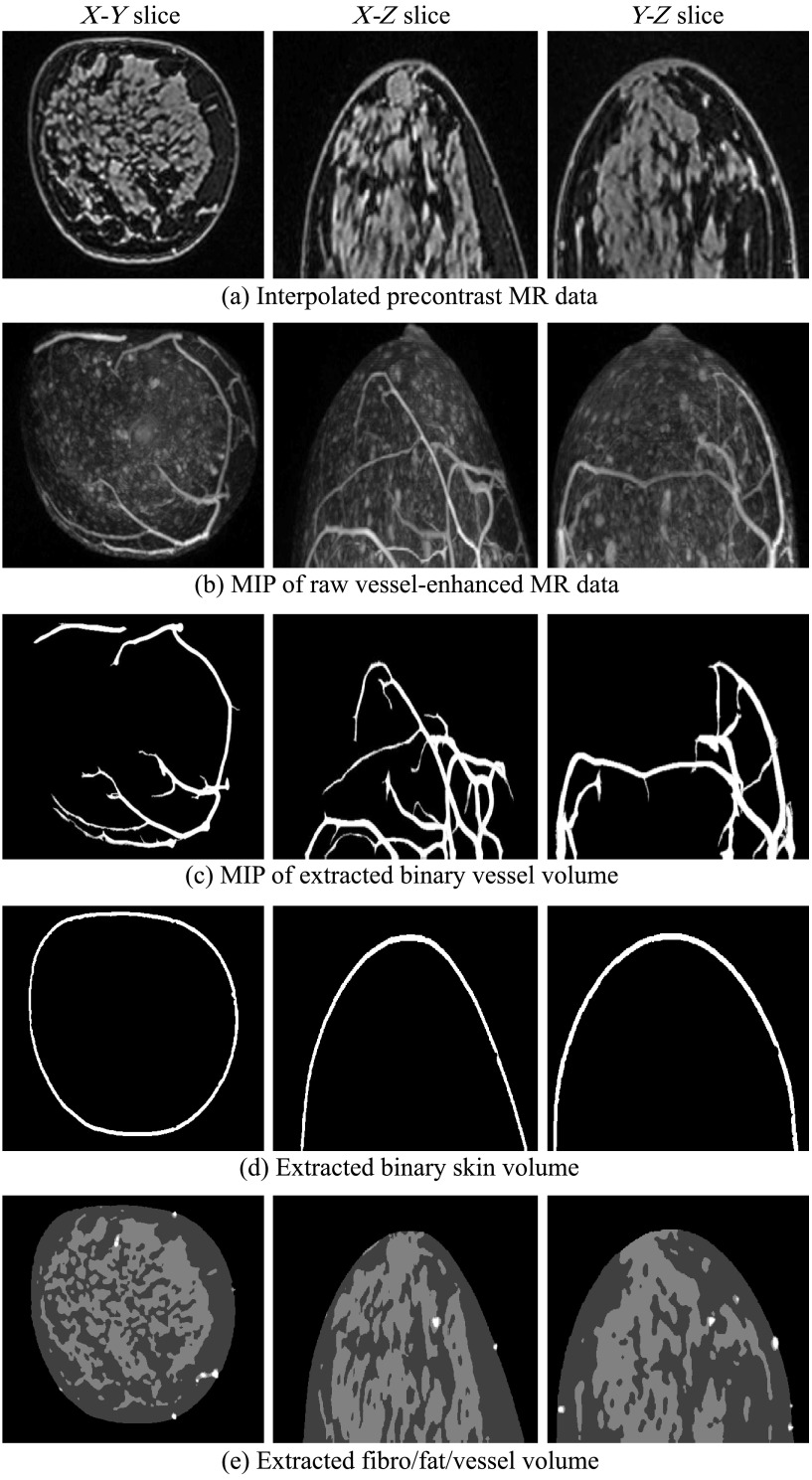
Fig. 5.

Extracted blood vessels, skin, fat, and fibroglandular tissues from patient 2, with heterogeneously dense breasts. Colors in (e): white, vessel; light gray, fibroglandular; dark gray, fat.

Fig. 6.

Extracted blood vessels, skin, fat, and fibroglandular tissues from patient 3, with extremely dense breasts. Colors in (e): white, vessel, light gray, fibroglandular, dark gray, fat.

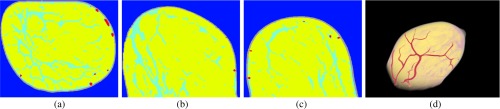
Fig. 7.

From left to right: the $X\text{-}Y$ slice, $X\text{-}Z$ slice, $Y\text{-}Z$ slice, and the 3-D rendered view of the segmented-tissue phantom for patient 1, with scattered fibroglandular breasts.

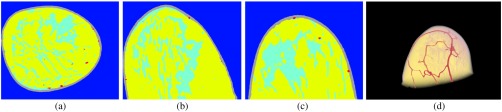
Fig. 8.

From left to right: the $X\text{-}Y$ slice, $X\text{-}Z$ slice, $Y\text{-}Z$ slice, and the 3-D rendered view of the segmented-tissue phantom for patient 2, with heterogeneously dense breasts.

Fig. 9.

From left to right: the $X\text{-}Y$ slice, $X\text{-}Z$ slice, $Y\text{-}Z$ slice, and the 3-D rendered view of the segmented-tissue phantom for patient 3, with extremely dense breasts.

Figures 4–6 show intermediate outputs obtained following the first four steps in our methodology. Each figure depicts the outputs for one patient. The columns in Figs. 4–6 show, from left to right, either example slices of $X\text{-}Y$, $X\text{-}Z$, and $Y\text{-}Z$ planes or MIP images along the $Z$, $Y$, and $X$ directions, respectively. The rows in Figs. 4–6 show outputs at different stages of the breast phantom generation process. The first row shows slices of the precontrast MR data ${\mathbf{V}}_{\mathrm{pre}}$, obtained following the preprocessing step (step 1). The second row shows MIP images of the vessel-enhanced MR data ${\mathbf{V}}_{R\_\text{enhanced}}$, which represents the difference between the averaged postcontrast MR data and the precontrast MR data. The third row shows MIP images of the extracted binary vessel volume ${\mathbf{B}}_{\text{vessel}}$. The second and third rows are both obtained as part of the vessel extraction step (step 2). The fourth row shows slices of the extracted binary skin volume ${\mathbf{B}}_{\text{skin}}$, which is the output at the end of the skin extraction step (step 3). Finally, the fifth row shows slices indicating the segmentation of fat and fibroglandular tissues, obtained following the fat/fibroglandular extraction step (step 4). For ease of visualization, the binary volumes generated by this step, ${\mathbf{B}}_{\text{fat}}$ and ${\mathbf{B}}_{\mathrm{fibro}}$, along with the vessel volume ${\mathbf{B}}_{\text{vessel}}$ from step 2, are combined into a single grayscale volume. The vessels are shown in white, the fibroglandular tissue is shown in light gray, and the fatty tissue is shown in dark gray. Comparison with the original MR data shows that the proposed method accurately extracts different tissue types for breasts with various density types.

Figures 7–9 show the results of the fifth step in our methodology. As mentioned above, for sake of brevity, the segmented-tissue phantoms are shown in lieu of the optical and acoustic phantoms themselves. The first three columns in each figure show the same example $X\text{-}Y$, $X\text{-}Z$, and $Y\text{-}Z$ slices as in Figs. 4–6. The final column shows a 3-D rendered view of the segmented-tissue phantom. For the tissue types in the first three columns, vessels are shown in red, skin in gray, fat in yellow, and fibroglandular in light blue. The colors in the 3-D rendered views for all the tissues are the same except that fibroglandular is now shown in light pink. The generated segmented-tissue phantoms display close representations of the realistic anatomical structures of the breast indicated in the original MR data.

5. PACT Simulation Employing the Generated Phantoms

A PACT computer-simulation study employing one of the numerical breast phantoms was performed to demonstrate the usefulness of the phantoms in comparing different image reconstruction methods.

The phantom generated from patient 1 was chosen for the study. The assigned optical and acoustic properties for the phantom are given in Table 1. These values were chosen from the literature.^37,38 The optical properties were chosen for a wavelength of 760 nm. While the 3-D phantom permits both the optical and acoustic simulations to be performed in 3-D, a 2-D acoustic simulation was employed for expediency. The measured data recorded by a collection of ultrasonic transducers arranged on a 2-D ring surrounding the breast were simulated in two steps. First, a 3-D optical simulation was performed to estimate the photoacoustically induced initial pressure distribution. Second, a slice from this 3-D volume was selected, and a 2-D acoustic simulation was performed to propagate the initial pressure distribution forward in time to obtain the pressure field at each transducer location.

Table 1.

Optical and acoustic property values used in simulation.

Tissue type	${\mu }_{\mathrm{a}}$ (${\mathrm{cm}}^{-1}$)	${\mu }_{\mathrm{s}}$ (${\mathrm{cm}}^{-1}$)	$g$	$n$	Sound speed (m/s)	Density ($\mathrm{kg}/{\mathrm{m}}^3$)
Background (water)	0	0	0.99	1.33	1500	1000
Blood vessel	9	179	0.975	1.38	1584	1040
Skin	0.08	500	0.99	1.40	1650	1150
Fat	0.05	159	0.95	1.40	1470	937
Fibroglandular	0.04	133	0.95	1.40	1515	1040

Note: ${\mu }_{\mathrm{a}}$, optical absorption coefficient; ${\mu }_{\mathrm{s}}$, optical scattering coefficient; $g$, scattering anisotropy; $n$, refractive index.

The 3-D optical simulation was performed using a GPU-accelerated Monte Carlo (MC) method.³⁹ The initial pressure distribution was calculated as the product of absorbed optical energy density, given by the MC simulation, and the Grueneiser parameter, which was assumed to be a constant. The simulation volume was $94.8\times 160.6\times 4{\mathrm{mm}}^3$ with a voxel size of 0.2 mm. Light was delivered via four slit-shaped illuminations that enclosed the central $X\text{-}Y$ plane ($z=0\mathrm{mm}$).

The $z=0\mathrm{mm}$ slice was selected for the 2-D simulation study. The transducer ring had a radius of 100 mm and was consisted of 512 equally spaced transducer elements. The pressure was simulated using the k-Wave toolbox⁴⁰ for a record time of $200\mu \mathrm{s}$ at a sampling frequency of 50 MHz. When generating the forward pressure, a pixel size of 0.1 mm was employed. No stochastic noise was added to the measured data.

The initial pressure distribution was reconstructed using the full-wave iterative image reconstruction method described by Huang et al.¹² No regularization was employed. To avoid inverse crime,⁴¹ different temporal and spatial sampling rates were employed for the reconstruction as compared with the generation of the measurement data. For the reconstruction, a pixel size of 0.2 mm and a temporal sampling rate of 25 MHz were employed.

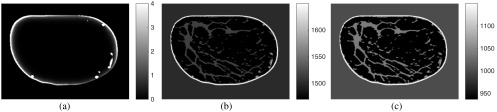
Two variants of this reconstruction approach were considered. In the first, the acoustic properties were chosen to be homogeneous with values equal to their corresponding background values. In the second, the acoustic properties of the medium were set to their true values. The initial pressure distribution along with the speed of sound and density distributions is shown in Fig. 10. Note that in the initial pressure distribution, only superficial blood vessels are visible. This is partly due to the limited light penetration within the breast. The reconstructed images, after 40 iterations, are shown in Fig. 11. From these results, we see that failure to compensate for acoustic heterogeneities can result in errors in the estimated initial pressure distribution. This is consistent with previous studies^7–10,12 that have demonstrated that consideration of the acoustic properties of the medium is necessary for accurate PACT image reconstruction.

Fig. 10.

(a) Initial pressure distribution computed from the MC simulation. (b) Speed of sound distribution, with units of m/s. (c) Density distribution, with units of ${\mathrm{kg}/\mathrm{m}}^3$.

Fig. 11.

Reconstructed images from the PACT simulation study. (a) Reconstructed image assuming homogeneous acoustic properties. (b) Reconstructed image with true acoustic properties. (c) Profile plot of the phantom and reconstructed images through a vessel structure.

6. Summary

In this work, we proposed a computational methodology for generating 3-D optical and acoustic breast phantoms from contrast-enhanced MR data for use in PACT and USCT. The generated phantoms depict the skin layer, vascular structures, and the volumetric distribution of different tissue types in the breast. Examples of generated phantoms were presented.

The generated phantoms can be employed to facilitate many simulation tasks. In addition to the PACT validation study performed in this paper, another example is the computation of task-based measures. It is advocated in the modern imaging science literature to utilize task-based measures of imaging system performance to guide the optimization of system design and image reconstruction algorithms^18,42–44 to produce images that are not simply visually attractive, but are the most informative with respect to the diagnostic task at hand. For the computed task-based measures to be informative not only for a specific subject but also for a general patient population, the structural variations in breasts across different patients need to be taken into consideration. This cannot be achieved using simple phantoms made from blobs or cylinders, which do not accurately reflect the complex structures in the breast. Our method provides a viable and convenient way for generating an ensemble of breast phantoms that include structural variations across different people, thereby enabling more reliable task-based measures to be computed for breast imaging research.

This work also has certain limitations. First, the phantoms in this study correspond to breasts in a free-hanging position. Some imaging systems may arrange the breast in other positions or may require the breast to be compressed during the imaging procedure. In these cases, the generated phantoms need to be carefully adjusted and distorted to compensate for the change in breast shape. Second, in our study, MR data from healthy patients were employed, and as a result, the methodology does not consider the segmentation of tumors nor their inclusion in the produced phantoms. Segmenting tumors from MR breast data remains an area for future work. For simulation studies that involve tumors, artificial synthetic tumors can be manually inserted into our phantoms.

Biographies

Yang Lou received his BS degree from Tsinghua University in 2012. He is currently a PhD candidate under the supervision of Dr. Mark A. Anastasio at Washington University in St. Louis. His research focuses on modern reconstruction algorithms for medical imaging, breast cancer imaging, and application of Bayesian approaches and deep learning in medical imaging.

Weimin Zhou received his BS degree from Beijing University of Posts and Telecommunications in 2014, and his MS degree from Washington University in St. Louis in 2016. He is currently a PhD candidate under the supervision of Dr. Mark A. Anastasio at Washington University in St. Louis. His research focuses on X-ray phase contrast imaging and advanced algorithms for image reconstruction.

Thomas P. Matthews received his BE and AB degrees from Dartmouth College in 2009 and 2008, and his MS degree from Washington University in St. Louis in 2013. He is currently a PhD candidate and a research assistant in Dr. Mark A. Anastasio’s laboratory at Washington University in St. Louis. His research focuses on image reconstruction algorithms for ultrasound computed tomography and photoacoustic computed tomography with applications for breast imaging and small animal imaging.

Catherine M. Appleton is Chief of Breast Imaging and an associate professor of Radiology at the Mallinckrodt Institute of Radiology at Washington University School of Medicine in St. Louis. Her clinical practice focuses on multimodality breast imaging and image-guided breast intervention. She is active in the American College of Radiology, the Society of Breast Imaging and the Radiological Society of North America.

Mark A. Anastasio earned his PhD at the University of Chicago in 2001. He is currently a professor of biomedical engineering at Washington University in St. Louis (WUSTL). His research interests include tomographic image reconstruction, imaging physics, and the development of novel computed biomedical imaging systems. He is an internationally recognized expert in the fields of imaging science, phase-contrast x-ray imaging, and photoacoustic computed tomography.

Disclosures

No conflicts of interest, financial or otherwise, are declared by the authors.