Threshold Dynamics in Stochastic SIRS Epidemic Models with Nonlinear Incidence and Vaccination

Abstract

In this paper, the dynamical behaviors for a stochastic SIRS epidemic model with nonlinear incidence and vaccination are investigated. In the models, the disease transmission coefficient and the removal rates are all affected by noise. Some new basic properties of the models are found. Applying these properties, we establish a series of new threshold conditions on the stochastically exponential extinction, stochastic persistence, and permanence in the mean of the disease with probability one for the models. Furthermore, we obtain a sufficient condition on the existence of unique stationary distribution for the model. Finally, a series of numerical examples are introduced to illustrate our main theoretical results and some conjectures are further proposed.

1. Introduction

As is well known, transmissions of many infectious diseases are inevitably affected by environment white noise, which is an important component in realism, because it can provide some additional degrees of realism compared to their deterministic counterparts. Therefore, in recent years, stochastic differential equation (SDE) has been used widely by many researchers to model the dynamics of spread of infectious disease (see [1–5] and the references cited therein). There are different possible approaches to include effects in the model. Here, we mainly introduce three approaches. The first one is through time Markov chain model to consider environment noise in SIS model (see, e.g., [6] and the references cited therein). The second is with parameters perturbation (see [2, 5, 7] and the references cited therein). The last issue to model stochastic epidemic system is to perturb around the positive equilibria of deterministic models (see, e.g., [1, 8, 9] and the references cited therein).

Now, we consider stochastic epidemic models with parameters perturbation. The incidence rate of a disease denotes the number of new cases per unit time, and this plays an important role in the study of mathematical epidemiology. In many epidemic models, the bilinear incidence rate βSI is frequently used (see [2, 5, 7, 8, 10–17]), and the saturated incidence rate βSI/(1 + aI) is also frequently used (see, e.g., [18–22]). Comparing with bilinear incidence rate and saturated incidence rate, Lahrouz and Omari [23] and Liu and Chen [24] introduced a nonlinear incidence rate βSI/φ(I) into stochastic SIRS epidemic models. In [25], Tang et al. investigated a class of stochastic SIRS epidemic models with nonlinear incidence rate βf(S)g(I):

$$\begin{array}{c}dS=\left(\mathrm{\Lambda }-\beta f\left(S\right)g\left(I\right)-\mu S+\delta R\right)dt\\ -\sigma f\left(S\right)g\left(I\right)dB\left(t\right),\\ dI=\left(\beta f\left(S\right)g\left(I\right)-\left(\mu +\alpha +\gamma \right)I\right)dt\\ +\sigma f\left(S\right)g\left(I\right)dB\left(t\right),\\ dR=\left(\gamma I-\left(\mu +\delta \right)R\right)dt.\\ \end{array}$$ (1)

Lahrouz et al. [26] studied a deterministic SIRS epidemic model with nonlinear incidence rate βSI/φ(I) and vaccination. If the transmission of the disease is changed by nonlinear incidence rate βf(S)g(I), and to make the model more realistic, let us suppose that the death rates of the three classes in the population are different, then a more general deterministic SIRS model is described by the following ordinary differential equation:

$$\begin{array}{c}\dot{S}=\left(\mathrm{1}-q\right)\mathrm{\Lambda }-\beta f\left(S\right)g\left(I\right)-\left(d_S+p\right)S+\epsilon R,\\ \\ \dot{I}=\beta f\left(S\right)g\left(I\right)-\left(d_I+\gamma \right)I,\\ \\ \dot{R}=q\mathrm{\Lambda }+pS+\gamma I-\left(d_R+\epsilon \right)R,\\ \end{array}$$ (2)

where S(t), I(t), and R(t) denote the numbers of susceptible, infectious, and recovered individuals at time t, respectively. Λ denote a constant input of new members into the susceptible per unit time. q is the rate of vaccination for the new members. p is the rate of vaccination for the susceptible individuals. d_S is the natural mortality rate or the removal rate of the S. d_I is the removal rate of the infectious and usually is the sum of natural mortality rate and disease-induced mortality rate. d_R is the removal rate of the recovered individual. γ is the recovery rate of infective individual. ε is the rate at which the recovered individual loses immunity. β represents the transmission coefficient between compartments S and I, and βf(S)g(I) denotes the incidence rate of the disease. For biological reasons, we usually assume that functions f(S) and g(I) satisfy the following properties:

• (H₁)g(I) is two-order continuously differentiable function; g(I)/I is monotonically nondecreasing with respect to I; g(0) = 0 and g′(0) > 0.
•  (H₂)f(S) is two-order continuously differentiable function; f′(S) ≥ 0 and f′′(S) ≤ 0 for all S ≥ 0, and f(0) = 0.

It is well known that the basic reproduction number for model (2) is defined by R₀ = βf(S₀)g′(0)/(d_I + γ), where S₀ = [(1 − q)d_R + ε]Λ/(d_S(d_R + ε) + pd_R). Applying the Lyapunov function method and the theory of persistence for dynamical systems, we can prove that, when R₀ < 1, model (2) has a globally asymptotically stable disease-free equilibrium E₀ = (S₀, 0, R₀) and, when R₀ > 1, model (2) has a unique endemic equilibrium E^∗(S^∗, I^∗, R^∗) and disease I is permanent.

In this paper, we extend model (1) to more general cases. As in [11], taking into account the effect of randomly fluctuating environment, we assume that fluctuations in the environment will manifest themselves mainly as fluctuations in parameters β, d_S, d_I, and d_R in model (2) change to random variables $\tilde{\beta }$, ${\tilde{d}}_S$, ${\tilde{d}}_I$, and ${\tilde{d}}_R$ such that

$$\begin{array}{c}\tilde{\beta }=\beta +{\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}}_{\mathrm{0}},\\ \\ {\tilde{d}}_S=d_S+{\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}}_{\mathrm{1}},\\ \\ {\tilde{d}}_I=d_I+{\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}}_{\mathrm{2}},\\ \\ {\tilde{d}}_R=d_R+{\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}}_{\mathrm{3}}.\\ \end{array}$$ (3)

Accordingly, model (2) becomes

$$\begin{array}{c}dS=\left(\left(\mathrm{1}-q\right)\mathrm{\Lambda }-\beta f\left(S\right)g\left(I\right)-\left(d_S+p\right)S+\epsilon R\right)dt\\ -f\left(S\right)g\left(I\right){\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}}_{\mathrm{0}}\hspace{0.17em}dt-S\hspace{0.17em}{\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}}_{\mathrm{1}}\hspace{0.17em}dt,\\ dI=\left(\beta f\left(S\right)g\left(I\right)-\left(d_I+\gamma \right)I\right)dt\\ +f\left(S\right)g\left(I\right){\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}}_{\mathrm{0}}\hspace{0.17em}dt-I\hspace{0.17em}{\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}}_{\mathrm{2}}\hspace{0.17em}dt,\\ dR=\left(q\mathrm{\Lambda }+pS+\gamma I-\left(d_R+\epsilon \right)R\right)dt-R\hspace{0.17em}{\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}}_{\mathrm{3}}\hspace{0.17em}dt.\\ \end{array}$$ (4)

By the central limit theorem, the error term error_i dt (0 ≤ i ≤ 3) may be approximated by a normal distribution with zero mean and variance σ_i²dt (0 ≤ i ≤ 3), respectively. That is, ${\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}}_i\hspace{0.17em}dt=\tilde{N}(\mathrm{0},{\sigma }_i^{\mathrm{2}}dt)$. Since these error_i dt may correlate with each other, we represent them by l-dimensional Brownian motion B(t) = (B₁(t),…, B_l(t)) as follows:

$$\begin{array}{c}{\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}}_i\hspace{0.17em}dt={\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{ij}d{B}_j\left(t\right),\mathrm{0}\le i\le \mathrm{3},\end{array}$$ (5)

where σ_ij are all nonnegative real numbers. Therefore, model (4) is characterized by the following Itô stochastic differential equation:

$$\begin{array}{c}dS=\left(\left(\mathrm{1}-q\right)\mathrm{\Lambda }-\beta f\left(S\right)g\left(I\right)-\left(d_S+P\right)S+\epsilon R\right)dt\\ -f\left(S\right)g\left(I\right){\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}d{B}_j\left(t\right)-S{\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{1}j}d{B}_j\left(t\right),\\ dI=\left(\beta f\left(S\right)g\left(I\right)-\left(d_I+\gamma \right)I\right)dt\\ +f\left(S\right)g\left(I\right){\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}d{B}_j\left(t\right)-I{\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{2}j}d{B}_j\left(t\right),\\ dR=\left(q\mathrm{\Lambda }+pS+\gamma I-\left(d_R+\epsilon \right)R\right)dt\\ -R{\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{3}j}d{B}_j\left(t\right).\end{array}$$ (6)

Model (6) in the special case where f(S) = S, g(I) = I, and p = q = 0 has been investigated by Yang and Mao in [11] and in the special case where σ_1j = σ_2j = σ_3j = 0  (1 ≤ j ≤ l) and p = q = 0 also has been discussed in [25]. It is well known that, in a stochastic epidemic model, the dynamical behaviors, like the extinction, persistence, stationary distribution, and stability of the model, are the most interesting topics. Therefore, in this paper, as an important extension and improvement of the results given in [11, 25], we aim to discuss the dynamical behaviors of model (6). Particularly, we will explore the stochastic extinction and persistence in the mean of disease with probability one and the existence of stationary distribution.

This paper is organized as follows. In Section 2, we introduce some preliminaries to be used in later sections. In Section 3, we establish the threshold condition for stochastic extinction of disease with probability one of model (6). In Section 4, we deduce the threshold conditions for the disease being stochastically persistent and permanent in the mean with probability one. In Section 5, we discuss the existence of the stationary distribution of model (6) under some sufficient conditions. In Section 6, the numerical simulations are presented to illustrate the main results obtained in this paper and some conjectures are further proposed. Finally, in Section 7, a brief conclusion is given.

2. Preliminaries

Through this paper, we let (Ω, ℱ, {ℱ_t}_t≥0, P) be a complete probability space with a filtration {ℱ_t}_t≥0 satisfying the usual conditions (that is, it is right continuous and increasing while ℱ₀ contains all P-null sets). In this paper, we always assume that stochastic model (6) is defined on probability space (Ω, ℱ, {ℱ_t}_t≥0, P). Furthermore, we denote R₊³ = {(x, y, z) : x > 0, y > 0, z > 0}, σ_i² = ∑_j=1^lσ_ij², 0 ≤ i ≤ 3, and σ² = ∑_i=0³σ_i².

Firstly, on the existence and uniqueness of global positive solution for model (4) we have the following result.

Lemma 1 . —

Assume that (H₁) and (H₂) hold; then, for any initial value (S(0), I(0), R(0)) ∈ R₊³, model (6) has a unique solution (S(t), I(t), R(t)) defined for all t ≥ 0, and the solution will remain in R₊³ with probability one.

This lemma can be proved by using a similar argument as in the proof of Theorem 3.1 given in [11]. We hence omit it here.

Lemma 2 . —

Assume that (H₁) and (H₂) hold and let (S(t), I(t), R(t)) be the solution of model (6) with initial value (S(0), I(0), R(0)) ∈ R₊³. Then lim sup_t→∞(S(t) + I(t) + R(t)) < ∞  a.s. Moreover, let h(x, y, z) be any continuous function defined on R₊³; then for each 1 ≤ j ≤ l we have

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}h\left(S\left(s\right),I\left(s\right),R\left(s\right)\right)d{B}_j\left(s\right)=\mathrm{0}.\end{array}$$ (7)

Proof —

Let N(t) = S(t) + I(t) + R(t); then we have from model (6)

$$\begin{array}{c}dN\left(t\right)\left(\mathrm{\Lambda }-d_{S}S\left(t\right)-d_{I}I\left(t\right)-d_{R}R\left(t\right)\right)dt-P\left(t\right)\\ \le \left(\mathrm{\Lambda }-\mu N\left(t\right)\right)dt-P\left(t\right),\end{array}$$ (8)

where μ = min {d_S, d_I, d_R} and P(t) = ∑_j=1^l(σ_1jS(t) + σ_2jI(t) + σ_3jR(t))dB_j(t). By the comparison theorem of stochastic differential equations, we further have

$$\begin{array}{c}N\left(t\right)\le N\left(\mathrm{0}\right)e^{-\mu t}+\frac{\mathrm{\Lambda }}{\mu }\left(\mathrm{1}-e^{-\mu t}\right)-Q\left(t\right),\end{array}$$ (9)

where

$$\begin{array}{c}Q\left(t\right)={\displaystyle \sum }_{j=\mathrm{1}}^l\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-\mu \left(t-s\right)}\left({\sigma }_{\mathrm{1}j}S\left(s\right)+{\sigma }_{\mathrm{2}j}I\left(s\right)+{\sigma }_{\mathrm{3}j}R\left(s\right)\right)d{B}_j\left(s\right).\end{array}$$ (10)

Define X(t) = N(0) + A(t) − U(t) − Q(t), where A(t) = (Λ/μ)(1 − e^−μt) and U(t) = N(0)(1 − e^−μt). It is clear that from Lemma 1 and (9) X(t) is nonnegative for t ≥ 0, and A(t) and U(t) are continuous adapted increasing processes for t ≥ 0 and A(0) = U(0) = 0. Therefore, by Theorem 3.9 given in [27], we obtain that lim_t→∞X(t) < ∞  a.s. exists. From (9), we further have

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{limsup}}\hspace{0.17em}N\left(t\right)<\infty \text{\hspace{0.17em}\hspace{0.17em}a.s}.\end{array}$$ (11)

Denote

$$\begin{array}{c}{M}_j\left(t\right)=\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}h\left(S\left(s\right),I\left(s\right),R\left(s\right)\right)d{B}_j\left(s\right).\end{array}$$ (12)

By (11), we have

$$\begin{array}{c}\frac{\mathrm{1}}{t}〈M_j,M_j〉\left(t\right)\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{\left(h\left(S\left(s\right),I\left(s\right),R\left(s\right)\right)\right)}^{\mathrm{2}}ds\\ \le \underset{t\ge \mathrm{0}}{\mathrm{s}\mathrm{u}\mathrm{p}}\left\{{\left(h\left(S\left(t\right),I\left(t\right),R\left(t\right)\right)\right)}^{\mathrm{2}}\right\}<\infty .\end{array}$$ (13)

Hence, the strong law of large number (see [27, 28]) implies lim_t→∞(1/t)M_j(t) = 0  a.s. This completes the proof.

For any function h(t) defined on R₊₀ = [0, +∞), we denote the average value on [0, t] by 〈h(t)〉 = (1/t)∫₀^th(s)ds.

Lemma 3 . —

Assume that (H₁) and (H₂) hold. Let (S(t), I(t), R(t)) be any positive solution of model (6); then

$$\begin{array}{c}〈S\left(t\right)〉=\frac{\left[\left(\mathrm{1}-q\right)d_R+\epsilon \right]\mathrm{\Lambda }}{d_S\left(d_R+\epsilon \right)+p{d}_R}\\ -\frac{d_I\left(d_R+\epsilon \right)+d_R\gamma }{d_S\left(d_R+\epsilon \right)+p{d}_R}〈I\left(t\right)〉+\phi \left(t\right),\end{array}$$ (14)

where function φ(t) is defined for all t ≥ 0 satisfying lim_t→∞φ(t) = 0.

Proof —

Taking integration from 0 to t for model (6), we get

$$\begin{array}{c}\frac{S\left(t\right)-S\left(\mathrm{0}\right)}{t}\\ =\left(\mathrm{1}-q\right)\mathrm{\Lambda }-\beta 〈S\left(t\right)g\left(I\left(t\right)\right)〉-\left(d_S+p\right)〈S\left(t\right)〉\\ +\epsilon 〈R\left(t\right)〉\\ -\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{\displaystyle \sum }_{j=\mathrm{1}}^l\left(S\left(s\right)g\left(I\left(s\right)\right){\sigma }_{\mathrm{0}j}+S\left(s\right){\sigma }_{\mathrm{1}j}\right)d{B}_j\left(s\right),\\ \frac{I\left(t\right)-I\left(\mathrm{0}\right)}{t}\\ =\beta 〈S\left(t\right)g\left(I\left(t\right)\right)〉-\left(d_I+\gamma \right)〈I\left(t\right)〉\\ +\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{\displaystyle \sum }_{j=\mathrm{1}}^l\left(S\left(s\right)g\left(I\left(s\right)\right){\sigma }_{\mathrm{0}j}-I\left(s\right){\sigma }_{\mathrm{2}j}\right)d{B}_j\left(s\right),\\ \frac{R\left(t\right)-R\left(\mathrm{0}\right)}{t}\\ =q\mathrm{\Lambda }+\gamma 〈I\left(t\right)〉+p〈S\left(t\right)〉-\left(d_R+\epsilon \right)〈R\left(t\right)〉\\ -\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{\displaystyle \sum }_{j=\mathrm{1}}^{l}R\left(s\right){\sigma }_{\mathrm{3}j}d{B}_j\left(s\right).\end{array}$$ (15)

Hence, we have

$$\begin{array}{c}\left(d_R+\epsilon \right)\left(\frac{S\left(t\right)-S\left(\mathrm{0}\right)}{t}+\frac{I\left(t\right)-I\left(\mathrm{0}\right)}{t}\right)+\epsilon \\ ·\frac{R\left(t\right)-R\left(\mathrm{0}\right)}{t}=\left[\left(\mathrm{1}-q\right)d_R+\epsilon \right]\mathrm{\Lambda }-\left(d_S\left(d_R+\epsilon \right)+p{d}_R\right)〈S\left(t\right)〉-\left[d_I\left(d_R+\epsilon \right)+d_R\gamma \right]〈I\left(t\right)〉-\frac{\mathrm{1}}{t}\\ ·\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{\displaystyle \sum }_{j=\mathrm{1}}^N\left[\left(d_R+\epsilon \right)\left(S\left(s\right){\sigma }_{\mathrm{1}j}+I\left(s\right){\sigma }_{\mathrm{2}j}\right)+\epsilon R\left(s\right){\sigma }_{\mathrm{3}j}\right]d{B}_j\left(s\right).\end{array}$$ (16)

With a simple calculation from (16) we can easily obtain formula (14) with which φ(t) is defined by

$$\begin{array}{c}\phi \left(t\right)=-\frac{\mathrm{1}}{d_S\left(d_R+\epsilon \right)+p{d}_R}\left[\left(d_R+\epsilon \right)·\left(\frac{S\left(t\right)-S\left(\mathrm{0}\right)}{t}+\frac{I\left(t\right)-I\left(\mathrm{0}\right)}{t}\right)+\epsilon \frac{R\left(t\right)-R\left(\mathrm{0}\right)}{t}+\frac{\mathrm{1}}{t}·\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{\displaystyle \sum }_{j=\mathrm{1}}^l\left[\left(d_R+\epsilon \right)\left(S\left(s\right){\sigma }_{\mathrm{1}j}+I\left(s\right){\sigma }_{\mathrm{2}j}\right)+\epsilon R\left(s\right){\sigma }_{\mathrm{3}j}\right]d{B}_j\left(s\right)\right].\end{array}$$ (17)

By Lemma 2, we further have lim_t→∞φ(t) = 0  a.s.

Lemma 4 . —

Assume that (H₁) and (H₂) hold and σ_1j = σ_2j = σ_3j = 0  (1 ≤ j ≤ l). Then, for any solution (S(t), I(t), R(t)) of system (6) with (S(0), I(0), R(0)) ∈ R₊³, one has

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{limsup}}\left(S\left(t\right)+I\left(t\right)+R\left(t\right)\right)\le \overline{S},\mathit{\text{\hspace{0.17em}\hspace{0.17em}a.s.}},\end{array}$$ (18)

where $\overline{S}=\Lambda /\mu$. Furthermore, the region

$$\begin{array}{c}\mathrm{\Gamma }=\left\{\left(S,I,R\right):S>\mathrm{0},I>\mathrm{0},R>\mathrm{0},S+I+R\le \overline{S}\mathit{\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}a.s.}}\right\}\end{array}$$ (19)

is positive invariant with probability one for model (6), where μ = min⁡{d_S, d_I, d_R}.

In fact, for N(t) = S(t) + I(t) + R(t), from model (6) we have

$$\begin{array}{c}dN\left(t\right)\left(\mathrm{\Lambda }-d_{S}S\left(t\right)-d_{I}I\left(t\right)-d_{R}R\left(t\right)\right)dt\\ \le \left(\mathrm{\Lambda }-\mu N\left(t\right)\right)dt,\text{\hspace{0.17em}\hspace{0.17em}a.s}.\end{array}$$ (20)

This implies that (18) holds, and set Γ is positive invariant with probability one for model (6).

Lemma 5 . —

Assume that (H₁) and (H₂) hold, σ_1j = σ_2j = σ_3j = 0  (1 ≤ j ≤ l), d_S = d_R, and d_I = d_S + α with constant α ≥ 0. Then, for any solution (S(t), I(t), R(t)) of model (6) with (S(0), I(0), R(0)) ∈ R₊³, one has

$$\begin{array}{c}S\left(t\right)=\frac{\mathrm{\Lambda }\left[\left(\mathrm{1}-q\right)d_S+\epsilon \right]}{d_S\left(d_S+\epsilon +p\right)}+H\left(t\right)+G\left(t\right),\mathit{\text{\hspace{0.17em}\hspace{0.17em}a.s}}.\\ \forall t\ge \mathrm{0},\end{array}$$ (21)

where

$$\begin{array}{c}H\left(t\right)=\frac{p\mathrm{\Lambda }\left[\left(\mathrm{1}-q\right)d_S+\epsilon \right]}{d_S\left(d_S+\epsilon \right)\left(d_S+\epsilon +p\right)}{e}^{-\left(d_S+\epsilon +p\right)t}\\ -\left(R\left(\mathrm{0}\right)-\frac{q\mathrm{\Lambda }}{d_S+\epsilon }\right)\frac{\mathrm{1}}{p}\left(\mathrm{1}-e^{-pt}\right)e^{-\left(d_S+\epsilon \right)t}\\ +\left(\frac{\mathrm{\Lambda }}{d_S}-\left(S\left(\mathrm{0}\right)+I\left(\mathrm{0}\right)+R\left(\mathrm{0}\right)\right)\right)\\ ·\frac{\mathrm{1}}{p+\epsilon }\left(\mathrm{1}-e^{-\left(p+\epsilon \right)t}\right)e^{-d_{S}t},\end{array}$$ (22)

$$\begin{array}{c}G\left(t\right)=-I\left(t\right)-\alpha \underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-d_S\left(t-s\right)}I\left(s\right)ds\\ -\gamma \underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon \right)\left(t-s\right)}I\left(s\right)ds\\ +p\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon +p\right)\left(t-s\right)}I\left(s\right)ds+p\alpha \underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon +p\right)\left(t-s\right)}\\ ·\underset{\mathrm{0}}{\overset{s}{{\displaystyle \int }}}{e}^{-d_S\left(s-u\right)}I\left(u\right)du\hspace{0.17em}ds+p\gamma \underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon +p\right)\left(t-s\right)}\\ ·\underset{\mathrm{0}}{\overset{s}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon \right)\left(s-u\right)}I\left(u\right)du\hspace{0.17em}ds.\end{array}$$ (23)

Proof —

Since

$$\begin{array}{c}dN\left(t\right)=\left(\mathrm{\Lambda }-d_{S}N\left(t\right)-\alpha I\left(t\right)\right)dt,\text{\hspace{0.17em}\hspace{0.17em}a.s.},\end{array}$$ (24)

then

$$\begin{array}{c}N\left(t\right)=\frac{\mathrm{\Lambda }}{d_S}+\left(N\left(\mathrm{0}\right)-\frac{\mathrm{\Lambda }}{d_S}\right)e^{-d_{S}t}\\ -\alpha \underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-d_S\left(t-s\right)}I\left(s\right)ds,\text{\hspace{0.17em}\hspace{0.17em}a.s.},\end{array}$$ (25)

where N(0) = S(0) + I(0) + R(0). From the third equation of model (6) we have

$$\begin{array}{c}R\left(t\right)=\frac{q\mathrm{\Lambda }}{d_S+\epsilon }+\left(R\left(\mathrm{0}\right)-\frac{q\mathrm{\Lambda }}{d_S+\epsilon }\right)e^{-\left(d_S+\epsilon \right)t}\\ +p\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon \right)\left(t-s\right)}S\left(s\right)ds+\gamma \underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon \right)\left(t-s\right)}I\left(s\right)ds,\text{\hspace{0.17em}\hspace{0.17em}a.s.}\end{array}$$ (26)

Therefore,

$$\begin{array}{c}S\left(t\right)=\frac{\mathrm{\Lambda }\left[\left(\mathrm{1}-q\right)d_S+\epsilon \right]}{d_S\left(d_S+\epsilon \right)}-I\left(t\right)\\ -\left(R\left(\mathrm{0}\right)-\frac{q\mathrm{\Lambda }}{d_S+\epsilon }\right)e^{-\left(d_S+\epsilon \right)t}\\ +\left(N\left(\mathrm{0}\right)-\frac{\mathrm{\Lambda }}{d_S}\right)e^{-d_{S}t}\\ -p\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon \right)\left(t-s\right)}S\left(s\right)ds\\ -\alpha \underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-d_S\left(t-s\right)}I\left(s\right)ds-\gamma \underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon \right)\left(t-s\right)}I\left(s\right)ds.\end{array}$$ (27)

Let y(t) = ∫₀^te^{(d_S + ε)s}S(s)ds; then

$$\begin{array}{c}dy\left(t\right)=\left[e^{\left(d_S+\epsilon \right)t}S\left(t\right)\right]dt=\left[-py\left(t\right)+\frac{\mathrm{\Lambda }\left[\left(\mathrm{1}-q\right)d_S+\epsilon \right]}{d_S\left(d_S+\epsilon \right)}{e}^{\left(d_S+\epsilon \right)t}-I\left(t\right)e^{\left(d_S+\epsilon \right)t}-\left(R\left(\mathrm{0}\right)-\frac{q\mathrm{\Lambda }}{d_S+\epsilon }\right)+\left(N\left(\mathrm{0}\right)-\frac{\mathrm{\Lambda }}{d_S}\right)e^{\left(\epsilon \right)t}-\alpha e^{\epsilon t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{d_{S}s}I\left(s\right)ds-\gamma \underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{\left(d_S+\epsilon \right)s}I\left(s\right)ds\right]dt.\end{array}$$ (28)

Solving y(t), we obtain

$$\begin{array}{c}y\left(t\right)=e^{-pt}\left[\frac{\mathrm{\Lambda }\left[\left(\mathrm{1}-q\right)d_S+\epsilon \right]}{d_S\left(d_S+\epsilon \right)\left(d_S+\epsilon +p\right)}\left(e^{\left(d_S+\epsilon +p\right)t}-\mathrm{1}\right)-\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{\left(d_S+\epsilon +p\right)s}I\left(s\right)ds-\left(R\left(\mathrm{0}\right)-\frac{q\mathrm{\Lambda }}{d_S+\epsilon }\right)\frac{\mathrm{1}}{p}\left(e^{pt}-\mathrm{1}\right)+\left(N\left(\mathrm{0}\right)-\frac{\mathrm{\Lambda }}{d_S}\right)\frac{\mathrm{1}}{\epsilon +p}\left(e^{\left(\epsilon +p\right)t}-\mathrm{1}\right)-\gamma \underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{ps}\underset{\mathrm{0}}{\overset{s}{{\displaystyle \int }}}{e}^{\left(d_S+\epsilon \right)u}I\left(u\right)du\hspace{0.17em}ds-\alpha \underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{\left(d_S+\epsilon +p\right)s}\underset{\mathrm{0}}{\overset{s}{{\displaystyle \int }}}{e}^{-d_S\left(s-u\right)}I\left(u\right)ds\hspace{0.17em}ds\right]dt.\end{array}$$ (29)

Substituting (29) into (27), we immediately obtain (21)–(23). This completes the proof.

Remark 6 . —

When d_S ≠ d_R in model (6), whether we can also establish a similar result as in Lemma 5 still is an interesting open problem.

Consider the following n-dimensional stochastic differential equation:

$$\begin{array}{c}dx\left(t\right)=b\left(x\right)dt+{\displaystyle \sum }_{r=\mathrm{1}}^m{\sigma }_r\left(x\right)d{B}_r\left(t\right),\end{array}$$ (30)

where x = (x₁, x₂,…, x_n), σ_r(x) = (σ_r¹(x), σ_r²(x),…, σ_rⁿ(x)), and B_r(t)  (1 ≤ r ≤ m) are standard Brownian motions defined on the above probability space. The diffusion matrix is defined by

$$\begin{array}{c}A\left(x\right)={\left(a_{ij}\left(x\right)\right)}_{n\times n},\\ \\ a_{ij}\left(x\right)={\displaystyle \sum }_{r=\mathrm{1}}^m{\sigma }_r^i\left(x\right){\sigma }_r^j\left(x\right).\\ \end{array}$$ (31)

For any second-order continuously differentiable function V(x), we define

$$\begin{array}{c}LV\left(x\right)={\displaystyle \sum }_{i=\mathrm{1}}^n\frac{\partial V\left(x\right)}{\partial x_i}{b}_i\left(x\right)+\frac{\mathrm{1}}{\mathrm{2}}{\displaystyle \sum }_{i,j=\mathrm{1}}^n\frac{{\partial }^{\mathrm{2}}V\left(x\right)}{\partial x_i\partial x_j}{a}_{ij}\left(x\right).\end{array}$$ (32)

The following lemma gives a criterion for the existence of stationary distribution in terms of Lyapunov function.

Lemma 7 (see [27]). —

Assume that there is a bounded open subset D in Rⁿ with a regular (i.e., smooth) boundary such that

• (i)there exist some i = 1,2,…, n and positive constant η > 0 such that a_ii(x) ≥ η for all x ∈ D;
• (ii)there exists a nonnegative function V(x) : D^c → R such that V(x) is second-order continuously differentiable function and that, for some θ > 0, LV(x)≤−θ for all x ∈ D^c, where D^c = Rⁿ∖D.

Then (30) has a unique stationary distribution π. That is, if function f is integrable with respect to the measure π, then for all x₀ ∈ Rⁿ

$$\begin{array}{c}P\left\{\underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}f\left(x\left(u,x_{\mathrm{0}}\right)\right)du={{\displaystyle \int }}_{R^n}f\left(x_{\mathrm{0}}\right)\pi \left(d{x}_{\mathrm{0}}\right)\right\}\\ =\mathrm{1}.\end{array}$$ (33)

To study the permanence in mean with probability one of model (6) we need the following result on the stochastic integrable inequality.

Lemma 8 (see [13]). —

Assume that functions Y ∈ C(R₊ × Ω, R₊) and Z ∈ C(R₊ × Ω, R₊) satisfy lim_t→∞(Z(t)/t) = 0  a.s. If there is T > 0 such that

$$\begin{array}{c}\ln Y\left(t\right)\ge {\nu }_{\mathrm{0}}t-\nu \underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}Y\left(s\right)ds+Z\left(t\right)\mathit{\text{\hspace{0.17em}\hspace{0.17em}a.s.}},\end{array}$$ (34)

for all t ≥ T, then

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}\hspace{0.17em}\mathrm{i}\mathrm{n}\mathrm{f}}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}Y\left(s\right)ds\ge \frac{{\nu }_{\mathrm{0}}}{\nu }\mathit{\text{\hspace{0.17em}\hspace{0.17em}a.s.}}\end{array}$$ (35)

3. Extinction of Disease

For the convenience of following statements, we denote

$$\begin{array}{c}{S}_{\mathrm{0}}=\frac{\left[\left(\mathrm{1}-q\right)d_R+\epsilon \right]\mathrm{\Lambda }}{d_S\left(d_R+\epsilon \right)+p{d}_R},\\ \\ S_{\mathrm{1}}=\frac{d_I\left(d_R+\epsilon \right)+d_R\gamma }{d_S\left(d_R+\epsilon \right)+p{d}_R}.\\ \end{array}$$ (36)

We further define a threshold value

$$\begin{array}{c}{\tilde{R}}_{\mathrm{0}}=\frac{f\left(S_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)\left(\beta +{\sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)}{d_I+\gamma }\\ -\frac{{\left(f\left(S_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}}{\mathrm{2}\left(d_I+\gamma \right)}-\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}\left(d_I+\gamma \right)}.\end{array}$$ (37)

Theorem 9 . —

Assume that (H₁) and (H₂) hold. If one of the following conditions holds:

• (a)${\tilde{R}}_{\mathrm{0}}<\mathrm{1}$  and  σ₀²f(S₀)g′(0) ≤ β + ∑_j=1^lσ_0jσ_2j,
• (b)σ₀ > 0  and  (β + ∑_j=1^lσ_0jσ_2j)²/2σ₀² − (d_I + γ + (1/2)σ₂²) < 0,

then, for any initial value (S(0), I(0), R(0)) ∈ R₊³, one has

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{limsup}}\frac{\ln I\left(t\right)}{t}<\mathrm{0}\mathit{\text{\hspace{0.17em}\hspace{0.17em}a.s.}}\end{array}$$ (38)

That is, disease I is stochastically extinct exponentially with probability one. Moreover,

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}〈S\left(t\right)〉=S_{\mathrm{0}},\\ \\ \underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}〈R\left(t\right)〉=\frac{\mathrm{\Lambda }\left(q{d}_S+p\right)}{d_S\left(d_R+\epsilon \right)+p{d}_R}\mathit{\text{\hspace{0.17em}\hspace{0.17em}a.s.}}\\ \end{array}$$ (39)

Proof —

Applying Itô's formula to model (6) leads to

$$\begin{array}{c}\ln I\left(t\right)=\ln I\left(\mathrm{0}\right)+\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}f\left(x\left(s\right)\right)ds\\ +{\displaystyle \sum }_{j=\mathrm{1}}^l\left({\sigma }_{\mathrm{0}j}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}f\left(S\left(s\right)\right)\frac{g\left(I\left(s\right)\right)}{I\left(s\right)}d{B}_j\left(s\right)-{\sigma }_{\mathrm{2}j}{B}_j\left(t\right)\right),\end{array}$$ (40)

where x = (S, I) and

$$\begin{array}{c}f\left(x\right)=f\left(S\right)\frac{g\left(I\right)}{I}\left(\beta +{\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)\\ -\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\right)-\frac{\mathrm{1}}{\mathrm{2}}{\left(f\left(S\right)\frac{g\left(I\right)}{I}\right)}^{\mathrm{2}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}.\end{array}$$ (41)

Assume that condition (b) holds. Since

$$\begin{array}{c}f\left(x\left(t\right)\right)\le \frac{{\left(\beta +{\sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)}^{\mathrm{2}}}{\mathrm{2}{\sigma }_{\mathrm{0}}^{\mathrm{2}}}-\left(d_I+\gamma +\frac{\mathrm{1}}{\mathrm{2}}{\sigma }_{\mathrm{2}}^{\mathrm{2}}\right),\end{array}$$ (42)

then from (40)

$$\begin{array}{c}\frac{\ln I\left(t\right)}{t}\le \frac{\ln I\left(\mathrm{0}\right)}{t}+\frac{{\left(\beta +{\sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)}^{\mathrm{2}}}{\mathrm{2}{\sigma }_{\mathrm{0}}^{\mathrm{2}}}-\left(d_I+\gamma +\frac{\mathrm{1}}{\mathrm{2}}{\sigma }_{\mathrm{2}}^{\mathrm{2}}\right)+{\displaystyle \sum }_{j=\mathrm{1}}^l\left({\sigma }_{\mathrm{0}j}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}f\left(S\left(s\right)\right)\frac{g\left(I\left(s\right)\right)}{I\left(s\right)}d{B}_j\left(s\right)-{\sigma }_{\mathrm{2}j}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}d{B}_j\left(s\right)\right).\end{array}$$ (43)

By Lemma 2, we have

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}S\left(s\right)\frac{g\left(I\left(s\right)\right)}{I\left(s\right)}d{B}_j\left(s\right)=\mathrm{0},\\ \\ \underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}d{B}_j\left(s\right)=\mathrm{0}\text{\hspace{0.17em}\hspace{0.17em}a.s.},\\ \\ \mathrm{1}\le j\le l.\end{array}$$ (44)

Therefore,

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{limsup}}\frac{\ln I\left(t\right)}{t}\frac{{\left(\beta +{\sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)}^{\mathrm{2}}}{\mathrm{2}{\sigma }_{\mathrm{0}}^{\mathrm{2}}}\\ -\left(d_I+\gamma +\frac{\mathrm{1}}{\mathrm{2}}{\sigma }_{\mathrm{2}}^{\mathrm{2}}\right)<\mathrm{0}.\end{array}$$ (45)

Assume that condition (a) holds. Choose constant ϵ > 0 such that β + ∑_j=1^lσ_0jσ_2j ≥ g′(0)f(ϵ)σ₀². We compute that

$$\begin{array}{c}f\left(x\right)\\ =f\left(S\right)\frac{g\left(I\right)}{I}\left(\beta +{\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)-\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\right)\\ -\frac{\mathrm{1}}{\mathrm{2}}{\left(f\left(S\right)\frac{g\left(I\right)}{I}\right)}^{\mathrm{2}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}\\ =f\left(S\right)\frac{g\left(I\right)}{I}\left(\beta +{\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)-\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\right)\\ +\frac{\mathrm{1}}{\mathrm{2}}{f}^{\mathrm{2}}\left(ϵ\right)\frac{g^{\mathrm{2}}\left(I\right)}{I^{\mathrm{2}}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}\\ -\frac{\mathrm{1}}{\mathrm{2}}{\left(f\left(S\right)-f\left(ϵ\right)\right)}^{\mathrm{2}}\frac{g^{\mathrm{2}}\left(I\right)}{I^{\mathrm{2}}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}\\ -f\left(S\right)f\left(ϵ\right)\frac{g^{\mathrm{2}}\left(I\right)}{I^{\mathrm{2}}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}\\ \le \left[\left(\beta +{\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)\frac{g\left(I\right)}{I}-f\left(ϵ\right){\sigma }_{\mathrm{0}}^{\mathrm{2}}\frac{g^{\mathrm{2}}\left(I\right)}{I^{\mathrm{2}}}\right]f\left(S\right)\\ -\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{\left(f\left(ϵ\right)g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}.\end{array}$$ (46)

When σ₀² = 0, which implies σ_0j = 0  (1 ≤ j ≤ l), we have from (46)

$$\begin{array}{c}f\left(x\right)\beta f\left(S\right)\frac{g\left(I\right)}{I}-\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\right)\\ \le \beta g^{\prime }\left(\mathrm{0}\right)f\left(S\right)-\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\right).\end{array}$$ (47)

Since

$$\begin{array}{c}f\left(S\right)f\left(S_{\mathrm{0}}\right)+f\left(S\right)-f\left(S_{\mathrm{0}}\right)\\ =f\left(S_{\mathrm{0}}\right)+f^{\prime }\left(\xi \right)\left(S-S_{\mathrm{0}}\right),\end{array}$$ (48)

where ξ ∈ (S, S₀), from (H₂), we can obtain f′(ξ)(S − S₀) ≤ f′(S₀)(S − S₀). Hence, we have

$$\begin{array}{c}f\left(S\right)\le f\left(S_{\mathrm{0}}\right)+f^{\prime }\left(S_{\mathrm{0}}\right)\left(S-S_{\mathrm{0}}\right).\end{array}$$ (49)

According to (14), (40), and (49), we have

$$\begin{array}{c}\frac{\ln I\left(t\right)}{t}\le \frac{\ln I\left(\mathrm{0}\right)}{t}+\beta g^{\prime }\left(\mathrm{0}\right)\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}f\left(S\left(s\right)\right)ds-\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\right)+{\displaystyle \sum }_{j=\mathrm{1}}^l\left({\sigma }_{\mathrm{0}j}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}f\left(S\left(s\right)\right)\frac{g\left(I\left(s\right)\right)}{I\left(s\right)}d{B}_j\left(s\right)-{\sigma }_{\mathrm{2}j}\frac{B_j\left(t\right)}{t}\right)=\frac{\ln I\left(\mathrm{0}\right)}{t}+\beta g^{\prime }\left(\mathrm{0}\right)f\left(S_{\mathrm{0}}\right)-\beta g^{\prime }\left(\mathrm{0}\right)\\ ·f^{\prime }\left(S_{\mathrm{0}}\right)S_{\mathrm{1}}〈I\left(t\right)〉+\beta f^{\prime }\left(S_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)\phi \left(t\right)-\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\right)+{\displaystyle \sum }_{j=\mathrm{1}}^l\left({\sigma }_{\mathrm{0}j}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}f\left(S\left(s\right)\right)\frac{g\left(I\left(s\right)\right)}{I\left(s\right)}d{B}_j\left(s\right)-{\sigma }_{\mathrm{2}j}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}d{B}_j\left(s\right)\right).\end{array}$$ (50)

Hence, from (44) and Lemma 3, we finally have

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{limsup}}\frac{\ln I\left(t\right)}{t}\le \beta f\left(S_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)-\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\right)\text{\hspace{0.17em}\hspace{0.17em}a.s.}\end{array}$$ (51)

When σ₀² ≠ 0, from (40) and (46) we have

$$\begin{array}{c}\frac{\ln I\left(t\right)}{t}\le \frac{\ln I\left(\mathrm{0}\right)}{t}+\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}\left[\left(\beta +{\displaystyle \sum }_{j=\mathrm{1}}^N{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)\frac{g\left(I\left(s\right)\right)}{I\left(s\right)}-f\left(ϵ\right){\sigma }_{\mathrm{0}}^{\mathrm{2}}\frac{g^{\mathrm{2}}\left(I\left(s\right)\right)}{I{\left(s\right)}^{\mathrm{2}}}\right]f\left(S\left(s\right)\right)ds\\ +{\displaystyle \sum }_{j=\mathrm{1}}^N\left({\sigma }_{\mathrm{0}j}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}f\left(S\left(s\right)\right)\frac{g\left(I\left(s\right)\right)}{I\left(s\right)}d{B}_j\left(s\right)-{\sigma }_{\mathrm{2}j}\frac{B_j\left(t\right)}{t}\right)-\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{\left(f\left(ϵ\right)g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}\\ ·{\sigma }_{\mathrm{0}}^{\mathrm{2}}.\end{array}$$ (52)

Define a function

$$\begin{array}{c}F\left(u\right)=\left(\beta +{\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)u-f\left(ϵ\right){\sigma }_{\mathrm{0}}^{\mathrm{2}}{u}^{\mathrm{2}}.\end{array}$$ (53)

Clearly, F(u) is a monotone increasing for u ∈ [0, (β + ∑_j=1^lσ_0jσ_2j)/2f(ϵ)σ₀²] and monotone decreasing for u ∈ [(β + ∑_j=1^lσ_0jσ_2j)/2f(ϵ)σ₀², ∞). With condition β + ∑_j=1^lσ_0jσ_2j ≥ g′(0)f(ϵ)σ₀², that is, g(I)/I ≤ g′(0) ≤ (β + ∑_j=1^lσ_0jσ_2j)/2f(ϵ)σ₀², we have

$$\begin{array}{c}F\left(\frac{g\left(I\right)}{I}\right)F\left(g^{\prime }\left(\mathrm{0}\right)\right)\\ =\left(\beta +{\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)g^{\prime }\left(\mathrm{0}\right)\\ -f\left(ϵ\right){\sigma }_{\mathrm{0}}^{\mathrm{2}}{\left(g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}.\end{array}$$ (54)

Hence, by (14) and (49), we have

$$\begin{array}{c}\frac{\ln I\left(t\right)}{t}\le \frac{\ln I\left(\mathrm{0}\right)}{t}+g^{\prime }\left(\mathrm{0}\right)\left(\beta +{\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}-f\left(ϵ\right)·{\sigma }_{\mathrm{0}}^{\mathrm{2}}{g}^{\prime }\left(\mathrm{0}\right)\right)\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}f\left(S\left(s\right)\right)ds\\ +{\displaystyle \sum }_{j=\mathrm{1}}^l\left({\sigma }_{\mathrm{0}j}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}f\left(S\left(s\right)\right)\frac{g\left(I\left(s\right)\right)}{I\left(s\right)}d{B}_j\left(s\right)-{\sigma }_{\mathrm{2}j}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}d{B}_j\left(s\right)\right)-\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{\left(g^{\prime }\left(\mathrm{0}\right)·f\left(ϵ\right)\right)}^{\mathrm{2}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}\le \frac{\ln I\left(\mathrm{0}\right)}{t}+g^{\prime }\left(\mathrm{0}\right)\left(\beta +{\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}-f\left(ϵ\right){\sigma }_{\mathrm{0}}^{\mathrm{2}}{g}^{\prime }\left(\mathrm{0}\right)\right)\left[f\left(S_{\mathrm{0}}\right)+f^{\prime }\left(S_{\mathrm{0}}\right)\phi \left(t\right)\right]-\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{\left(g^{\prime }\left(\mathrm{0}\right)f\left(ϵ\right)\right)}^{\mathrm{2}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}\\ +{\displaystyle \sum }_{j=\mathrm{1}}^l\left({\sigma }_{\mathrm{0}j}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}S\left(s\right)\frac{g\left(I\left(s\right)\right)}{I\left(s\right)}d{B}_j\left(s\right)-{\sigma }_{\mathrm{2}j}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}d{B}_j\left(s\right)\right).\end{array}$$ (55)

Choose ϵ = S₀; from (44) and Lemma 3, we finally have

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{limsup}}\frac{\ln I\left(t\right)}{t}\le f\left(S_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)\left(\beta +{\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)\\ -\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\right)-\frac{\mathrm{1}}{\mathrm{2}}{\left(f\left(S_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}\text{\hspace{0.17em}\hspace{0.17em}a.s.}\end{array}$$ (56)

From (45), (51), and (56), it follows that (38) holds.

Since lim_t→∞I(t) = 0  a.s., by (14) of Lemma 3 and the last equation of (15), we further obtain

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}〈S\left(t\right)〉=S_{\mathrm{0}},\\ \\ \underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}〈R\left(t\right)〉=\frac{\mathrm{\Lambda }\left(q{d}_S+p\right)}{d_S\left(d_R+\epsilon \right)+p{d}_R}\text{\hspace{0.17em}\hspace{0.17em}a.s.}\\ \end{array}$$ (57)

This completes the proof.

Remark 10 . —

Condition (b) in Theorem 9 can be rewritten in the following form:

$$\begin{array}{c}{\sigma }_{\mathrm{0}}^{\mathrm{2}}>\frac{{\left(\beta +{\sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)}^{\mathrm{2}}}{\mathrm{2}\left(d_I+\gamma +\left(\mathrm{1}/\mathrm{2}\right){\sigma }_{\mathrm{2}}^{\mathrm{2}}\right)}.\end{array}$$ (58)

It is clear that

$$\begin{array}{c}\frac{f\left(S_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)\left(\beta +{\sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)}{d_I+\gamma +\left(\mathrm{1}/\mathrm{2}\right){\sigma }_{\mathrm{2}}^{\mathrm{2}}}\\ -\frac{{\left(f\left(S_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}{\left(\beta +{\sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)}^{\mathrm{2}}}{\mathrm{4}{\left(d_I+\gamma +\left(\mathrm{1}/\mathrm{2}\right){\sigma }_{\mathrm{2}}^{\mathrm{2}}\right)}^{\mathrm{2}}}\le \mathrm{1}.\end{array}$$ (59)

Therefore, when condition (b) holds, from (58) we also have

$$\begin{array}{c}{\tilde{R}}_{\mathrm{0}}=\frac{f\left(S_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)\left(\beta +{\sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)}{d_I+\gamma }\\ -\frac{{\left(f\left(S_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}}{\mathrm{2}\left(d_I+\gamma \right)}-\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}\left(d_I+\gamma \right)}\\ <\frac{f\left(S_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)\left(\beta +{\sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)}{d_I+\gamma }\\ -\frac{{\left(f\left(S_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}{\left(\beta +{\sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)}^{\mathrm{2}}}{\mathrm{4}\left(d_I+\gamma \right)\left(d_I+\gamma +\left(\mathrm{1}/\mathrm{2}\right){\sigma }_{\mathrm{2}}^{\mathrm{2}}\right)}\\ -\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}\left(d_I+\gamma \right)}=\left[\frac{f\left(S_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)\left(\beta +{\sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)}{d_I+\gamma +\left(\mathrm{1}/\mathrm{2}\right){\sigma }_{\mathrm{2}}^{\mathrm{2}}}-\frac{{\left(f\left(S_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}{\left(\beta +{\sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\right)}^{\mathrm{2}}}{\mathrm{4}{\left(d_I+\gamma +\left(\mathrm{1}/\mathrm{2}\right){\sigma }_{\mathrm{2}}^{\mathrm{2}}\right)}^{\mathrm{2}}}\right]\\ \times \frac{d_I+\gamma +\left(\mathrm{1}/\mathrm{2}\right){\sigma }_{\mathrm{2}}^{\mathrm{2}}}{d_I+\gamma }-\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}\left(d_I+\gamma \right)}\le \mathrm{1}.\end{array}$$ (60)

Remark 11 . —

From Remark 10 above, we see that in Theorem 9 if condition (a) holds, then we directly have ${\tilde{R}}_{\mathrm{0}}<\mathrm{1}$, and if condition (b) holds, then we also have ${\tilde{R}}_{\mathrm{0}}<\mathrm{1}$. Therefore, an interesting open problem is whether we can establish the extinction of disease I with probability one for model (6) only when ${\tilde{R}}_{\mathrm{0}}<\mathrm{1}$.

4. Stochastic Persistence in the Mean

In this section, we discuss the stochastic persistence and permanence in the mean with probability one for model (6) only for the following two special cases: (1) σ_0j = 0  (1 ≤ j ≤ l) and (2) σ_1j = σ_2j = σ_3j = 0  (1 ≤ j ≤ l). Furthermore, we also assume that in model (6) function f(S) ≡ S.

4.1. Case σ_0j = 0  (1 ≤ j ≤ l)

When f(S) = S and σ_0j = 0  (1 ≤ j ≤ l) in model (6), we have

$$\begin{array}{c}{\tilde{R}}_{\mathrm{0}}=\frac{S_{\mathrm{0}}{g}^{\prime }\left(\mathrm{0}\right)\beta }{d_I+\gamma }-\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}\left(d_I+\gamma \right)}.\end{array}$$ (61)

Theorem 12 . —

Assume that (H₁) holds, f(S) = S, and σ_0j = 0  (1 ≤ j ≤ l). If ${\tilde{R}}_{\mathrm{0}}>\mathrm{1}$; then disease I in model (6) is stochastically persistent in the mean; that is,

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}\hspace{0.17em}\mathrm{i}\mathrm{n}\mathrm{f}}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}I\left(r\right)dr>\mathrm{0}\mathit{\text{\hspace{0.17em}\hspace{0.17em}a.s.}}\end{array}$$ (62)

Proof —

Let (S(t), I(t), R(t)) be any positive solution of model (6). Lemma 2 implies that there is a constant M₀ > 0 such that S(t) + I(t) + R(t) ≤ M₀  a.s. for all ≥0. Define a Lyapunov function

$$\begin{array}{c}U\left(I\right)=\underset{I\left(\mathrm{0}\right)}{\overset{I\left(t\right)}{{\displaystyle \int }}}\frac{\mathrm{1}}{g\left(I\right)}dI.\end{array}$$ (63)

Using Itô's formula to model (6) leads to

$$\begin{array}{c}dU\left(I\right)=\left(\beta S-\left(d_I+\gamma \right)\frac{I}{g\left(I\right)}-\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\frac{I^{\mathrm{2}}}{g^{\mathrm{2}}\left(I\right)}{g}^{\prime }\left(I\right)\right)dt\\ -{\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{2}j}\frac{I}{g\left(I\right)}d{B}_j\left(t\right)=\left(\beta S-\left(d_I+\gamma \right)\left(\frac{I}{g\left(I\right)}-\frac{\mathrm{1}}{g^{\prime }\left(\mathrm{0}\right)}\right)-\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\left(\frac{I^{\mathrm{2}}}{g^{\mathrm{2}}\left(I\right)}{g}^{\prime }\left(I\right)-\frac{\mathrm{1}}{g^{\prime }\left(\mathrm{0}\right)}\right)-\left(\frac{d_I+\gamma }{g^{\prime }\left(\mathrm{0}\right)}+\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}{g}^{\prime }\left(\mathrm{0}\right)}\right)\right)dt-{\displaystyle \sum }_{j=\mathrm{1}}^l{\sigma }_{\mathrm{2}j}\frac{I}{g\left(I\right)}d{B}_j\left(t\right).\end{array}$$ (64)

From (H₁), which implies that g′(I) ≤ g(I)/I ≤ g′(0), we have

$$\begin{array}{c}\frac{I^{\mathrm{2}}}{g^{\mathrm{2}}\left(I\right)}{g}^{\prime }\left(I\right)-\frac{\mathrm{1}}{g^{\prime }\left(\mathrm{0}\right)}\\ =\frac{I^{\mathrm{2}}}{g^{\mathrm{2}}\left(I\right)}\left(g^{\prime }\left(I\right)-g^{\prime }\left(\mathrm{0}\right)\right)\\ +g^{\prime }\left(\mathrm{0}\right)\left(\frac{I^{\mathrm{2}}}{g^{\mathrm{2}}\left(I\right)}-\frac{\mathrm{1}}{{\left(g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}}\right)\\ \le g^{\prime }\left(\mathrm{0}\right)\left(\frac{I}{g\left(I\right)}+\frac{\mathrm{1}}{g^{\prime }\left(\mathrm{0}\right)}\right)\left(\frac{I}{g\left(I\right)}-\frac{\mathrm{1}}{g^{\prime }\left(\mathrm{0}\right)}\right)\\ \le \left(M{g}^{\prime }\left(\mathrm{0}\right)+\mathrm{1}\right)\left(\frac{I}{g\left(I\right)}-\frac{\mathrm{1}}{g^{\prime }\left(\mathrm{0}\right)}\right),\end{array}$$ (65)

where M = sup_0≤I≤M0{I/g(I)}. Since lim_I→0⁺(I/g(I)) = 1/g′(0), then 0 < M < ∞. Substituting (65) into (64) and then integrating from 0 to t ≥ 0, we get

$$\begin{array}{c}\frac{U\left(I\right)}{t}\ge \frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}\left[\beta S\left(r\right)-\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\left(M{g}^{\prime }\left(\mathrm{0}\right)+\mathrm{1}\right)\right)·\left(\frac{I\left(r\right)}{g\left(I\left(r\right)\right)}-\frac{\mathrm{1}}{g^{\prime }\left(\mathrm{0}\right)}\right)-\left(\frac{d_I+\gamma }{g^{\prime }\left(\mathrm{0}\right)}+\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}{g}^{\prime }\left(\mathrm{0}\right)}\right)\right]dr\\ -{\displaystyle \sum }_{j=\mathrm{1}}^l\frac{\mathrm{1}}{t}{M}_j\left(t\right),\end{array}$$ (66)

where M_j(t) = ∫₀^tσ_2j(I(r)/g(I(r)))dB_j(r). From Lemma 2, we have

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\mathrm{1}}{t}{M}_j\left(t\right)=\mathrm{0}\text{\hspace{0.17em}\hspace{0.17em}a.s.},\mathrm{1}\le j\le l.\end{array}$$ (67)

Define a function G(I) as follows. When I > 0, G(I) = I/g(I), and when I = 0, G(0) = lim_I→0(I/g(I)) = 1/g′(0). Then G(I) is continuous for I ≥ 0 and differentiable for I > 0. Applying Lagrange's mean value theorem to G(I) − G(0), we have from (66)

$$\begin{array}{c}\frac{U\left(I\right)}{t}\ge \frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}\left[\beta S\left(r\right)-\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\left(M{g}^{\prime }\left(\mathrm{0}\right)+\mathrm{1}\right)\right)·\underset{\mathrm{0}\le I\le M_{\mathrm{0}}}{\mathrm{s}\mathrm{u}\mathrm{p}}\left\{G^{\prime }\left(I\right)\right\}I\left(r\right)-\left(\frac{d_I+\gamma }{g^{\prime }\left(\mathrm{0}\right)}+\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}{g}^{\prime }\left(\mathrm{0}\right)}\right)\right]dr\\ -{\displaystyle \sum }_{j=\mathrm{1}}^l\frac{\mathrm{1}}{t}{M}_j\left(t\right),\end{array}$$ (68)

Substituting (14) into (68), it follows that

$$\begin{array}{c}\frac{U\left(I\right)}{t}\ge \beta S_{\mathrm{0}}-\left[\beta S_{\mathrm{1}}+\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\left(M{g}^{\prime }\left(\mathrm{0}\right)+\mathrm{1}\right)\right)\underset{\mathrm{0}\le I\le M_{\mathrm{0}}}{\mathrm{s}\mathrm{u}\mathrm{p}}\left\{G^{\prime }\left(I\right)\right\}\right]\\ ·〈I\left(t\right)〉-\left(\frac{d_I+\gamma }{g^{\prime }\left(\mathrm{0}\right)}+\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}{g}^{\prime }\left(\mathrm{0}\right)}\right)-{\displaystyle \sum }_{j=\mathrm{1}}^l\frac{\mathrm{1}}{t}{M}_j\left(t\right)\\ +\beta \phi \left(t\right).\end{array}$$ (69)

Since

$$\begin{array}{c}\frac{U\left(I\right)}{t}\frac{\mathrm{1}}{t}\underset{I\left(\mathrm{0}\right)}{\overset{I\left(t\right)}{{\displaystyle \int }}}\frac{I}{g\left(I\right)}\frac{\mathrm{1}}{I}dI\le \frac{\mathrm{1}}{t}\underset{I\left(\mathrm{0}\right)}{\overset{I\left(t\right)}{{\displaystyle \int }}}M\frac{\mathrm{1}}{I}dI\\ =M\frac{\ln I\left(t\right)-\ln I\left(\mathrm{0}\right)}{t},\end{array}$$ (70)

we have

$$\begin{array}{c}\frac{\ln I\left(t\right)}{t}\ge \frac{\mathrm{1}}{M}\left\{\beta S_{\mathrm{0}}-\frac{d_I+\gamma }{g^{\prime }\left(\mathrm{0}\right)}-\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}{g}^{\prime }\left(\mathrm{0}\right)}\right\}-\frac{\mathrm{1}}{M}\left[\beta S_{\mathrm{1}}+\left(d_I+\gamma +\frac{{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}\left(M{g}^{\prime }\left(\mathrm{0}\right)+\mathrm{1}\right)\right)\underset{\mathrm{0}\le I\le M_{\mathrm{0}}}{\mathrm{s}\mathrm{u}\mathrm{p}}\left\{G^{\prime }\left(I\right)\right\}\right]\\ ·〈I\left(t\right)〉+\mathrm{\Phi }\left(t\right),\end{array}$$ (71)

where

$$\begin{array}{c}\mathrm{\Phi }\left(t\right)=-\frac{\mathrm{1}}{M}{\displaystyle \sum }_{j=\mathrm{1}}^l\frac{\mathrm{1}}{t}{M}_j\left(t\right)+\frac{\beta \phi \left(t\right)}{M}+\frac{\mathrm{1}}{t}\ln I\left(\mathrm{0}\right).\end{array}$$ (72)

From (67) and Lemma 3 we have lim_t→∞Φ(t) = 0. Finally, by Lemma 8, we obtain

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}\hspace{0.17em}\mathrm{i}\mathrm{n}\mathrm{f}}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}I\left(r\right)dr\ge I^{\ast },\end{array}$$ (73)

where

$$\begin{array}{c}{I}^{\ast }=\frac{\left(d_I+\gamma \right)\left({\tilde{R}}_{\mathrm{0}}-\mathrm{1}\right)}{\left(\beta S_{\mathrm{1}}+\left(d_I+\gamma +\left(\mathrm{1}/\mathrm{2}\right){\sigma }_{\mathrm{2}}^{\mathrm{2}}\left(M{g}^{\prime }\left(\mathrm{0}\right)+\mathrm{1}\right)\right){\sup }_{\mathrm{0}\le I\le M_{\mathrm{0}}}\left\{G^{\prime }\left(I\right)\right\}\right)g^{\prime }\left(\mathrm{0}\right)}.\end{array}$$ (74)

This completes the proof.

Remark 13 . —

In the proof of Theorem 12, we easily see that three constants M₀, M = sup_0≤I≤M0{I/g(I)}, and I^∗ given in (74) are dependent on every solution (S(t), I(t), R(t)) of model (6). This shows that in Theorem 12 we only obtain the stochastic persistence in the mean of the disease.

4.2. Case σ_1j = σ_2j = σ_3j = 0  (1 ≤ j ≤ l)

When f(S) = S and σ_1j = σ_2j = σ_3j = 0  (1 ≤ j ≤ l) in model (6), we have

$$\begin{array}{c}{\tilde{R}}_{\mathrm{0}}=\frac{\beta S_{\mathrm{0}}{g}^{\prime }\left(\mathrm{0}\right)}{d_I+\gamma }-\frac{S_{\mathrm{0}}^{\mathrm{2}}{\left(g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}}{\mathrm{2}\left(d_I+\gamma \right)}.\end{array}$$ (75)

In order to obtain the stochastic permanence in the mean with probability one for model (6), we need to introduce a new threshold value

$$\begin{array}{c}{\overline{R}}_{\mathrm{0}}=\frac{\beta S_{\mathrm{0}}{g}^{\prime }\left(\mathrm{0}\right)}{d_I+\gamma }-\frac{{\overline{S}}^{\mathrm{2}}{\left(g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}}{\mathrm{2}\left(d_I+\gamma \right)}.\end{array}$$ (76)

Obviously, we have ${\overline{R}}_{\mathrm{0}}\le {\tilde{R}}_{\mathrm{0}}$.

Theorem 14 . —

Assume that (H₁) holds, f(S) = S, and σ_1j = σ_2j = σ_3j = 0  (1 ≤ j ≤ l). If ${\overline{R}}_{\mathrm{0}}>\mathrm{1}$, then disease I in model (6) is stochastically permanent in the mean, that is,

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}\hspace{0.17em}\mathrm{i}\mathrm{n}\mathrm{f}}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}I\left(r\right)dr\\ \ge \frac{\left(d_I+\gamma \right)\left({\overline{R}}_{\mathrm{0}}-\mathrm{1}\right)}{\left(\beta S_{\mathrm{1}}+\left(d_I+\gamma \right){\max }_{\mathrm{0}\le I\le \overline{S}}\hspace{0.17em}{G}^{\prime }\left(I\right)\right)g^{\prime }\left(\mathrm{0}\right)}\mathit{\text{\hspace{0.17em}\hspace{0.17em}a.s.}},\end{array}$$ (77)

where function G(I) is defined in Theorem 12 above.

Proof —

Let U(I) = ∫_I(0)^I(t)(1/g(I))dI; using Itô's formula to model (6) and (18) leads to

$$\begin{array}{c}dU\left(I\right)=\left(\beta S-\left(d_I+\gamma \right)\frac{I}{g\left(I\right)}-\frac{{\sigma }_{\mathrm{0}}^{\mathrm{2}}}{\mathrm{2}}{S}^{\mathrm{2}}{g}^{\prime }\left(I\right)\right)dt\\ -{\displaystyle \sum }_{j=\mathrm{1}}^{l}S{\sigma }_{\mathrm{0}j}d{B}_j\left(t\right)\ge \left(\beta S-\left(d_I+\gamma \right)\left(\frac{I}{g\left(I\right)}-\frac{\mathrm{1}}{g^{\prime }\left(\mathrm{0}\right)}\right)-\left(\frac{{\sigma }_{\mathrm{0}}^{\mathrm{2}}{\overline{S}}^{\mathrm{2}}{g}^{\prime }\left(\mathrm{0}\right)}{\mathrm{2}}+\frac{d_I+\gamma }{g^{\prime }\left(\mathrm{0}\right)}\right)\right)dt-{\displaystyle \sum }_{j=\mathrm{1}}^{l}S{\sigma }_{\mathrm{0}j}d{B}_j\left(t\right).\end{array}$$ (78)

Similarly to above proof of Theorem 12, we have

$$\begin{array}{c}\frac{U\left(I\right)}{t}\ge \frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}\left(\beta S\left(r\right)-\left(d_I+\gamma \right)\underset{\mathrm{0}\le I\le \overline{S}}{\max }\hspace{0.17em}{G}^{\prime }\left(I\right)I\left(r\right)-\left(\frac{{\sigma }_{\mathrm{0}}^{\mathrm{2}}{\overline{S}}^{\mathrm{2}}{g}^{\prime }\left(\mathrm{0}\right)}{\mathrm{2}}+\frac{d_I+\gamma }{g^{\prime }\left(\mathrm{0}\right)}\right)\right)dr\\ -{\displaystyle \sum }_{j=\mathrm{1}}^l\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}S\left(r\right){\sigma }_{\mathrm{0}j}d{B}_j\left(r\right).\end{array}$$ (79)

Substituting (14) into (79) yields

$$\begin{array}{c}\frac{U\left(I\right)}{t}\ge \beta S_{\mathrm{0}}\\ -\left[\beta S_{\mathrm{1}}+\left(d_I+\gamma \right)\underset{\mathrm{0}\le I\le \overline{S}}{\max }\hspace{0.17em}{G}^{\prime }\left(I\right)\right]\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}I\left(r\right)dr\\ -\left(\frac{{\sigma }_{\mathrm{0}}^{\mathrm{2}}{\overline{S}}^{\mathrm{2}}{g}^{\prime }\left(\mathrm{0}\right)}{\mathrm{2}}+\frac{d_I+\gamma }{g^{\prime }\left(\mathrm{0}\right)}\right)-{\displaystyle \sum }_{j=\mathrm{1}}^l\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}S\left(r\right){\sigma }_{\mathrm{0}j}d{B}_j\left(r\right)+\beta \phi \left(t\right).\end{array}$$ (80)

Since by (18)

$$\begin{array}{c}\frac{U\left(I\right)}{t}\le \frac{\mathrm{1}}{t}\underset{I\left(\mathrm{0}\right)}{\overset{I\left(t\right)}{{\displaystyle \int }}}\frac{\overline{S}}{g\left(\overline{S}\right)}\frac{\mathrm{1}}{I}dI\le \frac{\overline{S}\left(\ln \overline{S}-\ln I\left(\mathrm{0}\right)\right)}{g\left(\overline{S}\right)t},\end{array}$$ (81)

(80) can be rewritten as

$$\begin{array}{c}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}I\left(r\right)dr\\ \ge \frac{\left(d_I+\gamma \right)\left({\overline{R}}_{\mathrm{0}}-\mathrm{1}\right)+g^{\prime }\left(\mathrm{0}\right)\mathrm{\Phi }\left(t\right)}{\left(\beta S_{\mathrm{1}}+\left(d_I+\gamma \right){\max }_{\mathrm{0}\le I\le \overline{S}}\hspace{0.17em}{G}^{\prime }\left(I\right)\right)g^{\prime }\left(\mathrm{0}\right)},\end{array}$$ (82)

where

$$\begin{array}{c}\mathrm{\Phi }\left(t\right)=-{\displaystyle \sum }_{j=\mathrm{1}}^l\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}S\left(r\right){\sigma }_{\mathrm{0}j}d{B}_j\left(r\right)+\beta \phi \left(t\right)\\ -\frac{\overline{S}\left(\ln \overline{S}-\ln I\left(\mathrm{0}\right)\right)}{g\left(\overline{S}\right)t}.\end{array}$$ (83)

By Lemmas 2 and 3, it follows that lim_t→∞Φ(t) = 0. Therefore, taking t → ∞ in (82) it follows that (77) holds. This completes the proof.

Using Lemma 5, we can establish the following result which shows that ${\tilde{R}}_{\mathrm{0}}$ can be a threshold value for the stochastic permanence of disease I in the mean for a more special case of model (6): d_S = d_R and d_I = d_S + α with constant α ≥ 0.

Theorem 15 . —

Assume that (H₁) holds, f(S) = S, σ_1j = σ_2j = σ_3j = 0  (1 ≤ j ≤ l), d_S = d_R, and d_I = d_S + α with constant α ≥ 0. If ${\tilde{R}}_{\mathrm{0}}>\mathrm{1}$; then disease I in model (6) is stochastically permanent in the mean; that is,

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}\hspace{0.17em}\mathrm{i}\mathrm{n}\mathrm{f}}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}I\left(r\right)dr\\ \ge \frac{\left(d_S+\alpha +\gamma \right)\left({\tilde{R}}_{\mathrm{0}}-\mathrm{1}\right)}{\left(\beta S_{\mathrm{1}}+\left(d_I+\gamma \right){\max }_{\mathrm{0}\le I\le \overline{S}}\hspace{0.17em}{G}^{\prime }\left(I\right)+M_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)}\mathit{\text{\hspace{0.17em}\hspace{0.17em}a.s.}},\end{array}$$ (84)

where function G(I) is defined in above Theorem 12 and

$$\begin{array}{c}{M}_{\mathrm{0}}=\mathrm{6}\left[\mathrm{1}+\frac{{\alpha }^{\mathrm{2}}}{d_S^{\mathrm{2}}}+\frac{{\gamma }^{\mathrm{2}}}{{\left(d_S+\epsilon \right)}^{\mathrm{2}}}+\frac{p^{\mathrm{2}}}{{\left(d_S+\epsilon +p\right)}^{\mathrm{2}}}+\frac{{\left(p\alpha \right)}^{\mathrm{2}}}{d_S^{\mathrm{2}}{\left(d_S+\epsilon +p\right)}^{\mathrm{2}}}+\frac{{\left(p\gamma \right)}^{\mathrm{2}}}{{\left(d_S+\epsilon \right)}^{\mathrm{2}}{\left(d_S+\epsilon +p\right)}^{\mathrm{2}}}\right]\frac{\mathrm{\Lambda }}{d_S}.\end{array}$$ (85)

Proof —

Firstly, when d_S = d_R and d_I = d_S + α, then threshold value ${\tilde{R}}_{\mathrm{0}}$ becomes

$$\begin{array}{c}{\tilde{R}}_{\mathrm{0}}=\frac{\beta S_{\mathrm{0}}{g}^{\prime }\left(\mathrm{0}\right)}{d_S+\alpha +\gamma }-\frac{S_{\mathrm{0}}^{\mathrm{2}}{\left(g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}}{\mathrm{2}\left(d_S+\alpha +\gamma \right)},\end{array}$$ (86)

where S₀ = Λ[(1 − q)d_S + ε]/d_S(d_S + ε + p).

Let U(I) = ∫_I(0)^I(t)(1/g(I))dI; similarly to above proof of Theorem 12, we have

$$\begin{array}{c}dU\left(I\right)\ge \left(\beta S-\left(d_S+\alpha +\gamma \right)\underset{\mathrm{0}\le I\le \overline{S}}{\mathrm{m}\mathrm{a}\mathrm{x}}\hspace{0.17em}{G}^{\prime }\left(I\right)I-\frac{\mathrm{1}}{\mathrm{2}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}{S}^{\mathrm{2}}{g}^{\prime }\left(\mathrm{0}\right)-\frac{d_S+\alpha +\gamma }{g^{\prime }\left(\mathrm{0}\right)}\right)dt\\ -{\displaystyle \sum }_{j=\mathrm{1}}^{l}S{\sigma }_{\mathrm{0}j}d{B}_j\left(t\right).\end{array}$$ (87)

Since S² = S₀² + 2S₀(S − S₀)+(S − S₀)², we further have

$$\begin{array}{c}\frac{U\left(I\right)}{t}\ge \beta 〈S\left(t\right)〉-\left(d_S+\alpha +\gamma \right)\underset{\mathrm{0}\le I\le \overline{S}}{\mathrm{m}\mathrm{a}\mathrm{x}}\hspace{0.17em}{G}^{\prime }\left(I\right)〈I\left(t\right)〉\\ -\frac{\mathrm{1}}{\mathrm{2}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}{S}_{\mathrm{0}}^{\mathrm{2}}{g}^{\prime }\left(\mathrm{0}\right)-{\sigma }_{\mathrm{0}}^{\mathrm{2}}{S}_{\mathrm{0}}{g}^{\prime }\left(\mathrm{0}\right)〈S\left(t\right)-S_{\mathrm{0}}〉\\ -\frac{d_S+\alpha +\gamma }{g^{\prime }\left(\mathrm{0}\right)}-\frac{\mathrm{1}}{\mathrm{2}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}{g}^{\prime }\left(\mathrm{0}\right)〈{\left(S\left(t\right)-S_{\mathrm{0}}\right)}^{\mathrm{2}}〉-{\displaystyle \sum }_{j=\mathrm{1}}^l\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}S{\sigma }_{\mathrm{0}j}d{B}_j\left(s\right).\end{array}$$ (88)

Substituting (14) and (21) of Lemma 5 into (88), using inequality (a + b)² ≤ 2(a² + b²), it follows that

$$\begin{array}{c}\frac{U\left(I\right)}{t}\ge \frac{d_S+\alpha +\gamma }{g^{\prime }\left(\mathrm{0}\right)}\left({\tilde{R}}_{\mathrm{0}}-\mathrm{1}\right)\\ -\left[\beta S_{\mathrm{1}}+\left(d_S+\alpha +\gamma \right)\underset{\mathrm{0}\le I\le \overline{S}}{\mathrm{m}\mathrm{a}\mathrm{x}}\hspace{0.17em}{G}^{\prime }\left(I\right)\right]〈I\left(t\right)〉\\ +\left(\beta -{\sigma }_{\mathrm{0}}^{\mathrm{2}}{S}_{\mathrm{0}}{g}^{\prime }\left(\mathrm{0}\right)\right)\phi \left(t\right)\\ -{\sigma }_{\mathrm{0}}^{\mathrm{2}}{g}^{\prime }\left(\mathrm{0}\right)\left(〈H^{\mathrm{2}}\left(t\right)〉+〈G^{\mathrm{2}}\left(t\right)〉\right)-{\displaystyle \sum }_{j=\mathrm{1}}^l\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}S{\sigma }_{\mathrm{0}j}d{B}_j\left(s\right).\end{array}$$ (89)

From expression (22) of H(t), we easily have lim_t→∞〈H²(t)〉 = 0. By (18), without loss of generality, we can assume that S(t) + I(t) + R(t) ≤ Λ/d_S  a.s. for all t ≥ 0. Hence,

$$\begin{array}{c}{G}^{\mathrm{2}}\left(t\right)\le \mathrm{6}\left[I^{\mathrm{2}}\left(t\right)+{\alpha }^{\mathrm{2}}{\left({\int }_{\mathrm{0}}^t{e}^{-d_S\left(t-s\right)}I\left(s\right)ds\right)}^{\mathrm{2}}+{\gamma }^{\mathrm{2}}{\left({\int }_{\mathrm{0}}^t{e}^{-\left(d_S+\epsilon \right)\left(t-s\right)}I\left(s\right)ds\right)}^{\mathrm{2}}+p^{\mathrm{2}}{\left({\int }_{\mathrm{0}}^t{e}^{-\left(d_S+\epsilon +p\right)\left(t-s\right)}I\left(s\right)ds\right)}^{\mathrm{2}}+{\left(p\alpha \right)}^{\mathrm{2}}·{\left({\int }_{\mathrm{0}}^t{e}^{-\left(d_S+\epsilon +p\right)\left(t-s\right)}{\int }_{\mathrm{0}}^s{e}^{-d_S\left(s-u\right)}I\left(u\right)du\hspace{0.17em}ds\right)}^{\mathrm{2}}+{\left(p\gamma \right)}^{\mathrm{2}}{\left({\int }_{\mathrm{0}}^t{e}^{-\left(d_S+\epsilon +p\right)\left(t-s\right)}·{\int }_{\mathrm{0}}^s{e}^{-\left(d_S+\epsilon \right)}\left(s-u\right)I\left(u\right)du\hspace{0.17em}ds\right)}^{\mathrm{2}}\right]\le \mathrm{6}\left[\frac{\mathrm{\Lambda }}{d_S}I\left(t\right)+\frac{{\alpha }^{\mathrm{2}}\mathrm{\Lambda }}{d_S^{\mathrm{2}}}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-d_S\left(t-s\right)}I\left(s\right)ds+\frac{{\gamma }^{\mathrm{2}}\mathrm{\Lambda }}{d_S\left(d_S+\epsilon \right)}·\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon \right)\left(t-s\right)}I\left(s\right)ds+\frac{p^{\mathrm{2}}\mathrm{\Lambda }}{d_S\left(d_S+\epsilon +p\right)}·\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon +p\right)\left(t-s\right)}I\left(s\right)ds+\frac{{\left(p\alpha \right)}^{\mathrm{2}}\lambda }{d_S^{\mathrm{2}}\left(d_S+\epsilon +p\right)}·\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon +p\right)\left(t-s\right)}\underset{\mathrm{0}}{\overset{s}{{\displaystyle \int }}}{e}^{-d_S\left(s-u\right)}I\left(u\right)du\hspace{0.17em}ds+\frac{{\left(p\gamma \right)}^{\mathrm{2}}\mathrm{\Lambda }}{d_S\left(d_S+\epsilon \right)\left(d_S+\epsilon +p\right)}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon +p\right)\left(t-s\right)}·\underset{\mathrm{0}}{\overset{s}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon \right)}\left(s-u\right)I\left(u\right)du\hspace{0.17em}ds\right].\end{array}$$ (90)

By computing, we obtain

$$\begin{array}{c}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}\underset{\mathrm{0}}{\overset{s}{{\displaystyle \int }}}{e}^{-d_S\left(s-u\right)}I\left(u\right)du\hspace{0.17em}ds\le \frac{\mathrm{1}}{d_S}〈I\left(t\right)〉,\\ \frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}\underset{\mathrm{0}}{\overset{s}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon \right)\left(s-u\right)}I\left(u\right)du\hspace{0.17em}ds\le \frac{\mathrm{1}}{d_S+\epsilon }〈I\left(t\right)〉,\\ \frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}\underset{\mathrm{0}}{\overset{s}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon +p\right)\left(s-u\right)}I\left(u\right)du\hspace{0.17em}ds\le \frac{\mathrm{1}}{d_S+\epsilon +p}〈I\left(t\right)〉,\\ \frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}\underset{\mathrm{0}}{\overset{s}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon +p\right)\left(s-u\right)}\underset{\mathrm{0}}{\overset{u}{{\displaystyle \int }}}{e}^{-d_S\left(u-v\right)}I\left(v\right)dv\hspace{0.17em}du\hspace{0.17em}ds\\ \le \frac{\mathrm{1}}{d_S\left(d_S+\epsilon +p\right)}〈I\left(t\right)〉,\\ \frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}\underset{\mathrm{0}}{\overset{s}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon +p\right)\left(s-u\right)}\underset{\mathrm{0}}{\overset{u}{{\displaystyle \int }}}{e}^{-\left(d_S+\epsilon \right)\left(u-v\right)}I\left(v\right)dv\hspace{0.17em}du\hspace{0.17em}ds\\ \le \frac{\mathrm{1}}{\left(d_S+\epsilon \right)\left(d_S+\epsilon +p\right)}〈I\left(t\right)〉.\end{array}$$ (91)

Therefore, we finally have

$$\begin{array}{c}〈G^{\mathrm{2}}\left(t\right)〉\le M_{\mathrm{0}}〈I\left(t\right)〉.\end{array}$$ (92)

From (81), (89), and (92) we further obtain

$$\begin{array}{c}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}I\left(r\right)dr\\ \ge \frac{\left(d_S+\alpha +\gamma \right)\left({\tilde{R}}_{\mathrm{0}}-\mathrm{1}\right)+g^{\prime }\left(\mathrm{0}\right)\mathrm{\Phi }\left(t\right)}{\left(\beta S_{\mathrm{1}}+\left(d_I+\gamma \right){\max }_{\mathrm{0}\le I\le \overline{S}}\hspace{0.17em}{G}^{\prime }\left(I\right)+M_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)},\end{array}$$ (93)

where

$$\begin{array}{c}\mathrm{\Phi }\left(t\right)=-{\displaystyle \sum }_{j=\mathrm{1}}^l\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}S\left(r\right){\sigma }_{\mathrm{0}j}d{B}_j\left(r\right)\\ +\left(\beta -{\sigma }_{\mathrm{0}}^{\mathrm{2}}{S}_{\mathrm{0}}{g}^{\prime }\left(\mathrm{0}\right)\right)\phi \left(t\right)-{\sigma }_{\mathrm{0}}^{\mathrm{2}}{g}^{\prime }\left(\mathrm{0}\right)〈H^{\mathrm{2}}\left(t\right)〉-\frac{\overline{S}\left(\ln \overline{S}-\ln I\left(\mathrm{0}\right)\right)}{g\left(\overline{S}\right)t}.\end{array}$$ (94)

By Lemmas 2 and 3, it follows that lim_t→∞Φ(t) = 0. Therefore, taking t → ∞ in (93) it follows that (84) holds. This completes the proof.

5. Stationary Distribution

In this section, we discuss the stationary distribution of model (6) by using Lyapunov function method. We firstly define the diffusion matrix A(x) = h(x)h^T(x), where x = (S, I, R),

$$\begin{array}{c}h\left(x\right)=\left(\begin{array}{cccc}{h}_{\mathrm{11}}\left(x\right)& h_{\mathrm{12}}\left(x\right)& \cdots & h_{\mathrm{1}l}\left(x\right)\\ h_{\mathrm{21}}\left(x\right)& h_{\mathrm{22}}\left(x\right)& \cdots & h_{\mathrm{2}l}\left(x\right)\\ h_{\mathrm{31}}\left(x\right)& h_{\mathrm{32}}\left(x\right)& \cdots & h_{\mathrm{3}l}\left(x\right)\end{array}\right),\\ \\ h_{\mathrm{1}j}\left(x\right)=-f\left(S\right)g\left(I\right){\sigma }_{\mathrm{0}j}-f\left(S\right){\sigma }_{\mathrm{1}j},\\ \\ h_{\mathrm{2}j}\left(x\right)=f\left(S\right)g\left(I\right){\sigma }_{\mathrm{0}j}-I{\sigma }_{\mathrm{2}j},\\ \\ h_{\mathrm{3}j}\left(x\right)=-R{\sigma }_{\mathrm{3}j}.\\ \end{array}$$ (95)

Furthermore, we denote by a_ii(x)  (i = 1,2, 3) the diagonal elements of matrix A(x). We have a_ii(x) = ∑_j=1^lh_ij²(x).

Theorem 16 . —

Assume that (H₁) holds, f(S) = S, and there is a constant ρ > 0 such that a_ii(x) > ρ, for any x ∈ R₊³ and i = 1,2, 3, γ > p, d_I > d_S, and γ(d_S + d_R) > p(d_I + d_R). If R₀ > 1 and

$$\begin{array}{c}\left[\frac{\left(d_S+p\right)\left[\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right]}{\left(\gamma -p\right)\epsilon }+d_S-C_{\mathrm{1}}\right]{S^{\ast }}^{\mathrm{2}}\wedge \left[\frac{\left(d_I+\gamma \right)\left[\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right]}{\left(\gamma -p\right)\epsilon }+d_I-C_{\mathrm{2}}\right]{I^{\ast }}^{\mathrm{2}}\\ \wedge \left[\frac{\left(d_I-d_S\right)\left(d_R+\epsilon \right)}{\gamma -p}+d_R-C_{\mathrm{3}}\right]{R^{\ast }}^{\mathrm{2}}>\frac{\left[\left(d_S+d_I\right)\left(\gamma -p\right)\epsilon +\left(d_S+p+d_I+\gamma \right)\left(\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right)\right]I^{\ast }{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\epsilon \beta g\left(I^{\ast }\right)\left(\gamma -p\right)}\\ +C_{\mathrm{1}}{S^{\ast }}^{\mathrm{2}}+C_{\mathrm{2}}{I^{\ast }}^{\mathrm{2}}+C_{\mathrm{3}}{R^{\ast }}^{\mathrm{2}},\end{array}$$ (96)

where

$$\begin{array}{c}{C}_{\mathrm{1}}=\frac{\mathrm{2}\left[\left(d_S+d_I\right)\left(\gamma -p\right)\epsilon +\left(d_S+p+d_I+\gamma \right)\left(\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right)\right]I^{\ast }{\left(g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}{\sigma }_{\mathrm{0}}^{\mathrm{2}}}{\epsilon \beta g\left(I^{\ast }\right)\left(\gamma -p\right)}\\ +\frac{\mathrm{2}\left[\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right]{\sigma }_{\mathrm{1}}^{\mathrm{2}}}{\left(\gamma -p\right)\epsilon }+{\sigma }^{\mathrm{2}},\\ C_{\mathrm{2}}=\frac{\mathrm{2}\left[\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right]{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\left(\gamma -p\right)\epsilon }+{\sigma }^{\mathrm{2}},\\ C_{\mathrm{3}}=\frac{\left(d_I-d_S\right){\sigma }_{\mathrm{3}}^{\mathrm{2}}}{\gamma -p}+{\sigma }^{\mathrm{2}}\end{array}$$ (97)

and (S^∗, I^∗, R^∗) is the unique endemic equilibrium of model (2), then model (6) has a unique stationary distribution.

Proof —

We here use the Lyapunov function method to prove this theorem. The proof given here is similar to Theorem 5.1 in [11]. But, due to nonlinear function g(I), the Lyapunov function structured in the following is different from that given in [11].

By Lemma 7, it suffices to find a nonnegative Lyapunov function V(x) and compact set K ⊂ R₊³ such that LV(x)≤−C for some C > 0 and x ∈ R₊³/K.

Denote x = (S, I, R) ∈ R₊³. Define the function

$$\begin{array}{c}{V}_{\mathrm{1}}\left(x\right)=\frac{\mathrm{1}}{\mathrm{2}}{\left(R-R^{\ast }\right)}^{\mathrm{2}}.\end{array}$$ (98)

Calculating LV₁(x), we have

$$\begin{array}{c}L{V}_{\mathrm{1}}\left(x\right)=\left(R-R^{\ast }\right)\\ ·\left(p\left(S-S^{\ast }\right)+\gamma \left(I-I^{\ast }\right)-\left(d_R+\epsilon \right)\left(R-R^{\ast }\right)\right)\\ +\frac{\mathrm{1}}{\mathrm{2}}{\sigma }_{\mathrm{3}}^{\mathrm{2}}{R}^{\mathrm{2}}\le -\left(d_R+\epsilon -{\sigma }_{\mathrm{3}}^{\mathrm{2}}\right){\left(R-R^{\ast }\right)}^{\mathrm{2}}\\ +p\left(S-S^{\ast }\right)\left(R-R^{\ast }\right)+\gamma \left(I-I^{\ast }\right)\left(R-R^{\ast }\right)\\ +{\sigma }_{\mathrm{3}}^{\mathrm{2}}{R^{\ast }}^{\mathrm{2}}.\end{array}$$ (99)

Define the function

$$\begin{array}{c}{V}_{\mathrm{2}}\left(x\right)=I-I^{\ast }-I^{\ast }\ln \frac{I}{I^{\ast }}.\end{array}$$ (100)

Calculating LV₂(x), we have

$$\begin{array}{c}L{V}_{\mathrm{2}}\left(x\right)=\left(\mathrm{1}-\frac{I^{\ast }}{I}\right)\left(\beta Sg\left(I\right)-\left(d_I+\gamma \right)I\right)+\frac{I^{\ast }}{\mathrm{2}}\\ ·{\displaystyle \sum }_{j=\mathrm{1}}^l{\left(S\frac{g\left(I\right)}{I}{\sigma }_{\mathrm{0}j}-{\sigma }_{\mathrm{2}j}\right)}^{\mathrm{2}}=\left(I-I^{\ast }\right)\\ ·\left(\beta S\left(\frac{g\left(I\right)}{I}-\frac{g\left(I^{\ast }\right)}{I^{\ast }}\right)+\beta \frac{g\left(I^{\ast }\right)}{I^{\ast }}\left(S-S^{\ast }\right)\right)\\ +\frac{\mathrm{1}}{\mathrm{2}}{I}^{\ast }{\sigma }_{\mathrm{2}}^{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{I}^{\ast }{\sigma }_{\mathrm{0}}^{\mathrm{2}}{S}^{\mathrm{2}}\frac{g^{\mathrm{2}}\left(I\right)}{I^{\mathrm{2}}}-{\displaystyle \sum }_{j=\mathrm{1}}^l{I}^{\ast }S\frac{g\left(I\right)}{I}{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\\ \le \beta \frac{g\left(I^{\ast }\right)}{I^{\ast }}\left(S-S^{\ast }\right)\left(I-I^{\ast }\right)+\frac{\mathrm{1}}{\mathrm{2}}{I}^{\ast }{\sigma }_{\mathrm{2}}^{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\\ ·I^{\ast }{\sigma }_{\mathrm{0}}^{\mathrm{2}}{\left(g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}{S}^{\mathrm{2}}-{\displaystyle \sum }_{j=\mathrm{1}}^l{I}^{\ast }S\frac{g\left(I\right)}{I}{\sigma }_{\mathrm{0}j}{\sigma }_{\mathrm{2}j}\le \beta \\ ·\frac{g\left(I^{\ast }\right)}{I^{\ast }}\left(S-S^{\ast }\right)\left(I-I^{\ast }\right)+\mathrm{2}{I}^{\ast }{\sigma }_{\mathrm{0}}^{\mathrm{2}}{\left(g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}\\ ·{\left(S-S^{\ast }\right)}^{\mathrm{2}}+\mathrm{2}{I}^{\ast }{\sigma }_{\mathrm{0}}^{\mathrm{2}}{\left(g^{\prime }\left(\mathrm{0}\right)\right)}^{\mathrm{2}}{S^{\ast }}^{\mathrm{2}}+I^{\ast }{\sigma }_{\mathrm{2}}^{\mathrm{2}}.\end{array}$$ (101)

Define the function

$$\begin{array}{c}{V}_{\mathrm{3}}\left(x\right)=\frac{\mathrm{1}}{\mathrm{2}}{\left(S+I-S^{\ast }-I^{\ast }\right)}^{\mathrm{2}}.\end{array}$$ (102)

Calculating LV₃(x), we get

$$\begin{array}{c}L{V}_{\mathrm{3}}\left(x\right)=\left(S+I-S^{\ast }-I^{\ast }\right)\left(-\left(d_S+p\right)\left(S-S^{\ast }\right)+\epsilon \left(R-R^{\ast }\right)-\left(d_I+\gamma \right)\left(I-I^{\ast }\right)\right)+\frac{\mathrm{1}}{\mathrm{2}}{\sigma }_{\mathrm{1}}^{\mathrm{2}}{S}^{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\\ ·{\sigma }_{\mathrm{2}}^{\mathrm{2}}{I}^{\mathrm{2}}+{\displaystyle \sum }_{j=\mathrm{1}}^{l}SI{\sigma }_{\mathrm{1}j}{\sigma }_{\mathrm{2}j}\le -\left(\left(d_S+p\right)-\mathrm{2}{\sigma }_{\mathrm{1}}^{\mathrm{2}}\right){\left(S-S^{\ast }\right)}^{\mathrm{2}}-\left(d_I+\gamma -\mathrm{2}{\sigma }_{\mathrm{2}}^{\mathrm{2}}\right){\left(I-I^{\ast }\right)}^{\mathrm{2}}+\epsilon \left(S-S^{\ast }\right)\left(R-R^{\ast }\right)-\left(d_S+p+d_I+\gamma \right)\left(S-S^{\ast }\right)\left(I-I^{\ast }\right)+\epsilon \left(I-I^{\ast }\right)\left(R-R^{\ast }\right)+\mathrm{2}{\sigma }_{\mathrm{1}}^{\mathrm{2}}{S^{\ast }}^{\mathrm{2}}+\mathrm{2}{\sigma }_{\mathrm{2}}^{\mathrm{2}}{I^{\ast }}^{\mathrm{2}}.\end{array}$$ (103)

Define the function

$$\begin{array}{c}{V}_{\mathrm{4}}\left(x\right)=\frac{\mathrm{1}}{\mathrm{2}}{\left(S+I+R-S^{\ast }-I^{\ast }-R^{\ast }\right)}^{\mathrm{2}}.\end{array}$$ (104)

Calculating LV₄(x), we get

$$\begin{array}{c}L{V}_{\mathrm{4}}\left(x\right)=\left(S+I+R-S^{\ast }-I^{\ast }-R^{\ast }\right)\\ ·\left(\mathrm{\Lambda }-d_{S}S-d_{I}I-d_{R}R\right)+\frac{\mathrm{1}}{\mathrm{2}}\\ ·{\displaystyle \sum }_{j=\mathrm{1}}^l{\left(S{\sigma }_{\mathrm{1}j}+I{\sigma }_{\mathrm{2}j}+R{\sigma }_{\mathrm{3}j}\right)}^{\mathrm{2}}\le -d_S{\left(S-S^{\ast }\right)}^{\mathrm{2}}\\ -d_I{\left(I-I^{\ast }\right)}^{\mathrm{2}}-d_R{\left(R-R^{\ast }\right)}^{\mathrm{2}}-\left(d_S+d_I\right)\\ ·\left(S-S^{\ast }\right)\left(I-I^{\ast }\right)-\left(d_S+d_R\right)\left(S-S^{\ast }\right)\left(R-R^{\ast }\right)\\ -\left(d_I+d_R\right)\left(I-I^{\ast }\right)\left(R-R^{\ast }\right)+\frac{\mathrm{1}}{\mathrm{2}}\left({\sigma }_{\mathrm{1}}^{\mathrm{2}}+{\sigma }_{\mathrm{2}}^{\mathrm{2}}+{\sigma }_{\mathrm{3}}^{\mathrm{2}}\right)\\ ·\left(S^{\mathrm{2}}+I^{\mathrm{2}}+R^{\mathrm{2}}\right)\le -\left(d_S-{\sigma }^{\mathrm{2}}\right){\left(S-S^{\ast }\right)}^{\mathrm{2}}\\ -\left(d_I-{\sigma }^{\mathrm{2}}\right){\left(I-I^{\ast }\right)}^{\mathrm{2}}-\left(d_R-{\sigma }^{\mathrm{2}}\right){\left(R-R^{\ast }\right)}^{\mathrm{2}}\\ -\left(d_S+d_I\right)\left(S-S^{\ast }\right)\left(I-I^{\ast }\right)-\left(d_S+d_R\right)\left(S-S^{\ast }\right)\\ ·\left(R-R^{\ast }\right)-\left(d_I+d_R\right)\left(I-I^{\ast }\right)\left(R-R^{\ast }\right)\\ +{\sigma }^{\mathrm{2}}\left({S^{\ast }}^{\mathrm{2}}+{I^{\ast }}^{\mathrm{2}}+{R^{\ast }}^{\mathrm{2}}\right).\end{array}$$ (105)

Define the Lyapunov function for model (6) as follows:

$$\begin{array}{c}V\left(x\right)=\frac{\left[\left(d_S+d_I\right)\left(\gamma -p\right)\epsilon +\left(d_S+p+d_I+\gamma \right)\left(\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right)\right]I^{\ast }}{\epsilon \beta g\left(I^{\ast }\right)\left(\gamma -p\right)}{V}_{\mathrm{2}}\left(x\right)+\frac{d_I-d_S}{\gamma -p}{V}_{\mathrm{1}}\left(x\right)\\ +\frac{\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)}{\left(\gamma -p\right)\epsilon }{V}_{\mathrm{3}}\left(x\right)+V_{\mathrm{4}}\left(x\right).\end{array}$$ (106)

Then from (99), (101), (103), and (105) we have

$$\begin{array}{c}LV\left(x\right)-\left[\frac{\left(d_S+p\right)\left[\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right]}{\left(\gamma -p\right)\epsilon }+d_S-C_{\mathrm{1}}\right]{\left(S-S^{\ast }\right)}^{\mathrm{2}}\\ -\left[\frac{\left(d_I+\gamma \right)\left[\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right]}{\left(\gamma -p\right)\epsilon }+d_I-C_{\mathrm{2}}\right]{\left(I-I^{\ast }\right)}^{\mathrm{2}}-\left[\frac{\left(d_I-d_S\right)\left(d_R+\epsilon \right)}{\gamma -p}+d_R-C_{\mathrm{3}}\right]{\left(R-R^{\ast }\right)}^{\mathrm{2}}\\ +C_{\mathrm{1}}{S^{\ast }}^{\mathrm{2}}+C_{\mathrm{2}}{I^{\ast }}^{\mathrm{2}}+C_{\mathrm{3}}{R^{\ast }}^{\mathrm{2}}+\frac{\left[\left(d_S+d_I\right)\left(\gamma -p\right)\epsilon +\left(d_S+p+d_I+\gamma \right)\left(\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right)\right]I^{\ast }{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\epsilon \beta g\left(I^{\ast }\right)\left(\gamma -p\right)}.\end{array}$$ (107)

If condition (96) holds, then the surface

$$\begin{array}{c}\left[\frac{\left(d_S+p\right)\left[\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right]}{\left(\gamma -p\right)\epsilon }+d_S-C_{\mathrm{1}}\right]{\left(S-S^{\ast }\right)}^{\mathrm{2}}\\ +\left[\frac{\left(d_I+\gamma \right)\left[\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right]}{\left(\gamma -p\right)\epsilon }+d_I-C_{\mathrm{2}}\right]{\left(I-I^{\ast }\right)}^{\mathrm{2}}+\left[\frac{\left(d_I-d_S\right)\left(d_R+\epsilon \right)}{\gamma -p}+d_R-C_{\mathrm{3}}\right]{\left(R-R^{\ast }\right)}^{\mathrm{2}}\\ =\frac{\left[\left(d_S+d_I\right)\left(\gamma -p\right)\epsilon +\left(d_S+p+d_I+\gamma \right)\left(\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right)\right]I^{\ast }{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\epsilon \beta g\left(I^{\ast }\right)\left(\gamma -p\right)}+C_{\mathrm{1}}{S^{\ast }}^{\mathrm{2}}+C_{\mathrm{2}}{I^{\ast }}^{\mathrm{2}}+C_{\mathrm{3}}{R^{\ast }}^{\mathrm{2}}\end{array}$$ (108)

lies in the interior of R₊³. Hence, we can easily obtain that there exists a constant C > 0 and a compact set K of R₊³ such that, for any x ∈ R₊³/K,

$$\begin{array}{c}LV\left(x\right)\le -C.\end{array}$$ (109)

Therefore, model (6) has a unique stationary distribution. This completes the proof.

Remark 17 . —

In fact, the variances of errors usually should be small enough to justify their validity of real data; otherwise, the data may not be considered as a good one. It is clear that when σ_ij are very small, condition (96) is always satisfied.

6. Numerical Examples

To verify the theoretical results in this paper, we next give numerical simulations of model (6).

Throughout the following numerical simulations, we choose l = 2 and g(I) = I/(1 + ωI²), where ω is a positive constant. It is easy to verify that assumption (H₁) holds. By Milstein's higher-order method [29, 30], we drive the corresponding discretization equations of model (6):

$$\begin{array}{c}{S}_{i+\mathrm{1}}=S_i\\ +\left(\left(\mathrm{1}-q\right)\mathrm{\Lambda }-\frac{\beta f\left(S_i\right)I_i}{\mathrm{1}+\omega I_i^{\mathrm{2}}}-\left(d_{S_i}+P\right)S_i+\epsilon R_i\right)\mathrm{\Delta }t\\ -\frac{f\left(S_i\right)I_i}{\mathrm{1}+\omega I_i^{\mathrm{2}}}{\displaystyle \sum }_{j=\mathrm{1}}^l\left({\sigma }_{\mathrm{0}j}{\xi }_{ji}\sqrt{\mathrm{\Delta }t}+\frac{\mathrm{1}}{\mathrm{2}}{\sigma }_{\mathrm{0}j}^{\mathrm{2}}\left({\xi }_{ji}^{\mathrm{2}}-\mathrm{1}\right)\mathrm{\Delta }t\right)\\ -S_i{\displaystyle \sum }_{j=\mathrm{1}}^l\left({\sigma }_{\mathrm{1}j}{\xi }_{ji}\sqrt{\mathrm{\Delta }t}+\frac{\mathrm{1}}{\mathrm{2}}{\sigma }_{\mathrm{1}j}^{\mathrm{2}}\left({\xi }_{ji}^{\mathrm{2}}-\mathrm{1}\right)\mathrm{\Delta }t\right),\\ I_{i+\mathrm{1}}=I_i+\left(\frac{\beta f\left(S_i\right)I_i}{\mathrm{1}+\omega I_i^{\mathrm{2}}}-\left(d_I+\gamma \right)I_i\right)\mathrm{\Delta }t+\frac{f\left(S_i\right)I_i}{\mathrm{1}+\omega I_i^{\mathrm{2}}}\\ ·{\displaystyle \sum }_{j=\mathrm{1}}^l\left({\sigma }_{\mathrm{0}j}{\xi }_{ji}\sqrt{\mathrm{\Delta }t}+\frac{\mathrm{1}}{\mathrm{2}}{\sigma }_{\mathrm{0}j}^{\mathrm{2}}\left({\xi }_{ji}^{\mathrm{2}}-\mathrm{1}\right)\mathrm{\Delta }t\right)\\ -I_i{\displaystyle \sum }_{j=\mathrm{1}}^l\left({\sigma }_{\mathrm{2}j}{\xi }_{ji}\sqrt{\mathrm{\Delta }t}+\frac{\mathrm{1}}{\mathrm{2}}{\sigma }_{\mathrm{2}j}^{\mathrm{2}}\left({\xi }_{ji}^{\mathrm{2}}-\mathrm{1}\right)\mathrm{\Delta }t\right),\\ R_{i+\mathrm{1}}=R_i+\left(q\mathrm{\Lambda }+p{S}_i+\gamma I_i-\left(d_R+\epsilon \right)R_i\right)\mathrm{\Delta }t\\ -R_i{\displaystyle \sum }_{j=\mathrm{1}}^l\left({\sigma }_{\mathrm{3}j}{\xi }_{ji}\sqrt{\mathrm{\Delta }t}+\frac{\mathrm{1}}{\mathrm{2}}{\sigma }_{\mathrm{3}j}^{\mathrm{2}}\left({\xi }_{ji}^{\mathrm{2}}-\mathrm{1}\right)\mathrm{\Delta }t\right).\end{array}$$ (110)

Here, ξ_ji  (i = 1,2,…, j = 1,…, l) are N(0,1)-distributed independent Gaussian random variables and Δt > 0 is time increment.

Example 1 . —

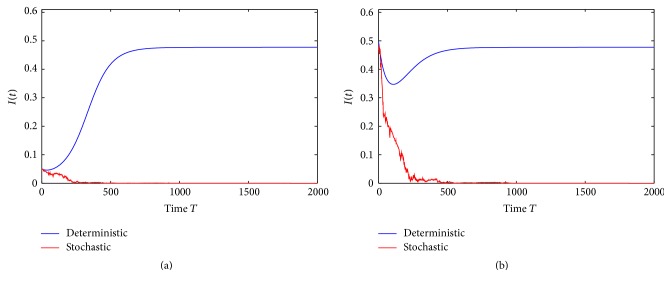
In model (6), we take f(S) = S/(1 + 0.2S), Λ = 1.85, q = 0.52, β = 0.52, p = 0.24, ε = 0.2, γ = 0.3, ω = 2, d_S = 0.4, d_I = 0.21, d_R = 0.3, σ₀₁ = 0.15, σ₀₂ = 0.99, σ₁₁ = 0.23, σ₁₂ = 0.17, σ₂₁ = 0.14, σ₂₂ = 0.72, σ₃₁ = 0.47, and σ₃₂ = 0.93. By computing, we obtain ${\tilde{R}}_{\mathrm{0}}=\mathrm{0.8939}<\mathrm{1}$, σ₀²f(S₀)g′(0)−(β + ∑_j=1²σ_0jσ_2j) = 0.3442 > 0, and (β + ∑_j=1²σ_0jσ_2j)²/2σ₀² − (d_I + γ + (1/2)σ₂²) = 0.005 > 0. This shows that conditions (a) and (b) of Theorem 9 do not hold. The numerical simulations (see Figure 1) suggest that disease I(t) of model (6) is still stochastically extinct with probability one. Therefore, as an improvement of Theorem 9, we have the following interesting conjecture.

Figure 1.

The path of I(t) for the stochastic model (6) with parameters in Example 1, compared to the corresponding deterministic model. (a) is trajectories of the solution I(t) with the initial value I(0) = 0.05 and (b) with the initial value I(0) = 0.5. The disease of model (6) is extinct with probability one.

Conjecture 2 . —

Assume (H₁) holds. The disease I(t) in model (6) is stochastically extinct with probability one only when ${\tilde{R}}_{\mathrm{0}}<\mathrm{1}$ holds.

Example 3 . —

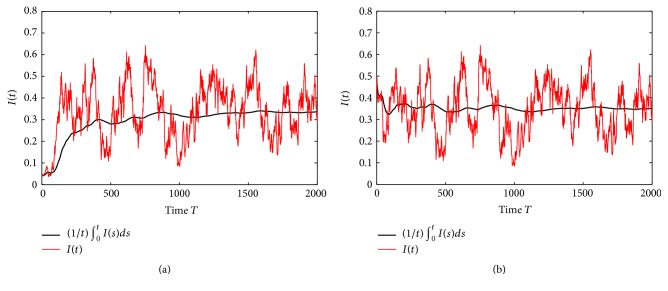
In model (6), we take f(S) = S/(1 + 1.5S), Λ = 3, q = 0.2, β = 2.1, p = 0.3, ε = 0.8, γ = 0.1, ω = 2, d_S = 0.5, d_I = 0.8, d_R = 0.4, σ₀₁ = 0.8, σ₀₂ = 1.2, σ₁₁ = 0.3, σ₁₂ = 0.75, σ₂₁ = 0.45, σ₂₂ = 0.8, σ₃₁ = 0.8, and σ₃₂ = 0.3. By computing, we obtain ${\tilde{R}}_{\mathrm{0}}=\mathrm{1.3554}>\mathrm{1}.$ From the numerical simulations given in Figure 2, it is shown that disease I(t) of model (6) is not only stochastically persistent in the mean but also stochastically persistent with probability one. Therefore, as an improvement of Theorem 12, we have the following interesting conjecture.

Figure 2.

The paths of I(t) and (1/t)∫₀^tI(s)ds for the stochastic model (6) with parameters in Example 3, (a) with the initial value I(0) = 0.05 and (b) with the initial value I(0) = 0.5.

Conjecture 4 . —

Assume (H₁) holds. The disease I(t) in model (6) is stochastically persistent in the mean only when ${\tilde{R}}_{\mathrm{0}}>\mathrm{1}$.

Example 5 . —

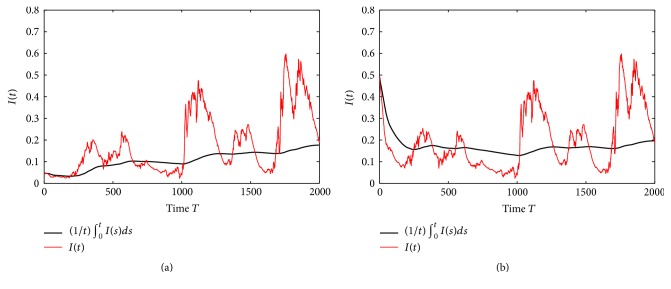
In model (6), we take f(S) = S/(1 + 0.1S), Λ = 1.2, q = 0.5, β = 1.5, p = 0.9, ε = 1.1, γ = 0.9, ω = 2, d_S = 0.6, d_I = 0.35, d_R = 0.4, σ₀₁ = 0.4, σ₀₂ = 0.2, σ₁₁ = 0.1, σ₁₂ = 0.45, σ₂₁ = 0.2, σ₂₂ = 0.1, σ₃₁ = 0.2, and σ₃₂ = 0.3. By computing, we obtain ${\overline{R}}_{\mathrm{0}}=\mathrm{0.8687}<\mathrm{1}$ and ${\tilde{R}}_{\mathrm{0}}=\mathrm{1.2931}>\mathrm{1}.$ The numerical simulations given in Figure 3 show that disease I(t) of model (6) is still stochastically permanent in the mean. Therefore, combining Theorem 12 and Theorem 14, we can obtain the following interesting conjecture about the stochastic permanence in the mean of disease I(t).

Figure 3.

The paths of I(t) and (1/t)∫₀^tI(s)ds for the stochastic model (6) with parameters in Example 5, (a) with the initial value I(0) = 0.05 and (b) with the initial value I(0) = 0.5.

Conjecture 6 . —

Assume (H₁) holds. The disease I(t) in model (6) is stochastically permanent in the mean only when ${\tilde{R}}_{\mathrm{0}}>\mathrm{1}$.

Example 7 . —

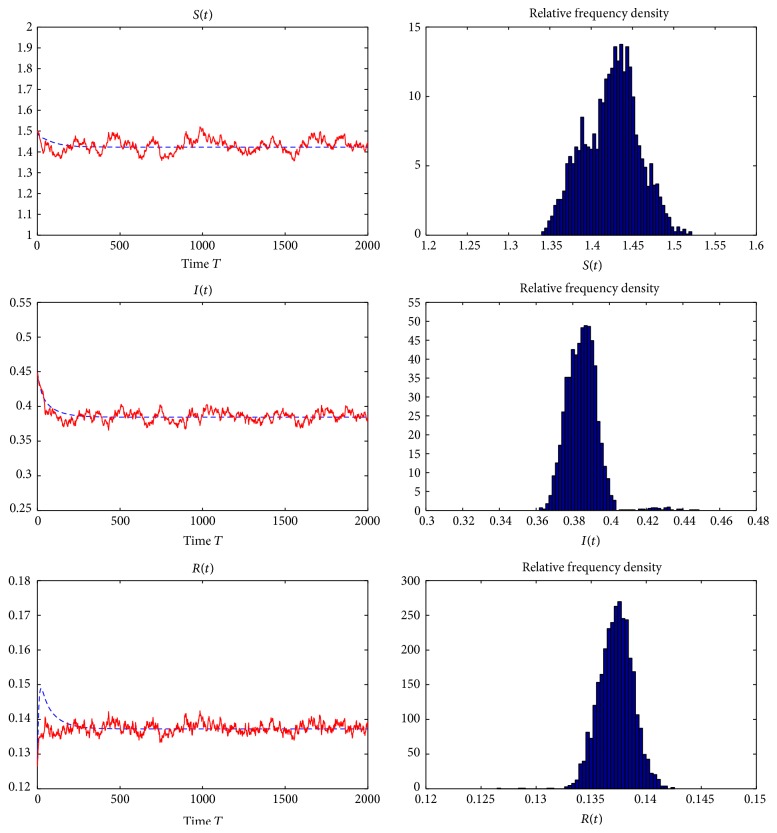
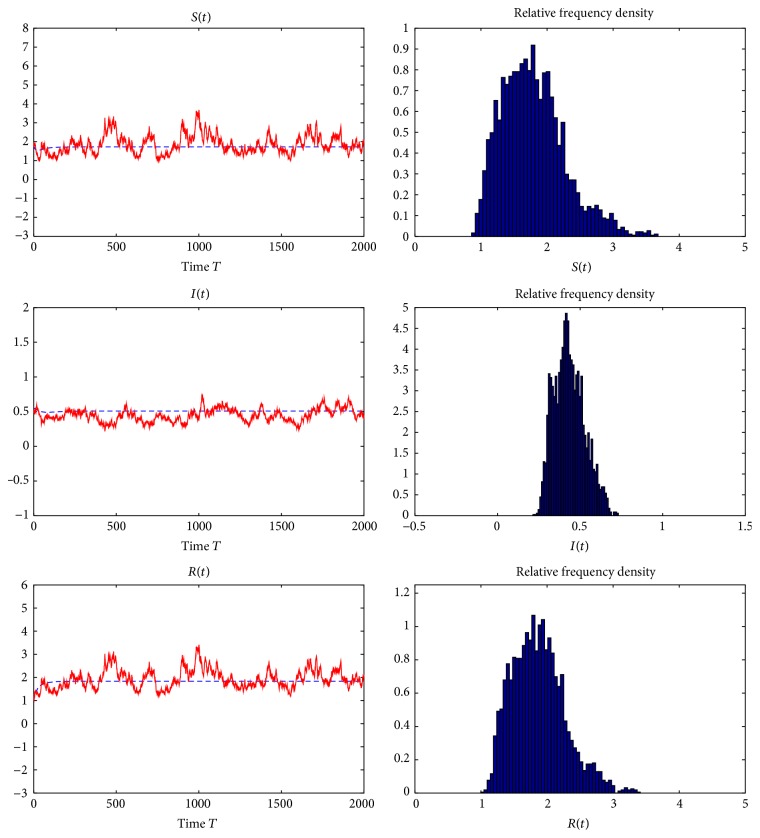
In model (6), we take f(S) = S, Λ = 0.67, q = 0.02, β = 1.7, p = 0.05, ε = 3, γ = 0.99, ω = 4, d_S = 0.29, d_I = 0.53, d_R = 0.39, σ₀₁ = 0.025, σ₀₂ = 0.02, σ₁₁ = 0.0121, σ₁₂ = 0.01, σ₂₁ = 0, σ₂₂ = 0, σ₃₁ = 0.02, and σ₃₂ = 0.01. By computing, we obtain that the basic reproduction number for deterministic model (2) is R₀ = 2.5279 > 1 and the unique endemic equilibrium of model (2) is (S^∗, I^∗, R^∗) = (1.4230,0.3845,0.1372). Furthermore, we can verify that there is a constant ρ > 0 such that a_ii(x) > ρ for any x ∈ R₊³  (i = 1,2, 3), d_I  −  d_S = 0.24 > 0, γ  −  p = 0.94 > 0, γ(d_S + d_R) − p(d_I + d_R) = 0.6272 > 0, and

$$\begin{array}{c}\left[\frac{\left(d_S+p\right)\left[\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right]}{\left(\gamma -p\right)\epsilon }+d_S-C_{\mathrm{1}}\right]{S^{\ast }}^{\mathrm{2}}\wedge \left[\frac{\left(d_I+\gamma \right)\left[\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right]}{\left(\gamma -p\right)\epsilon }+d_I-C_{\mathrm{2}}\right]{I^{\ast }}^{\mathrm{2}}\\ \wedge \left[\frac{\left(d_I-d_S\right)\left(d_R+\epsilon \right)}{\gamma -p}+d_R-C_{\mathrm{3}}\right]{R^{\ast }}^{\mathrm{2}}-\frac{\left[\left(d_S+d_I\right)\left(\gamma -p\right)\epsilon +\left(d_S+p+d_I+\gamma \right)\left(\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right)\right]I^{\ast }{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\epsilon \beta g\left(I^{\ast }\right)\left(\gamma -p\right)}\\ +C_{\mathrm{1}}{S^{\ast }}^{\mathrm{2}}+C_{\mathrm{2}}{I^{\ast }}^{\mathrm{2}}+C_{\mathrm{3}}{R^{\ast }}^{\mathrm{2}}=\mathrm{0.0147}>\mathrm{0}.\end{array}$$ (111)

That is, all conditions in Theorem 16 are satisfied. The stationary distributions about the susceptible, infected, and removed individuals obtained through the numerical simulations are reported in Figure 4, which shows that after some initial transients the population densities fluctuate around the deterministic steady-state values S^∗ = 1.4230, I^∗ = 0.3845, and R^∗ = 0.1372.

Figure 4.

The solution of stochastic model (6) and its histogram with parameters in Example 7.

Example 8 . —

In model (6), we take f(S) = S/(1 + 0.4S), Λ = 2.5, q = 0.5, β = 1.4, p = 0.7, ε = 0.9, γ = 0.51, ω = 1.89, d_S = 0.7, d_I = 0.45, d_R = 0.58, σ₀₁ = 0.4, σ₀₂ = 0.2, σ₁₁ = 0.21, σ₁₂ = 0.1, σ₂₁ = 0.1, σ₂₂ = 0.24, σ₃₁ = 0.2, and σ₃₂ = 0.1. By computing, we obtain that the basic reproduction number for deterministic model (2) is R₀ = 1.6484 > 1 and the unique endemic equilibrium of model (2) is (S^∗, I^∗, R^∗) = (1.7242,0.5082,1.8352). Furthermore, we can verify that there is not a constant ρ > 0 such that a_ii(x) > ρ for any x ∈ R₊³ and i = 1,2, 3, d_I − d_S = −0.25 < 0, γ − p = −0.19 < 0, γ(d_S + d_R) − p(d_I + d_R) = −0.0682 < 0 and

$$\begin{array}{c}\left[\frac{\left(d_S+p\right)\left[\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right]}{\left(\gamma -p\right)\epsilon }+d_S-C_{\mathrm{1}}\right]{S^{\ast }}^{\mathrm{2}}\wedge \left[\frac{\left(d_I+\gamma \right)\left[\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right]}{\left(\gamma -p\right)\epsilon }+d_I-C_{\mathrm{2}}\right]{I^{\ast }}^{\mathrm{2}}\\ \wedge \left[\frac{\left(d_I-d_S\right)\left(d_R+\epsilon \right)}{\gamma -p}+d_R-C_{\mathrm{3}}\right]{R^{\ast }}^{\mathrm{2}}-\frac{\left[\left(d_S+d_I\right)\left(\gamma -p\right)\epsilon +\left(d_S+p+d_I+\gamma \right)\left(\gamma \left(d_S+d_R\right)-p\left(d_I+d_R\right)\right)\right]I^{\ast }{\sigma }_{\mathrm{2}}^{\mathrm{2}}}{\epsilon \beta g\left(I^{\ast }\right)\left(\gamma -p\right)}\\ +C_{\mathrm{1}}{S^{\ast }}^{\mathrm{2}}+C_{\mathrm{2}}{I^{\ast }}^{\mathrm{2}}+C_{\mathrm{3}}{R^{\ast }}^{\mathrm{2}}=-\mathrm{5.5051}<\mathrm{0}.\end{array}$$ (112)

That is, the conditions in Theorem 16 are not satisfied. However, we obtain that threshold value ${\tilde{R}}_{\mathrm{0}}=\mathrm{2.7192}>\mathrm{1}.$ The numerical simulations given in Figure 5 show the stationary distributions about the susceptible, infected, and removed individuals. Therefore, we can obtain the following interesting conjecture about the stationary distribution for model (6), as described in the conclusion part.

Figure 5.

The solution of stochastic model (6) and its histogram with parameters in Example 8.

Conjecture 9 . —

Assume (H₁) holds. Model (6) has a unique stationary distribution only when ${\tilde{R}}_{\mathrm{0}}>\mathrm{1}$.

7. Conclusion

In this paper, as an extension of the results given in [11, 25], we investigated the dynamical behaviors for a stochastic SIRS epidemic model (6) with nonlinear incidence and vaccination. In model (6), the disease transmission coefficient β and the removal rates d_S, d_I, and d_R are affected by noise. Some new basic properties of model (6) are found in Lemmas 2, 3, and 5. Applying these lemmas, we established a series of new threshold value criteria on the stochastic extinction, persistence in the mean, and permanence in the mean of the disease with probability one. Furthermore, by using the Lyapunov function method, a sufficient condition on the existence of unique stationary distribution for model (6) is also obtained.

The stochastic persistence and permanence in the mean of the disease for model (6) are established in this paper only for the special cases: f(S) ≡ S and (1) σ_0j = 0  (1 ≤ j ≤ l) or (2) σ_1j = σ_2j = σ_3j = 0  (1 ≤ j ≤ l). However, for the general model (6), particularly, f(S) ≠ S and (σ_1j, σ_2j, σ_3j)≠(0,0, 0)  (1 ≤ j ≤ l), whether we also can establish similar results still is an interesting open problem.

In fact, under the above case, from the proofs of Theorems 12 and 14, we can see that an important question is to deal with terms βf(S(t)) and f²(S(t))g′(I(t)). If we may get

$$\begin{array}{c}\beta f\left(S\left(t\right)\right)\ge \beta f\left(S_{\mathrm{0}}\right)+v_{\mathrm{1}}\left(S\left(t\right)-S_{\mathrm{0}}\right)\text{\hspace{0.17em}\hspace{0.17em}a.s.},\\ \\ f^{\mathrm{2}}\left(S\left(t\right)\right)g^{\prime }\left(I\left(t\right)\right)\le f^{\mathrm{2}}\left(S_{\mathrm{0}}\right)g^{\prime }\left(\mathrm{0}\right)\\ +v_{\mathrm{2}}\left(S\left(t\right)-S_{\mathrm{0}}\right)\text{\hspace{0.17em}\hspace{0.17em}a.s.},\end{array}$$ (113)

where v₁ and v₂ are two positive constants; then the following perfect result may be established.

Assume that (H₁) holds. If ${\tilde{R}}_{\mathrm{0}}>\mathrm{1}$, then disease I in model (6) is stochastically persistent in the mean; that is,

$$\begin{array}{c}\underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}\hspace{0.17em}\mathrm{i}\mathrm{n}\mathrm{f}}\frac{\mathrm{1}}{t}\underset{\mathrm{0}}{\overset{t}{{\displaystyle \int }}}I\left(r\right)dr>\mathrm{0}\text{\hspace{0.17em}\hspace{0.17em}a.s.}\end{array}$$ (114)

Another important open problem is about the existence of stationary distribution of model (6), that is, whether we can establish a similar result as in Theorem 16 when f(S) is a nonlinear function. The best perfect result on the stationary distribution is to prove that model (6) possesses a unique stationary distribution only when threshold value ${\tilde{R}}_{\mathrm{0}}>\mathrm{1}$. But this is a very difficult open problem.

However, the numerical examples given in Section 6 propose some affirmative answer for above open problems.

Competing Interests

The authors declare that they have no competing interests.