Antibody structure determination using a combination of homology modeling, energy-based refinement, and loop prediction

Abstract

We present the blinded prediction results in the Second Antibody Modeling Assessment (AMA-II) using a fully automatic antibody structure prediction method implemented in the programs BioLuminate and Prime. We have developed a novel knowledge based approach to model the CDR loops, using a combination of sequence similarity, geometry matching, and the clustering of database structures. The homology models are further optimized with a physics-based energy function (VSGB2.0), which improves the model quality significantly. H3 loop modeling remains the most challenging task. Our ab initio loop prediction performs well for the H3 loop in the crystal structure context, and allows improved results when refining the H3 loops in the context of homology models. For the 10 human and mouse derived antibodies in this assessment, the average RMSDs for the homology model Fv and framework regions are 1.19 Å and 0.74 Å, respectively. The average RMSDs for five non-H3 CDR loops range from 0.61 Å to 1.05 Å, and the H3 loop average RMSD is 2.91 Å using our knowledge-based loop prediction approach. The ab initio H3 loop predictions yield an average RMSD of 1.28 Å when performed in the context of the crystal structure and 2.67 Å in the context of the homology modeled structure. Notably, our method for predicting the H3 loop in the crystal structure environment ranked first among the seven participating groups in AMA-II, and our method made the best prediction among all participants for seven of the ten targets.

INTRODUCTION

Computational structure prediction of antibodies is an important step in the modeling, engineering, and design of novel antibodies with desired therapeutic properties. The variable domains (Fvs) of the heavy and light chain are of special interest, as they typically impart most or all of the specificity of an antibody for its antigen target. The Fv can be further divided into the hypervariable regions and the framework regions (FRs). The hypervariable regions are so called complementarity-determining-regions (CDRs), which are composed of 6 hypervariable loops on the surface of the antibody, thereafter denoted as H1, H2 and H3 of the heavy variable domain (VL), and L1, L2, and L3 of the light variable domain (VH). Due to the highly conserved nature of the framework regions of the VL and VH domains, research into Fv structure prediction has largely focused on the prediction of the six CDR loops. Analysis of antibody crystal structures led to the discovery of “canonical” classes for the five non-H3 CDR loops in the 1980s and 1990s.^1–4 Antibody structure predictions based on this type of analysis and categorization are often qualitatively successful for loops L1-L3 and H1-H2, although predictions of H3 are more problematic. Recently, Dunbrack et al. performed clustering of a new expanded set of crystal structures (>1300 antibody structures in the PDB) and proposed 72 clusters for the five non-H3 loops.⁵ Approximately 85% of the non-H3 sequences can be assigned to one of these conformational clusters based on gene source and sequence. Prediction of the H3 loops remains difficult, however. In contrast to the other CDR loops, the H3 loops are extremely diverse in the length and conformation. Although there have been a number of attempts, no satisfying classification has been possible for the H3 loops.^6–10

The modeling of non-H3 loops has traditionally relied on the canonical classes, beginning with those based on the first studies that derived loop classifications from only a small number of crystal structures.^1,2 However, with the rapidly increasing number of the antibody structures in the PDB, the methods that use sequence similarity and other generic criteria in homology modeling instead of antibody rules have become popular and perform comparably well to the canonical classes based approach.¹¹ An advantage to these generic homology based approaches is that new structures can be added to the dataset more easily than with the older canonical class analyses. The large number of available structures has revealed the limitation of sequence based analysis and its predictive power. For example, Martin and Thornton observed that a loop might be closer in sequence to one class, but structurally belongs to another.³ Clearly, the loop conformation is not determined by its sequence alone—the interactions between a loop and its environment must be considered to make an accurate prediction.

On the other end of the spectrum of the loop modeling techniques are ab initio prediction methods.^12–18 These methods generally use a discretized rotamer library to sample the conformational space and a scoring function or energy function to rank the candidates. One of the advantages of ab initio methods is that they are independent of the protein structure database and thus can be used when no suitable template is available. With progress in sampling techniques and increased sophistication of the energy function, ab initio prediction methods have demonstrated high accuracy in the prediction of loops generally,^19–23 and in the prediction of loops for antibodies,^24–26 and other protein families.^27,28

In this article, we describe our approach to antibody structure modeling and present our results for the Antibody Modeling Assessment II (AMA-II).^29,30 Antibody Modeling Assessment is a community-wide blinded test of the state of the art antibody modeling methods, and is similar in form to CASP.³¹ The first assessment (AMA-I) was organized in 2011, in which four approaches (three software packages and a web server) were evaluated by predicting nine then-unpublished antibody crystal structures.¹¹ For AMA-II, six groups and an automated Web server attempted to predict 11 then-unpublished antibody crystal structures, and the results were used to benchmark the modeling performance. The AMA-II assessment consisted of two stages. In the first stage, the participants were asked to predict the full Fv structures of 11 antibodies from sequence. In the second stage, the crystallographic coordinates of each of the antibody structures minus the coordinates of the H3 loops were made available, and each participating group was then asked to predict the coordinates of the H3 loops. The second stage of the assessment is new to AMA-II, and reflects the known difficulty in predicting H3 loops.

We have developed a novel knowledge-based method to predict the CDR loops using a combination of sequence similarity, geometry matching, and conformational clustering of the database structures. The homology models are optimized with a physics-based energy function (VSGB2.0),¹⁹ which we show significantly improves the quality and accuracy of the models. Subsequently, we present and discuss the results using our ab inito approach for the second stage of the assessment—H3 loop predictions in the context of the crystallographic structure scaffolds—and compare these to the results of the same approach when carried out in the context of homology models for the remainders of the Fv regions.

MATERIALS AND METHODS

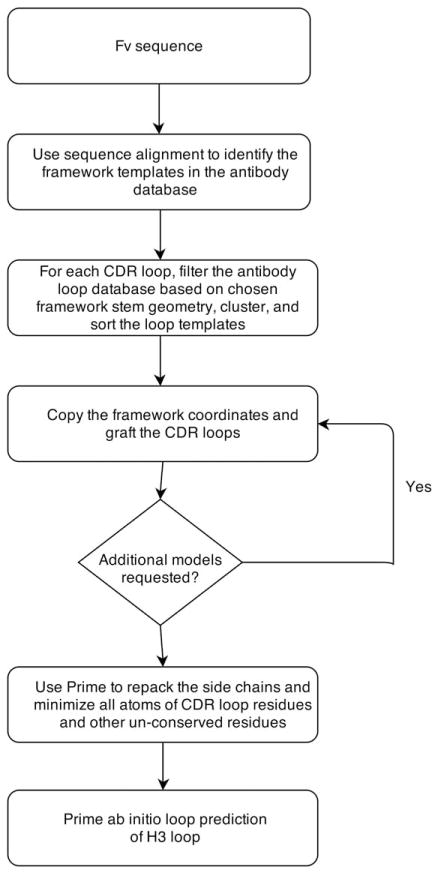
Figure 1 depicts the flowchart of the steps in our antibody homology modeling protocol. Our protocol starts with a template search for the framework region (FR) in our curated antibody database, which is derived from the publically available crystal structures in the Protein Data Bank (PDB). Instead of a heuristic search algorithm such as BLAST³² or PSI-BLAST,³³ we do a direct alignment of the query sequence to every sequence in the database using the Smith-Waterman algorithm³⁴ with BLO-SUM62³⁵ for the scoring matrix. Because there are only about 1200 antibody structures in the curated database, this direct alignment can be done relatively quickly, usually in 1 to 3 s. We select a matching pair of light and heavy chain templates from a single antibody template. There has been discussion in the literature^36,37 regarding the question of whether one should use the light and heavy chain templates from a single structure, or whether selecting them from different templates (requiring subsequent structural alignment) might be preferable. Although there is no systematic benchmark study, there is evidence that using both chains derived from a single antibody template offers some advantage.³⁷ The framework region and CDRs are defined according to the Chothia numbering. The templates are ranked by the average framework sequence similarity of the heavy and the light chain, and the best template is chosen as the one with the highest average similarity.

Figure 1.

The antibody homology modeling flowchart.

The selection of the templates for CDR loops has three steps. First, a set of loop sequences and conformations is derived individually for each loop position (L1, L2, L3, H1, H2, and H3). Next, each of the six resulting loop databases is dynamically filtered based on the query sequence, loop length, and the stem residue geometry of the framework template that has been selected. The stem residues are the adjacent residues in the N- and C- termini of the loop. The stem geometry is defined using the distance, angles, and torsions by the Cα and C atoms in N-terminal stem residue and the N and Cα atoms in C-terminal stem residue.³⁸ After the filtering for each of the six loops, all remaining loop candidates are clustered with a complete linkage algorithm based on their backbone RMSDs with the stem residues being aligned. The clusters are ranked by the cluster size, and the “representative loop” of each cluster is defined as the one with the highest sequence similarity (as defined by BLOSUM62) to the query loop within that cluster. If the sequence similarity of the representative loop in the largest cluster exceeds a sequence similarity cutoff, this loop candidate will be chosen for the template; otherwise, the representative loop in the second largest cluster will be checked against the sequence similarity cutoff, and so on. If none of the representative loops in any cluster exceeds the similarity cutoff, then the representative loop with the highest sequence similarity will be chosen. The similarity cutoff for H3 loops and non-H3 loops are 0.3 and 0.6, respectively.

Once the templates for the framework and the six CDRs are chosen, we construct the initial homology model by first copying over the backbone coordinates and also side chains for conserved residues in the framework region, then mutating the nonconserved residues in the framework, and finally grafting the CDR loops onto the framework homology model. The nonconserved residues of the framework, and all CDR loop residues, are subject to a rotamer search to remove clashes and are then minimized with the OPLS 2005 force field³⁹ in vacuum. Lastly, a side-chain prediction and minimization using the implicit solvent energy model VSGB2.0 are performed on all the non-conserved residues to further refine the model.

In the AMA-II, each modeler was asked to submit three models. The workflow, as described above, was used to produce our model #1. Our model #2 was generated by using the template loop candidate with the highest sequence similarity regardless the CDR loop clusters (framework selection was not changed). For model #3, we used Prime ab initio loop prediction to re-predict the H3 loops on model #1. The loop prediction follows the protocol in our previous study,²⁴ and the side chains within 5 Å were also repacked simultaneously.

The second stage of the antibody modeling assessment was based on the well-known observation (also reflected in the aggregate results for the first stage of this assessment) that the H3 loop is generally the most difficult loop to correctly predict. Each participating modeling lab was challenged to predict the H3 loop conformations for a set of unpublished crystal structures, given the Fv crystal structure coordinates without the H3 loop. Our prediction strategy follows the protocol in our previous study,²⁴ which is based on the Prime loop prediction method, but with some slight variations. Before the loop prediction job, the protein structure was prepared with Protein Preparation Wizard⁴⁰ available in Maestro 9.4,⁴¹ which assigns the polar hydrogen positions, protonation states, and amide group flips. Because the starting structure does not have the coordinates for the H3 loop, we run the “preparation-then-prediction” process twice, first on the provided structure without H3 loop, and then again once a loop has been modeled in the H3 position. The loop predictions are performed on the H3 loop plus one extra residue on each end to make the loop terminal residues fully flexible. The rest of the model is kept fixed. Five models are submitted for each target, ranked by Prime energy function.

RESULTS AND DISCUSSION

The homology model accuracy

Tables I and II show the PDB templates for constructing our homology models (the number 1 model submission) and the RMSD values of different regions to the crystal structure. The 11 antibody targets are denoted as AM1 to AM11. All CDRs are defined according to Chothia numbering. The structure alignment uses the Cα atoms, and the RMSD is calculated based on the backbone atoms (N, Cα, and C). The first target is a rabbit antibody, which does not have high similarity to any templates in the PDB, especially for the light chain. The sequence similarity of the best template is significantly lower than other antibodies, which results in significantly worse RMSDs. (In the AMA-II assessment, no participant was able to produce an acceptable model for the rabbit antibody due to lack of homologous data in existing crystallographic databases. Prediction of this structure was deemed a failure for all participants and it was subsequently removed before the second phase of the competition.^29,30 Excluding the rabbit antibody, the average RMSDs of the Fv region and of just the frameworks for the 10 targets are 1.19 Å and 0.74 Å, respectively. The five non-H3 CDR loop RMSDs range from 0.61 Å to 1.05 Å. Not surprisingly, the H3 loop remains to the most challenging constituent of the structure to predict, with an RMSD of 2.91 Å. In comparison, all modeling groups in AMA-II generate similar results on the FR and non-H3 loop predictions with no appreciable differences in the average RMSDs.²⁹ Predictions of the H3 loops exhibit a larger spread among the different groups and our results rank in third place by the average RMSD. Note that the RMSDs in Ref. 29 are calculated using only backbone carbonyl atoms and the values are slightly different from here.

Table I.

The PDB Templates for Constructing the Homology Models (Model 1, Stage 1) and the Corresponding Sequence Similarities

Model 1	FR		L1		L2		L3		H1		H2		H3
AM1	2X7L	0.87	3LMJ	0.54	3L95	0.71	3MLW	0.15	2VXS	0.86	3MLX	0.60	2BDN	0.50
AM2	4H20	0.95	3O2D	1.00	2I9L	1.00	3O2D	0.88	1F11	1.00	4HK0	1.00	1EHL	0.73
AM3	2XTJ	0.99	2A6D	0.91	1RZI	1.00	3CMO	0.63	1OPG	0.86	3GBM	0.83	1A2Y	0.63
AM4	3MXV	0.92	2R0L	1.00	1T4K	0.86	3IY0	1.00	1EGJ	1.00	1UWX	1.00	1FL6	0.63
AM5	3MLW	0.95	2JB6	0.71	1Q1J	1.00	2J6E	0.73	2B1H	1.00	4DGI	1.00	2R0L	0.75
AM6	3HR5	0.96	1VGE	1.00	2ZUQ	0.71	2J4W	0.89	2VXV	0.86	3GIZ	0.67	2AAB	0.50
AM7	1F58	0.97	1I7Z	0.87	4F9L	0.71	2ZCH	0.67	2AJU	1.00	3J1S	0.60	1QFW	0.63
AM8	2I9L	0.92	1AP2	1.00	1XCT	1.00	1MCP	1.00	1P2C	0.86	1P2C	0.83	1A6U	0.64
AM9	3HMW	0.98	3HI5	0.91	2JIX	1.00	1KCV	0.89	1C5C	1.00	3MLT	0.83	4DN3	1.00
AM10	2I9L	0.94	3W11	1.00	1XCT	1.00	1JRH	0.75	3IY3	0.86	1Z3G	0.83	1E6J	0.55
AM11	2OZ4	0.93	4DGI	0.91	4F2M	1.00	3D9A	0.89	4HK3	1.00	4FQH	0.83	2UUD	0.80

The light and heavy chain templates are taken from a common template framework. The CDR loop templates are chosen according to a combination of stem residue geometry, sequence similarity and database loop clustering (see main text). For each column, the template PDB ID and sequence similarity are listed.

Table II.

The Backbone RMSDs Between the Predicted Antibody Models and Those of the Associated Crystal Structures, Divided into Various Structural Elements

Align	ALL	FR	L	H	FRL	FRL	FRL	FRL	FRH	FRH	FRH	FRH
RMSD	ALL	FR	L	H	FRL	L1	L2	L3	FRH	H1	H2	H3
AM1	1.80	0.85	1.73	1.54	0.68	3.13	0.99	3.68	0.83	1.12	2.05	4.74
AM2	1.64	0.81	0.64	1.90	0.65	0.40	0.39	1.04	0.61	0.45	0.82	6.49
AM3	0.92	0.64	0.45	1.04	0.39	0.59	0.50	0.71	0.55	3.12	1.18	1.41
AM4	1.25	1.14	0.71	1.32	0.72	0.54	1.12	0.43	1.07	0.93	1.23	3.31
AM5	1.12	0.89	1.03	0.80	0.54	1.82	0.58	2.54	0.70	0.84	0.40	1.80
AM6	1.06	0.72	0.46	1.14	0.33	0.49	0.77	1.07	0.54	0.92	0.51	3.04
AM7	0.78	0.54	0.64	0.70	0.44	1.31	0.55	0.84	0.38	1.12	0.86	1.88
AM8	1.21	0.66	0.49	1.18	0.45	0.82	0.35	0.62	0.64	0.61	0.83	3.34
AM9	0.70	0.50	0.44	0.78	0.37	0.47	0.85	0.56	0.38	0.60	0.84	2.50
AM10	2.06	0.69	0.75	0.82	0.40	1.99	0.32	0.50	0.44	1.10	0.62	2.27
AM11	1.12	0.81	0.51	1.16	0.44	0.39	0.68	0.82	0.75	0.82	1.57	3.10
Avg	1.19	0.74	0.61	1.08	0.47	0.88	0.61	0.91	0.61	1.05	0.89	2.91

The structure alignment uses the Cα atoms and the RMSD is calculated on the backbone atoms (N, Cα, and C) in Å. The average RMSD for antibody target AM2-AM11 is given in the last row of the table.

ALL: whole Fv; FR: framework; FRL: light chain framework; FRH: heavy chain framework.

The CDR loop homology modeling protocols: Clustering and sequence similarity

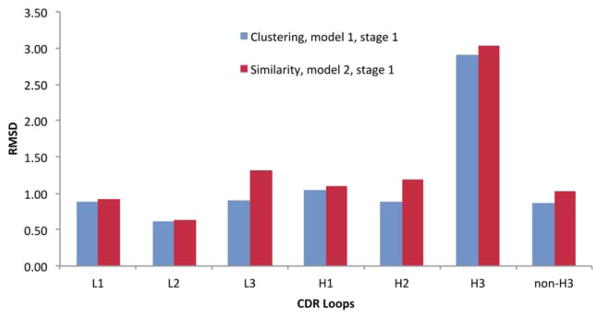
CDR loops can have identical sequences with very different conformations. This poses an issue for methods that rely on sequence alone to select the loop template. To overcome this issue, our primary model (model #1) is produced using a method that combines sequence similarity, stem geometry matching, and conformation clustering, as detailed in the Methods. Our second submitted model uses only sequence similarity to select the CDR loop templates. This experiment provides a blind assessment of the two methods. Figure 2 compares the backbone RMSDs of six CDR loops generated by these two methods. The clustering method shows some advantage over the similarity method with smaller RMSDs on all six CDR loops. The biggest improvement is for L3 with an improvement of 0.4 Å in the RMSD, followed by H2 with an improvement of 0.3 Å. On average, the RMSDs are about 0.1 to 0.2 Å better with the clustering approach. It should be pointed out that this observation is based on a relatively small data set, which is not sufficient to make a definitive conclusion about these two methods. A large scale test should be conducted in the future to compare these methods.

Figure 2.

The backbone RMSDs of six CDR loop predictions using loop clustering and sequence similarity. “Non-H3” is the average of five CDR loops excluding H3.

H3 loop prediction

In the first stage of this assessment, our third submitted model is different from the first model only in the H3 loop, which is based on ab initio prediction by Prime in the context of a homology model for the remainder of the Fv. Analysis of the blinded predictions for these loops in model #3 versus model #1 allows us to evaluate the ability this ab initio method to improve the predictions derived using standard homology templates. The loop prediction methodology in Prime has been extensively validated and recently we have shown encouraging H3 loop predictions in the context of crystal structure scaffolds, as well as when a highly homologous scaffold is available.²⁴ Table III shows the backbone RMSDs of H3 loop homology models and Prime predictions. On average, Prime refinement improves the backbone RMSD by 0.2 Å. This improvement, although small, would have put us in the second place among AMA-II participants if we had submitted the ab initio models as the #1 models. The accuracy of ab initio loop prediction in the context of homology models is heavily influenced by the quality of the homology model itself, but this influence is largely local instead of global (i.e. the structures near the loop in question) in a way that is hard to quantify.

Table III.

The Comparison Between Prime Ab Initio H3 Loop Predictions and the Predictions made by Knowledge Based Homology Modeling

H3 RMSD	AM2	AM3	AM4	AM5	AM6	AM7	AM8	AM9	AM10	AM11	Average
Homology	6.49	1.41	3.31	1.80	3.04	1.88	3.34	2.50	2.27	3.10	2.91
Ab initio	2.29	1.49	2.04	1.78	4.69	1.50	3.99	3.78	2.05	3.10	2.67

The homology models are the submitted model #1 in stage 1, and the Prime ab initio models are the submitted model #3. The accuracy is measured by backbone RMSDs in Å.

MolProbity

In constructing our homology models, we keep the side-chain conformations from the template for all conserved residues. The side chains of non-conserved residues and CDR loop residues are first optimized by a simple rotamer search to minimize the steric clashes. Then a Prime side-chain prediction is performed to optimize the side-chain conformations. Finally, all atoms on non-conserved residues and CDR loops are minimized with the VSGB2.0 energy function in Prime. In Table IV, we compare the MolProbity assessment of the homology models before and after Prime refinement. MolProbity score and clash score are improved significantly by the refinement. We should note that MolProbity is a measurement of structure model quality or self-consistency of the model. It does not necessarily correlate with the “correctness” of a model. Nevertheless, the side-chain accuracy after Prime refinement is also improved and for some models the improvements are substantial. The backbone accuracy does not change significantly (RMSD data not shown), which can also be seen from the relatively minor change in Ramachandran favored backbone torsions.

Table IV.

Prime Side Chain Prediction and Minimization Improves MolProbity Score (Model 1, Stage 1)

	Before prime refinement				After prime refinement
	Clash score (Perc)	Rama favored	MolP score	Side Acc (%)	Clash score (Perc)	Rama favored	MolP score	Side Acc (%)
AM1	19.3(34)	87.6	3.2	38	7.3(85)	89.4	2.8	38
AM2	17.4(40)	93.7	2.8	45	8.7(78)	94.2	2.0	54
AM3	6.4(89)	91.6	2.4	51	4.6(95)	93.0	2.2	51
AM4	9.6(74)	94.4	2.4	49	1.8(99)	95.3	1.3	50
AM5	22.2(27)	93.6	3.0	36	5.7(92)	93.6	2.4	43
AM6	10.3(70)	95.5	2.6	41	5.9(91)	95.5	2.1	52
AM7	16.3(44)	94.5	2.6	54	3.8(96)	95.0	1.8	56
AM8	24.5(22)	93.7	3.1	44	15.5(48)	92.9	2.7	49
AM9	19.2(35)	93.1	3.0	48	11.7(64)	94.1	2.7	62
AM10	25.7(20)	92.4	3.2	46	15.9(46)	92.8	2.8	48
AM11	12.8(59)	94.0	2.6	42	4.5(95)	95.4	1.8	39

Compared with the crystal structure, the refinement also improves the side chain accuracy. A correct side chain prediction is defined as the χ1 angle within 30 degrees of the corresponding crystal structure. “Side Acc” is the percentage accuracy of all side chains on the model. “Clash score” shows both the raw score and the percentile in parenthesis. “Rama favored” is the percentage of backbone torsional angles falling within favored Ramachandran region.

H3 loop prediction in the context of the crystal structure scaffold

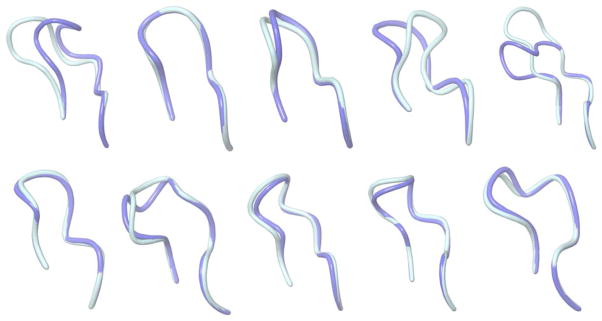
In the second stage of the assessment, all modelers were given the 10 crystal structures (the first rabbit antibody was excluded) with the H3 loops removed and asked to predict the conformations of the missing H3 loops. The purpose of this phase of the assessment is to determine how much the prediction depends on the scaffolds and how much improvement can be made if the perfect scaffolds are available. Figure 3 shows graphical illustrations of our predicted H3 loop (the first model among five submitted models) and the comparison with the crystal structure. Table V provides the backbone RMSD and side-chain χ1 angle accuracy of all five submitted models for each antibody, as well as our #1 model performance relative to that of other AMA-II participants. The average backbone RMSD of the first models is 1.28 Å. The five models are ranked by their Prime energy, and the model backbone accuracy is generally consistent with their ranking. Notably, our predictions rank the best among all AMA-II participants for 7 of the 10 targets in this category, and are within a fraction of an Å to the best model for two more of targets. In only one case (target 5) is our method significantly worse than the best approach by another group. Interestingly, in this case, one of our alternative models (#4 model) would have placed this prediction as the best among all groups.

Figure 3.

Graphical illustrations of the predicted H3 loop structures (model 1, stage 2) and corresponding crystal structures. The crystal structures and the predictions are colored turquoise and blue, respectively. From left to right: top: AM2-AM6; bottom: AM7-AM11.

Table V.

Top Five Models for the H3 Loop Prediction in the Context of the Crystal Structure Scaffold

	Model 1		Model 2		Model 3		Model 4		Model 5		Model 1 rank versus other methods29
	RMSD	χ1 (%)	RMSD	χ1 (%)	RMSD	χ1 (%)	RMSD	χ1 (%)	RMSD	χ1 (%)
AM2	2.78	63	1.78	63	2.54	50	2.14	25	2.81	38	2
AM3	0.37	63	1.28	75	0.80	75	1.14	75	0.89	50	1
AM4	0.65	75	1.09	63	1.27	63	1.18	63	0.74	75	4
AM5	2.37	63	3.42	38	2.10	38	0.36	50	3.92	50	6
AM6	3.11	46	4.53	54	4.04	31	8.54	15	6.08	31	1
AM7	0.45	43	1.67	29	1.69	86	1.15	57	0.37	57	1
AM8	1.25	57	1.61	71	3.57	57	1.77	43	1.33	43	1
AM9	0.54	75	3.40	38	3.14	25	3.72	50	3.10	63	1
AM10	0.85	63	1.74	63	3.30	63	3.54	50	5.49	63	1
AM11	0.40	50	1.46	75	2.17	50	0.89	38	0.45	50	1
Average	1.28	60	2.20	57	2.46	54	2.44	47	2.52	52

For each model, the backbone RMSD and side chain χ1 angle accuracy are reported. Side chain accuracy is defined as the χ1 angle within 30 degrees of the corresponding crystal structure. The model 1 ranks among all participating groups in AMA-II are also reported in the last column based on Ref. 29.

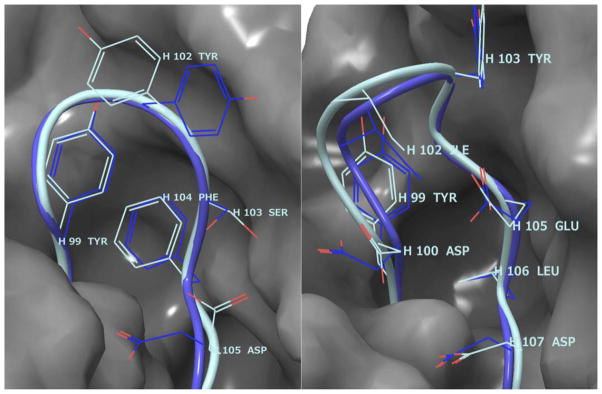
Considering the high accuracy of loop backbone predictions, it is interesting to examine how well the side chains are predicted. From Table V, however, we do not see strong correlations of side chain prediction accuracy and the backbone RMSDs. For example, the side chain accuracy of model 1 averaged over the six H3 loops where the backbone RMSD is less than 1.0 Å is 63%; for the three H3 loops where the backbone RMSD is greater than 2.0 Å, the average side chain accuracy is 57%. The side-chain prediction accuracy for very accurate loop backbone predictions is not much better than that for the incorrectly predicted loops. A possible explanation for this is that the side-chain conformations are highly opportunistic—they can take distinctively different states depending on slight variation of the backbone positions. For buried side chains, the flexibility may be very limited, but surface residues can have much freedom to take different conformations without much energy costs. Figure 4 shows the side-chain predictions of AM7 and AM9. Both predictions have excellent backbone RMSDs (0.45 Å and 0.54 Å, respectively), but side-chain predictions are very different: 43% versus 75%. The buried side chains are always predicted correctly according to the crystal structure, but the surface residues may not necessarily assume the crystal structure conformations, although the loop backbones are predicted very accurately. This suggests that the observed difference in the side chain fine detail may not reflect a weakness of the prediction algorithm as much as the ability of these residues to adjust based on their environment.

Figure 4.

H3 loop Side chain prediction accuracies of AM7 (left) and AM9 (right). The H3 loops are shown on the surface of the rest of the protein. The turquoise is the crystal structure and the blue is the prediction. The backbone RMSD and side chain accuracy for AM7 are 0.45 Å and 43%, respectively. The correct side predictions are H99, H100 and H104, and the incorrect predictions are H102, H103, H105, and H106. The backbone RMSD and side chain accuracy for AM9 are 0.54 Å and 75%, respectively. The correct side predictions are H99, H102, H103, H105, H106, and H107; the incorrect predictions are H100 and H108. Some of the side chains are omitted for clarity.

Knowledge-based and energy-based methods on H3 loop prediction

Table VI shows a direct comparison of H3 loop predictions made using both homology modeling and the Prime ab initio method. As more antibody structures become available, the chances of finding a good template for H3 loop in the database will continue to improve. However, there is still much room for improvement for homology modeling, as demonstrated by the fact that homology model predictions are often significantly worse than the best available template (columns 3 and 4). The ab initio prediction method in Prime does not depend on the structure database, and its accuracy on crystal structure scaffolds is in most cases as good as the best template in the database. In fact, in several cases the ab initio H3 prediction is significantly better than any template in the PDB. On the other hand, Prime performance is sensitive to the loop environment. The relative advantages to homology modeling decreases as we move from a “perfect” crystal structure to an inaccurate homology model for the remainder of the structure. One of the reasons is that the Prime energy function is sensitive to structural errors in the “fixed” regions, such as shifted backbone positions, misplaced side-chain rotamers, and incorrect protonation states. A direct Prime energy evaluation of the knowledge based homology model with minimization usually does not yield favorable energy. Furthermore, the sampling problem is more challenging for homology models, as a small change in the nearby environment can greatly influence the generation of a structural candidate ensemble.

Table VI.

Comparison of H3 Loop Predictions with Homology Modeling and the Prime Ab Initio Method

H3 RMSD (Å)	H3 length	Best in database	Using crystal structure		Using homology model
			Homology prediction	Prime prediction	Homology prediction	Prime prediction
AM2	11	1.69	4.35	2.78	6.49	2.29
AM3	8	0.88	1.48	0.37	1.41	1.49
AM4	8	0.72	2.20	0.65	3.31	2.04
AM5	8	1.00	2.35	2.37	1.80	1.78
AM6	14	2.60	3.12	3.11	3.04	4.69
AM7	8	1.46	2.33	0.45	1.88	1.50
AM8	11	1.68	3.30	1.25	3.34	3.99
AM9	10	0.73	1.89	0.54	2.50	3.78
AM10	11	1.53	2.79	0.85	2.27	2.05
AM11	10	0.37	2.56	0.40	3.10	3.10
Average		1.26	2.64	1.28	2.91	2.67

Best in database: The H3 loop in the PDB database with the best backbone RMSD to the crystallographic conformation of the target H3 loop. Using crystal structure: H3 loops built in the context of the remainder of the antibody structure taken from crystallographic coordinates. Using homology model: H3 loops built in the context of the remainder of the antibody structure taken from our “Model #1” submission from the first part of this assessment.

CONCLUSIONS

AMA-II has offered an opportunity for blinded testing of our approach to antibody homology modeling and refinement, as implemented in the programs BioLuminate and Prime within Schrodinger Suite. Our homology modeling features a novel knowledge based approach to modeling the CDR loops, using a combination of sequence similarity, geometry matching, and the clustering of database structures. This method does not rely on the antibody canonical classes or other specific rules, and performs on par with the state of the art antibody modeling methods. Our homology models benefit significantly from the energy-based refinement, as demonstrated by the side-chain placement and H3 loop prediction. The ab initio loop prediction method in Prime performs very well when applied to repredicting the H3 loops in the context of crystal structures. Its accuracy on homology models degrades, but the method still performs better than the best database approach presented here. The refinement of homology models, in terms of reducing backbone RMSDs, still remains a very challenging problem. Its success depends heavily on the starting homology models and it should be used with caution. One particular situation where we have shown Prime works well²⁴ is when the template and target structure are highly homologous and the structural differences are relatively isolated (e.g. two antibodies with only differences in H3 loops and with minor changes in other CDR loops). This is a relatively common real-world scenario in antibody optimization, for which we expect our methods will be useful.