Ensemble perception of size in 4–5 year-old children

Abstract

Groups of objects are nearly everywhere we look. Adults can perceive and understand the “gist” of multiple objects at once, engaging ensemble-coding mechanisms that summarize a group’s overall appearance. Are these group-perception mechanisms in place early in childhood? Here, we provide the first evidence that 4–5 year-old children use ensemble coding to perceive the average size of a group of objects. Children viewed a pair of trees, with each containing a group of differently sized oranges. We found that, in order to determine which tree had the larger oranges overall, children integrated the sizes of multiple oranges into ensemble representations. This pooling occurred rapidly, and it occurred despite conflicting information from numerosity, continuous extent, density, and contrast. An ideal observer analysis showed that although children’s integration mechanisms are sensitive, they are not yet as efficient as adults’. Overall, our results provide a new insight into the way children see and understand the environment, and they illustrate the fundamental nature of ensemble coding in visual perception.

Introduction

Take a trip to the market and you will appreciate how readily people perceive and evaluate groups. Dozens of oranges are seen not as individual objects, but as collectives of small and large, groups of clementines and Valencia. Gestalt impressions such as these provide a window into the phenomenology of visual experience, revealing that much of awareness is at the level of the group (Koffka, 1935). But there is an apparent paradox about this kind of perception. The capacity limits of attention and memory only allow us to perceive and remember precise information about a few objects at a time (Awh, Barton, & Vogel, 2007; Luck & Vogel, 1997; Scholl & Pylyshyn, 1999; Simons & Levin, 1997; Whitney & Levi, 2011). How then, does the visual system overcome these bottlenecks and enable us to see what a group of objects is like all at once, as a collective?

To see groups, adults engage a process known as ensemble coding. In ensemble coding, information about multiple objects is compressed into a summary statistic—a singular representation that provides access to the group in the form of a gist percept (for reviews, see Alvarez, 2011; Whitney, Haberman, & Sweeny, 2013). This compression is what allows ensemble codes to overcome capacity limits, providing more information about groups than would be possible by inspecting each member of a set, one after another. In fact, with ensemble coding, precise information about individuals, like each orange’s unique size, is lost in favor of the group percept, like the average size of all the oranges in the group (Ariely, 2001; Haberman & Whitney, 2009, 2011). Moreover, ensemble codes need not be drawn from every member in a group (Dakin, Bex, Cass, & Watt, 2009)—rapid averaging across a subset of members is enough to provide surprisingly high sensitivity, even when there is insufficient time to serially attend to individual group members (e.g., Sweeny, Haroz, & Whitney, 2013). In fact, this averaging process overcomes noise in local representations (Alvarez, 2011), allowing adults to perceive crowds more precisely than they perceive individuals (Sweeny, Haroz, & Whitney, 2013). Efficient and sensitive, ensemble codes underlie an important part of conscious phenomenology, providing the gist experience that allows adults to regard sets of objects as holistic groups with particular collective characteristics. We might think of ensemble perception as involving a kind of “lantern consciousness” in which many objects are seen at once, rather than the more focused “spotlight consciousness” that comes with attention to individual objects (Gopnik, 2009).

Less is known about what visual experience is like early in life. Do children see their surroundings like adults, appreciating multiple objects as groups with collective properties? Or is children’s visual experience simply noisier, or less cohesive in general than adults’? Children’s perception is certainly coarse—spatial and temporal resolution develop slowly (Benedek, Benedek, Kéri, & Janáky, 2003; Ellemberg, Lewis, Liu, & Maurer, 1999; Farzin, Rivera, & Whitney, 2010, 2011; Jeon, Hamid, Maurer, & Lewis, 2010), and crowding, the impairment in perceiving an individual item when it is surrounded by clutter, is particularly strong in childhood (Jeon, et al., 2010; Semenov, Chernova, & Bondarko, 2000). Moreover, children’s attentional capacities are also limited compared to those of adults, particularly their capacities for focused, endogenous top-down attention (Enns & Girgus, 1985; Goldberg, Maurer, & Lewis, 2001; Johnson, 2002; Ristic & Kingstone, 2009). These limitations make it easy to imagine that, when children are viewing many objects at once, their visual experience would be noisy and fractured rather than holistically coherent.

On the other hand, studies of cognitive development show that even infants are remarkably sensitive to statistical and relational features of scenes, and that they seem to discriminate scenes based on judgments about those features (e.g., Spelke, Breinlinger, Macomber, & Jacobson, 1992; Fiser & Aslin, 2002; Kirkham, Slemmer, & Johnson, 2002; Xu & Garcia, 2008). Furthermore, children are adept at making inferences from subtle statistical cues even by preschool age (see Gopnik & Wellman, 2013, for a review).

Children, might, in fact, be able to mitigate their perceptual and attentional limitations by engaging ensemble-coding strategies. By pooling independent samples of similar objects, children may be able to average out the noise, improving their visual sensitivity to perceive groups of objects in scenes. Here, we sought to test these competing hypotheses by determining whether or not ensemble perception mechanisms are in place in childhood.

Specifically, we asked: when 4–5 year-old children see many objects at once, do they determine the average object size in the group by considering information from multiple objects (i.e., ensemble coding), or do they make coarse judgments about the group based only on a single object? Judgments of ensemble size based on just one object are likely to be coarse, and, not ideal, because the size of the sampled object may not necessarily be representative of the entire group. We investigated perception of size for two reasons. First, ensemble size perception is robust and well understood with adults (e.g., Ariely, 2001; Chong & Treisman, 2003). Second, size is a relatively simple visual feature in the hierarchy of visual processing (Desimone & Schein, 1987; Dumoulin & Hess, 2007). We therefore reasoned that if any ensemble coding is operative in childhood, it is likely to be manifested in a judgment of size.

While the perception of basic collective properties of homogeneous groups, like numerosity, comes online early in life (Zosh, Halberda, & Feigenson, 2011), it is still unclear if children possess the ensemble processes necessary to summarize properties of heterogeneous groups. This distinction is critical. Only ensemble coding affords humans the ability to average information across many individuals that differ in appearance, telling us not just how much stuff there is, but what that stuff is like. Thus, the current research represents an important advance in understanding the development of complex group perception.

Why would it matter if ensemble mechanisms were or were not in place in childhood? Adults are already known to use ensemble coding to overcome their own perceptual limitations. Specifically, pooling information into gist percepts allows adults to recover information about individuals that would otherwise be inaccessible or unrecognizable due to crowding (Fischer & Whitney, 2011), visual short term memory capacity (Alvarez & Oliva, 2008; Haberman & Whitney, 2011), attentional capacity (Chong & Treisman, 2003), or even congenital deficits in recognition ability (Yamanashi Leib et al., 2012). If children also possess ensemble mechanisms, they could, in principle, use them to overcome their own capacity limits. This would be especially useful at 4–5 years of age, when children’s perception of individual objects is already more limited than that of adults’, and is constrained by gradually developing spatial resolution (Farzin, et al., 2010), selective attention (Enns & Girgus, 1985; Goldberg, et al., 2001; Johnson, 2002; Ristic & Kingstone, 2009), and visual working memory capacity (Cowan, AuBuchon, Gilchrist, Ricker, & Saults, 2011; Simmering, 2012; Wilson, Scott, & Power, 1987). For these reasons, we tested 4–5 year old children. Testing children at this age has an additional benefit—we could ask them to make explicit judgments of groups in the same experimental paradigms as those used with adults, which would allow us to directly compare the strength of children’s and adults’ ensemble integration capabilities.

If ensemble perception mechanisms are in place early in life, then just like adults, children should be able to use ensemble coding to extract information about average size in a group of objects. Alternatively, finding that children are unable to access summary information at the level of the group would reveal that their visual experience is even more limited than previously thought. As such, our results should have far-reaching implications, not just for characterizing the development of ensemble coding for the first time, but also for providing new insights into the phenomenology of visual experience in childhood.

Experiment 1

Methods

Observers

Ten children (M = 4.67 years, SD = 0.58 years, five females and five males), and ten adults (M = 28.9 years, SD = 4.6 years, five females and five males) participated in the experiment.

Stimuli

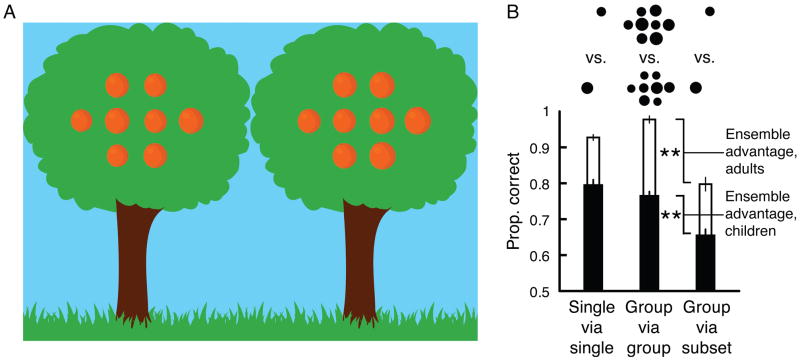
Children were seated in front of a laptop but were free to move during the experiment, so the visual angles noted below represent the size of the stimuli from an average distance of 57 cm. These values would have varied between −15% and +20% given 10cm of movement forward or backward. Because children are more likely to cooperate when an experiment is presented as a game, we created a cartoon scene which we described as a chance to help a “hungry monkey” determine which of two trees had the largest oranges (Figure 1A). Every aspect of this cartoon scene was prepared in Photoshop (Adobe Photoshop CS5 Version 12.0). Oranges had an orange hue. The two trees were identical (16.1° × 19.2°), each with a green top and a brown trunk. The edges of the trees abutted one another. The cartoon monkey (2.1° × 4.81°) had brown fur. Green grass lined the bottom border of the screen (30.1° × 2.61°). Oranges were presented along an invisible grid (9.85° × 6.6°) centered in each tree. The entire scene appeared over a blue background.

Figure 1.

A) Each tree had a range of differently sized oranges. In the group condition, multiple orange were available within each tree for determining which had the largest oranges, overall. In the single condition (not shown), only a randomly selected pair of oranges from different sets of full groups was visible. Both the single-via-single analysis and the group-via-subset analysis were conducted on the same data from the single condition. B) Children (black bars) selected the tree with the largest oranges, overall, more often when the full sets of oranges were visible (shown in the group-via-group analysis) compared to when only a single orange (a subset) was visible in each tree (shown in the group-via-subset analysis). This occurred despite high sensitivity for discriminating individual oranges observed in the single-via-single analysis. Adults (white bars) showed the same pattern. ** represents p < .01. Error bars reflect ±1 SEM (adjusted for within-observer comparisons).

On each trial, we generated groups of eight oranges for each tree. Each tree contained four different orange sizes, and one tree (randomly determined as the right or left) had slightly larger oranges, on average. Individual orange sizes ranged from 1.69° – 2.58° across trials. On each trial, the range of orange sizes within each tree (0.294°) and the difference in average orange size between the trees (0.147°) remained constant. Each orange in the left tree was always a different size than any orange in the right tree. Across trials, the average orange size collapsed across both trees ranged from small to large (1.91°, 1.97°, 2.02°, 2.06°, 2.11°, 2.16°, 2.21°, 2.26°, 2.31°, or 2.36°). On a given trial, the average orange size in either tree was always .074° smaller or larger than one of these values. Oranges based around these ten sizes were each generated four times for a total of 40 trials across two blocks of 20 trials each. The variability in orange sizes within each tree and the overlapping sizes between the trees served an important purpose – it ensured that sampling multiple oranges from each tree (i.e., building ensemble representations) would lead to better judgments of average size than simply comparing a single orange from each tree (see Table 1 for a detailed description of orange sizes, conditions, and analyses in two hypothetical trials).

Table 1.

Conditions, analyses, individual oranges sizes, and group average sizes from two hypothetical trials in Experiment 1. In each trial of each condition, a separate group of eight oranges was generated for the left and right tree. For simplicity in this table, the sizes (diameter, in pixels) of the oranges in each tree are listed in order from smallest to largest. In the group condition, in which all eight oranges were presented and visible in each tree, we analyzed how well children and adults evaluated the average size in each tree—the group-via-group analysis. In this trial of the group condition, the right tree happens to have the larger average orange size (80 pixels). Note, however, that the largest orange in the left tree was larger than the smallest orange in the right tree. This illustrates how comparing a random pair of oranges in each tree would not always lead to a correct response about the groups. In the single condition, eight oranges were again generated for each tree, but only one randomly selected orange (in bold) was visible in each tree. The rest of the oranges (in italics) were not presented. We conducted two analyses—the single-via-single analysis and the group-via-subset analysis—on the same data from the single condition. The single-via-single analysis allowed us to evaluate sensitivity for comparing individual oranges. Here, the orange in the right tree (92 pixels) is the largest, and selecting the right tree leads to a correct answer in the single-via-single analysis. The group-via-subset analysis allowed us to determine what performance in the group condition would have been like had observers based their estimates on a single randomly selected orange in each tree. Here, accurately comparing this randomly selected pair of oranges would not have led to a correct response about the groups. Better performance in the group condition relative to this simulated performance in the group-via-subset analysis would mean that observers’ did not simply compare random pairs of oranges in the group condition

Condition	Analysis		Tree	Orange sizes (1–8)								Group Avg
GROUP	Group-via-group		L	68	68	72	72	76	76	82	82	74
			R	74	74	78	78	82	82	86	86	80
SINGLE	Single-via-Single	Group-via-Subset	L	86	86	90	90	94	94	98	98	92
			R	80	80	84	84	88	88	92	92	86

Procedure

Each trial began with a cartoon monkey standing equidistant from the pair of trees. Each observer was free to look directly at the oranges for an unlimited duration, and then indicated which tree had the larger oranges, overall, by moving the monkey (4.31° leftward or rightward) under one of the trees using the left or right arrows on a keypad. Next, the observer pressed the spacebar once to finalize his or her response and again to start a new trial. A practice block of four trials preceded the main experiment. In this practice block, the experimenter explained (1) that the monkey was hungry and preferred to eat large oranges, (2) that the observer could help the monkey by moving him to the tree with the larger oranges, overall, and (3) that the observer should consider the sizes of all of the oranges visible to him or her when making a decision.

On half of the trials, full groups of eight oranges appeared in each tree (Figure 1A) – the group condition. In our analysis of this condition, we calculated the proportion of trials in which each observer selected the tree with the largest average orange size, presumably via an evaluation of the groups. We refer to this as the group-via-group analysis.

However, the main objective of this investigation was not simply to determine if children performed well when comparing groups. Rather, it was to determine how much information they used to evaluate these groups. To answer this question, we included a control condition—the single condition—to determine what performance would have looked like if children judged the groups simply by comparing a single orange from each tree. Specifically, on the other half of trials, we again generated full groups of eight oranges for each tree, but only displayed a single randomly selected orange (i.e., a subset) from each tree. We recorded the average orange size in each full group as well as the sizes of the single randomly displayed oranges. Trials from both conditions were intermixed within both blocks.

We analyzed the data from this same set of trials in the single condition in two different ways. In the group-via-subset analysis, we calculated the proportion of trials in which each observer’s selection (made via the subsets, each of which always contained just one orange) happened to also be the tree with the largest group average. This calculation simulated what performance would have looked like in the group condition if observers had based their judgments on a single orange in each tree. The purpose of this single condition, as analyzed in this way, was not to ask observers to make judgments of groups that they could not see, which would be impossible. Rather, this analysis is analogous to an empirical simulation of what performance in the group-via-group condition would have looked like if observers had not engaged crowd perception, combining information from several objects, but instead had based their judgment on a single object that we randomly selected for them.

In the single-via-single analysis, we calculated the proportion of trials in which each observer selected the tree that contained the subset with the largest orange. That is, within the single condition, we simply determined how often the observer chose the tree with the larger single orange. This latter calculation allowed us to measure baseline sensitivity to individual size differences (see Table 1 for a detailed description of these analyses in two hypothetical trials).

If observers utilize ensemble coding, they will select the tree with the largest oranges, overall, more often when the full groups are visible. Performance should be better in the group condition than in the group-via-subset analysis of the single condition —the ensemble advantage. This should occur despite high baseline sensitivity for comparing individual oranges and concomitant high performance in the single-via-single analysis.

Results

Children showed high sensitivity for comparing the sizes of individual oranges; they were very accurate at determining which single orange was larger (the single-via-single analysis; Figure 1B). They were also highly precise and accurate when they compared groups of oranges (the group-via-group analysis). Performance in the single-via-single analysis and the group condition were strongly correlated (R² = .868, p < .01). Most importantly, children’s comparisons of groups would have been less precise if they had been made via a single random pair of oranges; children selected the tree with the larger oranges less often when only a single randomly selected orange was visible from each group (t[9] = 4.13, p < .01, Figure 1B). This difference—the ensemble advantage—directly shows that when children made judgments about groups of oranges, they did so by evaluating information from multiple oranges and not just by using a single orange within each group.

Adults were excellent at discriminating the sizes of individual oranges, making even fewer errors than children in the single-via-single analysis, t(18) = 2.61, p < .05). Adults were also adept at perceiving groups, and they made more precise comparisons of groups via consideration of multiple oranges in each tree (the ensemble advantage: t[9] = 4.91, p < .01, Figure 1B). Overall, the similar pattern of results from children and adults suggests that ensemble coding is in place even at 4–5 years-of-age. Thus, while children’s perception is certainly noisier, consistent with previous results (Benedek, Benedek, Kéri, & Janáky, 2003; Ellemberg, Lewis, Liu, & Maurer, 1999; Farzin, Rivera, & Whitney, 2010, 2011; Jeon, Hamid, Maurer, & Lewis, 2010), they appear to employ an ensemble coding strategy which averages out noise and achieves a more precise percept of the group than would otherwise be possible.

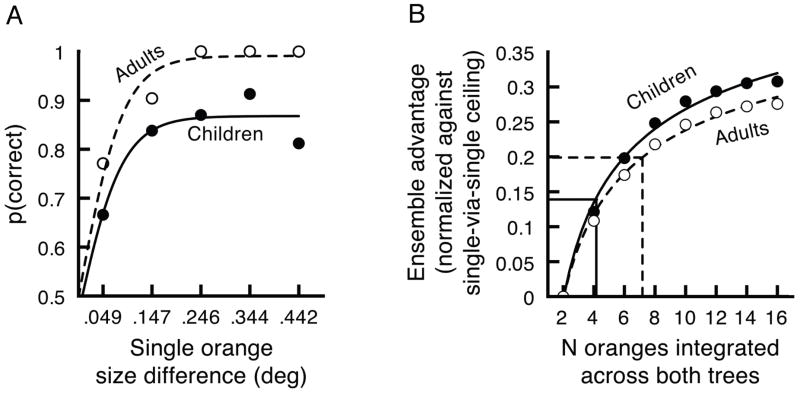
Exactly how refined are children’s group perception mechanisms? In order to properly evaluate children’s sensitivity to groups, it was first necessary to determine if their lower overall performance was due to perceptual limitations, or instead due to lapses in attention or motivation. We accomplished this by deconstructing data from the single-via-single analysis, evaluating performance across the wide range of size differences that resulted from randomly selecting and displaying a single orange from each tree. Specifically, we separately concatenated data from children and adults, and then measured each group’s discrimination performance as a function of the differences in size between the two randomly visible oranges. For both children and adults, the proportion of correct responses increased with larger differences in size, and these increases were well fit by logistic functions (children; R² = .852, adults; R² = .911, Figure 2A). We then used these logistic fits to separately derive probability density functions representing children and adults’ sensitivities to size differences. Specifically, using our logistic fits from Figure 2A, we simply determined the increase in percent correct that accompanied incremental increases (in 0.2 degree steps) in the size difference of the two oranges being compared. This yielded half of a Gaussian-shaped distribution, which we then mirrored to produce a full probability density function separately for children and adults. The standard deviations of these density functions were remarkably similar (children; SD = .098°, adults; SD = .10°).

Figure 2.

A) Children’s and adults’ abilities to discriminate size in the single-via-single analysis. Both groups’ performances improved with larger differences in size and were well fit by logistic functions. We used these logistic fits to simulate early-stage noise in our ideal observer analysis. B) Number of oranges that children and adults integrated across both trees, estimated from our ideal observer analysis. We used a linear pooling algorithm to predict the ensemble advantages that children (filled circles) and adults’ (open circles) would gain from integrating different numbers of oranges in each tree. The intersection of children and adults’ observed ensemble advantages (horizontal lines) with power functions fitted to our predicted ensemble advantages provided estimates of the number of oranges each group integrated across both trees (vertical lines).

This similarity has two important implications. First, it indicates that children’s sensitivity for comparing the sizes of individual objects is fully developed at 4–5 years-of-age. Second, it shows that children’s lower baseline level of performance reflected non-perceptual limitations, meaning that any comparison of children and adults’ sensitivity to groups should be made independently of this baseline difference. That is, the differences between children and adults were not due to basic differences in their perceptual abilities, but were more likely due to lapsing, inattentiveness, or a decision stage process. Children might, for example, be less good than adults at actually implementing the decision to pick a particular tree.

Ideal Observer Analysis

How sensitive are children’s group perception mechanisms compared to adults’? How many oranges did children and adults integrate into their ensemble codes? To answer these questions, it was first necessary to calculate children’s and adult’s improvements in proportion correct—their ensemble advantages—independently of baseline differences in performance. Specifically, we divided each observer’s ensemble advantage by his or her ceiling performance in the single-via-single analysis. We then performed an ideal observer analysis to estimate the number of oranges children and adults would have needed to integrate to produce these observed ensemble advantages. This analysis is straightforward and conservative; similar linear pooling models have successfully characterized ensemble coding in adults (Parkes, Lund, Angelucci, Solomon, & Morgan, 2001; Sweeny, Haroz, & Whitney, 2012). This assumption of linearity is reasonable considering (1) the small range of sizes in this experiment (Chong & Treisman, 2003), and (2) the very similar results we obtained when we ran this same ideal observer analysis using values adjusted to reflect the compressive-non-linear nature of size perception (Teghtsoonian, 1965).

We began our ideal observer analysis by simulating performance in the group-via-group analysis and the group-via-subset analysis. First, we generated eight orange sizes for each tree using actual values from the experiment. Next, we simulated noisy perception of each orange by (1) centering Gaussian-shaped sampling distributions at each simulated orange size, each with a standard deviation equal to our estimates of children’s or adults’ single-orange sensitivity (see above) and (2) sampling a random value from each distribution. This sampling produced groups of eight noise-perturbed oranges in each tree. Last, we simulated performance that would have occurred with different numbers of oranges integrated. We started by randomly selecting subsets (1–7) of our simulated oranges or the full group of eight oranges from each tree. For each simulated subset in each tree, we calculated the average orange size (the linear mean of the subset) and selected the tree with the largest average value as the simulated response. We did not add noise in this integration stage. As in our experiment, we noted if the simulated response (based on each subset) matched the correct response that would be obtained from comparing the averages of the full groups in each tree.

We completed this procedure 50,000 times and determined the proportion of these trials in which each number of oranges integrated (e.g., four across both trees, five across both trees, etc.) produced the correct response. We then calculated the difference between these values and the proportion of correct responses that would have been obtained from using a subset of one orange from each tree. In this way, we simulated the ensemble advantages children and adults would have produced by integrating different numbers of oranges (Figure 2B). We then fit the increase in these simulated ensemble advantages with a power function. The fits were excellent (R² > .977, p < .01 for children and adults). By locating the points where children’s and adults’ observed ensemble advantages intersected with these fits, we were able to estimate the number of oranges that each group integrated into their respective ensemble codes (Figure 2B). We found that, across both trees, children integrated at least 4.24 oranges and adults integrated at least 7.18 oranges. We obtained similar patterns of results by comparing subsets with different sizes but equivalent totals (e.g., averaging four and two oranges from each tree instead of three and three from each tree). However, for each combination with unbalanced subsets, it would have been necessary to integrate more oranges than with balanced subsets, with even the closest estimates requiring an extra orange to be integrated. While we cannot be sure what approach observers used, especially on any given trial, our approach of using balanced subsets at least provides the most conservative estimate of the number of oranges integrated.

This analysis takes into account the differences in attention, motivation, decision-making and other sources of noise that are reflected in the differences between adults and children on the single-orange task. However, like other ideal-observer simulations of ensemble coding (Myczek & Simons, 2008), ours does not include late-stage noise in the integration process. Accounting for this attribute of real, imperfect observers would only increase estimates of integration efficiency since more samples would need to be pooled to reach the observed enhancement. As such, our simulation provides a conservative, lower-bound estimate of integration efficiency. We also do not know whether there might be developmental differences in this late-stage noise, or whether such differences would influence the relative size of the ensemble advantage for adults and children.

Experiment 2

The children in our first experiment showed a pattern of results consistent with integrating multiple oranges to perceive average size. Nevertheless, their sensitivity to single oranges was positively correlated with their sensitivity to groups. In order to be sure that children possess a distinct mechanism for evaluating crowds, it is important to demonstrate that sensitivity to crowds persists even when it is dissociated from sensitivity to individual objects. We thus conducted Experiment 2 to determine if children can be good at perceiving crowds despite poor sensitivity to individuals. Such a result would clearly show that children do indeed possess unique ensemble size representation. Additionally, we wanted to determine whether or not sensitive crowd perception persists when children have insufficient time to serially attended to individual oranges and cognitively compute the average size. This alternative strategy could have been possible with the unlimited viewing duration in Experiment 1, and might not qualify as ensemble coding (Myczek & Simons, 2008), in which the average percept is achieved through rapid integration in parallel, bypassing the need for focused attention. Rejection of this kind of focused-attention strategy has been important for providing rigorous evidence of summary statistical perception (Ariely, 2008; Chong, Joo, Emmanouil, & Treisman, 2008; Myczek & Simons, 2008), and it is especially relevant here, since larger objects are known to draw bottom-up attention over smaller objects when in groups (Proulx, 2010; Treisman & Gormican, 1988).

To evaluate both of these questions, in Experiment 2, we tested whether the integration we observed in Experiment 1 could occur when children viewed groups for only 1,500 msec. We reasoned that, with this shorter viewing time, children would be more likely spread their attention to access the gist of the crowds independent from, and at the expense of, sensitivity to individual oranges. Although 1,500 msec may seem relatively long compared to durations typically used in research with adults, it was the shortest duration that children would endure in a round of pilot testing. Importantly, we began Experiment 2 with a preliminary investigation (Experiment 2A), which confirmed that 1,500 msec was an insufficient amount of time for children to engage a serial search strategy for the largest orange.

Experiment 2A

Methods

Observers

A new group of twenty children (M = 4.26 years, SD = .877 years, seven females and thirteen males), and a new group of twenty adults (M = 20.28 years, SD = 2.39 years, twelve females and eight males) participated in the experiment.

Stimuli and Procedure

The stimuli and procedure were identical to those in Experiment 1, with oranges displayed until each observer responded. The only exception was that observers were instructed to point to the largest orange on the screen as quickly as possible. The experimenter made sure that each child was looking at the screen before pressing the spacebar to initiate the trial. The experimenter pressed the right- or left-arrow key as soon as the child pointed to the screen, taking care to respond as soon as the child’s finger clearly indicated the orange of his or her choice. The experimenter repeated the instructions to find the largest orange and point to it as quickly as possible throughout the experiment. The same procedure was used for testing adults so that any experimenter-imposed response delay would be equivalent across reaction times for children and adults. Children completed ten trials from the group condition and ten trials from the single condition, all in a single block of testing. Adults completed twice the number of trials intermixed across two-blocks of testing.

Results

To obtain a conservative estimate of reaction times, we removed trials in which RTs were greater than 2.5 standard deviations from each observer’s mean reaction time. We conducted this trimming separately for trials where an observer viewed groups and trials where that same observer viewed a single orange in each tree. We did not exclude trials based on whether or not the observer actually pointed to the largest orange.

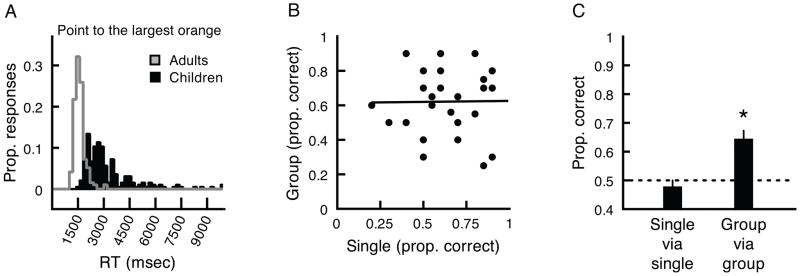
Not surprisingly, children responded faster on trials where a single orange was presented in each tree (M = 2,607 msec, SD = 780 msec) compared to when a group was presented in each tree (M = 2,984 msec, SD = 1,042 msec), t(19) = 2.77, p < .01, d = .619. Critically, mean RTs on trials where children viewed groups were longer than 1,500 msec, t(19) = 6.37, p < .01, d = 1.42. A histogram combining raw RTs from all children clearly shows that, on trials from the group condition, 99.48% of individual RTs were greater than 1,500 msec (Figure 3A). There was no relationship between RT in the group condition and age, R² = .087, n.s. While some portion of children’s reaction times reflects the additional time it took for the experimenter to record his or her response, this added time would have been equivalent for each observer in each condition, and it is reasonable to expect that it would have been relatively small, as the experimenter recorded the child’s response as soon as his or her finger touched the screen.

Figure 3.

A) Histograms of children’s (black bars) and adults’ (gray line) reactions times for pointing to the largest orange on the screen in Experiment 2A. RTs from individual trials were pooled for each group after extreme RTs were excluded separately for each observer (see text for details). Note that children’s RTs were overwhelmingly longer than the 1,500 msec they had to view the oranges in Experiment 2B. B) With the shorter presentation time in Experiment 2B, there was no relationship between children’s sensitivity to single orange size differences and group size differences. C) Based on a median split, the children who had the lowest sensitivity for comparing individual orange sizes (not above chance-level performance, left bar) showed higher sensitivity for comparing the sizes of groups. * represents p < .01. Error bars reflect ±1 SEM (adjusted for within-observer comparisons).

Like children, adults responded faster on trials where a single orange was presented in each tree (M = 1,180 msec, SD = 112 msec) compared to when a group was presented in each tree (M = 1,387 msec, SD = 171 msec), t(19) = 7.29, p < .01, d = 1.63. Unlike with children, adult’s mean RTs on trials from the group condition were shorter than 1,500 msec, t(19) = 2.81, p < .05, d = .629. A histogram combining raw RTs from all adults illustrates that 77.2% of individual RTs were less than 1,500 msec (Figure 3A). Note that adult RTs included the same experimenter-produced additional delay included in child RTs.

We mention reaction times from adults merely to illustrate the relatively long amount of time it takes children to complete this particular type of visual search. While it would be odd to describe 1,500 msec as a brief duration in an experiment designed for adults, this time is indeed brief and challenging for 4–5 year-old children. Most importantly, these results confirm that 1,500 msec is an insufficient amount of time for 4–5 year-old children to point to what they believe to be the largest orange on the screen. We can thus be confident that, should children display any sensitivity for perceiving groups displayed for this duration in Experiment 2B, this sensitivity will not have emerged from engaging a serial search strategy, and it should not be related to sensitivity for perceiving single oranges.

Experiment 2B

Methods

Observers

A new group of twenty-seven children (M = 4.35 years, SD = .81 years, fifteen females and twelve males), and twenty adults (the same observers from Experiment 2A) participated in the experiment.

Stimuli and Procedure

Stimuli and procedure were identical to those in Experiment 1 in which children were instructed to determine which tree had larger oranges overall, except that the oranges were shown for only 1,500 msec. On each trial, the experimenter made sure that each child was looking at the screen before pressing the spacebar to initiate the trial.

Results

Even with the shorter duration, children were above chance for comparing the sizes of individual oranges in the single condition, (M = .642, SD = .193), t(26) = 3.84, p < .01, d = .741, and for comparing groups of oranges in the group condition, (M = .62, SD = .183), t(26) = 3.42, p < .01, d = .658. Unlike with an unlimited presentation time, sensitivity for discriminating mean size in briefly presented crowds was not related to sensitivity for discriminating the sizes of individual oranges (R² = .0001, n.s., Figure 3B). These results show that children are able to make comparisons of average size in groups without relying on their sensitivity to individual oranges.

The fact that perception of crowds and individuals were independent in this experiment allowed us to more conclusively evaluate the possibility that some observers, as a group, might have been better at extracting information from groups than from single oranges. We did this by dividing the children into two groups using a median split based on single-orange sensitivity. The thirteen children who discriminated single oranges with the lowest sensitivity (M = 47.7% correct, not significantly different from chance-level performance, t[12] = 0.68, n.s.) nevertheless discriminated the average sizes of groups of oranges above chance level (t[12] = 2.78, p < .05, Figure 3C). Moreover, and surprisingly, these children’s group discriminations were actually better than their discriminations of a single orange from each tree (t[12] = 3.13, p < .01, Figure 3C). Overall, these surprising patterns of results show that rapid-acting ensemble perception mechanisms are in place by 4–5 years-of-age and that they operate independently of sensitivity for perceiving individual objects.

Experiment 3

The findings from Experiments 1 and 2 converge to suggest that children do indeed integrate and summarize size information from multiple oranges to make evaluations of groups—ensemble coding. However, it is still possible that they could have used other information related to average size, like increased density or the amount of orange color on the screen, to make their choices. We conducted Experiment 3 to directly rule out these image-based explanations.

Specifically, we manipulated the numerosity of the groups such that one tree always had eight oranges (as in the previous experiments) and the other always had six oranges, with reduced density and total orange color displayed. This design allowed us to conclusively determine whether or not ensemble size integration is available at 4–5 years of age, and if so, how it interacts with orthogonal image-based information.

Methods

Observers

A new group of twenty children (M = 4.34 years, SD = .63 years, 13 females and 7 males), and twenty adults (the same adult observers from Experiment 2) participated in the experiment.

Stimuli and Procedure

Most stimuli and procedures were identical to those in Experiment 1, with oranges displayed until each observer responded. The only exceptions were that (1) we only included the group condition – there were no trials where a single randomly selected orange was visible in each tree, and that (2) only six oranges were visible in one of the two trees, randomly determined to be the left or right tree.

As in the single condition in Experiment 1, we generated a full set of eight oranges for each tree even when only six were displayed in one of them. For the six-orange tree, we randomly selected six oranges from this full set and displayed them in six randomly selected locations out of the eight locations possible. Thus, across trials, the oranges on the tree with six oranges were less densely spaced than those on the tree with eight oranges. Children completed 20 trials from the group condition in a single block of testing. Adults completed 40 trials across two-blocks of testing.

Results

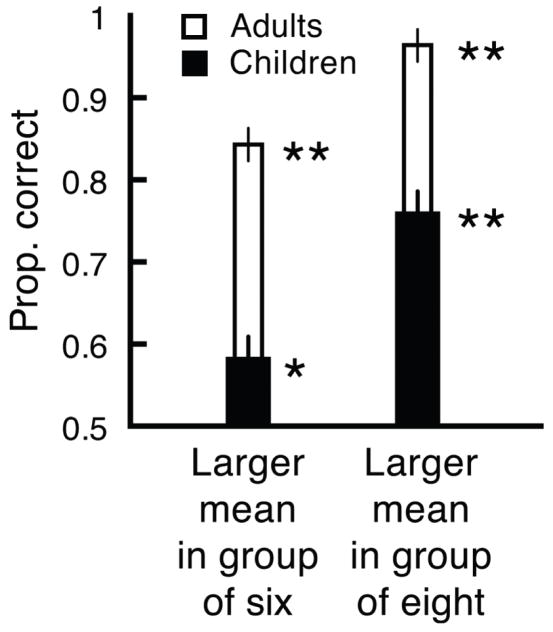
When the tree with the largest oranges also happened to be the tree showing the most (eight) oranges, both children and adults easily discriminated average orange size across the groups, and were significantly above chance (children; t[19] = 5.32, p < .01, d = 1.18, adults; t[19] = 46.9, p < .01, d = 10.49, Figure 4). More importantly, when the tree with the largest oranges happened to be the tree with lower numerosity, showing just six oranges, children and adults still discriminated the groups above chance (children; t[19] = 2.64, p < .05, d = .59, adults; t[19] = 8.50, p < .01, d = 1.90, Figure 4). Average size perception was not completely independent of numerosity, density, or the amount of orange on the screen; both children and adults showed reduced sensitivity for comparing average size when the largest-sized oranges were in the less numerous group (children; t[19] = 3.24, p < .01, d = .726, adults; t[19] = 3.14, p < .01, d = .702, compare left bars with right bars in Figure 4).

Figure 4.

Despite baseline differences in sensitivity, children (black bars) and adults (white bars) were able to indicate which group had the largest oranges, on average, even when that group had lower numerosity, density, and contrast (the group of six oranges, left bars). However, extraction of mean size was not completely independent of these orthogonal visual cues; both children and adults correctly indicated which group had larger oranges more often when that group had higher numerosity, density, and contrast.

The important point here, however, is that children can still reliably extract ensemble size information even in the face of strong interference from orthogonal image-based information. Moreover, there were actually no numerosity differences in Experiment 1, and though the density differences in Experiment 3 were larger than those in Experiment 1, the children still showed ensemble perception. Hence, the ensemble advantage in Experiment 1 could not have been due to numerosity, and is unlikely to have been due to density.

Discussion

We showed, for the first time, that ensemble-coding mechanisms are in place early in childhood. Even at 4–5 years-of-age, children were able to make precise and rapid comparisons of average size between groups. A conservative ideal-observer analysis revealed that children integrated information from more than four objects to estimate which group had larger objects overall. This value is nearly double the capacity of visual working memory at 3–5 years-of-age (Simmering, 2012), arguing against the possibility that children serially searched and compared the sizes of just a few random objects. A control experiment further ruled out this alternative hypothesis, showing that ensemble size integration proceeds even when children are unable to engage serial search. This integration process is independent of sensitivity to individual objects, and it even allowed children to extract average size information from groups despite poor sensitivity for perceiving individual objects. We also verified that this early summary-statistical pooling cannot be explained entirely by non-ensemble information, like numerosity, density, or contrast. While surprisingly sensitive, children pooled information across fewer objects than adults, indicating that adults’ remarkable ability to perceive the gist of groups and crowds develops gradually.

Our investigation provides a novel perspective on the sophistication of Gestalt perception in childhood. Previous investigations using hierarchical stimuli and coherent motion have shown that young children gradually develop sensitivity to global information in patterns and scenes (Dukette & Stiles, 2001; Ellemberg et al., 2004; Narasimhan & Giaschi, 2012; Parrish, Giaschi, Boden, & Dougherty, 2005; Porporino, Iarocci, Shore, & Burack, 2004; Prather & Bacon, 1986; Scherf, Berhmann, Kimchi, & Luna, 2009). Even sensitivity to collective information, like numerosity, is in place in infancy (e.g., Zosh, Halberda, & Feigenson, 2011). But perceiving groups–heterogeneous collectives of unique individuals–cannot occur by accessing global image attributes alone; it requires an extra step of averaging heterogeneous local information from many objects to extract a summary representation. Our findings demonstrate that ensemble coding allows children to do just this, even with some independence from numerosity, density, or contrast. Our results also lay the groundwork for future investigations to determine if, like adults, young children’s developing ensemble-coding mechanisms are flexible enough to enhance perception of complex social information in groups of people, like facial expression or crowd motion (Haberman & Whitney, 2007; Sweeny et al., 2012, 2013. They also motivate future investigation on the relative role and prevalence of ensemble coding and individual object coding in young children’s perception.

Perhaps most interestingly, our results are an important step in understanding the phenomenology of early visual experience. Many critical visual functions are still immature or limited at 4–5 years-of-age, including acuity and contrast sensitivity (e.g., Benedek, et al., 2003; Ellemberg, et al., 1999; Jeon, et al., 2010; Skoczenski & Norcia, 2002), selective attention (e.g., Johnson, 2002), attentional resolution in space and time (Farzin, et al., 2010, 2011), visual working memory capacity (Cowan, et al., 2011; Simmering, 2012; Wilson, et al., 1987), and multiple object tracking (O’Hearn, Landau, & Hoffman, 2005). Unchecked, these limitations would severely constrain the capacity of children’s conscious experience, leaving cohesive groups to instead appear noisy and fragmented. However, we have shown that compressed summary representations may allow children to surmount these limitations and regard groups as ensembles. Just as prosopagnosics compensate for noisy perception of individual faces by accessing the gist of an entire crowd (Yamanashi Leib, et al., 2012), our findings show that children have the requisite ensemble mechanisms that could, in principle, allow them to overcome their own perceptual limitations, grasping the broader gist of a scene instead of focusing on individual details.