Acute Kidney Injury Risk Factors For ICU Patients Following Cardiac Surgery: The Application of Joint Modeling

Abstract

Background

Admission to the ICU (intensive care unit) is frequently complicated by early AKI (acute kidney injury). The development of AKI following cardiac surgery is particularly associated with increased mortality and morbidity. According to AKIN (acute kidney injury network) criteria, UO (urinary output) is a predictor for AKI.

Objectives

The goal of this study was to determine the effects of some AKI risk factors on AKI and also to investigate changes in UO as a predictor of AKI using joint modeling.

Patients and Methods

In a retrospective study, 300 cardiac-operated patients, who had been admitted over a period of three years, were selected according to the consecutive sample selection method, using the ICU at Masih Daneshvari Hospital in Iran as a referral center. The random mixed effect model and the survival model were used to investigate UO changes and estimate the effect of UO and other risk factors on the hazard rate of AKI in a joint analysis.

Results

AKI occurred in 38.0% of patients. A significant decrease of UO occurred more often in female and infected patients, as well as those with a low DBP (diastolic blood pressure). The survival model showed that the risk of AKI in females, older patients and patients with low DBP, lower UO and with infection was higher (P = 0.001). Using joint modeling, the association parameter between the risk of AKI and UO was estimated (-0.3, P = 0.002).

Conclusions

Where there is a relationship between two longitudinal and survival responses, joint modeling can estimate it.

1. Background

The development of AKI (acute kidney injury) following cardiac surgery is associated with increased mortality and morbidity (1). According to the definition, post-operative AKI occurs in 3% - 30% of patients (2). In a study conducted to identify the AKI incidence in patients who were operated on through the off-pump coronary artery bypass (OPCAB) technique, 33.3% in the OPCAB group had AKI (3). Over the last few decades, more than 35 different definitions have been proposed to define AKI, many of which were complicated. A substantial number of publications focused on the AKIN (acute kidney injury network) and RIFLE (risk injury failure loss end-stage kidney disease) classifications are widely accepted by the medical community. They were based on UO (urinary output) and/or SCr (serum creatinine) biomarkers (4, 5). Because of some advantages, in many studies, UO has been suggested over other biomarkers, such as serum creatinine. The use of UO has been especially preferred for the study of AKI in cardiac surgery, ICU and hospitalized patients (6, 7). Furthermore, using UO as an AKI biomarker is not dependent on the knowledge of a baseline UO, and particularly in critical care settings, where hourly UO is routinely measured, a reduced UO is potentially the first symptom of kidney dysfunction (7, 8). A decrease in UO is usual among critically ill patients (9). Therefore, urinary diagnostic indices are principally used to aid in the early diagnosis of AKI and in measuring its severity (10).

As many studies have investigated, the risk factors associated with the development of AKI after cardiac surgery, the precise monitoring of UO and a better understanding of risk factors of its variation, could improve the clinical management of patients in the ICU and allow clinicians to quickly recognize AKI (7). In almost all studies, explicit risk factors have been frequently associated with an increased risk for AKI (11-17). These include female gender, reduced left ventricular function or the presence of congestive heart failure, diabetes, peripheral vascular disease, pre-operative use of an intra-aortic balloon pump, chronic obstructive pulmonary disease, the need for emergent surgery and an elevated pre-operative serum creatinine (18). Other risk factors for AKI have also been established, such as sepsis, pneumonia, infusion of contrast medium, rhabdomyolysis and preexisting renal disease (19, 20). The study of the risk factors associated with the variation of UO changes as a predictor of AKI in ICU patients has been performed less frequently than AKI. Using joint modeling of longitudinal and survival data, it is possible to estimate the effects of risk factors for UO changes and then investigate the effects of UO and other AKI risk factors.

Many clinical trials produce both repeated measurements (longitudinal) and time-to-event (survival) data. Many classic methods exist for analyzing such data separately, including linear mixed effects models for longitudinal responses and parametric, nonparametric or semiparametric models for survival responses (21-24). Using these methods separately, however, may be inappropriate when two outcomes are correlated. A joint model is less likely to cause biased statistical inferences (22, 25, 26). By jointly maximizing the likelihood from both the longitudinal process and the time-to-event data, one uses information from both sources to get parameter estimates for the two processes simultaneously. By doing so, we can correctly assess the dependence of the failure time and the longitudinal data (26). In addition to correcting biases, joint modeling can improve the efficiency of parameter estimates in both parts of the model, because extra information is being used. Many studies have been further extended by using the Bayesian approach (27-31) or the frequentist approach (32-35). However, when a more complicated longitudinal model is used, an EM algorithm may not be feasible. For example, when the longitudinal model requires a large number of random effects to capture the structure of the observations, the EM algorithm for estimation may involve high-dimensional integration in the E-step. This task is very challenging and may even be impossible (26). Therefore, in this study, a Bayesian joint modeling of longitudinal and survival data was used to determine the effects of certain risk factors, such as gender, age, infection (the majority of patients were septic), cardiac disease, DBP (diastolic blood pressure) and chronic pulmonary disease, on time-to-AKI as the survival outcome, and UO as the longitudinal outcome.

A Bayesian approach was used to estimate the joint posterior distribution of model parameters. We used AKIN criteria for the AKI definition, which was defined as a reduction in urinary volume to 0.5 mL/kg per hour for more than six hours. The present retrospective study was conducted on patients admitted to the ICU of Masih Daneshvari Hospital as a referral center over a period of three years. The patients’ demographic data, laboratory data and the reason for ICU admission were recorded in constructed forms during the ICU admission.

2. Objectives

In this study, for the first time, we assessed the association between UO and AKI using the joint modeling of longitudinal and survival data.

3. Patients and Methods

We analyzed the data from a retrospective study. All participants were consecutively sampled adult patients (n = 380) who underwent a cardiac surgical procedure with cardiopulmonary bypass at Masih Daneshvari Hospital, Tehran, Iran, between October 2010 and October 2012. Patients who underwent more than one cardiac surgical procedure during hospitalization (n = 40) were excluded from the study. Additional exclusion criteria were surgeries performed off-pump (n = 15) and pre-operative renal failure requiring dialysis (n = 25). Overall, 300 patients could be included in the study. After surgery, patients were admitted to the ICU and were followed from the day of ICU admission until ICU discharge or the end of the study. UO and other physiological variables were repeatedly measured every two hours in the first eight hours of admission in the ICU. The patients’ demographics, laboratory data, the reason for ICU admission, the length of hospitalization and the length of ICU stay were recorded in prepared forms during the ICU admission. The main survival endpoint was the time of occurrence of AKI after cardiac surgery, which was defined as an amount of urinary output less than 0.5 mL/kg per hour for more than six hours. Patients were followed from ICU admission until AKI occurrence. The dosage of dopa, dobutamine, epinephrine, norepinephrine and vassopresinare was scaled based on the individual patient characteristics and comorbid conditions. Blood pressure was measured twice at ten-minute intervals, and patients were sitting for at least five minutes before the measurement.

3.1. Statistical Analysis

A joint modeling of longitudinal and survival data, proposed by Guo-Carlin, was used for data analysis in this study (25-37). Guo-Carlin’s method applied a Bayesian hierarchical model obtaining estimates for the parameters of interest by Markov chain Monte Carlo (MCMC) methods. The joint modeling approach links two sub-models, one for the longitudinal process and one for the event time. The linkage is modeled via a set of random effects that are assumed to consider the associations between these two outcomes. In this study, the longitudinal and survival responses were, respectively, UO and the time of occurrence of AKI (in hours) in patients with cardiac surgery since the time of entry into the ICU. A mixed effect model was assumed for UO, and the time-to-AKI was analyzed using parametric models (Weibull and exponential models), respectively, according to Equations 1 and 2:

$${\displaystyle {\mathrm{UO}}_{\mathrm{ij}}={\mathrm{intercept}}_i+{{\beta }_{11}\mathrm{age}}_i+{\beta }_{12}{\mathrm{sex}}_i+{\beta }_{13}{\mathrm{DBP}}_{\mathrm{ij}}+{\beta }_{14}{\mathrm{infection}}_{\mathrm{ij}}}$$ Equation 1.

$${\displaystyle {\lambda }_i(t)={\lambda }_0(t)\exp ({\gamma *\mathrm{intercept}}_i+{{\beta }_{21}\mathrm{Age}}_i+{\beta }_{22}{\mathrm{sex}}_i+{\beta }_{23}{\mathrm{DBP}}_i+{\beta }_{24}{\mathrm{Infection}}_i+{\beta }_{25}{\mathrm{COPD}}_i+{\beta }_{26}{\mathrm{CD}}_i)}$$ Equation 2.

Where i = 1…300, the number of patients, and j for each i equals j = 1, 2, 3, 4. λ_i (t) is the hazard of AKI for patient i at time t.

The free software OpenBUGS 3.2.2 (http://www.mrc-bsu.cam.ac.uk) was used for data analysis and estimation of unknown parameters. Deviance information criterion (DIC) was used for model selection. A Bayesian joint modeling approach with vague prior distributions (assuming a multivariate normal distribution with mean 0 and variance-covariance matrix Z_4×4 with diagonal elements 0.01 and zero covariances for main effects vector β₁ = ( β₁₁, β₁₂, β₁₃, β₁₄), and postulating a gamma distribution with parameters α₁ = 0.1 and α₂ = 0.1 for the error variance. We similarly selected vague normal distribution prior for β₂ = (β₂₁, β₂₂, β₂₃, β₂₄, β₂₅, β₂₆). A normal distribution with mean 0 and variance 0.01 for the association parameter γ was assumed. In addition, we for random intercepts chose normal prior. Results are based on 100 draws from a Markov chain Monte Carlo (MCMC) of length 11,000 iterations, with a burn-in of 1,000 iterations, to characterize posterior distributions for the parameters.

4. Results

The characteristics of some variables that were used in the modeling have been reported in Table 1. Continuous variables are presented as the mean ± SD. To summarize, the mean ± SD age was 57.7 ± 9.8 years, 52% were women and AKI developed in 38% of patients. From among the 300 patients included in this analysis, 114 patients had observed event times and 25 patients died. 46 and 156 patients, respectively, had chronic pulmonary disease and cardiac disease.

Table 1. Demographic and Laboratory Characteristics of Patients (n = 300)^a.

Variable	Cardiac Surgery Patients
Urinary
2 hours	1.8 ± 0.2
4 hours	1.1 ± 0.2
6 hours	0.9 ± 0.3
8 hours	1.2 ± 0.2
HOS-LOS, days	17.8 ± 3.8
ICU-LOS, days	7.8 ± 2.9
Age, y	57.6 ± 9.8
Additive EuroSCORE	3.9 ± 1.3
Logistic EuroSCORE	4.7±6.9
APACHI II SCORE	11.2 ± 5.0
COPD, No. (%)	62 (20.7)
CD, No. (%)	242 (80.7)
Sex, (Female), No. (%)	156 (52.0)
Infection, No. (%)	45 (15.0)

Abbreviations: APACHE II SCORE, acute physiology and chronic health evaluation II score; CD, cardiac disease; COPD, chronic obstructive pulmonary disease; EuroSCORE, European system for cardiac operative risk evaluation; HOS-LOS, hospital length of stay; ICU-LOS, ICU length of stay.

^aValues are expressed as mean ± SD unless otherwise indicated.

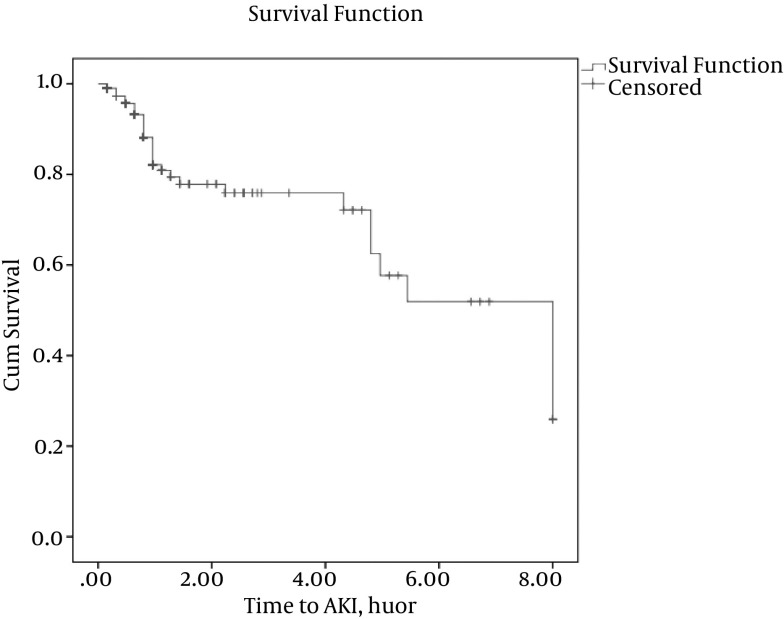
The survival estimates of patients are shown in Figure 1. A decreasing survival curve of patients means an increasing risk of AKI over time. The vertical dashes on the line of survival function in Figure 1 to denote that AKI for some patients did not occur because the study ended or because the patient died. The total number of UO longitudinal measurements was 880, and the average of the measurements was 3.2 per patient. The amount of UO was reduced over time overall. In Table 2, we compared the results of the joint analysis for the effect estimation of some covariates on two interested responses. The association parameter that described the strength of association between values of UO and risk of AKI was estimated to be -0.31 with a 95% confidence interval (-0.55, -0.10), which indicated that UO and the risk of AKI were negatively associated. The HR (hazard ratio) was exp (1.34) = 3.8 for patients with infection problems with respect to non-infected patients. The patients without an infection problem had a better average survival rate. Females had a worse survival rate (i.e., a higher risk of AKI following cardiac surgery) than male patients, and the differences were significant. The HR of AKI following cardiac surgery in female to male was exp (0.69) = 1.99. In the survival model, we found that age was significant; every 10-year increase in age elevated the AKI rate by 50%. In the longitudinal sub-model, it was seen that the decrease of UO occurred significantly more in female and infected patients, and also in those with low DBP. A decrease of one unit in DBP corresponds to a decrease of 11.9 in UO. The mean UO of a female patient was 55.7 lower than the mean UO of a male patient in this study. The final joint modeling, presented in Table 2, had less (DIC = 56.8) over other models with different predictors. In other joint models, chronic obstructive pulmonary disease (COPD) and cardiac disease were entered into the longitudinal sub-model, but they had no significant effects, and their DICs were near to the final joint model DIC in this study.

Figure 1. Survival Estimate of Patients.

Table 2. The Estimated Effects of Risk Factors Associated With UO and AKI in ICU Data Using Joint Analysis.

Sub-Model Parameter	β (SE)
Longitudinal (UO)
Age	2.98 (1.57)
Sex	-55.72a (13.63)
DBP	11.90a (1.56)
Infection	-649.8a (6.00)
Survival (AKI)
Age	0.04 (0.40)
Sex	0.69a (0.39)
DBP	-0.31a (0.08)
Infection	1.34a (0.52)
COPD	0.67a (0.55)
CD	1.42a (0.79)
Association Parameter
Association	-0.31* (0.70)

Abbreviations: COPD, chronic obstructive pulmonary disease; CD, cardiac disease.

^aSignificance of the effect at significance level of 5%.

5. Discussion

AKI following cardiac surgery is a common and serious post-operative problem, and it is an independent predictor of mortality after cardiac surgery (38). AKI is highly prevalent and predictable. AKI is a significant predictor of mortality using multivariate logistic regression (39-41).

By most estimates, up to 30% of cardiac surgery patients develop clinically relevant kidney injury (42). Some studies have found that using UO as a biomarker of AKI in cardiac surgery in ICU and hospitalized patients is preferable (6). Many studies have developed models to predict AKI, but statistical modeling of the risk factors associated with the variation of UO in ICU patients has been described less than AKI. Moreover, there was no numeric quantity for association of UO and risk of AKI (2).

The novelty of this study was in describing the relationship between the time of AKI following cardiac surgery and UO by an association parameter, using joint modeling. Joint modeling takes into account the interdependence of the two types of survival and longitudinal responses.

After using joint modeling, our findings showed a negative significant association between the risk of AKI following cardiac surgery and UO in patients (-0.31, P = 0.04), which demonstrated the suitable selection of the joint modeling for this research. According to the results of the mixed model of joint analysis, a significant decrease of UO occurred more often in female and infected patients as well as those with low DBP. Female gender (HR = 1.99, P = 0.01), older age (HR = 1.1), cardiac diseases (HR = 4.2, P = 0.02), low DBP (HR = 1.4, P = 0.03) and chronic pulmonary diseases (HR = 1.9, P = 0.02) had significant effects on the risk of AKI after cardiac diseases. Similar results were obtained by other researchers (10, 38, 43-46). Sepsis was also introduced as a considerable risk factor of AKI. In fact, the majority of infected patients were septic in this study. Many other factors are associated with an increased risk of AKI, but their influence will be highly dependent on the specific nature of the population (19). Through using joint modeling, a reduction in the standard error of estimates occurred, thus more accurate parameter estimates and valid inferences concerning the effect of covariates on the survival and longitudinal outcomes could be obtained (25, 47).

However, the occurrence of AKI after cardiac surgery is often slow, and other factors concerning intra-operative and post-operative management of patients could be relevant. We recommend definite prevention programs in the ICU target patients with traditional risks of AKI, such as older age, sex, cardiovascular surgery and chronic pulmonary disease. Moreover, some factors might be measurable some time before the occurrence of AKI, which more importantly could suggest appropriate strategies to prevent or limit AKI (1).

To the best of our knowledge, it is not clear whether the addition of variables that are not known before surgery, but are easily accessible before AKI occurrence, can also be easily collected, recorded and monitored (1). The strength of this study was the estimation of the association parameter of AKI and UO using joint modeling for the first time.

5.1. Conclusions

We concluded that when there was a relationship between two longitudinal and survival responses, joint modeling presented considerable improvements in estimations compared to longitudinal and survival models separately.