Inertial imaging with nanomechanical systems

Abstract

Mass sensing with nanoelectromechanical systems has advanced significantly during the last decade. With nanoelectromechanical systems sensors it is now possible to carry out ultrasensitive detection of gaseous analytes, to achieve atomic-scale mass resolution and to perform mass spectrometry on single proteins. Here, we demonstrate that the spatial distribution of mass within an individual analyte can be imaged—in real time and at the molecular scale—when it adsorbs onto a nanomechanical resonator. Each single-molecule adsorption event induces discrete, time-correlated perturbations to all modal frequencies of the device. We show that by continuously monitoring a multiplicity of vibrational modes, the spatial moments of mass distribution can be deduced for individual analytes, one-by-one, as they adsorb. We validate this method for inertial imaging, using both experimental measurements of multimode frequency shifts and numerical simulations, to analyse the inertial mass, position of adsorption and the size and shape of individual analytes. Unlike conventional imaging, the minimum analyte size detectable through nanomechanical inertial imaging is not limited by wavelength-dependent diffraction phenomena. Instead, frequency fluctuation processes determine the ultimate attainable resolution. Advanced nanoelectromechanical devices appear capable of resolving molecular-scale analytes.

Over the past decade, mass measurements with nanomechanical devices have systematically improved to the point where they now offer an interesting capability for engendering a new approach to mass spectrometry. Nanoelectromechanical systems (NEMS) resonators are extremely responsive to the added mass of adsorbed particles^1–6 and this has led to advances including the mass detection of individual proteins^7,8, nanoparticles⁹ and large biomolecules^10,11, as well as demonstrations of near-atomic-scale mass resolution^12–15. Given its capability for measuring neutral, single particles in both the low and high mass (>500 kDa) domains, NEMS-based mass spectrometry (NEMS-MS) is now being developed as an analytical approach for proteomics, structural biology and nanoparticle detection⁷.

Here, we propose and demonstrate a new methodology that represents a paradigm shift in real-time, NEMS-based measurements of individual analytes. It can be implemented using existing NEMS sensors, or even larger mechanical devices, and simply involves the analysis of data obtained from standard measurements. We show that this approach enables simultaneous measurement of the mass, position and molecular size and shape of individual adsorbates (that is, it enables the acquisition of what we term their ‘inertial image’) through real time measurements of the frequency shifts of the mechanical sensor’s multiple vibrational modes, induced by discrete single-molecule adsorption events. We validate our approach through detailed experimental measurements on a series of adsorbates and by numerical simulation. We also establish that measurement of the size and shape of molecular-scale analytes can be achieved using state-of-the-art NEMS devices. In fact, we find that there are no fundamental wavelength (or diffraction-based) limits to the resolution of this technique. Instead, it is the mechanical resonator’s intrinsic frequency-fluctuation processes that impose the ultimate resolution limits.

Calculating spatial moments of a mass distribution

In NEMS-MS, adsorption of an individual analyte on the resonant sensor affects each of its vibrational modes differently. The mode shapes of the resonator themselves give rise to a distinct position dependence of these adsorbate-induced modal frequency shifts^7,16,17. For each mode, the induced frequency shift is maximal for analyte adsorption at vibrational antinodes, whereas it vanishes for an analyte that adsorbs at a node. In a previous study we used two resonator modes to measure simultaneously the mass and position-of-adsorption of individual biomolecular analytes, in real time, as they adsorbed on a NEMS resonator⁷. Deduction of the masses and positions of pairs and triplets of small particles after their manual attachment to a microcantilever has also been demonstrated using multiple vibrational modes¹⁸. In these previous efforts it was assumed that the analytes were point-like particles. Here we go further and show that our methodology, which involves measurements of additional adsorbate-induced frequency shifts for higher modes, permits deduction of all spatial moments of the mass distribution for each adsorbate (which are now assumed spatially finite), in real time. These moments not only include information about each analyte’s total mass, but also, importantly, its spatial distribution—its position-of-adsorption and its size and shape. Once acquired, the measured moments of the mass distribution can be used to reconstruct an inertial image of the analyte.

Without loss of generality, we present here the ultimate and practical sensitivity limits to inertial imaging of small adsorbate masses, which inherently do not perturb resonator mode shapes. Our focus is on small, soft and compliant adsorbates; this includes biological molecules and molecular complexes, which are of significant current interest⁷. For such analytes, effects that may arise from adsorbate stiffness^19–21 can be neglected. Our analysis proceeds by defining coefficients F_n, which represent the surface loading of a NEMS device by a small analyte (Supplementary Section 1):

$$F_n={\int }_{{\mathrm{\Omega }}_{\mathrm{s}}}\mu (\mathbf{r}){\mid {\mathbf{\Phi }}_n(\mathbf{r})\mid }^2\mathrm{d}S$$ (1)

Here, μ is the areal mass density distribution of the adsorbed analyte (evaluated normal to the device surface), Φ_n(r) are the natural (vector) vibrational modes of the device in the absence of analyte adsorption (normalized such that ∫_Ω ρ_device(r)|Φ_n(r)|²dV = M, where ρ_device is the mass density of the device and M is the device mass), Ω represents the region in space occupied by the device and Ω_s is its surface. Implicit in equation (1) is that mass loading arises from an adsorbate that is thin relative to the dimensions of its contact region and that the adsorbate is both compliant and strongly adherent to the NEMS surface. When this holds, the adsorbate’s rotary inertia, induced while following the NEMS vibrations, exerts a negligible effect. Classical linear elasticity²² allows these coefficients, F_n, to be related directly to the discrete, experimentally measured fractional-frequency shifts induced by each analyte adsorption event, ${\mathit{\Delta }}_n=\left({\omega }_n-{\omega }_n^{(0)}\right)/{\omega }_n^{(0)}$. Here, ${\omega }_n^{(0)}$ is the unperturbed angular frequency of the nth mode and ω_n is the shifted angular frequency after adsorption of the analyte. As detailed in Supplementary Section 1, our analysis yields the connection between these F_n and experimental measurements:

$$F_n=-2{\mathit{\Delta }}_{n}M$$ (2)

Equation (1) indicates the relevance of these coefficients: F_n are weighted spatial averages of the analyte’s mass distribution function. It follows then, that moments of the analyte’s mass distribution, m^(k), can be determined directly by forming linear combinations of these functions,

$${\mathrm{m}}^{(k)}={\sum }_{n=1}^N{\alpha }_n^{(k)}{F}_n={\int }_{{\mathrm{\Omega }}_s}\mu (\mathbf{r}){\mathrm{g}}^{(k)}(\mathbf{r})\mathrm{d}S$$ (3)

Here, $g^{(k)}(\mathbf{r})={\sum }_{n=1}^N{\alpha }_n^{(k)}{\left|{\mathbf{\Phi }}_n(\mathbf{r})\right|}^2$ are linear superpositions with N terms (N is the total number of measured modes), involving the squared magnitudes of the unperturbed mode shapes evaluated at the device surface. These are, in turn, superposed using coefficients ${\alpha }_n^{(k)}$ chosen in a specific manner described immediately below. Superscript (k) represents the moment order. Using equations (2) and (3), we can then relate the moments m^(k) directly to the experimentally measured set of analyte-induced fractional-frequency shifts {Δ_n} through

$${\mathrm{m}}^{(k)}=-2M{\sum }_{n=1}^N{\alpha }_n^{(k)}{\mathit{\Delta }}_n$$ (4)

For example, the adsorbate mass m can be deduced from experiments by first picking a particular set of coefficients ${\alpha }_n^{(0)}$ to create a superposition that ideally yields g⁽⁰⁾(r) = 1 over the integration region Ω_s. In this case ∫_Ωs μ(r)dS = m = m⁽⁰⁾ = ∫_Ωs μ(r)g⁽⁰⁾(r)dS. Similarly, by picking a different set of coefficients a different superposition g⁽¹⁾(r) = x can be created; this allows the analyte’s position-of-adsorption (its centre-of-mass along the x-direction) to be deduced. This analysis can be generalized trivially to all higher-order moments.

Case study for a doubly-clamped beam

As an example, we consider a one-dimensional doubly-clamped elastic beam. The position vector r in this case simplifies to the beam coordinate x, and we solve for the linear mass density, λ(x). We can calculate m⁽⁰⁾, m⁽¹⁾ and in turn, 〈x〉 = m⁽¹⁾/m⁽⁰⁾, which is the analyte’s centre-of-mass along the beam coordinate (its position); this is proportional to ${\int }_0^{L}x\lambda (x)\mathrm{d}x$, where L is the beam length. Creating a higher-order expansion along x, we form g⁽²⁾(x) = x² to obtain m⁽²⁾. This, in turn, allows deduction of the analyte’s standard deviation in x; that is, its average size along the x coordinate, (σ_x = √m⁽²⁾/m⁽⁰⁾ − (m⁽¹⁾/m⁽⁰⁾)²). Analogous relations yield even higher spatial moments of the analyte’s mass distribution along x, which represent its width-averaged shape along x—for example the analyte’s skewness and kurtosis, which involve g⁽³⁾(x) = x³ and g⁽⁴⁾(x) = x⁴, respectively (Supplementary Section 2).

With a sufficiently complete set of spatial moments of the analyte’s mass distribution {m^(k)}, which can be deduced for each adsorbing analyte in real time from experimentally measured multimodal NEMS frequency shifts, a one-dimensional inertial image (that is, the width-averaged density distribution of the analyte along the beam’s longitudinal axis) can be determined^23,24. Equation (3) illustrates that the spatial dimensionality of m^(k) arises directly from the spatial variation of the vibrational modes used in its expansion. For example, the out-of-plane displacements of a doubly-clamped beam or a singly-clamped cantilever change with one spatial variable along the longitudinal axis, x. Vibrational mode shapes that vary with two coordinates, such as those for thin plates or membranes, can provide two-dimensional moments of the adsorbate distribution. These devices will permit extraction of a two-dimensional inertial image of the mass distribution of the particle. An example of image reconstruction using inertial imaging theory is discussed in the following. Note that equation (2) applies generally to mechanical devices of any size, geometry and composition (Supplementary Section 1).

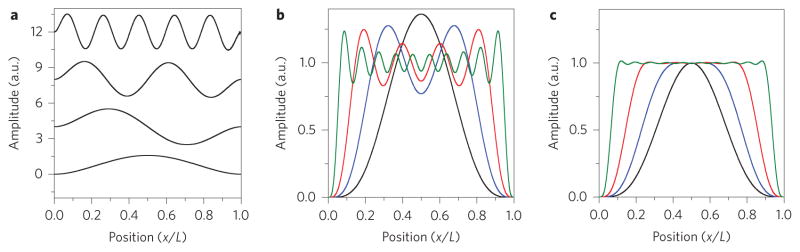
Figure 1 presents mode shapes and superpositions for the out-of-plane displacements of an ideal doubly-clamped beam of length L. For such a one-dimensional device the entire (linear) spatial domain Ω_l is x ∈ [0, L], because variations over the transverse direction are implicitly integrated. Figure 1a depicts the first, second, fourth and tenth mode shapes along the longitudinal coordinate, x. In Fig. 1b we demonstrate use of superpositions to approximately yield g⁽⁰⁾(x) = 1 over the full length of the beam; these involve from one up to ten modes. We determine the optimal coefficients ${\alpha }_n^{(0)}$ for the expansion of g⁽⁰⁾(x) through least-squares analysis. It can be shown rigorously that a unique analytic solution for these coefficients exists (Supplementary Section 3).

Figure 1. Superposition of resonator mode shapes.

a, Mode shapes of a doubly-clamped beam (from bottom to top) for the first, second, fourth and tenth out-of-plane flexural modes. b, A linear combination of mode shapes intended to yield a superposition g⁽⁰⁾(x) = 1 over an interval Ω_l spanning the entire beam [0, 1], using the first mode (black), first two modes (blue), first four modes (red) and first ten modes (green). Significant over- and undershoot is evident. c, Superpositions with a slightly foreshortened interval provide greatly improved convergence. Here, Ω_l spans [δ,1 − δ], where δ = N/(1 + N²). For an expansion involving the first ten modes (green), the interval [0.099, 0.901] covers about 80% of the beam. L, cantilever length. N, number of modes used.

The fidelity of the adsorbate’s inertial image is determined by how well, over the entire integration region Ω_s, the finite superpositions g^(k)(r) used in equation (3) converge to their targeted spatial functions. For the specific case illustrated in Fig. 1 involving one-dimensional modes of a doubly-clamped beam, we seek an expansion g⁽⁰⁾(x) = 1 that converges over Ω_l. Figure 1b indicates that a choice of Ω_l to span the full beam length L is not ideal and gives poor convergence (over- and undershoot); this choice will yield moments that poorly approximate those of the analyte mass distribution. Figure 1c shows that convergence to g⁽⁰⁾(x) = 1 over Ω_l improves very significantly with the choice of a slightly foreshortened region of integration. Practically, foreshortening Ω_l implies a reduced measurement zone; in other words, such improvement comes with the cost of excluding a small fraction of experimental data (from analytes that adsorb outside Ω_l). The effect of this small reduction in the measurement zone, Ω_l, is minimal; in fact, adaptive fitting (described below) can render it inconsequential.

As long as Ω_l spans the spatial extent of the analyte, the error for the kth moment, ε^(k), varies as a power of the measurement zone: ${\epsilon }^{(k)}\propto {\mathrm{\Omega }}_l^{N+1/2}/N!$. Here N is the number of modes, and this expression holds for N > k + 1. For an accurate estimation of the kth moment, at least k + 1 modes are needed, and the accuracy obtained increases rapidly as more modes are employed (Supplementary Section 4). Moreover, in the limit where the adsorbate is infinitesimal compared to the device size, only k + 1 modes are required to determine the kth moment, and the use of additional modes does not improve resolution (Supplementary Section 5).

Adaptive fitting to minimize error

To be useful in mass spectrometry and inertial imaging of biomolecules, the NEMS mass sensor must be of sufficient size that individual analytes are small compared to the device dimensions. In this case it is possible to markedly enhance resolution by fitting the measurement zone, Ω_s, adaptively to the analyte size using a minimal set of modes (see above). This straightforward computational procedure can be implemented in real time after each set of adsorption-induced frequency shifts is acquired; no additional measurements are involved. Figure 2 demonstrates adaptive fitting with a doubly-clamped beam. The expansion interval Ω_l is progressively shrunk around the analyte’s adsorption position in an iterative process after the analyte’s location is determined from a first pass of analysis. An exponential decrease in uncertainty is attainable (Supplementary Sections 6 and 7). Figure 2 demonstrates a decrease in residual error by six orders of magnitude as Ω_l is ultimately reduced to a region somewhat larger than the size of the analyte. We find adaptive fitting converges (that is, the residual error saturates at a minimum level), typically after less than ten iterations (Supplementary Section 7). In fact, this procedure enables convergent measurements over a larger fraction of the beam. Hence, the extent of the region excluded to obtain convergent expansions of g^(k)(r) can be significantly reduced. In practice, the ultimate attainable resolution is determined by the frequency stability of the resonator modes, as described in the following.

Figure 2. Adaptive fitting for enhanced resolution and accuracy.

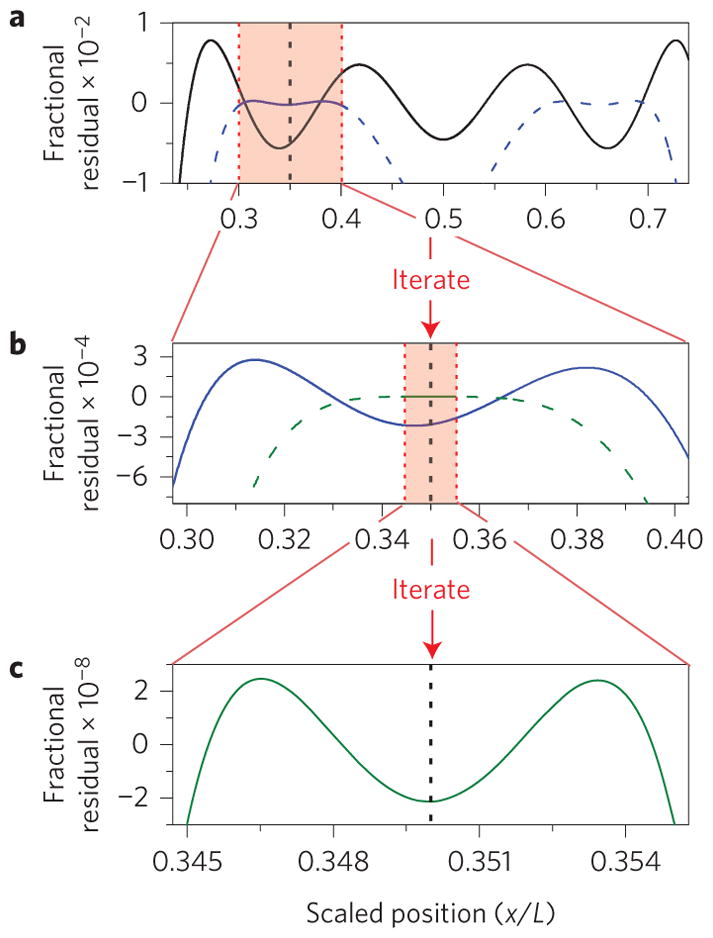
Superposition fit to g⁽⁰⁾(x) = 1 (to calculate mass) using the first four modes of a doubly-clamped beam, showing the effect of measurement zone reduction. a, Initial superposition (black curve) before the initial values for the location and size of the particle are determined. After determination of the location and size of the particle, the measurement zone can be reduced. In this case, the position is determined to be near x/L = 0.35 (dotted vertical line) and a measurement zone smaller than the original is chosen (pink shaded area). This measurement zone (pink shaded area) is centred on the particle position and commensurate with particle size. With this reduction in measurement zone, a new superposition can be calculated (blue curve: solid is within zone, dashed is outside). b, Zoomed-in view of new superposition. Further reduction of the measurement zone by a factor of 10 leads to another superposition (green curve: solid is within zone, dashed is outside). This is again superior to the previous superposition (blue curve). c, Zoomed-in view of final superposition (dotted vertical line is the position of the particle). Error is reduced by six orders of magnitude from a.

Mass and position validation using published data

We first validate our methodology for mass and position determination using (1) our own previous study of soft biological adsorbates (IgM antibodies) on NEMS resonators⁷ and (2) an independent study of Au nanoparticles attached to a microcantilever at various positions along its length¹⁷. Analysis of these published data permits benchmarking the results of inertial imaging against reported literature values. In the following section we shall present new measurements that validate analysis of analyte size and shape by inertial imaging.

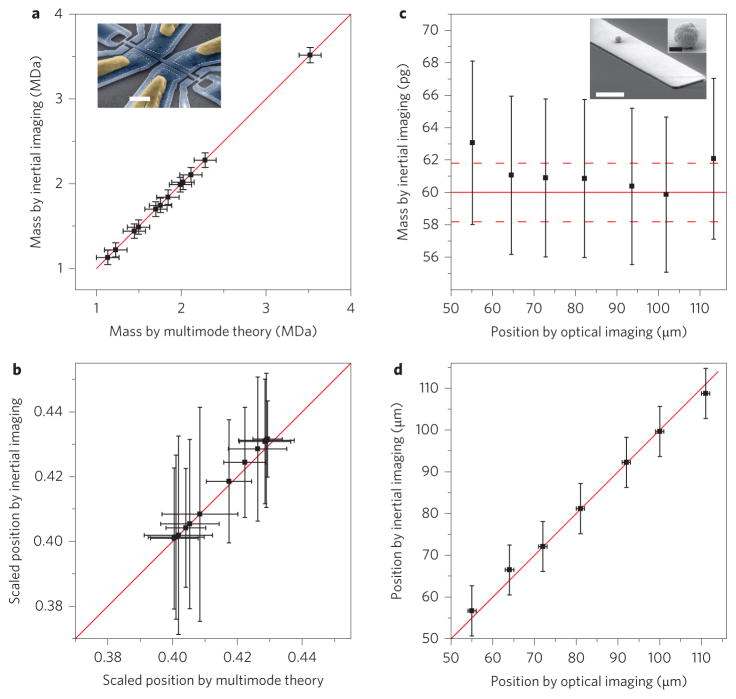
The results of our new analysis of the data from ref. 7 are shown in Fig. 3a,b. The two-mode frequency shift data measured in ref. 7 are used here to independently determine particle mass (Fig. 3a) and position (Fig. 3b) using inertial imaging. These results are compared to those obtained from previously validated multimode theory⁷, which implicitly assumes that analytes are point particles. As seen, the deduced masses and positions from both methods are in excellent agreement.

Figure 3. Mass and position analysis using published experimental data.

a,b, Mass (a) and position (b) calculations for the experimental data from ref. 7 using two modes of a doubly-clamped beam. The values for mass and position are compared with the previous values from ref. 7 using multimode theory. Position is scaled to the device length. Error bars in inertial imaging theory reflect the total error due to both the fitting residual and frequency fluctuations (2σ, 95% confidence level). c, Analysis of particle mass for different positions using the four-mode measurement of the same particle along a cantilever device¹⁶. The particle expected mass is estimated from the scanning electron microscopy (SEM) measurements of ref. 16 (solid red line) with 2% assumed uncertainties in that measurement (dotted red lines). d, Position calculation using the same data, compared with the optically measured position. Red lines in a,b,d represent curves of exact agreement between the two methods. Insets in a and c: Electron micrographs of representative devices used in the two respective studies. Scale bars, 2 μm (a); white, 5 μm and black, 500 nm (c). In all figures, error bars represent the 2σ, 95% confidence level.

Figure 3c,d compares the results of ref. 16 with those obtained from inertial imaging and direct measurements of the gold bead on the cantilever from optical microscopy. The four-mode frequency measurements reported in ref. 17 are used to determine the mass and position of the bead from inertial imaging. This comparison shows excellent agreement for both mass and position. Although the high-aspect-ratio Au nanoparticles used in ref. 17 are obviously not thin or compliant with the device surface, this does not compromise the validity of inertial imaging for mass and position. We find these moments are relatively unaffected by the rotary inertia of the adsorbate.

Size and shape validation using droplet arrays

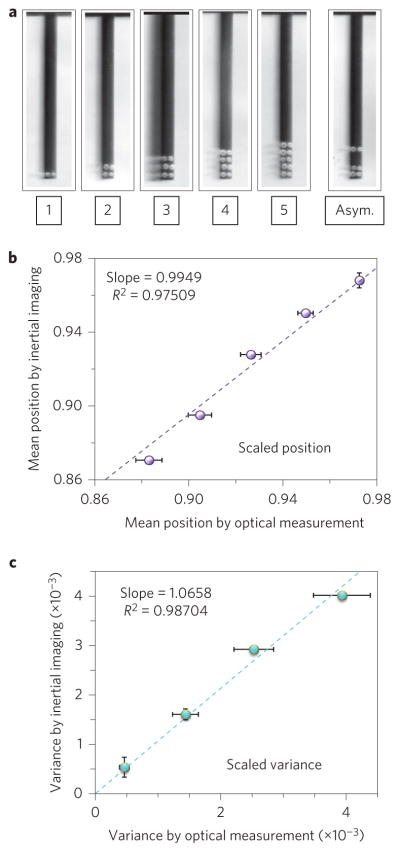
With the capabilities of inertial imaging established for both mass and position, we turn to validation of higher moments—variance and skewness—which represent the size and shape of the adsorbate. As mentioned, inertial imaging measurements of mass and position are robust for non-compliant adsorbates, but the same is not true for the higher moments. To ensure the overarching assumptions of our method are upheld, we used non-volatile liquid micro-droplet arrays (see Methods). Figure 4a presents optical images of the droplet array systems studied.

Figure 4. Size and shape analysis via frequency-shift measurements of droplet arrays.

a, Optical images of liquid droplet arrays deposited on a silicon microcantilever (397 μm long, 29 μm wide, 2 μm thick) using AFM dip-pen lithography. Inverted black–white images serve to highlight the droplets. Inertial imaging using the lowest four vibrational modes resolves these addenda as constituting a composite, thin, spatially distributed analyte that is strongly adherent to the cantilever surface. Measurement details are provided in the Methods and Supplementary Section 11. The numbers of two-droplet rows in the symmetric distributions are specified, and the asymmetric distribution used to assess skewness is indicated. b, Comparison of mean position of the droplet array distribution, measured using both inertial imaging and optical microscopy. c, Comparison of the variance in the droplet array distribution measured using both inertial imaging and optical microscopy. Position and standard deviation are scaled to cantilever length. The single row (denoted ‘1’ in a, does not satisfy the requirement of being a thin and compliant adsorbate and hence is not included in the comparison of variance. Dashed lines are linear regressions of data centred at the origin. Slopes of lines and R² values are indicated. Vertical and horizontal error bars in b,c represent the 2σ uncertainty levels due to frequency noise and droplet mass variability, respectively.

We compare results deduced from inertial imaging to optical measurements of the droplet arrays in Fig. 4b,c. As shown, inertial imaging of symmetric array distributions provides excellent agreement with optical measurements for both position and standard deviation. Also, the results for position are consistent with the analysis of previously published data, as discussed above.

Our variance measurements of Fig. 4 provide the first validation of the capabilities of inertial imaging to provide the spatial variance (size) of an adsorbate. Additionally, these data also deliver a first demonstration of the measurement of mass distribution asymmetry: inertial imaging data yield a skewness of −0.453, which is in close agreement with the optically measured value of −0.537. (Slight non-uniformities in droplet size contribute to the small, ~15% difference in skewness values.)

These experimental validations of inertial imaging are consistent with our full numerical simulations (Supplementary Sections 8 and 9), which permit absolute specification of adsorbate properties. In Supplementary Section 8, we also show how the spatial mass distribution of the adsorbate (that is, its ‘inertial image’) can be reconstructed from the measured moments.

Practical implications

In frequency-shift-based mass sensing, both the mass distribution function of the analyte and its mechanical coupling to the surface of the NEMS sensor play important roles in determining the magnitude of the induced fractional-frequency shifts, {Δ_n}. Hence, the nature of the physical attachment of the analyte to the resonator is also probed. Soft biological analytes, such as proteins, are ideal targets for inertial imaging. Our standard NEMS-MS protocol of cooling the sensor below ambient promotes strong physisorption of the analytes⁷. Accordingly, van der Waals and chemical forces will cause the analyte to conform to the surface topography of the sensor. However, results inferred from the frequency shifts induced by rigid analytes, such as for metallic nanoparticles, will instead yield an inertially imaged size reflecting the region of attachment. In general, this can be smaller than the diameter of a rigid analyte.

Beyond such experimental details, the primary source of uncertainty—and the ultimate limit to the resolution of inertial imaging—arises from the frequency instability of the resonator. This fundamental uncertainty in deducing the moments of the analyte’s mass distribution function can be evaluated using equation (4) and standard methods of error propagation, together with knowledge of the spectral density of the resonator’s frequency fluctuations (Supplementary Section 10). In Table 1 we provide examples of the frequency-noise-limited resolvable size of an analyte that is attainable with current micro- and nanoscale resonator technology. These projections are based on strongly driven devices, which provide optimal frequency resolution. As shown, today’s smallest devices are clearly capable of resolving molecular-scale analytes.

Table 1.

Imaging resolution capabilities of current micro- and nanomechanical resonators.

Device type	Dimensions (L × w × t)	Frequency resolution	Resolvable feature size
Closed-loop frequency measurements: predicted resolution
Silicon microbeam11	200 × 33 × 7 (μm)	AD = 1 × 10−8	370 nm
Silicon nanobeam7	10 × 0.3 × 0.1 (μm)	AD = 8 × 10−8	15 nm
Graphene nanoribbon6	1760 × 200 × 0.14 (nm)	AD = 1.3 × 10−6	4.2 nm
Single-walled carbon nanotube15	150 × 1.7 × 1.7 (nm)	AD = 2 × 10−6	0.3 nm
Passive thermal-noise frequency measurements in current study
Silicon microcantilever	397 × 29 × 2 (μm)	SD = 10−4	9 μm

For closed-loop frequency measurements the diameters of the smallest measureable analytes are tabulated for the cases of a hollow silicon microbeam¹¹, silicon nanobeam⁷, graphene nanoribbon⁶ and a single-walled carbon nanotube¹⁵. Doubly-clamped beam geometries are employed. The actual device dimensions and deduced experimental values for resonator frequency instability are listed. Frequency fluctuations are characterized by the Allan deviation (AD), which was either reported in the reference indicated, or deduced from the reported mass sensitivity. The resolvable feature size is defined as the approximate size (standard deviation) of an analyte for which the measurement signal-to-noise ratio is unity. The resolvable feature size is calculated assuming a hemispherical particle with a mass density of 2 g cm⁻³ that strongly adsorbs onto these resonators. We use the analyte-induced frequency shifts in the four lowest-frequency mechanical modes, which are assumed to have identical frequency stabilities (consistent with our experimental findings). For passive thermal-noise frequency measurements we use the observed resolvable feature size in current proof-of-concept measurements. The measured standard deviation (SD) in frequency is given. The differences in resolvable feature size for passive measurement of the microcantilever and the closed-loop measurements of the microbeams are due to their disparity in frequency noise.

Inertial imaging enables measurements of both the mass and molecular size and shape of analytes that adsorb on a nanomechanical resonator. Analogous to the previous nanomechanical measurements of mass and position-of-adsorption of individual proteins⁷, inertial imaging is possible in real time as individual analytes adsorb on a NEMS sensor, one by one. This represents a paradigm shift in the realm of resonator-based particle sensing, in that it permits spatially resolved imaging of single analytes using current measurement technology. The ultimate resolution of this technique is not limited by the modal wavelengths, but instead only by the inherent frequency instability of the nanomechanical resonators used. Hence, NEMS-based inertial imaging can enable single-molecule mass spectrometry and, simultaneously, the evaluation of the size and shape of individual molecules with nanometre-scale dimensions.

Methods

The liquid droplet arrays were deposited on a tipless reference microcantilever (Bruker, CLFC-NOBO) using atomic force microscopy (AFM) dip-pen lithography²⁵. These ‘soft’ adsorbates are both thin and compliant with the device, which mitigates any effect of the adsorbates’ rotary inertia, as required with our formulation of inertial imaging. The liquid droplet arrays also mimic the soft material properties of a biological specimen, while enabling both precise dimensional control and independent characterization of adsorbate shape (difficult with a biomolecular test specimen). We used ideally rectangular single-crystal silicon microcantilevers for these studies. This minimized potential non-idealities in the mode shapes and thus simplified application of inertial imaging theory.

The droplets were sequentially deposited in rows, beginning from the distal end of the cantilever. The droplets were deposited in configurations to produce both symmetric and asymmetric adsorbate mass distributions (the latter permitting an assessment of skewness). We measured the undriven, thermomechanical response of the cantilever before and after deposition of the droplet arrays to obtain, with high precision, the induced resonant frequency shifts for the first four flexural modes (which lie within the bandwidth of our measurement system). Although this thermal-noise-based measurement scheme limited the practically achievable frequency resolution (Table 1)²⁶, it permitted a controlled, artefact-free first experimental demonstration of the inertial imaging method. Additional measurement details are described in Supplementary Section 11.