Abstract
The hypoxia inducible transcription factors (HIF) play a central role in the human oxygen sensing signalling pathway. The binding of the von Hippel Lindau tumour-suppressor protein (pVHL)-ElonginC-ElonginB complex (VCB) to HIF-1α is highly selective for the trans-6-hydroxylated form of when Pro564 in the C-terminal oxygen dependent degradation domain (ODDD) of HIF-1α. The binding of HIFα for VCB is increased by ∼1000-fold upon addition of a single oxygen atom to either of two conserved proline-residues. Here, we address how this addition governs selective recognition, and characterize the strength of the interaction of this ‘switch-like’ signalling event. A new set of molecular mechanics parameters for 4-hydroxyl-proline has been developed following the CHARMM force field philosophy. Using the free energy perturbation (FEP) formalism, the difference in the binding free energies between HIF-1α in the non-hydroxylated and hydroxylated forms with the VCB complex was estimated using over 3 microseconds (µs) of MD trajectories. These results can favourably be compared to an experimental value of ∼4 kcal mol−1. It is observed that the optimized hydrogen bonding network to the buried hydroxyprolyl group confers precise discrimination between hydroxylated and unmodified prolyl residues. These observations provide insight that will aid in developing therapeutic agents that block HIF-α recognition by pVHL.
Keywords: Hypoxia inducible factor, hydroxyproline, VHL/HIF-1α, protein-protein interaction, free energy of binding
Graphical Abstract
Introduction
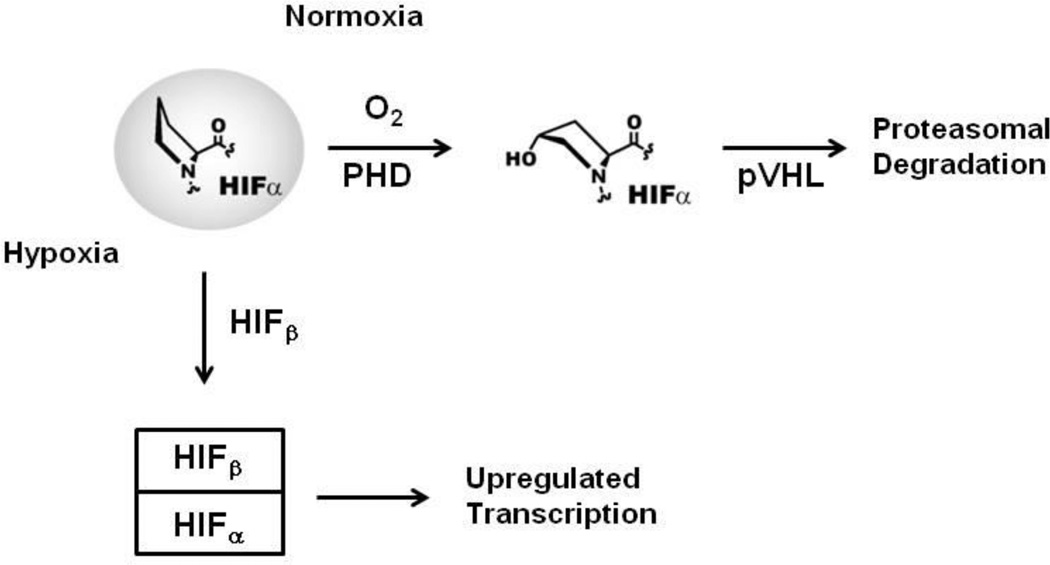
The von Hippel-Landau tumor suppressor protein (pVHL) plays an important role in the regulation of oxygen homeostasis in animals through its interaction with the hypoxia inducible factors1 HIF-1α and HIF-2α, referred to collectively as HIFα. As the background level of oxygen increases from a hypoxic to a normoxic condition, two proline residues of HIF-1α and HIF-2α undergo post-translational hydroxylation.2 HIF-α hydroxylation is catalyzed by prolyl hydroxylase domain containing enzymes (PHDs)3 which are FeII and 2-oxoglutarate dependent oxygenases. pVHL is the recognition component of a multi-component ubiquitin ligase that targets HIFα subunits for proteasomal proteolysis.4 pVHL associates and interacts with elongin C/B and form a multi-component ubiquitin ligase complex (VCB) that binds to prolyl-hydroxylated HIFα, leading to its ubiquitination and subsequent degradation via the ubiquitin-proteasome pathway of HIFα (Figure 1).5 As such, the prolyl-hydroxylation of HIFα operates as a hypoxia sensing switch.6 In vitro studies have shown that 4-prolyl hydroxylated CODD peptides bind ∼1,000 fold more tightly to the VCB complex than non-hydroxylated CODD.4 X-Ray diffraction analyses have revealed that the post-translationally introduced alcohol is positioned to bind via hydrogen-bonds formed between the alcohol of the hydroxylated proline and two other residues of pVHL (Ser111 and His115).4, 7 The remarkable selectivity of the switch-like HIF signaling pathway is proposed to be a key determinant in human oxygen sensing.8
Figure 1.
Overview of the human HIF oxygen sensing pathway. In normoxia, the PHD enzymes catalyze HIFα trans-4-prolyl hydroxylation, leading to specific recognition of hydroxylated HIFα by the E3 ubiquitin ligase targeting subunit pVHL, and subsequent proteasomal degradation. Conversely, in hypoxia, the PHD enzymes are less active, leading to accumulation of HIFα, its translocation to the nucleus and dimerization with HIFβ. The transcriptionally active HIFα/β heterodimer binds to specific recognition motifs on HIF target genes, to activate their transcription.
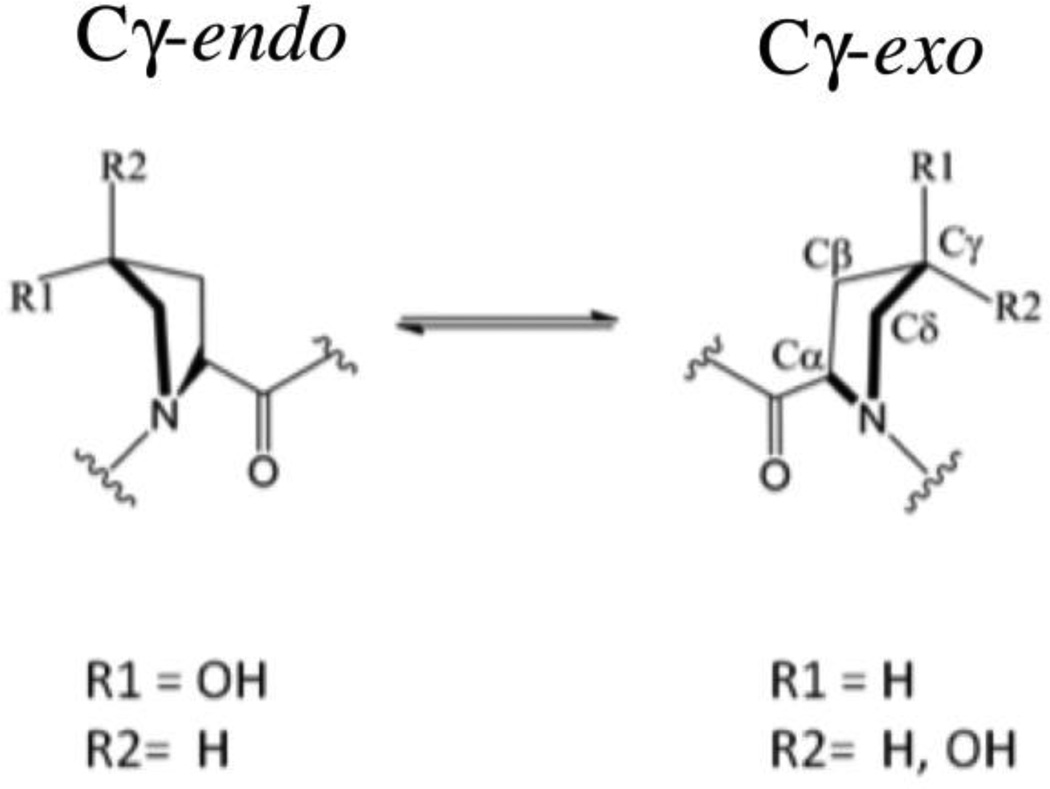
Some study has led to the proposal that the conformation of the targeted HIFα prolyl ring has important roles both in the binding of hydroxylated HIFα to VCB, and in the binding of non-hydroxylated HIFα to the PHDs.9 The pyrrolidine ring of prolyl residues can adopt Cγ-exo and Cγ-endo conformations, with unsubstituted prolyl residues exhibiting a small preference for the Cγ-endo conformation (Scheme 1).10 This ‘gauche effect’ was proposed to be responsible for the preference for the trans-4 and cis-4 prolyl substituent to adopt the Cγ-exo and Cγ-endo conformations, respectively. Therefore, it is predicted that prolyl trans-4-hydroxylation will bias the Cγ-endo/exo equilibrium to the exo form. The role of the gauche effect in the HIF system has already been described experimentally. Firstly, in VCB⋅HIF crystal structures,4, 7 the HIF trans-4-hydroxyprolyl-564 residue adopts the Cγ -exo conformation and the hydroxy group makes two hydrogen bonds with pVHL Ser111 and His115 that contribute significantly to the binding of HIF to pVHL. The ability of the VCB protein complex to discriminate between hydroxylated and non-hydroxylated HIF-1α556–574 is remarkable (Kd=33nM and 34 µM, respectively).4 These observations suggest selectivity of the pVHL binding pocket for HIF trans-4-hydroxyproline. Secondly, it was reported that PHD catalysis proceeds by hydroxylation of HIF-1α Pro564 in its Cγ-endo conformation and with retention of stereochemistry. It was suggested that upon hydroxylation, a bias to the Cγ-exo conformation may aid in product release.9 Here, we report computational studies aimed at investigating the relative free energy of binding of the VCB complex and HIF-1α, while describing the protein–protein interactions that signals for HIF degradation.
Materials and Methods
Force field
The form of the CHARMM potential energy function used to calculate the energy, U(r), where r represents the Cartesian coordinates of the system, is shown in Equation 1.
| Equation 1 |
The bonded (sometimes refereed as intramolecular) contribution to the potential energy function includes terms for the bonds, angles, torsion or dihedral angles, improper dihedral angles and a Urey-Bradley 1,3-term, where b0, θ0, ψ0, and r1,3;0 are the bond, angle, improper, and Urey-Bradley equilibrium terms, respectively, n and δ are the dihedral multiplicity and phase and the K’s are the respective force constants and amplitudes. The non-bonded (sometimes less precisely referred to as intermolecular) or non-bonded terms include electrostatic and van der Waals (vdW) interactions, where qi and qj is the partial atomic charge of atom i and j, respectively, εij is the well depth, and Rmin,ij is the radius in the Lennard-Jones (L–J) 6–12 term used to treat the vdW interactions, and rij is the distance between i and j. In addition, the energy function in Equation 1 has been extended to include a 2D dihedral energy correction map, referred to as CMAP, which has been used to improve the treatment of the conformational properties of the φ and ψ terms in the peptide backbone.11
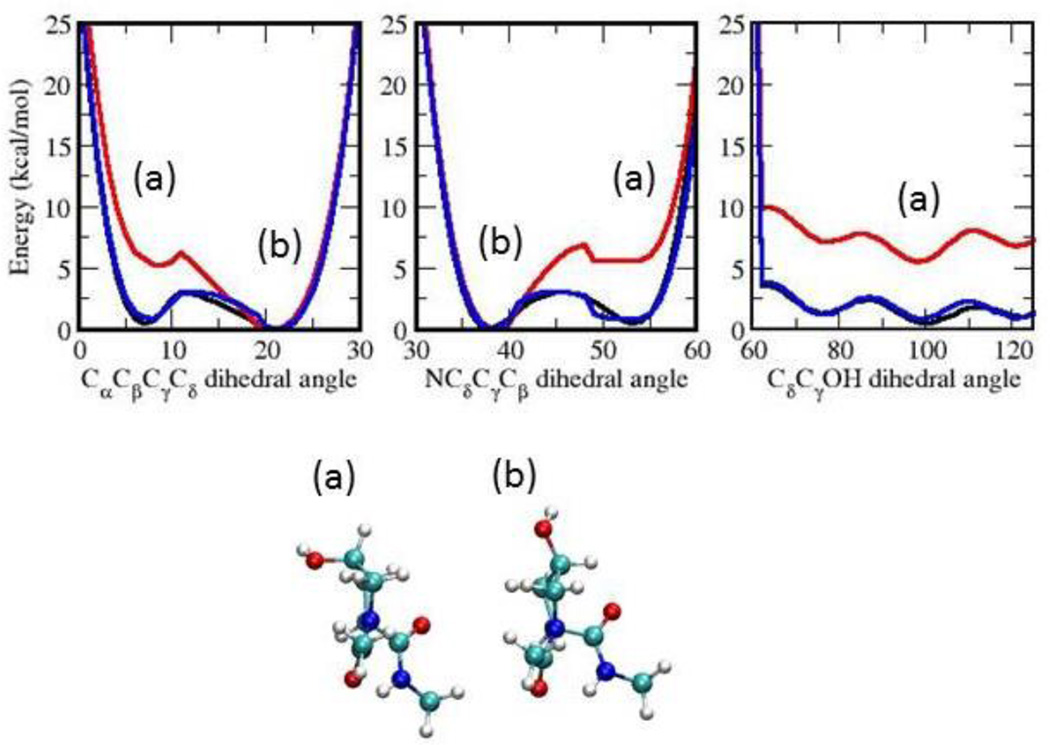
To simulate 4-hydroxyproline with the required accuracy, it was necessary to extend the CHARMM protein force field12 to included optimized parameters for 4-hydroxyproline . Atom types from the CHARMM22 protein force were used along with their corresponding L-J parameters. Likewise, the charges for 4-hydroxyproline were assigned following standard CHARMM additive charge assignment rules (Table S3 in Supplementary Material). Obtaining the bonded terms involved performing the appropriate Quantum Mechanics (QM) calculations to generate target data, followed by the analogous MM calculations and optimization of the parameters so that the target properties are adequately reproduced. All parameters are interdependent and need to be optimized in a self-consistent way. Bond, valence angle, and Urey-Bradley equilibrium terms were optimized targeting a geometry optimized at the MP2/6–31G* level of theory. Bond, valence angle, Urey-Bradley and improper dihedral constants are based on MP2/6–31G* vibrational spectra. Vibrational frequencies should ideally be within 5% of their MP2 values though in some cases this could not be achieved due to the limited number of parameters that were not already in the protein force field. The dihedral angle N-Cδ-Cγ-O is analogous to N-Cδ-Cγ-Hγ in proline, where Hγ is the hydrogen atom that is replaced with the hydroxyl group in the hydroxylation. The value of this dihedral angle is positive for the endo-pucker and negative for the exo-pucker. Amplitudes for the NCδCγO, CαCβCγO, CδCγOH and CβCγOH torsions were optimized based on one-dimensional potential energy scans performed at the MP2/6–31G* level. A Monte Carlo simulated annealing conformational-energy fitting algorithm was used to automatically optimize the targeted parameters.13 Compared to the QM, the initial (transferred) MM parameters produced large differences in some particular areas of the potential energy scans, while the scans with the optimised parameters are in excellent agreement (Figure 4). This is discussed in more detail under ‘Results and Discussion’ below. The final parameter and topology data are listed Table S1, S2 and S3 in the Supplementary Material.
Figure 4.
Ab inito and empirical potential energy surfaces for torsional angles CαCβCγCδ, NCδCγCβ and CδCγOH. Data was obtained from fully relaxed torsional scans at the MP2 level of theory (QM; black) and from the initial (MMi; red) and final (MMf; blue) molecular mechanics set of dihedral parameters. Geometries of some representative minima in each of the dihedral angle scans are shown: (a) exo and (b) endo forms.
System preparation
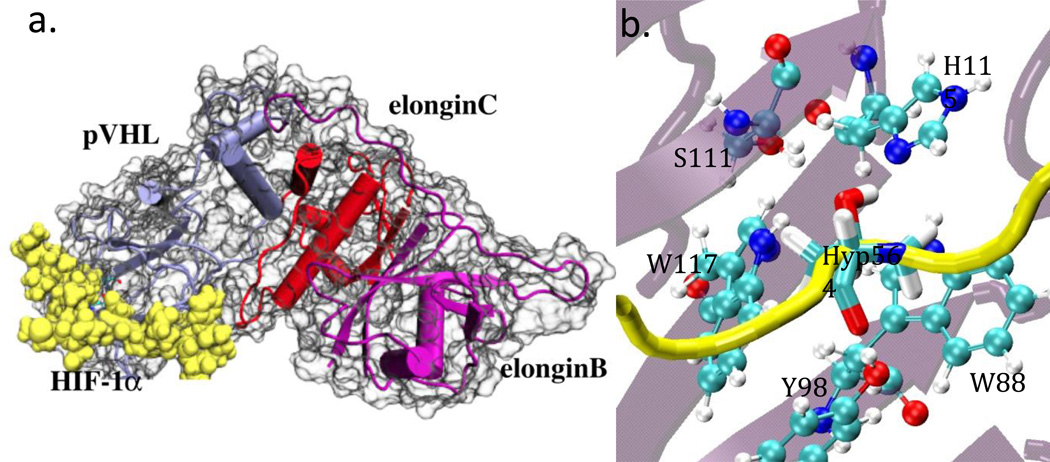
Crystal structures of VCB bound to the C-terminal ODD (CODD) fragment of HIF-1α including hydroxylated Pro564 have been reported (PDB ID: 1LM87 and 1LQB4) at 1.85 Å and 2.00 Å resolution. The higher resolution structure (PDB 1LM8) was used as a starting model in this study (Figure 2). In this structure, the HIFα peptide lies in an extended conformation across one side of the β-domain of pVHL, binding to one of the β-sheets as if it were a complementary β-strand. Hyp564 is almost entirely buried in a deep pocket in the binding cavity. The pocket is lined by W88, Y98, S111, H115 and W117. The N-terminus of the CODD peptide (HIF-1α561–575) was acetylated; an N-methylamide group was present at the C-terminus. Two segments of unresolved residues in the VCB X-ray structures were built using the Wloop homology modeling server (http://bioserv.rpbs.jussieu.fr/cgi-bin/WLoop).14 These loops correspond to residues 49–58 and 107–118 in elongin C and B, respectively.
Figure 2.
a) Schematic representation of the pVHL-Elongin B- Elongin C complex (VCB) with the COOD fragment HIF-1α bound. pVHL in purple, Elongin C in blue and Elongin B in red and HIF-1α in yellow respectively. b) Close-up view of the HIF-1α and pVHL interactions in the Hyp564 binding site. Hyp564 is presented in licorice representation, and the pVHL residues in CPK representation. The backbones of HIF-1α and pVHL are depicted in cartoon representation in yellow and light purple respectively.
Molecular Dynamics Simulations
All force field parameterization was performed with CHARMM15 while the MD simulations and free energy calculations were carried out with NAMD.16 Molecular dynamics (MD) simulations of the wild type VCB with the bound CODD peptide were carried out including all water molecules observed in its crystal structure (PDB 1LM8). The system was trans-4-hydroxylated P564CODD and neutral H115VHL protonated on its Nε nitrogen. An identical system where P564CODD was not hydroxylated was also studied. Additional solvent water molecules were added using the Solvate plug-in of VMD17 using a box padding of 11.5×11.5×11.5 Å3. Sodium and chloride ions were added to neutralize the system. The total system included 70,600 atoms, of which ∼64,600 were water atoms. Two other independent systems with the peptide P564CODD and the trans-4-hydroxylated P564CODD peptide in solution were also set up for further free energy perturbation calculations.
The CHARMM22 force field with CMAP correction18 was used for the protein complex, supplemented with the 4-hydroxyroline parameters discussed above, together with the TIP3P model for water molecules.19 Default CHARMM parameters were used for ions in bulk solution. Long-range electrostatic interactions were treated using the particle mesh Ewald algorithm, 20 with a grid spacing lower than 1 Å, and van der Waals forces were smoothly switched off between 10–12 Å. Bonds with hydrogen atoms were restrained by the SETTLE algorithm,21 with a 2 fs time step. The multi time step algorithm r-RESPA22 was used to integrate the equations of motion. Non-bonded short-range forces were computed for each time step, while longer-range electrostatic forces were updated every 2 time steps. Pressure was kept at 1 atm by the Nose-Hoover Langevin piston,23 with a damping time constant of 100 ps and a period of 200 ps. The temperature was maintained at 298 K by coupling to a Langevin thermostat, with a damping coefficient of 5 ps−1. MD simulations were performed using version 2.8 of NAMD.16 The energy was first minimized by 10,000 steps of steepest descent followed by 50 ns of dynamics. Starting points for the free energy calculations were taken from the last nanosecond of the trajectory.
Free Energy Perturbation calculations
The difference in the free energy of binding between HIF-1α with either P564CODD or Hyp564CODD and pVHL was calculated using the Free Energy Perturbation (FEP) technique24 under the dual-topology paradigm, using version 2.8 of NAMD. Soft-core (SC) potentials were used with a shifting coefficient for the van der Waals radii of 5.0, to prevent the issue of van der Waals endpoint catastrophes arising at λ=1.0 due to the unbounded potential arising from contacts between the decoupled particles and the environment.25 By employing a dimensionless shift coefficient λshift>0 to repel overlapping particles and the dimensionless coefficient λvdW and λelec to independently tune the van der Waals and electrostatic interactions, a bounded van der Waals potentials is guaranteed. Electrostatics interactions are turned on for the created residue and are turned off for the annihilated residue. Van der Waals interactions are turned on for the created residue and are turned off for the annihilated residue.
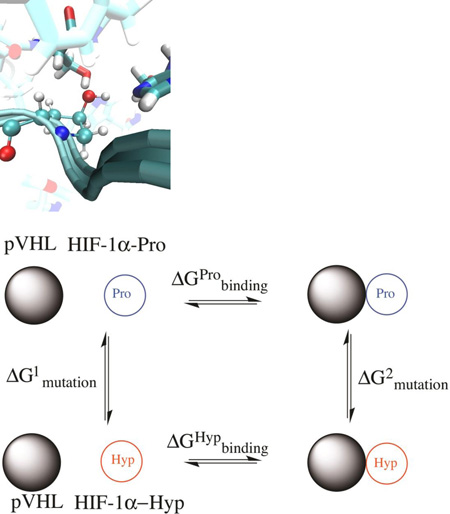
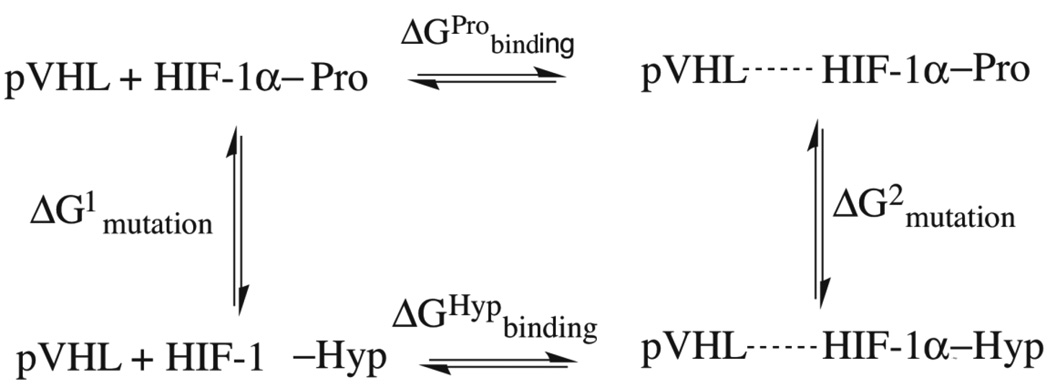
The dual-topology FEP methodology amounts to performing an alchemical transformation, where a chemical species is transformed into another via a pathway of nonphysical (alchemical) states. In a typical FEP calculation involving the transformation of two chemical species in the course of a simulation, the atoms in the molecular topology can be classified into three groups: (i) a group of atoms that do not change during the simulation, e.g. the environment, (ii) the atoms of the reference or initial state, and (iii) the atoms of the final state. In the dual topology paradigm (26 and references therein), the changes are specified in terms of a coupling parameter λ, which is used as a weighting factor for the concurrently existing initial and final states of the group of atoms that are changing. Specifically, the initial state is weighted by a factor (1 – λ) while the final state is weighted by a factor λ, where λ evolves stepwise from 0 to 1. Atoms of the initial state do not interact with those of the final state throughout the simulation, although they interact with the rest of the system. The starting point for the forward FEP calculations was chosen from the last equilibrated snapshot of the MD production run trajectory of pVHL:HIF-1α(Pro564) and the reverse FEP calculations from the last equilibrated snapshot of the MD trajectory of pVHL:HIF-1α(Hyp564). According to the thermodynamic cycle shown in Figure 3, the net free-energy change can be written:
| Equation 2 |
Here, double-wide sampling with full forward and reverse simulations was employed. Each perturbation step was independently equilibrated. ΔG1 was calculated by mutating P564CODD into hydroxylated proline in water, and ΔG2 was calculated by mutating P564CODD into hydroxylated proline in complex to VCB in solution. The FEP calculations were carried out using 10, 16 or 20 intermediate states (λ= 0.1, 0.0625, 0.05), and window lengths of 50, 100, 150 and 200 ps. In total, these calculations amount between 0.5 to 4 ns for each unidirectional simulation. Both forward (λ = 0 → λ = 1) and backward transformations (λ = 1 → λ = 0) were performed, where λ = 0 is the reference state, P564CODD, and λ = 1 is the perturbed, hydroxylated state.
Figure 3.
Thermodynamic cycle utilized to estimate relative protein-peptide binding free energies between hydroxylated and non-hydroxylated proline. Horizontal transformations are described through respective experimental data and vertical transformations described computationally through ‘alchemical transformation’ of an amino acid of the peptide in the bound (left) and the free state (right).
Error analysis was performed on the resulting potential energy ΔU profile obtained from the simulation. This allows for the calculation of the forward potential energy probability distributions. The FEP estimator of the true free-energy was obtained using N independent values of ΔU obtained in the FEP/MD simulation:26–27
| Equation 3 |
The FEP estimator constitutes a biased distribution of ΔU values, such that its estimate will only match the value obtained from the FEP/MD simulation ΔG in the limit of using every single configuration from the run.26 The variance of a FEP estimator distribution can be found. This distribution consists of N0 sampled values of ΔU:
| Equation 4 |
A bidirectional FEP estimator was used by combining the probability distributions P0(ΔU) and P1(ΔU) for both the forward and backward FEP runs.
| Equation 5 |
A simple-overlap sampling (SOS) was applied,28 where the intermediate state is located halfway between the initial and final states ln w with an arbitrary parameter w (rN, λ):
| Equation 6 |
Results and Discussion
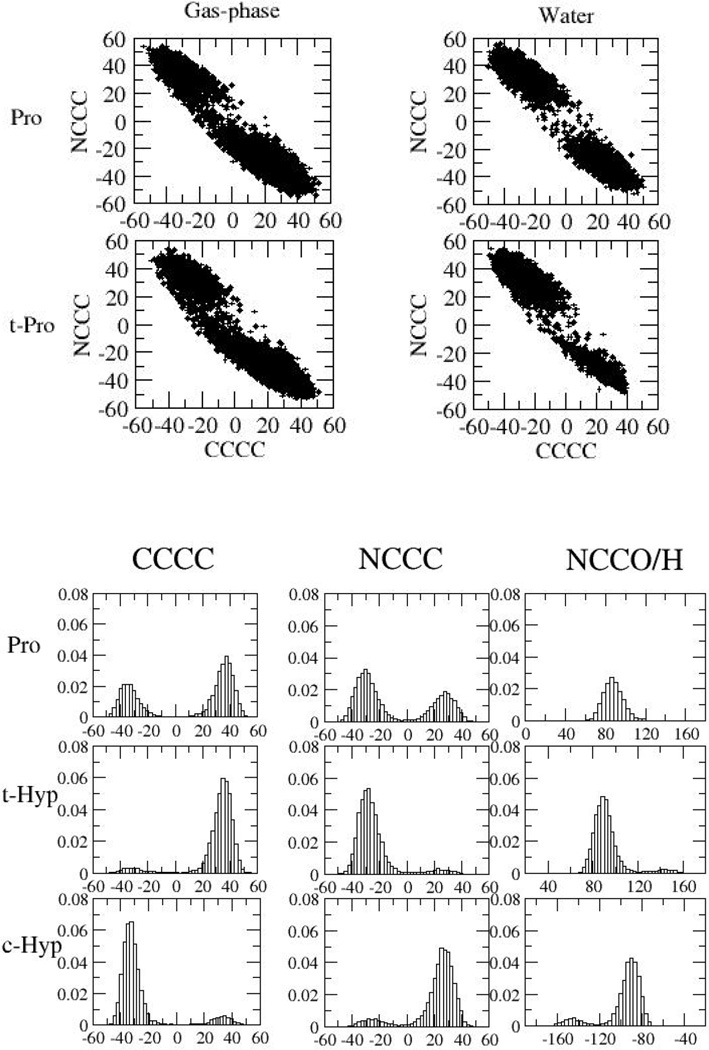
MD simulations, using the optimized parameters, were performed to test the validity of the crystal structures, to investigate the conformational preferences of HIF-1α P564CODD, and the contribution of S111VHL and H115VHL in HIFα:VCB binding. In the MD simulations of non-substituted P564CODD, the observed conformational preferences were almost the same as in the corresponding solution simulations. A preference for the exo conformation when COOD was trans-4-hydroxylated at 564 was observed (Figure 5). Overall, the results for prolyl and trans-4-hydroxyprolyl 564CODD were consistent with the crystallographic and substrate analog studies that predict trans-4-hydroxyprolyl-564CODD to adopt the C4-exo conformation when bound to VCB.4, 7, 9
Figure 5.
Distribution of CαCβCγCδ, NCδCγCβ, and CδCγOH angles in simulations of 4-hydroxyproline and proline in aqueous solution. Note that NCδCγH was uniquely measured in proline, and the measurement was performed using the (diastereotopic) hydrogen atom that corresponds to the oxygen atom in hydroxyproline.
Probability distributions of CαCβCγCδ, NCδCγCβ, and CδCγOH angles in simulations of proline and 4-hydroxyproline in solution are presented in Figure 5. The two minima in both the CαCβCγCδ and NCδCγCβ scan in Figure 4 correspond to the exo (a) and endo (b) conformations. The energy difference between these conformations was 5.23 kcal/mol using the initial guess MM parameters compared to 0.48 kcal/mol using the QM reference data, and a very similar value for the optimized MM parameters. Using the initial guess could hypothetically have led to large qualitative differences in the conformational sampling during MD simulations and FEP calculations. Clearly, optimization of the dihedral parameters yields MM energy profiles that are in very good agreement with the corresponding QM profiles; the locations and heights of the different minima and barriers are an excellent fit, as is the overall energy landscape. This quality of fit at the model compound level is encouraging for the accuracy of (respectively) the thermodynamics and kinetics of the endo/exo equilibrium obtained from the MD simulation will be accurate and good agreement with experiment was indeed observed.
Free energy perturbation calculations were performed to understand the molecular contributions to the relative binding of the proline and hydroxyproline motives. Results are summarized in Tables 1 to 4, giving values for the difference in free energy of binding of HIF-1α in the hydroxylated and non-hydroxylated forms and pVHL.
Table 1.
Average free energy for the transformation of the bound VCB-HIF-1α complex with Pro564 (Enz-Pro) and Hyp564 (Enz-Hyp), when employing hard- and soft-core potentials.
| λshift | λvdW | λelec | Average ΔG ± σ (kcal mol−1) | |
|---|---|---|---|---|
| Enz-Pro | Enz-Hyp | |||
| 1 | 0 | 0 | −23.49 ± 1.22 | +25.70 ± 0.31 |
| 5 | 0 | 0 | −23.59 ± 1.80 | +25.88± 0.37 |
| 5 | 0 | 0.5 | −24.18± 1.23 | +26.27± 0.38 |
| 5 | 1 | 0.5 | −23.65 ± 1.68 | +24.75± 1.38 |
Table 4.
Difference in free energy of binding of pVHL and HIF-1α, in the hydroxylated and non-hydroxylated forms. Simulations were performed with different number of windows, and different window lengths. In order to increase the statistical precision of the FEP calculations each simulation was run bi-directionally, involving transformations to and from the hydroxylated and non-hydroxylated states. The statistical data accrued in the forward and backward transformations were used to evaluate the convergence of the FEP calculations.
| Number of Windows |
Window length (ps window−1) |
Total simulation time (ns) |
ΔΔG ± RMS σ (kcal mol−1) | |
|---|---|---|---|---|
| Forward | Reverse | |||
| 10 | 50 | 0.5 | 4.70 ± 0.90 | −6.68 ± 0.43 |
| 100 | 1.0 | 5.80 ± 0.38 | −6.20 ± 0.42 | |
| 150 | 1.5 | 5.91 ± 0.52 | −6.70 ± 0.73 | |
| 200 | 2.0 | 5.49 ± 0.56 | −6.49 ± 0.47 | |
| 16 | 50 | 0.8 | 4.26 ± 1.10 | −6.67 ± 0.34 |
| 100 | 1.6 | 5.64 ± 0.21 | −6.48 ± 0.30 | |
| 150 | 2.4 | 5.55 ± 0.29 | −6.07 ± 0.61 | |
| 200 | 3.2 | 6.31 ± 0.28 | −6.21 ± 0.38 | |
| 20 | 50 | 1.0 | 5.26 ± 0.82 | −6.60 ± 0.20 |
| 100 | 2.0 | 6.00 ± 0.33 | −6.43 ± 0.30 | |
| 150 | 3.0 | 5.97 ± 0.39 | −6.38 ± 0.32 | |
| 200 | 4.0 | 5.92 ± 0.38 | −6.20 ± 0.42 | |
Several computational technicalities are considered in order to evaluate and attain convergence and precision. The outcome of using soft-core (SC) and hard-core scaling is given in Table 1, as was detailed in the FEP Methods section. In order to increase the statistical precision of the FEP calculations, each simulation was run bi-directionally, involving transformations to and from the hydroxylated and non-hydroxylated states both for the peptide on its own or in complex with pVHL. The statistical data accrued in the forward and backward transformations were used to evaluate the convergence of the FEP calculations. The results are presented in Table 2. A stratification approach was adopted, and the effect of the number of windows and window length on the precision for the alchemical transformation in solution of the unbound HIF-1α in the hydroxylated and non-hydroxylated forms was considered; the results are presented in Tables 3 and 4. The free energy change ΔG was obtained from the mean of ten independent FEP runs starting from the same snapshot, and the error estimate σ was obtained as the standard error from the mean of those 10 simulations (Table 1, and 3, and the final binding energy in Table 4).
Table 2.
Reversibility of the transformation in solution. In order to increase the statistical precision of the FEP calculations each simulation was run bi-directionally, involving transformations to and from the hydroxylated and non-hydroxylated states, with pVHL in complex with HIF-1α or HIF-1α on its own. A representative set of simulations using 20 windows of 200 ps per window was used to evaluate the convergence of the FEP calculations, with the cut-off criteria of a simulation with a hysteresis of < 0.5 kcal mol−1.
| Pep-Pro to Pep-Hyp | Pep-Hyp to Pep-Pro | Enz-Pro to Enz-Hyp | Enz-Hyp to Enz-Pro |
|---|---|---|---|
| −18.64 | 18.44 | −23.59 | 24.83 |
| −18.74 | 18.77 | −25.38 | 25.35 |
| −18.61 | 18.51 | −24.38 | 25.60 |
| −18.64 | 18.54 | −24.24 | 24.71 |
| −18.53 | 18.59 | −24.86 | 25.39 |
| −18.63 | 18.67 | −24.46 | 24.63 |
| −18.41 | 18.58 | −24.99 | 24.55 |
| −18.59 | 18.60 | −24.13 | 25.28 |
| −18.70 | 18.55 | −24.06 | 23.16 |
| −18.64 | 18.72 | −25.27 | 24.41 |
| Average (kcal/mol) −18.62 ± 0.09 |
Average (kcal/mol) 18.60 ± 0.10 |
Average (kcal/mol) −24.54 ± 0.58 |
Average (kcal/mol) 24.79 ± 0.64 |
Table 3.
Influence of optimal window length on precision. Alchemical transformations were carried out in solution with pVHL in complex with HIF-1α, or HIF-1α on its own, in the hydroxylated and non-hydroxylated forms and the reverse.
| Window length (ps window−1) |
Number of Windows |
Pep-Pro → Pep-Hyp | Enz-Pro →Enz-Hyp |
|---|---|---|---|
| Average ΔG ± RMS σ (kcal mol−1) |
Average ΔG ± RMS σ (kcal mol−1) |
||
| 50 | 10 | −18.51 ± 0.30 | −23.21 ± 1.51 |
| 16 | −18.70 ± 0.15 | −22.96 ± 2.05 | |
| 20 | −18.60 ± 0.14 | −23.86 ± 1.50 | |
| 100 | 10 | −18.59 ± 0.13 | −24.38 ± 0.62 |
| 16 | −18.53 ± 0.18 | −24.41 ± 0.31 | |
| 20 | −18.67 ± 0.14 | −24.67 ± 0.51 | |
| 150 | 10 | −18.58 ± 0.12 | −24.49 ± 0.80 |
| 16 | −18.62 ± 0.17 | −24.17 ± 0.24 | |
| 20 | −18.67 ± 0.09 | −24.64 ± 0.59 | |
| 200 | 10 | −18.69 ± 0.13 | −24.18 ± 0.85 |
| 16 | −18.55 ± 0.10 | −24.86 ± 0.36 | |
| 20 | −18.62 ± 0.09 | −24.54 ± 0.58 |
We now proceed to analyse the FEP results, detailing our choice of protocol starting with the choice of soft-core (SC) potential parameters. In Table 1, the soft-core (SC) and hard-core (SC) simulation parameters tested for the VCB complex with HIF-1α bound, in both the forward and backward directions (Enz-Pro and Enz-Hyp states) are presented. We use a NAMD-default soft-core (SC) potential with λshift=5, λvdW=1 and λelec=0.5, for which there is evidence of its advantage over hard-core (HC) potentials that do not scale non-bonded forces (λshift=1, λvdW=0 and λelec=0). A recent review of scaling methods found that HC potentials gave rise to a >5 kcal mol−1 error in the converged free-energy estimate.27, 29 This preference of SC scaling is due to its ability to alleviate end-point catastrophes of unbounded van der Waals forces of annihilated moiety. This is argued on the basis that SC yields smaller hysteresis in the ΔG when compared to HC scaling; compare the hysteresis of 2.2 kcal mol−1 for HC and 1.1 kcal mol−1 for SC.
In Table 2, the typical values of ΔG obtained in 10 individual and repeated FEP simulations for each system, Pep-Pro, Pep-Hyp, Enz-Pro and Enz-Hyp are illustrated. The average of each set of 10 simulations is reported, and this procedure of averaging is also adopted for results in Tables 1, 3, and 4. Good sampling is essential for capturing the structural rearrangements and yielding converged free energies. The trends displayed in the hysteresis of ΔG (forward minus reverse transformation) in Table 2 is overall below 0.5 kcal/mol, suggesting that sampling of phase space in the simulations has been efficient. The standard deviations on individual free energy difference values provide an estimate of the errors involved in their calculation. These errors are small relative to the magnitude of the calculated free energies.
Secondly, the choice of optimal window numbers and length was selected based on three different window values, 10, 16 and 20, corresponding to values of λ=0.1, λ=0.0625, and λ=0.05, respectively, and four different times: 50, 100, 150 and 200 ps per window. This equates to total simulation times for a 10-window set of 0.5 ns, 1.0 ns, 1.5 ns and 2.0 ns, respectively; for a 16-window set the total simulation time was 0.8 ns, 1.6 ns, 2.4 ns, and 3.2 ns, respectively; for a 20-window set the total simulation time 1.0 ns, 2.0 ns, 3.0 ns, and 4.0 ns, respectively. The use of window stratification ensures that there is sufficient overlap between the reference (ΔU0) and target (ΔU1) state potential energy distributions during the alchemical transformation, which improves hysteresis.27 In Table 3, the ΔG average of the forward alchemical transformation of the unbound solvated peptide, and the bound enzyme complex, reveals that window number did not strongly affect the statistical precision of results, with the standard deviation error all within same order of magnitude and with no statistically-significant deviation between window number. These results suggest that this alchemical transformation is not affected by a stratification approach above 10 window partitions. It is however revealed that the window length was a determinant of hysteresis. When comparing the set of 50 ps to sets 100, 150 and 200 ps, the error reduces from σ=2.05 kcal mol−1 (50 ps) to σ=0.31 kcal mol−1 (100 ps), 0.24 kcal mol−1 (150 ps) and 0.36 kcal mol−1 (200 ps). Thus, it can be concluded that simulations using window lengths greater than 50 ps yield equivalent results, but that simulations with 50 ps yield unacceptable hysteresis. This in accordance with the result that longer sampling correlates with increases precision in ΔG, by reducing the finite-time sampling error.26–27
Finally, to demonstrate the micro-reversibility of the FEP simulation procedure, the free energy was evaluated in the forward (Pro564 to Hyp564) and backward (Hyp564 to Pro564) transformations. In both directions, the free energy must have the same absolute magnitude such that . Table 2 summarizes the free energy values for the transformation of the peptide bound to the enzyme in the forward (Enz-Pro) and reverse (Enz-Hyp) direction. The hysteresis (forward minus reverse transformation) of the average value of ten simulations observed is 0.26 ± 0.06 kcal mol−1 below the threshold of 0.5 kcal mol−1. This result is indicative of the micro-reversibility of the transformation. For the alchemical transformation of Pep-Pro to Pep-Hyp (forward process), and Pep-Hyp to Pep-Pro (reverse process) the hysteresis of the average value of ten simulations being 0.02 ± 0.10 kcal mol−1, below the 0.5 kcal mol−1 threshold.
The relative difference in binding energy (ΔΔGcomp) between the non-hydroxylated peptide (Pep-Pro) and enzyme (Enz-Pro) for the forward direction simulation, and the difference between the hydroxylated peptide (Pep-Hyp) and enzyme (Enz-Hyp) states for the reverse direction simulation, was estimated using Equation 2, and results are summarised in Table 4. The free energy profile of the Pep-Pro and Enz-Pro transformations with ΔΔGcomp being the difference in free energies at λ=1 are shown in Figure S4. Consistent with previous results, simulations that employed window lengths above 50 ps yield comparable binding free energies of the order of ~ 10–11 kT, such as 5.92 kcal mol−1 when using 20 windows, which constitutes an acceptable hysteresis of 0.28 kcal mol−1, which is <1 kcal mol−1 (<2 kT) within the RMS error bound. Based upon this analysis, a representative value, such as 5.92 ± 0.38 kcal mol−1 constitutes the computational relative free energy of binding, ΔΔGcomp.
That the binding energy values all range from 5.26 to 6.00 kcal mol−1 (of the order ~ 10–11 kT) is indicative of a moderate strength peptide-protein interaction between HIF-1α and pVHL (at least in terms of the regions studied). This is an important result, because the moderate strength interaction enables the subsequent proteasomal degradation of HIF-1α via an E3 uniquitin ligase complex during normoxic conditions, as outlined in the signalling pathway in Figure 1. If binding was too strong, association would remain permanent and the further degradation would not be possible or it would be difficult. Hence, this moderate strength binding interaction is responsible for HIF-1α not accumulating physiologically except during hypoxic crises when it builds up and signals for physiological adaptation to low-oxygen conditions.
A full error analysis is presented in Table 5. This analysis was performed on the potential-energy distributions ΔU obtained in the previous FEP simulations. By using free energy estimators (unidirectional, bidirectional and SOS) three estimates of the relative computational binding free energy were obtained. The SOS analysis yielded a relative binding free energy estimate whose error was smallest (4.78 ± 0.13 kcal mol−1), and was also the closest estimate to the experimental ∼4 kcal mol−1 binding energy.
Table 5.
Error analysis for the Enz-Pro and Pep-Pro systems and the binding energy estimate ΔΔG.
|
(kcal mol−1) |
(kcal mol−1) |
(kcal mol−1) |
|
|---|---|---|---|
| Unidirectional FEP | −24.0 ± 0.08 | −18.89 ± 0.10 | 5.09 ± 0.18 |
| Bidirectional FEP | −24.0 ± 0.12 | −18.89 ± 0.13 | 5.09 ± 0.25 |
| Simple Overlap Sampling | −23.5 ± 0.06 | −18.72 ± 0.07 | 4.78 ± 0.13 |
For an assessment of the hydrogen bond interactions present, the distance profile between HIF-1α/S111 and HIF-1α/H115 as a function of simulation time was calculated. Two stable interactions during the classical MD simulation, between the H-bond donor S111 hydrogen atom and the acceptor HIF-1α-Hyp564 oxygen atom, and between the H-bond acceptor H115 imidazole nitrogen and the donor HIF-1α-Hyp564 hydroxyl hydrogen, confirm the existence of S111(H)-HIF-1α-Hyp564(O) and HIF-1α-Hyp564(H)-H115(N) native contacts. The overall trend observed is that a hydrogen-bond between HIF-1α and S111 or H115 is only detected when Pro564 is hydroxylated. These findings support the currently proposed HIF-1α/VCB binding model.
In Table 6, the per-residue RMSD of the pVHL:HIF-1α(Hyp564) and pVHL:HIF-1α(Pro564) is presented. In the case of pVHL:HIF-1α(Hyp564), a low RMSD of Hyp564 (0.46 ± 0.14 Å) is observed due to its highly conserved H-bonds to S111 (0.62 ± 0.30 Å) and H115 (0.57 ± 0.16 Å with 67% and 74.5% life time respectively. This is absence in the complex pVHL:HIF-1α(Pro564), in which the Pro564 pocket has a larger RMSD of 1.47 ± 0.24 Å and 1.02 ± 0.29 Å for H115 and S111 respectively. For Y112, a value of 0.72 ± 0.18 Å is obtained which supports its nature of key native contact. In the Pro pocket, the loss of significant H-bond interactions results in a conformational change in the Y112 side-chain with the rotation of the phenol group, raising the RMSD (1.79 ± 0.86 Å), despite conserving a significant H-bond to H115 (residence time of 85.4%). For L562, due to increased pocket flexibility, this residue can tumble in the Pro pocket, thus explaining the significant RMSD drift (2.61 ± 1.04 Å).
Table 6.
RMSD values per residue and total pocket average (Å) for pVHL:HIF-1α(Hyp564) trajectory and pVHL:HIF-1α(Pro564) trajectory.
| Residue | Hyp RMSD ± σ (Å) | Pro RMSD ± σ (Å) |
|---|---|---|
| W88 | 0.71 ± 0.16 | 0.49 ± 0.14 |
| W117 | 0.73 ± 0.23 | 0.55 ± 0.11 |
| Hyp564 | 0.45 ± 0.13 | 0.90 ± 0.37 |
| A563 | 1.04 ± 0.30 | 0.99 ± 0.29 |
| H115 | 0.63 ± 0.16 | 1.47 ± 0.24 |
| Y112 | 0.70 ± 0.18 | 1.79 ± 0.84 |
| S111 | 0.70 ± 0.32 | 1.03 ± 0.29 |
| Y98 | 0.73 ± 0.23 | 0.71 ± 0.23 |
| L562 | 1.60 ± 0.55 | 2.30 ± 0.88 |
| Y565 | 0.95 ± 0.32 | 0.90 ± 0.27 |
| H110 | 0.78 ± 0.23 | 1.39 ± 0.20 |
| I109 | 2.29 ± 0.34 | 2.39 ± 0.46 |
| Avg. RMSD | 1.17 ± 0.13 | 1.44 ± 0.23 |
In Table 7, the occupancy of native contacts in the pVHL:HIF-1α(Hyp564) and pVHL:HIF-1α(Pro564) trajectories is compared using a contact threshold of 3.5 Å. The conformation of Y98 remains unaffected by the hydroxylation of Pro564, maintaining the contact for 68.8% toward Pro564 and 54.4% for Hyp564. H115 and S111 are only bonded to residue 564 in the hydroxylated state (H115 74.50% in Hyp versus 1.74% in Pro, and S111:67.00 % in Hyp versus 0.03% in Pro). An analysis was also performed to study pVHL-pVHL contacts. Tyr112 loses its highly conserved donor interaction with H115 (85.4% residence time) upon hydroxylation, due to H115 rearranging to bind strongly to Hyp564 while H110 retains a highly conserved interaction with Y565 independent of hydroxylation state (82.5% in Pro and 76.01% in Hyp). In addition, W117 retains its interaction with S111 independent of hydroxylation state (71.00% in Pro and 65.78% in Hyp) and H115 retains its donor interaction with Y112 independently of the hydroxylation state (60.00% in Pro and 50.88% in Hyp). The S111–H115 interaction in the Pro state is completely lost upon hydroxylation, due to the two newly gained interactions with Hyp564. The alchemical transformation introducing the OH hydroxyl group that replaces a hydrogen atom was monitored. It was ensured that this transformation does not induce disruptions in the pocket (typical value of 0.42 ± 0.07 Å) and or large-scale conformational changes on the protein backbone (typical value of 0.96 ± 0.14 Å), as illustrated in Supplementary Figure S5.
Table 7.
H-bond persistence for (a) pVHL interactions with segment Hyp564 in HIF-1α, and (b) environment-environment (pVHL-pVHL) interactions
| Contact pVHL-HIF | Persistence | Contact pVHL-pVHL | Persistence |
|---|---|---|---|
| Hyp564-H115 | 74.5% | W117-S111 | 65.8% |
| S111-Hyp564 | 67.0% | H115-Y112 | 50.9% |
| Y98-Hyp564 | 54.4% | W88-H115 | 20.1% |
| Y112-Hyp564 | 13.3% | Y112-H115 | 9.60% |
| Hyp564-W88 | 0.50% | Y112-A563 | 7.43% |
| Y112-Hyp564 | 0.90% | H115–W88 | 0.20% |
| Hyp564-Y98 | 0.37% | H115–Y112 | 0.33% |
| W117-Hyp564 | 0.07% | - | - |
| Hyp564-H110 | 0.03% | - | - |
| Y564–Y112 | 1.57% | - | - |
| H110-Y565 | 76.0% | - | - |
| Y565-H110 | 53.9% | - | - |
| H115-L562 | 17.5% | - | - |
Summary
Substitution of a hydrogen atom by a hydroxyl group in the oxygen-dependent degradation domain substantially increases binding of HIFα to the VCB complex. As described previously,30 residues other than the (hydroxylated) proline (P564CODD) are important in HIFα:VCB binding, but hydroxylation of P564CODD alone accounts for the experimentally observed ∼1,000-fold difference in binding affinity (equivalent to ∼4 kcal/mol) for VCB between hydroxylated/non-hydroxylated CODD. That the selectivity of VCB for its HIFα binding partner is predominantly determined by binding events arising from modifications to residue P564CODD alone is consistent with the signaling mechanisms for binding to E3 ubiquitin ligases other than VCB.31 It had been proposed that trans-4-hydroxylation of prolyl-residues in HIFα biases the conformation of the targeted prolyl residues to the Cγ-exo state, i.e. that the stereoelectronic gauche effect pre-organizes32 HIFα for binding to VCB.4, 30 Here, a new set of molecular mechanics parameters for hydroxyproline has been developed following the CHARMM force field philosophy, paying particular attention to the endo/exo pucker conformations. These QM-based parameters qualitatively reproduce the expected pucker preference of hydroxyproline based on the gauche effect and indirect experimental evidence. Subsequently, a systematic study using the FEP technique amounting over 3 microsecond (µs) of simulation time yielded a change in free energy of binding of P564CODD or Hyp564CODD with pVHL consistent with the difference of at least 4.09 kcal/mol that can be estimated from the Ki values at 25°C, i.e., ΔΔGexp = RT ln KPro/KHyp. Thus, it appears that the calculations reproduce the experimental observation, and provide a rigorous method for studying in greater depth the origin of the selectivity arising from hydroxylation. More generally spoken, the present methodology demonstrates that relative binding free energy calculations between structurally similar sites can be computed with good precision and a reasonable computational expense.
The interaction between HIF-1α and the von Hippel Lindau tumour-suppressor protein complex is attractive for drug targets due to its exquisite substrate specificity. However, the development of inhibitors has proven extraordinarily challenging as its modulation requires the targeting of protein-protein interactions. Characterising the interactions of this protein complex with computational and experimental tools will aid guiding future development of therapeutics for the treatment of some types of cancer and cardiovascular diseases where clinically observed mutations to pVHL are thought to cause weaker binding of HIF-1α.33
Supplementary Material
Scheme 1.
Ring conformations of proline and 4-hydroxyproline. The pyrrolidine ring of prolyl residues can adopt Cγ-exo and Cγ-endo conformations. Proline exhibits a small preference for the Cγ-endo conformation. trans-4 and cis-4 prolyl substituents prefer the Cγ-exo and Cγ-endo conformations respectively.10
Acknowledgments
C.D. thanks The Royal Society for a University Research Fellowship and grants from the EPSRC. The Oxford Supercomputing Centre and HECToR are acknowledged for providing computational resources. A.D.M. thanks the NIH (GM051501, GM0720855 and GM070855) and NSF (CHE-0823198) for support.
Footnotes
SUPPORTING INFORMATION PARAGRAPH. The contents of Supporting Information include the following: 1) Tables with hydroxyl-proline force field parameters and topology, 2) Scaled ab initio and MM vibrational spectra of cis- and trans-hydroxyproline, 3) Average RMSD values and standard deviation for the peptide in solution and the enzyme complexes, 4) Key H-bond differences between clusters of pVHL:HIF-1α(Hyp564) and pVHL:HIF-1α(Pro564), 5) Snapshots indicating distances between HIF-1α:Pro564(H) to S111(O) and H115(N), and HIF-1α-Hyp564(O)-S111(H) and HIF-1α-Hyp564(H)-H115(N) 6) Free energy profile for an Enz-Hyp simulation with different scaling parameters, 7) Effect of window number in ΔG for the Enz-Hyp transformation, 8) Free energy profile for the Pep-Pro state considering simulations with different lengths, 9) Free energy of binding as the difference between the free energy of the transformation of Pro564 to Hyp564 in the peptide (Pep-Pro) and enzyme (Enz-Pro) states. This information is available free of charge via the Internet at http://pubs.acs.org/.
REFERENCES
- 1.Kaelin WG, Jr, Ratcliffe PJ. Oxygen sensing by metazoans: The central role of the HIF hydroxylase pathway. Mol Cell. 2008;30:393–402. doi: 10.1016/j.molcel.2008.04.009. [DOI] [PubMed] [Google Scholar]
- 2.Chan DA, Sutphin PD, Yen S-E, Giaccia AJ. Coordinate regulation of the oxygen-dependent degradation domains of hypoxia-inducible factor 1α. Mol Cell Biol. 2005;25:6415–6426. doi: 10.1128/MCB.25.15.6415-6426.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Berra E, Benizri E, Ginouves A, Volmat V, Roux D, Pouyssegur J. HIF prolyl-hydroxylase 2 is the key oxygen sensor setting low steady-state levels of HIF-1alpha in normoxia. EMBO J. 2003;22:4082–4090. doi: 10.1093/emboj/cdg392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hon WC, Wilson MI, Harlos K, Claridge TDW, Schofield CJ, Pugh CW, Maxwell PH, Ratcliffe PJ, Stuart DI, Jones EY. Structural basis for the recognition of hydroxyproline in HIF-1α by pVHL. Nature. 2002;417:975–978. doi: 10.1038/nature00767. [DOI] [PubMed] [Google Scholar]
- 5.(a) Epstein ACR, Gleadle JM, McNeill LA, Hewitson KS, O’Rourke J, Mole DR, Mukherji M, Metzen E, Wilson MI, Dhanda A, Tian Y-M, Masson N, Hamilton DL, Jaakkola P, Barstead R, Hodgkin J, Maxwell PH, Pugh CW, Schofield CJ, Ratcliffe PJ. C. elegans EGL-9 and mammalian homologs define a family of dioxygenases that regulate HIF by prolyl hydroxylation. Cell. 2001;107:43–54. doi: 10.1016/s0092-8674(01)00507-4. [DOI] [PubMed] [Google Scholar]; (b) Bruick RK, McKnight SL. A conserved family of prolyl-4-hydroxylases that modify HIF. Science. 2001;294:1337–1340. doi: 10.1126/science.1066373. [DOI] [PubMed] [Google Scholar]
- 6.Jaakkola P, Mole DR, Tian Y-M, Wilson MI, Gielbert J, Gaskell SJ, Kriegsheim Av, Hebestreit HF, Mukherji M, Schofield CJ, Maxwell PH, Pugh CW, Ratcliffe PJ. Targeting of HIF-alpha to the von Hippel-Lindau ubiquitylation complex by O2-regulated prolyl hydroxylation. Science. 2001;292:468–472. doi: 10.1126/science.1059796. [DOI] [PubMed] [Google Scholar]
- 7.Min J-H, Yang H, Ivan M, Gertler F, Kaelin WG, Jr, Pavletich NP. Structure of an HIF-1alpha -pVHL complex: hydroxyproline recognition in signaling. Science. 2002;296:1886–1889. doi: 10.1126/science.1073440. [DOI] [PubMed] [Google Scholar]
- 8.(a) Kaelin WG., Jr The von Hippel-Lindau protein, HIF hydroxylation, and oxygen sensing. Biochem Biophys Res Comm. 2005;338:627–638. doi: 10.1016/j.bbrc.2005.08.165. [DOI] [PubMed] [Google Scholar]; (b) Schofield CJ, Ratcliffe PJ. Oxygen sensing by HIF hydroxylases. Nat. Rev. Mol. Cell. Biol. 2004;5:343–354. doi: 10.1038/nrm1366. [DOI] [PubMed] [Google Scholar]; (c) Semenza GL. Hydroxylation of HIF-1: oxygen sensing at the molecular level. Physiology. 2004;19:176–182. doi: 10.1152/physiol.00001.2004. [DOI] [PubMed] [Google Scholar]
- 9.Loenarz C, Mecinovic J, Chowdhury R, McNeill Luke A, Flashman E, Schofield Christopher J. Evidence for a stereoelectronic effect in human oxygen sensing. Angew. Chem., Int. Ed. 2009;48:1784–1787. doi: 10.1002/anie.200805427. [DOI] [PubMed] [Google Scholar]
- 10.Hodges JA, Raines RT. Stereoelectronic and steric effects in the collagen triple helix: Toward a code for strand association. J. Am. Chem. Soc. 2005;127:15923–15932. doi: 10.1021/ja054674r. [DOI] [PubMed] [Google Scholar]
- 11.MacKerell AD, Feig M, Brooks CL. Improved treatment of the protein backbone in empirical force fields. J. Am. Chem. Soc. 2004;126:698–699. doi: 10.1021/ja036959e. [DOI] [PubMed] [Google Scholar]
- 12.MacKerell AD, Bashford D, Bellott; Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiórkiewicz-Kuczera J, Yin D, Karplus M. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 13.Guvench O, MacKerell AD. Automated conformational energy fitting for force-field development. J Mol Modell. 2008;14:667–679. doi: 10.1007/s00894-008-0305-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.(a) Kwasigroch JM, Chomilier J, Mornon JP. A global taxonomy of loops in globular proteins. J Mol Biol. 1996;259:855–872. doi: 10.1006/jmbi.1996.0363. [DOI] [PubMed] [Google Scholar]; (b) Wojcik J, Mornon JP, Chomilier J. New efficient statistical sequence-dependent structure prediction of short to medium-sized protein loops based on an exhaustive loop classification. J Mol Biol. 1999;289:1469–1490. doi: 10.1006/jmbi.1999.2826. [DOI] [PubMed] [Google Scholar]
- 15.Brooks BR, Brooks CL, III, Mackerell AD, Jr, Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, Caflisch A, Caves L, Cui Q, Dinner AR, Feig M, Fischer S, Gao J, Hodoscek M, Im W, Kuczera K, Lazaridis T, Ma J, Ovchinnikov V, Paci E, Pastor RW, Post CB, Pu JZ, Schaefer M, Tidor B, Venable RM, Woodcock HL, Wu X, Yang W, York DM, Karplus M. CHARMM: The Biomolecular Simulation Program. J Comput Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.(a) Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. Scalable molecular dynamics with NAMD. J Comput Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Kale L, Skeel R, Bhandarkar M, Brunner R, Gursoy A, Krawetz N, Philips J, Shinozaki A, Varadarajan K, Schuten K. Molecular dynamics programs design - NAMD2: Greater Scalability for Parallel Molecular Dynamics. J. Comput Phys. 1999;151:283–312. [Google Scholar]
- 17.Humphrey W, Dalke A, Schulten K. VMD: Visual molecular dynamics. J. Mol. Graphics. 1996;14:33–37. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 18.Mackerell AD, Jr, Feig M, Brooks CL., 3rd Extending the treatment of backbone energetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J Comput Chem. 2004;25:1400–1415. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- 19.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulations of liquid water. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 20.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. A smooth particle mesh Ewald method. J. Chem. Phys. 1995;103:8577–8593. [Google Scholar]
- 21.Miyamoto S, Kollman PA. SETTLE - an analytical version of the Shake and Rattle algorithm for rigid water models. J Comput Chem. 1992;13:952–962. [Google Scholar]
- 22.Tuckerman M, Berne BJ, Martyna GJ. Reversible Multiple Time Scale Molecular-Dynamics. J Chem Phys. 1992;97:1990–2001. [Google Scholar]
- 23.(a) Martyna GJ, Tobias DJ, Klein ML. Constant pressure molecular-dynamics algorithms. J Chem Phys. 1994;101:4177–4189. [Google Scholar]; (b) Feller SE, Zhang YH, Pastor RW, Brooks BR. Constant-pressure molecular dynamics simulation- the langevin piston method. J Chem Phys. 1995;103:4613–4621. [Google Scholar]
- 24.Pearlman DA. Free energy derivatives - a new method for probing the convergence problem in free-energy calculations. J Comput Chem. 1994;15:105–123. [Google Scholar]
- 25.Zacharias M, Straatsma TP, McCammon JA. Separation-shifted scaling, a new scaling method for Lennard-Jones interactions in thermodynamic integration. J Chem Phys. 1994;100:9025–9031. [Google Scholar]
- 26.Chipot C, Pohorille A. Free Energy Calculations. Springer; 2007. [Google Scholar]
- 27.Pohorille A, Jarzynski C, Chipot C. Good Practices in Free-Energy Calculations. J Phy Chem B. 2010;114:10235–10253. doi: 10.1021/jp102971x. [DOI] [PubMed] [Google Scholar]
- 28.Lu N, Kofke DA, Woolf TB. Improving the efficiency and reliability of free energy perturbation calculations using overlap sampling methods. J Comput Chem. 2004;25:28–40. doi: 10.1002/jcc.10369. [DOI] [PubMed] [Google Scholar]
- 29.Steinbrecher T, Mobley DL, Case DA. Nonlinear scaling schemes for Lennard-Jones interactions in free energy calculations. J Chem Phys. 2007;127:214108. doi: 10.1063/1.2799191. [DOI] [PubMed] [Google Scholar]
- 30.Illingworth CJR, Loenarz C, Schofield CJ, Domene C. Chemical Basis for the Selectivity of the von Hippel Lindau tumor suppressor pVHL for prolyl-hydroxylated HIF-1 alpha. Biochemistry. 2010;49:6936–6944. doi: 10.1021/bi100358t. [DOI] [PubMed] [Google Scholar]
- 31.Ciechanover A, Orian A, Schwartz AL. The ubiquitin-mediated proteolytic pathway: mode of action and clinical implications. J Cell Biochem Suppl. 2000;34:40–51. doi: 10.1002/(sici)1097-4644(2000)77:34+<40::aid-jcb9>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- 32.Warshel A. Electrostatic origin of the catalytic power of enzymes and the role of preorganized active sites. J Biol Chem. 1998;273:27035–27038. doi: 10.1074/jbc.273.42.27035. [DOI] [PubMed] [Google Scholar]
- 33.Domene C, Illingworth CJR. Effects of point mutations in pVHL on the binding of HIF-1 alpha. Proteins: Struct., Funct., Bioinf. 2012;80:733–746. doi: 10.1002/prot.23230. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.