A new approach to detect epidemic of DHF by combining ARIMA model and adjusted Tukey’s control chart with interpretation rules

Abstract

The aim of this study was to propose a new method to detect the epidemic of dengue hemorrhagic fever (DHF) using seasonal autoregressive integrated moving average model [ARIMA(1,0,2)(0,1,2)₁₂] with no constant and adjusted Tukey’s control chart and the results obtained were interpreted using seventh interpretation rule. Data on the number of DHF cases in Chonburi reported during 2007–2013 were used. The results indicated that this new approach efficiently detected the epidemic of DHF in October 2015 with the forecasted number of DHF (257 cases) and root-mean-squared error (RMSE = 46.71).

Introduction

Dengue hemorrhagic fever (DHF) occurs after infection with a dengue virus. It is a single-stranded RNA positive-strand virus of the family Flaviviridae and four different serotypes (DEN1–DEN4) of dengue viruses are known to cause DHF [1, 2]. The first outbreak of dengue fever in Thailand was reported in Bangkok in 1958 [3]. Chonburi is one of the eastern provinces of Bangkok facing the outbreak of DHF [4]. Although there were several studies on prediction of the number of DHF cases [5–7], only few studies have focused on detecting the epidemic of DHF. Hence, the aim of this study was to propose a new approach to detect the epidemic of DHF in Chonburi by combining seasonal autoregressive integrated moving average (ARIMA) model and adjusted Tukey’s control chart (ATCC).

Materials and Methods

Data on the number of DHF cases reported in Chonburi during January 2007 to December 2013 were collected from the Bureau of Epidemiology, National Trustworthy and Competent Authority in Epidemiological Surveillance and Investigation, Thailand.

• 1.ATCC: the control chart was constructed following upper control limit (UCL) = F⁻¹(0.75) + (3 × MADM), center line (CL) = MADM, and lower control limit (LCL) = F⁻¹(0.25) − (3 × MADM), where the MADM stands for the median absolute deviation to the median [8].
• 2.The seasonal ARIMA model: this model was defined by p = 1, d = 0, q = 2, P = 0, D = 1, Q = 2, and S = 12 with no constant or ARIMA(1,0,2)(0,1,2) [5].
• 3.
  Detecting the epidemic of DHF: the procedures are listed as follows:

  • (i)
    Forecasting the number of DHF cases used the model in Step 2 and the results are shown in Table I.
  • (ii)
    Adding up one forecasted number of DHF cases into the original data (2007–2013).
  • (iii)
    Setting up UCL, CL, and LCL of the process used the data from Step (ii) with ATCC.
  • (iv)
    Detecting the epidemic of DHF occurred when the process was out-of-control using the interpretation rules [9], and the epidemic DHF did not occur when the process was in-control.
  • (v)
    Repeating Steps (ii)–(iv) until the process was found to be out-of-control state.

Table I.

The forecasted number of DHF cases in Chonburi using ARIMA(1,0,2)(0,1,2)₁₂

Year	Month
	1	2	3	4	5	6	7	8	9	10	11	12
2014	82.1	57.1	86.4	103.6	232.2	279.5	307.7	244.0	215.7	114.7	117.3	68.7
2015	98.3	85.6	108.5	135.0	195.1	240.8	241.4	257.3	232.9	151.9	145.8	89.8

The Bureau of Epidemiology has approved and informed consent to the above data according to the study about the epidemic of DHF in Chonburi. The data have not been published in whole or in part elsewhere.

Results and Discussion

The UCL, CL, and LCL of ATCC were set up when the forecasted number of DHF case 82.1 was added up the original data, and the results are shown in Tables II and III. After setting up the ATCC, the epidemic of DHF was detected, and the results indicate that the epidemic of DHF would occur in October 2015 by the seventh interpretation rule with the forecasted number of DHF (257 cases) and root-mean-squared error (RMSE = 46.71), as illustrated in Fig. 1. The forecasted number of DHF cases from January 2014 to September 2015 was not found at the outbreak in Chonburi.

Table II.

Control limit of ATCC using data between 2003 and 2014

To	Month
	1	2	3	4	5	6	7	8	9	10	11	12
UCL
−3σ	3.04	3.00	2.84	2.87	3.04	2.95	2.91	2.93	2.87	2.85	2.87	2.87
−2σ	2.01	1.98	1.89	1.90	2.00	1.96	1.93	1.94	1.89	1.88	1.90	1.89
−1σ	0.98	0.96	0.93	0.93	0.96	0.96	0.94	0.95	0.91	0.91	0.92	0.92
CL	0.04	0.06	0.05	0.05	0.03	0.00	0.01	0.02	−0.02	−0.03	−0.04	−0.03
LCL
−3σ	3.06	−3.03	−2.93	−2.97	−3.09	−3.00	−2.98	−2.99	−2.97	−2.94	−2.96	−2.95
−2σ	−2.03	−2.01	−1.98	−2.00	−2.05	−2.00	−2.00	−2.00	−1.99	−1.97	−1.98	−1.97
−1σ	−1.00	−1.00	−1.03	−1.02	−1.01	−1.00	−1.01	−1.01	−1.01	−1.00	−1.00	−1.00

Table III.

Control limit of ATCC using data between 2003 and 2015

To	Month
	1	2	3	4	5	6	7	8	9	10	11	12
UCL
−3σ	2.89	2.89	2.92	2.91	2.90	2.89	2.84	2.79	2.76	2.77	2.82	2.85
−2σ	1.91	1.89	1.92	1.91	1.91	1.90	1.87	1.84	1.83	1.83	1.86	1.88
−1σ	0.93	0.90	0.91	0.91	0.92	0.92	0.89	0.89	0.89	0.90	0.90	0.91
CL	−0.03	−0.03	−0.04	−0.03	−0.02	−0.03	−0.04	−0.05	−0.05	−0.05	−0.05	−0.06
LCL
−3σ	−2.97	−3.00	−3.03	−3.01	−2.98	−2.96	−2.95	−2.90	−2.86	−2.86	−2.90	−2.95
−2σ	−1.99	−2.01	−2.03	−2.01	−1.99	−1.98	−1.98	−1.95	−1.93	−1.92	−1.95	−1.98
−1σ	−1.00	−1.02	−1.02	−1.01	−1.00	−1.00	−1.00	−0.99	−0.99	−0.98	−0.99	−1.01

Fig. 1.

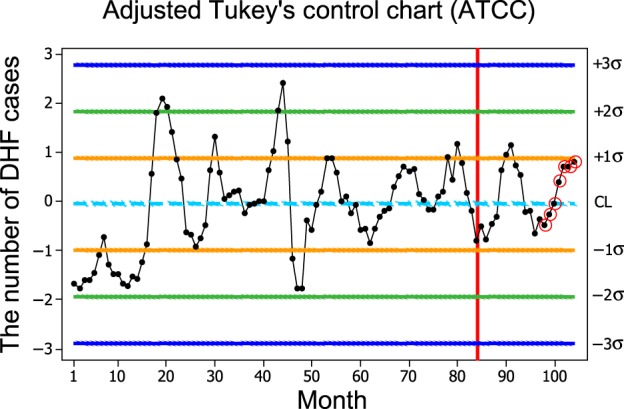
The control limit of ATCC for the combination of the original data and the forecasted number of DHF

Authors’ contributions

JM designed for the study. KS collected and analyzed data. JM and KS interpreted the data. JM made the article draft. JM and KS commented and approved the version to be published.

Conflict of interest

None declared.

Funding Statement

Funding sources: None declared.