Drug Distribution Part 2. Predicting Volume of Distribution from Plasma Protein Binding and Membrane Partitioning

Ken Korzekwa; Swati Nagar

doi:10.1007/s11095-016-2086-y

. Author manuscript; available in PMC: 2018 Mar 1.

Published in final edited form as: Pharm Res. 2016 Dec 13;34(3):544–551. doi: 10.1007/s11095-016-2086-y

Drug Distribution Part 2. Predicting Volume of Distribution from Plasma Protein Binding and Membrane Partitioning

Ken Korzekwa ¹, Swati Nagar ^1,^*

PMCID: PMC5285473 NIHMSID: NIHMS836462 PMID: 27966088

Abstract

Purpose

Volume of distribution is an important pharmacokinetic parameter in the distribution and half-life of a drug. Protein binding and lipid partitioning together determine drug distribution.

Methods

Here we present a simple relationship that estimates the volume of distribution with the fraction of drug unbound in both plasma and microsomes. Model equations are based upon a two-compartment system and the experimental fractions unbound in plasma and microsomes represent binding to plasma proteins and cellular lipids, respectively.

Results

The protein and lipid binding components were parameterized using a dataset containing human in vitro and in vivo parameters for 63 drugs. The resulting equation explains ~84% of the variance in the log of the volume of distribution with an average fold-error of 1.6, with 3 outliers.

Conclusions

These results suggest that V_ss can be predicted for most drugs from plasma protein binding and microsomal partitioning.

Keywords: Volume of distribution, microsomal partitioning

Introduction

Predicted pharmacokinetic properties play a large role in selecting drug candidates. It is unlikely that a compound will enter a drug development program without some knowledge of its pharmacokinetic properties. The two most important factors that determine the plasma concentration-time profile are the clearance and volume of distribution (1,2). The steady-state volume of distribution (V_ss) is the most useful parameter to describe drug distribution, and can be impacted by plasma protein binding, permeability, partitioning, and active transport. Drug distribution parameters are important components of both compartmental and physiologically based pharmacokinetic (PBPK) models. Compartmental PK models define volumes as mathematical empirical terms to convert amounts to concentrations, whereas PBPK models use partition coefficients and tissue volumes to describe drug distribution.

The Oie-Tozer equation was the first physiological model for volume of distribution of drugs and remains a simple and useful standard (3). This model states that prediction of volume of distribution requires knowledge of drug plasma protein binding and tissue partitioning. It is understood that tissue partitioning will depend upon the physicochemical characteristics of a drug molecule, and numerous studies have been published with models for the prediction of drug tissue or membrane partitioning, with subsequent prediction of volume of distribution. For example, Lombardo et al. (4,5) used the rearranged form of the Oie-Tozer equation to calculate f_ut (free fraction of drug in tissue) for neutral and basic drugs using experimental LogD, fraction ionized at pH 7.4, and plasma protein binding (f_up). Acidic drugs were not included in this work, and V_ss was predicted for 18 neutral and basic compounds with a mean 2.26-fold error. Importantly, even if calculated LogD and pKa are used, experimental f_up data are necessary for the f_ut prediction with Lombardo’s method.

Another approach to predict tissue partitioning and V_ss is provided within the framework of PBPK models (6–12)}. A summary of the accuracy of these approaches to predict V_ss has been recently published (13).

These models use a ‘bottom-up’ approach to predict drug disposition. Thus, tissue lipid composition, f_up, blood:plasma ratio (BP), pKa and LogP are used to predict tissue partitioning. Lipid composition is characterized by three lipid categories: neutral lipids, neutral phospholipids, and acidic phospholipids. The following assumptions are made: The original Poulin method models partitioning into the neutral lipid fraction with the vegetable oil:water partition coefficient (usually calculated from LogP) and assumes that phospholipids can be represented as 30% neutral lipids and 70% water (14). Only unionized drugs are assumed to bind to neutral lipids. A more recent unified algorithm (12) and the methods of Rodgers et al. (8–10) assume that cationic molecules bind only to acidic phospholipids. Partitioning into acidic phospholipids is modeled with BP and f_up. Although these methods are purported to be based on first principles only, the underlying assumptions and approaches suggest that these models are actually semi-empirical in nature.

Since microsomes are essentially unsorted phospholipid membranes and since the primary determinants of distribution are plasma protein binding and lipid partitioning, we explored the possibility of using f_um to represent tissue lipid partitioning in a model for V_ss. Thus, the goal of the overall work was to develop simple models for V_ss prediction with experimental f_up and f_um input. Next, predicted f_um values from Part 1 of this work were used to predict V_ss. The results of these studies are presented here.

Methods

Development of the V_ss model

Similar to the approach by Oie and Tozer that considers intracellular, extracellular, and plasma compartments (3), we use the simple two compartment model (plasma and tissue) shown in Figure 1. In this model, plasma proteins exist in both the vascular (plasma) and extravascular (tissue) space. Unbound drug in the plasma is at equilibrium with drug bound to plasma protein and with free drug in the tissue. The free drug in tissue can bind to extravascular plasma proteins (P) and to lipids (L). Additionally, binding to neutral lipids and lysosomes is represented by the dashed arrows. The model without neutral lipids and lysosomal partitioning was derived as follows. As described by Rowland and Tozer (2), a plasma-tissue model can be described with Equation 1:

C_{p} V_{s s} = C_{p} V_{p} + C_{t} V_{t}

Equation 1

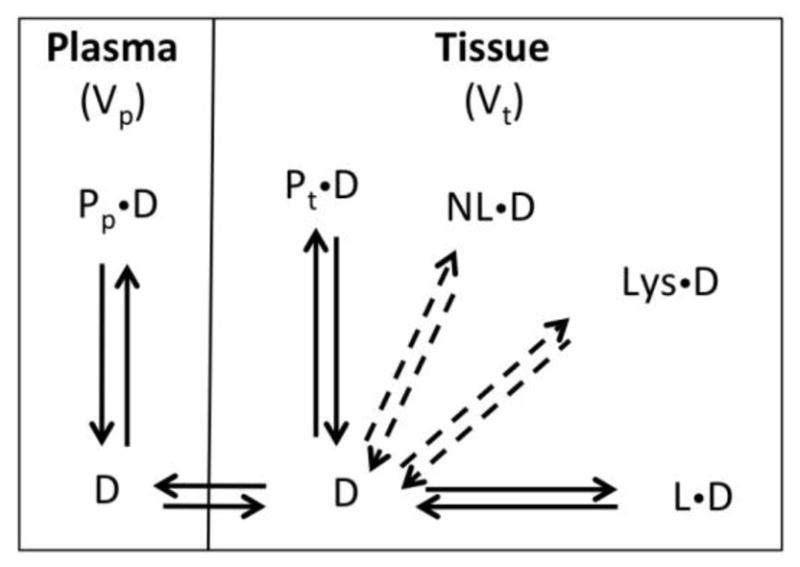
A model with two compartments is used, with plasma and tissue represented by the two compartments. Plasma proteins exist in both the vascular (plasma; P_p) and extravascular (tissue; P_t) space. Unbound drug (D) in the plasma is at equilibrium with drug bound to plasma protein (P_pD) and with free drug (D) in the tissue. The free drug in tissue can bind to extravascular plasma proteins (P_tD) and to lipids (LD). Additionally, binding to neutral lipids (NLD) and lysosomes (LysD) are represented by the dashed arrows.

V_P is the plasma volume, V_t is the tissue volume, C_p is the concentration in the plasma, and C_t is the concentration in the tissue. Substituting for bound and unbound components of plasma and tissue gives Equation 2.

V_{s s} = V_{p} + \frac{(C_{u} + C_{t b} + C_{l}) V_{t}}{(C_{p b} + C_{u})}

Equation 2

In Equation 2, C_u is the concentration of unbound drug, C_pb is the concentration of drug bound to plasma proteins in the plasma, C_tb is the concentration of drug bound to plasma proteins in the tissue, and C_l is the concentration of lipid–associated drug. Equation 3 can be derived using the following relationships: f_up = C_u/(C_u+C_bp); R₁ = P_t/P_p = C_tb/C_pb; C_l = C_u LK_L, where f_up is the unbound fraction in plasma, R₁ is the ratio of the concentration of plasma proteins in the tissue to the concentration of plasma proteins in the plasma, L is the amount of lipid in the tissue, and K_L is the association constant for drug binding to the lipid. R₁ is analogous to R_E/I in the Oie-Tozer equation (3) with the exception that R₁ is based on protein concentration and R_E/I is based on protein amounts.

V_{s s} = V_{p} + V_{t} f_{u p} + V_{t} R_{1} (1 - f_{u p}) + V_{t} f_{u p} L K_{L}

Equation 3

Volumes and plasma protein levels were used as described by Rowland and Tozer (2), with V_p = 0.043 L/kg, V_t = 0.557 L/kg. R₁ is calculated to be 0.116 for neutral and acidic compounds (60% extraplasma albumin in 0.557 L/kg divided by 40% plasma albumin in 0.043 L/kg). An R1 value of 0.052 was used for basic drugs that are expected to bind to α-acid glycoprotein, AAG (40% extraplasma AAG in 0.557 L/kg divided by 60% plasma AAG in 0.043 L/kg).

In order to use the fraction unbound in microsomes as a measure of LK_L, we assume that LK_L is proportional to (1−f_um)/f_um:

V_{s s} = V_{p} + V_{t} f_{u p} + V_{t} R_{1} (1 - f_{u p}) + V_{t} f_{u p} c (\frac{1 - f_{u m}}{f_{u m}})

Equation 4

In Equation 4, c is the proportionality constant that relates microsomal membrane partitioning to the partitioning of drug into the tissue membranes. Combining V_t and c in the last term to give the constant a gives Equation 5:

V_{s s} = V_{p} + V_{t} f_{u p} + V_{t} R_{1} (1 - f_{u p}) + f_{u p} a (\frac{1 - f_{u m}}{f_{u m}})

Equation 5

If the relationship between microsomal partitioning in vitro and partitioning in vivo is linear instead of simply proportional, a constant b can be added to the last term in equation 5 to give equation 6.

V_{s s} = V_{p} + V_{t} f_{u p} + V_{t} R_{1} (1 - f_{u p}) + f_{u p} (a (\frac{1 - f_{u m}}{f_{u m}}) + b)

Equation 6

Accounting for pH differences inside versus outside the cell, equation 6 can be further revised to include the unionized fraction of drug entering the cell, as follows (Equation 7).

V_{D} = V_{p} + V_{t} R_{1} (1 - f_{u p}) + \frac{X}{Y} V_{t} f_{u p} + \frac{X}{Y} f_{u p} (a (\frac{1 - f_{u m}}{f_{u m}}) + b)

Equation 7

Where X = 1 + 10^pKa,b^–^pHiw + 10^pKiw^–^pHa,a and Y = 1 + 10^pKa,b^–^pHp + 10^pKp^–^pHa,a

The pH values for intracellular water and plasma are pHiw=7.2, and pHp=7.4, respectively.

Finally, in order to account for non-specific binding of ionized bases to acidic tissue components, a fraction ionized term can be added to Equation 6, as shown in equation 8.

V_{D} = V_{p} + V_{t} R_{1} (1 - f_{u p}) + V_{t} f_{u p} + f_{u p} (a (\frac{1 - f_{u m}}{f_{u m}}) + b) + d f_{u p} \frac{X - 1}{X}

Equation 8

Equations that include binding to neutral lipids and lysosomes can be derived in an analogous manner (equations 9 and 10, respectively). In Equation 9, the neutral lipid binding is represented by LogP (13), and lysosomal partitioning in equation 10 is modeled as pH partitioning terms (10a for acids and 10b for bases) (15). Table S1 in supplementary materials further lists all the V_ss models developed and tested.

V_{s s} = V_{p} + V_{t} f_{u p} + V_{t} R_{1} (1 - f_{u p}) + f_{u p} (a (\frac{1 - f_{u m}}{f_{u m}}) + b + cLogP)

Equation 9

V_{s s} = V_{p} + V_{t} f_{u p} + V_{t} R_{1} (1 - f_{u p}) + f_{u p} (a (\frac{1 - f_{u m}}{f_{u m}}) + b + d (\frac{10^{4.8 - pKa, a} + 1}{10^{7.2 - pKa, a} + 1}))

Equation 10a

V_{s s} = V_{p} + V_{t} f_{u p} + V_{t} R_{1} (1 - f_{u p}) + f_{u p} (a (\frac{1 - f_{u m}}{f_{u m}}) + b + d (\frac{10^{pKa, b - 4.8} + 1}{10^{pKa, b - 7.2} + 1}))

Equation 10b

For V_ss model development, a subset of 63 drugs (Table S2) was selected, based on the availability of f_up and V_ss from a single meta study (16). The careful considerations and strict calculation criteria for each V_ss value of each compound are described in great detail in Obach et al.(16). Briefly, strictly IV dosing studies were selected, and the steady state volume of distribution (as against central compartment volume or beta-phase volume) was calculated with standard compartmental equations for V_ss. For studies where only C-t profiles were presented but no compartmental analysis was reported, the authors in the meta-study calculated the V_ss with the standard noncompartmental statistical moment equation. It is noteworthy that variation in study populations and therefore variability in V_ss across populations has not been considered in this analysis. The experimental f_um values are from sources provided in Part 1. The experimental f_um values were normalized to 1 mg/ml microsomal protein by assuming linearity and calculating an average binding constant and predicting the value at 1 mg/ml. Due to the sensitivity of the resulting model to very low f_up and f_um values (see discussion), we excluded drugs with f_up < 0.005. Equations 6–10 were fit to this dataset. Log transformed equations were fit using the NonlinearModelFit routine in Mathematica. For models that included lysosomal partitioning, the equations for acids and bases were fit simultaneously. Model selection was based on corrected Akaike Information Criteria (AICc) (17). Outliers were identified using the BoxWhisker function in Mathematica with the upper and lower fences defined as 1.5 times the interquartile range. Finally, the best models were used to predict V_ss using predicted f_um values derived in Part 1.

Results

For V_ss prediction, a total of ten models was derived (Eqs.6–10, Table S1), and the five models with the best AICc values are shown in Tables 1 and 2. The five models had essentially similar AICc values (Table 1). Addition of a neutral lipid component, correction for fraction ionized, or addition of a lysosomal compartment did not result in a substantially lower AICc.

Table 1.

Model selection and parameter estimates for V_ss prediction for n = 60^a drugs. Corrected AIC values (AICc) are reported for models derived from equations 6–10.

Model	AICc^b	AICc	R², AAFE	Parameter Estimate ± error
	n=63	n=60		a	b	c	d	e
Linear LK_L $V_{D} = V_{p} + V_{t} R_{1} (1 - f_{u p}) + V_{t} f_{u p} + f_{u p} (a (\frac{1 - f_{u m}}{f_{u m}}) + b)$	39.6	15.4	0.84, 1.6	20.0±0.2	0.76±0.43	--	--	--
Linear LK_L + neutral lipids $V_{D} = V_{p} + V_{t} R_{1} (1 - f_{u p}) + V_{t} f_{u p} + f_{u p} (a (\frac{1 - f_{u m}}{f_{u m}}) + b + c P_{O W})$	39.3	15.3	0.84, 1.6	19.9±2.5	0.76±0.43	0	--	--
Linear LK_L + fraction ionized^c $V_{D} = V_{p} + V_{t} R_{1} (1 - f_{u p}) + V_{t} f_{u p} + f_{u p} (a (\frac{1 - f_{u m}}{f_{u m}}) + b) + d f_{u p} \frac{X - 1}{X}$	38.2	14.0	0.85, 1.6	18.8±2.4	0.49±0.40	--	2.94±1.9	--
Linear LK_L + lysosomes (bases^d) $V_{s s} = V_{p} + V_{t} f_{u p} + V_{t} R_{1} (1 - f_{u p}) + f_{u p} (a (\frac{1 - f_{u m}}{f_{u m}}) + b + e (\frac{10^{pKa, b - 4.8} + 1}{10^{pKa, b - 7.2} + 1}))$	38.1	14.7	0.84, 1.6	18.1±2.6	0.62±0.40	--	--	0.003±0.002
Linear LK_L + neutral lipids + fraction ionized $V_{D} = V_{p} + V_{t} R_{1} (1 - f_{u p}) + V_{t} f_{u p} + f_{u p} (a (\frac{1 - f_{u m}}{f_{u m}}) + b + c P_{O W}) + d f_{u p} \frac{X - 1}{X}$	37.0	13.9	0.85, 1.6	17.5±2.6	0.63±0.39	0	0.63±0.40	--

Open in a new tab

Outliers excluded were nicardipine, quinine and zidovudine.

AICc values with all n=63 compounds are shown.

X = 1 + 10^pKa,b^–^pHiw + 10^pKiw^–^pHa,a

Equation 10b is shown but equations 10a and 10b were simultaneously fit.

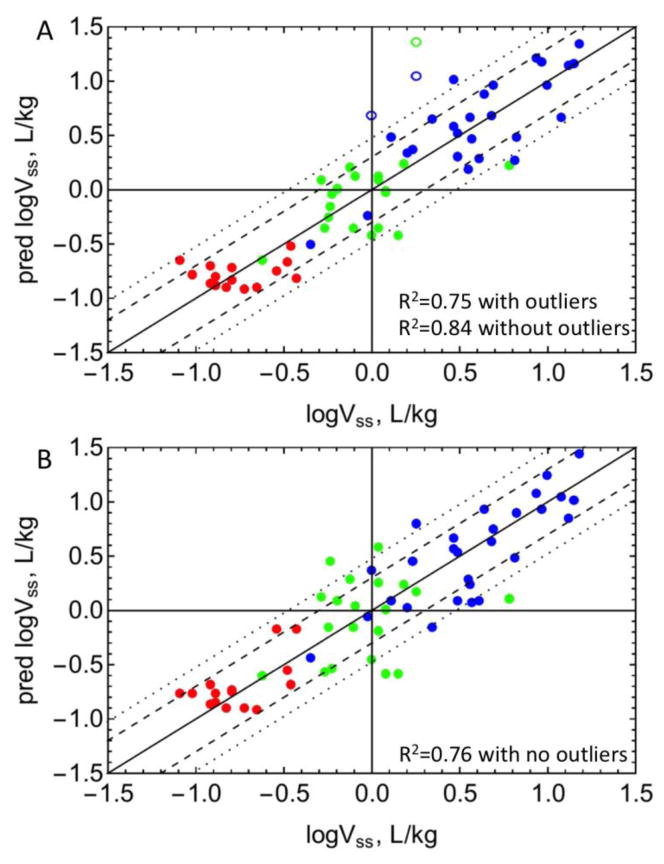
For models in Tables 1 and S1, three outliers were identified: nicardipine, quinine and zidovudine. After excluding outliers, the R² values, average absolute fold error (AAFE), and best fit parameters for the 5 models are listed in Table 1. In general, about 85% of the variance could be explained by all models and parameters were consistent. The linear LK_L model with inclusion of neutral lipids and fraction ionized had a slightly lower AICc value (13.9), relative to the linear LK_L model (AICc = 15.4). However, this difference is insufficient to distinguish between the two models. Therefore the simpler linear LK_L model was selected, and the fit for this model is shown in Figure 2a. It can be seen that 75% of the 60 drugs have predicted V_ss values within 2-fold error and 92% drugs were within 3-fold. The AAFE values were 1.6 for all models.

Predicted versus observed V_ss are plotted with A) experimental f_um or B) f_um predicted with equation 1. See drug list (n=63) in Table S2. Red: acidic drugs, blue: basic drugs, green: neutral drugs. Open circles represent outliers. The dashed and dotted lines represent 2-fold and 3-fold error, respectively. R² values including and excluding outliers are listed.

Figure 2b shows the predicted versus observed V_ss values for all 63 drugs using the linear LK_L model in Table 1, with predicted f_um values from Part 1. With predicted f_um values, the R² of the V_ss prediction was 0.75 with no outliers. Of the 63 drugs analyzed, 71% of drugs have predicted V_ss values within 2-fold error and 86% of drugs were within 3-fold.

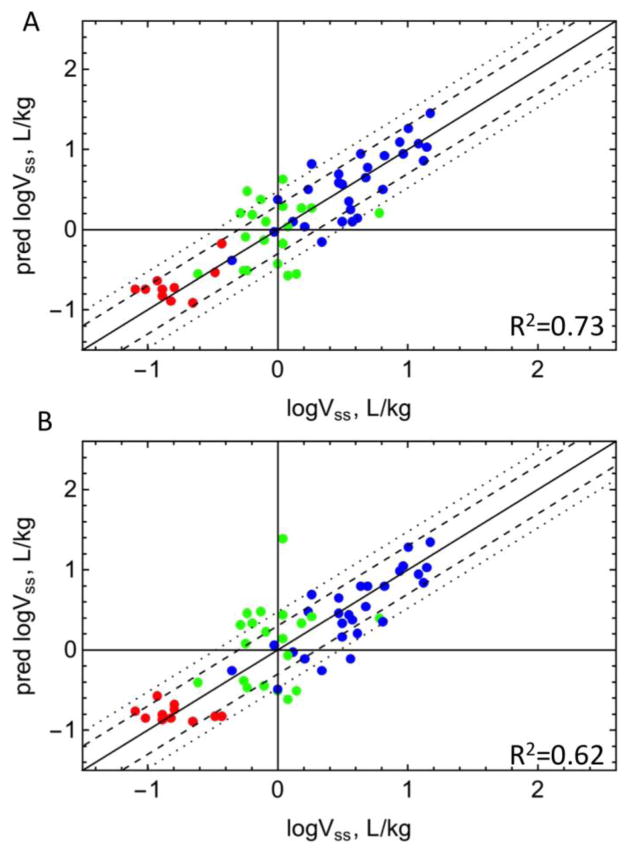
In addition to the model to predict f_um in Part 1, other models to predict f_um are available. A commonly used model predicts f_um with a quadratic relationship between f_um and LogP/D (18). A dataset for which experimental f_um, V_ss, and LogP or LogD are available (n = 59) was used to compare the Hallifax model with the f_um model in Part 1. V_ss predictions using the quadratic relationship and Equation 11 from Part 1 is shown in Figure 3. Using the predictions from the model in Part 1, 81% of LogV_ss values were predicted within 3-fold and 71% within 2-fold error with R² = 0.73. Using the quadratic equation, 81% of LogV_ss values were predicted within 3-fold and 58% within 2-fold error with R² = 0.62.

V_ss predicted versus experimental values (n = 59) using predicted f_um were compared with either (A) equation 11 of Part 1, or (B) the quadratic equation by Hallifax et al (18). Red: acidic drugs, blue: basic drugs, green: neutral drugs. The dashed and dotted lines represent 2-fold and 3-fold error, respectively.

Discussion

Much of the effort in preclinical drug metabolism and pharmacokinetics is focused on predicting human drug disposition. Significant progress has been made in the area of in vitro- in vivo correlations (IVIVCs). Although we have been relatively successful at predicting drug clearance from in vitro data (19–22), predicting the half-life of a drug requires an estimation of both clearance and volume. Lombardo et al have developed quantitative structure-property relationships to predict volume of distribution (4,5). These models were based on the Oie-Tozer equation (3) and the tissue binding parameters were fit to the experimental parameters, LogD, pKa, and the unbound fraction in the plasma. More recently standard QSAR techniques were used to make a model that predicts V_ss from structural descriptors (23–25). Sui et al. has used artificial immobilized membrane partitioning coefficients, pKa, and plasma protein binding data to predict volume (26).

In addition to models that directly predict V_ss, PBPK models estimate V_ss with tissue volumes and drug partition coefficients (8,27). Although these models are bottom-up, some of the assumptions call into question the basis of these models (see Perspective in this issue). In Part 1 of these manuscripts, we developed models to predict f_um from physicochemical properties. Here, we evaluate the ability to predict V_ss with a minimum set of experimental measurements. Specifically, interactions with phospholipid membranes are parameterized with microsomal partitioning (f_um), interactions with neutral lipids with LogP, and lysosomal partitioning with pKa.

We compare a total of ten V_ss models (Table S1) that include either proportional or linear relationships between microsomal partitioning and tissue partitioning. Other model components tested include: partitioning into neutral lipid (represented by LogP), lysosomal partitioning (fraction ionized in lysosomes and cytosol), cellular partitioning of ionizable drugs (fraction ionized in cells and plasma), and non-specific binding of ionizable bases to tissue acidic components (pKa of basic compounds). The use of LogP to represent neutral lipid partitioning is similar to that used by Poulin (28,29) and Rodgers (9) in PBPK modeling. To model plasma protein binding, acids and neutrals were assumed to bind to albumin and bases were assumed to bind AAG. This assumption is a limitation because many compounds can bind to both proteins. Lysosomal sequestration was modeled using standard pH partitioning methods. Cellular partitioning between cytosol and plasma is a common component of PBPK models (8,30). A very good correlation between unbound V_ss and the unbound partition coefficient for erythrocytes has been observed for basic drugs (31). While the mechanisms underlying this correlation are unknown, one possibility is that bases can bind to the ample sialic acid groups on the erythrocyte membrane, and by extension, to tissue capillaries. Therefore, non-specific binding of ionizable bases was included.

It was found that the linear LK_L model was the simplest model with an AICc value of 39.6 (Table 1). Inclusion of terms for neutral lipids, fraction ionized, or lysosomes did not significantly improve the AICc (Table 1). The parameters for these models (Table 1) have consistent values for the constants a and b, and similar R² values. The constant a is estimated to be ~ 20. Multiplying the lipid amount in a microsomal incubation (~ 0.7 uL in a 1 mg/mL microsomal protein incubation) by 20 results in 14 mL lipid/L. This can be compared to the range of 3 to 30 mL phospholipid/L non-adipose tissue. Given the complexities of the tissues, a direct correlation may not be expected. For example, as discussed in the manuscript, lysosomal partitioning certainly occurs but is likely too covariant with the partitioning of bases into phospholipids to allow inclusion in these models.

Also, the coefficient for the lysosomal sequestration term is 0.003, representing ~0.3% lysosomal volume. This is consistent with values reported previously (32,33). A comparison of the five models with essentially non-distinguishable AICcs (Table 1) indicates that, due to its simplicity, the linear LK_L model was the most appropriate model for further analyses. The ability to explain most of the variance in V_ss using only f_up and f_um suggests that interactions with membranes are an important determinant of V_ss. The fact that the additional terms e.g. neutral lipid partitioning and lysosomal partitioning, do not reach statistical significance does not imply that these processes do not occur. Lysosomal partitioning is expected for ionizable bases, and ionizable bases are also more likely to partition into phospholipid membranes. Likewise, hydrophobic molecules partition into both neutral lipids and phospholipids. These correlated properties might mask the individual contributions of each phenomenon. We may need to incorporate these processes for other datasets or when modeling partition coefficients for specific tissues. As more and better data become available, additional components may emerge, resulting in more complex but more accurate models.

The linear LK_L model had three outliers, zidovudine, nicardipine and quinine, and lower residuals were observed for all 3 when predicted f_um values were used. As discussed in Part 1, zidovudine may have an inaccurate experimental f_um value. When using predicted versus experimental f_um for nicardipine and quinine, the residuals were −0.37 versus −0.59, and −0.55 versus −0.7, respectively. It is interesting that quinidine, a diastereomer of quinine, was well predicted. For quinidine, the experimental and predicted f_um values were similar (LK_L = 0.67 and 0.8, respectively; Table S2). However, for quinine, the predicted LK_L was 0.5 log units lower than the experimental LK_L. The result is that the experimental LK_L value for quinine was 13-fold higher than that for quinidine, whereas the predicted values are only 3-fold higher. Although diastereomers can have different physicochemical properties, the better V_ss prediction with the predicted f_um suggests that the experimental quinine f_um may be inaccurate.

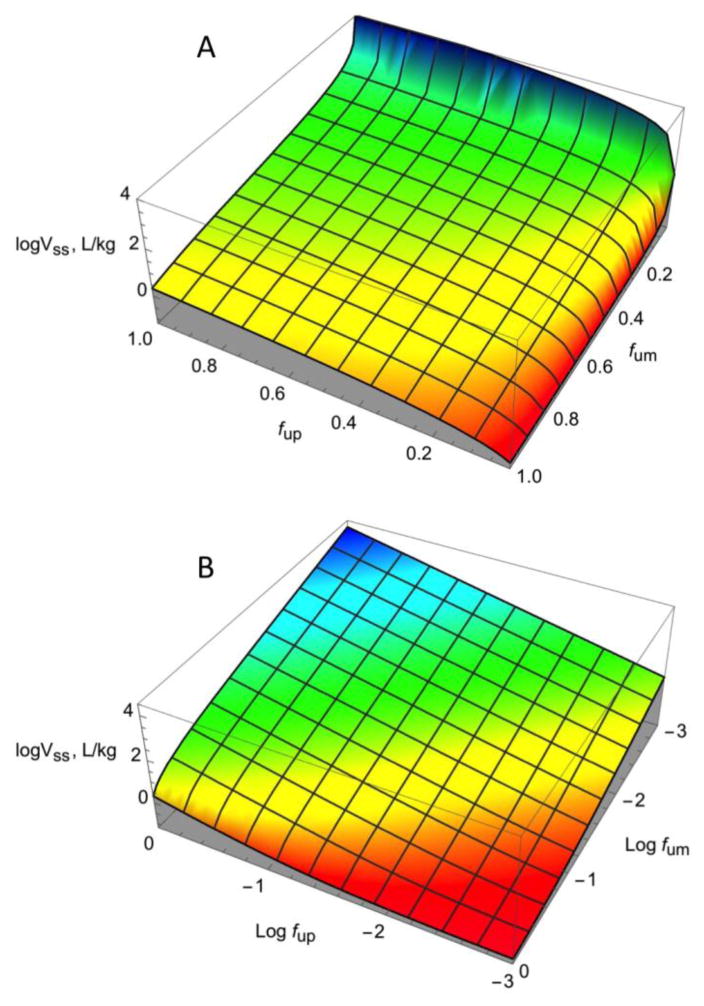
Figure 2 shows the fits for V_ss prediction with experimental (A) and predicted (B) f_um values. Using the experimental f_um values, there were three outliers. Of the remaining 60 drugs, 92% were within 3-fold and 75% were within 2-fold error, with an R² of 0.83. Using predicted f_um values, there were no outliers, 86% of the predictions were within 3-fold, 71% were within 2-fold, and the R² was 0.75. Since these models are mechanistic with a minimum number of fitted parameters, overfitting is unlikely. The results suggest that using only two experimental inputs, ~80% of the variance in V_ss can be explained. However the model is very sensitive to both low f_up and low f_um values (Figure 4). Therefore V_ss for compounds with very high binding to plasma proteins and/or high partitioning to membranes may be poorly predicted. Figure 4 also shows that all regions are sensitive to the value of f_um except when there is very high protein binding and moderate membrane partitioning.

The relationship between f_um, f_up, and V_ss is plotted. The green surface indicates a stable relationship. The red surface indicates instability in the region of very low f_up values, and the blue surface indicates instability in the region of very low f_um values. The f_um and f_up values are depicted on a (A) linear scale or (B) log scale.

This model can be compared to a number of descriptor-based volume models (34), such as QSAR models (23–25), models based on the Oie-Tozer equation (4,5), and tissue partitioning models used in PBPK approaches (8–11,13,29,35,36). Descriptor-based models could predict volume values within 2-fold of the observed approximately 70% of the time (23,24). With the PBPK approach, V_ss can be calculated as the sum of the individual tissue partition constants (K_p) times their tissue volumes plus the volume of the plasma. Methods to predict K_p values generally use experimental f_up values and relationships involving LogP, pKa, and tissue lipid composition (8–11,13,29,35). In addition, the Rodgers method to calculate K_p values for bases used an experimental blood-to-plasma ratio. A recent analysis to evaluate the accuracy of the various methods showed that 63–87% of the predicted volumes were within 3-fold of the experimental values (13). In light of these analyses, any new predictive model for V_ss should have better predictability and/or greater simplicity than previous models. Including outliers, the model reported here with experimental f_um values can predict 92% of V_ss values within 3-fold, and 86% with predicted f_um values. Therefore, the models reported here are comparable to or more predictive than previously reported approaches. More notable is the simplicity of this model.

The availability of a model to predict f_um reduces the required experimental input for V_ss prediction to f_up, provided that estimations of LogP and pKa are available. Although models to predict f_um have been reported (18,37,38), a commonly used model proposes a quadratic relationship between f_um and LogP or LogD (18). A comparison of V_ss predictions using the predicted f_um values from the quadratic relationship and Equation 11 in Part 1 is shown in Figure 3. With the f_um model developed in Part 1, 81% of LogV_ss values were predicted within 3-fold and 71% within 2-fold error with R² = 0.73. Using the quadratic equation, 81% of LogV_ss values were predicted within 3-fold and 58% within 2-fold error with R² = 0.62. The recent models published by Poulin et al. (12,39,40) cannot be directly compared to the present model because Poulin’s model requires an additional experimental input (blood:plasma ratio), and errors are reported as deviations from f_um instead of deviations from Log LK_L.

It should be noted that the models presented here are preliminary in that the experimental data used in these models came from literature sources. If plasma protein binding is not conducted in the presence of CO₂, f_up can be underestimated (41). This, together with the large inter-laboratory variability in f_um values, suggests that these models can be improved. Although the present models have only been applied to predict V_ss, they can also be used in PBPK models to predict tissue partitioning. It may be necessary to develop tissue-specific models for prediction of tissue partition coefficients. This will allow for prediction of perfusion-limited distribution kinetics in addition to V_ss. These studies are currently underway.

In summary, we report a simple model for V_ss prediction based on f_up and f_um. This simple two compartment model can explain >80% of the variance in V_ss. The f_um and V_ss models in Parts 1 and 2 of this work can be used together to predict V_ss with only an experimental f_up as an in vitro input. The use of f_um instead of LogP to predict lipid partitioning may result in quantitatively better models to predict human drug distribution.

Supplementary Material

11095_2016_2086_MOESM1_ESM

Table S1. Model selection for V_ss prediction. Corrected AIC values (AICc) are reported for models derived from equations 6–10.

NIHMS836462-supplement-11095_2016_2086_MOESM1_ESM.docx^{(21.8KB, docx)}

11095_2016_2086_MOESM2_ESM

Table S2. Dataset (n = 63) for V_SS model development, including experimental f_up, V_SS, V_ss predicted (Linear LK_L model), L K_L, and predicted L K_L from equation 1.

NIHMS836462-supplement-11095_2016_2086_MOESM2_ESM.docx^{(23.9KB, docx)}

Acknowledgments

This work was partially funded by NIH/NIGMS grants 1R01GM104178 and 1R01GM114369 to KK and SN. The authors acknowledge Drs. Jiunn Lin and Mark Stroh for early discussions of this project and Obioma Chikwendu for her modeling efforts.

Abbreviations

AAG: α-acid glycoprotein
AICc: corrected Akaike Information Criteria
C_l: concentration of lipid–associated drug
C_p: drug concentration in the plasma
C_pb: concentration of drug bound to plasma proteins in the plasma
C_tb: concentration of drug bound to plasma proteins in the tissue
C_u: concentration of unbound drug
f_um: fraction unbound in microsomal incubation
f_up: unbound fraction in plasma
IVIVC: in vitro in vivo correlation
K_L: association constant for drug binding to the lipid
K_p: tissue partition constant
L: amount of lipid in the tissue
PBPK: physiologically based pharmacokinetic models
pKa,a and pKa,b: pKa values for acids and bases are respectively
PLS: partial least squares
R₁: ratio of the concentration of plasma proteins in the tissue to the concentration of plasma proteins in the plasma
V_ss: steady-state volume of distribution of a drug
V_t: tissue volume

References

1.Gibaldi M, Perrier D. Pharmacokinetics. 2. Taylor & Francis; 1982. [Google Scholar]
2.Rowland M, Tozer TN. Clinical Pharmacokinetics and Pharmacodynamics: Concepts And Applications. Wolters Kluwer Health/Lippincott William & Wilkins; 2010. Membranes and distribution. [Google Scholar]
3.Oie S, Tozer TN. Effect of altered plasma protein binding on apparent volume of distribution. J Pharm Sci. 1979;68(9):1203–1205. doi: 10.1002/jps.2600680948. [DOI] [PubMed] [Google Scholar]
4.Lombardo F, Obach RS, Shalaeva MY, Gao F. Prediction of volume of distribution values in humans for neutral and basic drugs using physicochemical measurements and plasma protein binding data. J Med Chem. 2002;45(13):2867–2876. doi: 10.1021/jm0200409. [DOI] [PubMed] [Google Scholar]
5.Lombardo F, Obach RS, Shalaeva MY, Gao F. Prediction of human volume of distribution values for neutral and basic drugs. 2. Extended data set and leave-class-out statistics. J Med Chem. 2004;47(5):1242–1250. doi: 10.1021/jm030408h. [DOI] [PubMed] [Google Scholar]
6.Ballard P, Leahy DE, Rowland M. Prediction of in vivo tissue distribution from in vitro data 1. Experiments with markers of aqueous spaces. Pharm Res. 2000;17(6):660–663. doi: 10.1023/a:1007565828856. [DOI] [PubMed] [Google Scholar]
7.Ballard P, Arundel PA, Leahy DE, Rowland M. Prediction of in vivo tissue distribution from in vitro data. 2. Influence of albumin diffusion from tissue pieces during an in vitro incubation on estimated tissue-to-unbound plasma partition coefficients (Kpu) Pharm Res. 2003;20(6):857–863. doi: 10.1023/a:1023879001294. [DOI] [PubMed] [Google Scholar]
8.Rodgers T, Leahy D, Rowland M. Physiologically based pharmacokinetic modeling 1: predicting the tissue distribution of moderate-to-strong bases. J Pharm Sci. 2005;94(6):1259–1276. doi: 10.1002/jps.20322. [DOI] [PubMed] [Google Scholar]
9.Rodgers T, Rowland M. Physiologically based pharmacokinetic modelling 2: predicting the tissue distribution of acids, very weak bases, neutrals and zwitterions. J Pharm Sci. 2006;95(6):1238–1257. doi: 10.1002/jps.20502. [DOI] [PubMed] [Google Scholar]
10.Rodgers T, Rowland M. Mechanistic approaches to volume of distribution predictions: understanding the processes. Pharm Res. 2007;24(5):918–933. doi: 10.1007/s11095-006-9210-3. [DOI] [PubMed] [Google Scholar]
11.Poulin P, Theil FP. Development of a novel method for predicting human volume of distribution at steady-state of basic drugs and comparative assessment with existing methods. J Pharm Sci. 2009;98(12):4941–4961. doi: 10.1002/jps.21759. [DOI] [PubMed] [Google Scholar]
12.Peyret T, Poulin P, Krishnan K. A unified algorithm for predicting partition coefficients for PBPK modeling of drugs and environmental chemicals. Toxicol Appl Pharmacol. 2010;249(3):197–207. doi: 10.1016/j.taap.2010.09.010. [DOI] [PubMed] [Google Scholar]
13.Graham H, Walker M, Jones O, Yates J, Galetin A, Aarons L. Comparison of in-vivo and in-silico methods used for prediction of tissue: plasma partition coefficients in rat. J Pharm Pharmacol. 2012;64(3):383–396. doi: 10.1111/j.2042-7158.2011.01429.x. [DOI] [PubMed] [Google Scholar]
14.Poulin P, Krishnan K. A biologically-based algorithm for predicting human tissue: blood partition coefficients of organic chemicals. Human & Experimental Toxicology. 1995;14(3):273–280. doi: 10.1177/096032719501400307. [DOI] [PubMed] [Google Scholar]
15.de Duve C, de Barsy T, Poole B, Trouet A, Tulkens P, Van Hoof F. Commentary. Lysosomotropic agents. Biochem Pharmacol. 1974;23(18):2495–2531. doi: 10.1016/0006-2952(74)90174-9. [DOI] [PubMed] [Google Scholar]
16.Obach RS, Lombardo F, Waters NJ. Trend analysis of a database of intravenous pharmacokinetic parameters in humans for 670 drug compounds. Drug Metab Dispos. 2008;36(7):1385–1405. doi: 10.1124/dmd.108.020479. [DOI] [PubMed] [Google Scholar]
17.Akaike T. A new look at the statistical model identification. IEEE Trans Automat Contr. 1974:19716–723. [Google Scholar]
18.Hallifax D, Houston JB. Binding of drugs to hepatic microsomes: comment and assessment of current prediction methodology with recommendation for improvement. Drug Metab Dispos. 2006;34(4):724–6. doi: 10.1124/dmd.105.007658. author reply 727. [DOI] [PubMed] [Google Scholar]
19.Hallifax D, Foster JA, Houston JB. Prediction of human metabolic clearance from in vitro systems: retrospective analysis and prospective view. Pharm Res. 2010;27(10):2150–2161. doi: 10.1007/s11095-010-0218-3. [DOI] [PubMed] [Google Scholar]
20.Obach RS. Predicting clearance in humans from in vitro data. Curr Top Med Chem. 2011;11(4):334–339. doi: 10.2174/156802611794480873. [DOI] [PubMed] [Google Scholar]
21.Houston JB, Carlile DJ. Prediction of hepatic clearance from microsomes, hepatocytes, and liver slices. Drug Metab Rev. 1997;29(4):891–922. doi: 10.3109/03602539709002237. [DOI] [PubMed] [Google Scholar]
22.Ito K, Houston JB. Prediction of Human Drug Clearance from in Vitro and Preclinical Data Using Physiologically Based and Empirical Approaches Pharmaceutical Research. 2005;22(1):103–112. doi: 10.1007/s11095-004-9015-1. [DOI] [PubMed] [Google Scholar]
23.Lombardo F, Obach RS, Dicapua FM, Bakken GA, Lu J, Potter DM, Gao F, Miller MD, Zhang Y. A hybrid mixture discriminant analysis-random forest computational model for the prediction of volume of distribution of drugs in human. J Med Chem. 2006;49(7):2262–2267. doi: 10.1021/jm050200r. [DOI] [PubMed] [Google Scholar]
24.Berellini G, Springer C, Waters NJ, Lombardo F. In silico prediction of volume of distribution in human using linear and nonlinear models on a 669 compound data set. J Med Chem. 2009;52(14):4488–4495. doi: 10.1021/jm9004658. [DOI] [PubMed] [Google Scholar]
25.Zhivkova Z, Doytchinova I. Prediction of steady-state volume of distribution of acidic drugs by quantitative structure-pharmacokinetics relationships. J Pharm Sci. 2012;101(3):1253–1266. doi: 10.1002/jps.22819. [DOI] [PubMed] [Google Scholar]
26.Sui X, Sun J, Li H, Wang Y, Liu J, Liu X, Zhang W, Chen L, He Z. Prediction of volume of distribution values in human using immobilized artificial membrane partitioning coefficients, the fraction of compound ionized and plasma protein binding data. Eur J Med Chem. 2009;44(11):4455–4460. doi: 10.1016/j.ejmech.2009.06.004. [DOI] [PubMed] [Google Scholar]
27.Poulin P, Theil FP. Prediction of pharmacokinetics prior to in vivo studies. II. Generic physiologically based pharmacokinetic models of drug disposition. J Pharm Sci. 2002;91(5):1358–1370. doi: 10.1002/jps.10128. [DOI] [PubMed] [Google Scholar]
28.Poulin P, Schoenlein K, Theil FP. Prediction of adipose tissue: plasma partition coefficients for structurally unrelated drugs. J Pharm Sci. 2001;90(4):436–447. doi: 10.1002/1520-6017(200104)90:4<436::aid-jps1002>3.0.co;2-p. [DOI] [PubMed] [Google Scholar]
29.Poulin P, Theil FP. Prediction of pharmacokinetics prior to in vivo studies. 1. Mechanism-based prediction of volume of distribution. J Pharm Sci. 2002;91(1):129–156. doi: 10.1002/jps.10005. [DOI] [PubMed] [Google Scholar]
30.Rodgers T, Rowland M. Physiologically based pharmacokinetic modelling 2: predicting the tissue distribution of acids, very weak bases, neutrals and zwitterions. J Pharm Sci. 2006;95(6):1238–1257. doi: 10.1002/jps.20502. [DOI] [PubMed] [Google Scholar]
31.Hinderling PH. Red blood cells: a neglected compartment in pharmacokinetics and pharmacodynamics. Pharmacol Rev. 1997;49(3):279–295. [PubMed] [Google Scholar]
32.Blouin A, Bolender RP, Weibel ER. Distribution of organelles and membranes between hepatocytes and nonhepatocytes in the rat liver parenchyma. A stereological study. J Cell Biol. 1977;72(2):441–455. doi: 10.1083/jcb.72.2.441. [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Oude Elferink RP, Harms E, Strijland A, Tager JM. The intralysosomal pH in cultured human skin fibroblasts in relation to cystine accumulation in patients with cystinosis. Biochem Biophys Res Commun. 1983;116(1):154–161. doi: 10.1016/0006-291x(83)90394-7. [DOI] [PubMed] [Google Scholar]
34.Zou P, Zheng N, Yang Y, Yu LX, Sun D. Prediction of volume of distribution at steady state in humans: comparison of different approaches. Expert Opin Drug Metab Toxicol. 2012;8(7):855–872. doi: 10.1517/17425255.2012.682569. [DOI] [PubMed] [Google Scholar]
35.Poulin P, Theil FP. A priori prediction of tissue:plasma partition coefficients of drugs to facilitate the use of physiologically-based pharmacokinetic models in drug discovery. J Pharm Sci. 2000;89(1):16–35. doi: 10.1002/(SICI)1520-6017(200001)89:1<16::AID-JPS3>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
36.De Buck SS, Sinha VK, Fenu LA, Gilissen RA, Mackie CE, Nijsen MJ. The prediction of drug metabolism, tissue distribution, and bioavailability of 50 structurally diverse compounds in rat using mechanism-based absorption, distribution, and metabolism prediction tools. Drug Metab Dispos. 2007;35(4):649–659. doi: 10.1124/dmd.106.014027. [DOI] [PubMed] [Google Scholar]
37.Austin RP, Barton P, Cockroft SL, Wenlock MC, Riley RJ. The influence of nonspecific microsomal binding on apparent intrinsic clearance, and its prediction from physicochemical properties. Drug Metab Dispos. 2002;30(12):1497–1503. doi: 10.1124/dmd.30.12.1497. [DOI] [PubMed] [Google Scholar]
38.Li H, Sun J, Sui X, Yan Z, Sun Y, Liu X, Wang Y, He Z. Structure-based prediction of the nonspecific binding of drugs to hepatic microsomes. AAPS J. 2009;11(2):364–370. doi: 10.1208/s12248-009-9113-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
39.Poulin P, Haddad S. Microsome composition-based model as a mechanistic tool to predict nonspecific binding of drugs in liver microsomes. J Pharm Sci. 2011;100(10):4501–4517. doi: 10.1002/jps.22619. [DOI] [PubMed] [Google Scholar]
40.Poulin P, Haddad S. Hepatocyte composition-based model as a mechanistic tool for predicting the cell suspension: aqueous phase partition coefficient of drugs in in vitro metabolic studies. J Pharm Sci. 2013;102(8):2806–2818. doi: 10.1002/jps.23602. [DOI] [PubMed] [Google Scholar]
41.Kochansky CJ, McMasters DR, Lu P, Koeplinger KA, Kerr HH, Shou M, Korzekwa KR. Impact of pH on plasma protein binding in equilibrium dialysis. Mol Pharm. 2008;5(3):438–448. doi: 10.1021/mp800004s. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

11095_2016_2086_MOESM1_ESM

Table S1. Model selection for V_ss prediction. Corrected AIC values (AICc) are reported for models derived from equations 6–10.

NIHMS836462-supplement-11095_2016_2086_MOESM1_ESM.docx^{(21.8KB, docx)}

11095_2016_2086_MOESM2_ESM

Table S2. Dataset (n = 63) for V_SS model development, including experimental f_up, V_SS, V_ss predicted (Linear LK_L model), L K_L, and predicted L K_L from equation 1.

NIHMS836462-supplement-11095_2016_2086_MOESM2_ESM.docx^{(23.9KB, docx)}

[R1] 1.Gibaldi M, Perrier D. Pharmacokinetics. 2. Taylor & Francis; 1982. [Google Scholar]

[R2] 2.Rowland M, Tozer TN. Clinical Pharmacokinetics and Pharmacodynamics: Concepts And Applications. Wolters Kluwer Health/Lippincott William & Wilkins; 2010. Membranes and distribution. [Google Scholar]

[R3] 3.Oie S, Tozer TN. Effect of altered plasma protein binding on apparent volume of distribution. J Pharm Sci. 1979;68(9):1203–1205. doi: 10.1002/jps.2600680948. [DOI] [PubMed] [Google Scholar]

[R4] 4.Lombardo F, Obach RS, Shalaeva MY, Gao F. Prediction of volume of distribution values in humans for neutral and basic drugs using physicochemical measurements and plasma protein binding data. J Med Chem. 2002;45(13):2867–2876. doi: 10.1021/jm0200409. [DOI] [PubMed] [Google Scholar]

[R5] 5.Lombardo F, Obach RS, Shalaeva MY, Gao F. Prediction of human volume of distribution values for neutral and basic drugs. 2. Extended data set and leave-class-out statistics. J Med Chem. 2004;47(5):1242–1250. doi: 10.1021/jm030408h. [DOI] [PubMed] [Google Scholar]

[R6] 6.Ballard P, Leahy DE, Rowland M. Prediction of in vivo tissue distribution from in vitro data 1. Experiments with markers of aqueous spaces. Pharm Res. 2000;17(6):660–663. doi: 10.1023/a:1007565828856. [DOI] [PubMed] [Google Scholar]

[R7] 7.Ballard P, Arundel PA, Leahy DE, Rowland M. Prediction of in vivo tissue distribution from in vitro data. 2. Influence of albumin diffusion from tissue pieces during an in vitro incubation on estimated tissue-to-unbound plasma partition coefficients (Kpu) Pharm Res. 2003;20(6):857–863. doi: 10.1023/a:1023879001294. [DOI] [PubMed] [Google Scholar]

[R8] 8.Rodgers T, Leahy D, Rowland M. Physiologically based pharmacokinetic modeling 1: predicting the tissue distribution of moderate-to-strong bases. J Pharm Sci. 2005;94(6):1259–1276. doi: 10.1002/jps.20322. [DOI] [PubMed] [Google Scholar]

[R9] 9.Rodgers T, Rowland M. Physiologically based pharmacokinetic modelling 2: predicting the tissue distribution of acids, very weak bases, neutrals and zwitterions. J Pharm Sci. 2006;95(6):1238–1257. doi: 10.1002/jps.20502. [DOI] [PubMed] [Google Scholar]

[R10] 10.Rodgers T, Rowland M. Mechanistic approaches to volume of distribution predictions: understanding the processes. Pharm Res. 2007;24(5):918–933. doi: 10.1007/s11095-006-9210-3. [DOI] [PubMed] [Google Scholar]

[R11] 11.Poulin P, Theil FP. Development of a novel method for predicting human volume of distribution at steady-state of basic drugs and comparative assessment with existing methods. J Pharm Sci. 2009;98(12):4941–4961. doi: 10.1002/jps.21759. [DOI] [PubMed] [Google Scholar]

[R12] 12.Peyret T, Poulin P, Krishnan K. A unified algorithm for predicting partition coefficients for PBPK modeling of drugs and environmental chemicals. Toxicol Appl Pharmacol. 2010;249(3):197–207. doi: 10.1016/j.taap.2010.09.010. [DOI] [PubMed] [Google Scholar]

[R13] 13.Graham H, Walker M, Jones O, Yates J, Galetin A, Aarons L. Comparison of in-vivo and in-silico methods used for prediction of tissue: plasma partition coefficients in rat. J Pharm Pharmacol. 2012;64(3):383–396. doi: 10.1111/j.2042-7158.2011.01429.x. [DOI] [PubMed] [Google Scholar]

[R14] 14.Poulin P, Krishnan K. A biologically-based algorithm for predicting human tissue: blood partition coefficients of organic chemicals. Human & Experimental Toxicology. 1995;14(3):273–280. doi: 10.1177/096032719501400307. [DOI] [PubMed] [Google Scholar]

[R15] 15.de Duve C, de Barsy T, Poole B, Trouet A, Tulkens P, Van Hoof F. Commentary. Lysosomotropic agents. Biochem Pharmacol. 1974;23(18):2495–2531. doi: 10.1016/0006-2952(74)90174-9. [DOI] [PubMed] [Google Scholar]

[R16] 16.Obach RS, Lombardo F, Waters NJ. Trend analysis of a database of intravenous pharmacokinetic parameters in humans for 670 drug compounds. Drug Metab Dispos. 2008;36(7):1385–1405. doi: 10.1124/dmd.108.020479. [DOI] [PubMed] [Google Scholar]

[R17] 17.Akaike T. A new look at the statistical model identification. IEEE Trans Automat Contr. 1974:19716–723. [Google Scholar]

[R18] 18.Hallifax D, Houston JB. Binding of drugs to hepatic microsomes: comment and assessment of current prediction methodology with recommendation for improvement. Drug Metab Dispos. 2006;34(4):724–6. doi: 10.1124/dmd.105.007658. author reply 727. [DOI] [PubMed] [Google Scholar]

[R19] 19.Hallifax D, Foster JA, Houston JB. Prediction of human metabolic clearance from in vitro systems: retrospective analysis and prospective view. Pharm Res. 2010;27(10):2150–2161. doi: 10.1007/s11095-010-0218-3. [DOI] [PubMed] [Google Scholar]

[R20] 20.Obach RS. Predicting clearance in humans from in vitro data. Curr Top Med Chem. 2011;11(4):334–339. doi: 10.2174/156802611794480873. [DOI] [PubMed] [Google Scholar]

[R21] 21.Houston JB, Carlile DJ. Prediction of hepatic clearance from microsomes, hepatocytes, and liver slices. Drug Metab Rev. 1997;29(4):891–922. doi: 10.3109/03602539709002237. [DOI] [PubMed] [Google Scholar]

[R22] 22.Ito K, Houston JB. Prediction of Human Drug Clearance from in Vitro and Preclinical Data Using Physiologically Based and Empirical Approaches Pharmaceutical Research. 2005;22(1):103–112. doi: 10.1007/s11095-004-9015-1. [DOI] [PubMed] [Google Scholar]

[R23] 23.Lombardo F, Obach RS, Dicapua FM, Bakken GA, Lu J, Potter DM, Gao F, Miller MD, Zhang Y. A hybrid mixture discriminant analysis-random forest computational model for the prediction of volume of distribution of drugs in human. J Med Chem. 2006;49(7):2262–2267. doi: 10.1021/jm050200r. [DOI] [PubMed] [Google Scholar]

[R24] 24.Berellini G, Springer C, Waters NJ, Lombardo F. In silico prediction of volume of distribution in human using linear and nonlinear models on a 669 compound data set. J Med Chem. 2009;52(14):4488–4495. doi: 10.1021/jm9004658. [DOI] [PubMed] [Google Scholar]

[R25] 25.Zhivkova Z, Doytchinova I. Prediction of steady-state volume of distribution of acidic drugs by quantitative structure-pharmacokinetics relationships. J Pharm Sci. 2012;101(3):1253–1266. doi: 10.1002/jps.22819. [DOI] [PubMed] [Google Scholar]

[R26] 26.Sui X, Sun J, Li H, Wang Y, Liu J, Liu X, Zhang W, Chen L, He Z. Prediction of volume of distribution values in human using immobilized artificial membrane partitioning coefficients, the fraction of compound ionized and plasma protein binding data. Eur J Med Chem. 2009;44(11):4455–4460. doi: 10.1016/j.ejmech.2009.06.004. [DOI] [PubMed] [Google Scholar]

[R27] 27.Poulin P, Theil FP. Prediction of pharmacokinetics prior to in vivo studies. II. Generic physiologically based pharmacokinetic models of drug disposition. J Pharm Sci. 2002;91(5):1358–1370. doi: 10.1002/jps.10128. [DOI] [PubMed] [Google Scholar]

[R28] 28.Poulin P, Schoenlein K, Theil FP. Prediction of adipose tissue: plasma partition coefficients for structurally unrelated drugs. J Pharm Sci. 2001;90(4):436–447. doi: 10.1002/1520-6017(200104)90:4<436::aid-jps1002>3.0.co;2-p. [DOI] [PubMed] [Google Scholar]

[R29] 29.Poulin P, Theil FP. Prediction of pharmacokinetics prior to in vivo studies. 1. Mechanism-based prediction of volume of distribution. J Pharm Sci. 2002;91(1):129–156. doi: 10.1002/jps.10005. [DOI] [PubMed] [Google Scholar]

[R30] 30.Rodgers T, Rowland M. Physiologically based pharmacokinetic modelling 2: predicting the tissue distribution of acids, very weak bases, neutrals and zwitterions. J Pharm Sci. 2006;95(6):1238–1257. doi: 10.1002/jps.20502. [DOI] [PubMed] [Google Scholar]

[R31] 31.Hinderling PH. Red blood cells: a neglected compartment in pharmacokinetics and pharmacodynamics. Pharmacol Rev. 1997;49(3):279–295. [PubMed] [Google Scholar]

[R32] 32.Blouin A, Bolender RP, Weibel ER. Distribution of organelles and membranes between hepatocytes and nonhepatocytes in the rat liver parenchyma. A stereological study. J Cell Biol. 1977;72(2):441–455. doi: 10.1083/jcb.72.2.441. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R33] 33.Oude Elferink RP, Harms E, Strijland A, Tager JM. The intralysosomal pH in cultured human skin fibroblasts in relation to cystine accumulation in patients with cystinosis. Biochem Biophys Res Commun. 1983;116(1):154–161. doi: 10.1016/0006-291x(83)90394-7. [DOI] [PubMed] [Google Scholar]

[R34] 34.Zou P, Zheng N, Yang Y, Yu LX, Sun D. Prediction of volume of distribution at steady state in humans: comparison of different approaches. Expert Opin Drug Metab Toxicol. 2012;8(7):855–872. doi: 10.1517/17425255.2012.682569. [DOI] [PubMed] [Google Scholar]

[R35] 35.Poulin P, Theil FP. A priori prediction of tissue:plasma partition coefficients of drugs to facilitate the use of physiologically-based pharmacokinetic models in drug discovery. J Pharm Sci. 2000;89(1):16–35. doi: 10.1002/(SICI)1520-6017(200001)89:1<16::AID-JPS3>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]

[R36] 36.De Buck SS, Sinha VK, Fenu LA, Gilissen RA, Mackie CE, Nijsen MJ. The prediction of drug metabolism, tissue distribution, and bioavailability of 50 structurally diverse compounds in rat using mechanism-based absorption, distribution, and metabolism prediction tools. Drug Metab Dispos. 2007;35(4):649–659. doi: 10.1124/dmd.106.014027. [DOI] [PubMed] [Google Scholar]

[R37] 37.Austin RP, Barton P, Cockroft SL, Wenlock MC, Riley RJ. The influence of nonspecific microsomal binding on apparent intrinsic clearance, and its prediction from physicochemical properties. Drug Metab Dispos. 2002;30(12):1497–1503. doi: 10.1124/dmd.30.12.1497. [DOI] [PubMed] [Google Scholar]

[R38] 38.Li H, Sun J, Sui X, Yan Z, Sun Y, Liu X, Wang Y, He Z. Structure-based prediction of the nonspecific binding of drugs to hepatic microsomes. AAPS J. 2009;11(2):364–370. doi: 10.1208/s12248-009-9113-4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R39] 39.Poulin P, Haddad S. Microsome composition-based model as a mechanistic tool to predict nonspecific binding of drugs in liver microsomes. J Pharm Sci. 2011;100(10):4501–4517. doi: 10.1002/jps.22619. [DOI] [PubMed] [Google Scholar]

[R40] 40.Poulin P, Haddad S. Hepatocyte composition-based model as a mechanistic tool for predicting the cell suspension: aqueous phase partition coefficient of drugs in in vitro metabolic studies. J Pharm Sci. 2013;102(8):2806–2818. doi: 10.1002/jps.23602. [DOI] [PubMed] [Google Scholar]

[R41] 41.Kochansky CJ, McMasters DR, Lu P, Koeplinger KA, Kerr HH, Shou M, Korzekwa KR. Impact of pH on plasma protein binding in equilibrium dialysis. Mol Pharm. 2008;5(3):438–448. doi: 10.1021/mp800004s. [DOI] [PubMed] [Google Scholar]

PERMALINK

Drug Distribution Part 2. Predicting Volume of Distribution from Plasma Protein Binding and Membrane Partitioning

Ken Korzekwa

Swati Nagar