Rapid In Vivo Detection of Rat Spinal Cord Injury with Double Diffusion Encoded Magnetic Resonance Spectroscopy

Abstract

Purpose

Diffusion weighted imaging is a common experimental tool for evaluating spinal cord injury (SCI), yet suffers from complications decreasing its clinical effectiveness. The most commonly used technique, Diffusion Tensor Imaging (DTI), is often confounded by effects of edema accompanying acute SCI, limiting its sensitivity to the important functional status marker of axonal integrity. The purpose of this study is to introduce a novel diffusion acquisition method with the goal of overcoming these limitations.

Methods

A Double Diffusion Encoding (DDE) pulse sequence was implemented with a diffusion-weighted filter orthogonal to the spinal cord for suppressing non-neural signals prior to diffusion weighting parallel to the cord. A Point-RESolved Spectroscopy readout (DDE-PRESS) was used for improved sensitivity and compared with DTI in a rat model of SCI with varying injury severities.

Results

The DDE-PRESS parameter, restricted fraction, showed a strong relationship with injury severity (p<0.001, R²=0.67). Whereas whole-cord averaged DTI parameter values exhibited only minor injury relationships, a weighted ROI-based DTI analysis improved sensitivity to injury (p<0.001, R²=0.66).

Conclusion

In a rat model of SCI, DDE-PRESS demonstrated high sensitivity to injury with substantial decreases in acquisition time and data processing. This method shows promise for application in rapid evaluation of SCI severity.

Introduction

SCI is a debilitating neurological event in which medical care immediately following onset has important implications for outcomes. However, current clinical techniques to evaluate function during the acute stage are insufficient since the pathophysiology of SCI and shock can complicate functional testing. While MRI has played an important role in diagnosis and patient management, relaxivity-based MRI methods during this critical period show only weak correlations with injury severity and functional outcome (1).

Diffusion weighted imaging (DWI) has shown promise as a noninvasive MRI tool to detect injury severity. DWI measures the diffusion of water and model fitting of the DWI signal permits inferences to the microstructural composition of tissues. The most widely used model, diffusion tensor imaging (DTI), has revealed important insights into SCI. Fractional anisotropy (FA), a measure obtained from DTI that quantifies the directional preference of diffusion, is high in the coherent white matter (WM) tracts of the spinal cord and is typically decreased following SCI. This decrease in FA reflects a disruption of normal tissue microarchitecture and is strongly correlated with functional status and outcome (2). Directionally-specific DTI measures, including axial (AD) and radial diffusivity (RD), have brought increased pathological specificity. In particular, axial diffusivity (AD), the diffusivity along the fastest axis of diffusion, is decreased rapidly after SCI and is generally associated with axonal damage and correlates strongly with histological-measured axonal injury (3,4), which is the strongest correlate of functional outcome in experimental (5) and human SCI (6). AD has shown some of the strongest correlations with injury severity (7,8) and is predictive of outcome in experimental models of SCI (3). However, despite encouraging findings in experimental models, diffusivity measured with DTI is confounded by the presence of other pathologies including edema, hemorrhage, demyelination, and inflammation, among others, which cause ambiguity, particularly in chronic stages after injury (2,8).

To remedy these limitations, alternative models of the DWI signal have been proposed to more faithfully represent the underlying pathology. However, adoption of DTI and advanced DWI models to clinical settings has been limited by many technical challenges. The small size of the cord, respiratory and cardiac motion, and susceptibility differences between the cord and surrounding spine are hurdles that can preclude high-quality diffusion weighted images, and the additional data required for advanced models can increase scan durations beyond a clinically feasible time. Furthermore, injury disrupts the normal anatomical structure of the cord, which complicates subsequent image analysis. With white and gray matter (GM) being no longer discernible (9), whole-cord measures are commonly used for quantification (10).

A promising alternative to modeling the DWI signal involves the application of multiple diffusion gradient weightings within a single measurement (11–14). Techniques such as double diffusion encoding (DDE; also referred to as the double pulsed field gradient, dPFG) and q-vector magic angle spinning (qMAS) probe features of the tissue not available through standard single pulsed field gradient methods (15–17). While these techniques aim to remove the effects of macroscopic tissue organization, such as crossing fibers or intra-voxel fiber dispersion, the DDE contrast can also be used to improve the specificity for axonal injury, as previous simulations have demonstrated (18). The combination of multiple diffusion gradients within a single measurement has provided new avenues to probe microstructure in novel and more efficient methods than DWI signal modeling alone (19,20).

In this report, a DDE sequence was specifically tailored to enhance sensitivity to axonal injury in the spinal cord. With white matter tracts of the cord aligned with its main axis, a diffusion gradient pulse applied perpendicular to the cord acts as a diffusion filter to suppress signal from spins exhibiting free or hindered diffusion behavior, while spins restricted in the perpendicular direction retain their coherent magnetization. A second diffusion gradient pulse applied parallel to the cord with varying magnitude probes the diffusion behavior of these restricted spins. Since the filtering diffusion pulse suppresses signal from the non-cord tissues, including muscle and CSF, a Point RESolved Spectroscopic (PRESS) readout of the signal can provide whole-cord measurements without contribution of these non-neuronal tissues, thereby reducing post-processing analysis and acquisition duration.

Based on previous simulations showing improvements in injury detection using DDE (18), its application was tested using an in vivo rat model of SCI and compared to standard DTI metrics. First, the diffusion characteristics of the normal rat spinal cord were examined in vivo using a standard PGSE diffusion imaging sequence to guide the implementation of the DDE sequence. The DDE sequence was then evaluated in a rat model of graded spinal cord injury. The results demonstrate that DDE-PRESS is a method with high sensitivity to injury severity and can be achieved in a substantially reduced scan duration and fewer post-processing requirements than DTI.

Methods

Animals

All animal procedures were approved by the Institutional Animal Care and Use Committees (IACUC) at the Medical College of Wisconsin and the Zablocki VA Medical Center. Twenty-nine female Sprague–Dawley rats (200–250 g) were used for this study. Initial MRI experiments were performed in the spinal cord of naïve rats (n=7) to characterize diffusion in vivo using the PGSE and DDE sequences. Subsequent experiments were performed in a rat model of spinal cord contusion in the thoracic cord with varying levels of injury severity or sham injury (n=22).

Magnetic Resonance Imaging

Experiments were performed on a Bruker 9.4 T Biospec System using a commercial 3.8 cm inner diameter quadrature Litz coil (Doty Scientific) for signal transmission and reception in the cervical cord. Animals were placed prone in a custom head holder with ear bars to minimize motion. For thoracic spinal cord imaging, a commercial, 4-channel surface coil array (Bruker Biospin) was used for signal reception along with a 9 cm inner diameter quadrature volume coil for transmission. Animals were placed supine for thoracic studies. All MRI acquisitions used respiratory gating as described previously (21).

Conventional pulsed gradient spin echo (PGSE) acquisitions employed a diffusion weighted echo planar imaging (DW-EPI) sequence. A 4-shot, respiratory-gated EPI acquisition (TE=28 ms; TR=>1500 ms, varied by respiratory rate) was used with a 25.6 mm² field of view and matrix of 128² with partial Fourier sampling of 6/8 for a nominal spatial resolution of 0.20×0.20 mm² and slice thickness of 1.0 mm and 0.5 mm gap. In order to characterize signal attenuation in the spinal cord and surrounding tissues, experiments in naive rats (n=4) employed diffusion weighting along either the parallel or perpendicular axis of the cord at b-values of 0, 250, 500, 750, 1000, 2000, 2500, 3500 s/mm², with a diffusion duration (δ) of 8.25 ms and separation (Δ) of 12.5 ms. Eight signal averages at each b-value were used. Subsequent experiments in SCI animals were performed with 30 unique diffusion directions (22) at b-values of 500, 1000, and 2000 s/mm², with δ=7 ms and Δ=13.4 ms in addition to 15 non-diffusion-weighted images. Identical spatial resolution was used with 4 signal averages. A total of 12 slices were collected, centered over the lesion epicenter at the T10 vertebral level. A sagittal FLASH image was used as a reference to position slices at the lesion epicenter. It consisted of a respiratory gated acquisition with 4 signal averages, TR/TE = 100/6 ms, slice thickness = 0.5 mm, slice gap = 0.5 mm, matrix size = 128 × 256. This full DW-EPI acquisition required approximately 1 hour of imaging time.

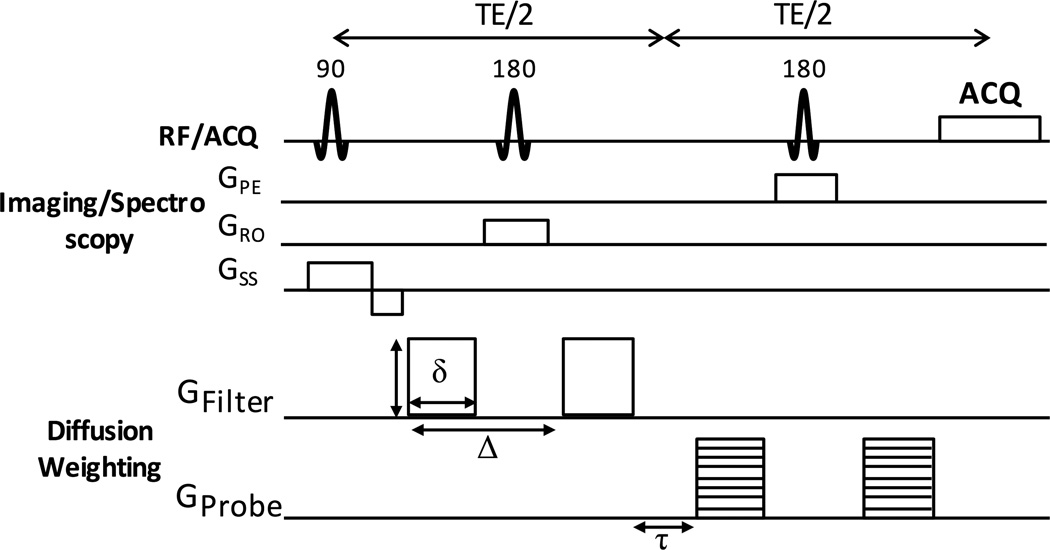
DDE implementation was first tested in the rat cervical spinal cord (n=3) to examine the effects of the filter pulse on the measured diffusivity values. For these experiments, a twice-refocused spin echo sequence was modified to include two pairs of Stejskal-Tanner diffusion weighting gradients surrounding each of the refocusing radiofrequency pulses (Fig. 1), in which the diffusion gradients were independently adjustable in their direction, timing, and magnitude. The DDE encoding was coupled with an echo planar imaging (EPI) readout. The DDE-EPI used identical parameters as the PGSE, except for the following: 2 mm thick slices, no slice gap, and TR/TE=1750/51.07 ms. The diffusion encoding in the DDE consisted of an initial diffusion weighting pair (“filtering pulse”) applied perpendicular to the spinal cord axis, and a second diffusion weighting gradient pair (“probe pulse”) applied parallel to the spinal cord axis. The filter b-value of 4000 s/mm² and probe b-values ranging from 0–1000 s/mm² in increments of 250 s/mm² were used with equivalent diffusion gradient duration (12 ms) and separation (6 ms) for each of the diffusion gradient pairs.

Figure 1. DDE Pulse Sequence.

The DDE is composed of two pairs of Stejskal-Tanner diffusion sensitizing gradients. The first pair, G_Filter, is applied perpendicular to the spinal cord at a constant b-value. The second pair, G_Probe, is applied parallel to the spinal cord at a range of b-values. The DDE preparation is shown with a PRESS localization and spectroscopic readout of the signal, but it is also compatible with imaging.

Since the diffusion filter pulse suppressed signals from CSF and tissues outside of the spinal cord, the DDE preparation was coupled with a Point-RESolved Spectroscopy readout (DDE-PRESS) to assess the potential for whole-cord measurements (23). The DDE-PRESS voxel (10×10×6 mm³) was oriented along the main axis of the spinal cord, with sagittal FLASH images used as a reference for the lesion epicenter, as described above. Shimming within the voxel was performed using the Bruker MAPSHIM protocol to adjust first-order and Z² shims. Outer volume suppression used six saturation bands positioned along the sides of the voxel, each with a thickness of 10 mm and with no gap to the voxel edge. The other acquisition parameters were: TR=3000 ms, TE=42.26 ms, sweep width=4960 Hz, number of points=256. No water suppression was used. A b-value of 2000 s/mm² was used for the filter diffusion pair and 9 probe b-values from 0 to 2000 s/mm² in increments of 250 s/mm² were collected with 1 additional non-weighted spectra. The full DDE-PRESS acquisition was repeated 4 times with a single average for each repetition, which required approximately 3 minutes, varying slightly by respiratory rate. Respiratory and cardiac gating was enabled, where the cardiac gating trigger occurred 30 ms after the R-wave detected from the ECG signal. The DDE-PRESS sequence was utilized for all animals with SCI.

Data Analysis

Analysis of DDE-PRESS data used custom Matlab scripts for derivation of diffusion parameters. The complex signals were Fourier transformed, and the peak of the water signal in the non-diffusion weighted spectra was set as the frequency reference for the correction and integration of all other spectra. No line broadening was used. All spectra were phase corrected and the signal between ±2 ppm of the water peak was integrated, which excluded the contribution from lipids at approximately 3.5 ppm relative to water. A comparison between the real-valued and absolute-valued (magnitude) signal integrals was performed, and it was shown that the two analysis approaches were equivalent when normalized to the non-diffusion weighted signal integral (Sup. Fig. S2). All subsequent procedures employed the signal magnitude for fitting. SNR was computed at each b-value defined as the mean signal divided by the standard deviation from a region of pure noise. For all DDE experiments, only the images or spectra acquired with the diffusion filter pulse were used for subsequent analysis, and the probe diffusion gradient strength (b-value) was the only weighting value used for calculating diffusion characteristics in the subsequent fitting. DDE-PRESS data quality was assessed using the full width half maximum of the spectra as well as the coefficient of variation between repetitions.

DW-EPI data were motion and eddy current corrected using the Spinal Cord Toolbox (24). DTI parameter maps were calculated using weighted linear least squares implemented in FSL (25). For whole-cord regions of interest, the spinal cord including both white and gray matter were manually traced on the non-diffusion weighted (b=0 s/mm²) images taking care to avoid inclusion of CSF, fluid-filled cysts, and regions with obvious hemorrhage. The reported mean DTI parameter values consist of the average of the 4 slices covering the same extent of spinal cord as the DDE-PRESS voxel. A subsequent analysis was performed to more systematically compare the DTI with the DDE-PRESS using weighted ROI. First, the diffusion weighted images were each corrected for Rican noise according to the equation in (26,27), A_corr=A₀/(M_noise/sqrt(π/2)−c), where A_corr is the corrected magnitude signal at each voxel, A₀ is the original magnitude signal in each voxel, M_noise is the mean of a region of pure noise, and c is the signal correction term (26,27). The high b-value (2000 mm²/s) DW-EPI images were averaged voxelwise across all diffusion directions, where each image was weighted by the angle between the diffusion weighting vector and the spinal cord main axis to achieve a perpendicular-weighted average image. The weighting image was subsequently masked by the PRESS voxel mapped into DTI space to constrain the analysis to the same comparable region. The voxelwise weights within this region reflect the relative contribution of each voxel to the total signal, which in addition to the perpendicular restricted diffusion, also incorporate spin density and coil inhomogeneity. The voxelwise perpendicular weights were applied to the diffusion-weighted images and fit to the DTI model using FSL. An additional analysis to assess the contribution of non-cord signals used whole-cord ROIs to mask the voxelwise perpendicular weighting (Supporting Material and Sup. Table. S1).

DW Signal Models

Several different signal models were evaluated, including a monoexponential model:

$$S_i=S_0\times e^{-bD}$$ [1]

where S_i is the diffusion-weighted signal, S₀ is the signal without diffusion encoding, D is the estimated diffusivity, and b is the strength of the diffusion weighting given by

$$b={\gamma }^2·G^2·{\delta }^2(\Delta -\frac{\delta }{3})$$ [2]

for a given gradient strength, G, gradient duration, δ, gradient separation, Δ, and the gyromagnetic ratio, γ. This monoexponential model was used for conventional DTI (28) as well as modeling the DDE signal parallel to the spinal cord, referred to as axial diffusivity (D_‖).

A biexponential model was also used to evaluate the DDE-PRESS data with the equation:

$$S_i=S_0(1-f_R)e^{-b{D}_{\mathit{\text{fast}}}}+S_0{f}_R{e}^{-b{D}_{\mathit{\text{slow}}}}$$ [3]

where f_R is the fraction of the restricted or slow diffusing component (D_slow) and D_fast is the diffusivity of the fast diffusing component. While this model is a simplification of physiologic tissue compartments, it does provide a more detailed fitting routine than the monoexponential DTI model. Without explicitly assigning these components to physical compartments, the addition of a slow diffusion term is thought to better capture diffusion restriction related to injury (29) while D_fast captures the freely diffusing component. This model was evaluated with an upper bound on the diffusivity of free water of 3.0 um²/s at the in vivo temperature of 37 °C.

Spinal Cord Injury Procedure

Rats underwent a contusion injury at T10 using the MASCIS impactor (W.M. Keck Center for Collaborative Neuroscience; Piscataway, NJ). Rats were anesthetized with 4% inhaled isoflurane, ensuring absence of leg flexion-withdrawal and corneal reflexes. The back was shaved and sterilized with povidone-iodine, and an incision was made over the mid-thoracic region. A laminectomy was performed on the T10 spinal segment, the animal was positioned in the impactor, and a 10 g rod was dropped from a height of 0, 10, 25, or 50 mm to induce a sham (n=6), mild (n=5), moderate (n=5), or severe (n=6) injury, respectively. The distance (mm) that the rod compressed into the cord at impact was obtained from the impactor as a continuous measure of injury severity. After surgery, rats were placed on postoperative care, including twice-daily bladder expression, one dose of enrofloxacin (10 mg/kg subcutaneously; Bayer Healthcare LLC; Shawnee Mission, KS), buprenorphine hydrochloride (0.1–0.5 mg/kg subcutaneously; Rickitt Benckiser Health Care Ltd; Hull, UK), and 6 cc of lactated Ringer's solution. Animals were kept under postoperative care procedures until bladder function returned and no signs of infection or stress were evident. All rats survived the injury procedures and recovered without unforeseen complications related to this injury model. MRI procedures were performed in injured animals at 48 hours post-injury.

Statistical Analysis

For the SCI data, a group-wise one-way ANOVA was used to test for a significant effect of injury severity for each DTI and DDE parameter. Further posthoc testing was performed in models with a significant main effect (p<0.05) with pairwise comparisons assessed in which each injury group was compared to the sham group and all adjacent severity groups were compared to one another using Bonferroni’s method for multiple comparison correction. The relationship between the severity of injury quantified as the impact velocity and each DDE or DTI parameter was assessed using a linear regression analysis, and corrected for multiple comparisons using by correcting for the false discovery rate (30). Parameters achieving significance were also assessed with sham animals omitted. Statistical analysis was performed using the Stata software program (StataCorp. 2011. Stata Statistical Software: Release 12. College Station, TX: StataCorp LP.).

Results

Single-Axis Behavior in the Rat Spinal Cord White Matter

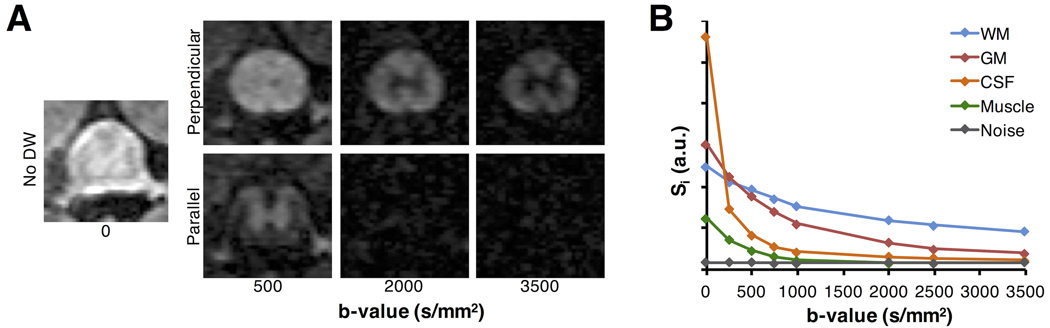
The diffusion weighted signal attenuation for tissues in and around the normal rat spinal cord was examined to guide the implementation of the DDE sequences. A PGSE applied perpendicular to the main cord axis in normal rats (n=4) exhibited a non-monoexponential response in both the WM and GM (Fig. 2). With increasing b-value, WM signal was less attenuated compared to that of the GM, and there was a complete loss of signal in the CSF and muscle at b-values above approximately 2000 s/mm². Non-weighted signal from the WM had an SNR of 13.87 (± 1.25) with values in the GM of 16.89 (± 1.34). At the largest b-value used here (3500 s/mm²), the SNR values from the WM and GM were 6.46 (±0.54) and 2.68 (±0.12), respectively, which were both greater than a region of only noise (1.02 ± 0.05). However, the contrast-to-noise ratio (CNR) between WM and GM did not change as b-value increased beyond a b-value of 2000 s/mm², where the CNR between WM and GM (2.88) at a b-value of 2000 s/mm² was not different from the CNR at b=3500 s/mm² (2.88). The WM and GM SNR values at the b=2000 s/mm² weighting were 7.74 (± 0.69) and 4.04 (± 0.36) respectively. At a b-value of 2000 s/mm², the SNR from CSF (1.34 ± 0.37) and muscle (1.05 ± 0.041) were not statistically different from noise, with p-values of 0.067 and 0.033, respectively. Collectively, the results indicate that a diffusion gradient with a b-value of 2000 s/mm² applied perpendicular to the cord was sufficient to suppress signals from the CSF and muscle, and no substantial gain in selectivity for WM signal was noted for values lager than this. As such, the resulting signal consists primarily of spinal cord tissue without a significant contribution from non-neural signal.

Figure 2. Perpendicular PGSE Signal Characteristics.

Signal decay in a standard PGSE sequence was acquired with gradients directed perpendicular or parallel to the spinal cord (A). Regions of interest from the white matter (WM), gray matter (GM), cerebrospinal fluid (CSF), muscle, and noise demonstrate the signal behavior of a perpendicular diffusion weighting (B). As evidenced by the image and signal plot, a perpendicular diffusion gradient at a b-value of 2000 s/mm² attenuates GM signal, and suppresses CSF and muscle signal, whereas WM signal was less attenuated.

Modeling the mean WM and GM signals with a biexponential model, the fraction of the restricted diffusing component in WM was f_R = 0.616 ± 0.13, and the diffusivities of the fast (1.4 ± 0.59 um²/ms) and slow (0.104 ± 0.040) compartments were separated by approximately an order of magnitude. By comparison, the GM had a smaller f_R (0.35 ± 0.11) and higher diffusivities for both the fast (1.702 ± 0.38) and slow (0.253± 0.073) components. Monte Carlo diffusion simulations in non-exchanging cylinders (Supporting Methods and Sup. Fig. S1) were consistent with the experimental results (Fig. 2B), suggesting that the fraction of the total signal originating from the intracellular (restricting) space did not substantially change with b-values above 2000 s/mm².

Double Diffusion Encoding

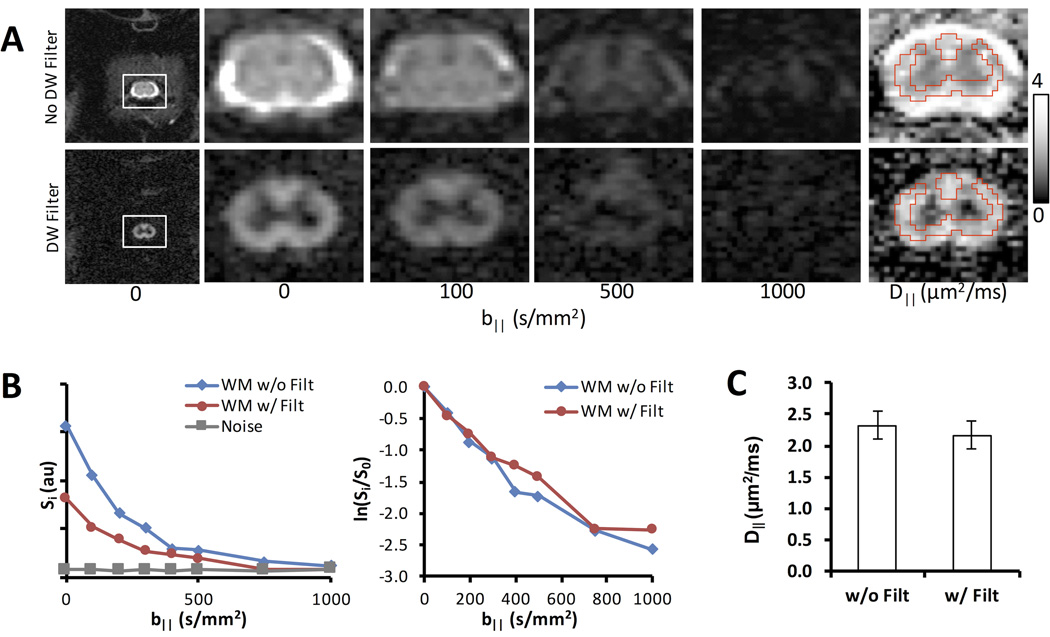
The DDE-EPI in the spinal cord of naive animals enabled further analysis of diffusion behavior in the cervical WM (Fig. 3). As in the PGSE, the perpendicular diffusion filter attenuated signal in the WM and suppressed signal from the CSF (Figs. 3A&B). D_‖ measured in the white matter (Fig. 3C) revealed no significant difference (n=3) with (2.16 ± 0.22 µm²/ms) or without the filter (2.32 ± 0.22 µm²/ms).

Figure 3. Imaging Application of DDE.

(A) DDE-EPI without (top) and with (bottom) the perpendicular diffusion weighted preparation with identical diffusion weighting parallel to the spinal cord. A region of interest analysis from the white matter demonstrated that while the filter decreases the absolute signal compared to the non-filtered data (B), the normalized signal was nearly identical. Moreover, there was no significant difference in the measured D_‖ between the filtered and non-filtered data (C) (n=3).

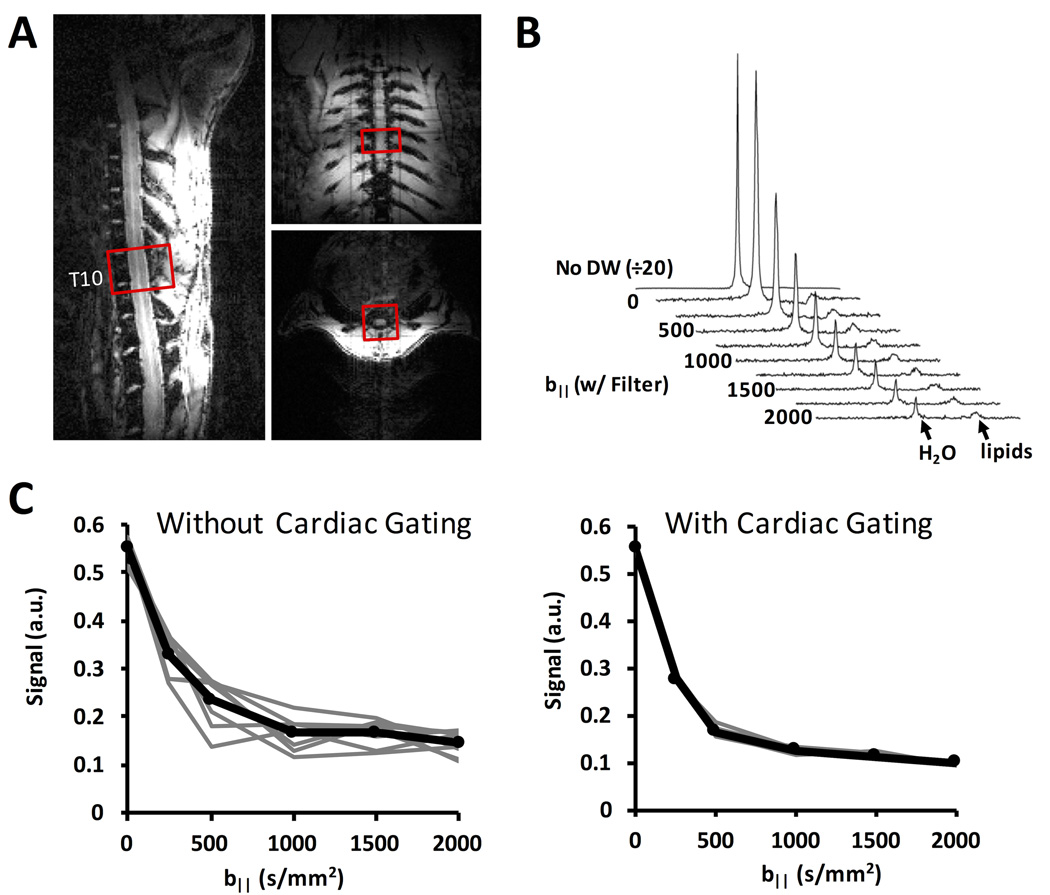
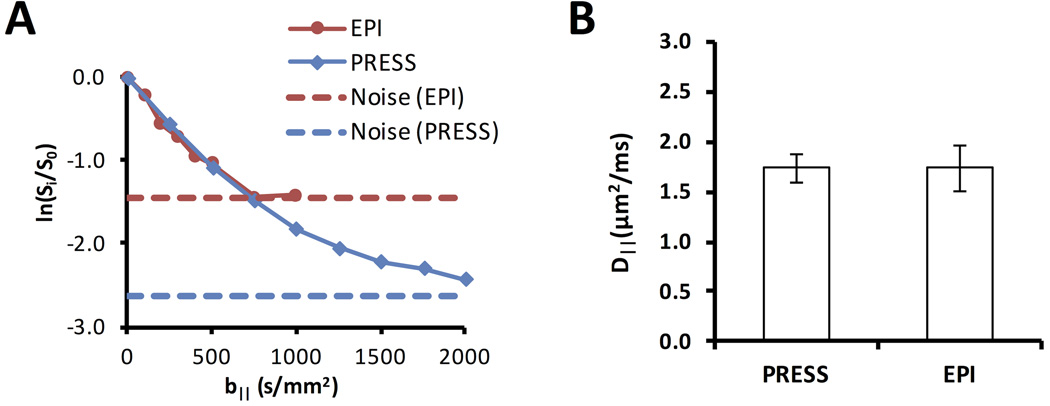
The adequate suppression of non-cord tissues enabled use of the DDE-PRESS sequence for whole-cord measurements (Fig. 4). The resulting spectra exhibited a strong water peak, with a lipid peak separated approximately 3.5 ppm from the water peak (Fig. 4B), thus avoiding signal contamination. The within-subject repeatability was improved with cardiac gating (Fig. 4C) compared to respiratory gating alone. The DDE-EPI and DDE-PRESS measurements performed in the same animals at the same spinal cord region (Fig. 5) exhibited similar diffusion weighted signal behavior. At low b-values, the normalized signals were nearly identical (Fig. 5A). The greater SNR afforded in the DDE-PRESS though the use of a whole-cord voxel allowed characterization of larger b-values. The estimated D_‖ (n=3) from the DDE-PRESS (1.74 ± 0.14 µm²/ms) was similar to that of the whole-cord DDE-EPI (1.73 ± 0.23 µm²/ms) with only b-values up to 1000 s/mm² used for both methods (Fig. 5B).

Figure 4. Spectroscopy Application of DDE.

A 10×10×6 mm³ voxel was positioned in the spinal cord at T10 with the short axis aligned parallel the cord axis on all three orthogonal views (A). The water signal from the spectra with the filter gradient is shown at multiple values for the parallel probe diffusion gradient (B). The lipid peak at approximately 3.5 ppm is also shown and exhibited almost no change with respect to b-value. Integration of the water peak from multiple repetitions and b-values shows that intra-subject repeatability is improved with the addition of a cardiac gating trigger in addition to the respiratory trigger (C).

Figure 5. Comparison of DDE-PRESS and DDE-EPI.

The normalized signal (A) from the DDE-PRESS demonstrated a similar diffusion weighted signal decay as a whole-cord region of interest from the DDE-EPI. The SNR from the DDE-PRESS was improved and sufficiently above the noise floor at even the largest b-values. The D_‖ values (B) were similar to one another using b-values ≤ 1000 s/mm² for estimation.

Double Diffusion Encoding in Spinal Cord Injury

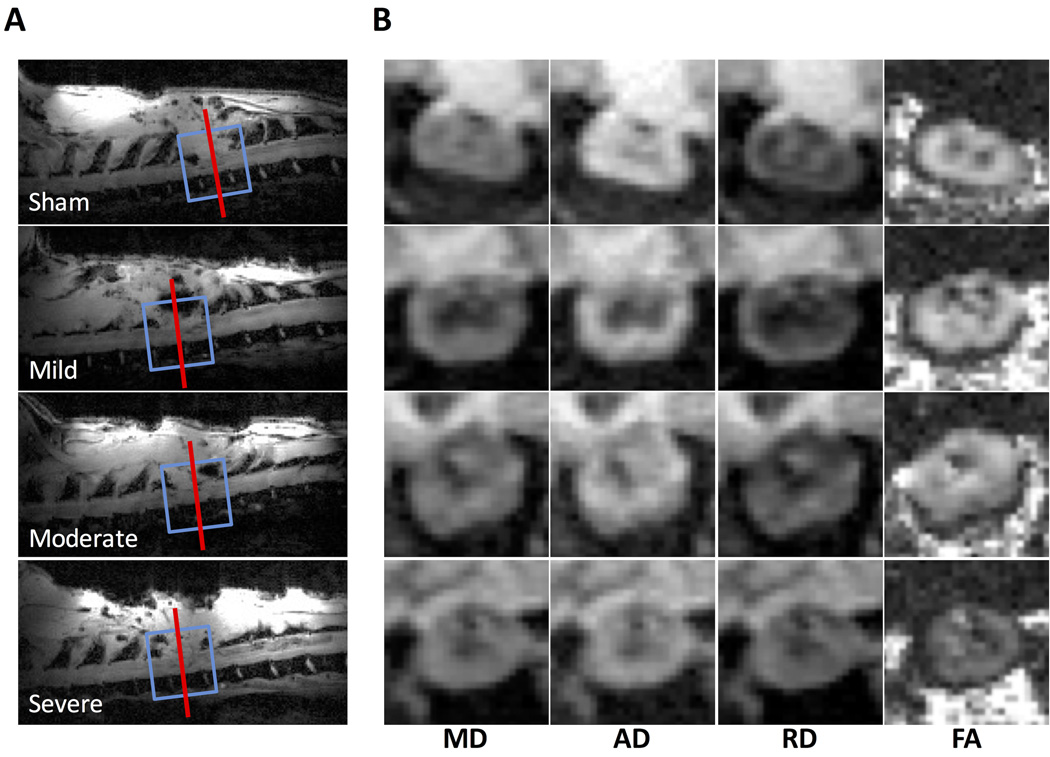
DDE-PRESS and DW-EPI was performed in a cohort of animals (n=22) at 2 days post injury after varying degrees of spinal cord injury to the thoracic (T10) cord (Fig. 6). Voxels and imaging slices were centered at the lesion epicenter. Sagittal FLASH images depicted the lesion site as evidenced by the dorsal laminectomy and were used for voxel and imaging slice placement (Fig. 6A). No obvious or consistent DTI parameter changes were evident qualitatively. Across all animals, the mean FWHM of the water peak measured in the DDE-PRESS was 47.3 ± 22.1 Hz using the filtered acquisition with b_‖=0. The coefficient of variation across each of the repetitions in the individual subject measurements was calculated as a measure of data quality, and the average across all animals was 8.9 ± 7.0 %. Based on these measures of data quality, two animals were removed from subsequent analysis. The FWHM for one moderate injury was 128.6 Hz (z-score = 3.67) and the CoV for one severe animal was 34.1 % (z-score = 3.59). In sham animals, a biexponential model provided a better fit to the DDE-PRESS data than the monoexponential model (Sup. Fig. S3), although both models were evaluated in all animals for completeness and comparison.

Figure 6. Injury Localization.

Sagittal scans were used to localize the injury site (A). The DDE-PRESS voxel (blue line) and DTI slices (red line showing center slice) were positioned at the center of the lesion and aligned with the main axis of the cord. Representative DTI maps (B) from the center slice show mean diffusivity (MD), axial diffusivity (AD), radial diffusivity (RD), and fractional anisotropy (FA). Diffusivity maps are windowed from 0 – 2.5 and FA is windowed from 0 – 1.

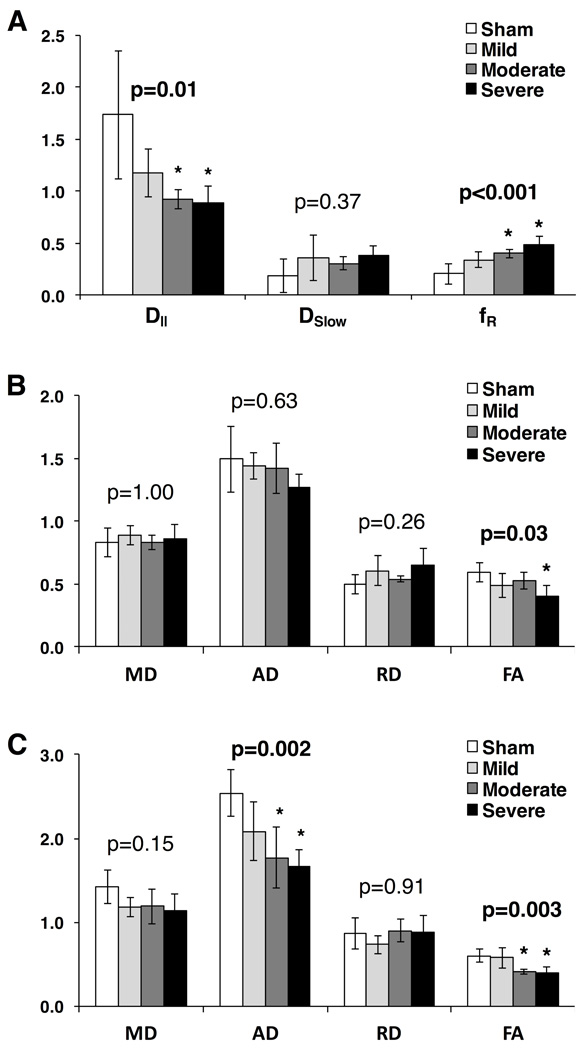
Diffusivity parameters showed varying levels of stratification based on injury severity (Fig. 7). DDE-PRESS exhibited a clear relationship with injury severity (Fig. 7A) with a significant effect of injury severity using a one-way ANOVA in both D_‖ (F(3,10)=5.94, p=0.0064) and f_R (F(3,10)=12.15, p=0.002). Post-hoc testing for pairwise differences revealed that the moderate (p=0.024) and severe (p=0.011) injury groups were significantly different from the sham group for D_‖, though the mild group was not significantly different from the sham (p=0.15). The f_R similarly demonstrated that the moderate (p=0.008) and severe (p<0.001) groups were significantly different than the sham group, whereas the mild group was not (p=0.078). The whole-cord ROI DTI parameters (Fig. 7B), showed a significant effect of injury severity for only FA (F(3,10)=4.64, p=0.016) and only the severe injury group demonstrated a significant difference from the sham injury group (p=0.013) in post-hoc analysis. On the other hand, weighted-ROI DTI analysis showed more prominent changes (Fig. 7C) with significant injury effect in AD (F(3,10)= 9.26, p=0.001) and FA (F(3,10)=8.73, p=0.001). Post-hoc pairwise analysis of AD demonstrated a significant difference from the sham group in the moderate and severe groups (p=0.007 and 0.001 respectively) with the mild group showing less separation (p=0.144). A similar difference from the sham group was seen for FA in the moderate (p=0.014) and severe (p=0.005) injury groups, but not in the mild group (p=1.00).

Figure 7. Comparison of DTI to DDE.

Mean values of the DDE-PRESS parameters of axial diffusivity (D_‖) from the monoexponential model and slow diffusion constant (D_slow) and the Restricted Fraction (f_R) from the biexponential model both exhibit consistent relationships with injury severity (A). Mean values of the DTI parameters of mean diffusivity (MD), axial diffusivity (AD), radial diffusivity (RD), and fractional anisotropy (FA) over the 6 slices centered at the lesion epicenter are shown (B), with only weak relationship to injury effect. Weighted ROI analysis of DTI parameters (C) showed an improvement in injury stratification in MD, AD and FA. Error bars reflect standard deviation. P-values indicate the one-way ANOVA for each parameter, and asterisks represent a significant group difference compared to the sham group in a post-hoc comparison.

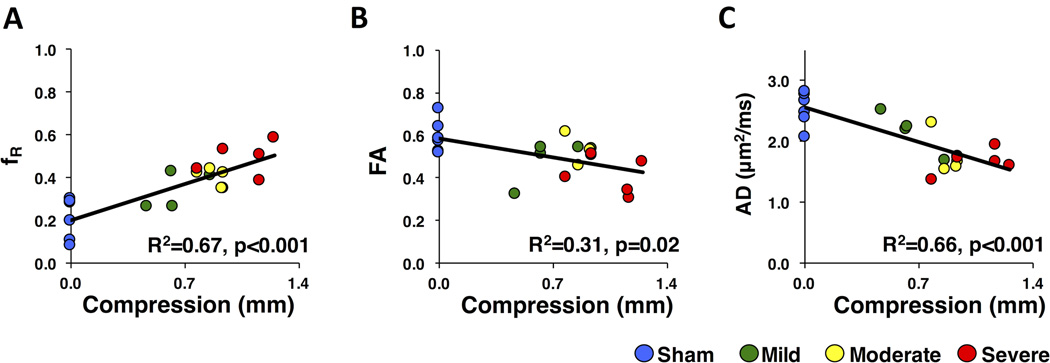
A linear regression analysis assessed the relationship between impact velocity, a continuous measure of injury severity, and DDE or DTI parameters, with the results shown in Table 1. The DDE-PRESS parameters showed a significant linear relationship with severity for D_‖ (p=0.002, R²=0.46), D_slow (p=0.02, R²=0.30), and f_R (p<0.001, R²=0.67). Whole-cord ROI DTI parameters showed a significant regression only for FA (p=0.015, R²=0.29). However, using the weighted ROI analysis, DTI parameters showed a significant relationship in MD (p=0.01, R²=0.34), AD (p<0.001, R²=0.66), and FA (p=0.001, R²=0.50). To ensure values from sham animal did not bias the regression estimates, an addition regression was assessed for those achieving significance in the full analysis. With the removal of the sham group, f_R (p=0.01, R²=0.44) from the DDE-PRESS and AD (p=0.02, R²=0.39) and FA (p<0.01, R²=0.50) from the weighted ROI DTI analysis all maintained significance, although the significance was reduced for all parameters. Scatter plots of the best performing parameter for each model are shown in Figure 8. To directly compare the derived parameters, a multiple linear regression incorporated the best performing parameter from each model. The DDE-PRESS parameter f_R maintained significance f_R (p<0.001, beta=0.71) with whole-cord ROI FA included as a covariate, which was not significant (p=0.12, beta=−0.24). On the other hand, a regression model including AD (p=0.03, beta=−0.48) from the weighted ROI as a covariate along with f_R (p=0.05, beta=−0.43) indicated that both metrics performed similarly in detecting injury severity.

Table 1.

Linear Regression.

Method	Parameter	Sham Included		Sham Excluded
		R2	p-value	R2	p-value
DDE-PRESS	D‖	0.46	0.002	0.09	0.29
	Dslow	0.30	0.02	0.13	0.21
	fR	0.67	<0.001	0.44	0.009
DTI-Whole Cord ROI	MD	0.00	1.00	--	--
	AD	0.14	0.16	--	--
	RD	0.15	0.14	--	--
	FA	0.31	0.02	0.03	0.49
DTI-Weighted ROI	MD	0.34	0.01	0.03	0.57
	AD	0.66	<0.001	0.39	0.018
	RD	0.00	1.00	--	--
	FA	0.50	0.001	0.50	0.005

p-values corrected for multiple comparisons

Figure 8. Linear Regression.

Scatter plots and the best-fit regression line including R² and p-values are shown for DDE-PRESS restricted fraction (f_R) (A), whole-cord DTI Fractional Anisotropy (FA) (B), and weighted DTI Axial Diffusivity (AD) (C), which are the best performing parameter from each model.

Discussion

A priori knowledge of fiber orientation allows application of the filter-probe model of DDE, which has several distinct advantages over DTI through removal of the effects of edema and CSF. Coupling with a spectroscopic readout reduced acquisition times and post-processing demands needed for DWI model fitting or region of interest analysis. Previous simulation results (18) showed sensitivity of this DDE technique to axonal injury in coherent fiber tracts, which was demonstrated in vivo in this study. While the DDE orthogonal diffusion filter resulted in an overall SNR decrease in the spinal cord white matter, it enabled an improvement in specificity to injury through suppression of the free and hindered component of the diffusion signal while preserving the restricted component (31–33). Although the relationship between mathematical compartments and biological tissue compartments is not straightforward, this slow diffusing fraction is generally believed to represent intra-axonal water. In the spinal cord white matter of humans (34,35) and rats (Fig. 2) in vivo, the fraction of the slow diffusing compartment is approximately 40–60 % of the total measured signal, which is largely consistent with histological estimates, although some discrepancies remain.

While the coherent signal remaining after the ‘filtering pulse’ is likely associated with intra-axonal water, no attempt was made to strictly assign it to this compartment, nor did it require this assumption. Instead, the sensitivity to intra-axonal water in the DDE was enhanced by directly suppressing signal from freely or fast diffusing water, most notably the CSF and extra-axonal tissue water. This approach is in contrast to other advanced DWI models wherein geometrical approximations and assumptions of diffusion signal behavior are often necessary to enable robust fitting and reduction of the parameter space. Interestingly, diffusivities measured parallel to white matter fibers with and without the filter were not significantly different from one another, suggesting little difference between intra- and extra-axonal parallel diffusivities in the normal white matter (Fig. 3C). In the injured cord, the restricted fraction is believed to represent axonal injury, though isotropically-restricting cells such as inflammatory cells are also compatible with the measured changes. Nonetheless, the DDE-PRESS demonstrated differences based on injury severity, which is the ultimate goal for a clinically-relevant measurement for SCI quantification.

Axial diffusivity has been shown to be a sensitive and predictive marker of SCI in the hyperacute setting (3) and exhibits evolving changes during the subacute and chronic period, likely due to axonal beading (29) and other degenerative breakdown processes contributing to altered intra-axonal diffusivity. Since axonal integrity is the best indicator of functional status following injury (6), diffusion changes within the axon related to degeneration are expected to represent a useful biomarker of injury severity. However, processes that obscure the intra-axonal signal, such as edema and cyst formation, confound standard DTI diffusion measurements. Our whole-cord DTI results demonstrate poor sensitivity to injury severity at the lesion epicenter. In contrast, DDE-PRESS measurements demonstrated an increased restricted diffusion fraction (f_R) with increased injury severity, showing a substantial improvement in sensitivity to injury by utilizing the filter pulse. Weighting the DTI analysis based on its perpendicular signal fraction rescued the sensitivity of DTI to injury severity and was comparable to the DDE-PRESS. However, as these results demonstrate, the method of ROI analysis can leads to very different DTI outcomes and can involve complex post-processing, the DDE-PRESS is a more straightforward and simplistic method while retaining a high sensitivity to injury. Hence, there is promise for this technique to be utilized as a clinically-feasible and sensitive biomarker of spinal cord injury severity.

Among limitations of the DDE-PRESS is the loss of spatial information, which may not be suitable for all applications. The inability to discern varying signal contributions from GM or spinal nerve roots may also be a complicating factor. The need for spatial resolution must be considered against SNR limitations and ease of analysis. Further work is needed to define and improve the limitations of this technique in SCI and other applications. Most notably, validation in patients is essential, as the current work was limited to a pre-clinical rat model. Nonetheless, in this application of acute SCI, we have shown a fast and efficient method by which to quantify injury severity, which was optimized based on the pathophysiology of injury and exploiting the known anatomy of the spinal cord.

Conclusions

The DDE sequence, and in particular the DDE-PRESS implementation, shows promise for use in the evaluation of spinal cord injury. It benefits from improved selectivity for white matter injury while suppressing other confounders to the diffusion signal. Furthermore, the spectroscopic acquisition improves SNR, decreases scan time, and eliminates much of the post-processing often required for imaging-based diffusion MRI methods. Application in a rat injury model showed sensitive quantification of injury which may have promise for future applications in pre-clinical and clinical evaluation of spinal cord integrity and injury.

Abbreviations

SCI

Spinal Cord Injury

DTI

Diffusion Tensor Imaging

DDE

Double Diffusion Encoding

WM

White Matter

GM

Gray Matter

CSF

Cerebrospinal Fluid