Model-based analysis of DNA replication profiles: predicting replication fork velocity and initiation rate by profiling free-cycling cells

Abstract

Eukaryotic cells initiate DNA synthesis by sequential firing of hundreds of origins. This ordered replication is described by replication profiles, which measure the DNA content within a cell population. Here, we show that replication dynamics can be deduced from replication profiles of free-cycling cells. While such profiles lack explicit temporal information, they are sensitive to fork velocity and initiation capacity through the passive replication pattern, namely the replication of origins by forks emanating elsewhere. We apply our model-based approach to a compendium of profiles that include most viable budding yeast mutants implicated in replication. Predicted changes in fork velocity or initiation capacity are verified by profiling synchronously replicating cells. Notably, most mutants implicated in late (or early) origin effects are explained by global modulation of fork velocity or initiation capacity. Our approach provides a rigorous framework for analyzing DNA replication profiles of free-cycling cells.

In eukaryotic cells, DNA replication is initiated from hundreds of replication origins that are distributed across the chromosomes and fire at different times in S phase (Ferguson et al. 1991; Friedman et al. 1997; Yamashita et al. 1997; Raghuraman et al. 2001). This temporal replication pattern is measured by DNA replication profiles, which define the times in S phase at which each genomic region is replicated (Raghuraman et al. 2001; Yabuki et al. 2002). Replication profiles are used for studying mutants implicated in DNA replication. For example, deleting a gene that activates a specific subset of origins will specifically delay the activation time of these origins. Indeed, multiple replication profiles have been reported, in which the firing of late origins was preferentially suppressed, implicating a specific regulation of this subset of origins (McCune et al. 2008; Yamazaki et al. 2013; Hiraga et al. 2014; Yoshida et al. 2014).

A central difficulty in interpreting replication profiles is the passive replication of origins before firing, by forks emanating from nearby origins (Dubey et al. 1991; Santocanale and Diffley 1998; Retkute et al. 2011). This passive replication introduces effective interactions between origins, which impacts the replication profiles. Further, the probability of passive replication depends on global dynamic parameters such as fork velocity or overall initiation capacity, so that changes in these parameters modulate the effective interactions between origins, leading to what appears as origin-specific effects. For example, a recent study explained the apparent effects of Rpd3 on late origins by an overall increase in initiation capacity due to decreased competition with rDNA replication (Yoshida et al. 2014).

Replication profiles are often generated by following cells as they progress synchronously through S phase. Measuring DNA content during this progression can capture origin firing times and replication fork velocity (Raghuraman et al. 2001; Yabuki et al. 2002). This approach requires cell synchronization and is therefore subject to several limitations (Davis et al. 2001; Cooper 2003). First, synchronization is difficult to achieve in many cell types. Second, synchronization necessarily perturbs normal cell cycle progression, which could, in principle, perturb the replication pattern, although, at least in wild-type cells, this does not appear to be the case (Müller et al. 2014). Finally, to achieve a good time resolution, many samples need to be sequenced, limiting the capacity to analyze a large number of mutants. An alternative approach is to profile DNA content in free-cycling cells. Indeed, in a population of asynchronously dividing cells, early replicating origins will be proportionally more abundant than late replicating ones. This analysis, termed marker frequency analysis (MFA), was designed to study chromosomal properties (Yoshikawa and Sueoka 1963; Altenbern 1971) and was recently applied for capturing genome-wide replication timing (Müller et al. 2014). A variant of this method enriches for actively replicating cells by staining the DNA and FACS-sorting S phase population (Schübeler et al. 2002; Koren et al. 2010; Müller and Nieduszynski 2012; Müller et al. 2014). This method does not perturb the cell cycle and requires sequencing a single sample for each mutant. Replication profiles generated this way, however, do not report directly on fork velocity or initiation rates; hence, interpreting these profiles to deduce dynamic replication parameters is less intuitive.

In this study, we propose and validate a model-based approach for analyzing replication profiles of free-cycling cells in a way that distinguishes changes in the global fork velocity and initiation capacity from changes that affect specific origins. We apply this method for analyzing a compendium of replication profiles from 25 budding yeast mutants, classifying mutants based on their effect on the global fork velocity, initiation capacity, or origin-specific effects.

Results

Modeling DNA replication

We consider replication profiles obtained by measuring DNA abundance in a population of free-cycling cells. Such data is obtained by FACS-sorting the subset of cells that are present in S phase, or by considering a population of growing cells in which a subset of cells is actively replicating. Replication profiles are visualized by plotting the measured DNA content as a function of chromosomal coordinates: Peaks represent replication origins, and peak heights capture the firing times of these origins (Fig. 1A). Sequencing data is often noisy, and therefore data smoothing is required prior to the analysis of the profiles. When comparing different samples, it is often difficult to distinguish changes that are significant from those that occur due to noisy sampling.

Figure 1.

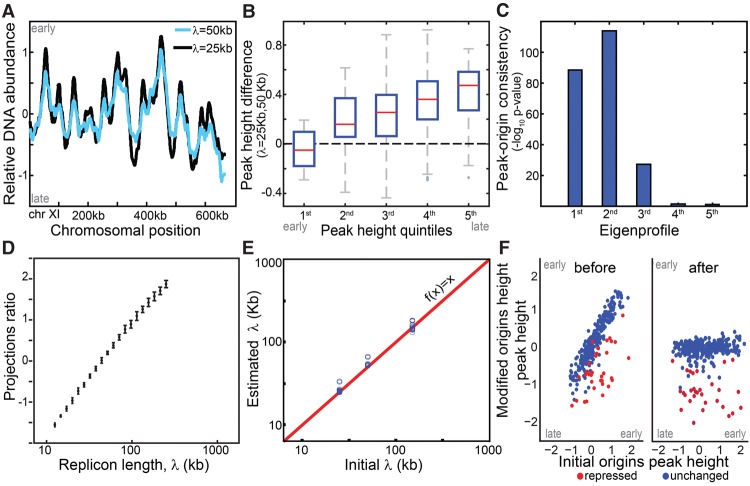
Simulation wild-type and mutated replication profiles. (A) Replication profile is sensitive to replicon length: Shown are simulated profiles corresponding to replicon lengths of λ = 25 kb (black) and λ = 50 kb (light blue). High DNA abundance indicates early replicating regions, and peaks represent replication origins. (B) Late origins show increased sensitivity to replicon length: Origin activation time was approximated by DNA content at the origin position (peak height). The figure compares activation times of all origins based on a reference and a perturbed profile (λ = 50 and 25 kb, respectively) grouped to quintiles. (C,D) Replicon length is retrieved using singular value decomposition (SVD). Origins were accurately predicted by the two leading eigenprofiles defined by SVD analysis (Methods) (C). Each profile was projected into the two leading eigenprofiles. This projection ratio is tightly correlated with the (log) replicon lengths (D). (E,F) Predicting origin-specific effects. Mutants that perturbed both the replicon length and origin-specific efficiencies were simulated. Replicon length was retrieved when projecting the simulated profile on the two leading eigenprofiles (E). Normalizing the replication profiles for the predicted changes in replicon lengths highlights origin-specific effects (F).

Our goal here is to use replication profiles in order to classify S phase mutants. To better understand the consequences of perturbing different replication parameters, we formulated a model of DNA replication that enables simulating three types of perturbations: change in the efficiency of individual origins, change in fork velocity, and change in the overall initiation capacity (Supplemental Material). Following the formulation used in previous models (Jun and Bechhoefer 2005; Lygeros et al. 2008; Brümmer et al. 2010; Hyrien and Goldar 2010; Rhind et al. 2010; Koutroumpas and Lygeros 2011; Bechhoefer and Rhind 2012), we simulated genome replication in a straightforward manner (Yang et al. 2010; Baker and Bechhoefer 2014): Given fork velocity, v, initiation capacity, I, and origin-specific parameters (chromosomal positions and relative firing probabilities of all replication origins, x_i and n_i), we compute the temporal increase in DNA content across the genome. The replication profile of free-cycling cells is obtained by averaging the DNA contents over the simulated times. Notably, this averaged profile depends on fork velocity v and initiation capacity I only through their ratio λ = v/I (Methods). This ratio is proportional to the average DNA length replicated by a highly efficient origin, and we therefore term it the replicon length.

Late-replicating origins are sensitive to replicon length

We simulated the wild-type replication profile by setting the local (x_i, n_i) and global (v, I) parameters based on the literature (Supplemental Material; Yang et al. 2010). Mutant profiles were simulated by perturbing these parameters. First, we changed the replicon length, λ. Notably, although origin-specific parameters were kept fixed, the mutated profile showed late-origin effects: Increasing λ preferentially delayed replication of late origins (Pearson correlation r²= −0.44) (Fig. 1A,B). This was explained by the increased probability for passive replication at longer replicon length.

We reasoned that this characteristic effect may enable predicting changes in replicon length directly from the averaged (asynchronous) replication profile, although this single profile doesn't contain explicit temporal information. To examine that, we generated 400 simulated profiles that differed only in their replicon length (and stochastic noise), and analyzed this data using the robust approach of singular value decomposition (SVD, closely related to principal component analysis). SVD represents each profile as a weighted sum of uncorrelated eigenprofiles, ordered by the fraction of data variance they explain (Alter et al. 2000). In our simulated data set, the two leading eigenprofiles captured 84% of the variance and accurately predicted replication origins: The first identified fewer origins (191 peaks) than the second (223 peaks) but predicted origin efficiencies more accurately (r²= 0.85 vs. r²= 0.15, respectively) (Fig. 1C).

Each replication profile is therefore well approximated as a weighted sum of these two eigenprofiles. Notably, the ratio of these projections was proportional to the (log) replicon length λ, in a manner that was robust to noise (Fig. 1D; Supplemental Figs. 1,2). This ability to predict changes in replicon length was maintained also when combined with perturbations of local origin efficiencies (Fig. 1E,F; Supplemental Fig. 3; Supplemental Material, Section A).

Testing the model—limiting the abundance of essential replication factors decreases replicon length

Perturbations of the replicon length can therefore be deduced from replication profiles using SVD analysis. To examine this result using experimental data, we first verified that our model can simulate the measured experimental profiles. Indeed, the wild-type replication profile was well described by our model with origin positions and efficiencies (x_i, n_i) used in our simulations and replicon length estimated as 51 kb (Supplemental Fig. 4).

Next, we examined whether the model can report on a perturbed replicon length. Replicon length is given by the ratio of fork velocity and initiation capacity. We perturbed the global initiation capacity by reducing the abundance of genes that code for factors that are essential for origin firing: POL2, POL12, CDC45, DPB11, POL30, and SLD5 (Takayama et al. 2003; Lydeard et al. 2010). This was done using a TET-repressible promoter, calibrated to prolong S phase but maintain viability (Mnaimneh et al. 2004). Replication profiles were measured by sorting S phase cells and measuring their DNA content. Replicon length values were predicted by projecting the resulting profiles on the two leading eigenprofiles obtained from the simulated data sets. As predicted, the measured replication profiles were assigned a longer λ (Fig. 2). Conversely, the predicted short-λ phenotype was obtained when increasing initiation capacity by overexpressing several initiation-limiting factors: CDK targets Sld2 and Sld3, their binding partner Dpb11, and Dbf4, which is required for phosphorylation of the Mcm2-7, abbreviated as SSDD (P-value < 0.04) (Mantiero et al. 2011). Note that, as in previous studies, this overexpression was analyzed in the background of rpd3Δ (Mantiero et al. 2011).

Figure 2.

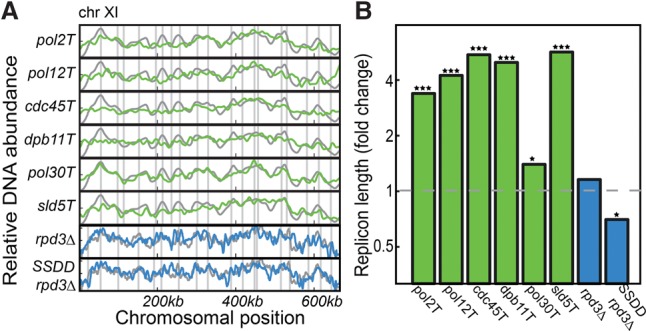
Replicon length is reduced when limiting abundance of initiation factors. Shown are the replication profiles (A, Chromosome XI) and the inferred replicon lengths (B), for the indicated genes expressed under the control of a TET-repressible promoter (green) and overexpression of the limiting factors SLD2, SLD3, DPB11, and DBF4 in the background of rpd3Δ ([Mantiero et al. 2011], denoted as SSDD rpd3Δ), with the rpd3Δ as control (blue). All experiments were done in duplicate, with the exception of rpd3Δ and SSDD rpd3Δ, which were done in triplicate, and the wild-type control, for which 13 independent replicates were performed. All changes in λ were significant, based on a one-sided two sample t-test between replicates (P-value = 0.01 for pol30Δ mutant, <10⁻¹⁰ for all other mutants showing higher λ, and 0.04 for the lower λ of SSDD rpd3Δ; the rpd3Δ control showed no significance at all). (*) P < 0.05, (***) P < 0.001.

A compendium of budding yeast mutant profiles

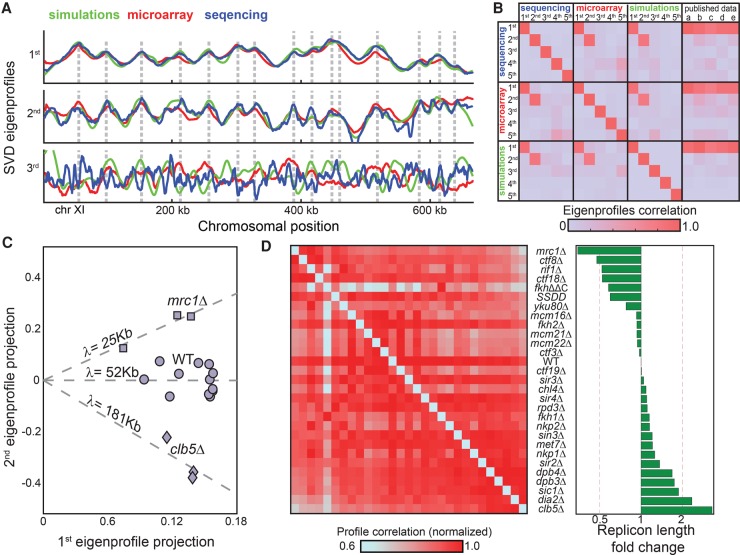
To more systematically test our approach, we analyzed a compendium of replication profiles, including most viable budding yeast mutants implicated in DNA replication. To enable unified analysis, we considered two data sets. First, a data set of 22 mutant profiles (98 profiles including biological replicates) generated using microarrays, some of which were reported previously (Koren et al. 2010). Second, we generated a new data set of 21 mutants (55 profiles), partially overlapping the first set, using high-throughput sequencing. Notably, SVD analysis, applied separately to each data set, generated practically the same two leading eigenprofiles, and these were strikingly similar to the respective eigenprofiles defined by the simulated data set described above (Fig. 3A,B; Supplemental Fig. 4). The compendium of profiles is therefore well explained by just two eigenprofiles: the mean of all profiles, which captures the origin replication times, and a sharper profile that predicts replication origins but doesn't capture their activation times.

Figure 3.

S phase mutants differ in their replicon lengths. (A) SVD analysis of a compendium of budding yeast mutant profiles: The three leading eigenprofiles defined by SVD analysis of experimental and simulated data sets are shown (blue, red, and green; Chromosome XI). (B) Distinct data sets define the same two leading eigenprofiles. Shown are the correlations between the five leading eigenprofiles from each data set (simulations, microarray, and sequencing), and their correlations with previously published wild-type data: (a) Alvino et al. (2007); (b) Feng et al. (2006); (c) McCune et al. (2008); (d) Müller and Nieduszynski (2012); and (e) Raghuraman et al. (2001). (C) Predicted replicon lengths are consistent between replicates. The replication profiles of wild-type cells, cells deleted of CLB5, and cells deleted of MRC1 were measured with 12, four, and three replicates, respectively. Shown are the projections of each individual repeat on the two leading eigenprofiles. The (log) replicon length is predicted by the slope (projection ratio). (D) Predicted replicon lengths. Shown are the predicted replicon lengths for the mutants in our data set. The left panel shows the correlation between respective profiles. For each mutant, correlation values were normalized by their maximum to control for differences in noise levels.

We predicted the replicon length λ of each mutant by projecting it onto the two leading eigenprofiles. The predicted λs were highly reproducible between independent replicates (Fig. 3C). In fact, these λ values best discriminated between strains (relative to replicates, P-value < 10⁻¹¹; ANOVA test). Ordering the mutants by their replicon lengths was in a good agreement with the pattern of correlations between the profiles (Fig. 3D), suggesting that changes in replicon length capture a large portion of the differences between the strains.

Notably, most mutants prolonged replicon length, indicating either an increase in fork velocity or decrease in initiation capacity. Since most mutants were chosen based on having a prolonged S phase, a longer λ predicts reduced initiation capacity. Indeed, initiation capacity depends on many factors required for origin initiation, consistent with the multiplicity of genes affecting it.

Validating predicted changes in fork velocity and initiation capacity using time-resolved profiling

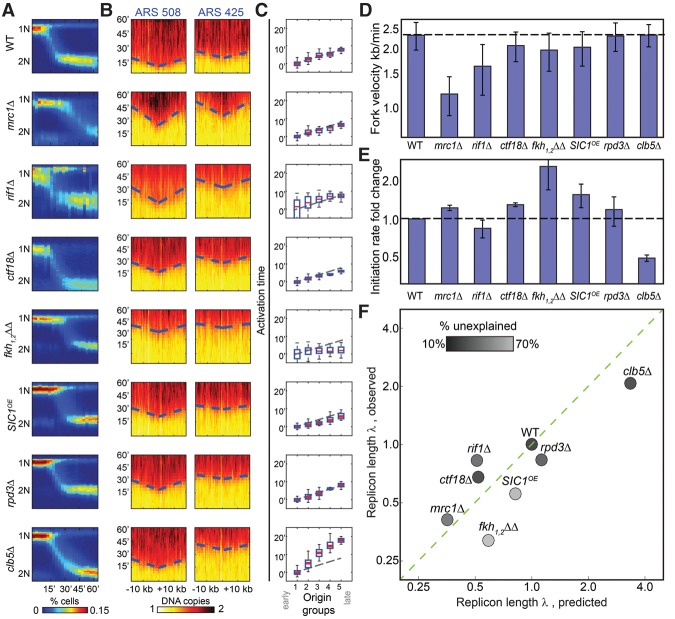
We next wished to verify predicted changes in fork velocity or initiation capacity. This required an independent means for measuring these parameters. To this end, we profiled cells that progress synchronously through S phase. Cells were arrested at the end of G1 using α-factor and were followed for 60 min upon release, with samples taken every 3 min for DNA sequencing. Synchronized progression was verified by DNA staining (Fig. 4A). Plotting DNA content as a function of chromosomal coordinates at different times showed the expected v-shape increase in DNA content around replication origins, capturing the symmetric progression of the replication fork (Fig. 4B). Based on this pattern around well-characterized origins, we estimated wild-type fork velocity to be 2.3 kb/min, consistent with previous estimates (1.6–3 kb/min) (Raghuraman et al. 2001; Yabuki et al. 2002; Hyrien and Goldar 2010; Sekedat et al. 2010; Yang et al. 2010). To estimate the initiation capacity, we measured the time at which each origin fires, approximated by the time at which DNA content reached its half-maximum. This time, t_i, is inversely proportional to the initiation capacity I, t_i∼1/I, if measured from the beginning of S phase. To obtain a robust estimate, we classified all origins into five clusters based on their replication time in wild-type cells and defined I based on the time-differences between the average replication times of origins assigned to each cluster (Fig. 4C). Note that, by definition, we can only measure changes in I but not its absolute level.

Figure 4.

Temporal profiling validates predicted changes in fork velocity and initiation rates. (A) Synchronous progression through S phase. Cells were followed for 60 min following release from α-factor arrest and sampled at 3-min time resolution. Shown in color-code are the distributions of total DNA content (y-axis, measured using flow-cytometer) at different times (x-axis) for the indicated mutants. (B) Defining fork velocity from the temporal progression of replication around replication origins. Shown in color-code are DNA content around early (ARS508) and late (ARS425) origins (x-axis, measured using whole-genome sequencing) as a function of time (y-axis). Fork velocity is estimated by the slope, obtained by linear fit (dashed blue lines) of the estimated times at which different genomic regions around the origins replicated (t_rep, black). (C) Defining origin activation time from the gradual delay in origin activation time. Origins were classified into five groups based on their wild-type efficiency. Shown is the average activation time for origins in each cluster. Initiation capacity is inferred by the proportional delay in activation time between clusters (Supplemental Material). (D) Fork velocities of the indicated mutants. Velocities shown are an average over all origins. (E) Initiation capacities of the indicated mutants. Initiation capacity was inferred from the proportional delay in activation time between clusters, as shown in B (Supplemental Material). (F) Measured replicon lengths tightly correlated with the predicted values. Replicon lengths were calculated from the measured fork velocity v and initiation capacity l (λ = v/I) and are shown as a function of the replicon length predicted form the respective profiles of free-cycling cells. Both measures are normalized by the wild-type value. The shading-code indicates the extent to which the mutant profile is explained by the model assuming no origin-specific effects (residual score; black indicates high agreement) (Supplemental Material).

We applied this approach to seven mutants predicted to change fork velocity or initiation capacity. First, we considered cells deleted of MRC1 or RIF1, which were predicted to reduce fork velocity based on their shorter replicon length and longer S phase relative to wild type. Mrc1 was previously shown to promote fork velocity (Szyjka et al. 2005; Tourriere et al. 2005; Hodgson et al. 2007; Gispan et al. 2014), while Rif1 was implicated in regulating telomeric origins (Hayano et al. 2012; Yamazaki et al. 2013; Peace et al. 2014). Second, we considered the clb5Δ and fkh_1,2ΔΔ mutants, predicted to respectively increase or decrease initiation rate (Donaldson et al. 1998; Knott et al. 2012): clb5Δ, a B-type cyclin, increased replicon length and S phase duration, while fkh_1,2ΔΔ decreased replicon length but did not increase S phase. Both Clb5 and Fkh1,2 were implicated in controlling the replication timing of a subset of origins but not with global effects. We included in this class also cells deleted of CTF18, which showed a similar, yet weaker, effect as fkh_1,2ΔΔ, and also cells overexpressing SIC1, an inhibitor of Cdc28-Clb kinase complexes (Lengronne and Schwob 2002) which was predicted to increase initiation capacity based on the increase of replicon length and longer S phase duration of SIC1-deleted cells. Finally, we considered cells deleted of RPD3, which showed no significant change in replicon length or S phase duration.

As can be appreciated from Figure 4, D and E, fork velocity and initiation capacity derived from this temporal profiling were fully consistent with the predictions described above. Further, the replicon length derived from the two temporal measurements (v/I) was well correlated with the replicon length predicted by our analysis of the asynchronous profile (r²= 0.85) (Fig. 4F).

Changes in replicon length explain the majority of apparent origin-specific effects

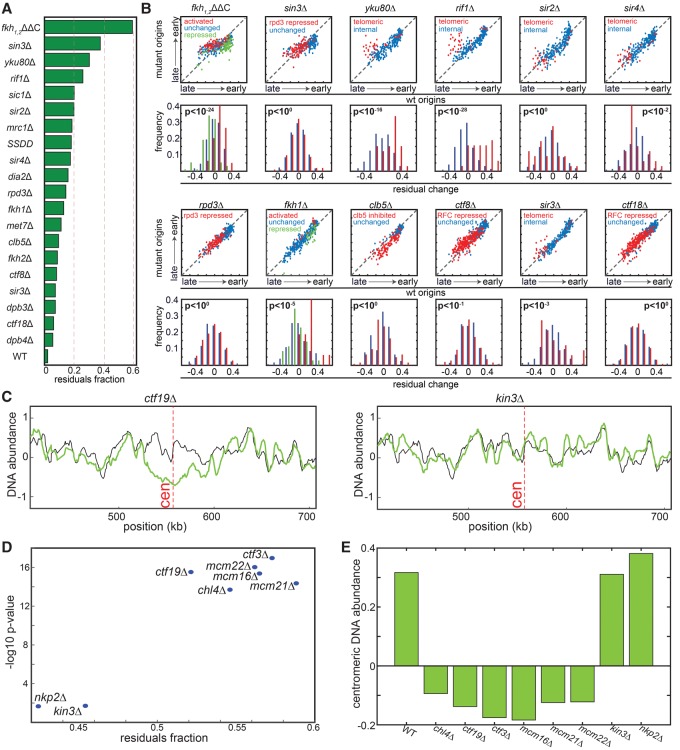
Our analysis suggests that many of the mutants analyzed perturb the replicon length. We next wished to characterize origin-specific effects that are not explained by the global changes in replicon length. To this end, we normalized each profile by the inferred λ and measured the remaining changes. As a measure of these remaining changes, we scored each mutant by the % variance not explained by the global changes (Methods; Fig. 5A). A high score predicts origin-specific effects, while a low score suggests that the mutant is well explained by global changes in fork velocity and initiation capacity.

Figure 5.

Mutants showing origin-specific effects. (A) Scoring mutants by the fraction of replication profile not explained by global changes. Shown are the fractions of the variances of the measured replication signals not explained by a model assuming no origin-specific effects. (B) Change in the replication timings of individual origins: For each mutant, the upper figure shows the inferred replication timing (DNA abundance) of each origin in the mutant vs. wild type. The group of origins predefined in previous experiments as regulated in the respective mutant is color-coded. The distributions of residual changes, following normalization by the predicted replicon length, are also shown (lower panel). P-values are measured based on a two-sample t-test (or one-way ANOVA in the case of the number of groups > 2) comparing the distribution of residuals in the regulated vs. unregulated origin groups. Origin classification is based on the following references: fkh_1,2ΔΔC and fkh1Δ taken from Knott et al. (2012); rpd3Δ and sin3Δ were classified based on the up-regulated origins in rpd3Δ from Knott et al. (2009); ctf8Δ and ctf18Δ classification was taken from Crabbe et al. (2010). Classification of clb5Δ origins was taken from McCune et al. (2008). Subtelomeric origins in yku80Δ, rif1Δ, sir2Δ, sir3Δ, and sir4Δ were defined within 50 kb from the telomeres (Methods). (C) Replication profile around centromeres. Shown are the replication profiles around the centromere (marked in a dashed red line) of Chromosome 16 for the indicated strains (green) compared to the wild-type strain (black). (D) The unexplained profile score correlates with local changes. For the indicated strains, the unexplained percentage of the signal (x-axis) is compared to the significance of change in centromere replication. Significance is defined by the −log₁₀(P-value) of a t-test comparing changes in replication time of centromeric vs. noncentromeric origins (y-axis). (E) DNA abundance around centromeric regions. Shown are 10-kb windows around the centromere for the indicated strains.

The highest scoring mutant was fkh_1,2ΔΔC, deleted of the two forkhead transcription factors (but rescued for expression effects) (Knott et al. 2012). This mutant was previously shown to perturb many origins, both advancing late origins and delaying early ones. Our analysis is consistent with these reported changes (P-value < 10⁻²⁴) (Fig. 5A,B). Additional mutants that received high scores in this analysis are rif1Δ, and yku80Δ (Cosgrove et al. 2002; Lian et al. 2011). Also here, our analysis was fully consistent with previous data showing specific effects of these factors on replication of subtelomeric origins (Fig. 5B). In contrast, local effects were significantly less pronounced in cells deleted of SIR2, a histone modifier involved in silencing which was also implicated in replication of subtelomeric origins (Fig. 5B; Stevenson and Gottschling 1999; Blander and Guarente 2004), suggesting that previously described effects in these mutants are due primarily to changes in the global initiation capacity (Yoshida et al. 2014).

The Ctf8 and Ctf18 components of the alternative clamp loader suppress late origins (Crabbe et al. 2010). These effects were observed in our data but were explained by reduced replicon length (Fig. 5A,B). Similarly, late-origin effects associated with clb5Δ were explained by its longer replicon length. Mutants deleted of the interacting histone deacetylases, Rpd3 and Sin3, were reported to advance late origins replication (Aparicio et al. 2004; Knott et al. 2009). Deletion of RPD3 in our strain had a minor effect on replication. SIN3 deletion was assigned a high residual score, but the previously described effects on late origins were consistent with global, rather than origin-specific, perturbations (Fig. 5A,B).

As an additional test for the ability of our method to capture origin-specific effects, we considered cells deleted of CTF19, an outer kinetochore protein needed for accurate chromosome segregation. Previous studies have shown that the Ctf19 complex mediates the interaction between the kinetochore and DNA replication machinery and that CTF19 deletion delays replication of centromeric origins (Natsume et al. 2013; Tirupataiah et al. 2014). We extended this analysis by profiling all eight nonessential protein subunits of the Ctf19 complex. In this analysis, which was performed at later stages of our study when our sequencing capacity increased, we did not sort S phase cells but directly profiled logarithmically growing cells, in which ∼20%–25% are actively replicating. With the increasing sequencing capacity, the mutant effects on the replicon length were captured also without sorting, as we verified by profiling many mutants (Supplemental Fig. 5).

Six subunits of the Ctf19 complex (ctf19Δ, ctf3Δ, chl4Δ, mcm22Δ, mcm21Δ, and mcm22Δ) showed the expected delay in replication of the centromeric region (Fig. 5C–E). This delay was not observed, however, in cells deleted for NKP1 and NKP2, suggesting that these subunits are not required for connecting the kinetochore with the replication machinery. Notably, the residual scores, indicative of origin-specific effects, were highly correlated with these effects on centromeric origins, confirming these residuals as a good measure for detecting origin-specific effects.

Discussion

Replication profiles provide a useful tool for analyzing mutants that perturb DNA replication. In this work, we proposed and validated a four-step approach for analyzing DNA replication profiles of free-cycling cells: First, a model of DNA replication is constructed based on wild-type parameters. Second, global perturbations are simulated, and the two eigenprofiles summarizing the data are identified using SVD analysis. Third, the replication profile of the mutant strain is projected onto those eigenprofiles to deduce changes in replicon length. Finally, the mutant profile is normalized by the inferred replicon length, allowing detection of origin-specific effects.

The SVD approach is suited for comparing mutant phenotypes with the wild-type one, identifying differences between the profiles. It is less well suited for characterizing wild-type cells, primarily because the SVD projections are not intuitive and do not provide explicit information about the parameters controlling replication. Curve-fitting methods that attempt to more directly model the full replication profile are better suited for characterizing the wild-type profiles and were indeed applied to multiple systems ranging from a Xenopus embryo (Goldar et al. 2008; Yang and Bechhoefer 2008; Gauthier and Bechhoefer 2009), budding yeast (Brümmer et al. 2010; de Moura et al. 2010; Yang et al. 2010; Retkute et al. 2011), regions of human cells (Gindin et al. 2014), and others (Hyrien and Goldar 2010; Koutroumpas and Lygeros 2011; Retkute et al. 2012; Baker and Bechhoefer 2014). These methods are labor-intensive and require an expert user to set up. Further, they rely on many assumptions regarding, e.g., the explicit parametric forms of initiation rates, which are not available. While critical for understanding the wild-type phenotype, these parametric details are less important for defining mutant effects, justifying the use of a simplified approach which provides a faster, robust, and easy to compute way of analysis.

We applied our approach to a large compendium of replication profiles, including most viable budding yeast mutants implicated in replication progression. Many mutants were found to affect initiation capacity. An example is the CLB5 deletion, which showed the most significant reduction in initiation rate. Notably, reduced initiation capacity fully explained the previous reports of late-origin effects of this mutant (McCune et al. 2008). In retrospect, the abundance of initiation-limited mutants is expected: Origin initiation requires the assembly of the full replication machinery and therefore depends on multiple proteins. While it can still compensate for missing components, it is not surprising that compensation is not complete, leading to some reduced initiation capacity. In contrast, once the machinery was assembled and began replicating, its velocity should not be too sensitive to missing components, unless these components directly function to modulate fork velocity.

Two classes of models were proposed to explain the ordered replication program. In the first, different subsets of origins are assumed to be regulated by different protein factors whose activities change during S phase. In this model, an early origin that (by chance) didn't fire at early S phase is unlikely to fire at late S (Friedman et al. 1997). In the second, origins are assumed to fire stochastically at rates that differ between origins (Rhind 2006). An apparent temporal order is generated since origins that fire at high rates will be activated, on average, early, while origins that fire at low rates will be activated, on average, late. Our model is based on the purely stochastic formulation but is still capable of accounting not only for the wild-type replication profiles but also for the profiles of the vast majority of S phase mutants, including mutants that dramatically modulate their S phase duration. Regulated changes in origin efficiency during S phase are therefore not needed to account for observed phenotypes, supporting the stochastic model as the basis for the ordered replication program in Saccharomyces cerevisiae.

Methods

Strain used in the study: Tet strains were generated by replacing the promoters with a cassette (kan^R-TetO₇-TATA_CYC1) from plasmid RP188 in the strain R1158 (Mnaimneh et al. 2004). Overexpression of SIC1 was done by replacing the gene promoter with the Nat-Tef1 promoter using the plasmid pYM-N19. All other strains used in this study are listed in Supplemental Table S1.

Growth condition for measuring replication profiles using unsynchronized cells: The cells were grown in YPD overnight, diluted to OD₆₀₀ 0.1 in YPD, grown at 30°C, and harvested in 70% ethanol at optical density OD₆₀₀ = 0.5. Tet strains were grown in YPD overnight at 30°C diluted to OD₆₀₀ of 0.05 in fresh YPD medium with 10 µg/mL doxycycline, grown for 6 h, and harvested in 70% ethanol in logarithmic OD.

Growth condition for measuring replication profiles using synchronized cells: The cells were grown in YPD overnight at 30°C, and then inoculated to fresh medium to OD₆₀₀ of 0.03. Cells were harvested after having reached an OD₆₀₀ of 0.15–0.2. Cells were washed from the media in order to remove secreted Bar1. Cells were then resuspended in an equal volume fresh warm YPD with α-factor in a final concentration of 5 µg/mL, and incubated for 3 h at 30°C. Cells were washed twice with warm YPD to remove α-factor and resuspended in an equal volume of fresh YPD. Samples for RNA and DNA sequencing were taken every 3 min, centrifuged, the supernatant removed, and pellets were immediately frozen in liquid nitrogen. One milliliter of each sample was aliquotted for DNA staining by fixation in 70% ethanol.

Library preparation and sequencing

Synchronous cells/asynchronous nonsorted cells (MFA)

DNA was extracted by blending the cells in 300 µL lysis buffer (50 mM HEPES pH 7.5, 140 mM NaCl, 1mM EDTA, 1% TritonX-100, 0.1% sodium deoxycholate) with 0.5 mm zirconium oxide beads in a Bullet Blender 24 (Next Advance) for 1 min at level 8. Cleared lysate was sonicated for 20 min (0.5 sec on, 0.5 sec off) in a Bioruptor plus (Diagenode) cooled water bath sonicator, resulting in an average DNA fragment size of ∼200 bp. Lysates were RNase A-treated for 1 h at 37°C, and then Proteinase K treated for an additional 2 h at 37°C. Twenty microliters of the lysate were taken from each sample, and a multiplexed library was prepared for sequencing as previously described (Blecher-Gonen et al. 2013). Libraries were sequenced in an Illumina HiSeq 2500 with 50-bp paired-end sequencing.

Asynchronous sorted cells for DNA-seq

DNA was digested with DpnII and multiplexed as previously described (Blecher-Gonen et al. 2013). The resulting tagged library was sent to sequencing using an Illumina HiSeq 2500.

Asynchronous sorted cells for microarray

Logarithmic cultures were fixated with 70% ethanol, stained with SYBR Green, and sorted for G1 and S phase with the Beckton-Dickinson FACSAria sorter. DNA was extracted with the MasterPure Yeast DNA purification kit (Epicentre), digested with DpnII, and amplified by four rounds of random-octamer-primed Exo-Klenow DNA synthesis (Invitrogen BioPrime ArrayCGH amplification kit) with amino-allyl modified nucleotides. DNA was labeled with Cy dyes, hybridized to the Agilent yeast ChIP-on-chip 44×4 arrays, and scanned using an Agilent microarray scanner as described in Koren et al. (2010).

DNA staining and cell sorting

Standard procedures were applied; see Supplemental Material for details.

Processing and analysis of microarray data

The signal was calculated by dividing the S fraction channel in the G1 fraction channel. See Supplemental Material for details.

Processing and analysis of DNA sequencing—free cycling cells

The sequencing reads were aligned and counted into bins representing the genome positions. The signal was calculated as S fraction divided by G1 and then smoothed. See Supplemental Material for details.

Processing and analysis of DNA sequencing—synchronized cells

The sequencing reads were aligned and counted into bins representing the genome positions. Each time point was normalized to have an average value of its DNA content (values between 1 and 2). See Supplemental Material for details.

Estimation of initiation capacity and fork velocity

Initiation capacity was calculated comparing the difference in firing time between early and late origins. Lower initiation capacity increased the delay of late origins compared to the early ones. Velocity was calculated by the linear fit of the replication time around origins to their distance from the origin. See Supplemental Material for details.

Model: simulating DNA replication

Model formulation

This model is a based on previous work (Yang et al. 2010; Baker and Bechhoefer 2014). The model consists of the following parameters:

• I – initiation capacity (1/min).

• x_i – locus of origin i.

• n_i – relative efficiency of origin i (unitless).

• v – replication fork velocity (kb/min).

Note that, while previous works have considered initiation rate that increases in time (Goldar et al. 2009; Rhind et al. 2010), here, we consider origin activation as a homogeneous Poisson process. This simplifies the analysis but does not affect our results or, in particular, our ability to identify changes in replicon length (see below).

For each origin i, the probability of firing before time t is given by

$$f(t)=\{\begin{array}{cc}0\hfill & t<0\hfill \\ 1-e^{-tI{n}_i}\hfill & t\ge 0\hfill \end{array}$$ (1)

The firing time of the origin is therefore defined as

$$t_{1/2}=\frac{\log \left(2\right)}{I{n}_i}.$$

From Equation (1), we get our local measure of origin firing, which is linear with time:

$$g(\mathrm{\Delta }{x}_i,t)=\text{max}(t,0)\cdot I{n}_i.$$ (2)

In order to describe the replication fraction f(x, t) of locus x at time t min after the start of S phase, we use Equation (7) from Yang et al. (2010):

$$f(x,t)=1-\exp \left[-\sum _{i=0}^{N-1}g\left(\mathrm{\Delta }{x}_i,t-\frac{\left|x-x_i\right|}{v}\right)\right]$$

and we get

$$f(x,t)=1-\exp \left[-\sum _{i=0}^{N-1}max\left(t-\frac{\left|x-x_i\right|}{v},0\right)\cdot I{n}_i\right].$$ (3)

In an asynchronous experiment, we sample cells with a distribution of cells p(t),0 ≤ t ≤ t*. t* is the end-time of replication. So the replication fraction of locus x in an S-phase sorted sample is

$$f(x)={\int }_0^{t^{\ast }}f(x,t)p\left(t\right)\text{d}t.$$ (4)

We assume that p(t) is uniform, so p(t) = 1/t*.

$$\begin{array}{rl}f\left(x\right)& ={\int }_0^{t^{\ast }}f(x,t)\frac{1}{t^{\ast }}\mathrm{d}t\\ & =1-\frac{1}{T}{\int }_0^{t^{\ast }}\exp \left[-\sum _{i=0}^{N-1}max\left(t-\frac{\left|x-x_i\right|}{v},0\right)\cdot I{n}_i\right]\mathrm{d}t.\end{array}$$ (5)

To solve Equation (5), we need to set the parameter t*, namely the time at which all DNA was replicated. In the simulations, we stopped the simulation when the DNA was fully replicated at probability f(x) > 1 − ε for all positions x. We chose ε = 0.001. We verified that the results are independent on this ε value.

One important consequence of our model in the scenario of asynchronous cell population is that the replication profile depends on fork velocity v and initiation capacity I only through their ratio λ = v/I (the replicon length). To see that, define an effective, unitless variable u = It. Define also an effective (unitless) end-time to be u* = It*. Using these variables, we can write equation (5) as

$$f(x)=1-\frac{1}{u^{\ast }}{\int }_0^{u^{\ast }}\exp \left[-\sum _{i=0}^{N-1}max\left(u-\frac{\left|x-x_i\right|}{\lambda },0\right)n_i\right]\mathrm{d}u.$$ (6)

To show that this equation indeed depends only λ, we still need to show that u* is not defined by v or I separately but again depends only on their ratio λ. This is indeed the case; based on Equation (1), for each 0 < ε < 1, the time it will take an origin o* to fire with probability >1 − ε is −log(ε)/In* minutes. t* is given by t* = a/I + b/v, where a and b are some parameters that depend on the specifics of the system (e.g., origin positions x_i and efficiencies n_i) but not on the global parameters I or v. Therefore, the parameter u* is given by u* = a + b/λ. Together, the replication profiles depends only on λ.

We note that previous studies considered a distribution of end-times p(t*) (Yang and Bechhoefer 2008), while we consider a specific value t* (given our resolution ε) The reason for this difference is the biological properties of the systems investigated. Thus, this previous work considered origins which are not located in fixed positions. Therefore, the end-time depends primarily on the selection of origin position, leading to a Gumbel distribution of end-times. In contrast, in S. cerevisiae, the origin positions are fixed, and therefore, the major source of end-time distribution is not present.

The parameters used in the model were selected based on known properties of the replication. See Supplemental Material for details.

The significance value of the origins predicted by principal eigenprofiles was calculated based on the binomial distribution, where N, K, and p are the number of predicted origins, successfully predicted origins, and fraction of genome adjacent to known origins, respectively. See Supplemental Material for details.

The details of the list of known active origins in the Supplemental Material and the list itself is available in the Supplemental Material file: Supplemental_Code.rar.

Defining replicon length

Each mutant profile was assigned a replicon length by projecting the profile onto the two principal eigenprofiles obtained from our global simulations. See Matlab procedure: estimateLambda.m available in the Supplemental Material file: Supplemental_Code.rar. Details of the computation of the unexplained fraction are in the Supplemental Material.

Data access

The microarray data in this study have been submitted to the NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) under accession number GSE32002. The sequencing data in this study have been submitted to the NCBI Sequence Read Archive (SRA; https://www.ncbi.nlm.nih.gov/sra) under accession number SRP049026. The source codes used to process and analyze the data are available in the Supplemental Material: Supplemental_Code.rar file.