Abstract
We introduce a novel optimization-based motion planner, Stochastic Extended LQR (SELQR), which computes a trajectory and associated linear control policy with the objective of minimizing the expected value of a user-defined cost function. SELQR applies to robotic systems that have stochastic non-linear dynamics with motion uncertainty modeled by Gaussian distributions that can be state- and control-dependent. In each iteration, SELQR uses a combination of forward and backward value iteration to estimate the cost-to-come and the cost-to-go for each state along a trajectory. SELQR then locally optimizes each state along the trajectory at each iteration to minimize the expected total cost, which results in smoothed states that are used for dynamics linearization and cost function quadratization. SELQR progressively improves the approximation of the expected total cost, resulting in higher quality plans. For applications with imperfect sensing, we extend SELQR to plan in the robot's belief space. We show that our iterative approach achieves fast and reliable convergence to high-quality plans in multiple simulated scenarios involving a car-like robot, a quadrotor, and a medical steerable needle performing a liver biopsy procedure.
Keywords: motion planning under uncertainty, nonholonomic motion planning
I. Introduction
When a robot performs a task, the robot's motion may be affected by uncertainty from a variety of sources, including unpredictable external forces or actuation errors. Uncertainty arises in a variety of robotics applications, including aerial robots moving in turbulent conditions, mobile robots maneuvering on unfamiliar terrain, and robotic steerable needles being guided to clinical targets in soft tissue. A deliberative approach that accounts for uncertainty during motion planning before task execution can improve the quality of computed plans, increasing the chances that the robot will complete the desired motion in a manner that avoids obstacles and minimizes costs.
We introduce an optimization-based motion planner that explicitly considers the impacts of motion uncertainty. Recent years have seen the introduction of multiple successful optimization-based motion planners, although most have focused on robots with deterministic dynamics (e.g., [29], [18], [7]). Compared to commonly used sampling-based motion planners [9], optimization-based motion planners produce plans that are smoother (without requiring a separate smoothing algorithm) and that are computed faster, albeit sometimes with a loss of completeness and global optimality. Prior optimization-based motion planners that consider deterministic dynamics can only minimize deterministic cost functions (e.g., minimizing path length while avoiding obstacles). In this paper we focus on robots with stochastic dynamics, and consequently minimize the a priori expected value of a cost function when a plan and corresponding controller are executed. The user-defined cost function can be based on path length, control effort, and obstacle collision avoidance.
We first introduce the Stochastic Extended LQR (SELQR) motion planner, a novel optimization-based motion planner with fast and reliable convergence that explicitly considers robot motion uncertainty. The method is designed for motion planning problems involving robotic systems with non-linear (but linearizable) dynamics, any cost function with positive (semi)definite Hessians, and motion uncertainty that can be reasonably modeled using Gaussian distributions that can be state- and control-dependent. Our approach builds on the linear quadratic regulator (LQR), a commonly used linear controller that does not explicitly consider obstacle avoidance. As an optimization-based approach, SELQR starts motion planning from a start state and returns a high-quality trajectory and an associated linear control policy that consider uncertainty and are optimized with respect to the given cost function.
To achieve fast performance, our approach in each iteration uses both the stochastic forward and inverse dynamics in a manner inspired by an iterated Kalman smoother [2]. In each iteration's backward pass, SELQR uses the stochastic dynamics to compute a control policy and estimate the cost-to-go of each state, which is the minimum expected future cost assuming the robot starts from each state. In each iteration's forward pass, SELQR estimates the cost-to-come to each state, which is the minimum cost to reach each state from the initial state. SELQR then approximates the expected total cost at each state by summing the cost-to-come and the cost-to-go. SELQR progressively improves the approximation of the cost-to-come and cost-to-go and hence improves its estimate of the expected total cost. A key insight in SELQR is that we locally optimize each state along a trajectory at each iteration to minimize the expected total cost, which results in smoothed states that are cost-informative and used for dynamics linearization and cost function quadratization. These smoothed states enable the fast and reliable convergence of SELQR.
We next extend SELQR to consider uncertainty in both motion and sensing. Although the robot in such cases often cannot directly observe its current state, it can estimate a distribution over the set of possible states (i.e., its belief state) based on noisy and partial sensor measurements. We introduce B-SELQR, a variant of SELQR that plans in belief space rather than state space for robots with both motion and sensing uncertainty, where belief states are modeled with Gaussian distributions. For such robots, the motion planning problem can be modeled as a Partially Observable Markov Decision Process (POMDP). Exact global optimal solutions to POMDPs are prohibitive for most applications since the belief space (over which a control policy is to be computed) is, in the most general formulation, the infinite-dimensional space of all possible probability distributions over the finite dimensional state space. B-SELQR quickly computes a trajectory and locally-valid controller from scratch in belief space.
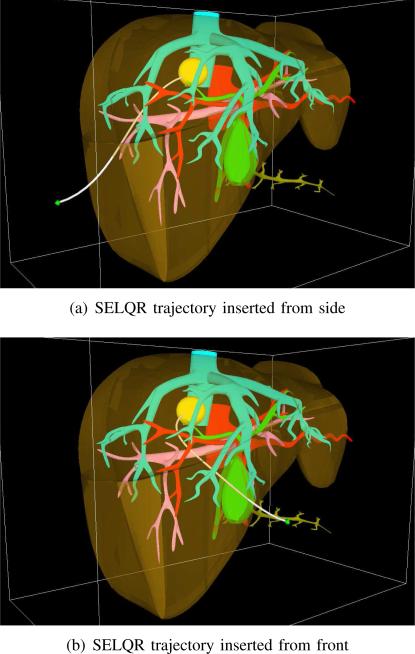
In this work, we provide a refined archival version of the results presented at a conference [19] and incorporate several important extensions. We added detail to the method derivation and expanded the experiments to include a non-Gaussian noise scenario, different Gaussian noise levels for B-SELQR, and a new beacons-based scenario for B-SELQR. We demonstrate the speed and effectiveness of SELQR in simulation for a car-like robot, quadrotor, and medical steerable needle (see Fig. 1). We also demonstrate B-SELQR for scenarios with imperfect sensing.
Fig. 1.
We show plans computed by SELQR for needle steering for a liver biopsy with motion uncertainty. The objective is to access the tumor (yellow) while avoiding the hepatic arteries (red), hepatic veins (blue), portal veins (pink), and bile ducts (green). The smooth trajectories explicitly consider uncertainty and minimize the a priori expected value of a cost function that considers obstacle avoidance and path length.
II. Related Work
Optimization-based motion planners have been studied for a variety of robotics applications and typically consider robot dynamics, trajectory smoothness, and obstacle avoidance. Optimization-based approaches have been developed that plan from scratch as well as that locally optimize a feasible plan created by another motion planner (such as a sampling-based motion planner), e.g. [29], [7], [18], [3], [5], [11]. These methods work well for robots with deterministic dynamics, whereas SELQR is intended for robots with stochastic dynamics.
Our approach builds on Extended LQR [23], [24], which extends the standard LQR to handle non-linear dynamics and non-quadratic cost functions. Extended LQR assumes deterministic dynamics, implicitly relying on the fact that the optimal LQR solution is independent of the variance of the motion uncertainty. In contrast to Extended LQR, SELQR explicitly considers stochastic dynamics and incorporates the stochastic dynamics into backward value iteration when computing a control policy, enabling computation of higher quality plans. Approximate Inference Control [22] formulates the optimal control problem using Kullback-Leibler divergence minimization but focuses on cost functions that are quadratic in the control input. Our approach also builds on Iterative Linear Quadratic Gaussian (iLQG) [21], which uses a quadratic approximation to handle state- and control-dependent motion uncertainty but, in its original form, did not implement obstacle avoidance. To ensure that the dynamics linearization and cost function quadratization are locally valid, iLQG requires special measures such as a line search. Our method does not require a line search, enabling faster performance.
For problems with partial or noisy sensing, the planning and control problem can be modeled as a POMDP [6]. Solving a POMDP to global optimality has been shown to be PSPACE complete. Point-based algorithms (e.g., [14], [8], [1]) have been developed for problems with discrete state, action, or observation spaces. Another class of methods [4], [16], [25], [13] utilize sampling-based planners to compute candidate trajectories or roadmaps in the state space in which paths can be evaluated based on metrics that consider stochastic dynamics. These approaches can be highly effective, although the methods [16], [4] require the existence of a two-point boundary value problem solver that can connect any two sampled configurations (which for nonholonomic robots may be computationally expensive), while the methods [25], [13] focused on cost functions corresponding to estimates of collision. Optimization-based approaches have been developed for planning in belief space [26], [15], [10], [12] by approximating beliefs as Gaussian distributions and computing a value function valid only in local regions of the belief space. Platt et al. [15] achieve fast performance by defining deterministic belief system dynamics based on the maximum likelihood observation assumption. Methods [10], [12] based on TrajOpt [17] effectively generate high quality plans, but they do not compute closed-loop policies, meaning they may require replanning at each time step during execution. Van den Berg et al. [26] require a feasible plan for initialization and then use iLQG to optimize the plan in belief space. We will show that B-SELQR, which considers stochastic dynamics, converges faster and more reliably than using iLQG in belief space, generates a local policy, and can plan from scratch.
III. Problem Definition
Let be the n-dimensional state space of the robot and let be the m-dimensional control input space of the robot. We consider robotic systems with differentiable stochastic dynamics and state- and control-dependent uncertainty modeled using Gaussian distributions. Let τ ∈ denote time, and let us be given a continuous-time stochastic dynamics:
| (1) |
with f : and , where and is a Wiener process with . We have .
We assume time is discretized into intervals of duration Δ, and the time step t ∈ starts at time τ = tΔ. As we will see in Sec. IV-E, by integrating the continuous time dynamics both backward and forward in time, we can construct the stochastic discrete dynamics and the deterministic inverse discrete dynamics:
| (2) |
| (3) |
where , with and as derived in Sec. IV-E. Note that gt is the deterministic part of the dynamics; for any x′, x, and u such that x′ = gt(x, u), we have gt(ḡt (x′, u), u) = x′ and ḡt(gt(x, u), u) = x.
Let the control objective be defined by a cost function that can incorporate metrics such as path length, control effort, and obstacle avoidance:
| (4) |
where is the given time horizon and cl : and are user-defined local cost functions. The expectation is taken because the dynamics are stochastic. We assume the local cost functions are twice differentiable and have positive (semi)definite Hessians: , , . The objective is to compute a control policy π (defined by πt : for all t ∈ [0, l)) such that selecting the controls ut = πt(xt) minimizes Eq. (4) subject to the stochastic discrete-time dynamics. This problem is addressed in Sec. IV.
For robotic systems with imperfect (e.g., partial and noisy) sensing, it is often beneficial during planning to explicitly consider the sensing uncertainty. We assume sensors provide data according to a stochastic observation model:
| (5) |
where zt is the sensor measurement at step t and the noise is state-dependent and drawn from a given Gaussian distribution. We formulate this motion planning problem as a POMDP by defining the belief state , which is the distribution of the state xt given all past controls and sensor measurements. We approximate belief states using Gaussian distributions. In belief space we define the cost function as
| (6) |
where the local cost functions are defined analogously to Eq. (4). The objective for this problem is to compute a control policy π (defined by πt : for all t ∈ [0, l)) in order to minimize Eq. (6) subject to the stochastic discrete-time dynamics. This problem is addressed in Sec. V.
IV. Stochastic Extended LQR
SELQR explicitly considers a system's stochastic nature in the planning phase and computes a nominal trajectory and an associated linear control policy that consider the impact of uncertainty. With the control policy from SELQR, the robot then executes the plan in a closed-loop fashion with sensor feedback. As in related methods such as iLQG [21], SELQR approximates the value functions quadratically by linearizing the dynamics and quadratizing the cost functions. But, as we will show, SELQR uses a novel approach to compute promising candidate trajectories around which to linearize the dynamics and quadratize the cost functions, enabling faster performance.
A. Method Overview
To consider non-linear dynamics and any cost function with positive (semi)definite Hessians, SELQR uses an iterative approach that linearizes the (stochastic) dynamics and locally quadratizes the cost functions in each iteration. As shown in Algorithm 1 and described below, each iteration includes both a forward pass and a backward pass, where each pass performs value iteration.
Algorithm 1.
SELQR
| Input: stochastic continuous-time dynamics (Eq. (1)); ct: local cost functions for 0 ≤ t ≤ l; Δ: time step duration; l: number of time steps | |
| Data: x̂: smoothed states; π: control policy; : inverse control policy; vt: cost-to-go function; v̄t: cost-to-come function | |
| 1 | πt = 0, St = 0, st = 0, st = 0 |
| 2 | repeat |
| 3 | S̄0 := 0, s̄0 := 0, s̄0 := 0 |
| 4 | for t := 0; t < l; t := t + 1 do |
| 5 | x̂t = –(St + S̄t)–1 (st + s̄t) (smoothed states) |
| 6 | ût = πt(x̂t), x̂t+1 = g(x̂t, ût) |
| 7 | Linearize inverse discrete dynamics around (x̂t+1, ût) (Eq. (16)) |
| 8 | Quadratize ct around (x̂t, ūt) (Eq. (12)) |
| 9 | Compute S̄t+1, s̄t+1, s̄t+1, v̄t+1, (forward value iteration in Sec. IV-C) |
| 10 | end |
| 11 | Quadratize cl around x̂l in the form of Eq. (12) to compute Ql, ql, and ql |
| 12 | Sl := Ql, sl := ql, and sl := ql. |
| 13 | for t := l – 1; t ≥ 0; t := t – 1 do |
| 14 | x̂t+1 = –(St+1 + S̄t+1)–1(st+1 + s̄t+1) (smoothed states) |
| 15 | , x̂t = ḡ(x̂t+1, ût) |
| 16 | Linearize stochastic discrete dynamics around (x̂t, ût) (Eq. (11)) |
| 17 | Quadratize ct around (x̂t, ût) (Eq. (12)) |
| 18 | Compute St, st, st, vt, πt (backward value iteration in Sec. IV-B) |
| 19 | end |
| 20 | until Converged (e.g., v0 stops changing significantly); |
| 21 | return πt for 0 ≤ t ≤ l |
As in LQR, SELQR uses backward value iteration to compute a control policy π and, for all t, the cost-to-go vt(x), which is the minimum expected future cost that will be accrued between time step t (including the cost at time step t) and time step l if the robot starts at x at time step t. The backward value iteration, as described in Sec. IV-B, considers stochastic dynamics. SELQR also uses forward value iteration to compute the cost-to-come , which computes the minimum past cost that was accrued from time step 0 to step t (excluding the cost at time step t) assuming the robot's dynamics is deterministic, as described in Sec. IV-C. The sum of vt(x) and provides an estimate of , the minimum expected total cost for the entire task execution given that the robot passes through state x at step t. Selecting x to minimize yields a sequence of smoothed states
| (7) |
At each iteration, SELQR linearizes the (stochastic) dynamics and quadratizes the cost function around the smoothed states. With each iteration, SELQR progressively improves the estimate of the cost-to-come and cost-to-go at each state along a plan, and hence improves its estimate of the minimum expected total cost. With this improved estimate comes a better control policy. The algorithm terminates when the estimated total cost converges. The output of the motion planner is the control policy πt for all t, where each πt is computed during the backward value iteration, which considers the stochastic dynamics. During execution, a robot at state x executes control ut = πt(x) at time step t.
SELQR accounts for non-linear dynamics and non-quadratic cost functions in a manner inspired in part by the iterated Kalman Smoother [2], which iteratively performs a forward pass (filtering) and a backward pass (smoothing) and at each iteration linearizes the non-linear system around the states from the smoothing pass. Likewise, SELQR consists of a backward pass (a backward value iteration) and a forward pass (a forward value iteration). The combination of these two passes at each iteration enables us to compute smoothed states around which we linearize the (stochastic) dynamics and quadratize the cost functions.
B. Backward Pass
We assume the cost-to-come functions , the inverse control policy , and the smoothed state are available from the previous forward pass. The backward pass computes cost-to-go functions vt(x) and control policy πt, using the approach of backward value iteration [20] in a backward recursive manner:
| (8) |
To make the backward value iteration tractable, SELQR linearizes the stochastic dynamics and quadratizes the local cost functions to maintain a quadratic form of the cost-to-go function . The backward pass starts from step l by quadratizing cl(x) around x̂l (line 11) as
| (9) |
and constructing quadratic vl(x) by setting Sl = Ql, sl = ql, and sl = ql. Starting from t = l – 1, vt+1(x) is available. To proceed to step t, SELQR first computes
| (10) |
Minimizing the quadratic with respect to x gives the smoothed states x̂t+1 (line 14). With the inverse control policy from the last forward pass, SELQR computes ût and x̂t (line 15), around which the stochastic discrete dynamics can be linearized as
| (11) |
where denotes the i'th column of matrix Mt, and At, Bt, , , at, and are given matrices and vectors of the appropriate dimension, and the cost function ct can be quadratized as
| (12) |
By substituting the linear stochastic dynamics and quadratic local cost function into Eq. 8, expanding the expectation, and then collecting terms, we get a quadratic expression of the value function vt(x),
| (13) |
where
following the similar derivation in [21]. The minimization on the right-hand side of Eq. (13) gives the linear control policy:
| (14) |
Filling u back into Eq. (13) gives vt(x) as a quadratic function of x with , , and (line 18).
C. Forward Pass
The forward pass recursively computes the cost-to-come functions and the inverse control policy using for ward value iteration [23]:
| (15) |
To make the forward value iteration tractable, we linearize the inverse dynamics and quadratize the local cost functions so that we can maintain a quadratic form of the cost-to-come function .
The forward pass starts from time step 0 (line 3) to construct the quadratic by setting S̄0 = 0, s̄0 = 0, and s̄0 = 0. At time step t, we assume and vt(x) are available. To proceed to step t + 1, SELQR first computes the smoothed state x̂t by minimizing the sum of vt(x) and (line 5) which are quadratic. (We note that in our implementation of matrix inversion for St + S̄t in line 5, we add a small positive regularization ηI, to zero matrices to avoid computing the inverse of a zero matrix and so x̂0 = 0 in the first iteration.) Since πt is available, SELQR then computes the ût and x̂t+1 as shown in line 7. Then, the deterministic inverse discrete dynamics is linearized around (x̂t+1, ût):
| (16) |
where Āt, B̄t, and āt are given matrices and vectors of the appropriate dimension, and the local cost function ct is quadratized around (x̂t, ût) to get the quadratic form as in Eq. (12).
Substituting the linearized inverse dynamics and quadratic local cost function into Eq. (15), expanding the expectation, and then collecting terms, we get a quadratic expression for ,
| (17) |
where
following the derivation in [23]. Take derivative of Eq. 17 with respect to u and equal to zero, the solution gives the inverse control policy for stage t:
| (18) |
Plugging ut into Eq. (17) gives as a quadratic function of x with , , and (line 9).
D. Iterative Forward and Backward Value Iteration
Without any a priori knowledge, SELQR initializes the cost-to-go functions and the control policy to 0's (line 1). As shown in Algorithm 1, SELQR starts with a forward pass and then iteratively performs backward passes and forward passes until convergence (e.g., v0 stops changing significantly). Similar to the iterated Kalman Smoother and to Extended LQR [23], SELQR performs Gauss-Newton like updates toward a local optimum.
Informed search methods often achieve speedups in practice by exploring from states that minimize a heuristic cost function. Analogously, in SELQR, the cost-to-go provides the minimum expected future cost, and the cost-to-come estimates the minimum expected cost that has been already accrued. The forward value iteration uses a deterministic inverse dynamics due to the intractability of computing a stochastic discrete inverse dynamics. Hence, the function estimates the minimum total cost assuming the robot passes through a given state x at time step t. Previous methods such as iLQG choose states for linearization and quadratization by blindly shooting the control policy from the last iteration without any information about the cost functions. These methods usually need measures such as line search to maintain stability. By computing smoothed states that are informed by cost for linearization and quadratization, we show, experimentally, that our method provides faster convergence.
E. Discrete-Time Dynamics Implementation
If f(x, u, τ) in Eq. (1) is linear in x and N is not dependent on x, then the distribution of the state at any time τ is given by x(τ) , where x̂(τ) and Σ(τ) are defined by the following system of differential equations:
For non-linear f and state- and control-dependent N, the equations provide first-order approximations. Instead of using an Euler integration [21], we use the Runge-Kutta method (RK4) to integrate the differential equations for x̂ and Σ forward in time simultaneously to compute gt and Mt in Eq. (2), and integrate the differential equation for x̂ to compute the ḡt in Eq. (3).
V. Stochastic Extended LQR in Belief Space
We introduce B-SELQR, a belief-state variant of SELQR for robotic systems with both motion and sensing uncertainty, where beliefs are modeled with Gaussian distributions. With an imperfect sensing model defined in the form of Eq. (5) and an objective function in the form of Eq. (6), the motion planning problem is a POMDP. B-SELQR needs a stochastic discrete forward belief dynamics and a deterministic discrete inverse belief dynamics. While the stochastic belief dynamics (Sec. V-A) can be modeled by an Extended Kalman Filter (EKF) [28] as shown in [26], the key challenge here is to develop the deterministic discrete inverse belief dynamics. We will show in Sec. V-B that the inverse belief dynamics can be derived by inverting the EKF.
A. Stochastic Discrete Belief Dynamics
Let us be given the belief of the robot's state at time step t as and a control input ut that the robot will execute at time step t. The EKF is used to model the stochastic forward belief dynamics [26] by
| (19) |
where
| (20) |
| (21) |
| (22) |
| (23) |
We refer readers to [26] for details of the derivation. Defining the belief bt = (x̂t, Σt), the stochastic belief dynamics is given by
| (24) |
where and Φ(bt, ut) stands for the deterministic part of Eq. 19. The dynamics is stochastic since the observation is treated as a random variable.
B. Deterministic Inverse Discrete Belief Dynamics
The deterministic inverse discrete belief dynamics takes belief bt+1 at time step t + 1 and control ut as input, and outputs belief bt.
Proposition V.1
(Deterministic Inverse Discrete Belief Dynamics) Given bt+1 = (x̂t+1, Σt+1) and the control input ut applied at time step t, there exists a belief bt = (x̂t, Σt) such that bt+1 = Φ(bt, ut) and bt is represented by
| (25) |
| (26) |
where
| (27) |
| (28) |
| (29) |
Proof
We show the proposition by substituting Eq. (25) and Eq. (26) into Φ(bt, u) (deterministic part of Eq. (19)) and proving the equality to bt+1.
First, substitute Eq. (25) into g(x̂t, ut), we get
| (30) |
which proves the correctness of Eq. (25).
Hence, substituting Eq. (25) to Eq. (27), we can see that Āt = At and M̄t = Mt(x̂t, ut). Substituting x̂t+1 = g(x̂t, ut) into Eq. (29), we can show that H̄t = Ht and V̄t = V(g(x̂t, ut)).
Secondly, substitute Eq. (26) back into Eq. (20), we can see that Γt+1 = . Substitute Γt+1 = into Eq. (22), we get:
| (31) |
| (32) |
Substitute Kt (Eq. (32)) and Γt+1 = into Eq. (19):
where the second equality follows from Sherman-Morrison-Woodbury Identity and the third equality follows from Eq. (28). Hence we prove the correctness of Eq. (26).
Eqs. (25) and (26) model the deterministic discrete inverse belief dynamics, which we write as . One can show that . With the stochastic discrete forward belief dynamics and deterministic inverse belief dynamics, together with cost objective Eq. (6) defined over belief space, we can directly apply SELQR to planning in belief space.
VI. Experiments
We demonstrate SELQR in simulation for a car-like robot, a quadrotor, and a medical steerable needle. Each robot must navigate in an environment with obstacles. We also apply B-SELQR to a car-like robot. We implemented the methods in C++ and ran scenarios on a PC with an Intel i3 2.4 GHz processor.
In our experiments, we used the local cost functions
| (33) |
where is the initial state, is the goal state, and Q0, Ql, and R are positive definite matrices. In our experiments, we use the first term in ct(x, u) to represent control effort where each control has independent cost, so assume R is a scaled identity matrix. We also set Q0 and Ql to scaled identity matrices, where the scaling parameter is large in order to fix the initial state and goal state for planning. We set function f(x) to enforce obstacle avoidance. For SELQR we used the same cost term as in [23],
| (34) |
where and di(x) is the signed distance between the robot at state x and the i'th obstacle. The parameter q controls the preferred clearance from the obstacles: lower values will result in more aggressive motion plans that allow the robot to move close to obstacles, while higher values encourage safer plans by heavily penalizing the robot being close to the obstacles. Since the Hessian of f(x) is not always positive semidefinite, we regularize the Hessian by computing its eigendecomposition and setting the negative eigenvalues to zeros [23]. We assume each obstacle is convex. For non-convex obstacles, we apply convex decomposition. For B-SELQR, to approximately consider the probability of collision we set , where di(b) is the minimum number of standard deviations of the mean of the robot's belief distribution needed to move to the obstacle's surface [26].
A. Car-like Robot in a 2-D Environment
We first apply SELQR to a non-holonomic car-like robot that navigates in a 2-D environment and can perfectly sense its state. The robot's state x = [x, y, θ, v] consists of its position (x, y), orientation θ, and speed v. The control inputs u = [a, ϕ] consist of acceleration a and steering wheel angle ϕ. The deterministic continuous dynamics is given by
| (35) |
where d is the length of the car-like robot. We assume the dynamics is corrupted by noise from a Wiener process (Eq. 1) and define . For the cost functions we set Q0 = Ql = 200I, R = 1.0I, and q = 0.2.
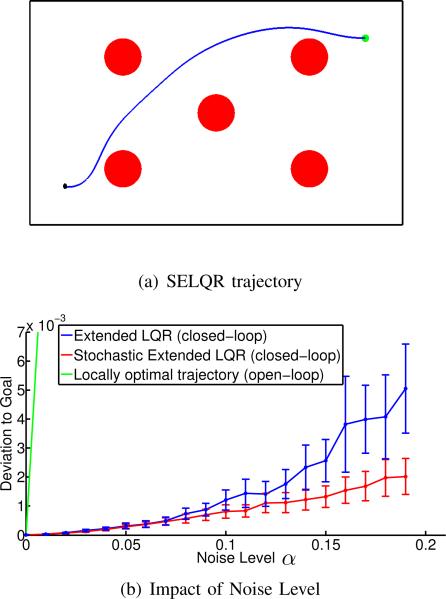
Fig. 2(a) shows the environment and the SELQR trajectory (illustrated by the path that results from following the control policy computed by SELQR in a simulation with zero noise). Consideration of stochastic dynamics is important for good performance. Fig. 2(b) shows the deviation from the goal for varying levels of noise α. We compare with Extended LQR, which uses deterministic dynamics to compute the control policy, and with simply executing the locally optimal trajectory, which is the open-loop execution of SELQR's nominal trajectory. We ran each method for 1,000 independent simulated runs. The locally optimal trajectory performs poorly since it is executed in an open-loop manner; the use of a closed-loop policy is needed for good performance in this scenario. The control policies from SELQR result in a smaller deviation from the goal since SELQR explicitly considers the control-dependent noise.
Fig. 2.
(a) The SELQR trajectory for a car-like robot moving to a green goal while avoiding red obstacles. (b) Mean and standard deviations for the deviation from the goal over 1,000 simulations for SELQR and related methods with different noise levels.
In Table I, we show SELQR's fast convergence for different values of Δ. The results are averages of 100 independent runs for random instances. In each instance, the initial state was chosen by uniformly sampling in the workspace, and the corresponding goal state was (where the origin is the center of the workspace). Compared to iLQG, our method achieved approximately equal costs but required substantially less computation time.
TABLE I.
Quantitative Comparison of SELQR and iLQG. Results averaged over 100 independent runs.
| Scenario | Δ (s) | SELQR | iLQG | ||||
|---|---|---|---|---|---|---|---|
| Average Cost | Average Time (s) | Average # Iterations | Average Cost | Average Time (s) | Average # Iterations | ||
| Car-like robot | 0.05 | 79.4 | 0.4 | 5.7 | 80.5 | 1.1 | 13.4 |
| 0.1 | 55.5 | 1.0 | 16.0 | 53.4 | 2.5 | 43.2 | |
| 0.2 | 50.8 | 1.2 | 18.4 | 51.7 | 2.0 | 35.4 | |
| Quadrotor | 0.025 | 552.1 | 30.3 | 7.7 | 798.0 | 52.7 | 23.4 |
| 0.05 | 272.7 | 50.1 | 14.4 | 292.1 | 113.7 | 51.6 | |
| 0.1 | 191.1 | 66.3 | 20.0 | 197.1 | 163.9 | 76.4 | |
| Steerable needle | 0.075 | 53.6 | 0.79 | 5.3 | 58.3 | 1.2 | 12.5 |
| 0.1 | 42.6 | 0.95 | 6.36 | 44.5 | 1.4 | 14.6 | |
| 0.125 | 39.1 | 1.3 | 10.1 | 40.0 | 1.5 | 15.6 | |
B. Quadrotor in a 3-D Environment
To show that SELQR scales to higher dimensions, we apply it to a simulated quadrotor with a 12-D state space. Its state consists of position p, velocity v, orientation r (angle-axis representation), and angular velocity w. Its control input u = [u1, u2, u3, u4] consists of the forces exerted by each of the four rotors. We directly adopt the continuous dynamics ẋ = f(x, u) with physical parameters of the quadrotor and the environment from [23]. The non-linear dynamics are given by
where ei are the standard basis vectors, g = 9.8 m/s2 is the acceleration due to gravity, kv = 0.15 is a constant relating the velocity to an opposite force related to rotor drag, m = 0.5 kg is the mass, J = 0.05I kg m2 is the moment of inertia matrix, ρ = 0.17 m is the distance between the center of mass and the center of the rotors, and km = 0.025 is a constant relating the force of a rotor to its torque. The notation [a] refers to the skew-symmetric cross product matrix of a. We add noise defined by , where .
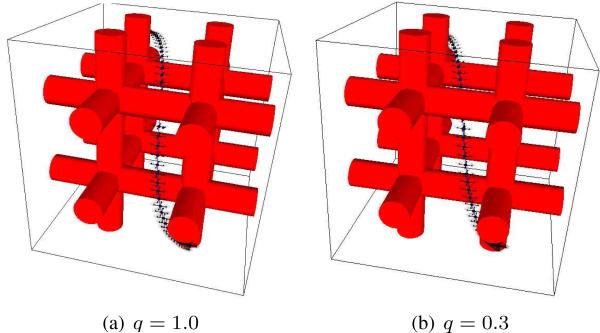
Fig. 3 shows the SELQR trajectory for two different values of q, where we set α = 2%, Q0 = Ql = 500I, and R = 20I. As expected, the trajectory with larger q has larger clearance from obstacles. In Table I, we show SELQR's fast convergence for the quadrotor scenario for different values of Δ. We conducted randomized runs in a manner analogous to Sec. VI-A. For the quadrotor, compared to iLQG, our method achieved slightly better costs while requiring substantially less computation time.
Fig. 3.
SELQR trajectories for a quadrotor in an 8 cylindirical obstacle environment.
C. Medical Needle Steering for Liver Biopsy
We also demonstrate SELQR for steering a flexible bevel-tip needle through liver tissue while avoiding critical vasculature modeled by a triangular surface mesh (Fig. 1). We use the stochastic needle model introduced in [27], where the kinematics are defined in SE(3). We represent the state x by the tip's position p and orientation r (angle-axis). The control input is u = [v, w, κ]T, where v is the insertion speed, w is the axial rotation speed, and κ is the curvature, which can vary from 0 to a maximum curvature of κ0 using duty-cycling. For the cost function, we set u* = [0, 0, 0.5κ0]T . Hence, we penalize large insertion speed, which given l and Δ corresponds to penalizing path length. It also penalizes curvatures that are too large (close to the kinematic limits of the device) or too small (requiring high-rate duty cycling, which may cause tissue damage). For motion noise, we set Mt from Eq. 2 to σ∥ut∥2I, where is a positive constant that controls the size of the noise. The noise is proportional to the norm of control input.
Fig. 1 shows the SELQR trajectories for two insertion locations with Δ = 0.1s, l = 30, Q0 = Ql = 100I, R = I, q = 0.5, σ = 0.01. Table I shows SELQR's fast convergence for the steerable needle for varying Δ. The results are averages of 100 independent runs for random instances. In each instance, the goal state was held constant, and we set the initial state such that the needle was inserted into the tissue from a uniformly-sampled point on the left (corresponding to the skin surface). Compared to iLQG, our method achieved approximately equal costs but required substantially less computation time.
Although SELQR is designed to compute policies for robotic systems with Gaussian noise, the policies may in some cases in practice also be effective for robotic systems with non-Gaussian noise. For the needle steering scenario, we evaluated the computed policy in simulation under two different types of noise: (1) Gaussian noise sampled from the Gaussian distribution that was used for computing the policy, and (2) uniform noise sampled from a 6D super-ball with radius σ∥u∥2. Namely, we set the radius of the ball equal to the standard deviation of the Gaussian distribution and evaluated the probability of success of the policy (i.e., the motion does not collide with obstacles). We conducted 1000 independent simulated runs for both types of noise. For α = 0.005, the probability of success was 99.8% for the Gaussian distribution and 99.5% for the uniform distribution. For α = 0.007, the probability of success was 97.4% for the Gaussian distribution and 97.0% for the uniform distribution. For α = 0.01, we achieved 93.1% for Gaussian distribution and 92.5% for uniform distribution. The results show that the computed locally optimal policy can, in some cases, handle motion noise from non-Gaussian distributions.
D. Belief Space Planning for a Car-like Robot
We apply B-SELQR to the car-like robot in Sec. VI-A but now with added uncertainty in sensing. We consider two environments, discussed below, in which the robot localizes itself using noisy measurements from sensors in the environment. The reliability of the measurement varies as a function of the robot's position.
For belief space planning we use the cost functions
We set Q0 = 1000I, R = 2I, Qt = 10I, Ql = 500I, and q = 0.1.
1) Light-dark Environment
We first consider the light-dark scenario suggested in [15]. The robot receives reliable measurements in the bright region and noisier measurements in the darker regions. Formally, the observation model is
| (36) |
where is a given constant.
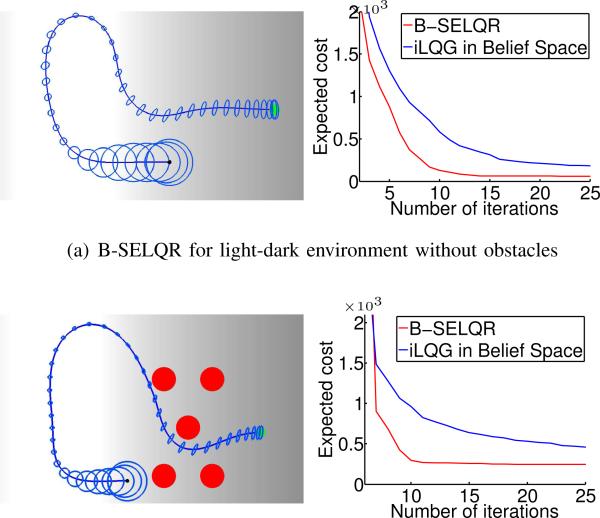
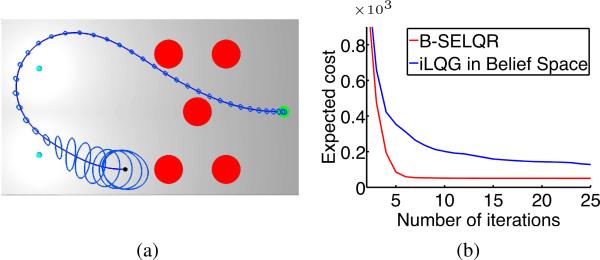
Fig. 4 shows the B-SELQR trajectory (illustrated by the path that results from following the control policy computed by B-SELQR in a simulation with zero noise) and associated beliefs along the trajectory for a scenario with and without obstacles with β = 0.01. The computed control policies steer the robot to the light region where the measurement noise is smallest in order to better localize the robot before proceeding to the goal. We also show the convergence of B-SELQR. We compare with iLQG executed for the same cost functions in belief space using the method in [26]. The statistics were computed by averaging the results of 100 random instances. (For each random instance, we randomly sampled the initial state .) On average, B-SELQR requires fewer iterations to reach a desired solution quality.
Fig. 4.
(a) B-SELQR trajectory for a car-like robot navigating to a goal (green) in a 2-D light-dark environment (adapted from [15]). (b) B-SELQR trajectory for the environment with obstacles (red circles). The blue ellipsoids show 3 standard deviations of the belief distributions. B-SELQR converges faster than iLQG in belief space in both scenarios.
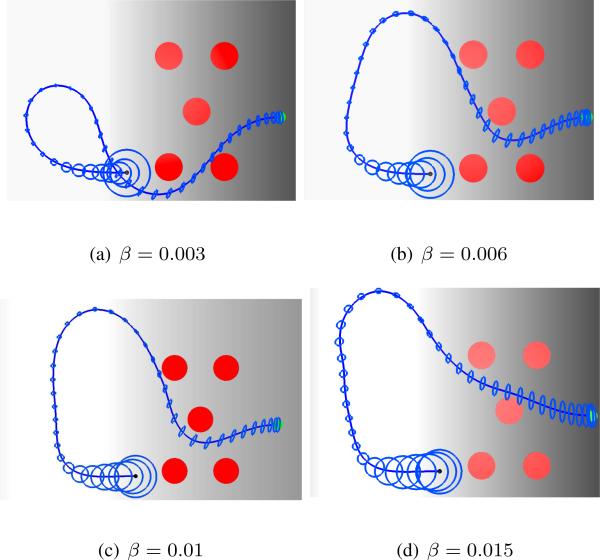
We also tested B-SELQR under different sensing noise levels. Fig. 5 shows the computed trajectories under four different βs. When the noise is small (Fig. 5 (a) and (b)), the robot travels less distance in the light domain since it can localize itself more quickly. On the other hand, when the noise is larger, the robot usually needs to travel more distance in the light domain to better localize itself. For large sensing noise as shown in Fig. 5 (d), the uncertainty increase quickly again after the robot leaves the light domain and causes the possibility of collision.
Fig. 5.
B-SELQR trajectories under different sensing noise levels
2) Environment with Beacons
We also consider a scenario where the car-like robot estimates its location using measurements from two beacons, b1 and b2, placed in the environment at positions (xb1, yb2) and (xb2, yb2). The strength of the signal decays quadratically with the distance to the beacon. The robot also measures its current speed and orientation angle. The measurement uncertainty is scaled by a constant matrix N. This gives us the non-linear observation model
| (37) |
where and . Fig. 6 (left) shows the quadratic decay in the signal strength of the beacons in the environment, where white indicates a strong signal and dark gray indicates a weak signal.
Fig. 6.
B-SELQR trajectories for a car-like robot navigating to a goal (green) in an environment where two beacons are used for localization (adapted from [26]) while avoiding obstacles (red). (b) Comparison between B-SELQR and iLQG in belief space in terms of the number of iterations for convergence.
Fig. 6 shows the B-SELQR trajectory and associated beliefs along the trajectory. The computed control policies steer the robot to move in the vicinity of the two beacons in order to better localize the robot before proceeding to the goal. We also show the convergence of B-SELQR in Fig. 6. We compare with iLQG in belief space executed for the same cost functions in belief space using 100 random instances. Again, on average, B-SELQR requires fewer iterations to reach a desired solution quality.
VII. Conclusion
We presented Stochastic Extended LQR (SELQR), a novel optimization-based motion planner that computes a trajectory and associated linear control policy with the objective of minimizing the expected value of a user-defined cost function. SELQR applies to robotic systems that have stochastic non-linear dynamics and state- and control-dependent motion uncertainty. We also extended SELQR to applications with imperfect sensing, requiring motion planning in belief space. Our approach converges faster and more reliably than related methods in both the robot's state space and belief space for multiple simulated scenarios, ranging from a mobile robot to a steerable needle.
In future work, we hope to broaden the applicability of the approach. The approach currently assumes motion and sensing uncertainty are modeled using Gaussian distributions. While this assumption is often appropriate, it is not valid for some problems. Our approach also relies on first and second order information, so to improve stability we plan to investigate the use of automatic differentiation. We also plan to incorporate a line search into SELQR to facilitate formal analysis of the method's convergence properties. We also plan to apply the methods to physical robots like steerable needles in order to efficiently account for motion and sensing uncertainty.
Note to Practitioners.
The motion of a robot cannot be predicted with certainty in a variety of robotics applications, including aerial robots moving in turbulent conditions, mobile robots maneuvering on unfamiliar terrain, and robotic steerable needles being guided to clinical targets in soft tissue. Explicitly considering uncertainty during motion planning before task execution can improve the quality of computed plans. We introduce a novel optimization-based motion planner, Stochastic Extended LQR (SELQR), which computes a trajectory and associated linear control policy with the objective of minimizing the expected value of a user-defined cost function. For applications that include both motion uncertainty and imperfect sensing, we extend SELQR to plan in the space of the robot's beliefs, i.e., distributions over the set of possible states. We demonstrate the speed and effectiveness of SELQR in simulation for a variety of robotics applications.
Acknowledgments
This research was supported in part by the National Science Foundation under awards IIS-1117127 and IIS-1149965 and by the National Institutes of Health under award R21EB017952.
Biography
 Wen Sun received his B.Tech degree in Computer Science and Technology from Zhejiang University, China, in 2012, a B.S. degree with Distinction in the School of Computing Science from Simon Fraser University, Canada, in 2012 and an M.S. degree in Computer Science from the University of North Carolina at Chapel Hill, USA, in 2014. He is currently a Ph.D. student in the Robotics Institute, School of Computer Science, Carnegie Mellon University, USA. His research interests include machine learning and motion planning.
Wen Sun received his B.Tech degree in Computer Science and Technology from Zhejiang University, China, in 2012, a B.S. degree with Distinction in the School of Computing Science from Simon Fraser University, Canada, in 2012 and an M.S. degree in Computer Science from the University of North Carolina at Chapel Hill, USA, in 2014. He is currently a Ph.D. student in the Robotics Institute, School of Computer Science, Carnegie Mellon University, USA. His research interests include machine learning and motion planning.
 Jur van den Berg received the Ph.D. degree in computer science from Utrecht University, the Netherlands in 2007. After that, he was a postdoctoral research associate with the University of North Carolina at Chapel Hill and the University of California, Berkeley. Since 2011, he is assistant professor at the University of Utah where he heads the Algorithmic Robotics Laboratory. His research interests are in developing new algorithms with strong theoretical foundations for relevant practical applications in mobile robotics, medical robotics, artificial intelligence, crowd simulation, virtual environments and computer games, autonomous transportation, and personal robotics, with a particular focus on motion planning under uncertainty, reciprocal collision avoidance, and information-theoretic decision making for autonomous virtual and real-world agents. In 2014 he joined Google[x] to work on the self-driving car.
Jur van den Berg received the Ph.D. degree in computer science from Utrecht University, the Netherlands in 2007. After that, he was a postdoctoral research associate with the University of North Carolina at Chapel Hill and the University of California, Berkeley. Since 2011, he is assistant professor at the University of Utah where he heads the Algorithmic Robotics Laboratory. His research interests are in developing new algorithms with strong theoretical foundations for relevant practical applications in mobile robotics, medical robotics, artificial intelligence, crowd simulation, virtual environments and computer games, autonomous transportation, and personal robotics, with a particular focus on motion planning under uncertainty, reciprocal collision avoidance, and information-theoretic decision making for autonomous virtual and real-world agents. In 2014 he joined Google[x] to work on the self-driving car.
 Ron Alterovitz received his B.S. degree with Honors from Caltech, Pasadena, CA in 2001 and the Ph.D. degree in Industrial Engineering and Operations Research at the University of California, Berkeley, CA in 2006.
Ron Alterovitz received his B.S. degree with Honors from Caltech, Pasadena, CA in 2001 and the Ph.D. degree in Industrial Engineering and Operations Research at the University of California, Berkeley, CA in 2006.
In 2009, he joined the faculty of the Department of Computer Science at the University of North Carolina at Chapel Hill, NC, where he leads the Computational Robotics Research Group. His research focuses on motion planning for medical and assistive robots. Prof. Alterovitz has co-authored a book on Motion Planning in Medicine, was awarded a patent for a medical device, has received multiple best paper finalist awards at IEEE robotics conferences, and is the recipient of the National Institutes of Health Ruth L. Kirschstein National Research Service Award and the National Science Foundation CAREER Award.
Contributor Information
Wen Sun, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA 15213 USA..
Jur van den Berg, School of Computing, University of Utah, Salt Lake City, UT 84112 USA..
Ron Alterovitz, Department of Computer Science, University of North Carolina at Chapel Hill, Chapel Hill, NC 24799 USA (ron@cs.unc.edu)..
References
- 1.Bai H, Hsu D, Lee WS. Integrated perception and planning in the continuous space: A POMDP approach. Robotics: Science and Systems (RSS) 2013 Jun; [Google Scholar]
- 2.Bell BM. The iterated Kalman smoother as a Gauss-Newton method. SIAM J. Optimization. 1994;4(3):626–636. [Google Scholar]
- 3.Brock O, Khatib O. Elastic strips: A framework for motion generation in human environments. Int. J. Robotics Research. 2002 Dec;21(2):1031–1052. [Google Scholar]
- 4.Bry A, Roy N. Rapidly-exploring random belief trees for motion planning under uncertainty. Proc. IEEE Int. Conf. Robotics and Automation (ICRA) 2011 May;:723–730. [Google Scholar]
- 5.Hauser K, Ng-Thow-Hing V. Fast smoothing of manipulator trajectories using optimal bounded-acceleration shortcuts. Proc. IEEE Int. Conf. Robotics and Automation (ICRA) 2010 May;:2493–2498. [Google Scholar]
- 6.Kaelbling LP, Littman ML, Cassandra AR. Planning and acting in partially observable stochastic domains. Artificial Intelligence. 1998;101(1-2):99–134. [Google Scholar]
- 7.Kalakrishnan M, Chitta S, Theodorou E, Pastor P, Schaal S. STOMP: Stochastic trajectory optimization for motion planning. Proc. IEEE Int. Conf. Robotics and Automation (ICRA) 2011 May;:4569–4574. [Google Scholar]
- 8.Kurniawati H, Hsu D, Lee W. SARSOP: Efficient point-based POMDP planning by approximating optimally reachable belief spaces. Robotics: Science and Systems (RSS) 2008 Jun; [Google Scholar]
- 9.LaValle SM. Planning Algorithms. Cambridge University Press; Cambridge, U.K.: 2006. [Google Scholar]
- 10.Lee A, Duan Y, Patil S, Schulman J, McCarthy Z, van den Berg J, Goldberg K, Abbeel P. Sigma hulls for Gaussian belief space planning for imprecise articulated robots amid obstacles. Proc. IEEE/RSJ Int. Conf. Intelligent Robots and Systems (IROS) 2013 Nov;:5660–5667. [Google Scholar]
- 11.Pan J, Zhang L, Manocha D. Collision-free and smooth trajectory computation in cluttered environments. Int. J. Robotics Research. 2012 Sep;31(10):1155–1175. [Google Scholar]
- 12.Patil S, Kahn G, Laskey M, Schulman J, Goldberg K, Abbeel P. Scaling up Gaussian belief space planning through covariance-free trajectory optimization and automatic differentiation. Proc. Workshop on the Algorithmic Foundations of Robotics (WAFR) 2014 Aug; [Google Scholar]
- 13.Patil S, van den Berg J, Alterovitz R. Estimating probability of collision for safe motion planning under Gaussian motion and sensing uncertainty. Proc. IEEE Int. Conf. Robotics and Automation (ICRA) 2012 May;:3238–3244. [Google Scholar]
- 14.Pineau J, Gordon G, Thrun S. Point-based value iteration: An anytime algorithm for POMDPs. Int. Joint Conf. Artificial Intelligence (IJCAI) 2003:1025–1032. [Google Scholar]
- 15.Platt R, Jr., Tedrake R, Kaelbling L, Lozano-Perez T. Belief space planning assuming maximum likelihood observations. Robotics: Science and Systems (RSS) 2010 Jun; [Google Scholar]
- 16.Prentice S, Roy N. The belief roadmap: Efficient planning in belief space by factoring the covariance. Int. J. Robotics Research. 2009 Nov;28(11):1448–1465. [Google Scholar]
- 17.Schulman J, Duan Y, Ho J, Lee A, Awwal I, Bradlow H, Pan J, Patil S, Goldberg K, Abbeel P. Motion planning with sequential convex optimization and convex collision checking. International Journal of Robotics Research. 2014 Aug;33(9):1251–1270. [Google Scholar]
- 18.Schulman J, Ho J, Lee A, Awwal I, Bradlow H, Abbeel P. Finding locally optimal, collision-free trajectories with sequential convex optimization. Robotics: Science and Systems (RSS) 2013 Jun; [Google Scholar]
- 19.Sun W, van den Berg J, Alterovitz R. Stochastic Extended LQR: Optimization-based motion planning under uncertainty. Proc. Workshop on the Algorithmic Foundations of Robotics (WAFR) 2014 Aug; doi: 10.1109/TASE.2016.2517124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Thrun S, Burgard W, Fox D. Probabilistic Robotics. MIT Press. 2005 [Google Scholar]
- 21.Todorov E. A generalized iterative LQG method for locally-optimal feedback control of constrained nonlinear stochastic systems. Proc. American Control Conference. 2005 Jun;:300–306. [Google Scholar]
- 22.Toussaint M. Robot trajectory optimization using approximate inference. Proc. Int. Conf. Machine Learning (ICML) 2009:1049–1056. [Google Scholar]
- 23.van den Berg J. Extended LQR: Locally-optimal feedback control for systems with non-linear dynamics and non-quadratic cost. Int. Symp. Robotics Research (ISRR) 2013 Dec; [Google Scholar]
- 24.van den Berg J. Iterated LQR smoothing for locally-optimal feedback control of systems with non-linear dynamics and non-quadratic cost. Proc. American Control Conference. 2014 Jun;:1912–1918. [Google Scholar]
- 25.van den Berg J, Abbeel P, Goldberg K. LQG-MP: Optimized path planning for robots with motion uncertainty and imperfect state information. Int. J. Robotics Research. 2011 Jun;30(7):895–913. [Google Scholar]
- 26.van den Berg J, Patil S, Alterovitz R. Motion planning under uncertainty using iterative local optimization in belief space. Int. J. Robotics Research. 2012 Sep;31(11):1263–1278. [Google Scholar]
- 27.van den Berg J, Patil S, Alterovitz R, Abbeel P, Goldberg K. LQG-based planning, sensing, and control of steerable needles. In: Hsu D, Others, editor. Algorithmic Foundations of Robotics IX (Proc. WAFR 2010), ser. Springer Tracts in Advanced Robotics (STAR) Vol. 68. Springer; Dec, 2010. pp. 373–389. [Google Scholar]
- 28.Welch G, Bishop G. An introduction to the Kalman filter. University of North Carolina at Chapel Hill, Technical Report TR 95-041. 2006 Jul; [Google Scholar]
- 29.Zucker M, Ratliff N, Dragan AD, Pivtoraiko M, Matthew K, Dellin CM, Bagnell JA, Srinivasa SS. CHOMP: Covariant Hamiltonian optimization for motion planning. Int. J. Robotics Research. 2012 Aug;32(9):1164–1193. [Google Scholar]