Abstract
Ceramide (CER)-based biological membranes are used both experimentally and in simulations as simplified model systems of the skin barrier. Molecular dynamics studies have generally focused on simulating preassembled structures using atomistically detailed models of CERs, which limit the system sizes and timescales that can practically be probed, rendering them ineffective for studying particular phenomena, including self-assembly into bilayer and lamellar superstructures. Here, we report on the development of a coarse-grained (CG) model for CER NS, the most abundant CER in human stratum corneum. Multistate iterative Boltzmann inversion is used to derive the intermolecular pair potentials, resulting in a force field that is applicable over a range of state points and suitable for studying ceramide self-assembly. The chosen CG mapping, which includes explicit interaction sites for hydroxyl groups, captures the directional nature of hydrogen bonding and allows for accurate predictions of several key structural properties of CER NS bilayers. Simulated wetting experiments allow the hydrophobicity of CG beads to be accurately tuned to match atomistic wetting behavior, which affects the whole system since inaccurate hydrophobic character is found to unphysically alter the lipid packing in hydrated lamellar states. We find that CER NS can self-assemble into multilamellar structures, enabling the study of lipid systems more representative of the multilamellar lipid structures present in the skin barrier. The coarse-grained force field derived herein represents an important step in using molecular dynamics to study the human skin barrier, which gives a resolution not available through experiment alone.
I. Introduction
The stratum corneum (SC) is the outermost layer of the skin, and serves as the barrier between the internal and external environments of the body, preventing, among other things, rapid dehydration and pathogen invasion.1 In addition to cholesterol and free fatty acids (FFAs), several different ceramides (CERs) comprise the lipid matrix of the SC.2 To date, 14 subclasses of CER have been identified in human skin that differ in headgroup and acyl tail structure.3 Of these, non-alpha-hydroxy-sphingosine ceramide (CER NS, Figure 1a) is the most abundant in healthy human skin.4
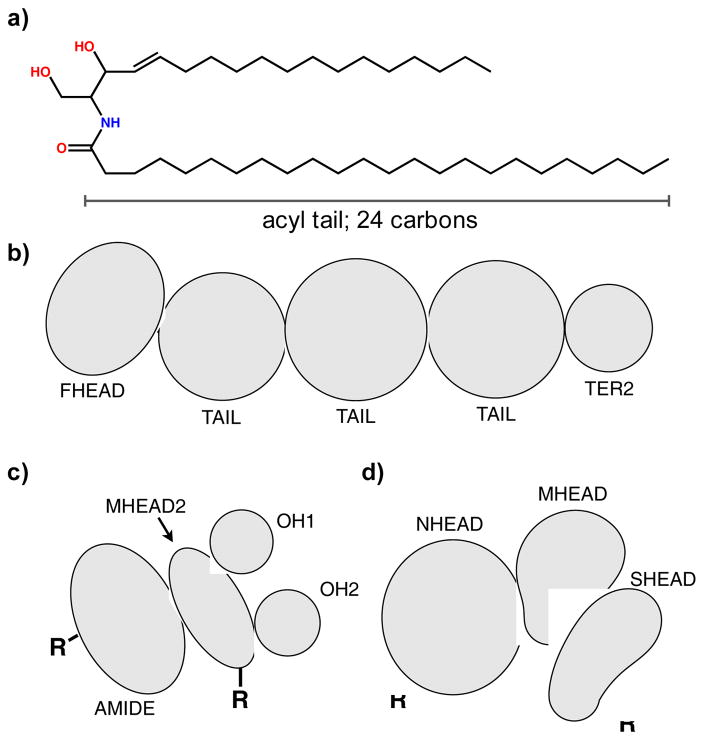
Figure 1.
CER NS structure and CG mappings used in this work. a) Molecular structure of CER NS C24, where C24 gives the length of the CER acyl chain; b) FFA mapping showing head (FHEAD), 3:1 tail beads (TAIL) and 2:1 terminal bead (TER2) as applied to C12:0; c) 4-site CER headgroup mapping proposed in this work; d) 3-site CER headgroup mapping. All beads interact through spherically symmetric potentials, even if drawn as irregular shapes. Note that beads are not drawn to scale, but rather to emphasize the mapping and connectivity.
Despite knowledge of the lipid composition in human SC, the connection between lipid composition, structure, and barrier function remains unclear.5,6 Understanding these connections is essential for developing effective models of skin for use in toxicology assessment and transdermal drug delivery development, as well as for developing effective treatments for skin diseases.6,7 Molecular simulation studies of SC lipid systems could allow the connections between lipid composition, structure, and barrier function to be probed, as simulation enables direct visualization of and explicit control over the molecular species in the system. For example, molecular simulations have been used extensively to better understand the structure, phase behavior, thermodynamics, and transmembrane permeability of phospholipid-based bilayer systems.8–13 However, CER-based bilayers have not been as widely studied as phospholipid-based systems, primarily because of the more complex nature of the lipid organization14–16 and a lack of accurate atomistic force fields, which was recently addressed.17 The limited atomistic (i.e., all-atom and united-atom) simulations that have been performed of CER bilayer structures have provided some insight into the lipid interactions,17–21 e.g., demonstrating strong connections between the phase transition temperature, CER headgroup structure, and lipid-lipid hydrogen bonding.17 However, the dense gel and crystalline packings found in CER-rich phases22–26 significantly reduce lipid mobility as compared to the liquid-crystalline phases typical of biological phospholipid-based bilayers at physiological conditions, resulting in the need for careful equilibration protocols and long equilibration times.19,27,28 As such, the time and length scales on which certain phenomena occur (e.g., phase separation, self-assembly) are limiting for all-atom models. Furthermore, bilayer structures consisting of a small number of components are highly simplified models of SC lipid lamellae; to study mixtures relevant to the multicomponent SC that form multilamellar structures, large system sizes must be employed, further increasing the computational cost.
Coarse-grained (CG) molecular models, where groups of atoms are treated as single interaction sites (CG beads), provide an attractive alternative to atomistic models. CG models typically require several orders of magnitude less computational cost to access the same timescale as the corresponding atomistic model, due to the simplified representation of the system. This simplification results in fewer pair interactions, allows implicit treatment of long-ranged electrostatics, and generally softens the energy landscape, allowing a larger timestep of integration. Combined, these properties allow CG models to access the long timescales needed to form equilibrium phases via self-assembly and probe the large system sizes needed to represent the SC lipid mixture. CG models have proven effective for the study of various lipid systems,29–31 including studies that examine the self-assembly of other lipids important to the skin barrier.32 Recently, Sovova et al.33 proposed a CG model of CER NS, which has been the most studied CER via all-atom molecular simulation.17–20,34 We note that this model predicts stable lamellar structures as expected of CER conformations in the SC,33 and is advantageous in that it is compatible with the popular MARTINI force field; however, since it was not derived to match CER structure, the model fails to accurately capture key structural properties of pure CER NS bilayers, overestimating the area per lipid by ~20% and substantially underestimating the tilt angle as compared to experimental and all-atom simulation results (i.e., no tilt is observed with this model).17,20,33 Furthermore, the CG mapping used in this model (i.e., how the atoms are grouped into CG beads), lacks directional headgroup interactions that have been shown to influence the properties of CER systems,17,35,36 overall making the CG model more representative of a generic lipid rather than CER NS, and thus of limited utility for accurately probing the behavior of systems representative of the SC.
In this paper, a CG mapping and force field for CER NS are derived to match structural properties calculated from all-atom simulations. The CER NS model proposed herein provides a more explicit treatment of hydroxyl groups than in the MARTINI-compatible CG CER model of Sovova et al.,33 allowing the model to capture directional headgroup interactions that exist between lipids due to hydrogen bonding.17,37–39 As CERs and FFAs contain identical tails (i.e., long alkyl chains), a CG FFA model is developed in parallel, using the same tail beads for CER and FFA. The recently developed multistate iterative Boltzmann inversion (MS IBI)40 scheme is used to optimize these CG force fields. While potentials derived with the original IBI scheme generally reproduce target RDFs with a high degree of accuracy, they often show limited transferability to other states,41,42 due to the single state nature of the scheme. They may also demonstrate significant artifacts associated with structural correlations between beads (e.g., potential wells and barriers associated with RDF peaks and valleys), and hence can be unrepresentative of the underlying potential landscape.40 The MS IBI algorithm was developed to address these issues; specifically, the multistate nature of the method provides additional constraints to the optimization, reducing structural artifacts, and yields potentials that are more generally applicable than those derived from the original (i.e., single state) IBI method,40,43 as is required for simulations that span multiple state points, such as simulations of lipid self-assembly. The structural properties and self-assembly of CER systems are studied using the derived CG model and compared to all-atom and experimental measurements, demonstrating close agreement and providing validation of the model.
The remainder of the paper is organized as follows: first we provide a description of the CG model and pair potential optimizations before discussing the results obtained for the derived potentials and the validations performed on states not used in the optimization process. We then examine the properties of preassembled CER bilayers and study the self-assembly behavior of both single bilayer (unilamellar) and stacked bilayer (multilamellar) structures. Finally, conclusions and future work is discussed.
II. Models and Methods
Deriving CG potentials via MS IBI involves several general steps. First, all-atom simulations are performed at various state points that are chosen to emphasize the different behaviors the CG model should reproduce. For example, for CERs, isotropic fluid and ordered lamellar states are included, which are both relevant for self-assembly. The all-atom trajectories are then used to create corresponding CG trajectories by mapping the all-atom trajectories to the CG level using a CG mapping operator that defines how the atoms are grouped into CG beads. Next, the CG trajectories mapped from the all-atom simulations are used to generate target data in the form of pair radial distribution functions (RDFs) for each pair type at each state. The MS IBI algorithm is then employed to iteratively derive the CG force field, such that the RDFs from the CG simulations match the target RDFs mapped from the all-atom simulations. As a last step, individual pair interactions in the force fields are refined to reproduce the correct balance between hydrophobic and hydrophilic interactions via simulated wetting experiments. The methodologies used in each of these steps are discussed in detail below.
Atomistic Simulations
All-atom simulations were performed with the fully atomistic CHARMM36 force field,44 employing the TIP3P water model45 and CHARMM-compatible headgroup parameters for CERs, which were derived and validated in previous work.17 All atomistic simulations were performed using the LAMMPS simulation engine,46,47 with a van der Waals interaction cutoff of 12 Å; the PPPM solver with a real space cutoff of 12 Å was used for the calculation of the long-ranged electrostatic interactions.48 A timestep of 1.0 fs was used with the Nose-Hoover thermostat in the canonical ensemble (i.e., NVT, constant number of molecules, volume, and temperature) and an additional barostat for simulations in the isothermal isobaric (i.e., NPT) ensemble.49 For NPT simulations, isotropic pressure control was used for bulk fluid states, while anisotropic pressure control was used for bilayer states, allowing the aspect ratio of the box to change. All-atom simulations used for gathering target data were run for 10 ns after sufficient equilibration with the trajectory written every 100 ps. A list of all the states used is given in Table S1 of the Supporting Information; the rationale for the choice of the specific states is discussed in the results section. Note that FFA C24:0 corresponds to a fully saturated FFA with length 24 carbons. CER NS C16 corresponds to CER NS with an acyl tail containing 16 carbons and is therefore of roughly equal length to the sphingosine tail. Similarly, CER NS C24 corresponds to a CER NS molecule with a longer acyl tail of 24 carbons (as in Figure 1a).
Bulk fluid simulations (both FFA and CER) were initialized by placing lipids on a 6 × 6 × 6 cubic lattice in a large simulation box to create a gas of 216 molecules. To randomize the lipids and distribute them evenly throughout the box, NVT simulations were performed for 5 ns at 1300 K. The box volume was then isotropically decreased to achieve the target density over 5 ns, followed by adjusting the temperature to that of the state point of interest. The systems were then equilibrated for 5 ns, which was found to be sufficient for the potential energy to converge, followed by 10 ns of simulation over which target data was collected; this was performed in either the NVT or NPT ensemble, depending upon the state point of interest. The mixed FFA-water systems were initialized in the same manner; these systems contained 6,480 water molecules and the appropriate number of lipids for the given concentration. This same approach was also used for the CER headgroups in water, which contained 4000 water molecules and 728 CER headgroups.
Atomistic gel-phase CER NS bilayers were initialized and equilibrated in the same manner as in our previous work.17 Specifically, initial configurations were generated by placing lipids on a 10 × 10 square lattice to create a leaflet. The leaflet was then replicated and inverted to create a bilayer and the bilayer solvated with 50 water molecules per leaflet. A short energy minimization was performed to remove any high-energy atomic overlaps, followed by 30 ps simulation in the NVT ensemble at 305K. The system was then simulated for 100 ns at 305 K and 1.0 atm in the anisotropic NPT ensemble and the final 10 ns used to collect target data; this time frame was found to be sufficient to converge both the potential energy and area per lipid. Furthermore, our previous work17 has shown that the structural properties of CER NS bilayer systems simulated for 100 ns at 305 K agree well with those from systems slowly cooled from just below the order-disorder transition, providing confidence that our systems are adequately equilibrated with this procedure. Dehydrated bilayer systems were initialized from the final configuration of the hydrated bilayer simulation, and simulated for an additional 40 ns to ensure convergence of the potential energy and area per lipid, with target data collected from the final 10 ns.
CG Simulations
All CG simulations utilized the HOOMD-Blue simulation engine.50,51 Integration of the equations of motion follows Martyna-Tobias-Klein49 for both NPT and NVT simulations. All CG simulations employed a nonbonded potential cutoff of 12Å. Since CG beads are treated as electroneutral, no treatment of long-ranged electrostatics was needed. In all cases, a timestep of 10 fs was used. Unless otherwise noted, the initial configuration of the CG simulation was the final configuration from the all-atom simulation, mapped to the CG level. For bulk fluid systems, this configuration was replicated twice in each direction so that the CG bulk fluid systems contained eight times more molecules than the corresponding atomistic systems. For lamellar states, this configuration was replicated twice in the lamellar plane so that CG lamellar systems contained four times more molecules than the corresponding atomistic systems.
CG Mappings
The CG mappings used for the lipids studied in this work are shown in Figure 1. The position of each CG bead is taken to be the center of mass of the atoms represented by the bead, with the mass of the CG bead defined to be the mass of the atoms it represents. The mapping for FFA is shown in Figure 1b. The carboxylic acid headgroup atoms are naturally mapped to a single CG bead (FHEAD), with the lipid tail described by “TAIL” beads that represent three methyl groups and a TER2 bead to describe the terminal two methyl groups when necessary, e.g., in FFA C12:0, as shown in Figure 1b. We collectively refer to the TAIL and TER2 beads in the FFA chain as TAILs. We note that this mapping closely resembles that of Hadley and McCabe,52 with the exception of using a 3:1 rather than a 4:1 mapping for the tail beads.
A 4-site mapping for the CER headgroups is used, as shown in Figure 1c. An “AMIDE” bead maps the amide group; an “MHEAD2” bead maps the C1, C2 and C3 carbons (and their associated hydrogens) of the sphingosine tail (note that the name “MHEAD” is reserved for the middle headgroup bead in the 3-site model, discussed below); an “OH1” bead maps the hydroxyl group on C1 of the sphingosine chain; and an “OH2” bead maps the hydroxyl group on C3 of the sphingosine chain. This CG mapping treats the hydroxyl groups explicitly to account for the strong directional interactions between the CER headgroups (i.e., hydrogen bonding). Additionally, this mapping scheme provides a simple route for extension to CER species with different headgroups, since the AMIDE and MHEAD2 beads are common to all CER subclasses. We refer to the beads in the CER headgroup collectively as CERHEADs. This mapping uses the same tail mappings as the FFAs, and as such, TAIL beads in CER and FFA are described by the same interaction potentials. Note, while optimizations use CER NS C24 (see Figure 1a), the validation studies performed also include CER NS C16.
A 3-site CER headgroup mapping was also investigated, as shown in Figure 1d to demonstrate the importance of the explicit treatment of hydroxyl groups. Here the effect of the hydroxyl groups is treated implicitly within the backbone structure, rather than being explicitly modeled as separate groups, and as such is similar to the MARTINI CER mapping of Sovova, et al.33 The tails are treated the same as in the 4-site CER headgroup model, using the same mappings and force fields for the TAILs as in the FFA.
In CG simulations where water is present a 4:1 k-means mapped CG water model was used following the work of Hadley and McCabe in which waters are dynamically assigned to CG beads.43,53 A dynamic mapping is necessary for water because a 4:1 mapping means atoms mapped to a common bead are necessarily parts of different molecules, and these molecules will not remain associated throughout the course of a simulation due to molecular diffusion. Thus, to map atomistic water to the CG level, a new mapping is effectively defined for each frame of the atomistic trajectory, with clusters of four molecules mapped to a single bead. The location of the center-of-mass of these beads is then used when calculating RDFs involving CG water. Since the original version of the water model was only optimized for bulk properties, it was recently reparameterized to also capture interfacial behavior.43 As detailed in Moore, et al., the CG water model was optimized against TIP3P all-atom simulations (that is, the same water model used in the all-atom lipid simulations) using both bulk and interfacial properties of water as target states, with the resulting force field accurately capturing structure, density, and droplet stability at 305 K and 1 atm.43
CG Force Field Derivation
The force field developed here consists of CG beads interacting through bonded and nonbonded potentials. These interactions are treated independently of one another, and are therefore derived separately.
The bonded interactions were derived from bond/angle distributions calculated from all-atom simulations. CG beads in a given molecule are considered bonded if they occur sequentially (i.e., if they each contain an atom that share a bond in the all-atom model). Additionally, any three consecutively bonded CG beads interact through an angle-bending potential. No torsional or dihedral interactions were included in the models. Instead, beads separated by 3 or more bonds interact only through nonbonded pair potentials, whereas the nonbonded pair potential is excluded from beads separated by 2 or fewer bonds. As in previous work,52,54 bonded interactions are determined from probability distributions following the approach of Milano et al.55 Bond and angle interactions were modeled as harmonic springs, with equilibrium values and spring constants derived from the distributions sampled in the fluid-state atomistic simulations mapped to its CG equivalent. After mapping the atomistic trajectories to the CG level, a normalized Gaussian distribution p(r) was fitted to the sampled distribution for each bond/angle type. A Boltzmann inversion of a Gaussian distribution yields a harmonic potential of the form
where kB is the Boltzmann constant, T is the absolute temperature, Kr is the spring constant determining the stiffness of the harmonic spring, r is the separation, and r0 is the equilibrium separation. This procedure was performed for each bond/angle type at each state, and the average Kr and r0 over all states for each type was used. Values of Kr and r0 for each bond/angle type are given in the Supporting Information.
Nonbonded interactions were iteratively optimized via MS IBI to match target RDFs. In MS IBI the non-bonded CG pair potential Vi(r) is iteratively updated based on deviations between RDFs from CG-mapped all-atom (AA) simulations, , and RDFs from a CG simulation, , using Vi(r) at state s. The pair potential is updated according to the sum of the differences between the Boltzmann-inverted target and CG RDFs at different state points:
where αs(r) is a scaling factor to prevent large updates, and to place emphasis on certain parts of the potential; kB is the Boltzmann constant; and Ts is the temperature of state s. Note that this expression reduces to the original IBI algorithm for a single state point. Following Ref. 40, αs(r) was chosen to be a linear function of the form , where αs,0 is the value at r = 0 and determines the maximum weight given to a particular state. This form places more emphasis at smaller separations, and ensures that the potential remains 0 at the cutoff. The pair potential is iteratively updated until some stopping criteria is met. Here, the value of the fitness function
was used to determine stopping criteria. The optimizations were terminated when |ffit,i − ffit,i−1| < 0.01 for each pair being optimized (i.e., when the fitness function became stable for each pair in the optimization). We note that MS IBI, like the original IBI method, yields numerical force fields that are not constrained to a functional form, thus allowing increased flexibility that is not available when fitting to an analytical form.
While potentials derived with IBI necessarily reproduce target RDFs, capturing the pressure-density relationship is not guaranteed. Rather than applying a pressure correction as in the original IBI method, CG models derived via MS IBI use a combination of NVT and NPT state points during the optimization. The RDFs are not likely to match if the pair potential predicts the wrong density, since the RDF is normalized by density; thus, NPT states can be used to account for the pressure, as was shown in the derivation of the CG water force field.43 A more detailed description of the theory behind the MS IBI method can be found in Moore, et al.40 and an example of using MS IBI to capture several key properties of water, including pressure-density relationships, can be found in a recent publication.43
Optimizations for particular pairs of interactions were performed successively. This was done for two reasons: 1) to reduce the number of interactions being simultaneously optimized during any single MS IBI optimization, and 2) to simplify the force field development by allowing pairs to be optimized from simulations of pure systems (e.g., pure CER) or single component hydrated systems where necessary (e.g., CER-WATER). The general order of the optimizations was to first optimize the lipid-lipid self-interactions, then, using the lipid-lipid self-interactions, derive the lipid-water interactions for each lipid species. The lipid-lipid cross-interactions (e.g., FFA-CER) were not derived in this work, since the focus is on the study of self-assembled CER structures; the cross-interactions will be reported in a future publication. Validation for each set of potentials was performed before using those potentials to optimize other interactions. For example, the TAIL-TAIL validation was performed before the TAIL-WATER potential was derived.
Seven distinct targets are used to optimize the FFA and CER nonbonded lipid self-interactions to capture a range of behaviors, including bulk fluid states (both FFA and CER), as well as an FFA monolayer and dehydrated CER bilayers. Target data from three different concentrations of FFA in water were used to optimize the TAILs-WATER interactions, and two distinct states were used to optimize the CERHEADs-WATER interactions, including hydrated CER NS C24 bilayers and CER NS headgroups solvated in water. Optimizations in both the NVT and NPT ensembles are carried out for select targets to ensure that the force field can reproduce the correct density in constant pressure simulations at 1 atm, as previously discussed. Note that not all pair potentials were optimized at all states. Instead, pair potentials were optimized at select states to capture specific behaviors. A complete list of the states used to optimize each pair potential is given in the Supporting Information. MS IBI calculations were carried out using the open source MSIBI Python library,56 which also makes use of the MDTraj Python library.57,58
Analysis
Several structural properties were used to characterize the ordered bilayer and multilamellar systems, including the area per lipid (APL), bilayer thickness, and nematic order parameter (S2) and tilt angle (θ) of the lipid tails. The hydrophobicity of a surface was characterized by calculating the contact angle that a droplet forms with the surface. A more detailed explanation of each of these calculations is provided in the Supporting Information.
III. Results
As mentioned above, the lipid-lipid self-interactions were derived first, followed by the lipid-water interactions. Even though our primary goal to is to derive a CG force field for CER NS, we note that the force field for FFA, also relevant to the SC, is simultaneously derived. Both CER and FFA contain the same tail beads (i.e., TAIL and TER2), however, the headgroups of FFA molecules interact less strongly than the headgroups of the CER molecules. As such, inclusion of FFA target states alongside CERs helps to lessen the influence of the strong CER headgroup interactions when optimizing potentials involving the TAILs beads.
III.1 Pure CER
TAIL-TAIL
Dehydrated CER bilayers (305 K, NPT and NVT) and an FFA monolayer (NVT, 305 K) are used in the TAIL bead optimizations to ensure the force field is able to capture the behavior of ordered lamellar structures. While an ordered structure is clearly an important target for capturing the SC bilayer structure, bulk FFA fluid states in both the NVT (800 K, 0.811 g/mL) and NPT (500 K, 1.0 atm) ensembles are also used to capture the behavior of disordered states expected prior to self-assembly. The inclusion of fluid states is also found to help decrease the level of structural artifacts in the force field that arise from the intermediate and long-ranged structural correlations found in the ordered phases, and thus ensures a better quality force field.40 Note that elevated temperatures were required to induce fluid phases at the density or pressure of interest. Also, due to periodic boundary conditions, the dehydrated bilayer is effectively an infinitely periodic multilamellar system.
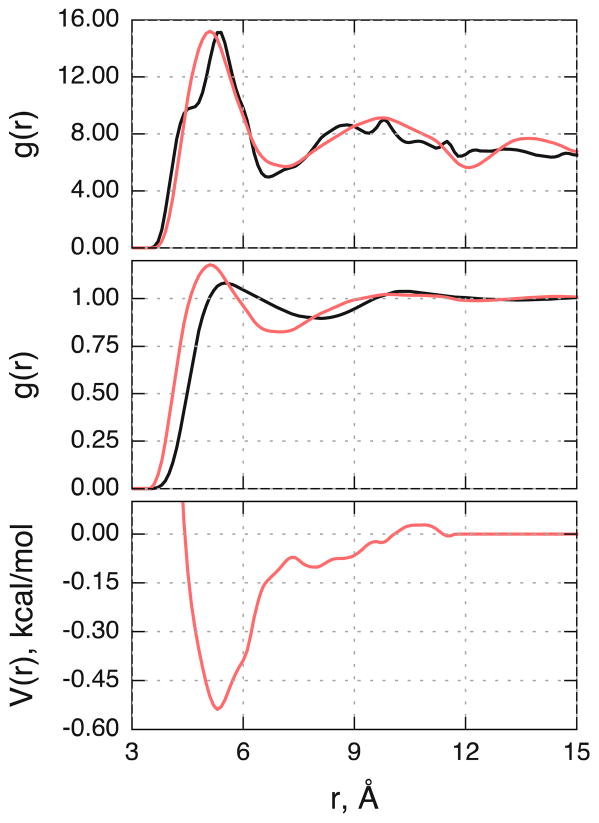
Figure 2 shows the TAIL-TAIL RDFs for the FFA monolayer state and the bulk FFA NPT state, comparing the target and optimized RDFs for each; the optimized pair potential is also shown. Considering the monolayer state, the CG model captures the main RDF peak locations and heights, although some of the smaller scale features are missed, likely due to the spherical symmetry of the CG potential. The in-plane density of this monolayer system closely compares with the density of the chains commonly found for CERs in a bilayer arrangement. Thus, this system provides a close approximation to the tail ordering found in the CER NS system. Note that this RDF does not decay to unity as the monolayer only fills a small region of the box, resulting in a system density that is lower than the local monolayer density, scaling the value of the RDF; however, this does not impact the optimization as the CG RDFs are normalized by the same factor. Satisfactory agreement is found for the bulk NPT state, where the CG model correctly predicts the presence of a fluid phase and accurately predicts the density at 1 atm, with ρCG = 0.68(5) g/mL as compared to ρAA = 0.69(1) g/mL. However, we note that the peaks in the CG RDF appear to be shifted to smaller separations by approximately 0.5 Å. As the main focus of the force field development is to accurately represent lamellar structures of the lipids in the SC, we consider such small deviations in the fluid state acceptable. We emphasize that via MS IBI, a single CG pair potential is optimized that is capable of modeling both ordered and fluid-like states; prior efforts to use the standard IBI methodology to generate CG FFA force fields required different force fields to capture different structural configurations, even though the CG mappings did not change.52
Figure 2.
RDFs and pair potential from the potential optimization for the interaction between TAIL beads. Top: target (black) and CG (red) RDFs from the FFA monolayer state; middle: target (black) and CG (red) RDFs from the FFA bulk fluid NPT state (500 K, 1 atm); bottom: the final potential used to calculate the CG RDFs above.
As further evaluation of the TAIL-TAIL interaction, structural properties of the CG FFA monolayer were also compared to results from atomistic simulations, since a matching TAIL-TAIL RDF does not guarantee that characteristic monolayer properties will also match. Well-ordered monolayers were observed in simulations of each model, with nematic order parameters S2,CG = 0.97 and S2,AA = 0.90, and tilt angles θCG = 40(5)° and θAA = 30(10)°. We note that the CG force field predicts a slightly increased level of ordering and increased tilt, although the differences in tilt angle are fully captured by the standard error of the two measurements, thus providing further validation of the pair potentials between TAILs beads.
CER Headgroups
The CG pair potentials between the four beads of the CER headgroup (collectively termed CERHEADs) are derived from both NVT and NPT ensemble simulations of dehydrated bilayers (305 K) and isotropic fluids of CER NS (500 K, 1.0 atm; 500 K, 0.721 g/mL), where, similar to the fluid FFA states, elevated temperatures were required to induce a fluid state. We note that while many prior simulations of CERs have focused on hydrated bilayers, the use of dehydrated lamellae removes the influence of the strong interactions with water and is more representative of the SC lamellae in vivo. Interactions with water are considered separately.
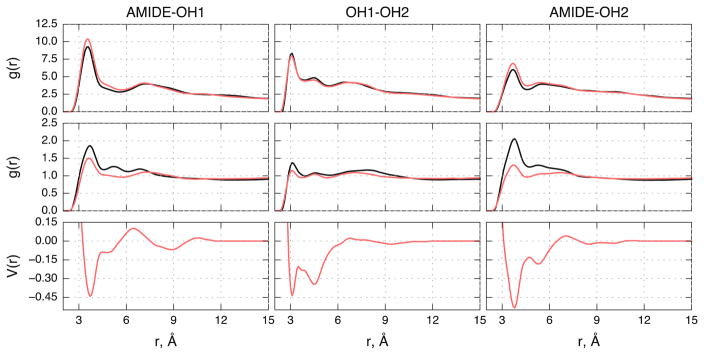
In the atomistic dehydrated CER NS bilayer, in-plane hydrogen bonding is most prevalent between atoms in the groups AMIDE-OH1, OH1-OH2, and AMIDE-OH2 (see Supporting Information). The RDFs for these pairs are shown in Figure 3. The target AMIDE-OH1 RDF from the dehydrated bilayer state, shown in Figure 3, shows a high, sharp peak at approximately 3.5 Å as a result of the significant hydrogen bonding capacity between atoms in these groups. The CG potential captures this peak and the weaker second peak in height and separation, indicating that the headgroup packing is correctly captured with the CG model. The fluid-phase CG AMIDE-OH1 RDF also agrees well with the target RDF, capturing the location of the first peak and the longer-ranged portion of the RDF (r > 7.5 Å), but missing some features in the range 4.5 Å < r < 7.5 Å. Since the primary goal of this CG force field is an accurate structural representation of lamellar structures relevant to the SC lipid matrix, a higher weight was given to the dehydrated bilayer state and thus again, this small deviation in fluid-phase behavior is considered acceptable.
Figure 3.
RDFs and the final derived potential between various CERHEAD-CERHEAD beads. Each column corresponds to a particular pair interaction, given at the top of the column. Top row: target (black) and CG (red) RDFs for each pair in the dehydrated NPT bilayer state. Middle row: target (black) and CG (red) RDFs for each pair in the bulk NPT fluid pure CER NS state (500 K, 1 atm). Bottom row: final derived potential used to calculate the CG RDFs in that column.
As shown in Figure 3, the atomistic and CG OH1-OH2 dehydrated bilayer RDFs agree very well, with the three peaks captured in both height and location in the CG simulation. This result indicates that the CG model correctly reproduces the in-plane ordering of the CER headgroups in the dehydrated bilayer. The sharp first peak in the dehydrated bilayer target RDF is a result of the large number of hydrogen bonds that form between atoms in these groups, which we note is reproduced by the CG model. The CG force field also accurately reproduces the fluid RDF, which is expected given the similarity between the fluid and dehydrated bilayer OH1-OH2 RDFs. Similarly, the target and CG dehydrated bilayer AMIDE-OH2 RDFs agree with a high level of accuracy, as shown in Figure 3. Several hydrogen bonds are also formed between atoms in these groups, which is manifested in the high peak in the dehydrated bilayer RDF at 3.5 Å. This peak is accurately captured in the CG simulation, again further indicating the in-plane packing of the CER headgroups in the dehydrated bilayer RDF is captured in the CG model. The CG model captures the general features of the bulk fluid phase, although, quantitative agreement is not see for the peak height; again, since our primary focus is the ordered phase, this deviation is considered to be acceptable.
In general, a good fit is found for all remaining RDFs at all states (see Figures S1–S7 of the Supporting Information), although we note that interactions involving the AMIDE bead tend not to reproduce the first peak in the fluid phase RDFs as accurately as seen in the other interactions. Whereas the other CERHEADs beads contain one or fewer polar groups, the AMIDE bead contains two polar groups, resulting in a high degree of shape anisotropy in the underlying interactions that is not easily accounted for by a spherically symmetric potential. Although this problem is not unique to MS IBI,42,59 it becomes more evident when using a multistate coarse-graining methodology, in which the derived potential must find the best compromise between the fluid structure at the different target states, as dictated by the weight given to each target state. Again, since our primary focus is quantitative agreement in the ordered phase, higher weight was given to those state points as compared to the bulk fluid, and thus the small quantitative deviations in the bulk fluid properties are considered acceptable. Additionally, we note that the density of the pure CER NS bulk fluid NPT state calculated with the CG model, 0.69(3) g/mL, only deviates from the atomistic value of 0.71(1) g/mL by 4%.
Compared to the 4-site model, relatively poor fits are observed for the ordered lamellar phases, as the CG models do not appear to capture the long range in-plane structure, although we note bulk fluid properties are captured with similar accuracy to the 4-site model. RDFs and potentials for the 3-site CER NS model are provided in Figures S12 and S13 of the Supporting Information.
Pure CER Validation
As validation of the CG CER interactions beyond RDFs, the structural properties of dehydrated CER NS C24 bilayers simulated using the CG model are compared to those calculated from simulations of the all-atom (AA) model. Table 1 summarizes the properties of the dry bilayer calculated with each model in the anisotropic NPT ensemble. The use of this ensemble allows the lengths of the orthogonal simulation box to change independently, allowing for a less biased comparison of the different models, as systems start from preassembled bilayer configurations.
Table 1.
Structural properties of dehydrated CER NS C24 bilayers simulated via CHARMM36-CER all-atom (AA) and the CG models derived here. The 4-site model corresponds to Figure 1c, while the 3-site model corresponds to Figure 1d. The numbers in parentheses indicate the variation in the last digit based on the standard deviation (e.g., 40.0(1) is 40.0 with a standard deviation of 0.1).
| Model | APL, Å2 | S2 | Thickness, Å | θ, deg |
|---|---|---|---|---|
| AA | 40.0(1) | 0.983 | 57.1(1) | 12(5) |
| 4-site CG | 41.90(7) | 0.976 | 55.44(7) | 7(1) |
| 3-site CG | 48.99(7) | 0.956 | 58.31(8) | 9.5(5) |
Overall, the CG force field provides accurate predictions of the key structural features of the dehydrated CER bilayer. Only minor variations in APL and S2 are found between the CG and atomistic simulations, with the CG simulations producing a slightly more compact bilayer (i.e, smaller thickness) than the atomistic simulations. The tilt angle is slightly underpredicted in the CG simulations, but is within the error of the atomistic system measurement. When comparing the volume per lipid (VPL) of the bilayers, only minor variations of the ratio of the CG to atomistic results is observed, with VPLCG/VPLAA = 1.02. As such, we can conclude that the CG CER force field accurately captures the structure and density of the dehydrated bilayer phase of CER NS. Table 1 also shows the properties of the dehydrated bilayer simulations of the 3-site headgroup model depicted in Figure 1d. Note that the TAIL and TER2 beads are the same for both mappings and identical targets were used for optimizing both the 3- and 4-site mappings. Thus, differences in properties are a direct result of the chosen mapping. The simulation of the 3-site model shows a significant overprediction of the APL as compared to the atomistic simulation. This inaccuracy is likely related to the lack of in-plane ordering in the 3-site model, which is apparent in the dry bilayer RDFs, as shown in the Supporting Information (see Figures S12 and S13). The VPL of this model is also overpredicted compared to the atomistic simulations, with VPLCG/VPLAA = 1.25. We note that the APL for the 3-site CG CER model is comparable to that obtained from the 3-site MARTINI-compatible model of Sovova et al.,33 although the lipids in our 3-site CG model show appreciable tilt, which is not captured by the MARTINI model. As such, it is clear that the 3-site CER headgroup model is an improvement over the MARTINI model, but that the 4-site CER headgroup mapping better captures the in-plane packing of the CER headgroups, enabled by the more explicit description of the hydroxyl groups; thus, this treatment is essential to accurately capture the properties of CER NS. This is also observed for the hydrated bilayer systems, as discussed below.
III.2 Optimization of Lipid-Water Interactions
Here, the results of the lipid-water potential derivations are presented, focusing on beads within the CER molecule. Interactions are first derived using MS IBI. However, we note that system density alone can drive lipid-water structural correlations, even in systems that are hydrophobic; the MS IBI routine (and IBI in general) cannot necessarily differentiate between a correlation that is induced by density and one induced by an underlying attraction. Thus, even though MS IBI produces a potential that captures the structural features of the target RDFs, the resulting potential may not provide adequate hydrophobic behavior. To address this issue, MS IBI is coupled with surface wetting simulations, which are used to validate and, if necessary, tune specific interactions such that the atomistic wetting behavior is observed in the CG model. In this approach, targeted modifications are made to the CG interactions that were derived via MS IBI and that reproduce the correct excluded volume and RDFs, such that the appropriate hydrophobic/hydrophilic character is captured in the surface wetting simulations.
TAILs-WATER
The TAILs-WATER interaction potentials were first derived using target data from simulations of FFA in water. As before, FFA was used instead of CER to remove the effect of the strong interactions between the CER headgroups and water; CERHEADs-WATER interactions were optimized separately. The FFA-WATER optimization uses three distinct states, each with a different concentration of FFA in water, such that different sized FFA aggregates are represented in the target RDFs. The CG simulations start from the final configuration of the atomistic simulations, in which the FFA is phase-separated from the water. To ensure that the CG potential can allow FFA to phase-separate, rather than just stabilize a phase-separated configuration, an additional state with the same concentration and target RDF as the most concentrated system is considered, except that the CG simulation starts with FFA dispersed in water; if FFA and water cannot phase separate with the given CG potential, the CG RDF will not match the phase separated target and the CG potential will be further refined by the MS IBI algorithm. Thus, inclusion of this state helps ensure that TAILs are sufficiently hydrophobic to drive phase-separation. While this only determines a minimum level of hydrophobicity needed for phase-separation, as a more hydrophobic system would also phase-separate, inclusion of this state greatly contributes to the realistic behavior of the CG model.
Figure 4 shows the RDFs for the most dilute and concentrated FFA-water targets, along with the optimized CG potential. Note that the highest concentration state corresponds to the system that starts from a dispersed state at each stage in the CG optimization. From the figure we can see that both target RDFs are accurately reproduced by the CG pair potential and it is also apparent that the hydrophobic interactions are sufficient to drive phase-separation, given that the system starts dispersed and visually, the FFA phase separates from water, as shown in Figure 5a.
Figure 4.
TAIL-WATER RDFs, target (black) and CG (red), from the most dilute (top) and most concentrated (middle) states; bottom: final derived potential, before tuning to match the wetting behavior.
Figure 5.
Snapshots of FFA-water simulations using different force fields. Left: CG simulation using the derived force field before tuning the interactions; middle: CG system with potentials after scaling the FHEAD-WATER and TAILs-WATER interactions; right: atomistic system mapped to the CG level. CG beads colored as follows: FFA chains: silver with yellow FHEAD beads; water: blue spheres.
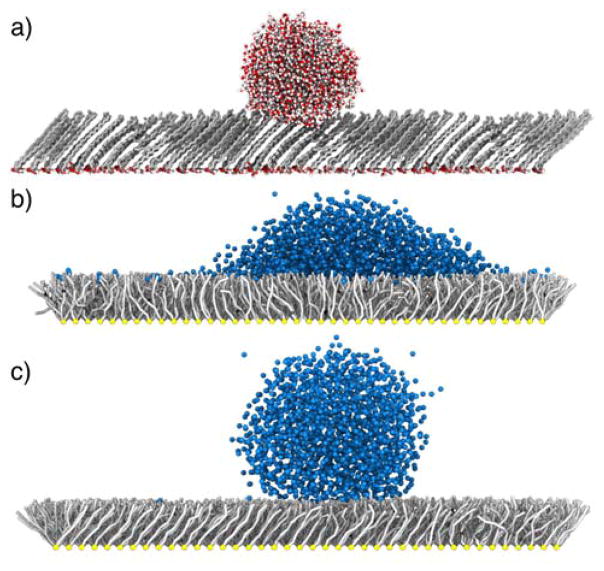
To ensure the interactions are sufficiently hydrophobic, a wetting simulation was performed in which a FFA monolayer was initialized with a water droplet on the tail side of the leaflet (as opposed to the headgroup side). The droplet forms a spherical cap on the surface with a characteristic contact angle. Snapshots of the droplet from atomistic and CG simulations are shown in Figure 6a and b, respectively. From the figure we can see that the atomistic model shows formation of a droplet with little surface wetting and thus a large contact angle φAA = 133°, while the contact angle calculated using the MS IBI-derived TAILs-WATER potentials is φCG = 40°. We note that the WATER-WATER CG potential was derived to capture the stability of a water droplet and provides a close approximation of the atomistic surface tension of a water droplet in a (near) vacuum.60 As such, the deviation from atomistic behavior lies in the TAILs-WATER interactions, indicating the derived CG force field contains insufficient hydrophobic character, despite the ability to phase separate, as discussed above. To adjust the hydrophobic character of the TAILs beads, the MS IBI derived potentials were systematically scaled, with a factor of 0.25 found to provide good agreement with a contact angle of φCG′ = 135° (where the prime indicates use of the scaled potentials), as shown in Figure 6c. Examining the behavior of the hydrated monolayer, the atomistic simulations demonstrate a high level of nematic ordering with S2,AA = 0.950 at the droplet contact (where a lipid is considered in contact with the droplet if the terminal bead is within 7 Å of a water bead in the droplet). The unscaled CG potential optimized via MS IBI, which does not capture the contact angle, appears to show a disruption in ordering near the droplet with S2,CG = 0.622, as compared to S2,CG′ = 0.921 with the scaled potential. This result suggests that the lipid hydrophobicity affects not only the lipid-water interface, but also plays a role in the structure of the lipid phase, which is relevant to hydrated lipid systems. Simulating the bulk FFA-WATER system with the scaled potentials results in behavior that also better matches the atomistic model, as shown in Figure 5c, where the simulation using the scaled CG potentials produces a cylindrical FFA aggregate in better agreement with the atomistic model, rather than an elliptical aggregate produced with the unscaled CG potential. By scaling the TAILs-WATER potentials, the CG force field is able to phase separate, reproduce the atomistic wetting behavior, and maintain the lipid order upon wetting. Therefore, the derived TAIL-WATER and TER2-WATER potentials scaled by a factor of 0.25 are transferred to the CER-water optimizations and used henceforth.
Figure 6.
Snapshots from the droplet simulations of a) the atomistic model, b) the CG model before tuning TAILs-WATER potentials, and c) the CG model with the TAILs-WATER potentials scaled by 0.25. Atoms colored as follows: C – silver, O – red, H – white; methyl hydrogens not shown for clarity. CG beads colored as follows: TAILs – silver, FHEAD – yellow, WATER – blue.
CERHEADs-WATER
While hydrophobicity-driven phase-separation is the first step in lipid self-assembly, hydrophilic interactions help drive the formation of organized structures.32,61 Therefore, it is important that the lipid headgroups possess the correct hydrophilic character to drive self-assembly. The CER-WATER MS IBI optimization used three states to optimize the interactions between water and the CER headgroup beads: hydrated CER NS C24 bilayers (305 K, NVT and NPT) to capture the interfacial behavior and CER NS headgroups dispersed in water (1.0 atm, 400 K) to capture the solvation of the lipid headgroups necessary for bilayer self-assembly. We note that the headgroups in water were simulated at 400 K to ensure that the headgroups were well dispersed throughout the water. Close matches to the target RDFs are found, as shown in Figures S8–S11 of the Supporting Information along with the derived potentials. To determine if the CERHEAD beads have sufficient hydrophilic character, we examine the wetting properties of a CER-WATER interface. Atomistic wetting simulations of CER headgroups show complete wetting of the headgroups by water, viz., θAA → 0°, indicating a hydrophilic surface. This is expected, given the available hydrogen bonding sites in the CER headgroups. Wetting simulations using the derived CG force field show the same behavior – complete wetting of the surface, indicating the MS IBI optimizations captured the hydrophilic nature of the CER headgroups. As such, the CERHEADs-WATER potentials were not modified from their derived form. We note that the same procedure was performed for the 3-site CER headgroup mapping model; sufficient hydrophilicity of these headgroup beads was observed and hence no scaling was performed.
III.3. Validation
As validation of the fully derived CG model (i.e., where all interactions are represented), we simulate hydrated preassembled single-component bilayers composed of CER NS C16 and CER NS C24 with the derived CG model and compare to results obtained from simulations of atomistic models and to experimental data, where available. Table 2 summarizes the comparison between the CG and atomistic CHARMM-CER simulation results, where overall, good agreement is seen, with the APL, nematic order, and bilayer thickness accurately reproduced. While neither model shows a strong correlation between CER length and tilt angle, appreciably more tilt is observed in the atomistic systems than the CG systems. While this and other differences between the atomistic and CG simulations in Table 2 can be attributed, at least in part, to the loss of details in the CG model, the softened free energy landscape associated with the CG models should allow the systems to relax more efficiently than atomistic models, even over the same timescale. Furthermore, as we discuss in the context of self-assembly below, small deviations in lipid packing in the CG simulations result in measurable differences in tilt angle, which may also account for the perceived underprediction of tilt angles in the CG simulations. Note that only CER NS C24 was used in the force field derivation, therefore, these results also illustrate the predictive power of the CG model in the ability to accurately capture CER NS C16 behavior. Additionally, comparisons are made for CER NS C24 simulated with the 3-site CG model derived here (see Table 2), where, again, the APL is overpredicted as compared to the atomistic simulation and is similar to the APL calculated with the MARTINI CER model (46 Å2).33
Table 2.
Structural properties of CER NS C16/CER NS C24 bilayers at 305 K and 1.0 atm simulated using the CG models derived here and the CHARMM36-CER all-atom model (AA). For CER NS C24, the terminal 8 carbons of the acyl tail are excluded from the moment of inertia of the tail, so as to exclude the unequal portion of the tails from the calculation. The numbers in parentheses are the variation in the final reported digit, based on the standard deviation.
| system | model | APL, Å2 | S2 | d, Å | θ, deg |
|---|---|---|---|---|---|
| CER NS C16 | AA | 42.4(2) | 0.998 | 42.5(5) | 24.3(9) |
| CG | 42.0(1) | 0.982 | 44.51(9) | 6.3(7) | |
|
| |||||
| CER NS C24 | AA | 39.9(2) | 0.979 | 56.2(4) | 22(4) |
| CG | 41.99(9) | 0.981 | 56.6(1) | 7(1) | |
| 3-site CG | 46.2(1) | 0.914 | 61.5(2) | 9(2) | |
As additional validation, the properties calculated from simulations of the CG and atomistic models for pure systems in Table 2 compare favorably with the limited experimental data on CER-based systems. APL values calculated from experimental studies of CER monolayers range from 37.8–45 Å2 for CER NS C1662,63 and 39.0 Å2 for CER NS C18.38 Monolayers displaying tilt angles ranging from 0–14° for pure CER NS C16 and CER NS C18 have been reported from experimental measurements,38,63 which we note are closer to the values predicted by the CG models than the atomistic model. Other simulation studies using different atomistic force fields also fall within similar ranges: e.g., using the united atom GROMOS-based force field of Berger,64 Notman et al. calculated an APL of 37.4 Å2 for CER NS C24 at 323 K,20 while a value of 39.8 Å2 was reported for pure CER NS C16 at 305 K with the same model in other work.17 Additionally, Metcalf and Pandit calculated the APL of a pure CER NS C16 bilayer to be ~44 Å2 at 323 K using a different united atom model.65 Tilt angles ranging from 17° for pure CER NS C24 at 323 K20 to 26° for pure CER NS C16 at 323 K65 have been reported from simulation studies. We note that the tilt angle in CG simulations significantly deviates from the atomistic simulations; this may be related to the loss of detail in the CG model, in which the local packing of the tails is altered compared to the atomistic model, resulting in different tilt behavior. However, as noted above, the tilt angles calculated in the CG simulations are actually closer to experimental values than the tilt angles from the atomistic simulations. Thus, overall, the 4-site CER headgroup CG model developed here produces results for preassembled bilayers consistent with both experiment and various atomistic-level models.
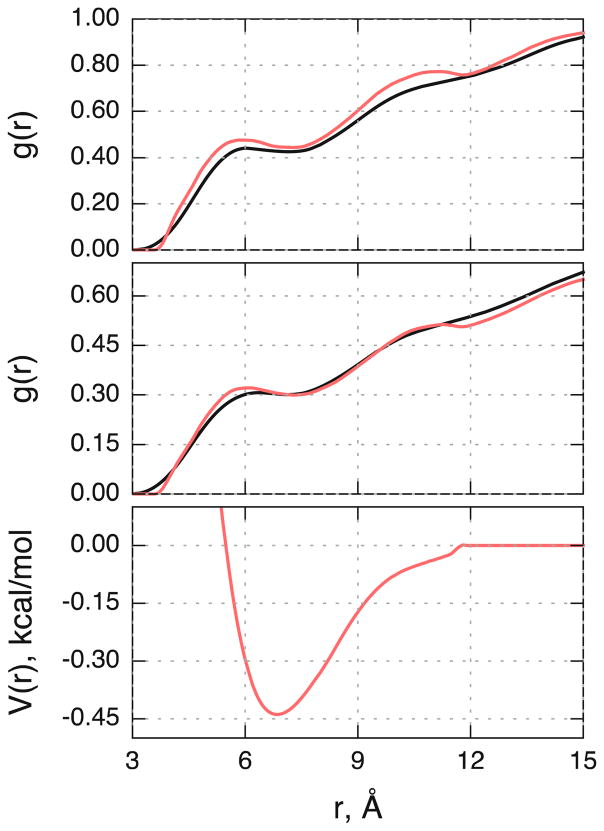
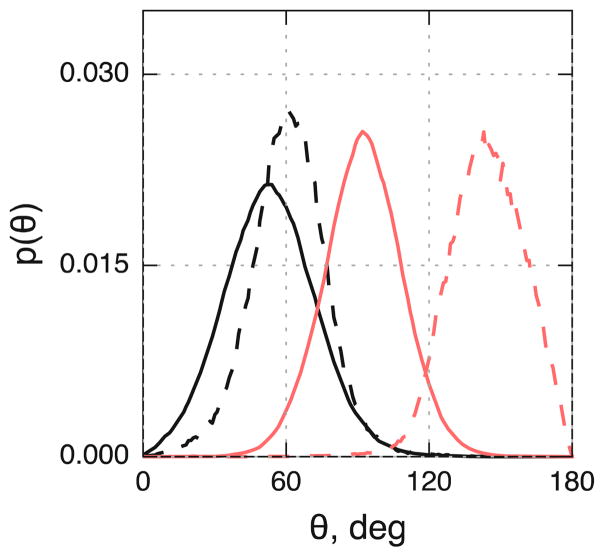
In addition to the aforementioned structural metrics, we also compare the orientation of the OH groups between the CG and atomistic models for the CER NS C24 systems because of the importance of hydrogen bonding network formation in CER-based systems.37–39 The orientation of the MHEAD2-OH1 vector relative to the outward bilayer normal (i.e., pointing towards the water) in the pure CER NS C24 bilayer, shown in Figure 7, is preferentially aligned approximately 60° off the bilayer normal in the atomistic simulation, suggesting the OH1 group interacts with the water phase. This behavior is captured with the CG model, where the MHEAD2-OH1 vector prefers an approximately 50° angle with respect to the bilayer normal. In contrast, the MHEAD2-OH2 vector prefers an orientation with the OH2 bead below the MHEAD2 bead (i.e., not between the MHEAD2 and WATER beads), indicating it is more involved in the hydrogen bonding network formed between the CER headgroups compared to the OH1 bead. This behavior is qualitatively captured by the CG model, where the MHEAD-OH2 vector tends to point away from the lipid-water interface, indicated by the MHEAD2-OH2 angle > 90° in Figure 7. However, there is a quantitative discrepancy between this property in the CG and atomistic simulations, where the CG system prefers an angle of approximately 95°, compared to 135° in the atomistic system. This discrepancy does not appear to have any significant impact on the APL or in-plane structure of the lipids, and is likely a consequence of the loss of detail inherent to CG models. This comparison further suggests that the CG model, at least on a qualitative level, captures the hydrogen bond network formation between the CER headgroups.
Figure 7.
Orientation of the MHEAD2-OH vectors with respect to the bilayer normal in the CER NS C24 bilayer. A value of 0° indicates the OH bead lies directly between the MHEAD2 bead and the lipid-water interface; a value of 90° means the OH group is lying flat in the bilayer plane. Black lines: OH1; red lines: OH2; solid lines: CG; dashed lines: atomistic mapped to the CG level.
IV. CER NS C24 Self-Assembly
It is unlikely that preassembled atomistic systems would be able to transition from metastable states to lower energy states because of the timescales on which major morphological transitions occur compared to the timescales that are accessible with atomistic models. Thus, pre- and self-assembled structures studied via atomistic simulations are likely to be “stuck” in metastable configurations. For example, Das et al. studied SC lipid self-assembly using a united-atom force field, finding that the lipids self-assemble into a lamellar phase under confinement but form micellar structures in bulk,28 in contrast to experimental studies that suggest the formation of lamellar phases in bulk systems;66,67 this discrepancy is likely due to the need for much longer simulation times to form equilibrium phases, currently inaccessible to atomistic models. Given the reduced computational cost of CG models, they can be used to access the timescales required to examine the self-assembly of SC lipids.
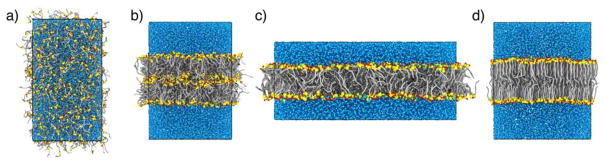
Here, we examine the self-assembly of CER NS C24 in water, motivated by its abundance in the SC. Systems composed of 800 lipids and 10,000 water beads are studied, which represents a water to lipid ratio well above that of a fully hydrated bilayer. To remove dependence on the initial configuration, the CG-mapped atomistic bilayer (replicated twice in the x and y directions to four times the original size) system was heated to 1500 K for 20 ns, during which time the lipids and water became completely mixed and disordered, as shown in Figure 8a. Upon cooling to 305 K, a bilayer containing structural defects formed, as shown in Figure 8b. To increase the relaxation rate of the defects, the system was then expanded in the bilayer plane to double the original area over 10 ns while preserving the box volume, as shown in Figure 8c. Upon deforming the box to the original aspect ratio over 10 ns, a defect-free bilayer formed, as shown in Figure 8d. After switching to the anisotropic NPT ensemble, the self-assembled bilayer was found to be stable for 200+ ns. This process was repeated three times with different expansion and compression rates to examine the influence of the relaxation rate on the final structure. The APL of the bilayers over the final 50 ns of the NPT simulations are compared in Table 3, with little variation between the different systems observed. Interestingly, the self-assembled CG systems are found to pack more densely than the comparable preassembled bilayers, resulting in APLs that are closer to the value from the atomistic simulation (see Table 2, CER NS C24). The timescale associated with this relaxation influences the distribution of lipids between the leaflets in the bilayer structure, with shorter timescales associated with larger deviations from an ideal (i.e., equal) distribution, although all deviations are within 2.6% of ideal. These small variations, however, do create noticeable changes to the average tilt angle of the leaflets (although the average APL is relatively unaffected), with a larger tilt observed in the leaflets with fewer lipids, as shown in Table 3. This trend is expected – with a fewer number of lipids in a leaflet, the lipid tails tilt relative to the bilayer normal to decrease their spacing to an optimal level.
Figure 8.
Self-assembly of CER NS C24 into an ordered bilayer. a) initial heating above mixing temperature; b) cooling from high temperature; c) full compression; d) final configuration after compression and expansion. CG beads colored as follows: TAILs – silver cylinders; AMIDE AND MHEAD2 – yellow spheres; OH1 and OH2 – red spheres; WATER – blue spheres.
Table 3.
Properties of self-assembled bilayers as a function of expansion and compression time (relaxation time). ftop/fbottom represents the of fraction of lipids in the top and bottom leaflets of the self-assembled bilayers; θtop/θbottom represents the average tilt angle of the lipids in the top and bottom leaflets. For the stacked systems, ntop/nbottom represents the number of lipids in each of the 4 layers, and θtop/θbottom represents the average tilt angle of the lipids in each of the 4 layers. The APL of the stacked systems was calculated using the average number of lipids in each layer. The standard error in the tilt angle was less than 3° for each measurement.
| final structure | relaxation time, ns | APL, Å2 | ftop/fbottom | θtop/θbottom, deg |
|---|---|---|---|---|
| bilayer | 20 | 40.00(2) | 0.513/0.487 | 5.2/9.2 |
| 40 | 40.10(2) | 0.511/0.489 | 5.0/7.2 | |
| 60 | 39.69(3) | 0.509/0.491 | 5.2/9.0 | |
|
| ||||
| stacked bilayer | 200 | 42.76(2) | 0.243/0.250/0.244/0.264 | 9.6/6.6/8.1/4.9 |
| 400 | 43.09(3) | 0.240/0.255/0.253/0.253 | 9.5/5.5/6.3/6.1 | |
| 600 | 42.83(2) | 0.258/0.246/0.253/0.244 | 5.6/7.1/5.9/11.1 | |
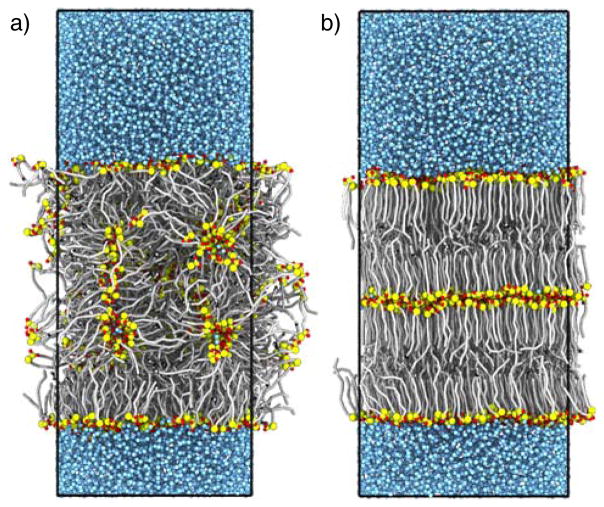
Since the simulated bilayer is a periodic structure (as periodic boundary conditions are used), it is reasonable to assume that the self-assembled structure is dependent on the size and shape of the box. For example, one would expect two bilayers to form in the previously-described CER NS C24 system if the box area parallel to the bilayer plane were reduced by a factor of 2. To explore this concept, the previous self-assembly protocol was repeated, with the exception that the aspect ratio of the simulation box at the end of the initial compression phase was set to half that of the initial self-assembly simulation (i.e., half the cross-sectional area of the bilayer and twice the thickness). As with the bilayer self-assembly, a defected lamellar structure initially formed, where the lipids were well-ordered at the lipid-water interface and less ordered in the interior of the membrane, as shown in Figure 9a. After subsequent expansion and compression cycles, well-ordered, multilamellar structures formed (i.e., stacked bilayers), with a small amount of water between the middle leaflets (0.35–0.5, water molecules per interior lipid, compared to 40 in the bulk). The relaxation rates of the stacked bilayer defects were much slower than that of the single bilayer systems, with 200 ns of both expansion and compression required to remove the defects, compared to 20 ns for the single bilayer assembly. Subsequent replication of this self-assembly protocol yielded similar structures, illustrating reproducibility. We note that without the expansion and compression to increase the relaxation rate of the defects, a defect-free stacked bilayer structure formed over the course of 1.3 μs at 305 K. Thus, the expansion and compression protocol is used as a means to increase the rate of exploration of the phase space of the CER-water system, rather than to influence the final state of the system.
Figure 9.
Self-assembly of CER NS C24 into a stacked bilayer. a) after changing the aspect ratio of the simulation cell; b) after subsequent area expansion and compression. Beads colored as follows: TAILs – silver cylinders; AMIDE and MHEAD2 – yellow spheres; OH1 and OH2 – red spheres; WATER – blue spheres.
Examining the multilamellar systems we note that similar structural trends are observed in comparison to the self-assembled single bilayer systems. For example, the self-assembled multilamellar systems also show deviations from an ideal distribution of lipids per leaflet, although the deviations are larger in the multilamellar systems (see Table 3), which may be expected given the differences between a lipid-water and lipid-lipid interface. A similar relationship between the tilt angle of a leaflet and the number of lipids in the leaflet is also observed for the single bilayer and multilamellar systems, where a higher tilt angle is observed for leaflets with fewer lipids. Compared to the self-assembled single bilayers, the APL of the self-assembled multilamellar systems is slightly larger and closer to the preassembled CG bilayers, which again, may be related to differences manifesting from the multilamellar organization.
The lipid-lipid interface in multilamellar structures makes it possible for lipids to adopt different configurations, which may alter the properties of the system. For example, several models of SC lipid organization have been proposed, with a key difference between the models being whether the CER tails adopt an extended conformation (with the two tails on opposite sides of the headgroup), a hairpin conformation (with both tails on the same side of the headgroup), or some combination of the two. For example, the stacked monolayer model assumes an extended conformation for the CERs,68 while the sandwich model assumes a hairpin conformation of the CERs.5,69 In contrast, the single gel phase model proposes a mixture of extended and hairpin CER conformations,70 and the armature reinforcement model proposes a transition from extended to hairpin CER conformations upon hydration.67,71
To explore the CER conformations in the stacked bilayer configurations, we examine the angle θtails between the two tails of each CER molecule. θtails was defined as the angle between the two vectors from the MHEAD2 bead to the terminal bead of each tail and thus distinguishes between the lipid being in a extended (θtails > 90°) or hairpin (θtails < 90°) conformation. From the simulations we find that the vast majority of the lipids in the multilamellar system exist in a hairpin conformation, with no correlation between conformation and expansion/compression time (for all systems, between 91 and 94% of lipids exist in a hairpin conformation). As might be expected, the hairpin configuration is strongly preferred at the lipid-water interface due to the hydrophobic nature of the lipid tails; however, when considering the lipids in the inner leaflets, the number of lipids adopting a hairpin conformation decreases to between 82 and 87%. Thus, while the hairpin conformation appears to be the preferred CER conformation in the pure, multilamellar CER NS C24 system, roughly 15% of the lipids in the inner leaflets adopt an extended conformation. Thus, the pure CER NS system is most consistent with the hairpin conformation assumed in the sandwich model. However, we note that the CER conformation in the complex lipid mixtures of human SC, which include both cholesterol and FFAs, could be different than observed for pure CER NS. It is reasonable to assume that the intramolecular bonded forces dictate the CER conformation to an extent. Therefore, to validate the intramolecular potentials and ensure they are not biasing the extended vs. hairpin conformations in the stacked bilayer system, a single CER molecule in a vacuum was simulated with the CG and atomistic force fields, and the distributions of the angle between the two tails (θtails) and end-to-end distance of the tails calculated with each model. Good agreement between the distributions calculated with the two models was found, with each predicting, on average, a hairpin conformation of the two tails (see Supporting Information). Therefore, we conclude the observed hairpin vs. extended distribution is physically relevant and not an artifact of the intramolecular bonded forces in the CG force field.
V. Conclusion
We have shown that MS IBI is an appropriate method for deriving CG models of SC lipids, specifically CER NS, which is the most abundant CER in human SC. The transferable nature of the MS IBI-derived force field is illustrated by the fact that the TAIL beads of CER NS and FFA are treated as the same type, and accurately model the tail behavior of the two different types of molecule. This transferability is promising for the development of models for other SC lipids, as the TAILs beads can confidently be transferred to describe the acyl tails, leaving only the headgroup interactions to be derived. Further, the inclusion of explicit hydroxyl groups on the CER headgroups allows the model to accurately capture the in-plane packing of the molecules. This is an important property of any CER model, especially, for example, when studying permeability, where the primary permeability barrier is at the lipid-water interface.72 In contrast, an implicit treatment of the hydroxyl groups does not allow the model to capture this behavior, which results in less accurate structural properties of lamellar phases with the CG model. This CG mapping also allows for easy extension to other CER species, since the AMIDE and MHEAD2 beads are common to all CERs.
The derived CG model was first validated through simulations of preassembled CER NS bilayers. Good agreement on several important bilayer properties was found between the CG and fully atomistic simulations and experimental data where available. Through preassembled bilayer simulations, we further showed that the CG mapping involving explicit hydroxyl groups more accurately reproduces the bilayer properties, and that this increased integrity of the model and incurs a minimal increase in computational expense. After validation on preassembled structures, self-assembly of CER NS into uni- and multilamellar structures was studied with the CG model, with the self-assembled structures exhibiting similar properties to the preassembled systems. Simulations of the CG model show a predominance of CERs adopting a hairpin configuration in the multilamellar systems.
While this paper derives a model specific to CER NS, it also provides the necessary framework for developing force fields to accurately model a realistic SC lipid mixture. Recent experimental work has focused on developing lipid mixtures that adequately reproduce the barrier properties of human skin.36,67,73–75 CG SC lipid models can offer molecular-level insight into phenomena that cannot be observed through experiment and atomistic molecular simulation, e.g., the self-assembly into and transitions between well-ordered lamellar phases. CG models are thus a practical tool for complementing experimental work in this field, e.g., aiding in the discovery of promising lipid mixtures that reproduce the properties of human SC. CG models for the other lipid classes of SC (FFA and cholesterol) will be published in a future publication, allowing simulation studies of representative SC lipid mixtures.
Supplementary Material
Acknowledgments
This work was supported by grant number R01 AR057886-01 from the National Institute of Arthritis and Musculoskeletal and Skin Diseases and National Science Foundation grant number CBET-1028374. This work was conducted in part using computational resources provided by the National Energy Research Scientific Computing Center, supported by the Office of Science of the Department of Energy under Contract No. DE-AC02-05CH11231, and the Advanced Computing Center for Research and Education at Vanderbilt University.
Footnotes
Tables containing the states used to gather target data and which states were used to optimize each pair interaction; a table containing the parameters for the CG bonded interactions; a description of the various analyses performed on the simulation trajectories; a summary of the hydrogen bonding calculated from atomistic bilayer simulations; and RDFs and potentials for interaction pairs that are not presented in the text.
References
- 1.Yardley HJ, Summerly R. Lipid composition and metabolism in normal and diseased epidermis. Pharmacol Ther. 1981;13:357–383. doi: 10.1016/0163-7258(81)90006-1. [DOI] [PubMed] [Google Scholar]
- 2.Gray GM, Yardley HJ. Different populations of pig epidermal cells: isolation and lipid composition. J Lipid Res. 1975;16:441–447. [PubMed] [Google Scholar]
- 3.Rabionet M, Gorgas K, Sandhoff R. Ceramide synthesis in the epidermis. Biochim Biophys Acta - Mol Cell Biol Lipids. 2014;1841:422–434. doi: 10.1016/j.bbalip.2013.08.011. [DOI] [PubMed] [Google Scholar]
- 4.Ponec M, Weerheim A, Lankhorst P, Wertz PW. New acylceramide in native and reconstructed epidermis. J Invest Dermatol. 2003;120:581–588. doi: 10.1046/j.1523-1747.2003.12103.x. [DOI] [PubMed] [Google Scholar]
- 5.Bouwstra JA, Dubbelaar FER, Gooris GS, Ponec M. The lipid organisation in the skin barrier. Acta Derm Venereol Suppl (Stockh) 2000;208:23–30. doi: 10.1080/000155500750042826. [DOI] [PubMed] [Google Scholar]
- 6.van Smeden J, Janssens M, Gooris GS, Bouwstra JA. The important role of stratum corneum lipids for the cutaneous barrier function. Biochim Biophys Acta - Mol Cell Biol Lipids. 2014;1841:295–313. doi: 10.1016/j.bbalip.2013.11.006. [DOI] [PubMed] [Google Scholar]
- 7.van Smeden J, et al. The importance of free fatty acid chain length for the skin barrier function in atopic eczema patients. Exp Dermatol. 2014;23:45–52. doi: 10.1111/exd.12293. [DOI] [PubMed] [Google Scholar]
- 8.Feller SE. Molecular dynamics simulations of lipid bilayers. Curr Opin Colloid Interface Sci. 2000;5:217–223. [Google Scholar]
- 9.Lindahl E, Sansom MS. Membrane proteins: molecular dynamics simulations. Curr Opin Struct Biol. 2008;18:425–431. doi: 10.1016/j.sbi.2008.02.003. [DOI] [PubMed] [Google Scholar]
- 10.Lyubartsev AP, Rabinovich AL. Recent development in computer simulations of lipid bilayers. Soft Matter. 2011;7:25. [Google Scholar]
- 11.Bennett WFD, Tieleman DP. Computer simulations of lipid membrane domains. Biochim Biophys Acta. 2013;1828:1765–76. doi: 10.1016/j.bbamem.2013.03.004. [DOI] [PubMed] [Google Scholar]
- 12.Rabinovich AL, Lyubartsev AP. Computer Simulation of Lipid Membranes: Methodology and Achievements. Polym Sci Ser C. 2013;55:162–180. [Google Scholar]
- 13.Bemporad D, Luttmann C, Essex JW. Computer simulation of small molecule permeation across a lipid bilayer: dependence on bilayer properties and solute volume, size, and cross-sectional area. Biophys J. 2004;87:1–13. doi: 10.1529/biophysj.103.030601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Groen D, et al. Disposition of ceramide in model lipid membranes determined by neutron diffraction. Biophys J. 2011;100:1481–9. doi: 10.1016/j.bpj.2011.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Školová B, et al. Different Phase Behavior and Packing of Ceramides with Long (C16) and Very Long (C24) Acyls in Model Membranes: Infrared Spectroscopy Using Deuterated Lipids. J Phys Chem B. 2014;118:10460–10470. doi: 10.1021/jp506407r. [DOI] [PubMed] [Google Scholar]
- 16.Mojumdar EH, et al. Skin Lipids: Localization of Ceramide and Fatty Acid in the Unit Cell of the Long Periodicity Phase. Biophys J. 2015;108:2670–2679. doi: 10.1016/j.bpj.2015.04.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Guo S, Moore TC, Iacovella CR, Strickland LA, McCabe C. Simulation study of the structure and phase behavior of ceramide bilayers and the role of lipid head group chemistry. J Chem Theory Comput. 2013;9:5116–5126. doi: 10.1021/ct400431e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pandit SA, Scott HL. Molecular-dynamics simulation of a ceramide bilayer. J Chem Phys. 2006;124:14708. doi: 10.1063/1.2140689. [DOI] [PubMed] [Google Scholar]
- 19.Das C, Noro MG, Olmsted PD. Simulation studies of stratum corneum lipid mixtures. Biophys J. 2009;97:1941–51. doi: 10.1016/j.bpj.2009.06.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Notman R, den Otter WK, Noro MG, Briels WJ, Anwar J. The permeability enhancing mechanism of DMSO in ceramide bilayers simulated by molecular dynamics. Biophys J. 2007;93:2056–68. doi: 10.1529/biophysj.107.104703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gupta R, Rai B. Molecular Dynamics Simulation Study of Skin Lipids: Effects of the Molar Ratio of Individual Components over a Wide Temperature Range. J Phys Chem B. 2015;119:11643–11655. doi: 10.1021/acs.jpcb.5b02093. [DOI] [PubMed] [Google Scholar]
- 22.Shah J, et al. Structural and thermotropic properties of synthetic C16:0 (palmitoyl) ceramide: effect of hydration. J Lipid Res. 1995;36:1936–44. [PubMed] [Google Scholar]
- 23.Bouwstra JA, et al. Phase behavior of isolated skin lipids. J Lipid Res. 1996;37:999–1011. [PubMed] [Google Scholar]
- 24.Moore DJ, Rerek ME, Mendelsohn R. FTIR Spectroscopy Studies of the Conformational Order and Phase Behavior of Ceramides. J Phys Chem B. 1997;101:8933–8940. [Google Scholar]
- 25.Brief E, et al. Phase behavior of an equimolar mixture of N-palmitoyl-D-erythro-sphingosine, cholesterol, and palmitic acid, a mixture with optimized hydrophobic matching. Langmuir. 2009;25:7523–7532. doi: 10.1021/la9003643. [DOI] [PubMed] [Google Scholar]
- 26.Paz Ramos A, Lafleur M. The chain length of free fatty acids influences the phase behaviour of stratum corneum model membranes. Langmuir. 2015;31:11621–11629. doi: 10.1021/acs.langmuir.5b03271. [DOI] [PubMed] [Google Scholar]
- 27.Hoopes MI, Noro MG, Longo ML, Faller R. Bilayer structure and lipid dynamics in a model stratum corneum with oleic acid. J Phys Chem B. 2011;115:3164–71. doi: 10.1021/jp109563s. [DOI] [PubMed] [Google Scholar]
- 28.Das C, Noro MG, Olmsted PD. Lamellar and Inverse Micellar Structures of Skin Lipids: Effect of Templating. Phys Rev Lett. 2013;111:148101. doi: 10.1103/PhysRevLett.111.148101. [DOI] [PubMed] [Google Scholar]
- 29.Marrink SJ, Risselada HJ, Yefimov S, Tieleman DP, de Vries AH. The MARTINI force field: coarse grained model for biomolecular simulations. J Phys Chem B. 2007;111:7812–24. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- 30.Shinoda W, DeVane RH, Klein ML. Multi-property fitting and parameterization of a coarse grained model for aqueous surfactants. Mol Simul. 2007;33:27–36. [Google Scholar]
- 31.Izvekov S, Voth GA. A multiscale coarse-graining method for biomolecular systems. J Phys Chem B. 2005;109:2469–73. doi: 10.1021/jp044629q. [DOI] [PubMed] [Google Scholar]
- 32.Hadley KR, McCabe C. A simulation study of the self-assembly of coarse-grained skin lipids. Soft Matter. 2012;8:4802. doi: 10.1039/C2SM07204A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sovova Z, Berka K, Otyepka M, Jurecka P. Coarse-Grain Simulations of Skin Ceramide NS with Newly Derived Parameters Clarify Structure of Melted Phase. J Phys Chem B. 2015;119:3988–3998. doi: 10.1021/jp5092366. [DOI] [PubMed] [Google Scholar]
- 34.Notman R, Anwar J, Briels WJ, Noro MG, den Otter WK. Simulations of skin barrier function: free energies of hydrophobic and hydrophilic transmembrane pores in ceramide bilayers. Biophys J. 2008;95:4763–71. doi: 10.1529/biophysj.108.138545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Moore DJ, Rerek ME, Mendelsohn R. Role of ceramides 2 and 5 in the structure of the stratum corneum lipid barrier. Int J Cosmet Sci. 1999;21:353–68. doi: 10.1046/j.1467-2494.1999.211916.x. [DOI] [PubMed] [Google Scholar]
- 36.Garidel P, Fölting B, Schaller I, Kerth A. The microstructure of the stratum corneum lipid barrier: mid-infrared spectroscopic studies of hydrated ceramide:palmitic acid:cholesterol model systems. Biophys Chem. 2010;150:144–56. doi: 10.1016/j.bpc.2010.03.008. [DOI] [PubMed] [Google Scholar]
- 37.Pascher I. Molecular Arrangements in Sphingolipids. Conformation and Hydrogen Bonding of Ceramide and Their Implication on Membrane Stability and Permeability. Biochim Biophys Acta. 1976;455:433–451. doi: 10.1016/0005-2736(76)90316-3. [DOI] [PubMed] [Google Scholar]
- 38.Löfgren H, Pascher I. Molecular arrangements of sphingolipids. The monolayer behaviour of ceramides. Chem Phys Lipids. 1977;20:273–84. doi: 10.1016/0009-3084(77)90068-8. [DOI] [PubMed] [Google Scholar]
- 39.Rerek ME, et al. Phytosphingosine and Sphingosine Ceramide Headgroup Hydrogen Bonding: Structural Insights through Thermotropic Hydrogen/Deuterium Exchange. J Phys Chem B. 2001;105:9355–9362. [Google Scholar]
- 40.Moore TC, Iacovella CR, McCabe C. Derivation of coarse-grained potentials via multistate iterative Boltzmann inversion. J Chem Phys. 2014;140 doi: 10.1063/1.4880555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bayramoglu B, Faller R. Coarse-Grained Modeling of Polystyrene in Various Environments by Iterative Boltzmann Inversion. Macromolecules. 2012;45:9205–9219. [Google Scholar]
- 42.Bayramoglu B, Faller R. Modeling of Polystyrene under Confinement: Exploring the Limits of Iterative Boltzmann Inversion. Macromolecules. 2013;46:7957–7976. [Google Scholar]
- 43.Moore TC, Iacovella CR, McCabe C. In: Foundations of Molecular Modeling and Simulation: Select Papers from FOMMS 2015. Snurr RQ, SAC, Kofke DA, editors. Springer; Singapore: 2016. pp. 37–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Klauda JB, et al. Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. J Phys Chem B. 2010;114:7830–43. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983;79:926. [Google Scholar]
- 46.Plimpton SJ. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J Comput Phys. 1995;117:1–19. [Google Scholar]
- 47.LAMMPS web page.
- 48.Plimpton SJ, Pollock R, Stevens MJ. Particle Mesh Ewald and rRESPA for Parallel Molecular Dynamics Simulations. Proc Eighth Siam Conf Parallel Process Sci Comput. 1997:1–13. doi:10.1.1.41.5174. [Google Scholar]
- 49.Martyna GJ, Tobias DJ, Klein ML. Constant pressure molecular dynamics algorithms. J Chem Phys. 1994;101:4177. [Google Scholar]
- 50.Anderson JA, Lorenz CD, Travesset A. General purpose molecular dynamics simulations fully implemented on graphics processing units. J Comput Phys. 2008;227:5342–5359. [Google Scholar]
- 51.HOOMD-blue web page. at < http://codeblue.umich.edu/hoomd-blue>.
- 52.Hadley KR, McCabe C. A coarse-grained model for amorphous and crystalline fatty acids. J Chem Phys. 2010;132:134505. doi: 10.1063/1.3360146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hadley KR, McCabe C. On the investigation of coarse-grained models for water: balancing computational efficiency and the retention of structural properties. J Phys Chem B. 2010;114:4590–9. doi: 10.1021/jp911894a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Hadley KR, McCabe C. A structurally relevant coarse-grained model for cholesterol. Biophys J. 2010;99:2896–905. doi: 10.1016/j.bpj.2010.08.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Milano G, Goudeau S, Müller-Plathe F. Multicentered Gaussian-based potentials for coarse-grained polymer simulations: Linking atomistic and mesoscopic scales. J Polym Sci Part B Polym Phys. 2005;43:871–885. [Google Scholar]
- 56.MSIBI. at < https://github.com/ctk3b/msibi>.
- 57.McGibbon RT, et al. MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys J. 2015;109:1528–1532. doi: 10.1016/j.bpj.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.MDTraj. at < http://mdtraj.org/latest/>.
- 59.Faller R, Reith D. Properties of poly(isoprene): Model building in the melt and in solution. Macromolecules. 2003;36:5406–5414. [Google Scholar]
- 60.Moore TC, Iacovella CR, McCabe C. Development of a coarse-grained water forcefield via multistate iterative. Boltzmann inversion. 2015 doi: 10.1007/978-981-10-1128-3_3. at < http://arxiv.org/abs/1509.07887>. [DOI] [PMC free article] [PubMed]
- 61.Marrink SJ, Lindahl E, Edholm O, Mark AE. Simulation of the spontaneous aggregation of phospholipids into bilayers. J Am Chem Soc. 2001;123:8638–9. doi: 10.1021/ja0159618. [DOI] [PubMed] [Google Scholar]
- 62.Brockman HL, et al. The 4,5-double bond of ceramide regulates its dipole potential, elastic properties, and packing behavior. Biophys J. 2004;87:1722–31. doi: 10.1529/biophysj.104.044529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Scheffer L, et al. Structure of cholesterol/ceramide monolayer mixtures: implications to the molecular organization of lipid rafts. Biophys J. 2005;88:3381–91. doi: 10.1529/biophysj.104.051870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Berger O, Edholm O, Jähnig F. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys J. 1997;72:2002–13. doi: 10.1016/S0006-3495(97)78845-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Metcalf R, Pandit SA. Mixing Properties of Sphingomyelin Ceramide Bilayers: A Simulation Study. J Phys Chem B. 2012;116:4500–4509. doi: 10.1021/jp212325e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Wartewig S, Neubert RHH. Properties of ceramides and their impact on the stratum corneum structure: a review. Part 1: ceramides. Skin Pharmacol Physiol. 2007;20:220–9. doi: 10.1159/000104420. [DOI] [PubMed] [Google Scholar]
- 67.Kessner D, Ruettinger A, Kiselev MA, Wartewig S, Neubert RHH. Properties of ceramides and their impact on the stratum corneum structure. Part 2: stratum corneum lipid model systems. Skin Pharmacol Physiol. 2008;21:58–74. doi: 10.1159/000112956. [DOI] [PubMed] [Google Scholar]
- 68.Swartzendruber DC, Wertz PW, Kitko DJ, Madison KC, Downing DT. Molecular Models of the Intercellular Lipid Lamellae in Mammalian Stratum Corneum. J Invest Dermatol. 1989;92:251–257. doi: 10.1111/1523-1747.ep12276794. [DOI] [PubMed] [Google Scholar]
- 69.Kuempel D, Swartzendruber DC, Squier CA, Wertz PW. In vitro reconstitution of stratum corneum lipid lamellae. Biochim Biophys Acta. 1998;1372:135–40. doi: 10.1016/s0005-2736(98)00053-4. [DOI] [PubMed] [Google Scholar]
- 70.Norlén L. Skin barrier structure and function: the single gel phase model. J Invest Dermatol. 2001;117:830–836. doi: 10.1038/jid.2001.1. [DOI] [PubMed] [Google Scholar]
- 71.Kiselev MA. Conformation of ceramide 6 molecules and chain-flip transitions in the lipid matrix of the outermost layer of mammalian skin, the stratum corneum. Crystallogr Reports. 2007;52:525–528. [Google Scholar]
- 72.Das C, Olmsted PD, Noro MG. Water permeation through stratum corneum lipid bilayers from atomistic simulations. Soft Matter. 2009;5:4549. [Google Scholar]
- 73.de Jager MW, et al. Novel lipid mixtures based on synthetic ceramides reproduce the unique stratum corneum lipid organization. J Lipid Res. 2004;45:923–32. doi: 10.1194/jlr.M300484-JLR200. [DOI] [PubMed] [Google Scholar]
- 74.Rerek ME, Van Wyck D, Mendelsohn R, Moore DJ. FTIR spectroscopic studies of lipid dynamics in phytosphingosine ceramide models of the stratum corneum lipid matrix. Chem Phys Lipids. 2005;134:51–58. doi: 10.1016/j.chemphyslip.2004.12.002. [DOI] [PubMed] [Google Scholar]
- 75.Gooris GS, Bouwstra JA. Infrared Spectroscopic Study of Stratum Corneum Model Membranes Prepared from Human Ceramides, Cholesterol, and Fatty Acids. Biophys J. 2007;92:2785–2795. doi: 10.1529/biophysj.106.094292. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.