Modeling Soft Tissue Damage and Failure Using a Combined Particle/Continuum Approach

Abstract

Biological soft tissues experience damage and failure as a result of injury, disease, or simply age; examples include torn ligaments and arterial dissections. Given the complexity of tissue geometry and material behavior, computational models are often essential for studying both damage and failure. Yet, because of the need to account for discontinuous phenomena such as crazing, tearing, and rupturing, continuum methods are limited. Therefore, we model soft tissue damage and failure using a particle/continuum approach. Specifically, we combine continuum damage theory with Smoothed Particle Hydrodynamics (SPH). Because SPH is a meshless particle method, and particle connectivity is determined solely through a neighbor list, discontinuities can be readily modeled by modifying this list. We show, for the first time, that an anisotropic hyperelastic constitutive model commonly employed for modeling soft tissue can be conveniently implemented within a SPH framework and that SPH results show excellent agreement with analytical solutions for uniaxial and biaxial extension as well as finite element solutions for clamped uniaxial extension in 2D and 3D. We further develop a simple algorithm that automatically detects damaged particles and disconnects the spatial domain along rupture lines in 2D and rupture surfaces in 3D. We demonstrate the utility of this approach by simulating damage and failure under clamped uniaxial extension and in a peeling experiment of virtual soft tissue samples. In conclusion, SPH in combination with continuum damage theory may provide an accurate and efficient framework for modeling damage and failure in soft tissues.

1 Introduction

Biological soft tissues are remarkably durable under the action of physiologic loads. Nevertheless, they are susceptible to load-induced damage and ultimate failure; common examples range from torn ligaments (Weiss and Gardiner 2001) to arterial dissections (Roccabianca et al. 2014). Given the complexity of tissue geometry and material properties, computational methods are often essential for studying tissue damage and failure, yet traditional continuum approaches are limited in this regard.

In this paper, we explore a novel combination of continuum and discrete particle methods to model damage and subsequent catastrophic failure in soft tissues that exhibit nonlinear anisotropic behaviors under finite deformations. Specifically, we meld a traditional continuum damage model with a Smoothed Particle Hydrodynamics (SPH) model. Although conceived for use in astrophysics, in the most general sense, SPH is a meshfree Lagrangian method for the numerical solution of differential equations of motion. Rather than requiring mesh-based discretization of the spatial domain, SPH relies on a list of particles over which quantities of interests are smoothed. Since its introduction by Gingold and Monaghan (1977) and Lucy (1977), SPH applications have ranged from the molecular level to galactic scales. Herein, however, our interest is in its potential advantages in the field of nonlinear solid mechanics, and in particular soft tissue mechanics (Monaghan 1992; Liu and Liu 2010; Springel 2010; Monaghan 2012). Among other advantages, SPH can account for large deformations without remeshing and, as we will see later, it can account for macroscopic damage and gross failure (Benz and Asphaug 1995).

The first application of SPH in solid mechanics dates back to Libersky and Petschek (1991). Yet, despite promising early results, applications in solid mechanics had until recently been limited by at least three major shortcomings: (i) In its original formulation, SPH particles tend to cluster locally while allowing non-physical gaps elsewhere in the domain. This poses a serious problem, especially for applications in damage mechanics (Swegle et al. 1995; Dyka et al. 1997; Monaghan 2000). (ii) An instability due to the rank-deficiency of the method (similar to hourglass modes in finite elements using reduced integration) can lead to non-physical solutions (Belytschko et al. 2000; Rabczuk et al. 2004). (iii) SPH does not provide first-order, or even zeroth-order, completeness. Thus, in its non-normalized form, gradients of constant and linear fields cannot be computed exactly (Belytschko et al. 1998).

Fortunately, all three of these challenges have essentially been overcome. Belytschko et al. (2000) traced SPH particle lumping back to its updated Lagrangian character, where the list of neighboring particles is updated frequently based on current particle coordinates. This problem is effectively circumvented by using a “Total Lagrangian” SPH, in which particle lists are established in the reference configuration and not, or seldom, updated. SPH “hourglassing” has been overcome by the introduction of “stress points” by Dyka and Ingel (1995) and Randles and Libersky (2000), and the recent introduction of an hourglass control algorithm by Ganzenmüller (2015). Finally, correct calculation of gradients of constant and linear functions have been achieved through “normalization” steps described below (Randles and Libersky 1996).

Consequently, only recently has SPH provided a reliable framework for applications in solid mechanics. While there are a few examples where SPH has been used to model the behavior of soft tissues, limitations yet include the use of an updated Lagrangian formulation, no normalization, restrictions to isotropic and/or linear elastic material behavior, or use of a background mesh/grid (Hieber et al. 2003; Hieber and Koumoutsakos 2008; Horton et al. 2010; Boyer et al. 2015). The purpose of this paper, therefore, is to review key equations of the Normalized Total Lagrangian SPH method as a representative meshless approach for modeling soft tissue mechanics and to demonstrate its potential utility in modeling damage and subsequent failure of a generic anisotropic soft tissue subjected to finite deformations.

2 Normalized Total Lagrangian SPH

2.1 Mathematical framework

As noted earlier, Total Lagrangian SPH computes all quantities in the reference configuration, herein denoted by capital letters to distinguish them from quantities in the current configuration, which are denoted by lower case letters. Note, too, that subscript indices do not imply summation; rather, they denote collocation points commonly referred to as “particles”. Thus, X_i is the location of particle “i” in the reference configuration whereas x_i is its coordinate location in the current configuration.

In the SPH framework, physical quantities are interpolated over a particle's immediate neighborhood. To this end, we assume that the function f(X), at point X_i, can be approximated by the convolution

$$\widehat{g}\left({\mathit{X}}_i\right)=\int f\left(\mathit{X}\right)W(\mathit{X}-{\mathit{X}}_i)\mathrm{d}\mathit{X},$$ (1)

where Ŵ is referred to as the kernel. If W takes the form of the Dirac delta, ĝ(X_i) is exactly f(X_i). Yet, because the Dirac delta has zero support, kernel functions with finite support radius h, the smoothing length, are preferred. Well-designed kernel functions nevertheless share the compact support property and the unity property with the Dirac delta and converge toward the Dirac delta for smoothing lengths h → 0.

For example, the kernel used herein is the so-called Spiky kernel, a third-order polynomial,

$$W({\mathit{R}}_j,h)=A\{\begin{array}{cc}{(h-R_j)}^3\hfill & R_j<h\hfill \\ 0\hfill & R_j\ge h\hfill \end{array}\phantom{\}},$$ (2)

where R_j is the reference distance vector, R_j = X_j − X_i, between particles i and j with the Euclidean length R_j with A = 10/(πh⁵) in two dimensions or A = 15/(πh⁶) in three dimensions (Fig. 1). We chose the Spiky kernel because it has been shown to prevent the clustering of neighboring particles in close proximity due to vanishing repulsive forces seen with other popular kernels (Desbrun and Gascuel 1996). Regardless of the specific choice of W, spatial discretization in SPH is performed by approximating the integral expression in (1) with a finite sum over discrete points, f_j = f(X_j), that lie in the neighborhood S of X_i, hence

$$g\left({\mathit{X}}_i\right)=\sum _{j\in S}{f}_j{V}_{j}W({\mathit{R}}_j,h).$$ (3)

X_j are thus the referential coordinates of all the neighbors of particle i at X_i within the support of the kernel as defined through the smoothing length h; V_j is the reference volume associated with each neighboring particle. The product of the neighboring particle's volume and its kernel weight may be interpreted as a “shape function”.

Fig. 1.

“Spiky” SPH kernel. Right Illustration of the kernel's weight distribution. Left Projection of the kernel function onto the 2D plane to illustrate the kernel's radius of influence (in this case three times the particle distance δ)

The referential gradient of g(X) at particle i follows accordingly,

$${\nabla }_{\mathit{X}}g\left({\mathit{X}}_i\right)=\sum _{j\in S}{f}_j{V}_j{\nabla }_{\mathit{X}}W({\mathit{R}}_j,h),$$ (4)

where gradients of the kernel functions are defined as

$${\nabla }_{\mathit{X}}W({\mathit{R}}_j,h)=\left(\frac{\partial W({\mathit{R}}_j,h)}{2{\mathit{R}}_j}\right)\frac{{\mathit{R}}_j}{{\mathit{R}}_j}.$$ (5)

Equations (1)–(5) hold true for the vector field f(X) as well, with the gradient becoming a second-order tensor,

$${\nabla }_{\mathit{X}}\mathit{g}\left({\mathit{X}}_i\right)=\sum _{j\in S}{\mathit{f}}_j\otimes V_j{\nabla }_{\mathit{X}}W({\mathit{R}}_j,h).$$ (6)

Albeit straightforward, this formulation cannot produce correct gradients of constant or linear functions, which is necessary for ensuring conservation of linear and angular momentum, respectively (Bonet and Lok 1999; Bonet et al. 2004). To remove this deficiency, two ad-hoc corrections have been introduced. First, Monaghan (1988) suggested a simple but effective way, known as symmetrization, to compute the correct gradient of constant fields. That is, let

$${\nabla }_{\mathit{X}}g\left({\mathit{X}}_i\right)=\sum _{j\in S}(f_j-f_i)V_j{\nabla }_{\mathit{X}}W({\mathit{R}}_j,h).$$ (7)

Alternatively, one can use Shepard functions (Bonet and Lok 1999). Second, Randles and Libersky (1996) suggested a method to compute correct gradients of linear fields. Based on the condition

$$\sum _{j\in S}{\mathit{R}}_j\otimes V_j{\tilde{\nabla }}_{\mathit{X}}W({\mathit{R}}_j,h)=\mathit{I}\text{with}{\tilde{\nabla }}_{\mathit{X}}W({\mathit{R}}_j,h)\equiv {\mathit{A}}_i^{-1}{\nabla }_{\mathit{X}}W({\mathit{R}}_j,h),$$ (8)

where the shape tensor A is

$${\mathit{A}}_i=\sum _{j\in S}{V}_j{\nabla }_{\mathit{X}}W({\mathit{R}}_j,h)\otimes {\mathit{R}}_j,$$ (9)

with R_j = X_j − X_i, as noted above.

2.2 Mechanical implementation

To explicitly solve the equilibrium equations in referential form,

$$\mathrm{Div}\mathit{P}+{\rho }_0\mathit{b}={\rho }_0\ddot{\mathit{x}},$$ (10)

where P is the first Piola–Kirchhoff stress tensor, b the body force vector, ρ₀ the referential mass density, and ẍ the acceleration, we first compute the deformation gradient F_i = ∂x_i/∂X_i associated with each particle i. Using the definition of the Total Lagrangian SPH gradient and requisite normalizations, the deformation gradient follows as

$${\mathit{F}}_i=\sum _{j\in S}{\mathit{r}}_j\otimes V_j{\tilde{\nabla }}_{\mathit{X}}W({\mathit{R}}_j,h),$$ (11)

where r_j = x_j − x_i is the distance vector in the current configuration corresponding to each R_j.

In the following, we focus on hyperelastic materials in which stress is derived from a strain energy function $\mathcal{W}\left(\mathit{C}\right)$, which, by material frame indifference, is a function of the right Cauchy–Green tensor C = F^TF. The stress tensor P at X_i can therefore be calculated according to (Humphrey 2013)

$${\mathit{P}}_i=2{\mathit{F}}_i\frac{\partial \mathcal{W}\left({\mathit{C}}_i\right)}{\partial {\mathit{C}}_i},$$ (12)

using the relationship P = FS, where the second Piola–Kirchhoff stress tensor $\mathit{S}=2\partial \mathcal{W}∕\partial \mathit{C}$.

We express the local strong form of the equilibrium equation explicitly in terms of its external and internal forces,

$$m_i{\ddot{\mathit{x}}}_i={\mathit{f}}_i^{\mathrm{int}}+{\mathit{f}}_i^{\mathrm{ext}},$$ (13)

in which the internal forces emerge from the divergence of the first Piola–Kirchhoff stress P as per the introduced approximations and normalizations shown in Bonet and Lok (1999) and Ganzenmüller (2015),

$${\mathit{f}}_i^{\mathrm{int}}=\sum _{j\in S}{V}_i{V}_j({\mathit{P}}_i{\tilde{\nabla }}_{\mathit{X}}W({\mathit{R}}_j,h)-{\mathit{P}}_j{\tilde{\nabla }}_{\mathit{X}}W({\mathit{R}}_i,h)).$$ (14)

Once the accelerations ẍ_i are updated at t + Δt as a function of internal and external forces, we obtain particle locations x_i through integration via the Leap Frog scheme (Ganzenmüller 2015; Ganzenmüller et al. 2015). Displacement boundary conditions can then be enforced by overwriting the integrated particle displacements with their respective boundary values. The total procedure is summarized in Algorithm 1.

Algorithm 1.

Normalized Total Lagrangian SPH Algorithm, adapted from (Ganzenmüller 2015)

1:	for all times t do
2:	for all particles i do
3:	for all neighbors j ∈ S do
4:	${\mathit{F}}_i\leftarrow {\mathit{F}}_i+{\mathit{r}}_j\otimes V_j{\nabla }_{\mathit{X}}W({\mathit{R}}_j,h)$	▷ Compute uncorrected deformation gradient
5:	${\mathit{A}}_i\leftarrow {\mathit{A}}_i+{\mathit{R}}_j\otimes V_j{\nabla }_{\mathit{X}}W({\mathit{R}}_j,h)$	▷ Compute shape matrix
6:	end for
7:	${\mathit{F}}_i\leftarrow {\mathit{F}}_i{\mathit{A}}_i^{-1}$	▷ Correct deformation gradient
8:	${\mathit{P}}_i\leftarrow 2{\mathit{F}}_i\partial \mathcal{W}∕\partial {\mathit{C}}_i$	▷ Compute first Piola–Kirchhoff stress tensor
9:	${\mathit{P}}_i\leftarrow {\mathit{P}}_i{\mathit{A}}_i^{-1}$	▷ Correct stress tensor
10:	end for
11:	for all particles i do
12:	for all neighbors j ∈ S do
13:	${\mathit{f}}_i^{\mathrm{int}}\leftarrow {\mathit{f}}_i^{\mathrm{int}}+V_i{V}_j({\mathit{P}}_i+{\mathit{P}}_j){\nabla }_{\mathit{X}}W({\mathit{R}}_j,h)$	▷ Compute internal particle forces
14:	end for
15:	end for
16:	${\ddot{\mathit{x}}}_i\leftarrow 1∕m_i{\mathit{f}}_i^{\mathrm{t}}$	▷ Compute particle accelerations $({\mathit{f}}_i^{\mathrm{t}}={\mathit{f}}_i^{\mathrm{int}}+{\mathit{f}}_i^{\mathrm{ext}}+{\mathit{f}}_i^{\mathrm{hg}})$
17:	end for

It is also worth mentioning that in contrast to the Finite Element Method, where homogeneous traction boundary conditions emerge naturally, this is not the case for the SPH method. Thus, special considerations must be employed to apply zero traction boundary conditions on free surfaces. In the current work, we followed what seems to be standard procedure in the SPH literature (Randles and Libersky 2000). We identified all free surface particles in the reference configuration and calculated their surface normals. Subsequently, we rotated the first Piola–Kirchhoff stress tensors at each time step into a local system parallel to the surface normal and set the necessary stress components of the tensor to zero before rotating the modified tensors back into their global system.

2.3 Mechanical stabilization

As mentioned above, we suppress spurious zero-energy modes using an hourglass control algorithm introduced by Ganzenmüller (2015). To reduce effects of non-physical motions of particles, the algorithm adds a penalty force to the right hand side of Eq. (13), namely

$${\mathit{f}}_i^{\mathrm{hg}}=\sum _{j\in S}-\alpha \frac{E{V}_i{V}_{j}W({\mathit{R}}_j,h)}{2R_j^2}({\delta }_i+{\delta }_j)\frac{{\mathit{r}}_j}{r_j},$$ (15)

where E is the assigned hourglass stiffness and α is a control parameter. δ_i and δ_j estimate the error due to zero-energy modes. For all examples considered below, we used α = 50 as recommended in Ganzenmüller (2015); for the hourglass stiffness, we used the initial modulus of the hyperelastic material. This approach was shown to yield quadratic convergence in the problem studied; for more details, we refer the reader to the original publication.

Rather than including an artificial viscosity term for stabilizing the SPH solution, we introduce such dissipation constitutively. Specifically, we model soft tissue as mildly “viscohyperelastic” by adding a Newtonian viscous stress tensor τ to the expression in (12),

$${\mathit{P}}_i=2{\mathit{F}}_i\frac{\partial \mathcal{W}\left({\mathit{C}}_i\right)}{\partial {\mathit{C}}_i}+\mathit{J}{\tau }_i{\mathit{F}}_i^{-T},$$ (16)

with J = detF and τ_i = 2μd_i, where μ is the viscosity and d is the stretching tensor. The latter is the symmetric part of the velocity gradient l = ∂v/∂x = ḞF⁻¹, which can be written as

$$\mathit{d}=\frac{1}{2}\left(\mathit{l}+{\mathit{l}}^{\mathrm{T}}\right).$$ (17)

The rate of change of the deformation gradient Ḟ can be computed with a simple finite difference scheme,

$$\stackrel{.}{\mathit{F}}=\frac{1}{\Delta t}\left({\mathit{F}}^{t+1}-{\mathit{F}}^t\right).$$ (18)

Finally, note that one of the more costly steps in Algorithm 1 is a neighbor search for each particle. Here, the Total Lagrangian approach provides an additional advantage in that this search is performed only once. Similarly, all other Lagrangian entities, such as reference distance vectors, shape matrices, and particle weights (volume and kernel value), can be typically calculated once at the beginning of the simulation. Exceptions include cases when very large deformations require an update of the neighboring particles or when a failure event disconnects particles, as we will see later. Fortunately, the SPH method lends itself very well to parallelization as the above equations are calculated for each particle independently. Thus, the domain can be easily split and distributed to multiple processors.

3 Damage and failure modeling of soft tissue

3.1 Material modeling of soft tissue

Soft tissues are complex composite materials which are highly heterogeneous, anisotropic, typically residually stressed and can exhibit viscoelastic characteristics (Rausch and Kuhl 2013). For illustrative purposes, we assume the behavior is dominated by nonlinear hyperelastic behavior (with mild added viscosity), with one dominant fiber family, and we ignore effects due to residual stress for the illustrative problems of interest. To this end, we employ a Fung-type constitutive relation defined through a strain energy function $\mathcal{W}(\mathit{C},\mathit{M})$ that depends on the right Cauchy–Green tensor C as well as the referential fiber orientation vector M (Holzapfel et al. 2000),

$$\mathcal{W}(\mathit{C},\mathit{M})=\frac{{\mu }_0}{2}(I_1-3)-p(J-1)+\frac{k_1}{4k_2}\left[\exp \left(k_2{(I_4-1)}^2\right)-1\right],$$ (19)

where coordinate invariant quantities I₁, j , and I₄ are defined as

$$I_1=\mathit{C}:\mathit{I},J=\det \mathit{F},I_4=\mathit{C}:\mathit{M}\otimes \mathit{M}.$$ (20)

The isotropic ground substance is thus described by the neo-Hookean strain energy having shear modulus μ₀, while the anisotropic fibrous extracellular matrix contributes to the strain energy though an exponential relationship determined by parameters k₁ and k₂. The remaining component of the strain energy function in Eq. (19) enforces incompressibility via the Lagrange multiplier p.

Note that the fibers only bear tensile load, thus the fiber term stores energy only if I₄ > 1. The second Piola–Kirchhoff stress can then be calculated through the Doyle–Ericksen relationship S = 2∂W/∂C,

$$\mathit{S}={\mu }_0\mathit{I}+k_1(I_4-1)\exp \left(k_2{(I_4-1)}^2\right)\mathit{M}\otimes \mathit{M}-p{J}^{-1}{\mathit{C}}^{-1}.$$ (21)

Unless otherwise stated, the following simulations are performed under the assumption of plane stress. In this case, the incompressiblity condition detF = 1 can be enforced analytically (Rausch and Kuhl 2014; Checa et al. 2015),

$$p=\frac{{\mu }_0}{C_{11}{C}_{22}-C_{12}{C}_{21}}.$$ (22)

Once the second Piola–Kirchhoff stress is known, the first Piola–Kirchhoff stress, as required for the present SPH formulation, can be obtained through P = FS.

3.2 Damage modeling of soft tissue

To model damage and ultimately the failure behavior of soft tissue, we propose a combined approach. We model microstructural damage accumulated throughout the load history of the soft tissue using a stretch-based continuum damage approach (Lee et al. 2015), then use SPH to capture macroscopic, discontinuous damage and ultimate failure. For the first part, isotropic damage evolution, we employ a simple model based on an approach popularized by Simo (Simo 1987; Rausch and Humphrey 2015). Let the strain energy function ${\mathcal{W}}_0(\mathit{C},\mathit{M})$ be augmented by damage D ∈ [0, 1]. D accumulates as the material experiences maximum principal stretch beyond a critical stretch level λ_crit,

$$\mathcal{W}(\mathit{C},\mathit{M},D)=(1-D){\mathcal{W}}_0(\mathit{C},\mathit{M}),$$ (23)

with D > 0 if λ > λ_crit, where ${\mathcal{W}}_0$ takes the form introduced in Eq. (19). Following standard arguments of thermodynamics, the second Piola–Kirchhoff stress is

$$\mathit{S}=2(1-D)\frac{\partial {\mathcal{W}}_0}{\partial \mathit{C}},$$ (24)

with the additional condition on the evolution of the damage variable,

$$-\frac{\partial \mathcal{W}}{\partial D}\stackrel{.}{D}\ge 0.$$ (25)

For the damage function D, we consider a simple, exponential evolution equation,

$$D=\{\begin{array}{cc}\exp \left({(({\lambda }_m-{\lambda }_{\mathrm{crit}})∕\tau )}^2\right)-1\hfill & {\lambda }_m\ge {\lambda }_{\mathrm{crit}}\hfill \\ 0\hfill & {\lambda }_m<{\lambda }_{\mathrm{crit}}\hfill \end{array}\phantom{\}}.$$ (26)

Thus, damage increases as the largest previously experienced maximum principal stretch λ_m(t) = max_{s∈(−∞,t]} λ(s) exceeds the critical stretch λ_crit at a rate determined through τ. This process is by definition irreversible as indicated in Eq. (25). Once λ_m exceeds λ_crit, the virgin strain energy function ${\mathcal{W}}_0$ is modified through the reduction factor (1 − D) and from then on, the deformation path is altered permanently. For ${\lambda }_m=\sqrt{\ln 2}\tau +{\lambda }_{\mathrm{crit}}$ the damage D equals one and the material can no longer store strain energy and is, thus, fully damaged. Figure 2a, b illustrate the sensitivity of the damage model to the parameters λ_crit and τ.

Fig. 2.

A continuum damage model for soft tissue. a Sensitivity to the damage parameter λ_crit that determines the stretch at which damage begins to accumulate in the material. b Sensitivity to the damage parameter τ that determines the rate at which damage accumulates

3.3 Failure modeling of soft tissue

As pointed out in the previous section, continuum damage mechanics predicts complete material failure at a point when the damage D has reached a value of one. Thereafter, the model has no capacity to predict discontinuous failure behaviors such as crazing, delamination, or rupture. Yet, because such behaviors are of most importance, they may render effects of newly created surfaces critical. Noting that these new surfaces may, in turn, be subjected to applied tractions, the SPH method provides a natural way of introducing such situations. Since the connection between particles is determined through the neighbor list established at the beginning of the simulation, modifications to this list can, in a straightforward manner, create discontinuities. Thus, the only task lies in determining which particles should be removed from the list of neighbors.

Figure 3 illustrates a simple algorithm based on what we call the visual radius of the damaged particles. Say at time t, before internal forces for the current particle i are determined through equations (11)–(22), we check whether any of the neighboring particles have been completely damaged (D = 1); if so, we add them to a second list of damaged neighboring particles. Next, we send “visual rays” from the current particle i to each undamaged neighboring particle. If a ray intersects the visual radius of a damaged particle, we remove the undamaged particle in the “shadow” of the damaged particle from our list of neighbor particles (all particles contained in the gray area in Fig. 3). For a good choice of the visual radius, this approach generates impenetrable ruptures in two dimensions and rupture surfaces in three dimensions. While this method becomes computationally more expensive with a large number of damaged particles and long lists of neighboring particles, the algorithm is never entered until catastrophic failure is eminent. Thus, its cost is limited in comparison to the total simulation time. Note, too, that once a particle is fully damaged (i.e. D = 1), we remove it from the simulation. Thus, mass of the damaged material is not preserved per se, though overall mass is yet conserved (that of the remnant material plus that of the material that is lost). This effect is otherwise negligible for sufficiently large numbers of particles.

Fig. 3.

Discontinuous SPH damage & failure algorithm. All undamaged neighboring particles in the shadow of fully damaged particles are excluded from the neighbor list (gray area). The damaged particles thus create a rupture path (in 2D) or surface (in 3D) along which the domain is disconnected

4 Illustrative examples

4.1 Verification under uniaxial and biaxial extension

To verify the implementation of Eqs. (11)–(22), we compared stresses generated in response to uniaxial and biaxial extension of a 20 mm × 20 mm tissue strip predicted by the SPH method and analytically (Fig. 4). Such loading protocols are routinely employed to characterize the mechanical behavior of soft tissues. To test the sensitivity of SPH to key parameters, such as particle density, smoothing length, and the hourglass stiffness, we studied their effect on the maximum error relative to the analytical solutions. To minimize inertial effects, we chose a fifth-order polynomial loading curve with a mean displacement speed of 10 mm/s.

Fig. 4.

SPH predicts well the stress and reaction force under homogenous deformation and under inhomogeneous deformation, respectively, with an error of ~1%. a Comparison of the uniaxial stress–stretch response in the fiber direction (blue curve) and orthogonal to the fiber direction (red curve) with the analytical solution. b Comparison of the biaxial stress–stretch response with the analytical solution. c Comparison of the clamped uniaxial reaction force-stretch response with a finite element solution (FEM) for a uniform SPH particle distribution and d a non-uniform SPH particle distribution. The 20mm × 20mm tissue sample was discretized with 441 particles and 400 quadrilateral finite elements

As expected, accuracy of the SPH method increased with increasing particle density. Interestingly, however, a smoothing length h three to four times the characteristic particle distance δ resulted in the smallest errors. Lastly, a hourglass stiffness equal to the initial stiffness of the material provided a good compromise between suppressing zero-energy modes and artificially increasing model stiffness. Figure 4a, b shows results for both loading scenarios in the fiber and orthogonal directions with material parameters μ₀ = 0.1 MPa, k₁ = 0.1 MPa, k₂ 1.5 as well as a characteristic particle distance δ = 1 mm, smoothing length h four times δ, an hourglass stiffness of 0.1 MPa. As seen in Fig. 4a, b, under simple deformations such as uniaxial and biaxial extension, the SPH method, with the given parameters, agrees well with the analytical solutions (maximum error of 0.89%).

4.2 Validation under clamped uniaxial extension

To validate the SPH method, we compared reaction forces for the clamped uniaxial extension of a 20 mm × 20 mm tissue strip predicted by SPH and a finite element method (FEM). This loading protocol is routinely employed during damage and failure testing of anisotropic soft tissues (Stemper et al. 2007) and will be repeated in subsequent sections. In addition, this problem, in contrast to the verification problems in the previous section, will test the accuracy of SPH for inhomogeneous problems. All parameters and properties for the SPH simulation are identical to the verification problems under uniaxial and biaxial extension. The FEM simulation was performed on a 20 mm × 20 mm tissue strip discretized with 400 quadrilateral shell finite elements. We chose the same material model for the FEM simulation as for the SPH simulation and incompressibility was enforced through the penalty method in combination with a three field solution strategy. Finally, the FEM simulations were carried out in the open source finite element software FEBio 2.3.1 (Maas et al. 2012). The results for the SPH simulation and the FEM simulation are shown in Fig. 4c. Agreement of the reaction force for the two methods demonstrates the accuracy of SPH under a large, inhomogenous deformation (maximum error 1.01%). Because SPH convergence has previously been shown to deteriorate with irregular particle spacing, the same comparison was also carried out with non-uniformly spaced particles. While the error for the non-uniform particle distribution increased to 1.12%, the comparison resulted nonetheless in good agreement between SPH and FEM, see Fig. 4d.

Lastly, we extended the validation experiment under clamped uniaxial extension to the three dimensional case. In this example, for both SPH and FEM, we chose a neo-Hookean material model,

$$\mathcal{W}\left(\mathit{C}\right)=\frac{{\mu }_0}{2}(I_1-3)-{\mu }_0\ln J+\frac{\widehat{\lambda }}{2}{\left(\ln J\right)}^2,$$ (27)

with a shear modulus μ₀ of 0.1 MPa and a Lamé parameter $\widehat{\lambda }$ of 9 MPa. I₁ and J are invariants introduced in Eq. (20). The FEM solution to the clamped uniaxial extension problem was, again, obtained using FEBio. Figure 5a, b shows, qualitatively, that an excellent agreement was obtained between the two solutions. Quantitatively, errors are smaller than 1% throughout most of the domain. Not surprisingly errors were highest at the boundary (as high as 5%), likely due to SPH's non-local support and the lack of neighbors beyond the outer surfaces, see Fig. 5c, d.

Fig. 5.

Clamped uniaxial extension of a soft tissue strip in 3D. a, b SPH compares well with the finite element method (FEM) for clamped uniaxial extension in 3D—note that we show both solutions separately for SPH (particles) and FEM (exterior faces of the elements). c, d Errors between SPH and FEM under clamped uniaxial extension are <1% throughout most of the domain, but are as high as 5% at the domain boundaries. e Comparison between SPH and FEM for clamped uniaxial extension to failure of a soft tissue strip in 3D (because SPH particles are removed upon failure, their corresponding finite elements are depicted as transparent). In both SPH and FEM, tissue was modeled as neo-Hookean with shear modulus of 0.1MPa and Lamé parameter of 9MPa. The 20mm × 20mm × 4mm strip was discretized with 2205 SPH particles and 1600 linear hexahedral finite elements

4.3 Failure under clamped uniaxial extension

Consider again a clamped uniaxial extension of a virtual soft tissue sample having one of two different fiber directions: vertical and diagonal. Using the same spatial and temporal descritization, loading curve, and SPH parameters as in Sect. 3.1, we chose the visual radius of the discontinuous damage model to be $\sqrt{2}$ times the particle distance. To further mimic the natural variation in damage patterns, we assigned each particle a λ_crit according to a normal distribution with a mean of 1.4 and standard deviation of 0.01; τ was set to 0.3. The lowest viscosity that prevented instabilities was chosen. Figure 6 shows the damage evolution of the virtual tissue samples from the undeformed configuration to complete failure. The curves demonstrate the seamless interplay between the continuum damage model and the discontinuous failure model. While the stress–stretch function follows the characteristic response curve of soft tissues during the initial loading, damage begins to accumulate at a clamp-to-clamp stretch of ~1.35, at which point the simulations begin to diverge as probabilistic effects of the randomly distributed damage thresholds gain in significance. Once the first particle fails, focal stretches quickly drive other particles to fail leading to catastrophic failure soon thereafter.

Fig. 6.

Stress–stretch response to uniaxial extension with clamped ends (i.e., non-homogenous deformation) predicted by the combined damage and failure model. Damage begins to accumulate at a clamp-to-clamp stretch of ~1.35, at which point the simulations begin to diverge as probabilistic effects of the randomly distributed damage thresholds gain in significance. a Fibers in the vertical direction. b Fibers in the diagonal direction. All curves represent the mean of n = 10 samples and shaded areas represent the range of solutions due to variations in critical stretch values

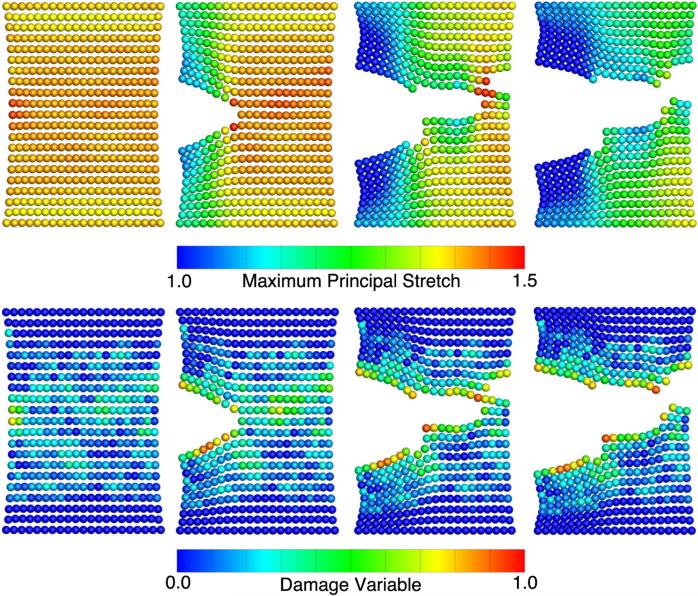
Expectedly, the fiber orientation strongly determines the failure behavior. Most markedly, the vertical fiber distribution results in the higher failure stress and higher failure stretch. On the other hand, the diagonal fiber distribution results in the lower failure stress and stretch. A time sequence with stretch and damage distributions for vertical and diagonal fiber orientation are further illustrated in Figs. 7 and 8.

Fig. 7.

SPH time sequence for a vertical fiber orientation in a soft tissue strip under clamped uniaxial extension to failure. The 20 mm × 20 mm strip was discretized with 441 SPH particles

Fig. 8.

SPH time sequence for a diagonal fiber orientation in a soft tissue strip under clamped uniaxial extension to failure. The 20 mm × 20 mm strip was discretized with 441 SPH particles

We further validate our approach by repeating a simplified failure experiment under clamped uniaxial extension in 3D and comparing it to a finite element solution. For both simulations, we used again a neo-Hookean material model with a shear modulus μ₀ of 0.1 MPa and a Lamé parameter $\widehat{\lambda }$ of 9 MPa. For the SPH simulation, we further used a particle density of 2205 within the 20 mm × 20 mm × 4 mm sample. However, in contrast to the 2D case, we virtually cut the initial soft tissue sample by removing a set of particles on the lateral side of the domain effectively predetermining the subsequent failure path. In addition, we omitted the damage softening effect in these simulations. We also built a finite element model of the same soft tissue sample that included cohesive elements between a lower and upper half of the domain. The cohesive elements were modeled as nonlinear springs between nodes of the cohesive interface, where the spring constants were chosen very large before failure and set to zero at the time of tissue failure. Subsequently, we calibrated the spring constants in the finite element simulation to fail at the same times as particles in the SPH simulation. A comparison of the dynamic response to these discrete failure events are shown in Fig. 5e.

4.4 Virtual peeling experiment

Peeling experiments are performed, for example, to characterize the delamination behavior of arterial wall tissue. In our next example, we model these experiments on an idealized tissue strip (Sommer et al. 2008; Tong et al. 2011). Similar to simulations carried out previously (Gasser and Holzapfel 2006), we consider a 4mm × 1.2mm tissue sample. Opposing Dirichlet boundary conditions were applied to the particles of the left and right side of the top surface, while all other boundaries remained traction free. In the first time step, we also introduce a 1mm cut in the long-axis direction as per the experiments performed by Sommer et al. (2008). Material parameters and SPH-specific parameters were chosen the same as in the example in Sect. 4.3, except that we assigned each particle a λ_crit according to a normal distribution with a mean of 1.6 and standard deviation of 0.05. Fibers are oriented in the direction of the long axis.

Figure 9 shows the temporal progression of a representative experiment. The reference configuration is shown at the bottom, while the last configuration before failure is shown on top. The results are qualitatively similar to previous simulations on the same geometry that employed the Partition of Unity Finite Element Method (Gasser and Holzapfel 2006). Figure 10 shows the peeling force recorded as a function of the separation path averaged over ten tissue samples. Upon initiation of separation, the force stays approximately constant with intermediate spikes that are related to individual particles failing and the following rebound effect. The average force curve shows good qualitative agreement with experimental data (Sommer et al. 2008), which also show an approximately constant peeling force throughout the experiment though with intermediate spikes. It is noted that if the tear is not initiated with an initial cut, as in the experiment, there is a transient increase then decrease in the pulling force toward the steady state value. This transient may occur due to changes in tear depth during the initial phase of the experiment that essentially serves as a lever for the lateral pulling force.

Fig. 9.

Temporal evolution of tissue sample in virtual peeling experiment using the SPH method. The tissue was modeled as solid mixture of neo-Hookean ground substance with long-axis-wise-oriented Fung-type fibers. The 4 mm × 1.2 mm strip was discretized with 480 SPH particles

Fig. 10.

Reaction force during a virtual peeling experiment. The tissue sample was modeled as a solid mixture of neo-Hookean ground substance with long-axis-wise-oriented Fung-type fibers. The 4 mm × 1.2 mm strip was discretized with 480 SPH particles. Shown is the mean response (in black) for ten samples along with ±1 standard deviation (in grey)

5 Discussion

The goal of the present work was to review the Normalized Total Lagrangian SPH method and to explore its potential for application in soft tissue mechanics. We found that the method introduced in Sect. 2 lends itself well to the implementation of standard constitutive relations of finite strain anisotropic elasticity and thus applies to soft tissue modeling. We demonstrated this capability using a Fung-type relation frequently employed in soft tissue mechanics (Famaey et al. 2013; Genet et al. 2015) and that, for simple cases of uniaxial and biaxial extension as well as clamped uniaxial extension, the SPH method predicts elastic responses under large deformations. To illustrate potential utility of the SPH method, we implemented a combined continuum damage and discontinuous failure model that builds on the SPH's natural ability to create material discontinuities. Applied to modeling clamped uniaxial extension and peeling of a generic soft tissue sample to failure, we found that the Total Lagrangian SPH model yields behaviors closely resembling experimental observations (Stemper et al. 2005; Sommer et al. 2008; Tong et al. 2011).

While the hourglass control algorithm was recently shown to stabilize SPH simulations and to improve accuracy when compared to analytical solutions to simple deformations, this was only for linearly elastic, isotropic materials. Here, we found that the hourglass stiffness parameter must be chosen strategically in nonlinear elasticity; there is a balance between artificially increasing the material stiffness too much and not suppressing the instability sufficiently. Especially due to the nonlinear, anisotropic nature of soft tissues, the effect of the hourglass algorithm varies with fiber orientation and degree of deformation. As can be seen from the present results, however, it is possible to find parameter values that enable realistic simulations. Future developments may provide an automatic adaptation algorithm for material anisotropy and nonlinearity.

Lastly, we chose SPH as a well-known, well-documented representation of meshless methods. SPH is not the only tool of this type available. Other methods, such as Peridynamics (Silling et al. 2007) and the Element-Free Galerkin Method (Jin et al. 2014) as well as the closely related Meshless Total Lagrangian Explicit Dynamics method (MTLED) (Miller et al. 2012; Li et al. 2016), may provide a good alternative to the method introduced in the current work. Note, too, that methods such as the one discussed here as well as MTLED lend themselves well to surgical simulations because of straight-forward spatial discretization as well as their algorithmic simplicity. Horton et al. (2010), for example, discuss the potential of meshless, Total Lagrangian explicit methods for real-time simulations. Our method was implemented in Matlab R2013b and no attempts were made toward optimizing this code in regard to efficiency or parallelization. As a result, the per time step cost was approximately 0.3s for the problem in Fig. 7a on an Intel^® Xeon^® E5-2630 at 2.3GHz. Implementation in a more efficient framework as well as parallelization and the utilization of graphics processing units (GPUs) will show whether Total Lagrangian SPH has potential toward real-time simulations for problems defined on large domains.

In conclusion, SPH previously suffered from a number of challenges that limited its use in solid mechanics, but the aforementioned recent advances by others have yielded new promise. Via initial verifications and validations as well as subsequent examples, we have demonstrated that the SPH method should now be considered a more useful numerical tool in solid mechanics, and soft tissue mechanics in particular. Especially where catastrophic failure such crazing, dissection, and rupture is modeled, the natural way of creating such discontinuities in SPH may provide some advantages over more established mesh-dependent numerical methods such as the finite element method. Further development of the method is thus warranted.