White matter predicts functional connectivity in premanifest Huntington's disease

Abstract

Objectives

The distribution of pathology in neurodegenerative disease can be predicted by the organizational characteristics of white matter in healthy brains. However, we have very little evidence for the impact these pathological changes have on brain function. Understanding any such link between structure and function is critical for understanding how underlying brain pathology influences the progressive behavioral changes associated with neurodegeneration. Here, we demonstrate such a link between structure and function in individuals with premanifest Huntington's.

Methods

Using diffusion tractography and resting state functional magnetic resonance imaging to characterize white matter organization and functional connectivity, we investigate whether characteristic patterns of white matter organization in the healthy human brain shape the changes in functional coupling between brain regions in premanifest Huntington's disease.

Results

We find changes in functional connectivity in premanifest Huntington's disease that link directly to underlying patterns of white matter organization in healthy brains. Specifically, brain areas with strong structural connectivity show decreases in functional connectivity in premanifest Huntington's disease relative to controls, while regions with weak structural connectivity show increases in functional connectivity. Furthermore, we identify a pattern of dissociation in the strongest functional connections between anterior and posterior brain regions such that anterior functional connectivity increases in strength in premanifest Huntington's disease, while posterior functional connectivity decreases.

Interpretation

Our findings demonstrate that organizational principles of white matter underlie changes in functional connectivity in premanifest Huntington's disease. Furthermore, we demonstrate functional antero–posterior dissociation that is in keeping with the caudo–rostral gradient of striatal pathology in HD.

Introduction

Huntington's disease (HD) is a fully penetrant monogenic neurodegenerative disorder. As the timing of clinical onset can be predicted with relative certainty, it provides a unique opportunity to study the earliest structural changes in the brain occurring years before clinical onset.1 Such pathological changes to brain structure do not occur randomly but in a stereotyped fashion. Recent research shows that this characteristic pattern of structural change is linked to the organizational principles of the healthy human brain. Specifically, brain regions with stronger anatomical links to distant regions and fewer connections to neighboring regions in a healthy brain show greater white matter (WM) loss in patients with Huntington's disease.2 Such organizational principles are also connected to the structural change seen in Alzheimer's disease, frontotemporal dementia and corticobasal syndrome.3

However, an unresolved question is how such characteristic patterns of structural change impact brain function and the activity‐based (functional) coupling between brain regions. Understanding such a relationship is critical to understanding the link between structural degeneration and behavioral change in neurodegeneration. It is changes in functional coupling between brain areas (and activity within those brain areas) that ultimately underlies behavioral change. Change in brain structure and anatomical connectivity in pre‐HD occurs well before clinical presentation in the absence of behavioral change, suggesting some form of functional compensation.4 Thus, a model of neurodegeneration in HD where reduction in anatomical links between brain areas is always associated with loss of functional connections (and consequent behavioral change) may be too simple. Some regions may potentially show increased functional coupling as a compensatory mechanism for decreased anatomical coupling in order to maintain sensory, cognitive or motor function in the face of structural change.5 It is important to determine whether there are principles or patterns underlying changes in functional coupling between brain areas in neurodegeneration that either follow or dissociate from structural change.

To resolve this question, we studied a large and well‐characterized cohort of pre‐HD patients from the TrackOn‐HD study.5 Using graph theoretical measures to characterize the organization of healthy WM, we tested the hypothesis that regions with fewer anatomical (WM) connections might show the greatest capacity for upregulation of their functional connectivity in pre‐HD relative to controls. Strong evidence was found in support of our hypothesis. Furthermore, we found that strong functional connections in healthy controls were stronger in the pre‐HD group in anterior brain regions. However, in more posterior regions strong functional connections showed reduced functional coupling. This striking antero–posterior dissociation of functional coupling in individuals with pre‐HD provides new evidence concerning the potential for compensatory mechanisms in preclinical neurodegeneration.

Materials and Methods

Cohort

The cohort included participants from the first visit of the Track‐On HD study from all sites (London, Leiden, Paris and Vancouver).5 From a total Track‐On HD cohort of 243, participants were excluded (see Kloppel et al.5 for detailed inclusion/exclusion criteria) due to; manifest disease (21), left handed or ambidextrous (24), poor quality fMRI data (11) and poor quality diffusion‐weighted imaging (DWI) data (36; see imaging sections). To age‐match the remaining cohort 21 participants <30 and >60 years of age were excluded. This left a cohort of 64 pre‐HD individuals and 66 healthy controls described in Table 1. Of the participants included, 31 pre‐HD and 29 controls had participated previously in Track‐HD. Our recently published structural connectivity analysis was conducted using 2011 Track‐HD data thus there is no overlap in imaging data used in this study.2

Table 1.

Demographics

	Pre‐HD	Control	Statistical test	P‐value
N	64	66	—	—
Age (SD)	43.5 (8)	45.5 (7.5)	2 tail t‐test	0.15
Gender (M/F)	35/29	26/40	Chi‐square	0.081
Education (2/3/4/5/6)	3/13/22/24/1	5/11/21/27/2	Chi‐square	0.851
Study site (N) (Leiden/London/Paris/Vancouver)	11/24/16/13	15/24/17/10	Chi‐square	0.8
CAG (SD)	42.67 (2.03)	—	—	—
DBS (SD)	300.3 (53.6)	—	—	—
CPO (SD)	0.24 (0.15)	—	—	—

SD, standard deviation; M, male; F, female; N, number; ISCED, International standard classification of education. CAG, CAG repeat expansion length, DBS, disease burden scale37, CPO, cumulative probability of onset.38

MRI acquisition

3T MRI data were acquired on two different scanner systems (Philips Achieva at Leiden and Vancouver and Siemens TIM Trio at London and Paris). Diffusion‐weighted images were acquired with 42 unique gradient directions (b = 1000 sec/mm²). Eight images with no diffusion weighting (b = 0 sec/mm²) and one image with no diffusion weighting (b = 0 sec/mm²) were acquired from the Siemens and Philips scanners, respectively. For resting state fMRI, 165 whole‐brain volumes were acquired at a repetition time (TR) of 3 sec using a T2*‐weighted echo planar imaging (EPI) sequence. Scanning time was approximately 12 min for T1‐weighted, 10 min for diffusion‐weighted acquisitions and 15 min for rsfMRI. Scanning times of between 12 and 16 min have previously been shown to increase the reliability of resting state fMRI connectivity estimates.6 See Kloppel et al.5 for detailed acquisition parameters and quality control procedures.

MRI data analysis

Structural MRI data

Cortical and subcortical regions of interest (ROIs) were generated by segmenting a T1‐weighted image, using Freesurfer.7 These included 70 cortical regions and 6 subcortical regions (caudate, putamen and thalamus bilaterally). The globus pallidus, nucleus accumbens and amygdala were not included as automatic segmentation of these regions is not sufficiently reliable.8 The cerebellum was not included as associated diffusion data was incomplete.

Diffusion tensor imaging data

Data preprocessing

Initial preprocessing steps were performed using FSL.9 For the diffusion data the b = 0 image was used to generate a brain mask using FSL's brain extraction tool.10 Eddy current correction was used to align the diffusion‐weighted volumes to the first b = 0 image and the gradient directions updated to reflect the changes to the image orientations. Finally, diffusion tensor metrics were calculated and constrained spherical deconvolution (CSD) applied to the data as implemented in MRtrix.11 Freesufer ROIs were warped into diffusion space by mapping between the T1‐weighted image and fractional anisotropy (FA) map using NiftyReg12 and applying the resulting warp to each of the ROIs. A foreground mask was generated by combining Freesurfer segmentations with the WM mask. A summary of the processing pipeline is provided in Figure 1.

Figure 1.

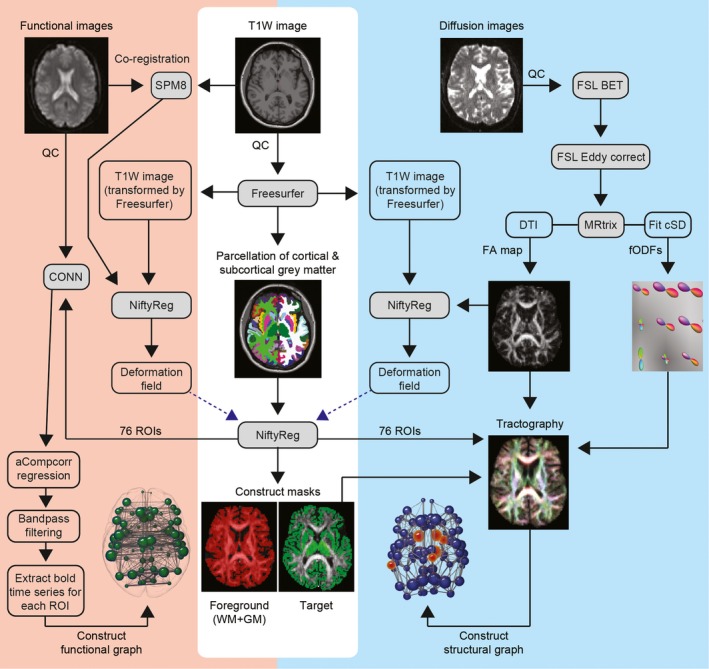
Resting state fMRI and diffusion tractography processing pipelines. BET, brain extraction tool; CONN, functional connectivity toolbox; CSD, constrained spherical deconvolution; DTI, diffusion tensor imaging; FA, fractional anisotropy; fODF, fibre orientation distribution function; GM, gray matter; QC, quality control; WM, white matter; SPM, statistical parametric mapping.

Diffusion tractography

Whole brain probabilistic tractography was performed using the iFOD2 algorithm in MRtrix.11 Specifically, 5 million streamlines were seeded throughout the WM, in all foreground voxels where FA > 0.2. Streamlines were terminated when they either reached the cortical or subcortical gray‐matter mask or exited the foreground mask. The spherical deconvolution informed filtering of tractograms (SIFT) algorithm13 was used to reduce biases. The resulting set of streamlines was used to construct the structural brain network.

Functional MRI

Data preprocessing

Preprocessing was performed using SPM8 and the CONN functional connectivity toolbox version 14 (https://www.nitrc.org/projects/conn/)14 running under MATLAB v8.3. Segmented images were used to create an improved anatomical scan for coregistration. The first four EPI images were discarded to allow for steady state equilibrium. Functional images were first realigned, incorporating field maps for inhomogeneity correction whenever available and then coregistered to the new anatomical image. Freesurfer ROIs were also coregistered to the anatomical image using NiftyReg.12 Using the CONN toolbox regression of noise ROIs (without global signal regression) was carried out using the anatomical Compcorr method,15 along with 6 movement parameters, followed by band‐pass filtering between 0.009 and 0.08 Hz, calculation of bivariate correlations and application of a Fisher transform. In addition to the inclusion of motion parameters, our main strategy for guarding against the effects of motion generated artifacts was through the implementation of stringent quality control procedures on the raw data and at each stage of preprocessing and analysis (see Kloppel et al5 for further details). Our study included only pre‐HD participants who have not yet developed the motor manifestations of HD.

Construction of structural and functional connectivity matrices

For structural connectivity matrices ROIs were defined as connected if a fibre originated in ROI 1 and terminated in ROI 2. For functional matrices ROIs were defined as functionally connected if there was a correlation between the time series of ROI 1 and ROI 2. Structural connections were weighted by streamline count, while functional connections were weighted by magnitude of correlation. Connections were then combined into 76 × 76, undirected and weighted matrices. A control group threshold of 75% was applied in order to remove weak spurious connections.16 This was performed for both structural and functional connectivity matrices where only those connections present in 75% of control subjects were retained. This 75% group threshold is consistent with group threshold strategies prevalent in the literature.2, 17, 18

Structural hub regions

Structural hub regions were defined to enable interpretation of the role of hub regions in the subsequent functional regulation analysis. Hubs were defined as the top 12 brain regions with highest degree for the group averaged control brain‐network in keeping with previous studies.2, 17, 18

Calculation of graph theory metrics

All graph theory metrics were calculated using the brain connectivity toolbox16 and have been discussed in detail elsewhere.19 Degree, defined as the number of binary connections to a brain region, was calculated for the control‐averaged structural connectivity matrix to define structural hub regions. Graph theory strength, defined as the sum of weighted connections for each brain region, was calculated for the analyses using healthy WM to predict functional and structural connectivity changes, in pre‐HD relative to controls, and for the antero–posterior (A‐P) analysis.

Characteristics of healthy white matter organization

To define healthy WM organization degree, clustering coefficient, betweenness centrality and eigenvector centrality were calculated for each brain region. Clustering coefficient is the fraction of brain regions neighbours that are also neighbors of each other. Betweenness centrality is defined as the fraction of shortest paths in the network that pass through a given brain region. Eigenvector centrality is a self‐referential measure that assigns a high level of importance to brain regions if they are connected to other highly connected brain regions (see Fig. 2 for a schematic representation of graph theory measures). These metrics were calculated for the un‐weighted average control WM brain‐network. Streamline weighting was not included to allow direct comparison with structural and functional modalities.

Figure 2.

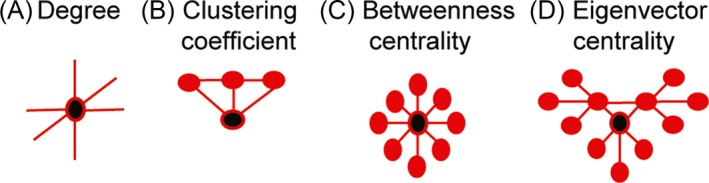
Schematic description of graph theory metrics. (A) Degree is the number of connections a brain region has. (B) Clustering coefficient indicates how highly connected a region is to its neighbors and (C) Betweenness centrality represents brain region network traffic. (D) Eigenvector centrality represents network traffic along the brains ‘busiest’ pathways. Black circles represent regions with high degree, clustering coefficient, betweenness centrality or eigenvector centrality. These graph theory metrics correspond to the graph metrics on the y‐axis of Figures 2, 3 and 4.

Brain‐network analyses

Prediction of structural and functional change using healthy white matter organization

Correlations were performed against both functional regulation coefficients (calculation of functional regulation coefficients is detailed below) and changes in functional strength (pre‐HD relative to controls) for each brain region and the corresponding graph theory metric of that brain region in the average control WM brain network; degree, clustering coefficient, betweenness centrality and eigenvector centrality. A Bonferroni correction (P < 0.0125) was applied for multiple comparisons. To allow comparison between structural and functional changes, correlations were also performed between changes in structural strength (pre‐HD relative to controls) for each brain region and their corresponding graph theory metrics in the average control WM brain‐network as outlined above. Similarly a Bonferroni correction (P < 0.0125) was applied for multiple testing of 4 graph theory metrics.

Split‐site and ‘off medication’analyses

To establish whether our findings were influenced by study site a split‐site analysis was carried out. Sites were paired based on type of MRI scanner; London‐Paris (Siemens) (40 pre‐HD individuals and 41 healthy controls) and Leiden‐Vancouver (Philips) (24 pre‐HD individuals and 25 healthy controls). As psychoactive medications influence brain activation in fMRI studies20 we also performed a control analysis in only those off psychoactive medications for more than 6 months. Patients excluded from the ‘off medication’ cohort included 2 on anti‐psychotics, 16 on selective serotonin reuptake inhibitors, 1 on a serotonin‐noradrenaline reuptake inhibitor, 1 on bupropion, 5 on benzodiazepines, 2 on tri‐cyclic anti‐depressants and 1 on melatonin. This resulted in a cohort of 43 pre‐HD individuals and 59 controls. See Table 2 for results of split‐site and ‘off medication’ control analyses.

Table 2.

Split‐site analyses and Off medication analyses

(A) Structural strength	Degree (rho)	Clustering coefficient (rho)	Betweenness centrality (rho)	Eigenvector centrality (rho)
Off medication	0.45	−0.33	0.36	0.41
Leiden‐Vancouver	0.22	−0.23	0.12	0.21
London‐Paris	0.43	−0.26	0.27	0.43
(B) Functional regulation
Off medication	−0.47	0.49	−0.26	−0.48
Leiden‐Vancouver	−0.32	0.3	−0.11	−0.39
London‐Paris	−0.33	0.38	−0.3	−0.3
(C) Functional strength
Off medication	−0.32	0.31	−0.16	−0.33
Leiden‐Vancouver	−0.17	0.19	−0.02	−0.21
London‐Paris	—0.33	0.34	—0.27	—0.33

rho, correlation coefficient.

Functional regulation analysis

We introduce the ‘functional regulation coefficient’ as a summary measure of the relative change in functional connectivity of a pair of brain regions comparing pre‐HD with healthy controls. This measure is designed to identify brain regions were strong connections in the healthy brain get stronger in pre‐HD and regions were strong connections in the healthy brain get weaker in pre‐HD. This was based on our previous observation that strong connections in the healthy brain show structural connectivity loss in manifest HD.2 The functional regulation coefficient was calculated as follows; an averaged control and an averaged pre‐HD functional connectivity matrix were created. Subtracting the averaged pre‐HD matrix from the averaged control matrix then created a difference matrix. For each brain region, the magnitude of a connection in the average control matrix was correlated against the magnitude of that connection in the difference matrix. Upregulation was defined as a positive correlation (stronger control connections show greater increases in pre‐HD), whereas downregulation was defined as a negative correlation (stronger control connections show greater decreases in pre‐HD). For example if region 3 was connected to regions 5, 26, and 74, magnitude of connections for region pairs 3–5, 3–27 and 3–74 for averaged controls were plotted against the differences in those connections (average pre‐HD− average controls). This provides a measure of how much the functional connectivity with a brain region is modified in pre‐HD as a function of the preexisting functional connectivity in healthy control brains. A Bonferroni correction (P < 0.0007) was then applied to account for the 76 brain regions tested.

Antero–posterior (A–P) analysis

Following our initial observations of a possible A–P pattern we investigated the spatial distribution of relative changes in functional connectivity across the brain. This was done by calculating the correlation between A–P axis coordinates of each brain region and its corresponding functional regulation coefficient. To investigate whether any relationship was common to changes in both structural and functional connectivity, correlations were also performed against A–P axis co‐ordinate and functional and structural changes in (graph theory) strength (pre‐HD relative to controls). A Bonferroni correction (P < 0.017) was applied to account for multiple testing of functional regulation coefficient, functional strength and structural strength (i.e., P < 0.05/3).

Results

Healthy white matter organization and structural connectivity loss in pre‐HD vs. controls

There were significant correlations (df = 74) between decreases in structural strength (in pre‐HD relative to controls) and degree (ρ = 0.45, P = 3.94 × 10⁻⁵); clustering coefficient (ρ = −0.35, P = 0.0023); betweenness centrality (ρ = 0.31, P = 0.0074) and eigenvector centrality (ρ = 0.43, P = 1.1 × 10⁻⁴) of healthy WM. All correlations survived Bonferroni‐correction (P < 0.0125) for number of graph theoretic measures. Consistent with previous reports2, this indicates that specific features of healthy WM organization can predict decreases in corresponding structural connectivity in pre‐HD relative to healthy controls.

Healthy white matter organization and functional connectivity increase in pre‐HD vs. controls

There were significant correlations (df = 74) between the regulation coefficient and degree (ρ = −0.45, P = 3.66 × 10⁻⁵); clustering coefficient (ρ = 0.5, P = 3.9 × 10⁻⁶); betweenness centrality (ρ = −0.29, P = 0.01) and eigenvector centrality (ρ = −0.48, P = 1.21 × 10⁻⁵) of healthy WM. See Figure 3.

Figure 3.

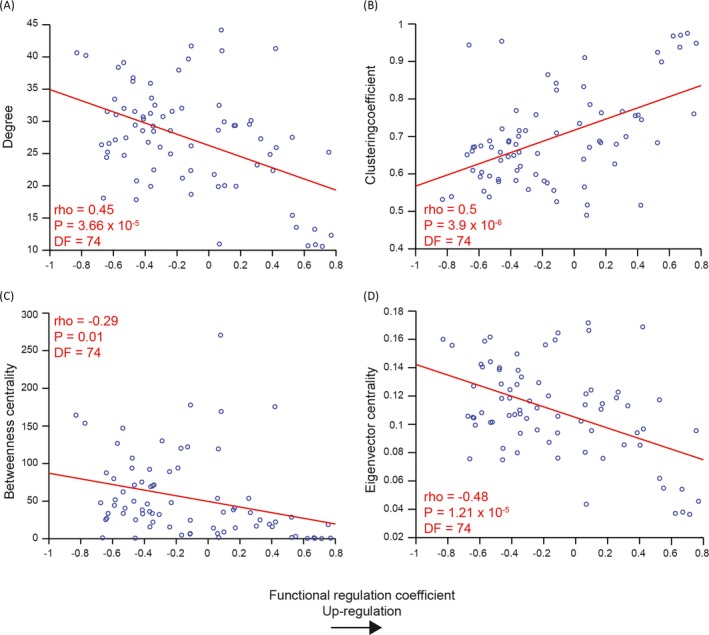
Prediction of functional upregulation based on healthy white matter organization. Regions with (A) low degree, (B) high clustering and (C,D) low network traffic (betweenness and eigenvector centrality) show greatest functional upregulation in pre‐HD. The graph theory metric value of a brain region in the average control WM brain network, on the y‐axis, is plotted against the functional regulation coefficient for that corresponding brain region, on the x‐axis. The red line represents a least squares linear regression line. rho, correlation coefficient; DF, degrees of freedom; WM, white matter.

Similar patterns were seen for correlations between increases in functional strength (in pre‐HD relative to controls) (df = 74) and degree (ρ = −0.36, P = 0.0016); clustering coefficient (ρ = 0.36, P = 0.0014) and eigenvector centrality (ρ = −0.38, P = 6 × 10⁻⁴) of healthy WM. There was no significant correlation between increases in functional strength and betweenness centrality (ρ = −0.19, P = 0.0948). All significant correlations survived Bonferroni‐correction (P < 0.0125) for number of graph theoretic measures. This indicates that as with structural neurodegeneration, specific features of healthy white organization can predict corresponding inter‐regional increases in functional connectivity in pre‐HD relative to healthy controls.

Split‐site and ‘off medication’ analyses

Correlations between healthy WM graph metrics and changes in structural strength, functional strength (pre‐HD relative to controls) and functional regulation for split‐site and ‘off medication’ cohorts revealed qualitatively similar findings with the exception of betweenness centrality (see Table 2). Thus, neither site nor medication status affected the results reported here.

Functional regulation in pre‐HD relative to controls

While the functional regulation of all brain regions were tested, structural hub regions were defined specifically in order to investigate whether these regions showed ‘up‐regulation’ (positive functional correlation coefficient) or ‘down‐regulation’ (negative functional correlation coefficient). Hub regions included the caudate, thalamus, superior frontal, precentral, precuneus, and insula bilaterally. Only anterior nonhub regions, with the exception of the left superior frontal, showed functional upregulation (an increase in functional connectivity in pre‐HD relative to controls) while predominantly posterior regions, including the caudate, precuneus and insula hubs (bilaterally) showed functional downregulation. Significant changes in the functional regulation of hub and nonhub regions is shown in Figure 4 along with example scatter plots for the top regions showing upregulation and downregulation. See Table 3 for a list of all significant functional regulation coefficients.

Figure 4.

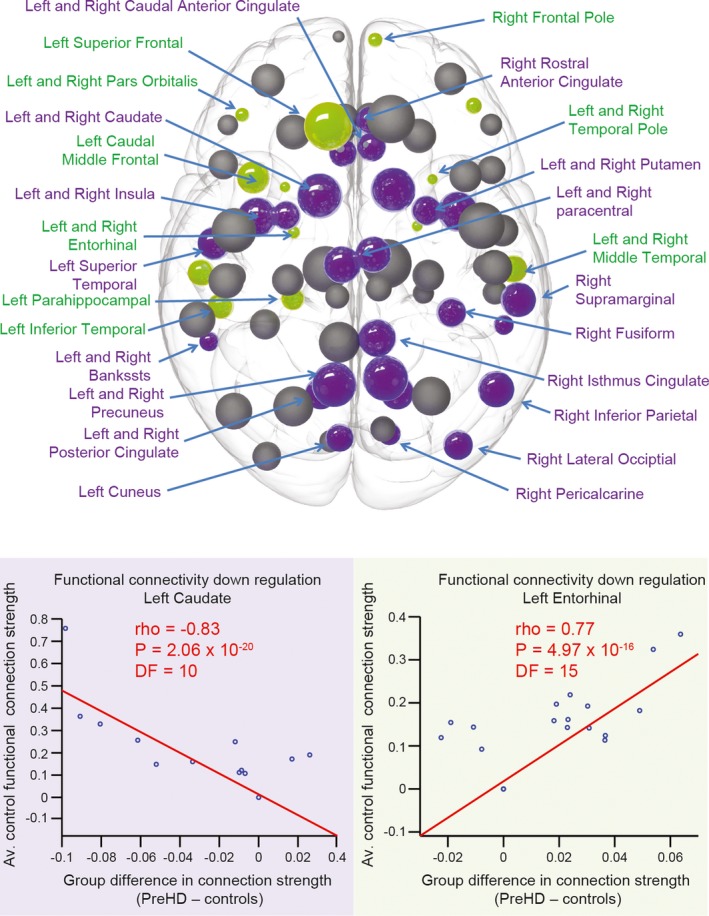
Functional regulation analysis. For each brain region in the average control network, correlations were performed against the strength of functional connection to all other 75 regions in the network (where a functional connection was present) and average group differences (pre‐HD minus controls) in these functional connections. Upregulation is defined as a positive correlation (stronger control connections show greater increases in pre‐HD), whereas downregulation is defined as a negative correlation (stronger control connections show greater decreases in pre‐HD). Brain regions that show significant positive (green) and negative (purple) correlations are highlighted. The size of the sphere represents the number of structural connections (thus largest spheres indicate hub brain regions). Correlation plots showing the brain regions with the most significant positive (green) and negative (purple) correlations are also displayed below. For each plot each data point represents a connection to the brain region specified. The strength of that connection for the avaerage control network, on the y‐axis, is plotted against the difference (pre‐HD minus controls) of that connection's strength on the x‐axis. The red line represents a least squares linear regression line. rho, correlation coefficient; DF, degrees of freedom.

Table 3.

Functional regulation analysis: regional correlations

Upregulation			Downregulation
Region	rho	P	Region	rho	P
L.entorhinal	0.77	4.97 × 10−16	L.caudate	−0.83	2.06 × 10−20
L.middle temporal	0.75	3.52 × 10−15	R.caudate	−0.77	2.79 × 10−16
R.temporal pole	0.71	4.64 × 10−13	R.rostral anterior cingulate	−0.67	2.35 × 10−11
R.entorhinal	0.67	3.21 × 10−11	R.bankssts	−0.66	6.96 × 10−11
L.pars orbitalis	0.67	5.10 × 10−11	L.caudal anterior cingulate	−0.64	3.99 × 10−10
L.temporal pole	0.62	1.75 × 10−09	R.lingual	−0.64	5.43 × 10−10
R.frontal pole	0.55	2.51 × 10−07	R.caudal anterior cingulate	−0.64	6.45 × 10−10
R.pars orbitalis	0.53	1.07 × 10−06	L.putamen	−0.63	1.29 × 10−09
L.caudal middle frontal	0.53	1.11 × 10−06	R.isthmus cingulate	−0.59	1.78 × 10−08
R.middle temporal	0.42	1.32 × 10−04	R.lateral occipital	−0.59	2.34 × 10−08
L.superior frontal	0.42	1.56 × 10−04	R.posterior cingulate	−0.58	3.10 × 10−08
L.para hippocampal	0.40	3.06 × 10−04	L.precuneus	−0.57	8.25 × 10−08
L.inferior temporal	0.39	5.79 × 10−04	R.precuneus	−0.54	6.39 × 10−07
			L.posterior cingulate	−0.53	6.84 × 10−07
			L.cuneus	−0.53	7.22 × 10−07
			R.putamen	−0.52	1.35 × 10−06
			L.insula	−0.48	1.26 × 10−05
			R.insula	−0.48	1.36 × 10−05
			R.inferior parietal	−0.47	2.23 × 10−05
			L.lingual	−0.46	2.54 × 10−05
			L.bankssts	−0.46	3.31 × 10−05
			R.pericalcarine	−0.46	3.63 × 10−05
			R.fusiform	−0.42	1.88 × 10−04
			L.superior temporal	−0.41	2.06 × 10−04
			R.supramarginal	−0.41	2.25 × 10−04

rho, correlation coefficient. Brain regions derived from the Freesurfer Desikan–Killiany atlas.7

Antero–posterior (A–P) analysis

Correlations (df = 74) were also performed between the functional regulation coefficient and the corresponding A–P axis coordinate for each brain region. This analysis revealed a significant positive correlation between functional regulation and the co‐ordinate of each brain region along the A‐P axis (ρ = 0.35, P = 0.0018). Finally, we investigated the A‐P effect for both structural and functional (connectivity) by calculating the correlations between increase in functional and decrease in structural strength in pre‐HD relative to controls and the corresponding A‐P axis co‐ordinate for each brain region. Significant Bonferroni‐corrected correlations were found for functional (ρ = 0.28, P = 0.0148), but not structural strength (ρ = −0.12, P = 0.31) (see Fig. 5).

Figure 5.

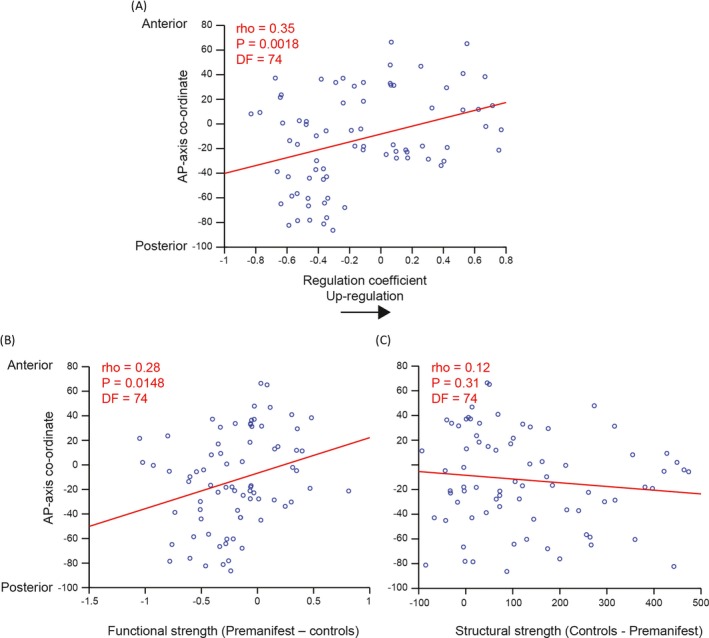
A–P correlation analysis for functional regulation, functional and structural strength. More anterior regions show greater increases in (A) regulation coefficient and (B) functional but not (C) structural strength in pre‐HD. Each data point represents a brain region. The coordinate of that brain region along the anterior–posterior axis, on the y‐axis, is plotted against regulation coefficient or strength on the x‐axis.The red line represents a least squares linear regression line. rho, correlation coefficient; DF, degrees of freedom.

Discussion

We found that the organizational properties of healthy WM could predict increases in functional connectivity in pre‐HD relative to controls. Through novel modeling of functional regulation, we demonstrated an antero–posterior dissociation of changes in functional connectivity in pre‐HD. Pre‐HD participants showed both functional upregulation (relative to healthy controls), where strong connections in anterior nonhub regions were stronger; and downregulation where strong connections in posterior hub regions were weaker.

Changes in resting‐state functional connectivity have consistently been observed in pre‐HD.5, 21, 22, 23 However, until now how such changes related to underlying WM organization and structural connectivity changes was unknown. To date only one study has investigated the relationship between structural and functional connectivity in HD.24 This was performed in a manifest HD cohort. While structural and functional connectivity differences relative to controls were observed independently no correlation was found between structure and functional connectivity in manifest HD participants. Using functional connectivity analyses combined with structural characterization of WM connectivity, our findings go significantly beyond those earlier observations by demonstrating that features of healthy WM organization can predict regional increases in resting state functional connectivity in pre‐HD relative to controls. In keeping with these findings, brain regions with low structural connectivity in the healthy brain showed the greatest increases in functional connectivity in pre‐HD.

While our study was not designed to detect whether these increases in functional connectivity are compensatory or pathological, the fact these increases are seen in regions with low WM connectivity loss suggest they may either represent the earliest signs of the disease process prior to structural connectivity loss or may indeed represent regions with intact structural connectivity upregulating as a compensatory mechanism.5 If the latter is correct then this has important implications for therapies aimed at enhancing compensatory mechanisms. Two such therapies, repetitive transcranial stimulation (rTMS)25 and neurofeedback26 are efficacious in other neurodegenerative diseases. If the functional increases we observed are compensatory this suggests targeting these therapies specifically to anterior brain regions may provide the optimal approach, as these are the regions with greatest capacity for functional upregulation based on the observations in this study.

Our functional regulation analysis revealed a striking A‐P dissociation where anterior regions in the brain showed functional upregulation of connectivity while posterior regions in the brain showed downregulation. A similar anterior–posterior shift in brain activation (rather than connectivity) is seen in healthy aging using task‐based fMRI27, which the authors interpret as a compensatory mechanism used to maintain cognitive performance as the brain ages. Although the physiology of aging and pathology of Huntington's disease are clearly very different processes, this anterior–posterior shift may possibly represent a shared mechanism of compensation common to both healthy aging and preclinical neurodegeneration. However it is difficult to make direct comparisons as Davis and colleagues measured brain activation during the performance of a cognitive task while we investigated brain activation at rest.

We provide additional evidence for an A‐P dissociation in functional connectivity changes in pre‐HD by showing a positive correlation between the location of a brain region along the A–P axis and the increase in functional regulation and functional strength observed in pre‐HD. As no such spatial correlation was seen with structural connectivity strength this suggests the A–P effect is not mediated by underlying structural connectivity but may reflect a solely functional process. Thus, if this is a compensatory mechanism it suggests this may be driven by a functional neurochemical process as opposed to structural alterations. Indeed the concentration of dopamininegric D2 receptors show a rostro–caudal gradient, present in highest concentrations in prefrontal cortex and lowest concentrations in the occipital cortex,28 furthermore D2 receptors are implicated in HD pathogenesis.29, 30, 31 It is therefore possible that changes in dopamine levels in pre‐HD may facilitate compensation and thus account for this A–P dissociation.

Grading of striatal neuropathology in HD reveals that degeneration occurs along a caudo–rostral gradient.32 In keeping with this previous studies in manifest HD have shown greater loss of WM volume33 and cortical thickness34, 35 in posterior compared to anterior areas of the brain. This suggests a common gradient of striatal and cortical pathology from posterior to anterior along the A–P axis. Therefore, we postulate that the functional A‐P dissociation we demonstrate in pre‐HD may be a precursor to the structural changes in gray and white matter seen in manifest disease. With clinical trials currently underway for potential disease‐modifying therapies,36 the presence of this functional dissociation may represent the optimum time for therapeutic intervention prior to irreversible structural damage. Future multimodal imaging studies in young adults far from disease onset will allow us to confirm if this functional A‐P dissociation is indeed one of the earliest brain changes in HD prior to disease onset.

Conclusion

Our findings reveal the organizational principles of healthy WM that determine functional connectivity changes in pre‐HD. Specifically, regions with low WM (structural) connectivity show increases in functional connectivity in pre‐HD relative to healthy controls. In addition, we demonstrate a functional A–P dissociation in pre‐HD where anterior regions in the brain show upregulation, while posterior regions show downregulation. This is in keeping with the caudo–rostral gradient of striatal pathology in HD and suggests these increases in functional connectivity may represent either compensatory change or the earliest brain changes of pre‐HD prior to structural connectivity loss.

Conflict of Interest

None declared.

Track‐On HD Investigators

A. Coleman, J Decolongon, M Fan, T. Petkau (University of British Columbia, Vancouver); C Jauffret, D Justo, S Lehericy, K Nigaud, R Valabrègue (ICM and APHP, Pitié‐ Salpêtrière University Hospital, Paris). A Schoonderbeek, E P t Hart (Leiden University Medical Centre, Leiden); DJ Hensman Moss, H Crawford, E Johnson, M Papoutsi, C Berna, (University College London, London). R Reilmann, N Weber (George Huntington Institute, Munster); J Stout, I Labuschagne (Monash University, Melbourne); B Landwehrmeyer, M Orth (University of Ulm, Ulm); H Johnson (University of Iowa).