Foot placement relies on state estimation during visually guided walking

Accurate foot placement is essential for safe walking. We used computational models and human walking experiments to test how our nervous system achieves this accuracy. We find that our control of foot placement beneficially combines sensory feedback with internal forward model predictions to accurately estimate the body's state. Our results match recent computational neuroscience findings for reaching movements, suggesting that state estimation is a general mechanism of human motor control.

Abstract

As we walk, we must accurately place our feet to stabilize our motion and to navigate our environment. We must also achieve this accuracy despite imperfect sensory feedback and unexpected disturbances. In this study we tested whether the nervous system uses state estimation to beneficially combine sensory feedback with forward model predictions to compensate for these challenges. Specifically, subjects wore prism lenses during a visually guided walking task, and we used trial-by-trial variation in prism lenses to add uncertainty to visual feedback and induce a reweighting of this input. To expose altered weighting, we added a consistent prism shift that required subjects to adapt their estimate of the visuomotor mapping relationship between a perceived target location and the motor command necessary to step to that position. With added prism noise, subjects responded to the consistent prism shift with smaller initial foot placement error but took longer to adapt, compatible with our mathematical model of the walking task that leverages state estimation to compensate for noise. Much like when we perform voluntary and discrete movements with our arms, it appears our nervous systems uses state estimation during walking to accurately reach our foot to the ground.

NEW & NOTEWORTHY Accurate foot placement is essential for safe walking. We used computational models and human walking experiments to test how our nervous system achieves this accuracy. We find that our control of foot placement beneficially combines sensory feedback with internal forward model predictions to accurately estimate the body's state. Our results match recent computational neuroscience findings for reaching movements, suggesting that state estimation is a general mechanism of human motor control.

walking requires accurate foot placement to balance an otherwise unstable inverted pendulum-like motion (Bauby and Kuo 2000) and to accommodate changes in terrain and the environment. Consider the situation of avoiding an icy patch or a hole in a sidewalk, and thus the need to direct your foot to a specific location. This involves identifying the hazard and a safe step location, and knowledge of body/limb position. The nervous system heavily relies on vision to make these measurements. For instance, individuals use visual feedback to make rapid stepping corrections, as evident when a ground target shifts to a new location (Reynolds and Day 2005) or when avoiding a sudden ground obstacle (Marigold et al. 2007). Furthermore, occluding vision of a target during the step prior reduces accuracy and increases variability of foot placement (Matthis et al. 2015).

However, visual feedback does not provide a true measure of limb state and the properties of the environment in which we navigate. Limited spatial resolution of sensory receptors, delays in sensory processing, and physiological noise inherent in neural transduction create uncertainty in sensory input (Faisal et al. 2008; Franklin and Wolpert 2011). How then, do we perform movements so effectively and adapt to changes in the properties of our body (e.g., reduced visual acuity with age or disease) and our surrounding environment despite this sensory noise?

Rather than relying entirely on imperfect sensory feedback, more accurate estimates of body and environmental states may be achieved by using a forward model to first predict these states and the associated sensory output. The mismatch between predicted and actual sensory feedback, termed sensory prediction error, adjusts the predicted states in a process called state estimation (Shadmehr and Mussa-Ivaldi 2012). However, forward prediction also suffers from uncertainty, termed process noise, because it is based on imperfect body representations and perturbation expectations. The relative levels of sensory and process noise determine the optimal combination between sensory feedback and forward prediction; the contribution of the latter grows with increases in sensory noise.

Although walking is rarely studied in this context, there is considerable evidence that state estimation underlies the control of upper limb reaching movements. Studies demonstrate, for example, that sensory prediction error drives adaptation to an imposed visuomotor rotation or displaced visual feedback of a hand-controlled cursor (Mazzoni and Krakauer 2006; Tseng et al. 2007; Wei and Körding 2010). This adaptation, which stems from a reweighting of visual feedback, depends on the prior history of errors and the certainty of information received and generated by the brain (Burge et al. 2008; Wei and Körding 2010). Given that visually guiding the foot to specific ground locations and reaching the hand to a target share similar motor planning features, these actions may be controlled similarly, as well. However, locomotion is often studied from the perspective that pattern-generating, reflexive, and balancing circuits located in the spinal cord and brain stem dominate its control (Duysens and van de Crommert 1998; Grillner et al. 2008; Pearson 2008). In this study, we determined whether foot placement control during walking also leverages state estimation. To test this hypothesis, subjects performed a visually guided walking task that required precise foot placement to a target while wearing prism lenses. The lenses altered the mapping relationship between the perceived target location and the motor command necessary to direct the foot to that position. We varied the magnitude and direction of prism shifts on a trial-to-trial basis to add noise to the visual feedback and induce a reweighting of this input. A state estimation-based controller suggests that subjects would rely more on a forward model prediction to best estimate target position with increased measurement uncertainty. To expose altered weighting of visual feedback after noise familiarization, we added a consistent prism shift requiring subjects to adapt their mapping estimate to reduce foot placement errors.

We contrasted the state estimation controller with another commonly used adaptation controller driven by task error (Haith and Krakauer 2013). In the former controller, subjects step toward the estimated target location, which is updated by weighted sensory prediction errors. In the latter controller, subjects step toward the sensed target location adjusted by a correction term, which is updated by weighted sensed foot placement (or task) error. Both controllers predict that reweighting should result in a slower error correction in response to the consistent prism shift for higher noise conditions. However, the state estimation controller uniquely predicts that reweighting results in smaller initial foot placement errors and a tendency for error to increase before decreasing following the consistent prism shift.

MATERIALS AND METHODS

Subjects.

Twenty-four subjects (age 21.8 ± 2.8 yr; 15 men, 9 women; 21 of 24 right-leg dominant, as defined by the leg used to kick a soccer ball) with no known musculoskeletal, neurological, or visual disease participated in this study. Six subjects wore corrective lenses (glasses or contacts) during the experiments. The Office of Research Ethics at Simon Fraser University approved all experimental procedures, and all subjects gave informed written consent before participating.

Experimental task.

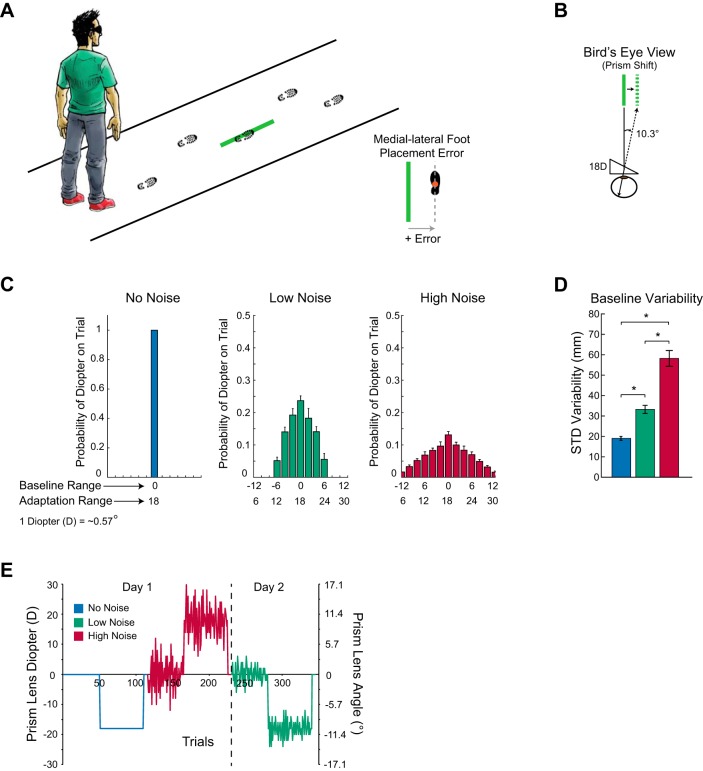
Subjects performed a modified visually guided, precision walking task (Alexander et al. 2011, 2013) characterized by having to walk across a 6-m path and step with the right foot onto the medial-lateral center of one target (36 × 3 cm) without stopping (Fig. 1A). An LCD projector (Epson EX7200) displayed the green target on the ground. Because we were interested in medial-lateral foot placement error, we used a long target length to reduce the accuracy demand in the anterior-posterior direction, which also prevented subjects from needing to shuffle their steps as they approached the target area. To diminish the effect of environmental references and increase target visibility, subjects walked under reduced light (∼0.7 lux, as measured with a calibrated digital light meter; model DML-2200, Circuit Test Electronics, Burnaby, BC, Canada). An Optotrak Certus motion capture camera (Northern Digital, Waterloo, ON, Canada), positioned perpendicular to the walking path, recorded infrared-emitting diodes placed on the chest and bilaterally on each midfoot over the lateral cuneiforms at a sampling frequency of 100 Hz. A Panasonic high-definition camcorder (model HDC-SD60) also was used to record videos of each walking trial.

Fig. 1.

Experimental setup and design. A: schematic of the visually guided walking task. Subjects walked and stepped with their right foot on a thin green line projected on the ground from above. Medial-lateral foot placement error, defined as the distance between a position marker on the foot and the center of the target line, quantified performance (inset). B: a simulated view of the target through the prism lenses and the perceived target shift for 18-diopter lenses. C: distribution of prism lenses in each noise condition for the baseline and adaptation phases. D: increasing noise created greater foot placement error variability during the baseline phase, supporting the notion that our prism noise had the intended effect on performance. *P < 0.05, significant post hoc test effects. E: an example of one of the protocols. In this case, the subject first experienced the no-noise condition with a leftward prism shift in the adaptation phase, followed by the high-noise condition with a rightward prism shift in the adaptation phase, and then the low-noise condition with a leftward prism shift in the adaptation phase. In each condition, 50 baseline phase trials preceded 60 adaptation phase trials and 5 postadaptation phase trials.

Subjects wore goggles housing wedge prism lenses that shifted the visual perception of the target either left or right with respect to its actual location (see Fig. 1B) or flat lenses that did not shift perceived target position. The type of lenses depended on the trial and phase of the protocol. The goggles blocked peripheral vision, forcing subjects to look only through the lenses. Visually guided movements require that the brain maintain an accurate mapping between the perceived target location and the motor command necessary to direct the limb to that position. Prism lenses disrupt the normal visuomotor mapping. This induces movement errors after walking and stepping to the perceived location of the target, thereby requiring subjects to adapt (Alexander et al. 2011, 2013). By setting a new mean prism shift during a block of trials while randomly changing prism lenses around this constant mean on a trial-by-trial basis (prism noise), we studied how subjects adapted when faced with different amounts of measurement uncertainty. We based these prism noise perturbations on the third experiment of Burge et al. (2008), which used trial-by-trial visual perturbations to induce measurement errors. Although it is unknown whether subjects interpret the prism noise as visual (sensory) noise or a randomly changing internal state, either interpretation allows testing of the state estimation hypothesis. A state estimation controller would rely more on a forward model prediction with increased prism noise, because prism noise reduces the certainty with which the controller can estimate the mean prism shift from measured errors. Therefore, this type of perturbation shares a common characteristic with other experiments that use blur to degrade visual information: there is little to no benefit to adapt, based on measurement error. However, unlike blur, the statistics of the noise can only be observed over many trials.

Subjects started each trial at random anterior-posterior locations within a 1.8- to 3-m distance from the target. This helped to avoid subjects learning a specific stepping sequence and ensured the task remained under visual guidance. To begin a trial, subjects opened their eyes and immediately started walking. We instructed subjects to walk at a quick and constant pace during the task (as if late for class). Although locomotion is a continuous process that relies on real-time sensory information, these guidelines minimized online corrections of the leg/foot trajectory to more closely match previous reaching experiments, in which the movements are ballistic and emphasize use of sensory feedback prior to the movement. Recent work in precision walking also demonstrates that visual feedback is used before, but not during, a step to a target (Matthis et al. 2015). Subjects walked with an average speed (±SD) of 1.9 ± 0.3 m/s, and we verified the presence of smooth foot marker velocity profiles and absence of sudden changes in foot marker trajectory during steps to the target to confirm the lack of online corrections. Our instructions also emphasized that the goal of the task was to step onto the center of the medial-lateral location of the target, to look down to see foot contact on the target, and to not stop until taking at least one step after the target. Subjects kept their eyes closed before each trial and again when walking back (under experimenter guidance) to the start position to avoid additional adaptation between trials. To ensure that subjects performed the task correctly, we provided them with familiarization trials (n ≈ 5) that preceded the actual experiment. Subjects wore flat lenses (0 diopters) in the goggles during these trials.

Experimental protocol.

Each protocol consisted of 50 baseline, 60 adaptation, and 5 postadaptation trials. The mean prism shift in these phases was 0 diopters (0°), 18 diopters (∼10.3°), and 0 diopters (0°), respectively. We used different ranges of trial-by-trial prism shifts to create three distinct levels of measurement uncertainty (referred to as noise) during the baseline and adaptation phases: no noise, low noise, and high noise (Fig. 1C). The no-noise condition consisted of constant 0-diopter lenses in the baseline phase and constant 18-diopter lenses in the adaptation phase. In the low-noise condition, we used a range of ±6 diopters (in 2-diopter increments) around the mean prism shift of the baseline (SD = 3.03 diopters) and adaptation (SD = 3.16 diopters) phases. The high-noise condition consisted of lenses with a range of ±12 diopters (in 2-diopter increments) around the mean prism shift of the baseline (SD = 5.66 diopters) and adaptation (SD = 5.84 diopters) phases. After each adaptation phase, we included five postadaptation trials with no prism shifts to assess the magnitude of each adaptation. To mask the strength and direction of the prism perturbations, an experimenter removed the prism lenses from the goggles every trial in each condition and phase and then replaced them, regardless of whether the subsequent trial used the same lenses.

A custom-written MATLAB (The MathWorks, Natick, MA) program randomly generated the order and frequency of the specific prism lenses based on a Gaussian distribution for each experimental condition and the total number of trials per baseline and adaptation phases. The program then reordered the sequence to reduce the likelihood that sequential trials used similar lenses and increase the perception of noise about the mean shift. Regardless, the prism shift values were fixed at 0 and 18 diopters for the last baseline phase trial and first adaptation phase trial, respectively, and the distance to the target was fixed at 1.8 m in these trials to ensure that the same perturbations occurred in the first adaptation trial across all conditions.

To establish that our noise conditions created three different levels of uncertainty, we determined the variability of foot placement error in the baseline phase for each condition, defined by the standard deviation across baseline trials. A one-way repeated-measures ANOVA and subsequent Tukey's post hoc test demonstrated that, compared with the no-noise condition, variability in foot placement error increased by 74.6% and 206% in the low- and high-noise conditions, respectively (Fig. 1D; F_2,46 = 73.3, P < 0.0001).

To minimize the order effects and to allow for a within-subject analysis, we used a fully counterbalanced design that accounted for the order of noise conditions and direction of the mean prism shifts in the adaptation phases. Specifically, we randomly assigned 2 subjects to 1 of 12 noise order-prism direction protocols, each with a unique noise condition order and with the direction of the mean prism shift in the adaptation phase alternated in a rightward-leftward-rightward sequence or leftward-rightward-leftward sequence (see Fig. 1E for example). The alternating mean prism shift during the adaptation phase also served to reduce the effect of learning the mean shift across conditions (Krakauer et al. 2005). Because of time constraints and to prevent fatigue, subjects performed two conditions separated by a 10-min rest break on the first day and performed the third condition during a second day, with an average interval between testing sessions of 6.3 ± 3.1 days. The first and second testing session lasted ∼2.5 and 1 h, respectively.

Visually guided walking model.

We used a mathematical model to simulate foot placement errors, as well as sensory feedback in response to foot placement motor command inputs, during the visually guided precision walking task. We then used this model to test two competing control schemes for planning these motor commands (described in Sensory prediction error controller and Task error controller). The model has three system states: medial-lateral target position relative to the starting location x₁, the mean prism shift x₂, and foot placement error x₃. A simulated subject measures the target location y₁ through prism lenses, walks toward the target position, and then measures foot placement error y₂ through the same prism lenses. These variables represent the minimum number of actual and sensed states necessary to represent a generic target-reaching task with visual perturbations. We chose not to include other sources of sensory feedback such as proprioception, since others also have excluded them (Burge et al. 2008), because relative target location could only be measured from visual information. The simulation is represented as a set of difference equations (Eq. 1), which model the trial-by-trial dynamics of the state vector $\stackrel{\rightharpoonup }{x}$ and sensory input vector $\stackrel{\rightharpoonup }{y}$, where $\stackrel{\rightharpoonup }{x}$ = [x₁ x₂ x₃]′ and $\stackrel{\rightharpoonup }{y}$ = [y₁ y₂]′.

$$\begin{array}{l}\stackrel{\rightharpoonup }{x}\left(k\right)=A\cdot \stackrel{\rightharpoonup }{x}\left(k-1\right)+B\cdot u\left(k-1\right)+\stackrel{\rightharpoonup }{w}\left(k-1\right)+{\left[0p\left(k-1\right)0\right]}^{\prime }\\ \stackrel{\rightharpoonup }{y}\left(k\right)=C\cdot \stackrel{\rightharpoonup }{x}\left(k\right)+\stackrel{\rightharpoonup }{v}\left(k\right)\end{array}$$ (1)

System states at trial k − 1 are mapped to future states by state transition matrix A and adjusted by foot placement motor command u(k − 1), which represents the input to the model. Since the foot placement action u(k − 1) represents the transition from trial k − 1 to trial k, the same target is associated with x₁(k − 1) and x₃(k). States are also perturbed by a prism-associated parameter p and process noise $\stackrel{\rightharpoonup }{w}$, where $\stackrel{\rightharpoonup }{w}$ = [w₁ w₂ w₃]′ and where $\stackrel{\rightharpoonup }{w}\left(k-1\right)$ is drawn from independent, zero-mean, normal distributions with covariance matrix Q. Process noise components w₁, w₂, and w₃ are associated with unmodeled variations (e.g., random perturbations or other aspects of the task not captured by the model) in subject's initial starting position that affect relative target position, relative head-body rotation that contributes to the visuomotor mapping, and foot placement, respectively. The actual states at trial k are mapped to the observations available to the subjects by the output matrix C and also corrupted by sensory noise $\stackrel{\rightharpoonup }{v}$, where $\stackrel{\rightharpoonup }{v}$ = [v₁ v₂]′ and where $\stackrel{\rightharpoonup }{v}\left(k\right)$ is drawn from independent, zero-mean, normal distributions with covariance matrix R.

There are two equivalent options for representing the prism noise so as to cause Gaussian-like measurement perturbations. Prism noise may be represented as perturbations of x₂, where parameter p would model both the mean prism shift and the trial-by-trial prism noise effects. Prism noise may also be represented as sensory noise. In this case, parameter p would model the mean prism shift and parameter $\stackrel{\rightharpoonup }{v}$ would model the prism noise. Although it is unclear which model form best represents a subject's neural representation of prism noise, simulations validated that these options are mathematically equivalent (data not shown). We chose to model the prism noise as sensory noise because it allows direct use of the Kalman equations to predict controller feedback gains and thus subject responses to prism noise perturbations (see Sensory prediction error controller).

Sensory noise components v₁ and v₂ are then associated with the effect of prism noise on target sensing and foot placement error sensing, respectively. Since the foot placement action demarcates individual trials, the same prism lenses affect sensing of target location at trial k − 1 and foot placement error at trial k. We parameterized the relative effect of the prism noise on these two measurements with a scaling factor α, where v₂(k) = α·v₁(k − 1). Therefore, we directly varied v₁ to mimic the experimental prism noise conditions, whereas we considered α fixed across conditions. Matrix parameters are defined in Table 1.

Table 1.

Modeling parameters

Parameter	Values	Description
A	$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ -1& 0& 0\end{array}\right]$	State transition matrix
B	$\left[\begin{array}{ccc}0& 0& 1\end{array}\right]\prime$	Input matrix
C	$\left[\begin{array}{ccc}1& 1& 0\\ 0& 0& 1\end{array}\right]$	Output matrix
Q	$\left[\begin{array}{ccc}\mathrm{var}\left(w_1\right)& 0& 0\\ 0& \mathrm{var}\left(w_2\right)& 0\\ 0& 0& \mathrm{var}\left(w_3\right)\end{array}\right]$	Process noise covariance matrix
R	$\left[\begin{array}{cc}\mathrm{var}\left(v_1\right)& 0\\ 0& \mathrm{var}\left(\alpha \cdot v_1\right)\end{array}\right]$	Sensory noise covariance matrix

To simulate the visually guided walking model, the model input u must be defined at each trial, and we tested two competing control models for planning this command (described in Sensory prediction error controller and Task error controller). We compared their ability to predict experimentally measured adaptations in response to perturbations of the visuomotor mapping. In the sensory prediction error controller, a state estimator predicts target line location and the subject steps toward that estimate. The target location estimate updates at each trial on the basis of sensory prediction error. In contrast, the task error controller estimates a correction term and steps toward the sensed line position plus the correction term. The correction term updates at each trial on the basis of sensed foot placement error. In both controllers, sensed errors are corrupted by prism noise.

Sensory prediction error controller.

In the sensory prediction error controller (SPEC), a state estimation controller uses a forward model that parallels the dynamics of the visually guided walking model to produce estimates of relative target position x^₁, mean prism shift x^₂, and foot placement error x^₃ (Eq. 2). The foot placement command is planned by the simple strategy of stepping directly to x^₁, after which feedback measurements $\stackrel{\rightharpoonup }{y}$ are used to update the state estimates.

$$\begin{array}{l}u\left(k-1\right)=\left[\begin{array}{ccc}1& 0& 0\end{array}\right]\cdot \widehat{\stackrel{\rightharpoonup }{x}}\left(k-1\right)\\ {\widehat{\stackrel{\rightharpoonup }{x}}}_{\ast }\left(k\right)=A\cdot \widehat{\stackrel{\rightharpoonup }{x}}\left(k-1\right)+B\cdot u\left(k-1\right)\\ \widehat{\stackrel{\rightharpoonup }{x}}\left(k\right)={\widehat{\stackrel{\rightharpoonup }{x}}}_{\ast }\left(k\right)+L\cdot \left(\stackrel{\rightharpoonup }{y}\left(k\right)-C\cdot {\stackrel{\rightharpoonup }{x}}_{\ast }\left(k\right)\right)\end{array}$$ (2)

The state estimator is composed of a forward model that generates an initial state estimate ${\widehat{\stackrel{\rightharpoonup }{x}}}_{\ast }\left(k\right)$, where $\widehat{\stackrel{\rightharpoonup }{x}}$ = [x^₁ x^₂ x^₃]′ based on the previous state estimate $\widehat{\stackrel{\rightharpoonup }{x}}\left(k-1\right)$ and the foot placement motor command u(k − 1). The final estimate $\widehat{\stackrel{\rightharpoonup }{x}}\left(k\right)$ is obtained by adjusting the initial estimate by the sensory prediction error feedback $\stackrel{\rightharpoonup }{y}\left(k\right)-C\cdot {\stackrel{\rightharpoonup }{x}}_{\ast }\left(k\right)$, scaled by the estimator feedback gain L. Reflected in these equations is the assumption that the state estimator has access to the control input u.

Under this interpretation, L is a matrix of sensory weightings that affect how strongly sensory prediction errors update the estimated system states. The Kalman filter method is one design approach for solving for these weightings. Assuming Gaussian sensory and process noise, the Kalman filter optimally designs L to minimize the variance of the sensory prediction error (Simon 2001) using the Riccati equation (Bryson and Ho 1975). This takes into account system parameters, A and C, and noise parameters, Q and R. In our model, the estimator is assumed to initially know the values of Q and R, whereas the subjects in our experiments must learn these statistics during the baseline phase.

The Kalman filter algorithm produces relatively large entries for L when the process noise perturbing a state is large compared with the sensory noise corrupting measurement of that state. Conversely, relatively small weightings are optimal when sensory noise dominates. Importantly, L also allows some measurements to play a larger role in estimating a state than others, depending on their relative amounts of sensor noise. For very large weightings in the L matrix, the estimated state will closely follow the sensory feedback scaled by that weighting. When entries of L are zero, associated sensory feedback signals do not contribute. Intermediate choices of L produce a controller somewhere between these extremes, whereby sensory feedback information filters through a forward model of the state dynamics.

Simulation of the walking model using the SPEC requires two parameters directly estimated from the experimental conditions and five free parameters with unknown values. Noise parameters are defined by their variance. Prism noise v₁ matched the diopter variance in the low-noise and high-noise experiments, with values of 3.03² and 5.66², respectively. Variance of v₁ for the no-noise condition was assumed to be an order of magnitude lower than that of the low-noise condition (0.3²). The parameter p induced the mean prism shift from the human experiment, where p(trial 50) = 18 diopters, p(trial 110) = −18 diopters, and p equals zero for all other trials. Nominal values for the remaining parameters (g, α, w₁, w₂, w₃) were assumed constant across the no-, low-, and high-noise conditions, where parameter g scales the output of the model from prism diopter to foot placement coordinates. The identified parameters minimized the sum of the squared error between the model output (see Model simulations and predictions) and average foot placement error across all subjects for the three adaptation phases. To implement this system identification, we used MATLAB's fminsearch.m function.

Task error controller.

We also tested a task error controller (TEC), another commonly used representation of motor adaptation, as a competing control system for planning u (Eq. 3) (see Haith and Krakauer 2013 for a review). Here, the foot placement command u(k − 1) is planned on the basis of the measured target location y₁ biased by a corrected term, x^₂, which may be conceptualized as an estimate of the mean prism shift, or visuomotor mapping. The correction term at trial k depends on the previous term and measured foot placement or task error y₂.

$$\begin{array}{l}u\left(k-1\right)=y_1\left(k-1\right)-{\widehat{x}}_2\left(k-1\right)\\ {\widehat{x}}_2\left(k\right)=a\cdot {\widehat{x}}_2\left(k-1\right)+m\cdot y_2\left(k-1\right)\end{array}$$ (3)

Learning rate m is a weighting term that determines how strongly the previously measured task error updates the current correction term. Forgetting rate a determines how the previous correction influences the current correction and is generally close to but less than 1. Although m appears qualitatively similar to the estimator feedback gain L, which scales sensory prediction errors to update the visuomotor mapping estimate, the TEC adapts the correction term only on the basis of perceived foot placement error. The models are also differentiated by the fact that L is optimally derived from the noise parameters, whereas the TEC has no formal methodology to consider noise values when determining m. However, m does scale the influence of sensory noise, and therefore relatively smaller values of m are expected to improve performance if sensory noise increases. Otherwise, trial-to-trial variability of foot placement error would increase without increasing the average accuracy.

Simulation of the walking model using the TEC requires known parameter value p and three free parameters with unknown values (g, a, m), where g and a are fixed and m is assumed to vary across the no-, low-, and high-noise conditions. We performed parameter identification to determine (g, a, m) as described previously in Sensory prediction error controller.

Model simulations and predictions.

We paired the competing foot placement controllers with the visually guided walking equations and simulated task performance by integrating the difference equations over 115 trials. We completed SPEC-based simulations for the no-, low-, and high-noise conditions after first solving for L on the basis of the nominal parameter values derived from the parameter identification. We completed TEC-based simulations at varying levels of m on the basis of nominal values. Because the purpose of modeling was to generate average expected adaptation profiles, we set the noise values to zero during the simulations, and therefore only the mean prism shift p influenced the visuomotor mapping.

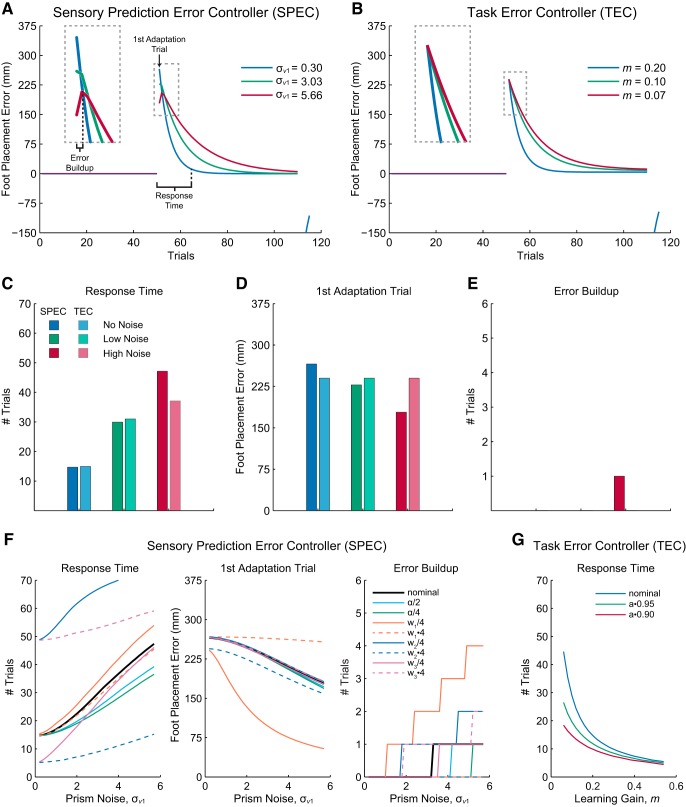
Both controllers adapt to the prism shift during the adaptation trials, reducing foot placement error over many trials (Fig. 2, A and B). The SPEC specifically predicts that this adaptation slows for increasing levels of prism noise (Fig. 2C). To compensate for increased noise, the state estimator decreases weightings on sensory prediction errors (components of L), and therefore these errors update the state estimates less at each trial. This controller result is robust across a wide range of noise parameters (Fig. 2F). For the TEC, decreases in learning rate m correspond with slowing of the foot placement adaptation (Fig. 2C), and this is true despite variations in the forgetting rate a (Fig. 2G). Both controllers therefore predict that compensations in L or m to reduce foot placement errors associated with prism noise will result in increased response times, defined as the number of adaptation trials necessary to achieve 95% of the total adaptation.

Fig. 2.

Model simulations. A: the sensory prediction error controller (SPEC) predicts foot placement error adaptation profiles across the no-noise (blue), low-noise (green), and high-noise (red) conditions. Response time and error buildup increase and first adaptation trial error decreases with increasing prism noise. B: task error controller (TEC) adaptation profiles for varying levels of learning rate m in which only response time varies. C–E: response time (C), first adaptation trial error (D), and error buildup values (E) measured from model adaptation profiles for each experimental noise condition. F: SPEC parameter study indicates that the effect of prism noise on response time, first adaptation trial error, and error buildup is robust to choices in other model parameters. G: TEC relationship between learning rate m and response time is robust to variations in forgetting rate a.

The SPEC also predicts that two additional features of the adaptation profile will vary with prism noise. Foot placement error in the first adaptation trial indicates the initial sensitivity to the shift in mean prism diopter and is expected to decrease with increasing prism noise because sensitivity to sensory prediction error feedback regarding target position is reduced (Fig. 2, A and D). As a result, the estimate of the target position relies more on the predicted target position determined by the forward model of the task, which is based on previous experience. For the same reason, foot placement error is expected to first increase before decreasing during the adaptation trials for high levels of prism noise (Fig. 2, A and E). Error buildup, the number of trials where error increases before decreasing during adaptation, occurs when the state estimator incorrectly attributes the mean prism shift to a change in relative target location x₁ instead of the visuomotor mapping x₂. Sensory prediction error feedback corrects the state estimates over time, but this correction is slower (error buildup increases) for increased prism noise. Both controller outcomes are robust across a wide range of noise parameters (Fig. 2F). Importantly, the TEC does not produce variations in first adaptation trial error and error buildup; we thus use their presence or absence in the empirical results to distinguish between these two competing controllers.

Data and statistical analyses.

We filtered the kinematic data from our experiments using a fourth-order low-pass Butterworth filter (cutoff frequency of 6 Hz). We determined foot placement on the target as the time at which point the foot marker anterior-posterior velocity and acceleration profiles stabilized to zero. The medial-lateral distance between the foot position marker and the center of the target at this time point defined the medial-lateral foot placement error (see Fig. 1A), where positive error represents foot placement to the right of the target. Because the direction of the mean prism shift during the adaptation phases rotated between the three noise conditions, we changed the sign of the errors during leftward prism shifts to positive for the purpose of our analyses and illustrations.

To test whether subjects adapted in the face of measurement uncertainty, we compared performance at specific “probe” trials (i.e., foot placement error in last baseline, first adaptation, last adaptation, and first postadaptation trials) using a two-way (condition × probe trial) repeated-measures ANOVA, and Tukey's post hoc tests for significant main effects or an interaction. These probe trials had prism shift values of the mean of each respective phase and thus allowed comparisons across noise conditions.

We quantified three metrics of the effects of measurement uncertainty on adaptation: 1) error in the first adaptation trial; 2) the number of trials of error buildup; and 3) two measures of adaptation rate, response time and early adaptation error. To calculate response time, we first smoothed the data using a five-trial running average and identified the trial, k, where the average error of trials k − 2:k + 2 fell below 95% of error in the first adaptation trial. We defined early adaptation error as the average foot placement error across trials 2–9 in the adaptation phase of each noise condition, similar to other research (Krakauer et al. 2005; Malone et al. 2011). We normalized this value to account for differences in the first adaptation trial between conditions by dividing it by the first adaptation trial error. Whereas the response time generally captures how long it takes subjects to reduce movement errors in the adaptation phase, the second measure instead focuses on the period of rapid early adaptation and does not depend on any extra treatment of the data. To test for differences with each measure, we used separate one-way repeated-measures ANOVAs and Tukey's post hoc tests when warranted. We analyzed data using custom-written MATLAB programs, and we used JMP 12 software (SAS Institute, Cary, NC) for all statistical analyses with an alpha level of 0.05.

RESULTS

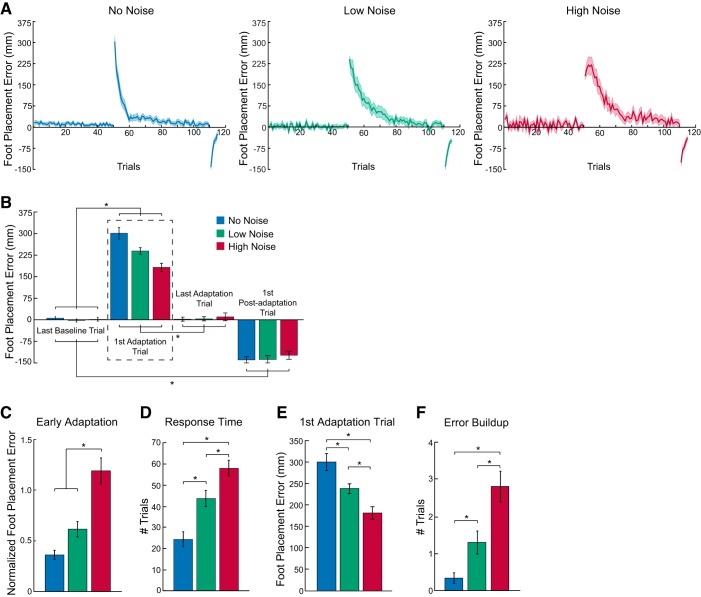
We first confirmed that subjects adapted in the face of measurement uncertainty. Figure 3A illustrates group mean (±SE) foot placement error across the baseline, adaptation, and postadaptation phases for each of the three noise conditions. Figure 3 demonstrates that error increased significantly in the adaptation phase compared with baseline but progressively decreased over repeated trials. In the postadaptation phase, we found large errors in the opposite direction that quickly decreased over five trials. As shown in Fig. 3B, a significant probe trial main effect (F_3,252 = 510.6, P < 0.0001) and condition × probe trial interaction (F_6,252 = 7.1, P < 0.0001) indicated that subjects fully adapted to the mean prism shift regardless of the underlying prism noise (compare first and last adaptation trials, and last baseline and adaptation trials). The significant negative aftereffect in the postadaptation phase (compare last adaptation trial with first postadaptation trial) indicates that subjects stored the new mean visuomotor mapping created by the prisms.

Fig. 3.

Increasing measurement uncertainty leads to decreasing first adaptation trial errors, decreasing adaptation rates, and increasing error buildup in response to a consistent prism shift. A: group mean (±SE) medial-lateral foot placement error across the no-noise (blue), low-noise (green), and high-noise (red) conditions. The direction of the mean prism shift during the adaptation phases rotated between the 3 noise conditions depending on the subject. Thus we changed the sign of the errors during leftward prism shift conditions for proper comparison with the rightward prism shift conditions for the purpose of our analyses. B: group mean (±SE) medial-lateral foot placement error in the probe trials across noise conditions. The dashed box highlights the first adaptation trial effects, in which significant differences between noise conditions are shown in more detail in E. C: group mean (±SE) medial-lateral foot placement error in early adaptation (average of trials 2–9, normalized by first adaptation trial error) across noise conditions. D: group mean (±SE) response time for each noise condition. F: group mean (±SE) error buildup. *P < 0.05, significant post hoc test effects.

Increasing measurement uncertainty slowed adaptation, a result predicted by both our controllers. Specifically, we found that greater prism noise led to slower adaptation when comparing foot placement error early in the adaptation phase (i.e., mean of trials 2–9) and the response time between noise conditions. The mean foot placement error in the high-noise condition greatly exceeded that in the low- and no-noise conditions (Fig. 3C; F_2,46 = 26.1, P < 0.0001). The response time measure showed similar results (Fig. 3D; F_2,46 = 24.1, P < 0.0001). In this case, response time in the high-noise condition exceeded response time in the low-noise condition, which differed significantly from the no-noise condition.

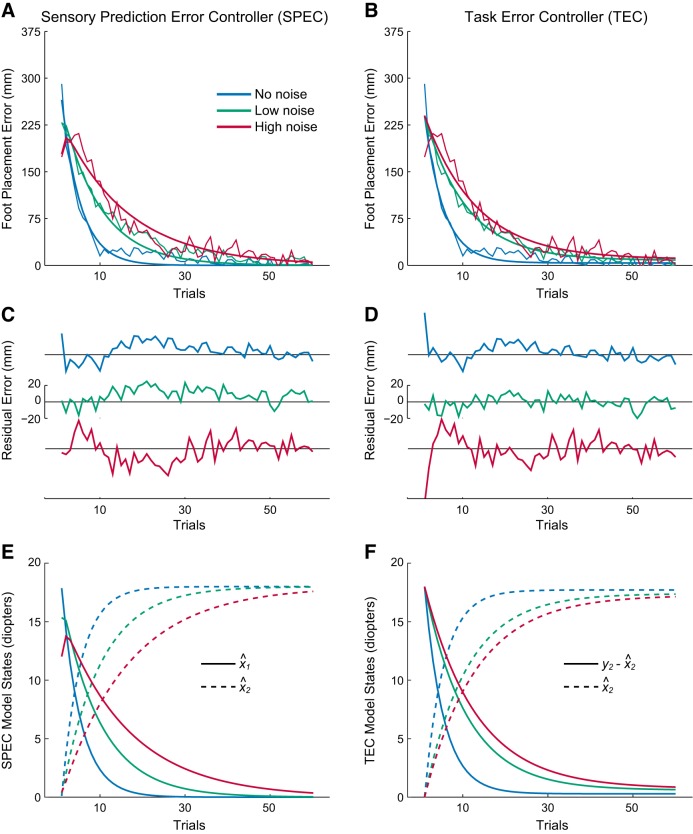
Both SPEC and TEC explained the average measured adaptation profiles (see Fig. 4). The SPEC captured 95.2% of the variance in the average data (Fig. 4, A and C). Process noise parameters w₁, w₂, and w₃, identified by least-squares optimization, were of comparable magnitude as the prism noise parameters, with values of 5.28 ± 1.42, 0.40 ± 0.12, and 2.41 ± 0.81 (mean ± CI), respectively. An identified value for α of 1.08 ± 0.48 suggests that the prism lenses equally affected target and foot placement error sensing. Interestingly, the TEC explained 95.8% of the variance in average data (Fig. 4B), although this controller does not capture the initial adaptation behavior, as demonstrated by the residuals (Fig. 4D). Identified values for m of 0.197 ± 0.018, 0.093 ± 0.007, and 0.076 ± 0.006 reflect the decreased adaptation rates across the no-, low-, and high-noise conditions, respectively. Thus direct fitting of the adaptation data does not distinguish the two controllers, because the total explained variance is equivalent. Differences in initial adaptation behavior between the two controllers are reflected in the model states (Fig. 4, E and F), where initial estimates of target location vary as a function of prism noise in the SPEC.

Fig. 4.

Model fits of foot placement error mean adaptation profiles, residuals, and model states for no-noise (blue), low-noise (green), and high-noise (red) conditions. A: SPEC model fits. B: TEC model fits. C: SPEC model residuals. D: TEC model residuals. E: SPEC model estimates for target location x^₁ and mean prism shift x^₂. F: TEC model correction term x^₂ and difference between sensed line position y₁ and the correction term.

As supported by the SPEC, foot placement error in the first adaptation trial decreases with increasing prism noise level. This trend is based on the expectation that subjects will reduce the weighting of sensory prediction error feedback regarding target position in favor of the forward model prediction of line position when faced with increased prism noise. When we focused on this trial (Fig. 3E), we found smaller error in the high noise condition compared with both the low- and no-noise conditions (P < 0.05, based on post hoc tests following a significant condition × probe trial interaction described earlier). Specifically, we observed 31.4% and 65.2% greater error in the low- and no-noise conditions, respectively, compared with the high-noise condition. Furthermore, we found smaller error in the low-noise condition compared with the no-noise condition.

We also observed error buildup in the adaptation profiles (Fig. 3A, right), a feature specifically predicted by the SPEC (see Fig. 2). The number of trials of error buildup, characterized by an initial increase in foot placement error prior to a gradual decrease, tended to increase with prism noise (Fig. 3F). We found greater error buildup in the high-noise condition compared with both the low- and no-noise conditions (F_2,46 = 16.0, P < 0.0001).

DISCUSSION

Our findings suggest that state estimation is used to accurately control foot placement during walking. Whereas increased measurement uncertainty increases foot placement errors, subjects learned to mitigate these effects by increasing reliance on a predictive model when given sufficient prior experience with this uncertainty in the baseline phase. This learning likely occurs in the context of adjusted weighting on sensory prediction error, and not measured task error, as evident by the timing and shape of subsequent corrective adaptations to a new visuomotor mapping condition.

Do our results clearly distinguish between the two foot placement controllers? Model outputs using both controllers fit the time course of the adaptation profiles equally well, although this outcome is partially explained by the fact that both controllers produce exponential decays and that this feature dominates the adaptation profile over the 60 measured trials. The other two factors, first adaptation trial error and error buildup, contribute significantly less to the variance of the adaptation signal and, therefore, to the strength of the model fits. However, coefficient of determination metrics are limited for nonlinear models (Spiess and Neumeyer 2010) and also are not the only way of determining goodness of fit. The SPEC is convincingly distinguished by its prediction that first adaptation trial error and error buildup vary as a function of measurement uncertainty. A graphical analysis of the residuals also emphasizes this point (Fig. 4, C and D).

Decreases in first adaptation trial error and adaptation rate with greater prism noise are substantiated by the results of reaching experiments (Herzfeld et al. 2014; Körding and Wolpert 2004; Wei and Körding 2010). Although other studies do not directly quantify first adaptation trial error, our findings about this measure correspond well with their error sensitivity metrics, which quantify the trial-to-trial relationship between visual perturbation value and the resultant error. In this context, the brain likely becomes less sensitive to sensory prediction error feedback (or uses vision less) with greater measurement uncertainty and thus relies more on forward prediction. This notion can also explain the lower adaptation rate, as shown in our results and previous research related to reaching (Experiment 1 in Burge et al. 2008; Wei and Körding 2010) and standing balance (Stevenson et al. 2009), that increases visual feedback uncertainty through target blur or dot clouds. Although Burge et al. (2008; see Experiment 3) used random trial-to-trial mappings to create greater measurement uncertainty, they found no effect on adaptation rate. However, their perturbations only affected visualized hand position, not the entire visual field as we have done in the present study, and were drawn randomly from a Gaussian distribution without consideration of order effects. In contrast, we reordered our randomly drawn perturbations to increase the perception of noise about a mean shift and applied them uniformly to the visual field, possibly increasing the likelihood that noise statistics were learned and attributed to sensory noise within the baseline period.

The presence of error buildup has not been observed in other motor adaptation studies or been proposed as evidence of state estimation-based control. Error buildup in our SPEC model occurs because the state estimator incorrectly attributes sensory prediction errors associated with the initial foot placement errors to a shift in estimated target location x^₁ instead of estimated mean prism shift x^₂ (Fig. 4E). This behavior is possible in a visually dominant task where a change in a sensed state (e.g., measured target location y₁) could be attributed to a change in multiple body states (e.g., x₁ or x₂), and other sensory information is not helpful for making the distinction. This behavior is also only expected to occur when subjects are exposed to measurement uncertainty prior to a sustained mean shift requiring adaptation, relatively uncommon conditions in motor adaptation studies. Our findings support the use of our experimental protocol and induction of error buildup as a possible tool for demonstrating and studying state estimation in future reaching and stepping motor control studies.

Given the perturbations applied in this study, we believe state estimation is the appropriate framework for developing a predictive model and drawing conclusions from the experimental findings. However, the nervous system likely relies on additional mechanisms to compensate for other perturbations. Foot placement in real-world environments would face a variety of perturbation types over a range of time scales. Presumably, the nervous system attempts to optimally respond to each of these perturbations. In the context of compensating for noise-like perturbations (zero mean and very low persistence) of varying amplitude, an optimal controller would inherently resemble a state estimator. In this context, persistence refers to the likelihood of a perturbation repeating from trial to trial (high persistence = high likelihood of a repeat). Therefore, any conservative strategy of aiming more centrally with increased noise-like perturbations will converge to be equivalent to optimal state estimation (Kalman filter) if the subject's actions are optimal or near optimal. Alternatively, when compensating for perturbations with varied persistence (zero mean and constant amplitude), an optimal controller would resemble those proposed by Herzfeld et al. (2014) and Körding et al. (2007).

Whereas purposeful stepping to a visual target represents a subset of walking behavior, state estimation control is likely applicable to walking control in general. Lateral instability requires significant active feedback control of foot placement, presumably based on a variety of sensory inputs, to ensure balance during walking (Bauby and Kuo 2000; Donelan et al. 2004; Fitzpatrick et al. 2006; O'Connor and Kuo 2009). State estimation may provide a means to improve stepping accuracy, and thus stability, by combining multiple noisy sensory channels with an internal model of the walking dynamics. Walking over rough terrain or complicated footpaths would similarly benefit by incorporating state estimation. Thus, although the sensory weightings during our experimental task are likely different than those in more typical walking scenarios, we expect that the general use of state estimation is common between them, even when a strong reliance of vision is absent.

The notion that state estimation drives foot placement during walking, as it does for hand position during reaching, implies that these tasks may share common neural substrates. However, locomotion is often studied from the perspective that pattern-generating, reflexive, and balancing circuits located in the spinal cord and brain stem dominate its control (Duysens and van de Crommert 1998; Grillner et al. 2008; Pearson 2008). Conversely, studies in reaching consider that the precise and often visually guided nature of arm movements require cortical control, involving the posterior parietal (PPC), premotor, and motor cortices in particular (Kalaska 2009; Rizzolatti et al. 2014; Vesia and Crawford 2012). Despite these differences, reaching is hypothesized to have evolved from quadrupedal locomotion (Dietz 2002; Georgopoulos and Grillner 1989). Indeed, the PPC and motor cortex are increasingly recognized as playing key roles in modifying gait on the basis of vision (Drew and Marigold 2015). In fact, many pyramidal tract neurons in the motor cortex demonstrate similar discharge activity, as well as temporal and magnitude relationships with muscle activity, during reaching and locomotion (Yakovenko and Drew 2015). In addition, recent neuroimaging work has shown that although effector-specific motor planning activity is encoded in certain PPC regions (e.g., anterior intraparietal sulcus, aIPS, for hand movements and anterior precuneous for foot movements), the anterior superior parietal lobe and medial intraparietal sulcus (mIPS) are active in planning visually guided eye, hand, and foot movements (Heed et al. 2011; Leoné et al. 2014). Interestingly, the pattern of activity in these regions does not distinguish between the two types of limb movement.

Generation of forward model predictions and state estimation are proposed functions of the cerebellum and PPC, respectively (Shadmehr and Krakauer 2008). For instance, predictive scaling of grip force is impaired in cerebellar patients relative to that in healthy control subjects (Nowak et al. 2004, 2007). The cerebellum is also necessary for sensory prediction error to drive visuomotor adaptation during reaching (Taylor et al. 2010; Tseng et al. 2007). In addition, neurons in the monkey PPC encode an estimate of the real-time angle of a joystick-controlled cursor used to make reaches to targets (Mulliken et al. 2008). Further indirect support comes from studies of rapid online corrective or change-in-direction movements, which test for rapid integration of visual feedback with a real-time estimate of limb and target state. For example, transcranial magnetic stimulation (TMS) to the lateral cerebellum disrupts the initial change in reaching direction to a target and increases endpoint finger error, and these results are consistent with the hand estimate being out of date (Miall et al. 2007). Additionally, TMS to mIPS at the onset of goal-directed reaches disrupts path corrections after unexpected target shifts (Desmurget et al. 1999), and TMS to aIPS impairs the ability to produce the appropriate forearm orientation when the grasp object is suddenly rotated (Tunik et al. 2005). We speculate that the cerebellum and PPC play a role in our task, and in walking in general, given that 1) cerebellar patients are slower and less able to adapt to prisms to control walking trajectory (Morton and Bastian 2004); 2) the PPC is important in adaptive gait modifications that result in changes in paw placement in cats (Lajoie and Drew 2007; Marigold and Drew 2011); and 3) neuroimaging work demonstrates that both regions are active during reaching prism adaptation (Clower et al. 1996; Luauté et al. 2009).

Our results have implications for understanding recovery of function and the design of rehabilitation programs following neurological injury that impairs walking. First, greater measurement noise (e.g., due to eye disease, brain injury, or peripheral neuropathy) may cause the nervous system to rely more on a predictive model during and after the adaptation process. Second, therapies or augmentations that actually reduce measurement uncertainty may help people adapt faster in rehabilitation settings.

In conclusion, we used prism noise in a visuomotor adaptation paradigm to demonstrate that state estimation underlies foot placement control during walking. A state estimation-based control model for planning foot placement specifically predicted how adaptation to a visuomotor mapping shift would change as a function of measurement uncertainty. This result not only parallels studies of reaching and grasping movements but also suggests that the robust theoretical and experimental framework for state estimation-based control is not confined to discrete voluntary upper limb tasks. Thus these findings expand the applicability of current models of motor adaptation for understanding central problems in motor control and for devising clinical corrections for improving upper and lower limb function.

GRANTS

This work was supported by Natural Sciences and Engineering Research Council of Canada Grants RGPIN-2014-04361 (to D. S. Marigold), RGPIN-371582 (to D. S. Marigold), and RGPIN-326825-2013 (to J. M. Donelan).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

R.S.M. performed experiments; R.S.M., S.M.O., J.M.D., and D.S.M. analyzed data; R.S.M., S.M.O., J.M.D., and D.S.M. interpreted results of experiments; R.S.M., S.M.O., and D.S.M. drafted manuscript; R.S.M., S.M.O., J.M.D., and D.S.M. approved final version of manuscript; S.M.O. and D.S.M. prepared figures; S.M.O., J.M.D., and D.S.M. edited and revised manuscript.