Automatic quantification of ischemic injury on diffusion-weighted MRI of neonatal hypoxic ischemic encephalopathy

Abstract

A fully automatic method for detection and quantification of ischemic lesions in diffusion-weighted MR images of neonatal hypoxic ischemic encephalopathy (HIE) is presented. Ischemic lesions are manually segmented by two independent observers in 1.5 T data from 20 subjects and an automatic algorithm using a random forest classifier is developed and trained on the annotations of observer 1. The algorithm obtains a median sensitivity and specificity of 0.72 and 0.99 respectively. F1-scores are calculated per subject for algorithm performance (median = 0.52) and observer 2 performance (median = 0.56). A paired t-test on the F1-scores shows no statistical difference between the algorithm and observer 2 performances. The method is applied to a larger dataset including 54 additional subjects scanned at both 1.5 T and 3.0 T. The algorithm findings are shown to correspond well with the injury pattern noted by clinicians in both 1.5 T and 3.0 T data and to have a strong relationship with outcome. The results of the automatic method are condensed to a single score for each subject which has significant correlation with an MR score assigned by experienced clinicians (p < 0.0001). This work represents a quantitative method of evaluating diffusion-weighted MR images in neonatal HIE and a first step in the development of an automatic system for more in-depth analysis and prognostication.

1. Introduction

Hypoxic-ischemic encephalopathy (HIE) is a condition associated with brain injury which, in newborn infants, is typically caused by perinatal asphyxia. The rates of mortality and morbidity in neonatal HIE remain high, even in the era of therapeutic hypothermia, the only treatment available to date. In neonates receiving therapeutic hypothermia, rates of death are reported between 10 and 40%, while amongsurvivors 20–30 % have moderate to severe disabilities (Azzopardi et al., 2014, Jacobs et al., 2008, Dec, Shankaran et al., 2005, Simbruner et al., 2010). Assessment and understanding of the type and severity of cerebral injury that has occurred is extremely important in the context of clinical decision making and prognostication (Bonifacio et al., 2015).

One of the principal ways to assess cerebral injury following suspected neonatal HIE is through magnetic resonance (MR) imaging, which has been shown to be one of the best predictors of outcome (Cheong et al., 2012, Weeke et al., 2016). While conventional T1 and T2 sequences may show signal changes in affected areas, it is well known that diffusion-weighted (DW) imaging should be acquired for early visualisation of hypoxic ischemic injury, optimally between 3 and 7 days after the hypoxic insult occurs (Alderliesten et al., 2011, Bednarek et al., 2012, Cowan et al., 1994, Aug, Johnson et al., 1999, Rutherford et al., 2006).

DW images depict water diffusion in the brain tissue, which, in neonatal HIE, is known to be reduced in ischemic regions in the first week after the injury occurs (Bednarek et al., 2012; Cowan et al., 1994). Since DW images may be affected by T2 relaxation and other factors which simulate restricted diffusion, it is recommended to acquire the apparent diffusion coefficient (ADC) map, which is essentially a voxel-by-voxel ratio between a diffusion-weighted and a non-diffusion-weighted image (Le Bihan et al., 1986). The ADC map eliminates any T2 shine-through effect and there is a large body of literature to suggest that this is optimal way to visualise ischemic injury in neonates with suspected HIE (Alderliesten et al., 2011, Barkovich et al., 2006, Cheong et al., 2012, de Vries et al., 2011, Heinz and Provenzale, 2009, Liauw et al., 2009, Rutherford et al., 2010, Vermeulen et al., 2008, Wolf et al., 2001).

The ADC value is a property of the tissue being imaged and expected normative ranges for particular cerebral regions have been defined for neonatal images (Bartha et al., 2007, Coats et al., 2009, Neil et al., 1998). Throughout the first week after the hypoxic insult, ischemic lesions are expected to have restricted diffusion, leading to lower than normal ADC values (McKinstry et al., 2002). Current clinical practice for analysing the ADC map is a visual assessment, where the clinician scrolls through the slices of the image looking for regions where intensity is visibly lower than expected, and makes a non-quantitative report based on an impression of the volume, severity and pattern of the injuries. To assist in the assessment, the clinician may use an on-screen tool to identify a 2D region of interest (e.g. an ellipse) and obtain a measurement (e.g. average ADC value) (Wolf et al., 2001), however, this is not a requirement and since it is manually laborious it is typically limited to a few small areas of the scan. Some scoring systems have been suggested and used in research studies (Barkovich et al., 1998, van Rooij et al., 2010), however the scores are based on visual assessment rather than quantifiable, precise, reproducible measurements. The aim of this work is to develop an automated method to assess ADC maps in neonatal HIE, providing quantitative, objective analysis which will aid the clinician in clinical decision-making and determination of prognosis.

In spite of the volumes of literature describing the visual interpretation of neonatal MR images in HIE there has been relatively little work to date on automating the image analysis tasks for effective and consistent injury quantification. Ghosh et al. (2011) used a hierarchical region splitting (HRS) method to automatically detect ischemic lesions on T2 images in an animal model of neonatal HIE, which showed promising agreement with manual delineations. In 2014 the authors compared the method with two others on a dataset including T2 images of animal model hypoxic ischemic injury and DW MR images from human neonatal subjects (n = 2) with arterial ischemic stroke (AIS) (Ghosh et al., 2014). It was found that the HRS method was most robust, while a method of symmetry-integrated region growing performed slightly better in comparison to the gold standard. Isgum et al. have also reported a method of injury detection and quantification in neonatal AIS using supervised voxel classification (Išgum et al., 2011). However, neonatal AIS presents very differently to hypoxia ischemia in an MR examination, with much larger and more focal injuries and an animal model of hypoxia may not provide a reliable representation of ischemia in human neonatal HIE. In this work we present a method to segment ischemic lesions in DW MR of neonatal HIE subjects. Lesions have been manually delineated by two expert observers, allowing for benchmarking of our reference-standard. The method is trained on manual annotations from 20 subjects and applied to a database of 74 subjects in total. The results of the algorithm are compared with manual annotations as well as with injury patterns and MRI scores provided by clinicians and neurodevelopmental outcomes.

2. Data

2.1. Cohort

Data from a total of 74 infants, admitted to the neonatal intensive care unit of the Wilhelmina Children's Hospital with suspected HIE, is used in this work. All MRI data was acquired at Wilhelmina Children's Hospital, University Medical Center Utrecht between 2005 and 2012. Infants with suspected genetic conditions or congenital anomalies have been excluded. Outcome (either death or developmental assessment results at 2 years of age (see Section 2.4)) is known for all subjects. This is a retrospective study using anonymous data analysis which was approved by the local ethics committee. The requirement to obtain informed consent for this study was waived.

2.2. Scanning

Scanning took place between day 2 and day 7 after birth (median was day 4). All scans were acquired in the axial direction on 1.5 T or 3 T MR scanners (whole-body Achieva system, Philips Medical Systems, Best, Netherlands) using an 8 channel head coil. For each subject the non-diffusion-weighted image was acquired with the attenuation factor, b, set at b = 0 (Le Bihan et al., 1986). The diffusion-weighted image was acquired in 3 perpendicular directions with b = 1000 (1.5 T) or b = 800 (3.0 T). The ADC map was calculated using the logarithm of the ratio of these two images as described in (Le Bihan et al., 1986). Purpose-built software was used for this calculation to avoid potential variation in software from different scanners. The main properties of the data are provided in Table 1 where the data is divided into 3 datasets for clarity, as follows: A) Subjects for which ischemic lesions have been fully annotated by 2 independent observers. (1.5 T data), B) Independent test set without annotations (1.5 T data), C) Independent test set without annotations (3 T data).

Table 1.

Properties of the three datasets included.

Set	Number subjects	Magnetic field	Manual annotations	Higher b-factor (bHigh)	Voxel sizes (mm)	Acquisition time period
A	20	1.5 T	Yes	1000	0.7 × 0.7 × 4.0	2005–2011
B	21	1.5 T	No	1000	0.7 × 0.7 × 4.0	2008–2012
C	33	3.0 T	No	800	0.9 × 0.9 × 4.0	2008–2012
All	74		20			2005–2012

2.3. MRI scores

A scoring system originally developed by Barkovich et al. (1998) to assess perinatal asphyxia by means of MR imaging was modified to include DW imaging as described in van Rooij et al. (2010). This scoring system is applied for each subject resulting in a ‘modified Barkovich’ MRI score (van Rooij et al., 2010), which ranges in value from 0 to 11 depending on the severity of visible injury. In determining this score the clinician has access to conventional MR images (T1- and T2-weighted) as well as the diffusion-weighted image and ADC map.

2.4. Outcome data

Of the 74 infants included, 24 died in the neonatal period following withdrawal of intensive care. The decision to redirect care was based on neurological examination, EEG/aEEG, MRI and ultrasound findings. The remaining 50 had neurodevelopmental assessments at 2 years of age. The Bayley Scale of infant and toddler development (third edition, BSID-III) (Bayley, 2006) was used for assessment in 44 cases and the remaining 6 were assessed using the Griffiths Mental Development Scales (GMDS) (Griffiths, 1984). The developmental assessments were carried out by specialists who were blinded to the MR findings. The results were processed to provide an outcome category for each subject as follows: For those that received the Bayley test the composite scores for both motor and cognition were considered and the minimum of these was used as the outcome score (in practice we found a very high degree of correlation between motor and cognition scores (Pearson's r = 0.98)). For those that received the GMDS the developmental quotient (DQ) was used. In both cases, a score of  <85 is considered to be abnormal, while a score of 100 matches the population average. We define 3 categories of surviving infants, abnormal (score  <85), normal [below mean] (85 ≤score < 100) and normal [above mean] (score ≥ 100).

3. Methods

3.1. Data annotation

Using proprietary software, observers were asked to identify and mark every pixel on the ADC map which they considered to represent ischemia (cytotoxic edema). The developed software allows the user to annotate individual pixels with a mouse-click and to draw pixel-based boundaries. Closed boundary regions could be filled with a single mouse-click. Annotations were carried out on a slice-by-slice basis, although observers could scroll freely to surrounding slices to assist their decision making. Observers were free to view the scan in coronal and sagittal directions, but because of the 4 mm slice thickness this was typically not found to be very useful. All annotations were made on the ADC map, however the observers also had access to the original diffusion-weighted and non-diffusion-weighted images as required, as well as to the conventional MR sequences. Intensity values for pixels under the mouse cursor were displayed at the bottom of the screen, allowing the observers to estimate region intensities by moving the cursor around. Typically the observers examined and marked the ADC map using the ADC intensities to help confirm suspicion of ischemia. The diffusion-weighted image was also consulted if there was any further doubt. Each observer was free to adjust the brightness and contrast (window level and width) as they wished both before and during analysis.

Annotations were made by SN and NvdA, clinicians with more than 2 and 8 years experience respectively in evaluating neonatal MRI. The observers worked independently and blind to subject outcome, each annotating all of the 20 ADC maps from dataset A. The markings of SN were all checked and corrected where necessary by MB, a neonatologist with over 10 years experience in evaluating neonatal MRI.

3.2. Automatic ischemia detection

Automatic detection of ischemia was carried out using features of the ADC map and the diffusion-weighted image in a system of supervised learning using random forest classification (Breiman, 2001). The first step in the method was to create a brain mask, eliminating background and non-brain structures. This was done using FSL's BET tool on the non-diffusion-weighted image (Smith, 2002). The default parameters of the tool were used in all cases, leading to very accurate brain segmentations in most subjects and only minor, partial over-segmentations in a small number. No manual correction was carried out. All subsequent processing excludes voxels outside the brain-mask and is carried out on 2D slices because of the slice-thickness of 4 mm. Each slice is first divided into superpixels (regions) which are relatively homogeneous in intensity. Features of each superpixel are then calculated and the manual annotations of observer 1 on dataset A are used as training data to build a random forest classifier (leave-one-subject-out training and testing is employed within dataset A). Classification using the random forest then yields a probability, for each superpixel, of it representing ischemia. The method is described in more detail in the remainder of this section.

3.2.1. Superpixel detection

The first step in the detection of intensity-based homogeneous superpixels was to process the ADC image such that voxels above threshold t_upper would be set to that value, and similarly for regions below threshold t_lower (clamping voxel values). This was done based on the fact that the ADC value is a physical property of the tissue type represented, and research in normative neonatal DW imaging (Coats et al., 2009, Neil et al., 1998, Toft et al., 1996) as well as a wealth of experience in imaging neonates with ischemic injuries (Alderliesten et al., 2011, Barkovich et al., 1998, Rutherford et al., 2010, Vermeulen et al., 2008, Wolf et al., 2001) provides an expectation of the ADC ranges within which ischemic tissue may fall. We wished to bundle regions which clearly cannot represent ischemia together rather than dividing them unnecessarily into homogeneous superpixels which will require further individual processing. We set t_upper at 1.5 × 10 ⁻³ mm²/s (which typically represents healthy white matter or CSF) and t_lower at 0.2 × 10 ⁻³ mm²/s (rarely occurring and typically representative of small artefacts). Fig. 1 (parts 1–2) illustrates how this affects image appearance.

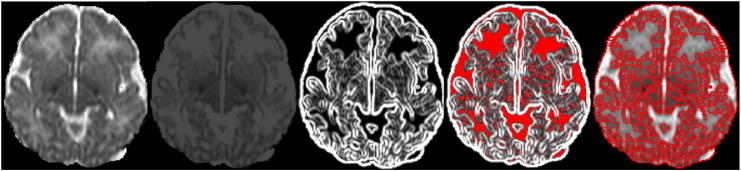
Fig. 1.

Detecting boundaries of homogeneous superpixels. From left to right: 1) A slice from the ADC map. 2) The same slice shown after clamping pixel values to a fixed range. Contrast and brightness settings are unchanged. 3)The in-slice gradient image (from clamped ADC image). 4) Pixels shown in red are below the gradient threshold to be zeroed. 5) Result of the watershed transform.

Each slice was then processed as follows: The sum of the squared image gradients in the in-slice directions (X and Y) was calculated, using a Gaussian kernel with σ = 0.5 mm. The lowest 10% of non-zero values in the gradient image were zeroed and a watershed transform (Meyer, 1994) was applied to determine the final superpixel boundaries. Fig. 1 (parts 3–5) shows an example of this process. All bounded regions are considered as superpixels, including those whose original ADC values fall outside the clamping thresholds.

This watershed-based method works well for our application, where the requirement for homogeneity of intensity values within the superpixel is foremost, while the size and shape of the superpixel is irrelevant. Experiments with previously developed methods to define superpixels, such as Achanta et al., 2012, Levinshtein et al., 2009, found that the aim to retain consistency of size and shape of the superpixels interfered with our requirement to place boundaries at image gradients. Tuning parameters to strongly prioritise this requirement obtained erratic and unsuitable results.

3.2.2. Feature calculation

For each detected superpixel, a total of 9 features were calculated, describing the grey-value of the superpixel in the ADC map and the diffusion-weighted image as well as the location of the superpixel within the brain. Location features are important since ischemia is most common in certain regions such as the basal ganglia/thalamus and white matter, while the healthy cerebellum and brainstem, for example, often contain grey-values which would represent ischemia in other tissues.

While ADC values are a property of the underlying tissue type, and have set ranges within which they may be expected to fall, this is not true of the original diffusion-weighted and non-diffusion-weighted scans, which can have extreme variation in the value ranges depending on the scanner and settings applied. This was an important consideration when developing a feature to represent image values in the diffusion-weighted image, since it was required that the feature values would be consistent across all scans. For each diffusion-weighted image we therefore obtained a reference value, d_ref, which corresponded to regions of ‘high diffusion’ in that image. This was done by obtaining the average value of all voxels in the diffusion-weighted image, where the corresponding ADC value was in the range 1.5 to 3.0 × 10 ⁻³ mm²/s (healthy white matter and CSF). The value of each voxel in the diffusion-weighted image was then modified by dividing it by d_ref to obtain a value d_mod, illustrating the level of diffusion at that voxel location, relative to the ‘high diffusion’ areas.

The full list of nine features calculated for each superpixel is provided as follows:

• 1.Superpixel volume. The largest components tend to be those regions which were excluded from further division based on their high ADC values. The volume further identifies them as unlikely ischemia candidates.
• 2.Average ADC value within the superpixel. The ADC value is the feature providing most weight in typical clinical analysis.
• 3.Average blurred ADC value within the superpixel. The average of the ADC values within the superpixel when the slice values are blurred using a Gaussian kernel with σ = 1.0 mm. This gives information about ADC in regions surrounding the superpixel.
• 4.Average d_mod value within the superpixel. This provides information about the diffusion level according to the diffusion-weighted image. Regions of true ischemia should show restricted diffusion in both ADC and diffusion-weighted images independently.
• 5.Average blurred d_mod value within the superpixel. The average when the slice of d_mod values is blurred using a Gaussian kernel with σ = 1.0 mm
• 6.Distance to brain mask edge. This helps to exclude regions around the cortex which can appear naturally darker (like ischemia) in ADC.
• 7.The signed distance (in mm) in the X (sagittal) direction between the superpixel centre of mass and the brain centre of mass.
• 8.The signed distance (in mm) in the Y (coronal) direction between the superpixel centre of mass and the brain centre of mass.
• 9.The signed distance (in mm) in the Z (axial) direction between the superpixel centre of mass and the brain centre of mass.

3.2.3. Random forest classification

A random forest classifier (Breiman, 2001) is a supervised classifier consisting of a number, n_trees, of binary decision trees. Each decision tree is built using randomly drawn training samples from the specified training set. The classification probabilities from all trees are combined to give the final random forest classification. Each sample, in this work, was a single superpixel (as described in Section 3.2.1), which was labelled as class 0 (healthy) if more than 90% of its pixels had been labelled healthy in the training data and class 1 (ischemia) if more than 50% of its pixels had been labelled as ischemia. (The threshold was set lower for class 1 in order to increase the number of ischemic samples, which are typically much fewer in number.) Superpixels with between 10 and 50% annotated ischemic were not included as training samples since their true classification was uncertain. Superpixel boundaries were excluded from the classification process. The classifiers were built using 100 trees with entropy as the splitting criterion, a maximum tree depth of 15 and bootstrapped samples. The average error when classifying out-of-bag samples was used to decide the number of trees and the maximum tree depth. Analysis of this error measure over 7 different subjects, randomly selected from dataset A, showed that it declined rapidly with the number of trees up to approximately 20–30 trees and levelled out thereafter. We settled on 100 to allow for any variation in unseen datasets, and since it incurs no penalty other than extra processing time. Tree-depth appeared to be optimal at around 15, with some minor variations between subjects. The classification process yielded a probabilistic output for each superpixel, indicating the chance of it representing ischemia. This final probability for each superpixel was obtained as the mean of all probability estimates across trees.

4. Experiments and results

The random forest classifier was trained using the annotations of observer 1 on the twenty subjects in dataset A. The annotations of observer 2 were retained for interobserver comparisons (the term ‘interobserver’ is used in this work to refer to the difference between our two specific observers and does not imply any more general meaning). For classification in dataset A (where training labels were defined), a system of leave-one-subject-out was employed and each subject was classified using training data from the other 19 subjects. Datasets B and C were classified using all training data from dataset A.

The output probabilities of ischemia for each superpixel are written to a probabilistic image I_prob. To obtain a binary segmentation I_prob is first thresholded with a specified threshold t_prob. Next, a morphological closing (square kernel, half-size = 1 pixel) is applied on each slice to close small gaps between remaining superpixels. This fills in superpixel boundaries, which have hitherto been ignored.

Where manual annotations are available (dataset A) the resulting binary image is then compared voxel-wise with the annotations of observer 1 to determine agreement in terms of sensitivity and specificity. Section 4.1 describes the results from these experiments in more detail, as well as the sensitivity and specificity of observer 2.

For the independent test sets (datasets B and C), and including dataset A as well, the algorithm output is validated by comparison with clinical information in the form of the modified Barkovich score for the MR data, the clinician's opinion of the injury pattern and the outcome of the subject. For this purpose the algorithm output is condensed into a heatmap for visualisation and a single system score which will be described in Section 4.2

4.1. Algorithm versus annotations

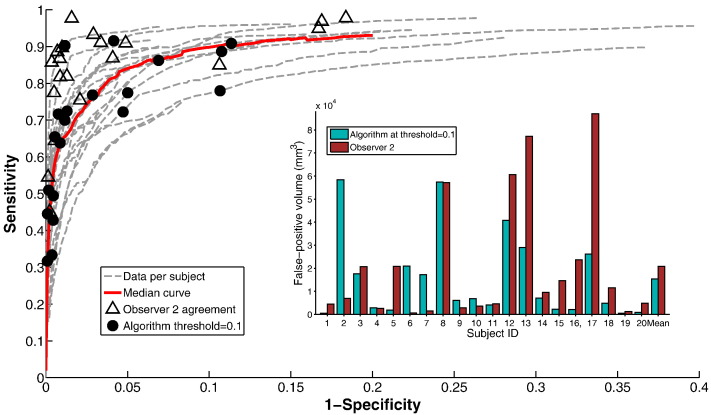
Binary segmentation results are obtained from the algorithm probabilistic output using different thresholds t_prob and used to create ROC curves as shown in Fig. 2. Actual volumes of false-positives (healthy tissue identified as ischemia) in mm³ are shown per-subject as an inset in Fig. 2. It should be noted that specificity (the percentage of healthy tissue detected correctly) is typically high since the volume of healthy tissue is (relatively) large in most cases, compared to the volume of ischemia. The number of false-positives identified by the algorithm may be small in the context of this large healthy region, but still be large in the context of what might be considered acceptable. An ‘acceptable’ level of false-positive detection is difficult to define, as it is a subjective matter, but this point should be taken into account when interpreting the ROC curves presented.

Fig. 2.

Performance of the algorithm compared with observer 1 annotations on dataset A (20 subjects). Inset: false-positive volumes in mm³.

Fig. 2 also shows the sensitivity and specificity values assigned to observer 2, when compared with observer 1 (triangles) and the sensitivity and specificity values of the algorithm at a fixed threshold t_prob = 0.1 (black dots). This threshold typically results in binary segmentations which have sensitivity and specificity values in a similar range to those of observer 2, and which appear visually correct. We do not suggest that there is an optimal value for t_prob across all subjects, nor even that binary thresholding is the best way to interpret the algorithm results, but it is useful for comparison with the binary markings of the observers. We refer to the algorithm result thresholded at t_prob = 0.1 as the ‘binary result’.

Considering algorithm performance on binary results, the spread of sensitivity and specificity values are, at first glance, reasonably similar to those obtained by observer 2, with slightly lower sensitivities, but also higher specificities. To compare performance directly we calculate F1-scores (harmonic mean of sensitivity and precision) for the algorithm binary result and for observer 2 in each case. The median F1-score for the algorithm is 0.52 (range 0.22–0.83), while for observer 2 the median is 0.56 (range 0.23–0.83).

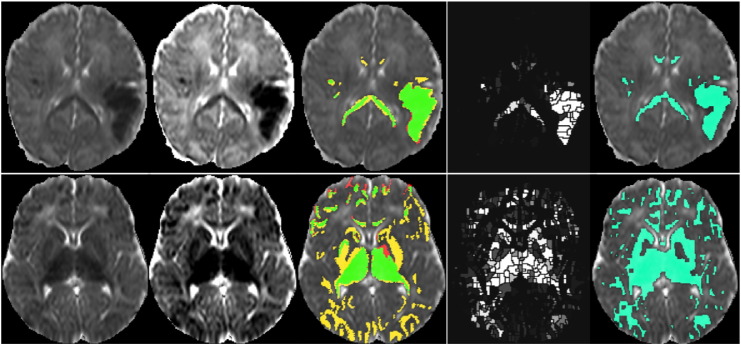
The algorithm performed best on subject 14 (consistently highest curve above sensitivity of 0.5). The top row of Fig. 3 shows a slice from the ADC map, along with the annotations from observers 1 and 2 and the algorithm output. The algorithm obtains sensitivity and specificity of 0.92 and 0.99 respectively for the binary result. Interobserver agreement is also good for this subject, with sensitivity = 0.90 and specificity = 0.99. By contrast, the lower row of Fig. 3 shows a slice from subject 8, which had one of the poorest performances. This subject has the lowest curve in the more acceptable specificity ranges and one of the poorest binary results with a sensitivity of 0.78 and specificity of 0.89. Interobserver agreement is also poor for this subject with sensitivity of 0.85 at a specificity of 0.89. The two different settings of brightness and contrast shown for this scan in Fig. 3 indicate a possible reason for the observer disagreement on the white-matter injury. The ADC values marked by observer 2 in the occipital region were low, but may not have appeared significant with window settings which easily captured the dominant basal-ganglia/thalamus injury.

Fig. 3.

Upper row: A slice from subject 14, the subject where the algorithm performs best against observer 1. Lower row: A slice from subject 8, the subject where the algorithm performs worst against observer 1. From left to right: 1) and 2) The ADC map seen with two different brightness and contrast settings. 3) The observer annotations (red = observer 1 only, yellow = observer 2 only, green = agreement). 4) The probabilistic outcome from the algorithm. 5) The final binary result from the algorithm at threshold t_prob = 0.1. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

It is clear from the lower row of Fig. 3 that (in this particular subject) the algorithm has better agreement with observer 2 than observer 1. An analysis of the algorithm performance in isolation from interobserver differences (on consensus regions) is provided in the supplementary material.

4.2. Assessing algorithm on independent test sets

Datasets B and C are completely independent of the training set and furthermore include 33 scans from a 3.0 T scanner. Based on visual analysis the algorithm performs in a similar manner on both these datasets as on dataset A, in spite of some differences (e.g. reduced resolution and smoother gradients) in the 3 T data. To illustrate its performance in the absence of any manual annotations we firstly condense the findings for each subject into a heatmap which shows the proportion of tissue identified with specific probabilities of ischemia and distances from the brain edge. These heatmaps are shown in conjunction with clinical scores and noted injury patterns as well as outcome at 2 years of age, to demonstrate the relationship between the algorithm findings and the clinical data. Further details on the heatmap construction are provided in Section 4.2.1.

Since clinical findings regarding the injury visible on MR have been condensed into a single measure, the modified Barkovich score, as described in Section 2.3, we further condense our algorithm findings to one measure to determine whether there is a correlation with the clinical score. This is described and illustrated in Section 4.2.2.

Dataset A is also included in all analysis detailed in this section.

4.2.1. Heatmaps

The heatmaps for each subject are created by traversing all voxels within the brain mask and determining, for each one, the probability of ischemia p according to the algorithm, and the distance d to the edge of the brain mask according to a 3D distance transform. The probability p is converted to a probability category p_c with 1 ≤ p_c ≤ 10 by p_c = ⌈10p⌉ while the distance d is similarly converted to a category d_c, 1 ≤ d_c ≤ 10, by d_c = ⌈10d/max_d⌉, where max_d is the maximum distance of any voxel to the edge of the brain mask. A 10 × 10 matrix, M, is maintained, with element M(i,j) being incremented when a voxel with p_c = i and d_c = j is encountered. When all voxels are traversed, the matrix values are converted to percentages of the grand sum of matrix entries, and visualised as a heatmap. Each voxel of the heatmap therefore represents the proportion of brain voxels detected with probability category p_c and distance category d_c. In practice, this visualisation does not place sufficient emphasis on small regions which are detected with high probability of being ischemia, because of the overwhelming majority of healthy tissue voxels. Therefore, we employ a weighting system to emphasize higher probabilities, whereby rather than simply incrementing element M(i,j) by 1, for each voxel traversed, we increment it by $a^{p_c/10}$, where a is set empirically at 50. The value for a was chosen by viewing the heatmaps alongside the determined probability values, to make the heatmap as representative as possible of the algorithm findings. This weighting is included purely to assist with visualisation in this condensed format and while the choice of weights is empirical, we note (assuming weights increase with ischemia probabilities) that weights cannot cause heat-maps to agree with clinically identified injury patterns unless the underlying probabilistic image is accurate.

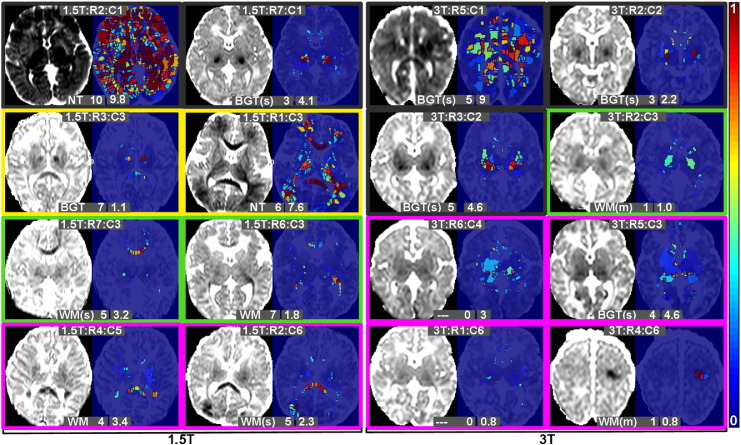
Fig. 4 illustrates the heatmaps for all subjects. In each case the X-axis denotes probability of ischemia while the Y-axis denotes distance from the brain edge. Colours are limited to representing regions from 0 to 1%, i.e. darkest red means 1% or more of the matrix grand total is represented at this location. The leftmost column of each heatmap is typically highly populated, since this represents the (usually large) region of the brain with probability of ischemia  <0.1. As an example of how to interpret the heatmaps, yellow/red towards the top right suggests an injury towards the brain centre (basal ganglia), while towards the bottom right suggests a more peripheral (white-matter) injury.

Fig. 4.

Per-subject heat maps which illustrate the findings of the algorithm at a glance. For each subject X-axis shows probability of ischemia, Y-axis shows distance to brain edge. Section 4.2.1 provides detailed information. The white text to the upper-left is the clinician note on injury pattern. The digits following this indicate the modified Barkovich score, while the number on the lower left indicates the algorithm score (see Section 4.2.2). The outline colour implies the outcome of the subject: black: subject died, yellow: abnormal, green: normal [below mean], magenta: normal [above mean]. (a) Heat maps for subjects scanned on 1.5 Tesla scanner (Datasets A and B). Subjects from Dataset A (training set) are denoted with an asterisk in the top right corner. (b) Heat maps for subjects scanned on 3 Tesla scanner. (Dataset C).

The text on the upper part of each heatmap denotes the injury pattern as per the clinician and the modified Barkovich score. Injury patterns are as follows: NT (near-total), WM (white-matter), BGT (basal-ganglia/thalamus), m (mild), s (severe), PH (parenchymal haemorrhage), - - (no parenchymal injury). The text on the lower part of the heatmap is the final algorithm score which will be described in Section 4.2.2.

The borders of the heatmaps in Fig. 4 are colour coded to denote the subject outcome (as described in Section 2.4).

Specific heatmaps are referred to, throughout the remainder of this work, by their MRI strength, row and column number in Fig. 4, e.g. 3T:R2:C4 will refer to the heatmap from the 3 T data in row 2, column 4 of Fig. 4b. In virtually all heatmaps in Fig. 4, the pattern of injury represented by the heatmap distribution corresponds well with the pattern described by the clinician, indicating that the algorithm has detected ischemia in the correct locations. One of the most visually striking results is the different patterns evident in the subjects that died, compared with survivors. Most of the heatmaps in those subjects show strong patterns of dark red towards the right hand side. Examining the non-surviving subjects with minimal heatmap activity (e.g. 1.5T:R7:C1), we see that there are still notably high values in the upper right area of the heatmap, suggesting a smaller, but significant focal basal-ganglia/thalamus injury.

In the surviving subjects, only 3 have a statistically abnormal result in their neurodevelopmental assessment at 2 years. For 2 of these subjects (1.5T:R1:C3 and 1.5T:R2:C3) a relatively severe injury was detected by the algorithm with the same injury pattern as that noted by the clinician. The third case (1.5T:R3:C3) was determined to be a basal-ganglia/thalamus injury by the clinician, and although the heatmap shows some ischemia towards the brain centre, the algorithm does not appear to have detected a very severe injury in this case.

The remainder of the subjects had normal neurodevelopmental assessments at 2 years, and for the majority of those the heatmap shows no evidence of significant injury. There is no particular distinction between the normal [below mean] group and the normal [above mean] group. A number of subjects with normal outcome which do show evidence of some injury (as well as other selected subjects) are included in Fig. 5 which (together with the heatmaps) illustrates the relationship between ADC, heatmaps, and injury patterns. (Subject 1.5T:R7:C5 is excluded, in spite of the apparent injury detection, since this is subject 14, already seen in the upper row of Fig. 3).

Fig. 5.

Examples showing representative ADC slices for a number of subjects along with the probabilistic algorithm findings. All ADC maps have the same contrast and brightness settings to enable comparisons. Probabilities are colour coded from 0 to 1 according to the colour-bar shown on the right. Border colours represent outcome as described in Section 4.2.1. The upper text represents the subject position in the heatmaps of Fig. 4. The lower text provides the clinician note and modified Barkovich score, as well as the algorithm final score (Section 4.2.2).

4.2.2. Algorithm and MRI scoring

As described in Section 2.3, the scans for each subject were assessed and provided with a (modified) Barkovich score by two experienced clinicians (FG, LdeV). To verify that the algorithm is assessing the scans correctly we next condense its results into a single score per subject, to determine whether these correlate with the clinical scores. For each subject, the 10 × 10 matrix, M, used to create the heatmaps in Fig. 4 was used as the basis for deriving the score. A straightforward method to convert M to a single score, S, is simply to sum the elements in columns 2–10. $S_{init}={\sum }_{i=1}^{10}{\sum }_{j=2}^{10}{M}_{ij}$. This gives the (weighted) proportion of the brain tissue that has probability  >0.1 of being ischemia (see Section 4.2.1). Scores derived in this way have excellent correlation with clinical scores (Pearson's r = 0.81), but it was noted that subjects with smaller localized basal-ganglia/thalamus injuries obtained lower scores by this method, compared with those assigned by clinicians. We therefore applied a weighting system, multiplying values in the upper half of the matrix (central region of the brain) by 10 before adding them to the summation. $\mathrm{S}={\sum }_{i=1}^5{\sum }_{j=2}^{10}10M_{ij}+{\sum }_{i=6}^{10}{\sum }_{j=2}^{10}{M}_{ij}$. The final score, in the range of 1–10 is given by

$$S_{final}=\frac{10S}{S+{\sum }_{i=1}^{10}{M}_{i1}}$$

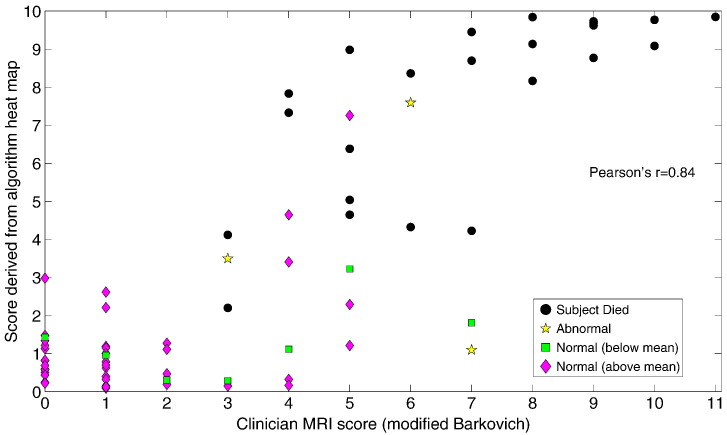
As with the weighting parameter, a, used in heatmap generation, this weighting factor is chosen empirically to better align the condensed algorithm score with those from the Barkovich system of scoring. This is done purely for illustration purposes, to indicate that the algorithm detects the same regions of ischemia as the clinician. The final scores are shown as additional information on the heatmaps of Fig. 4. In addition, Fig. 6 shows them plotted against the modified Barkovich scores given by the clinician. For information, the subject outcome is also provided by colour-coding in this figure.

Fig. 6.

Correlation of scores derived from the subject heat maps (see Section 4.2.2) with (modified) Barkovich scores assigned by a clinician. Subject outcome is shown by colour/shape coding.

Pearson's correlation coefficient, r, is calculated for the data in Fig. 6 at r = 0.84, which implies a significant correlation (p < 0.0001).

5. Discussion

A system has been developed to automatically identify ischemia on neonatal DW MR images. While previous work has attempted this task in animal models (Ghosh et al., 2011) and in stroke injuries in neonates (Ghosh et al., 2014, Išgum et al., 2011), this is the first time that the more diffuse and subtle hypoxic ischemic injuries have been automatically identified and quantified in newborn infants. As part of this development, 20 ADC maps were fully manually annotated by 2 independent observers, to provide system training and validation. This enables us to examine their interobserver agreement as well as the system performance compared with observer annotations. Furthermore, for the larger database with a total of 74 subjects, from both 1.5 T and 3.0 T scanners, the system findings are condensed to a heatmap format and shown with clinical MR scores, noted injury patterns and developmental outcome at 2 years to verify the relevance of the system output. In this section the major findings in each of these areas will be discussed.

5.1. Interobserver agreement

To our knowledge, this is the first time that neonatal ischemic lesions have been fully manually delineated on MR images. The annotation of the lesions was time-consuming and far from straight-forward. When annotating on a per-pixel basis, there were many occasions on which it could be debated whether ischemia was present, as evidenced by the relatively high levels of interobserver disagreement in some subjects (Fig. 2). This issue was exacerbated by the fact that we did not place any restrictions on brightness or contrast settings, which can make a significant difference to the appearance of the image (see e.g. Fig. 3). However, in the clinic, readers typically choose their own preferred settings and it was decided to follow this practice when annotating. There is no specified protocol on how to conclusively identify ischemia, which typically results in disagreement among experts when such discussion arises. In order to represent our application in this context, and also to provide a benchmark for algorithm performance, we did not attempt to force observers into consensus decisions. In spite of the moderate levels of interobserver agreement, we note that the observers almost always agreed in a general sense on the areas affected, but differed on the boundaries they chose (additional examples are shown in the supplementary material). It appears, therefore, that in most cases our observers formed the same overall impression of the injury, with differing boundaries attributable to factors such as contrast and brightness settings and variation of injury severity within a subject, which can cause milder injury to appear less significant. Agreement in qualitative reporting or scores based on visual impressions may not, it seems, translate to strong agreement in a pixel-by-pixel delineation of the injury.

We theorise that many of the regions of disagreement represent partial ischemia, since in biological terms ischemia occurs at a cellular level and therefore can occur to varying degrees within a fixed volume (i.e. a voxel) of tissue containing very many cells. Consideration of such ‘partially ischemic’ regions is likely to form part of a qualitative report or severity score, but it is not obvious whether they should be identified conclusively as ischemia in a binary annotation. It has become clear, in this respect, that binary markings are not the ideal way to interpret these images and that probabilistic outputs, such as those provided by the algorithm may, in fact, be a more natural way to quantify injury. In clinical practice it is unfeasible to manually annotate scans with binary markings, much less with probabilistic ones, which demonstrates an urgent need for an automatic tool which can provide quantitative, consistent and reproducible annotations.

5.2. Algorithm performance versus annotations

As described in Section 4.1 and illustrated in Fig. 2 the algorithm binary results compare well with those of observer 2, showing a similar range of sensitivities and specificities as well as F1-scores. A paired t-test on the F1-scores shows that the differences between the algorithm and observer 2 performances are not significant (p = 0.2), indicating that with this dataset, there is no statistical distinction between them.

The algorithm has its best performance on subject 14 (see Fig. 3, upper row) where it can be seen that the visually dominant injury is more typical of stroke than of hypoxia ischemia where injury patterns tend to be more diffuse and subtle. The nature of this stroke injury (large and focal with sharp edges) makes it very easy for both the algorithm and observers to identify and agree upon. Although it has not been tested, the algorithm performance on this subject suggests that it would also work well on data from a neonatal stroke cohort.

The worst algorithm performance coincided with large interobserver differences (Fig. 3, lower row), illustrating the difficulty of analysing performance accurately in the presence of such disagreement. For this reason analysis of consensus regions only was also carried out and the results are provided in the supplementary material. This analysis demonstrates that algorithm performance is markedly improved when only regions of observer consensus are evaluated. It also illustrates a case where the algorithm detects white-matter injury that was missed by both observers, demonstrating the value of the type of exhaustive and quantitative analysis that the automated system provides.

5.3. Algorithm performance on independent test sets

Datasets B and C consist of 54 subjects which are entirely independent of the training data, and include both 1.5 T data as well as 3.0 T data. This enables us to perform independent testing on a large dataset with scans from different imaging protocols. The ability to perform well on both 1.5 T and 3 T data, with very different imaging protocols, is significant, since many machine learning algorithms perform poorly on data which does not originate from the same source as the training set.

The heatmaps of Fig. 4 illustrate the algorithm performance, and it is notable that the algorithm shows very similar results and patterns on all data (1.5 T and 3.0 T), with the ischemia detections corresponding well with noted clinical injury patterns and outcome.

Fig. 5 shows representative slices from a varied group of subjects, including some of those where the heatmap may not seem to correspond precisely with the provided injury pattern or the outcome. In subjects 1.5T:R4:C5 and 1.5T:R7:C3 the clinician has noted a white-matter injury, while the heatmap shows the ischemia to be quite central (towards the top right of the heatmap), which usually suggests a detection in the basal-ganglia/thalamus region. In both these cases the injury is predominantly to the corpus callosum (see Fig. 5) which is relatively centrally located rather than peripheral, accounting for the heatmap pattern. This demonstrates a limitation of the heatmap, in that the location information relates only to distance from the brain edge.

Subject 3T:R5:C3 is noted to have a severe basal-ganglia/thalamus injury, in spite of which the subject has a positive developmental outcome. The heatmap looks dissimilar to heatmaps of those subjects that died with similarly labelled injuries, however, and in Fig. 5 it can be seen that the injury is much less focal and severe in this subject (compared to e.g. 1.5T:R7:C1 or 3T:R2:C2 in the same figure). This results in only moderate probabilities of ischemia, albeit across a larger region, and a different pattern on the heatmap, suggesting that the algorithm distinguishes well between injuries which result in different outcomes.

Subject 1.5T:R3:C3 is of particular interest since the outcome at 2 years was abnormal, while the heatmap does not suggest a very severe injury. The injury in this case was quite complex, with lesions in the anterior thalami, cerebral peduncles and corpus callosum, however the lesions are each relatively small and although the algorithm detects them correctly, neither the heatmap nor the final algorithm score reflects the fact that multiple different tissues were affected in numerous different areas of the brain. This is further evidence that the heatmap is lacking in location-specific information which would provide additional prognostic power.

In general the algorithm score (Section 4.2.2) correlates well with the clinician score, as evidenced in Fig. 6. In terms of outcomes, we can see that the scores of both clinician and algorithm provide a reasonable distinction between those that died and those that survived. Distinguishing between different normal outcomes is not to be expected since healthy children develop at different rates with many contributing factors. Unfortunately, since our data contains only 3 subjects with abnormal development we are unable to make any claim regarding the algorithm's ability to predict this outcome at present. Future work should endeavour to include data with a broader spectrum of outcome categories.

5.4. Future work

The system described provides the first step in developing assistive software to aid clinicians in the assessment and decision making process in a complex but crucially important application. While we have demonstrated here that binary algorithm detections are comparable to those of a human expert it should be noted that by thresholding the probabilistic findings, valuable information regarding varying injury severity is lost. The heatmaps and algorithm scores make better use of the variable ischemia probabilities, weighting strong probability categories more heavily. Although we have shown that these correlate well with clinical information and outcome, they were constructed to validate the algorithm findings only and we do not envisage such calculations to be the end-goal of the method. In fact, as discussed in Section 5.3, by reducing the per-voxel findings of the algorithm in this way, valuable quantifiable spatial and probabilistic information is lost, which we anticipate could be utilised in a much more detailed prognostication system. We envisage a system where the probability of ischemia for each voxel, along with its location within the brain, is taken into account. While the distance from brain-edge provides a rough estimate of which tissues have been affected, more precise location information is desirable (as seen in Section 5.3), in order to estimate the injury severity and predict prognosis. Application of an automatic tissue segmentation method (such as those described in Išgum et al., 2015) to the data, in combination with image registration (T1/T2 to DW), would define the tissue boundaries precisely. The white-matter might also be divided into regions of importance in this application, such as the corpus callosum. A supervised learning system is envisaged whereby this detailed location information is combined with the probability (severity) of ischemia at each voxel to learn, from existing data, what outcome may be expected for the subject. Additional information could be incorporated by specific analysis of the posterior limb of the interior capsule (PLIC), which has been shown to be important in prognostication (Martinez-Biarge et al., 2011, Rutherford et al., 1998), and by consideration of the timing of the scan when examining ADC values. Automatic analysis of other methods of injury assessment, such as the electroencephalogram (EEG), which measures brain function and has been shown to be independently predictive of outcome (Weeke et al., 2016) could also be incorporated in future systems to provide a comprehensive analysis of the injury severity.

Since the described method has been shown to work well in the detection of diffusion restriction in brain tissue it is also likely to be applicable in other conditions which affect the neonatal brain in a similar way, such as neonatal stroke (see Fig. 3, upper row) or hypoglycemia (Burns et al., 2008). A method to obtain consistent, quantitative results from neonatal DW images provides the potential to detect previously unknown relationships between particular injury types/locations, clinical course and specific developmental delays. This information is vital for prognostication and informed clinical decision-making regarding critical issues such as redirection of care or suitability for neuroprotective or neuroregenerative therapies.

Appendix A. Supplementary data

Evaluation Based on Observer Consensus Regions.