Abstract
Background
Drop foot resulting from degenerative lumbar diseases can impair activities of daily living. Therefore, predictors of recovery of this symptom have been investigated using univariate or/and multivariate analyses. However, the conclusions have been somewhat controversial. Bayesian network models, which are graphic and intuitive to the clinician, may facilitate understanding of the prognosis of drop foot resulting from degenerative lumbar diseases.
Questions/purposes
(1) To show a layered correlation among predictors of recovery from drop foot resulting from degenerative lumbar diseases; and (2) to develop support tools for clinical decisions to treat drop foot resulting from lumbar degenerative diseases.
Methods
Between 1993 and 2013, we treated 141 patients with decompressive lumbar spine surgery who presented with drop foot attributable to degenerative diseases. Of those, 102 (72%) were included in this retrospective study because they had drop foot of recent development and had no diseases develop that affect evaluation of drop foot after surgery. Specifically, 28 (20%) patients could not be analyzed because their records were not available at a minimum of 2 years followup after surgery and 11 (8%) were lost owing to postoperative conditions that affect the muscle strength evaluation. Eight candidate variables were sex, age, herniated soft disc, duration of the neurologic injury (duration), preoperative tibialis anterior muscle strength (pretibialis anterior), leg pain, cauda equina syndrome, and number of involved levels. Manual muscle testing was used to assess the tibialis anterior muscle strength. Drop foot was defined as a tibialis anterior muscle strength score of less than 3 of 5 (5 = movement against gravity and full resistance, 4 = movement against gravity and moderate resistance, 3 = movement against gravity through full ROM, 3− = movement against gravity through partial ROM, 2 = movement with gravity eliminated through full ROM, 1 = slight contraction but no movement, and 0 = no contraction). The two outcomes of interest were postoperative tibialis anterior muscle strength (posttibialis anterior) of 3 or greater and posttibialis anterior strength of 4 or greater at 2 years after surgery. We developed two separate Bayesian network models with outcomes of interest for posttibialis anterior strength of 3 or greater and posttibialis anterior strength of 4 or greater. The two outcomes correspond to “good” and “excellent” results based on previous reports, respectively. Direct predictors are defined as variables that have the tail of the arrow connecting the outcome of interest, whereas indirect predictors are defined as variables that have the tail of the arrow connecting either direct predictors or other indirect predictors that have the tail of the arrow connecting direct predictors. Sevenfold cross validation and receiver-operating characteristic (ROC) curve analyses were performed to evaluate the accuracy and robustness of the Bayesian network models.
Results
Both of our Bayesian network models showed that weaker muscle power before surgery (pretibialis anterior ≤ 1) and longer duration of neurologic injury before treatment (> 30 days) were associated with a decreased likelihood of return of function by 2 years. The models for posttibialis anterior muscle strength of 3 or greater and posttibialis anterior muscle strength of 4 or greater were the same in terms of the graphs, showing that the two direct predictors were pretibialis anterior muscle strength (score ≤ 1 or ≥ 2) and duration (≤ 30 days or > 30 days). Age, herniated soft disc, and leg pain were identified as indirect predictors. We developed a decision-support tool in which the clinician can enter pretibialis anterior muscle strength and duration, and from this obtain the probability estimates of posttibialis anterior muscle strength. The probability estimates of posttibialis anterior muscle strength of 3 or greater and posttibialis anterior muscle strength of 4 or greater were 94% and 85%, respectively, in the most-favorable conditions (pretibialis anterior ≥ 2; duration ≤ 30 days) and 18% and 14%, respectively, in the least-favorable conditions (pretibialis anterior ≤ 1; duration > 30 days). On the sevenfold cross validation, the area under the ROC curve yielded means of 0.78 (95% CI, 0.68–0.87) and 0.74 (95% CI, 0.64–0.84) for posttibialis anterior muscle strength of 3 or greater and posttibialis anterior muscle strength of 4 or greater, respectively.
Conclusions
The results of this study suggest that the clinician can understand intuitively the layered correlation among predictors by Bayesian network models. Based on the models, the decision-support tool successfully provided the probability estimates of posttibialis anterior muscle strength to treat drop foot attributable to lumbar degenerative diseases. These models were shown to be robust on the internal validation but should be externally validated in other populations.
Level of Evidence
Level III, therapeutic study.
Keywords: Bayesian Network, Posterior Lumbar Interbody Fusion, Cauda Equina Syndrome, Bayesian Network Model, Spinal Canal Stenosis
Introduction
Drop foot, which is the inability to dorsiflex the ankle resulting in a slapping gait pattern, can be caused by degenerative lumbar diseases. It can affect activities of daily living and postoperative patient function [29].
In previous studies that investigated predictors of residual drop foot (such as the duration of drop foot before surgery, and preoperative weakness of ankle dorsiflexors), multivariate logistic regression analyses were used to reinforce the results of univariate analyses [1, 3, 16, 21]. However, logistic regression analyses have several disadvantages in terms of interpreting results. Regression analyses are difficult to describe layered correlations among predictors if the sample size is not huge [9]. This means that predictors should be interpreted in parallel. In addition, they are vulnerable to missing data, which is a common occurrence in clinical records [11, 24]. Specifically, studies with relatively small sample sizes may lead to losing the statistical power.
Bayesian networks have been used in many fields of medicine [15, 20, 28], and have qualitative and quantitative aspects. The qualitative aspect provides a graphic map that is useful for interpreting the interactions among variables intuitively. The quantitative aspect can estimate the probability of outcomes. This graphic approach has several advantages. It enables clinicians to understand intuitively the layered correlations among predictors with graphs, it presents prognostic models that are tolerant of missing data [19], it incorporates all outcomes and covariates in a single network, and it readily updates network models when new data are added. To our knowledge, such methodology has rarely been applied in the field of orthopaedic surgery [5, 25].
We therefore sought to apply Bayesian networks to facilitate understanding of the prognosis of drop foot resulting from degenerative lumbar diseases. Specifically, we wished (1) to show a layered correlation among predictors of recovery from drop foot resulting from degenerative lumbar diseases, and (2) to develop our support tools for clinical decisions to treat drop foot resulting from lumbar degenerative diseases.
Patients and Methods
This study was conducted retrospectively. All patients were informed that clinical data could be used for scientific purposes according to the regulations of the medical ethics review board of our hospital, which approved our study. Additionally, the study complied with the World Medical Association’s Declaration of Helsinki [30].
Between 1993 and 2013, we treated 141 patients with decompressive lumbar spine surgery who presented with drop foot attributable to degenerative diseases. Of those, 102 (72%; 58 men, 44 women) were included in this retrospective study because they had recent development of drop foot and did not have diseases develop that affect the evaluation for drop foot after surgery (ie, cervical myelopathy). Specifically, 28 (20%) patients could not be analyzed because their records were not available at a minimum of 2 years followup after surgery and 11 (8%) were lost owing to postoperative conditions that affect the muscle strength evaluation.
Clinical Assessment
Tibialis anterior muscle strength was evaluated using a manual muscle test according to the Medical Research Council scale and as described in a previous study (Table 1) [1]. Drop foot was defined as a tibialis anterior muscle strength score less than 3 (of 5) [1, 2, 6, 8]. Tibialis anterior muscle strength was graded as 3- when patients could dorsiflex and invert their ankles while they were seated but could not achieve full ROM. If patients had bilateral drop foot, the weaker side was assessed. All patients underwent a physical examination immediately before surgery. Patients stayed in the hospital for approximately 2 to 4 weeks after surgery. Postoperative evaluations of motor recovery were performed regularly on an outpatient basis (at 4–6 weeks, 3 months, 6 months, 1 year, 1.5 years, and 2 years postoperatively, and once per year thereafter), and the results of the latest followup were analyzed. All examiners were orthopaedic spine surgeons (TF, MI, TO, SO, and HA).
Table 1.
Manual muscle test of the tibialis anterior muscle according to the Medical Research Council scale of muscle strength [1]
| Grade | Description |
|---|---|
| 0 | No contraction of the tibialis anterior muscle |
| 1 | Slight contraction of the tibialis anterior muscle is observed, but no joint motion of the ankle |
| 2 | Patient can invert and dorsiflex the ankle with gravity eliminated through full ROM |
| 3− | Patient can dorsiflex and invert the ankle against gravity through partial ROM |
| 3 | Patient can dorsiflex and invert the ankle against gravity through full ROM |
| 4 | Patient can dorsiflex and invert the ankle against gravity and moderate resistance |
| 5 | Patient can dorsiflex and invert the ankle against gravity and full resistance |
Candidate Variables and Outcomes
Eight candidate variables were chosen as predictors for the recovery of drop foot according to previous reports [1–3, 6, 7, 12, 13, 16, 17, 21]. These included: sex; age at surgery; diagnosis; duration of drop foot before surgery; preoperative tibialis anterior strength (pretibialis anterior); leg pain; cauda equina syndrome; and number of involved levels. Diagnosis was classified in three categories: herniated soft disc; spinal canal stenosis; and isthmic spondylolisthesis. Cauda equina syndrome was defined as perineal numbness and/or bowel and bladder dysfunction. Combined radicular and cauda equina symptoms were considered cauda equina syndrome.
For our Bayesian network model, continuous variables were converted into categorical variables (Table 2). Age at surgery was stratified in three groups (≤ 40 years, 41–60 years, and ≥ 61 years) based on a previous study in which age was identified as an important predictor [6]. The duration of drop foot before surgery was categorized in two groups (≤ 30 days and > 30 days) for two reasons. First, this cutoff value is considered to be useful for surgical decision-making. Second, using a longer cutoff value may exacerbate inaccuracies in assessment of the duration of drop foot before surgery. To simplify interpretation of the results, diagnosis was divided based on the presence of a herniated soft disc (herniated soft disc versus spinal canal stenosis and isthmic spondylolisthesis).
Table 2.
Description of the variables included in the Bayesian network
| Variable description | Node acronym | Variable type | States description |
|---|---|---|---|
| Sex | Sex | Discrete | Female; male |
| Age at surgery (years) | Age | Continuous | ≤ 40; 41–60; ≥ 61 |
| Diagnosis | Hernia | Discrete | Yes; no |
| Duration of drop foot before surgery | Duration | Continuous | ≤ 30; > 31 |
| Pretibialis anterior | Pre-TA | Discrete | 0 or 1; 2 or 3− |
| Leg pain | Pain | Discrete | Yes; no |
| Cauda equina syndrome | Cauda equina | Discrete | Yes; no |
| Number of involved levels | Number of levels | Discrete | Multiple; single |
| Posttibialis anterior | Post-TA | Discrete | < 3; ≥ 3 or < 4; ≥ 4 |
Pretibialis anterior = preoperative tibialis anterior muscle strength; posttibialis anterior = postoperative tibialis anterior muscle strength.
In the current study, there were two outcomes of interest: posttibialis anterior muscle strength (posttibialis anterior) of 3 or greater and posttibialis anterior muscle strength of 4 or greater. Posttibialis anterior strength of 3 or greater was used to access minimal recovery from drop foot, which corresponds to a “good” outcome, and posttibialis anterior strength of 4 or greater was considered an “excellent” outcome in previous studies [1, 2].
Statistical Analysis
Conventional Statistical Analysis
We used R software version 3.0.2 (R Development Core Team, Vienna, Austria) for conventional univariate and multivariate analyses. Statistical significance was set at a probability less than 0.05. The Mann–Whitney U test was used to compare clinical data between groups for continuous and ordinal variables. Fisher’s exact test was used to compare group differences for dichotomous variables. Multivariate logistic regression analyses were performed using variables that showed p values less than 0.20 in the univariate analyses.
Univariate Analysis
The analyses of posttibialis anterior strength of 3 or greater and 4 or greater indicated age at surgery (continuous variable) and the duration of drop foot before surgery (continuous and discrete variable) were significant negative predictors. A soft herniated disc and pretibialis anterior strength were shown to be significant positive predictors. In addition, analysis of posttibialis anterior strength of 3 or greater revealed age at surgery (discrete variable) and number of involved levels were significant negative predictors (Table 3).
Table 3.
Characteristics of the study population (n = 102)
| Variable | Total | Postsurgery tibialis anterior strength < 3 | Postsurgery tibialis anterior strength ≥ 3 | p Value | Postsurgery tibialis anterior strength < 4 | Postsurgery tibialis anterior strength ≥ 4 | p Value |
|---|---|---|---|---|---|---|---|
| Sex (men:women) | 58:44 | 26:13 | 32:31 | 0.151 Fisher’s exact | 34:17 | 24:27 | 0.071 Fisher’s exact |
| Age at surgery (years); continuous mean (median; IQR) | 59 (63; 49–72) | 65 (69; 55–75) | 56 (58; 40–66) | 0.003* Mann–Whitney U test | 63 (66; 51–75) | 56 (58; 42–66) | 0.027* Mann–Whitney U test |
| Age at surgery (years); discrete, ≤ 40:41–60:≥ 61 | 17:30:55 | 3:10:26 | 14:20:29 | 0.025* Mann–Whitney U test | 6:14:31 | 11:16:24 | 0.124 Mann–Whitney U test |
| Diagnosis, hernia:nonhernia | 52:50 | 27:12 | 25:38 | 0.005* Fisher’s exact | 30:21 | 22:29 | 0.165* Fisher’s exact |
| Duration of drop foot before surgery (days); continuous mean (median; IQR) | 106 (44; 20–120) | 214 (180; 60–360) | 39 (30; 17–52) | < 0.001* Mann–Whitney U test | 174 (90; 34–240) | 37 (30; 15–45) | < 0.001* Mann–Whitney U test |
| Duration of drop foot before surgery, discrete, ≤ 30 days:> 30 days | 47:55 | 8:31 | 39:24 | < 0.001* Fisher’s exact | 12:39 | 35:16 | < 0.001* Fisher’s exact |
| Pretibialis anterior, 0 or 1:2 or 3− | 36:66 | 25:14 | 11:52 | < 0.001* Fisher’s exact | 27:24 | 9:42 | < 0.001* Fisher’s exact |
| Leg pain, yes:no | 21:81 | 9:30 | 12:51 | 0.624 Fisher’s exact | 11:40 | 10:41 | 1.000 Fisher’s exact |
| Cauda equine syndrome, yes:no | 25:77 | 14:25 | 11:52 | 0.057 Fisher’s exact | 14:37 | 11:40 | 0.646 Fisher’s exact |
| Number of involved levels, multiple:single | 35:67 | 19:20 | 16:47 | 0.019* Fisher’s exact | 22:29 | 13:38 | 0.095 Fisher’s exact |
* Significant; IQR = interquartile range (25th–75th percentiles); pretibialis anterior = preoperative tibialis anterior muscle strength.
Multivariate Analysis
Multivariate logistic regression analyses revealed three significant predictors for posttibialis anterior muscle strength of 3 or greater: pretibialis anterior strength (p < 0.001), duration of drop foot before surgery (p < 0.001), and age at surgery (p = 0.014) (Table 4). When doing the same analysis for posttibialis anterior muscle strength of 4 or greater, two predictors were found: pretibialis anterior strength (p = 0.002), and the duration of drop foot before surgery (p = 0.001) (Table 4).
Table 4.
Results of the multivariate logistic regression analyses
| Posttibialis anterior muscle strength ≥ 3 | Posttibialis anterior muscle strength ≥ 4 | |||||
|---|---|---|---|---|---|---|
| Variable | p Value | Odds ratio | 95% CI | p Value | Odds ratio | 95% CI |
| Sex (men:women) | 0.069 | 5.35 | 0.88–32.7 | 0.111 | 2.48 | 0.81–7.59 |
| Age at surgery (years); continuous | 0.014* | 0.92 | 0.86–0.98 | 0.081 | 0.96 | 0.93–1.004 |
| Diagnosis, hernia:nonhernia | 0.650 | 1.57 | 0.22–11.2 | 0.100 | 3.40 | 0.79–14.6 |
| Duration of drop foot before surgery (days); continuous | < 0.001* | 0.97 | 0.95–0.99 | 0.001* | 0.97 | 0.96–0.99 |
| Pretibialis anterior 0 or 1:2 or 3− | < 0.001* | 44.5 | 6.78–292 | < 0.001* | 6.29 | 1.96–20.2 |
| Cauda equine syndrome, yes:no | 0.793 | 1.29 | 0.20–8.45 | NA | NA | NA |
| Number of involved levels, multiple:single | 0.990 | 1.01 | 0.14–7.20 | 0.413 | 1.79 | 0.44–7.18 |
* Significant; pretibialis = preoperative tibialis; posttibialis = postoperative tibialis; NA = not applicable.
Bayesian Network Analysis
A Bayesian network is a directed acyclic graph composed of nodes and arrows. “Acyclic” means that the graph does not contain any cycle or loop. These characteristics are necessary for calculating probabilities. Nodes represent random variables and arrows represent the probabilistic dependence relationship between connected nodes (ie, A → B means that A causes B). The Bayesian network has two aspects: qualitative and quantitative. The qualitative aspect provides a straightforward, transparent graphic map to enable clinicians to interpret the interactions among nodes intuitively. The quantitative aspect quantifies the degree of relationships by conditional probability distributions, which configures a Bayesian network model [18, 22].
The Bayesian network was constructed using the R package “deal” [4]. All eight candidate variables were considered. We set the equivalent sample size to five to achieve a good balance between the smoothing effect of the uniform prior distribution and accuracy of the model according to the recommendations of Koller and Friedman [14]. In the next step, we used the R package “gRain” to parameterize and perform inference in Bayesian networks [10]. Before structuring Bayesian networks, all arcs toward age or sex and all arcs from posttibialis anterior muscle strength were eliminated based on causality. We trained the Bayesian network to specify network structures and prior probability distributions to develop classifiers of estimated posttibialis anterior muscle strength of 3 or greater and 4 or greater, respectively. The former model is called the TA3 model and the latter is the TA4 model. As mentioned above, the two outcomes of interest correspond to “good” and “excellent” results. Direct predictors are defined as variables that have the tail of the arrow connecting the outcome of interest, whereas indirect predictors are defined as variables that have the tail of the arrow connecting either direct predictors or other indirect predictors that have the tail of the arrow connecting direct predictors.
Internal Validation
To assess the predictive accuracy of the final TA3 and TA4 models, we conducted the internal validation in two ways. First, the evaluation was conducted with the same set of data used to construct the Bayesian network models. However, this could have resulted in overestimation of the true predictive accuracy. Second, we performed sevenfold cross validation. The value of k in k-fold cross validation was set to seven based on Sturges’ formula [26]. Data were randomized into seven training sets containing 86% of the data with seven corresponding test sets containing the remaining 14%. Each matching set was unique, and there was no overlap between the independent test sets. A receiver-operating characteristic (ROC) curve was plotted to evaluate the predictive accuracy and robustness of the models. The ROC curve is a graphic plot of sensitivity versus 1-specificity at all discrimination threshold levels. The area under the ROC curve (AUC) then was calculated for each Bayesian network model to assess its overall accuracy and robustness. To reduce the arbitrariness in the choice of random number seeds, the AUC values were averaged by repeating the sevenfold cross validation 100 times. AUC values greater than 0.70 are generally considered to represent useful performance [27].
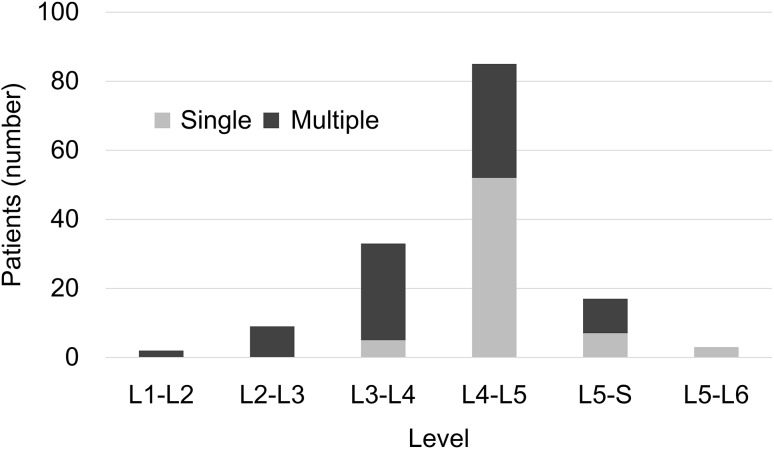
The median age of the patients at surgery was 63 years (interquartile range [IQR], 49–72 years). In terms of diagnosis, of the patients included, 50 had a herniated soft disc, 49 had spinal canal stenosis, and three had isthmic spondylolisthesis. The median duration of drop foot before surgery was 44 days (IQR, 20–120 days). Pretibialis anterior muscle strength was graded as 0 or 1 for 36 patients and as 2 or 3− for 66 patients. There were 21 patients who did not report leg pain. Cauda equina syndrome was diagnosed in 25 patients. There were multiple involved levels in 35 patients and a single involved level in 67 patients. Posttibialis anterior muscle strength recovered to 3 or greater in 63 patients and to 4 or greater in 51 patients, respectively. The median duration of followup was 30 months (IQR, 24–42 months). Drop foot was unilateral in 91 patients and bilateral in 11. Surgical procedures were performed, including a standard discectomy in 48 patients, bilateral fenestration (laminectomy with or without discectomy) in 37, posterior lumbar interbody fusion in 16, and repair of spondylolysis in one. The most frequent single lesion was at the L4-L5 level (Fig. 1).
Fig. 1.
Compromised levels affected in drop foot are shown. The most frequent single lesion occurred at the L4–L5 level.
Results
Predictors of Recovery after Drop Foot
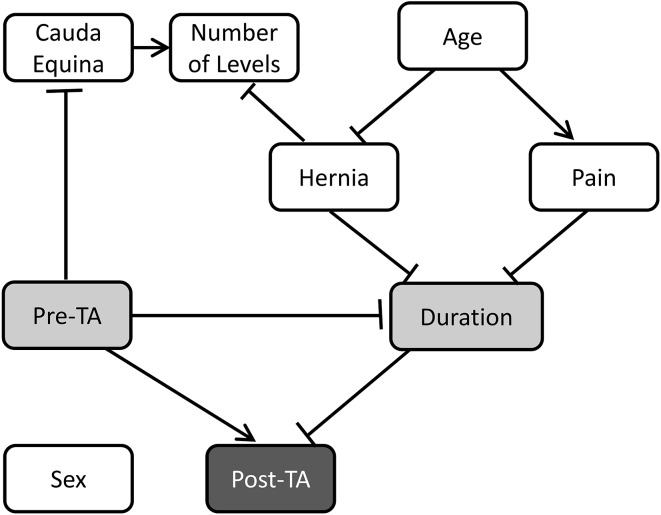
The T3 and T4 models, which are graphically the same, showed that weaker muscle power before surgery (pretibialis anterior strength ≤ 1) and longer duration of neurologic injury before treatment (> 30 days) were associated with a decreased likelihood of return of function by 2 years (Fig. 2). The network showed that two direct predictors of posttibialis anterior muscle strength are pretibialis anterior strength (0 or 1; 2 or 3−) and the duration of drop foot before surgery (≤ 30 days or > 30 days). In addition, we identified three indirect predictors, which are age at surgery (≤ 40 years, 41–60 years, or ≥ 61 years), leg pain, or diagnosis (hernia or nonhernia). These results do not imply that the three indirect predictors do not influence the estimate of posttibialis anterior, but rather that they are not included to calculate the estimate of posttibialis anterior muscle strength given the information of the two direct predictors.
Fig. 2.
The Bayesian network for the TA3 and TA4 models are shown. The arrow and bar edges are assigned to positive and negative correlations, respectively. The probability estimates for posttibialis anterior muscle strength necessitates direct predictors (posttibialis anterior muscle strength and duration). Indirect predictors (age, hernia, and pain) are not necessary for the prediction given the information of the two direct predictors (Table 5). Pre-TA = preoperative tibialis anterior muscle strength; post-TA = postoperative tibialis anterior muscle strength; duration = duration of drop foot before surgery.
Decision Support Tool for Drop Foot
We developed a decision-support tool in which the clinician can enter pretibialis anterior muscle strength and duration, and from this obtain the probability estimates of posttibialis anterior muscle strength. Both models suggest that the most favorable preoperative condition comprises the combination of pretibialis anterior strength of 2 or 3− and duration of drop foot before surgery of 30 days or less. With this condition combination, the probability estimates of posttibialis anterior muscle strength were 94% and 85% for the TA3 and TA4 models, respectively. However, with the least-favorable condition combination (pretibialis anterior strength of 0 or 1 and duration of drop foot before surgery greater than 30 days), the probability estimates of posttibialis anterior muscle strength were 18% and 14%, respectively. All four combinations of the two predictors can be used in the model to develop an inference table that estimates posttibialis anterior muscle strength and that can be used to derive clinical rules (Table 5).
Table 5.
Probability estimates of postoperative tibialis anterior strength of 3 or greater or 4 or greater
| Predictors | Outcome | |||
|---|---|---|---|---|
| Expected frequency (%) (actual frequency) | Pretibialis anterior muscle strength | Duration (days) | Posttibialis anterior muscle strength ≥ 3 (%) (actual rate) | Posttibialis anterior muscle strength ≥ 4 (%) (actual rate) |
| 30.4 (31.4, n = 32) | 2 or 3− | ≤ 30 | 93.5 (96.9 = 31/32) | 84.8 (87.5 = 28/32) |
| 33.0 (33.3, n = 34) | 2 or 3− | > 30 | 61.0 (61.7 = 21/34) | 41.8 (41.2 = 14/34) |
| 16.3 (14.7, n = 15) | 0 or 1 | ≤ 30 | 52.9 (53.3 = 8/15) | 47.1 (46.7 = 7/15) |
| 20.3 (20.6, n = 21) | 0 or 1 | > 30 | 18.1 (14.3 = 3/21) | 13.8 (9.5 = 2/21) |
Pretibialis anterior = preoperative tibialis anterior muscle strength; duration = duration of drop foot before surgery; posttibialis anterior = postoperative tibialis anterior muscle strength. The clinician can enter pretibialis anterior and duration in this decision-support tool and obtain the probability estimates of posttibialis anterior muscle strength.
The internal validation using ROC curve analyses with the same set of data used to construct the Bayesian network models indicated AUCs of 0.84 (95% CI, 0.73–0.91) and 0.81 (95% CI, 0.73–0.89) in the TA3 and TA4 models, respectively. On the sevenfold cross validation, AUC means were 0.78 (95% CI, 0.68–0.87) and 0.74 (95% CI, 0.64–0.84) in the TA3 and TA4 models, respectively. These results indicate the accuracy and robustness of both models.
Discussion
The prognosis of drop foot resulting from degenerative lumbar diseases has been a topic of interest for spine surgeons. Prior work using traditional analytic approaches (such as multivariate analyses) have suggested that duration of drop foot before surgery and preoperative motor weakness [1, 3, 16, 17] may be associated with recovery of active dorsiflexion after decompressive lumbar spine surgery; however, this is somewhat controversial, since other studies did not identify one or either of these factors as important in anticipating a patient’s neurologic recovery [2, 6, 7, 12, 13, 21]. We believe that those analytic approaches may not be ideal for this purpose because they are difficult to describe layered correlations among predictors, and we believe that Bayesian network analysis, which is graphic and intuitive to the clinician, may be better suited to the task because this approach readily describes the layered correlation among predictors. Using Bayesian networks, we found that pretibialis anterior muscle strength and duration of drop foot before surgery are associated with recovery of motor strength within 2 years of decompressive lumbar surgery in patients who presented with drop foot.
This study has several limitations. First, the Bayesian network models constructed in this study were internally validated with sevenfold cross validation, but external validation will be necessary in other patient populations in future studies. Second, the selection bias that is inherent in retrospective studies may have had some effect on the outcomes and a prospective study is ideal, but we thought the sufficient statistical power is important in overcoming the relative rarity of drop foot. Third, in this retrospective study, the possibility of assessment bias in manual muscle testing exists. However, all examiners were trained at the same institute and were considered to share the same standards for assessing muscle strength. In addition, pretibialis anterior muscle strength was categorized in two scores (≤ 1 or ≥ 2). This categorization may lessen the effect of assessment bias. Fourth, 28 patients (20%) were lost to followup owing to unavailable records and 11 (8%) were lost owing to postoperative conditions that affect the muscle strength evaluation. This followup rate (72%) is considered acceptable as a retrospective study. Finally, age and the duration of drop foot before surgery were categorized for Bayesian network analyses because they did not show a normal distribution. In some conditions, the categorization of variables may lead to loss of information, but this study showed sufficient robustness in the Bayesian network models. Moreover, the probability estimates of posttibialis anterior muscle strength using categorical data of the two predictors is practical for clinical use.
Predictors for residual drop foot in previous studies are varied, but the two main predictors have been preoperative motor weakness [1, 3, 6, 12, 16, 17, 21] and the duration of drop foot before surgery [2, 3, 7, 16, 17]. The former corresponds to pretibialis anterior muscle strength in the current study. Other predictors are age at surgery [6, 7, 16], herniated soft disc [7, 12, 13], and involvement of a single level [7]. In the current study, the two main predictors (pretibialis anterior strength and the duration of drop foot before surgery) were confirmed by the Bayesian network models as direct predictors. However, a herniated soft disc was found to influence the duration of drop foot before surgery directly, which in turn influenced posttibialis anterior strength. Similarly, age at surgery was an indirect predictor influencing posttibialis anterior strength through a herniated soft disc, leg pain, and the duration of drop foot before surgery. A herniated soft disc and age at surgery were shown to be indirect predictors influencing the outcome of interest through other predictors (Fig. 2). Using these direct and indirect predictors in parallel can lead to an overfitting model. Actually we performed the multivariate logistic regression analyses using the same cohort (Table 4). These results were similar compared with the Bayesian network models. However, in the analysis for posttibialis anterior strength of 3 or greater, age, pretibialis anterior strength, and duration of drop foot before surgery were significant predictors. The three variables were parallel as predictors in the multivariate logistic analysis, but the Bayesian network model successfully avoided overfitting with intuitive, understandable graphs and provided the layered correlation between these variables, showing that age was an indirect predictor.
We developed a decision-support tool to provide the probability estimates for posttibialis anterior strength of 3 or greater and 4 or greater, respectively. The readers may use this tool by entering pretibialis anterior strength and duration. Urgent surgery is indicated for progressive weakness of the lower limbs resulting from degenerative lumbar diseases, but the precise timing for surgery has not been established [23]. There are two purposes for developing a support tool for decision-making regarding surgical treatment of drop foot resulting from degenerative lumbar diseases. First, the probability estimates for posttibialis anterior strength can assist physicians in case-specific predictions. Second, the support tools may be useful for patients and physicians making a shared decision regarding surgery. A remarkable merit of a Bayesian network is that it enables these probability estimates to be updated after adding new clinical data.
The results of this study suggest that the clinician can understand intuitively the layered correlation among predictors by Bayesian network models. Based on the models, the decision-support tool successfully provides the probability estimates of posttibialis anterior muscle strength to treat drop foot attributable to lumbar degenerative diseases. These models were shown to be robust on internal validation but should be externally validated in other populations.
Acknowledgments
We thank Takeshi Fuji MD, PhD (Department of Orthopaedic Surgery, Japan Community Healthcare Organization Osaka Hospital), Motoki Iwasaki MD, PhD (Department of Orthopaedic Surgery, Osaka Rosai Hospital), Tetsuo Ohwada MD (Department of Orthopaedic Surgery, Kansai Rosai Hospital), and Shinya Okuda MD, PhD (Department of Orthopaedic Surgery, Osaka Rosai Hospital) for their dedication to the treatment and evaluation of the patients.
Footnotes
Each author certifies that neither he, nor any member of his immediate family, have funding or commercial associations (consultancies, stock ownership, equity interest, patent/licensing arrangements, etc) that might pose a conflict of interest in connection with the submitted article.
All ICMJE Conflict of Interest Forms for authors and Clinical Orthopaedics and Related Research ® editors and board members are on file with the publication and can be viewed on request.
Each author certifies that his institution approved the human protocol for this investigation, that all investigations were conducted in conformity with ethical principles of research, and that informed consent for participation in the study was obtained.
A comment to this article is available at http://dx.doi.org/10.1007/s11999-016-5225-1.
References
- 1.Aono H, Iwasaki M, Ohwada T, Okuda S, Hosono N, Fuji T, Yoshikawa H. Surgical outcome of drop foot caused by degenerative lumbar diseases. Spine (Phila Pa 1976). 2007;32:E262–266. [DOI] [PubMed]
- 2.Aono H, Nagamoto Y, Tobimatsu H, Takenaka S, Iwasaki M. Surgical outcomes for painless drop foot due to degenerative lumbar disorders. J Spinal Disord Tech. 2014;27:E258–261. doi: 10.1097/BSD.0000000000000102. [DOI] [PubMed] [Google Scholar]
- 3.Bhargava D, Sinha P, Odak S, Tyagi A, Towns G, Pal D. Surgical outcome for foot drop in lumbar degenerative disease. Global Spine J. 2012;2:125–128. doi: 10.1055/s-0032-1326947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bøttcher SG, Dethlefsen C. deal: a package for learning Bayesian networks. J Stat Soft. 2003;8:1–40. Available at: https://core.ac.uk/download/pdf/6303113.pdf. Accessed November 14, 2016.
- 5.Forsberg JA, Eberhardt J, Boland PJ, Wedin R, Healey JH. Estimating survival in patients with operable skeletal metastases: an application of a bayesian belief network. PLoS One. 2011;6:e19956. doi: 10.1371/journal.pone.0019956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ghahreman A, Ferch RD, Rao P, Chandran N, Shadbolt B. Recovery of ankle dorsiflexion weakness following lumbar decompressive surgery. J Clin Neurosci. 2009;16:1024–1027. doi: 10.1016/j.jocn.2008.10.017. [DOI] [PubMed] [Google Scholar]
- 7.Guigui P, Benoist M, Delecourt C, Delhoume J, Deburge A. Motor deficit in lumbar spinal stenosis: a retrospective study of a series of 50 patients. J Spinal Disord. 1998;11:283–288. doi: 10.1097/00002517-199808000-00002. [DOI] [PubMed] [Google Scholar]
- 8.Hara N, Oka H, Yamazaki T, Takeshita K, Murakami M, Hoshi K, Terayama S, Seichi A, Nakamura K, Kawaguchi H, Matsudaira K. Predictors of residual symptoms in lower extremities after decompression surgery on lumbar spinal stenosis. Eur Spine J. 2010;19:1849–1854. doi: 10.1007/s00586-010-1374-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Harrell FE, Jr, Lee KL, Mark DB. Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat Med. 1996;15:361–387. doi: 10.1002/(SICI)1097-0258(19960229)15:4<361::AID-SIM168>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- 10.Højsgaard S. Graphical independence networks with the gRain package for R. J Stat Soft. 2012;46:1–26. [Google Scholar]
- 11.Horton NJ, Kleinman KP. Much ado about nothing: a comparison of missing data methods and software to fit incomplete data regression models. Am Stat. 2007;61:79–90. doi: 10.1198/000313007X172556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Iizuka Y, Iizuka H, Tsutsumi S, Nakagawa Y, Nakajima T, Sorimachi Y, Ara T, Nishinome M, Seki T, Shida K, Takagishi K. Foot drop due to lumbar degenerative conditions: mechanism and prognostic factors in herniated nucleus pulposus and lumbar spinal stenosis. J Neurosurg Spine. 2009;10:260–264. doi: 10.3171/2008.12.SPINE08500. [DOI] [PubMed] [Google Scholar]
- 13.Jonsson B, Stromqvist B. Motor affliction of the L5 nerve root in lumbar nerve root compression syndromes. Spine (Phila Pa 1976). 1995;20:2012–2015. [DOI] [PubMed]
- 14.Koller D, Friedman N. Probabilistic Graphical Models: Principles and Techniques. Cambridge, MA: MIT Press; 2009. [Google Scholar]
- 15.Lee S, Ybarra N, Jeyaseelan K, Faria S, Kopek N, Brisebois P, Bradley JD, Robinson C, Seuntjens J, El Naqa I. Bayesian network ensemble as a multivariate strategy to predict radiation pneumonitis risk. Med Phys. 2015;42:2421–2430. doi: 10.1118/1.4915284. [DOI] [PubMed] [Google Scholar]
- 16.Liu K, Zhu W, Shi J, Jia L, Shi G, Wang Y, Liu N. Foot drop caused by lumbar degenerative disease: clinical features, prognostic factors of surgical outcome and clinical stage. PLoS One. 2013;8:e80375. doi: 10.1371/journal.pone.0080375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Macki M, Syeda S, Kerezoudis P, Gokaslan ZL, Bydon A, Bydon M. Preoperative motor strength and time to surgery are the most important predictors of improvement in foot drop due to degenerative lumbar disease. J Neurol Sci. 2016;361:133–136. doi: 10.1016/j.jns.2015.12.035. [DOI] [PubMed] [Google Scholar]
- 18.Nagarajan R, Scutari M, Lèbre S. Bayesian Networks in R with Applications in Systems Biology. New York, NY: Springer-Verlag; 2013. [Google Scholar]
- 19.Needham CJ, Bradford JR, Bulpitt AJ, Westhead DR. A primer on learning in Bayesian networks for computational biology. PLoS Comput Biol. 2007;3:e129. doi: 10.1371/journal.pcbi.0030129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nissan A, Protic M, Bilchik A, Eberhardt J, Peoples GE, Stojadinovic A. Predictive model of outcome of targeted nodal assessment in colorectal cancer. Ann Surg. 2010;251:265–274. doi: 10.1097/SLA.0b013e3181bd5187. [DOI] [PubMed] [Google Scholar]
- 21.Postacchini F, Giannicola G, Cinotti G. Recovery of motor deficits after microdiscectomy for lumbar disc herniation. J Bone Joint Surg Br. 2002;84:1040–1045. doi: 10.1302/0301-620X.84B7.12948. [DOI] [PubMed] [Google Scholar]
- 22.Scutari M, Denis JB. Bayesian Networks: With Examples in R. Boca Raton, FL: CRC Press; 2014. [Google Scholar]
- 23.Sharma H, Lee SW, Cole AA. The management of weakness caused by lumbar and lumbosacral nerve root compression. J Bone Joint Surg Br. 2012;94:1442–1447. doi: 10.1302/0301-620X.94B11.29148. [DOI] [PubMed] [Google Scholar]
- 24.Sterne JA, White IR, Carlin JB, Spratt M, Royston P, Kenward MG, Wood AM, Carpenter JR. Multiple imputation for missing data in epidemiological and clinical research: potential and pitfalls. BMJ. 2009;338:b2393. doi: 10.1136/bmj.b2393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Stojadinovic A, Kyle Potter B, Eberhardt J, Shawen SB, Andersen RC, Forsberg JA, Shwery C, Ester EA, Schaden W. Development of a prognostic naive bayesian classifier for successful treatment of nonunions. J Bone Joint Surg Am. 2011;93:187–194. doi: 10.2106/JBJS.I.01649. [DOI] [PubMed] [Google Scholar]
- 26.Sturges HA. The choice of a class interval. J Am Stat Assoc. 1926;21:65–66. doi: 10.1080/01621459.1926.10502161. [DOI] [Google Scholar]
- 27.Swets JA. Measuring the accuracy of diagnostic systems. Science. 1988;240:1285–1293. doi: 10.1126/science.3287615. [DOI] [PubMed] [Google Scholar]
- 28.Volzke H, Fung G, Ittermann T, Yu S, Baumeister SE, Dorr M, Lieb W, Volker U, Linneberg A, Jorgensen T, Felix SB, Rettig R, Rao B, Kroemer HK. A new, accurate predictive model for incident hypertension. J Hypertens. 2013;31:2142–2150. doi: 10.1097/HJH.0b013e328364a16d. [DOI] [PubMed] [Google Scholar]
- 29.Wang Y, Nataraj A. Foot drop resulting from degenerative lumbar spinal diseases: clinical characteristics and prognosis. Clin Neurol Neurosurg. 2014;117:33–39. doi: 10.1016/j.clineuro.2013.11.018. [DOI] [PubMed] [Google Scholar]
- 30.World Medical Association. WMA declaration of Helsinki—ethical principles for medical research involving human subjects. Available at: http://www.wma.net/en/30publications/10policies/b3/index.html. Accessed November 14, 2016.