Borrowing Strength with Non-Exchangeable Priors over Subpopulations

Summary

We introduce a non-parametric Bayesian model for a phase II clinical trial with patients presenting different subtypes of the disease under study. The objective is to estimate the success probability of an experimental therapy for each subtype. We consider the case when small sample sizes require extensive borrowing of information across subtypes, but the subtypes are not a priori exchangeable. The lack of a priori exchangeability hinders the straightforward use of traditional hierarchical models to implement borrowing of strength across disease subtypes. We introduce instead a random partition model for the set of disease subtypes. This is a variation of the product partition model that allows us to model a non-exchangeable prior structure. Like a hierarchical model, the proposed clustering approach considers all observations, across all disease subtypes, to estimate individual success probabilities. But in contrast to standard hierarchical models, the model considers disease subtypes a priori non-exchangeable. This implies that when assessing the success probability for a particular type our model borrows more information from the outcome of the patients sharing the same prognosis than from the others.

Our data arises from a phase II clinical trial of patients with sarcoma, a rare type of cancer affecting connective or supportive tissues and soft tissue (e.g., cartilage and fat). Each patient presents one subtype of the disease and subtypes are grouped by good, intermediate, and poor prognosis. The prior model should respect the varying prognosis across disease subtypes. The practical motivation for the proposed approach is that the number of accrued patients within each disease subtype is small. Thus it is not possible to carry out a clinical study of possible new therapies for rare conditions, because it would be impossible to plan for sufficiently large sample size to achieve the desired power.

We carry out a simulation study to compare the proposed model with a model that assumes similar success probabilities for all subtypes with the same prognosis, i.e. a fixed partition of subtypes by prognosis. When the assumption is satisfied the two models perform comparably. But the proposed model outperforms the competing model when the assumption is incorrect.

1. Introduction

We address statistical inference in a phase II trial of sarcoma. Sarcoma is a rare cancer affecting connective and soft tissues (e.g., cartilage and fat). Sarcoma is a very heterogeneous disease with many different subtypes that are characterized by different prognoses. In the proposed design we pay particular attention to the heterogeneous nature of the disease and the fact that different disease subtypes are related but cannot be considered a priori exchangeable.

We classify different subtypes by the overall prognosis as poor, intermediate or good. The classification is by subjective judgment of the clinical investigator. The objective of the study is to assess the efficacy of a new drug in patients with different subtypes of sarcoma. Let p_i, i = 1, …, n, denote the probability of response (defined below) for a patient with disease subtype i.

One possible approach is to analyze the different subtypes as separate studies. But due to the rare nature of some of the subtypes the enrollment in n = 12 separate studies would be unfeasibly slow. This and concerns related to ethics and efficiency of clinical trial design lead us to consider borrowing of strength across related subtypes. This could be done with a hierarchical model across subtypes that assumes separate models for each subtype that are linked only at the level of a common distribution for all p_i. The problem is that a hierarchical model would treat all subtypes symmetrically. Formally, the prior probability model for the p_i is exchangeable, i.e., invariant with respect to any permutation of the subtype indices i. This symmetry assumption is too strong for the application to the sarcoma study. Different sarcomas are not exchangeable. They are characterized by at least different prognosis, x_i ∈ {poor, intermediate, good}.

At the other extreme, we could accept the clinicians classification and assume a logistic regression of p_i on x_i. Then subtypes with the same prognosis are assumed to have equal success probabilities. The problem with this approach is that disease subtypes are grouped by overall prognosis and this grouping is fixed. However, while overall prognosis for a subtype is important, it is not obvious that it determines the most appropriate grouping. One of the eligibility criteria of the study is failure of prior therapy, i.e., in a sense all patients enter the study with a poor prognosis. The desired level of borrowing strength is somewhere between these two extremes, allowing the data to inform us about the appropriate grouping. We propose a novel approach that can be characterized as intermediate between an exchangeable hierarchical model and a regression. We treat the appropriate grouping as a random quantity, ρ, and define a probability model for this random partition ρ. The model is indexed with the covariates x_i. Thus the model includes a priori a preference for grouping by x_i, but allows for alternative grouping as the data dictates. In other words, we propose a semi-parametric model that respects the non-exchangeable nature of the data.

In a different context Dahl (2008) defines similar random partition models that are constructed to be non-exchangeable across experimental units. His models are based on pairwise distances and are used for inference in protein folding. Similar to the approach proposed in this paper, the models in Dahl (2008) are based on a modification of the product partition model. However, the nature of the modification is different.

Also Malec and Sedransk (1992) and Evans and Sedransk (2001) propose similar models. They introduce a meta-analysis technique to estimate the means corresponding to different experiments, in our context study arms. Like the model proposed in this paper, their approach considers a random grouping where one is able to control the prior preference for grouping. Their approach and ours are similar. Both models assume in a first level that outcomes of a particular experiment are i.i.d., and that, in a second level, given a partition ρ the group-specific parameters are similar, that is, i.i.d. The differences between the two models are in the prior distribution for ρ and the assumptions on the distributions of the outcomes and the means. The latter are assumed Gaussian in Malec and Sedransk (1992) and unconstrained in the proposed approach.

The rest of this article is organized as follows. Section 2 describes the motivating phase II sarcoma dataset. The non-exchangeable model is formalized and discussed in detail in Section 3. Section 4 reports a comparison of the proposed model versus several alternatives. In Section 5 the model is applied to the sarcoma data. Section 6 concludes with a discussion.

2. Data

A single arm phase II clinical trial for sarcoma is currently underway at M.D. Anderson Cancer Center. The objective of the study is to assess the efficacy of irinotecan on patients with different sarcoma subtypes. Irinotecan is a water soluble and commercially available chemical agent that is thought to reduce the sarcoma cancerigenic tumors. Its maximum tolerable dose has been established in a phase I clinical trial (Masuda et al, 2000). The dose limiting toxicity is defined as diarrhea and bone marrow suppression.

Treatment efficacy is measured as tumor shrinkage. More specifically, tumor sizes at the end of the second and fourth treatment cycles were compared with the size at the beginning of the study. If complete (total disappearance of tumor) or partial response (at least 30% shrinkage) is observed at the end of the second cycle, the treatment is considered a success for this patient. Progressive disease (20% or more increase) is reported as treatment failure. A change between 30% shrinkage and 20% increase is considered stable disease. In that case, the tumor is measured again after the fourth cycle, and the treatment is declared a failure only if progressive disease is reported.

This study is still ongoing. So far, a total of 179 patients have met the protocol criteria for eligibility and have been recruited in the study. Of them, 164 participants exhibited one out of eight sarcoma subtypes related with an intermediate prognosis and only 15 exhibited one out of two subtypes of the disease related to good prognosis. No patient with a sarcoma subtype related to poor prognosis has been reported yet. Table 1 shows the available data.

Table 1.

Reported number of successes/trials for each one of the sarcoma subtypes.

Intermediate Prognosis
subtype	successes/trials
Leiomyosarcoma	6/28
Liposarcoma	7/29
MFH	3/29
Osteosarcoma	5/26
Synovial	3/20
Angiosarcoma	2/15
MPNST	1/5
Fibrosarcoma	1/12
Good Prognosis
Ewing’s	0/13
Rhabdo	0/2

3. Non-Exchangeable Product Partition Model (NEPPM)

3.1 Model Definition

Let y_i and N_i respectively denote the number of successes (i.e., patients with positive outcome) and the total number of patients presenting with sarcoma subtype i, i = 1, …, n, n = 12. Denote also by pⁿ = (p₁, …, p_n) the vector of success probabilities. Let ρ = {S₁, …, S_K} denote a partition of {1, …, n} into K nonempty clusters S_k, k = 1, …, K, i.e., $\{1,\dots ,n\}={\cup }_{k=1}^K{S}_k$ and S_k∩S_k′ = ∅ for k ≠ k′. The partition ρ is equivalently characterized by cluster membership indicators φ_i, for i = 1, …, n with φ_i = k if i ∈ S_k. We use ρ or (φ, K) interchangeably. We assume that each subtype is characterized by a categorical covariate x_i taking values in 1, …, Q.

We first describe the proposed model in words. Given an assumed partition ρ we assume i.i.d. sampling across all subtypes within the same cluster. The sampling model is indexed by a subtype-specific parameter ${\theta }_k^{\star }$, in our case the logit of the success probability. The model is completed with a prior on the cluster arrangement ρ.We build on a popular random partition model known as the Pólya urn. It is the model that is implicitly defined in Dirichlet process mixture models. More details on this model are below. An important feature of that model is exchangeability across the subpopulations. We modify the basic Pólya urn model with an additional factor that introduces the desired non-exchangeability by favoring subtypes with matching prognosis x_i to share the same cluster.

We start the formal model definition by specifying the prior conditional on an assumed partition ρ. We adopt the following model, assuming in particular that all disease subtypes in the same cluster share the same success probability. Recall that y_i denotes the number of patient responses to treatment for N_i patients in disease subtype i. Let xⁿ = (x₁, …, x_n) denote the set of values of the categorical covariates, and similarly yⁿ = (y₁, …, y_n). Let Bin(p, N) denote the binomial distribution with success probability p and N trials, N(m, τ) the normal distribution with mean m and precision τ, and Ga(a, b) the gamma distribution with mean a/b.

$$y_i|p_i~\text{Bin}(p_i,N_i)\text{ with logit }(p_i)={\theta }_k^{*}\text{ for }i\in S_k$$

$${\theta }_k^{*}\stackrel{\mathrm{i}\mathrm{i}\mathrm{d}}{~}N(\mu ,{\tau }_{\theta }),\text{ for }k=1,\dots ,K$$

$$\mu ~N(0,{\tau }_{\mu }),{\tau }_{\theta }~\mathit{\text{Ga}}(a_{\tau },b_{\tau })\text{ and }\rho ~p(\rho |x^n),$$ (1)

The definition of p(ρ | xⁿ) will be discussed below. We fix τ_μ = 1/1000 and a_τ = b_τ = 1/10. These choices allow for a wide range of cluster-specific values ${\theta }_k^{\star }$. We investigated alternative choices, using priors that are recommended in the literature for variance components in mixed effects models, but found (results not shown) that these choices provided the best overall performance in terms of DIC. Note also that the use of a common precision parameter τ_θ implies the same amount of shrinkage in each cluster.

To define the model p(ρ) we build on the product partition models (PPMs) (Hartigan, 1990; Barry and Hartigan, 1993). The idea is to construct a probability distribution p(ρ) on the space of partitions of {1, …, n}, by introducing a function c(A) ≥ 0 for every A ⊆ {1, …, n} that measures how tightly grouped the elements in A are thought to be. A random partition model is called a product partition model (PPM) if p(ρ) factors into a product of subset specific factors c(S_k), known as cohesion functions:

$$p(\rho =\{S_1,\dots ,S_K\})=\frac{1}{g_n}\prod _{k=1}^{K}c(S_k),p(y^n|\rho )=\prod _{k=1}^{K}p(y_i:i\in S_k),$$ (2)

with g_n a normalizing constant. Model (2) is easily seen to be conjugate. There is an important connection between the PPM and the Dirichlet process (DP) prior (Ferguson, 1973). Assume θ_i ~ G, i = 1, …, n is an i.i.d. sample from a random probability measure G with a DP prior. The discrete nature of G implies a positive probability of ties among the θ_i. The distribution on the partition ρ induced by these ties is a PPM with cohesions c(S_k) = α (⧣S_k − 1)!. Here ⧣S_k denotes the number of elements in the cluster k and α > 0 is the total mass parameter of the DP prior. In many applications α is assumed random and the model is completed with a hyperprior on α. This feature of the DP is exploited in many applications and highlighted, for example, in Quintana and Iglesias (2003) and Dahl (2003). One important feature of the PPM induced by the DP is that it is a priori exchangeable with respect to the experimental units. This a priori exchangeability makes the PPM induced by the DP prior inappropriate to model the clustering of the disease subtypes in our application.

We now define a non-exchangeable PPM (NEPPM). In particular, applied to the clustering of disease sub-types {1, …, n} we define a model that increases the prior probability of any two subtypes i and i′ with equal prognoses x_i = x_i′ to cluster together. In other words, we define a probability model for random partitions of experimental units {1, …, n} with categorical covariates x_i ∈ {1, …, Q} such that clusters with homogeneous covariates are encouraged a priori. We use

$$p(\rho =\{S_1,\dots ,S_K\}|x^n)\propto \prod _{k=1}^{K}c(S_k),\text{ where }c(S_k)=c_D(S_k)d(S_k),$$

where xⁿ = (x₁, …, x_n), and c_D(S_k) = α (⧣S_k − 1)! is the cohesion induced by the DP and

$$d(S_k)={\left(\frac{{\prod }_{q=1}^Q{m}_{kq}!}{(⧣S_k+Q-1)!}\right)}^{\gamma }.$$ (3)

Here Q is the number of different categories, m_kq the number of subtypes of category q in the cluster S_k and γ is a nonnegative constant, common to all cohesions. We refer to d(S_k) as a “similarity function.” It serves the purpose of increasing the probability of forming clusters with more homogeneous covariate values x_i, i ∈ S_k, i.e., experimental units i in the same cluster include a minimum number of distinct x_i values. The higher the value of γ, the stronger the prior emphasis on homogeneous clusters. More homogeneous clusters S_k have larger d(S_k). In our specific application, we have Q = 3 prognoses, and m_kq for q = −1, 0, 1 are, respectively, the numbers of sarcoma subtypes with poor, intermediate and good prognosis in the cluster S_k (indexing starts at −1 as mnemonic for poor diagnosis). As desired, the resulting prior probability model is non-exchangeable.

3.2 Some Properties of the NEPPM

Let f_k(ρ) denote the predictive probability function, i.e., the conditional probability of a hypothetical new (n + 1)−th unit being allocated to cluster k, conditional on ρ. Let K(n) denote the number of clusters in ρ. We find

$$f_k(\rho )=\frac{c(S_k\cup \{n+1\})}{c(S_k)}\propto \{\begin{array}{cc}⧣S_k{\left(\frac{m_{k\ell }+1}{⧣S_k+Q}\right)}^{\gamma }\hfill & \text{for }1\le k\le K(n),\hfill \\ \alpha /{(Q!)}^{\gamma }\hfill & \text{for }k=K(n)+1.\hfill \end{array}$$ (4)

where x_n+1 = ℓ is the category of the new experimental unit and c(∅) ≔ 1. In the context of our application x_i is the prognosis for subtype i. Posterior simulation follows a simple modification of standard Gibbs-sampling schemes for DP or PPM models, as described in, e.g., MacEachern and Müller (1998) or Quintana (2006). See further details in the Appendix.

The proposed model reduces to the DP Pólya urn when all x_i are equal, i.e., Q = 1. As a consequence the NEPPM reduces to a DP mixture (DPM). That is, if Q = 1, then, m_k1 = ⧣S_k and d(S_k) reduces to

$$d(S_k)={\left[\frac{(⧣S_k)!}{(⧣S_k)!}\right]}^{\gamma }=1.$$

Similarly, when γ = 0 the similarity function drops out of the model and the NEPPM reduces to the DPM. On the other hand, the model can easily be extended for more complicated covariates x_i. For multiple categorical covariates one could introduce several similarity functions and use the product to modify the cohesion functions in (3).

For γ = 1 the model reduces to a special case of the model introduced in Müller et al. (2011) using the default similarity function for categorical covariates. In general, they suggest using a similarity function defined with an auxiliary probability model as

$$d(S_k)=\int \prod _{i\in S_k}q(x_i|{\xi }_k)q({\xi }_k)d{\xi }_k,$$

where ξ_k is a latent variable, and q(· | ξ_k) and q(·) are auxiliary probability models. The auxiliary model q(·) is introduced solely for the purpose of defining an easily evaluable cohesion function d(·). For categorical covariates x_i ∈ {1, …, Q} they introduce a vector ξ_k = (ξ_k1, …, ξ_kQ) and use q(x_i = q | ξ_kq) = ξ_kq and q(ξ) as a Dirichlet distribution with parameters β₁, …, β_Q. Assuming that the parameters of this Dirichlet distribution are all equal to, say, β, the expression for d(S_k) reduces to:

$$d(S_k)=\frac{\mathrm{\Gamma }(Q\beta )}{\mathrm{\Gamma }{(\beta )}^Q}\frac{{\prod }_q\mathrm{\Gamma }(\beta +m_{kq})}{\mathrm{\Gamma }(⧣S_k+Q\beta )}.$$

With β = 1 this is exactly the factor d(S_k) in (3), assuming γ = 1.

The proposed model p(ρ | xⁿ) defines a sequence of probability models across n. The question arises whether the model is coherent across n. Ideally the model for n should arise from marginalization of the model under n + 1. Below we show that, in general, this is not true. We let ρ_n = {S₁, …, S_K} denote a partition of the set {1, …, n}, and use a subindex_n on ρ_n to highlight the dependence of ρ on the sample size n. For simplicity we focus on the case γ = 1 and find

$$\sum _{\ell =1}^{K+1}p({\rho }_n,{\phi }_{n+1}=\ell |x^n,x_{n+1}=q)=\prod _{k=1}^{K}c(S_k)[\sum _{\ell =1}^K\frac{c(S_{\ell }\cup \{n+1\})}{c(S_{\ell })}+c(\{n+1\})]\propto p({\rho }_n|x^n)[\sum _{\ell =1}^K⧣S_{\ell }\frac{m_{\ell q}+1}{⧣S_{\ell }+Q}+\frac{\alpha }{Q!}].$$

The expression in square brackets varies with ρ_n and xⁿ. Thus in general under p(ρ_n+1 | xⁿ, x_n+1) the implied marginal on the first n experimental units is not equal to p(ρ_n | xⁿ). This limits the use of the model for prediction. However, for the envisioned use for data analysis over multiple subgroups this is not a major concern.

4. Simulation Study

4.1 Competing Models

In this section we compare via simulation the performance of the proposed model vs. alternative models. The comparison is in terms of bias, mean square error, and coverage probability (CP). In the implementation of the proposed NEPPM model we complete the NEPPM with a Ga(10, 0.5) hyperprior on α. The Gamma hyper-prior was proposed in Escobar and West (1995). See also, Dorazio (2009).

We compare the proposed NEPPM (1) with the following alternative models. The first model entirely abandons borrowing strength across subtypes (stratified models). The second model borrows strength, but assumes a priori exchangeable subtypes (fully exchangeable model). The third model respects the lack of exchangeability across sub-types, but goes to the extreme of grouping the subtypes by the covariate, in our case prognosis, and fixing this grouping for the rest of the analysis (partially exchangeable model).

Stratified Models

Assume a separate model for each disease subtype. There is no borrowing of strength or pooling of information across subtypes. That is, for i = 1, …, n,

$$y_i|p_i~\text{Bin}(p_i,N_i)\text{ and logit }(p_i)~N(0,1/1000)$$ (5)

Fully exchangeable model

The model borrows strength across subtypes, but treats a priori all subtypes symmetrically. No prognosis information is considered.

$$y_i|p^n\stackrel{\mathrm{i}\mathrm{i}\mathrm{d}}{~}\text{Bin}(p_i,N_i)$$

$$\text{logit }(p_i)\stackrel{\mathrm{i}\mathrm{i}\mathrm{d}}{~}N(\mu ,1/{\sigma }^2)$$

$$\mu ~N(0,{\tau }_{\mu })\text{ and }\sigma \propto {\mathrm{N}}^{+}(0,1),\sigma >0$$ (6)

with τ_μ = 1/1000. Here N⁺(0, 1) denotes a half normal distribution, i.e., a standard normal distribution restricted to the positive real line. The half normal prior for the standard deviation σ is recommended, for example, in Spiegelhalter et. al. (2004, p. 170). The use of hierarchical models with a priori exchangeable subpopulations is a standard approach for many biomedical inference problems that require borrowing of strength across subpopulations.

Partially exchangeable model (PEM)

The PEM assumes partial exchangeability by fixing the subgroup-specific cluster means as a logistic regression on x_i, the overall prognosis of disease subtype i. In other words, ρ is fixed as the grouping determined by the categorical prognosis covariate. There is no learning about the partition.

$$y_i|p^n\stackrel{\mathrm{i}\mathrm{i}\mathrm{d}}{~}\text{Bin}(p_i,N_i)$$

$$\text{logit }(p_i)~N({\beta }_0+{\beta }_{-1}1(x_i=-1)+{\beta }_{1}1(x_i=1),\tau )$$

$${\beta }_j\stackrel{\mathrm{i}\mathrm{i}\mathrm{d}}{~}N(0,{\tau }_{\mu }),j=-1,0,1$$ (7)

with τ_μ = 1/1000 and τ = 18. The covariate x_i is equal to −1, 0 or 1 when i indexes a sarcoma subtype with poor, intermediate, or good prognosis, respectively. Fixing τ = 18 implies Pr(|logit (p_i) − logit (p_i′)| ≤ 0.65) = 95% for any two subtypes i and i′ with the same prognosis, i.e., the odds ratio for any two subtypes in the same cluster is a priori bounded between 1/2 and 2 with probability 95%. For any two subtypes with different prognoses the same prior probability is close to zero. In contrast, under model (6) with σ fixed at 0.65 (the prior median of σ) the same probability is approximately equal to 50%, leaving the two models comparable with respect to the overall prior shrinkage of the p_i.

The PEM (7) and the fully exchangeable hierarchical model (6) are two extreme cases of borrowing strength. The latter assumes that all subpopulations are exchangeable; the earlier allows partial exchangeability using the groups defined by x_i, but freezes the grouping. The proposed NEPPM model strikes a compromise between the two extremes by including grouping in clusters, but allowing the clusters to be random.

4.2 Simulation Study Results

In the comparison, we consider n = 12 different experimental units (sarcoma subtypes) with a categorical covariate x_i ∈ {−1, 0, 1}. Each simulated trial realization consists of n independent observations y_i ~ Bin(p_i, N_i) with success probabilities fixed at an assumed simulation truth, and fixed sample size N_i. We use N_i = 6, 6, 8, 40, 40, 30, 20, 20, 10, 7, 7 and 6, respectively. The first three subtypes have poor overall prognosis, x_i = −1, i = 1, 2, 3. The last three subtypes have good prognosis, x_i = 1, i = 10, 11, 12. The remaining six subtypes have x_i = 0. The sample sizes N_i are chosen to match the expected accrual under the 12 sarcoma subtypes in the motivating phase II sarcoma trial. For the simulation truth on p_i we consider four scenarios, S0 through S3, summarized in Table 2.

Table 2.

Simulation truth p_i under four alternative scenarios

scenario	good	intermediate	poor
Ni	6, 6, 8	40, 40, 30, 20, 20,10	7, 7, 6
S0	.59,.55,.47	.45,.4,.36,.34,.3,.26	.23,.19,.17
S1	.28,.26,.24	.18,.16,.15,.17,.2,.19	.12,.13,.1
S2	.28,.26,.18	.24,.16,.15,.17,.10,.19	.12,.20,.10
S3	.30,.40,.15	.20,.10,.30,.20,.15,.12	.15,.40,.30

Scenarios S0 and S1 favor the PEM model. The grouping by prognosis is perfect. S1 includes a wider gap between success probabilities for subtypes with intermediate and good prognosis. The remaining scenarios represent varying levels of mismatch between prognosis and true success probabilities. Under S2 only two pairs of success probabilities are switched between intermediate and poor and intermediate and good prognosis, respectively. Under S3 prognosis and success probability are unrelated. We will demonstrate that we lose little in scenarios S0 and S1 by using the more flexible NEPPM compared to the PEM, which happens to be favored by the assumed simulation truth. However, in S2 and S3, when the assumption of the fixed grouping under the PEM is violated, the proposed NEPPM model correctly recognizes that the a priori assumed clustering is inappropriate and leads to better performance.

We generated M = 1000 repeat simulations of the entire trial under these four scenarios. For each simulation m = 1, …, M, and for each i = 1, …, n, we estimated p_i by the posterior mean ${\overline{p_i}}^m$. We evaluated bias and mean square error (MSE) by

$$\text{bias}({\overline{p}}_i)\approx \frac{1}{M}\sum _{m=1}^M{\overline{p}}_i^m-p_i\text{ and }\mathrm{M}\mathrm{S}\mathrm{E}({\overline{p}}_i)\approx \frac{1}{M}\sum _{m=1}^M{({\overline{p}}_i^m-p_i)}^2,$$

i.e., we use Monte Carlo averages to evaluate the means with respect to repeat experimentation.

For scenario S0, we estimated models (5) through (7), as well as the proposed NEPPM with γ = 1 in (3). The results of this comparison are discussed in Web Appendix A and summarized in Figures 1 and 2 of the Supplemental Web Materials. The PEM (7) produces the estimators with the lowest values of the MSE. This is to be expected since scenario S0 strongly favors the PEM. The NEPPM and PEM report better summaries than the remaining models, due to the fact that these are the only models that borrow strength across sarcoma subtypes and acknowledge the similarity of the success probabilities corresponding to the same prognosis. Stratified inference with separate models (5) and inference under the fully exchangeable model (6) suffer from the small sample sizes, leading to increased MSE. These models fail to sufficiently borrow strength across the subtypes. We therefore restrict the further comparison to NEPPM versus PEM.

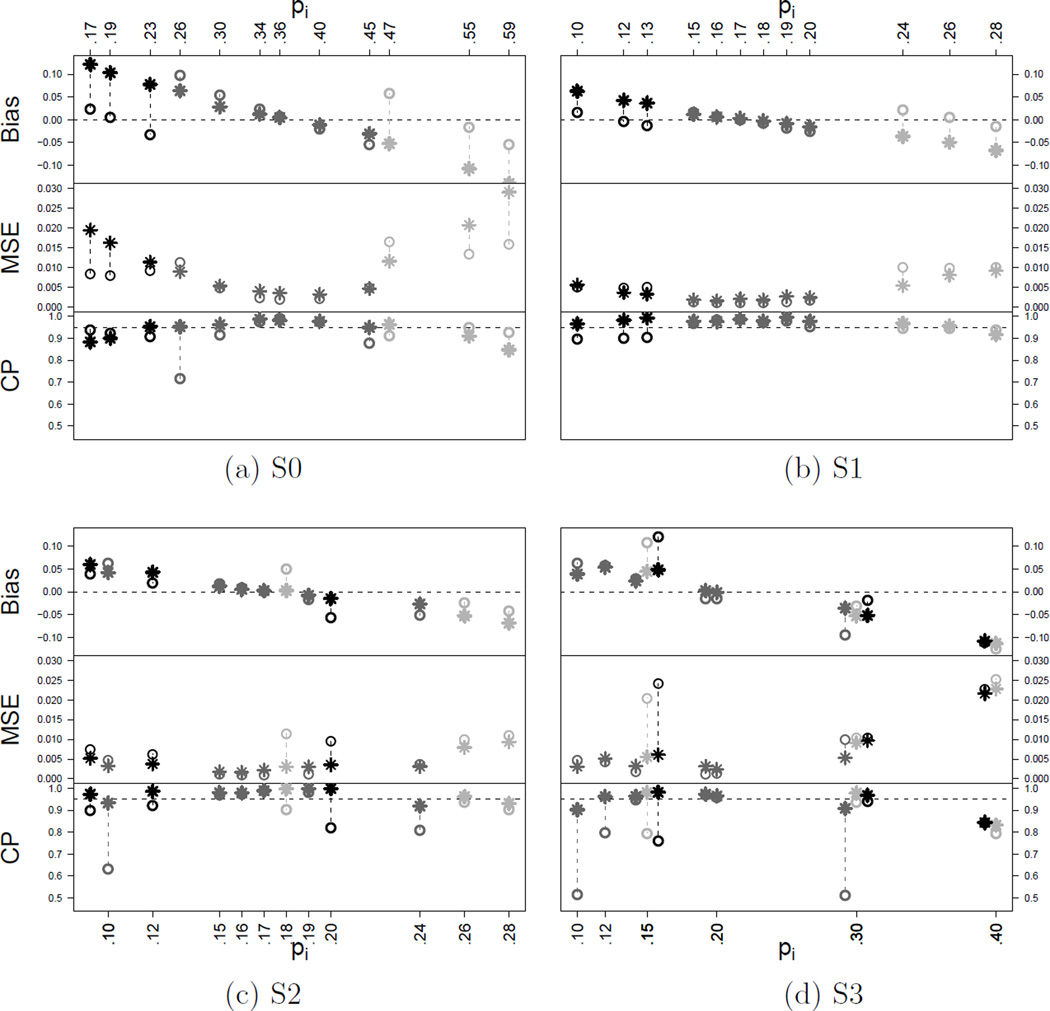
Figure 1 compares NEPPM vs. PEM under scenarios S0–S3. Panel (a) shows the results under S0. Inference under the PEM reports smaller MSE in almost all subtypes. The bottom figure in panel (a) compares the coverage probability (CP) of the central 95% credible interval (CI) under the PEM vs. the NEPPM with γ = 1. The PEM has low CP for the subtypes with lowest and largest intermediate prognosis success probabilities (p_i = 0.26 and 0.45). Note in particular the low CP for the large subgroup with p_i = 0.26. This is due to the fixed grouping of all intermediate prognosis subtypes, leading to excessive shrinkage for the subtypes with lowest and greatest true p_i within each fixed cluster. The PEM model does not allow any change or weighting of the grouping.

Figure 1.

Summary of simulation results under scenarios S0 through S3. The plots compare the estimated success probabilities under the NEPPM (star “*”) vs. the PEM (circle “○”). The horizontal axis shows the n = 12 true success probabilities under the assumed scenario. The upper, medium and lower panels show the bias, mean square error and coverage probability of the central 95% credible interval, respectively. Under S0 and S1, from left to right, the first three success probabilities correspond to poor prognosis (x_i = −1), the following six to intermediate (x_i = 0) and the last three to good prognosis (x_i = 1). The p_i with equal values were jittered in the plot for display purposes.

Panel (b) reports the comparison under scenario S1. Although scenario S1 still favors the PEM, inference under the two models seems comparable. Scenario S2 is the same as S1, with only two pairs of success probabilities interchanged. The summaries in panel (c) show that the PEM fails to accurately estimate the swapped probabilities. Under S3 the grouping by prognosis is meaningless. As panel (d) demonstrates, the NEPPM performs better than the PEM under this scenario.

In summary, we gain precision when incorporating the information of the covariates in the model and the covariates have predictive power. Among the four competing models considered in Section 4.1, the partially exchangeable PEM and the NEPPM with random partitions show the best overall performance. Comparing these two models directly, as long as the assumed true success probabilities with the same prognosis are similar, the PEM is optimal in terms of bias, MSE, and coverage probability. However, when the assumed simulation truth does not match the grouping by prognosis x_i, we find better performance under NEPPM. By its nature, the PEM introduces strong prior beliefs about the similarity of the success rates. The model groups subtypes by x_i, and allows no modification of this fixed clustering. Inference is precise when these beliefs happen to be right. In contrast, the NEPPM introduces similar beliefs, but allows for uncertainty. The model allows the data to speak and correct the clustering in case the prior beliefs were in conflict with the data.

5. Application to Sarcoma Data

We implemented inference for the data described in Section 2 using the proposed non-exchangeable partition model (1) with γ = 1. The total mass parameter α of the Dirichlet process was modeled with a Ga(10, 0.5) prior.

Saving every 10^th iteration after a 10,000 iteration burn-in, a Monte Carlo posterior sample of size 10,000 was saved to estimate the success probabilities. The Markov chain mixed well. Posterior simulations are implemented as a C program. Running under OS X on a Macbook Pro laptop, the 110,000 iterations took 165.72 seconds CPU time.

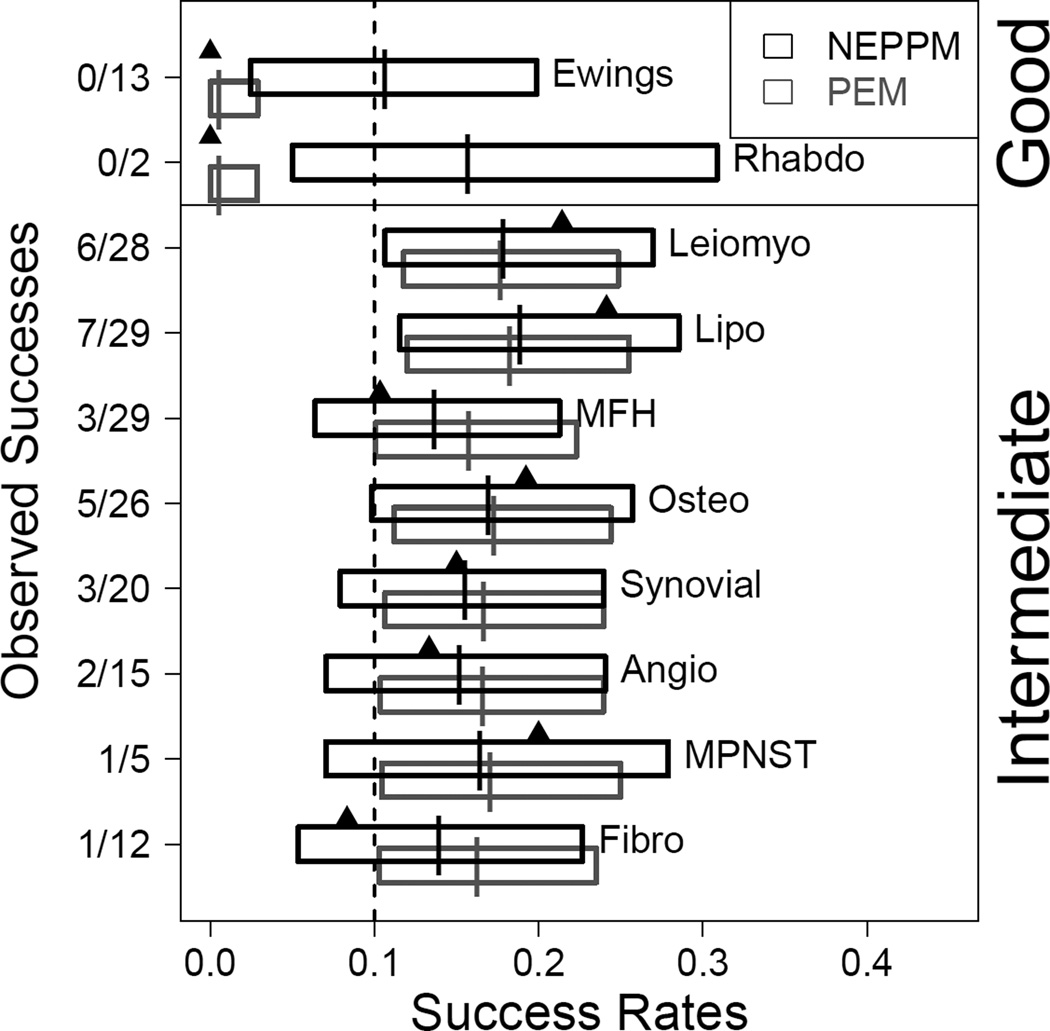
Figure 2 shows the central 90% posterior credible intervals of the success probability p_i for each sarcoma subtype. For example, only for Leiomyosarcoma and Liposarcoma the 5% posterior percentile is greater than 0.1.

Figure 2.

Central 90% credible intervals of the success probabilities for each sarcoma subtype under the proposed NEPPM (black boxes) with parameter γ = 1 and under the PEM (grey boxes). The vertical lines in the boxes indicate the posterior means, and the triangles represent the proportion of successes within each subtype. For reference the dashed vertical line marks 0.1. The first two subtypes are sarcoma subtypes with good prognosis. The remaining eight are subtypes with intermediate prognosis. Note how the PEM borrows strength across all disease subtypes within the same (fixed) prognosis group.

For comparison, we carried out the same inference under the PEM. We note that the small sample sizes in some of the subtypes and the uncertainty about the effect of prognosis in the treatment would lead most analysts to consider the PEM as an inappropriate model for this data. We use it here for comparison only. The central 90% credible intervals for the success probabilities under the PEM are shown in Figure 2 (dashed lines). The fixed grouping of subtypes in the PEM forces similar inference for all intermediate prognosis subtypes. In particular, Liposarcoma and MFH report almost the same inference, despite very different numbers of reported successes for the same number of patients in both subtypes. Also note the inappropriately short credible interval for Rhabdo. Despite the only N_i = 2 enrolled patients, posterior inference borrows strength from the data on the 13 Ewing’s patients.

Finally we computed the Deviance Information Criterion (DIC) (Spiegelhalter et al., 2002) for each one of the models described earlier. See the supplementary web materials, Table 1. PEM has the lowest DIC followed by the NEPPM. While the DIC indicates the PEM as the best fitting model, the comparison of the reported posterior credible intervals lead us to prefer the NEPPM. The substantive prior knowledge that different sarcomas are not necessarily exchangeable leads us to prefer, for example, the much larger credible interval for Rhabdo, even when pooling with Ewings might report a lower DIC. Even lower DIC is reported for a logistic regression (see Web Appendix B and Table 1 in the Supplemental Web Materials), i.e., for 1/τ = 0 and exactly matching inference for all subtypes in the same prognosis group.

6. Discussion

We proposed an approach to borrow strength across non-exchangeable subpopulations. The usual approach to borrow strength across subpopulations, through hierarchical models, is perhaps one of the most successful Bayesian approaches in biomedical data analysis. In a hierarchical model, the estimation of any subpopulation-specific parameter borrows strength from all observations in other subpopulations, treating all subpopulations symmetrically. In a partially exchangeable hierarchical regression model, inference borrows strength across all subpopulations that are grouped together in some fixed a priori grouping by covariates. In contrast, the proposed model introduces the non-exchangeability only stochastically, with random partitions. The estimation of subpopulation success probability p_i borrows more strength from the subset of observations, that according to our prior beliefs, are more likely to be exchangeable with the observation i. The proposed model allows the data to speak and correct prior assumptions when the prior beliefs are not confirmed by the data. However, the precision of estimates under the proposed model can be lower than under a partially exchangeable hierarchical regression because inference has to account for the uncertainty in the grouping. This was confirmed in the simulation study.

The proposed model is useful when sample sizes are small in some subpopulations. With large samples in all subpopulations, a stratified analysis with separate models for each subpopulation could be considered. However, small sample sizes are typical for early phase clinical trials. In particular due to the rare nature of the sarcomas studied in the motivating phase II clinical trial borrowing strength is essential to obtain useful inference.

The proposed model included a novel distribution over random partitions that gives increased a priori weights to homogeneous partitions. The additional computational effort compared to a conventional Pólya urn (induced by a Dirichlet process mixture) is minimal. Depending on the application, in principle any sampling model and any distribution for the cluster-specific effects can be considered. The proposed model is a particular case of the more general PPMx model introduced in Müller et al. (2011). Their model uses covariate information to change the prior probability of clustering. They consider continuous, ordinal, and nominal covariates.

Finally, the proposed approach is not a viable alternative to subgroup analysis as discussed in the clinical trial literature (Pocock et al 2002, Simon, 2002). Subgroup analysis investigates whether a conclusion about effectiveness or lack of effectiveness in the overall population remains valid for subpopulations characterized by covariates, including age, prior treatment history, different disease subtypes, biomarkers, etc. The main concerns are related to data dredging and multiplicity issues when many potential subgroups are available and the search for subgroups is carried out in an unplanned fashion. The model and approach discussed in this article included no consideration of a possible selection of subgroups for reporting or multiplicity controls. We consider the approach most suitable for early phase trials, such as the motivating sarcoma study.

In summary, we have proposed an extension of hierarchical modeling to non-exchangeable subpopulations. The approach is easy to implement. It strikes a compromise between borrowing too much strength as, for example, in a logistic regression, versus no borrowing at all, as in a stratified analysis. The proposed model is suitable to estimate the success probabilities in the motivating sarcoma trial presented here by borrowing strength across the different subtypes of the disease.

Appendix

Gibbs Sampling Scheme

We describe posterior Markov chain Monte Carlo (MCMC) posterior simulation under the proposed NEPPM model (1) and (3). Ties among any set of imputed parameters θ₁, …, θ_n define a partition ρ = {S₁, …, S_K} of the indices {1, …, n}. Let ${\theta }_1^{*},\dots ,{\theta }_K^{*}$ denote the unique values in the sample, indexed in order of appearance and define $S_k=\{i:{\theta }_i={\theta }_k^{*}\}$.

Let θ⁻ⁱ = (θ₁, …, θ_i−1, θ_i+1, …, θ_n) denote all values but θ_i. Let K⁻ⁱ be the number of unique values in θ⁻ⁱ, let ${\theta }_1^{*-i},\dots ,{\theta }_{K^{-i}}^{*-i}$ be these different values in order of appearance and ρ⁻ⁱ be the partition implied by θ⁻ⁱ. Use equation (4) with the n − 1 observations and let the observation i be the future observation (partial exchangeability allows us to permute the indices) to get:

$$p({\theta }_i|{\mathit{\theta }}^{-i})=f_{K^{-i}+1}({\rho }^{-i})g_0({\theta }_i)+\sum _{k=1}^{K^{-i}}{f}_k({\rho }^{-i}){\delta }_{{\theta }_k^{*-i}}({\theta }_i),$$

where δ_x is a pointmass at x and g₀ is the pdf corresponding to G₀. Therefore,

$$p({\theta }_i|{\mathit{\theta }}^{-i},y^n)\propto p(y^n|{\theta }_i,{\mathit{\theta }}^{-i})p({\theta }_i|{\mathit{\theta }}^{-i})\propto \{\prod _{j=1}^{n}p(y_j|{\theta }_j)\}\{f_{K^{-i}+1}({\rho }^{-i})g_0({\theta }_i)+\sum _{k=1}^{K^{-i}}{f}_k({\rho }^{-i}){\delta }_{{\theta }_k^{*-i}}({\theta }_i)\}\propto p(y_i|{\theta }_i)f_{K^{-i}+1}({\rho }^{-i})g_0({\theta }_i)+\sum _{k=1}^{K^{-i}}{f}_k({\rho }^{-i})p(y_i|{\theta }_i){\delta }_{{\theta }_k^{*-i}}({\theta }_i)$$

Using (4) we get:

$$p({\theta }_i|{\mathit{\theta }}^{-i},y^n)\propto \frac{\alpha }{{(Q!)}^{\gamma }}p(y_i|{\theta }_i)g_0({\theta }_i)+\sum _{k=1}^{K^{-i}}⧣S_k{\left(\frac{m_{kl}+1}{⧣S_k+Q}\right)}^{\gamma }p(y_i|{\theta }_k^{*-i}){\delta }_{{\theta }_k^{*-i}}({\theta }_i),$$ (8)

where l is the value of the categorical covariate (in our particular, the prognosis) corresponding to the i^th experimental unit (subpopulation).

The expression above has an important practical implication. Assume we have code for posterior simulation under the Dirichlet process (DP) mixture prior with parameters α and G₀. Only a slight modification in the predictive probability function, i.e., in $\mathit{\text{Pr}}({\theta }_i={\theta }_k^{*}|{\mathit{\theta }}^{-i},y^n)$ is necessary to implement posterior simulation under the proposed nonexchangeable product partition model. Compared with a corresponding model with a DP mixture prior for p_i, only two additional factors appear in (8), the (Q!) in the denominator of the first term, and the expression between (…)^γ in the second term.