Exploring the energy landscape of GFP by single-molecule mechanical experiments

Abstract

We use single-molecule force spectroscopy to drive single GFP molecules from the native state through their complex energy landscape into the completely unfolded state. Unlike many smaller proteins, mechanical GFP unfolding proceeds by means of two subsequent intermediate states. The transition from the native state to the first intermediate state occurs near thermal equilibrium at ≈35 pN and is characterized by detachment of a seven-residue N-terminal α-helix from the beta barrel. We measure the equilibrium free energy cost associated with this transition as 22 k_BT. Detachment of this small α-helix completely destabilizes GFP thermodynamically even though the β-barrel is still intact and can bear load. Mechanical stability of the protein on the millisecond timescale, however, is determined by the activation barrier of unfolding the β-barrel out of this thermodynamically unstable intermediate state. High bandwidth, time-resolved measurements of the cantilever relaxation phase upon unfolding of the β-barrel revealed a second metastable mechanical intermediate with one complete β-strand detached from the barrel. Quantitative analysis of force distributions and lifetimes lead to a detailed picture of the complex mechanical unfolding pathway through a rough energy landscape.

Mechanical stability is a property of protein structure that has recently become accessible through single-molecule experiments (1-3). The importance of protein stability under a mechanical force becomes immediately obvious for proteins bearing mechanical function in vivo, like in muscle (4) and cytoskeletal proteins (5). Because mechanical single-molecule experiments exhibit single amino acid-length resolution and can thus also provide important structural information (5-7), they have become a valuable tool to explore the energy landscape of proteins (8). Most proteins investigated in folding studies to date are small, containing <200 amino acid residues. Folding studies of larger proteins in classical bulk experiments are generally difficult because their folding kinetics are slow and many large proteins tend to aggregate in the unfolded state. Moreover, growing structural complexity causes more intermediate states to become populated; therefore, analysis and interpretation of multiexponential kinetics becomes difficult. For single-molecule mechanical experiments, however, large protein sizes can be handled easily (9).

Here, we use GFP to investigate the energy landscape of a complex protein in single-molecule force experiments. GFP is among the most important proteins used in biotechnology (10). Numerous applications ranging from localization studies of proteins in living cells to fluorescent pH or Ca sensors have been developed (10). Nevertheless, folding studies of this protein are rare (10-12) for the above reasons.

A detailed knowledge of the mechanical stability of GFP would open the door to an application of GFP as a molecular force sensor. Because fluorescence is closely coupled to an intact GFP structure (13), understanding the determinants of mechanical GFP stability will allow us to develop mutants with known unfolding forces that can report by means of their fluorescence signal the forces acting on the single-molecule level inside a living cell. The many known fluorescent GFP analogs, like red fluorescent protein and yellow fluorescent protein (10) may already exhibit different mechanical stability.

Materials and Methods

Cloning and Protein Expression. We investigated Cycle3-GFP (14) with an additional point mutation, S2G. The Ig8 titin construct, containing the domains I27-I34 from human cardiac titin was as described in ref. 9. The shortened actin crosslinker dictyostelium filamin (DdFLN1-5) construct was as described in ref. 5. To insert a single Cycle3-GFP domain into the Ig8 construct, two restriction sites (NcoI and BstEII) were introduced into the Ig8 expression vector between the Ig30 and Ig31 domain sequences by using the QuikChange mutagenesis kit (Stratagene). The same restriction sites were introduced into the DdFLN1-5 expression vector between domains DdFLN3 and DdFLN4 by using the QuikChange Multi Site-Directed Mutagenesis kit (Stratagene). The vectors were digested, and the GFP sequence was introduced and relegated. Protein purification was done by using an N-terminal His-6-Tag. The presence of the inserted GFP domain in the two constructs was verified by DNA sequencing and protein gel electrophoresis. The sample solutions showed the typical GFP fluorescence.

Force Spectroscopy of Single Proteins. All single-molecule force measurements were performed on a custom-built atomic force microscope. Calibration of cantilevers was done in solution by using the equipartition theorem (15, 16). This method provides a resolution in force of ≈10%. Two types of gold-coated cantilevers (Bio-Levers, Olympus, Tokyo) with spring constants and resonance frequencies of either 30 pN/nm and 8.5 kHz (type A), respectively, or 6 pN/nm and 1.5 kHz (type B) were used. For the measurements, ≈20 μl of protein solution (PBS buffer, pH 7.4; protein concentration, ≈0.5 g/liter) were applied on a freshly evaporated gold surface and incubated for 5 min at room temperature. The force curves on the Ig8-GFP construct were collected at pulling speeds ranging from 100 to 1,000 nm/s. The force curves on the DdFLN1-5-GFP construct used in the analysis of unfolding forces and contour lengths as well as in the lifetime analyses were collected at a pulling speed of 300 nm/s with Olympus type A Bio-Levers. All experiments were conducted at room temperature.

Measurement of Contour Lengths and Unfolding Forces. For quantitative analysis of contour lengths and unfolding forces the force-extension traces were fit to an interpolation formula of the worm-like chain model (WLC), F(x) = (k_BT/p)[0.25(1 - x/L)^-2 - 0.25 + x/L] as introduced by Bustamante et al. (17). L denotes the contour length of the stretched protein, p is the persistence length, k_B is Boltzmann's constant, T is the temperature in Kelvin, and x is the distance between attachment points of the protein (extension or end-to-end distance). A value of 0.5 nm for p provided the best fit for the investigated force regime (20-150 pN) and was held fixed at this value for all fits. Unfolding forces were determined from the points where the WLC fits intersect the cantilever relaxation phase after unfolding of a protein domain. All fits and calculations were performed with igor pro 4.01 (WaveMetrics, Lake Oswego, OR).

Interpretation of Unfolding Forces. To interpret the distributions of observed unfolding forces, Monte Carlo simulations were performed as described in ref. 18. Experimental conditions could be simulated by including the measured distribution of contour lengths at which GFP unfolding was observed. The simulated unfolding force distributions were then fitted to those obtained from experiment (see Fig. 1e) to yield the unloaded lifetime τ₀(F = 0) under zero force and Δx, which denotes the distance from the folded state to the transition state, along the reaction coordinate defined by the end-to-end distance of the protein and by the direction of the applied force (see supporting information, which is published on the PNAS web site).

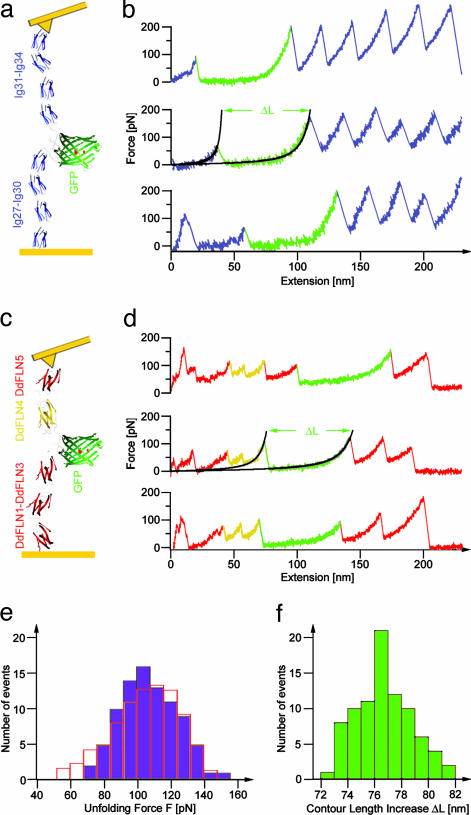
Fig. 1.

Single-domain force spectroscopy of GFP. (a) Scheme of Ig8-GFP chimera protein, stretched between a gold surface and a gold-coated cantilever tip. (b) Three typical force-extension traces measured with Ig8-GFP. GFP unfolding and the subsequent stretching phase of the unfolded polypeptide now lengthened by ΔL is marked in green. Black lines show WLC fits by using a persistence length, p, of 0.5 nm and contour lengths L and L + ΔL. (c) Scheme of DdFLN1-5-GFP chimera protein. (d) Three typical force-extension traces measured with DdFLN1-5-GFP. The GFP unfolding pattern is marked in green, and the double peak indicating DdFLN domain 4 unfolding (5) is marked in yellow. Black lines show WLC fits as in b. (e) Distribution of GFPΔα unfolding forces F (see Materials and Methods) obtained from measurements with DdFLN1-5-GFP. Open red bars show results from a Monte Carlo unfolding kinetics simulation of GFPΔα with τ₀ = 14 s and Δx = 0.28 nm. (f) Distribution of the contour length increase, ΔL, because of GFPΔα unfolding as measured by WLC fits to DdFLN1-5-GFP traces (compare to d).

Elastically Coupled Two-State Model. To analyze the observed force plateaus in the rising slopes before the unfolding of GFPΔα, we fitted force-extension traces calculated by an equilibrium elastically coupled two-state model (18, 19) to our data (see Fig. 3). From the fits we obtain the free energy cost ΔG = 22 ± 4k_BT for the transition and the contour length increase ΔL = 3.2 ± 1 nm.

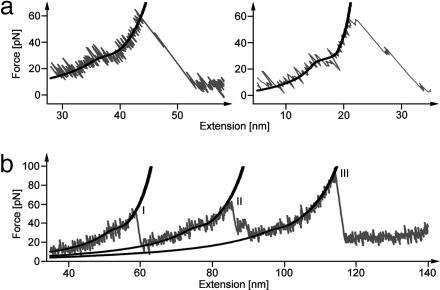
Fig. 3.

Detachment of the N-terminal α-helix. (a) Gray lines show detail of the region before GFPΔα unfolding of two Ig8-GFP force-extension traces. Black lines shows a fit with an elastically coupled two-state model (for fit parameters see text) (b) Gray line shows detail of a DdFLN1-5-GFP force-extension trace. Peak I corresponds to the unfolding of a DdFLN domain. Peak II corresponds to the unfolding of DdFLN domain 4. Peak III corresponds to the unfolding of GFPΔα. Black lines show a fit with an elastically coupled two-state model.

Calibration and Interpretation of Contour Lengths. The contour lengths L, measured by means of the WLC fits to the data, had to be calibrated to obtain the number of amino acids involved in an unfolding event. For calibration, we used Ig domains of DdFLN, which contain exactly 100 amino acids per domain (20). The average contour length increase after the unfolding of a single DdFLN domain is ΔL = 32.5 ± 0.3 nm. Taking into account an N-terminal-to-C-terminal distance, d_N;C, of 4 ± 0.1 nm of the folded domain from the NMR structure (21) we arrive at a total unfolded contour length of L = ΔL + d_N;C = 36.5 nm. From this we derive a contour length, L_aa, of 0.365 nm per unfolded amino acid residue. We used this calibration factor for all contour length analyses. A value of 0.365 nm is a lower limit for L_aa, because in our estimate we assume all 100 amino acids in the DdFLN domains are tightly folded.

The distributions of contour length increases, ΔL, we show in this paper are mainly even distributions around a well defined average value, which indicates that the structural transitions are well defined. The width of these contour length increase distributions is due to a measurement error of 3 nm for a single trace. The error of the mean for a sample of 87 measurements is therefore 0.33 nm.

In this study we use the full structural information available from the Cycle3-GFP crystal structure (Protein Data Bank ID code 1B9C) (22) to map measured contour length increases to changes in the protein structure. The contour length of a protein is determined by two contributions: the contour length of the unfolded amino acids and the distance between the first structured residue at the N terminus and the last structured residue at the C terminus (see supporting information). The first part is given by m·L_aa, assuming m unfolded amino acids. The second part, d_N;C, can be extracted from the coordinates in the crystal structure. If a protein undergoes an unfolding transition from a state I to a state II, during which m amino acid residues unfold, the measured change in contour length will be given by ΔL = m·L_aa + d_N;C(II) - d_N;C(I). Both distances, d_N;C(I) and d_N;C(II), can be calculated from the coordinates of the backbone C^α atoms of the first and last amino acid of the folded structure provided in x-ray diffraction or NMR data. As an example, if in a first transition seven N-terminal amino acids (the N-terminal α-helix) of GFP would detach from the folded portion (residues 4-230), we would expect a length increase of ΔL = 7·L_aa + d_11;230(II) - d_4;230(I) = 2.9 ± 0.2 nm. The indices denote the respective folded residues. In Fig. 2a, we identify structural candidates for GFPΔα. For unfolding events leading to complete unfolding of GFP d_N;C(II) = 0. We calculated the expected contour length increase for GFP structures lacking an increasing number of amino acids from either the N or C terminus, respectively. This contour length increase is given then by ΔL = (227 - i)·L_aa - d_4+i;230(I) if i amino acid residues detach from the N terminus or by ΔL = (227 - i)·L_aa - d_4;230-i(I) if detachment occurs from the C terminus. The result is plotted in Fig. 2a as a function of index i.

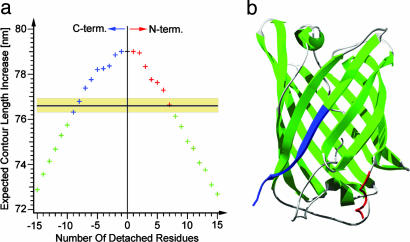
Fig. 2.

Contour length mapping. (a) Expected contour length increase because of unfolding of GFP as a function of the number of residues detached from either the N or C terminus from the native Cycle3-GFP structure (Protein Data Bank ID code 1B9C) (22). The black line with the shaded yellow region marks the measured contour length increase of 76.6 ± 0.3 nm. (b) Cycle3-GFP crystal structure (22). The regions marked in blue and red correspond to the C-terminal and N-terminal solution of the calculation in a.

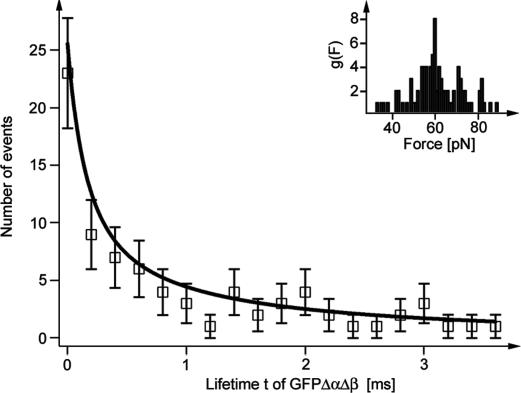
Lifetime Measurements. In this study, we observed a stable GFP intermediate (GFPΔαΔβ) with a lifetime under load in the microsecond to millisecond range. To investigate the lifetimes we performed measurements with a fast atomic force microscope cantilever (Bio-Lever type A, Olympus) by using a sampling rate of 20 kHz. We analyzed the cantilever relaxation phase after the unfolding of GFPΔα for deviations from the temporal relaxation of an overdamped cantilever. Under our experimental conditions, this relaxation phase is completed within three data points. Relaxation phases of three data points were therefore counted as zero lifetime events, whereas longer relaxation phases with intermediate levels were counted with a precision of ±50 μs (compare with Fig. 4b) to yield the lifetime histogram of GFPΔαΔβ (see Fig. 5).

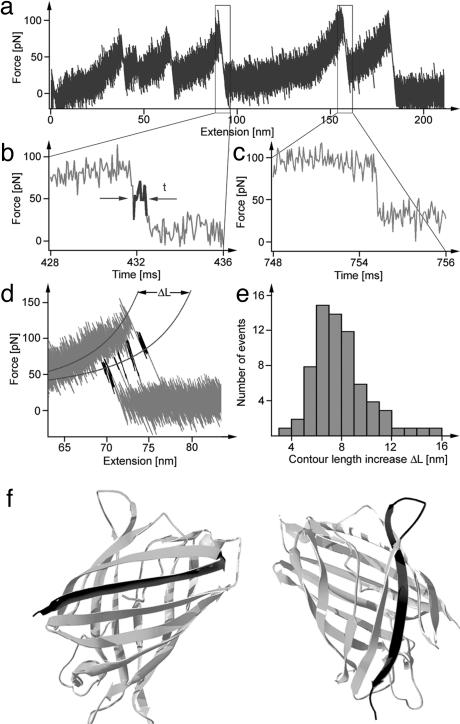
Fig. 4.

Another short-lived intermediate. (a) DdFLN1-5-GFP force-extension trace measured at 10 kHz bandwidth with an Olympus type A Bio-Lever (resonance in water at 8.5 kHz). (b) Detail of the time course of the cantilever relaxation phase after unfolding of GFPΔα. The region marked in black indicates the presence of a short-lived intermediate state. (c) Detail of the time course of the cantilever relaxation phase after unfolding of a DdFLN domain. No deviations from normal damped oscillator relaxation were detected. (d) Six force-extension traces measured with DdFLN1-5-GFP and superimposed in the region of GFPΔα unfolding. The regions marked in black indicate the short-lived intermediate. All six intermediate levels fall on a WLC curve with a contour length increased by 6.8 nm. (e) Distribution of the contour length increase, ΔL, determined by WLC fits as shown in d. (f) Two possible structures of GFPΔαΔβ (light gray). Marked in dark gray are residues that unfold from the GFP barrel in the transition of GFPΔα to GFPΔαΔβ. (Left) A full β-strand detaches from the N terminus, and the folded GFP core comprises residues 25-230. (Right) A full β-strand detaches from the C terminus, and the folded GFP core comprises residues 11-209.

Fig. 5.

Lifetime distribution. Open squares indicate the distribution of measured lifetimes of GFPΔαΔβ. The black solid line shows a fit with a two-state model with Δx = 0.55 nm and τ₀ = 10 s (see Materials and Methods). (Inset) Distribution of forces acting on GFPΔαΔβ.

Interpretation of Lifetimes. The average measured lifetime of GFPΔαΔβ is <t>= 1.3 ms. The increase in force during this period at a pulling velocity of 300 nm/s is only 2 pN, which is in the range of 1% of the absolute forces acting on the intermediate. Thus, the forces acting on the GFP intermediate can be readily assumed constant. To interpret the distribution of observed lifetimes, the force dependence of lifetimes had to be included into the analysis. Poisson statistics predicts the probability to measure a certain lifetime t of the intermediate to

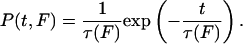P(t, F) is a function of the applied force because the average lifetime, τ(F), is a function of force. This average lifetime is predicted by Bell's formula, τ(F) = τ₀exp(-FΔx/k_BT), where τ₀ denotes the unloaded lifetime and Δx denotes the potential width as described above (23). This formula has recently been shown to describe protein unfolding kinetics very well (24). In our experiments, the forces acting on GFPΔαΔβ obey a broad distribution, g(F), determined by the unfolding forces of the preceding peak. We derived this force distribution, g(F), from the force distribution of the unfolding of GFPΔα shown in Fig. 1e. We corrected the forces of this distribution by the calculated force drop in a WLC polymer when its contour length is increased by 6.8 nm. By including the force distribution g(F) of acting forces (see Fig. 5 Inset), we arrive at a weighted probability to measure a certain lifetime of the structure:

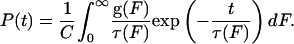The probabilities P(t) to measure a certain lifetime were calculated and fitted to the measured distribution of lifetimes (see Fig. 5) to obtain the unloaded lifetime τ₀ and the potential width Δx of the intermediate state GFPΔαΔβ.

Estimating Transition Barrier Heights. The barrier height ΔG for a transition state from a conformational state can be estimated by means of the Arrhenius equation ΔG = -k_BT·ln(τ_A/τ₀), where τ₀ denotes the unloaded lifetime of the state and 1/τ_A is the Arrhenius frequency factor. For protein dynamics, τ_A has a value of 10^-9 s (25). We chose this value for all barrier height estimations.

Results and Discussion

Single Domain Force Spectroscopy. In mechanical, single-molecule unfolding experiments, it is crucial to distinguish unfolding events from multiple molecule interactions and nonspecific interactions between tip and substrate. The design of modular proteins with multiple repeating subunits leading to a characteristic sawtooth-shaped mechanical unfolding pattern has proven a robust strategy to detect and measure unfolding forces of the individual subunits (9, 26-28). In the present experiment, we have combined this strategy with the possibility to investigate single protein domains (5). Therefore, we sandwiched GFP between four N-terminal and four C-terminal Ig domains of human cardiac titin to create an Ig8-GFP chimera protein (Fig. 1a). Force extension curves of this construct should exhibit a clear sawtooth pattern because of the unfolding of the Ig domains (9) and an additional unfolding event reflecting GFP unfolding. Force extension curves from this construct are shown in Fig. 1b. In all traces at extensions >80 nm, the well studied sawtooth pattern of titin domain unfolding is visible (colored in blue). In contrast to curves obtained from an Ig8 construct lacking the GFP insert (9), at shorter extensions and lower forces, an additional unfolding event appears (colored in green). The length increase associated with this unfolding event is 2.5 times larger than that of an individual Ig domain. Comparing the number of amino acids constituting GFP (238 amino acids) with that folded in an Ig domain (89 amino acids), we arrive at a length for the unfolded polypeptide chain of GFP longer by a factor of 2.7 as compared with Ig domains, which suggests that the observed unfolding event reflects GFP unfolding. Titin Ig domains exhibit a much higher unfolding force than GFP; thus, GFP unfolding events always occur at small extensions close to the surface where nonspecific interactions often mask true unfolding events. To rule out any nonspecific contributions, we designed a construct comprising five Ig domains from the actin crosslinker DdFLN with GFP sandwiched between domain 3 and 4 (DdFLN1-5-GFP) (Fig. 1c). The Ig domains of DdFLN exhibit unfolding forces in a range between 40 and 100 pN (5), and GFP unfolding in this chimera construct should occur at higher extensions after the weakest Ig domains have already unfolded. In force extension traces obtained with DdFLN1-5-GFP (Fig. 1d), the GFP unfolding events are indeed shifted toward higher extensions. Nonetheless, both the length gain and the unfolding force are identical to Ig8-GFP. Results for the two constructs are therefore in agreement, and we conclude that at pulling velocities of 300 nm/s GFP on average can bear mechanical loads of 104 ± 40 pN (Fig. 1e) before it unfolds.

Unfolding of the β-Barrel Occurs from an Intermediate. Evans and Ritchie (29) have shown that the distribution of unfolding forces (Fig. 1e) contains information about the underlying energy profile, that is, both the lifetime of the domain in the absence of force τ₀ and the N-terminal -to-C-terminal distance from the folded structure to the transition state Δx. We have used a Monte Carlo simulation to extract τ₀ and Δx from the data (open bars in Fig. 1e). We get a good fit to our histogram by using a value of 0.28 ± 0.03 nm for Δx and 14 ± 6 s for τ₀. A value of 0.3 nm for Δx is typical for β-sheet domains (9, 30, 31). However, a lifetime of 14 s stands in stark contrast to values of 10¹⁰ s obtained from solution experiments (12). Moreover, comparing the folding time of GFP of 600 s (10, 11) with our measured lifetime of 14 s suggests the state before mechanical unfolding has a positive free energy of at least 3.7 k_BT in contrast to ΔG = -16 k_BT, which is determined from bulk measurements (12). This seeming discrepancy can be resolved if we consider that the GFP structure unfolding at 104 pN may not be the native state but an intermediate state, during which part of the structure has already unfolded at lower forces. Clear evidence for the existence of such an intermediate comes from measuring the contour length increase ΔL upon GFP unfolding (see Materials and Methods). Force spectroscopy has an excellent length resolution down to the single amino acid (5, 6). The average length increase, ΔL, we measure is 76.6 ± 0.3 nm, n = 87 (Fig. 1f). If all of the 227 amino acids resolved in the x-ray structure of Cycle3-GFP (amino acids 4-230) by Battistutta et al. (22) contributed to the measured length increase, the expected value for ΔL would be 79.4 nm. This difference is well resolvable with our instrument, and it shows that the force-bearing structure unfolding at 104 pN is smaller than the native structure. A more detailed analysis, for which we plotted the calculated ΔL for structures that lack a certain amount of amino acids from either the N terminus (red) or the C terminus (blue) of the crystal structure of GFP is shown in Fig. 2a (see Materials and Methods for details). This analysis suggests two possible structures for the shorter intermediate state. The intersection points of the horizontal line indicating our measured value of ΔL = 76.6 ± 0.3 nm with the calculated curve in Fig. 2a lead to either seven amino acids removed from the N terminus or eight to nine amino acids removed from the C terminus. Intriguingly, the seven N-terminal amino acids constitute an α-helix that ends at the first β-sheet of the GFP barrel. The other possibility of eight to nine C-terminal amino acids detaching would require removal of half a β-strand (Fig. 2b). This possibility can be ruled out given the cooperative nature of β-strand breakage so far observed in mechanical experiments (5, 6). Here, we refer to the unfolding intermediate with the N-terminal α-helix detached as GFPΔα. It is important to note that single-molecule force spectroscopy allows us to measure precisely the number of amino acid residues constituting the folded part of an unfolding intermediate. However, we have no indication whether the structures of these intermediates will be native-like, as we assume in our study.

Can we observe detachment of the N-terminal α-helix directly in our data? To address this question, we filtered our data in the rising slope of the GFP unfolding peak to increase the force resolution. Both in the data of Ig8-GFP and DdFLN1-5-GFP we now observe consistently a hump-like transition at forces between 30 and 40 pN (Fig. 3). This transition is absent in curves obtained with DdFLN1-5 and Ig8 constructs lacking the inserted GFP domain (5, 9). In force curves with DdFLN1-5-GFP, on average, two to three weaker Ig domains unfold before the GFP domain unfolds (Figs. 1d, 3b, and 4a). These unfolding events before GFP unfolding exhibit the same hump-like transition (Fig. 3b), indicating that the structure that gives during the transition recovers quickly as soon as the force drops below 20 pN (within <1 ms). The hump vanishes after GFP has unfolded. Near-equilibrium transitions are often characterized by hump-shaped force plateaus in force-extension traces (6, 19, 32), similar to the one we observe here. We used an equilibrium two-state model (19) to fit the hump-like transition (black curves in Fig. 3 a and b). The fit yields a contour length increase ΔL of 3.2 ± 1 nm (n = 44) and an equilibrium free energy for this transition of ΔG = 22 ± 4k_BT (n = 44). A value of 3.2 ± 1 nm for the length increase during this transition is very close to the expected length gain upon unfolding of the N-terminal α-helix (2.9 nm) that is calculated from the GFP structure. This finding strongly supports our picture that the N-terminal α-helix detaches before the GFP barrel breaks. Remarkably, the energy required for the detachment of the N-terminal α-helix is even slightly higher than the total free energy (16 k_BT) of the GFP fold (12). The GFP structure lacking the α-helix (GFPΔα) is therefore thermodynamically unstable. This finding is in good agreement with its short unloaded lifetime of 14 ± 6 s determined above from the distribution of unfolding forces. Moreover, deletion studies by Li et al. (33) of GFP have shown that removal of the N-terminal α-helix leads to nonfluorescent protein. Our results now provide an explanation for this result. Because GFPΔα has a positive folding free energy of at least 3.7 k_BT above the unfolded state, a construct lacking the α-helix will not fold into a barrel-like structure. Thermodynamic stability of GFP is dominated by the presence of the N-terminal α-helix. Mechanical stability on the subsecond timescale yet depends on the integrity of the β-barrel. For Ig domain 27 from titin, Marszalek et al. (6) have reported an unfolding intermediate during which a short β-strand detaches before the major mechanical unfolding event. In that study, however, the intermediate state governing mechanical stability was still thermodynamically stable (34). In contrast, our data demonstrate that mechanical experiments can be used to drive a protein into metastable states that are not populated thermally.

β-Strand Breakage Leads to Another Short-Lived Intermediate. In the data, when displayed with the full measurement bandwidth (10 kHz) of our cantilevers (Fig. 4a), we consistently observe deviations from the expected overdamped time course in the cantilever relaxation phase after the unfolding of GFPΔα (Fig. 4b). These deviations occur both in Ig8-GFP (see traces in Fig. 3a) and in DdFLN1-5-GFP (Fig. 4 b and d). We did not observe such deviations in the relaxation phase of two-state unfolders, like the Ig domains from titin or DdFLN (Fig. 4c). These deviations therefore indicate the existence of yet another short-lived intermediate state during GFP unfolding, which is stable only on the submillisecond timescale at the forces applied. In Fig. 4d we superimposed six traces exhibiting this intermediate level (marked in black) in their relaxation phase. A similar superposition strategy led to the detection of an unfolding intermediate in bacteriorhodopsin (35). Because the unfolding of GFPΔα has a broad force distribution (Fig. 1e), the intermediate level must also occur at different forces and extensions. Yet all six intermediate levels fall on a force extension curve predicted by the WLC of polymer elasticity, indicating that the structured portion of this additional intermediate also contains a well defined number of residues. A histogram of contour length increases during the transition from GFPΔα to the new short-lived intermediate shows an average lengthening of 6.8 ± 0.6 nm (Fig. 4e). Mapping this length increase to the structure of GFP (analogous to the method shown in Fig. 2a), we arrive at two possible structures for the intermediate state. Again, in our analysis we only consider possible structures in which a complete secondary structural element detaches from the barrel, and we thus disregard structures with partially frayed β-sheets at both ends. The two structures are shown in Fig. 4f and correspond to the GFP barrel lacking a full β-strand from either the N or the C terminus. Choosing between those two structures requires further experiments with GFP mutants. We will call the folded portion of this intermediate GFPΔαΔβ.

The observation of the short-lived intermediate GFPΔαΔβ in the relaxation phase of the cantilever sheds new light on the interpretation of unfolding forces commonly used in force spectroscopy experiments. First, it becomes obvious that the relaxation phase of the cantilever spring does not impose a “blind window” on our experiments as assumed in earlier studies (9). In contrast, every intermediate state exhibiting structural stability will interfere with the free relaxation of the cantilever and leave a signature in the force curve. Lifetimes of these intermediates can be extremely short, because they are subject to forces determined by the force of the previous unfolding event, the length increase, polymer elasticity, and the cantilever spring constant. We anticipate that increasing the measurement bandwidth into the microsecond timescale (36) or below will lead to the discovery of intermediate states, even in domains hitherto believed to be two-state unfolders.

Another aspect of these measurements concerns the analysis of unfolding forces for such short-lived intermediates. During a lifetime in the submillisecond range of the intermediate, the pulling experiment can be considered quasistatic. Therefore, the force will be approximately constant during this time. Consequently, unfolding of a short-lived intermediate must be treated as a constant force experiment. Unfolding force histograms in such a case will lead to trivial force distributions because the force remains constant during the short lifetime of the intermediate. All of the important information now resides in the lifetime distribution of the intermediate state (37).

The lifetime distribution of GFPΔαΔβ is given in Fig. 5. It appears strongly multiexponential. This distribution, however, does not reflect nonexponential protein unfolding kinetics but can be entirely explained by a single Poisson process. The multiexponential behavior is a consequence of the broad distribution of forces by which the structure is loaded until it breaks. This distribution (Fig. 5 Inset) is entirely governed by the unfolding force distribution of GFPΔα (Figs. 1e and 4d). The solid line in Fig. 5 is a superposition of lifetimes calculated for the measured force distribution. Our analysis yields values of 0.55 ± 0.1 nm for the position of the transition state Δx and a range of 1-100 s for the unloaded lifetime at zero force τ₀.

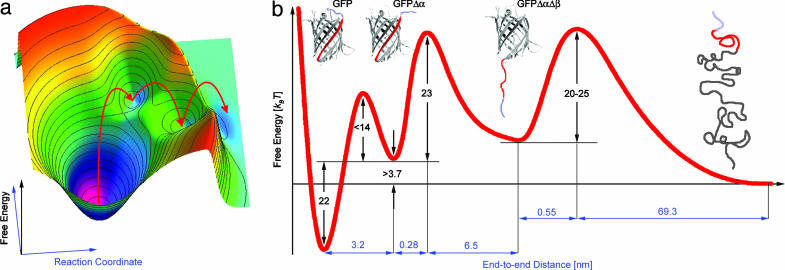
GFP Unfolding Is Governed by a Rough Energy Landscape. By combining our results, we are now able to reconstruct detailed features of a section through the energy landscape of GFP along a path determined by the application of mechanical force. A cartoon of this path is shown in Fig. 6a. Starting from the completely folded structure in the global minimum, the pathway is biased along the N-terminal-to-C-terminal direction. Upon unfolding of the N-terminal α-helix, we arrive at a local minimum (GFPΔα). It is important to note that now the direction of the pathway changes, because the protein will respond to the detachment of the α-helix by turning and reorienting along the new N-terminal-to-C-terminal direction determined by the connecting line between the first structured residue at the N terminus and the last structured residue at the C terminus of the folded portion of the intermediate. The new bias induces detachment of a β-strand leading to the second local minimum (GFPΔαΔβ). Again, the protein will reorient and the direction of the path changes. From here, the protein will transition directly into the completely unfolded state, at least at the current temporal resolution of our experiment. In Fig. 6b we show a projection of the zig-zag-shaped unfolding pathway onto one coordinate. This projection summarizes our current picture of the barrier heights and positions along the mechanical GFP unfolding pathway. Yet, it is important to bear in mind that the reaction coordinate changes from minimum to minimum as explained above. For simplicity, the distances in this diagram contain our directly measured contour length increases upon detachment of amino acids. Of course, these numbers will be smaller at small stretching forces, at which the polymer will not be completely stretched.

Fig. 6.

Free energy surface. (a) Cartoon of the multidimensional energy landscape of GFP. The red arrows indicate the course of the mechanical unfolding pathway. (b) Projection of the energy landscape along the unfolding pathway onto one reaction coordinate.

The first transition from GFP to GFPΔα occurs close to equilibrium. From our data, we can extract a difference of ΔG = 22 ± 4k_BT between GFP and GFPΔα. The contour length increase upon detachment of seven amino acids is ΔL = 3.2 ± 1 nm. From our equilibrium data, we cannot conclude directly the position or height of the transition barrier. However, from our estimate for the refolding time of the α-helix of <1 ms we can estimate an upper limit for this barrier height of 14k_BT.

The position of the barrier for the transition from GFPΔα to GFPΔαΔβ is 0.28 ± 0.03 nm from the minimum, with an activation barrier of 23 k_BT. Detachment of the β-strand from the barrel leads to an additional contour length increase of 6.8 ± 0.6 nm. From the GFPΔαΔβ state, GFP unfolds into the completely denatured state leading to a contour length increase of 69.8 nm. The associated barrier height is 20-25 k_BT at a position of 0.55 nm.

Conclusion

Our experimental results show that the mechanical unfolding of GFP proceeds by means of at least two metastable intermediate states, with unloaded lifetimes on the second timescale. The rough energy landscape we reconstructed from our data shows deep local minima reflecting largely structured, however metastable, intermediates with a positive free energy compared with the unfolded state. It appears that such intermediates are much more likely to occur in topologically complex proteins, like GFP, as compared with simpler, fast-folding two-state proteins. We propose that force spectroscopy is an ideal tool to investigate energy landscapes of complex proteins not amenable to bulk studies because of their slow kinetics or tendency of aggregation. The detailed picture we have obtained for the mechanical unfolding pathway will allow the tailoring of GFP mutants with altered stability that are useful for application as molecular force sensors. Such mechanical stability mutations have already been successfully realized with other proteins (31, 34, 38). A precise correlation of the breakdown of fluorescence with the breakdown of structure is an important task for the future.