Electron transfer between hemes in mammalian cytochrome c oxidase

Abstract

Fast intraprotein electron transfer reactions associated with enzymatic catalysis are often difficult to synchronize and therefore to monitor directly in non-light-driven systems. However, in the mitochondrial respiratory enzyme cytochrome oxidase aa₃, the kinetics of the final electron transfer step into the active site can be determined: reverse electron flow between the close-lying and chemically identical hemes a₃ and a can be initiated by flash photolysis of CO from reduced heme a₃ under conditions where heme a is initially oxidized. To follow this reaction, we used transient absorption spectroscopy, with femtosecond time resolution and a time window extending to 4 ns. Comparison of the picosecond heme a₃-CO photodissociation spectra under different redox states of heme a shows significant spectral interaction between both hemes, a phenomenon complicating the interpretation of spectral studies with low time resolution. Most importantly, we show that the intrinsic electron equilibration, corresponding to a ΔG⁰ of 45-55 meV, occurs in 1.2 ± 0.1 ns. This is 3 orders of magnitude faster than the previously established equilibration phase of ≈3 μs, which we suggest to reflect a change in redox equilibrium closely following CO migration out of the active site. Our results allow testing a number of conflicting predictions regarding this reaction between both experimental and theoretical studies. We discuss the potential physiological relevance of fast equilibration associated with this low-driving-force redox reaction.

Electron transfer (ET) reactions in proteins occur on time-scales ranging from subpicosecond to millisecond. Determination of the pathway and dynamics of ET and their regulation is of crucial importance for the understanding of many catalytic reactions. The dynamics of biological ET has been extensively studied in naturally photoactive proteins and in particular in photosynthetic reaction centers, where even the fastest reactions can naturally be synchronized by populating their excited-state precursors using ultrashort light pulses (1, 2). Monitoring intraprotein electron flow in other bioenergetic systems must rely on synchronization of nonnaturally photoactivatable electron sources. In fact, to our knowledge, the direct observation of such ET has been limited to microseconds and slower. Here we set out to determine the intrinsic rate of electron equilibration between the two chemically identical hemes of mitochondrial cytochrome c oxidase (CcO), a key step in respiratory oxygen reduction. The kinetics of this ET step are currently a subject of controversy among experimentalists (3, 4), and a broad range of rates has been predicted in theoretical studies (5-7).

CcO is the membranous protein complex that reduces molecular oxygen to two water molecules in mitochondrial respiration. During this process, it accepts electrons from one side of the mitochondrial membrane and protons from the other and thus creates an electrochemical proton gradient across the membrane. In addition, this enzyme is a proton pump, using the energy released during the oxygen chemistry to transfer four additional protons across the membrane. The resulting proton gradient is used by ATP-synthase to synthesize ATP, the preeminent energy storage molecule. A number of crystallographic structures of CcO of mammalian (bovine heart) (8) and bacterial (9, 10) origin have been solved at high resolution.

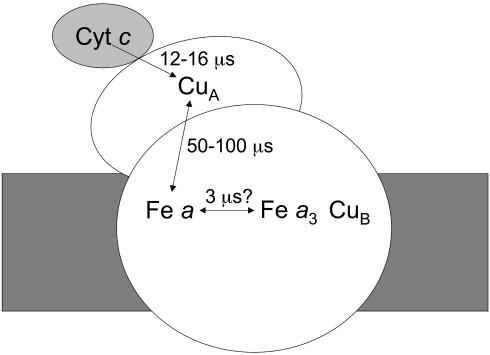
CcO contains four redox-active cofactors, two a-type hemes, and two copper centers, and accommodates four electrons in its fully reduced (FR) form. During catalysis, the enzyme accepts electrons from soluble ferro-cytochrome c (Scheme 1). The primary acceptor is the diatomic copper center Cu_A (11), bound to a polar domain of subunit II. In the physiological electron pathway, Cu_A transfers electrons to high-spin heme a located, at a distance of 19.5 Å, in subunit I in the intramembrane moiety. Heme a serves as an electron donor to the so-called binuclear center, where the actual oxygen chemistry takes place, and which is formed by low-spin heme a₃ and the copper atom Cu_B. Cu_B plays a crucial role in the redox chemistry and also serves as a “gate” for ligand transfer to and from heme a₃. The two hemes approach each other at a minimal edge-to-edge distance of 4.7 Å and make an interplanar angle of ≈100° (8). The intraprotein ET chain operates at low driving forces: free energy differences for ET between the hemes and CuA are in the tens of meV range, and the equilibration constants can be “fine tuned” by the environment of the redox factors.

Scheme 1.

Pathway for ET from cytochrome c to the active site of CcO.

ET into CcO using external synchronizable electron sources has been studied by using a variety of techniques, including pulse radiolysis (12), ruthenium-containing dyes (13), and modified cytochromes (14, 15). Using these methods, it has been established that, starting from the oxidized enzyme, CuA is reduced and reoxidized on the microsecond timescale, as indicated in Scheme 1. However, ET between hemes cannot be studied in this way, because it occurs faster than ET from CuA to heme a, presumably due to the great difference in distance between these redox cofactors. Insight into the intrinsic interheme rate of ET is needed, however, to understand the sequence and rate limitation of events during the binding of oxygen and its four-electron reduction. For instance, several models have invoked an important role of ET to heme a₃ in the kinetic trapping of oxygen (16) and gating of proton translocation (17), albeit without explicitly discussing the timescale of these processes.

A different experimental approach makes use of the possibility of reversing electron flow. Here, photodissociation of CO bound to the mixed valence (MV, 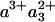-CO) enzyme instantly lowers the apparent midpoint potential of heme a₃, causing a flow of electrons from the binuclear center to heme a and to Cu_A (18-24). In the early 1990s, using this method with microsecond instrumentation, in studies using subsequently single-wavelength kinetics in the heme α and Soret bands (22) and full spectral characterization in the Soret region (23), two phases with time constants of 3-5 and 77 μs were observed and assigned to ET between heme a₃ and heme a and between heme a and Cu_A, respectively. The 3-μs phase was then thought to reflect the fastest ET process in CcO.

More recently, doubt was shed on this assessment by Verkhovsky et al. (3), based on a detailed comparison of the “photolysis” spectra of the FR (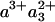-CO) and MV-CO states measured with submicrosecond time resolution. From the difference of these spectra, the authors (3) proposed that in MV-CO, ≈20% oxidation of heme a₃ should happen faster than 3 μs and presumably faster than 30 ns, because no additional ET had been observed in Einarsdóttir and coworkers' (14) work with 30-ns time resolution (24, 25). In this view, the intrinsic interheme ET rate should be in the subnanosecond-nanosecond time regime, as also predicted by the semiempirical distance ruler of Dutton and coworkers (26). The slower 3-μs phase would then result from a secondary effect that modifies the redox equilibrium between the two hemes.

This view was subsequently challenged by Brzezinski and coworkers (4). From their failure to observe nanosecond ET-attributable phases with a temporal resolution of 10 ns, and from the spectral properties of the “photolysis” spectra, they concluded that all interheme ET occurs in microseconds. In the present work, we carefully explored the timescale up to 4 ns with femtosecond time resolution in both α and Soret spectral regions upon selective excitation of carbonmonoxy-heme a_3. We present clear evidence for nanosecond ET upon photolysis from the MV-CO complex. In addition, the influence of steady-state spectral interactions between the two hemes on the CO dissociation spectrum is established, implying that the two hemes cannot be strictly treated as independent entities.

Materials and Methods

Sample Preparation. The protein was purified from beef heart mitochondria by using van Buuren's method (27) with minor modifications. CcO was solubilized in 0.1% β-dodecylmaltoside/50 mM Tris, pH 7.4, and then stored at -80°C. The sample was thoroughly degassed in a gas-tight vessel, and ≈100 μl was transferred to a degassed gas-tight optical cell (Hellma, Müllheim, Germany; 117.007 QS, optical path length, 1 mm) sealed with a rubber septum. Two-electron reduced MV CcO was obtained by overnight incubation of the protein in 1 atm (1 atm = 101.3 kPa) CO at 4°C. For the FR CO-bound complex, the sample was thoroughly degassed and 20 mM sodium dithionite (identical spectroscopic results were obtained by using 10 mM sodium ascorbate) was added as reductant and equilibrated with 1 atm CO. The redox state of the proteins was followed by absorption spectroscopy by using a Shimadzu 1601 UV-VIS spectrophotometer. The enzyme concentrations were 45 and 150 μM for measurements in the Soret and α band, respectively. After each experiment, it was spectroscopically verified that the redox state was unchanged.

Experimental Procedures. Multicolor transient absorption pump-probe spectroscopy (28) was performed with a 55-fs pump pulse centered at 590 nm and a <30-fs white light continuum probe pulse, at a repetition rate of 30 Hz. The beams were focused in the sample to ≈50 μm, yielding an excitation volume of ≈2 nl per shot. The sample cell was translated at ≈1 Hz and an amplitude of ≈2 cm, in a direction perpendicular to the beam. In this way, the excitation volume of subsequent pulse pairs did not overlap, and full rebinding of CO (occurring on the 10- to 30-ms timescale; ref. 24) between excitation of the same sample volume is assured.

The probe continuum was generated by using the fundamental beam of the laser system, which was centered at ≈615 nm. For this reason, the required low noise could not be obtained around 615 nm, and the α band data could be exploited in the spectral region <606 nm. The probe beam is split into test and reference beams. The polarization of the pump pulse could be rotated with respect to that of the continuum probe pulse with a half-wavelength plate. In the α band experiments, noise due to scattering of the pump pulse was avoided by setting the polarization of the pump beam perpendicular to that of the probe beam and filtering the scattered light with a polarizer. The system was equipped with a delay line allowing temporal delays up to 4 ns (corresponding to an optical path-length difference of 1.2 m). The alignment of the delay line was verified by using CO-myoglobin. Full spectra of the test and reference beams were recorded by using a combination of a polychromator and a charge-coupled device camera. During each experiment, data were accumulated corresponding to ≈10⁵ pulse pairs in the whole sample volume. All experiments were carried out at 21°C.

Data Analysis. Basic data matrix manipulations and presentation were done with matlab (Mathworks, Natick, MA). The absorbance changes were treated by using the SPLYMOD algorithm (29), with a matlab interface developed by Morgan and Verkhovsky and detailed in ref. 30. Singular value decomposition was used to subtract baseline fluctuations in some cases.

Results

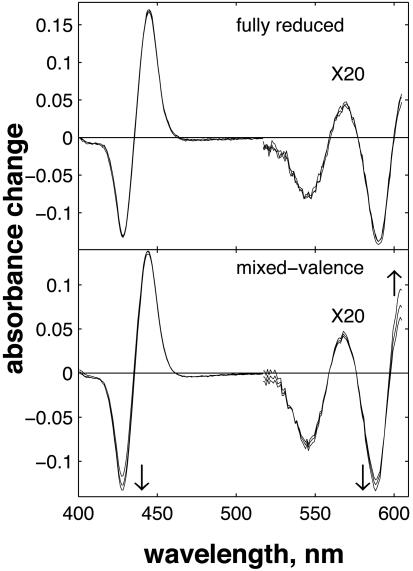
We recorded optical absorbance changes after CO photolysis in the FR and MV states of CcO on the timescale up to 4 ns. In the case of the FR enzyme, spectral changes associated with the subpicosecond (31) and presumably ballistic (32) transfer of CO to CuB and the full decay of the excited states of both hemes in <30 ps have been described (32, 33). In the following, we will refer to the spectrum following these decay phases as the photolysis spectrum and focus on the subsequent spectral evolution. The overview of the transient spectra of Fig. 1 clearly shows that for MV, there is significant spectral evolution after photolysis, whereas for FR, the spectrum hardly changes, implying a significant difference in the dynamics involving the hemes.

Fig. 1.

Evolution of the spectrum after CO photolysis in the FR (Upper) and MV (Lower) states of CcO. Time points: 40 ps, 1 ns, and 4 ns. Pump and probe pulses were perpendicular. The α band region measurements, obtained in separate experiments, were normalized to the Soret band experiments by using an overlapping region near 550 nm and multiplied by 20.

Photolysis Spectra. To be able to take into account photoselection effects, the experiments in the Soret region were performed under both parallel (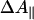) and perpendicular (ΔA⊥) polarization of the pump pulse with respect to the probe pulse. Generally, for hemes, because of the near two-fold symmetry of the porphyrin ring, the two in-plane optical transitions are thought to be close-lying or “degenerate”, and therefore the polarization effects are expected to be small. For FR, small differences were observed in the photolysis spectrum (data not shown). The extrema of the spectra were at the same positions, but the isosbestic points were shifted by ≈1 nm. At the extrema, 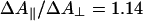, close to the value reported for dissociated carboxy-myoglobin, but somewhat lower than the theoretical value for planar (two-fold degenerate) optical transitions of 4/3 (34). These findings indicate that the two transitions composing the Soret band of heme a₃ are not completely degenerate, indicating asymmetry in the heme environment. Interactions between the optical transitions of hemes a and a₃ (see below) may also contribute to these observations. Unfortunately, scattering from the pump-pulse around 590 nm precludes collection of high-quality spectra under parallel polarization conditions over the whole α band region, and a similar assessment of polarization effects was not possible.

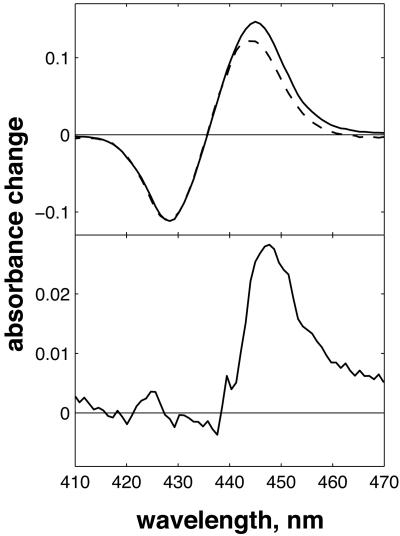
Significantly larger differences in spectral shape were found between CO photolysis spectra of the FR and MV states of CcO (Fig. 2). To eliminate polarization effects, here the data are isotropically represented as 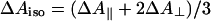, corresponding to magic angle configuration. To take into account incomplete formation of the MV state (a small fraction remained oxidized and did not contribute to the signal at t >30 ps), the spectra were normalized at the absorption minimum at 428 nm. Even though the spectra coincide in the blue region, differences are observed at λ>440 nm, as shown in Fig. 2 Lower. This difference spectrum deviates strongly from that expected for a₃→a ET, which should have its main features at λ < 440 nm (see below). Thus, whereas interheme electron equilibration appears insignificant before 30 ps, considerable spectral differences are observed in the (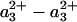-CO) photolysis difference spectrum. Hence, the redox state of heme a influences this spectrum, an observation pointing to spectral interactions between the two hemes; i.e., the charges on each heme contribute to the electronic absorption spectrum of the other heme, and the electronic structure of the aa₃ complex cannot be strictly considered as that of the sum of the individual hemes. Similar spectral interactions have been proposed (35) from variations in the spectra of heme a under different configurations of the active site and from variations in the spectrum associated with CO migration out of the active site under different redox state of heme a and Cu_A (25).

Fig. 2.

CO photolysis spectra in CcO, obtained from extrapolating global fits to the data at t >30 ps to t = 0. (Upper) CO photolysis spectra in FR (solid line) and MV (dashed line) states, normalized at 428 nm. Both spectra are calculated to be isotropic (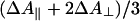). (Lower) the difference spectrum.

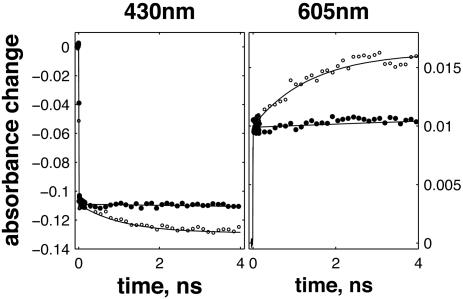
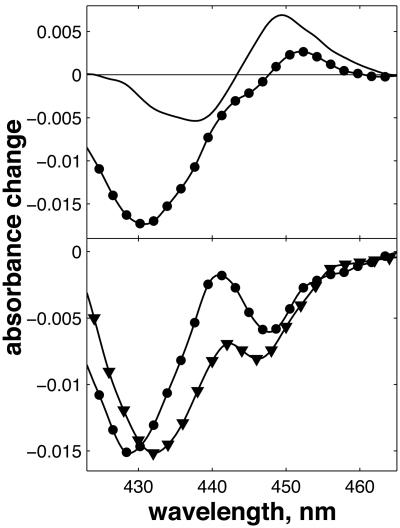
Spectral Evolution and ET. For the case of the FR enzyme, after photolysis, the kinetics at all wavelengths stay almost unchanged during the whole time span of 4 ns (Fig. 3, filled circles). Only in the Soret region, a small but reproducible, yet unassigned, phase with a time constant 100-200 ps was observed. The maximal amplitude of this phase was more than five times smaller than that of the 1.2-ns phase observed in MV-CO (see below). By contrast, in the case of the MV enzyme, we observed a substantial evolution of the spectrum on this timescale (Figs. 1 and 3, open circles). By fitting these data separately in the Soret and α regions, using a global multiexponential procedure, we found that they can be adequately described by a single exponential component of 1.2 ns in both spectral regions. The spectral shape of the nanosecond component is shown as dots in Fig. 4. We modeled this spectrum as a (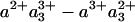) difference spectrum, i.e., assuming that heme a₃ is oxidizing and heme a reducing with a 1:1 ratio, using the basis set of the a and a₃ hemes absorbance from Liao and Palmer (36). The best correspondence between the experimental and the model spectra was obtained by assuming a quantum yield of this ET process of 11% for the α band and 16% for the Soret band, as determined by normalizing the corresponding photodissociation spectra to the steady-state photodissociation spectra. The difference in the calculated extent of heme a reduction in the two spectral regions may be due to photoselection effects, differences between steady-state and time-resolved difference spectra that influence the normalization involving the CO dissociation spectrum, and interactions among hemes (see below).

Fig. 3.

Kinetics after photolysis of CO at 430 nm (Left) and at 605 nm (Right) of the FR (filled circles) and MV (open circles) state of CcO, normalized at t = 30 ps.

Fig. 4.

The spectrum of the 1.2-ns component in the Soret (Left) and α (Right) regions is represented as dots. The solid line is the calculated difference spectrum heme a₃ - heme a. The estimated extent of the ET between hemes is 11-16%.

The striking similarity of the measured 1.2-ns component and the model spectrum implies that the component can safely be ascribed to a₃→ a ET. The determined extent of ET implies that after CO dissociation (and when CO is presumably bound to CuB), the difference in free energy between the states 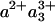and 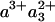is 45-55 meV.

Discussion

Using sensitive pump-probe transient absorption spectroscopy with a time window out to several nanoseconds, and the concept of back-flow ET, we have been able to establish the intrinsic timescale of electron injection into the active site of CcO at 1.2 ns. This value probably corresponds to the highest rate directly established for a physiological ET reaction in a nonnaturally photoactivatible system.

ET on the nanosecond timescale in bovine CcO was predicted indirectly, by comparing the transient absorption spectra in the α band region after CO photolysis from the FR and MV states measured with submicrosecond time resolution (3). These spectral differences were confirmed, their assessment extended to the Soret region, and the timescale of the spectra trimmed down to ≈10 ns (at -20°C) by Namslauer et al. (4). These authors did not observe spectral evolution on the supra-10-ns timescale and mentioned that they could not observe any absorption changes associated with ET on a timescale below 600 ps using femtosecond spectroscopy. Our present assessment that the “missing” ET component has a time constant of 1.2 ns can be considered consistent with these findings, because it falls in the time-window gap not investigated in ref. 4. However, we clearly do not share their conclusion that no submicrosecond interheme ET occurs. The relatively small amplitude of the experimentally measured component, compared with that of the CO photolysis spectrum (Fig. 1), may additionally have played a role in the difficulty to assess this phase.

We modeled the spectral shape of the determined component using a basis set of heme a and heme a₃ steady-state reduced-minus-oxidized difference spectra. Several different decompositions were discussed by Namslauer et al. (4) in the framework of their different FR-CO and MV-CO transient spectra on a much longer timescale but were judged not to correspond well with interheme ET as an origin. Presumably, this is due to the added complexity of spectral interactions, as documented (25, 35), and as witnessed to play a role in the heme a₃ photodissociation spectra in a direct way by our CO photolysis spectra (Fig. 2).

The spectrum associated with the 1.2-ns component and the corresponding model spectrum display considerable differences from that of the 3-μs component (23) also ascribed to interheme electron equilibration. As will be discussed below, these differences can be well understood in terms of synchronous CO migration associated with the latter phase, a finding that further strengthens the assignment of the 1.2-ns phase.

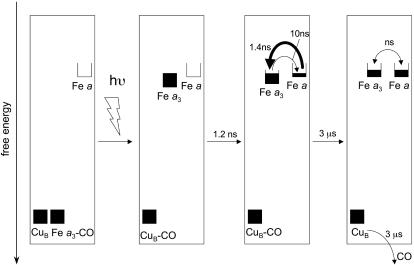
The scheme of Fig. 5 summarizes the interpretation of our findings. Initially, heme a₃ and Cu_B are the only reduced cofactors. Light-induced transfer of CO from heme a₃ to Cu_B (in <1 ps; ref. 31) lowers the effective midpoint potential of heme a₃ to a value close to that of heme a. Subsequently, redistribution of the electron density takes place by partial ET from heme a₃ to heme a, in 1.2 ns. Our experiments indicate that this phase corresponds to oxidation of 11-16% of the initially reduced heme a₃. Assuming that the 1.2-ns phase corresponds to full equilibration, this implies that the equilibrium constant K is ≈6-9, and that the difference in free energy ΔG⁰ between the states 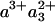Cu_B-CO and 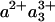Cu_B-CO amounts to ≈45-55 meV. The measured equilibration rate of (1.2 ns)^-1 corresponds to the sum k_for+ k_back of the microscopic rate constants of forward (a→a₃) and backward (a₃→a) ET and K = k_for/k_back. Taking these together, we determine k_for and k_back at (1.4 ns)^-1 and (10 ns)^-1, respectively. We conclude that the microscopic time constant of heme a₃ reduction by heme a is ≈1.4 ns.

Fig. 5.

Scheme summarizing our findings. The boxes reflect filling of the reduced forms of the redox centers. Starting from the MV-CO complex, CO photolysis from heme a₃ results in its binding to CuB and a rise of the effective midpoint potential of heme a₃. Electron redistribution between the two hemes according to the new equilibrium occurs in 1.2 ns. We suggest that the previously observed 3-μs ET phase (transition to rightmost box) reflects a modest change in redox equilibrium due to CO migration out of the active site.

Origin of the Previously Established Microsecond ET Component. As mentioned in the Introduction, an additional well established further equilibration phase, corresponding to oxidation of ≈25% of heme a₃, occurs with a time constant 3 orders of magnitude longer, ≈3 μs (22, 23). However, the spectral characteristics of this phase (23) differ significantly from the one assessed here as intrinsic equilibration and cannot be well described (4) by the model spectra of Liao and Palmer (36) used here. Under the hypothesis of the now-established 1.2-ns intrinsic equilibration time, Verkhovsky et al. (3) suggested that this phase is related either to a very slow protein relaxation or to CO migration out of the active site. For reasons outlined below, we favor the latter suggestion, as indicated in the right-most box of Fig. 5.

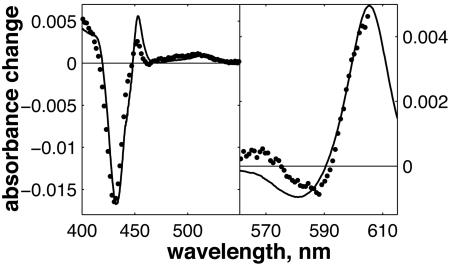
In the FR-CO complex, transient IR spectroscopy has shown that the Cu_B—CO bond is broken, and CO is presumably released by the protein, with a time constant of ≈1.5 μs (37). Einarsdóttir and coworkers (24) have shown that this phase is accompanied by a small shift in the optical spectrum of the 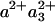state, presumably mostly due to the heme a₃ contribution, which is located closest to Cu_B. Assuming that similar CO release in the MV-CO complex takes place in 3 μs and gives rise to a similar spectral shift,‡ the total 3-μs spectral component can be described by adding this spectral shift to the “pure” ET component. This has been done by Namslauer et al. (ref. 4, figure in supporting information), where the ≈1.5-μs phase in the FR enzyme was added to the 3-μs component in the MV, and this sum was compared with different steady-state decompositions of heme absorbance. Fig. 6 shows that with the opposite approach, adding the ≈1.5-μs phase from ref. 24 to our measured nanosecond component compares favorably with the 3-μs ET phase shown in ref. 4. Thus, electron equilibration and CO migration would occur simultaneously, most likely because the free energy gap between the states 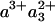and 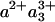would be lowered by CO migration. Because intrinsic equilibration is on the nanosecond timescale, this implies that this ET phase closely follows CO migration. Altogether, this proposal thus offers a consistent spectral interpretation of the ensemble of interheme ET phases observed after the photolysis of the MV-CO complex. Determination of the microsecond CO migration kinetics in the MV complex by infrared spectroscopy could further test this proposition.

Fig. 6.

Simulation of this spectrum associated with the 3-μs ET phase. (Upper) Solid line, the 1.5-μs phase in FR CcO taken from ref. 24; circles, the 1.2-ns ET component measured in the MV complex, taken from Fig. 4. The amplitude ratio between two phases was taken as 100% for the 1.5-μs FR phase and 25% for the 1.2-ns phase. (Lower) The sum of the 1.2-ns phase and the inverse (the sign convention in ref. 24 is the inverse of ours) of the 1.5-μs phase (circles) and the spectrum of the 3-μs ET phase shown in ref. 4. Solid lines between points are splines to guide the eye.

In this view, the 3-μs ET phase can thus be considered as an additional equilibration phase related to the need to use CO to initiate the reaction.

Mechanism of ET. The rate k of intraprotein ET can be described, in the nonadiabatic limit, as factorized into electronic and nuclear terms:

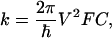1

where V is the electronic matrix coupling element, and FC is the Frank-Condon factor, describing the influence of the nuclear motions. In the classical Marcus description,

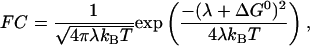2

where λ is the reorganization energy, k_B the Boltzmann factor, and T the temperature (38). The nuclear coupling V decreases strongly with distance between redox centers.

Different approaches have been used to estimate V and therewith the rate. One is to consider the protein as a homogeneous material and describe V = V⁰ exp(-βr), where r is the edge-to-edge distance of the redox partners. This approach, applied to a compilation of biological ET reactions, led to the semiempirical “ruler” advocated by Moser, Dutton, and coworkers (26, 39, 40), which directly correlates distance and optimal (activationless, ΔG⁰ = -λ) rate. Using this ruler and the interheme edge-to-edge distance of 4.7 Å (8), the thus-found optimal rate is ≈(1 ps)^-1. This value is ≈3 orders of magnitude faster than the observed rate. The difference could then be ascribed to substantial reorganization energy. Indeed, λ = 0.7 eV was invoked by Verkhovsky et al. (3) to predict a rate of (1.4 ns)^-1, exactly the rate that we observe. However, we note that the rather large value of 0.7 eV for λ is obtained from the temperature dependence of the ≈3-μs interheme ET equilibration phase (5, 41). If this phase is controlled by CO dissociation from CuB and migration out of the protein, as discussed above, then the temperature dependence reflects the activation barrier for CO dissociation from Cu_B rather than the ET reaction itself. In this case, the extremely close agreement between the thus-predicted (3) and measured (our work) rates may be fortuitous.

A more “intimist” approach to estimate the coupling V is to identify and calculate explicitly through-bond and through-space ET pathways between donor and acceptor (42). This strategy has been applied to interheme ET in CcO by several groups (5-7). Medvedev et al. (6) identified two major ET pathways, one major involving protein residues and one direct, and calculated the rate at (17 μs)^-1. Because this rate was obtained assuming a large λ (0.76 eV) (see above), the optimal rate could be ≈2 orders of magnitude faster, bringing it closer to, but still 2 additional orders of magnitude slower than, the measured rate. A very similar optimal rate of (140 ns)^-1 was calculated by Regan et al. (5) from a model including three through-protein pathways. Very recently, Tan et al. (7) combined pathway analysis and molecular dynamics simulations. By thus including the effect of thermal motions, the dominant pathway was found to be direct through-space interheme transfer. The estimated optimal rate of (3 ns)^-1 from this work is in remarkably good agreement with our experimental rate of (1.4 ns)^-1. Future work on the temperature dependence of this ET step may allow verification of the correspondingly predicted near-activationlessness of the reaction.

Potential Functional Implications. One might question the functional relevance of the final step of electron injection into the binuclear site being orders of magnitude faster than discrete established steps of the catalytic cycle of CcO. Under physiological turnover conditions, before oxygen binding, the enzyme is more likely near the two-electron reduced form than near the FR form (43). Oxygen can bind only to reduced heme a_3. For the two-electron reduced form, one electron resides on CuB, and one is in equilibrium between hemes a and a₃, which operate at very close redox potential. We can assume that O₂ is efficiently trapped if heme a₃ is in the reduced form at any time during the dwell time of a passage of unbound oxygen in the active site. If electron equilibration is slow compared with this dwell time, the trapping rate will be equal to the frequency of O₂ passages to the active site multiplied by the 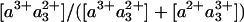equilibrium constant. However, if electron equilibration is fast compared with this dwell time, the trapping rate will be equal to the frequency of O₂ passages to the active site. Hence, once O₂ is bound, the electron will remain on heme a₃ until O₂ is released or reduced, but to optimize the overall chances of trapping O₂ after its passage to CuB (44) under conditions of limited O₂ availability, it may appear useful that interheme electron equilibration is much more rapid than microseconds. In this context, we note that it has been shown that intrinsic transfer of O₂ from CuB to heme a₃, a reaction competing with O₂ migration out of the protein, occurs faster than 1 μs (44).

On the same note, one might even speculate that the efficiency of initial reduction of the active site, which is gated by the arrival of a proton (45), benefits from rapid ET to the active site to stabilize the new state.

Conclusion

We have demonstrated that, in bioenergetic systems, very fast and functional intraprotein ET reactions are not restricted to photosynthetic systems. This notion may help to construct realistic models of the coupling and temporal adaptation of these reactions to other functional, and also often not time-resolved, intraprotein events, such as proton translocation and substrate transport toward the active site. Because the intrinsic timescale of global protein motions guiding such events is (sub)picosecond, even faster ET reactions than the one elucidated in this work may be expected to play a role.