Interventional effects for mediation analysis with multiple mediators

Abstract

The mediation formula for the identification of natural (in)direct effects has facilitated mediation analyses that better respect the nature of the data, with greater consideration of the need for confounding control. The default assumptions on which it relies are strong, however. In particular, they are known to be violated when confounders of the mediator–outcome association are affected by the exposure. This complicates extensions of counterfactual-based mediation analysis to settings that involve repeatedly measured mediators, or multiple correlated mediators.

VanderWeele, Vansteelandt, and Robins²¹ introduced so-called interventional (in)direct effects. These can be identified under much weaker conditions than natural (in)direct effects, but have the drawback of not adding up to the total effect. In this article, we adapt their proposal in order to achieve an exact decomposition of the total effect, and extend it to the multiple mediator setting. Interestingly, the proposed effects capture the path-specific effects of an exposure on an outcome that are mediated by distinct mediators, even when – as often – the structural dependence between the multiple mediators is unknown; for instance, when the direction of the causal effects between the mediators is unknown, or there may be unmeasured common causes of the mediators.

Introduction

The introduction of counterfactual-based distribution-free definitions of direct and indirect effects in epidemiology^9,10 – so-called natural (in)direct effects – has spurred a major revival of mediation analysis^5,14,20. It has led to a renewed and improved understanding of the ignorability assumptions required to identify (in)direct effects. It has moreover enabled the development of a formal framework for mediation analysis that is applicable to nonlinear models. These developments have facilitated applications of mediation analysis that better respect the nature of the data and reflect greater consideration of the need for confounding control. Notwithstanding these advances, mediation analysis based on natural (in)direct effects has been the subject of recent critiques. The usefulness of natural (in)direct effects has been called into question because they are not directly informative about real-life interventions^8,11. Concerns have moreover been raised about the impossibility to conduct experiments in which the identification assumptions for natural (in)direct effects are guaranteed to be satisfied^3,6,11. Remaining concerns arise from the difficulty or impossibility of identifying these effects in realistic settings that involve multiple and/or repeatedly measured mediators^2,4,15, and settings that involve exposure-induced confounding of the mediator–outcome association^1,21,22. These concerns all originate from the fact that natural (in)direct effects are defined in terms of so-called cross-world counterfactuals¹¹ that are unobservable, even from experimental data; they call for alternative effect measures that are less remote from the observed data.

In this article, we revisit and refine so-called interventional (in)direct effects, previously introduced by VanderWeele, Vansteelandt and Robins²¹. These are not defined in terms of cross-world counterfactuals. They can therefore be identified under weaker conditions, but have the drawback of not always adding up to the total effect. We will adapt this proposal to overcome this, and then extend it to the case of multiple mediators. Interestingly, our proposal decomposes the total effect into different path-specific effects via the different mediators, even when – as often happens – the structural dependence between the multiple mediators (for instance, the direction of the causal effect, or the possible presence of unmeasured common causes) is unknown. It thus opens avenues towards a flexible and realistic mediation analysis with multiple mediators.

Single mediator models

Effect measures

Let A, M, and Y denote the exposure, mediator, and outcome. Let C represent baseline covariates not affected by the exposure. We let Y_a and M_a denote respectively the values of the outcome and mediator that would have been observed had the exposure A been set to level a; let Y_am denote the value of the outcome that would have been observed had A been set to level a, and M to m. Throughout, we make the consistency assumption¹⁷ that Y_a = Y and M_a = Y when A = a, and that Y_am = Y when A = a and M = m.

Suppose a and a* are two values of the exposure we wish to compare, e.g. a = 1 and a* = 0. The corresponding average controlled direct effect, fixing the mediator to level m, is then defined by E(Y_am − Y_a*m). It captures the effect of exposure A on outcome Y, intervening to fix M to m^10,14; it may be different for different levels of m. The natural direct effect, E(Y_aMa* − Y_a*Ma* ), differs from the controlled direct effect in that the intermediate M is set to the level M_a*, the level that it would have naturally been under some reference condition a* for the exposure^10,14. By subtracting it from the total effect, E(Y_a − Y_a* ), one obtains the average natural indirect effect, E(Y_aMa − Y_aMa* ); this compares the effect of the mediator at levels M_a and M_a* on the outcome when exposure is set to A = a. Finally, we define the interventional direct effect as

$$E\left(Y_{a{G}_{a*|C}}-Y_{a*G_{a*|C}}\right)=E\left[{\displaystyle \sum _m\left\{E(Y_{am}|C)-E(Y_{a*m}|C)\right\}P(M_{a*}=m|C)}\right].$$

It differs from the controlled direct effect in that the intermediate is set for each subject to a random draw from the conditional distribution of M_a*, given the observed covariates C for that subject (a related definition²¹ uses P (M = m|a*, C) in lieu of P (M_a* = m|C)). It may thus be viewed as the controlled direct effect of comparing exposure levels a versus a* under a stochastic intervention, G_a*|C, which controls the mediator for each subject at some value randomly drawn from the distribution of M_a*, given the observed covariates C. We will moreover call

$$E\left(Y_{a{G}_{a|C}}-Y_{a{G}_{a*|C}}\right)=E\left[{\displaystyle \sum _{m}E(Y_{am}|C)\{P(M_a=m|C)-P(M_{a*}=m|C)\}}\right]$$

the interventional indirect effect. For this effect to be non-zero, the exposure would have to change the mediator, which in turn would have to change the outcome, thus confirming that it captures a notion of mediation. For instance, VanderWeele et al. ¹⁶ investigate pack-years of smoking as a mediator of the effect of genetic variants on lung cancer. The interventional indirect effect expresses the change in lung cancer risk that would be seen if the distribution of pack-years of smoking were shifted from what it would be if all subjects carried two risk alleles to what it would otherwise be. Arguably, this effect is more relevant than the corresponding natural indirect effect, as it is informative about the effect of particular interventions on smoking. One could alternatively define interventional (in)direct effects with respect to a mediator distribution other than P(M_a = m|c). This can be of interest when interventions on the exposure are not conceivable. For instance, changing P(M_a = m|c) to P(M = m|a, c) would change the interpretation to the average change in lung cancer risk that would be seen if the distribution of pack-years of smoking were shifted from what it is in subjects with two risk alleles to what it is in the remaining subjects²¹. In the remainder of the article, we choose not to do this because unmeasured confounding may render P(M = m|a, c) dependent on a, even when the exposure has no effect on the mediator.

Assumptions

Controlled direct effects can be identified when:

• (i)the effect of exposure A on outcome Y is unconfounded conditional on C (i.e., Y_am ⫫ A|C, where X ⫫ Y|Z denotes that X is independent of Y conditional on Z);
• (ii)the effect of mediator M on outcome Y is unconfounded conditional on A, C and possibly some additional covariate vector L that may be affected by A (i.e., Y_am ⫫ M|{A = a, C, L}).

  Average interventional (in)direct effects are identified if, in addition to these assumptions,

• (iii)the effect of exposure A on mediator M is unconfounded conditional on C (i.e., M_a ⫫ A|C).
  Randomisation of the exposure (possibly conditional on C) ensures the validity of this additional assumption as well as assumption (i). Under (i)-(iii), the interventional direct and indirect effect can be identified as²¹

  $${\displaystyle \sum _c{\displaystyle \sum _l{\displaystyle \sum _m\{E(Y|a,l,m,c)P(l|a,c)-E(Y|a*,l,m,c)P(l|a*,c)\}P(m|a*,c)P(c)}}}$$ (1)

  $${\displaystyle \sum _c{\displaystyle \sum _l{\displaystyle \sum _{m}E(Y|a,l,m,c)P(l|a,c)\{P(m|a,c)-P(m|a*,c)\}P(c).}}}$$ (2)

  These expressions reveal a major weakness that we will attempt to overcome: the sum of the effects (1) and (2), which is sometimes called the ‘overall effect’ ²¹, may differ from the total effect. One exception is when assumptions (i) and (iii) hold, and in addition, assumption (ii) holds with L empty. In that case, the direct and indirect interventional effects sum to the total effect E(Y_a − Y_a* ), even when there are interactions and non-linearities.

  Natural direct and indirect effects always sum to the total effect. However, their identification requires much stronger assumptions. It requires that assumptions (i) and (iii) hold, that assumption (ii) holds with L empty (thus excluding the possible presence of exposure-induced confounders), and in addition that a technical cross-world independence assumption⁹ holds, which places an independence restriction on the joint distribution of the variables Y_am and M_a* :

• (iv)Y_am ⫫ M_a* |C.

  Under these assumptions, these effects reduce to expressions (1) and (2) obtained for average direct and indirect interventional effects, but with L empty. It thus follows that in single mediator models without post-treatment confounding, natural (in)direct effects obtained under assumption (iv) can also be interpreted as interventional (in)direct effects (even when that assumption is violated).

Natural versus interventional (in)direct effects

Average interventional direct effects encode the exposure effect that would be realised while controlling the mediator distribution to be fixed. This is realised by setting the mediator for each subject to a random draw from the distribution of the mediator at exposure level a*, given covariate values c. Natural direct effects adopt a similar notion, but fixing the mediator at the counterfactual mediator value (corresponding to exposure level a*) itself. This may yield a direct effect of a different magnitude, in part because the counterfactual level of the mediator may depend on much more than the considered covariates c. Both measures would thus be relatively close if the covariate set c were so rich as to leave little variation in M_a* for a given c (beyond the variation due to causes unrelated to Y_am), but not necessarily otherwise. While the natural direct effect may thus more closely capture the notion of mechanism, this need not lead us to prioritise them. First, natural direct effects employ cross-world counterfactuals like Y_aMa* about which information cannot be obtained even from experimental data. The data analyst who reports natural direct effects is thus obligated to make strong untestable assumptions like (iv) (and/or to conduct a sensitivity analysis¹²), under which these effects reduce to the interventional direct effect (1) (with L empty). Second, the relevance of natural (in)direct effects has been questioned on the basis that they do not connect to the effect of particular policies⁸.

In contrast to natural (in)direct effects, interventional (in)direct effects are policy-relevant¹⁸: they are relevant about a policy that involves fixing the mediator distribution, or shifting it to the extent that it is affected by the exposure. They continue to be meaningful, even when assumptions (i) and (iii) fail or when the exposure is not manipulable (e.g. when the exposure is race¹⁹), so long as assumption (ii) is satisfied. For instance, when L is empty, then the interventional direct effect (1) reduces to

$${\displaystyle \sum _c{\displaystyle \sum _m\{E(Y_m|a,c)-E(Y_m|a*,c)\}P(m|a*,c)P(c),}}$$

since E(Y |a, m, c) = E(Y_m|a, c) under assumption (ii). This can be interpreted as the average outcome difference that would remain between exposure groups A = a and A = a* if the mediator distribution in the former group were shifted to equal that in the latter group¹⁹. Similar comments are relevant for indirect effects.

Multiple mediator models

Review

For pedagogic purposes, we consider a setting with two mediators M₁ and M₂, and defer more general results to the eAppendix. VanderWeele and Vansteelandt (2013) define the natural direct effect of A on Y, not mediated by either or both mediators, as E(Y_aM1a*M2a* − Y_a*M1a*M2a* ). The remaining indirect effect via both mediators is then E(Y_aM1aM2a − Y_aM1a*M2a* ). These effects can be identified as

$${\displaystyle \sum _c{\displaystyle \sum _{m_1}{\displaystyle \sum _{m_2}\{E(Y|a,m_1,m_2,c)-E(Y|a*,m_1,m_2,c)\}P(m_1,m_2|a*,c)P(c)}}}$$ (3)

and

$${\displaystyle \sum _c{\displaystyle \sum _{m_1}{\displaystyle \sum _{m_2}E(Y|a,m_1,m_2,c)\{P(m_1,m_2|a,c)-P(m_1,m_2|a*,c)\}P(c)}}},$$ (4)

when

• (i’)the effect of exposure A on outcome Y is unconfounded conditional on C (i.e., Yam₁m₂ ⫫ A|C);
• (ii’)the effect of both mediators M₁ and M₂ on outcome Y is unconfounded conditional on A and C (i.e., Y_am1m2 ⫫ (M₁, M₂)|{A = a, C});
• (iii’)the effect of exposure A on both mediators is unconfounded conditional on C (i.e., (M_1a, M_2a) ⫫ A|C);
• (iv’)the cross-world assumption holds that Y_am1m2 ⫫ (M_1a*, M_2a* )|C.

Unfortunately, these effects provide no insight into the distinct pathways that may exist between exposure and outcome.

When the mediators are sequential (i.e., M₁ may affect M₂ but not vice versa), further progress^15,21 can sometimes be made by supplementing the previous analysis with a single mediator analysis with respect to M₁. In particular, if assumptions (i)-(iv) hold with M₁ in lieu of M, one can additionally identify the natural direct effect E(Y_aM1a* − Y_a*M1a* ). This can be decomposed as

$$E(Y_{a{M}_{1a*}}-Y_{a{M}_{1a*}{M}_{2a*}})+E(Y_{a{M}_{1a*}{M}_{2a*}}-Y_{a*M_{1a*}{M}_{2a*}}),$$

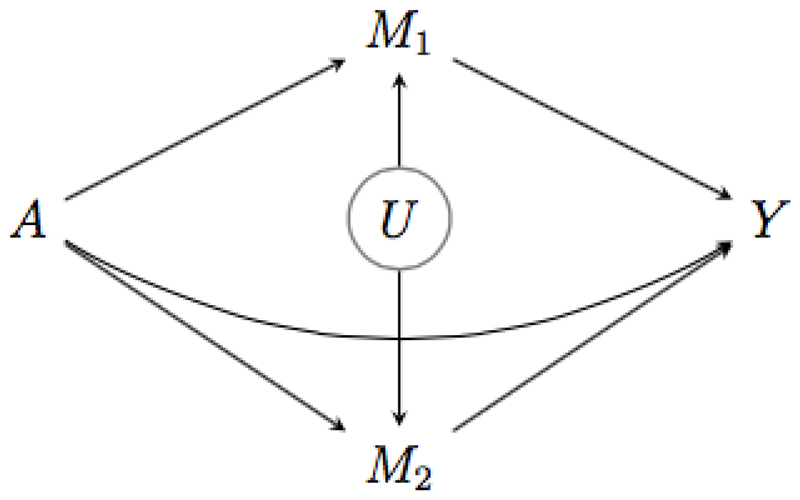
where the first component represents the effect mediated by M₂ but not M₁, and the second component can be identified as detailed in the previous paragraph. Such sequential analysis thus enables one to infer the direct effect that is not mediated by either M₁ or M₂ or both, i.e. E(Y_aM1a*M2a* − Y_a*M1a*M2a* ), the effect that is mediated by M1, i.e. E(Y_aM1a − Y_aM1a* ) (including any effect mediated by both M₁ and M₂), and the effect that is mediated by M₂ but not M₁, i.e. E(Y_aM1a* − Y_aM1a*M2a* ). However, one important limitation is that the causal structure between M₁ and M₂ (i.e. whether M₁ affects M₂, or vice versa) is often not known when different mediators are assessed at the same time. Moreover, even when assumptions (i’)-(iv’) hold, assumptions (i)-(iv) (with M₁ in lieu of M) will often not be satisfied¹⁵. For instance, when both mediators share an unmeasured common cause, as in the causal diagram of Figure 1, then M₂ confounds the association between M₁ and Y, thereby inducing a violation of assumption (ii). In that case, the effect mediated via M₁ is not identified because the data carry no information about the effect of M₁ on M₂. Regression adjustment for M₂ provides no remedy because M₂ is an exposure-induced confounder so that adjusting for it would violate assumption (iv). This problem is important because the mediators are strongly related in many applications; for instance M₁ and M₂ may represent realisations of a repeatedly measured mediator, or be manifestations of an underlying latent process.

Figure 1.

Causal diagram 1: M₁ and M₂ share an unmeasured common cause.

In view of these limitations, we will next propose novel definitions of interventional (in)direct effects for the multiple mediator setting, which do not have the disadvantage that they do not sum to the total effect. The proposed formalism will decompose the total effect of exposure on outcome into various path-specific effects. It can be used even when the causal structure between the mediators is unknown or when various mediators share unmeasured common causes.

Proposal

We define the interventional direct effect of exposure on outcome other than via the given mediators as

$$E[{\displaystyle \sum _{m_1}{\displaystyle \sum _{m_2}\{E(Y_{a{m}_1{m}_2}|c)-E(Y_{a*m_1{m}_2}|c)\}P(M_{1a*}=m_1,M_{2a*}=m_2|c)}}].$$ (5)

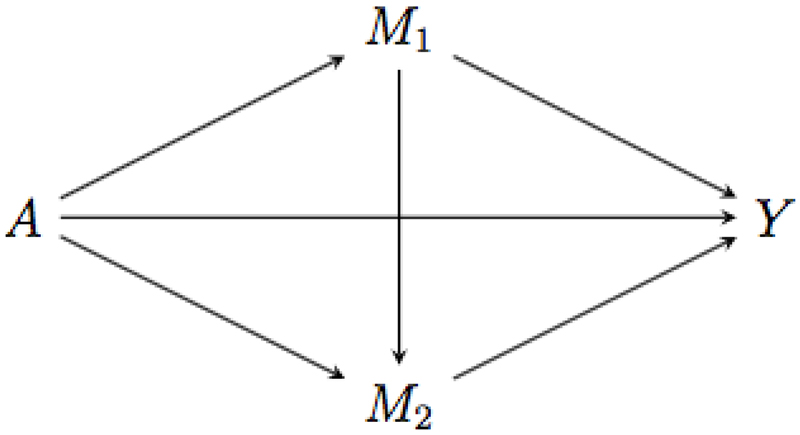
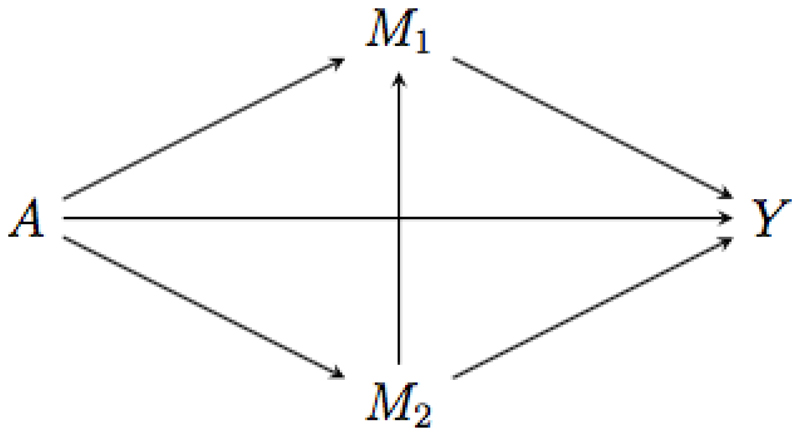
This expresses the exposure effect when fixing the joint distribution of both mediators (by controlling the mediators for each subject at a random draw from their counterfactual joint distribution with the exposure set at a*, given covariates C). This corresponds to the effect A → Y in the causal diagrams of Figures 1, 2, and 3.

Figure 2.

Causal diagram 2: M₁ affects M₂.

Figure 3.

Causal diagram 3: M₂ affects M₁.

We define the interventional indirect effect of exposure on outcome via M₁ as

$$E[{\displaystyle \sum _{m_1}\sum _{m_2}}E(Y_{a{m}_1{m}_2}|c)\{P(M_{1a}=m_1|c)-P(M_{1a*}=m_1|c)\}P(M_{2a*}=m_2|c)].$$ (6)

This expresses the effect of shifting the distribution of mediator M₁ from the counterfactual distribution (given covariates) at exposure level a* to that at level a, while fixing the exposure at a and the mediator M₂ to a random subject-specific draw from the counterfactual distribution (given covariates) at level a* for all subjects. The latter is chosen independently of M₁, so as to avoid assumptions on the joint distribution of the counterfactuals M_1a and M_2a* corresponding to different exposure levels.

The effect (6) corresponds to the effect A → M₁ → Y in the causal diagrams of Figures 1 and 2, and to the combination of the effects A → M₁ → Y and A → M₂ → M₁ → Y in Figure 3. The latter can be seen upon noting that the difference P(M_1a = m₁|c) − P(M_1a* = m₁|c) encodes the combination of the effects A → M₁ and A → M₂ → M₁. The interventional indirect effect of exposure on outcome via M₁ thus captures all of the exposure effect that is mediated by M₁, but not by causal descendants of M₁ in the graph. Interestingly, this interpretation holds regardless of the underlying causal structure.

We define the interventional indirect effect of exposure on outcome via M₂ similarly as

$$\begin{gathered} E[{\displaystyle \sum _{m_1}{\displaystyle \sum _{m_2}E\left(Y_{a{m}_1{m}_2}|c\right) \\ \left\{P\left(M_{2a}=m_2|c\right)-P\left(M_{2a*}=m_2|c\right)\right\}P\left(M_{1a}=m_1|c\right)}}]. \end{gathered}$$ (7)

This corresponds to the effect A → M₂ → Y in the causal diagrams of Figures 1 and 3, and to the combination of the effects A → M₂ → Y and A → M₁ → M₂ → Y in Figure 2. It thus captures all of the exposure effect that is mediated by M₂, but not by causal descendants of M₂ in the graph; again, this interpretation holds regardless of the underlying causal structure.

The difference between the total effect and these three effects equals

$$\begin{gathered} E[{\displaystyle \sum _{m_1}\sum _{m_2}}E\left(Y_{{\mathrm{am}}_1{m}_2}|c\right)\{P(M_{1a}=m_1,M_{2a}=m_2|c) \\ -P(M_{1a}=m_1|c)P(M_{2a}=m_2|c)-P(M_{{1a}^{*}}=m_1,M_{{2a}^{*}}=m_2|c) \\ +P(M_{{1a}^{*}}=m_1|c)P(M_{{2a}^{*}}=m_2|c)\}]. \end{gathered}$$ 8

This captures the indirect effect resulting from the effect of exposure on the dependence between the counterfactuals M_1a and M_2a, given C. This effect would be zero when both mediators are conditionally independent⁷, given exposure and covariates, but also under much weaker conditions. Under linear models, for instance, this effect can only be non-zero when both mediators interact in their effect on the outcome and, moreover, one of the mediators interacts with the exposure in its effect on the other mediator. Because of this, we would often expect (8) to be much closer to zero than the other components (6) and (7) of the indirect effect, though not always (see Section 4).

In some cases, the effect (8) may be of primary scientific interest. For instance, consider the mediating roles of cancer stage at diagnosis and treatment in the effect of socioeconomic status (SES) on 1-year survival in breast cancer patients. Suppose that the treatment decision process takes cancer stage into account in a manner that may be different for women with high versus low SES. The resulting effect of SES on 1-year survival that is mediated by this possibly differential decision process is encoded in (8).

Regardless of whether the component (8) is of scientific interest, it is important to consider it when expressing how much of the exposure effect is explained by specific pathways. For instance, in utero tobacco smoke exposure M₁ is known to have an effect on asthma and wheeze only in children with the GSTM1-null genotype M₂¹³. If an intervention to reduce smoking during pregnancy were only effective in mothers of infants without the GSTM1-null genotype, then the intervention would have no indirect effect via smoking. Yet, the indirect effect (6) would be non-zero because it would consider the characteristics M₁ and M₂ independently. Only by acknowledging that part of the indirect effect via M₁ is also expressed by the term (8) may valid conclusions be drawn.

Estimation

Under assumptions (i’), (ii’) and (iii’), the effects (5), (6), (7) and (8) can be identified upon substituting E (Y_am1m2 |c) by E (Y|a, m₁, m₂, c) and P (M_ja = m_j|c) for j = 1, 2 by P (M_j = m_j|a, c) in the above expressions. Suppose for instance that the outcome obeys model

$$E\left(Y|a,m_{1,}{m}_{2,}c\right)={\theta }_0+{\theta }_{1}a+{\theta }_2{m}_1+{\theta }_3{m}_2+{\theta }_4{m}_1{m}_2+{\theta }_{5}a{m}_1+{\theta }_{6}a{m}_2+{\theta }_{7}c$$

and that the mediators (M₁, M₂), conditional on A and C, have means

$$E\left(M_j|a,c\right)={\beta }_{0j}+{\beta }_{1j}a+{\beta }_{2j}c,$$

with residual variances ${\sigma }_j^2,$ j = 1, 2, and covariance σ₁₂. Then the interventional direct effect (5) is given by

$$E[\{{\theta }_1+{\theta }_5({\beta }_{01}+{\beta }_{11}a*+{\beta }_{21}C)+{\theta }_6({\beta }_{02}+{\beta }_{12}a*+{\beta }_{22}C)\}(a-a*)]=\{{\theta }_1+{\theta }_5({\beta }_{01}+{\beta }_{11}a*+{\beta }_{21}E(C))+{\theta }_6({\beta }_{02}+{\beta }_{12}a*+{\beta }_{22}E(C))\}(a-a*).$$

It equals θ₁(a − a*) in the absence of exposure–mediator interactions. Upon fitting the appropriate regression models to the observed data, thus obtaining estimates of the above parameters, these estimates can be plugged in to the expression above to obtain an estimate of the interventional direct effect. The interventional indirect effect (6) via M₁ equals

$$\{{\theta }_2+{\theta }_4({\beta }_{02}+{\beta }_{12}a*+{\beta }_{22}E(C))+{\theta }_{5}a\}{\beta }_{11}(a-a*),$$

which is θ₂β₁₁(a − a*) in the absence of exposure–mediator and mediator–mediator interactions. The interventional indirect effect (7) via M₂ is

$$\{{\theta }_3+{\theta }_4({\beta }_{01}+{\beta }_{11}a+{\beta }_{21}E(C))+{\theta }_{6}a\}{\beta }_{12}(a-a*).$$

Finally, the indirect effect (8) resulting from the effect of exposure on the mediators’ dependence is θ₄σ₁₂ − θ₄σ₁₂ = 0. The total effect can thus be decomposed into the direct effect and the two indirect effects defined above. If instead, A and M₁ interacted in their effect on M₂ in the sense that

$$E\left(M_2|m_1,a,c\right)={\beta }_{02}+{\beta }_{12}a+{\beta }_{22}c+{\beta }_{32}{m}_1+{\beta }_{42}a{m}_1,$$

then (8) would evaluate to ${\sigma }_1^2{\theta }_4{\beta }_{42}\left(a-a*\right)$.

This regression approach has the drawback that it requires a new derivation each time a different outcome or mediator model is considered. This can be remedied via a Monte-Carlo approach, which involves sampling counterfactual values of the mediators from their respective distributions. For instance, to evaluate the first component

$$E\left[{\displaystyle \sum _{m_1}{\displaystyle \sum _{m_2}E\left(Y_{a{m}_1{m}_2}|c\right)P\left(M_{1a}=m_1|c\right)P\left(M_{2a*}=m_2|c\right)}}\right],$$

of (6), one may take a random draw M_2a*,i for each subject i from the (fitted) distribution P(M₂|a*, c_i). Next, one takes a random draw M_1a,i for each subject i from the (fitted) distribution P(M₁|a, c_i). Finally, one may predict the outcome as the expected outcome under a suitable model with exposure set to a, M₁ set to M_1a,i, M₂ set to M_2a*,i, and covariate C_i. The average of these fitted values across subjects then estimates the above component. Its performance can be improved by repeating the random sampling many times and averaging the results across the different Monte-Carlo runs. In practice, we recommend the bootstrap for inference.

A health disparity analysis

We illustrate our proposal using data for all 29,580 women diagnosed with malignant, invasive breast cancer from 2000 to 2006 in the Northern and Yorkshire Cancer Registry Information Service (NYCRIS) – a population-based cancer registry covering 12% of the English population – who have information on cancer stage at diagnosis recorded. Our analysis is covered by approval PIAG 1-05(c)/2007 entitled ‘Linkage of National Cancer Registry data to national Hospital Episode Statistics (HES) data’ held by the Cancer Survival Group (LSHTM) which supported this research.

Our aim is to investigate possible explanations for the disparity in breast cancer survival between women of higher and lower SES; 95.9% (64.7%) of women with higher SES survive to one (five) year(s) after diagnosis, compared with 93.2% (54.1%) in the lower SES group. One possible explanation is that women with lower SES are less likely to attend screening and as a result, are more likely to be diagnosed when the disease is already more advanced. A difference in treatment choice is another possible explanation.

Our analyses are included mainly for illustration and some caution is warranted, as they involve several simplifications. In particular, we consider a binary SES exposure (A) which is whether or not the woman resides (at diagnosis) in an affluent area. The mediator M₁ comprises age at diagnosis and cancer stage at diagnosis, classified as early (tumor-node-metastasis [TNM] stage 1/2) or advanced (TNM stage 3/4). The mediator M₂ is a treatment variable that classifies women either as having ‘major surgery’ or ‘minor or no surgery’. The outcome (Y ) is one-year survival from the date of diagnosis. Calendar year at diagnosis and region are considered as baseline confounders (C).

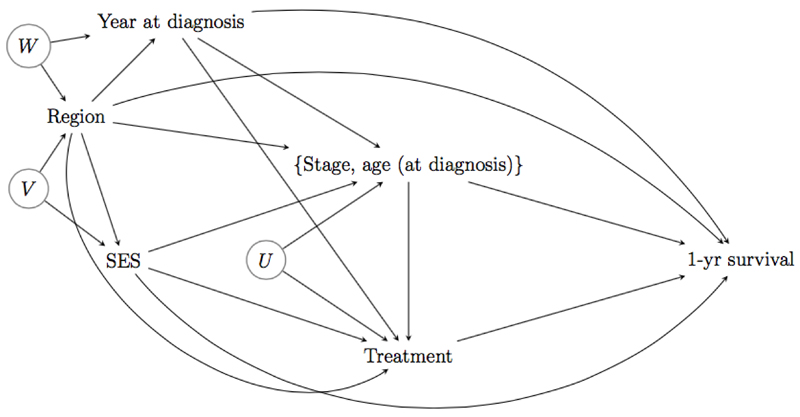
All analyses assume that the causal diagram of Figure 4 holds, and are based on 6 million Monte-Carlo draws in total (to ensure that the results were free of Monte-Carlo error to the number of decimal places given), with the distribution of the two confounders equal to their empirical distribution. Standard errors are obtained using the nonparametric bootstrap, with 1,000 bootstrap samples. Stata code is given in eAppendix D.

Figure 4.

Causal diagram 4: data example.

Sequential mediation analysis

Details on the sequential mediation analysis of Section 3.1 are given in the eAppendix. The results in Table 1 suggest that, of the 2.8% (95% CI 2.3%–3.4%) total difference in survival probability, about half of this (1.4%, 95%CI 1.1%–1.6%) is mediated by some combination of age and stage at diagnosis and treatment. Assuming that there are no unmeasured common causes of age/stage at diagnosis and treatment (i.e. no U in Figure 4), we can further decompose this indirect effect into an effect through age/stage (some of which may also act through treatment) (1.0%, 95% CI 0.8%–1.2%) and an effect through treatment alone (0.3%, 95% CI 0.2%–0.5%), thus indicating that only a small proportion of the effect is through the treatment variable alone.

Table 1.

Results of sequential mediation analysis (CI: confidence interval; SE: standard error)

Effect	Interpretation	Estimate	Bootstrap	95% CI
			SE	lower	upper
E(Y1 – Y0)	Total causal effect	0.028	0.0028	0.023	0.034
E(Y1M10M20 – Y0M10M20)	Direct effect not through {M1, M2}	0.013	0.0028	0.008	0.018
E(Y1M11M21 – Y1M10M20)	Indirect effect through {M1, M2}	0.014	0.0014	0.011	0.016
E(Y1M10 – Y0M10)	Direct effect not through M1	0.017	0.0028	0.011	0.022
E(Y1M11 – Y1M10)	Indirect effect through M1	0.010	0.0011	0.008	0.012
E(Y1M10 – Y1M10M20)	Indirect effect through M2 only	0.003	0.0008	0.002	0.005

Multiple mediator analysis based on interventional effects

Without relying on any cross-world assumptions or any assumptions about the causal structure of the mediators, thus allowing U in Figure 4, the results in Table 2 (obtained as detailed in the eAppendix) suggest that, of the 2.8% (95% CI 2.3%–3.4%) total difference in survival probability, about a quarter of this (0.7%, 95%CI 0.5%–0.9%) is mediated by the dependence of treatment on stage and age at diagnosis, i.e. (8). Recall that we expected this effect to be small, except when there are particular interactions present, as is the case here (see eTable 2). Among women of a lower SES, there is a strong negative association between stage and treatment, meaning that those diagnosed at an advanced stage are less likely to receive major surgery. One possible interpretation would be that doctors and/or patients decide that treatment is not likely to be beneficial for patients with advanced disease, or that surgical treatment is substantially delayed for these patients due to tumor-reducing treatments such as chemotherapy being prioritised first. We see from eTable 2 that this negative association is much less pronounced for women of higher SES. Therefore, we would interpret this estimated 0.7% as the increase in survival that would be expected if the treatment decision, as a function of stage and age at diagnosis (and baseline confounders), would be made for poorer women as it is currently made for higher SES women. There is little evidence of further mediation through the treatment variable (estimated effect 0.02%, 95% CI: –0.05, 0.08%), and evidence of an effect through age and stage at diagnosis (estimated effect 0.7%, 95%CI 0.5%–0.8%). This would suggest that an additional 0.7% reduction in one-year mortality for lower SES women could be achieved if the distribution of age and stage at diagnosis (given year of diagnosis and region) were changed from that seen in lower SES women to that of higher SES women, a change that could perhaps be affected by encouraging better uptake of screening and other health-seeking behaviour among lower SES women.

Table 2.

Results of multiple mediator analysis based on interventional effects (CI: confidence interval; SE: standard error)

Effect	Estimate	Bootstrap	95% CI
		SE	lower	upper
Total causal effect	0.028	0.0028	0.023	0.034
Interventional direct effect not through {M1, M2} (5)	0.013	0.0027	0.008	0.018
Interventional indirect effect through M1 (6)	0.007	0.0008	0.005	0.008
Interventional indirect effect through M2 (7)	0.0002	0.0003	–0.0005	0.0008
Interventional indirect effect through the dependence of M2 on M1 (8)	0.007	0.0009	0.005	0.009

Discussion

Most mediation analyses involve multiple mediators, either because of scientific interest in multiple pathways, or because certain confounders are mediators at the same time. When the mediators are independent⁷ or can be causally ordered¹⁵, but share no (unmeasured) common causes, then distinct pathways via those mediators can be identified. We have shown that progress can be made even in the likely event that mediators share unmeasured common causes, or when the direction of causality is unknown. This is possible by redirecting the focus on less ambitious interventional (in)direct effects. In this article, we have focused on effects defined on the additive scale. We refer to eAppendix A for similar result for effects on other (e.g. multiplicative) scales.

The proposed effect decomposition is relatively easy to perform via a (Monte-Carlo based) regression approach. It delivers effects mediated via each of the mediators separately, but also via the mediators’ dependence.