Multi-domain structure and correlated dynamics determined by self-consistent FRET networks

Abstract

We present an approach that allows us to simultaneously access structure and dynamics of a multi-domain protein in solution. Dynamic domain arrangements are experimentally determined by combining self-consistent networks of distance distributions with known domain structures. Local structural dynamics are correlated with the global arrangements by analyzing networks of time-resolved single-molecule fluorescence parameters. The strength of this hybrid approach is shown by an application to the flexible multi-domain Hsp90. The average solution structure of Hsp90’s closed state resembles the known x-ray crystal structure with Angstrom precision. The open state is represented by an ensemble of conformations with inter-domain fluctuations of up to 25 Å. The data reveal a state-specific suppression of the sub-millisecond fluctuations by dynamic protein-protein interaction. Finally, the method enables localization and functional characterization of dynamic elements and domain interfaces.

Molecular machines in most organisms consist of multiple domains. These machines rely on the dynamic interaction between their domains and components. Time-resolved x-ray scattering and NMR relaxation methods provide important information on local small-scale dynamics. But especially multi-domain proteins often undergo large (nm-scale) global conformational changes on slow timescales of milliseconds to seconds, while local dynamics depend on these global states and occur on the timescale of microseconds to milliseconds¹. Our method uniquely covers this temporal and spatial range and therefore simultaneously accesses local and global equilibrium dynamics.

We demonstrate our method by using the example of the multi-domain heat shock protein Hsp90, which is an important and abundant protein in eukaryotic cells. It is essential for the activation of numerous signal transduction and key regulatory proteins^2–4 and has been assigned critical functions in chaperoning oncogenic proteins^5,6 and evolution⁷. The ATP-dependent functional Hsp90 dimer performs large conformational rearrangements involving its N-terminal and middle domains⁸. The x-ray crystal structure of the C- and N-terminally dimerized closed state⁹ of yeast Hsp90 triggered several studies including extensive searches for inhibitors as cancer drugs¹⁰. However, the dynamic nature of Hsp90 in the N-terminal open state, which is important for client binding, has challenged established structure determination methods. Different open and closed conformations of Hsp90 have been discussed in order to explain the experimental observations^11,12. We show that the previously postulated additional conformations are snapshots within the dynamic structural ensemble determined in the presented study for Hsp90’s closed and open state.

Dynamic interconversion between an open and a closed structure is frequently observed in many multi-domain protein machines. Such large-scale dynamics have been extensively studied by single molecule Förster resonance energy transfer (smFRET) in a protein under near-native conditions (buffered solution and room temperature)^13–17. For these experiments, two fluorophores (i.e. FRET dyes) were attached at defined positions to the protein under investigation. Unfortunately, such “two point” kinetics cannot be linked unambiguously to structural information obtained, for example, from x-ray or cryoEM.

Recent approaches combined several FRET pairs for the docking of rigid structures of small proteins^18–20. However, these approaches were optimized for rigid complexes excluding dynamic information. Our approach provides both structure and dynamics of complete multi-domain proteins by combining single molecule FRET with x-ray structure information and a novel type of data evaluation. It is readily applicable to any dynamic multi-domain protein or multi-subunit assembly if site-specific dye labeling is possible and structures of individual (sub)domains are known.

Results

Multi-domain arrangement and refinement

The investigation of a dynamic multi-domain protein structure requires the separation of global and local rearrangements, which we achieved in three basic steps (for a detailed flowchart see Supplementary Fig. 1). First, we determined the optimal domain compilation and its optimal spatial arrangement for each global state by means of a network of averaged experimental distances. Second, we examined local dynamics and its correspondence to the global states by using position-specific and time-resolved fluorescence parameters. Third, we combined the optimal domain compilation from the first step with networks of distance distributions to generate dynamic ensembles of structures. In the following we describe this procedure using the example of the multi-domain Hsp90.

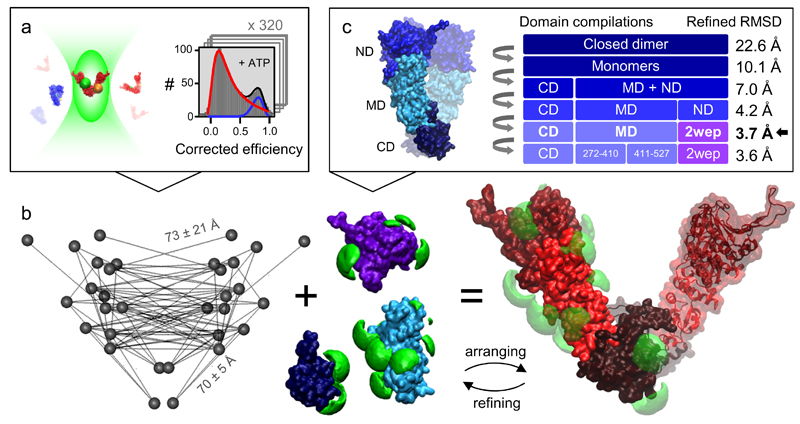
We measure more than 100 pairs of FRET dyes across the entire Hsp90 dimer under various nucleotide conditions in solution. Each resulting FRET efficiency histogram comprises at least 1000 single molecules (Fig. 1a). In the presence of ATP, Hsp90 slowly interchanges between the closed state (blue) and the open state (red). The efficiency populations are assigned to these global states by shifting the equilibrium towards the closed state with the ATP analog AMPPNP or towards the open state with ADP. At this point, mean distances and their uncertainties are extracted from the efficiency histograms assuming Gaussian distributed distances. Two distance networks are generated; one for the closed and one for the open state (Supplementary Table 1). See next section for verification and consistency tests.

Figure 1. Global domain arrangement of Hsp90’s open state.

(a) Corrected FRET efficiencies are calculated from photon bursts of single molecules using a confocal setup with alternating excitation and color- and polarization-sensitive detection. Photophysical correction parameters are verified within a global network. Each measurement consists of at least 1000 single molecules and is repeated at least three times. See main text and Supplementary Notes 2, 3 for determination and verification of precise distances from efficiencies. (b) The self-consistent distance network of Hsp90’s open state is visualized for the final model structure (left). It is used to optimally arrange domain structures (middle, blue/violet) considering the accessible volumes of the dyes (green). The initial global domain arrangement is refined considering changes of accessible volumes and local structural elements to obtain an optimal arrangement (right). (c) The arrangement procedure is repeated for different compilations of domains and subdomains. The full-length x-ray structure of yeast Hsp90 in the closed state (pdb: 2cg9) and x-ray structures of individual domains and homologues served as basic components. The final model structure fulfills the distances with an RMSD of 3.7 Å. The procedure is verified with subsets of the data (see Fig. 2b).

The distance network for the open state is used to optimally arrange domain structures in their position and orientation (Fig. 1b). For this purpose, dye accessible volumes are calculated considering equally distributed position densities¹⁸. Then, the deviations between measured distances and efficiency-averaged inter-dye model distances are minimized. In the first run, flexible domain interfaces are considered ignoring domain clashing. For definitions of minimization criteria and uncertainties see Online Methods. The global domain arrangement is iteratively refined by considering modified accessible volumes at domain interfaces. The refined structural arrangement is completed with dynamic elements (e.g. loops) not present in the x-ray crystal structure and then equilibrated with MD simulations for further local structural refinements (Online Methods).

This arrangement is done for different domain compilations (Fig. 1c). An optimal arrangement was found when using the C-terminal and middle domains (C- and M-domains) from the x-ray structure of the AMPPNP-bound closed conformation (pdb: 2cg9⁹) and the N-domains from the x-ray structure of an isolated ADP-bound N-domain (pdb: 2wep²¹). The final model structure matched the distance network with a root mean square deviation (RMSD) of 3.7 Å. Further splitting into subdomains did not significantly decrease the RMSD. We have found that an average symmetric structure is more likely than an average asymmetric structure for the open state of Hsp90, although asymmetric intermediates are possible (Supplementary Note 1).

Verifying the experimental distance networks

The accuracy of single pair distance determination via smFRET depends mainly on (i) photophysics, (ii) the Förster radius R₀ and (iii) dye mobility. The accuracy of three dimensional structures from smFRET is additionally challenged by (iv) local structural rearrangements and (v) an incomplete set of experimental distances. The exceptionally large set of distances determined for the Hsp90 system and their connection enabled us to derive consistency tests and the following general approach.

• (i)Photophysical correction parameters are determined for every single FRET pair²². Dark states are not considered by these parameters and are therefore excluded separately with FCS (Supplementary Note 2). The self-consistency of these parameters is verified within the FRET network and therefore outliers can be easily detected (Supplementary Note 3).
• (ii)The Förster radius is calculated for each FRET pair individually considering overlap spectra, donor quantum yield and the average dipole orientation factor <κ²>. State specific heterogeneities of the Förster radius are directly monitored within the FRET network. We assume <κ²> to be 2/3, because we explicitly select distances that are dynamically averaged as detailed in the following.
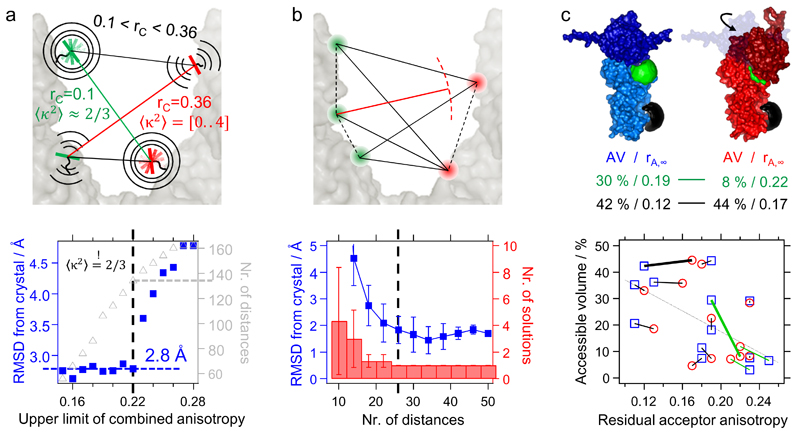
• (iii)We derive a threshold value for the geometric mean of the residual anisotropies of both dyes – i.e. the combined anisotropy (Supplementary Note 4). A low combined anisotropy represents sufficient isotropic averaging of orientation factors. By decreasing the threshold for the combined anisotropy, the deviations between the distance network and the closed structure of Hsp90 is significantly reduced (Fig. 2a, bottom). With a threshold of r_C=0.22, the x-ray structure of the closed conformation (pdb: 2cg9⁹, resolution: 3.1 Å) is described with an RMSD of 2.8 Å by the remaining 134 distances. This threshold is chosen as a prior threshold for the open state. In our study we use dyes with a dipole axis approximately perpendicular to the dye linker enabling fast isotropic motions at most labeling positions.
• (iv)The distance deviations remaining after applying the anisotropy threshold do not significantly correlate with the dye anisotropies. In addition, simulations show a high isotropic averaging of orientation factors for these remaining distances (Supplementary Note 4). Thus, we believe that the underlying cause for the deviations is not κ², but local differences of structural elements (e.g. loops) between the solution structure and the crystal structure.
• (v)Remaining uncertainties due to small structural rearrangements are addressed by measuring several redundant distances. To answer the question how many distances are sufficient for an unambiguous domain arrangement, the middle domains of Hsp90 are arranged with subsets of distances. The results are compared with the x-ray structure of the closed state (Fig. 2b). In this example, a unique solution is obtained if more than 26 distances are used; this corresponds to 13 measured distances in the homo dimer. The RMSD between this arrangement and the x-ray structure is (2±0.5) Å.

Figure 2. Analyzing networks of distances and fluorescence parameters.

(a) If the combined anisotropy r_C is low enough, κ²=2/3 is normally justified (green distance, top). The threshold for the combined anisotropy r_c=0.22 is found by determining the RMSD between experimental distances and the x-ray crystal structure of the closed state (bottom). (b) Subsets of distances were systematically generated from 50 experimental distances to arrange Hsp90’s middle domains. The RMSD from the x-ray structure, its variability and the number of possible solutions strongly decrease with an increasing number of redundant distances. The number of possible solutions was reduced to one if using 26 distances or more (dashed black line). We use a χ² criterion (Online Methods) to rate the solutions. The error bars represent the standard deviations, each calculated from 5 random subsets. (c) Dyes may change their residual anisotropy due to a changing accessible volume (top, green) or due to local conformational changes (top, black). Correlating accessible volumes and residual anisotropies for various dye positions within the closed structure (blue squares) and the arranged open structure (red circles) allows us to find state dependent local conformational changes. The green lines denote positions at domain interfaces. Long black lines indicate a state-dependent local conformational change not located at interfaces. The dashed gray line denotes the average anti-correlation between accessible volume and residual anisotropy for all dye positions.

Generally, the required number of distances for a protein system can be found by checking the number of solutions or convergence of the RMSD. This can be done with the accompanying software. A good starting point is 4 mutations for two domains (i.e. 16 distances) or 3 mutations for three domains (i.e. 27 distances). Contact restraints reduce the minimum number of distances.

Localizing dynamic and functional elements

Localizing functionally relevant elements is an important contribution towards the understanding of multi-domain proteins and their interactions. A change in the global state of a multi-domain protein involves a global rearrangement of structural domains. In addition, there are local rearrangements of structural elements including local changes of structural dynamics. We present three ways of correlating local and global rearrangements.

First, if different x-ray structures exist for one functional domain, local differences can be assigned to the global states. This is achieved by arranging different domain compilations with the measured distance network (Fig. 1c). In this way, we found that the N-terminal beta-sheet strand binds to its own monomer in the open dimer state according to the x-ray structure of the isolated ADP-bound N-domain (pdb: 2wep). This agrees with the observation for the bacterial homologue HtpG²³.

Second, we developed an approach to uncover small local rearrangements and dynamic elements in solution which are not resolved in the crystal structures. We compared the position-specific and state-specific dye anisotropies within the FRET networks. In that way, we found that the loop-positon 452 rearrange upon the global conformational change. Combining the anisotropy information with accessible volumes, local and global structural arrangements could be further verified (Fig. 2c). For further explanations and all dye positions and accessible volumes refined with MD simulations see Supplementary Note 3.

Third, intra-domain distances can be measured in the presence of different interactors that shift the equilibrium of the global states. A difference in the intra-domain distance distribution elucidates either a state-dependent local rearrangement of a structural element or a state-dependent change of local dynamics.

Quantifying local and global dynamics

In addition to the mean distances, we quantified the spatial fluctuations for every FRET pair on timescales from microseconds to milliseconds within the closed and open state, respectively. Distance distributions were separated from shot noise with a probability distribution analysis of the FRET efficiencies (Supplementary Note 5). Several verifications excluded photophysics as a source of the efficiency broadening. Varying the binning times of the photon traces revealed the timescale of the fluctuations (Supplementary Note 6). Efficiency histograms and time-correlated fluctuation amplitudes measured under different conditions are depicted exemplarily for one FRET pair in Figure 3a, b (for all distances and their fluctuations see Supplementary Table 1). In the presence of AMPPNP (blue) Hsp90 is in the closed state and undergoes very small fluctuations from 0.1 to 10 milliseconds. The open state is mainly populated in the presence of ADP (red) or ATP (gray) and shows very large fluctuations on this timescale. Of particular note is the suppression of the fast sub-millisecond fluctuations in the presence of the model client Δ131Δ (violet).

Figure 3. Network of time-correlated distance distributions.

(a) Efficiency histograms recorded under different conditions are shown for a photon binning time of 1 ms for the FRET pair highlighted in the top right. The fits indicate the efficiency distribution of Hsp90’s closed state (blue) or Hsp90’s open state (red) assuming Gaussian distributed distances. (b) Time-correlated distance distributions – i.e. fluctuations versus observation time – are quantified for the closed state (blue), the open state (red), the open state in the presence of 2mM ATP (gray) and the open state in the presence of 2mM ATP and 20 µM of the model client Δ131Δ (purple). See Supplementary Fig. 4 for additional data and Supplementary Note 5 for the calculation of distance fluctuations. (c) The distance fluctuations for an observation time of 1 ms are represented as average value and standard error over all distances of the indicated domain pair. The individual distance distributions are listed in Supplementary Table 1 for every FRET pair.

Figure 3c illustrates the standard deviation of the distance fluctuations at 1 ms as average values per domain pair, contrasting the closed AMPPNP-bound with the open ADP-bound state. As expected, the overall closed state was rigid with fluctuations smaller than 3 Å. The open state revealed large fluctuations of up to 25 Å between several domains. The inter-domain dynamics were checked for consistency with further fluorescence-based methods such as efficiency-lifetime correlation (Supplementary Note 6).

Dynamic ensemble of multi-domain structures

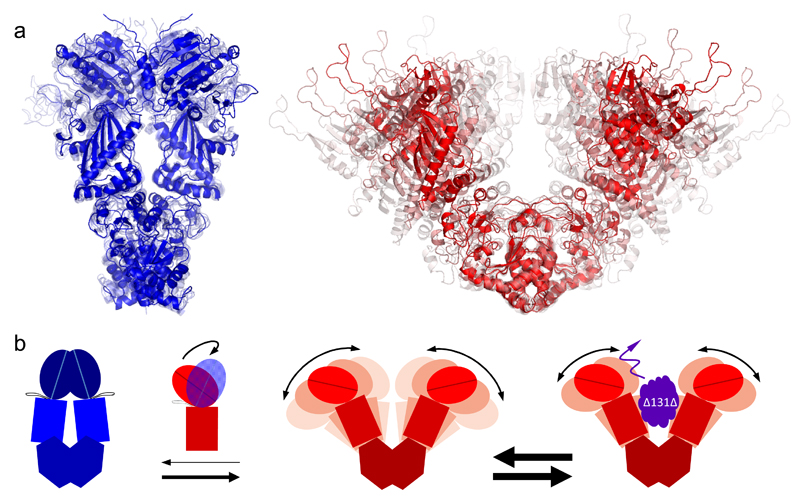
Figure 4a shows the final dynamic ensemble for the closed state (blue). The average closed structure in solid color was arranged with the measured distance network for AMPPNP-bound Hsp90. The four transparent structures are snapshots from MD simulations, which represent the standard deviation of the experimental distance distributions with regard to the average structure. The experimentally arranged ATP-bound closed conformation and AMPPNP-bound closed conformation match within 2.0 Å.

Figure 4. Time-correlated structural ensembles and dynamics of Hsp90.

(a) Dynamic ensembles of Hsp90 structures for the closed state (blue) and open state (red) for an observation time of 1 ms. The mean structures are shown in solid color and the less probable structures in transparent colors. (b) Global conformational dynamics and state-dependent inter-domain fluctuations of Hsp90 are illustrated for an observation time of 0.1 ms to emphasize the effect of the interaction with the client protein. The rigid closed state (left) is mainly stabilized by NN-contacts. The highly dynamic open state (middle) is characterized by globally stable but locally flexible domain interfaces. The CM-interface enables large but defined inter-monomer fluctuations on the millisecond timescale. The MN-interface enables a transient rotational motion of the N-terminal domain on the sub-millisecond timescale (see Supplementary Note 6). The CC-interface remains globally unchanged during the described conformational changes. The interconversion between the global states occurs on the seconds timescale. The model client Δ131Δ suppresses inter-monomer fluctuations on timescales shorter than 0.1 ms (right). The transition rates are indicated by the arrow thickness in a logarithmic scale.

The dynamic ensemble for Hsp90’s open state was generated directly from experimental data, whereas MD simulations were only used for structural refinement. This was necessary, because the large fluctuations were not sampled on the timescale of current simulation times.

To determine an ensemble of model structures, we developed a domain arrangement procedure for dynamic proteins based on a global distance distribution analysis and on the average domain arrangement (Online Methods). Three model structures were generated that fulfilled all measured efficiency histograms simultaneously. One structure equaled the average symmetric structure and the other two structures corresponded either to the left or to the right interval of single Gaussian distance distributions. Hence, further model structures were generated representing the standard deviations ±σ and ±2σ of single Gaussian distance distributions at an observation time of 1 ms. The average structure and the ±σ-structures matched the experimental distances with an RMSD of about 4 Å. The resulting structural ensemble represented the most likely average trajectory within the open state (Fig. 4a, red).

Superposition of the average open structure with the closed x-ray structure of yeast Hps90 at the C-domains emphasized an opening perpendicular to the N-terminal dimerization interface. Prominent average rearrangements between the global states were a partial shift of the CM-interface and a significant change of the NM-interface with a rotation of the N-domain by 90° (see also Figs. 5b, c).

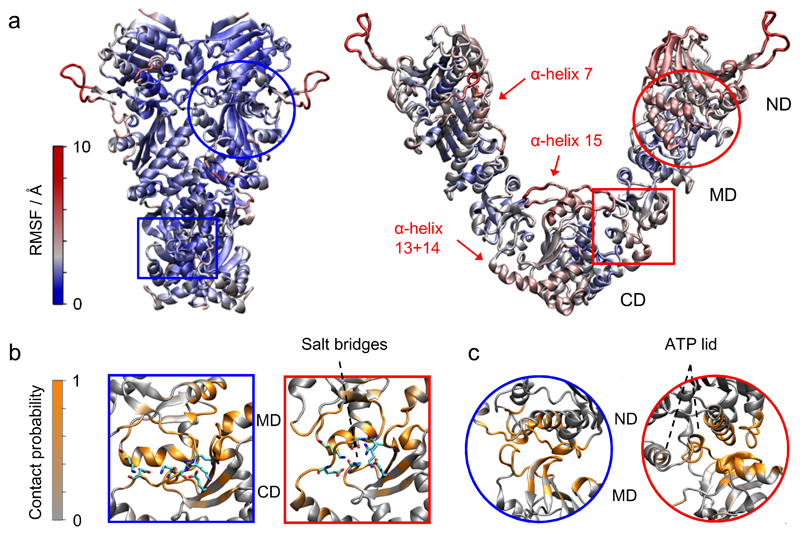
Figure 5. Structural insights from unrestrained MD simulations.

(a) Root mean square fluctuations from MD simulations for Hsp90 indicating several flexible elements in the open state. (b, c) The number of contributions per residue to the buried surface area (i.e. the contact probability) was calculated within the closed state (blue frames) and the open state (red frames) for the CM-interface (b) and the MN-interface (c). Interfacial salt-bridges are highlighted as sticks.

Beyond providing average structures for each state, the global distance distribution analysis revealed state-dependent inter-domain dynamics, which are a basis for understanding the overall mechanism. The CM- and MN-interface can be seen as flexible hinges. Both enable large and fast fluctuations of the open dimer state. The large dwell time of the global open state is likely caused by the low conditional probability that the N-terminal domains are in close proximity at the correct orientation. Figure 4b summarizes the global conformational dynamics of Hsp90 and the effect of a model client.

The NM-arrangements of the average open structure matches the x-ray structures of the endoplasmic reticulum homologue Grp94 (pdb: 2o1v²⁴) with an RMSD of 3 Å. The full-length -2σ-structure of the open state even resembles the overall Grp94 x-ray structures with an RMSD of 4.5 Å (Supplementary Fig. 2). The overall σ-structure is similar to the open x-ray structure of the bacterial homologue HtpG (pdb: 2ioq²³). Altogether, several structures of Hsp90 homologues are contained as snapshots within our dynamic structural ensemble.

Further structural insights from unrestrained MD simulations

To test the stability and fast dynamics of the Hsp90 structure, unrestrained MD simulations in explicit solvent were performed (Online Methods), starting from the experimentally arranged average closed structure and average open structure. The RMSD between the simulated open structure and the start structure reached a plateau regime of 6-8 Å (Supplementary Fig. 3a), indicating indeed a stable open structure. Thousands of snapshots of open structures sampled during the simulations were compared to the experimental distance distribution network resulting in an average χ² of 1.5.

Root mean square fluctuations (RMSF) were calculated and color-coded in Figure 5a. The closed conformation resulted in an overall rigidness with fluctuations in almost all regions of only 3 Å. In contrast, the open structure revealed several flexible elements.

The interfacial rearrangements in Hsp90’s open state likely enable the large conformational changes and flexibility of this multi-domain protein. Therefore, we quantified the buried surface areas at the CM-interface (Fig. 5b) and NM-interface (Fig. 5c). The normalized buried surface areas per atom are shown in Supplementary Figure 3b. The NM-interface of the open state significantly differs from that of the closed state. Interestingly, the ATP lid remains in an α-helix conformation while contacting the M-domain. The loop conformation of the ATP lid as in the AMPPNP-bound x-ray structure is sterically not accessible. This agrees well with the previous suggestion that the ATP lid might regulate the NM-arrangement²³.

At the CM-interface a clear shift of interface contacts from the closed to the open state is observed. The α-helix 10, the loop 568-575 and the loop 524-533 contribute mostly to the CM-interface, which conforms well with hydrogen exchange experiments²⁵. Remarkably, the CM-interface in the open state seems to be stabilized by (complex) salt bridges between charged residues (highlighted in Fig. 5b right) that are not present in the closed state. Most of these charged residues show (anti-) correlated switching (Supplementary Fig. 3c) additionally supporting the experimentally found flexibility of this interface.

Discussion

The presented study demonstrates that our hybrid method can reveal unique structural and dynamic properties of multi-domain proteins. The dynamics of small structural motifs and complete domains is captured simultaneously and therefore complements time-resolved x-ray scattering and NMR, both of which address only local dynamics. Finally, the accuracy and reliability of distance determination with smFRET were raised to a new level by means of the unprecedented self-consistent network and novel quality controls.

Application to Hsp90 in solution reproduced the x-ray crystal structure of the closed state within its resolution of 3.1 Å. In addition, we determined an ensemble of open solution structures with similar precision. The presented structural ensemble includes previously found structures of Hsp90 homologues. Beyond previous efforts, we revealed and correlated local and global dynamics of the closed and open state. In this way, we uncovered state-dependent flexible elements and revealed that the model client protein only changes the dynamics within the open dimer state while not affecting the interconversion times between the global states.

Such a disentanglement of global and local dynamics and its regulation by interaction partners is to our knowledge not accessible with other methods. Our approach provides a new tool in structural biology for determining time-correlated structural ensembles on length- and timescales relevant for multi-domain proteins. The methodology is applicable if an x-ray structure is available for one functional state of a multi-domain protein, but also if the structures of individual (sub)domains, e.g. obtained from cryoEM studies, are known. We anticipate that this kind of hybrid method will be necessary for understanding transient protein-protein interactions, for finding novel interaction sites and for a thorough understanding of regulation and signaling in multi-protein systems.

Software and Data Availability

The software is available at: http://www.singlemolecule.uni-freiburg.de.

Program files, example applications and measured data to dynamically arrange multi-domain proteins are provided in the “MDA.zip” file.

Programs files and example applications to setup FRET derived distance restrained MD simulations are included in the “MD-restraining-support.zip” file.

Online Methods

Sample preparation

The Hsp90 dimer was site-specifically labeled with dyes via cysteine-maleimide chemistry. Dyes used in this study were Atto532, Atto550 as donor fluorophores, Atto647N (AttoTec, Germany) and Alexa647 (Life Technologies, Germany) as acceptor fluorophores.

The influence of the dyes on the protein itself was checked for each position and FRET pair in three ways: First, there had to be significant ATPase activity (Supplementary Fig. 5), second the conformational equilibrium had to be shifted by nucleotides and third several positions were double checked by different FRET pairs and donor and acceptor positions were swapped. The following positions were selected out due to low ATPase activity: 51, 141, 109, 179, 466.

Homo dimers (i.e. Hsp90 dimers with two equal dyes at the same position per monomer) were exchanged with different homo dimers to obtain about 50 % hetero dimers that have exactly one acceptor dye at one monomer and one donor dye at the other monomer. The exchange was done by incubating the mixed sample for about 20 minutes at 47°C in order to accelerate the opening of the coiled coil zipper. In contrast, intra-monomer mutants (two labels within one monomer) were exchanged with 100-fold excess of wild type Hsp90 to exclude inter-monomer FRET. In this case, equimolar dye concentrations were added at the same time. FRET between these positions did not significantly depend on which dye reacted to which site, indicated by dye swapping in the heterodimer. By correlating FRET efficiency with stoichiometry in a scatter plot, remaining homo dimers were sorted out.

Experimental conditions

The samples were measured in aqueous solution containing 150 mM KCl, 40 mM Hepes-KOH (pH 7.5) and 10 mM MgCl. All samples were measured at room temperature and several samples were double checked at 30°C. The measurement concentration was 50 pM for Hsp90, the K_D of the native Hsp90 dimer is 60 nM and less than 1 pM for the zipped construct used in this study. The measurement concentration for the client was 10 µM. The K_D of the client is about 10 µM.

Experimental methods

Single molecule fluorescence parameters of freely diffusing molecules were measured in a homebuilt confocal microscope similar to other published setups^22,26,27. Time-resolved fluorescence intensities were recorded with picosecond time resolution with single photon avalanche photodiodes (PDM-50μm and τ-SPAD, PicoQuant, Germany) for color- and polarization-sensitive detection and processed with a commercial data acquisition system (HydraHarp 400, PicoQuant). The data is stored in the ht3 format, i.e. the micro-time data with 16 ps resolution (for the determination of lifetimes and time-resolved sub-ensemble anisotropies) and macro-time data with 200 ns resolution (for the determination of FRET efficiencies and stoichiometries) using the Symphotime acquisition software (PicoQuant). We used two alternating, pulsed diode lasers (532 nm LDH-P-FA-530 and 640 nm LDH-D-C-640, PicoQuant) as excitation sources and an Apo 60x water immersion objective (Nikon).

The heatable measurement chambers consisting of glass slides and Teflon cavities were passivated with PEG to reduce surface interactions and preserve the analyte concentrations. Laser scanning and moderate laser intensities (50 µW) reduced blinking and bleaching of the dyes.

Fluorescence spectra were measured on a Jasco FP8500 spectrafluorimeter (Jasco, Germany). Absorbance spectra were recorded on a Lambda25 UV/VIS spectrometer (PerkinElmer, USA).

Analysis methods

FRET efficiencies were corrected according to Lee et al.²² and an individual Förster radius was determined for each distance (Supplementary Note 2).

Networks of redundant distances and parameters were generated to test their self-consistency and to probe local conformational changes (Supplementary Note 3).

Time-resolved sub-ensemble anisotropies were determined for each distance and each state to obtain the combined anisotropy as a selection criterion (Supplementary Note 4).

For the average and dynamic domain arrangement, distance distributions were extracted from pre-corrected FRET efficiency histograms by separation from shot noise and by excluding non-structural heterogeneities (Supplementary Note 5 and Supplementary Table 1).

Variation of the binning time of the photon traces in combination with the distance distribution analysis revealed the timescale of the distance fluctuations (Supplementary Note 6).

Average domain arrangement

For each selected domain structure and for each labeling position, dye accessible volumes are calculated¹⁸. The center coordinates of these volumes are used to transform each domain structure into one polyhedron. On the one hand, this accelerates the optimization process, especially for multiple states. On the other hand, the independency from the protein structure prevents steric hindrance which is necessary for dynamic interfaces consisting of flexible elements. Furthermore, this procedure enables an additional control of the plausibility of the results.

The domain polyhedrons are randomly positioned and orientated in space and stepwise translated and rotated. A gradient-descent algorithm with stochastically varied starting parameters²⁸ is used to minimize the sum of the squared deviations between n measured distances R^exp and the corresponding model distances R^mod:

$${\chi }_{\mathit{\text{single}}}^2=\frac{1}{n}{{\displaystyle \sum _{i=1}^n\left(\frac{R_i^{\mathit{\text{exp}}}-R_i^{\mathit{\text{mod}}}}{\Delta R_i^{\mathit{\text{exp}}}}\right)}}^2$$ (1)

The experimental uncertainty ΔR^exp strongly weights the distance deviations. In other words, this uncertainty can be seen as the reciprocal stiffness of distance springs that are applied to center dye positions.

The evidence of other local minima arrangements is tested, too. The final unambiguous solution is completed with dynamic elements (e.g. loops) not present in the x-ray crystal structures and then equilibrated with MD simulations for further local structural refinement. For the final structure, new dye accessible volumes are calculated and efficiency-averaged inter-dye distances are compared with the measured distances. We define the total distance uncertainty as the quadratic mean of the efficiency-related distance uncertainty ΔR^eff and of the uncertainty due to anisotropic orientation factors ΔR^ani and of the standard deviation σ_R of the Gaussian distributed distances:

$${(\Delta R^{\mathit{\text{exp}}})}^2={(\Delta R^{eff})}^2+{(\Delta R^{ani})}^2+{({\sigma }_R^{\mathit{\text{exp}}})}^2$$ (2)

The efficiency-related distance uncertainty can be expressed as:

$$\Delta R^{eff}=-\frac{1}{6}{\left(1+{\left(\frac{R^{\mathit{\text{exp}}}}{R_0}\right)}^6\right)}^2{\left(\frac{R^{\mathit{\text{exp}}}}{R_0}\right)}^{-5}{R}_0\cdot \Delta E$$ (3)

The efficiency error ΔE is estimated at 0.02. This number is the standard deviation derived by repeating several experiments with our confocal setup. Notably, the precision was very similar for low, medium and high transfer efficiencies. The error includes possible fluctuations in the background signal. It has to be noted that the uncertainty for the measured distance R^exp can differ significantly from the uncertainty of the real distance for very low or very high efficiencies. For this and other reasons, distances with average efficiencies below 0.05 or above 0.95 are excluded from the further analysis.

The average anisotropy-related distance uncertainty accounts for deviations from the assumption of isotopically distributed orientation factors and can be roughly classified as:

$$\Delta R^{ani}=\{\begin{array}{r}5\%\cdot R^{\mathit{\text{exp}}}for\hspace{0.17em}{r}_C<r_{threshold}\\ 15\%\cdot R^{\mathit{\text{exp}}}for\hspace{0.17em}{r}_C>r_{threshold}\end{array}$$ (4)

The percentages of uncertainty were empirically calculated by comparing 160 measured distances with the crystal structure of Hsp90 and measuring the combined anisotropies r_C. Very few distances can have larger errors due to rare scenarios (Supplementary Note 4). However, such distances are directly monitored within the distance networks.

The standard deviation σ_R of the Gaussian distributed distances is determined with the distance distribution analysis derived in Supplementary Note 5.

Notably, the efficiency average can differ from the distance average of the possible inter-dye distances between the dye accessible volumes. For large accessible volumes, the difference is non-negligible. In this case, the experimental efficiency-averaged distances can be conveniently transformed into preliminary distance-averaged distances with a numeric look-up table (Supplementary Note 1). This allows a fast and effective minimization necessary for the dynamic domain arrangement of multiple states.

Dynamic domain arrangement

If a protein state can be described by a single structure with small fluctuations, the distance of a FRET dye pair can be extracted from a single efficiency histogram with a distance distribution analysis (Supplementary Note 5). If a global state exists of several sub-states, their unambiguous determination from a single efficiency histogram is not possible in most cases. Therefore, a global distance distribution analysis has been developed that simultaneously fits all measured efficiency histograms while arranging a minimum number of s structures necessary to describe the broadest of all efficiency histograms.

The above-described average domain arrangement reveals the optimal compilation of rigid domains and preferably large domains to reduce the degrees of freedom for the dynamic domain arrangement. The average domain arrangement can be used as a start arrangement for the following optimization.

The domains of each structure are rotated and translated in space and a gradient descent algorithm²⁸ is used to find the global minimum, at which all measured efficiency histograms are best described by model histograms. The model histograms are generated by using the model distances of the arranged domain structures as input parameters for the distance distribution analysis. For each FRET dye pair, s normal distributions of distances P_N according to s model distances R^mod are summed and transformed into normalized efficiency histograms E^R (Supplementary Note 2) which are convoluted with shot noise limited efficiency distributions E^shot. The sum of the squared deviations between n measured efficiency histograms E^exp and the corresponding model efficiency histograms is used as a minimization criterion:

$$\begin{array}{c}{\chi }_{multi}^2=\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{{\left[{\mathit{\text{E}}}_i^R({\mathit{\text{P}}}_R)\ast {\mathit{\text{E}}}_i^{shot}(N)-{\mathit{\text{E}}}_i^{\mathit{\text{exp}}}\right]}^2}{{\left({\mathit{\text{E}}}_i^R({\mathit{\text{P}}}_R)\ast {\mathit{\text{E}}}_i^{shot}(N)\right)}^2+{\left({\mathit{\text{E}}}_i^{\mathit{\text{exp}}}\right)}^2},}\\ with\hspace{0.17em}{\mathit{\text{P}}}_R={\displaystyle \sum _{k=1}^s{\mathit{\text{P}}}_N(R_{i,k}^{\mathit{\text{mod}}},\sigma R_{i,k}^{\mathit{\text{mod}}})\cdot {\rho }_k}\end{array}$$ (5)

The standard deviation σ of the normal distributed distances P_N is set to a maximum value of 3 Å. The other free parameter is the relative frequency ρ of each of the s states. In contrast to the standard minimization χ_single for the average domain arrangement, this minimization χ_multi intrinsically includes the efficiency-related distance uncertainty. But, inclusion of the anisotropy-related distance uncertainty is difficult; therefore only distances with a low combined anisotropy are selected (Supplementary Note 4).

Pre-correction of the measured efficiency histograms dramatically increased the computational expense of the optimization procedure. Therefore, corrected shot noise limited efficiency distributions were calculated considering the changed Poisson statistics of the corrected fluorescence intensities (Supplementary Note 5). Additional acceleration was achieved by calculating the corrected shot noise limited efficiency histograms already before starting the optimization procedure.

Restrained MD simulations

Molecular dynamics simulations and energy minimization to generate Hsp90 structural models were performed using the sander module of the Amber14 molecular simulation package²⁹. During structural modeling the core structures of the N-, M- and C-domains were restrained to experimental reference structures by adding distance restraints between Cα atoms within 15 Å (force constant 3 kcal mol^-1 Å^-2). This allows translational and rotational mobility but only limited internal flexibility in each domain. Additionally, the core structure of the C-domains was kept close to the geometry of the x-ray structure, due to the corresponding experimental distances being equal in the presence of ADP and AMPPNP. For the structure generation steps, an implicit solvent model with a distance dependent dielectric constant (ε=4r) was employed.

As start structure the -2σ domain arrangement – which is similar to the closed conformation, but with rotated N-domains – was used. The connection between N- and M-domains was modeled by a short Gly₁₀ linker inserted between residue 216 and 261. For inclusion of the FRET derived distance data, pseudo atoms with a van der Waals radius of 6.5 Å, representing approximately the size of the dyes, were connected to the Cβ atoms of the dye labeled residues using a pseudo bond (linker) of 11 Å. The distance between each donor-acceptor pseudo atom pair was allowed to vary within an interval given by the experimentally determined FRET derived distance range. Beyond the allowed distance interval further variation was penalized with a force constant of 3 kcal mol^-1 Å^-2. In addition, the optimal spatial MN-arrangement in the dimer served as additional positional restraints (on heavy atoms, with a force constant 1.0 kcal mol^-1 Å^-2) during MD-based structure generation. In order to keep the structure symmetric with respect to the spatial arrangement of each monomer, the option to penalize the difference between two distances implemented in sander module of the Amber14 package was employed. The option was applied to a subset of equivalent backbone distances within each monomer and between monomers. MD simulations were performed for 0.5 ns at 450 K followed by 0.5 ns at 300 K using a time step of 0.001 ps. Structures were finally energy minimized within 7500 steps of conjugate gradient minimization. Structural models of the open Hsp90 structure were re-evaluated by the FPS approach¹⁸ to check compatibility with the FRET data. The final mean-structure yielded an average deviation from the FRET distance data of χ² < 0.3 (see above for the definition of χ²).

Unrestraint MD simulations

In addition to restrained MD simulations in implicit solvent for structure generation, unrestrained MD simulations starting from the mean open ADP-bound Hsp90 structure were performed in the presence of explicit solvent and surrounding ions. The structure was solvated in a truncated octahedral box with explicit TIP3P water molecules³⁰ and neutralized with sodium and chloride ions by means of the leap module and employing the parm14SB force field³¹. Long range electrostatic interactions were calculated with the Particle Mesh Ewald (PME) method³² and a real space cutoff radius of 9Å. During 0.5 ns equilibration the system was heated up to 300 K while heavy atoms of the protein were harmonically restrained (25 kcal mol^-1 Å^-2) to positions in the starting structure. After removing positional restraints gradually during another 0.15 ns the structures were being equilibrated for 0.2 ns in an unrestrained simulation. The simulation was extended to 100 ns at 300 K and a pressure of 1 bar. For comparison explicit solvent MD simulations were started from the closed crystal structure of Hsp90 (pdb: 2cg9) after removing the p23 cofactor and supplemented with the same (Gly)₁₀ linker between N- and M-domain as used for modeling the open Hsp90 structures. Equilibration followed the same protocol and simulations were extended to 100 ns. Several thousand structures in form of simulation snapshots were evaluated by the FPS approach¹⁸ resulting in an average χ² of 1.5.The generated trajectories were evaluated using the cpptraj module of the Amber14 package. Calculations of the root mean square deviation (RMSD) of the backbone and root mean square fluctuations (RMSF) were performed using the cpptraj module. The RMSF was calculated as the mean over all heavy atoms of each residue.

For a subset of 200 snapshots of the open and closed simulations the buried surface area (BSA) of the CM interface was calculated. Therefore the solvent accessible surface area of the C, M and CM domains has been calculated atom wise using the SHRAKE algorithm³³. This was done for both monomers of the Hsp90 dimer and the arithmetic mean was used in the following. For each residue the normalized total contribution as well as the number of contributions to the BSA was determined. The same procedure was repeated for the NM interface.

The protein structures were illustrated using³⁴.