Identifying T Cell Receptors from High-Throughput Sequencing: Dealing with Promiscuity in TCRα and TCRβ Pairing

Abstract

Characterisation of the T cell receptors (TCR) involved in immune responses is important for the design of vaccines and immunotherapies for cancer and autoimmune disease. The specificity of the interaction between the TCR heterodimer and its peptide-MHC ligand derives largely from the juxtaposed hypervariable CDR3 regions on the TCRα and TCRβ chains, and obtaining the paired sequences of these regions is a standard for functionally defining the TCR. A brute force approach to identifying the TCRs in a population of T cells is to use high-throughput single-cell sequencing, but currently this process remains costly and risks missing small clones. Alternatively, CDR3α and CDR3β sequences can be associated using their frequency of co-occurrence in independent samples, but this approach can be confounded by the sharing of CDR3α and CDR3β across clones, commonly observed within epitope-specific T cell populations. The accurate, exhaustive, and economical recovery of TCR sequences from such populations therefore remains a challenging problem. Here we describe an algorithm for performing frequency-based pairing (alphabetr) that accommodates CDR3α- and CDR3β-sharing, cells expressing two TCRα chains, and multiple forms of sequencing error. The algorithm also yields accurate estimates of clonal frequencies.

Author Summary

Our repertoires of T cell receptors (TCR) give our immune system the ability to recognise a huge diversity of foreign and self antigens, and identifying the TCRs involved in infectious disease, cancer, and autoimmune disease is important for designing vaccines and immunotherapies. The majority of T cells express a TCR made up of two chains, the TCRα and TCRβ, and high-throughput sequencing of samples of T cells results in the loss of this pairing information. One can identify TCRαβ clones using single-cell sequencing, but this is costly and typically probes only part of the diversity of T cell populations. Statistical approaches are potentially more powerful by sequencing the TCRα and TCRβ in multiple samples of T cells and pairing them using their frequency of co-occurrence. However, T cells involved in immune responses frequently share TCRα and TCRβ chains with other responding cells. This promiscuity, combined with a high prevalence of T cells with two TCRα chains and sequencing errors, presents significant challenges to frequency-based pairing methods. Here we present a new algorithm that addresses these challenges and also provides accurate estimates of the abundances of T cell clonotypes, allowing us to build a more complete picture of T cell responses.

Introduction

The ability of T cells to recognise antigens is conferred by a process of gene rearrangement that generates a diverse repertoire of T cell receptors (TCR), or clonotypes. Identifying the clonotypes involved in responses against pathogens and tumours or those involved in autoimmune disease can guide the design of vaccines and immunotherapies. In addition, the breadth of a T cell response correlates positively with the efficiency of control in many viral infections [1–3]. Thus, a method to characterise the diversity of antigen-specific responses—that is, the participating TCRs and their relative abundances—may yield potential correlates of protection.

The αβ TCR is a heterodimer, generated by a combination of ordered recombination of V, D, and J gene segments for the β chain and V and J gene segments for the α chain, together with random nucleotide insertions and deletions between the gene segments. The hypervariable CDR3α and CDR3β regions contact the peptide-loaded MHC (pMHC) most closely and so are considered the primary source of specificity in binding. From hereon we will use the term ‘chain’ interchangeably with the CDR3 region of the TCRα or TCRβ. Historically, the CDR3β has been thought to contribute more to the interaction with pMHC due to its greater theoretical diversity. However, studies of crystal structures have demonstrated that CDR3α loops can have equal or greater contact with pMHC, as measured by buried surface area [4]. Epitope-specific immune responses also show biases for certain V and J segments in both α and β chains [5, 6], suggesting both chains contribute to the binding affinity. The α chain may even play a dominant role in the recognition of certain antigens [7]. Characterising the true extent of clonal diversity within T cell populations therefore requires resolving the paired CDR3α and CDR3β sequences within them.

Standard methods of multiplex PCR and high-throughput sequencing lose this pairing information and as a result are commonly used to analyze either the α or β chains alone [8–11]. More recent studies have used single-cell sequencing approaches to identify TCRαβ pairs, and, analogously, the paired CDR3 sequences from the heavy and light chains of the B cell receptor. These approaches include using single-cell sorting and RT-PCR [12–14], also with barcoding [15–18]; and variations of emulsion techniques to isolate single cells and amplify with PCR [18–20]. Drawbacks of these techniques include limited scalability, the risk of undersampling rare clones and so underestimating diversity, imprecise information regarding clonal abundances, and the need to use customised equipment [18, 21].

An alternative strategy is to use statistical methods to associate the CDR3α and CDR3β sequences obtained from bulk sequencing of multiple subsamples of T cells taken from the parent population of interest [22]. This approach exploits the fact that paired chains will tend to appear together in samples and uses the frequencies of these co-occurrences to associate them. A similar approach has been used to pair the heavy and light chains of B cells [23]. Because frequency-based pairing can be applied to large samples of cells, it has the potential to recover antigen receptors in greater depth and more economically than single-cell approaches, as well as providing more precise estimates of clonal frequencies. However, several properties of antigen-specific T cell populations present difficult challenges to this method. First, there is accumulating evidence from single-cell sequencing studies that, within an individual, T cell clonotypes specific for a given pMHC can exhibit sharing of both α and β chains [13, 14, 17, 19]. Second, between 10–30% of T cells possess two productive α chains [13, 24, 25] and 6–7% of T cells possess two productive β chains [25, 26]. The combination of sharing of α or β chains, dual TCRs, and sequencing errors can confound frequency-based methods that assume unique pairings. To illustrate, frequent co-occurrences of the three chains α₁α₂β in samples may derive from a single clone possessing two α chains or two clones α₁β and α₂β present at similar abundances, and the two possibilities are difficult to distinguish.

Here we describe a novel approach to frequency-based pairing that addresses these issues and identifies TCRαβ clones and their relative abundances using high-throughput sequencing of CDR3α and CDR3β regions. Our approach is optimised for antigen-specific populations and designed for use with cells recovered from typically-sized human blood samples. It is specifically designed to deal with promiscuity in αβ pairing, dual TCRα clones, and high rates of sequencing errors. By drawing on bulk sequencing data, we increase the efficiency of detection of rare responding clones and reduce the costs associated with single-cell high-throughput sequencing methods. The method also goes beyond other currently available approaches, yielding estimates of the frequencies of clones within their parent populations.

Results

Sharing of TCRα and TCRβ chains across epitope-specific clones within an individual is common

Performing frequency-based pairing is in principle relatively straightforward if each clone is identified by two unique TCRα and TCRβ chains. However, single-cell analyses of epitope-specific T cell populations in mice and humans have revealed significant levels of sharing of both CDR3α and CDR3β sequences at the amino acid level across clones within individuals (Table 1).

Table 1. A summary of the degrees of sharing of CDR3α and CDR3β at the amino acid level across clones within epitope-specific T cell populations, found in published single-cell TCR sequencing data and our own.

Unless indicated otherwise, the samples were obtained from influenza-infected mice. The data clearly demonstrate that sharing of both α and β chains within an individual occurs in different infection/inoculation settings.

Citation	Peptide/System	Status	Number of clones	Number of distinct α chains	Number of distinct β chains	Number of shared α chains	Number of shared β chains	% of α chains that are shared	% of β chains that are shared
[13]	KbPB1703	Immune	35	16	24	3	2	18.8	8.3
[17]	Human CD4+ TILs	Colon cancer	216	226	216	7	0	3.1	0.0
	CD4+ T cells from adjacent colon		305	239	237	15	0	6.3	0.0
[14]	DbNP366	Naive 1	17	17	15	0	2	0.0	13.3
		Naive 2	11	11	11	0	0	0.0	0.0
		Naive 3	7	7	7	0	0	0.0	0.0
		Naive 4	10	7	9	3	1	42.9	11.1
		Naive 5	13	13	12	0	1	0.0	8.3
		Naive 6	9	9	9	0	0	0.0	0.0
		Immune 1	12	10	8	2	3	20.0	37.5
		Immune 2	15	9	8	4	3	44.4	37.5
		Immune 3	12	11	8	1	1	9.1	12.5
		Immune 4	10	10	8	0	1	0.0	12.5
	DbPA244	Naive 1	11	11	11	0	0	0.0	0.0
		Naive 2	10	10	10	0	0	0.0	0.0
		Naive 3	8	8	8	0	0	0.0	0.0
		Naive 4	25	25	25	0	0	0.0	0.0
		Naive 5	43	40	43	2	0	5.0	0.0
		Immune 1	17	15	15	2	1	13.3	6.7
		Immune 2	27	21	20	5	6	23.8	30.0
		Immune 3	14	14	12	0	2	0.0	16.7
		Immune 4	20	14	20	3	0	21.4	0.0
	DbPB1-F262	Naive 1	13	13	13	0	0	0.0	0.0
		Naive 2	13	12	13	1	0	8.3	0.0
		Naive 3	9	9	9	0	0	0.0	0.0
		Naive 4	41	41	41	0	0	0.0	0.0
		Naive 5	21	21	21	0	0	0.0	0.0
		Naive 6	24	22	23	2	1	9.1	4.4
		Naive 7	16	16	16	0	0	0.0	0.0
		Immune 1	9	9	8	0	1	0.0	12.5
		Immune 3	11	11	11	0	0	0.0	0.0
		Immune 4	20	15	17	1	2	6.7	11.8
		Immune 5	16	15	16	1	0	6.7	0.0
This study	Human CD8+ YFV	Immune	184	169	179	15	3	8.9	1.7

The current upper limits on estimates of the number of unique TCRβ chains in the naive CD4 or CD8 pools are 10⁶ in mice [27] and 10⁸ in humans [28]. As a consequence, sequencing of samples of naive T cells typically results in nearly every cell possessing a unique TCRβ (see S1 Text, Section 1). Nevertheless, the true diversity of the naive repertoire may be even greater; due to the sequence of events involved in the generation of the TCR in the thymus, we expect each TCRβ to be shared with many TCRα within the naive CD4 and CD8 T cell pools. In mice, thymocytes undergo 6–9 divisions following TCRβ rearrangement at the DN3 stage [29–32], generating 64–512 cells which then undergo independent TCRα rearrangements. Assuming 5% of these TCRαβ precursors survive selection [33–36] leaves TCRβ clone sizes of 3–25 cells post-selection [27]. Thymocytes may undergo 1 or 2 divisions at the single-positive CD4 or CD8 stage before leaving the thymus [36]; if we assume a 2-fold expansion here on average, each αβ T cell precursor at DN3 generates 6–50 new naive cells with identical TCRβ chains, comprising 3–25 unique TCRαβ clones of typically 2 cells. Comparable estimates of TCRβ clone sizes have been obtained elsewhere [27, 32]. There is also evidence that TCRβ-clone sizes can be augmented by convergent recombination of the TCRβ chain [8, 37]. If a particular CDR3β contributes strongly to the affinity of binding to a given peptide-MHC, then because the recruitment of naive antigen-specific T cells appears to be highly efficient [38], our rough quantification of TCRαβ clonality in thymopoesis is consistent with the observation that TCRβ-sharing is commonly found within epitope-specific populations (Table 1).

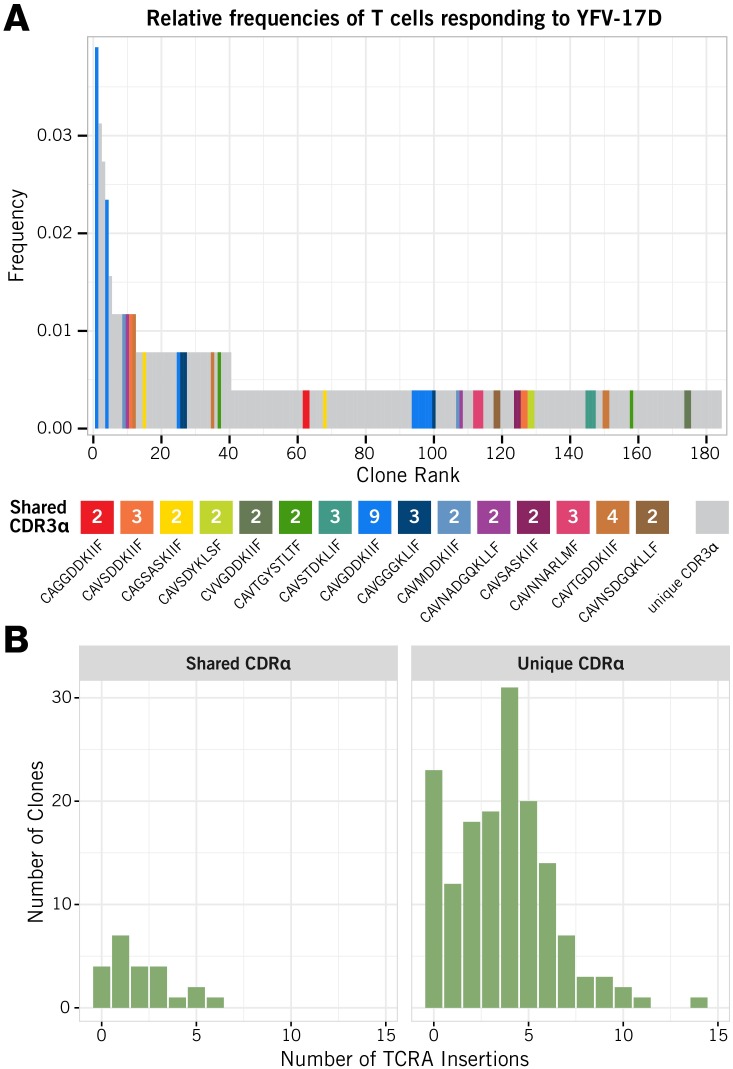
Because the rearrangement of the TCRα follows that of the TCRβ, any sharing of CDR3α sequences across clones presumably arises from convergent recombination. Sharing then would be expected to arise most frequently for sequences that are close to germline, containing relatively few random N-nucleotide insertions. To examine this possibility, we immunised an HLA-A2 human volunteer with the live attenuated yellow fever vaccine YFV-17D, took a peripheral blood sample 15 days post-vaccination, and used dextramer staining and single-cell RNAseq to recover paired TCRαβ sequences from CD8⁺ T cells specific for the immunodominant epitope HLA-A02:01/LLWNGPMAV (see Methods; data provided in S1 Dataset). Out of 256 cells, we observed 169 unique CDR3α, with 15 (8.9%) of them shared between two or more clones (Fig 1A). We examined the numbers of nucleotide insertions at the V-J junction of the CDR3α and indeed saw significantly fewer in CDR3α sequences that were shared between two or more clones (mean 2.04 insertions, n = 23) than in sequences that were unique to a single clone (mean 3.62 insertions, n = 154; p < 0.005, Wilcoxon rank sum test; Fig 1B). In summary, it appears that convergent TCRα recombination may derive at least in part from the reduced junctional diversity of clones possessing CDR3 regions that are closer to germline.

Fig 1. Analysis of TCRα usage in human, YFV-specific peripheral-blood CD8⁺ T cells.

(A) Observed distribution of relative clone sizes within the population specific for the HLA-A02:01/LLWNGPMAV epitope. Clones expressing a unique CDR3α are shown in grey; clones that share a CDR3α are coloured, and the numbers in the coloured boxes represent the number of clones sharing each CDR3α. (B) The distributions of CDR3α nucleotide insertion lengths in clones with shared CDR3α (left hand panel) and unique CDR3α (right hand panel).

Experimental overview and computational approach

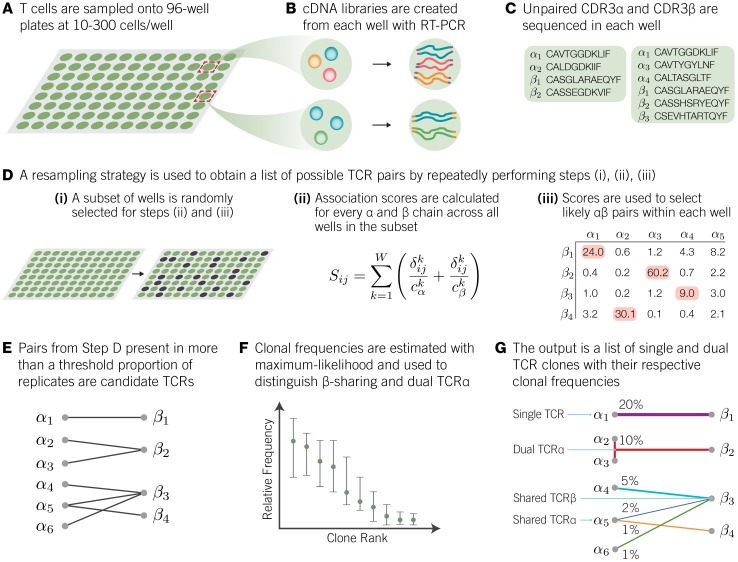
Motivated by this promiscuity of TCRα and TCRβ pairings, we developed a semi-heuristic procedure alphabetr (ALgorithm for Pairing alpHA and BEta T cell Receptors) that recovers TCRαβ pairs from high-throughput sequencing data. Fig 2 shows the algorithm schematically. The experimental procedure is to sequence the CDR3α and CDR3β regions from multiple samples of T cells from the same parent population (Fig 2A–2C). The input to the algorithm is a list of these unpaired sequences (Fig 2C), each associated with the sample it belonged to (e.g. a given well in one or more 96-well plates). Fig 2C illustrates amino acid sequences as inputs, but the algorithm can be applied equally well to data comprising nucleotide sequences and/or the addition of V(D)J segment information. The number of cells in each well can be freely varied, and indeed as we describe below, varying the sample size across the plate(s) helps to increase both the number and accuracy of pairings. Given this information, alphabetr then calculates association scores between every α and every β chain found in a randomly chosen subsample of wells. This score is the sum of the number of co-occurrences of chains in each well, each weighted inversely by the total number of chains recovered from that well (Fig 2D(ii)). The weighting factor reflects the intuitive idea that our confidence that a co-occurring α and β pair derive from the same clone decreases as the number of unique chains recovered from that well increases. The algorithm then solves a linear sum assignment problem within each well based on these plate-wide association scores to generate a list of candidate pairs of α and β sequences within each well (Fig 2D(iii)). This is a list of αβ pairs in which each α is paired with only one β, and vice versa, such that the sum of the association scores is maximised. After repeating this assignment for every well in the subset, we generate a matrix of dimensions n × m where n and m are the total numbers of unique α and β chains recovered across the plate(s), respectively, and whose entries are the number of times that each candidate pair α_i β_j (i ∈ {1…n}, j ∈ {1…m}) have been associated. Sharing of chains across clones is now possible in this list. Those αβ pairs that appear in a number of wells greater than the mean of the non-zero elements of this matrix are retained as a refined list of candidate pairs. The pairing and filtering process is repeated on subsets of the data (Fig 2D), and a consensus list of putative paired CDR3 sequences comprises those appearing in more than a threshold proportion of these lists (Fig 2E). This pseudo-jacknife procedure acts to reduce the effect of very common clones pushing up the threshold for inclusion in the filtered list and increases the efficiency of pairing of rarer clones, while minimising the inclusion of incorrect αβ pairs. Steps A-D are described in more detail in Methods.

Fig 2. An overview of the implementation of alphabetr.

(A) From the population of interest, multiple samples of 10–300 T cells are sorted into 96-well plates. This design allows for a given clone to be sampled in multiple wells. (B) Multiplex RT-PCR is used to create cDNA libraries of CDR3α and CDR3β from each well, and (C) high-throughput sequencing is used to recover the unpaired CDR3α and CDR3β sequences of the clones sampled in each well. (D)(i) A random subset of the wells is chosen, (ii) association scores between every unique α and β found across the wells within this sample are calculated, and (iii) the set of unique αβ pairs that maximises the sum of association scores is identified using the Hungarian algorithm [39]. Step (iii) is illustrated for a particular set of CDR3α and CDR3β recovered from one well, as a matrix of association scores calculated across all wells in the subsample. (E) Steps D(i)-(iii) are repeated to generate a consensus list of pairs, filtering out candidates that appear rarely across replicates. (F) The frequencies of each remaining candidate αβ pair within the parent population are estimated using a maximum-likelihood approach, assuming only sharing (no dual TCR). Dual TCRα clones α₁ α₂ β₁ are then distinguished from clones apparently sharing a TCRβ chain (α₁ β₁ and α₂ β₁), by examining the patterns of co-occurrences of the three chains, and the frequencies of these clones are re-calculated. (G) The output of the algorithm is a list of single and dual TCRα clones, each with their estimated frequency within the parent population. See text and Methods for more details.

The algorithm then uses a maximum likelihood approach to estimate the relative frequencies of the clones associated with each candidate αβ pair (Fig 2F; Methods). These estimated frequencies are then used with the patterns of co-occurrences of chains to distinguish between β-sharing and dual TCRα clones (see Methods). This step also yields refined estimates of the frequencies of dual TCRα clones. The output of the algorithm is a list of single or dual TCRα clones together with estimates of their abundances within the parent population (Fig 2G).

Testing on synthetic datasets

To test the performance of alphabetr, we first used artificially generated datasets mimicking the bulk sequencing of CDR3α and CDR3β regions from polyclonal T cell populations. We assumed skewed distributions of clone sizes, with between 5 and 50 clones comprising the most abundant 50% of the population and the remainder, approximately 2000 clones, forming a flat tail at low frequency (see Methods). These distributions were chosen to reflect plausible immunodominance hierarchies within T cell responses, motivated by analysis of epitope-specific cells recovered from human subjects immunised with live attenuated yellow fever virus vaccine (our analysis and ref. [11]). We also analysed different sizes of parent populations (see S1 Text, Section 2). Within these hierarchies we allowed the virtual clones to exhibit sharing of CDR3α and CDR3β at ranges of frequencies consistent with published single-cell TCR sequencing studies (Table 1) and our own data (Fig 1A). We also allowed between 10% and 30% of clones to express two productive TCRα chains and 6% of clones to express two productive TCRβ chains. The sequences in each ‘well’ were then generated by sampling between 10 and 300 T cells from the parent population with replacement. Selecting an optimal pattern of sampling is an issue we return to below.

To assess the robustness of alphabetr, we simulated the properties of two forms of sequencing error: dropping of chains and productive in-frame sequencing errors. Dropping of chains represents the failure of CDR3α and/or CDR3β regions to amplify or be detected, a process which likely has both purely random and clone-specific elements [22]. To model this, each clone was assigned a drop rate at random from a lognormal distribution with mean 0.15 and standard deviation of 0.01, with the rate capped at 0.9. Each instance of a CDR3α and CDR3β from that clone was then removed from the well with probability equal to the drop rate. To model productive in-frame sequencing errors, every unique CDR3α and CDR3β was assigned an error rate randomly drawn from a lognormal distribution with mean 0.02 and standard deviation 0.005. Each instance of a sequence at the per-cell level was replaced at random by one of three erroneous ‘daughter’ sequences, unique and specific to the parent sequence, with probability equal to the sequence-specific in-frame error rate. Thus on average each CDR3α and CDR3β generated mutant offspring sequences at the rate of 2% per instance in each cell in the plate(s).

We then assigned identifiers to the remaining CDR3α and CDR3β sequences, associating them with the sample’s location in a virtual 96-well plate. The input to the algorithm is the list of these unpaired CDR3α and CDR3β sequences together with their well-identifiers. This process was repeated for different sampling strategies (varying the sample sizes within each well, and using one or five 96-well plates); different clonal size distributions; and different degrees of CDR3α and CDR3β sharing. Under these ranges of conditions, the algorithm was tested for the following:

1. Overall depth, the number of αβ pairs that were correctly identified, as a proportion of the total number in the parent population (here a dual TCRα clone α_j α_k β is treated as two clones α_j β and α_k β—see points 4 and 5)

2. Depth of top clones, the proportion of those clones that comprise 50% of the population after ranking by abundance that were correctly identified

3. False pairing rate, the proportion of identified αβ pairs that were incorrect

4. Adjusted dual depth, a measure of how well dual TCRα clones can be identified from candidate pairs:

   $$=\frac{\#\text{ correctly identified dual TCR}\alpha \text{ clones}}{\#\text{ true dual TCR}\alpha \text{ clones whose two }\alpha \text{ chains are in the list of candidate }\alpha \beta \text{ pairs}}$$

5. False dual rate, the proportion of candidate dual TCRα clones that were incorrectly identified.

alphabetr does not attempt to identify dual TCRβ expressing cells because dealing with this relatively infrequent phenomenon together with dual TCRα chains and sharing of both TCRα and TCRβ chains across clones is extremely challenging algorithmically. However, we include dual TCRβ cells in our simulated data at the level of 6% to establish their impact on the algorithm’s performance.

A mixed sampling strategy with stringent co-incidence criteria strikes a balance of depth and accuracy of pairing

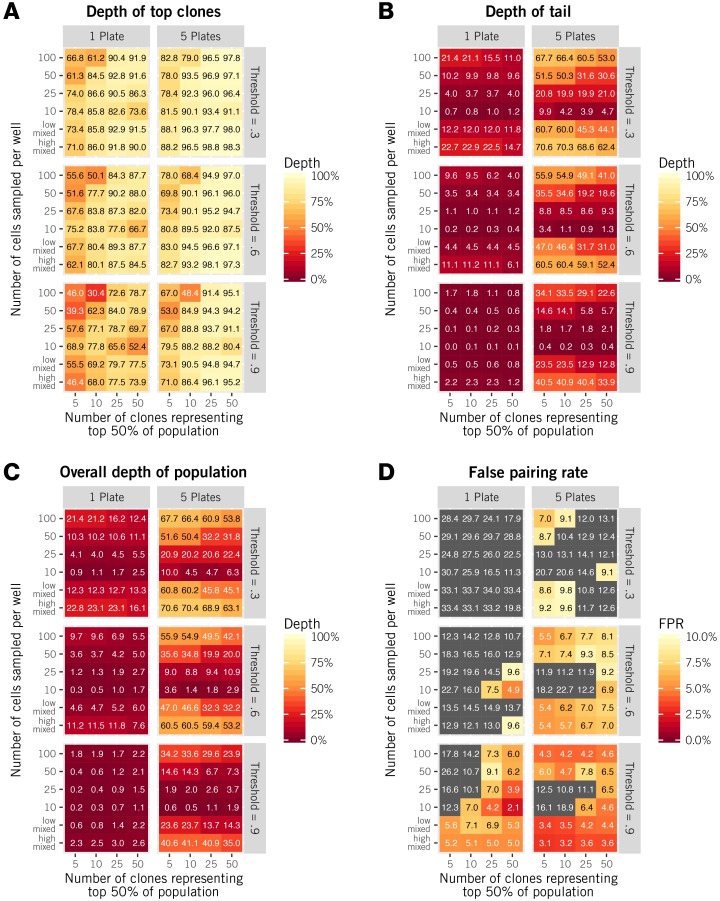
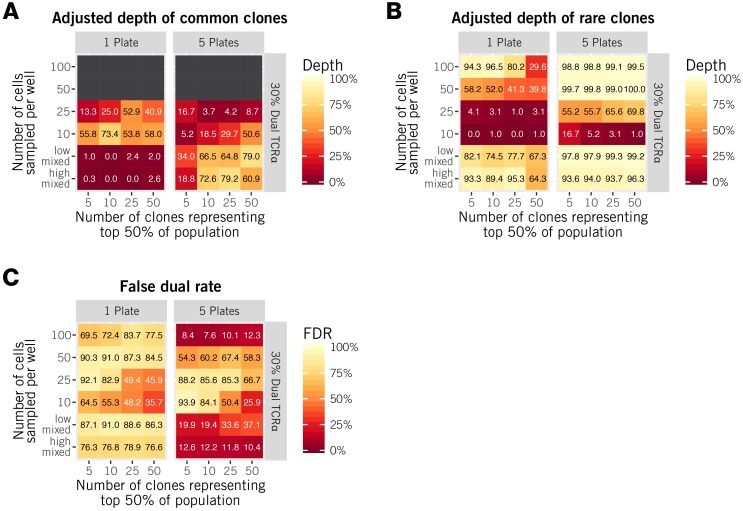
Fig 3 shows the depth and accuracy of pairing using simulated data. These were generated by sampling from parent populations of 2100 clonotypes exhibiting sharing of both TCRα and TCRβ chains, with drop rates and in-frame error rates of the CDR3α and CDR3β sequences drawn from lognormal distributions as described above. To test the algorithm robustly, we assumed 30% of clones expressed two TCRα, a prevalence at the upper limit of estimates from the literature [24]. We tested the ability of the algorithm to associate CDR3α and CDR3β sequences for different distributions of clonal frequencies and for different sampling strategies, using fixed numbers of cells per well (10, 25, 50, 100) or two mixed strategies (Table 2). We also show results for different degrees of consensus required for pair selection. For each set of conditions, performance metrics were computed by averaging the results of 100 simulated experiments.

Fig 3. Depth and accuracy of αβ pairings generated by alphabetr, for a range of overall sample sizes, sampling strategies and underlying distributions of clone sizes.

Simulations were performed using in silico data sets of one or five plates using six different sampling strategies (see text) and different degrees of skewness in clonal frequencies, as indicated by the number of clones comprising 50% of the population when ranked by frequency. ‘Threshold’ refers to the stringency of pair association, T (see Methods). (A) The proportion of the most abundant 50% of clones that were identified. (B) The proportion of the least abundant 50% of clones that were identified. (C) The overall depth was influenced strongly by the tail depth, indicating that data from one plate may be sufficient for recovering the most common clones. (D) The rate at which CDR3α and CDR3β sequences were incorrectly paired (false positive rate, FPR).

Table 2. The mixed sampling strategies used in the simulations.

Sampling Strategy	Number of plates	Number of wells × number of cells per well
High-Mixed	1	26 × 20	13 × 50	19 × 100	19 × 200	19 × 300
	5	128 × 20	64 × 50	96 × 100	96 × 200	96 × 300
Low-Mixed	1	26 × 15	6 × 20	13 × 30	19 × 50	19 × 100	19 × 150
	5	96 × 15	32 × 20	64 × 30	96 × 50	96 × 100	96 × 150

With only a single plate, the most abundant 50% of clones can be recovered with depths between 62% and 89% with a moderate threshold of 0.6 and the mixed sampling strategies, improving with less skewed distributions (Fig 3A). Coverage of rare clones (Fig 3B, left panels) is much more limited, particularly—and unsurprisingly—for sparse sampling strategies, but improves with a more lenient consensus threshold of 0.3. Using five plates boosts the recovery of rare clones considerably (Fig 3B, right panels), providing up to 61% depth with a threshold of 0.6 and 70% with a threshold of 0.3. As a result, for all sampling strategies, the effect of increasing the number of plates—and hence total sample size—is to increase overall depth (Fig 3C), almost entirely through greater recovery of rarer clones.

Increasing the number of plates also significantly reduces the false pairing rate (Fig 3D), which can be as low as 3.1% for 5 plates and a stringent threshold of 0.9 (Fig 3D, lower right panel). In general, and as expected, increasing the stringency threshold reduces false pairing rates. However, the stringency of the threshold can be relaxed if there is no significant presence of dual TCRβ clones in the T cell population of interest (S1 Text, Section 2 and Fig F).

Increasing the stringency (threshold) of the pseudo-jacknife procedure—that is, requiring a high frequency of occurrence of candidate pairs across subsets of the data—results in a lower false pairing rate at the cost of lower depth, largely for rarer clones (Fig 3C and 3D). This is because rarer clones will be excluded from the jacknife replicates more often than common ones; as the stringency of pair selection is increased, rare clones will therefore tend to be filtered out.

In summary, mixed sampling strategies with moderate to high acceptance thresholds yield the lowest false pairing rates (Fig 3D) while maintaining good depth of recovery of rare clones (Fig 3B). The high-mixed strategy requires a larger overall sample size and thus achieves greater depths, particularly of rare clones.

Sampling strategies for epitope-specific T cells may be constrained by the ability to recover sufficient cells

In practice, the availability of cells may place constraints on the sampling strategy. For example, with five plates the high- and low-mixed strategies require a total of 64,000 and 33,000 cells respectively. A typical sample of four tubes (approximately 30ml) of human blood yields roughly 3 × 10⁷ PBMCs, of which roughly half are αβ T cells. With such a sample, numbers of T cells specific for immunodominant epitopes of highly immunogenic infections such as Epstein-Barr virus and cytomegalovirus [40–43], numbers are unlikely to be limiting. A conservative estimate is that to acquire 100,000 cells with which to implement the high-mixed sampling strategy on five 96-well plates requires epitope-specific frequencies in excess of 1% of αβ T cells, or 0.5% of PBMC. Frequencies below this may dictate fewer plates and/or a sparser sampling strategy (S1 Text, Section 2).

Exploring different degrees of TCRα- and TCRβ-sharing, richness in clonal structure, and prevalence of dual TCRβ

Our simulation approach allowed us to explore other plausible datasets. We simulated populations exhibiting sharing at the high and low ends of the levels quoted in the literature, as well as different levels of clonal diversity (S1 Text, Section 2). For mixed sampling strategies with five plates, higher sharing levels increased the false pairing rate by at most 4% in absolute terms, although the magnitude of this effect decreased as the stringency of pair selection was increased (S1 Text, Fig B). Lower levels of sharing decreased the false pairing rate by approximately 1% in absolute terms (S1 Text, Fig C). In both cases, the depths of recovery were very similar to those presented in Fig 3.

Simulations of populations with higher diversity (3000 clones) show similar false pairing rates, similar top depths, and slightly lower tail depths to those for 2000 clones, while simulations of populations with 500 clones show slightly lower top depths, higher tail depths, and higher false pairing rates (S1 Text, Fig D and E). Populations comprising fewer clones overall will by definition display higher relative abundances, and as we discuss below, in such situations frequency-based pairing approaches will benefit from sparser sampling strategies.

Although alphabetr does not identify dual TCRβ clones, we performed simulations to compare how the presence of such clones in the parent population affects the ability of alphabetr to associate TCRα and TCRβ correctly (S1 Text, Fig F). The presence of dual TCRβ clones at a frequency of 6% increases the false pairing rate by approximately 3% in absolute terms, while not affecting the top and tail depths. Since significant levels of dual TCRβ clones have been shown in only a small number of studies sequencing antigen-specific T cell populations [25, 26], we believe this represents an upper bound on the effect of dual TCRβ clones on the performance of alphabetr.

Precise estimation of frequencies of common clones benefits from sparse or mixed sampling strategies

The probability that all chains associated with a clone co-appear in a given number of wells can be calculated straightforwardly from the binomial distribution. We can then use maximum likelihood to estimate this clone’s abundance within the parent population (see Methods).

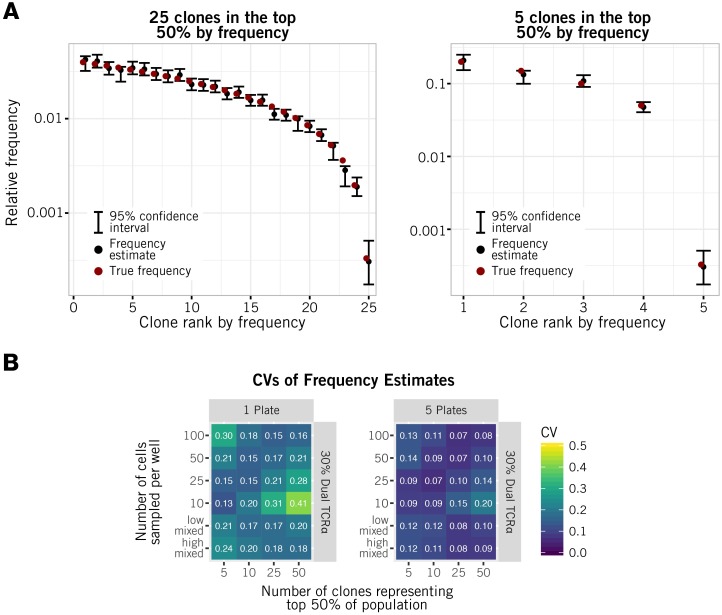
We used this procedure to assess the ability of alphabetr to estimate clonal abundances over a range of clonal size distributions and sampling strategies (Fig 4). We show results only for the most abundant clones making up 50% of the population. The left and right panels of Fig 4A show typical sets of abundance estimates for populations with moderately and highly skewed clonal distributions, with 25 and 5 clones respectively making up the top 50% of clones by size. We tested the method of construction of point estimates and confidence intervals using simulated data and confirmed that close to 95% of such intervals contained the true frequency (results not shown).

Fig 4. Assessment of the precision of clonal frequency estimation.

(A) Point estimates of clonal abundances generated by alphabetr, derived from representative simulations using five plates and distributions with 25 and 5 clones in the top 50% (left and right panels respectively). (B) The coefficient of variation (precision) of abundance estimates for a range of skewnesses of clone sizes and sampling strategies. Values quoted are averages over 100 simulations.

Fig 4B summarises the precision of the abundance estimation for a variety of sampling strategies and skewnesses. We quote an approximate coefficient of variation (CV) $\widehat{\sigma }/\widehat{f}$, where $\widehat{\sigma }$ is estimated using a quadratic approximation to the 95% confidence interval, 3.92$\widehat{\sigma }$, and $\widehat{f}$ is the estimated abundance. The procedure yielded CVs in the range 0.13–0.41 for one plate and 0.07–0.20 for five plates (Fig 4B).

Intuitively, the impact of skewness arises because we maximise the information regarding a given clone’s abundance when sample sizes are such that the clone appears in an intermediate proportion of wells. Sampling low numbers of cells is therefore optimal for determining the abundance of highly immunodominant clones, and larger numbers are optimal for determining the abundance of rare clones. For the clone distributions considered here, for common clones the sparsest sampling strategy (uniformly 10 cells/well) gives the greatest precision. In general, however a mixed sampling strategy strikes a balance between precision over a wide range of abundances (Fig 4B, bottom row in each panel), false pairing rates, and depth.

The clonal abundances shown in Fig 4A depend on prior knowledge or estimation of the mean drop rate, or the mean probability that any CDR3α or CDR3β of a clone will fail to be sequenced (see Methods). Neglecting this error rate yields lower bounds on clonal abundances (S1 Text, Section 3).

Efficient discrimination of dual TCRα and TCRβ-sharing clones requires a mixed sampling strategy and distinct methods for common and rare clones

The final step in the algorithm is to decide whether each candidate pair of clones that share a β chain (e.g. α₁β and α₂β) are indeed two clones or derive from one clone with a dual TCRα (α₁α₂β). To do this, we exploit the fact that the patterns of co-occurences of all three chains will be different under the two hypotheses. Initially, we use the estimated frequencies of a putative β-sharing clone pair α₁ β and α₂ β to calculate the expected number of wells in which all three chains should co-occur. Essentially, the three chains will tend to co-occur more frequently if they derive from a dual TCRα clone than if they derive from two β-sharing clones. We construct the ratio of the expected to the observed numbers of three-way co-occurrences for each β-sharing pair and perform k-means clustering on these ratios. The cluster of higher values forms the first list of candidate dual TCRα clones. See Methods for details and S1 Text, Section 5 for a visual example of the clustering of clones into two groups.

However, performing k-means clustering on only the numbers of three-way occurrences is inefficient at discriminating β-sharing and dual TCRα clones that are relatively abundant because the expected frequencies of co-occurrences become indistinguishable, particularly for rich sampling strategies in which the three chains co-occur in many wells. We therefore added a second step which utilises more information from the plates, calculating the likelihoods of all three- and two-way concurrences of α₁, α₂ and β under both hypotheses. Exact computation of these likelihoods is only practical for the low-occupancy wells (less than 50 cells/well), which conveniently are also the wells that contain maximal information regarding common clones. As a result, this second approach can be performed only when using sparse sampling strategies or the low-occupancy wells used in the mixed sampling strategies. We determined empirically that differences in the log-likelihoods of more than 10 distinguish the β-sharing and dual TCRα hypotheses.

The ability of these procedures to identify dual TCRα clones depends on alphabetr associating both TCRα chains with the TCRβ chains of these clones (e.g. associating α₁ and α₂ with β for a dual α₁α₂β clone). We therefore assess the efficiency of the discrimination using the ‘adjusted dual depth’—the number of correctly identified dual TCRα clones divided by the number of true dual TCRα clones whose constituent chains appeared in the candidate list of αβ pairs (that is, those dual TCRα clones α₁α₂β for which α₁ and α₂ were both paired with β in the first stage of the algorithm). We also calculate the false dual rate (FDR)—the proportion of the putative dual TCRα clones that were incorrectly identified.

Fig 5 summarises the ability of the algorithm to distinguish TCRβ-sharing and dual TCRα clones. Common clones are identified through the three-way likelihood approach, and mixed sampling strategies give the best results in this case, with adjusted depths of up to 79% for less skewed distributions (Fig 5A). The likelihood approach still performs relatively poorly with very highly skewed populations, distinguishing dual TCRα from β-sharers correctly at most 34% of the time for population with 5 clones making up the top 50% of the population (Fig 5A). Under these circumstances, the statistics of co-incidence of the three chains are very similar under the two hypotheses of dual TCRα or TCRβ-sharing clones. In contrast, the k-means procedure achieves adjusted depths of 93–99% for rare clones when using 5 plates and the high-mixed strategy (Fig 5B). Averaging over all clones, this strategy gives false dual rates of between 10–13% (Fig 5C).

Fig 5. Discriminating between dual TCRα and β-sharing clones.

We assess the degree of recovery of dual TCRα clones with the ‘adjusted depth,’ which is the proportion of dual TCRα clones correctly assigned out of the list of candidate dual TCRα and TCRβ-sharing clones. Panel (A) shows the adjusted depth of common clones; panel (B), rare clones. For common clones, we used likelihood-based discrimination; for rare clones we used a clustering approach. Both procedures are detailed in Methods. Panel (C) shows the false dual rate averaged over all clones—the proportion of identified dual TCRα that are incorrect. All results are shown for a threshold of 0.3 with 30% prevalence of dual TCRα and are averages over 100 simulations.

Extensive single-cell sequencing is required to achieve equivalent overall depth to alphabetr

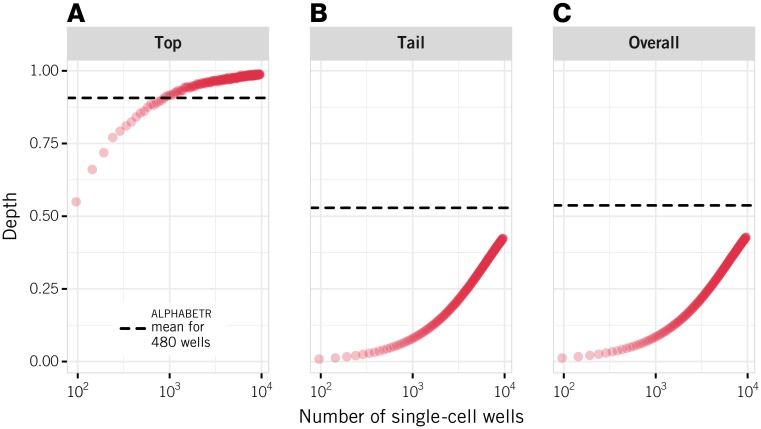
A key issue is whether implementing alphabetr improves upon single-cell approaches. One way to assess this would be to take a sample of antigen-specific cells, perform single-cell sequencing on a subset of these cells, and apply alphabetr to the remainder to compare their performance on the same set of parent clones. An alternative, which we perform here, is to simulate both scenarios. The advantages of the simulation approach are that it allows us to (i) triangulate both methods with the gold-standard of the true sequences, which are not known in practical settings due to dropping of chains and in-frame sequencing errors, and (ii) explore levels of single-cell sequencing that are currently prohibitively costly.

We simulated the sequencing of between 96 and 9600 single cells sampled from the same synthetic T cell populations used for evaluating alphabetr, and using the same model of sequencing errors. Fig 6 compares the performance of the two methods for a population of 2100 clones, with 25 clones making up the top 50% by abundance. alphabetr was implemented with the high-mixed sampling strategy of five plates and with a stringency threshold T = 0.6. We show performance comparisons using other distributions of clone sizes in S1 Text, Section 7. Under the conditions used for Fig 6, almost double the number of single-cell sequencing runs was required to achieve the same top depth yielded by alphabetr with five plates, and more than 100 plates of single cells are required to approach alphabetr’s level of recovery of rare clones. With the same clone size distribution, even a single plate analysed with alphabetr yields top depths from 78% to 92%, depending on the threshold parameter used (Fig 3A), whereas 96 single cells yield a top depth of 60% (Fig 6A). Single-cell sequencing will exhibit a false positive rate that is approximately twice the mean of the in-frame error rate, or 4% in our simulations, an accuracy that is comparable to that of alphabetr at its most stringent.

Fig 6. Comparison of single-cell approaches and alphabetr.

Single-cell sequencing was simulated by sampling from the same populations used to evaluate alphabetr and including both the dropping of chains and in-frame sequencing errors. In these simulations, the parent population contains 2100 clones with 25 clones representing the top 50% of the clones ranked by abundance. The results were evaluated for (A) top depth, (B) tail depth, and (C) overall depth. The dashed lines show the mean performance of alphabetr applied to five plates using the high-mixed sampling strategy and a threshold of 0.6 (values taken from Fig 3). The single-cell sequencing results are averages of 200 simulations.

Applying alphabetr to real sequencing data

Using simulated data allowed us to assess the performance of alphabetr directly using the gold standard of known TCRαβ sequences and under a range of plausible experimental conditions. However, to illustrate a real-world application, we applied alphabetr to a published dataset derived from the TCRs of tumour-infiltrating lymphocytes (TILs) from human subjects [22]. The study also used a frequency-based method to pair the TCRα and TCRβ obtained by sampling TILs from nine different tumours into the wells of one 96-well plate and sequencing the CDR3α and CDR3β chains found in each. One tumour (Breast 1) yielded only 7 pairs, and we excluded it from the analysis. We applied alphabetr to the chains from each of the remaining 8 tumours in turn. We then compared the pairs determined by alphabetr to those identified explicitly by ref. [22] (Table 3; see Section 8 of S1 Text for details). The true TCR clonotypes are unknown and so our aim was to measure degrees of concordance and conflict between the two methods. In 6 out of 8 tumours, alphabetr recovered fewer clones; however we found average concordance rates of 77%, defined as the proportion of the pairs identified by alphabetr that were also identified in ref. [22]. Perhaps more strikingly, we also found a very low incidence of conflicting pairs (mean 2% across tumours, as a proportion of all pairs identified by alphabetr). Conflicts were defined as those clones determined by the two methods that have only one chain in common.

Table 3. Recovery of tumour-infiltrating lymphocyte TCR pairs using alphabetr and data from ref. [22].

The data were processed by associating chains with their tumour sources through exact matching of the CDR3 nucleotide sequences from the mixed tumour samples to CDR3 libraries obtained from blood samples from each patient. The data were then simplified by selecting only those chains associated with one tumour. We then used alphabetr to identify TCRαβ pairs. The numbers of pairs unambiguously identified in ref. [22] were determined by directly matching nucleotide sequences to the CDR3 libraries, and only those pairs for which both chains could be directly associated with the corresponding tumour sample were included in the analysis.

Tumour Sample	Number of pairs identified by alphabetr	Number of pairs unambiguously identified by ref. [22]	Number of identical identified pairs	Percentage of alphabetr pairs agreeing with ref. [22]	Number of conflicting pairs	Number of novel pairs from alphabetr
Breast 2	98	85	74	75.5%	0	24
Breast 3	109	129	94	86.2%	1	14
Breast 4	50	85	26	52.0%	1	23
Kidney 1	74	112	58	78.4%	3	13
Kidney 2	145	286	126	86.9%	5	5
Kidney 3	213	282	166	77.9%	8	39
Kidney 4	157	176	131	83.4%	1	25
Lung 1	173	163	124	71.7%	1	48

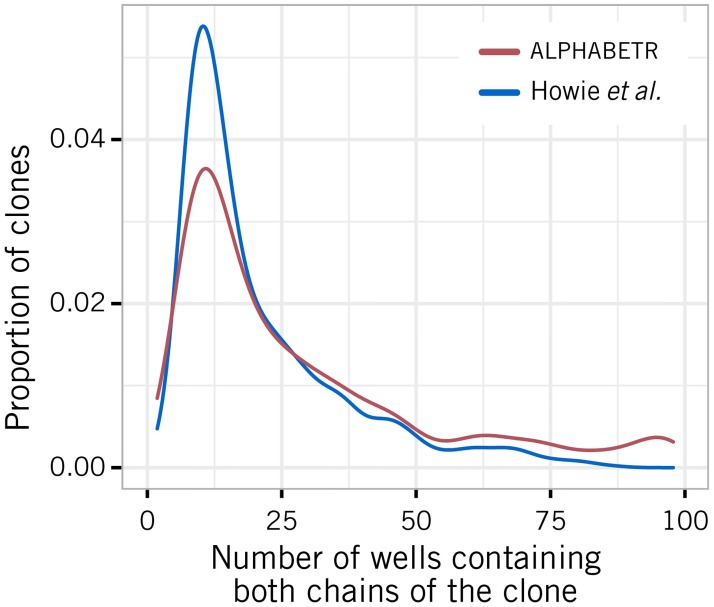
To compare the abilities of the two algorithms to identify rare or common clones, we stratified the identified αβ chain pairs by the frequency with which they co-appeared in wells. With stringency thresholds greater than 0.7, we find that with a single 96-well plate and a sampling strategy optimised for use by the algorithm described in ref. [22], alphabetr is less efficient at identifying rare clones but identifies clones with moderate to high abundances—for which the TCRα and TCRβ chains co-appear in more than a quarter of the wells—more efficiently (Fig 7; see Fig J in S1 Text for a breakdown by tumour). The clones identified by alphabetr alone exhibit moderate levels of sharing (TCRα-sharing, mean 16%, range 0–60%; TCRβ-sharing, mean 13%, range 4–31%). Of the sharers, an average of 76% share a chain with a clone that was identified by both methods.

Fig 7. Comparison of well occupancy patterns of the clones identified by alphabetr and in ref. [22].

For each method, TCRαβ pairs identified for all tumour samples were combined to estimate the distribution of the number of wells in which the chains co-appeared. The differences between these distributions indicate the relative efficiency with which the two algorithms identify clones, as a function of their abundance.

Discussion

Applying high throughput single-cell sequencing technologies to very large numbers of T cells is becoming increasingly within reach, but smaller-scale solutions using frequency-based sampling potentially remain far more economical. While another implementation of this strategy exists [22], the promiscuous nature of TCRα and TCRβ usage within epitope-specific populations presents multiple challenges to frequency-based methods that have not been addressed to date, to our knowledge. The combination of alphabetr and relatively low-cost sequencing strategies addresses these issues, being capable of handling a wide range of clonal structures—skewed abundances, dual TCRα, sharing of both TCRα and TCRβ between clones—as well as providing estimates of clonal abundances. The algorithm is available as a documented package in R [44] from http://github.com/edwardslee/alphabetr.

Single-cell technologies clearly allow the identification of large clonal expansions within populations. Our algorithm offers the potential to both identify these common clones as well as achieve depths of coverage of rarer clones that far exceed those currently possible with reasonable levels of single-cell sequencing. Given the correlation between diversity of immune responses and protection, this characterisation of the full diversity of T cell responses may be a better prognostic indicator than simply identifying common clones. Further, establishing the levels of TCRα- and TCRβ-sharing within populations sheds light on mechanisms of antigen recognition, repertoire diversity, and the efficiency of recruitment into immune responses.

Our analysis demonstrates that the most difficult of these challenges is to reliably distinguish between abundant TCRβ-sharing or dual TCRα clones within highly skewed populations because the expected patterns of co-occurrences of the three chains under the two alternatives are very similar when sequencing samples of a few tens of cells per well; all three chains typically appear in nearly all the wells. The difference in patterns can be magnified to an extent by sampling very few numbers of cells per well, but this solution comes with the cost of a reduction in total sample size, sacrificing depth of recovery of rarer clones. One might suppose that the high prevalence of dual TCRα clones in the naive T cell pool favours that scenario over TCRβ-sharing. However, our immunological intuition here may be misleading. Naive T cell precursor numbers may be in the range 10–1000 cells in mice [45–47], which we estimate is comparable to or larger than the size of TCRβ-sharing populations exported from the thymus. If the sharing of a TCRβ between clones confers overlap in their TCR specificities, and if recruitment into immune responses is efficient, we might expect to see significant levels of TCRβ-sharing within expanded, epitope-specific populations. Indeed, as shown in Table 1, TCRβ-sharing has been seen to reach levels of up to 25% in responses to influenza epitopes in naive mice [13, 14] and almost 40% in secondary responses [14]. It also occurred at a level of 2% in our analysis of TCRα and TCRβ usage among CD8⁺ cells specific for a YFV epitope in a human volunteer. The TCRβ-sharing/dual TCRα ambiguity is therefore a robust feature of epitope-specific responses, and is challenging to unravel fully with statistical approaches.

There are at least three ways to address this problem. One solution is to pair alphabetr with, for example, one plate of single-cell samples. Since the ambiguity is only manifest strongly with common clones, this limited amount of extra information may serve to resolve the issue. A second approach is to exploit the fact that 30%-40% of clones will yield both an in-frame and an out-of-frame CDR3α sequence [13]. Currently, out-of-frame sequences are not utilised by alphabetr; one could extend it to include them and associate clones with their out-of-frame sequences. Clones possessing one in-frame and one out-of-frame CDR3α could then be excluded from the list of dual TCRα candidates, which would assist β-sharing/dual TCRα discrimination. A third possibility is to extend the algorithm to exploit the sequence information itself. If dealing with epitope-specific populations, we might expect more sequence similarity in the CDR3α in two β-sharing clones than in a dual TCRα case. In the latter, the two CDR3α sequences are likely unrelated because presumably only one of the TCRα chains is involved in antigen recognition and they rearrange independently.

In practice, one needs a strategy for implementing alphabetr on a given sample of T cells with no a priori knowledge of the number or size distribution of clones. Assuming the number of cells is not limiting, we advocate a high-mixed sampling approach that involves sampling 20–300 cells per well and deals efficiently with a wide range of clonal abundances. When alphabetr is implemented as described here, a standard desktop computer with 16 Gb of RAM is able to handle samples from parent distributions of up to 4000 clones. When sampling populations with much fewer clones, lower numbers of cells/well are needed to avoid high false pairing rates. Assuming cell numbers are not limiting, bulk sequencing of the β chain could be used to gain a rough estimate of the richness of the parent distribution and so indicate when a sparse sampling strategy would be beneficial. In situations where cell numbers are limiting, one approach could be to begin with a single plate of 10 cells/well to obtain a rough lower bound on the richness of the distribution and apply a low or high mixed sampling strategy with the remaining cells from the sample, as appropriate. The single plate of 10 cells/well is then still usable for the pairing process and for frequency estimation.

While we have framed our analysis around the sequencing of epitope-specific populations, alphabetr can equally well be applied more generally to T cell populations of restricted and potentially skewed polyclonality, such as tumour infiltrating lymphocytes or T cells extracted from sites of autoimmune responses. It therefore has immediate applications in cancer immunotherapy and other personalised immunomodulatory treatments. Until single-cell sequencing becomes more affordable, frequency-based pairing methods provide a rapid and economical means of characterising the clonal structure of T cell populations.

Methods

Ethics statement

All experimental procedures were approved by the Regional Ethical Review Board in Stockholm, Sweden: 2008/1881-31/4, 2013/216-32, and 2014/1890-32.

Algorithm for TCRαβ pairing

Our approach exploits the fact that TCRα and TCRβ sequences (referred to as α and β chains) will tend to appear together in wells. Let N_α be the total number of unique α chains, N_β be the total number of unique β chains, and the α and β chains found in the data set be labelled from 1 to N_α and from 1 to N_β respectively. The degree of association between chains α_i and β_j is measured by a score S_ij,

$$S_{ij}=\sum _{k=1}^W\left(\frac{{\delta }_{ij}^k}{c_{\alpha }^k}+\frac{{\delta }_{ij}^k}{c_{\beta }^k}\right),$$ (1)

where the wells in the data are labelled from 1, 2, …, W, the numbers of distinct α and β chains in well k are $c_{\alpha }^k$ and $c_{\beta }^k$ respectively, and ${\delta }_{ij}^k$ is 1 if both α_i and β_j are found in well k and 0 otherwise. Eq 1 sums the co-appearances in wells, each weighted inversely by the total number of α and β chains recovered from the well. The scaling accounts for the fact that the larger the number of unique chains in a well, the lower our confidence that a co-occurring α and β pair derive from the same clone.

The algorithm begins by sampling a proportion p_J of the wells in the data without replacement. For all analyses presented here, we used p_J = 0.75, which provided a good balance between depth and false pairing rate. The algorithm computes the association scores between every unique α and β chain using Eq 1 based on the sampled subset of wells. Let ${\mathcal{A}}_k$ denote the set of A distinct α chains found in well k, that is ${\mathcal{A}}_k=\{{\alpha }_{m_1^k},{\alpha }_{m_2^k},\dots ,{\alpha }_{m_A^k}\}$, where the $m_i^k\in \{1,\dots ,N_{\alpha }\}$ are integers that denote the labels of the A TCRα chains found in well k. Similarly, let ${\mathcal{B}}_k$ denote the set of B distinct β chains found in well k, that is ${\mathcal{B}}_k=\{{\beta }_{n_1^k},{\beta }_{n_2^k},\dots ,{\beta }_{n_B^k}\}$, where the $n_i^k\in \{1,\dots ,N_{\beta }\}$ subscripts denote the labels of the B TCRβ chains found in well k. The algorithm solves the following linear assignment problem using the Hungarian algorithm [39]:

$$\begin{array}{ll}\text{maximize}\hfill & {\displaystyle \sum _{{\alpha }_i\in {\mathcal{A}}_k}}{\displaystyle \sum _{{\beta }_j\in {\mathcal{B}}_k}}{S}_{ij}{x}_{ij}\hfill \\ \text{subject\hspace{0.17em}to}\hfill & {\displaystyle \sum _{{\alpha }_i\in {\mathcal{A}}_k}}{x}_{ij}=1\text{\hspace{0.17em}for\hspace{0.17em}}{\beta }_j\in {\mathcal{B}}_k\hfill \\ \hfill & {\displaystyle \sum _{{\beta }_j\in {\mathcal{B}}_k}}{x}_{ij}=1\text{\hspace{0.17em}for\hspace{0.17em}}{\alpha }_i\in {\mathcal{A}}_k\hfill \\ \hfill & x_{ij}\ge 0,{\alpha }_i\in {\mathcal{B}}_k,{\beta }_j\in {\mathcal{A}}_k,\hfill \end{array}$$ (2)

where x_ij = 1 indicates that α_i and β_j are assigned as a candidate TCR pair and x_ij = 0 otherwise. A pair α_iβ_j is defined as an assigned pair of well k if x_ij = 1 for Eq 2 associated with well k. The number of assignments made for every pair of α and β is recorded as X_ij, i.e. X_ij equals the number of times x_ij = 1 from the solutions of Eq 2 for each well in the subset. We then calculate a filter level F that determines the minimum number of assignments required for an assigned candidate pair of α and β chains to be determined as a true TCR pair. The filter-level F is chosen to be the mean of the elements of the set {N(i, j) : N(i, j) > 0, i ∈ 1, 2, …, N_α, j ∈ 1, 2, …, N_β}, where N(i, j) is the number of times α_i β_j are assigned to each other, The output of this algorithm is then a list of candidate αβ pairs that may be associated with T cell clone. At this stage, dual TCRα cells are not identified; thus a clone α₁α₂β may be represented in this list as one or both of α₁β and α₂β.

The procedure above is performed N_r times on random subsets of the wells (all simulations in this paper use N_r = 100), and each replicate yields a list of candidate αβ pairs. We then perform a filtering or consensus step in which only αβ pairings that appear in more than a threshold proportion T of these lists are retained as candidates. The simulations we present in the text explore thresholds of T = 0.3, 0.6, and 0.9.

Maximum-likelihood estimation of clonal frequencies

We use maximum likelihood to infer clonal frequencies based on the number of wells in which a pair of α and β chains both appear. Let N = {n₁, n₂, …, n_s} be the set of s distinct sample sizes (n_i cells per well) in all of the wells and W = {w₁, w₂, …, w_s} where w_i represents the number of wells with samples of size n_i cells. Let c_ij denote the clone with chains α_i and β_j and let $k_{ij}^l$ denote the number of wells of sample size n_l cells per well that contain chains α_i and β_j. The likelihood of the observations $k_{ij}^{(.)}$, given that the clone c_ij is present at frequency f_ij within the population, is

$$\mathcal{L}\left(\text{observed}\text{incidence}\text{of}\text{clone}{c}_{ij}|f_{ij}\right)=\prod _{l=1}^s\left(\begin{array}{c}{w}_l\\ k_{ij}^l\end{array}\right){\left(1-q_l\right)}^{k_{ij}^l}{q}_l^{w_l-k_{ij}^l}$$ (3)

where q_l is the probability of clone c_ij not being found in well l and is given by

$$q_l={\left(1-f_{ij}\right)}^{n_l}+\sum _{m=1}^{n_l}\left(2{ϵ}^m-{ϵ}^{2m}\right)\left(\begin{array}{c}{n}_l\\ m\end{array}\right)f_{ij}^m{\left(1-f_{ij}\right)}^{n_l-m}.$$ (4)

Here ϵ is the average probability that a CDR3 sequence in a cell fails to be amplified and sequenced. For every clone c_ij, the algorithm maximises Eq 3 to estimate its frequency f_ij, and 95% confidence intervals are defined by the frequencies yielding $log\mathcal{L}=log{\mathcal{L}}_{\text{max}}-\text{1.96}$. Details of the derivation of Eqs 3 and 4 are given in Section 4 of S1 Text.

This procedure is applied to every αβ pair identified in the first phase of the algorithm. These estimated frequencies are used to distinguish TCRβ-sharing clone pairs from single TCR clones expressing two TCRα. This procedure is described in the following section. When a clone with two TCRα is identified, we revise the frequency estimate as follows. Let c_(ij)t denote a clone with chains α_i, α_j, and β_t, and $k_{\left(ij\right)t}^l$ denote the number of wells of size n_l that contain chains α_i, α_j, and β_t. The likelihood of the observations given that clone c_(ij)t has a frequency f_(ij)t ∈ (0, 1] is

$$\mathcal{L}\left(\text{observed}\text{incidence}\text{of}\text{clone}{c}_{\left(ij\right)t}|f_{\left(ij\right)t}\right)=\prod _{l=1}^s\left(\begin{array}{c}{w}_l\\ k_{\left(ij\right)t}^l\end{array}\right){\left(1-q_l\right)}^{k_{\left(ij\right)t}^l}{q}_l^{w_l-k_{\left(ij\right)t}^l}$$ (5)

where q_l is the probability of clone c_(ij)t not being found in well l and is given by

$$q_l={\left(1-f_{\left(ij\right)t}\right)}^{n_l}+\sum _{m=1}^{n_l}\left(3{ϵ}^m-3{ϵ}^{2m}+{ϵ}^{3m}\right)\left(\begin{array}{c}{n}_l\\ m\end{array}\right)f_{\left(ij\right)t}^m{\left(1-f_{\left(ij\right)t}\right)}^{n_l-m}$$ (6)

where ϵ is the mean drop rate as described above. Eq 5 is then maximised to estimate f_(ij)t, and again $log\mathcal{L}=log{\mathcal{L}}_{\text{max}}-\text{1.96}$ is used to calculate 95% confidence intervals.

Discriminating between dual TCRα and shared TCRα chains

If the algorithm yields two clones that appear to share a TCRβ (α₁β and α₂β), we must decide whether this is indeed a β-sharing pair of clones or that the association derives from one dual TCRα clone (α₁α₂β). To do this, we use the likelihoods of observed co-occurrences of the three chains to assess the relative support for the two alternatives.

Let c_ij = (α_i, β_j) and c_kj = (α_k, β_j) be two putative clones with a common TCRβ chain β_j. We count the number of wells containing all three-way, two-way, and single appearances of the three chains. We then calculate the ‘full’ likelihoods of this pattern of occurrences under two hypotheses: (A) that c_ij and c_kj are indeed two β-sharing clones, with frequencies f_ij and f_kj estimated using Eq 3; and (B) that the chains derive from one dual TCRα clone c_(ij)k present at frequency f_(ij)k, estimated using Eq 5. If the difference $log{\mathcal{L}}_B-log{\mathcal{L}}_A\ge 10$, we assume the three chains derive from dual TCRα clone.

The calculation of these full likelihoods is in Section 6 of S1 Text but is computationally tractable only for wells with less than 50 cells due to the need to calculate large multinomial coefficients. The full-likelihood method is therefore only appropriate for estimating frequencies of those relatively abundant clones that are commonly found in the wells with smaller sample sizes. We use a more restricted likelihood-based approach for discriminating β-sharing and dual TCRα among rare clones, which tend to appear only in larger samples. Let clones c_ij = (α_i, β_j) and c_kj = (α_k, β_j) be two clones with a common beta chain β_j, and let f_ij and f_kj be their estimated frequencies. The algorithm calculates the ratio $r_{ik}^j$ of the observed to the expected number of wells in which all three chains from the putative β-sharing pair c_ij and c_kj co-appear, under the hypothesis that they are indeed two clones and not a dual TCRα:

$$R=\left\{r_{ik}^j=\frac{A\left(c_{ij},c_{kj}\right)}{E\left(c_{ij},c_{kj}\right)}:i\ne k,j\in 1,2,\dots ,N_{\beta }\right\}$$ (7)

where A(c_ij, c_kj) is the number of times clones c_ij and c_kj are observed to appear in the same well and N_β is the number of distinct β chains, and the expected number is

$$E\left(c_{ij},c_{kj}\right)=\sum _{l=1}^s{w}_l\left(1-{\left(1-f_{ij}\right)}^{n_l}-{\left(1-f_{kj}\right)}^{n_l}+{\left(1-f_{ij}-f_{kj}\right)}^{n_l}\right)$$ (8)

(see S1 Text, Section 5 for a derivation and discussion of this equation). We then partition the set of ratios R into two groups C₁ and C₂ using k-means clustering, where the mean of ratios of C₁ is greater than the mean of the ratios of C₂ (see S1 Text, Fig G for an example). The clones associated with the ratios in C₁ are chosen as dual TCR clones, such that if $r_{ik}^j\in C_1$, then clones c_ij and c_kj are removed from the list of TCR pairs and replaced with a dual TCRα clone α_i α_k β_j.

Creation of in silico data sets for validation

We created synthetic data sets reflecting the properties of antigen-specific T cell populations and sequencing errors. The data sets were sampled from a population of T cell clones where a significant proportion of α and β chains are shared and 10%-30% of clones have dual TCRα chains (e.g. three clones can have the following chains: α_i β_k, α_j β_k, and α_j α_h β_l). The sharing of β chains was set such that 85.9% of β chains were uniquely from one clone, 7.6% shared by two clones, 3.7% shared by three clones, 1.9% by four clones, and 0.9% by five clones. The sharing of α chains was set such that 81.6% of α chains were uniquely from one clone, 8.5% shared by two clones, 2.1% shared by three clones, 0.7% shared by four clones, 3.3% shared by five clones, 0.5% shared by six clones, and 3.3% shared by seven clones. We determined these levels of sharing by averaging those from the published single-cell data shown in Table 1.

The frequencies of the N clones were drawn from a skewed distribution in which n_s clones comprise a proportion p_s of the population and the other N − n_s clones evenly represent 1 − p_s of the population. The clone ranked i^th in abundance then has frequency f_i where

$$f_i=\left\{\begin{array}{cc}{f}_1+r\left(i-1\right)\hfill & \text{if}i=1,2,\dots ,n_s\hfill \\ p_s/(N-n_s)\hfill & \text{if}i=n_s+1,n_s+2,\dots ,N\hfill \end{array}\right.$$ (9)

where the frequency of the largest clone f₁ and the step size r are determined by solving the equations

$$\sum _{i=1}^{n_s}{f}_i=p_s,f_{n_s}=1.1\times \frac{p_s}{N-n_s}.$$ (10)

The frequency of the smallest clone in the top 50%, f_ns, is set to be 10% higher than the frequency of the clones in the tail. All simulations were based on p_s = 0.5. We varied the number of top clones n_s between 5 to 50 to test how skewness in the antigen-specific T cell population impacts the performance of the algorithm.

In order to make the simulated data more realistic, experimental noise was included in the forms of ‘dropped’ chain errors and in-frame sequencing errors. Dropped chains are CDR3 sequences that fail to be sequenced due to PCR errors and/or sorting problems, and studies utilising both single-cell and many-cell techniques have reported average drop rates of 8% to 10% [17, 22]. In the simulations, each clone was assigned a drop rate from a lognormal distribution with a mean of 0.15 and standard deviation of 0.01, and every TCRα and TCRβ chain belonging to that clone was assigned that drop rate. In-frame errors cause a CDR3 sequence to be falsely identified with an incorrect productive nucleotide and/or amino acid sequence. In the simulations, each distinct sequence was assigned an in-frame error rate drawn from a lognormal distribution with a mean of 0.02 and a standard deviation of 0.005. The error model was simulated as follows: when a cell is sampled into a virtual well, each of its chains fails to be sequenced with probability equal to the pre-assigned, clone-specific drop rate. Every surviving chain produces one of three randomly chosen, distinct, and chain-specific false sequences with probability equal to that chain’s pre-assigned in-frame error rate.

TCR sequencing

A human volunteer was identified as HLA-A2⁺/HLA-B7⁺ and received the live attenuated yellow fever vaccine (YFV-17D). On day 15 post-vaccination, peripheral blood samples were taken, and live CD3⁺CD8⁺ T cells were isolated by negative selection using magnetic columns (Miltenyi Biotec, CD8⁺ T cell negative isolation kit). Cells were labeled with a panel of antibodies and the HLA-A02:01/LLWNGPMAV dextramer representing the immunodominant response. Single dextramer-specific CD3⁺CD8⁺ T cells were sorted into individual wells in 96 well plates containing a lysis buffer (0.4% Triton, RNAse inhibitor, dNTP, OligodT) and immediately stored on dry ice. Single cell transcriptome libraries were subsequently generated from these cells using an adapted version of the SMRT-Seq2 protocol [48]. Libraries were prepared for sequencing by tagmentation and labelling individual single cell transcriptomes with a custom Tn5 enzyme [49] and Nextera XT dual indexes. Pooled libraries were then sequenced using an Illumina Hiseq2500 on high output mode (2 × 100bp or 2 × 125bp reads), and individual TCRα and TCRβ chains were identified using the MiTCR algorithm with default parameters. The default settings for MiTCR were used to align the CDR3 sequences. These were then manually filtered to remove erroneous sequences (e.g. early stop codons and CDR3 sequences that were greater than 30 amino aids in length), and then BLAST was used on the remaining sequences to check for mapping to other parts of the genome, removing as appropriate. All clones used in the comparative analysis of CDR3α lengths were curated manually to exclude the possibility of contaminating TCR sequences.

CDR3 amino acid sequences are provided as a CSV file in S1 Dataset, and the raw reads are deposited in the Gene Expression Omnibus (GEO), GSE75659; Sequence Read Archive (SRA), SRP066963.

Supporting Information

S1 Text. Supporting analyses.

(PDF)

S1 Dataset. TCR sequences of HLA-A02:01/LLWNGPMAV-specific cells.

(CSV)

Data Availability

All relevant data are within the paper, its Supporting Information files and in publicly available repositories as described in the manuscript. An implementation of the algorithm is available as an R package, with vignettes, from http://github.com/edwardslee/alphabetr.

Funding Statement

This study was funded by Arthritis Research UK and the NIH (R01 AI 093870). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.