Abstract
Magnetic nanoparticles (MNPs) have been used in many diagnostic and therapeutic biomedical applications over the past few decades to enhance imaging contrast, steer drugs to targets, and treat tumors via hyperthermia. Optical coherence tomography (OCT) is an optical biomedical imaging modality that relies on the detection of backscattered light to generate high-resolution cross-sectional images of biological tissue. MNPs have been utilized as imaging contrast and perturbative mechanical agents in OCT in techniques called magnetomotive OCT (MM-OCT) and magnetomotive elastography (MM-OCE), respectively. MNPs have also been independently used for magnetic hyperthermia treatments, enabling therapeutic functions such as killing tumor cells. It is well known that the localized tissue heating during hyperthermia treatments result in a change in the biomechanical properties of the tissue. Therefore, we propose a novel dosimetric technique for hyperthermia treatment based on the viscoelasticity change detected by MM-OCE, further enabling the theranostic function of MNPs. In this paper, we first review the basic principles and applications of MM-OCT, MM-OCE, and magnetic hyperthermia, and present new preliminary results supporting the concept of MM-OCE-based hyperthermia dosimetry.
Keywords: Magnetomotive nanoparticles, optical coherence tomography, optical coherence elastography, biomechanics, magnetic hyperthermia, thermotherapy, theranostic
I. Introduction
Magnetic nanoparticles (MNPs) have been used in biomedicine for various applications, which can be broadly grouped into the following three categories: (1) diagnostic applications such as biosensing, where MNPs have been used as proximity sensors and imaging or biomechanical contrast agents [1, 2], (2) therapeutic applications such as drug delivery and hyperthermia treatment [3], and (3) theranostic applications that incorporate both therapeutic and diagnostic functions [4]. To date, these techniques have been demonstrated in ex vivo, in vivo, and pre-clinical studies, and have been an emerging field of research.
From a biological point-of-view, MNPs (usually magnetite Fe3O4 and maghemite γ-Fe2O3) have several desirable properties that make them suitable for in vivo clinical applications. First, MNPs have controllable particle size (tens of nanometers), which is comparable to or smaller than several basic biological entities such as cells (10-100 μm) and proteins (5-50 nm), providing the possibility of cellular uptake [5]. When used in cancer treatment, MNPs can be delivered intravascularly and will ‘leak’ into a tumor (with a pore size of 380-780 nm) by the enhanced permeability and retention (EPR) effect, which facilitates their diagnostic and therapeutic effectiveness [6, 7]. Second, MNPs can degrade into iron and oxygen, which can be recycled in iron metabolic and oxygen transport systems and be safely eliminated from the systematic circulation by macrophages [8]. Additionally, the biocompatibility and biodegradability of MNPs can be further enhanced by surface functionalization [9]. Third, conjugation of specific functional groups or ligands allows for additional functions, such as targeting of specific tissues and enabling a more effective transport to the targeted sites by extending blood circulation time [10-12].
Considered from an engineering point-of-view, the advantages of using MNPs for biomedical applications are numerous. MNPs are magnetic and can respond to an external magnetic field, allowing remote manipulation. This implies that MNP-based diagnosis and therapy can be performed in a non-contact manner. Since, most tissues exhibit very little magnetism as compared to MNPs, the MNPs contained within the tissue can be sensed with high selectivity and specificity. Additionally, MNPs can be used to induce a localized heating and temperature increase by subjecting them to an alternating magnetic field. Generally, the heat induced only occurs in the MNP-laden malignant tissue while sparing the non-targeted healthy tissues. This is useful in thermotherapy such as magnetic hyperthermia, where the use of MNPs has been shown to provide improved treatment outcomes [5, 13]. Finally, MNPs possess negligible mass and inertia. This is particularly desirable for the diagnostic approaches that rely on the assessment of biomechanical tissue properties, where a non-negligible addition of mass may significantly alter the physical properties of the tissue.
Due to their versatility, MNPs have been used as imaging contrast agents in various biomedical imaging modalities including magnetic resonance imaging (MRI), computed tomography (CT), positron emission tomography (PET), and optical imaging [14]. In this paper, we focus on the review of MNPs combined with optical coherence tomography (OCT) techniques including magnetomotive optical coherence tomography and elastography (MM-OCT and MM-OCE), which allow for diagnostic measurements based on imaging and biomechanical contrast, respectively. OCT is a noninvasive optical imaging modality that provides cross-sectional images of tissues up to 1-2 mm in depth and with cellular level (micron scale) resolution, surpassing the resolution of the aforementioned imaging modalities [15, 16]. Additionally, we also discuss the use of MNPs as therapeutic agents, with hyperthermia therapy being our main focus. Finally, the feasibility of using MNPs as theranostic agent for both magnetic hyperthermia and dosage evaluation based on MM-OCE, including new preliminary results and discussion, will be presented.
The rest of the paper is organized as follows. In Section II, the underlying physics of MNPs, including their magnetic properties, will be discussed. In Section III, an overview of MM-OCT and MM-OCE, along with MNP-based diagnostic and therapeutic applications, will be presented. In Section IV, the theranostic use of MNPs will be discussed, followed by Sections V and VI, where new preliminary results of MM-OCE-based hyperthermia dosimetry are reported. Finally, in Section VII, we conclude with a discussion on the significance of our findings along with possible future research directions.
II. Background
A. Classification of Magnetic Materials
Magnetic materials can be categorized based on the degree of the magnetization induced in response to an applied magnetic field. The relation between the magnetic field strength and the magnetization (magnetic moment per unit volume of the material) is given by the following equation
| (1) |
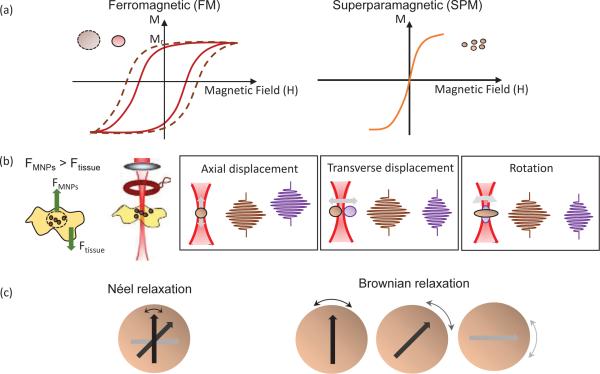
The constant of proportionality χ in the above equation is a dimensionless quantity, called the volumetric magnetic susceptibility, which specifies the degree of magnetization of a material. Typically, ferromagnetic (FM) materials have magnetic susceptibilities that are orders of magnitude larger than that of paramagnetic (PM) and diamagnetic (DM) materials. While PM materials are characterized by a positive magnetic susceptibility (χPM > 0) and are attracted by the magnetic field, DM materials have a negative magnetic susceptibility (χDM < 0) and are repelled by a magnetic field. Most materials are PM or DM, and can only be magnetized when a magnetic field is present. Hence, the curve passes through the origin and exhibits a one-to-one correspondence. In contrast, FM materials can acquire magnetization without an external field, which is indicated by a non-zero value of magnetization for a zero value of the magnetic field strength . Consequently, a typical curve for a FM material shows a hysteresis loop as shown in Fig. 1(a). Hysteresis results from domain boundary shifting by the change of intrinsic magnetic anisotropy energy of the crystalline material [18], and the shape of the hysteresis loop is inversely related to the particle size— the larger the particles, the narrower the loop [5]. For particles as small as 10-100 nm, the particle as a whole can be regarded as a single ‘giant’ spin due to the rigidly aligned atomic moments [19]. This ‘superparamagnetic’ (SPM) particle can then fluctuate freely in response to thermal energy. Like PM materials, SPM nanoparticles are only magnetized under an external field as shown in Fig. 1(a). However, the susceptibilities of SPM materials, much like FM materials, greatly exceed that of PM materials. The magnetization characteristics of a SPM nanoparticle is described by the Langevin function [20].
Fig. 1.
Classification and properties of magnetic nanoparticles. (a) Typical curve of (left) ferromagnetic (FM) and (right) superparamagnetic (SPM) particles, where the hysteresis loop and remnant magnetization () is present in the FM particles. (b) Schematic of the sample arm in a MM-OCT setup where (left) MNP-laden tissue is located beneath the magnetic coil. (Left) The magnetic force on the tissue and (right) different forms of magnetomotion are illustrated in relation to the OCT imaging beam (adapted from [11, 21]). (c) Heating mechanisms of SPM nanoparticles, where (left) Néel rotation describes the internal rotation of the magnetic moment (shown as arrows), and (right) Brownian rotation is the rotation of the entire particle.
While most human tissues are slightly DM and have susceptibilities within ±20% of that of water (χH20 = −9.05 × 10−6 in SI unit), a PM response is exhibited by vascular tissues, where iron-containing hemoglobin molecules are present
(χdeoxygenated,ferrous hemoglobin = 2.08 × 10−6 in SI unit [22]. For either case though, the susceptibility of tissue is far in SI unit) less than that of typical MNPs (either FM or SPM), which implies that the magnetic response induced within MNP-laden tissue is mainly determined by the MNPs. Thus, a high selectivity of the MNPs can be achieved in biomedical applications [5].
B. Magnetomotion
MNPs are capable of being actuated by an external magnetic field gradient and induces the movement of MNPs, which we have termed as ‘magnetomotion’ [23]. While magnetism can be sensed by the nonlinear magnetization and relaxation of the magnetic moment [24, 25], the presence of MNPs can also be detected by magnetomotion. The magnetomotion can offer dynamic imaging contrast at specific targeted tissue sites, or be modulated to reveal the biomechanical properties of the MNP-laden tissues [1], and both will be discussed in detail later.
Magnetomotion can arise when a magnetic force is exerted on the MNPs in a non-contact configuration. The magnetic force acting on a single spherical MNP can be described by the following equation [5, 26].
| (2) |
Here VMNP is the volume of the MNP, Δχ is the difference of the magnetic susceptibilities of the MNP and the environmental medium, μo is the permeability constant, and is the magnetic induction. Since no magnetic field gradient will be generated under a uniform magnetic field (i.e. ), the MNPs must be located outside the electromagnetic coil for motion generation.
Shown in Fig. 1(b), magnetomotion can have various forms. FM nanoparticles with remnant magnetization 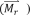 experience a torque and lead to rotation, while a translation will be observed for materials without
experience a torque and lead to rotation, while a translation will be observed for materials without 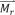 [27]. If a field is applied to SPM nanoparticles
[27]. If a field is applied to SPM nanoparticles 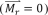 in the z direction under the assumption that it would not be affected by the magnetization within the material and that is the same throughout the particle volume V, the magnetic force on each individual MNP can be approximated as [28]. For NMNP amount of MNPs embedded within the tissue matrix, the net magnetic force of the ensemble of MNPs can hence be given by
in the z direction under the assumption that it would not be affected by the magnetization within the material and that is the same throughout the particle volume V, the magnetic force on each individual MNP can be approximated as [28]. For NMNP amount of MNPs embedded within the tissue matrix, the net magnetic force of the ensemble of MNPs can hence be given by
| (3) |
Tissues are often slightly DM . Hence, to achieve a net PM response , a threshold value of the MNP concentration should be met such that (Fig. 1(b))
| (4) |
The above inequality shows that although the tissue to MNP magnetization ratio is typically small (since χMNP ~1 >> |χtissue|~10−5), yet, to estimate the concentration of MNPs, the tissue to MNP volume ratio must be taken into consideration as well [28].
At magnetic field strengths sufficiently smaller than saturation, is linear to the applied and is proportional to (since in Eq. 2 can be written alternatively as , assuming no currents or time-varying electric field is present). Thus, to temporally modulate the MNPs with a sinusoidal wave, one can supply a voltage of [28]. If the induced magnetomotion is small enough so that the system undergoes a linear (Hookean) mechanical response, the displacement can then be written as
| (5) |
where A is the maximum displacement amplitude, fB is the modulation frequency, and φ is the phase lag in which a shift can be observed for a PM and DM response, reflecting directionality of the net magnetic force [28].
C. Energy Transfer
Electromagnetic energy can be transferred from an external magnetic field to the MNPs in the form of heat, equipping MNPs with the ability to deliver a thermal dose for therapeutic applications, such as hyperthermia treatment. The heat induction is mainly due to hysteresis loss and magnetic relaxation, while eddy current and magnetic resonance effects are neglected owing to the small size of the MNPs and the low field frequency typically applied in hyperthermia [5, 18].
For FM particles, the enclosed area of the hysteresis loop pertains to the energy loss per magnetization cycle [29]. If a time-varying magnetic field is applied repeatedly, a constant flow of energy can then be transferred to the MNPs. The heating power can therefore be determined from the energy loss per cycle times the frequency f of the excited alternating excitation field [5], given by
| (6) |
However, a substantial heating power from hysteresis loss is difficult to achieve if the field strength is not sufficiently strong, or if the uniaxial nanoparticles are not well-aligned with the excitation field, which impose challenges for in vivo applications [5].
The energy barrier for magnetization reversal decreases with decreasing MNP size, and hence the ambient thermal energy kT (the product of the Boltzmann constant k and temperature T) could allow the macroscopic magnetization of SPM nanoparticles to relax back to an equilibrium state once the magnetic field is removed [29]. This phenomenon is associated with both Néel and Brownian relaxations [29, 30], and can be characterized through an effective relaxation time τ, given by
| (7) |
where
| (8) |
Through Néel relaxation, the magnetic moment rotates within each particle (internal dynamics, Fig. 1(c)), and is affected by the magnetic anisotropy energy KV (the product of the magnetic anisotropy constant K and particle volume V). In Brownian relaxation, the entire particle suspended within a fluid rotates (external dynamics, Fig. 1(c)), which can be influenced by the frictional losses due to the liquid viscosity η and the hydrodynamic volume Vh, and is also affected by the additional volume of the adhered fluid layer or particle coating [29, 30]. Néel rotation dominates in the case where MNP are immobilized, such as when the MNPs are injected directly (interstitially) into a tumor [31]. In addition, Néel relaxation is more favorable for small particles, as can be seen from the size-dependent characteristics (i.e. Néel ~ exponential; Brownian ~ power law) [32].
The volumetric power dissipation in magnetic particles subjected to an alternating magnetic field is given by the following equation [29, 33].
| (9) |
Energy transfer only exists with a non-zero χ″, which denotes the imaginary part of the complex magnetic susceptibility (loss component) that depends on both the relaxation time τ and field frequency f [30, 32]. It has been reported that the magnetic fluid (a colloidal suspension of single domain particles) has a higher specific absorption rate (SAR) as compared to multi-domain particles, suggesting a prohibitively high field or frequency is not necessary for SPM nanoparticles to generate an adequate amount of heat [18, 34].
III. Magnetomotive nanoparticle applications
A. Magnetomotive optical coherence tomography
Nanoparticles, with their potentially higher targeting efficiency, have been utilized as image contrast agents in various imaging modalities such as MRI, CT, PET, ultrasound imaging, and optical imaging to enable visualization and recognition of specifically localized tissues in the body, such as tumors [35]. In OCT, which is a coherent imaging technique, image contrast can be provided by modulation of optical properties, either static (e.g. scattering, absorption, and polarization change) or dynamic (e.g. pump-probe OCT techniques) [21].
Magnetomotive OCT (MM-OCT) is a functional extension of OCT that employs MNPs or MNP-containing magnetic microspheres (MSs) as dynamic imaging contrast agents [23]. Actuated by an external magnetic field, the MNPs or magnetic MSs can undergo magnetomotion and modify the amplitude and phase of the OCT interferogram. The exogenous magnetic contrast agents can be delivered to the biological target via intravenous administration, followed by passive cellular uptake as macrophages in the reticuloendothelial system (RES) engulf the agents [36], or by actively targeting specific receptors or molecules with functionalized MNPs/magnetic MSs containing specific binding agents [37].
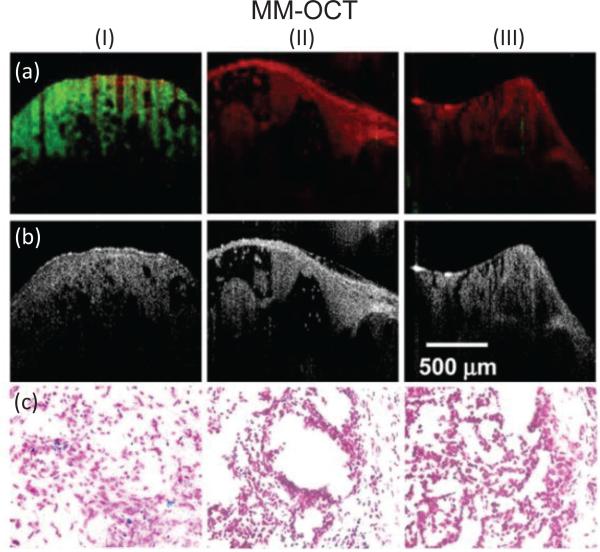
Using MM-OCT, the detection and sensitivity of MNPs at nanomole-scale concentrations can be achieved using a low field strength (less than 0.1 T) [11, 27, 28]. While the diffusion dynamics of MNPs in ex vivo tissues can be monitored [38], MM-OCT can also be used for in vivo tissue imaging [23] and targeting (Fig. 2). For instance, magnetite nanoparticles carrying antibodies to target human epidermal growth factor receptor (HER2neu) have been used to achieve in vivo mammary tumor imaging in a pre-clinical rat mammary tumor model [11]. In [1], thrombi within ex vivo porcine arteries can be marked by the adhesion of MNP-laden, rehydrated, lyophilized platelets to the injured sites. Likewise, arginine-glycine-aspartic acid (RGD)-functionalized protein MSs were shown to target the αvβ3 integrin that is overexpressed in atherosclerotic lesions [37], enabling early-stage detection of atherosclerotic changes by intravascular MM-OCT [39]. Finally, an application of MM-OCT to detect hemoglobin within blood based on its inherent magnetically responsive properties under a high-strength magnetic field (0.7 T) has also been demonstrated [40].
Fig. 2.
In vivo MM-OCT results showing targeted delivery and detection of MNPs. (I) targeted MNP-injected, (II) non-targeted MNP-injected, and (III) saline-injected rats. (a) The MM-OCT signal (green) is overlaid on the structural OCT signal (red). (b) Structural OCT images. (c) Corresponding histologic microscopic images of the Prussian-blue stained slices of tumors at 40x magnification [11].
Multimodal imaging contrast can also be achieved using MNPs or magnetic MSs [14]. Since MNPs also exhibit strong negative T2* contrast in MRI, MNPs can act as dual modality contrast agents in both MM-OCT and MRI [11]. Supplied with both MNPs and fluorescent dyes, MM-OCT can be complemented with fluorescence imaging [37]. The magnetomotive principle has also been applied in ultrasound and demonstrated with multimodal imaging [41].
A dual electromagnetic coil configuration has been applied for sensing and imaging magnetic MSs in liquid-based samples which lack the viscoelastic restoring force present in tissues [42], and a volumetric full-range OCT technique has been introduced to achieve rapid three-dimensional MM-OCT imaging acquisition [43].
B. Magnetomotive optical coherence elastography
Diseased tissues are known to have different biomechanical properties than healthy ones (e.g. tumors are often stiffer than the surrounding normal tissue in breast). This motivates the use of elastography, an imaging technique which can facilitate diagnostic imaging by introducing mechanical contrast to biomedical images non-invasively [44]. The success of ultrasound elastography (USE) [45, 46] has stimulated extensive elastography studies using other imaging modalities such as magnetic resonance elastography (MRE) [47] and optical coherence elastography (OCE) [48-50]. OCE surpasses MRE and USE in the following aspects: (1) higher spatial resolution (micrometer scale), which allows for the discrimination of fine morphological features, (2) higher displacement sensitivity (hundreds of nanometers scale), which enables the detection of subtle changes in tissue deformation, and (3) faster image acquisition time [49]. However, compared to USE or MRE, OCE has a lower penetration depth (1-2 mm).
In general, all elastography techniques require a certain mechanical excitation source and some means of measuring the resulting deformation or dynamic response. OCE techniques can be categorized in several ways, such as being based on the time-scale of the measurements (static or dynamic), configuration of the excitation source (internal or external), or the detection approach [48, 49]. In terms of mechanical properties, to date, most OCE techniques have assumed the tissue to be linear and viscoelastic. In this section, we will briefly summarize the current OCE techniques, particularly focusing on MM-OCE.
Static OCE is a conventional OCE technique that relies on the spatial characteristics of the biological material, such as the deformation under a uniform stress field (intuitively, a stiffer material exhibits less deformation under the same loading). Stiffness is a one-dimensional characteristic often quantified by the Young's modulus, which has the widest dynamic range as compared to other elasticity parameters [51]. In general, for small deformations of an elastic material (usually less than 10% of the original length), the material will respond in a linear (Hookean) fashion. The Young's modulus E of such a material undergoing a uniaxial deformation can be given by
| (10) |
where σ is the imposed stress that can be obtained by the ratio of force loading to the area , and ε is the fractional change in sample length of the material along the axial direction [52]. The elastic contrast is typically revealed in a strain map in response to a uniform stress field. Using this approach, static OCE has been demonstrated in postmortem aorta and cornea [53, 54], ex vivo human breast, lymph node, and ovary [55, 56], and in vivo human skin [57, 58]. However, strain mapping only provides a relative measurement. To quantify Young's modulus, techniques such as micro-indentation based on the Hertz contact theory [59], and optical palpation where a translucent compliant silicone stress sensor is placed on the sample surface [60], can be implemented. Most static OCE techniques rely on contact-based, external excitation sources, such as a glass plate with a ring actuator or piston [55, 61], or a needle probe configuration [62].
Viscoelastic features can also be inferred from temporally-resolved dynamics characteristics. This is the basic idea of dynamic OCE, where a mechanical vibrator and glass plate with mechanical actuators can be used as contact-based excitation [63-65]. Contact-free excitation configurations have also been utilized, including acoustic radiation forces [66, 67], laser-pulses [68], air-puffs [69, 70], or magnetic forces [1, 71-75]. The mechanical responses can be detected by motion-tracking techniques including speckle tracking (e.g. cross-correlation or speckle decorrelation [76, 77]) and phase-sensitive OCT [78, 79], where the latter is more common due to its larger dynamic range and the lower data acquisition requirement [49].
Magnetomotive OCE (MM-OCE) is a variant of dynamic OCE that employs a non-contact mechanical perturbation with the use of magnetic components that are manipulated through an alternating magnetic field at a distance. MM-OCE techniques are commonly performed with phase-sensitive OCT, where the displacement response of the stimulated sample is estimated from the phase profile by [71]
| (11) |
Here, dt is the time interval between adjacent scans, dφ(dt) is the phase change, n is the refractive index of the material, λ0 is the center wavelength of the OCT light source, and dz is the displacement induced during the time interval dt.
It is important to note that MM-OCE is conceptually different from MM-OCT. While MM-OCT relies on the dynamic modulation of MNPs for image contrast, MM-OCE extracts the motion characteristics of the medium surrounding the MNPs in order to assess its biomechanical properties [1]. In MM-OCE, MNPs [1, 71-74] or magnetic microbeads [80, 81] can respond to a magnetic field and serve as force transducers. MNPs have negligible inertia compared to biological tissues, and hence the responsive motion reflects the viscoelasticity of the surrounding tissue in which the MNPs are embedded [49]. Here, we focus our discussion on MNP-based MM-OCE techniques. For the remainder of this paper, unless specifically noted, MM-OCE denotes the OCE techniques that use MNPs as internal force transducers.
The magnetically-induced motion of a sample depends not only on the sample viscoelasticity and geometry, but also on the gradient of the applied field, the concentration and the distribution of the MNPs, and the characteristics of the electromagnetic coil [74]. However, the localized dynamic excitation scheme in MM-OCE provides a more effective means of alleviating the problems associated with geometric constraints in an external static loading scheme, and hence the MM-OCE measurements, compared to static OCE, are potentially more quantitative and less subjective to boundary conditions [49, 74].
1) Transisent-response MM-OCE
Biological soft tissue is a complex material composed of both fluids and solids. Under certain assumptions, the viscoelastic mechanical response of the tissue can be described by empirical rheological models such as the Kelvin-Voigt and Maxwell models. In the Kelvin-Voigt model, the elastic and viscous components coexist in a parallel configuration [52]. When a step-wise magnetic field is applied, and which eventually leads to a steady magnetic field gradient, the MNPs along with the neighboring tissue will be driven by the magnetic force and settle at a new equilibrium position while undergoing an underdamped oscillation [71]. Similarly, when the magnetic field is removed, the MNP-laden tissue is released from the magnetic force and the restoring force of the sample microenvironment will again result in an underdamped harmonic oscillation around its original equilibrium position, which can be described by the second order differential equation expressed below [71, 82].
| (12) |
Here, z(t) is the displacement as a function of time in response to the driving force f(t), m is the total mass of the sample neglecting the minute mass of the MNPs, and γ and κ are the damping coefficient and spring constant that are associated with the viscous and elastic properties, respectively. Note that these values can be regarded as constants since the variation of the biomechanical properties across the scale displacement (hundreds of nm) is sufficiently small [63]. Solving Eq. 12, the underdamped response to the loading can be written as
| (13) |
where A is the amplitude component, φ is an arbitrary phase, C is a constant, and f0 is the natural frequency provided by
| (14) |
Using Hooke's law, Young' s modulus E can be retrieved from the spring constant k and is geometrically related through the sample thickness L and the cross-sectional area S that the force has been applied to, given by
| (15) |
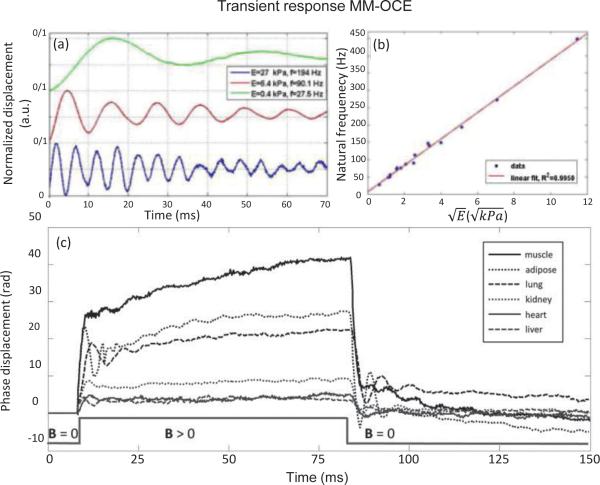
where the spring constant k can be obtained from Eq. 14. MM-OCE excitation can be performed with a step or square-wave function, followed by M-mode acquisition as the tissue undergoes an underdamped oscillation, as shown in Fig. 3(a) and (c) [71]. With negligible viscosity, the natural frequency can be simplified to . If the sample mass and shape are relatively constant, a linearity between the natural frequency and the square root of the Young's modulus can be observed, as plotted in Fig. 3(b) [67, 71]. Hence, the higher the natural frequency, the stiffer the sample.
Fig. 3.
Transient-responses MM-OCE detecting the natural frequency of a material. (a) A correlation between the natural frequency and stiffness can be seen. This correlation is quantitatively shown in (b), where a linear dependence between the natural frequency and square root of the Young's modulus can be observed [71]. (c) shows how the natural frequency can be used to characterize the viscoelastic behavior of different ex vivo rabbit tissues [73].
For viscoelastic media that have a time-dependent stress-strain relation, other descriptive parameters can be introduced to the model. Creep is a transient phenomenon that occurs when the fluid redistributes within a biosample under a constant stress (e.g. in a step-wise loading scheme). In such a case, an increase of strain with time would be observed. Using the Kelvin-Voigt model, the responding strain of creep can be given as [52, 83]
| (16) |
Here, τc is referred to as the creep retardation time and is defined by the ratio , which includes the viscosity η and elasticity E of the medium. The term ε0 is the instantaneous strain and is the viscoelastic (delayed) strain amplitude. In [73], the creep retardation time was extracted for a quantitative comparison of viscoelasticity between ex vivo rabbit muscle and lung (Fig. 3(c)). The τc metrics, along with a constant strain parameter, have also been demonstrated with static OCE, where a four-parameter Kelvin-Voigt model was utilized and parametric B-scan images of ex vivo rat and mouse muscles were generated [84]. In addition, the creep phenomenon can be explained by applying a harmonic oscillation force F0eiwt with angular frequency ω = 2πf to the sample using Eq. 12. The particular solution reveals an additional displacement of [64]
| (17) |
where . It can be seen from Eq. 17 that the displacement Δz attains maximum value for . This is the condition for resonance. In terms of the resonant frequency, this condition is achieved when the frequency of the forced oscillation f is equal to the natural frequency f0 of the sample. For the case when either f > f0 (above resonance) or f < f0 (below resonance), the sample displacement Δz is less than the maximum displacement (achieved at the resonant frequency). The phase and frequency conditions for these different cases are summarized in the equation below [64]. response can also be reflected in the rise time, which is defined as the time interval between the time the magnetic field is applied and the time the first peak of displacement amplitude is observed [73].
2) Spectroscopic MM-OCE
If a material undergoes a forced vibration oscillating at the natural frequency of the sample, the sample would exhibit the largest displacement and hence a resonant peak would be observed within the frequency-swept mechanical spectrum. The resonance
| (18) |
It must also be mentioned that the width of the resonant peak in the frequency spectrum (or the change of phase angle φ toward 0 or π on either side of the resonant peak) is directly proportional to the damping coefficient of the sample. This means that a highly viscous medium leads to a resonant peak that is wide and distributed across a broad frequency range in the frequency-swept mechanical spectrum [64].
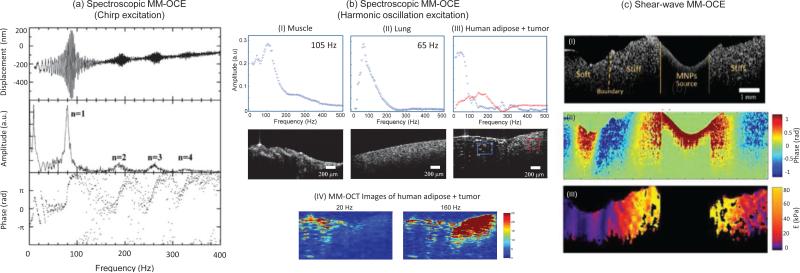
Spectroscopic principles have been demonstrated previously with USE [85, 86] and other dynamic OCE techniques [64]. A frequency-varying load can be applied with a chirp (Fig. 4(a)), which probes the system impulse response while offering a higher signal-to-noise ratio (SNR), as compared to an impulse excitation, due to a longer time duration of the applied frequency components across the spectrum [1, 72]. Alternatively, one can produce a harmonic oscillation by delivering one frequency at a time across the acquisition of one frame, and then sweeping across a wide range of frequencies. Though more computationally expensive, this approach allows for a two-dimensional imaging scheme which probes both the spatial and temporal characteristics of the sample simultaneously [64, 75]. As shown in Fig. 4(b), the elastic contrast of a mechanically heterogeneous sample, such as along a tumor margin, where the stiff tumor is adjacent to the soft adipose tissue, can be revealed by this technique.
Fig. 4.
Spectroscopic and shear-wave MM-OCE. (a, b) Spectroscopic MM-OCE is an alternative way of determining the resonant/natural frequency. (a) Excited by a chirp waveform, a cylindrical agarose sample exhibits (top) a frequency-dependent displacement, where (middle) the computed amplitude reveals the longitudinal resonance modes n =1,2,3,4, and (bottom) the phase shift from 0 to π across each resonance mode agrees with theoretical expectation [72]. (b) Spectroscopic MM-OCE with a two-dimensional imaging scheme was applied to probe the biomechanical properties of the sample both spatially and temporally, where the mechanical spectral response can be revealed in both (I, II) homogenous rat muscle and lung tissues and (III, IV) more heterogeneous tissues such as at the tumor-adipose margin in human breast tissue. (IV) A stronger MM-OCT signal is seen at lower excitation frequencies for softer tissue and at higher frequencies for the stiffer areas (tumor) [75]. (c) Shear wave MM-OCE shown in (I) a heterogeneous agarose sample where a clear boundary between stiff and soft regions can be seen. (II) The wave propagation can be visualized and further used for (III) Young's moduli quantification and mapping [74].
As in the case of transient-response MM-OCE, estimating Young's modulus from spectroscopic MM-OCE requires knowledge of the sample geometry and physical properties such as mass and Poisson's ratio (relating the axial strain to the shear strain). For example, for a homogeneous, isotropic, elastic, cylindrical sample with stress-free walls, the Young's modulus can be estimated by solving the Love equation [72]. Although a precise estimation of Young's modulus from solid tissues with arbitrary shapes is generally difficult, a spectroscopic approach is effective for comparing the viscoelasticity of the same sample longitudinally if the mass and geometry remain relatively unchanged.
3) Shear wave MM-OCE
The propagation behavior of elastic waves through materials provides another way to assess the biomechanical properties. Originating from the equation of motion and linked through the constitutive equation, shear wave propagation within an isotropic, linear elastic, homogeneous, incompressible material can be described by the Helmholtz equation [47, 49]
| (19) |
Here u is the displacememt, ρ is the sample density, and v is the Poisson's ratio. The shear modulus G is related to Young's modulus E through = , where v of soft tissue is typically close to 0.5 (v of liquid). Young's modulus can then be approximated as E ≈ 3G. The shear modulus can be extracted from the shear wave velocity using [87]
| (20) |
In shear wave MM-OCE, both an impulse and a harmonic oscillation waveform can be sent to propagate across the sample, where the group and phase velocity can be used for shear wave velocity calculations, respectively. When the excitation source has a point-wise characteristic in the lateral direction, a phase gradient can be obtained by linearly fitting the phase profile Δϕ with respect to the radial spatial interval Δr, which can be used to compute the empirical phase velocity [74]. In [74], MNPs were deployed into tissue-mimicking phantoms and tissue specimens, and act as a cylindrically-shaped excitation source. As shown in Fig. 4(c), the stiffness of the sample can be related to the wavelength of the shear wave (i.e. larger shear wave wavelength implies higher shear wave speed, and hence the elasticity). For a viscoelastic body, the shear modulus is complex and the frequency-dependent shear wave speed (dispersion) can be quantified assuming a certain tissue model. Using the Kelvin-Voigt model, the shear wave speed dispersion can be given as [88]
| (21) |
where G is the real part of the complex shear modulus, ω is the angular frequency of excitation, ρ is the mass density, and η is the viscosity. The viscosity can be inferred from the slope of the shear wave speed dispersion curve – the steeper the slope, the greater the viscosity [74]. When η = 0 or the shear modulus is much greater than the viscosity, the above equation become non-dispersive and reduces to Eq. 20.
Numerous rheological models have been employed for biomechanical characterization, yet erroneous results may often appear due to violations of various mechanical assumptions. One way to alleviate this issue is by using the finite element method (FEM), which is an effective numerical tool that iteratively approximates the boundary value solutions [89]. FEM has been implemented in both static [90] and dynamic [75, 91] OCE. In [75], a dynamic FEM model using the structural mechanics module in COMSOL was used to simulate spectroscopic MM-OCE, where the simulation results were close to the empirical measurements.
Among these major MM-OCE techniques, whether one approach would be favored over another depends on the specific application. Shear wave approaches are suitable in a scenario where Young's modulus quantification is needed, while a transient or a spectroscopic technique might be more preferable in scenarios where localized MNP aggregation is not readily achieved (such as during the intravascular administration of MNPs).
C. Magnetic hyperthermia
Hyperthermia is a clinical therapeutic treatment process that utilizes adequate temperature elevation to traumatize targeted cells or tissues, such as in cancer. Different effects of cell injury and killing are induced depending on the level of temperature rise. In [13, 34], investigations summarize that thermoablation occurs at temperatures above 46 °C (up to 56 °C), where the cells undergo direct necrosis, coagulation, and/or carbonization. Moderate hyperthermia occurs around 41-46 °C, which activates cellular and tissue level degradation, such as irreversible protein damage, induction of apoptosis and multidrug resistance. Temperatures below 41 °C but above normal body temperature (37 °C) are in the range of diathermia, which is commonly used to treat rheumatic diseases in physiotherapy. Hyperthermia treatment usually refers to moderate hyperthermia that induces protein damage and triggers cellular dysfunction [13]. At the tissue level, if hyperthermia effects occur in tumor tissues, blood vessels may not appropriately respond with vasodilation when tissue temperature increases [92]. Hyperthermia is capable of introducing impressive regression or destruction of tumors, thermally affecting hypoxic cancerous cells, impairing the repair process of DNA after radiation damage, and making cancerous cells more sensitive to radiation or anticancer drugs [34, 93]. Hyperthermia can also be performed alone, or as an adjunctive therapy to facilitate and improve the effectiveness of other cancer therapies.
External and internal heating sources can be utilized for heat delivery and induction of hyperthermia during treatments. Microwaves, radiofrequency energy, ultrasound waves, infrared radiators, and lasers are examples of external energy sources commonly used [92]. In contrast, MNPs such as SPM nanoparticles or magnetic fluids can serve as internal heating sources, albeit driven by external alternating magnetic fields. These agents can be delivered through the vasculature or by direct (interstitial) injection into a solid tumor, where Brownian and Néel relaxation govern the heating mechanisms [31, 32]. Ever since the first demonstration of magnetic hyperthermia in 1957 [94], investigations into this therapeutic approach have thrived. Related research has been performed in many in vivo animal studies [95-97], and investigations have moved on to preclinical studies for human glioblastoma and prostate cancer [98-100], to name only a few.
IV. Magnetic nanoparticles as theranostics agents
A. Conventional hyperthermia dosimetry
Evaluation and measurement of thermal energy dose is essential to avoid the undesirable overtreatment that induces collateral damage to adjacent healthy tissues. The total thermal energy dose is dependent on the amount of energy applied, heating duration, the cumulative number of times that a treatment is delivered, and the thermal sensitivity of the tissue [101]. Inhomogeneous distributions of thermal energy are inevitable due to the inherent heterogeneous composition of tissue, the inhomogeneity of the blood perfusion field, and the relatively uncontrollable distribution of MNPs on the microscopic scale [102-104]. Cumulative equivalent minute at 43°C (CEM43°C Tx) is an ‘isoeffect thermal dose’ commonly used to describe the time-temperature history of the applied thermal dose, with the non-uniform temperature distribution also taken into account [105-107].
| (22) |
Here, ti is the i-th minute time interval and R is number of minutes required to compensate for a 1 °C change of the breakpoint. The variable Tx describes the temperature exceeded by x % of the intratumoral measurement. Temperatures around 43 °C are near the breakpoint of the rate of cell death for several cell lines [106]. Usually, a thermal dose of 5-10 CEM43°C T90 is the target for clinical hyperthermia combined with radiotherapy [108]. However, the resulting temperature does not directly refer to the biological destruction as the cell death rate could be affected by several other factors, including the well-known thermotolerence effect [106]. This imposes difficulty in associating the actual thermal damage with the thermal dose applied.
B. Heat-induced stiffness changes
Heat-stress can trigger several cell- and tissue-level degradation processes, such as protein denaturation, folding, aggregation, DNA cross-linking, coagulation, and tissue necrosis [13]. These physiological changes subsequently alter the biomechanical properties of the tissue, which are a result of changes in the configurational entropy from denaturation [109] or fibrin crosslinking and platelet adhesion during coagulation [110].
USE and MRE have been utilized for thermal ablation monitoring in excised animal liver and muscle tissues [111, 112], and for in vivo monitoring in animal muscle, human liver, and human prostate [113-115]. These studies report the correlation between stiffness and thermal damage, while some further investigated the reversible and irreversible changes due to different states of the heat-modified proteins [111, 112, 115]. The findings of these studies suggest that heat-induced stiffness changes measured via elastography not only offers an alternative metric for thermal dosimetry, but may also be more indicative of biological status over temperature-based metrics.
C. Magnetic hyperthermia dosimetry by MM-OCE
Theranostic agents represent a single platform with combined diagnostic and therapeutic functions, and have the potential to facilitate a more personalized medicine approach [116]. MNPs can provide theranostic functions by combining tissue targeting, imaging contrast, and disease treatment in a single agent [4]. In cancer chemotherapy, fluorophores can be added to liposomal nanoparticles, where chemotherapeutic agents and iron-oxide can also be included within the shell to produce a therapeutic, magneto-fluorescent agent [117]. MNPs can also be used to deliver a thermal dose to targeted cancerous sites while providing image contrast in MRI [118].
Therapy monitoring, or dosimetry (the measurement of a therapeutic dose or intervention), is another theranostic application of MNPs. Traditionally, most dosimetric techniques have utilized imaging modalities to visualize and detect changes in structural image features that represent the interventional effects, while dosimetric methods that rely on direct elastographic measurements of the changing biomechanical properties of the tissue have not been thoroughly explored. Previously, researchers have demonstrated combining USE imaging with high intensity focused ultrasound (HIFU) to monitor the mechanical changes of the prostate before, during, and after thermal ablation [114]. An analogous approach may be provided by using MNPs as theranostic agents, where magnetic hyperthermia can be applied for therapeutic purpose and the dynamic evolving viscoelastic properties of the tissue can be probed by MM-OCE for dosimetry.
Here we propose and investigate the feasibility of monitoring the thermal dose delivered by magnetic hyperthermia based on the viscoelastic tissue properties revealed by MM-OCE. The main goal of this preliminary study of MM-OCE-based magnetic hyperthermia dosimetry was to explore the potential correlation between heat-induced treatments and changes in the elasticity of ex vivo chicken breast tissue. We simulated the intravenous administration of MNPs by placing the tissues in suspensions of MNPs and allowing for diffusion of the MNPs into the ex vivo tissue specimens prior to magnetic hyperthermia treatment.
V. Method
A. Experimental setup and magnetic hyperthermia treatment
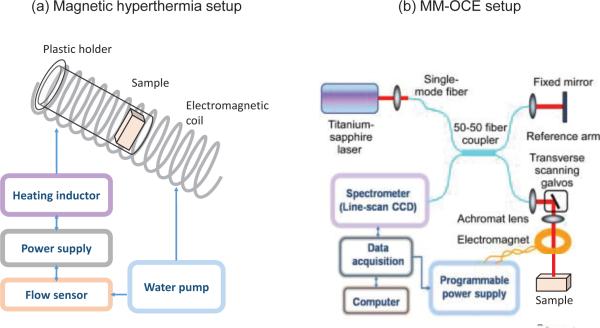
The magnetic hyperthermia setup included a custom-made power supply which supplied an alternating voltage at 64.7 kHz to drive a water-cooled magnetic coil formed from copper tubing. The coil was 10 cm in length (1.3 turns per cm), and had an internal diameter of 3 cm. The coil was used to induce a magnetic field with peak-to-peak field strength of 50 kA/m (~629.3 Gauss, assuming negligible magnetization of air) inside the coil. Since the magnetic field is uniform along the central longitudinal axis of the coil, each sample was placed at the center of the coil to reduce the radial variation of the magnetic field inside the sample (Fig. 5(a)). The hyperthermia treatment consisted of delivering the alternating magnetic field continuously to the sample for 15 minutes. Immediately before and after treatment, for each tissue sample, tissue temperatures were measured at the surface within one minute (T1-min) from six locations using a digital thermometer (HH-20A, Omega Engineering, Inc., Stamford, CT). Temperature measurements were performed only on the sample surface since the MNPs were diffused from the outer surface and the insertion of temperature sensing probe would have affected the mechanical coupling within the tissue and also possibly alter the boundary conditions. The thermometer was kept in contact at each location for ~10 seconds in order to reach a steady-state value. Inevitably, the tissue temperature dropped between sequential measurements. Therefore, we also report the temperature measured within the first 10 seconds (T10-sec), which is expected to be least influenced by the cooling effect from the ambient temperature.
Fig. 5.
Schematic of (a) the magnetic hyperthermia and (b) MM-OCE systems. The MM-OCE setup schematic is adapted from [11].
The MM-OCT/MM-OCE system utilized for this study was described previously [75]. Briefly, a custom-made electromagnetic coil was placed in the sample arm of a 1310 nm spectral domain OCT imaging system that utilized a superluminescent diode source with a 170 nm bandwidth (giving axial and transverse resolutions of ~6 μm and ~16 μm, respectively). Shown in Fig. 5(b), the sample was placed beneath the electromagnetic coil, which had a bore diameter of ~ 2 mm to allow the optical beam to pass through for imaging the tissue beneath the coil. Immediately following the MM-OCE measurements, gold-standard mechanical indentation testing (TA.XT Plus Texture Analyzer, Texture Technologies Corp., Algonquin, IL) was performed on the samples. Both MM-OCE and indentation measurements were performed after the samples were allowed to cool down to room temperature after the magnetic hyperthermia treatment.
B. Sample preparation
Chicken breast tissue was cut into pieces (~1.5 × 1.5 × 0.5 cm3) and marinated for approximately 2.5 hours in a Fe3O4 (#637106, Sigma-Aldrich, St. Louis, MO, characterized in [28]) solution (100 mg Fe3O4/ml PBS) to simulate passive uptake of MNPs in tissues, while the control group specimens were marinated in PBS solutions for the same time duration.
C. Data collection and processing
We performed MM-OCT and MM-OCE, including both spectroscopic and transient-response approaches. For MM-OCT, a line scan rate of 1,983 Hz was used and 4,000 A-scans were acquired across a 1.6 mm range in the transverse direction. The data processing followed the standard MM-OCT processing procedure [28]. For spectroscopic MM-OCE, an excitation chirp over the range of 10-400 Hz and 10-500 Hz was applied depending on the level of tissue stiffness, and 4,000 M-mode scans were acquired with a line scan rate of 1,983 Hz. The frequency range of the chirp excitation was selected according to a prior knowledge of the resonant frequency of muscle tissue (~100 Hz [38, 73]). A line scan rates of 1,983 Hz was chosen to ensure that the sampling rate meets Nyquist criteria without excessive oversampling. The data were processed in a similar manner as in [64]. In brief, the data was first processed following the standard OCT data processing. Then, phase differences between each adjacent M-scan were computed based on the complex OCT signals. Next, an average was taken across 10 rows in depth where the highest SNR values were present, followed by phase unwrapping. Sequentially, discrete Fourier transforms were performed across 4,000 M-scans to obtain a frequency-swept mechanical spectrum. For the transient-response MM-OCE, a square wave of ~10 Hz was applied while the line scan rate and the number of M-scans were set to 20,730 Hz and 4,000, respectively. The phase profile was extracted from the angle of the complex OCT signal, followed by phase unwrapping. Then, the underdamped oscillation occurring during each magnetic field ‘on’ and ‘off’ period was processed individually. After the trend of increasing displacement over time was first removed, the natural frequencies were determined from the inverse of the time period between the first and the second displacement peaks detected from the signal. The natural frequency was estimated by the average across 10 rows in depth, where the highest signal SNR was obtained.
VI. Results
As noted earlier, MM-OCE was used to evaluate the heat-induced change in elasticity of ex vivo chicken breast tissue.
To first verify the effectiveness of magnetic hyperthermia induction by our system, we investigated the contributions of both the alternating magnetic field (AMF) and the MNPs. As a result, four groups were analyzed: (1) MNP-laden tissue treated with AMF (MNP+, AMF+), (2) non-treated MNP-laden tissue (MNP+, AMF−), (3) PBS-soaked tissue treated with AMF (MNP−, AMF+), and (4) non-treated PBS-soaked tissue (MNP−, AMF−). Additionally, the presence of MNPs was validated by MM-OCT measurements.
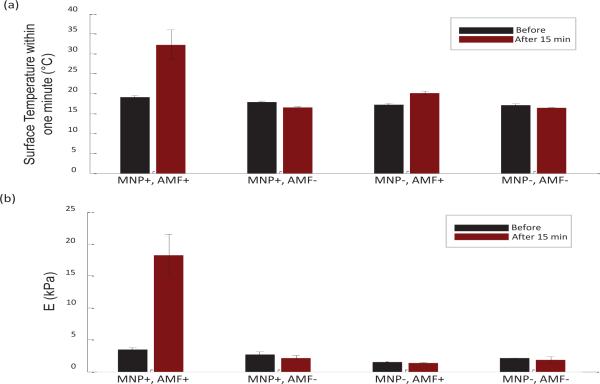
Validating the effectiveness of magnetic hyperthermia treatment through temperature measurements, the results are shown in Fig. 6(a). Comparing within the MNP+ samples, an increase in temperature (T1-min from 19.08 ± 0.49 °C to 32.25 ± 3.75 °C; T10-sec from 19.9 °C to 37.5 °C after treatment) was only observed from the sample that was exposed to the AMF (i.e. AMF+). In contrast, no significant temperature rise was observed in the MNP+, AMF− tissue (T1-min from 17.92 ± 0.2 °C to 16.53 ± 0.16°C; T10-sec from 18.2 °C to 16.8 °C), or MNP- tissues for both AMF+ (T1-min from 17.18 ± 0.37 °C to 20.07 ± 0.53°C; T10-sec from 17.4 °C to 21.1 °C ) and AMF-(T1-min from 17.07 ± 0.38 °C to 16.43 ± 0.05°C; T10-sec from 17.8 °C to 16.5 °C) samples. This demonstrates that the customized magnetic hyperthermia system and its operating parameters were able to successfully induce a significant temperature rise inside the MNP+ tissues.
Fig. 6.
Surface temperature and Young's modulus results of the four groups (black) before and (dark red) after 15 minutes of treatment. (a) Surface temperature measured within a one-minute time interval (T1-min) at six different locations on each sample. A significant temperature rise is observed only in the MNP+ AMF+ case, indicating the effectiveness of the magnetic hyperthermia. (b) Validating Young's moduli were obtained from indentation testing. A significant increase in stiffness occurred only in the MNP+,AMF+tissue.
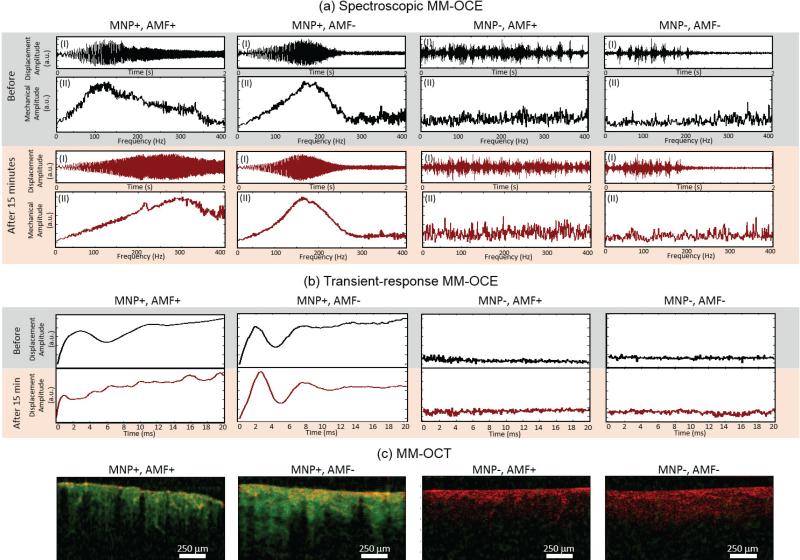
Following this validation experiment, MM-OCT and MM-OCE measurements were performed, and results are shown in Fig. 7. As expected, strong MM-OCT signals, along with higher SNR in MM-OCE, are only observed in the MNP+ groups. The elastic properties were revealed from spectroscopic and transient-response MM-OCE, and were further confirmed with gold-standard indentation testing. Both MM-OCE techniques showed a substantial increase in the resonant/natural frequency for the MNP+, AMF+ tissue (from 120.35 ± 1.12 Hz to 272.97 ± 7.75 Hz), while the MNP+, AMF− sample manifested almost no frequency shift (from 189.79 ± 3.57 Hz to 191.74 ± 2.95 Hz). This can be visualized in both the temporal displacement profile (i.e. larger displacement amplitude as the excited chirp is swept through a higher frequency) and the mechanical spectral response (resonant peak shifting toward a higher frequency), as well as in the shortened periods of the underdamped oscillations.
Fig. 7.
MM-OCE and MM-OCT results from ex vivo tissue before and after a magnetic hyperthermia treatment. In both MM-OCE results, a higher SNR is only present in the MNP+ groups. (a) Spectroscopic MM-OCE results of (black) before and (dark red) after 15 minutes, with or without hyperthermia treatment. (I) Normalized temporal displacement in response to chirp excitation (10-400 Hz or 10-500 Hz) is plotted with the x-axis representing the time from 0 to 2 sec. (II) Resonance spectrum showing relative mechanical amplitude across 0-400 Hz. (b) Transient-response MM-OCE results for (black) before and (dark red) after 15 minutes, with or without treatment, where relative displacement amplitude is plotted throughout 0-20 ms. From both (a) and (b), a significant resonant/natural frequency shift can only be observed in the MNP+, AMF+ sample. (c) The presence of MNPs was further verified using MM-OCT. Displayed images are the superposition of both MM-OCT (green channel) with structural OCT (red channel) signals. Strong MM-OCT signals are evident only in the MNP+ tissues and not in the MNP− tissues. The excitation frequencies for MM-OCT are 280 Hz, 170 Hz, 200 Hz, and 200 Hz, respectively for MNP+AMF+, MNP+AMF−, MNP−AMF+, and MNP−AMF− samples. The excitation frequency for both MNP+ cases were chosen near the values of their post-treatment (with or without AMF) resonant frequency. For both MNP− cases, the excitation frequency were selected arbitrarily for display since our data exhibit no significant difference in the MM-OCT results when various frequencies within the range 50-300 Hz have been applied.
The Young's moduli of the samples were also extracted by a commercial indentation device, which further validated the stiffening effect of the MNP+, AMF+ sample and enabled the comparison between the elasticity of the MNP+ and MNP-samples. It can be seen from Fig. 6(b) that a large increase in elasticity is only achieved in the MNP+, AMF+ group (from 3.48 ± 0.29 kPa to 18.25 ± 3.26 kPa), while the samples without AMF treatment and the tissues without MNPs have an elasticity that is relatively unchanged (from 2.67 ± 0.42 kPa to 2.17 ± 0.35 kPa for MNP+, AMF−; from 1.49 ± 0.01 kPa to 1.36 ± 0.07 kPa for MNP−, AMF+; from 2.11 ± 0.04 kPa to 1.84 ± 0.48 kPa for MNP−, AMF−). This suggests that the stiffening of the tissues are a result of the combination of both the MNPs and the AMF (i.e. magnetic hyperthermia). A brief summary of the results is available in Table. 1.
TABLE I.
Summary of Initial results
| MNP-laden tissue (MNP+) | PBS-soaked tissue (MNP−) | |
|---|---|---|
| AMF-treated (AMF+) | Strong MM-OCT signal | Weak MM-OCT signal |
| Significant rise in T | No significant rise in T | |
| Significant rise in E | No significant rise in E | |
| Significant rise in fo | (fo not applicable) | |
| Non-treated (AMF−) | Strong MM-OCT signal | Weak MM-OCT signal |
| No significant rise in T | No significant rise in T | |
| No significant rise in E | No significant rise in E | |
| No significant rise in fo | (fo not applicable) |
VII. Discussion and Conclusion
MM-OCE is an optics-based elastography technique that takes advantage of MNPs as small internal excitation sources with negligible inertia to enable the assessment of viscoelastic properties of soft tissues based on temporally-resolved magnetomotion characteristics. Here, we proposed and demonstrated a theranostic function of MNPs, where MM-OCE was also used for dosimetry of magnetic hyperthermia by monitoring the thermal dose delivery via changes in the biomechanical properties of the tissue.
In this study, a substantial temperature rise (13.17 °C increase in the averaged T1-min ; 17.6 °C increase in the averaged T10-sec) was successfully induced by a 15-minute treatment of magnetic hyperthermia (~64.7 kHz, 50 kA/m or ~629.3 Gauss) on ex vivo MNP-laden chicken breast tissue. The evaluation of tissue stiffness was performed with both spectroscopic and transient-response MM-OCE, both of which correlate with the measurements obtained from gold-standard indentation testing. Our initial results show that a large increase in both temperature (69% increase in the averaged T1-min value; 88.4% increase in the averaged T10-sec value) and elasticity (14.77 KPa, corresponding to 424.4% increase in the averaged Young's modulus value) could be achieved in the hyperthermia-treated MNP-laden tissue, while the samples either without MNPs or without exposure to an AMF show negligible change in both temperature and elasticity. This implies that magnetic-hyperthermia-induced elasticity changes may serve as a good biomarker of thermal damage of tissue, where both therapeutic and mechanical contrast monitoring processes can be achieved with the same MNPs embedded inside the tissue matrix. In this initial study we only performed relative measurements (resonant/natural frequency) by MM-OCE with an intra-sample elasticity comparison. In the future, the empirical information of the MNP distribution within the tissue could be obtained from MRI or micro-CT [119], followed by FEM simulations for improved understanding of the dynamically evolving biomechanical properties.
The initial new results presented in this review may serve as proof-of-concept, where only one representative sample per group was included due to the physical, mechanical and physiological variabilities across each individual biological sample. In future studies, a systematic characterization of tissue properties or MNP distribution outcome will be carried out before including a larger sample size for statistical analysis. Potentially, the correlation between the various magnetic hyperthermia parameters with the heating outcome could be investigated as well. Moreover, due to the limitations of the current experimental setup, it was difficult to achieve a precise temperature measurement both spatially (throughout the tissue volume) and temporally (real-time monitoring). To more accurately investigate the induced temperature before, during, and after hyperthermia treatment, and access the thermodynamics history (i.e. heating or cooling), real-time temperature monitoring can be implemented via a metal-free fiber optic sensor that is not affected by the strong applied AMF, or by temperature mapping performed using magnetic resonance temperature imaging [120] or a remote infrared camera. Additionally, the conventional CEM43°C T90 value and FEM simulations of the bio-heat transfer equation [121] can also be obtained for correlation and comparison. Moreover, to evaluate the extent of thermal damage to the tissues, histology can be performed and compared with both the elasticity and temperature changes.
The assessment of the spatial biodistribution of MNPs can also provide a more accurate thermal dosimetry estimation. Although the MNP distribution appeared relatively uniform in our MM-OCT data (Fig. 7 (c)), we hypothesize a non-uniform MNP concentration in depths that exceed our imaging depth (~2.2 mm optical distance). Experimentally, the MNP distribution could be assessed by MRI or micro-CT and compared with the corresponding theoretical diffusion models [122, 123] for detailed investigation. This will be beneficial when comparing the influence of different MNP administration approaches to the hyperthermia outcome. Here, we modeled an intravascular injection of MNPs by allowing the MNPs to diffuse into the tissue samples while immersed in a suspension of MNPs. However, a direct injection of MNPs into the tissue samples, simulating the scenario of direct interstitial injection, should also be investigated, where both the characterization of the MNP distribution and the corresponding heating and biomechanical results can be compared in the future.
In vivo animal models could be used to better simulate more practical clinical scenarios where physiological factors such as blood circulation, cooling effects, and coagulation will affect the magnetic hyperthermia dose and effectiveness. Magnetic hyperthermia has been successfully demonstrated in vivo, as have other types of interventional techniques that ablate diseased tissues (tumors) via hyperthermia or hypothermia techniques. In all these therapeutic interventions there remains an important need for dosimetry, to precisely measure the amount of dose delivered, and track the dynamic tissue response to that dose. While traditionally this has been accomplished with biomedical imaging, many rely on changes in the structural features visualized in the images. Few examples exist where elastography has been used to measure the dynamically changing biomechanical properties of the tissue for dosimetry.
Finally, a number of improvements in the MM-OCE based dosimetry system can be made in future studies. The MM-OCT/MM-OCE monitoring system used in this initial study was a separate system from the magnetic hyperthermia treatment system, however, the two systems can be conceivably combined with one another, enabling rapid hyperthermia dosimetry. Another area of improvement could be enhancing the image acquisition speed in MM-OCE monitoring. This can be done through a volumetric scan approach which can potentially allow rapid monitoring across tissue volume [43]. On the other hand, characterization of the sensitivity of MM-OCE for measurement of heat-induced stiffness changes also needs to be evaluated. This will be performed experimentally and compared with both analytical estimation and FEM simulation, incorporating both the bio-heat transfer and structural analysis methods in the future.
This review paper, along with the presented preliminary results, support the potential for using MM-OCE for biomechanical dosimetry during magnetic hyperthermia interventions. By extension, OCE techniques (without the use of MNPs) can also be used to dynamically monitor tissue biomechanical changes during thermal or cryo ablation of tissue. In vivo MM-OCE for magnetic hyperthermia dosimetry applications should be feasible not only for superficial tumors, but also for internal tissue/tumor sites, where optical fibers can be inserted to perform optical sensing for the changes in tissue biomechanics. Collectively, the magnetomotion of MNPs induced by the application of an external AMF offers novel theranostic approaches for contrast enhancement, optical coherence elastography, and dosimetry of therapeutic interventions that alter the biomechanical properties of tissue.
Acknowledgment
The authors would like to thank Prof. Michael Insana and his research group from the Beckman Institute for Advanced Science and Technology for sharing their TA.XT Plus Texture Analyzer during this study. Also, the authors appreciate the valuable discussions with our colleague, Eugene D. Ark, from the Biophotonics Imaging Laboratory. Additional information can be found at http://biophotonics.illinois.edu.
This work was supported in part by the National Institutes of Health (R01 CA166309).
Biography
Pin-Chieh Huang received the B.S. degree in electrophysics from National Chiao Tung University, Taiwan in 2013. She is currently working toward the Ph.D. degree in bioengineering at the University of Illinois at Urbana-Champaign, USA. Her research interests include optical imaging and elastography.
Paritosh Pande received the B.Tech. (Hons) degree in electrical engineering and M.Tech. degree in instrumentation engineering, both from the Indian Institute of Technology, Kharagpur, India, in 2008, and the Ph.D. degree in biomedical engineering from Texas A&M University, College Station, TX, in 2014. He is currently a postdoctoral research associate in the Biophotonics Imaging Laboratory at the University of Illinois at Urbana-Champaign. His research interests include biomedical signal and image processing, pattern recognition, and the development of optical imaging technologies for biomedical diagnostics.
Adeel Ahmad received the B.S. degree in electrical engineering from National University of Sciences and Technology, Pakistan in 2006 and the M.S. and Ph.D. degrees in electrical engineering from the University of Illinois at Urbana-Champaign, USA in 2010 and 2014, respectively. In his graduate research, he worked on utilizing magnetic particles for contrast enhancement in optical imaging and elastography applications.
Marina Marjanovic received the B.S. degree in molecular biology and physiology in 1979, M.S. and Ph.D. degrees in physiology, in 1987 and 1992 respectively, from the University of Belgrade, Belgrade, Serbia. She was a postdoctoral fellow at the University of Illinois at Urbana-Champaign from 1992-1996. In 1996 she accepted a faculty position at the Eastern Illinois University, Charleston, IL. In 2009, she returned to the University of Illinois at Urbana-Champaign where she is currently Associate Director of Imaging at Illinois and Adjunct Associate Professor in the department of bioengineering. Dr. Marjanovic authored and co-authored 2 book chapters, 37 peer-reviewed publications, 41 presentations with published proceedings and 48 meeting presentations. Her research interests include physiological studies, especially those with medical relevance, using novel imaging technologies.
Darold R. Spillman Jr. received the A.A. degree in human resources from the Community College of the Air Force, Maxwell AFB, GA in 2005 and the B.A. degree in general studies from Eastern Illinois University, Charleston, IL in 2015. He served in the United State Air Force from 1984 – 2007. Mr. Spillman brings real world experience to the Biophotonics Imaging Laboratory. His focus in research is in the design and development of novel ideas in the form of packaging and use of equipment. He has also studied the effects of probiotics on lactose intolerance as well as imaging of chromatophores on live cuttlefish to explore how the chromatophores provide camouflage. He was a 1993 Presidential Point of Light Award nominee and was spotlighted in the Inside Illinois publication.
Boris Odintsov received the M.S. degree in radio-electronics and the Ph.D. degree in physics and math from State University of Kazan, Russia, in 1971 and 1978, respectively, and the Doctor of Science in physics and math from St. Petersburg State University, Russia in 1993. He is a senior research scientist in Biomedical Imaging Center, Beckman Institute for Advanced Science and Technology and Adjunct Professor in bioengineering department at the University of Illinois at Urbana-Champaign since 2002 and 2012, respectively.
Dr. Odintsov has over 30 years of funded experience in different magnetic resonance areas, such as NMR and EPR spectroscopy and relaxation, MRI and DNP. He has numerous honors, patents and peer-reviewed publications, including book and book chapters. During the last 20 years (1996 – 2015) at the University of Illinois he pursued an extensive microimaging program of National and International supported studies in collaboration with different scientific groups in US and abroad. For the past 10 years, his research and engineering interests are related to ultra-high magnetic field MR methods development and application in microimaging studies.
Stephen A. Boppart (S’90–M’90–SM’06–F’11) was born in Harvard, IL, in 1968. He received the B.S. degree in electrical and bioengineering and the M.S. degree in electrical engineering from the University of Illinois at Urbana-Champaign, IL, in 1990 and 1991, respectively, the Ph.D. degree in medical and electrical engineering from the Massachusetts Institute of Technology, Cambridge, in 1998, and the M.D. degree from Harvard Medical School, Boston, MA, in 2000.
He was a Research Scientist with the Air Force Laser Laboratory, Brooks Air Force Base, San Antonio, TX, where he was engaged in research on developing national (ANSI) and Air Force laser safety standards. Since 2000, he has been with the University of Illinois at Urbana-Champaign. He is currently an Able Bliss Professor of Engineering in the departments of Electrical and Computer Engineering, Bioengineering, and Medicine, the Head of the Biophotonics Imaging Laboratory at the Beckman Institute for Advanced Science and Technology, and also the Director of Imaging at Illinois. He has authored or coauthored more than 300 invited and contributed publications, and more than 670 invited and contributed presentations. He holds more than 40 patents. His research interests include the development of novel optical imaging technologies for biological and medical applications, with particular emphasis on translating these to clinical applications.
Dr. Boppart is a Fellow of IEEE, AAAS, OSA, SPIE, and AIMBE. He was named one of the top 100 innovators in the world by the Technology Review Magazine for his research in medical technology, and received the IEEE Engineering in Medicine and Biology Society Early Career Achievement Award. He received the Paul F. Forman Engineering Excellence Award from the Optical Society of America for dedication and advancement in undergraduate research education, and recently, the international Hans Sigrist Prize for his work in diagnostic laser medicine.
Footnotes
T denotes surface temperature measured. E denotes the Young's modulus obtained from gold-standard indentation testing. fo indicates the natural frequency measured from transient-response MM-OCE.
Contributor Information
Pin-Chieh Huang, Biophotonics Imaging Laboratory, Beckman Institute for Advanced Science and Technology, and the Department of Bioengineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801 USA (phuang16@illinois.edu)..
Paritosh Pande, Biophotonics Imaging Laboratory and the Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL 61801 USA (pande@illinois.edu)..
Adeel Ahmad, Biophotonics Imaging Laboratory and the Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL 61801 USA (aahmad5@illinois.edu)..
Marina Marjanovic, Biophotonics Imaging Laboratory, Beckman Institute for Advanced Science and Technology, and the Department of Bioengineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801 USA (marinam@illinois.edu)..
Darold R. Spillman, Jr., Biophotonics Imaging Laboratory and the Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL 61801 USA (dspillm2@illinois.edu).
Boris Odintsov, Biophotonics Imaging Laboratory and the Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL 61801 USA (bodintso@illinois.edu)..
Stephen A. Boppart, Biophotonics Imaging Laboratory, Beckman Institute for Advanced Science and Technology, and the Departments of Electrical and Computer Engineering, Bioengineering, and Medicine, University of Illinois at Urbana-Champaign, Urbana, IL 61801 USA (phone: 217-333-8598; fax: 217-333-5833; boppart@illinois.edu)..
References
- 1.Oldenburg AL, Wu G, Spivak D, Tsui F, Wolberg AS, Fischer TH. Imaging and elastometry of blood clots using magnetomotive optical coherence tomography and labeled platelets. IEEE J. Sel. Top. Quantum Electron. 2012;18:1100–1109. doi: 10.1109/JSTQE.2011.2162580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Haun JB, Yoon T-J, Lee H, Weissleder R. Magnetic nanoparticle biosensors. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 2010;2:291–304. doi: 10.1002/wnan.84. [DOI] [PubMed] [Google Scholar]
- 3.Pankhurst QA, Thanh NTK, Jones SK, Dobson J. Progress in applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2009 Nov 21;42:224001. [Google Scholar]
- 4.Yoo D, Lee JH, Shin TH, Cheon J. Theranostic magnetic nanoparticles. Acc. Chem. Res. 2011 Oct 18;44:863–74. doi: 10.1021/ar200085c. [DOI] [PubMed] [Google Scholar]
- 5.Pankhurst QA, Connolly J, Jones SK, Dobson J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2003 Jul 7;36:R167–R181. [Google Scholar]
- 6.Brigger I, Dubernet C, Couvreur P. Nanoparticles in cancer therapy and diagnosis. Adv. Drug Deliv. Rev. 2002 Sep 13;54:631–51. doi: 10.1016/s0169-409x(02)00044-3. [DOI] [PubMed] [Google Scholar]
- 7.Iyer AK, Khaled G, Fang J, Maeda H. Exploiting the enhanced permeability and retention effect for tumor targeting. Drug Discov. Today. 2006 Sep;11:812–8. doi: 10.1016/j.drudis.2006.07.005. [DOI] [PubMed] [Google Scholar]
- 8.Reddy LH, Arias JL, Nicolas J, Couvreur P. Magnetic nanoparticles: Design and characterization, toxicity and biocompatibility, pharmaceutical and biomedical applications. Chem. Rev. 2012 Nov 14;112:5818–78. doi: 10.1021/cr300068p. [DOI] [PubMed] [Google Scholar]
- 9.Laurent S, Forge D, Port M, Roch A, Robic C, Elst LV, et al. Magnetic iron oxide nanoparticles: Synthesis, stabilization, vectorization, physicochemical characterizations, and biological applications. Chem. Rev. 2008 Jun;108:2064–110. doi: 10.1021/cr068445e. [DOI] [PubMed] [Google Scholar]
- 10.Rezaeipoor R, John R, Adie SG, Chaney EJ, Marjanovic M, Oldenburg AL, et al. Fc-directed antibody conjugation of magnetic nanoparticles for enhanced molecular targeting. J. Innov. Opt. Health Sci. 2009 Oct 1;2:387–396. doi: 10.1142/S1793545809000693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.John R, Rezaeipoor R, Adie SG, Chaney EJ, Oldenburg AL, Marjanovic M, et al. In vivo magnetomotive optical molecular imaging using targeted magnetic nanoprobes. Proc. Natl. Acad. Sci. USA. 2010 May 4;107:8085–8090. doi: 10.1073/pnas.0913679107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Moghimi SM, Hunter AC, Murray JC. Long-circulating and target-specific nanoparticles: theory to practice. Pharmacol. Rev. 2001 Jun;53:283–318. [PubMed] [Google Scholar]
- 13.Kumar CS, Mohammad F. Magnetic nanomaterials for hyperthermia-based therapy and controlled drug delivery. Adv. Drug Deliv. Rev. 2011 Aug 14;63:789–808. doi: 10.1016/j.addr.2011.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Thomas R, Park IK, Jeong YY. Magnetic iron oxide nanoparticles for multimodal imaging and therapy of cancer. Int. J. Mol. Sci. 2013;14:15910–30. doi: 10.3390/ijms140815910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Huang D, Swanson EA, Lin CP, Schuman JS, Stinson WG, Chang W, et al. Optical coherence tomography. Science. 1991 Nov 22;254:1178–81. doi: 10.1126/science.1957169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Schmitt JM. Optical coherence tomography (OCT): A review. IEEE J. Sel. Top. Quantum Electron. 1999 Jul-Aug;5:1205–1215. [Google Scholar]
- 17.Griffiths DJ. Introduction to Electrodynamics. 4 ed. Vol. 3. Addison-Wesley; Massachusetts, USA: 2012. [Google Scholar]
- 18.Jordan A, Wust P, Fähling H, John W, Hinz A, Felix R. Inductive heating of ferrimagnetic particles and magnetic fluids: Physical evaluation of their potential for hyperthermia. Int. J. Hyperthermia. 2009;25:499–511. doi: 10.3109/02656730903287790. [DOI] [PubMed] [Google Scholar]
- 19.Kodama RH. Magnetic nanoparticles. J. Magn. Magn. Mater. 1999;200:359–372. [Google Scholar]
- 20.Bean CP, Livingston JD. Superparamagnetism. J. Appl. Phys. 1959;30:S120–S129. [Google Scholar]
- 21.Boppart SA, Oldenburg AL, Xu C, Marks DL. Optical probes and techniques for molecular contrast enhancement in coherence imaging. J. Biomed. Opt. 2005 Jul-Aug;10:41208. doi: 10.1117/1.2008974. [DOI] [PubMed] [Google Scholar]
- 22.Schenck JF. Physical interactions of static magnetic fields with living tissues. Prog. Biophys. Mol. Biol. 2005 Feb-Apr;87:185–204. doi: 10.1016/j.pbiomolbio.2004.08.009. [DOI] [PubMed] [Google Scholar]
- 23.Oldenburg AL, Toublan FJ-J, Suslick KS, Wei A, Boppart SA. Magnetomotive contrast for in vivo optical coherence tomography. Opt. Express. 2005 Aug 22;13:6597–614. doi: 10.1364/opex.13.006597. [DOI] [PubMed] [Google Scholar]
- 24.Gleich B, Weizenecker R. Tomographic imaging using the nonlinear response of magnetic particles. Nature. 2005 Jun 30;435:1214–1217. doi: 10.1038/nature03808. [DOI] [PubMed] [Google Scholar]
- 25.Brown RW, Cheng Y-CN, Haacke EM, Thompson MR, Venkatesan R. Magnetic Resonance Imaging: Physical Principles and Sequence Design. 2 ed. John Wiley & Sons; New Jersey, USA: 2014. [Google Scholar]
- 26.Shevkoplyas SS, Siegel AC, Westervelt RM, Prentiss MG, Whitesides GM. The force acting on a superparamagnetic bead due to an applied magnetic field. Lab Chip. 2007;7:1294–1302. doi: 10.1039/b705045c. [DOI] [PubMed] [Google Scholar]
- 27.Oldenburg AL, Gunther JR, Boppart SA. Imaging magnetically labeled cells with magnetomotive optical coherence tomography. Opt. Lett. 2005 Apr 1;30:747–9. doi: 10.1364/ol.30.000747. [DOI] [PubMed] [Google Scholar]
- 28.Oldenburg AL, Crecea V, Rinne SA, Boppart SA. Phase-resolved magnetomotive OCT for imaging nanomolar concentrations of magnetic nanoparticles in tissues. Opt. Express. 2008 Jul 21;16:11525–39. [PMC free article] [PubMed] [Google Scholar]
- 29.Hergt R, Dutz S, Muller R, Zeisberger M. Magnetic particle hyperthermia: Nanoparticle magnetism and materials development for cancer therapy. J. Phys. Condens. Matter. 2006 Sep 27;18:S2919–S2934. [Google Scholar]
- 30.Rosensweig RE. Heating magnetic fluid with alternating magnetic field. J. Magn. Magn. Mater. 2002 Nov;252:370–374. [Google Scholar]
- 31.Dutz S, Kettering M, Hilger I, Muller R, Zeisberger M. Magnetic multicore nanoparticles for hyperthermia-influence of particle immobilization in tumour tissue on magnetic properties. Nanotechnology. 2011 Jul 1;22:265102. doi: 10.1088/0957-4484/22/26/265102. [DOI] [PubMed] [Google Scholar]
- 32.Dutz S, Hergt R. Magnetic particle hyperthermia—a promising tumour therapy? Nanotechnology. 2014;25:452001. doi: 10.1088/0957-4484/25/45/452001. [DOI] [PubMed] [Google Scholar]
- 33.Jeyadevan B. Present status and prospects of magnetite nanoparticles-based hyperthermia. J. Ceram. Soc. Jpn. 2010 Jun;118:391–401. [Google Scholar]
- 34.Jordan A, Scholz R, Wust P, Fahling H, Felix R. Magnetic fluid hyperthermia (MFH): Cancer treatment with AC magnetic field induced excitation of biocompatible superparamagnetic nanoparticles. J. Magn. Magn. Mater. 1999 Jul;201:413–419. [Google Scholar]
- 35.Hahn MA, Singh AK, Sharma P, Brown SC, Moudgil BM. Nanoparticles as contrast agents for in-vivo bioimaging: current status and future perspectives. Anal. Bioanal. Chem. 2011 Jan;399:3–27. doi: 10.1007/s00216-010-4207-5. [DOI] [PubMed] [Google Scholar]
- 36.Oh J, Feldman MD, Kim J, Kang HW, Sanghi P, Milner TE. Magneto-motive detection of tissue-based macrophages by differential phase optical coherence tomography. Lasers Surg. Med. 2007 Mar;39:266–72. doi: 10.1002/lsm.20473. [DOI] [PubMed] [Google Scholar]
- 37.Kim J, Ahmad A, Marjanovic M, Chaney EJ, Li J, Rasio J, et al. Magnetomotive optical coherence tomography for the assessment of atherosclerotic lesions using αvβ3 integrin-targeted microspheres. Mol. Imaging Biol. 2014;16:36–43. doi: 10.1007/s11307-013-0671-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.John R, Chaney EJ, Boppart SA. Dynamics of magnetic nanoparticle-based contrast agents in tissues tracked using magnetomotive optical coherence tomography. IEEE J. Sel. Top. Quantum Electron. 2010 May-Jun;16:691–697. doi: 10.1109/JSTQE.2009.2029547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kim J, Ahmad A, Li J, Marjanovic M, Chaney EJ, Suslick KS, et al. Intravascular magnetomotive optical coherence tomography of targeted early-stage atherosclerotic changes in ex vivo hyperlipidemic rabbit aortas. J. Biophotonics. 2015;9999 doi: 10.1002/jbio.201400128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kim J, Oh J, Milner TE, Nelson JS. Hemoglobin contrast in magnetomotive optical Doppler tomography. Opt. Lett. 2006 Mar 15;31:778–80. doi: 10.1364/ol.31.000778. [DOI] [PubMed] [Google Scholar]
- 41.Evertsson MM, Kjellman PP, Cinthio MM, Fredriksson SS, Zandt R. I. t., Persson HW, et al. Multimodal detection of iron oxide nanoparticles in rat lymph nodes using magnetomotive ultrasound imaging and magnetic resonance imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2014 Aug;61:1276–1283. doi: 10.1109/TUFFC.2014.3034. [DOI] [PubMed] [Google Scholar]
- 42.Kim J, Ahmad A, Boppart SA. Dual-coil magnetomotive optical coherence tomography for contrast enhancement in liquids. Opt. Express. 2013 Mar 25;21:7139–47. doi: 10.1364/OE.21.007139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ahmad A, Kim J, Shemonski ND, Marjanovic M, Boppart SA. Volumetric full-range magnetomotive optical coherence tomography. J. Biomed. Opt. 2014 Dec;19:126001. doi: 10.1117/1.JBO.19.12.126001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sarvazyan A, Hall TJ, Urban MW, Fatemi M, Aglyamov SR, Garra BS. An overview of elastography-An emerging branch of medical imaging. Curr. Med. Imaging Rev. 2011 Nov;7:255–282. doi: 10.2174/157340511798038684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ophir J, Cespedes I, Ponnekanti H, Yazdi Y, Li X. Elastography: A quantitative method for imaging the elasticity of biological tissues. Ultrasonic Imag. 1991 Apr;13:111–34. doi: 10.1177/016173469101300201. [DOI] [PubMed] [Google Scholar]
- 46.Krouskop TA, Wheeler TM, Kallel F, Garra BS, Hall T. Elastic moduli of breast and prostate tissues under compression. Ultrasonic Imag. 1998 Oct;20:260–74. doi: 10.1177/016173469802000403. [DOI] [PubMed] [Google Scholar]
- 47.Manduca A, Oliphant TE, Dresner MA, Mahowald JL, Kruse SA, Amromin E, et al. Magnetic resonance elastography: Noninvasive mapping of tissue elasticity. Med. Image Anal. 2001 Dec;5:237–54. doi: 10.1016/s1361-8415(00)00039-6. [DOI] [PubMed] [Google Scholar]
- 48.Liang X, Crecea V, Boppart SA. Dynamic optical coherence elastography: A review. J. Innov. Opt. Health Sci. 2010 Oct;3:221–233. doi: 10.1142/S1793545810001180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kennedy BF, Kennedy KM, Sampson DD. A review of optical coherence elastography: Fundamentals, techniques and prospects. IEEE J. Sel. Top. Quantum Electron. 2014 Mar-Apr;20:272–288. [Google Scholar]
- 50.Wang S, Larin KV. Optical coherence elastography for tissue characterization: A review. J. Biophotonics. 2015 Apr;8:279–302. doi: 10.1002/jbio.201400108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Greenleaf JF, Fatemi M, Insana M. Selected methods for imaging elastic properties of biological tissues. Annu. Rev. Biomed. Eng. 2003;5:57–78. doi: 10.1146/annurev.bioeng.5.040202.121623. [DOI] [PubMed] [Google Scholar]
- 52.Tschoegl NW. The Phenomenological Theory of Linear Viscoelastic Behavior: An Introduction. Springer-Verlag Berlin Heidelberg; Berlin, German: 1989. [Google Scholar]
- 53.Rogowska J, Patel NA, Fujimoto JG, Brezinski ME. Optical coherence tomographic elastography technique for measuring deformation and strain of atherosclerotic tissues. Heart. 2004 May;90:556–62. doi: 10.1136/hrt.2003.016956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ford MR, J. D. W. J., Rollins AM, Roy AS, Hu Z. Method for optical coherence elastography of the cornea. J. Biomed. Opt. 2011 Jan-Feb;16:016005. doi: 10.1117/1.3526701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kennedy BF, McLaughlin RA, Kennedy KM, Chin L, Curatolo A, Tien A, et al. Optical coherence micro-elastography: mechanical-contrast imaging of tissue microstructure. Biomed. Opt. Express. 2014 Jul 1;5:2113–24. doi: 10.1364/BOE.5.002113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Nandy S, Salehi HS, Wang T, Wang X, Sanders M, Kueck A, et al. Correlating optical coherence elastography based strain measurements with collagen content of the human ovarian tissue. Biomed. Opt. Express. 2015;6:3806–3811. doi: 10.1364/BOE.6.003806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kennedy BF, Liang X, Adie SG, Gerstmann DK, Quirk BC, Boppart SA, et al. In vivo three-dimensional optical coherence elastography. Opt. Express. 2011 Mar 28;19:6623–34. doi: 10.1364/OE.19.006623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Kennedy BF, Hillman TR, McLaughlin RA, Quirk BC, Sampson DD. In vivo dynamic optical coherence elastography using a ring actuator. Opt. Express. 2009 Nov 23;17:21762–72. doi: 10.1364/OE.17.021762. [DOI] [PubMed] [Google Scholar]
- 59.Yang Y, Bagnaninchi PO, Ahearne M, Wang RK, Liu K-K. A novel optical coherence tomography-based micro-indentation technique for mechanical characterization of hydrogels. J. R. Soc. Interface. 2007 Dec 22;4:1169–73. doi: 10.1098/rsif.2007.1044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Kennedy KM, Es'haghian S, Chin L, McLaughlin RA, Sampson DD, Kennedy BF. Optical palpation: optical coherence tomography-based tactile imaging using a compliant sensor. Optics letters. 2014;39:3014–3017. doi: 10.1364/OL.39.003014. [DOI] [PubMed] [Google Scholar]
- 61.Nahas A, Bauer M, Roux S, Boccara AC. 3D static elastography at the micrometer scale using Full Field OCT. Biomed. Opt. Express. 2013 Oct 1;4:2138–2149. doi: 10.1364/BOE.4.002138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Kennedy KM, McLaughlin RA, Kennedy BF, Tien A, Latham B, Saunders CM, et al. Needle optical coherence elastography for the measurement of microscale mechanical contrast deep within human breast tissues. J. Biomed. Opt. 2013 Dec;18:121510–121510. doi: 10.1117/1.JBO.18.12.121510. [DOI] [PubMed] [Google Scholar]
- 63.Liang X, Oldenburg AL, Crecea V, Chaney EJ, Boppart SA. Optical micro-scale mapping of dynamic biomechanical tissue properties. Opt. Express. 2008 Jul 21;16:11052–65. doi: 10.1364/oe.16.011052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Adie SG, Liang X, Kennedy BF, John R, Sampson DD, Boppart SA. Spectroscopic optical coherence elastography. Opt. Express. 2010 Dec 6;18:25519–34. doi: 10.1364/OE.18.025519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Liang X, Boppart SA. Biomechanical properties of in vivo human skin from dynamic optical coherence elastography. IEEE Trans. Biomed. Eng. 2010 Apr;57:953–9. doi: 10.1109/TBME.2009.2033464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Adie SG, Kennedy BF, Armstrong JJ, Alexandrov SA, Sampson DD. Audio frequency in vivo optical coherence elastography. Phys. Med. Biol. 2009 May 21;54:3129–39. doi: 10.1088/0031-9155/54/10/011. [DOI] [PubMed] [Google Scholar]
- 67.Qi W, Li R, Ma T, Li J, Shung KK, Zhou Q, et al. Resonant acoustic radiation force optical coherence elastography. Appl. Phys. Lett. 2013 Sep 2;103:103704. doi: 10.1063/1.4820252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Li C, Huang Z, Wang RK. Elastic properties of soft tissue-mimicking phantoms assessed by combined use of laser ultrasonics and low coherence interferometry. Opt. Express. 2011 May 23;19:10153–10163. doi: 10.1364/OE.19.010153. [DOI] [PubMed] [Google Scholar]
- 69.Wang S, Li J, Manapuram RK, Menodiado FM, Ingram DR, Twa MD, et al. Noncontact measurement of elasticity for the detection of soft-tissue tumors using phase-sensitive optical coherence tomography combined with a focused air-puff system. Opt. Lett. 2012 Dec 15;37:5184–5186. doi: 10.1364/OL.37.005184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Wang S, Larin KV. Noncontact depth-resolved micro-scale optical coherence elastography of the cornea. Biomed. Opt. Express. 2014 Nov 1;5:3807–21. doi: 10.1364/BOE.5.003807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Crecea V, Oldenburg AL, Liang X, Ralston TS, Boppart SA. Magnetomotive nanoparticle transducers for optical rheology of viscoelastic materials. Opt. Express. 2009 Dec 7;17:23114–22. doi: 10.1364/OE.17.023114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Oldenburg AL, Boppart SA. Resonant acoustic spectroscopy of soft tissues using embedded magnetomotive nanotransducers and optical coherence tomography. Phys. Med. Biol. 2010 Feb 21;55:1189–1201. doi: 10.1088/0031-9155/55/4/019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Crecea V, Ahmad A, Boppart SA. Magnetomotive optical coherence elastography for microrheology of biological tissues. J. Biomed. Opt. 2013 Dec;18:121504. doi: 10.1117/1.JBO.18.12.121504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Ahmad A, Kim J, Sobh NA, Shemonski ND, Boppart SA. Magnetomotive optical coherence elastography using magnetic particles to induce mechanical waves. Biomed. Opt. Express. 2014 Jul 1;5:2349–2361. doi: 10.1364/BOE.5.002349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Ahmad A, Huang P-C, Sobh NA, Pande P, Kim J, Boppart SA. Mechanical contrast in spectroscopic magnetomotive optical coherence elastography. Phys. Med. Biol. 2015 Sep 7;60:6655–68. doi: 10.1088/0031-9155/60/17/6655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Ahmad A, Adie SG, Chaney EJ, Sharma U, Boppart SA. Cross-correlation-based image acquisition technique for manually-scanned optical coherence tomography. Opt. Express. 2009 May 11;17:8125–36. doi: 10.1364/oe.17.008125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Kirkpatrick SJ, Wang RK, Duncan DD. OCT-based elastography for large and small deformations. Opt. Express. 2006 Nov 27;14:11585–97. doi: 10.1364/oe.14.011585. [DOI] [PubMed] [Google Scholar]
- 78.Wang RK, Kirkpatrick S, Hinds M. Phase-sensitive optical coherence elastography for mapping tissue microstrains in real time. Appl. Phys. Lett. 2007 Apr 16;90:164105. [Google Scholar]
- 79.Song S, Huang Z, Wang RK. Tracking mechanical wave propagation within tissue using phase-sensitive optical coherence tomography: motion artifact and its compensation. J. Biomed. Opt. 2013 Dec;18:121505–121505. doi: 10.1117/1.JBO.18.12.121505. [DOI] [PubMed] [Google Scholar]
- 80.Wu G, Krebs CR, Lin FC, Wolberg AS, Oldenburg AL. High sensitivity micro-elastometry: Applications in blood coagulopathy. Ann. Biomed. Eng. 2013 Oct;41:2120–9. doi: 10.1007/s10439-013-0817-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Crecea V, Graf BW, Kim T, Popescu G, Boppart SA. High resolution phase-sensitive magnetomotive optical coherence microscopy for tracking magnetic microbeads and cellular mechanics. IEEE J. Sel. Top. Quantum Electron. 2014 Mar;20:25–31. doi: 10.1109/JSTQE.2013.2280501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Gatti PL. Applied Structural and Mechanical Vibrations: Theory and Methods. 2 ed. CRC Press, Taylor & Francis Group; Boca Raton, FL: 2014. [Google Scholar]
- 83.Sridhar M, Liu J, Insana MF. Viscoelasticity imaging using ultrasound: parameters and error analysis. Phys. Med. Biol. 2007 May 7;52:2425–2443. doi: 10.1088/0031-9155/52/9/007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Wijesinghe P, McLaughlin RA, Sampson DD, Kennedy BF. Parametric imaging of viscoelasticity using optical coherence elastography. Phys. Med. Biol. 2015 Mar 21;60:2293–2307. doi: 10.1088/0031-9155/60/6/2293. [DOI] [PubMed] [Google Scholar]
- 85.Migliori A, Sarrao JL, Visscher WM, Bell TM, Lei M, Fisk Z, et al. Resonant ultrasound spectroscopic techniques for measurement of the elastic-moduli of solids. Physica B Condens. Matter. 1993 Jan;183:1–24. [Google Scholar]
- 86.Kinney JH, Gladden JR, Marshall GW, Marshall SJ, So JH, Maynard JD. Resonant ultrasound spectroscopy measurements of the elastic constants of human dentin. J Biomech. 2004 Apr;37:437–41. doi: 10.1016/j.jbiomech.2003.09.028. [DOI] [PubMed] [Google Scholar]
- 87.Achenbach JD. Wave Propagation in Elastic Solids. North-Holland; Amsterdam, Netherlands: 1987. [Google Scholar]
- 88.Yamakoshi Y, Sato J, Sato T. Ultrasonic imaging of internal vibration of soft tissue under forced vibration. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1990;37:45–53. doi: 10.1109/58.46969. [DOI] [PubMed] [Google Scholar]
- 89.Hughes TJR. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis. Dover Publications; New York, USA: 2012. [Google Scholar]
- 90.Chin LX, Curatolo A, Kennedy BF, Doyle BJ, Munro PRT, McLaughlin RA, et al. Analysis of image formation in optical coherence elastography using a multiphysics approach. Biomed. Opt. Express. 2014 Sep 1;5:2913–2930. doi: 10.1364/BOE.5.002913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Han Z, Li J, Singh M, Aglyamov SR, Wu C, Liu C-H, et al. Analysis of the effects of curvature and thickness on elastic wave velocity in cornea-like structures by finite element modeling and optical coherence elastography. Appl. Phys. Lett. 2015 Jun 8;106:233702. doi: 10.1063/1.4922728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Chicheł A, Skowronek J, Kubaszewska M, Kanikowski M. Hyperthermia–description of a method and a review of clinical applications. Rep. Pract. Oncol. Radiother. 2007;12:267–275. [Google Scholar]
- 93.Salunkhe AB, Khot VM, Pawar SH. Magnetic hyperthermia with magnetic nanoparticles: A status review. Curr. Top. Med. Chem. 2014 Mar;14:572–94. doi: 10.2174/1568026614666140118203550. [DOI] [PubMed] [Google Scholar]
- 94.Gilchrist RK, Medal R, Shorey WD, Hanselman RC, Parrott JC, Taylor CB. Selective inductive heating of lymph nodes. Ann. Surg. 1957 Oct;146:596–606. doi: 10.1097/00000658-195710000-00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Jordan A, Scholz R, Wust P, Fahling H, Krause J, Wlodarczyk W, et al. Effects of magnetic fluid hyperthermia (MFH) on C3H mammary carcinoma in vivo. Int. J. Hyperthermia. 1997 Nov-Dec;13:587–605. doi: 10.3109/02656739709023559. [DOI] [PubMed] [Google Scholar]
- 96.Attaluri A, Ma R, Qiu Y, Li W, Zhu L. Nanoparticle distribution and temperature elevations in prostatic tumours in mice during magnetic nanoparticle hyperthermia. Int. J. Hyperthermia. 2011;27:491–502. doi: 10.3109/02656736.2011.584856. [DOI] [PubMed] [Google Scholar]
- 97.Zadnik PL, Molina CA, Sarabia-Estrada R, Groves ML, Wabler M, Mihalic J, et al. Characterization of intratumor magnetic nanoparticle distribution and heating in a rat model of metastatic spine disease: Laboratory investigation. J. Neurosurg. Spine. 2014;20:740–750. doi: 10.3171/2014.2.SPINE13142. [DOI] [PubMed] [Google Scholar]
- 98.Johannsen M, Gneveckow U, Eckelt L, Feussner A, Waldofner N, Scholz R, et al. Clinical hyperthermia of prostate cancer using magnetic nanoparticles: Presentation of a new interstitial technique. Int. J. Hyperthermia. 2005 Nov;21:637–647. doi: 10.1080/02656730500158360. [DOI] [PubMed] [Google Scholar]
- 99.Thiesen B, Jordan A. Clinical applications of magnetic nanoparticles for hyperthermia. Int. J. Hyperthermia. 2008 Sep;24:467–74. doi: 10.1080/02656730802104757. [DOI] [PubMed] [Google Scholar]
- 100.Johannsen M, Gneueckow U, Thiesen B, Taymoorian K, Cho CH, Waldofner N, et al. Thermotherapy of prostate cancer using magnetic nanoparticles: Feasibility, imaging, and three-dimensional temperature distribution. Eur. Urol. 2007 Dec;52:1653–1662. doi: 10.1016/j.eururo.2006.11.023. [DOI] [PubMed] [Google Scholar]
- 101.Thrall DE, Rosner GL, Azuma C, Larue SM, Case BC, Samulski T, et al. Using units of CEM 43 C T90, local hyperthermia thermal dose can be delivered as prescribed. Int. J. Hyperthermia. 2000;16:415–428. doi: 10.1080/026567300416712. [DOI] [PubMed] [Google Scholar]
- 102.Rhoon G. C. v., Samaras T, Yarmolenko PS, Dewhirst MW, Neufeld E, Kuster N. CEM43 degrees C thermal dose thresholds: A potential guide for magnetic resonance radiofrequency exposure levels? Eur. Radiol. 2013 Aug;23:2215–27. doi: 10.1007/s00330-013-2825-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Lagendijk JJ. Hyperthermia treatment planning. Phys. Med. Biol. 2000 May;45:R61–76. doi: 10.1088/0031-9155/45/5/201. [DOI] [PubMed] [Google Scholar]
- 104.Salloum M, Ma R, Zhu L. Enhancement in treatment planning for magnetic nanoparticle hyperthermia: Optimization of the heat absorption pattern. Int. J. Hyperthermia. 2009 Jun;25:309–21. doi: 10.1080/02656730902803118. [DOI] [PubMed] [Google Scholar]
- 105.Sapareto SA, Dewey WC. Thermal dose determination in cancer therapy. Int. J. Radiat. Oncol. Biol. Phys. 1984 Jun;10:787–800. doi: 10.1016/0360-3016(84)90379-1. [DOI] [PubMed] [Google Scholar]
- 106.Dewhirst MW, Viglianti BL, Lora-Michiels M, Hanson M, Hoopes PJ. Basic principles of thermal dosimetry and thermal thresholds for tissue damage from hyperthermia. Int. J. Hyperthermia. 2003 May-Jun;19:267–94. doi: 10.1080/0265673031000119006. [DOI] [PubMed] [Google Scholar]
- 107.Oleson JR, Samulski TV, Leopold KA, Clegg ST, Dewhirst MW, Dodge RK, et al. Sensitivity of hyperthermia trial outcomes to temperature and time: implications for thermal goals of treatment. Int. J. Radiat. Oncol. Biol. Phys. 1993 Jan 15;25:289–97. doi: 10.1016/0360-3016(93)90351-u. [DOI] [PubMed] [Google Scholar]
- 108.Krishnan S, Diagaradjane P, Cho SH. Nanoparticle-mediated thermal therapy: Evolving strategies for prostate cancer therapy. Int. J. Hyperthermia. 2010;26:775–89. doi: 10.3109/02656736.2010.485593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Wright NT, Humphrey JD. Denaturation of collagen via heating: an irreversible rate process. Annu. Rev. Biomed. Eng. 2002;4:109–28. doi: 10.1146/annurev.bioeng.4.101001.131546. [DOI] [PubMed] [Google Scholar]
- 110.Kaibara M. Rheology of blood coagulation. Biorheology. 1996 Mar-Apr;33:101–17. doi: 10.1016/0006-355X(96)00010-8. [DOI] [PubMed] [Google Scholar]
- 111.Wu T, Felmlee JP, Greenleaf JF, Riederer SJ, Ehman RL. Assessment of thermal tissue ablation with MR elastography. Magn. Reson. Med. 2001 Jan;45:80–7. doi: 10.1002/1522-2594(200101)45:1<80::aid-mrm1012>3.0.co;2-y. [DOI] [PubMed] [Google Scholar]
- 112.Brosses E. S.-d., Gennisson JL, Pernot M, Fink M, Tanter M. Temperature dependence of the shear modulus of soft tissues assessed by ultrasound. Phys. Med. Biol. 2010 Mar 21;55:1701–18. doi: 10.1088/0031-9155/55/6/011. [DOI] [PubMed] [Google Scholar]
- 113.Rivaz H, Fleming I, Assumpcao L, Fichtinger G, Hamper U, Choti M, et al. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2008. Springer; New York, USA: 2008. Ablation monitoring with elastography: 2D in-vivo and 3D ex-vivo studies; pp. 458–466. [DOI] [PubMed] [Google Scholar]
- 114.Souchon R, Rouviere O, Gelet A, Detti V, Srinivasan S, Ophir J, et al. Visualisation of hifu lesions using elastography of the human prostate in vivo: Preliminary results. Ultrasound Med. Biol. 2003 Jul;29:1007–1015. doi: 10.1016/s0301-5629(03)00065-6. [DOI] [PubMed] [Google Scholar]
- 115.Arnal B, Pernot M, Tanter M. Monitoring of thermal therapy based on shear modulus changes: II. Shear wave imaging of thermal lesions. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2011 Aug;58:1603–11. doi: 10.1109/TUFFC.2011.1987. [DOI] [PubMed] [Google Scholar]
- 116.Mura S, Couvreur P. Nanotheranostics for personalized medicine. Adv. Drug Deliv. Rev. 2012 Oct;64:1394–416. doi: 10.1016/j.addr.2012.06.006. [DOI] [PubMed] [Google Scholar]
- 117.Erten A, Wrasidlo W, Scadeng M, Esener S, Hoffman RM, Bouvet M, et al. Magnetic resonance and fluorescence imaging of doxorubicin-loaded nanoparticles using a novel in vivo model. Nanomedicine. 2010 Dec;6:797–807. doi: 10.1016/j.nano.2010.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Hayashi K, Nakamura M, Sakamoto W, Yogo T, Miki H, Ozaki S, et al. Superparamagnetic nanoparticle clusters for cancer theranostics combining magnetic resonance imaging and hyperthermia treatment. Theranostics. 2013;3:366–76. doi: 10.7150/thno.5860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Dähring H, Grandke J, Teichgräber U, Hilger I. Improved Hyperthermia Treatment of Tumors Under Consideration of Magnetic Nanoparticle Distribution Using Micro-CT Imaging. Mol. Imaging Biol. 2015:1–7. doi: 10.1007/s11307-015-0848-2. [DOI] [PubMed] [Google Scholar]
- 120.Quesson B, Zwart J. A. d., Moonen CT. Magnetic resonance temperature imaging for guidance of thermotherapy. J. Magn. Reson. Imaging. 2000 Oct;12:525–33. doi: 10.1002/1522-2586(200010)12:4<525::aid-jmri3>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- 121.Attar MM, Haghpanahi M, Amanpour S, Mohaqeq M. Analysis of bioheat transfer equation for hyperthermia cancer treatment. J. Mech. Sci. Technol. 2014 Feb;28:763–771. [Google Scholar]
- 122.Nacev A, Beni C, Bruno O, Shapiro B. Magnetic nanoparticle transport within flowing blood and into surrounding tissue. Nanomedicine. 2010;5:1459–1466. doi: 10.2217/nnm.10.104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Goodman TT, Chen J, Matveev K, Pun SH. Spatio-temporal modeling of nanoparticle delivery to multicellular tumor spheroids. Biotechnol. Bioeng. 2008;101:388–399. doi: 10.1002/bit.21910. [DOI] [PMC free article] [PubMed] [Google Scholar]